Most Natural Machine Learning Method: KNN Classification and Inference

1. KNN Guided Actions

KNN (K-Nearest Neighbors) classification is a two-step procedure of supervised machine learning: (1) finding K closest data points (neighbors) to a test data and, (2) predicting the class of this test data with the majority class in the K closest data points. It is apparent that this procedure is naturally consistent with the way in which human-beings conduct their daily affairs. In other words, the KNN is the means of guiding human’s actions.

Starting a new job: Facing a new job, you have certainly two choices as follows. One is to start the new job based on oneself closest related data if it is applicable. And another is to start the new job guided by a supervisor. The second way is similar to transfer learning, i.e., the closest related data of your supervisor are passed to you. This has definitely showed that starting a new job must be simply guided by KNN.

Big problem solving: At first, you must understand this big problem with your closest experienced data/knowledge. And then, the big problem is divided into several sub-problems based on your related knowledge. Finally, each sub-problem is solved with your closest experienced knowledge. From the above problem-solving procedure, big problem solving must also be guided by KNN.

Children training: Before having a baby, parents often read many books concerning children training. After accumulating enough related data, they can train their babies to say, read, understand, do and decision-make, guided by most proper data, or information. It means that children training is truly a KNN guided action.

Intelligence developing: Under equal-education, different person can be with different powers of utilizing KNN. Consider an example as follows.

A person bought 10 bottles of beer in a bar, and 3 empty bottles can exchange one bottle of beer in the bar. How many can the person drink?

The Google AI immediately obtained an answer as follows.

The person can drink a total of 14 bottles of beer. They start with 10 bought bottles. They can exchange the empty bottles for 3 more bottles (10 / 3 = 3 with a remainder of 1). Then they have 3 + 1 = 4 bottles. They can exchange those for 1 more bottle (4 / 3 = 1 with a remainder of 1). Finally, they can exchange the last 1 bottle for 0 bottles. So, 10 + 3 + 1 = 14.

It is true that most people are only able to answer 14 bottles of beer using their closest knowledge in Mathematics, at most telling that there are 2 empty bottles left.

There are only few of people who can answer 15 bottles of beer based on their knowledge on played games. Because the person has 2 empty bottles left, he can temporally borrow one empty bottle for exchanging one bottle of beer. After quickly drinking this beer, or pour all the beer into a glass of cup, the person can immediately return this empty bottle. Therefore, it is a perfect answer that the person can drink 15 bottles of beer. This is really an intelligent answer at utilizing closest knowledge, or KNN.

From the above 4 cases, KNN algorithm is a machine learning method closest to human’s intelligence, as well as a way of guiding human’s everyday actions.

2. Modelling Lazy Learning

As mentioned previously, KNN algorithm is a lazy learning procedure that has become the bottleneck constraining its widely applications. Unlike model-based machine learning algorithms, the KNN need take up much more memory and data storage when making test data prediction. The reason is that it is clearly a complete sample space search at each time of finding all K nearest neighbors. Therefore, it has been an open problem to invent a model of KNN classification.

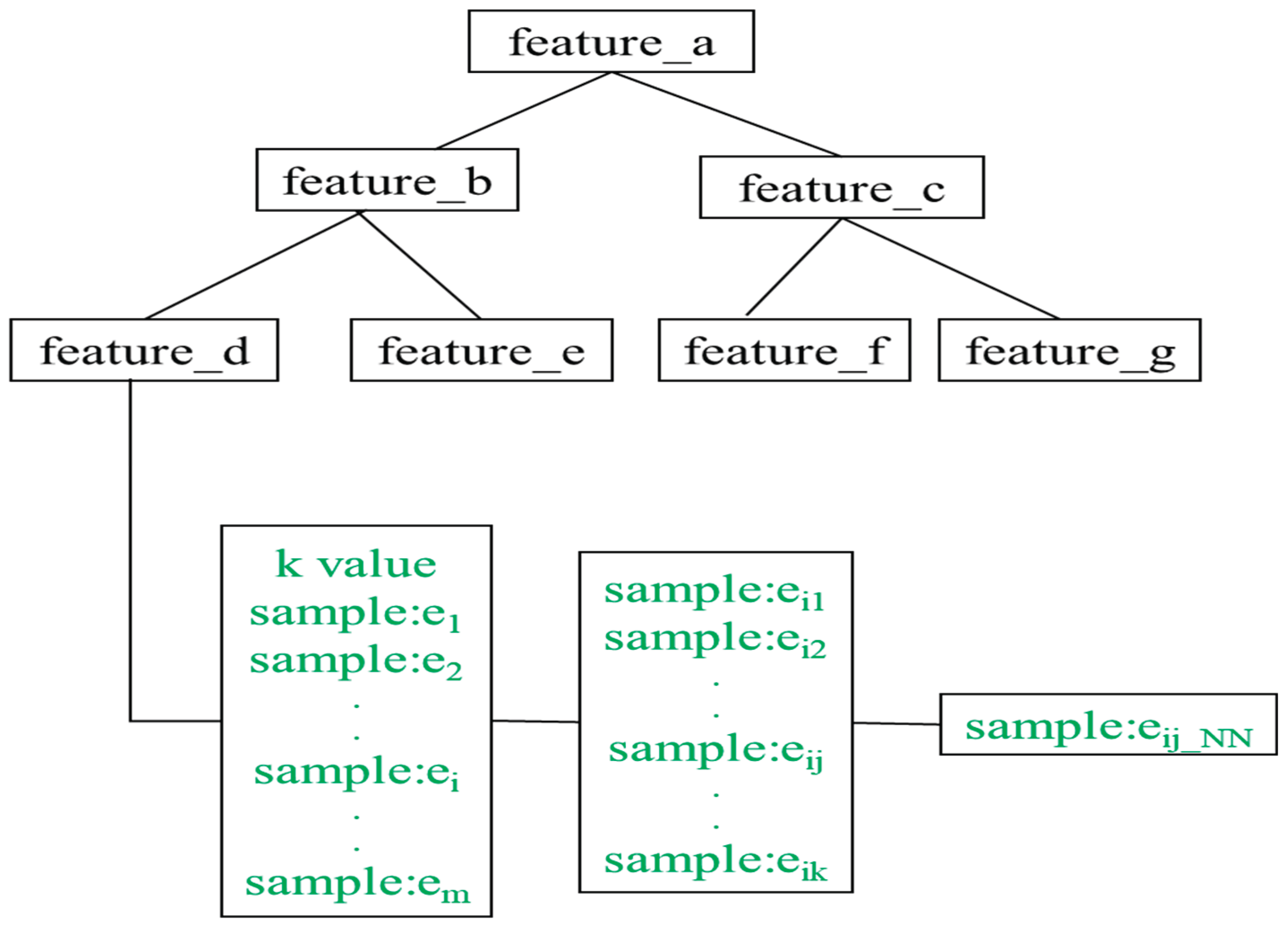
To break this bottleneck, Zhang, et al. (2018) advocated a tree model for KNN classification, called as K*Tree. The K*Tree is based on two assumptions as follows.

• Mutual Relation: A friend of a friend is a friend.
• Approximate solution: The K value is the same of its 1NN point.

The mutual relation can be applied to nearest neighbor selection: the nearest neighbour of the nearest neighbour may be the nearest neighbour. In this way, Zhang, et al. (2018) built a decision tree for a given training dataset, in which each leaf node of the decision tree contains a set of samples with the same K value, as well as each sample is attached with a set of its K nearest neighbors. This decision tree is the tree model of KNN classification, called as K*Tree, see Figure 1.

In Figure 1, only one of leaf nodes is showed, so as to reduce the graphic size, or the space occupied by a graphic. Each leaf node can contain one more samples and each sample has a set of pointers to its all K nearest neighbors. From the experimental results, the K*Tree performs much more efficient than existing KNN classification and, carries out the same effectiveness as standard KNN classification.

The K*Tree works as follows. For a given test data X, it first searches for the 1NN point, A, of X in the K*Tree. And then, the K value, the K nearest neighbors of A, {B1, B2, ..., BK}, are obtained from the K*Tree. Thirdly, the KNN points of X can be searched from the set, {A}∪{B1, B2, ..., BK}∪the KNN points of Bi for 1≤i ≤K. Finally, K*Tree predicts the class of X with the majority class in the K closest data points of X.

The K*Tree brings us two benefits as follows. One is to classify different test data with different K value. Another is as possible to reduce the search space of finding all the K nearest neighbors, i.e., the complete sample space search is changed and decreased to the union of the nearest neighbors and their direct nearest neighbors. Apparently, the K*Tree has provided the clue of modelling lazy learning.

The K*Tree is a seminal work and has received more than 1450 citations by July 2025. For example, many survey papers include, such as Halder, et al. (2024) and Syriopoulos, et al. (2025). A number of research articles include, such as Gallego, et al. (2018) and Cheng, et al. (2018).

3. Uneven Distribution

The natural flaw of training data is of uneven distribution. It has been an underlying logic issue in many fields, such as data mining, machine learning and databases. This leads to the inability of discovering the real mathematical models, not yet finding an effective solution to this issue.

Recent efforts to the uneven distribution mainly include “recursively generated data”. However, Shumailov, et al. (2024) have pointed out that AI models collapse when trained on recursively generated data. Therefore, machine learning must face this natural flaw of training data.

To deal with the above issue in KNN classification, Zhang (2011) advocated a strategy, detour to carry out classification task, i.e., to invent classification models and methods that are independent of the data distribution. Using the detour, a shell-nearest neighbors algorithm, Shell-NN, was proposed to perform the task of different test data prediction with different numbers of nearest neighbors. In the Shell-NN algorithm, all the nearest neighbors look like a shell around a test data. And these Shell-NN points are referred to ideal nearest neighbors of the test data, see Figure 2.

The determination of each shell is a quadratic selection of nearest neighbors as follows. In the first selection, K nearest neighbors of a test data are chosen from training samples. In the second selection, the left and right nearest neighbors of the test data are chosen from the K nearest neighbors attribute by attribute. In this way, only those data points tightly around the test data are kept among the K nearest neighbors. From the experimental results, the Shell-NN are efficient and promising.

For efficiency, Zhang, et al. (2017) advocated another classification algorithm independent of the data distribution with sparse learning. To improve this approach, Zhang and Li (2023) developed a one-step computation for KNN classification independent of the data distribution. The one-step computation only needs to calculate an optimal K values for each test data and, completely avoids finding all K nearest neighbors for each test data. Also, a quantum KNN classification algorithm was designed independent of the data distribution (Li, et al. 2024).

From the above KNN algorithms independent of the data distribution, one needs only to set different K values to different test data because the uneven distribution of training data can mainly impact on setting K values in KNN classification.

The above KNN algorithms independent of the data distribution have gained significant attention from different research areas and applications. There are many survey papers, such as Lin and Tsai (2020); Thomas and Rajabi (2021); Uddin, et al. (2022). Research articles in different research areas and applications include, such as Gou, et al. (2019); Shu, et al. (2025); Spinnato, et al. (2023).

4. Imbalanced Class Problem

Most people think imbalanced class dataset is an issue of uneven distribution data. Actually, imbalanced class problem is much different from the uneven distribution data because even if a dataset is of balanced distribution, it can still be an imbalanced dataset in which the number of instances in different classes is significantly unequal. This imbalance can lead to models that are biased towards the majority class, resulting in poor performance on the minority class. In real applications, instances in the minority class could win much more attention. This has motivated out a new research direction, cost-sensitive learning (Zhang 2020).

Because KNN is one of top learning algorithms Wu, et al. (2008), we proposed KNN-CF classification that provided an obvious-effect weighting method (Zhang 2010) that was significantly expanded in (Zhang 2022). Traditionally, the imbalance is naturally solved by weighting methods with up-weight minority class, or down-weight majority class. This needs to properly score the importance of all classes in a dataset for meeting the requirements in real applications.

Different from scoring the importance of classes in a dataset, Zhang (2022) advocated a weight self-lift to deal with the imbalance. The weight self-lift is a weighting model that takes the portion, or representative ratio of a class as the weight of a nearest neighbor point. For example, consider a set of 100 samples with 98 negative samples and 2 positive samples. Let X be the test data, K = 5, and X’s 5 nearest neighbors contain 4 negative samples and 1 positive sample. According to the majority rule, the class of X is predicted to “negative”. In the weight self-lift rule, the possibility of “negative” is 1/98 + 1/98 + 1/98 + 1/98 = 4/98，the possibility of “positive” is 1/2. Consequently, the class of X is predicted to “positive”.

This work has attracted much attention from real applications, such as Shalaby, Shennawy, Sarhan (2022); Pajouh, Dastghaibyfard, Hashemi (2017); Atlı and İlhan (2025); Kazangirler and Özkaynak (2024).