Integrating Biological Principles into Observational Entropy

1. Introduction

• “Information is not knowledge” – Albert Einstein

The uncertainty and indeterminacy of entropy arises from the interplay between the intrinsic variability of the observed physical system and limitations in the observer’s sensorial and epistemic framework (1). It is the lack of the observer’s substantive knowledge about the state of the system under consideration that is the operative factor in the definition of entropic uncertainty (2). Furthermore, observer indeterminacy and computational constraints really define the boundary of uncertainty and limits of knowability of the system state (3). This experiential boundary condition suggests that measures of entropy should be understood as dependent on the integration of the observed physical system with the observer rather than an independent property of the system alone. These considerations have led many to attempt to reconstitute the concepts of entropy in an observational framework wherein an observational entropy corresponds to uncertainty defined as a lack of knowledge about the system (4,5). Classical Shannon information is the average information expected to be gained in making an observation given the probability distribution of its possible states. Insightfully, investigators have used this Shannon information communication statistical model as the foundation for observational entropy with coarse-graining defined as:

$$S_C=\sum _i^n{p}_i\mathit{ln}\left({\displaystyle \frac{p_i}{V_i}}\right)$$

Where the observer cannot distinguish between microstates within the same macrostate i the probability ${\displaystyle \frac{p_i}{V_i}}$is given to every microstate and Vi is the volume of the macrostate (4).

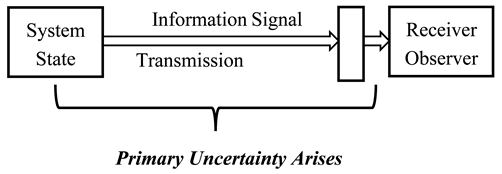
The Shannon model is generally concerned with the communication of information from a source to a receiver and the uncertainty of that transmission as depicted graphically below (6). It is important to note that while the true essence of information concerning a system’s state is in itself not necessarily probabilistic; probabilities are utilized to characterize the uncertainty and limitations inherent in this communication process. This uncertainty arises from the meshing of the system’s inherent characteristics with the deficiencies of the transmission channel and the limitations of the receiver’s sensory-perceptual processes.

2. Methods

• “But if the ultimate aim of the whole of Science is indeed, as I believe, to clarify man’s relationship to the Universe, then biology must be accorded a central position.” —Jacques Monod

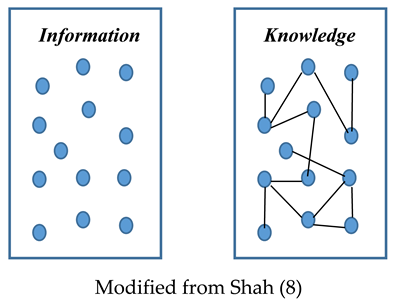
While Shannon provides an excellent measure of information transmission, there are limitations to this approach that do not reach the full potential of the observational perspective. There are several biologic principles of an observing living system that should be considered in such a reformulation of the concepts of entropy (2). For the living system as observer, the Shannon mappings reflect a potential to inform that is only a part of the total process for the acquisition of knowledge (7). Entropy is an uncertainty of knowledge and not just the uncertainty of the reception of information. Through the currency of information, knowledge occurs when the observer apprehends and contextualizes the nature or overall state of the system. Apprehension as the foundation of knowledge is more than just the reception of sensory input and involves an interconnected, coherent structuring of the information. It is through this information organizing process that system states are differentiated as ordered vs disordered and predictable vs random. In fact, establishing a cohesive structure for the incoming information is necessary to make it potentially useful and amenable to prediction. A graphical depiction of this contrasting view between information and knowledge for the observer is provided below.

“It is the quality, not the mere existence, of information that is the real mystery here.”

—Paul Davies

Shannon information is only concerned with the uncertainty of the transmission and reception of the message or signal. From Shannon’s perspective, two separate messages could be equivalent in terms of information content even if one message imparts knowledge and the other is uninterpretable, unusable, and appears random with uncertainty in the information being conveyed. For example, if I receive a message from a source written in a foreign language using a non-Greco-Roman alphabet or logographic characters, I can have some degree of certainty in the accurate reception of the character form details in this transmitted information. However, the knowledge of the message is unknowable to me as the observer and therefore I am uncertain of the state of things and unable to make conclusive predictions. The same message with the same Shannon information and same uncertainty of transmission and reception may provide a decidedly different knowledge concerning the state of things for another observer based on their background and prior knowledge. Fortunately, for most energy and material exchanges in the physical world, our shared biology and sensory-perceptive mechanisms provide for consistency in our translated knowledge of events. Mikhail Volkenstein first noted that the real practical value of Shannon information is determined by the consequences of its reception (9). The observer’s knowledge depends on a conception of the consequences of the received information. This conceptualization by the observer enables the ordering and predictive power of the information that makes it useful.

• “The observer, when he seems to himself to be observing a stone, is really, if physics is to be believed, observing the effects of the stone upon himself.” —Bertrand Russell

The process of further differentiating and evaluating the state of the physical system upon reception of the incoming information signals by the observer occurs through two mechanisms (2). First, upon reception of the communication the observer assesses the expectation of the incoming information (surprisal value) based on the observer’s prior knowledge of the probability of that state and condition (2,10). Typically, there is some superfluous information that is already known to the observer. Information that is expected based on this prior knowledge about the system state is considered as excess information (2,11). Some physicists consider this irrelevant and unusable excess information as a form of entropy (12). If there is no prior expectation, then the information to be communicated is simply the basic Shannon information as determined by the inherent signal probability distribution. This basic measure is considered to be the independent potential information before it is observed.

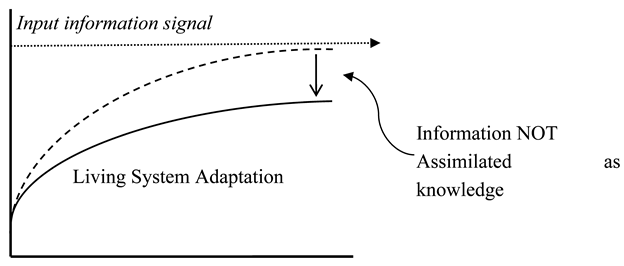
Secondly, the observer gauges if the information can be assimilated as knowledge into the general analytic framework of the observer’s conception of physical actuality and its interplay with that reality (2,13). Any information that does not “make sense” within this framework is deemed uncertain in the context of usefulness or predictability. We see an analog to this process in adaptive control system mechanics that are often used to describe the assimilation of signal information by biological systems (2). In this way, the signal drives the living system to adjust to the incoming information as a counteraction to any disorder (“control entropy” in engineering terms) (14,15,16). In most biological systems, there is imperfect system gain and adaptation with some residual signal information that is not assimilated as knowledge and is not useful (see graphic below) (17,18,19). Therefore, this residual information cannot be used by the living system for predictive functions.

3. Results

• “Observer participancy gives rise to information; and information gives rise to physics.”
• —John Archibald Wheeler

Integrating these biological principles with the Shannon information approach can be accomplished by considering the natural axiomatic procedures used by living systems for processing information and subsequent homeorhetic activities concerning the observed state of their biocontinuum (2). By incorporating the processing of Fisher’s Darwinian adaptive replicator functions into the Shannon information communication framework, the entropic dynamics of the observing living system can be ascertained (20, 21). The mathematical derivation of this integration has been described previously by Summers and is highly informed by the approaches of Harper and Baez in their analyses of evolutionary dynamics (2,22,23,24). System entropic information defined as the Kullback–Leibler divergence metric for relative information drives the interaction between the observer and the potential information of the physical system (13,25). The Kullback–Leibler information divergence of $\left(p\right)$ from $\left(q\right)$ (denoted as $D_{KL}(q\left|p\right)$ or $I\left(q,p\right)$) is where $\left(p\right)$ is the prior probability distribution of types as known to the observer and $\left(q\right)$ is the distribution that is found in the newly observed state. This relative information metric creates a codependence between the observer and the observed with an uncertainty of communication transmission and apprehension in the determination of the entropic state. The dynamics for this processing are described by the following equations.

The potential information (I) as the Kullback–Leibler information divergence at the point of observation is defined by:

$$I\left(q,p\right)=D_{KL}(q\left|p\right)=\sum _i^{n}ln\left({\displaystyle \frac{q_i}{p_i}}\right)q_i=\sum _i^n(ln\left(q_i\right){-ln\left(p_i\right))q}_i$$

The Kullback–Leibler information divergence changes during the procedure of control entropy and information assimilation by the observing living system is defined by:

$${\displaystyle \frac{d}{dt}}I\left(q,p\right)=-{\sum }_i^n{(f}_i\left(P\right)-〈f\left(P\right)〉)q_i={\sum }_i^n{f}_i\left(P\right){(p_i-q}_i)$$

Where:

$〈f\left(P\right)〉={\sum }_i^n{f}_i\left(P\right)p_i$ is the mean fitness of all the individual types.

In Fisher replicator dynamics, the fitness function assesses the congruence of each observation with the machinery of the observer’s biologic functioning and epistemic processes (20). Information that “fits” or coheres with the observer’s framework can then be assimilated as knowledge (2). Information that is unresolved within this processing context is considered to be in an indeterminate or uncertain state.

4. Discussion

• “…general relativity, quantum mechanics, and statistical mechanics are actually derivable, and from the same ultimate foundation: the interplay between computational irreducibility and the computational boundedness of observers.” —Stephen Wolfram.

As entropy is defined as a measure of uncertainty and randomness, the implicit question is “uncertain to whom?”. While most of science is oriented toward a third person perspective, it is evident that measures of entropy should include the perspective of the observer. When the observer is integrated into the determining calculus, information is considered to have a relative and ontologically subjective quality even if there is consilience amongst groups of observing agents secondary to their shared biology. A variety of investigators have astutely recognized this unique characteristic of entropy and a burgeoning area of research concerning “observational entropy” has been advanced based on the Shannon information communication model (4,5). While this model is an excellent framework for providing an accounting of the uncertainty in information transmission and reception, it does not resolve the amount of knowledge ascertained by the observer from that information. In this paper, the fundamental biological principles associated with observation and knowledge acquisition are integrated into the standard proposed observational entropy model. This approach could provide a clearer understanding of the impact of entropy as a qualification of energy usefulness and in describing disorder vs order of the physical system from the perspective of the observer.

Uncertainty is the condition of limited knowledge resulting in an inability to precisely determine or predict the current or future state of something. Uncertainty can be aleatory and due to the natural inherent variation in a physical system or secondary to the observer’s limitation in knowledge acquisition about the state of that system (2). In combination, uncertainty arises from an inadequacy of knowledge about the state of the object or system under consideration. The dictionary definition of knowledge implies that there is an apprehension of the significance of the information in a way that makes it interpretable and usable for actions such as predictions. In other words, knowledge provides the contextual connectivity of the information to the physical system and the observer so that it is predictable and does not appear random.

Perhaps the fundamental and existentially important biological principles to consider are:

• The capacity of observing living systems to differentiate incoming information signals and translating this information into knowledge concerning the state of the object or system being observed. This capacity has previously been considered to be the most fundamental and unifying principal process of living systems. Living observing organisms depend primarily on this ability for guiding adaptation and survival.
• The process of adaptation of living system functions in response to information signals as described by replicator dynamics is the procedure by which this information is made coherent with the observer’s epistemic framework and assimilated as knowledge. This process is at the foundation of natural selection, biological evolution, and the subsistence of living organism. Renowned physicist Carlo Rovelli suggests that considering these Darwinian principles in conjunction with modern information theory could bridge the current gap in our understanding of the physical world from the perspective of the observer (26).

The use of Kullback-Leibler divergence as relative information is also important in integrating and combining the facets of the observer with the observed. In his classic book, Fred Dretske contends that Shannon’s theory does not define what information is (27). Obviously, all physical phenomena are based on relational interactions. This has led some physicist to conclude that the Kullback–Leibler information divergence metric as relative information is the true physical version of the Shannon-type information (28).

From the beginning of the conception of entropy as a consequence of energy transitions, qualifications based on notions of certainty, order, predictability, usefulness and knowability are naturally dependent on the inclusion of an observer. If the observer is to hold a central place in the modern understanding of entropy, then it is important to incorporate biological principles in that description. In this study, the most salient of these biocentric tenets are integrated into the current model of observational entropy based on prior work considering the mechanics of entropic dynamics as first introduced by Ariel Caticha and Carlo Cafaro (29,30). Such an approach could broaden our understanding of entropy including a determination of the meaning of received information and the impact of unique sensory mechanisms (i.e. magnetic sensory apparatus of migratory birds) and living system complexity on energy qualifications (25, 31).