Energy Criterion for Tearing of Elastic and Elastic-Plastic Materials: Independent Derivations from Compliance Relations and a Thermodynamic Model with Internal Variables

1. Introduction

It typically occurs in scientific research that a given problem attracts attention for a time, and is then relegated to historical archives of the discipline in pursuit of newer problems. In the process, important aspects of the original problem are occasionally bypassed, and remain unaddressed in future research due to the perceived closed nature of the problem. This paper re-examines one such problem arising in fracture mechanics nearly eighty years ago, namely Irwin’s elastic-plastic extension [1] of Griffith’s brittle elastic fracture criterion [2].

Griffith’s criterion, adapted by Orowan [3,4,5] to distinguish between fixed-grips and fixed-load conditions, may be written for a linear elastic plate specimen of unit thickness and crack length a subjected to an external load P and load-point displacement X, as

$$-{\left({\displaystyle \frac{\partial U_e}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_e}{\partial a}}\right)}_P=2\gamma$$

(1)

where $U_e$ is the elastic energy of the specimen, ${\Pi }_e\equiv PX-U_e$ is the complementary energy and $\gamma$ is the specific crack surface energy.

In 1948 Irwin [1] postulated extending Griffith’s criterion to elastic-plastic conditions by adding a plastic dissipation term to the surface tension parameter. This effectively modified (1) to

$$-{\left({\displaystyle \frac{\partial U_e}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_e}{\partial a}}\right)}_P=2\gamma +{\displaystyle \frac{d{U}_p}{da}} \approx {\displaystyle \frac{d{U}_p}{da}}$$

(2)

where $U_p$ is the energy of plastic deformation in material surrounding the crack, and the final identity on the right arises from Irwin’s approximation $d{U}_p/da\gg 2\gamma$. Irwin recognized that the magnitude of the plastic dissipation term $d{U}_p/da$ depended on the size of the plastic zone surrounding the crack tip, but considered that the relations between energy derivatives expressed in (2) remained basic and useful. Orowan [4,5] initially questioned applicability of (2) under highly ductile conditions, but nevertheless used it as basis for postulating a tearing instability or “fast fracture” criterion for those same ductile conditions. Orowan’s instability criterion, obtained by differentiating [2], was of the fixed-grips form:

$${\left({\displaystyle \frac{{\partial }^2{U}_e}{\partial a^2}}\right)}_X={\displaystyle \frac{d^2{U}_p}{d{a}^2}}$$

(3)

Implicit in (2) and (3) was the notion that elastic unloading within a cracked elastic-plastic body constitutes a driving force not only for crack extension but also for plastic dissipation, an idea consistent with later thermodynamic models of elastoplasticity [6,7,8]. Indeed, if one identifies variations in $U_e$ as isothermal changes in Helmholtz energy, recognizes plastic deformation as a dissipative process and postulates crack extension as an observable macroscopic measure of internal variable changes, then (2) becomes very similar in structure and interpretation to a well-known thermodynamic constraint on inelastic constitutive laws, summarized in Equation (32) of Rice [6] and Equation (16) of Maugin [9]. This similarity provided much of the motivation for the present analysis.

A limitation of (2), recognized by both Orowan [4,5] and Irwin [10], is collapse of the unique LEFM relation between driving force derivatives and crack-tip stress distribution under ductile conditions, except in the limit of small-scale plasticity. Added to this is experimental indeterminacy of the surface and elastic energies $\gamma$ and $U_e$ in (2), the latter arising from indeterminate accumulations of residual or “cold working” elastic energy during cyclic loading processes involving non-uniform plastic deformation [11,12,13]. In view of such difficulties, the dominant tendency in macroscopic energy-based formulations of fracture has been to restrict (2) to conditions of small-scale plasticity, and replace it in the fully plastic domain with elastic-plastic adaptations of the J-integral.

J-integral theory [14,15,16] was originally formulated for non-linear elastic conditions, in which case J is formally and physically equivalent to the driving force partial derivatives ${\left(\partial U_e/\partial a\right)}_X \mathrm{a}\mathrm{n}\mathrm{d} {\left(\partial {\Pi }_e/\partial a\right)}_P$ in (1). Adaptation to the elastic-plastic domain was achieved by formally treating plastic deformation prior to incipient fracture as non-linear elastic, resulting in a “pseudo-elastic” parameter preserving the same form and contour-invariance as the elastic J integral, although losing its thermodynamic meaning as an elastic (Helmholtz) energy release rate. The thermodynamic discrepancy between elastic and fully plastic J values is partly offset whenever J contour measurements in small fully plastic specimens can be reliably extrapolated to far-field elastic contours in large specimens, since in the latter case the elastic interpretation of J is recovered [17,18]. However, for J measurements restricted to the fully plastic domain, indistinction between elastic and plastic deformation remains thermodynamically problematic. The redeeming feature in this case is the unique HRR relation between J and the crack tip stress field for proportional loading up to incipient tearing [19,20], allowing use of J as a characteristic stress intensity parameter at fracture initiation. The HRR model breaks down once crack extension with elastic unloading begins, although in practice small or moderate amounts of extension are usually admitted [18,21,22]. The meaning of J becomes increasingly obscure for extended ductile crack growth accompanied by significant elastic unloading.

In contrast, Irwin’s criterion (2), regardless of its limitations, has a formal structure explicitly admitting ductile crack extension accompanied by elastic unloading. In recognition of this fact, a small but significant number of researchers have continued to characterize elastic-plastic crack extension by means of measurable macroscopic parameters similar in form and meaning to the driving or resistance force derivatives in (2). One of the best known of these parameters is the energy dissipation rate D [23,24,25,26,27,28,29,30,31,32], which approximates the sum of resistive forces of the right-hand side of (2). Another postulated parameter, I, emulates the crack driving force derivatives on the left hand side of (2) associated with elastic unloading [25,26,33,34]. The parameter I reduces to Irwin’s parameter G [35] in the LEFM case, but deviates from it under elastic-plastic conditions by accounting for plastic deformation in addition to elastic unloading. A characteristic of both parameters I and D, to be considered in more detail later, is that they only consider “apparent” elastic unloading energy that does not account for indeterminate amounts of residual elastic energy.

Snyder [36] conducted an inspectional analysis of the mathematical definitions of I, D and unloading compliance C for the common special case of cracked elastic or elastic-plastic specimens with linear elastic unloading behavior, subjected to loading paths in X-P space typical of fracture tests. The definitions imposed that $I<D$ for loads P less than the critical load $P\prime$ at imminent crack extension, but whenever $P=P\prime$ a relation similar to Irwin’s criterion (2) was satisfied, namely

$$I=D$$

(4)

Since (4) follows directly from the mathematical definitions of measurable parameters I, C and D, it is valid under all experimental tearing conditions where the three parameters are defined, including LEFM and the fully plastic regime. Restrictions on (4) were its derivation for materials with linear elastic unloading, and (then) unknown effects of residual elastic energy.

Following Orowan’s rationale underlying (3), Snyder [36] postulated fixed-grips and fixed-load instability conditions associated with (4), as

$$-{\left({\displaystyle \frac{\partial I}{\partial a}}\right)}_X\ge {\displaystyle \frac{dD}{da}} (\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{g}\mathrm{r}\mathrm{i}\mathrm{p}\mathrm{s})$$

(5)

And

$${\left({\displaystyle \frac{\partial I}{\partial a}}\right)}_P\ge {\displaystyle \frac{dD}{da}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d})$$

(6)

where in general

$$-{\left({\displaystyle \frac{\partial I}{\partial a}}\right)}_X\ne {\left({\displaystyle \frac{\partial I}{\partial a}}\right)}_P$$

(7)

By combining (5) and (6]) with compliance relations, simple inequalities between system parameters were obtained that agreed qualitatively with typically observed stability behavior of load- and displacement-controlled systems.

Given that Snyder’s criterion (4) was derived using only the definitions of empirical parameters I, D and C for elastic or elastic-plastic materials with linear elastic unloading, it must on those grounds be considered a strictly empirical result. This leaves important issues unresolved, such as is if and how (4) relates to thermodynamic constraints. Additional questions are whether (4) can be extended to materials with non-linear elastic unloading behavior, how it is affected by indeterminate amounts of residual elastic energy, and if and how it relates to Irwin’s postulate (2). The objective here is to address these issues.

The remainder of the paper is divided into two main sections. Section 2 is primarily background material, expanding Snyder’s original derivation of (4), (5) and (6), which was limited to an Abstract in a Conference Proceedings [36]. In Section 3, a generalized form of criterion (4) is derived from a thermodynamic model with internal variables. This establishes consistency of (4) with the first and second laws of thermodynamics, generalizes it to admit both linear and non-linear elastic unloading, and demonstrates that it correctly accounts for changes in residual elastic energy associated with fracture. The analysis also shows that Irwin’s postulate (2) is consistent with the thermodynamic result.

2. Derivation of (4) and Associated Instability Conditions from the Definitions of C, D and I

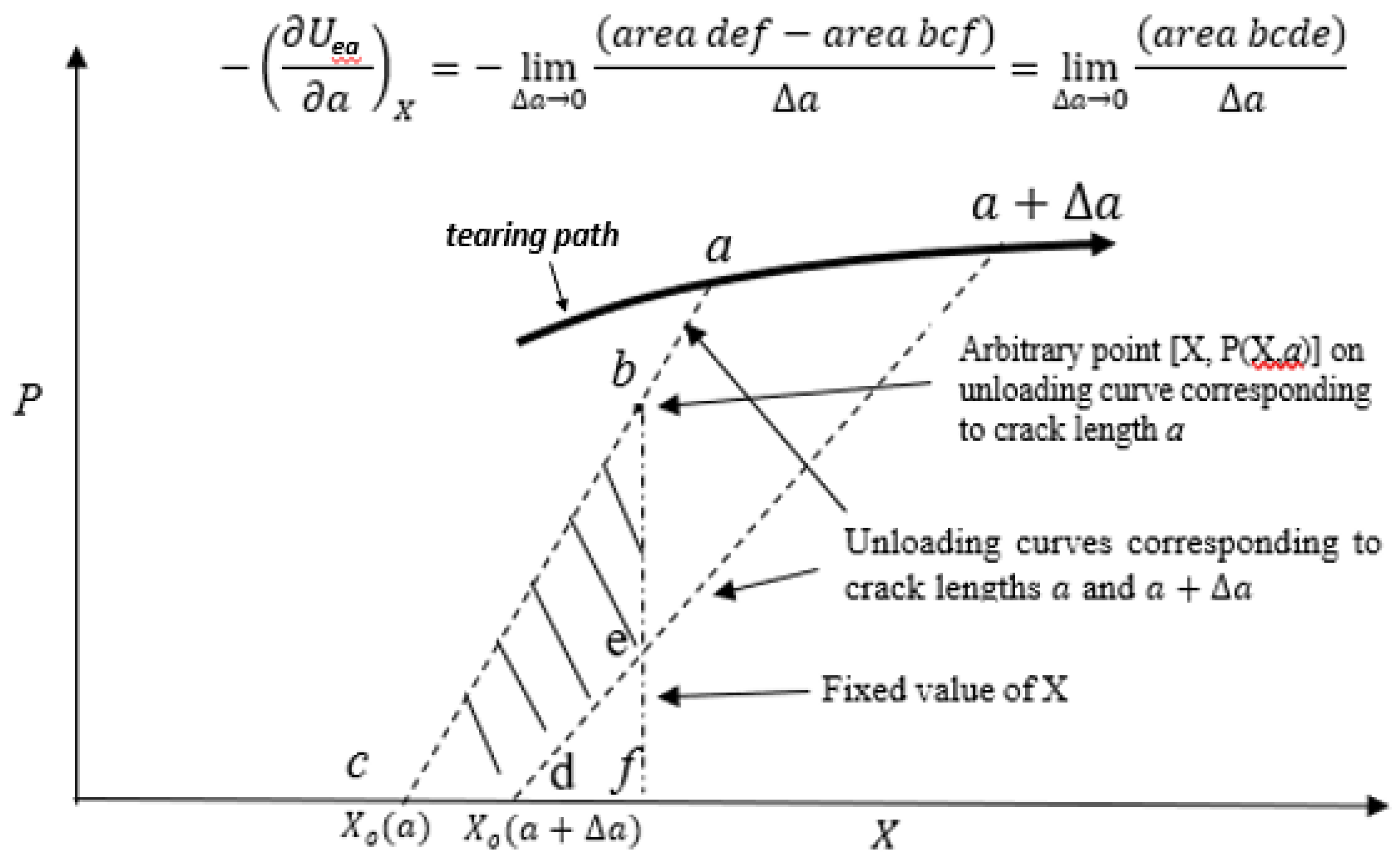
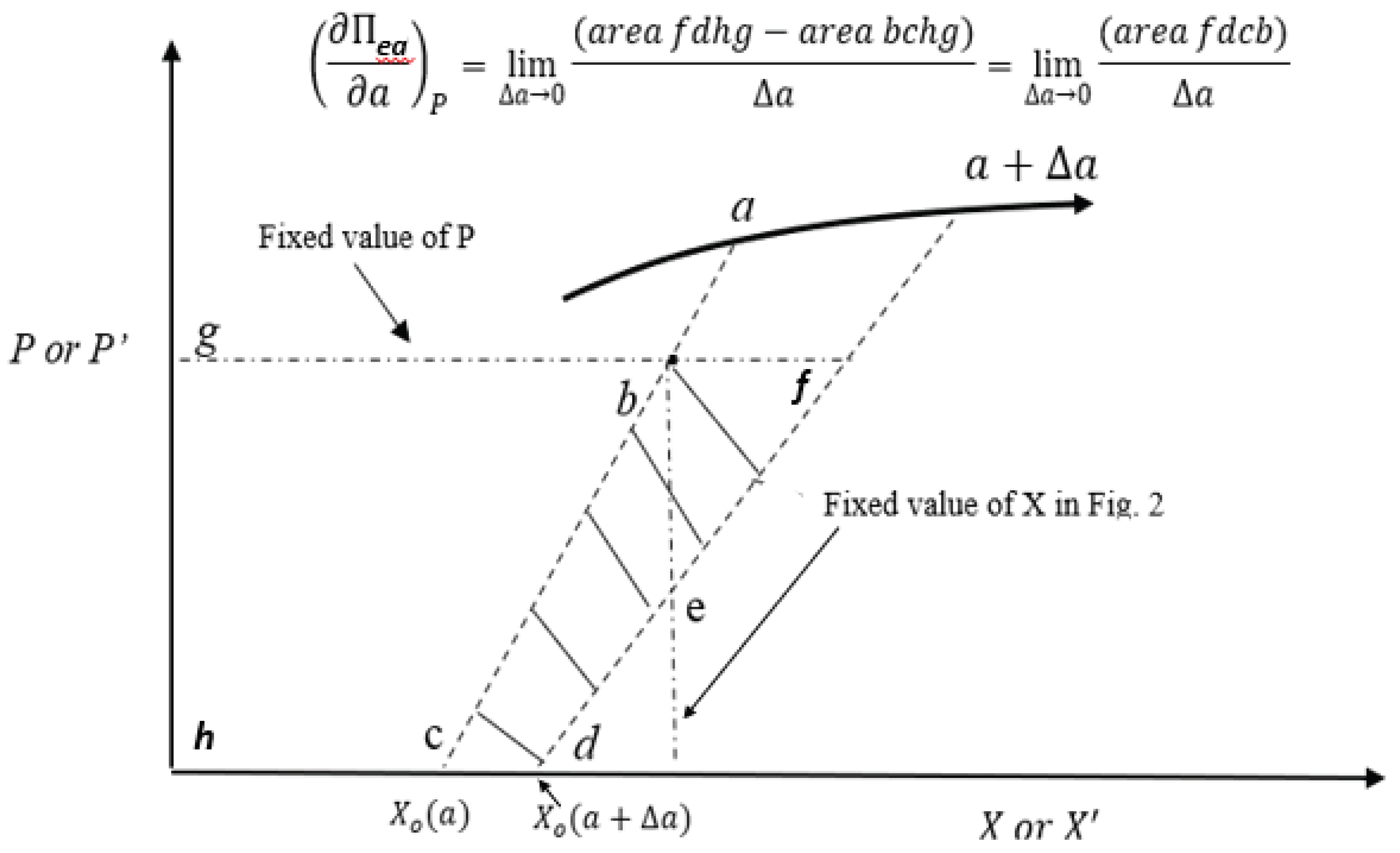
2.1. Definition and Derivative Properties of the Unloading Compliance Function

The compliance function C(a) defines the dependence of the unloading compliance C on the current crack length a of an elastic or elastic-plastic specimen of specified loading configuration and unloading elastic modulus. It is often used inversely to estimate crack extension from measured compliance changes during fracture tests [21,22].

The compliance relates the current load-point displacement X and conjugate external load P during linear elastic unloading of a fracture specimen as:

$$C\left(X,a\right)= {\displaystyle \frac{\left[X-X_o\left(a\right)\right]}{P(X,a)}}$$

(8)

The independent variable X in (8) is the abscissa of an arbitrary point e on the elastic unloading path corresponding to crack length a (Figure 1). The domain of possible values of X is $X_o\left(a\right)\le X\le X^{\prime }(a)$, where $X^{\prime }(a)$ is the critical load-point displacement at which the crack begins to extend, and $X_o\left(a\right)$ is the “plastic set” or point where the linear unloading curve extrapolates to the X-axis. The load $P(X,a)$ is the conjugate of X on the unloading path, restricted to the domain $0\le P(X,a)\le P^{\prime }(a)$, where $P^{\prime }\left(a\right)$ is the critical load required for crack extension. For linear unloading, the value of $C\left(X,a\right)$ is independent of the arbitrarily chosen value of X, so long as X is located somewhere on the unloading path corresponding to a. Under that condition, ${\left(\partial C/\partial X\right)}_a=0$ so that $C\left(X,a\right)=C(a).$

The apparent elastic energy $U_{ea}(X,a)$, illustrated by area def under the unloading curve in Figure 1, is defined by

$$U_{ea}\left(X,a\right)\equiv {\int }_{X_o}^{X}P\left(\tau ,a\right)d\tau ={\displaystyle \frac{1}{2}} P\left(X,a\right)· \left[X-X_o\left(a\right)\right]$$

(9)

$\mp$where the term “apparent” denotes that $U_{ea}(X,a)$ excludes any indeterminate residual elastic energy existing in the macroscopically unloaded state P=0.

Solving (8) for $P(X,a)$ gives

$$P\left(X,a\right)={\displaystyle \frac{\left[X-X_o\left(a\right)\right]}{C\left(a\right)}}$$

(10)

which substituted into (9) gives $U_{ea}$ in terms of X, $X_o\left(a\right)$ and C(a) as

$$U_{ea}\left(X,a\right)={\displaystyle \frac{1}{2}}{\left[X-X_o\left(a\right)\right]}^2/C\left(a\right)$$

(11)

Taking the partial derivative ${\left(\partial U_{ea}/\partial a\right)}_X$ of (11) and again making use of (10) giv

$${-\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X={\displaystyle \frac{1}{2}}{[X-X_o\left(a\right)]}^2/{\left[C\left(a\right)\right]}^2·{\displaystyle \frac{dC\left(a\right)}{da}}+{\displaystyle \frac{\left[X-X_o\left(a\right)\right]}{C\left(a\right)}}·{\displaystyle \frac{d{X}_o\left(a\right)}{da}}={\displaystyle \frac{1}{2}}{ P}^2{\displaystyle \frac{dC}{da}}+P{\displaystyle \frac{d{X}_o}{da}} (0\le P\le P^{\prime } )$$

(12)

where it should be noted that (12) is defined over the entire range $0\le P\le P^{\prime }$.

The apparent complementary energy ${\Pi }_{ea}$, shown by area bcde in Figure 1, is defined by

$${\Pi }_{ea}\equiv \mathrm{P}\mathrm{X}-U_{ea}= PX-{\displaystyle \frac{1}{2}}·{\displaystyle \frac{{\left[X-X_o\left(a\right)\right]}^2}{\mathrm{C}(\mathrm{a})}}=PX-{\displaystyle \frac{1}{2}} C(a)·P^2$$

(13)

where use has been made of (11) and then (10). Solving for X in (8) and substituting the result into (13), yields

$${\Pi }_{ea}={\displaystyle \frac{1}{2}} P^{2}C\left(a\right)+P{X}_o(a)$$

(14)

for which the partial derivative ${\left(\partial {\Pi }_{ea}/\partial a\right)}_P$ gives

$${\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P={\displaystyle \frac{1}{2}}{P}^2{\displaystyle \frac{dC}{da}}+P{\displaystyle \frac{d{X}_o}{da}}\hspace{1em}\hspace{1em}\hspace{1em}(0\le P\le P^{\prime })$$

(15)

Comparing (12) and (15) shows that

$${-\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P={\displaystyle \frac{1}{2}}{P}^2{\displaystyle \frac{dC}{da}}+P{\displaystyle \frac{d{X}_o}{da}}\hspace{1em}\hspace{1em}\hspace{1em}(0\le P\le P^{\prime })$$

(16)

This indicates that the partial derivatives -${\left(\partial U_{ea}/\partial a\right)}_X \mathrm{a}\mathrm{n}\mathrm{d} {\left(\partial {\Pi }_{ea}/\partial a\right)}_P$ are non-linear homogeneous functions of the current load P and also equal to each other for a given loading state (X, P). They represent virtual fixed-load and fixed-grips crack driving forces, respectively, i.e., elastic and complementary energy changes that would occur if the crack were to extend by an amount da for fixed-grips or fixed load conditions under an arbitrary applied load P. Note that this does not necessarily imply that the crack will extend under load P.

Graphical definitions of the partial derivatives ${\left(\partial U_{ea}/\partial a\right)}_X \mathrm{a}\mathrm{n}\mathrm{d} {\left(\partial {\Pi }_{ea}/\partial a\right)}_P$ are shown in Figure 2 and Figure 3, respectively. Comparing these figures to the graphical definition of the parameter I presented by various authors [25,27,34], shows that the partial derivatives in (16) are equivalent to I. In the LEFM case, where the plastic set term $Pd{X}_o/da$ vanishes, the parameter I defined by (16) reduces to Irwin’s [35] crack driving force $G={\displaystyle \frac{1}{2}}{ P}^{2}dC/da$.

For small-strain linear elastic unloading behavior of a loaded elastic-plastic fracture specimen, an elastic stress-strain field surrounding the crack tip can be defined, with the corresponding material reference configuration being the final unloaded state ($P=0$) of the specimen. This elastic field is identical to that in an LEFM specimen with the same loading configuration and elastic modus E’ as in the elastic-plastic specimen, and therefore admits the LEFM identity $K^2/E\prime ={\displaystyle \frac{1}{2}}{ P}^{2}dC/da$, where K’ is Irwin’s [35] stress intensity parameter. A distinction is that in LEFM specimens the elastic field represents the total stress field, whereas in the elastic-plastic case it represents an excess field relative to any residual stresses remaining in the specimen in its final unloaded state [11].

Substituting the identity $K^2/E\prime ={\displaystyle \frac{1}{2}}{ P}^{2}dC/da$ into the elastic-plastic relation (16) yields

$${-\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P={\displaystyle \frac{K^2}{E^{\prime }}}+P{\displaystyle \frac{d{X}_o}{da}} (0\le P\le P^{\prime } )$$

(17)

Presence of the independent dissipative term $Pd{X}_o/da$ in (17) negates the possibility of a unique relation between driving force derivatives on the left hand side of (17) and the elastic field represented by the term $K^2/E\prime$ on the right hand side. Uniqueness is only predicted in the limit of fully elastic LEFM behavior. In that case, the plastic dissipation term $Pd{X}_o/da$ vanishes, as does the residual elastic component of the apparent energy parameters $U_{ea}$ and ${\Pi }_{ea}$, rendering them equivalent to the total energy parameters $U_e \mathrm{a}\mathrm{n}\mathrm{d}$ ${\Pi }_e$ in [1], respectively. This reduces (16) and (17) to the set of well-known LEFM identities [22,37]:

$${-\left({\displaystyle \frac{\partial U_e}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_e}{\partial a}}\right)}_P\equiv G={\displaystyle \frac{1}{2}}{ P}^2{\displaystyle \frac{dC}{da}}={\displaystyle \frac{K^2}{E^{\prime }}} (0\le P\le P^{\prime } )$$

(18)

2.2. Definition of the Energy Dissipation Rate Function D*(a) and Associated Properties

The energy dissipation rate function ${\mathit{D}}^{\mathit{*}}$(a), essentially a quasi-static relative of the Charpy and Izod impact parameters, has been used as a measure of crack growth resistance [23,24,25,26,27,28,29,30,31,32]. It is defined by the total derivative

$$D^{\mathrm{*}}(a)\equiv {\displaystyle \frac{d\left(W^{\prime }-U_{ea}^{\prime }\right)}{da}}={\displaystyle \frac{P^{\prime }\left(a\right)d{X}^{\prime }\left(a\right)-d{U}_{ea}^{\prime }\left(a\right)}{da}}$$

(19)

where $d{W}^{\prime }\equiv P^{\prime }\left(a\right)d{X}^{\prime }\left(a\right)$is the external work on a specimen required to extend the crack by an amount $da$, and $U_{ea}^{\prime }(a)$ is the apparent elastic energy released by unloading the body from the critical load $P^{\prime }(a)$ to the state $P=0$. The above definition applies strictly for loading along the boldfaced tearing path in Figure 1, where the specimen is always in a state of imminent tearing such that the load P and displacement X are always at their respective critical values $P^{\prime }(a)$ and $X^{\prime }\left(a\right)$. Therefore, all variables in (19) may be considered functions of crack length a, justifying the definition of ${\mathit{D}}^{\mathit{*}}$ in the literature as a total derivative with respect to a. Note that this contrasts fundamentally with the partial derivatives ${\left(\partial U_{ea}/\partial a\right)}_X \mathrm{a}\mathrm{n}\mathrm{d} {\left(\partial {\Pi }_{ea}/\partial a\right)}_P$ in (16), which depend not only on current crack length a but also on the arbitrary loading state (X, P) on the corresponding elastic unloading curve.

The definition of ${\mathit{D}}^{\mathit{*}}$(a) in (19) is quite general, admitting elastic or elastic-plastic materials with either linear or non-linear elastic unloading behavior. For the special case of elastic-plastic specimens with linear elastic unloading, substituting the identities $U_{ea}^{\prime }\left(a\right)=1/2 P^{\prime }\left(a\right)·[X^{\prime }\left(a\right)-X_o\left(a\right)]$ and $P^{\prime }\left(a\right)=\left[X^{\prime }\left(a\right)-X_o\left(a\right)\right]/C(a)$ into (19), and performing the indicated differentiation, gives:

$$\mathit{D}\left(a\right)={\displaystyle \frac{\frac{1}{2}{\left[X^{\prime }\left(a\right)-X_o\left(a\right)\right]}^2}{{C\left(a\right)}^2}}{\displaystyle \frac{dC}{da}}+{\displaystyle \frac{\left[X^{\prime }\left(a\right)-X_o\left(a\right)\right]}{C\left(a\right)}}{\displaystyle \frac{d{X}_o}{da}}={\displaystyle \frac{1}{2}}{P^{\prime }(a)}^2{\displaystyle \frac{dC}{da}}+P^{\prime }(a){\displaystyle \frac{d{X}_o}{da}}$$

(20)

which is equivalent to the result obtained by Turner and Kolednik [26] in their Equation (3). The symbol $\mathit{D}\left(a\right)$ in (20) has been written without an asterisk to indicate its specificity for materials with linear elastic unloading behavior, contrasting with the more general definition of ${\mathit{D}}^{\mathit{*}}(a)$ in (19) admitting both linear and non-linear elastic unloading.

2.3. Tearing Criterion Implicit in (16) and (20)

Comparison of (16) and (20) shows that, whenever the arbitrarily variable load P reaches the critical value $P^{\prime }(a)$, and only then, the driving force partial derivatives become equal to D, yielding the tearing criterion

$${-\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P=D$$

(21)

which is the result anticipated earlier in (4). Since criterion (21) arises directly from the definitions of functions $\mathit{C}$, $\mathit{D}$ and I, it is valid under any experimental conditions where all three functions are defined. This includes crack extension in either the LEFM or elastic-plastic regimes. The most important (interim) restriction on (21) is the assumption of linear elastic unloading behavior, necessary for existence of the compliance function C(a).

2.4. Analysis of Stability Conditions

Snyder [36] proposed instability criteria by applying tangency conditions to (21) under fixed grips or fixed load as

$$-{\left({\displaystyle \frac{{\partial }^2{U}_{ea}}{\partial a^2}}\right)}_X\ge {\displaystyle \frac{dD}{da}} (\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{g}\mathrm{r}\mathrm{i}\mathrm{p}\mathrm{s})$$

(22)

Or

$${\left({\displaystyle \frac{{\partial }^2{\Pi }_{ea}}{\partial a^2}}\right)}_P\ge {\displaystyle \frac{dD}{da}} (\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d})$$

(23)

where in general $-{\left({\displaystyle \frac{{\partial }^2{U}_{ea}}{\partial a^2}}\right)}_X\ne {\left({\displaystyle \frac{{\partial }^2{\Pi }_{ea}}{\partial a^2}}\right)}_P$.

In the special case of materials with linear elastic unloading behavior, substituting the compliance relations (8), (11) and (14) into the derivative inequalities (22 ) and (23) gives the instability conditions as

$${\displaystyle \frac{d{P}^{\prime }}{da}}\le -{\displaystyle \frac{1}{C}}\left(P^{\prime }{\displaystyle \frac{dC}{da}}+{\displaystyle \frac{d{X}_o}{da}}\right) \left(\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{g}\mathrm{r}\mathrm{i}\mathrm{p}\mathrm{s}\right)$$

(24)

and

$$\left(P^{\prime }{\displaystyle \frac{dC}{da}}+{\displaystyle \frac{d{X}_o}{da}}\right){\displaystyle \frac{d{P}^{\prime }}{da}}\le 0 \left(\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}\right)$$

(25)

The quantities C, P’, $dC/da$and $d{X}_o/da$ are generally positive (see Section 3.1 for justification of positive P’), so that parameters $1/C$ and $\left(P^{\prime }dC/da+d{X}_o/da\right)$ in (24) and (25) are also positive. This allows making the following predictions on stability of fracture toughening vs. fracture weakening systems, which agree qualitatively with typical observations.

2.4.1. Stability of Fracture Toughening Systems

Fracture toughening systems, characterized by positive slope $d{P}^{\prime }/da$ of the tearing path in addition to the generally positive values of $\left(P^{\prime }dC/da+d{X}_o/da\right)$ and $(1/C)\left(P^{\prime }dC/da+d{X}_o/da\right)$, always violate both of the fixed grips and fixed load instability criteria (24) and (25), respectively. Such systems are therefore predicted to be always stable, consistent with observations.

2.4.2. Stability of Fracture Weakening Systems

Fracture-weakening systems, characterized by negative slope $d{P}^{\prime }/da$ of the tearing path, are predicted to be either stable or unstable, depending on the magnitude of $d{P}^{\prime }/da$ and whether displacement- controlled (fixed grips) or load – controlled (fixed load) conditions prevail. Under load-controlled conditions these systems always satisfy criterion (25) and are therefore predicted to be unstable, as typically observed experimentally. But under displacement-controlled conditions, the corresponding criterion (24) predicts that instability occurs only if $d{P}^{\prime }/da$ is sufficiently negative that $d{P}^{\prime }/da\le -(1/C)\left(P^{\prime }dC/da+d{X}_o/da\right)\le 0$. The condition is violated for values of $d{P}^{\prime }/da$ in the range $-(1/C)\left(P^{\prime }dC/da+d{X}_o/da\right)\le d{P}^{\prime }/da\le 0$, indicating stability in that range. This prediction is qualitatively consistent with empirical observations that fracture-weakening systems under displacement control can be stable within a certain loading range, beyond which instability sets in. Whether or not the critical value of $d{P}^{\prime }/da$ for transition from stability to instability is precisely $-(1/C)\left(P^{\prime }dC/da+d{X}_o/da\right)$, as predicted by (24), must be verified by experiment, which is beyond the scope of this paper.

3. Thermodynamic Formulation of Elastic-Plastic Tearing Processes

The thermodynamic model developed below relies heavily, with adaptations, on previous work by Rice [6,38] and Hill and Rice [7].

3.1. Conventions

The convention is adopted that any heat added to a body is a positive quantity, whereas heat transferred out of the body is negative. Similarly, work performed by the environment on the body, i.e., “loading work”, is positive, whereas working by the body on the environment or “unloading work” is negative. A load-point displacement $dX$ is always assigned the same algebraic sign as that of the work increment$dW\equiv PdX$ which it produces, so that dX is always positive for loading processes and negative for unloading. Under this convention P is always positive. For simplicity, a cracked body is considered as a closed system, subject to work and heat exchange with the environment but no mass exchange (no chemical reactions occur between exposed crack surfaces and environmental substances). Time independent conditions are assumed throughout, allowing Gibbs’ [39] convention of expressing parameter variations in time-implicit form.

A fundamental assumption is that fracture, even in the brittle elastic case, is an irreversible process characterized by the condition $da\ge 0$. That is, unlike fluid interfaces which extend or contract reversibly with loading or unloading, crack surfaces formed during loading of solids are assumed not to retract upon unloading, at least during the time frame of a typical experiment. Aside from its common experimental occurrence [38,40,41,42], crack growth irreversibility is implicit in much of the theoretical structure of fracture mechanics. Without it, elastic unloading at fixed crack length would be impossible (reversible cracks would simply close up as a function of the decreasing load), rendering foundational properties such as the unloading compliance function $C\left(a\right)\equiv {\left(\partial X/\partial P\right)}_a$ and its total derivative dC/da undefined. Also undefined would be partial derivatives of the form ${\left(\partial /\partial a\right)}_X$ or ${\left(\partial /\partial a\right)}_P$, such as those arising in (16).

In making the crack growth irreversibility assumption, it is fully recognized that certain solids exhibiting at least partially reversible crack extension have been documented [43]. Such materials are considered outside the domain of the present analysis.

3.2. State Functions and Internal Variables

A deforming and/or fracturing body, at all stages in its history, is assumed to have as state functions an internal energy (U ) and an entropy (S), with variations subject to the first and second laws of thermodynamics [44]. Irreversibility of load vs. displacement relations is formally accounted for by introducing internal state variables [6,9,38,41], The corresponding internal energy function can be written as

$$U=U(S, \left\{X_i\right\}, \left\{{\epsilon }_k\right\})$$

(26)

Here $\left\{X_i\right\}$ is the set of i=1, 2… I independently controlled macroscopic displacement parameters, and $\left\{{\epsilon }_k\right\}$ is a set of k=1, 2 … K internal variables accounting for irreversible changes in the internal structure of the body. For a typical fracture test specimen subject to variations in a single characteristic load-point displacement X, (26) simplifies somewhat to

$$U=U(X,S, \left\{{\epsilon }_k\right\})$$

(27)

Expanding in terms of partial derivatives gives

$$dU={\displaystyle \frac{\partial U}{\partial X}}dX+{\displaystyle \frac{\partial U}{\partial S}}dS+\sum _{k=1}^K{\displaystyle \frac{\partial U}{\partial {\epsilon }_k}}d{\epsilon }_k=PdX+TdS+\sum _{k=1}^K{\displaystyle \frac{\partial U}{\partial {\epsilon }_k}}d{\epsilon }_k$$

(28)

where T is temperature. Under isothermal conditions, (28) may be simplified by substituting the identity $d\left(TS\right)=TdS+SdT$ into (28) and setting dT=0, yielding

$$dA=PdX+\sum _{k=1}^K{\displaystyle \frac{\partial U}{\partial {\epsilon }_k}}d{\epsilon }_k$$

(29)

where $A\equiv U-TS$ is the Helmholtz energy.

The internal variable changes ${d\epsilon }_k$ in (29) are typically indeterminate, and furthermore the derivative sum $\sum _{k=1}^K\partial U/\partial {\epsilon }_{k}d{\epsilon }_k$ must in general be considered non-holonomic (dependent on the order of differentiation). One way of dealing with such problems is by representing internal variable changes in terms of measurable macroscopic parameters that, even though not controllable, are uniquely related to the $d{\epsilon }_k$ [9,41]. In considering the thermo-mechanics of micro-crack propagation, Rice [38] in his Equation (2.73) essentially took this approach and used crack extension da as a measure of internal variable fluctuations. Adapting this idea to irreversible extension of macroscopic cracks, it is assumed that for a given material and specimen loading configuration, all internal variable changes ${d\epsilon }_k$ are related to crack extension $da$ so that

$${d\epsilon }_k={\displaystyle \frac{{d\epsilon }_k}{da}}\left(a\right)da (k=\mathrm{1,2}\dots K)$$

(30)

where both the magnitude and order of occurrence of the ${d\epsilon }_k$ are assumed dependent on crack extension da. Combining (29) and (30) then gives

$$dA=PdX+{\left({\displaystyle \frac{\partial U}{\partial a}}\right)}_{X}da={\left({\displaystyle \frac{\partial A}{\partial X}}\right)}_{a}dX+{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_{X}da=dW+{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_{X}da$$

(31)

where the role of internal variable changes is now assumed by crack extension, and an implicit identity to be used later is

$${\left({\displaystyle \frac{\partial A}{\partial X}}\right)}_a=P$$

(32)

The postulated relation (30) between crack extension and internal variable changes is supported experimentally by the observation that, for an elastic or elastic-plastic fracture specimen of a given loading configuration, the isothermal load vs. displacement relation (compliance) is typically reversible for fixed crack length but varies irreversibly with crack extension, which would be expected for internal variables dependent on crack extension. Assumption (30) is also implicit in the definition (19) of the energy dissipation rate D*(a) typically given in the literature, where the dissipated energy during a tearing process is expressed as a total derivative with respect crack extension, implying that crack extension is the variable controlling internal variable changes and associated dissipation. Even more significant evidence for assumption (30), to be presented below, is that its incorporation into the general thermodynamic model (29) predicts results verifiable by experiment. Specifically, for the important class of elastic-plastic materials with linear elastic unloading behavior, the thermodynamic formulation (31) obtained by combining (29) and (30) reduces to the empirically verifiable result (21).

An important restriction on (30) and (31) must be noted. This is that, during the initial plastic crack tip blunting stage of loaded elastic-plastic specimens prior to fracture initiation, the crack tip remains stationary so that changes in internal variables cannot be related to changing crack length, rendering (30) and (31) invalid. In that case, a better macroscopic measure of internal variable changes might be an observable integral of the plastic deformation field, such as crack tip opening displacement (CTOD). It is only once post-yield tearing begins that constitutive linkage between internal variable changes and crack extension is assumed, leading to (30) and (31).

3.3. First and Second Laws of Thermodynamics and Resulting Constraints on State Functions

The first law of thermodynamics for a one-dimensional thermomechanical process in a fracture specimen requires that the internal energy change dU of the specimen is subject to

$$dU=dW+dq=dW+TdS-d{q}_{dis}$$

(33)

The differential $dW$is the work performed by external forces, $dq$ is the heat exchanged between the specimen and the environment and $d{q}_{dis}$ is the dissipation defined in Truesdell [44] as:

$$d{q}_{dis}\equiv TdS-dq\ge 0$$

(34)

where the inequality is imposed by the second law of thermodynamics. For isothermal conditions, substituting the identity $d\left(TS\right)=TdS+SdT$ into (33) and setting dT=0 gives the first law in terms of the Helmholtz energy A as

$$dA=dW-d{q}_{dis}$$

(35)

where again $A\equiv U-TS$is the Helmholtz energy.

Introducing the first and second law constraints (34) and (35) into the formal proposition (31) gives

$$d{q}_{dis}=dW-dA=-{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_{X}da\ge 0$$

(36)

which constitutes a thermodynamic condition on both reversible and irreversible processes in fracture specimens. For reversible loading and unloading at fixed crack length, both da and $d{q}_{dis}$ vanish from (36), reducing it to the result $dA=dW$. On the other hand, for irreversible tearing processes where da and $d{q}_{dis}$ are generally non-vanishing, and where load coordinates (X,P) are always at the critical values (X’, P’), (36) becomes

$$-{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_{X}da=d{W}^{\prime }-d{A}^{\prime }=d{q}_{dis}\ge 0$$

(37)

where again the prime notation denotes processes restricted to the tearing path.

As an interim check on results, we note that the fracture condition (37) is formally similar to a well-known thermodynamic constraint on inelastic constitutive laws, summarized in Equation (32) of Rice [6] and Equation (16) of Maugin [9]. Written in time implicit form, this constraint is

$$-{\left({\displaystyle \frac{\partial A}{\partial {\epsilon }_k}}\right)}_{X}d{\epsilon }_k=d{q}_{dis}\ge 0$$

(38)

where ${\epsilon }_k$ is an internal variable related to the extent of plastic deformation. Note that (37) and (38) are formally identical under variable transformation (30). The only essential difference is the type of irreversible process (tearing vs. plastic deformation) represented by the internal variable $d{\epsilon }_k$. It is this similarity between fracture and elasoplasticity theories that was anticipated earlier in the Introduction.

The domain of (37) can be extended beyond fixed-grips conditions to admit fixed load P, by substituting the identity $d\left(PX\right)=PdX+XdP$ into (31) yielding

$$d\left(PX-A\right)=d\Pi \left(P,a\right)=-{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_{X}da+XdP={\left({\displaystyle \frac{\partial \Pi }{\partial a}}\right)}_{P}da+{\left({\displaystyle \frac{\partial \Pi }{\partial P}}\right)}_{a}dP$$

(39)

where $\Pi \left(P,a\right)\equiv PX-A$ is the complementary energy. Comparing coefficients of the da in (39) gives the identity

$$-{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial \Pi }{\partial a}}\right)}_P$$

(40)

which substituted back into (37) gives the condition for tearing under either fixed grips or fixed load as

$$-{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_{X}da={\left({\displaystyle \frac{\partial \Pi }{\partial a}}\right)}_{P}da=d{W}^{\prime }-d{A}^{\prime }=d{q}_{dis}\ge 0$$

(41)

Dividing [41] by $da$ and recalling the crack growth irreversibility condition $da\ge 0$, gives the thermodynamic tearing criterion as:

$$-{\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial \Pi }{\partial a}}\right)}_P={\displaystyle \frac{d\left(W^{\prime }-A^{\prime }\right)}{da}}={\displaystyle \frac{d{q}_{dis}}{da}}\ge 0$$

(42)

where similarity with Irwin’s criterion (2) is clearly evident.

3.4. Indeterminacy of Helmholtz Energy and Transformation of (42) to a Determinate Form

A problem with thermodynamic criterion (42) is that the Helmholtz energy A can only be determined to within some unknown function of crack length, rendering the relation (42) in its present form difficult to apply experimentally. The indeterminacy is evident in constraint (32), requiring that the derivative ${\left(\partial A/\partial X\right)}_a$ must vanish in the unloaded state $P=0$. This admits a non-vanishing value of A at $P=0$ that is at most some unknown function ${\mathrm{A}}_{\mathrm{o}}$ of crack length a. We designate this function as the “residual Helmholtz energy” ${\mathrm{A}}_{\mathrm{o}}\left(a\right)$. Similar indeterminacy of A in elastic-plastic materials was noted by Hill and Rice [7], who observed that under isothermal conditions A could at most be specified to within some unknown function H of the set of internal variables.

The residual energy ${\mathrm{A}}_{\mathrm{o}}(a)$ in a fracture specimen may be considered as the set of all Helmholtz energy components that cannot be recovered as mechanical work by isothermal removal of the external load P. It admits, without necessarily being restricted to, non-dissipative irreversible energy forms such as residual elastic energy $U_{er}(a)$ trapped within unloaded elastic-plastic specimens due to the “warping” effect of non-uniform plastic deformation fields, and irreversible Griffith surface energy $\Gamma (a)$ associated with formation of crack surfaces that, due to stearic or other internal constraints, are prevented from retracting upon unloading. Accordingly, we write

$${\mathrm{A}}_{\mathrm{o}}\left(a\right)=U_{er}\left(a\right)+\Gamma \left(a\right)+\beta (a)$$

(43)

where $\beta (a)$ is a miscellaneous term accounting for any components of ${\mathrm{A}}_{\mathrm{o}}\left(a\right)$ not included in the terms $U_{er}\left(a\right)$ and $\Gamma \left(a\right)$. Note that these ${\mathrm{A}}_{\mathrm{o}}$ components represent currently irreversible energy forms, which could in principle become available as mechanical work on the environment if at some future time the internal constraints were removed. In this respect ${\mathrm{A}}_{\mathrm{o}}$ differs fundamentally from the dissipation d$q_{dis}$ defined by (34), which under isothermal conditions is rendered permanently irreversible by the second law of thermodynamics. Hence the term “non-dissipative irreversible energy” used to describe ${\mathrm{A}}_{\mathrm{o}}$.

The relation between A$(X,a)$ and $A_o\left(a\right)$ is obtained by integrating (32) with respect to X at fixed a, parting from the plastic set point ${X=X}_o\left(a\right)$ where $P=0$ and $A=A_o\left(a\right)$, giving $A(X,a)$ as

$$A(X,a)=A_o\left(a\right)+{\int }_{X_o\left(a\right)}^{X}P\left(\tau ,a\right)d\tau =A_o\left(a\right)+U_{ea}(X,a)$$

(44)

where $\tau$ is a dummy variable for X and the integral ${\int }_{X_o\left(a\right)}^{X}P\left(\tau ,a\right)d\tau$ defines the apparent elastic energy $U_{ea}\left(X,a\right)$. Relation (44) shows that $A(X,a)$ is equal to the (measurable) apparent elastic energy $U_{ea}(X,a)$ plus the indeterminate residual parameter $A_o(a)$. For later use, we note that the definition of $U_{ea}\left(X,a\right)$ in (44) admits both linear and non-linear elastic unloading, contrasting with the strictly linear compliance-based definition of $U_{ea}\left(X,a\right)$ in (9) and (16).

Making use of (44), the thermodynamic tearing criterion (42) can be transformed from its current indeterminate form to an equivalent form where all parameters are measurable. This is achieved by first substituting (44) into the derivative expressions ${\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_X$, ${\left({\displaystyle \frac{\partial \Pi }{\partial a}}\right)}_P$ and ${\displaystyle \frac{d{A}^{\prime }}{da}}$, giving the derivatives as

$${\left({\displaystyle \frac{\partial A}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X+{\displaystyle \frac{d{A}_o}{da}}$$

(45)

$${\left({\displaystyle \frac{\partial \Pi }{\partial a}}\right)}_P={\left({\displaystyle \frac{\partial (\mathrm{P}\mathrm{X}-\mathrm{A})}{\partial a}}\right)}_P={\left({\displaystyle \frac{\partial (\mathrm{P}\mathrm{X}-{[U}_{ea}+A_o)}{\partial a}}\right)}_P={\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P-{\displaystyle \frac{d{A}_o}{da}}$$

(46)

And

$${\displaystyle \frac{d{A}^{\prime }}{da}}={\displaystyle \frac{d{U}_{ea}^{\prime }}{da}}+{\displaystyle \frac{d{A}_o}{da}}$$

(47)

Substituting (45), (46) and (47) into thermodynamic criterion (42) yields the final desired result:

$$-{\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P=D^{*}={\displaystyle \frac{d{(q}_{dis}+A_o)}{da}} \ge 0 (?)$$

(48)

where $D^{*}\equiv d\left(W^{\prime }-U_{ea}^{\prime }\right)/da$ is the (measurable) energy dissipation rate defined earlier in (19). The derivatives ${\left(\partial U_{ea}/\partial a\right)}_X \mathrm{a}\mathrm{n}\mathrm{d} {\left(\partial {\Pi }_{ea}/\partial a\right)}_P$ on the left hand side of (48), expressed in terms of measurable apparent elastic energy, represent the parameter I illustrated in Figure 2 and Figure 3 but now generalized to admit both linear and non-linear elastic unloading. Accordingly, as was done with D, the generalized form of I is designated with an asterisk, so that criterion (48) may be written in abbreviated form

$$I^{*}=D^{*}$$

(49)

Note that, in contrast to the indeterminate parameter A in (42), all essential parameters in the equivalent relation (48) are measurable. The indeterminate residual energy parameter ${\mathrm{d}\mathrm{A}}_{\mathrm{o}}/da$ still appears on the right hand side of (48), but incorporated into the derivative sum $d(q_{dis}+A_o)/da$ which is measurable by virtue of its identity with the measurable parameter ${\mathit{D}}^{\mathit{*}}$.

The inequality condition “$\ge 0$” in thermodynamic criterion (42) has been retained in (48), but with a question mark (?) indicating that it is left as a postulate. Inspection of (48) shows that the condition $D^{*}\ge 0$ requires not only that $d{q}_{dis}/da\ge 0$ as imposed by the second law, but also that $d{A}_o/da\ge -d{q}_{dis}/da$. The latter constraint is satisfied whenever crack extension is associated with accumulation of residual Helmholtz energy A_o (a positive quantity), and also under release of A_o (negative quantity) so long as the amount released does not exceed the amount of dissipated heat. These conditions, regardless of their likelihood, are not guaranteed by any general thermodynamic principle with the same standing as the second law. Their likelihood is indicated by the fact that measurements of D in the literature [23,24,25,26,27,28,29,30,31,32] generally yield positive values.

Criterion (48) reduces to the empirical compliance-based result (21) in the special case of materials with linear elastic unloading behavior. This is significant, since it demonstrates that empirical relation (21) is consistent with thermodynamic constraints, and at the same time provides empirical verification of the thermodynamic model (48).

3.5. Application of Thermodynamic Criterion (48) to Fully Elastic Fracture

In the case of fully elastic materials, residual elastic energy vanishes so that the apparent elastic energy $U_{ea}$in (48) becomes equivalent to the total elastic energy $U_e$. The dissipation term $d{q}_{dis}/da$ also vanishes, reducing (48) to

$$-{\left({\displaystyle \frac{\partial U_e}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_e}{\partial a}}\right)}_P=D^{*}={\displaystyle \frac{d{A}_o}{da}}$$

(50)

Note that even though no heat dissipation is involved in this case, the residual Helmholtz energy component $d{A}_o/da$ of D* still remains. As observed earlier, this parameter admits non-dissipative irreversible processes such as accumulation of Griffith’s surface energy by extension of non-retractable cracks. Consequently, Griffith’s brittle fracture criterion (1) may be considered a special case of (50) where $D^{*}=2\gamma$. Also, note that (50) admits both linear and non-linear elastic materials, so that the partial derivatives on the left-hand side of (50) are the same as in the elastic J-integral. This allows writing (50) as

$$J=D^{*}={\displaystyle \frac{d{A}_o}{da}}$$

(51)

3.6. Stability Conditions Associated with Thermodynamic Criterion (48)

A set of instability conditions associated with thermodynamic tearing criterion constraint (48) has been postulated as:

$$-{\left({\displaystyle \frac{{\partial }^2{U}_{ea}}{\partial a^2}}\right)}_X\ge {\displaystyle \frac{d{D}^{*}}{da}} (fixed grips)$$

(52)

and

$${\left({\displaystyle \frac{{\partial }^2{\Pi }_{ea}}{\partial a^2}}\right)}_P\ge {\displaystyle \frac{d{D}^{*}}{da}} (\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d})$$

(53)

In situations where analytical forms of the functions $U_e(a,X)$, ${\Pi }_{ea}(a,P)$ and $D^{*}(a)$ are unknown a-priori, these functions and their derivatives must be determined experimentally on a case by case basis. However, as shown previously in Section 2, for the common case of linear elastic unloading it is possible to simplify (52) and (53) to inequalities involving easily measured system parameters C, P’, $dC/da$, $dP\prime /da$ and $d{X}_o/da$. These inequalities were noted to be consistent with typically observed fracture stability behavior.

3.7. Consistency of Irwin’s Elastic-Plastic Tearing Criterion (2) and Orowan’s Associated Instability Criterion (3) with Thermodynamic Constraint (48)

Irwin’s original elastoplastic tearing criterion (2) and Orowan’s associated instability condition (3) can be examined for consistency with thermodynamic result (48). Substituting expression (44) for the residual Helmholtz energy function $A_o(a)$ into the right-hand side of (48), and letting the miscellaneous energy term $\in (a)$vanish, (48) becomes

$$-{\left({\displaystyle \frac{\partial U_{ea}}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_{ea}}{\partial a}}\right)}_P=D^{*}={\displaystyle \frac{d{q}_{dis}^{\prime }}{da}}+2\gamma +{\displaystyle \frac{d{U}_{er}}{da}}$$

(54)

where the surface energy derivative $d\Gamma /da$ as been written as Griffith’s parameter $2\gamma .$ We next write the total elastic energy $U_e$as the sum of the apparent elastic energy $U_{ea}\left(a,X\right)$ and residual elastic energy $U_{er}\left(a\right)$:

$$U_e\left(a,X\right)\equiv U_{ea}\left(a,X\right)+U_{er}\left(a\right)$$

(55)

When (55) is substituted into the derivatives ${\left(\partial U_{ea}/\partial a\right)}_X \mathrm{a}\mathrm{n}\mathrm{d} {\left(\partial {\Pi }_{ea}/\partial a\right)}_P$in (54), the indeterminate residual energy terms $d{U}_{er}/da$ cancel out, transforming (54) to

$$-{\left({\displaystyle \frac{\partial U_e}{\partial a}}\right)}_X={\left({\displaystyle \frac{\partial {\Pi }_e}{\partial a}}\right)}_P={\displaystyle \frac{d{q}_{dis}^{\prime }}{da}}+2\gamma \approx {\displaystyle \frac{d{W}_p}{da}}+2\gamma$$

(56)

which is Irwin’s postulate (2). For fixed grips, taking derivatives of all terms in (56) with respect to a, and equating the right and left hand sides of the resulting expression, gives

$$-{\left({\displaystyle \frac{{\partial }^2{U}_e}{\partial a^2}}\right)}_X={\displaystyle \frac{d^2{W}_p}{d{a}^2}}+2{\displaystyle \frac{d\gamma }{da}}\approx {\displaystyle \frac{d^2{W}_p}{d{a}^2}}$$

(57)

which is Orowan’s instability postulate (3).

3.8. Implications Regarding Significance of the Energy Dissipation Rate D*

Although the energy dissipation rate D* has received some attention as an empirical fracture parameter in the scientific journal literature, it is difficult to find any mention of it in fracture mechanics textbooks. This seems to reflect uncertainty regarding the theoretical meaning of D*, a situation attributable in part to the frequently observed sensitivity of D* to specimen configuration and crack extension [32]. However, results obtained here clearly demonstrate the nature of D* as a measurable, rigorously defined thermodynamic parameter. Even though individual values of D* may depend on specimen configuration, the fracture condition ${\mathit{I}}^{\mathit{*}}={\mathit{D}}^{\mathit{*}}$ imposed by (48) is configuration independent, representing a macroscopic thermodynamic constraint that must be integrally satisfied by localized processes associated with fracture. Similar arguments, in a weaker sense, may be made regarding the meaning of common fracture indices such as the Charpy and Izod impact parameters, which are essentially dynamic extensions of D*.

4. Summary and Conclusions

A macroscopic energy-based tearing criterion, applicable for crack extension in both elastic and fully plastic regimes, has been independently derived from compliance relations and a thermodynamic model with internal variables. The two derivations are mutually supportive in that the thermodynamic formulation demonstrates consistency of the compliance-based result with the first and second laws of thermodynamics, whereas the compliance result provides empirical verification of the thermodynamic model. A crack driving force I* is predicted that is equivalent to the J-integral under linear or non-linear elastic tearing conditions, but differs fundamentally from J in the elastic-plastic case by admitting crack extension accompanied by both elastic unloading and plastic dissipation. Crack growth resistance is represented by the energy dissipation rate D*, which contrary to common perception is a rigorously defined thermodynamic parameter. It represents the sum of heat dissipated per unit crack extension, plus the rate of change of a residual Helmholtz energy component accounting for non-dissipative irreversible processes such as accumulation of residual elastic energy and Griffith surface energy. Instability of fracture is postulated to occur whenever ${\left(\partial I^{*}/\partial a\right)}_{X or P}\ge d{D}^{*}/da$, with the partial derivative evaluated at either fixed displacement X or fixed load P. For the common special case of elastic or elastic-plastic materials with linear elastic unloading behavior, the instability criteria reduce to simple inequalities between system parameters that predict commonly observed stability behaviors. These are: 1) general stability of fracture-toughening systems under either load or displacement control; 2) general instability of load-controlled fracture-weakening systems; and 3) transition from initially stable to ultimately unstable tearing of fracture-weakening systems under displacement-controlled loading. In the latter case a set of specific parameter values is predicted for transition from stable to unstable behavior, which has yet to be tested experimentally. Irwin’s original elastic-plastic tearing criterion is shown to be consistent with the thermodynamic model over a wide domain of material behaviors ranging from LEFM to fully plastic tearing conditions.