Submitted:
08 July 2025
Posted:
09 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
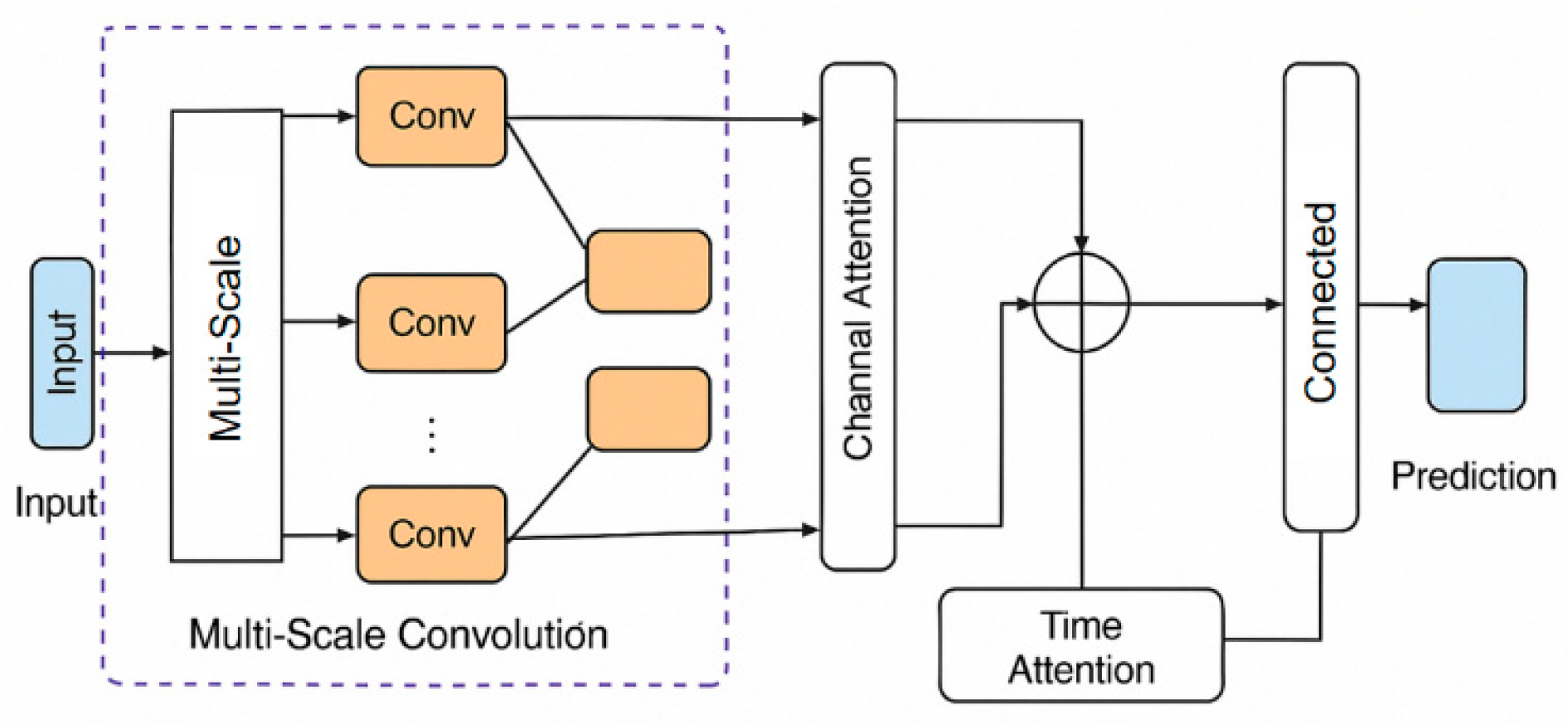
2. Method
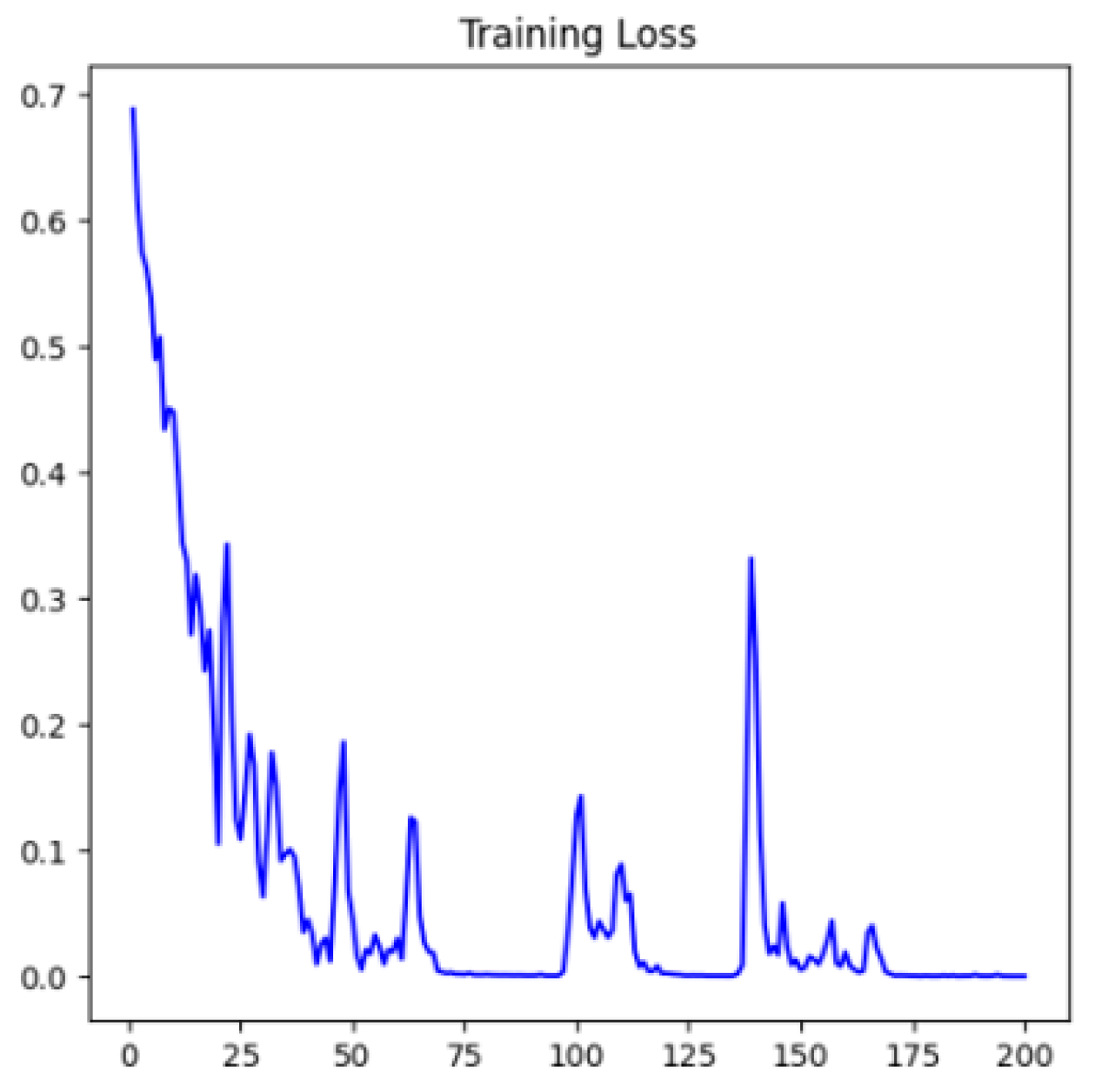
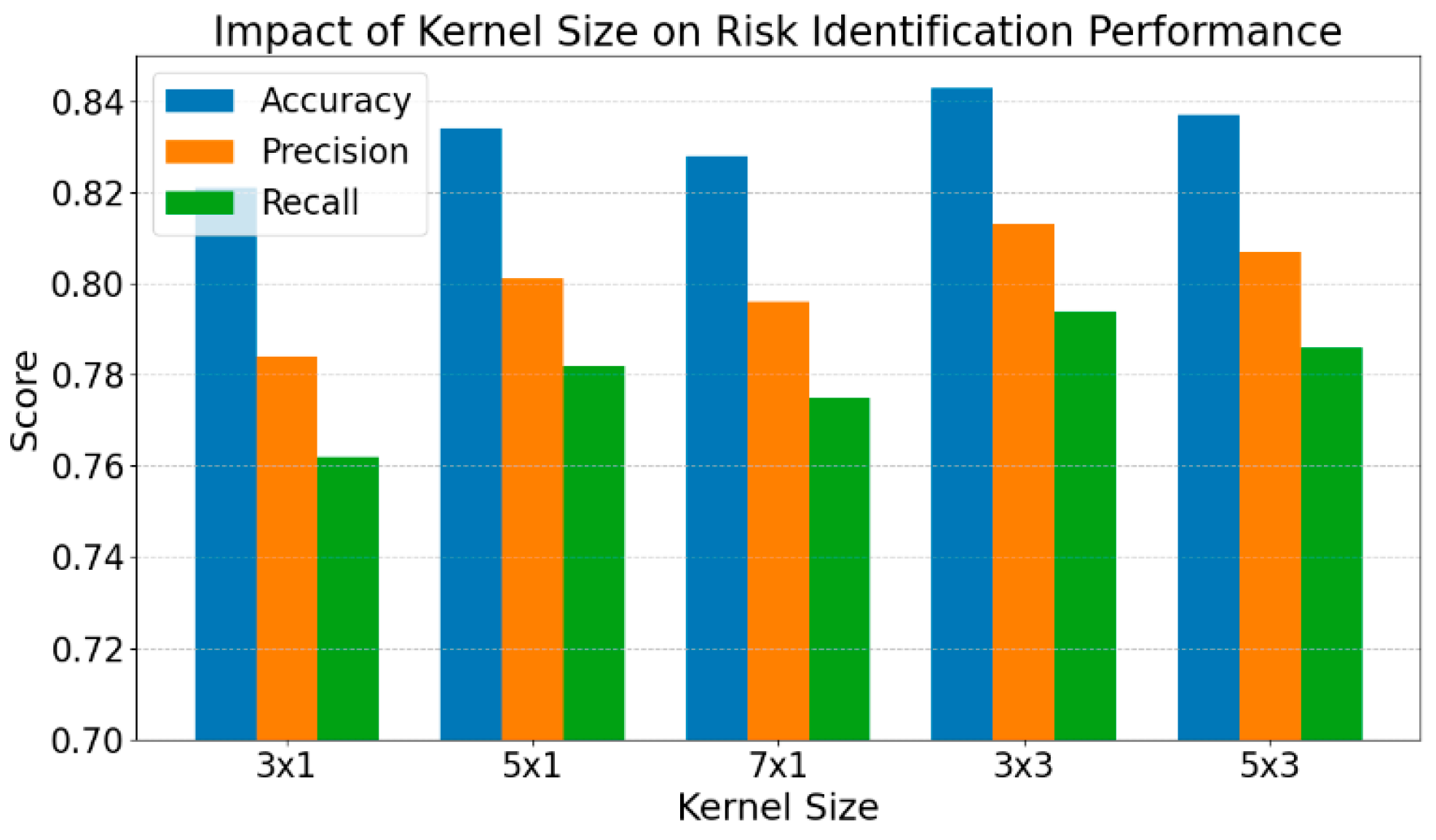
3. Experiment
A. Datasets
B. Experimental Results
4. Conclusions
5. Use of AI
References
- Y. Balmaseda, M. Coronado and G. de Cadenas-Santiago, "Predicting systemic risk in financial systems using deep graph learning," Proceedings of the 2023 Intelligent Systems with Applications Conference, pp. 200240, 2023.
- V. Kanaparthi, "Transformational application of Artificial Intelligence and Machine learning in Financial Technologies and Financial services: A bibliometric review," arXiv preprint arXiv:2401.15710, 2024.
- Y. Cheng, "Multivariate Time Series Forecasting through Automated Feature Extraction and Transformer-Based Modeling," Journal of Computer Science and Software Applications, vol. 5, no. 5, 2025.
- W. Cui and A. Liang, “Diffusion-Transformer Framework for Deep Mining of High-Dimensional Sparse Data,” Journal of Computer Technology and Software, vol. 4, no. 4, pp. 50–66, 2025. [CrossRef]
- J. Wang, “Credit Card Fraud Detection via Hierarchical Multi-Source Data Fusion and Dropout Regularization,” Transactions on Computational and Scientific Methods, vol. 5, no. 1, pp. 15–28, 2025. [CrossRef]
- B. Chen, F. Qin, Y. Shao, J. Cao, Y. Peng and R. Ge, "Fine-Grained Imbalanced Leukocyte Classification With Global-Local Attention Transformer," Journal of King Saud University - Computer and Information Sciences, vol. 35, no. 8, Article ID 101661, 2023.
- J. Luo, W. Zhuo and B. Xu, "A deep neural network-based assistive decision method for financial risk prediction in carbon trading market," Proceedings of the 2024 Journal of Circuits, Systems and Computers Conference, vol. 33, no. 08, pp. 2450153, 2024.
- X. Du, “Audit Fraud Detection via EfficiencyNet with Separable Convolution and Self-Attention,” Transactions on Computational and Scientific Methods, vol. 5, no. 2, pp. 33–45, 2025. [CrossRef]
- O. E. Ejiofor, "A comprehensive framework for strengthening USA financial cybersecurity: integrating machine learning and AI in fraud detection systems," Proceedings of the 2023 European Journal of Computer Science and Information Technology Conference, vol. 11, no. 6, pp. 62-83, 2023.
- Q. Bao, "Advancing Corporate Financial Forecasting: The Role of LSTM and AI in Modern Accounting," Transactions on Computational and Scientific Methods, vol. 4, no. 6, 2024. [CrossRef]
- X. Yan, J. Du, L. Wang, Y. Liang, J. Hu and B. Wang, "The Synergistic Role of Deep Learning and Neural Architecture Search in Advancing Artificial Intelligence," Proceedings of the 2024 International Conference on Electronics and Devices, Computational Science (ICEDCS), pp. 452-456, Sep. 2024.
- T. M. A. U. Gunathilaka, J. Zhang and Y. Li, "Fine-Grained Feature Extraction in Key Sentence Selection for Explainable Sentiment Classification Using BERT and CNN," IEEE Access, 2025.
- J. Gong, Y. Wang, W. Xu and Y. Zhang, "A Deep Fusion Framework for Financial Fraud Detection and Early Warning Based on Large Language Models," Journal of Computer Science and Software Applications, vol. 4, no. 8, 2024. [CrossRef]
- Y. Sheng, "Temporal Dependency Modeling in Loan Default Prediction with Hybrid LSTM-GRU Architecture," Transactions on Computational and Scientific Methods, vol. 4, no. 8, 2024. [CrossRef]
- J. Wei, Y. Liu, X. Huang, X. Zhang, W. Liu and X. Yan, "Self-Supervised Graph Neural Networks for Enhanced Feature Extraction in Heterogeneous Information Networks," 2024 5th International Conference on Machine Learning and Computer Application (ICMLCA), pp. 272-276, 2024.
- Y. Lou, “Capsule Network-Based AI Model for Structured Data Mining with Adaptive Feature Representation,” Transactions on Computational and Scientific Methods, vol. 4, no. 9, pp. 77–89, 2024. [CrossRef]
- L. Dai, W. Zhu, X. Quan, R. Meng, S. Cai and Y. Wang, "Deep Probabilistic Modeling of User Behavior for Anomaly Detection via Mixture Density Networks," arXiv preprint arXiv:2505.08220, 2025.
- M. Scholkemper, X. Wu, A. Jadbabaie and M. T. Schaub, "Residual connections and normalization can provably prevent oversmoothing in GNNs," arXiv preprint arXiv:2406.02997, 2024.
- P. Feng, “Hybrid BiLSTM-Transformer Model for Identifying Fraudulent Transactions in Financial Systems,” Journal of Computer Science and Software Applications, vol. 5, no. 3, pp. 45–58, 2025. [CrossRef]
- L. Almahadeen et al., “Enhancing Threat Detection in Financial Cyber Security Through Auto Encoder-MLP Hybrid Models,” International Journal of Advanced Computer Science and Applications, vol. 15, no. 4, pp. 924–933, 2024. [CrossRef]
- Y. Cheng et al., "A Deep Learning Framework Integrating CNN and BiLSTM for Financial Systemic Risk Analysis and Prediction," arXiv preprint arXiv:2502.06847, 2025.
- Y. Wei et al., "Financial Risk Analysis Using Integrated Data and Transformer-Based Deep Learning," Proceedings of the 2024 Journal of Computer Science and Software Applications Conference, vol. 4, no. 7, pp. 1-8, 2024. [CrossRef]
- E. Sy et al., "Fine-grained argument understanding with bert ensemble techniques: A deep dive into financial sentiment analysis," Proceedings of the 35th Conference on Computational Linguistics and Speech Processing (ROCLING 2023), 2023.
- Z. Xu et al., “Reinforcement Learning in Finance: QTRAN for Portfolio Optimization,” Journal of Computer Technology and Software, vol. 4, no. 3, 2025. [CrossRef]
- Y. Yao, "Time-Series Nested Reinforcement Learning for Dynamic Risk Control in Nonlinear Financial Markets," Transactions on Computational and Scientific Methods, vol. 5, no. 1, 2025. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




