Navigating Meta-Universes of Melded Infinities: A Theoretical Exploration of the Mind's Ontological Power

1. Introduction

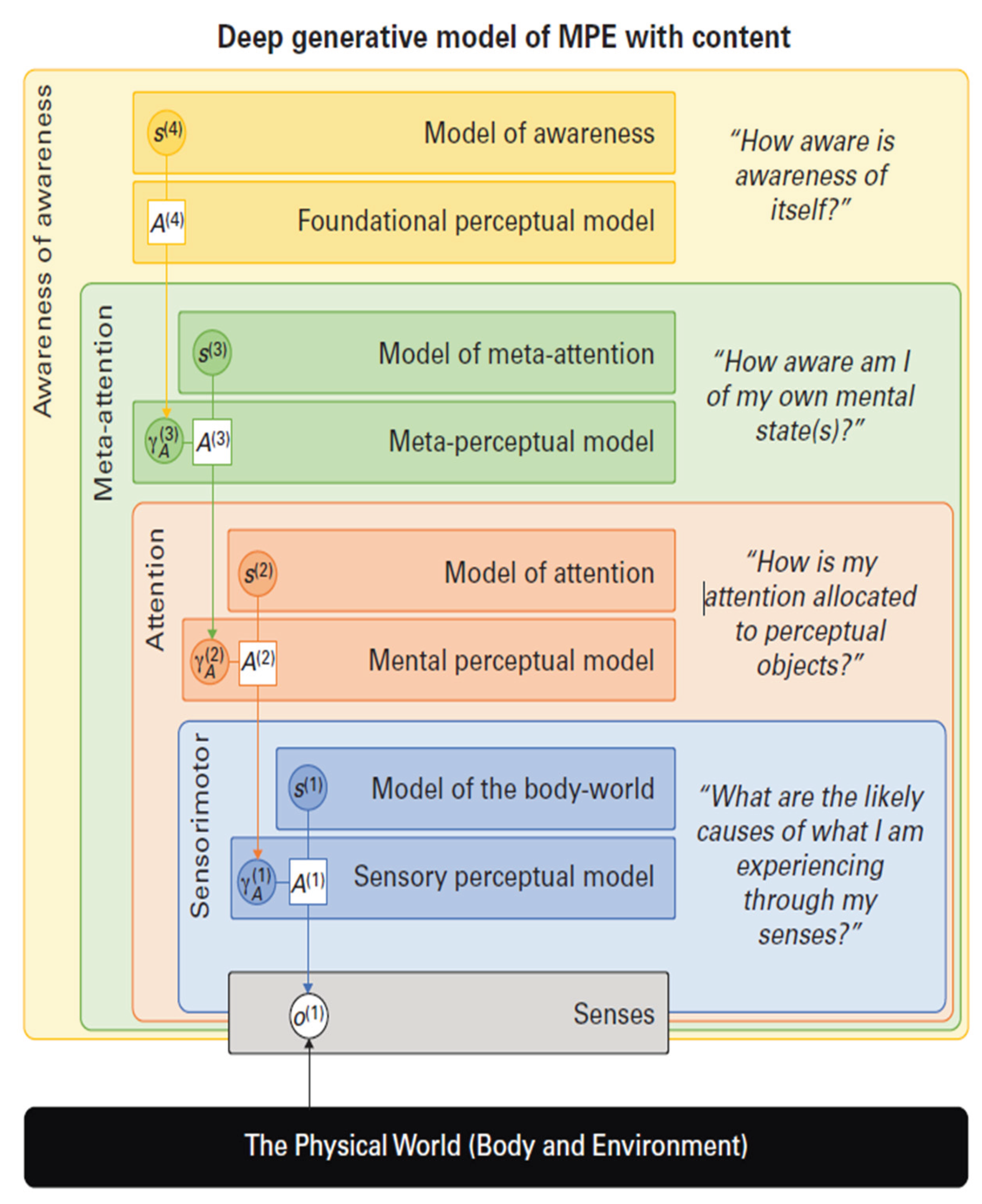
Often centered on its function as a mirror to the outside world—a complicated biological mechanism for perception, response, and survival. This questionnaire (Metzinger, 2024) investigates experiences of “awareness of awareness” or “consciousness of consciousness.” Our focus is the subjective experience of “consciousness as such,” also termed “pure awareness” or “pure consciousness.” We are not interested in mystical or dramatic spiritual experiences, but in states characterized by “pure awareness” or “consciousness itself.” This indicates that, regardless of other conscious contents, an “awareness of awareness” has emerged. We seek states where we distinctly experience the quality of “consciousness” itself. as manifested by Figure 1 and Figure 2 (Metzinger, 2024)—the persistent search for human consciousness has although this view is basic, it is highly insufficient It ignores the incredible creative capacity of the mind: its capacity to build complete worlds internally, to handle ideas of infinity(Mageed, 2025a; Mageed, 2025c), and to combine many fields of knowledge into fresh forms of understanding.

This article suggests that the human brain serves as a "meta-universe," an all-encompassing reality comprising, models, and merges innumerable sub-level "infinities" of thought, imagination, and possibility. Two main ideas underlie this framework. First, the "meta-universe" of the mind is an ontological one—a cosmos of being and meaning generated by neuronal processes—rather than a physical multiverse in the cosmological meaning (Peebles, 2020; Nahin, 2021).

Second, "melded infinities" is the cognitive alchemy by which the mind combines the boundless potential of symbolic systems (such as language, mathematics) with the qualitative richness of subjective experience (such as emotion, memory) (Wittgenstein, 2023). The human mind displays a power—one not only interpretive but also fundamentally creative—through predictive processing, symbolic abstraction, and recursive self-awareness—which helps it to create and live in worlds created of its own design.

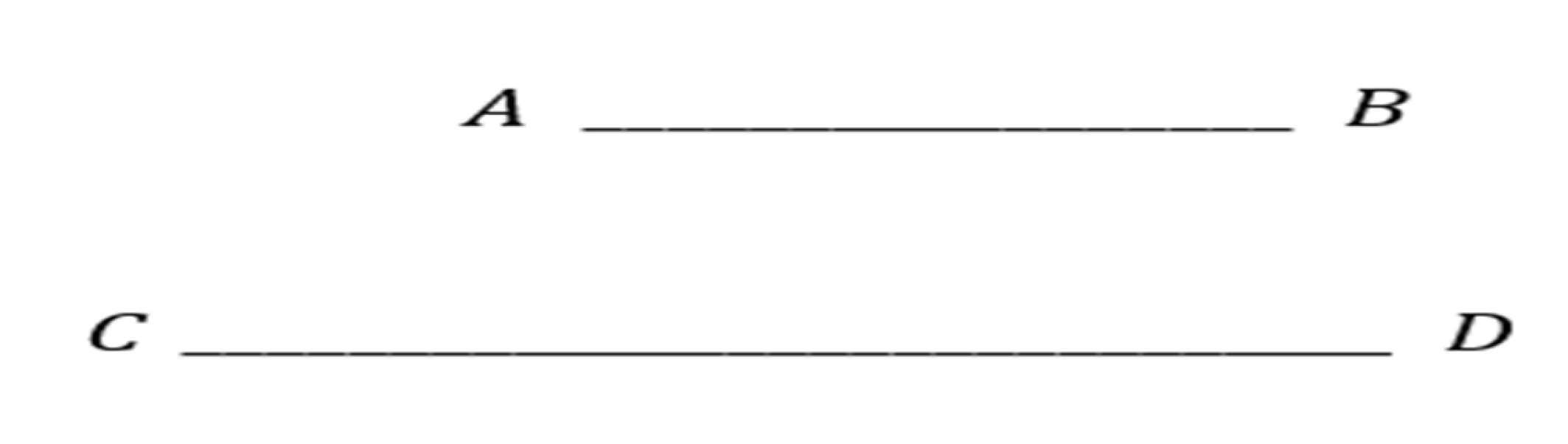
I do not support the existence of infinity as a mathematical entity. The number of points in a straight line appears infinite, such as in straight-line AB, as depicted in Figure 3 (Mageed, 2025c). The cardinal number Card of the sets forming line CD is infinite. Since the first line segment’s points are a subset of the larger segment, this creates a contradiction.

From a fractal geometric, information geometric, information-theoretic, and machine learning perspectives(Mageed and Kouvatsos,2021; Mageed and Bhat, 2022;Mageed and Zhang, 2022a ; Mageed and Zhang, 2022b; Mageed and Zhang, 2023;Mageed and Mohamed, 2023; Mageed, 2023 a-c; Mageed, 2024 a-c; Mageed et al., 2024 a-c; Mageed and Li, 2025; Mageed, 2025 a-c), a new line of enquiry can showcase that infinity is only a mere agreeable convention to limit our counting ability as humans, beyond certain numbers, and not as a mathematical entity.

2. The Brain as a Universe-Simulator: Predictive Processing and Neuroplasticity

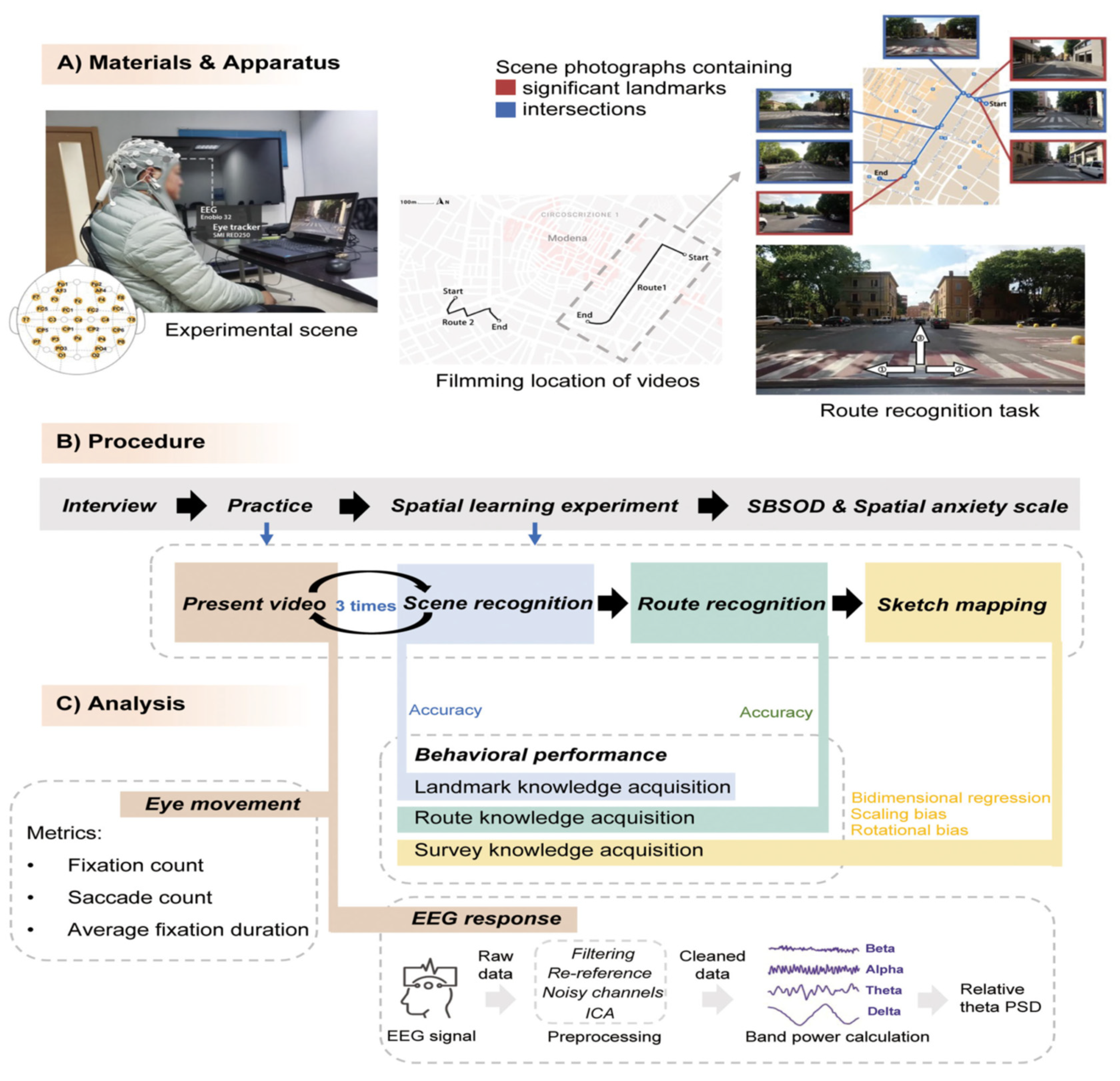
Modern neuroscience more and more depicts the brain not as a passive receiver of sensory input but as an active, prediction-generating system. The predictive processing framework holds that the brain continually creates models—or hypotheses—about the causes of its sensory data and then modifies those models according to prediction errors (Grossberg, 2021; Parr et al., 2022). According to this viewpoint, our perception of reality is not a direct reading of the outside world but a controlled hallucination, a "best guess" limited by sensory data (Seth, 2021). The starting point of the intellectual meta-universe is this continuous world-modeling action. The brain creates the reality of the chair based on prior experience and incoming light patterns, not just sees one. This simulation is not static. Neuroplasticity shows that our thoughts and experiences constantly reshape the very structure of the brain, namely its synaptic connections and neural pathways (Barrett, 2020). Every learning moment, every introspective experience, and every dreamed situation physically changes the architecture of the mental meta-universe , as in Figure 4 (Ying et al. , 2024). This implies the mind is a self-organizing and self-complicating cosmos rather than merely a simulator. The "laws of physics" in this inner world are malleable, rewritten by the very process of cognition itself, thereby enabling a level of dynamic production impossible in the physical world.

3. The Architecture of Infinity: Language, Mathematics, and Abstraction

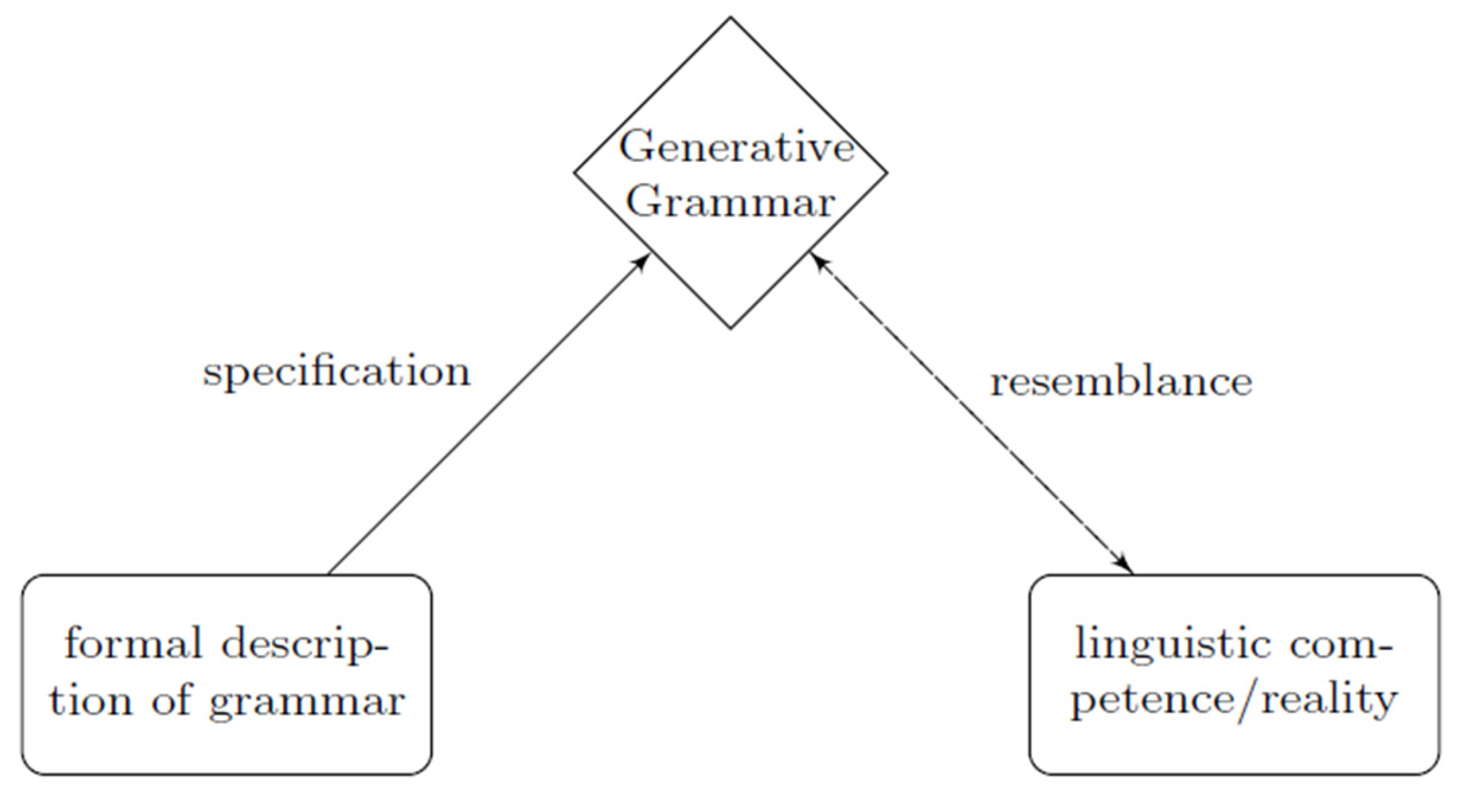
If predictive processing gives the canvas, symbolic systems give infinite color tools. The human invention of mathematics and language let us enter conceptual domains free from physical barriers. Human language, as Chomsky et al (2023) noted, has the characteristic of discrete infinity, enabling the production of an endless number of original sentences from a finite set of rules. Language is a world-building technique that carves reality into ideas, connections, and stories, so enabling us to create shared social realities and rich cultural histories (Bregman, 2020). Likewise, proof of the mind's capacity is its grasp of mathematical infinity—from the basic notion of a number line extending forever to Cantor's complex hierarchies of transfinite numbers created by Cantor (Bellos, 2020; Harford, 2020)— The brain can think of, control, and logically deal with infinities lacking a direct physical analogue. From cryptographic systems to cosmological models, these abstract systems are fundamental worlds of logic and structure that we can enter, explore, and build further realities—(Gaspar and Tambor, 2024). Operating inside entirely formal, infinite systems shows a cognitive capacity to go beyond the limited, biological container from whence it derives. When these abstract infinities are woven with our sensory and emotional realities, as when a mathematical formula defines the elegant arc of a thrown ball, merging the platonic realm of numbers with the phenomenal world of experience (Khatin-Zadeh et al. 2023). The diagram in Figure 5 (Nefdt,2019) shows grammar descriptions may involve merge or recursion, implying discrete infinity, unlike the target system. Hence, a grammatical model's closure under iterative operations does not imply the same for the language it models.

4. The Crucible of Imagination: Melding Realities Through Counterfactual Thought

The faculty of imagination best conveys the real power of the mental meta-universe. The crucible where several universes and infinities are "melded" is imagination. Stuart (2021) declares that it's the engine of counterfactual thinking—the capacity to imagine options not now real. Planning, regretting the past, story-telling, or developing a scientific hypothesis all comprise complex acts of reality-blending. We take elements from memory (one "universe"), project them into a hypothetical future (another "universe"), and imbue them with emotional valence and rational consequence (Gardner, 2020). This method enables entirely new theoretical worlds to be developed. Melded infinities are sophisticated systems created from the synthesis of current knowledge, logic, and imaginative leaps (Redelmeier, 2024), examples of which are the universe of a novel, the foundation of a new political philosophy, or the design for an unfinished machine. Although metaphysically debatable, philosophical ideas like "possible worlds" (Berto, 2022) offer a strong analogy for this cognitive capacity. By constantly imagining and evaluating potential universes, the mind becomes a par excellence simulation of constructing and testing new ones that represent the vast array of branching opportunities that exist within our physical world (Batchmann, 2020).

(Stuart, 2021) explored in depth, how we learn through imagination and explore the nature of imagination itself, questioning whether it is a mental state, ability, character trait, or cognitive process. (Stuart, 2021) proposed that imagination should be seen as a cognitive ability, which can be divided into two types: one that happens automatically and without effort (unconscious), and another that requires conscious thought and effort (controlled), aiming to create a framework that both philosophers and cognitive scientists can agree on, focusing on key aspects like how accessible imagination is to our awareness, how much control we have over it, and the effort it requires.

Aiming to create a framework (Stuart, 2021) for discussing how we understand imagination that both philosophers and cognitive scientists can agree on. So, (Stuart, 2021) propose using a dual process model, which distinguishes between two types of cognitive processes: one that is unconscious and effortless, and another that is conscious and requires effort. This framework allows for a clearer definition of imagination, where "imagination phase 1" refers to our overall ability to imagine, and "imagination phase 2 " describes the effortless, unconscious way we interact with things that are not currently in our sensory experience.

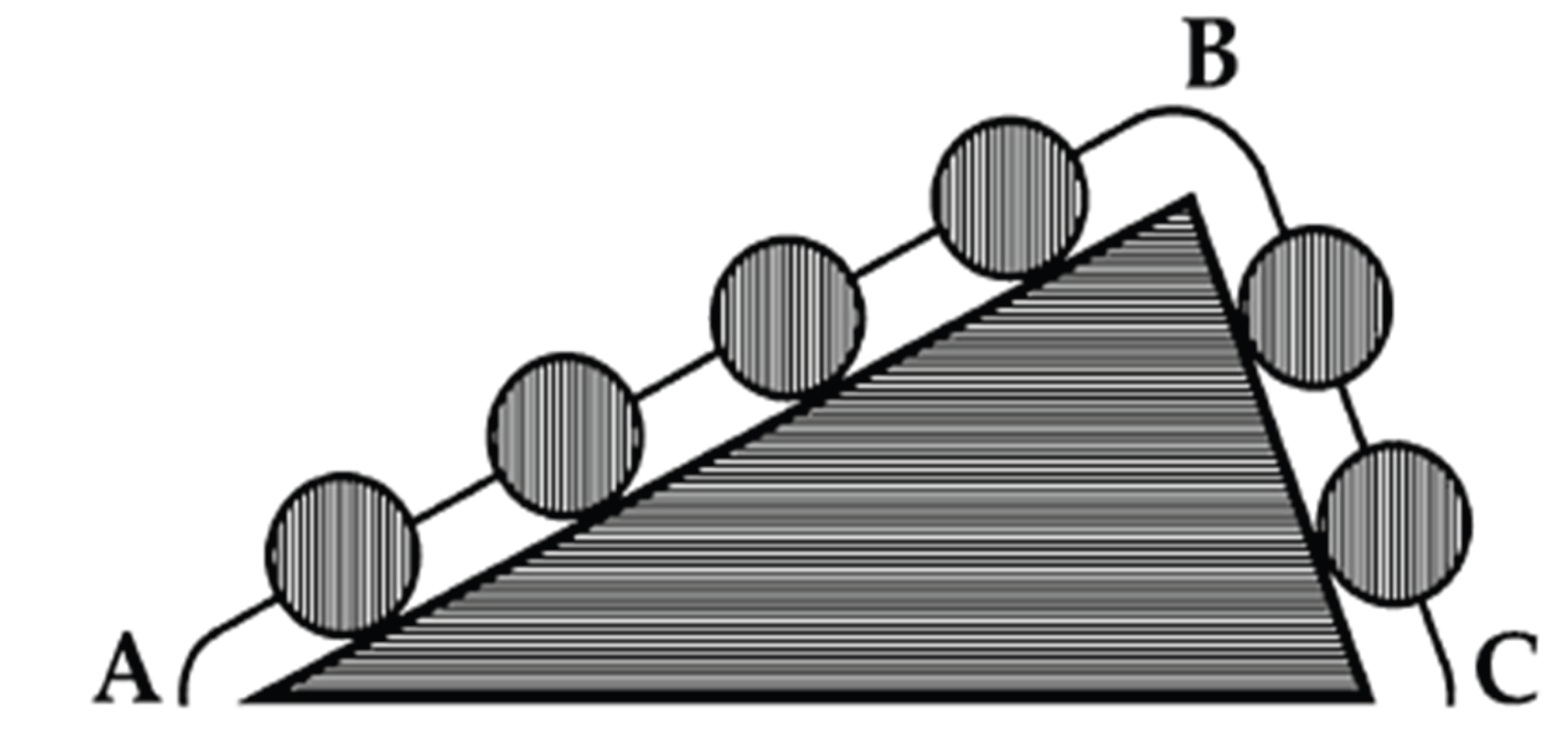
Table 1 visualizes two types of cognitive processes related to imagination and how they can be used together effectively to understand complex concepts. It uses the example of Stevin's prism(Stuart, 2021), which is a theoretical setup involving a triangular prism and a chain resting on it, to illustrate how we can use our imagination to predict the behavior of the chain in this frictionless environment. By asking ourselves (Stuart, 2021) how the chain will behave, we engage both types of imagination to explore and analyze the problem.

The text discusses how effective uses of imagination in understanding complex concepts often involve blending different types of imaginative thinking. For example, Stevin's prism, see Figure 6 (Stuart, 2021) is a theoretical setup that includes a triangular prism and a chain of mass resting on it, which helps us explore physical principles without friction. By imagining how the chain will behave on the prism, we can apply both creative and analytical thinking to gain insights into the problem.

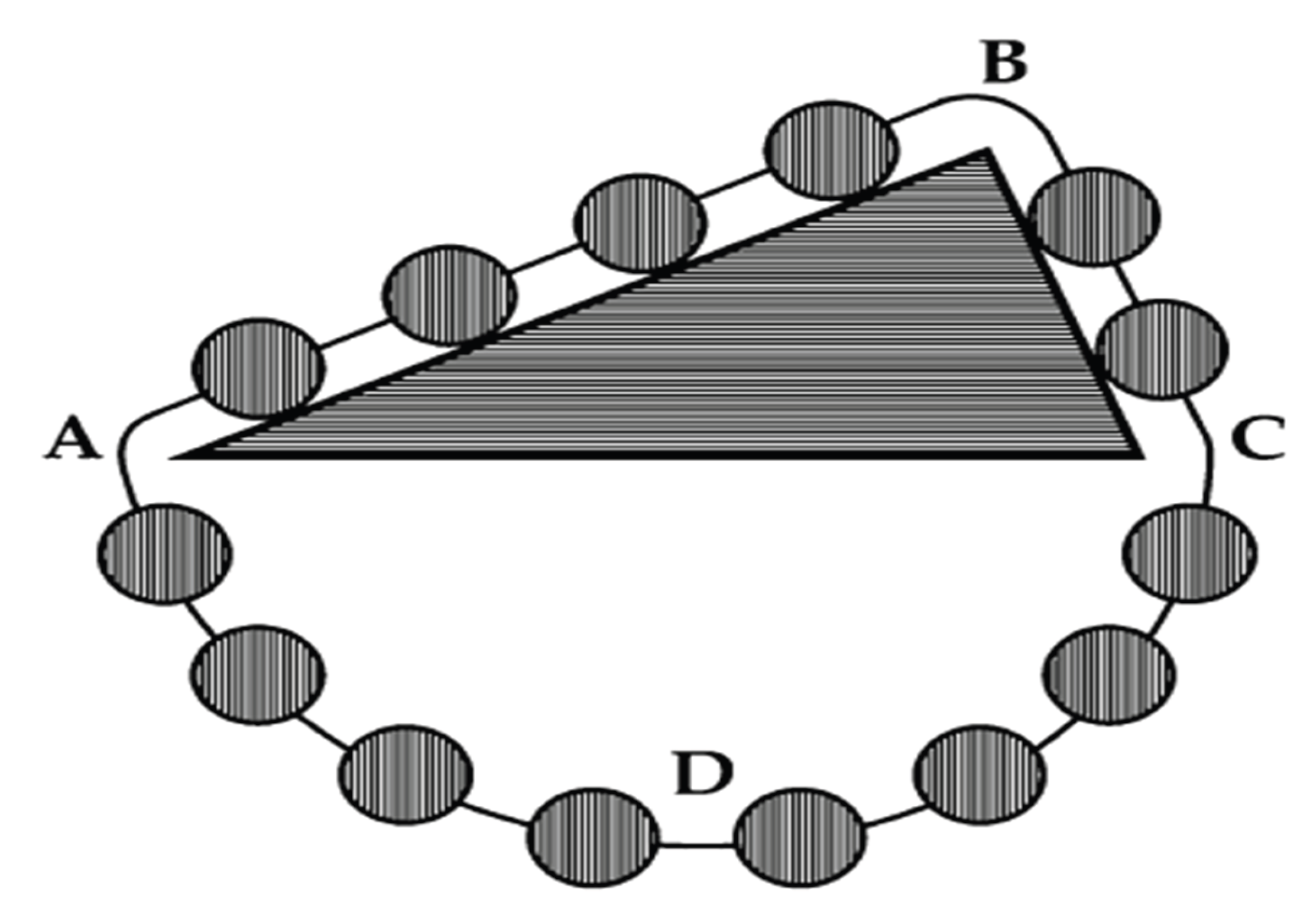
In this context, the text refers to a thought experiment involving a chain that is placed over a prism, which is a solid geometric shape. By imagining the chain connected around the bottom of the prism, as shown in Figure 7 (Stuart, 2021), we can explore how this change in configuration affects the chain's movement and the forces acting on it. This exercise encourages us to think critically about the physical principles at play, such as tension and equilibrium, in different setups.

This explains that if two systems (represented in Figure 6 and Figure 7) have the same balance of forces, their behavior will be identical; if one chain is still, the other will also remain still. This principle holds true for any chain with a uniform mass distribution placed over frictionless prisms of any shape, if the system is oriented correctly with respect to gravity. (Stuart, 2021) emphasized the importance of creative thinking (referred to as "imagination phases") in exploring and understanding these physical scenarios, leading to the conclusion that the chain will not slide regardless of the prism's shape.

5. Consciousness as the Meta-Observer: The Self and the Navigation of Worlds

An observer is needed to give coherence to a cosmos, even a mental one. In the mental meta-universe, self-awareness serves this part. Thinking about one's own ideas—metacognition—enables us to separate the various worlds we live: the dream from the memory, the fantasy from the strategy (Whitebread and Neale, 2020). This recursive capacity develops a steady "self" able to negotiate the internal landscape. Philosophers such as Gallagher and Zahavi (2020) suggested that the self is a type of internal model—a "phenomenal self-model" (PSM)—allowing the organism to represent itself acting in a world. The meta-universe's unifying core, this self-model is the site of phenomenal experience capable of deliberately focusing attention, blending opposing concepts, and recognizing its own products as such. This meta-awareness keeps us from getting lost in our own simulations (Seth, 2021). Not only to create worlds, but also to recognize that it is doing so and to do so intentionally is the greatest expression of the mind's ability.

6. Conclusions

Talking of "meta-universes of merged infinites" uses a simile but one that perfectly reflects the nature of the human mind. Our awareness is an active, world-generating energy not an inert slate. The brain builds, resides, and permanently reshapes an inner universe of remarkable complexity by means of the neurological bedrock of predictive processing and neuroplasticity, the limitless abstracting ability of math and language, the creative synthesis of imagination, and the unifying perspective of self-awareness. Perhaps the most defining trait of our species is this ontological ability—the ability to create new worlds even if only on a conceptual level. The statement implies that the laws of physics do not fix reality but are constantly expanded by the unfathomable potentiality of the human mind, which is always imaginative in its exploration of possibilities.