Advances in Large-Scale Spiking Neural Networks: Learning, Simulation, and Deployment

1. Introduction

The advent of deep learning has heralded remarkable advancements across a wide spectrum of artificial intelligence (AI) applications, ranging from image recognition and natural language processing to autonomous systems and scientific discovery [1]. Central to these successes are artificial neural networks (ANNs), which leverage dense matrix operations, gradient-based optimization, and backpropagation to learn representations from large-scale data [2]. However, despite their empirical prowess, conventional ANNs remain biologically implausible and computationally expensive, particularly in terms of energy consumption. In contrast, spiking neural networks (SNNs), inspired by the asynchronous and event-driven nature of biological neurons, have emerged as a promising paradigm offering both biological fidelity and computational efficiency, especially when deployed on neuromorphic hardware [3]. SNNs model the dynamics of biological neurons by encoding information in the timing of discrete spikes rather than in continuous-valued activations [4]. Formally, the membrane potential $V_i\left(t\right)$ of neuron i evolves according to a differential equation of the form:

$${\tau }_m{\displaystyle \frac{d{V}_i\left(t\right)}{dt}}=-V_i\left(t\right)+R\sum _j{w}_{ij}{S}_j\left(t\right),$$

where ${\tau }_m$ is the membrane time constant, R is the membrane resistance, $w_{ij}$ is the synaptic weight from neuron j to i, and $S_j\left(t\right)$ denotes the presynaptic spike train, typically modeled as a sum of Dirac delta functions:

$$S_j\left(t\right)=\sum _k\delta (t-t_j^k),$$

with $t_j^k$ representing the time of the k-th spike emitted by neuron j[5]. A spike is emitted by neuron i whenever $V_i\left(t\right)$ exceeds a threshold $\theta$, after which the potential is reset [6]. Despite their appeal, training SNNs at scale presents substantial challenges [7]. The primary obstacle arises from the non-differentiability of spike events, which precludes the direct application of backpropagation [8]. This has spurred a wide array of surrogate gradient methods, local learning rules such as spike-timing dependent plasticity (STDP), and hybrid approaches that combine ANN pretraining with SNN fine-tuning. Moreover, implementing large-scale SNNs necessitates overcoming limitations in memory, event-driven simulation, and communication overhead, especially in distributed settings [9]. The growing interest in SNNs has led to a proliferation of research focusing on their scalability in both hardware and algorithmic dimensions [10]. From a hardware perspective, neuromorphic platforms such as Intel Loihi, IBM TrueNorth, and BrainScaleS offer specialized architectures tailored to the event-driven nature of SNNs [11]. These platforms exploit sparse connectivity, temporal coding, and low-power operation to efficiently simulate large-scale networks with millions of spiking neurons and billions of synapses [12]. From a software and algorithmic standpoint, recent advances include spatio-temporal backpropagation frameworks, efficient spike encoding strategies, sparsity-aware optimization, and large-scale datasets and benchmarks designed specifically for spiking models. Mathematically, scaling SNNs involves careful treatment of several issues that do not arise in traditional ANNs [13]. For instance, the non-Euclidean nature of spike trains challenges conventional metrics for gradient computation and loss evaluation. Let $\mathcal{L}$ denote a generic loss function. The surrogate gradient approach replaces the non-differentiable spike activation function $\sigma \left(x\right)=H(x-\theta )$, where H is the Heaviside function, with a smooth approximation $\tilde{\sigma }\left(x\right)$, such as:

$$\tilde{\sigma }\left(x\right)={\displaystyle \frac{1}{1+e^{-\beta (x-\theta )}}},$$

where $\beta$ controls the steepness of the sigmoid approximation. This enables gradient-based updates via:

$${\displaystyle \frac{\partial \mathcal{L}}{\partial w_{ij}}}=\sum _t{\displaystyle \frac{\partial \mathcal{L}}{\partial S_i\left(t\right)}}·{\displaystyle \frac{\partial S_i\left(t\right)}{\partial V_i\left(t\right)}}·{\displaystyle \frac{\partial V_i\left(t\right)}{\partial w_{ij}}}.$$

[14] Such approximations must balance biological realism with computational tractability, particularly in deep and recurrent SNNs where temporal credit assignment becomes nontrivial [15]. Furthermore, scaling to larger networks raises questions of architectural design [16]. Analogous to the role of convolutional layers and attention mechanisms in ANNs, researchers are investigating architectural motifs in SNNs that support hierarchical temporal processing, recurrent feedback, and modular connectivity [17]. Incorporating these ideas necessitates novel formulations of time-dependent computation and learning rules that are compatible with spiking dynamics [18]. This survey aims to comprehensively review the current state of research on large-scale spiking neural networks, encompassing their mathematical underpinnings, training algorithms, architectural innovations, and hardware accelerators [19]. We explore the interplay between biological inspiration and computational pragmatism, highlighting the key breakthroughs and persistent challenges in scaling SNNs [20]. Our focus is on bridging the gap between theory and large-scale implementation, identifying principled methods that allow SNNs to perform competitively with deep ANNs on complex, real-world tasks. In what follows, we begin with a formal definition of spiking neuron models and their computational abstractions [21]. We then examine learning algorithms tailored to large-scale spiking systems, including supervised, unsupervised, and reinforcement learning paradigms. Subsequently, we review hardware and software infrastructures designed to support large-scale SNN training and inference [22]. Finally, we discuss current benchmarks, evaluation criteria, and future research directions toward the realization of brain-scale spiking intelligence.

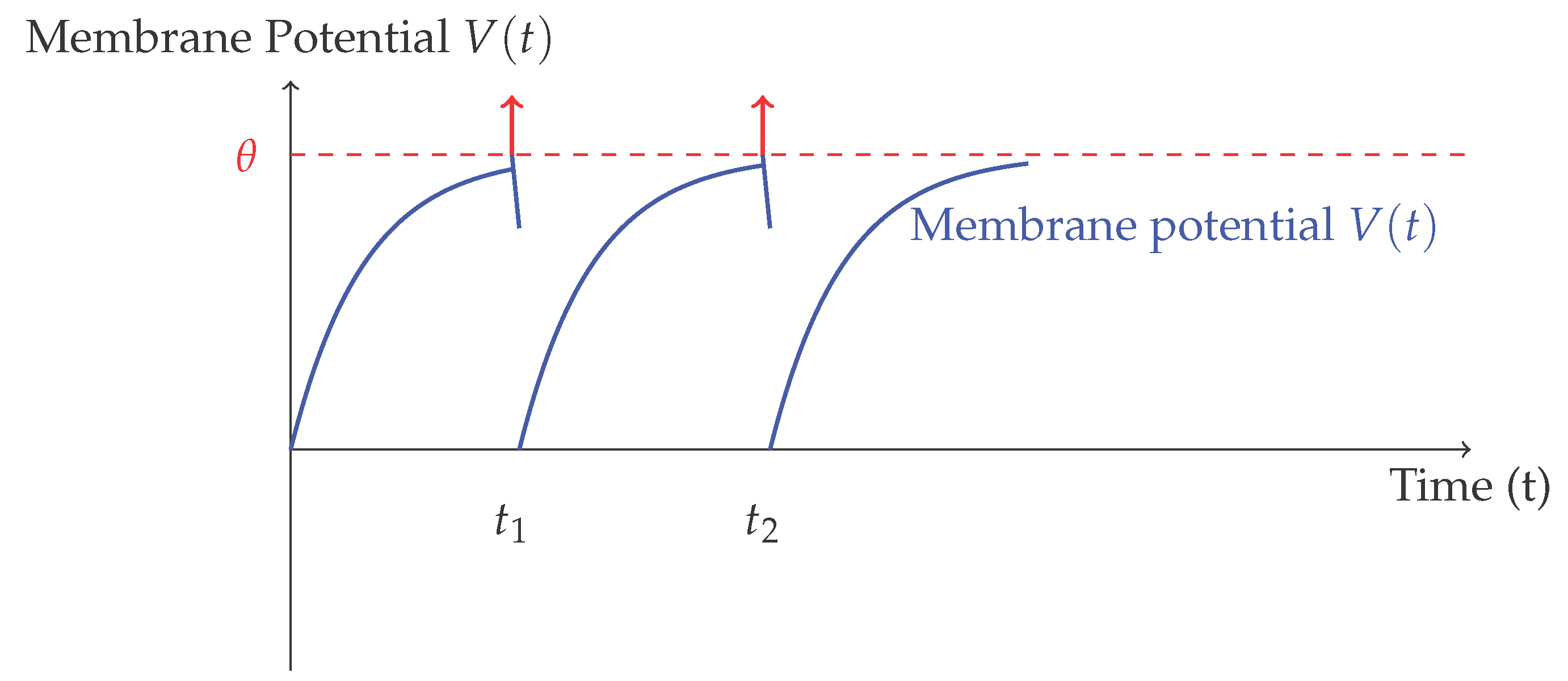
2. Spiking Neuron Models and Mathematical Formalism

Spiking neural networks (SNNs) differ fundamentally from traditional artificial neural networks (ANNs) in their encoding, processing, and communication of information. While ANNs typically rely on static, real-valued activations updated in synchronous rounds, SNNs use time as a critical dimension: neurons communicate through discrete, sparse, and temporally precise spike events. Consequently, modeling the behavior of a spiking neuron requires capturing its membrane potential dynamics, thresholding mechanism, and refractory behavior [23]. This section delves into the mathematical foundations of spiking neuron models and provides a unified framework for their analysis and simulation [24]. The most commonly used model is the leaky integrate-and-fire (LIF) neuron, which balances biological plausibility and mathematical tractability [25]. The membrane potential $V\left(t\right)\in \mathbb{R}$ of a neuron evolves according to:

$${\tau }_m{\displaystyle \frac{dV\left(t\right)}{dt}}=-V\left(t\right)+I\left(t\right),$$

where ${\tau }_m$ is the membrane time constant, and $I\left(t\right)$ is the input current, typically a weighted sum of incoming spikes [26]. When $V\left(t\right)$ reaches a threshold $\theta$, the neuron emits a spike and resets its membrane potential to a baseline value $V_{\mathrm{reset}}$[27]. In discrete time with timestep $\Delta t$, the update rule becomes:

$$V[t+1]=\alpha V\left[t\right]+\sum _j{w}_{ij}{S}_j\left[t\right],\mathrm{where}\alpha =e^{-\Delta t/{\tau }_m},S_j\left[t\right]\in \{0,1\}.$$

[28] Here, $S_j\left[t\right]$ is the spike output of the j-th presynaptic neuron at timestep t, and $w_{ij}$ is the synaptic weight [29]. The neuron spikes when $V\left[t\right]\ge \theta$, after which it enters a reset or refractory phase [30]. More complex models, such as the Izhikevich or Hodgkin–Huxley models, incorporate additional biophysical dynamics like recovery variables and ionic currents, but their complexity makes them less suitable for large-scale simulation.

As illustrated in Figure 1, the dynamics of a single spiking neuron involve an exponential rise of membrane potential in response to input spikes, followed by a rapid reset after the emission of a spike [32]. This mechanism yields sparse, temporally distributed spike patterns that encode rich temporal structure even in static stimuli. The model is deterministic if inputs are deterministic, but stochastic extensions, incorporating noise into input currents or thresholds, are often introduced to improve robustness and biological plausibility [33]. Another crucial concept is the encoding of analog information into spike trains [34]. A common approach is rate coding, where the information is represented by the spike rate over a fixed time window [35]. Mathematically, the firing rate $r_i$ of neuron i over an interval $[0,T]$ is given by:

$$r_i={\displaystyle \frac{1}{T}}\sum _{t=0}^T{S}_i\left[t\right],$$

which approximates the average spike count. However, such rate-based encodings may discard important temporal information [36]. Alternative schemes include temporal coding, where information is conveyed by precise spike times, and population coding, where ensembles of neurons jointly represent a stimulus [37]. Modeling large-scale SNNs requires constructing networks where each neuron’s dynamics are defined individually, but the global behavior emerges from the collective activity [38]. Let $\mathbf{V}\left(t\right)\in {\mathbb{R}}^N$ be the vector of membrane potentials for all N neurons, and $\mathbf{S}\left(t\right)\in {\{0,1\}}^N$ the corresponding spike outputs. The system evolves under:

$$V(t+1)=\alpha V\left(t\right)+W·S\left(t\right),S(t+1)=H\left(V\right(t+1)-\theta ),$$

where $\mathbf{W}\in {\mathbb{R}}^{N\times N}$ is the synaptic weight matrix and H is applied elementwise. This discrete-time dynamical system is piecewise-linear but non-smooth due to the Heaviside function. Analyzing such systems demands techniques from hybrid dynamical systems and event-driven simulation [39]. As we scale these models to millions of neurons and synapses, challenges arise in terms of numerical stability, efficient event scheduling, and the minimization of redundant computation in periods of inactivity [40]. Modern SNN simulators and neuromorphic hardware platforms address these by leveraging sparse event-driven updates, parallelization, and compressed memory representations of synaptic connectivity [41]. In the next section, we examine how to train such networks, focusing on surrogate gradient methods, biologically plausible learning rules, and techniques for enabling efficient, large-scale supervised and unsupervised learning in spiking architectures [42].

3. Learning Algorithms for Large-Scale Spiking Neural Networks

Training spiking neural networks (SNNs) at scale remains one of the most active and challenging areas of research in neuromorphic computing [43]. The core difficulty lies in the non-differentiability of the spiking function, which renders traditional gradient-based learning methods, such as backpropagation, inapplicable in their standard form [44]. Unlike artificial neural networks (ANNs), where gradients flow through continuously differentiable activation functions like ReLU or tanh, the discrete and binary nature of spikes—often modeled as Heaviside step functions—necessitates novel learning algorithms capable of handling temporal, non-differentiable dynamics [45]. The principal direction for supervised learning in SNNs is the use of surrogate gradient methods [46]. These methods circumvent the non-differentiability of the spiking function by replacing it with a smooth approximation during the backward pass [47]. Formally, let the spike output $S\left(t\right)=H\left(V\right(t)-\theta )$, where H is the Heaviside function. During training, we replace the derivative ${\displaystyle \frac{dH}{dV}}$ with that of a surrogate function ${\tilde{\sigma }}^{\prime }\left(V\right)$, such as:

$${\tilde{\sigma }}^{\prime }\left(V\right)={\displaystyle \frac{\beta }{2}}{\sec \mathrm{h}}^2\left({\displaystyle \frac{\beta (V-\theta )}{2}}\right),$$

where $\beta$ is a sharpness parameter [48]. This enables the use of backpropagation through time (BPTT), albeit with increased memory and computational requirements due to the need to store entire spike histories over time. In parallel, significant effort has been directed toward biologically inspired, local learning rules such as spike-timing dependent plasticity (STDP) [49]. STDP adjusts synaptic weights based on the relative timing of presynaptic and postsynaptic spikes [50]. A typical update rule takes the form:

$$\Delta w_{ij}=\left\{\begin{array}{cc}{A}_{+}exp\left(-{\displaystyle \frac{\Delta t}{{\tau }_{+}}}\right),\hfill & \mathrm{if}\Delta t>0,\hfill \\ -A_{-}exp\left({\displaystyle \frac{\Delta t}{{\tau }_{-}}}\right),\hfill & \mathrm{if}\Delta t<0,\hfill \end{array}\right.$$

where $\Delta t=t_i-t_j$ is the time difference between postsynaptic and presynaptic spikes, and $A_{+},A_{-},{\tau }_{+},{\tau }_{-}$ are hyperparameters [51]. Although STDP aligns closely with experimental neuroscience observations, it is typically limited to unsupervised or reinforcement learning contexts and scales poorly in terms of global task optimization [52]. Recent approaches explore hybrid models combining SNNs with deep learning frameworks. One method involves pretraining a conventional ANN and then converting it to an SNN through careful normalization of weights and activations, often known as ANN-to-SNN conversion [53]. While such methods allow SNNs to inherit the performance of deep ANNs, they do not fully leverage the temporal and event-driven nature of spikes, and they often incur high latency or precision loss due to rate coding [54]. The table below categorizes and compares prominent learning algorithms in terms of scalability, biological plausibility, hardware efficiency, and task performance [55]. It is designed to fit the full text width and provide a concise reference point for researchers exploring scalable training strategies for SNNs [56].

As Table 1 highlights, no single learning paradigm currently achieves optimal trade-offs across all desirable dimensions [57]. Surrogate gradient descent provides the best performance on standard benchmarks but lacks biological plausibility and imposes high memory usage during training [58]. Conversely, STDP and reinforcement-based rules align closely with biological observations and are well-suited for neuromorphic hardware but struggle with complex, structured tasks due to the lack of global credit assignment [59]. Recent efforts have introduced scalable alternatives such as e-prop, which replaces global gradients with locally computed eligibility traces combined with global learning signals [60]. This method offers a more hardware-friendly and biologically grounded alternative to BPTT and is amenable to online learning. Similarly, local error learning and dendritic computation-inspired models aim to retain performance while reducing computational overhead [61]. In summary, the design of learning algorithms for large-scale SNNs remains a dynamic research area. Future directions must reconcile three major demands: biological plausibility, computational scalability, and compatibility with event-driven hardware. In the following section, we examine the infrastructure supporting large-scale SNN deployment, focusing on the capabilities and limitations of contemporary neuromorphic platforms and simulation frameworks [62].

4. Hardware and Software Infrastructures for Large-Scale SNNs

The successful deployment of large-scale spiking neural networks (SNNs) critically depends on the availability of specialized hardware and efficient software frameworks that can accommodate the unique computational characteristics of spiking dynamics. Unlike conventional artificial neural networks, which are predominantly implemented on GPUs and TPUs optimized for dense linear algebra, SNNs demand event-driven, sparse, and temporally precise processing paradigms [63]. This section provides a detailed overview of state-of-the-art neuromorphic hardware platforms and software ecosystems tailored for large-scale SNN simulation and training, highlighting their architectures, operational principles, and current limitations [64]. Neuromorphic hardware architectures draw inspiration from biological neural systems to achieve orders of magnitude improvements in energy efficiency and latency [65]. Leading examples include Intel’s Loihi, IBM’s TrueNorth, and the BrainScaleS system developed at Heidelberg University [66]. These platforms implement massively parallel arrays of spiking neurons and synapses with dedicated circuits for spike generation, synaptic integration, and plasticity mechanisms [67]. For instance, the Loihi chip integrates on-chip learning through programmable microcode and supports asynchronous spike communication via a mesh network. The fundamental computational unit in these systems is the neuron, implemented as a state machine that evolves membrane potential and emits spikes according to configurable dynamics [68]. Mathematically, the neuromorphic chip architecture can be abstracted as a graph $G=(V,E)$, where vertices V correspond to neurons and edges E represent synapses [69]. Communication over the network is event-driven, with spikes propagating as discrete packets that trigger state updates in downstream neurons [70]. Formally, the state update of neuron i at time t can be described as:

$$V_i(t+1)=f\left(V_i\left(t\right),\sum _{j\in \mathcal{N}\left(i\right)}{w}_{ij}{S}_j\left(t\right),{\eta }_i\left(t\right)\right),$$

where $\mathcal{N}\left(i\right)$ denotes the set of presynaptic neurons connected to i, $w_{ij}$ are synaptic weights, and ${\eta }_i\left(t\right)$ models noise or stochasticity [71]. The function f encapsulates the neuron’s intrinsic dynamics, including leak, integration, thresholding, and reset. From a software perspective, simulators such as NEST, Brian2, and BindsNET provide flexible environments for prototyping and testing SNN models. These frameworks support both CPU- and GPU-based simulations and offer interfaces for custom neuron and synapse models [72]. To achieve scalability, simulators often employ event-driven kernels that update only active neurons and synapses, thereby exploiting the sparsity inherent in spiking activity [73]. The simulation time complexity thus scales with the number of spikes rather than the total number of neurons, an essential property for large networks [74]. Table 2 summarizes key characteristics of prominent neuromorphic hardware platforms and simulation frameworks relevant for large-scale SNNs [75].

Despite these advances, several challenges impede the widespread adoption of large-scale SNNs [76]. Neuromorphic chips are often limited by fixed precision arithmetic, restricted programmability, and nontrivial integration with existing machine learning pipelines [77]. Moreover, large networks spanning multiple chips require scalable interconnects with low latency and high bandwidth to maintain temporal coherence of spike events. On the software side, simulating biologically detailed models at scale remains computationally intensive, demanding innovations in parallelization, memory management, and model compression [78]. In conclusion, hardware-software co-design is paramount to realize the full potential of large-scale SNNs [79]. Emerging research focuses on hybrid systems that combine the flexibility of software simulators with the efficiency of neuromorphic hardware, alongside the development of standardized benchmarks and APIs for interoperability [80]. These advances will be critical to deploying SNNs in real-world applications such as robotics, sensory processing, and autonomous agents, where low power and real-time operation are essential [81]. The next section will delve into benchmark datasets and evaluation metrics, providing insights into how large-scale SNNs are assessed in terms of accuracy, latency, and energy efficiency [82].

5. Benchmarking and Evaluation Metrics for Large-Scale SNNs

Evaluating the performance of large-scale spiking neural networks (SNNs) requires a comprehensive framework that captures multiple dimensions including accuracy, temporal efficiency, energy consumption, and biological plausibility. Unlike traditional artificial neural networks (ANNs) whose evaluation predominantly focuses on task accuracy or loss metrics, SNNs introduce additional considerations owing to their event-driven and temporally dynamic nature [83]. This section explores common benchmark datasets used in the field, discusses standard and emerging evaluation metrics, and highlights the challenges involved in meaningful comparisons across different SNN models and hardware platforms.

5.1. Benchmark Datasets

Several benchmark datasets have become standard for assessing the capabilities of SNNs across various application domains, including classification, sensory processing, and temporal pattern recognition.

Static Image Datasets

Traditional image datasets such as MNIST and CIFAR-10 have been adapted for SNNs by converting static images into spike trains through rate coding or temporal encoding schemes [84]. For example, the MNIST handwritten digit dataset [85] is frequently encoded via Poisson spike trains where the firing rate corresponds to pixel intensity:

$$r_i={\lambda }_{max}{\displaystyle \frac{I_i}{I_{max}}},$$

with $I_i$ the pixel intensity, $I_{max}$ the maximum pixel intensity, and ${\lambda }_{max}$ a maximum firing rate parameter [85]. Although simple, these conversions do not fully exploit the temporal capabilities of SNNs, motivating the use of more biologically plausible neuromorphic datasets [86].

Neuromorphic Datasets

Neuromorphic event-based datasets recorded using dynamic vision sensors (DVS) have become prominent benchmarks, capturing asynchronous spikes directly from sensors [87]. Notable examples include N-MNIST [89], CIFAR10-DVS [90], and DVS Gesture [91]. These datasets provide spatiotemporal spike streams that test the SNN’s ability to process and learn from real-world event-driven data. Formally, the input data $\left\{(x_k,y_k,t_k)\right\}$ consists of spatial coordinates $(x_k,y_k)$ and timestamps $t_k$ of spikes, requiring SNNs to efficiently process sparse, high-temporal-resolution information [88].

Temporal Sequence Datasets

Tasks such as speech recognition or motor control utilize datasets like TIDIGITS and the spike-based Heidelberg dataset, emphasizing the network’s temporal integration and memory capabilities [89]. Evaluating performance on these datasets necessitates models that maintain internal states over extended durations and adapt to non-stationary input distributions [90].

5.2. Evaluation Metrics

Evaluation of large-scale SNNs extends beyond accuracy or classification error to include metrics capturing temporal dynamics, energy efficiency, and hardware compatibility [91].

Accuracy and Latency

Task accuracy remains a primary measure, computed as the fraction of correctly classified samples. However, latency—the time taken to produce a correct output—is crucial in real-time applications [92]. The latency L can be formally defined as:

$$L=\underset{t}{min}\{t\mid \widehat{y}\left(t\right)=y\},$$

where $\widehat{y}\left(t\right)$ is the network’s prediction at time t and y the true label [93]. Minimizing latency while maintaining accuracy reflects efficient temporal coding and fast spike propagation [94].

Energy Consumption

One of the most compelling advantages of SNNs is their potential for low energy consumption. Energy per inference, E, can be approximated as:

$$E=N_{\mathrm{spikes}}\times E_{\mathrm{spike}},$$

where $N_{\mathrm{spikes}}$ is the total number of spikes generated during inference and $E_{\mathrm{spike}}$ is the energy cost per spike, dependent on hardware implementation [95]. Measuring energy on real neuromorphic hardware, such as Loihi or TrueNorth, is essential for validating theoretical energy savings.

Sparsity and Spike Rate

The average firing rate per neuron is a proxy for network sparsity:

$$r_{\mathrm{avg}}={\displaystyle \frac{1}{NT}}\sum _{i=1}^N\sum _{t=1}^T{S}_i\left[t\right],$$

where N is the number of neurons and T the evaluation duration [96]. Sparse spiking activity is desirable to reduce energy and communication overhead, but excessive sparsity can impair representational capacity [97].

Biological Plausibility and Interpretability

Although harder to quantify, metrics assessing the degree to which network dynamics resemble biological neurons—such as spike timing precision, refractory period adherence, and synaptic plasticity rules—are increasingly considered. These factors influence the interpretability and potential translational relevance of SNN models [98].

5.3. Challenges and Future Directions

Benchmarking large-scale SNNs involves intrinsic difficulties [99]. Datasets vary widely in spike density, temporal resolution, and noise characteristics, complicating direct comparisons [100]. Moreover, many benchmarks rely on rate-coded inputs, which partially negate the advantages of temporal coding inherent in SNNs. Hardware variability further complicates performance and energy comparisons, as simulation-based evaluations often do not capture the nuances of real hardware behavior. To address these issues, the community is moving toward standardized benchmarking suites such as the Neuromorphic Benchmark Suite (NBS) and open challenges that integrate task complexity, energy budgets, and latency constraints [101]. Advances in synthetic dataset generation and task design aim to stress-test temporal dynamics and learning capabilities at scale [102]. In conclusion, developing rigorous, multi-dimensional benchmarks and metrics is crucial for driving progress in large-scale SNN research and facilitating fair, reproducible comparisons across algorithms, architectures, and platforms [103]. The following section will survey emerging applications of large-scale SNNs, highlighting their potential impact across diverse domains [104].

6. Applications and Future Directions of Large-Scale Spiking Neural Networks

The unique computational paradigm of spiking neural networks (SNNs) — characterized by sparse, event-driven processing and temporal dynamics — positions them as promising candidates for a wide range of applications that demand low latency, high energy efficiency, and biological plausibility [105]. As the scale of SNNs continues to grow, propelled by advances in learning algorithms and neuromorphic hardware, their deployment in real-world scenarios becomes increasingly feasible. This section surveys key application domains where large-scale SNNs have demonstrated or hold significant potential for impact, and outlines emerging research directions that are expected to shape the future landscape of the field [106].

6.1. Robotics and Autonomous Systems

One of the most natural application areas for large-scale SNNs is robotics, where systems must process continuous streams of sensor data in real-time while operating under stringent power and latency constraints [107]. Neuromorphic processors integrated with spiking networks enable robots to perform tasks such as visual perception, motor control, and navigation with reduced energy footprints compared to traditional deep learning pipelines [108]. In robotic control, SNNs excel at encoding temporal sequences and sensorimotor contingencies. For example, spiking models have been employed for dynamic obstacle avoidance, leveraging their ability to react to asynchronous event-based vision inputs [109]. Mathematically, sensorimotor mappings in these systems can be modeled as:

$$u\left(t\right)=\mathcal{F}\left({\left\{S_i(t-\tau )\right\}}_{i=1}^N,\tau \in [0,T]\right),$$

where $\mathbf{u}\left(t\right)$ denotes motor commands at time t, generated as a function $\mathcal{F}$ of recent spike trains from N sensory neurons over a temporal window T [110]. The sparse and event-driven nature of spikes enables low-latency feedback loops essential for agile robotic behavior.

6.2. Sensory Processing and Brain-Machine Interfaces

Large-scale SNNs are particularly well-suited to sensory processing tasks that naturally involve spatiotemporal patterns, such as auditory processing, tactile sensing, and vision [111]. Event-driven sensors, like Dynamic Vision Sensors (DVS) and silicon cochleae, produce asynchronous spikes that align seamlessly with SNN input representations [112]. In brain-machine interfaces (BMIs), SNNs offer the prospect of directly decoding neural activity in the form of spike trains to control prosthetic devices or restore sensory functions [113]. By mimicking biological neuronal dynamics, large-scale SNNs facilitate closed-loop systems that can adapt online to neural plasticity [114]. For example, the decoding function $D\left(\mathbf{S}\right)$ can be formalized as:

$$D\left(S\right)=arg\underset{y}{max}P(y\mid S),$$

where $\mathbf{S}$ denotes observed spike patterns from cortical neurons, and $\mathbf{y}$ the decoded motor or sensory output.

6.3. Neuromorphic Computing and Edge AI

The push towards edge computing and Internet of Things (IoT) devices has renewed interest in ultra-low power, always-on intelligent systems. Large-scale SNNs, implemented on neuromorphic hardware, are ideal candidates for edge AI applications, such as anomaly detection in sensor networks, real-time environmental monitoring, and wearable health diagnostics [115]. The event-driven computation model significantly reduces power consumption by activating processing only when spikes occur, a property quantified by the network’s duty cycle d:

$$d={\displaystyle \frac{\mathrm{active}\mathrm{time}}{\mathrm{total}\mathrm{time}}}\ll 1,$$

which directly translates to energy savings compared to continuously active ANN-based processors.

6.4. Future Research Directions

Despite promising advances, several open challenges must be addressed to fully harness the potential of large-scale SNNs:

• Scalable and Efficient Learning: Developing biologically plausible, online learning algorithms that scale to millions of neurons while supporting complex cognitive tasks remains an open problem. Novel hybrid approaches combining local plasticity with global error signals are a promising avenue [116].
• Standardization and Benchmarking: The establishment of comprehensive benchmarks, standardized APIs, and interoperable toolchains will accelerate reproducibility and facilitate comparison across methods and platforms [117].
• Integration with Conventional AI: Hybrid architectures that integrate SNNs with classical deep learning networks could leverage the strengths of both paradigms, enabling robust and energy-efficient systems [118,119].
• Advanced Neuromorphic Hardware: Progress in analog and mixed-signal neuromorphic chips with enhanced plasticity mechanisms and scalable interconnects is vital for deploying large-scale SNNs in practical applications [120].
• Theoretical Foundations: A deeper theoretical understanding of information encoding, computational capacity, and generalization in SNNs will inform better architecture and algorithm design [121].

In summary, large-scale spiking neural networks represent a frontier in both computational neuroscience and machine learning. Their event-driven, temporally rich dynamics offer unique advantages for next-generation intelligent systems. Continued interdisciplinary research combining algorithmic innovation, hardware development, and application-driven exploration promises to unlock their full potential in the coming years.

7. Conclusion

In this survey, we have examined the multifaceted landscape of large-scale spiking neural networks (SNNs), focusing on their foundational principles, learning algorithms, hardware-software infrastructures, benchmarking methodologies, and emerging applications. SNNs represent a paradigm shift from traditional artificial neural networks by leveraging discrete spike events to encode and process information temporally and sparsely, mirroring key aspects of biological neural systems.

We began by outlining the core challenges in scaling SNNs, notably the non-differentiability of spike functions and the need for efficient, biologically plausible learning algorithms. Surrogate gradient methods and local plasticity rules such as spike-timing dependent plasticity (STDP) provide complementary approaches, each with distinct trade-offs in scalability, performance, and hardware compatibility. The interplay between these methods remains a rich area of ongoing research.

Next, we reviewed the specialized neuromorphic hardware platforms and simulation frameworks that enable large-scale SNN implementation. Architectures like Intel’s Loihi and IBM’s TrueNorth illustrate the potential for ultra-low power, massively parallel spike processing, while software tools such as NEST and Brian2 facilitate flexible prototyping and algorithm development. However, hardware limitations, communication bottlenecks, and programmability constraints continue to challenge seamless large-scale integration.

Benchmarking efforts were discussed, emphasizing the need for multidimensional evaluation metrics that go beyond accuracy to include latency, energy consumption, and biological fidelity. The advent of event-based datasets and neuromorphic benchmarks highlights the community’s push towards more realistic and task-relevant assessments.

Finally, we surveyed the expanding range of applications where large-scale SNNs hold promise, including robotics, sensory processing, brain-machine interfaces, and edge AI. The event-driven nature of SNNs aligns naturally with real-time, power-constrained environments, offering distinct advantages over conventional deep learning approaches.

Looking forward, the convergence of scalable learning algorithms, advanced neuromorphic hardware, and rigorous evaluation frameworks will be essential to unlock the full potential of large-scale SNNs. Interdisciplinary collaboration bridging neuroscience, computer science, and engineering will drive innovations that bring us closer to realizing energy-efficient, adaptive, and intelligent systems inspired by the brain.

In conclusion, while significant hurdles remain, large-scale spiking neural networks stand poised to revolutionize how we design and deploy next-generation cognitive computing platforms, marking an exciting frontier at the intersection of artificial intelligence and neuroscience.