1. Introduction
The underactuated systems are characterized by having more Degrees of Freedom (DoF) than control inputs. There are several reasons why a system could become underactuated,
e.g. failure in one or more of the actuators. Still, some systems are naturally underactuated, namely, Ball-Beam, Traslational Oscillator with a Rotarinal Actuator (TORA), Acrobot, Two-Wheeled Self-Balancing robot, etc., and one of these systems is the BallBot Robotic System (BRS), or in a shorter form
ballbot. The BRS is an inverted pendulum type robot that balances itself on top of a ball, this ball acts as a spherical wheel and allows the BRS to move omnidirectionally. According to [
11], since the BRS must actively balance, it is said to have dynamic equilibrium which allows a greater maneuverability than robots with passive equilibrium. The main control objective is to maintain the body of the BRS in the upright position,
i.e. aligned with the vertical, but in some cases, trajectory tracking is sought.
In [
16], a BRS with two wheels placed orthogonally was used. To maintain the body balanced a Linear Quadratic Regulator (LQR) is implemented (this prototype of BRS was also used in [
10] and [
11]). A different type of prototype of BRS with three wheels placed at
between each other is developed in [
17]. In this case, a state feedback controller was implemented to maintain the BRS balanced. To take advantage of the maneuverability of the BRS, a BRS large enough to transport a person was developed in [
18] (this latter also known as
ballsegway). A PD controller was used to achieve the control objective.
Developing a BRS, as those discussed above, can require a lot of time and resources, an alternative is to design and build the BRS using a simpler platform like LEGO
® MINDSTORMS
®. The first prototype of a BRS using LEGO
® MINDSTORMS
® NXT, known as the NXT BRS (NXTBRS), is shown in [
12], but this is not the only BRS developed using this kit, different NXTBRS are shown in [
1,
19]. The newer version of the LEGO
® MINDSTORMS
® kit is the LEGO
® MINDSTORMS
® EV3, which is also used in the development of BRS, known as the EV3 BRS (EV3BRS). In [
5,
8], an EV3BRS was developed based on the NXTBRS proposed in [
1], in [
20] an EV3BRS was developed but also based on the BRS proposed in [
17]. Several controllers have been implemented on the NXTBRS and the EV3BRS. In [
1,
12,
19], linear controllers were implemented while a fuzzy adaptive controller for the EV3BRS was designed in [
8]. In [
5], a Takagi-Sugeno Fuzzy Model (TSFM) for the EV3BRS was designed based on the model proposed in [
1], from which a Takagi-Sugeno Fuzzy Controller (TSFC) was implemented on the same EV3BRS.
With the improvement of Computer-Aided Design (CAD), then it is possible to construct a three-dimensional (3-D) model of the BRS that more accurately approximates the real system since this software can consider real material properties as well as its complex dynamics. One of these tools is Simscape
™ Multibody
™ , previously known as
SimMechanics®, which specializes in modeling and simulation of 3-D mechanical systems like suspensions, robotic manipulators, construction machinery, etc., but with the interaction of Simscape
™ Multibody
™ with the rest of the components of Simscape
™ actuators for the systems can be model, like motors from a robotic system or the hydraulic piston from an excavator. In the case of the BRS, a simple model similar to the prototype presented in [
17] was developed in [
21], while a more detailed model is presented in [
22]. For the prototypes similar to the one in [
1], no model in Simscape
™ has been reported in the literature, the same can be said for the EV3BRS and NXTBRS.
The contributions from this work are threefold: (1) Design of a 3-D model of the EV3BRS in the Simscape™ environment, (2) Implementation of a TSFC on the EV3BRS Simscape™ model and, (3) Implementation on the EV3BRS Simscape™ model of a TSFC with attenuation.
The manuscript is organized as follows:
Section 2 shows the detailed process of the design of the EV3BRS Simscape
™ model. The mathematical model of the EV3BRS as well as the design of the TSFCs are shown in
Section 3. Simulation results from the performance of the TSFCs on the EV3BRS Simscape
™ model are included in
Section 4. In
Section 5 the discussion is presented, and, finally, in
Section 6 the conclusion is drawn.
2. Modeling of the EV3BRS in the Simscape™ Environment
Since the EV3BRS is composed of multiple solids, an assembly using SOLIDWORKS® is first done and then exported to the Simscape™ environment through the Simscape™ Multibody™ Link plugin. The EV3BRS comprises a body mounted on top of a rigid ball, with the control torques between the body and the ball applied through the wheels.
2.1. SOLIDWORKS® Assembly of the EV3BRS
Because LEGO
® MINDSTORMS
® is a widely known brand, many pieces are already designed and available in repositories, so, the majority of LEGO
® pieces used in the assembly are obtained from the projects [
2,
3,
4]. The only pieces designed in SOLIDWORKS
® by the authors are those shown in
Figure 1.
The assembly of the EV3BRS is based on the NXTBRS, proposed by [
1], which is very similar to that used in [
5]. One of the properties of the Simscape
™ Multibody
™ Link plugin is that the mating relationships defined in SOLIDWORKS
® are exported as joints to Simscape
™ , but mates defined in subassemblies will be interpreted as rigid transforms, that is to say, rigidly attached. Since the body is considered rigid, only the mates of the wheels are defined in the assembly.
Figure 2 shows the subassemblies for the body and the wheels.
The finished assembly of the EV3BRS is shown in
Figure 3.
2.2. Simscape™ Model of the EV3BRS
As stated previously, the assembly of the EV3BRS is exported to Simscape
™ through the Simscape
™ Multibody
™ Link plugin giving as a result the diagram in
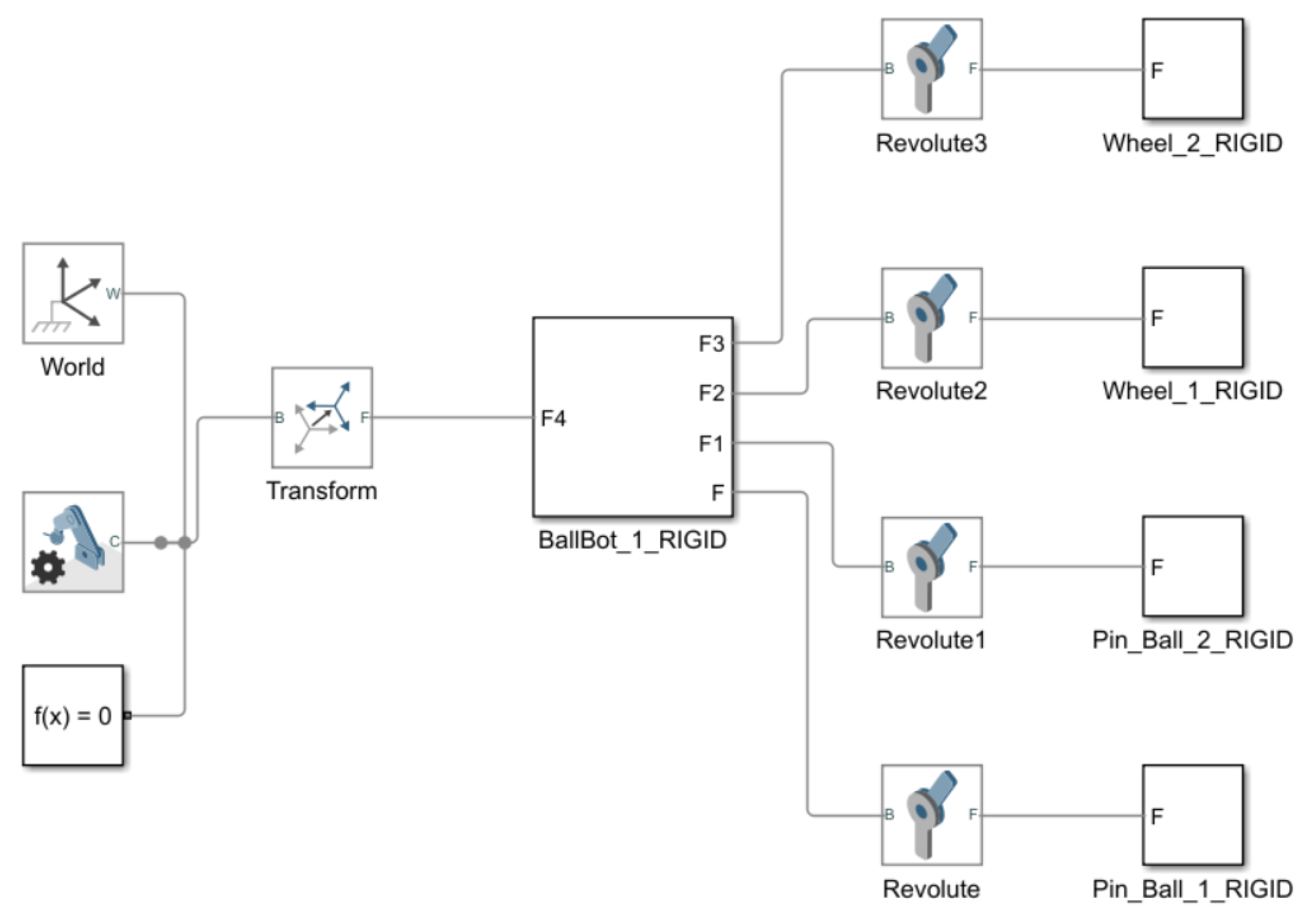
Figure 4. It can be seen that the body of the EV3BRS is rigidly connected to the
World Frame and therefore the only thing allowed to move are the wheels. To model the entire system, the ball, the floor, and the DoF from the ball and body are need to be added.
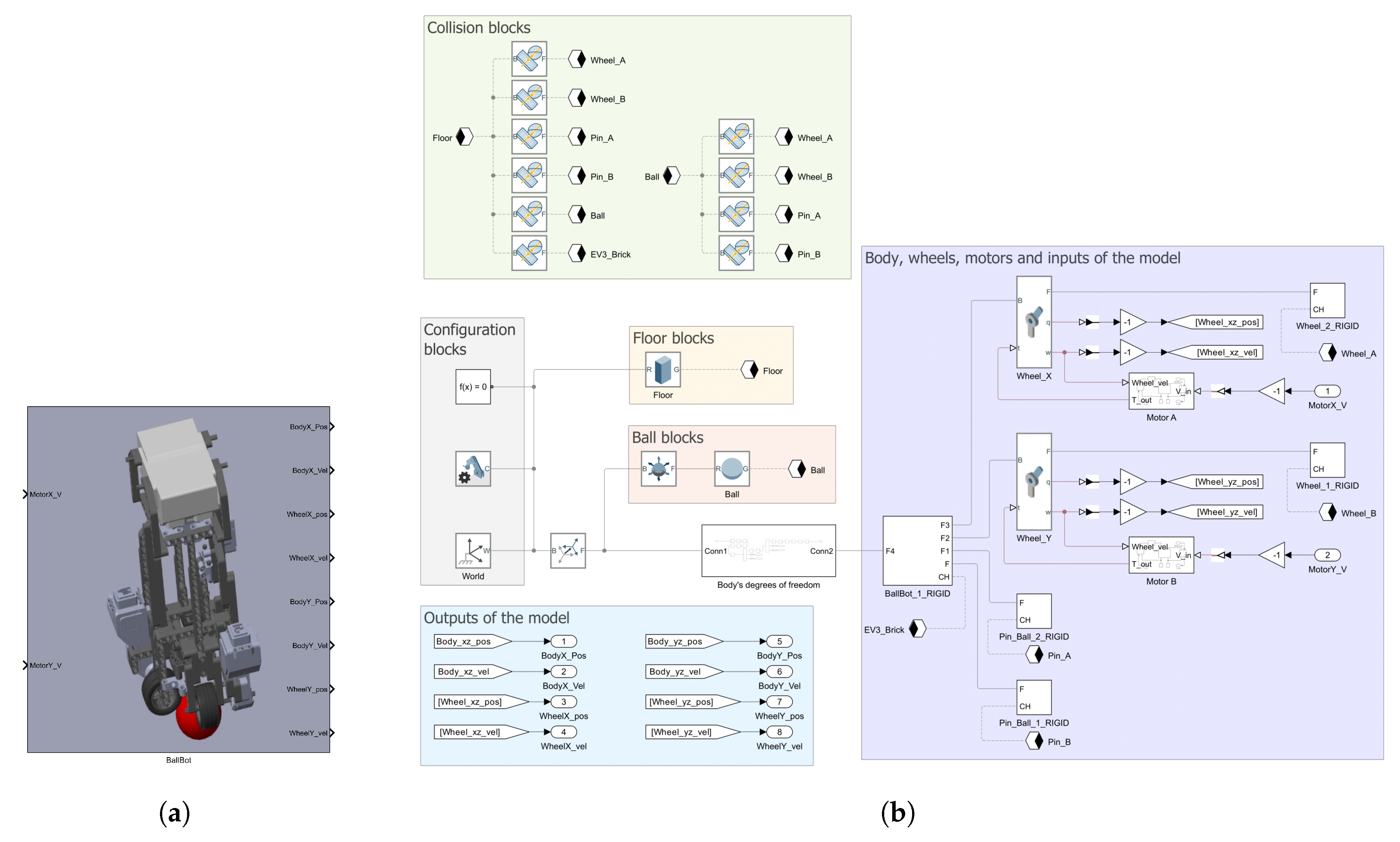
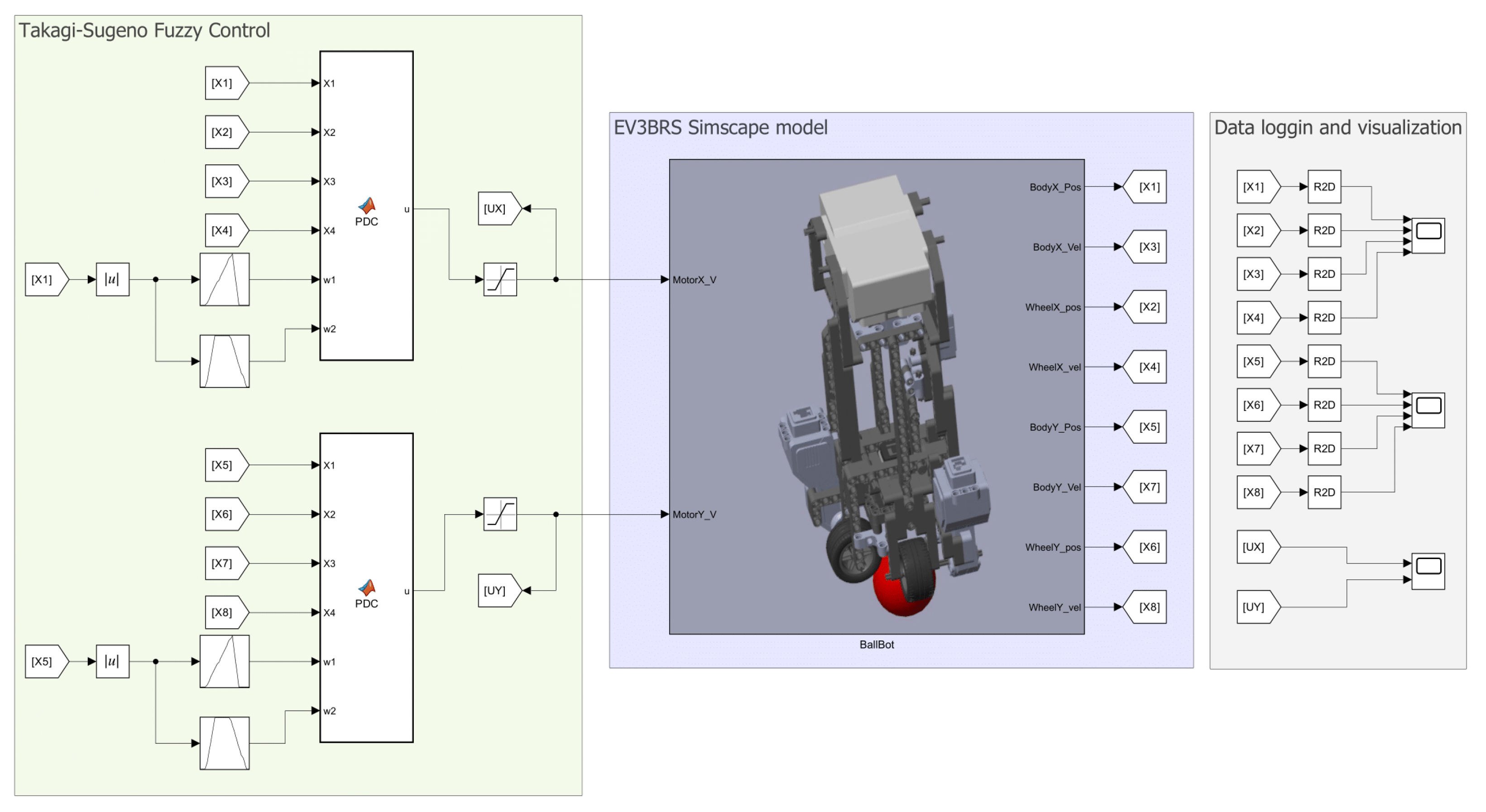
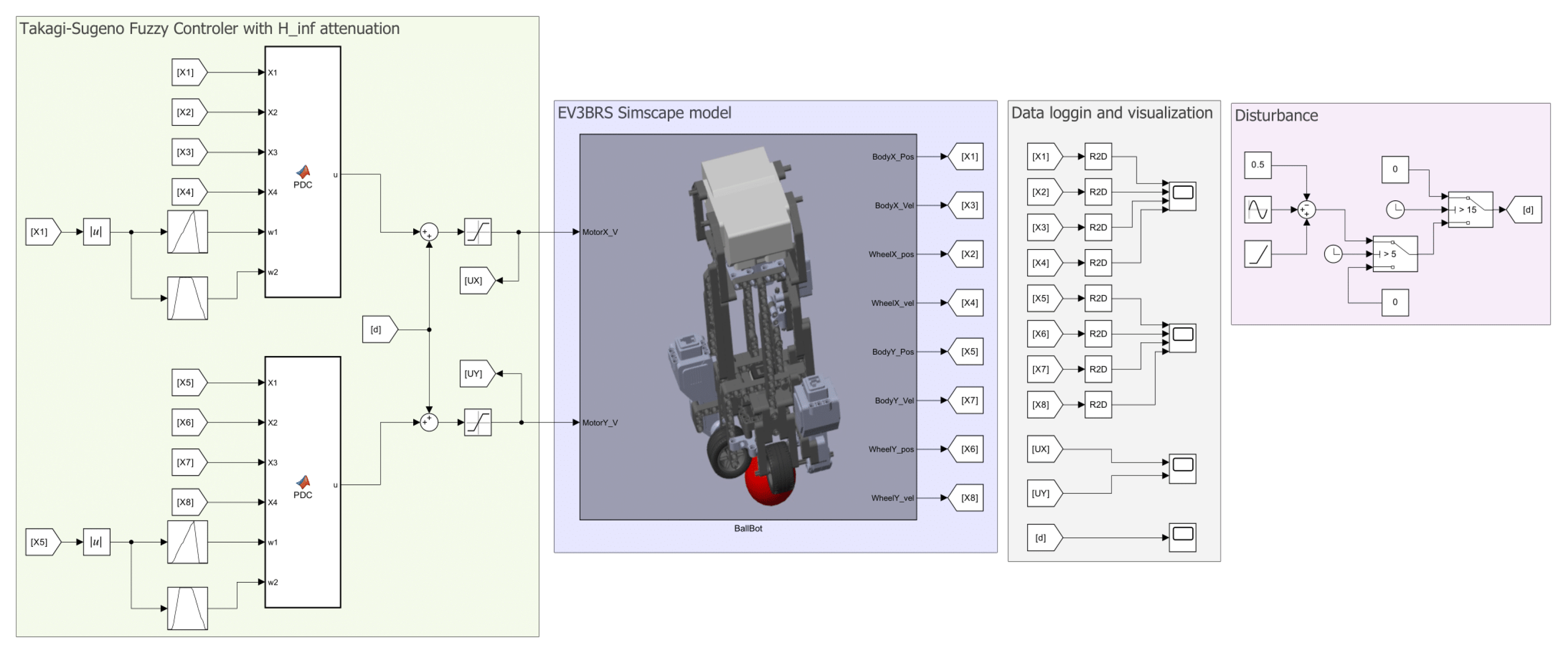
In
Figure 5, the whole model of the EV3BRS in Simscape
™ is shown. It can be seen that the model is divided in different areas which are described next.
2.2.1. Configuration Blocks
These blocks serve as the source for parametric configuration as starting point for the simulation. The Solver Configuration block defines the required parameters for the solver. The Mechanism Configuration block acts as the source of uniform gravity for the simulation. In our model, the gravity is defined pointing downwards along the vertical z-axis as . Finally, the World Frame serves as the main reference frame for the model and it is used to define all the remaining frames in the model.
2.2.2. Floor Blocks
The EV3BRS needs a surface on top of which it can move, in other words, it needs a floor. The floor is directly attached to the World Frame and consists of a Brick Solid with dimensions . The geometry of this block is exported to be used with the Collision blocks.
2.2.3. Ball Blocks
The ball is defined using the Spherical Solid block with a radius of and, like the floor, its geometry is exported to the Collision blocks. The DoF of the ball are given through the 6-DOF Joint. It can be noticed that before the 6-DOF Joint, a Rigid Transform block is used. This latter block is used to elevate the ball from the World Frame, in order to prevent that the ball stars “inside” the floor, that is to say, submerged inside the floor.
2.2.4. Outputs of the Model
These blocks are simply the states of the system measured from the joints of the model. The units for the outputs are given in , for position, and , for the velocity.
2.2.5. Body, Wheels, Motors and Inputs to the Model
The body and wheels are the same blocks and subsystems obtained from the Simscape™ Multibody™ Link plugin, but the geometry of the wheels, pins, and EV3 brick are exported to the Collision blocks. The position and velocity of the wheels are measured directly from the joints provided by the plugin.
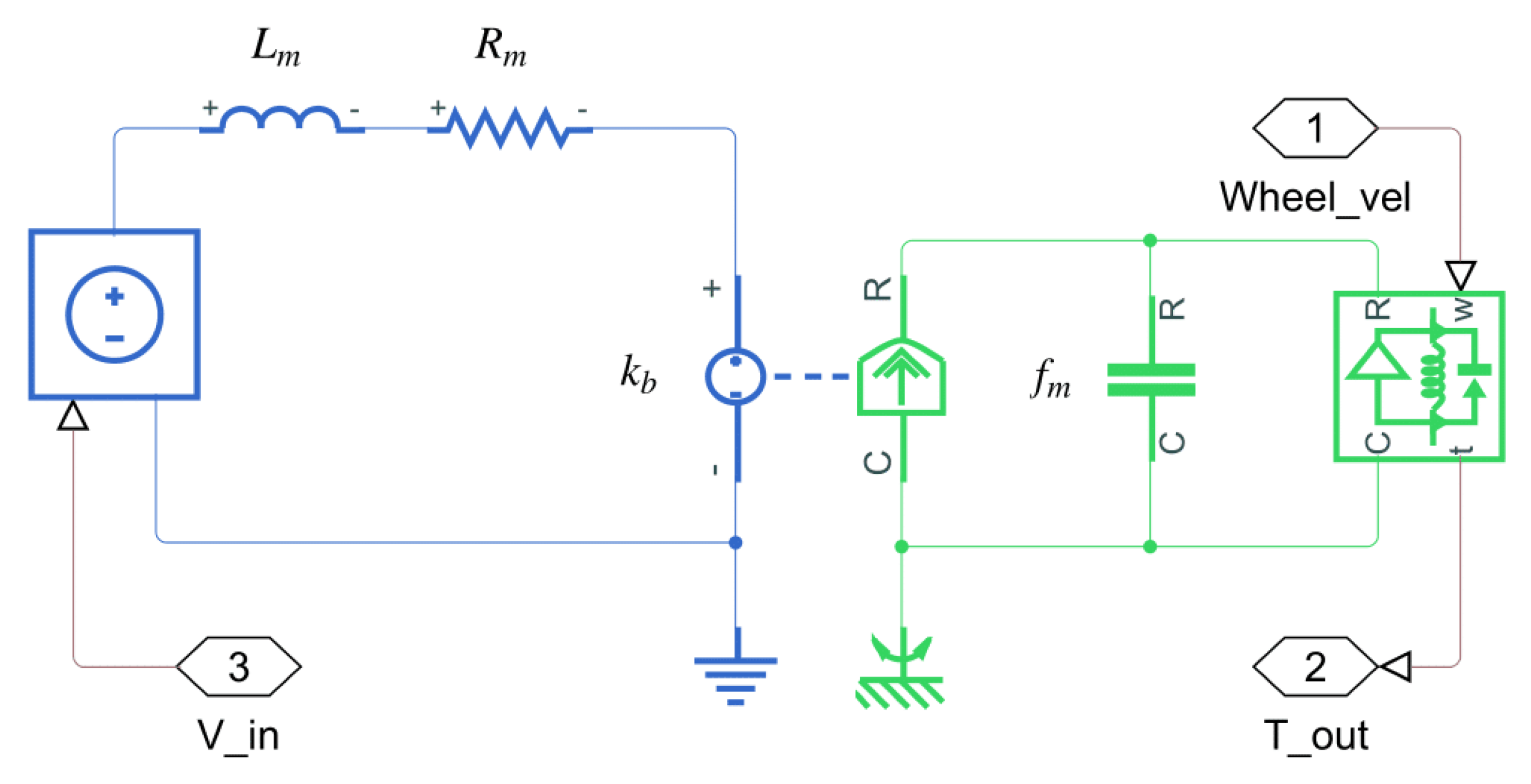
The motors are also modeled in Simscape
™. In
Figure 6 the model of the motors is shown and its parameters are given in
Table 1. These values are obtained from [
6] and [
7]. It must be noticed that only the viscous friction is considered; the remaining parameters for the
Rotational Friction are set to zero.
The inputs of the model are the motor input voltages. These are expected to be Simulink® input signals, so they must be converted into physical signals, namely Simscape™ signals, before they can interact with the model of the motors. This last task is done through the Simulink-PS Converter block.
2.2.6. Collision Blocks
To model the collision, the Spatial Contact Force block is used. This block allows to model the collision force between two bodies as well as the friction between them. The blocks used for the collisions with the floor are left with the default parameters. Instead, about the collisions with the ball only the coefficients of friction are changed; specifically, the Coefficient of Static Friction is set to while the Coefficient of Dynamic Friction is set to . It must be noticed that these coefficients were obtained heuristically.
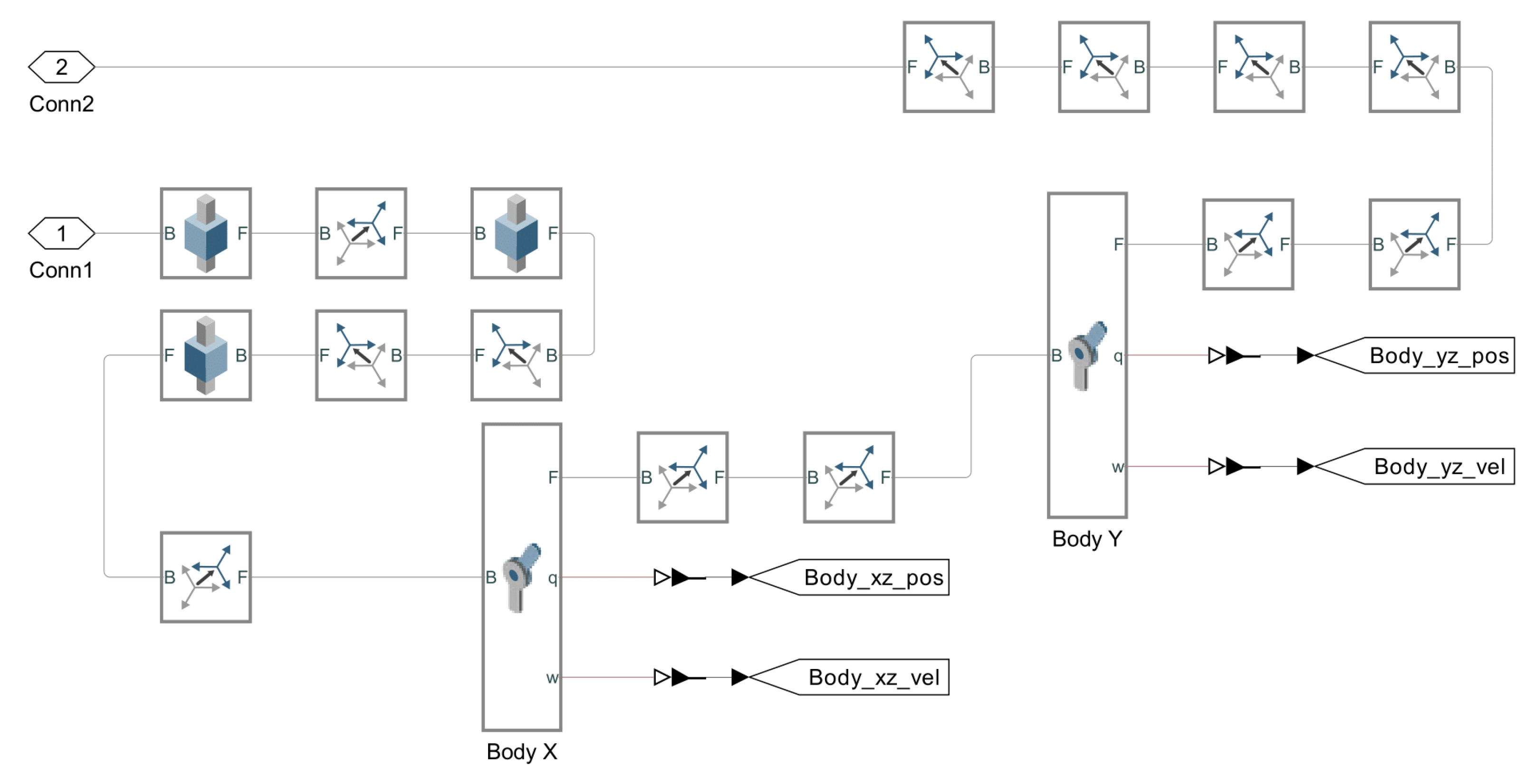
2.2.7. Body’s DoF
This subsystem contains all the blocks that define the DoF for the body and these are shown in
Figure 7. Unlike the ball, the body gets its DoF from several blocks; this is done in order to have straight access to the body’s angular position and velocity. The measurements of these states are given in physical signals, and similarly to the inputs of the model these must be converted to Simulink
® output signals, which can be accomplished through the
PS-Simulink Converter block.
3. Mathematical Model and Control Design
3.1. Mathematical Model
The mathematical model of the EV3BRS discribed below was proposed by [
1] and it was also used in [
5,
8,
9]. This model considers the assumptions proposed in [
16]:
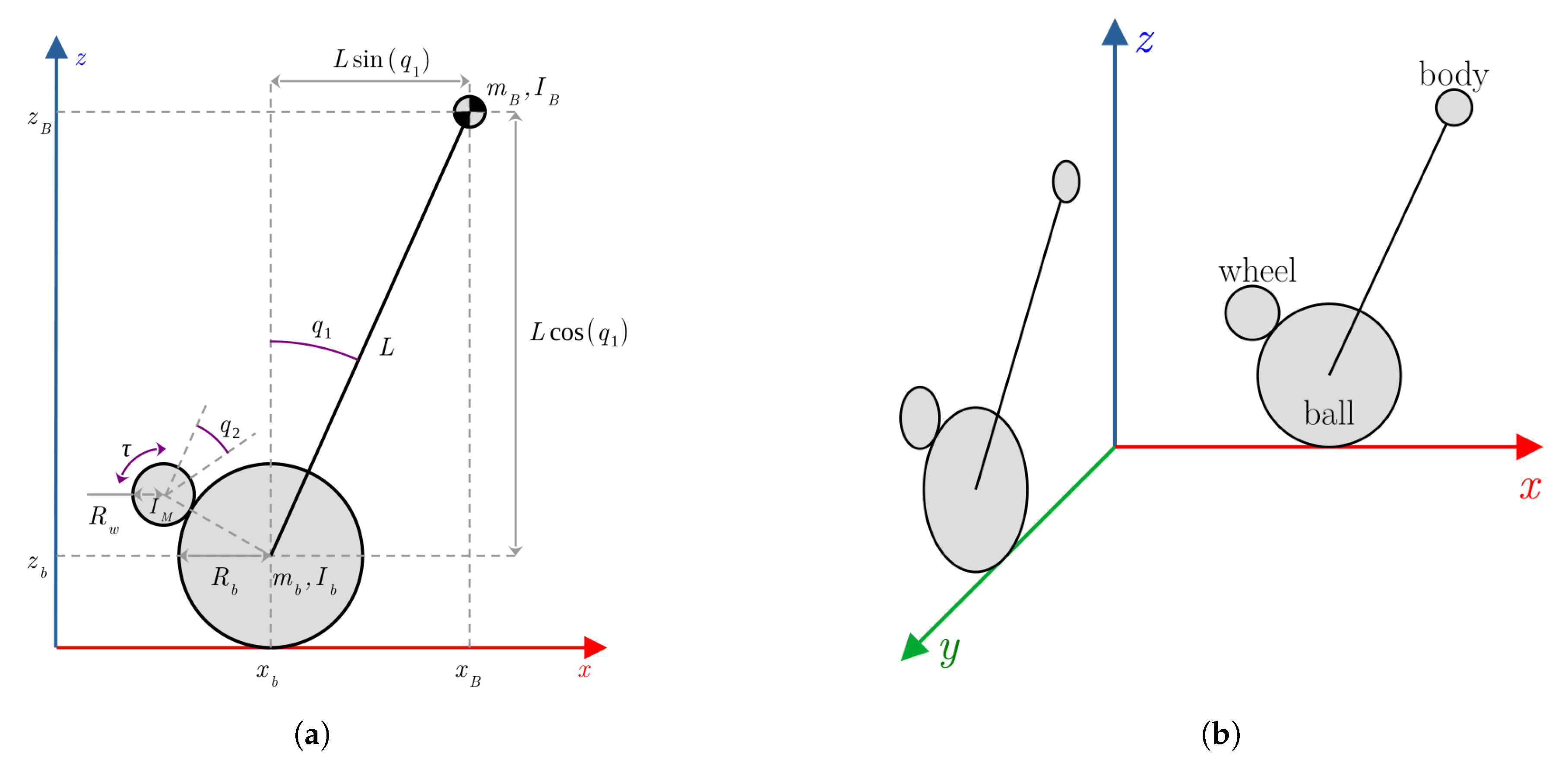
The EV3BRS is composed of two parts: a rigid body on top of a rigid ball.
The movement of the roll and pitch planes are uncoupled and the equations of motion between the two planes are identical (See
Figure 8b).
The control torques are applied between the body and the ball using the wheels.
Only viscous friction is considered.
There is no slip between the ball and the wheels.
3.1.1. Dynamic Model
The simplified model for the
plane is shown in
Figure 8a. As stated in [
11], it is convenient to choose the generalized coordinates in such way that these be directly related with measurable signals, so, in this case the angular displacement of the body (
) and wheels (
) are chosen.
The mathematical model is derived using the Euler-Lagrange method and can be expressed as follows:
where
,
is the control input vector, and
is the input torque control.
is the inertia matrix,
is the centripetal and Coriolis forces matrix,
is the gravity vector, and
is the friction vector. The elements of the matrices and vectors previously stated are the following:
where
The notation and values from these last parameters are given in
Table 2. The mass of both body and ball as well as the radius of the ball and wheels were measured experimentally. The distance to the center of mass is taken from [
1]. The moments of inertia of the body and ball are extracted from [
1] and [
12].
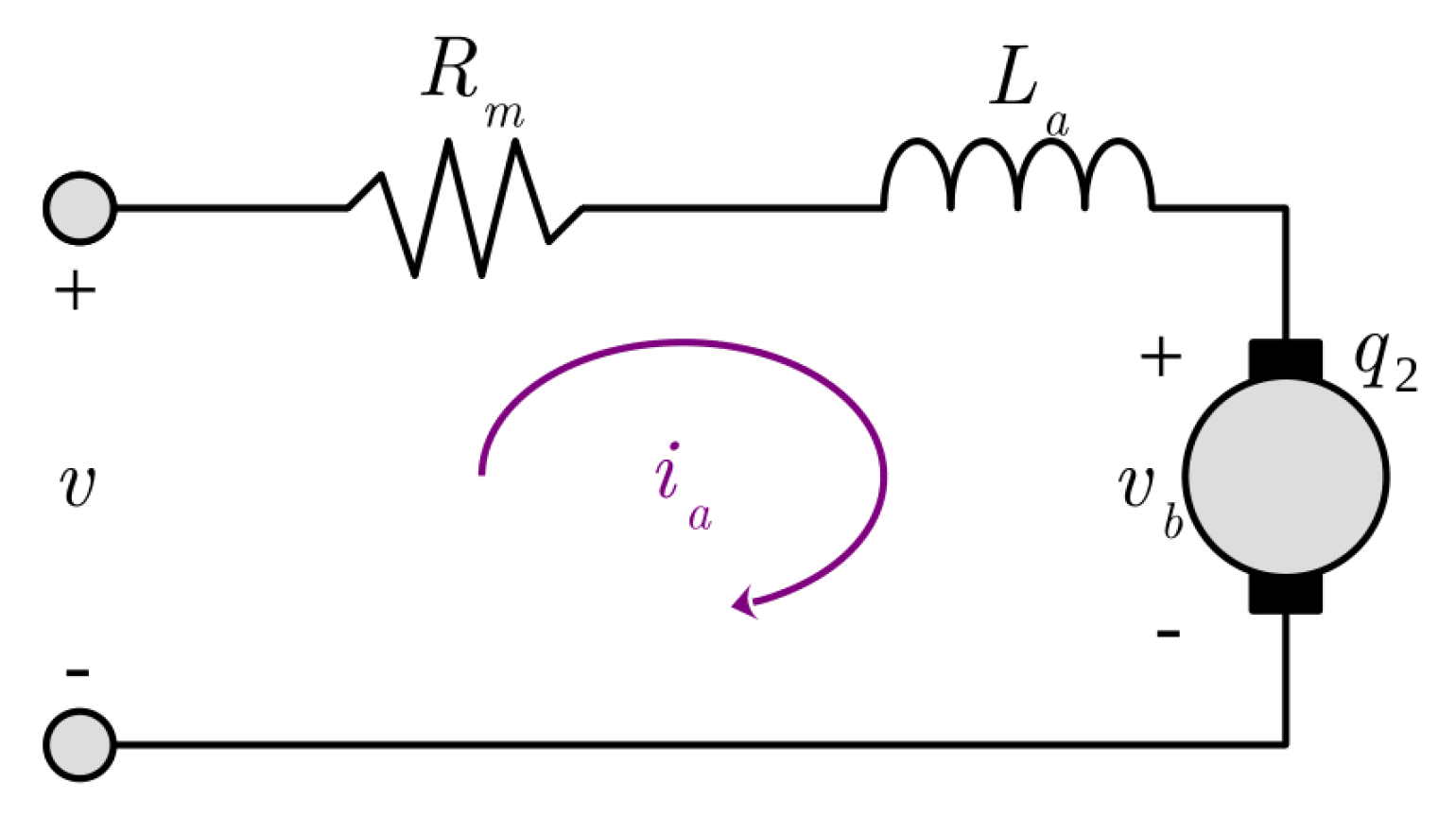
3.1.2. Dynamic of the Motor
The model proposed by [
1] takes into account a simplified model for the motors (see
Figure 9), the inductance and friction are considered negligible (
i.e. and
), so the control input vector is given by
where
v is the input voltage for the motor.
3.1.3. State Space Representation
Defining the state vector
, the control input
, and using (
2), the model (
1) can be rewritten as:
where
3.2. Takagi-Sugeno Fuzzy Model (TSFM)
A TSFM describes a system as a set of fuzzy
if-then rules [
13,
14]. Using the local approximation in fuzzy partitions spaces approach, each rule is linked to a local linear system obtained from the linearization around selected interest points. Then, the overall TSFM is derived by fuzzy blending of the local linear systems. The
i-th rule of a TSFM takes the form:
where
are fuzzy sets,
is the state vector,
is the output vector,
is the input vector,
is the state matrix,
is the input matrix,
is the output matrix,
are known premise variables and
r is the number of rules. Defining
, the final outputs of the TSFM, given a pair of
, are inferred as follows:
where
, with
as the grade of membership of
in
, and
the normalized weight of the
i-th rule.
3.2.1. Linearization of the EV3BRS’s Model
In order to derive the TSFM of the EV3BRS, the nonlinear model (
3) is linearized around
and
. Using small-angle linearization for
(
and
) the linear model takes the form
where
Given the parametric values from
Table 1 and
Table 2, the model (
6) takes the form
Now, for
the following is considered:
Thus, the local linear model takes the form
where
Again, using the parametric values from
Table 1 and
Table 2, equation (
8) takes the form
3.2.2. EV3BRS’s TSFM
Since the model (
3) is only linearized around two points, the TSFM is only comprised of two rules. Defining
, the rules of the TSFM are the following
These rules can be expressed in the form of (
5) using the membership functions shown in
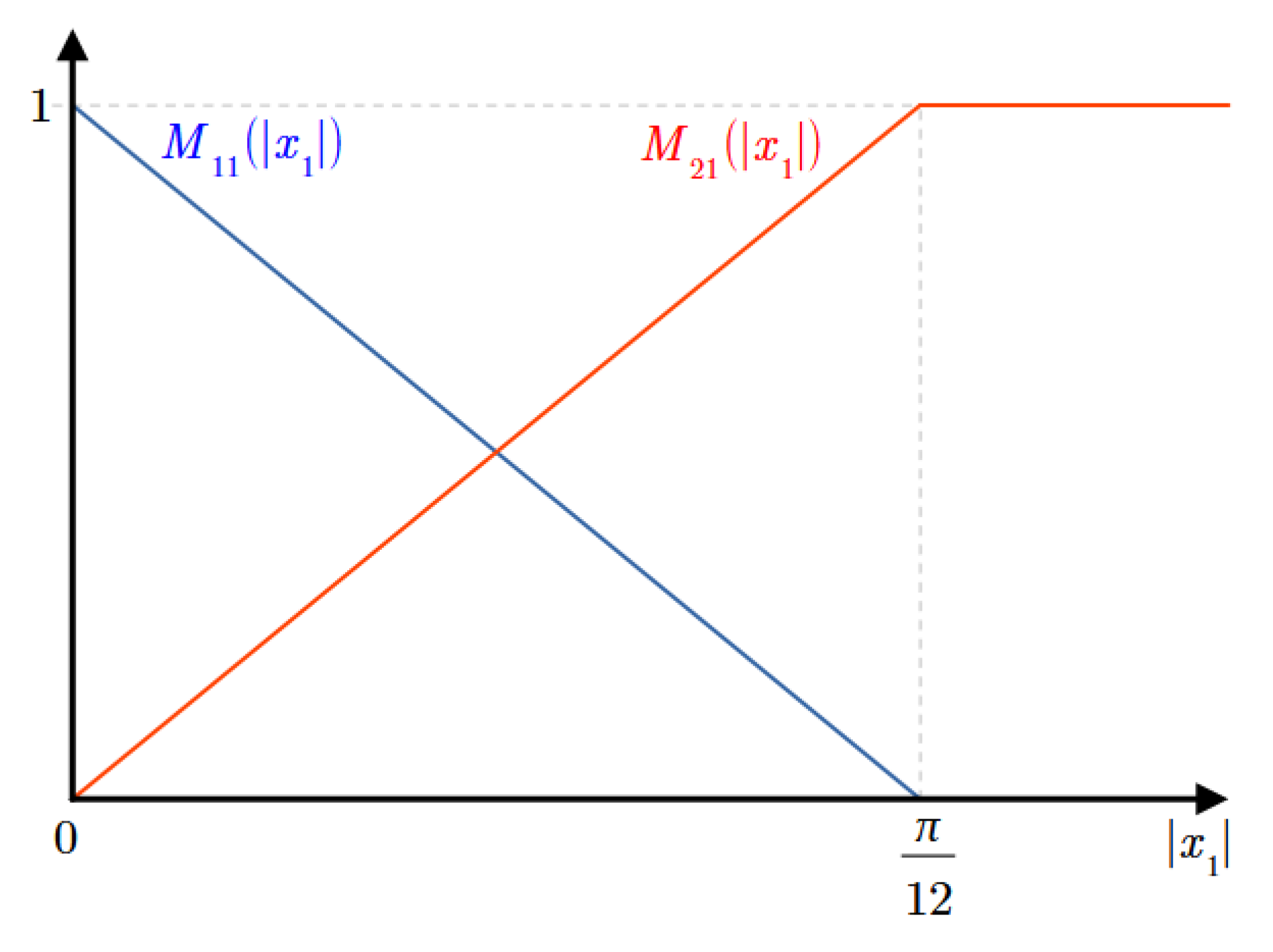
Figure 10. So, the TSFM of the EV3BRS takes the form
3.3. Takagi-Sugeno Fuzzy Control (TSFC)
To design a TSFC, the
Parallel Distributed Compensation (PDC) technique is used [
14]. A feedback control law
, where
is the
i-th feedback gains vector, to stabilize each local linear system of the TSFM can be applied. Thus, the PDC comprises of the same amount of rules as the TSFM and also shares its fuzzy sets. Then, the PDC can be described as a set of rules given in the following form
Using the same membership functions as in the TSFM, the overall PDC can be described in the form
3.3.1. Stable TSFC
To determine the feedback gains vector that ensures global stability, the following theorem must be satisfied.
Theorem 1 ([
15]).
The TSFM (5) with the PDC control law (14) is globally asymptotically stable if there exist matrices , and , such that
satisfies the following conditions
for and . If this conditions are satisfied, the PDC gains are .
Applying the Theorem 1 to the TSFM (
12) of the EV3BRS, and using the
YALMIP toolbox and choosing the
SeDuMi 1.3.7 solver with the
adaptative self-diferentiation method to solve the Linear Matrix Inequalities (LMIs), the following matrices are obtained
Thus, the feedback gains vector are
Therefore, using the membership functions from
Figure 10, the PDC control law can be expressed in the form
3.3.2. TSFC with Attenuation
Performance criteria can be added to the control using extra LMIs [
14,
15]. Consider the TSFM (
5) with external disturbance
,
i.e.,
Disturbance rejection can be achieved by minimizing
subject to
To add disturbance rejection to the PDC control law, the following theorem must be satisfied (it should be noted that denotes an identity matrix)
Theorem 2 ([
15]).
The TSFM (19) with PDC control law (14) is globally asymptotically stable and the disturbance is attenuated by at least γ, if there exist matrices , and , such that
satisfies the conditions (15). If this conditions are satisfied the PDC gains are .
Considering the following voltage disturbance
the model (
3) can be modified to include this disturbance as an input of the system. Thus, the EV3BRS’s model with input anomalies is then given as
Linearizing the model (
21) around
and
and using the membership functions depicted in
Figure 10, (
21) takes a form similar to (
19)
where
From applying Theorem 2, the following matrices are obtained from considering (
22)
Thus, the PDC gains are
Since the control law itself has not changed, the form (
18) holds.
4. Results
4.1. TSFC on Simscape™
The control law (
18) with PDC gains (
16) and (17) is applied to the EV3BRS Simscape
™ model as shown in
Figure 11. Since the maximum voltage that the EV3
intelligent brick can provide to the motors is
, a
saturation block is added. To simulate the system, the solver
ode45 with
variable step is used. The simulation is started from initial conditions
for the
plane, and
for the
plane.
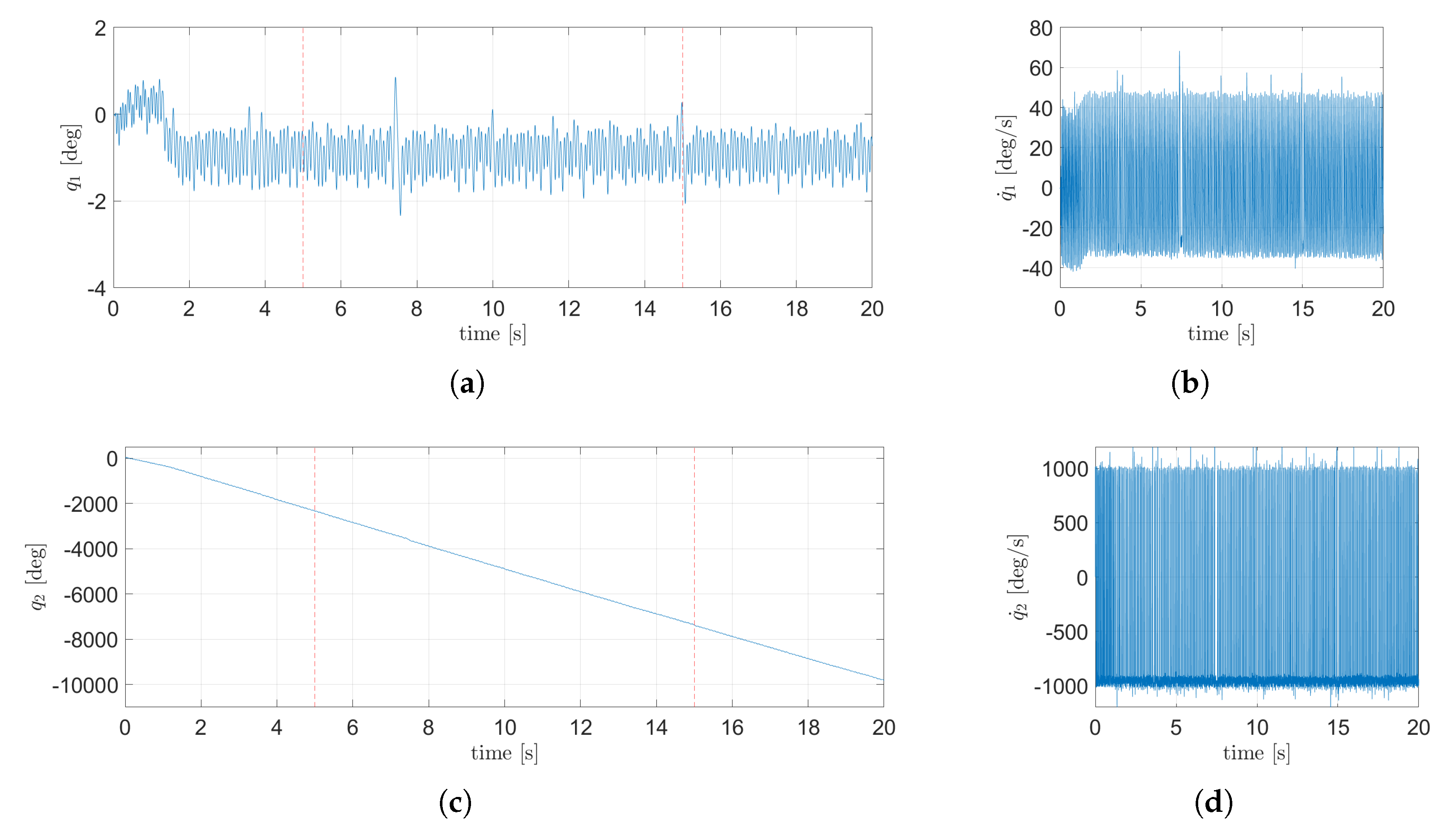
The evolution from the states of the system in the
plane are shown in
Figure 12, while the states corresponding to the
plane can be seen in
Figure 13. From
Figure 12(a) and
Figure 13(a), it can be seen that the TSFC can maintain the body of the EV3BRS balanced over the ball (
i.e., near the upright position).
Figure 12(c) and
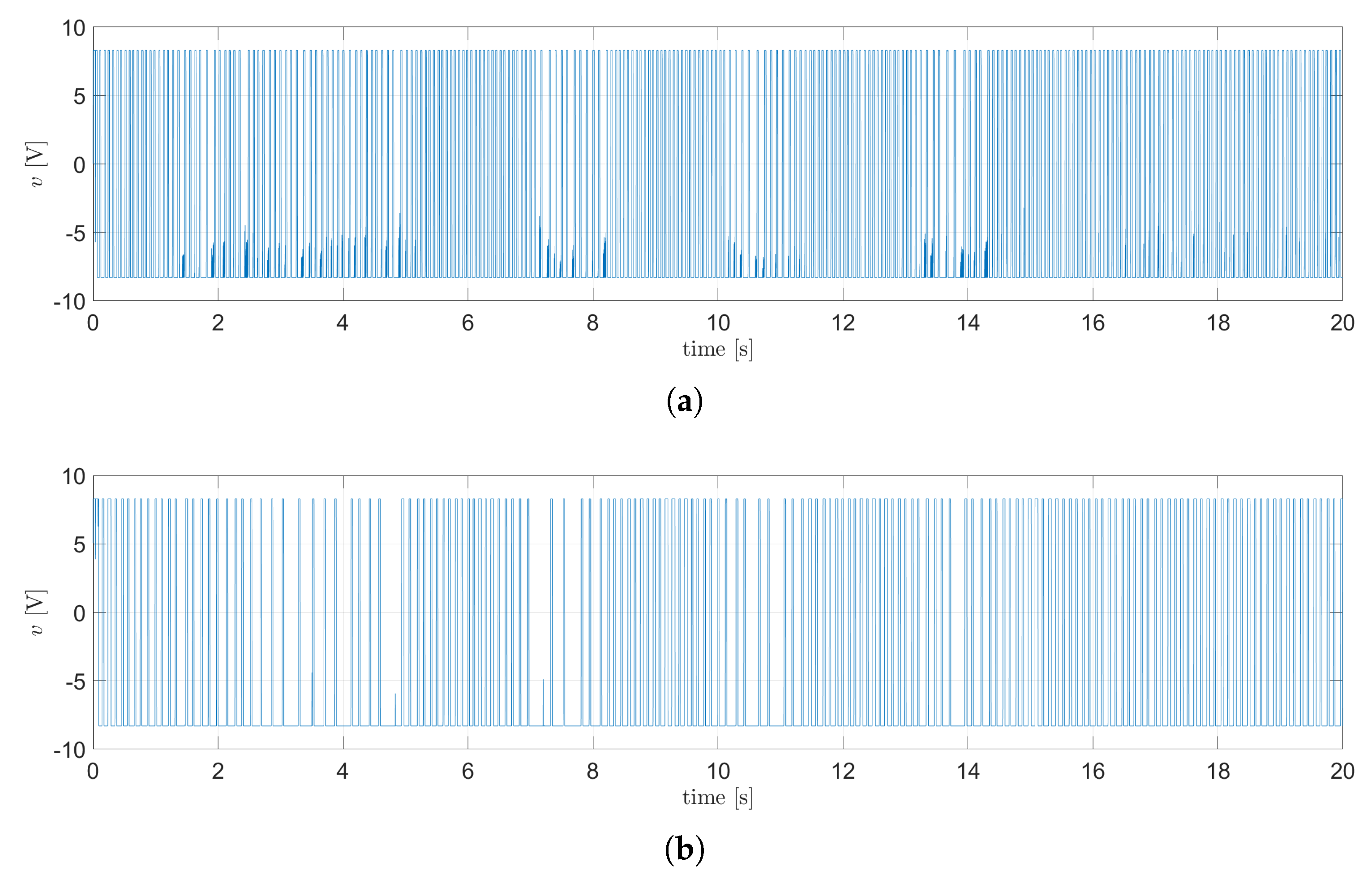
Figure 13(c) show the angular displacement of the wheels. The control signal for each motor is shown in
Figure 14. Since the tracking task is outside of the scope for this work, the displacement in the
plane is not taken into consideration, thus the TSFC successfully achieves the control objective. A video of the animation for this simulation is attache in the Supplementary Materials (
Video S1).
4.2. TSFC with Attenuation
In order to robustify the performance of the TSFC in presence of external disturbances, the
attenuation is invoked, where the gains (
23) and (24) are consider. In
Figure 15 the disturbance and the TSFC with
attenuation are applied to the EV3BRS Simscape
™ model.The same initial conditions, solver, and saturation imposed from the nominal TSFC are used.
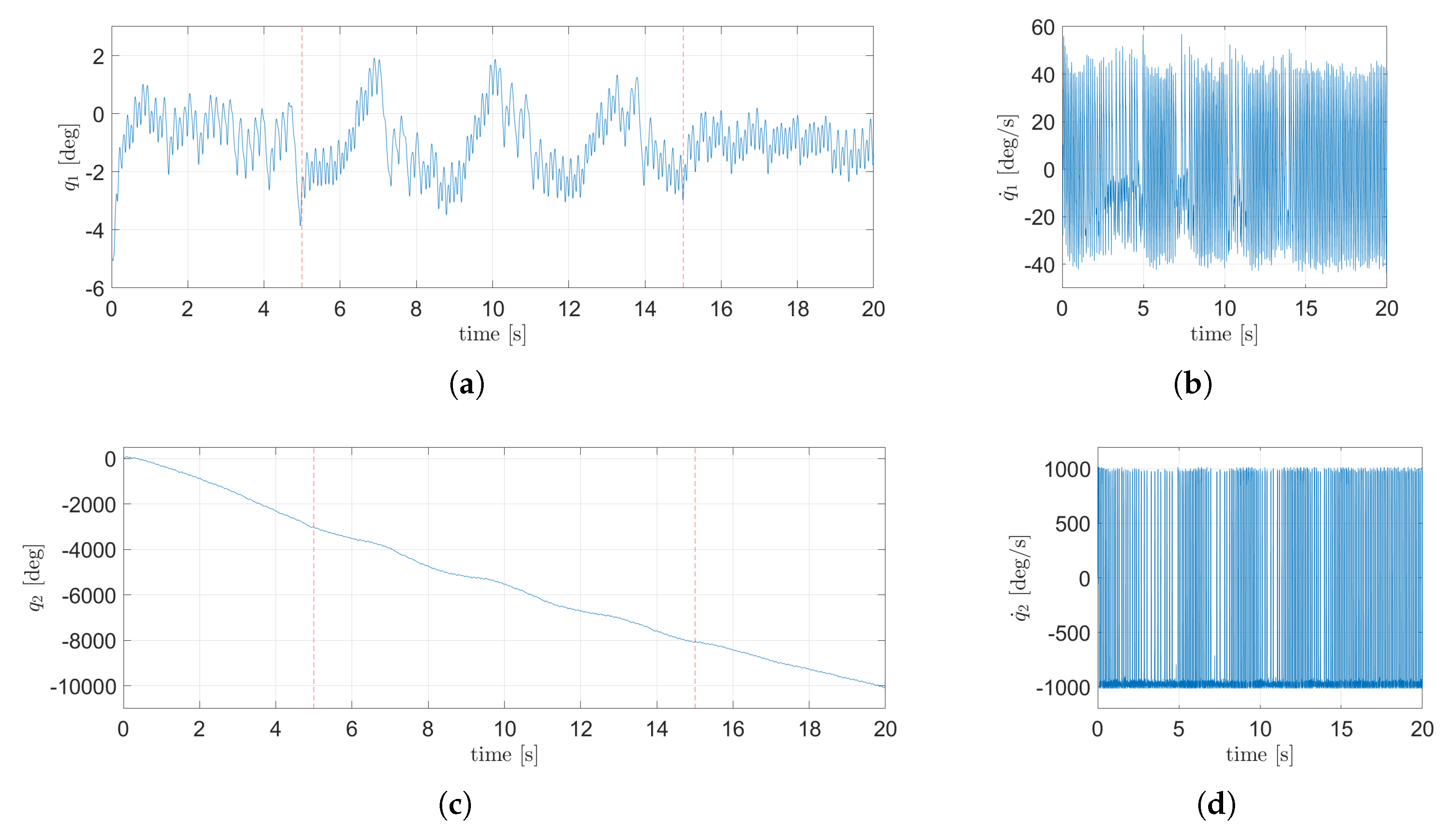
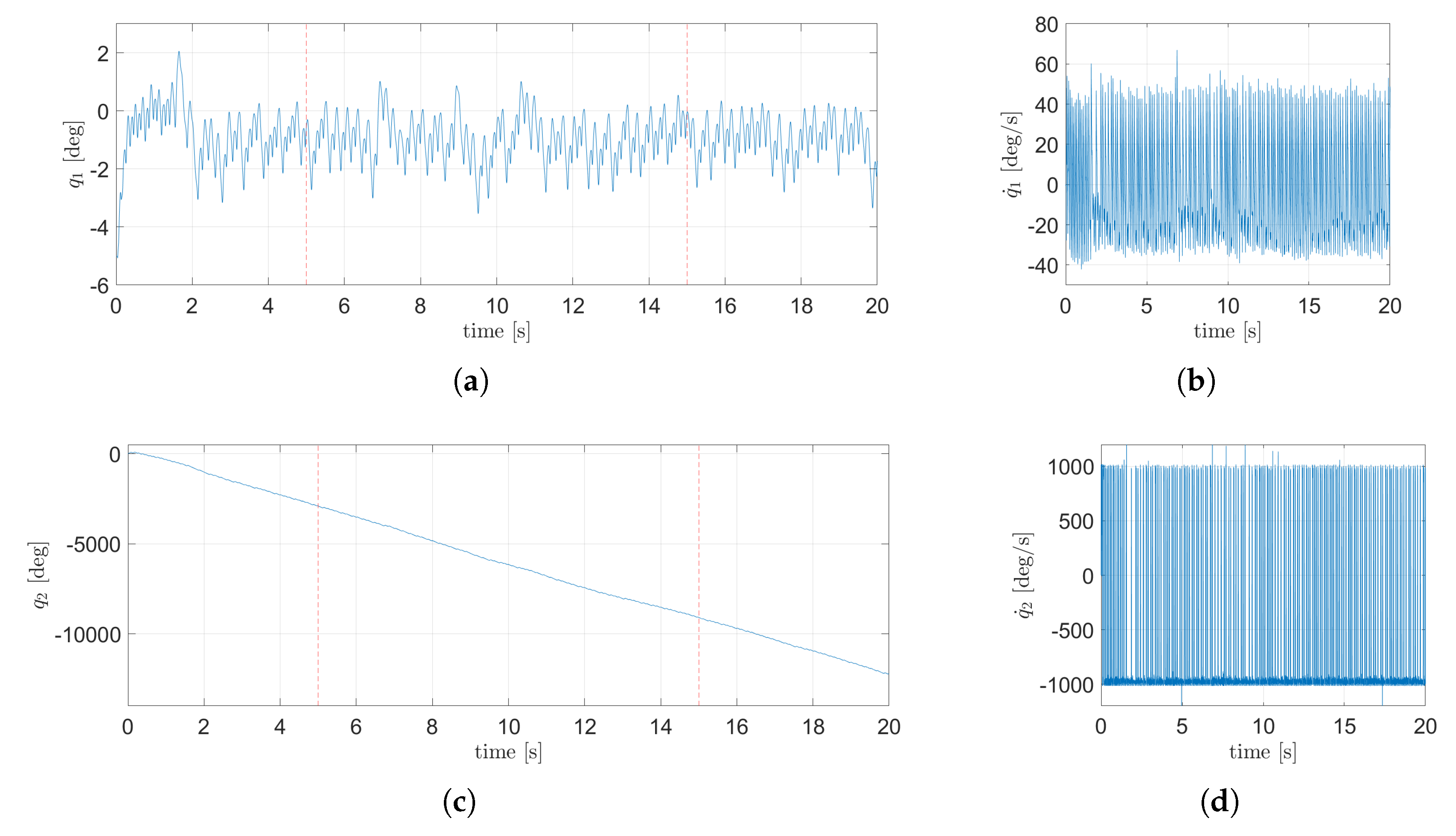
In
Figure 16, the dynamic of the states corresponding to the
plane are shown, while
Figure 17 shows the dynamic of the states from the
plane. In
Figure 16(a),
Figure 16(c),
Figure 17(a) and
Figure 17(c), the beginning and end of the duration range for the disturbance is limited and depicted by red dashed lines. From
Figure 16(a) and
Figure 17(a) it can be concluded that the control objective is achieved since the TSFC is able to maintain the body near the upright position. A video of the animation for this simulation is attache in the Supplementary Materials (
Video S2).
The attenuation of the disturbance is better seen when the performance of the nominal TSFC and the TSFC with
attenuation is compared.
Figure 19 compares the body position dynamics from plane
and plane
. It can be seen that the
attenuation managed to reduce the oscillations generated by the disturbance.
Table 3 compares the RMS and maximum error from both controllers.
5. Discussion
In summary, this work details the procedure to develop the model of the EVBRS by using the Simscape™ environment. The use of the Simscape™ Multibody™ Link plugin is essential to the development of the model since it allows the design of the body of the EV3BRS to take place in SOLIDWORKS® . Taking advantage of the popularity of LEGO® MINDSTORMS® the design of most of the pieces that comprise the body is already done, and thus, only four pieces needed to be designed before making the assembly in SOLIDWORKS® and exporting it to the Simscape™ environment.
Using the EV3BRS’s Simscape™ model allows the tuning of control gains without risking the physical platform and, although the next it is beyond the scope of this work, the displacement in the plane should be taken into consideration when preparing an area for experimental evaluation. The Simscape™ model may be used to delimit such displacement. Importantly, this model is expected to produce simulation results that more closely match experimental behavior, and because no other EV3BRS Simscape™ model has been reported in the literature, the model here developed can be considered a first virtual testbed that allows a more accurate control development.
Since the control objective is to maintain the body balanced on top of the ball, the TSFC here implemented is able to achieve such control objective even in presence of anomalies at the input, in our case, input voltage anomalies. In addition, in order to improve the control task performance, the attenuation approach has been exploited. Simulation results confirm that the effect of the anomaly on the body angle is reduced when the TSFC with attenuation is used.
6. Conclusions
From our study, the TSFC with attenuation has shown improvement in the performance of the EV3BRS Simscape™ model under anomalies at the input in contrast with the nominal TSFC version. Simulation results obtained through the EV3BRS Simscape™ model are expected to more closely resemble the dynamics of the real system.
The EV3BRS Simscape™ model here developed can be used in future work to simulate alternative control strategies, including those who aim to solve the trajectory tracking problem. Then, the model can be considered a first step toward the development of a digital twin of the EV3BRS.
Supplementary Materials
The following supporting information can be downloaded at: Preprints.org, Video S1: Simulation of the EV3BRS Simscape model with the TSFC with attenuation; Video S2: Simulation of the EV3BRS Simscape model with the nominal TSFC.
Author Contributions
Conceptualization, G.E.-E. and F.J.; methodology, G.E.-E. and F.J.; software, G.E.-E.; validation, G.E.-E. and F.J.; formal analysis, G.E.-E. and F.J.; investigation, G.E.-E. and F.J.; resources, F.J.; writing—original draft preparation, G.E.-E. and F.J.; writing—review and editing, G.E.-E. and F.J.; visualization, G.E.-E.; supervision, F.J.; project administration, F.J.; funding acquisition, F.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Tecnológico Nacional de México (TecNM) projects and, partially, under grant 47338 from EDD 2024 program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article/
Supplementary Material, further inquiries can be directed to the corresponding author.
Acknowledgments
The first author thanks to SECIHTI (previously CONAHCYT), México, for supporting this work under grant CVU 1323049.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3-D |
three-dimensional |
| BRS |
Ball Robotic System |
| CAD |
Computer-Aided Design |
| DoF |
Degrees of Freedom |
| EV3BRS |
EV3 Ballbot Robotic System |
| LMI |
Linear Matrix Inequality |
| LQR |
Linear Quadratic Regulator |
| NXTBRS |
NXT Ballbot Robotic System |
| PDC |
Parallel Distributed Compensation |
| TSFC |
Takagi-Sugeno Fuzzy Controller |
| TSFM |
Takagi-Sugeno Fuzzy Model |
References
- Fong, J.; Uppill, S. 899: Ballbot. Bachelor’s Thesis, University of Adelaide, Adelaide, Australia, 2009.
- Parker, B. GrabCAD Community. Available online: https://grabcad.com/library/lego-the-don-open-rescue-1 (accessed on 19 March 2025).
- Zdelarec, I. GrabCAD Community. Available online: https://grabcad.com/library/lego-wheels-1 (accessed on 19 March 2025).
- Downs, A. GrabCAD Community. Available online: https://grabcad.com/library/lego-nxt-light-sensor (accessed on 19 March 2025).
- Enemegio, R.; Jurado, F.; Villanueva-Tavira, J. Experimental Evaluation of a Takagi-Sugeno Fuzzy Controller for an EV3 Ballbot System. Appl. Sci. 2024, 14, 4103. [CrossRef]
- Akmal, M. A.; Jamin, N. F.; Ghani, N. M. A. Fuzzy logic controller for two wheeled EV3 LEGO robot. In Proceedings of 2017 IEEE Conference on Systems, Process and Control (ICSPC), Meleka, Malaysia, 15-17 December 2017; IEEE, 2018; pp 135-139. [CrossRef]
- Maxim Blogger. Available online: https://nxt-unroller.blogspot.com/2015/03/mathematical-model-of-lego-ev3-motor.html (accessed on 19 March 2025).
- Hernandez, R.; Jurado. F. Adaptive Neural Sliding Mode Control of an Inverted Pendulum Mounted on a Ball System. In Proceedings of 2018 15th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 5-7 September 2018; IEEE, 2018. [CrossRef]
- Ortiz, I.; Jurado,, F.; Ollervides-Vazquez, E. J. Discrete–Time Linear Quadratic Regulator for a NXT Ballbot System. In Proceedings of 2022 International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 5-9 December 2022; IEEE, 2024. [CrossRef]
- Lauwers, T.; Kantor, G.; Hollis, R. One Is Enough! In Robotics Research. Springer Tracts in Advanced Robotics; Thrun, S., Brooks, R., Durrant-Whyte, H., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2007; pp 327–336. [CrossRef]
- Schearer, E. M. Modeling Dynamics and Exploring Control of a Single-Wheeled Dynamically Stable Mobile Robot with Arms. Master’s Thesis, Carnegie Mellon University, Pittsburgh, U.S.A., 2006.
- Yamamoto, Y. NXT Ballbot Model–Based Design–Control of a Self–Balancing Robot on a Ball, Built with LEGO Mindstorm NXT, 1st ed.; Cybernet Systems: Tokyo, Japan, 2009.
- Wang, L. X. A Course in Fuzzy Systems and Control; Prentice-Hall International: Englewood Cliffs, 1997; pp. 265–275.
- Tanaka, K.; Wang, H. O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; John Wiley & Sons: New York, U.S.A., 2001; pp. 5–81.
- Lendek, Z.; Guerra, T. M.; Babuška, R.; De Schutter, B. Stability Analysis and Nonlinear Observer Design Using Takagi-Sugeno Fuzzy Models; Springer: Berlin-Heidelberg, Germany, 2010; pp. 5–41.
- Hollis, R. BALLBOTS. Sci. AM. 2006, 18, (1), 58–63. [CrossRef]
- Kumagai, M.; Ochiai, T. Development of a robot balancing on a ball. In Proceedings of 2008 International Conference on Control, Automation and Systems, Seoul, Korea , 14-17 October 2008; IEEE, 2008; pp 433-438. [CrossRef]
- Pham, D. B.; Kim, H.; Kim, J.; Lee, S. G. Balancing and Transferring Control of a Ball Segway Using a Double-Loop Approach [Applications of Control]. IEEE Control Systems Magazine 2018, 38, (2), 15–37. [CrossRef]
- Sanchez-Prieto, S.; Arribas-Navarro, T.; Gomez-Plaza, M.; Rodriguez-Polo, O. A Monoball Robot Based on LEGO Mindstorms [Focus on Education]. IEEE Control Systems Magazine 2012, 32, (2), 71–83. [CrossRef]
- Maly, J. Usage of the LEGO Mindstorms EV3 Robot- Design and Realization of the “Ball riding robot” for the Promotion of the Faculty. Bachelor’s Thesis, Czech Technical University in Prague, Prague, Czech Republic , 2018.
- Iemolo, R. Considerations about the development of a Ballbot system. Master’s Thesis, Politecnico di Torino, Turín, Italy , 2018.
- García-Luengo, O. Diseño, implementación y control de un prototipo de BallBot. Master’s Thesis, Universitat Politècnica de València, Valencia, Spain, 2022.
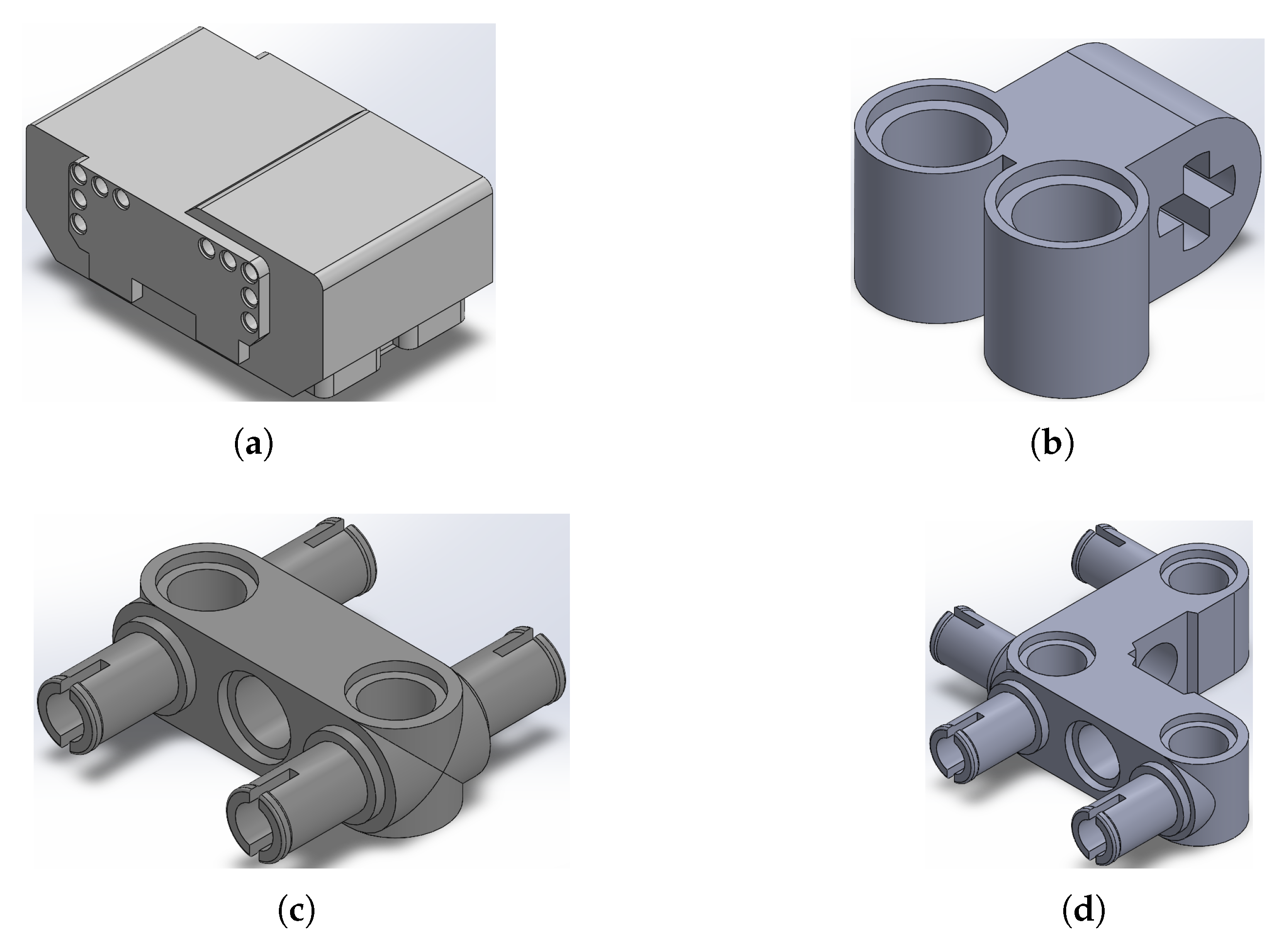
Figure 1.
Pieces designed by the authors: (a) LEGO®’s EV3 Brick, (b) LEGO®’s piece 32291, (c) LEGO®’s piece 48989, (d) LEGO®’s piece 55615.
Figure 1.
Pieces designed by the authors: (a) LEGO®’s EV3 Brick, (b) LEGO®’s piece 32291, (c) LEGO®’s piece 48989, (d) LEGO®’s piece 55615.
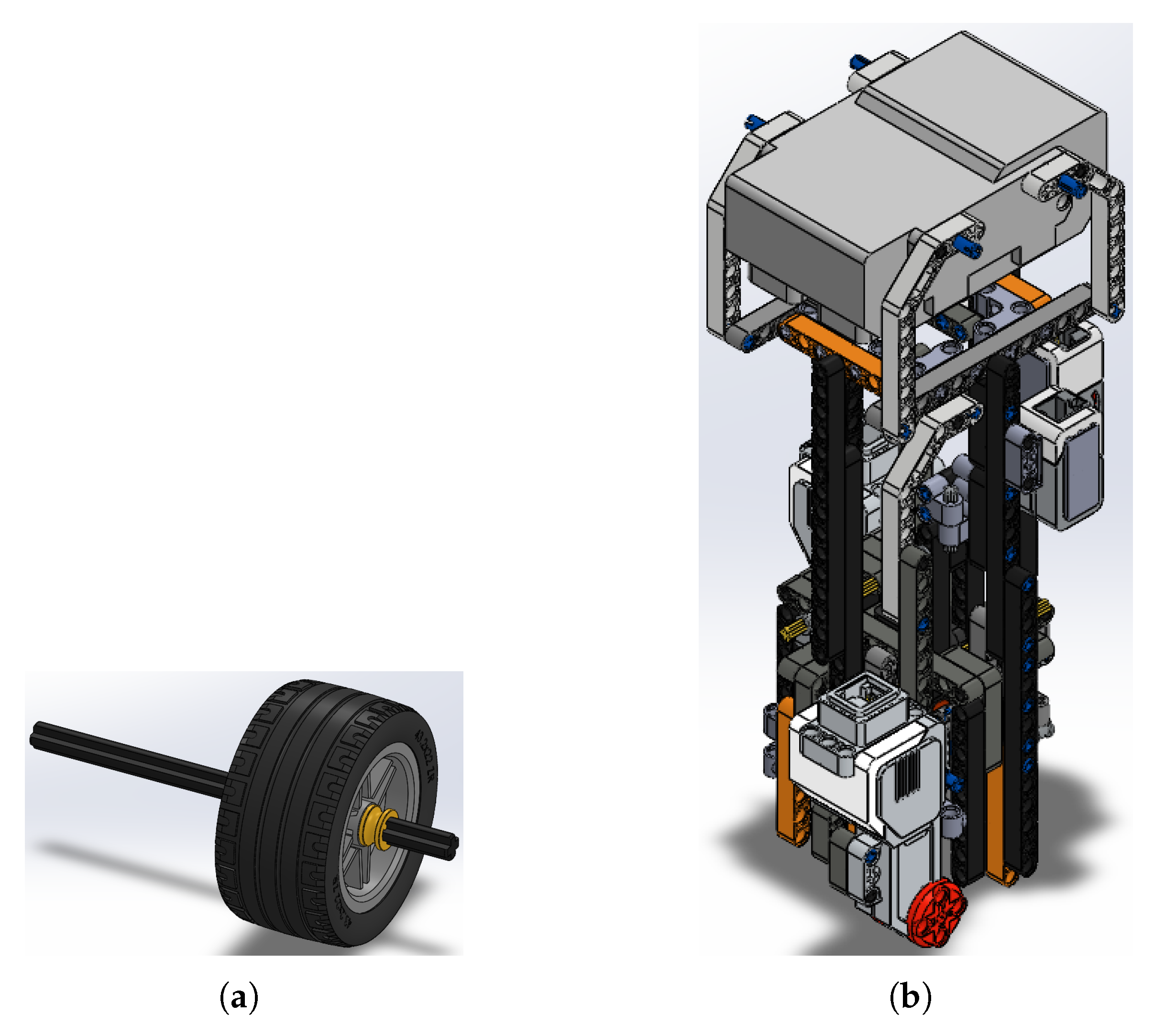
Figure 2.
Subassemblys used for the overall assembly of the EV3BRS: (a) subassembly of the EV3BRS’s wheels, (b) subassembly of the EV3BRS’s body.
Figure 2.
Subassemblys used for the overall assembly of the EV3BRS: (a) subassembly of the EV3BRS’s wheels, (b) subassembly of the EV3BRS’s body.
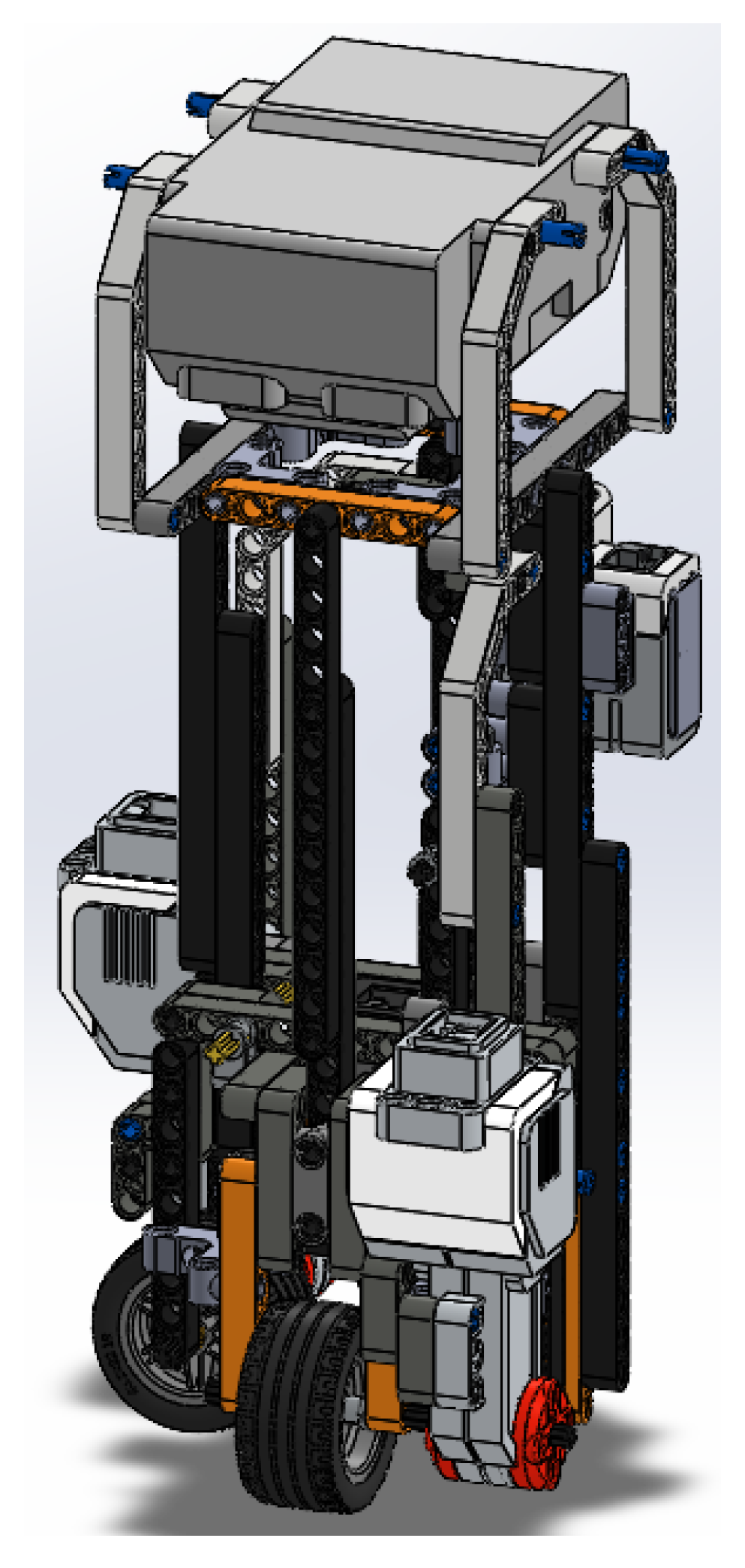
Figure 3.
Entire assembly of the EV3BRS in SOLIDWORKS®.
Figure 3.
Entire assembly of the EV3BRS in SOLIDWORKS®.
Figure 4.
Unmodified EV3BRS model in Simscape™.
Figure 4.
Unmodified EV3BRS model in Simscape™.
Figure 5.
Comprehensive model of the EV3BRS in Simscape™ :(a) main subsystem for the EV3BRS virtual model, (b) elements of the subsystem divided into areas according to their purpose.
Figure 5.
Comprehensive model of the EV3BRS in Simscape™ :(a) main subsystem for the EV3BRS virtual model, (b) elements of the subsystem divided into areas according to their purpose.
Figure 6.
Motor’s model in Simscape™.
Figure 6.
Motor’s model in Simscape™.
Figure 7.
Blocks of the body’s DoF subsystem.
Figure 7.
Blocks of the body’s DoF subsystem.
Figure 8.
Simplified model of the EV3BRS: (a) simplified model for the plane, (b) diagram that shows the and planes as identical and uncoupled.
Figure 8.
Simplified model of the EV3BRS: (a) simplified model for the plane, (b) diagram that shows the and planes as identical and uncoupled.
Figure 9.
Simplified model for the motor.
Figure 9.
Simplified model for the motor.
Figure 10.
Membership functions of the EV3BRS’s TSFM.
Figure 10.
Membership functions of the EV3BRS’s TSFM.
Figure 11.
Implementation of the whole TSFC to the EV3BRS’s Simscape™ model.
Figure 11.
Implementation of the whole TSFC to the EV3BRS’s Simscape™ model.
Figure 12.
States dynamic corresponding to the plane using the nominal TSFC: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 12.
States dynamic corresponding to the plane using the nominal TSFC: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 13.
States dynamic corresponding to the plane using the nominal TSFC: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 13.
States dynamic corresponding to the plane using the nominal TSFC: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 14.
Control signals for the motors using the nominal TSFC: (a) signal for the plane, (b) signal for the plane.
Figure 14.
Control signals for the motors using the nominal TSFC: (a) signal for the plane, (b) signal for the plane.
Figure 15.
Implementation of the TSFC with attenuation to the EV3BRS’s Simscape™ model.
Figure 15.
Implementation of the TSFC with attenuation to the EV3BRS’s Simscape™ model.
Figure 16.
States dynamic corresponding to the plane using the TSFC with attenuation: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 16.
States dynamic corresponding to the plane using the TSFC with attenuation: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 17.
States dynamic corresponding to the plane using the TSFC with attenuation: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 17.
States dynamic corresponding to the plane using the TSFC with attenuation: (a) angular position of the body, (b) angular velocity of the body, (c) angular position of the wheel, (d) angular velocity of the wheels.
Figure 18.
Control signals for the motors using the TSFC with attenuation: (a) signal for the plane, (b) signal for the plane.
Figure 18.
Control signals for the motors using the TSFC with attenuation: (a) signal for the plane, (b) signal for the plane.
Figure 19.
Comparison of the nominal TSFC and the TSFC with attenuation: (a) angular position dynamics of the body in the plane, (b) angular position dynamics of the body in the plane.
Figure 19.
Comparison of the nominal TSFC and the TSFC with attenuation: (a) angular position dynamics of the body in the plane, (b) angular position dynamics of the body in the plane.
Table 1.
Motor’s parameters.
Table 1.
Motor’s parameters.
| Parameter |
Notation |
Value |
Units |
| Armature inductance |
|
|
mH |
| Armature resistance |
|
|
|
| Body-Motor friction coefficient |
|
|
|
| Back EMF constant |
|
|
|
| Torque constant |
|
|
|
| Moment of inertia |
|
|
|
Table 2.
Parameters of the EV3BRS.
Table 2.
Parameters of the EV3BRS.
| Parameter |
Notation |
Value |
Units |
| Body mass |
|
|
Kg |
| Ball mass |
|
|
Kg |
| Ball radius |
|
|
m |
| Wheel radius |
|
|
m |
| Distance to the center of mass |
L |
|
m |
| Body moment of inertia |
|
|
|
| Ball moment of inertia |
|
|
|
| Gear ratio |
N |
|
- |
| Body-Ball friction coefficient |
|
|
|
| Body-Floor friction coefficient |
|
0 |
|
| Gravity acceleration |
g |
|
|
Table 3.
Quantitative index performance.
Table 3.
Quantitative index performance.
| Index* |
TSFC |
|
TSFC with attenuation |
| |
plane |
plane |
|
plane |
plane |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).