A Lightweight Batch Authenticated Key Agreement Scheme Based on Fog Computing for VANETs

1. Introduction

With the rapid proliferation of private vehicles and increasingly complex road traffic networks, traffic management faces significant challenges, resulting in frequent accidents and substantial losses of life and property. Meanwhile, modern vehicles have transcended their traditional role as mere transportation tools, evolving into mobile intelligent spaces that integrate travel, leisure, entertainment, and work functions. These factors collectively highlight the critical importance of establishing an intelligent traffic management platform. In recent years, the swift advancement of information technology has positioned vehicular ad-hoc networks (VANETs) as an emerging research focus [1,2]. By enabling wireless communication among multiple entities, VANETs provide crucial technical support for traffic control, autonomous driving, safety warnings, and vehicular services, thereby becoming a cornerstone of modern intelligent transportation systems.

The foundational architecture of conventional VANETs typically comprises three core components: traffic control center (TCC), roadside units (RSU), and vehicles equipped with on-board unit (OBU) [3]. Central to this architecture, the TCC serves as both the system’s centralized control hub and primary computation component. Its responsibilities encompass identity management, secure authentication, and security policy formulation for the entire network.

However, with the rapid advancement of VANETs and the exponential growth of smart vehicles, network data traffic has surged dramatically. Due to its centralized nature, traditional vehicular network architecture struggles to meet the requirements of high concurrency and real-time communication, often resulting in communication bottlenecks and single points of failure.

To overcome these challenges, cloud computing and fog computing-based vehicular architectures have gained significant attention in recent years [4,5]. As an extension of cloud computing, fog computing deploys computing and storage resources closer to the network edge, enabling more localized data processing. This approach effectively reduces communication latency and enhances network efficiency [6]. Furthermore, given the limited coverage of RSUs, introducing fog nodes (FNs) between TCCs and RSUs can significantly improve network stability and overall communication quality in vehicular networks.

In VANET environments, information exchange primarily relies on wireless communication technologies, such as WiFi and dedicated short-range communications (DSRC) [7,8]. However, the inherent security vulnerabilities in wireless technologies expose the entire system to both internal and external security threats, including man-in-the-middle attacks, replay attacks, and impersonation attacks. If VANETs suffer malicious attacks, they could result in serious casualties and substantial property damage. Therefore, ensuring communication security is a fundamental prerequisite for the widespread deployment of VANETs.

To ensure the security of VANETs, symmetric or asymmetric encryption is typically employed for secure data transmission. While asymmetric encryption offers robust security, its high computational and communication overhead makes it difficult to satisfy VANETs’ requirements for high-frequency, low-latency communication. In contrast, the authenticated key agreement (AKA) mechanism enables the establishment of a secure session key between two communicating entities. This allows subsequent data transmission using symmetric encryption based on the session key, thereby reducing the computational and communication overhead while ensuring security.

At present, a variety of AKA schemes have been proposed [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], However, these schemes commonly face the following challenges: (1) When a large number of vehicles request key agreement from TCC in a short period of time, each request is processed individually between the vehicle and TCC. This paradigm incurs two critical limitations: on the one hand, TCC has too much processing pressure in a short period of time; on the other hand, the communication overhead of the whole system increases greatly, and the processing efficiency of the whole system is relatively low; (2) Some schemes rely on complex cryptographic operations, which is difficult to meet the real-time requirements in the VANETs environment.

To solve the above problems, we propose an efficient batch AKA scheme based on fog computing (BAKAF), which can improve the overall efficiency of the system on the premise of ensuring security. Our key contributions are summarized as follows:

(1) For the scenario where a group of vehicles in a local area request AKA sessions within a short time frame, we propose a comprehensive AKA scheme based on the concepts of fog computing and Lagrange interpolation. In our scheme, the FN aggregates all AKA requests and, with the assistance of the TCC, establishes session keys for all vehicles by a round of operations. This approach effectively alleviates operational complexity of the entire system. During the process of generating multiple session keys via Lagrange interpolation, a shared random point is used across the straight lines corresponding to different vehicles at the FN, thereby reducing both computational and communication overhead.

(2) Our scheme incorporates a conditional privacy preserving mechanism and supports the revocation of malicious vehicles. The storage and computational overhead associated with tracking and revoking malicious vehicles is centralized at TCC, which is beneficial for resource-constrained vehicles.

(3) Our scheme employs cryptographic tools with low computational complexity, further reducing the overall computational overhead.

(4) Security analysis demonstrates that our scheme satisfies the security and privacy requirements of VANETs. Extensive experiments show that compared to existing advanced schemes, our approach achieves superior performance.

The remainder of this paper is organized as follows. Section 2 describes the related works. The preliminaries are presented in Section 3. Following this, the proposed scheme is detailed in Section 4. Subsequently, the security analysis and performance evaluation are presented in Section 5 and Section 6 respectively. Finally, there is the conclusion of the paper.

2. Related Works

To meet the high-security requirements for identity authentication and session key exchange, numerous AKA protocols have been proposed over the past decade.

In early schemes for foundational peer-to-peer communication scenarios, AKA mechanisms often relied on public key infrastructure (PKI). Islam et al. [9] proposed a device-to-device (D2D) AKA protocol based on elliptic curve cryptography (ECC) and self-certified public keys, which simplifies certificate management while achieving lightweight authentication. However, the lack of a complete mutual authentication mechanism makes this scheme vulnerable to typical threats such as replay and blocking attacks. To further simplify key management, Dang et al. [10] introduced a more efficient identity-based AKA protocol for VANETs, using an identity-based key generation model to reduce reliance on certificates. However, Deng et al. [11] pointed out that this scheme fails to ensure forward security in key leakage scenarios and proposed an improved version to enhance robustness under asymmetric attack models.

As privacy protection and practicality demands rise, Recent studies have incorporated multi-factor authentication, anonymous authentication, Chebyshev polynomials, and elliptic curve-based lightweight cryptographic primitives into AKA protocols. For instance, Xie et al. [12] proposed a dynamic ID-based anonymous two-factor AKA scheme combining smart cards and dynamic identities, supporting anonymity and password updates. However, Li et al. [13] revealed that the scheme [12] is vulnerable to offline guessing attacks and smart card loss scenarios. Liu et al. [14] proposed a reputation-based conditional privacy-preserving AKA scheme for VANETs, which enhances authentication credibility and supports dynamic trust management. However, it suffers from high computational overhead due to its use of bilinear pairing. Lee et al. [15] introduced an improved two-factor AKA scheme based on extended chaotic maps, constructing a timestamp verification mechanism to resist replay attacks, but the protocol still faces risks of key leakage and temporary data exposure. Jiang et al. [22] proposed a cloud-based three-factor authentication and key agreement protocol (CT-AKA) integrating passwords, biometrics, and smart cards to secure access between cloud systems and vehicles. Dua et al. [16] designed a two-tier AKA scheme based on ECC, where cluster head vehicles are authenticated by a central authority in the first tier, and ordinary vehicles are authenticated by cluster head vehicles in the second tier to achieve efficient V2V communication.

With rising device density and access demands in VANETs, traditional authentication methods struggle with communication latency and key synchronization inefficiencies. To overcome these issues, researchers have designed AKA protocols supporting batch verification and one-to-many authentication. Vijayakumar et al. [17] proposed an efficient batch AKA scheme for 6G-enabled VANETs. However, their scheme requires authentication prior to key agreement and supports only batch authentication rather than batch key agreement. Sun et al. [18] combined certificateless signatures with the Chinese Remainder Theorem to design an AKA protocol with batch processing capabilities, claiming it effectively resists man-in-the-middle, impersonation, and replay attacks. Madandi et al. [19] developed a binary-tree-based AKA protocol to share authentication loads among nodes and enhance structural scalability. It should be noted that while these one-to-many AKA protocols reduce the complexity of operations, they also introduce high-computational operations such as pairing and modular exponentiation, which impose significant computational burdens on resource-constrained VANET environments. As a result, increasing attention has been paid to designing lightweight AKA protocols tailored for VANET environments. Researchers have recognized that vehicle terminals have limited resources, while RSUs, Trusted Authorities (TAs), and FNs possess greater computational and storage capabilities, leading to fog computing-based AKA design models. Wazid et al. [24] proposed a secure AKA protocol for fog computing-based VANETs deployments, offering resource-aware advantages. However, some studies pointed out potential vulnerabilities in the scheme [24] under simulated attacks [25]. Ma et al. [26] designed a fog-based AKA scheme proven to provide session key security and protect V2I communication without using bilinear pairings. Wei et al. [20] proposed a symmetric encryption-based conditional privacy-preserving AKA scheme for fog-based VANETs, significantly reducing communication and computational costs. Qiao et al. [21] proposed a lightweight anonymous three-party AKA protocol using Chebyshev chaotic map operations to generate a shared session key while preserving anonymity, however, due to its focus on healthcare IoT, it is not suitable for VANETs. Cui et al. [23] proposed a robust and scalable VANET authentication scheme enabling vehicles to register with a trusted authority (TA) once and subsequently achieve rapid and efficient authentication with cloud service providers. Considering the limited computational and storage capacities of vehicles and drones, Cui et al. [27] further introduced a lightweight and provably secure two-factor AKA scheme based on chaotic maps for UAV-assisted VANETs, featuring fuzzy verifiers and honeywords to resist offline guessing and honeypot attacks. Zhou et al. [28] designed a vehicle-attribute-based AKA scheme supporting multi-user simultaneous authentication, offering formal security under the Canetti-Krawczyk (eCK) model and enabling session key agreement and anonymous identity updates. However, its use of bilinear pairing results in significant computational overhead.

In summary, although existing AKA protocols have made significant progress in improving VANET communication security, several key challenges remain. First, many schemes rely on complex cryptographic operations such as bilinear pairing and group signatures, leading to high computational and communication overheads that fail to meet the latency requirements of vehicular applications. Second, most of these protocols do not support batch AKA operations, which results in high operational complexity and poor service quality when facing large-scale AKA requests in localized and short-time scenarios.

3. Preliminaries

In this section, we introduce some basic knowledge, including system model, pseudo random function, elliptic curve cryptography, security and privacy requirements. The important symbols and definitions used in subsequent sections are shown in Table 1.

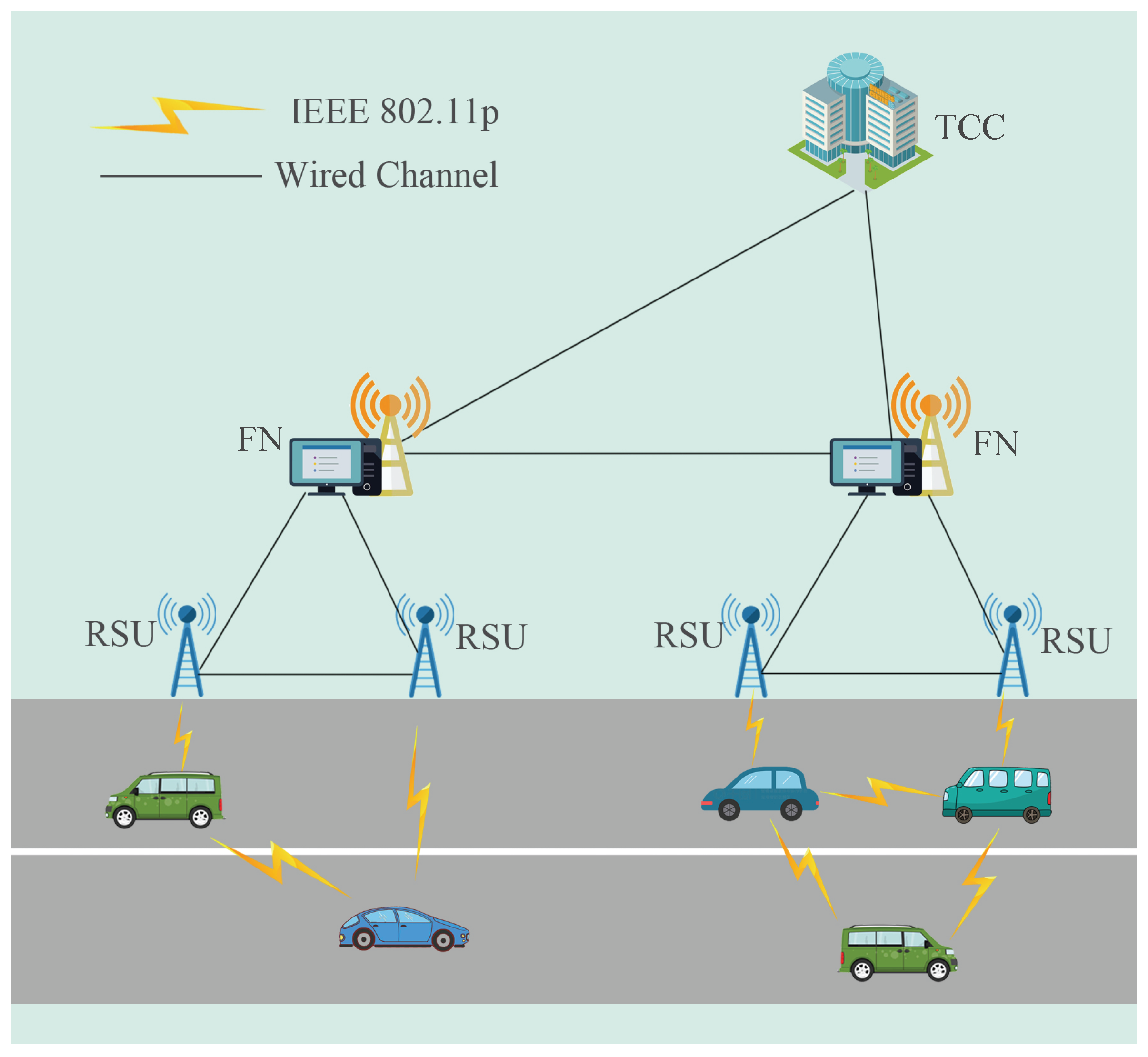
3.1. System Model

Our BAKAF scheme is based on the new architecture with FNs, as illustrated in Figure 1. This architecture mainly comprises of four entities, i.e., traffic control center (TCC), fog node (FN), roadside unity (RSU), and vehicle. The functions and features of each entity are as follows.

TCC: TCC as a fully trusted entity, is controlled by government agencies. It possesses robust storage capacity and computing power. TCC is responsible for the registration of FNs, RSUs, and vehicles, broadcasting system parameters, and tracking and revoking malicious vehicles. By leveraging technologies such as artificial intelligence and big data, TCC can provide data support for services like road navigation, real-time information sharing, public security investigation, traffic improvement, and urban data analysis.

FN: FNs have strong storage and processing capabilities, primarily responsible for collecting and processing data within their domains. they are generally arranged at the edges of the fogs, so that the vehicles can handle various tasks nearby, thereby enhancing overall system efficiency and meeting the low-latency requirements of the VANETs. FNs are connected to TCC and RSUs via wired links for various interactions. they are semi-trusted entities that, on one hand, faithfully execute protocol commands, and on the other hand, monitor and collect data from other entities.

RSU: RSUs typically feature small signal coverage areas and limited storage and computing capabilities. In our scheme, we assume that RSUs are only used for collecting and forwarding the information they received.

Vehicle: Vehicles are equipped with wireless sensing devices and tamper-proof devices (TPD). They are untrusted entities with weak computing and storage capabilities, making them vulnerable to various attacks. Vehicles collect surrounding information through sensing devices and transmit it to nearby vehicles or RSUs via wireless communication technology.

3.2. Pseudo Random Function (PRF)

Pseudo-random function (PRF) is an important cryptographic primitive that behaves similarly to a truly random function. Specifically, given an input consisting of a key $k\in \mathcal{K}$ and a binary string $x\in \mathcal{X}$, a PRF generates an output string $y\in \mathcal{Y}$ via the computation $y=\mathrm{PRF}(k,x)$. A secure PRF must ensure that its output is computationally indistinguishable from the output of a truly random function for any probabilistic polynomial time (PPT) adversary. PRF typically have the following characteristics: (1) Given the same key and input, they will generate the same output. (2) For different keys and inputs, the output should appear random and unpredictable.

3.3. Elliptic Curve Cryptography (ECC)

Since ECC was built by Kobilitz, it has been widely applied to encryption and other safety-related areas [29].

Let $F_p$ denote a finite field with a large prime number p as its order. We choose an elliptic curve E defined as $y^2=x^3+ax+b(modp)$, where $a,b\in F_p$. Then, an additive cyclic elliptic curve group G on E with order q and a generator P can be generated, which contains the point at infinity O. The properties of group G are as follows:

Scalar multiplication: Let $\alpha \in Z_q^{*}$, the scalar multiplication on E is defined as $\alpha P=P+P+\cdots +P$ ($\alpha$ times).

Elliptic curve discrete logarithm (ECDL) assumption: For randomly chosen $P,Q\in G$ satisfying $Q=\alpha P$, where $\alpha \in Z_q^{*}$ is unknown, there exists no efficient algorithm that can determine $\alpha$ from Q in PPT with non-negligible advantage.

3.4. Security and Privacy Requirements

Mutual authentication: In order to ensure identity legitimacy of the communication entity during AKA communication, mutual authentication should be performed among vehicles, FNs, and the TCC.

Confidentiality: The session key established through the AKA process can be kept confidential from any other entity except for the participating entities.

Data integrity: If a message is maliciously forged during transmission, the receiver should be capable of detecting the forgery.

Unlinkability: Unlinkability guarantees that no observable connection exists between different messages sent by the same vehicle. This security mechanism effectively prevents any entity from deducing whether two intercepted messages were transmitted by the identical sender.

Conditional privacy-preserving: During communication, the vehicle’s real identity remains hidden from all entities except TCC, which can retrieve any vehicle’s true identity when necessary.

Revocability: Once malicious vehicles are detected, TCC can prevent them from initiating further AKA sessions.

Forward and backward secrecy: From an adversarial perspective, session keys established across different sessions must be computationally indistinguishable. Knowledge of one session key provides no advantage in deriving another.

Resistance to various attacks: Our scheme must withstand various well-known attacks, such as impersonation attack, replay attack.

4. Prposed Scheme

In this section, we will describe our BAKAF scheme in detail, which consists of three phases, namely: setup phase, registration phase, and authentication and key agreement phase. In setup phase, TCC initializes the system and selects public parameters. In registration phase, all vehicles and fog nodes need to register with TCC, respectively. In authentication and key agreement phase, within the set time interval, a batch of vehicles simultaneously establishes corresponding session keys with the fog nodes.

4.1. Setup Phase

Given a security parameter $\lambda$, TCC defines $F_p$ as a finite field with a large prime number p as its order. TCC then generates an elliptic curve E defined by the equation $y^2\equiv x^3+ax+b(modp)$, where $a,b\in F_p$. Subsequently, TCC defines a additive cyclic elliptic curve group G with order q and generator P, which includes a point at infinity denoted as O. Finally, TCC selects a random number $s\in Z_q^{*}$ as the system’s master secret key and retains the corresponding system public key $P_{pub}=sP$.

TCC constructs a revocation list, denoted as $RevList$, which is used to store the real identities of malicious vehicles. Then chooses 7 cryptographic hash functions: $H_1:Z_q^{*}\times {\{0,1\}}^{l_i}\to Z_q^{*}$, $H_2:G\to {\{0,1\}}^{l_i}$, $H_3:Z_q^{*}\times {\{0,1\}}^{l_i}\times Z_q^{*}\times G\to {\{0,1\}}^{l_a}$, $H_4:Z_q^{*}\times {\{0,1\}}^{l_i}\times Z_q^{*}\times Z_q^{*}\times {\{0,1\}}^{*}\to Z_q^{*}$, $H_5:Z_q^{*}\times {\{0,1\}}^{l_i}\times Z_q^{*}\times Z_q^{*}\times Z_q^{*}\to Z_q^{*}$, $H_6:{\{0,1\}}^{*}\to Z_q^{*}$, $H_7:Z_q^{*}\times {\{0,1\}}^{l_i}\times {\{0,1\}}^{l_i}\times Z_q^{*}\times Z_q^{*}\times Z_q^{*}\to Z_q^{*}$, where $l_i$ represents the length of the real identity or pseudonym, $l_a$ represents the length of message authentication code.

TCC publishes the system parameters $parmas=\{p,q,a,b,P,P_{pub},H_1,H_2,H_3,H_4,H_5,H_6,H_7\}$ and secretly saves the system’s master secret key s.

4.2. Registration Phase

4.2.1. Registration for Vehicles

Assuming vehicle $V_i$ requests registration, TCC selects a specific string $I{D}_i$ as the vehicle $V_i$’s real identity, calculates the certificate $c_i=H_1(s,I{D}_i)$, and sends $(I{D}_i,c_i)$ to vehicle $V_i$ through a secure channel.

4.2.2. Registration for Fog Node

Assuming fog node $F{N}_f$ requests registration, TCC selects a specific string $I{D}_f$ as the fog node $F{N}_f$’s real identity, calculates the certificate $c_f=H_1(s,I{D}_f)$, and sends $(I{D}_f,c_f)$ to fog node $F{N}_f$ through a secure channel.

The certificate $c_i$ (or $c_f$) is owned exclusively by the vehicle $V_i$ (or fog node $F{N}_f$) itself and the TCC, and will play a vital role in both authentication and message integrity assurance.

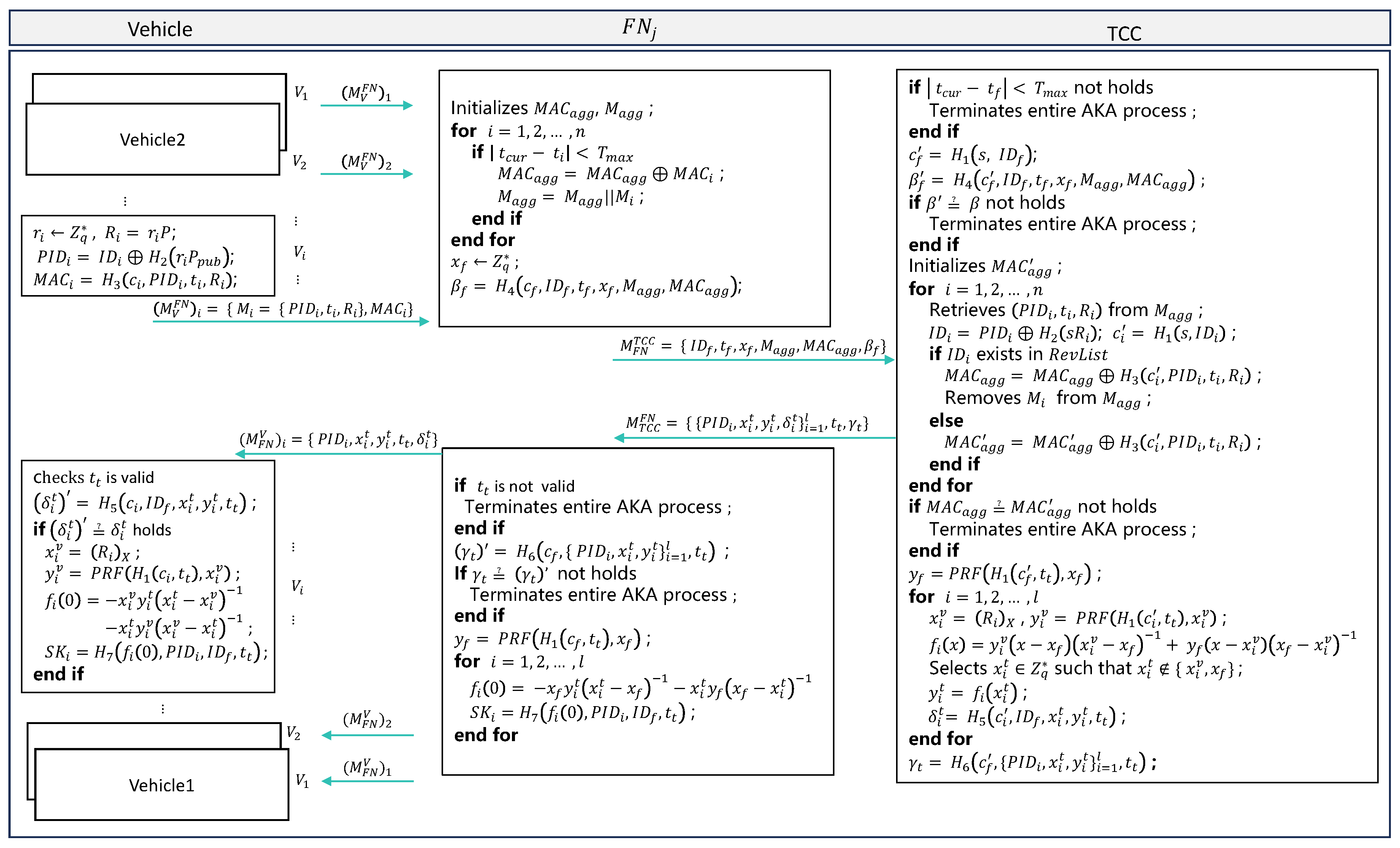
4.3. Authentication and Key Agreement Phase

Assume that there are n vehicles requesting key agreement with the fog node $F{N}_f$ in a short period of time. For the convenience of explanation, we will take vehicle $V_i$ as an example to elaborate. The main steps of this stage are shown in Figure 2.

4.3.1. Vehicle Requests to Generate a Session Key

Vehicle $V_i$ selects a random number $r_i\in Z_q^{*}$ and computes $R_i=r_{i}P$ to obtain a random point on the group G.

Vehicle $V_i$ retains its pseudonym $PI{D}_i=I{D}_i\oplus H_2\left(r_i{P}_{pub}\right)$. (The vehicle uses a different pseudonym each time it sends the requested information, helping to ensure conditional privacy-preserving.)

Generates the message authentication code $MA{C}_i=H_3(c_i,PI{D}_i,t_i,R_i)$, where $t_i$ is the timestamp, sets message ${\left(M_V^{FN}\right)}_i=\{M_i=\{PI{D}_i,t_i,R_i\},MA{C}_i\}$.

Finally, vehicle $V_i$ sends the message ${\left(M_V^{FN}\right)}_i$ to fog node $F{N}_f$. It notes that the subscript V denotes that the sender of message is a vehicle, while the superscript $FN$ denotes that the receiver of message is a FN, and the superscripts and subscripts of some symbols below have similar meanings.

4.3.2. FN Aggregates the Request Data from Each Vehicle

Upon receiving key agreement request information ${\{M_i,MA{C}_i\}}_{i=1}^n$ from n vehicles within the predetermined time interval, $F{N}_f$ initializes $MA{C}_{agg}$ (a binary string of length $|MA{C}_i|$, all bits set to 0) and $M_{agg}$ (an empty string) for storing the aggregated $MAC$ and message, respectively.

For each vehicle’s information $M_i$, checks whether the inequality $|t_{cur}-t_i|<T_{max}$ holds? where $t_{cur}$ and $T_{max}$ denote the current timestamp and max valid time interval, respectively. If not, discard the information. Otherwise, proceed to calculate $MA{C}_{agg}=MA{C}_{agg}\oplus MA{C}_i$ and $M_{agg}=M_{agg}\left|\right|M_i$. In this way, the information from all vehicles is aggregated into the variables $M_{agg}$ and $MA{C}_{agg}$.

$F{N}_f$ selects a random number $x_f\in Z_q^{*}$, such that $x_f\notin \{{\left(R_1\right)}_X,{\left(R_2\right)}_X,\cdots ,{\left(R_n\right)}_X\}$, where ${\left(R_i\right)}_X$ represents the X-coordinate of the point $R_i$ on the elliptic curve E. Calculates verification message ${\beta }_f=H_4(c_f,I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg})$, where $t_f$ is the timestamp of $F{N}_f$. Then, $F{N}_f$ sends the message $M_{FN}^{TCC}=\{I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg},{\beta }_f\}$ to TCC.

4.3.3. TCC Authenticates and Processes the FN’s Requests

Upon receiving the batch key agreement request message $M_{FN}^{TCC}$ from $F{N}_f$, TCC first checks whether the inequality $|t_{cur}-t_f|<T_{max}$ holds? If not, the entire AKA process will be terminated.

Next, TCC calculates $c_f^{\prime }=H_1(s,I{D}_f)$ and ${\beta }_f^{\prime }=H_4(c_f^{\prime },I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg})$, and checks whether the equation ${\beta }^{\prime }\stackrel{?}{=}\beta$ holds. If it holds, two conclusions can be drawn: the identity legality of $I{D}_f$ has been validated by TCC, and the integrity of $M_{FN}^{TCC}$ can be guaranteed; Otherwise, the entire AKA process will be terminated.

Next, TCC initializes an auxiliary variable $MA{C}_{agg}^{\prime }$, which is a binary string with the length equal to $|MA{C}_i|$ and each bit of which is 0, and $MA{C}_{agg}^{\prime }$ is used to re-record the information of legitimate vehicles. Then, TCC performs the following procedures for each vehicle $V_i$ to verify its identity legitimacy and information integrity.

• Retrieves the i-th tuple $(PI{D}_i,t_i,R_i)$ from $M_{agg}$ and obtains the real identity of $V_i$ by computing $I{D}_i=PI{D}_i\oplus H_2\left(s{R}_i\right)$.
• Calculates the vehicle $V_i$’s certificate $c_i^{\prime }=H_1(s,I{D}_i)$.
• Verifies whether vehicle $V_i$ is revoked by checking if its real identity $I{D}_i$ exists in the revocation list $RevList$.

  –

  If it is not revoked, it indicates that the vehicle is legal, then calculates $MA{C}_{agg}^{\prime }=MA{C}_{agg}^{\prime }\oplus H_3(c_i^{\prime },PI{D}_i,t_i,R_i)$.

  –

  If it is revoked, calculates $MA{C}_{agg}=MA{C}_{agg}\oplus H_3(c_i^{\prime },PI{D}_i,t_i,R_i)$, where the message authentication code $MA{C}_i$ of the illegal vehicle $V_i$ is removed from $MA{C}_{agg}$, at the same time, the message $M_i$ of the illegal vehicle $V_i$ should be removed from $M_{agg}$.

TCC checks whether the equation $MA{C}_{\mathrm{agg}}\stackrel{?}{=}MA{C}_{agg}^{\prime }$ holds. If it does not hold, it indicates that the messages from some legitimate vehicles have been tampered with, and the entire AKA process is terminated. Otherwise, it confirms that the information from all legitimate vehicles remains intact, and TCC proceeds with the following steps.

Computes $y_f=PRF(H_1(c_f^{\prime },t_t),x_f)$, where $t_t$ is the timestamp of $TCC$. Then, based on the message $\{PI{D}_i,t_i,R_i,I{D}_i\}$ of each legitimate vehicle $V_i$, TCC performs the following procedures.

• TCC sets $x_i^v={\left(R_i\right)}_X$, and $y_i^v=PRF(H_1(c_i^{\prime },t_t),x_i^v)$.
• Using the Lagrange interpolation formula, TCC can obtain the equation $f_i\left(x\right)=y_i^v(x-x_f){(x_i^v-x_f)}^{-1}+y_f(x-x_i^v){(x_f-x_i^v)}^{-1}$ of a straight line passing through points $(x_i^v,y_i^v)$ and $(x_f,y_f)$. These straight lines corresponding to all legitimate vehicles pass through a common point $(x_f,y_f)$, which can significantly reduce the computational and communication overhead.
• TCC selects a random number $x_i^t\in Z_q^{*}$ for vehicle $I{D}_i$, such that $x_i^t\notin \{x_i^v,x_f\}$, then substitutes $x_i^t$ into the straight line equation $f_i\left(x\right)$ to compute the corresponding Y-coordinate, i.e., evaluates $y_i^t=f_i\left(x_i^t\right)$. Therefore, in addition to the points $(x_i^v,y_i^v)$ and $(x_f,y_f)$, TCC has now obtained the third point $(x_i^t,y_i^t)$ on the straight line $f_i\left(x\right)$.
• TCC obtains verification message by computing ${\delta }_i^t=H_5(c_i^{\prime },I{D}_f,x_i^t,y_i^t,t_t)$.

Upon completing the above operations for each vehicle, TCC computes ${\gamma }_t=H_6(c_f^{\prime },{\{PI{D}_i,x_i^t,y_i^t\}}_{i=1}^l,t_t)$, where l represents the number of legitimate vehicles, sets message $M_{TCC}^{FN}=\{{\{PI{D}_i,x_i^t,y_i^t,{\delta }_i^t\}}_{i=1}^l,t_t,{\gamma }_t\}$, and transmits the $M_{TCC}^{FN}$ to the fog node $F{N}_f$. Since the information of illegitimate vehicles has been deleted by TCC, the pseudonyms of legitimate vehicles need to be returned to the fog node $F{N}_f$.

4.3.4. FN Generates Session Keys

Upon receiving message $M_{TCC}^{FN}$, fog nodes $F{N}_f$ checks whether $t_t$ is valid. If not, the entire AKA process is terminated. If it is, the following process continues.

$F{N}_f$ computes ${\left({\gamma }_t\right)}^{\prime }=H_6(c_f,{\{PI{D}_i,x_i^t,y_i^t\}}_{i=1}^l,t_t)$ and checks whether the equation ${\gamma }_t\stackrel{?}{=}{\left({\gamma }_t\right)}^{\prime }$ holds. If holds, it indicates that the legality of the vehicles ${\left\{V_i\right\}}_{i=1}^l$ and the integrity of $M_{TCC}^{FN}$ and $M_V^{FN}$ are guaranteed. Then, $F{N}_f$ performs the following steps.

• The fog node $F{N}_f$ sends the messages ${\left\{M_{FN}^V\right\}}_{i=1}^l={\{PI{D}_i,x_i^t,y_i^t,t_t,{\delta }_i^t\}}_{i=1}^l$ to the corresponding vehicles ${\left\{V_i\right\}}_{i=1}^l$ respectively.
• Computes $y_f=PRF(H_1(c_f,t_t),x_f)$, and performs the following operations for each legal vehicle.

  –

  Substitute $x=0$ into the straight line equation $f_i\left(x\right)$ to obtain the Y-coordinate of the intersection point between the line $f_i\left(x\right)$ and the Y-axis: $f_i\left(0\right)=-x_f{y}_i^t{(x_i^t-x_f)}^{-1}-x_i^t{y}_f{(x_f-x_i^t)}^{-1}$. The line $f_i\left(x\right)$ passes through points $(x_i^t,y_i^t)$ and $(x_f,y_f)$, where point $(x_f,y_f)$ is set by fog node $F{N}_f$ and point $(x_i^t,y_i^t)$ is set by TCC.

  Note: It’s unnecessary to first solve for the explicit expression of the linear equation here.

  –

  Gets the session key between the vehicle $V_i$ and the fog node $F{N}_f$ by computing $S{K}_i=H_7(f_i\left(0\right),PI{D}_i,I{D}_f,t_t)$.

  –

  Fog node $F{N}_f$ stores the session key $S{K}_i$.

4.3.5. Vehicle Generates Session Key

After receiving message ${\left(M_{FN}^V\right)}_i$, vehicle $I{D}_i$ checks whether $t_t$ is valid. If not, the entire AKA process is terminated. If it is, the following processes continue.

Computes ${\left({\delta }_i^t\right)}^{\prime }=H_5(c_i,I{D}_f,x_i^t,y_i^t,t_t)$ and checks whether the equation ${\left({\delta }_i^t\right)}^{\prime }\stackrel{?}{=}{\delta }_i^t$ holds. If holds, it indicates that the legality of the vehicles $V_i$ and the integrity of $M_{TCC}^{FN}$ and $M_V^{FN}$ are guaranteed. Then, $F{N}_f$ performs the following steps.

• Sets $x_i^v={\left(R_i\right)}_X$, and computes $y_i^v=PRF(H_1(c_i,t_t),x_i^v)$.
• Substitute $x=0$ into the linear equation $f_i\left(x\right)$ to obtain the Y-coordinate of the intersection point between the line $f_i\left(x\right)$ and the Y-axis: $f_i\left(0\right)=-x_i^v{y}_i^t{(x_i^t-x_i^v)}^{-1}-x_i^t{y}_i^v{(x_i^v-x_i^t)}^{-1}$. The line $f_i\left(x\right)$ passes through points $(x_i^t,y_i^t)$ and $(x_i^v,y_i^v)$, where point $(x_i^v,y_i^v)$ is set by vehicle $V_i$ and point $(x_i^t,y_i^t)$ is set by TCC.
  Note: For a specific vehicle $V_i$, the three points $(x_i^t,y_i^t)$, $(x_i^v,y_i^v)$, and $(x_f,y_f)$ lie on the same straight line. Therefore, the line determined by any two of these points is identical, denoted as $f_i\left(x\right)$.
• Gets the session key between the vehicle $V_i$ and the fog node $F{N}_f$ by computing $S{K}_i=H_7(f_i\left(0\right),PI{D}_i,I{D}_f,t_t)$.
• Vehicle $I{D}_i$ stores the session key $S{K}_i$.

Remark 1: Within a fixed time interval, if n vehicles request AKA sessions with the same FN, the FN aggregates all AKA session requests, and the system then performs batch AKA processing. This approach offers at least three advantages: (1) reducing the overall system complexity; (2) lowering the communication overhead between the FN and TCC; and (3) decreasing the computational overhead for both the FN and TCC.

Remark 2: On TCC side, even if some vehicles are found to be illegal, the remaining legal vehicles can still perform the batch AKA process, which greatly enhances the flexibility of batch AKA.

5. Security Analysis

In this section, we will analyze the security performance of our scheme from both informal and formal aspects.

5.1. Informal Security Analysis

Mutual authentication: Our scheme comprises four phases of information transmission, all employing identical authentication mechanisms. We illustrate this using the TCC-to-FN message transmission as an example. TCC first computes ${\gamma }_t=H_6(c_f^{\prime },{\{PI{D}_i,x_i^t,y_i^t\}}_{i=1}^l,t_t)$, where $c_f^{\prime }=H_1(s,I{D}_f)$ is the certificate of $F{N}_f$. Subsequently, TCC transmits the message $M_{TCC}^{FN}=\{{\{PI{D}_i,x_i^t,y_i^t,{\delta }_i^t\}}_{i=1}^l,t_t,{\gamma }_t\}$ to $F{N}_f$. Upon receiving message $M_{TCC}^{FN}$, $F{N}_f$ computes ${\left({\gamma }_t\right)}^{\prime }=H_6(c_f,{\{PI{D}_i,x_i^t,y_i^t\}}_{i=1}^l,t_t)$ and checks whether the equation ${\gamma }_t\stackrel{?}{=}{\left({\gamma }_t\right)}^{\prime }$ holds. If the equation holds, it confirms that the message must originate from TCC, since only $F{N}_f$ and TCC possess the certificate $c_f$. Therefore, the authenticity is guaranteed.

Confidentiality: In our scheme, the method for calculating the session key is $S{K}_i=H_7(f_i\left(0\right),PI{D}_i,I{D}_f,t_t)$. To obtain the session key between vehicle $V_i$ and $F{N}_j$, we first need to obtain $f_i\left(0\right)$, which represents the Y-coordinate of the line $f_i\left(x\right)$ at $x=0$. At least two points are required to determine a straight line. Even if a malicious entity intercepts a point on the straight line transmitted from TCC, since it cannot obtain the certificates of the vehicle $V_i$ or the FN $F{N}_j$, it cannot obtain the other point on the required straight line. Consequently, it cannot construct the linear equation and calculate $f_i\left(0\right)$. Therefore, the session key between vehicle $V_i$ and $F{N}_j$ remains confidential to any malicious entity.

Data integrity: Our scheme comprises four phases of information transmission, all employing identical message integrity protection mechanisms. We illustrate this using the FN-to-TCC message transmission as an example. $F{N}_f$ first sends the message $M_{FN}^{TCC}=\{I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg},{\beta }_f\}$ to TCC, where ${\beta }_f=H_4(c_f,I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg})$, and $c_f=H_1(s,I{D}_f)$ is the certificate of $F{N}_f$, which is owned exclusively by the fog node $F{N}_f$ itself and the TCC. If any field in $M_{FN}^{TCC}$ is tampered with (e.g., $t_f$ altered to $t_f^{*}$), the malicious attacker must recompute the verification value ${\beta }_f$. Without $F{N}_f$’s certificate, the attacker can only arbitrarily choose $c_f^{*}$, yielding: ${\beta }_f=H_4(c_f^{*},I{D}_f,t_f^{*},x_f,M_{agg},MA{C}_{agg})$.

Upon receiving the message $M_{FN}^{TCC}$ from $F{N}_f$, TCC first recalculates certificate $c_f^{\prime }=H_1(s,I{D}_f)$ and verification value ${\beta }_f^{\prime }=H_4(c_f^{\prime },I{D}_f,t_f^{*},x_f,M_{agg},MA{C}_{agg})$. Then, checks whether the equation ${\beta }_f^{\prime }\stackrel{?}{=}{\beta }_f$ holds. Because $c_f^{\prime }$ is not equal to $c_f^{*}$, the verification equation will not hold. In this way, the integrity of $M_{FN}^{TCC}$ can be guaranteed.

Unlinkability: For each AKA session request, the vehicle generates a fresh pseudonym, timestamp, and random ECC point, where neither the timestamp nor the ECC point correlates with the vehicle’s identity or pseudonym, and no other entity except the TCC and the vehicle itself can track the true identity through pseudonym. Therefore, these mechanism effectively prevents any malicious entity from deducing whether two intercepted messages were transmitted by the identical sender.

Conditional privacy-preserving: Prior to initiating an AKA session, vehicle $V_i$ generates a pseudonym $PI{D}_i=I{D}_i\oplus H_2\left(r_i{P}_{pub}\right)$, then uses $PI{D}_i$ for all subsequent communications. Once message is disputed, The TCC can recover the real identity via $I{D}_i=PI{D}_i\oplus H_2\left(s{R}_i\right)$, where s is the master secret key, $R_i$ is a random ECC point.

To derive the real identity from $PI{D}_i$, any entity must calculate either $I{D}_i=PI{D}_i\oplus H_2\left(s{R}_i\right)$ or $I{D}_i=PI{D}_i\oplus H_2\left(r_i{P}_{pub}\right)$. s is the system’s master private key, owned only by TCC, while $r_i$ is a random number, owned only by the vehicle $V_i$. Solving for $r_i$ from R or s from $P_{pub}$ requires solving the difficult ECDL problem. Therefore, except TCC, no other entities can obtain the real identity.

Revocability: TCC maintains a revocation list $RevList$. Upon detection of a malicious vehicle $V_i$, its real identity $I{D}_i$ is added to $RevList$. If $V_i$ attempts to initiate subsequent AKA sessions, TCC will detect that its real identity $I{D}_i$ is already in the revocation list $RevList$ and terminate the AKA procedure. All revocation operations are concentrated on TCC, which has abundant computing and storage resources, making it relatively friendly for vehicle terminals with limited resources.

Forward and backward secrecy: In our scheme, the session key is computed as $S{K}_i=H_7(f_i\left(0\right),PI{D}_i,I{D}_f,t_t)$, where: $f_i\left(0\right)$ depends on two fresh random nonces, $PI{D}_i$ is a randomly generated ECC point. The single-use and randomness of these parameters ensure no correlation between session keys $s{k}_i$ across different sessions, thus guaranteeing both forward and backward secrecy.

Resistance to impersonation Attack: In our scheme, any passed message contains a verification value, which is bound to the certificate of the entity (vehicle or FN) through a hash function. Since these certificates are exclusively held by TCC and the originating entity itself, no other party can forge valid verification values. Consequently, any impersonation attempt by malicious attackers will be detected during the recipient’s verification process.

Resistance to replay attack: In our scheme, each transmitted message incorporates a timestamp. For instance, during the FN-to-TCC message transmission, $F{N}_f$ sends the message $M_{FN}^{TCC}=\{I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg},{\beta }_f\}$ to TCC, where $t_f$ denotes the timestamp. As demonstrated in the “Data integrity” section, the timestamp $t_f$ is immutable. Upon receiving the message $M_{FN}^{TCC}$, TCC verifies its freshness by checking whether the inequality $|t_c-t_f|<\Delta T$ holds, where $t_c$ represents the current time. If not, TCC treats the message as expired. Therefore, this timestamp validation mechanism, combined with the immutability guarantee, ensures that our scheme can effectively defend against replay attack.

5.2. Formal Security Proof

In this section, we formally prove that our scheme satisfies session key security under the Real-Or-Random (ROR) model [30].

5.2.1. Security Model

We first establish a security model to define the adversaries’ capabilities and the interaction rules between the challenger and the adversaries, and the model includes the following definitions:

Participants: Let ${\Pi }_V^i$, ${\Pi }_{FN}^f$, and ${\Pi }_{TCC}^t$ denote the i-th instance of a vehicle, the f-th instance of a FN, the t-th instance of a TCC, respectively. The concrete instance of these participants can also be represented as ${\Pi }_{\Lambda }^{\chi }$, where $\Lambda$ indicates the instance type and $\chi$ represents the index. Notably, RSUs are excluded from being considered as participating entities, as they merely function as conventional base stations for message forwarding.

Partnering: Two participants are considered as partners if they (a) belong to the same session, (b) successfully exchange messages in sequence, and (c) want to mutually authenticate each other.

Freshness: If the adversary $\mathcal{A}$ does not obtain the session key shared among ${\Pi }_V^i$, ${\Pi }_{FN}^f$, and ${\Pi }_{TCC}^t$, then these instances are considered fresh.

Adversary: The adversary $\mathcal{A}$ can participate in interactions of ${\Pi }_V^i$, ${\Pi }_{FN}^f$, and ${\Pi }_{TCC}^t$ by adopting the following oracle queries.

• $Execute({\Pi }_V^i,{\Pi }_{FN}^f,{\Pi }_{TCC}^t)$: This query simulates the passive adversary $\mathcal{A}$ to intercept messages exchanged among ${\Pi }_V^i$, ${\Pi }_{FN}^f$, and ${\Pi }_{TCC}^t$.
• $Send({\Pi }_{\Lambda }^{\chi },m)$: The query models an active adversary $\mathcal{A}$ sending message m to ${\Pi }_V^i$, ${\Pi }_{FN}^f$, and ${\Pi }_{TCC}^t$. Upon receiving this query, these instances return corresponding response messages to $\mathcal{A}$.
• $Test\left({\Pi }_{\Lambda }^{\chi }\right)$: When challenger $\mathcal{C}$ receives this query from adversary $\mathcal{A}$, it randomly selects a bit $b\in \{0,1\}$, if $b=1$, $\mathcal{C}$ sends the real session key of ${\Pi }_{\Lambda }^{\chi }$ to $\mathcal{A}$; if $b=0$, $\mathcal{C}$ sends a random key of the same length as the session key to the $\mathcal{A}$. If the session key of ${\Pi }_{\Lambda }^{\chi }$ is undefined, or if a $\mathsf{Test}$ query has been made to ${\Pi }_{\Lambda }^{\chi }$ or its partners, $\mathcal{A}$ receives ⊥ as an invalid value.

Semantic security: Adversary $\mathcal{A}$ first perform $Test\left({\Pi }_{\Lambda }^{\chi }\right)$ query, and guess the random value of b in $Test\left({\Pi }_{\Lambda }^{\chi }\right)$ query, denotes as $b^{\prime }$, if $b^{\prime }=b$, $\mathcal{A}$ wins, We define our BAKAF scheme as $\mathcal{P}$, and the advantage of $\mathcal{A}$ to break the $\mathcal{P}$’s semantic security based on ROR model within PPT as $Ad{v}_{\mathcal{A}}^{\mathcal{P}}=|2Pr[b^{\prime }=b]-1|$, where $Pr\left[E\right]$ denotes the probability that the event E occurs, if $Ad{v}_{\mathcal{A}}^{\mathcal{P}}$ is negligible, our scheme is regarded as secure under the ROR model.

5.2.2. Security Proof

In this subsection, we prove that our BAKAF scheme satisfies the semantic security of the session key.

Theorem 1.

Let $N_i(i=1,2,\dots ,7)$, $|has{h}_i|(i=1,2,\dots ,7)$, $N_s$, $N_e$, $N_t$, and $Ad{v}_{\mathcal{A}}^{PRF}$ represent the maximum number of hash $H_i$($i=1,2,\dots ,7$) queries, the space range of hash function $H_i$($i=1,2,\dots ,7$), the number of $\mathsf{Send}$ oracle queries, the number of $\mathsf{Execute}$ oracle queries, the number of $\mathsf{Test}$ oracle queries, and the advantage of adversary $\mathcal{A}$ in breaking the PRF, respectively. Thus, the advantage $Ad{v}_{\mathcal{A}}^{\mathcal{P}}$ of adversary $\mathcal{A}$ in breaking the semantic security of the session keys in our BAKAF scheme within PPT, can be calculated as follows:

$$Ad{v}_{\mathcal{A}}^{\mathcal{P}}\le {\displaystyle \frac{N_s+N_e}{q}}+\sum _{i=1}^7{\displaystyle \frac{N_i^2}{|has{h}_i|}}+2Ad{v}_{\mathcal{A}}^{PRF}$$

(1)

Proof: Similar to [31,32], to prove Theorem 1, we construct a sequence of games ${\mathsf{Game}}_i$ ($i=0,1,2,3$). These games involve interactions between adversary $\mathcal{A}$ and challenger $\mathcal{C}$. We define ${\mathsf{succ}}_i$ as the event that adversary $\mathcal{A}$ wins in ${\mathsf{Game}}_i$.

$Gam{e}_0$: This game serves as the starting point of the entire proof process. It simulates a realistic environment in which adversary $\mathcal{A}$ launches actual attacks. A random number b is predetermined before the game begins. Based on the semantic security of the session key, we have

$$Ad{v}_{\mathcal{A}}^{\mathcal{P}}=2|Pr\left[suc{c}_0\right]-1/2|$$

(2)

$Gam{e}_1$: In this game, the adversary $\mathcal{A}$ is permitted to eavesdrop on communications among parties ${\Pi }_V^i$, ${\Pi }_{FN}^f$ and ${\Pi }_{TCC}^t$ by executing the Execute operation. Subsequently, $\mathcal{A}$ performs the Test operation to distinguish the real session key $S{K}_i$ from a random value. And because of $S{K}_i=H_7(f_i\left(0\right),PI{D}_i,I{D}_f,t_t)$, where $f_i\left(0\right)=-x_i^v{y}_i^t{(x_i^t-x_i^v)}^{-1}-x_i^t{y}_i^v{(x_i^v-x_i^t)}^{-1}$. Since determining the equation of a straight line requires at least two distinct points on the line, but $\mathcal{A}$ can obtain at most one point, the actual session key cannot be computed. Consequently, the probability of $\mathcal{A}$ winning ${\mathsf{Game}}_1$ is identical to that of winning ${\mathsf{Game}}_0$, as shown below:

$$Pr\left[suc{c}_1\right]=Pr\left[suc{c}_0\right]$$

(3)

$Gam{e}_2$: Based on $Gam{e}_1$, the adversary $\mathcal{A}$ can perform Send and hash oracle queries. In this game, $\mathcal{A}$ launches spoofing attacks by forging and sending malicious requests to ${\Pi }_V^i$, ${\Pi }_{FN}^f$, and ${\Pi }_{TCC}^t$. Our scheme allows $\mathcal{A}$ to modify messages $M_V^{FN}$, $M_{FN}^{TCC}$, $M_{TCC}^{FN}$, and $M_{FN}^V$, but these messages contain random elements ($r_i$, $x_f$, $x_i^t$) and independent timestamps ($t_i$, $t_f$, $t_t$). Hence, $\mathcal{A}$ must execute $\mathsf{Send}$ queries without causing collisions. By the birthday paradox, we derive the following probability bound:

$$|Pr\left[suc{c}_2\right]-Pr\left[suc{c}_1\right]|\le {\displaystyle \frac{N_s+N_e}{2q}}+\sum _{i=1}^7{\displaystyle \frac{N_i^2}{2|has{h}_i|}}$$

(4)

$Gam{e}_3$: In this game, the $\mathsf{Send}({\Pi }_{\mathsf{TCC}}^t,M_{FN}^{TCC})$ oracle is slightly modified compared to $Gam{e}_2$. Specifically, when processing queries from $\mathcal{B}$, the challenger $\mathcal{C}$ now substitutes the $\mathsf{PRF}$ outputs with truly random numbers. Since this modification affects exactly two $\mathsf{PRF}$ operations, namely $PRF(H_1(c_f^{\prime },t_t),x_f)$ and $PRF(H_1(c_i^{\prime },t_t),x_i^v)$), we can derive the following probability bound:

$$|Pr\left[suc{c}_3\right]-Pr\left[suc{c}_2\right]|\le Ad{v}_{\mathcal{A}}^{PRF}$$

(5)

After that, the adversary $\mathcal{A}$ has utilized all available oracles to challenge the semantic security of protocol $\mathcal{P}$. Adversary $\mathcal{A}$ attempts to win the game solely by guessing the value of b. All session keys $S{K}_i$ used to respond to Test queries in this game are independently and uniformly distributed. As a result, no information regarding the hidden bit b used by the Test oracle is leaked to the adversary. Consequently, we obtain:

$$Pr\left[suc{c}_3\right]=1/2$$

(6)

By combining the above formulas: (2), (3), (4), (5), (6), we can obtain:

$$\begin{array}{cc}\hfill Ad{v}_{\mathcal{A}}^{\mathcal{P}}& =2\left|Pr\right[suc{c}_0]-1/2|\hfill \\ \hfill & =2|Pr\left[suc{c}_1\right]-Pr\left[suc{c}_3\right]|\hfill \\ \hfill & =2|Pr\left[suc{c}_1\right]-Pr\left[suc{c}_2\right]+Pr\left[suc{c}_2\right]-Pr\left[suc{c}_3\right]|\hfill \\ \hfill & \le 2\left(\right|Pr\left[suc{c}_2\right]-Pr\left[suc{c}_1\right]|\hfill \\ \hfill & +|Pr\left[suc{c}_3\right]-Pr\left[suc{c}_2\right]\left|\right)\hfill \\ \hfill & \le {\displaystyle \frac{N_s+N_e}{q}}+\sum _{i=1}^7{\displaystyle \frac{N_i^2}{|has{h}_i|}}+2Ad{v}_{\mathcal{A}}^{PRF}\hfill \end{array}$$

(7)

Since q and $|Has{h}_i|$ are typically sufficiently large, and $Ad{v}_{\mathcal{B}}^{PRF}$ is small enough and infinitely close to 0, the adversary $\mathcal{A}$’s advantage $Ad{v}_{\mathcal{A}}^{\mathcal{P}}$ in breaking the semantic security of our BAKAF scheme is negligible. Thus, our scheme is semantically secure under the ROR model.

6. Peformance Evaluation

In this subsection, we evaluate the proposed scheme’s performance through two key metrics: computational overhead and communication overhead. We compare our BAKAF scheme with state-of-the-art provably secure AKA schemes [20,21,22,23]. The selection of these comparative schemes is based on two key criteria: (1) Our scheme employs three-party entity collaboration for key agreement, and all selected comparison schemes similarly adopt a three-party framework. (2) Since our scheme eliminates computationally expensive bilinear pairing operations, pairing-based AKA schemes are excluded from the comparison to ensure fairness.

As far as we know, this scheme is the first batch three-party AKA scheme in VANETs. Therefore, if other schemes perform n AKA sessions, the computational and communication overheads of those schemes are n times the respective overheads of a single AKA session.

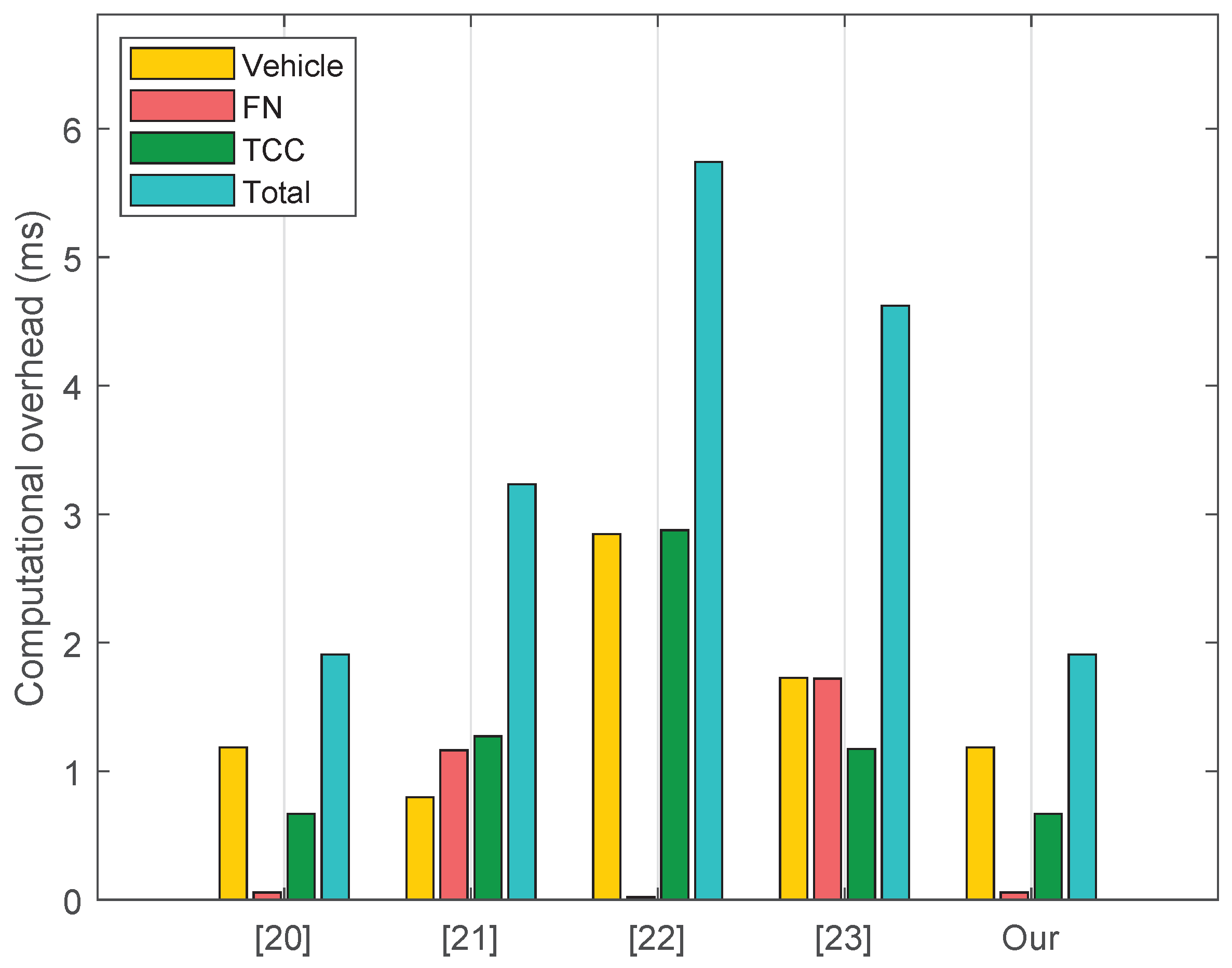
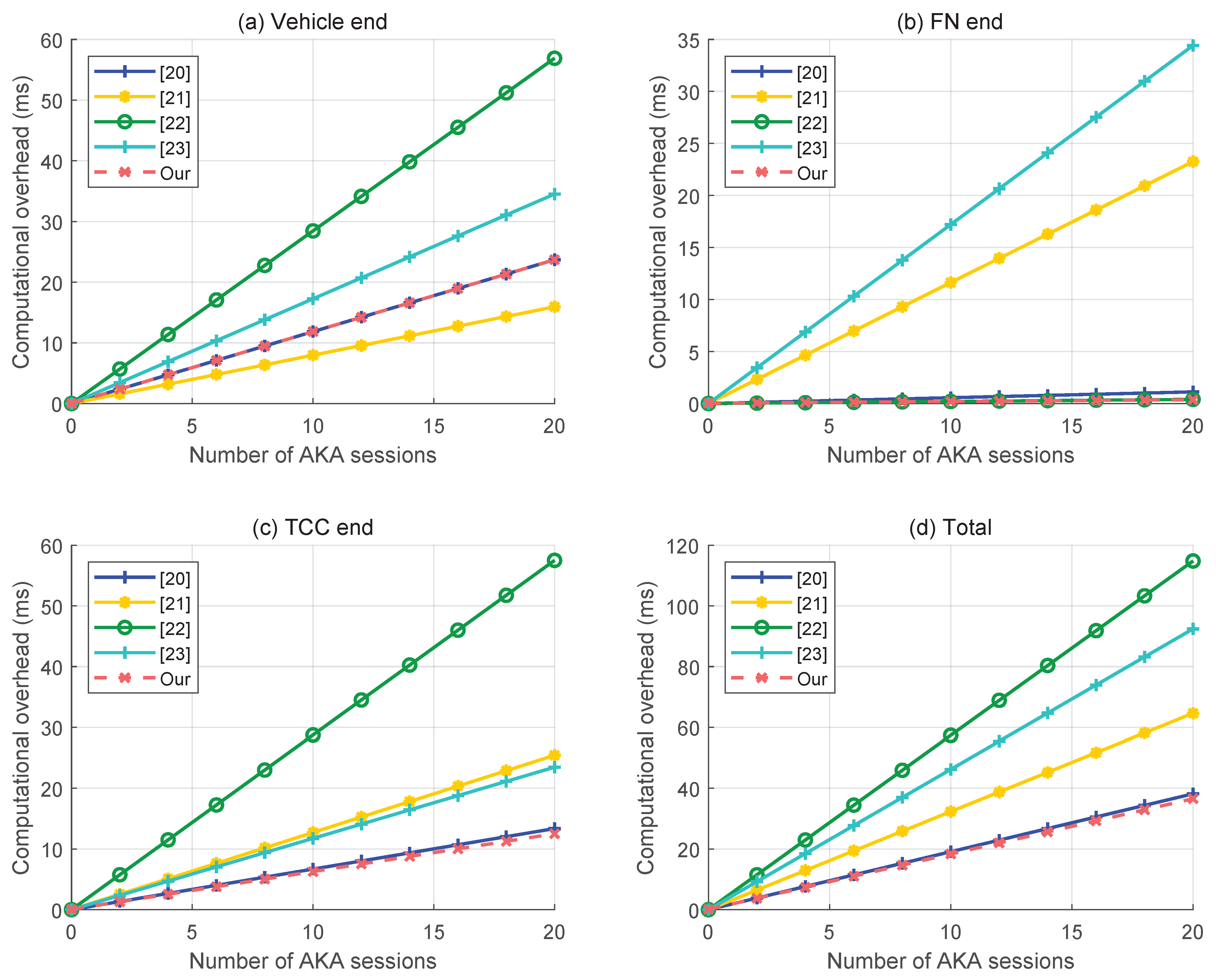
6.1. Computational Overhead Comparison

Before comparing the computational overhead, we use the MIRACL [33] library to measure all basic operations. All experiments are conducted on a laptop equipped with an Intel Core i5-12500 processor, 16 GB of memory, and the Windows 11 operating system. We omitted normal $Z_q^{*}$ operations (addition, multiplication) and string operations (concatenation, XOR) due to their negligible execution times. The experimental results for the average time consumption of basic operations are shown in Table 2. It is noted that each operation’s execution time was averaged across 1000 repetitions.

In a complete AKA session process of the Lu et al.’s scheme [20], a vehicle needs to execute 2 scalar multiplication operations based on ECC, 1 Lagrange interpolation operation, 1 PRF operation and 5 one-way hash operations, so the computational overhead of a vehicle is $2T_{sm}+T_{la}+T_{prf}+5T_h$; A fog node needs to execute 1 PRF operation, 1 Lagrange interpolation operation and 4 hash operations, so the computational overhead of the fog node is $T_{la}+T_{prf}+4T_h$; A sub-TA needs to execute 1 Lagrange interpolation operation, 1 scalar multiplication operation based on ECC, 2 PRF operations and 9 one-way hash operations, so the computational overhead of a sub-TA is $T_{sm}+T_{la}+2T_{prf}+9T_h$, in scheme [20], a lookup operation for real ID was performed on the Cuckoo Filter, however, since this functionality is not implemented in our proposed scheme, we omitted this operation to ensure fairness, the role of sub-TA is similar to that of TCC in our scheme. Thus, the total computational overhead of scheme [20] is $n(3T_{sm}+3T_{la}+4T_{prf}+18T_h)$.

In a complete AKA session process of the Qiao et al.’s scheme [21], a user needs to execute 2 Extended Chebyshev chaotic map operations, 7 one-way hash operations, so the computational overhead of a user is $2T_{cm}+7T_h$, and the role of user is similar to that of vehicle in our scheme; A fog node needs to execute execute 3 Extended Chebyshev chaotic map operations, 4 one-way hash operations, so the computational overhead of the fog node is $3T_{cm}+4T_h$; A server needs to execute 3 Extended Chebyshev chaotic map operations, 4 symmetric encryption operations, and 13 one-way hash operations, so the computational overhead of a cloud needs is $3T_{cm}+4T_{aes}+13T_h$, and the role of server is similar to that of TCC in our scheme. Thus, the total computational overhead of scheme [21] is $n(8T_{cm}+24T_h+4T_{aes})$.

In a complete AKA session process of the Jiang et al.’s scheme [22], a user needs to execute 5 scalar multiplication operations based on ECC, 7 one-way hash operations, so the computational overhead of a user is $5T_{sm}+7T_h$, and the role of user is similar to that of vehicle in our scheme; A autonomous vehicle needs to execute 4 one-way hash operations, and the role of autonomous vehicle is similar to that of fog node in our scheme; A cloud needs to execute 5 scalar multiplication operations based on ECC and 13 one-way hash operations, so the computational overhead of a cloud needs is $5T_{sm}+13T_h$, and the role of cloud is similar to that of TCC in our scheme. Thus, the total computational overhead of scheme [22] is $n(10T_{sm}+24T_h)$.

In a complete AKA session process of the Cui et al.’s scheme [23], a vehicle needs to execute 8 one-way hash operations and 3 scalar multiplication operations based on ECC, so the computational overhead of a vehicle is $8T_h+3T_{sm}$; A cloud service needs to execute 7 one-way hash operations and 3 scalar multiplication operations based on ECC, so the computational overhead of the cloud service is $7T_h+3T_{sm}$, and the role of cloud service is similar to that of fog node in our scheme; A TA needs to execute 10 one-way hash operations and 2 scalar multiplication operations based on ECC, so the computational overhead of a TA is $10T_h+2T_{sm}$, The role of TA is similar to that of TCC in our scheme. Thus, the total computational overhead of scheme [23] is $n(25T_h+8T_{sm})$.

In our BAKAF scheme, assume that AKA is executed in a batch for n vehicles, a vehicle needs to execute 2 scalar multiplication operations based on ECC, 1 Lagrange interpolation operation, 1 PRF operation and 5 one-way hash operations, so the computational overhead of a vehicle is $2T_{sm}+T_{la}+T_{prf}+5T_h$, and the computational overhead of n vehicle is $2n{T}_{sm}+n{T}_{la}+n{T}_{prf}+5n{T}_h$; A fog node needs to execute 1 PRF operation, n Lagrange interpolation operation and $3+n$ hash operations, so the computational overhead of the fog node is $n{T}_{la}+T_{prf}+(3+n)T_h$ for n vehicles and $T_{la}+T_{prf}+4T_h$ for $n=1$ vehicle; TCC needs to execute n Lagrange interpolation operations, n scalar multiplication operations based on ECC, $n+1$ PRF operations and $5n+4$ one-way hash operations, so the computational overhead of TCC is $n{T}_{sm}+n{T}_{la}+(n+1)T_{prf}+(5n+4)T_h$ for n vehicles and $T_{sm}+T_{la}+2T_{prf}+9T_h$ for $n=1$ vehicle. Thus, the total computational overhead is $3n{T}_{sm}+3n{T}_{la}+2(n+1)T_{prf}+(11n+7)T_h$ for n vehicles and $3T_{sm}+3T_{la}+4T_{prf}+18T_h$ for $n=1$ vehicle.

Consequently, the comparison results of computational overhead between our scheme and schemes [20,21,22,23] are presented in Table 3.

And we use Figure 3 to show the comparison results for a single AKA session, according to Figure 3, our scheme maintains identical computational overhead to Scheme [20], while demonstrating significant advantages over Schemes [21,22,23] in terms of both per-entity and total computational overhead. Meanwhile, Figure 4 compares the computational overhead (both per-entity and total) for all schemes when n AKA sessions are conducted within a fixed time interval. The results demonstrate that as the number of vehicles n increases, our scheme achieves lower computational overhead than baseline schemes.

The low computational overhead of our scheme primarily stems from two key factors: (1) Our scheme employs lightweight cryptographic primitives, while the more computationally intensive ECC-based scalar multiplication operations are exclusively used for anonymous credential generation; (2) The batch AKA approach significantly reduces the overall computational operations. Beyond reducing per-entity computational overhead, our scheme substantially decreases the interaction between FN and TCC through batch AKA session processing.

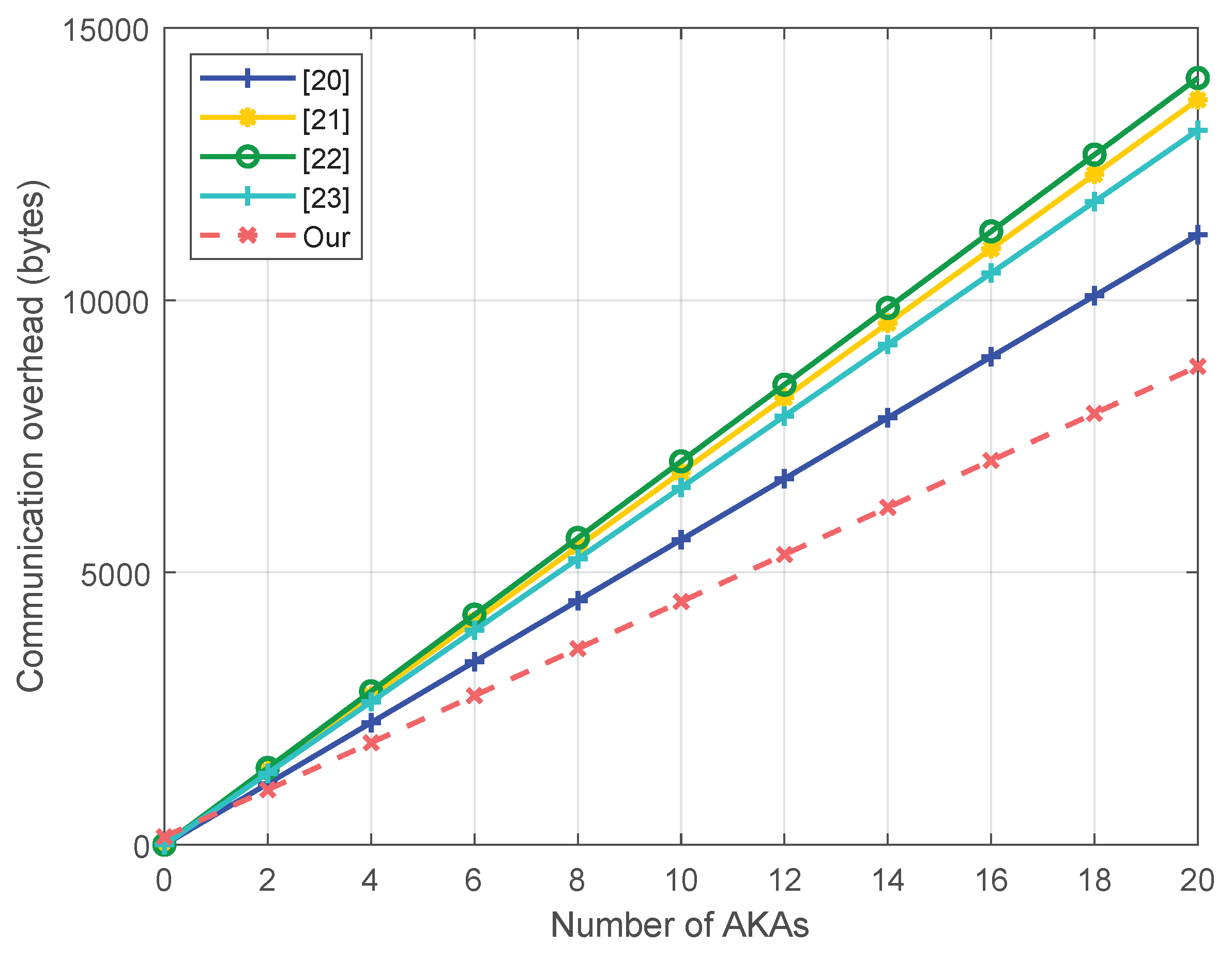
6.2. Communication Overhead Comparison

Before comparing the communication overhead, we assume that the security parameters of all schemes are 128 bits in length. The element types and lengths involved in information transmission for each scheme are listed in Table 4. To ensure fairness and simplicity, we adopt AES as the symmetric encryption algorithm across all schemes, with ciphertext length identical to plaintext length.

In Scheme [20], a vehicle transmits $\{pi{d}_i,t_i,R_i,{\alpha }_i\}$ to the FN in the first stage, where $pi{d}_i$ is the pseudonym, whose length is identical to $\left|ID\right|$, $t_i$ is the timestamp, $R_i$ is an element in elliptic curve group G, ${\alpha }_i\in Z_q^{*}$, so the communication overhead in the first stage is $\left|ID\right|+\left|t\right|+\left|G\right|+|Z_q^{*}|=120$ bytes. In the second stage, the FN transmits $\{i{d}_j,t_j,n_j,pi{d}_i,t_i,R_i,{\alpha }_i,{\beta }_j\}$ to TCC, where $i{d}_j$ is the real identity, $t_j$ is the timestamp, $n_j,{\beta }_j\in Z_q^{*}$, so the communication overhead in this stage is $2\left|ID\right|+2\left|t\right|+\left|G\right|+3|Z_q^{*}|=208$ bytes. In the third stage, TCC transmits $\{n_k,f{n}_k,t_k,{\gamma }_k,{\delta }_k\}$ to the FN, where $n_k,f{n}_k,{\gamma }_k,{\delta }_k\in Z_q^{*}$, and $t_k$ is the timestamp, so the communication overhead in this stage is $\left|t\right|+4|Z_q^{*}|=132$ bytes. In the fourth stage, the FN transmits $\{n_k,f{n}_k,t_k,{\delta }_k\}$ to the vehicle, so the communication overhead in this stage is $\left|t\right|+3|Z_q^{*}|=100$ bytes. Suppose n vehicles conducting AKA sessions during a fixed time interval, the total communication overhead is $(120+208+132+100)n=560n$ bytes.

In Scheme [21], a user transmits $M{S}_1=\{NI{D}_i,PI{D}_i,W_i,T_1,T_u\left(x\right)\}$ to the fog node $F{N}_j$ in the first stage, where $NI{D}_i=E_s(I{D}_i\left|\right|O_i)$ is obtained by symmetrically encrypting the concatenation of the identifier $I{D}_i$ and a random number $O_i$, whose length is identical to $\left|ID\right|+\left|Z_q^{*}\right|$, $T_1$ is timestamp, $PI{D}_i$ and $W_i$ are derived from one-way hash functions, since their data types are unspecified in the original paper, we adopt the 20-byte length defined therein, $T_u\left(x\right)$ is the extended Chebyshev polynomial, whose length is $\left|E\right|$. So the communication overhead in the first stage is $|M{S}_1|=|ID|+|Z_q^{*}|+2*20+|t|+|E|=128$ bytes. In the second stage, the $F{N}_j$ transmits $M{S}_2=\{M{S}_1,NI{D}_j,A,T_v\left(x\right),W_j,T_2\}$ to cloud server S, where $NI{D}_j=E_s(I{D}_j\left|\right|N_j)$ is obtained by symmetrically encrypting the concatenation of the identifier $I{D}_j$ and a random number $N_j$, whose length is $\left|ID\right|+|Z_q^{*}|$, A and $T_v\left(x\right)$ are the extended Chebyshev polynomial, $T_2$ is timestamp, $W_j$ is derived from one-way hash functions, so the communication overhead in this stage is $|M{S}_1|+|ID|+|Z_q^{*}|+|t|+2|E|+20=268$ bytes. In the third stage, cloud server S transmits $|M{S}_3|=\{V_i,V_j,A{u}_i,A{u}_j,B,C,T_3\}$ to the fog node $F{N}_j$, where $V_i,V_j,A{u}_i,A{u}_j$ are derived from one-way hash functions, B and C are the extended Chebyshev polynomial, and $T_3$ is the timestamp, so the communication overhead in this stage is $4\ast 20+2\left|E\right|+\left|t\right|=148$ bytes. In the fourth stage, the fog node $F{N}_j$ transmits $M{S}_4=\{V_i,A{u}_i,A,B,C,T_3\}$ to the user, where $T_3$ is timestamp, so the communication overhead in this stage is $2\ast 20+3\left|E\right|+\left|t\right|=140$ bytes. Suppose n users conducting AKA sessions during a fixed time interval, the total communication overhead is $(128+268+148+140)n=684n$ bytes.

Similarly, when executing n AKA sessions within a fixed time interval, the total communication overhead for Scheme [22] and Scheme [23] is calculated as $704n$ bytes and $656n$ bytes, respectively.

In our scheme, suppose there are n vehicles performing AKA sessions with the same fog node $F{N}_f$ within a fixed time interval, vehicle $V_i$ need to transmits ${\left(M_V^{FN}\right)}_i=\{M_i=\{PI{D}_i,t_i,R_i\},MA{C}_i\}$ to the fog node $F{N}_f$, where $PI{D}_i$ is pseudonym, $t_i$ is timestamp, $R_i$ is an element in elliptic curve group G, and $MA{C}_i$ is the message authentication code, so the communication overhead of n vehicles in the first stage is $\left(\right|ID|+|t|+|G|+|M\left|\right)n=108n$ bytes. In the second stage, the fog node $F{N}_f$ transmits the message $M_{FN}^{TCC}=\{I{D}_f,t_f,x_f,M_{agg},MA{C}_{agg},{\beta }_f\}$ to TCC, where $I{D}_f$ is real identity, $t_f$ is time timestamp, $x_f,{\beta }_f\in Z_q^{*}$, $M_{agg}$ is formed by sequentially concatenating n messages ${\left\{M_i\right\}}_{i=1}^n$, whose length is $n\left(\right|ID|+|t|+|G\left|\right)$, and $MA{C}_{agg}$ is message authentication code, so the communication overhead in this stage is $\left|ID\right|+\left|t\right|+2|Z_q^{*}|+n(\left|ID\right|+\left|t\right|+\left|G\right|)+|M|=108+88n$ bytes. In the third stage, TCC transmits the message $M_{TCC}^{FN}=\{{\{PI{D}_i,x_i^t,y_i^t,{\delta }_i^t\}}_{i=1}^l,t_t,{\gamma }_t\}$ to the fog node $F{N}_f$, where $t_t$ is timestamp, $x_i^t,y_i^t,{\delta }_i^t,{\gamma }_t\in Z_q^{*}$, here we assume $l=n$, implying that all vehicles’ data are both correct and complete. so the communication overhead in this stage is $n\left(\right|ID|+3|Z_q^{*}\left|\right)+\left|t\right|+|Z_q^{*}|=36+116n$ bytes. In the fourth stage, the fog node $F{N}_f$ sends the messages ${\left\{M_{FN}^V\right\}}_{i=1}^n={\{PI{D}_i,x_i^t,y_i^t,t_t,{\delta }_i^t\}}_{i=1}^n$ to the corresponding vehicles ${\left\{V_i\right\}}_{i=1}^n$ respectively,so the communication overhead in this stage is $n\left(\right|ID|+3|Z_q^{*}|+|t\left|\right)=120n$ bytes. Thus, for n vehicles executing the AKA sessions, the total communication overhead across all four stages amounts to $432n+144$ bytes.

Figure 5 compares the communication overhead of different schemes as the number of AKAs varies. As shown in the figure, our scheme demonstrates a clear advantage as the number of AKAs increases. This is primarily because our scheme processes multiple AKA requests in batches within a fixed time interval.

7. Conclusion and Remark

In this scheme, for a batch of vehicles initiating AKA requests to the same fog node within a fixed short time interval, We combine fog computing and Lagrange interpolation to complete these AKA processes in a round of operations. The interpolation points of the straight lines corresponding to each vehicle share a common point at the fog node. These mechanisms ensure that our scheme possesses very low computational and communication overhead while simplifying the overall system operations.

The authentication component of our scheme relies on the certificates of vehicles and fog nodes, as well as the system master secret key. It is assumed that the system master secret key and the certificate values remain perpetually secure. However, existing physical attack techniques (such as side-channel attacks) can obtain such sensitive information. Since existing technologies like physically unclonable functions and fuzzy extractor can effectively resist these physical attacks, our scheme does not focus on this aspect in-depth.

The batch AKA mechanism designed in our scheme requires participating vehicles to establish session keys with the same FN, which poses a certain limitation. How to perform batch AKA operations among different vehicles and different FNs within a short time interval is a key direction for our future research.