Exploring Novel Perspectives on Model Compression Techniques and Their Impact on Adversarial Robustness in Deep Learning: A Comprehensive Review and Analysis

1. Introduction

In recent years, the demand for real-time, on-device models has significantly increased, leading to their application across diverse fields. While large neural networks often achieve high accuracy, their substantial computational and memory requirements frequently render them impractical for on-device processing. To mitigate these challenges, model compression techniques—such as pruning, quantization, and knowledge distillation—are widely employed to reduce the size of neural networks without substantially compromising performance. These techniques have proven effective in practice, facilitating the broader deployment of Deep Neural Networks (DNNs) in resource-constrained applications[1].

However, a crucial aspect of model performance that is often overlooked in the context of compression is adversarial robustness [2,3]. Adversarial robustness refers to the model’s ability to withstand adversarial attacks, wherein minor, imperceptible modifications to input data can lead to incorrect predictions. Mathematically, given a model $f:{\mathbb{R}}^d\to {\mathbb{R}}^k$ and an input $\mathbf{x}\in {\mathbb{R}}^d$, an adversarial example can be formulated as:

$${\mathbf{x}}_{adv}=\mathbf{x}+\delta$$

(1)

where ${\parallel \delta \parallel }_p\le ϵ$ for a specified norm p (e.g., $L_2$ or $L_{\infty }$) and perturbation magnitude $ϵ$. Various strategies have been proposed to defend against such attacks, with one of the most prominent being adversarial training. This approach employs an adversary to generate adversarial examples, subsequently retraining the model on these examples to enhance its robustness [4]. Research has shown that adversarial training results in more accurate decision boundaries, as these boundaries attain a margin from data points, particularly within the $L_p$ ball of the example.

The potential risks posed by adversarial attacks are particularly concerning in high-stakes applications such as autonomous vehicles and medical diagnostics. The susceptibility of a model to adversarial attacks becomes increasingly problematic when it undergoes compression, as the reduction in parameters and precision may adversely affect its capacity to resist adversarial perturbations. Given the paramount importance of deploying robust and secure models, it is essential to comprehend how compression techniques influence adversarial robustness, both in research and practical applications. The interplay between model compression and adversarial robustness remains poorly understood [5]. While compression techniques are primarily designed to minimize the trade-off between model size and accuracy, their impact on a model’s security under adversarial conditions is not well characterized. Some studies suggest that model compression may render networks more vulnerable to attacks, while others propose that, under specific circumstances, compression could enhance robustness. However, most existing research treats model compression and adversarial robustness as distinct areas of study, thereby creating a critical gap in understanding how these compression methods influence robustness across varying model architectures and attack scenarios.

This paper seeks to address this gap by providing a systematic benchmarking study of model compression techniques within the context of adversarial robustness. We empirically evaluate three major compression techniques—pruning, quantization, and knowledge distillation—to ascertain their effects on the robustness of deep learning models against a spectrum of adversarial attacks. Our experiments investigate the trade-offs between model size, accuracy, and robustness, yielding new insights into how compression techniques can be optimized for real-world applications where efficiency and security are both critical.

To facilitate this empirical evaluation, we introduce a novel benchmarking pipeline that enables consistent comparisons across different models, compression rates, and attack methodologies. Our experiments investigate the trade-offs between model size, accuracy, and robustness, yielding new insights into how compression techniques can be optimized for real-world applications where efficiency and security are both critical.

1.1. Novelty of the Work

This study represents an effort to systematically examine the interplay between model compression techniques and adversarial robustness. The novelty of this work lies in its comprehensive approach to bridging two critical areas of deep learning research that have traditionally been treated in isolation. By providing empirical evidence on how different compression techniques affect the adversarial robustness of neural networks, we offer new perspectives on the trade-offs involved in deploying efficient models in real-world scenarios. Furthermore, the introduction of a standardized benchmarking pipeline sets a precedent for future research, facilitating more reliable comparisons and encouraging further investigations into this underexplored domain.

1.2. Paper Structure

The remainder of this paper is structured as follows: Section 2 presents a detailed review of existing literature on model compression and adversarial robustness, integrating both domains to provide a comprehensive background. Section 3 presents the methodology. Section 4 describes the experimental setup. In Section 5, we present the results of our evaluations, followed by a discussion in Section 6 that interprets the findings and their implications. Finally, Section 7 concludes the paper, summarizing the contributions and suggesting directions for future research.

By focusing on the intersection of model compression and adversarial robustness, this paper establishes a foundation for future research aimed at optimizing both model efficiency and security. Our findings illuminate critical considerations that researchers and practitioners must take into account when deploying compressed models in adversarial contexts, ultimately guiding the development of more robust and efficient neural networks for real-world applications.

2. Background

In this section, we investigate related works on model compression and adversarial robustness. We start by discussing the different model compression techniques that will be used in the study. Then, we will discuss adversarial attacks and defenses. Lastly, we will summarize the different studies that address the connection between robustness and model compression

2.1. Model Compression Techniques

Model compression is a crucial step in optimizing deep learning models for deployment in resource-constrained environments. This section outlines three widely used techniques for model compression: pruning, quantization, and knowledge distillation, providing theoretical explanations for each.

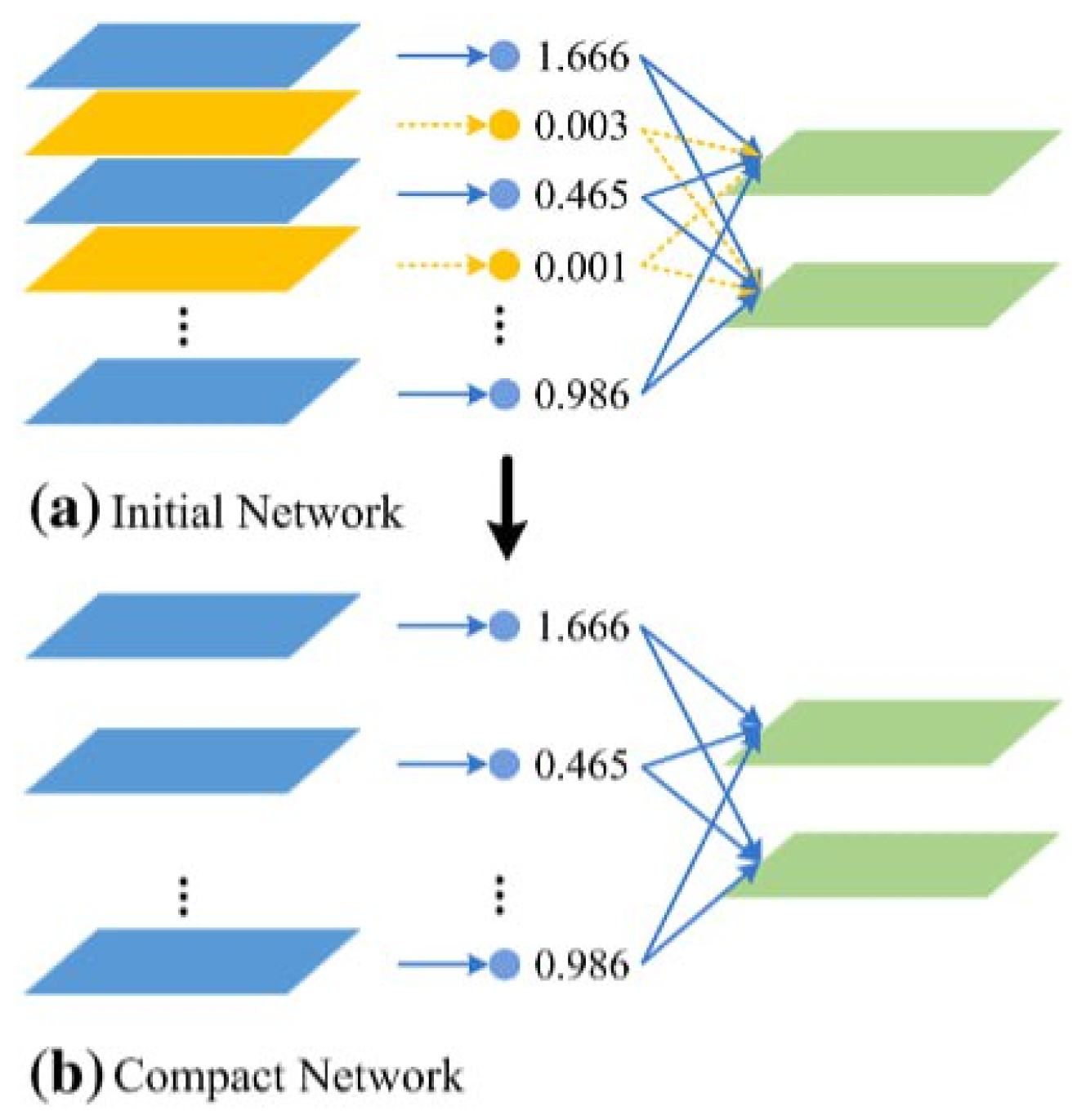
2.1.1. Pruning

Pruning reduces the size of neural networks by selectively removing parameters based on their importance as illustrated in Figure 1, which is often defined by the sensitivity of the loss function to these parameters [6]. Specifically, parameters that contribute minimally to the performance of the model are pruned, resulting in a sparser and more efficient model.

Let $f(x;W)$ represent the neural network function parameterized by the weight matrix W. The sensitivity of the loss function $L\left(f\right(x;W),y)$ concerning individual parameters can be used to determine which weights to prune. This sensitivity can be quantified using the magnitude of gradients or Hessian-based approaches:

$$S\left(w_{ij}\right)={\displaystyle \frac{\partial L}{\partial w_{ij}}}$$

(2)

Weights $w_{ij}$ with low sensitivity $S\left(w_{ij}\right)$ (i.e., those having little effect on the loss) are pruned, resulting in a new, sparse weight matrix $W^{\prime }$. Pruning can be expressed mathematically as:

$$W^{\prime }=W\odot {\mathbf{1}}_{S\left(W\right)>\theta }$$

(3)

where $\theta$ is a predefined threshold for sensitivity, and ${\mathbf{1}}_{S\left(W\right)>\theta }$ is an indicator function that retains only the weights with sensitivities greater than $\theta$.

It is important to note that after pruning, the resulting weight matrix $W^{\prime }$ is generally sparse, meaning that it contains many zero-valued weights. However, $W^{\prime }$ does not have the same size or number of parameters as W in terms of non-zero elements. Pruning, therefore, reduces the computational cost and memory footprint of the model by eliminating less important connections between neurons.

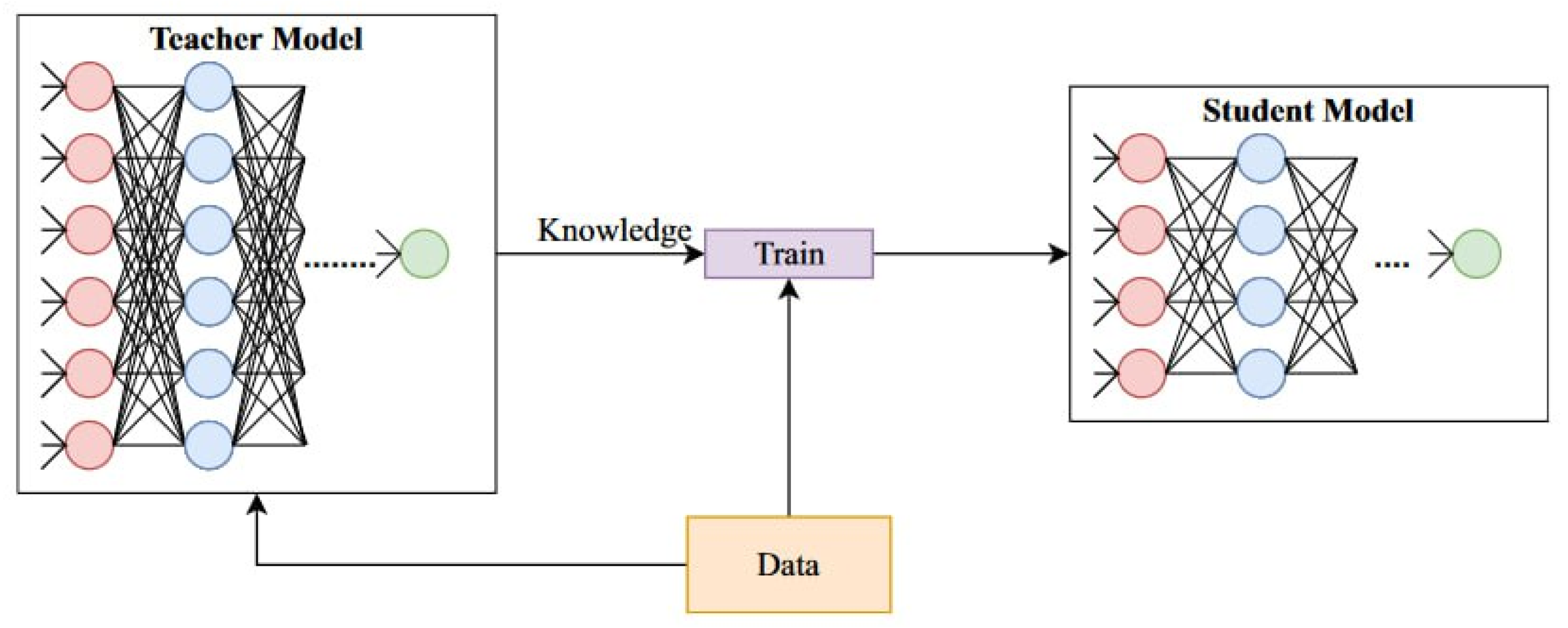
2.1.2. Knowledge Distillation

Knowledge distillation is a model compression technique in which a smaller model (student) is trained to mimic the behavior of a larger, more complex model (teacher) [7] as illustrated in Figure 2. The student model is optimized to reproduce the output distribution of the teacher model, allowing it to retain most of the performance benefits of the teacher while being more computationally efficient.

In this technique, the student model is trained using a combination of the true labels and the soft predictions of the teacher model. The distillation loss function is typically defined as:

$$L_{\mathrm{distill}}=\alpha L_{\mathrm{CE}}(M_s\left(x\right),y)+(1-\alpha )L_{\mathrm{KL}}(p_t\left|\right|p_s)$$

(4)

where:

• $M_s\left(x\right)$ and $M_t\left(x\right)$ are the outputs of the student and teacher models, respectively.
• $p_t=\mathrm{softmax}\left({\displaystyle \frac{M_t\left(x\right)}{T}}\right)$ is the teacher’s probability distribution over the output classes, softened by a temperature T.
• $p_s=\mathrm{softmax}\left(M_s\left(x\right)\right)$ is the student’s output distribution.
• $L_{\mathrm{CE}}$ is the cross-entropy loss with the true labels y, and $L_{\mathrm{KL}}$ is the Kullback-Leibler divergence between the teacher and student distributions.
• $\alpha$ is a weighting factor that balances the two loss terms.

The parameter T (temperature) controls the softness of the teacher’s output probabilities, allowing the student model to learn from the relative similarities between classes, rather than just the hard class assignments. By transferring the knowledge encoded in the teacher model’s outputs, knowledge distillation enables the student model to achieve comparable performance with fewer parameters, leading to efficient deployment.

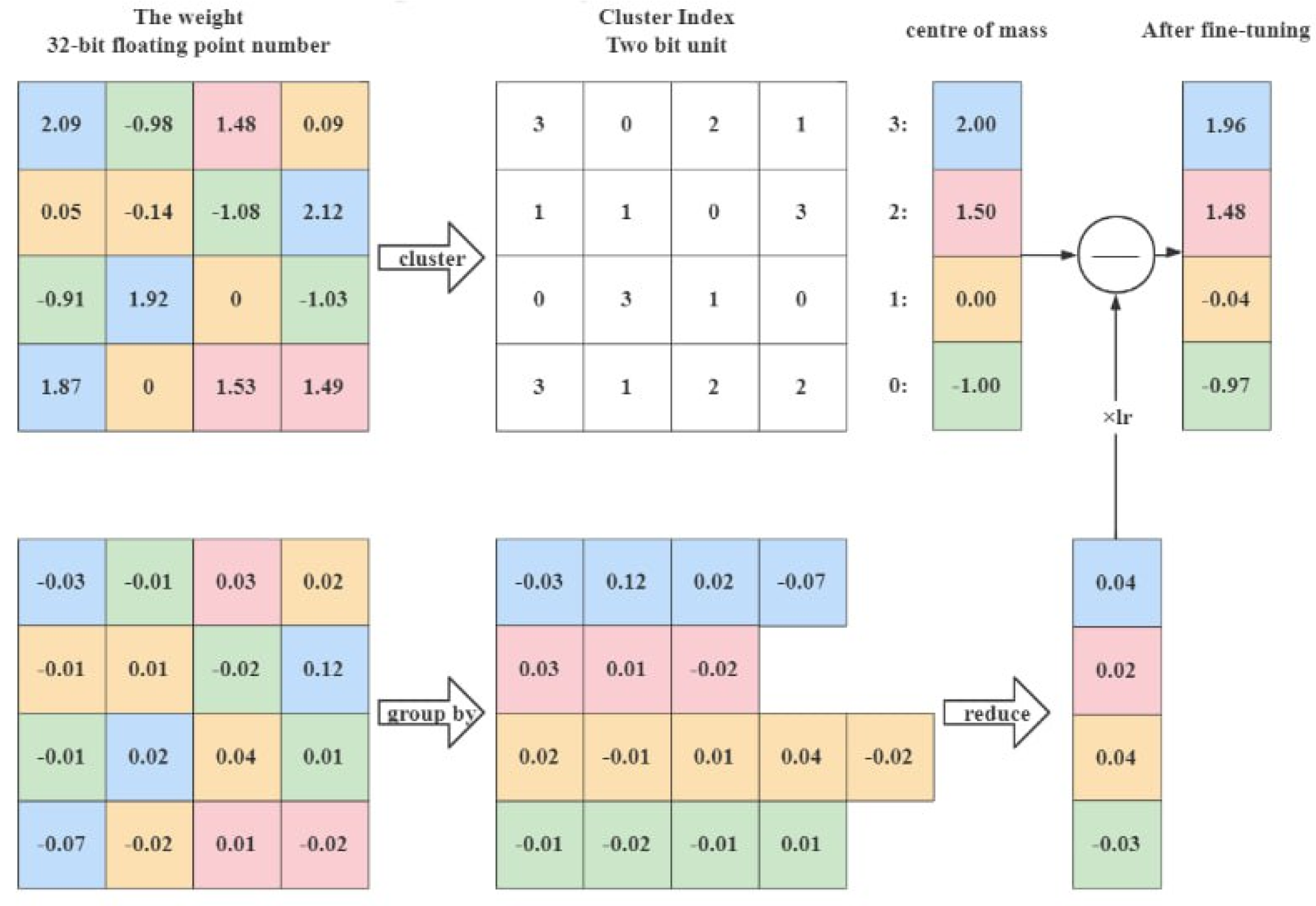
2.1.3. Quantization

Quantization compresses a model by reducing the precision of its parameters, often by converting floating-point weights and activations into lower-precision formats such as 8-bit integers as shown in the Figure 3. The goal of quantization is to minimize the model size and computational demands while retaining a similar level of performance [8].

Mathematically, quantization of a weight w involves mapping it to a discrete set of values, typically determined by a quantization step size $\mathrm{\Delta }$:

$$w_q=\mathrm{round}\left({\displaystyle \frac{w-w_{\min }}{\mathrm{\Delta }}}\right)·\mathrm{\Delta }+w_{\min }$$

(5)

where:

$$\mathrm{\Delta }={\displaystyle \frac{w_{\max }-w_{\min }}{N}}$$

(6)

Here, $\mathrm{\Delta }$ represents the quantization resolution, $w_{\min }$ and $w_{\max }$ are the minimum and maximum weight values, and N is the number of quantization levels. By reducing the precision of weights and activations, quantization significantly reduces the model’s memory requirements and speeds up inference, particularly in hardware accelerators like GPUs or TPUs [9].

Quantization is especially effective in scenarios where high precision is not necessary for maintaining the performance of the model, such as in inference tasks where slight variations in weight values have negligible effects on the final predictions.

2.2. Adversarial Attack Generation

Adversarial attacks involve crafting input perturbations that cause a machine-learning model to misclassify. These perturbations are often imperceptible to humans, making the attack especially dangerous in sensitive applications [10,11,12,13,14]. Several adversarial attack methods exist, including Fast Gradient Sign Method (FGSM) [15], Basic Iterative Method (BIM) [16], Carlini & Wagner (C&W) attacks [17], and Projected Gradient Descent (PGD) [18]. Among these, PGD is widely regarded as one of the most powerful first-order adversarial attacks, and thus, we will focus on it in our experiments. PGD iteratively modifies the input data to maximize the model’s loss function, constrained by a perturbation limit.

The iterative update rule for PGD is given by:

$$x_{t+1}^{\prime }=\mathrm{clip}(x_t^{\prime }+\alpha ·\mathrm{sign}\left({\nabla }_{x}L(M\left(x^{\prime }\right),y)\right),x-ϵ,x+ϵ)$$

(7)

where:

• $L(M\left(x^{\prime }\right),y)$ is the loss function with respect to the model M and the target label y,
• $x^{\prime }$ is the adversarial example,
• $ϵ$ is the perturbation limit, controlling the maximum allowable change to the input,
• $\alpha$ is the step size, determining how much the adversarial example is modified in each iteration.

We have chosen PGD because of its effectiveness in generating adversarial examples that are challenging for models to defend against, especially in a white-box setting where the model’s parameters are known to the attacker.

2.2.1. Evaluation Metrics for Adversarial Robustness

Evaluating a model’s robustness against adversarial attacks requires specific metrics that quantify the model’s ability to withstand attacks while maintaining classification performance [15,18]. The key metrics used in this evaluation are:

Robustness Accuracy:

This metric measures the percentage of adversarial examples that the model correctly classifies. It is defined as:

$$\mathrm{Robustness}\mathrm{Accuracy}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\mathbf{1}\{M\left(x_i^{\prime }\right)=y_i\}$$

(8)

where N is the total number of adversarial examples, $M\left(x_i^{\prime }\right)$ is the model’s prediction on the adversarial example $x_i^{\prime }$, and $y_i$ is the true label.

Average Perturbation:

This metric quantifies the average magnitude of the perturbations introduced by adversarial attacks. It is computed as:

$$\mathrm{Average}\mathrm{Perturbation}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\parallel x_i^{\prime }-x_i\parallel }_2$$

(9)

where $x_i$ is the original input, and $x_i^{\prime }$ is the corresponding adversarial example.

2.2.2. Defense Mechanisms

Various defense strategies have been proposed to counter adversarial attacks. These methods either train models to be more robust to adversarial perturbations or modify model predictions to mitigate the impact of such attacks. The most commonly used techniques include:

Adversarial Training:

Adversarial training involves augmenting the training process with adversarial examples. The model is trained using a loss function that combines the losses from both clean and adversarial data, thereby improving robustness. The combined loss is given by:

$$L={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(L_{\mathrm{CE}}(M\left(x_i\right),y_i)+\lambda ·L_{\mathrm{CE}}(M\left(x_i^{\prime }\right),y_i)\right)$$

(10)

where:

• $L_{\mathrm{CE}}$ denotes the cross-entropy loss,
• $M\left(x_i\right)$ is the model’s prediction on clean input $x_i$,
• $M\left(x_i^{\prime }\right)$ is the model’s prediction on the adversarial example $x_i^{\prime }$,
• $\lambda$ controls the balance between the losses from clean and adversarial examples.

Defensive Distillation:

This technique trains the model with softened labels (probabilities rather than hard class labels) to make the model less sensitive to adversarial perturbations. By using smoothed outputs from a teacher model during training, the student model learns to generalize better and becomes more resilient against adversarial attacks.

Adversarial Purification:

A recent approach related to our research group, adversarial purification focuses on transforming adversarial examples back into their clean form before feeding them into the model. This method leverages generative models or denoising algorithms to "purify" the adversarial input, reducing the adversarial impact without requiring the model itself to be altered. Empirical results show promising robustness against various attack methods.

Input Transformation:

Input transformation techniques, such as image resizing, rotation, or adding noise, are employed to preprocess inputs before feeding them into the model. This preprocessing can disrupt the carefully crafted nature of the adversarial attack, though its effectiveness is generally considered low compared to other techniques. However, recent advancements in adversarial purification suggest that input transformations, when integrated with more sophisticated approaches, may yield better results.

2.2.3. Comparison of Defense Techniques

Each defense mechanism offers different levels of robustness, with varying trade-offs in terms of computational cost, complexity, and effectiveness. Adversarial training remains the most widely used and empirically validated approach for enhancing model robustness, particularly against white-box attacks. Adversarial purification shows good results and can be integrated with other defense mechanisms to improve overall robustness.

The Table 1 reflects evaluations from studies on adversarial robustness [17,18,19,20,21,22], including advances in adversarial purification, which shows significantly improved results in various experimental settings.

2.3. Compression and adversarial robustness

Pruning is a widely utilized compression technique that reduces the number of parameters in Deep Neural Networks (DNNs). At its core, pruning seeks to eliminate nodes or edges in the network (parameters) that contribute minimally to the output during training. While importance-based pruning methods, such as magnitude pruning, are common, research has demonstrated that they can sometimes be ineffective. Pruning strategies can be broadly categorized into two types: Filter Pruning and Weight Pruning. Filter pruning involves the removal of entire filters from Convolutional Neural Networks (CNNs). Filters are typically ranked based on an importance score, often calculated using $L1$ or $L2$ norms, with the least important filters being pruned. This method is classified as a Regular Pruning technique because it systematically reduces the model’s complexity by eliminating entire filters, thereby affecting the network’s structure. Various methodologies have been applied in filter pruning, with differing focuses and outcomes. For instance, neuron pruning, which removes neurons from fully connected layers and subsequently all connected edges, represents another form of pruning. However, as our research is centered on image classification tasks involving CNNs, neuron pruning is not the primary focus of this discussion.

In contrast, Weight Pruning concentrates on removing individual weights within filters or channels while preserving the overall network structure, often referred to as Irregular Pruning. Several studies have examined the implications of combining pruning with adversarial training to enhance model robustness. For example, Han et al. [23] introduce a magnitude-based pruning technique that involves iterative stages of identifying, pruning, and retraining, resulting in a sparse model with significantly reduced storage requirements. This process is particularly effective when integrated with adversarial training. By adding a regularizer to the min-max optimization problem, as demonstrated in [23], models can achieve a compression rate of $4\times$ while maintaining both natural and adversarial accuracy. This approach combines regular and irregular pruning techniques to maximize the benefits of both methods. The relationship between pruning and adversarial training is further explored in the work [24] and the work [25], which empirically demonstrate that adversarial training post-pruning is critical for maintaining adversarial accuracy. Their findings highlight the inherent trade-offs between classification accuracy, compression size, and robustness. This idea is echoed in the work of other researchers [26], who propose dynamic network surgery as a comprehensive compression pipeline. This method iteratively prunes and splices redundant weights, followed by further compression through quantization and encoding, achieving faster and higher compression rates compared to earlier methods such as those proposed in the work [23].

Another innovative approach is introduced in work [27], which developed a pruning framework that operates on adversarially trained models without the need for adversarial examples, albeit with increased training time. This method employs self-distillation techniques and the Hilbert-Schmidt Independence Criterion (HSIC) metric to retain robustness, solving the problem using the Alternating Direction Method of Multipliers (ADMM). This technique addresses the combinatorial nature of the problem more effectively than traditional Stochastic Gradient Descent (SGD). Pruning techniques can be further divided into One-Shot Pruning and iterative pruning. One-shot pruning is exemplified in studies where pruning is completed in a single step, potentially enhancing model robustness in specific cases, as seen in [25]. Conversely, iterative pruning, which involves repeated cycles of pruning and retraining, is more commonly used in conjunction with adversarial training to refine model accuracy and robustness. For instance, [28] introduces a dynamic network rewiring (DNR) method that integrates pruning and adversarial training into a unified, non-iterative training framework. This approach leverages a hybrid loss function that combines clean image classification, adversarial training loss, and a dynamic L2 regularizer, dynamically adjusting inter-layer connectivity. DNR provides over $20\times$ compression on models such as VGG16 and ResNet-18 across datasets like CIFAR-10, CIFAR-100, and Tiny-ImageNet, with negligible accuracy loss. Subsequent research has enhanced this model with DNR++, which incorporates sparse parametric noise regularization to improve robustness, while FDNR++ employs a "free" adversarial training technique that significantly reduces training time.

On the other hand, quantization is a critical technique for reducing the precision of weights and activations in DNNs, thereby decreasing the model’s memory usage and computational cost. It can be broadly categorized into two main types: Weight Quantization, which focuses on reducing the precision of the model’s weights, and Activation Quantization, which targets the activations or outputs of neurons. Several studies have explored the implications of quantization on adversarial robustness, often employing different quantization-aware training techniques or evaluating models under various adversarial conditions.

A significant focus in the literature has been on understanding how quantization impacts model robustness against adversarial attacks. Both [29] and [30] examine the effects of quantization on model robustness, particularly under adversarial settings. Gorsline et al. demonstrate that under certain attack strengths, model accuracy remains largely stable or slightly improves regardless of the quantization rate, attributing this to the gradient masking effect of the ReLU activation function, which inherently resists stronger attacks. Duncan et al. expand on this by showing that quantized models retain almost all of the robustness of their full-precision counterparts, with relative robustness ranging from 98.6% to 99.7%. However, they observe that adversarial deficiencies in full-precision models are not entirely transferred to quantized models, with adversarial transfer rates varying between 52.0% and 98.9%. Another line of research focuses on the regularization effects of quantization and its ability to handle adversarial perturbations. [31] explores the dual role of quantization in reducing noise for small perturbations while potentially amplifying it for larger ones. They attribute this amplification to error propagation and propose adding a regularization term to the cost function to limit the network’s Lipschitz constant, thereby controlling the extent of this amplification. Similar concerns are addressed by Song et al. [32], who introduce layer-wise quantization to better preserve adversarial robustness. They critique prior work for focusing primarily on white-box attacks, arguing that a broader approach is necessary to validate robustness. Their method involves integrating a quantization loss term with general adversarial training loss, evaluated using the Lipschitz constant.

The interplay between quantization and adversarial training has also been a key area of exploration. Both [33] and [34] highlight the complex relationship between quantization and adversarial robustness. [33] focus on transformer-based text classifiers, showing that while quantization slightly decreases natural accuracy, it significantly enhances robustness against adversarial attacks. [34] provides an empirical analysis that reveals the conflicting conclusions about the effects of quantization on adversarial robustness often stem from variations in experimental setups, including different adversarial training techniques and quantization precisions. Research on hybrid quantization methods and their implications for robustness is also notable. The work [35] introduces a hybrid quantization approach driven by Adversarial Noise Sensitivity (ANS), which optimally balances energy efficiency, accuracy, and robustness. They quantify each layer’s sensitivity to adversarial perturbations and assign lower bit-widths to more sensitive layers. However, their approach overlooks the potential for error amplification during ANS calculation and does not address the optimal number of training epochs, which could vary based on the dataset.

Other innovative approaches include Binarized Neural Networks (BNNs) and non-linear mapping techniques. The work [36] proposes BNNs, which quantize models to 1-bit precision. While this method significantly reduces model size, it introduces challenges such as gradient masking and complicating adversarial training. Nevertheless, their results indicate that BNNs can outperform full-precision models under certain conditions, particularly in Fast Gradient Sign Method (FGSM) settings. In contrast, In work [37], the authors propose a non-linear mapping technique for the final layers of a model to enhance robustness against first-order white-box attacks. This method utilizes $\mu$-law non-linearity, slightly reducing natural accuracy while significantly improving adversarial robustness. However, they caution that adversarial training itself is susceptible to quantization effects, and non-linear mapping may not perform well in such settings. Lastly, Knowledge Distillation (KD) is another pivotal technique for model compression, particularly concerning adversarial robustness. This process involves training a smaller model (the student) to replicate the behavior of a larger, pre-trained model (the teacher). The knowledge distilled from the teacher to the student encompasses more than just the final output probabilities, including intermediate representations that can enhance the robustness of the distilled model.

Recent studies highlight the effectiveness of KD in enhancing adversarial robustness. For instance, The work [38] first introduced the idea of distillation, demonstrating that the student model could achieve competitive performance when trained with softened logits from the teacher model. Subsequent research has built on this foundation, with the work [39] which demonstrates that adversarial examples can be used as a training signal for the student, thereby improving its robustness. This approach is particularly relevant given that teacher models often exhibit heightened robustness due to adversarial training, making the distilled student models more resilient against similar attacks.

Overall, the synergy between model compression techniques—such as pruning, quantization, and knowledge distillation—and adversarial robustness remains a rich field of inquiry. The existing literature demonstrates that while these techniques can enhance model efficiency, they also introduce complex dynamics that warrant further investigation to fully understand their implications for adversarial training and robustness.

3. Methodology

This research introduces a benchmarking pipeline aimed at evaluating the trade-offs between model compression, adversarial robustness, and parameter efficiency in pre-trained models. The methodology is divided into four distinct phases: pretraining, compression, fine-tuning (if necessary), and evaluation. Each phase is designed to ensure a comprehensive analysis of how compression affects both model size and resilience to adversarial attacks, providing actionable insights for optimizing model performance under various constraints.

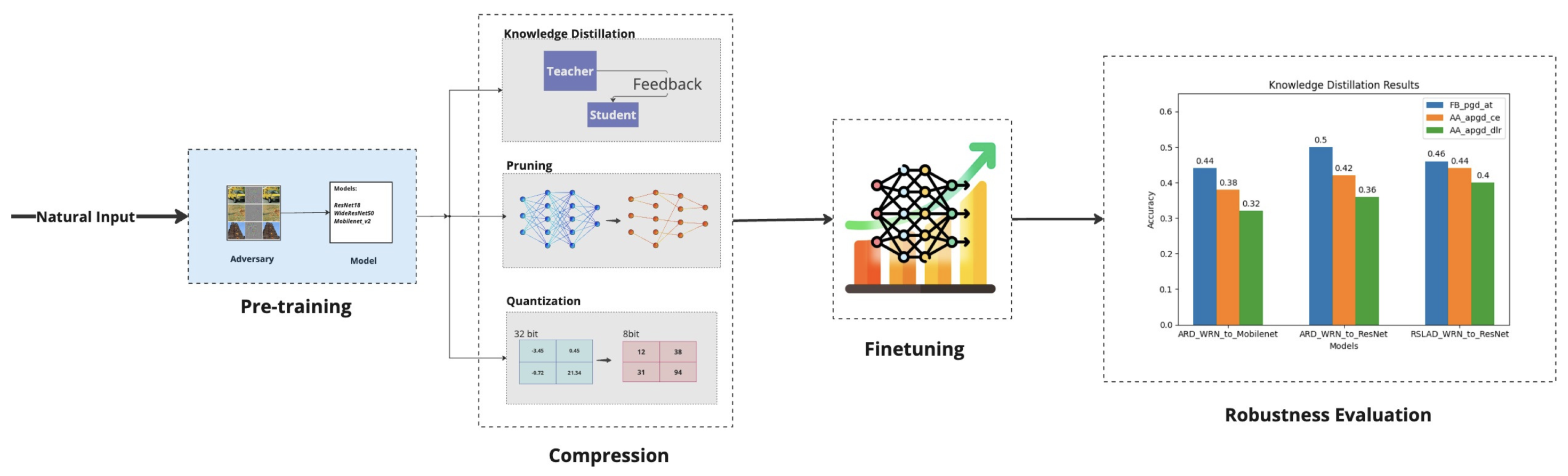
3.1. Pipeline Overview

The benchmarking pipeline, as illustrated in Figure 4, is structured into four primary stages:

• Pretraining
• Compression
• Fine-tuning
• Evaluation

Each stage plays a critical role in understanding the impacts of compression on model robustness and efficiency.

3.1.1. Pretraining

In the initial phase, the model M is pretrained on a dataset $\mathcal{D}$, establishing a baseline performance. The objective during pretraining is to minimize the loss function $\mathcal{L}(M,\mathcal{D})$ through standard optimization techniques, such as stochastic gradient descent (SGD).

$$\mathcal{L}(M,\mathcal{D})={\displaystyle \frac{1}{n}}\sum _{i=1}^n\ell \left(M\left(x_i\right),y_i\right)$$

(11)

Here, $x_i\in \mathcal{D}$ denotes the input data samples, $y_i$ represents the corresponding labels, and ℓ is the chosen loss function (e.g., cross-entropy loss). This step generates the pre-trained model M that will undergo compression.

3.1.2. Compression

Once pretrained, the model M is subjected to a compression algorithm $\mathcal{C}$, yielding the compressed model $M_c=\mathcal{C}\left(M\right)$. The goal of compression is to reduce the model’s size while maintaining its performance. This necessity arises from the need to deploy models efficiently in resource-constrained environments without sacrificing their effectiveness. The compression process involved Pruning, Quantization, Knowledge distillation, and techniques such as

3.1.3. Fine-Tuning

If the compression process results in a significant drop in model performance, fine-tuning is employed to restore accuracy. In this stage, the compressed model $M_c$ is further trained on the original dataset $\mathcal{D}$, optimizing its post-compression performance.

$$M_c^{*}=\mathrm{Fine}-\mathrm{Tune}(M_c,\mathcal{D})$$

(12)

Fine-tuning helps bridge the gap between the compressed model’s reduced size and its original performance.

3.1.4. Evaluation

The final stage involves rigorous evaluation of the compressed model $M_c$ using a series of adversarial attacks, specifically employing the Projected Gradient Descent (PGD) attack. The adversarial robustness $R\left(M_c\right)$ is quantified as the model’s accuracy under adversarial perturbations:

$$R\left(M_c\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathbb{I}(M_c(x_i+\delta )=y_i)$$

(13)

Here, $\delta$ represents the adversarial perturbation, and $\mathbb{I}(·)$ is the indicator function. Robustness is measured across various levels of perturbation $ϵ$, providing insight into the model’s stability under adversarial conditions.

3.2. Benchmarking Pipeline Key Components

The benchmarking pipeline integrates multiple dimensions to evaluate each model comprehensively. The key components include:

3.2.1. Model Compression Metrics

Each pretrained model M undergoes compression, with the compression ratio $\gamma$ and parameter count P computed. These metrics serve as indicators of compression efficiency and model size reduction:

$$\gamma ={\displaystyle \frac{P_{\mathrm{original}}}{P_{\mathrm{compressed}}}}$$

(14)

3.2.2. Adversarial Robustness Evaluation

The adversarial robustness R of compressed models is tested against various attack methods, focusing primarily on the PGD attack. For each perturbation level $ϵ$, the robustness metric is calculated by applying equation 13

This metric quantifies the model’s ability to maintain accuracy when subjected to adversarial attacks.

3.2.3. Categorization of Compression Techniques

After evaluation, the compressed models are categorized based on their compression technique (pruning, quantization, or knowledge distillation), as well as their respective compression ratio $\gamma$ and parameter count P. This categorization aids in understanding how different compression methods influence adversarial robustness and overall performance.

3.2.4. Performance Visualization

To facilitate comparative analysis, the pipeline generates detailed visualizations of the trade-offs between compression efficiency and adversarial robustness. These visualizations, generated using libraries such as matplotlib and seaborn, allow users to identify models that strike an optimal balance between size and robustness.

The pipeline summarizes the performance of each compressed model, providing recommendations based on the evaluation results. This includes identifying models that offer a favorable trade-off between compression ratio, parameter count, and robustness to adversarial attacks.

Algorithm 1Benchmarking Pipeline for Pretrained and Compressed Models

1: Input: Pretrained model M, Dataset $\mathcal{D}$ 2: Pretrain M on $\mathcal{D}$ 3: Compress M using compression algorithm $\mathcal{C}$ to obtain $M_c$ 4: if fine-tuning is required then 5:    Fine-tune $M_c$ on $\mathcal{D}$ 6:    $M_c^{*}=\mathrm{Fine}-\mathrm{Tune}(M_c,\mathcal{D})$ 7: end if 8: for each adversarial attack do 9:    Evaluate $M_c$ under attack A 10:    Compute adversarial robustness $R(M_c,A)$ 11: end for 12: Compute compression ratio $\gamma$ and parameter count P 13: Group models by compression technique, compression ratio $\gamma$, and parameter count P 14: Visualize performance trade-offs and summarize results

4. Experimental Setup

In this section, we present the experimental setup used to evaluate the adversarial robustness of six models, each utilizing different architectures and compression techniques, including pruning, knowledge distillation, and quantization. The models were subjected to three distinct adversarial attacks, all implemented using the Foolbox library [40,41]. The strength of the adversarial perturbations was controlled by an $ϵ$-value of $ϵ={\displaystyle \frac{8}{255}}$ under the $L_{\infty }$-norm. Table 2 provides a summary of the models, including their architectures, compression rates, and performance under adversarial attacks.

The evaluation includes two pruned models, RAP-ADMM [5] and Hydra [42], both of which apply different pruning strategies to neural networks. RAP-ADMM utilizes an adversarial pruning approach based on the WideResNet architecture, while Hydra implements layer-wise pruning on the ResNet architecture. These models were tested against both standard adversarial attacks and the more advanced Auto-PGD attack, ensuring consistent conditions across all experiments.

For knowledge distillation, three models were evaluated: RSLAD, ARD, and IAD. These models are based on distillation techniques and incorporate adversarial defense strategies. Their adversarial robustness was assessed using Projected Gradient Descent (PGD) attacks, with variations in loss functions such as Cross-Entropy and Difference of Logits Ratio (DLR) [43,44], providing a comprehensive view of their defense capabilities.

The evaluation also includes a quantized model, which applies low-bitwidth quantization to both weights and activations. Specifically, the model reduces the precision from full 32-bit ($w32\_a32$) to 1-bit ($w1\_a1$), achieving a 32x reduction in computational complexity. Despite this reduction, the model maintained a robust defense against adversarial attacks, demonstrating competitive accuracy relative to other quantization approaches [45]. The model was evaluated under identical attack parameters, including an $ϵ$-value of ${\displaystyle \frac{8}{255}}$ and the $L_{\infty }$-norm constraint.

Table 2 provides a consolidated overview of all the models, their architectures, applied compression techniques, and results from the adversarial attack evaluations.

5. Results

This study evaluated the impact of various model compression techniques under adversarial conditions across multiple architectures, including Wide Residual Networks (WRN), ResNet, and MobileNet. The evaluation focused on key performance metrics such as compression rate, parameter reduction, and adversarial robustness. The robustness was thoroughly tested using adversarial attacks, specifically the Fast Gradient Sign Method (FGSM) with Projected Gradient Descent (FB-PGD) and the AutoAttack (AA) framework, incorporating both APGD-CE and APGD-DLR variants.

The performance metrics for models compressed using the Hydra framework are presented in Table 3, showcasing the effectiveness of its pruning strategies. The results of the Intra-Architecture Distillation (IAD) approach, a form of knowledge distillation, are summarized in Table 4. Additionally, conventional knowledge distillation methods are evaluated, with results provided in Table 5.

For models subjected to the RAP-ADMM compression technique, performance metrics are detailed in Table 6, highlighting the balance between compression efficiency and adversarial robustness. The outcomes of the RSLAD methodology are encapsulated in Table 7, demonstrating its adversarial resilience. Finally, the performance results from the quantization framework are summarized in Table 8, emphasizing the trade-off between low-bitwidth quantization and adversarial defense capabilities.

This comprehensive analysis provides valuable insights into the trade-offs between model compression and adversarial robustness, with a focus on how different architectures and compression strategies respond to sophisticated adversarial attacks.

6. Discussion

The results presented herein elucidate a nuanced relationship between various model compression techniques and their corresponding adversarial robustness across distinct architectures. Each compression strategy exhibits unique characteristics that significantly influence performance metrics, particularly regarding resilience to adversarial attacks.

• Hydra Techniques: The Hydra methodologies demonstrate substantial compression rates (99x, 95x, and 90x); surprisingly, these high compression levels are accompanied by a marked increment in adversarial robustness, particularly when subjected to the FB-PGD and AA attacks.
• Knowledge Distillation (IAD vs. KD): The IAD framework displays superior performance compared to traditional KD approaches, evidenced by enhanced robustness metrics. Notably, IAD methods achieve higher accuracy under adversarial conditions, indicating a potential advantage in utilizing intra-architecture relationships to mitigate adversarial effects. Here IIAD-I stands for Introspective Adversarial Distillation based on ARD [44] and IAD-II Introspective Adversarial Distillation based on AKD2 [46].
• RAP-ADMM Techniques: Models subjected to RAP-ADMM compression exhibit varying degrees of adversarial resilience, suggesting that the selection of appropriate compression rates plays a critical role in optimizing both model size and robustness.
• RSLAD and Quanztion Frameworks: Both RSLAD and Quanztion frameworks present compelling results, particularly the Quanztion framework, which achieves notable accuracy metrics while maintaining a viable compression rate. This indicates a promising avenue for future research focusing on integrating quantization with adversarial robustness.

The observed results can be intuitively and theoretically explained by the interplay between model compression and adversarial robustness. Techniques like pruning in the Hydra methodologies remove redundant parameters, which intuitively reduces the model’s complexity and potential overfitting to adversarial perturbations. Theoretically, pruning acts as a form of regularization that simplifies the model’s decision boundaries, making it less sensitive to small, adversarially crafted input changes. Similarly, the Intra-Architecture Distillation (IAD) approach outperforms traditional Knowledge Distillation (KD) by internally preserving robust features within the same architecture. This internal distillation maintains the integrity of adversarial defenses more effectively than transferring knowledge from a separate teacher model, ensuring that crucial defensive mechanisms are retained in the compressed model.

Among all the techniques evaluated, quantization demonstrated the most remarkable results by achieving the highest compression rate while maintaining strong adversarial accuracy. By reducing the precision of the model parameters, quantization introduces discretization noise, which disrupts the gradient calculations used in adversarial attacks, thereby enhancing robustness. The quantization framework achieved a compression rate of 32x with an accuracy of 56.00% against PGD attacks and 49.20% against CWL2 attacks, outperforming other methods in both compression efficiency and adversarial resilience. This indicates that quantization not only effectively reduces the model size but also inherently strengthens the model against adversarial threats, making it the most effective technique among those evaluated.

The findings highlight the necessity for future explorations to delve deeper into the trade-offs between model compression and adversarial resilience. It remains imperative to formulate strategies that not only enhance model efficiency but also fortify defenses against adversarial attacks. Furthermore, employing a multi-faceted approach that incorporates advanced machine learning techniques may yield substantial improvements in model robustness.

7. Conclusions

In conclusion, this study has demonstrated the efficacy of various model compression techniques under adversarial conditions, emphasizing the complex interplay between compression rates and adversarial robustness. The results indicate that while aggressive compression strategies can significantly reduce model size, they may also compromise the model’s ability to withstand adversarial attacks. The Intra-Architecture Distillation (IAD) approach emerged as a particularly effective method for enhancing robustness while maintaining acceptable compression rates. Additionally, the RAP-ADMM and RSLAD techniques showed promise in balancing compression and adversarial performance. Future work should focus on addressing the limitations identified in this study, particularly through the exploration of hybrid approaches that integrate multiple compression techniques to optimize both model efficiency and resilience. Moreover, expanding the evaluation to include a wider array of architectures and adversarial attack scenarios could further elucidate the robustness and applicability of these compression methodologies in real-world settings.