The Impact of Optimization Approximation Algorithms on the Performance of BHT-QAOA

1. Introduction

In quantum computing, to solve combinatorial optimization problems, such as the MaxCut [1,2], the quantum approximate optimization algorithm (QAOA) was introduced by Farhi et al. [3,4]. The QAOA represents a combinatorial optimization problem in the form of an ansatz Hamiltonian oracle, which is the so-called “Hamiltonian clauses (H_C)”, and an ansatz Hamiltonian operator, which is the so-called “Hamiltonian mixer (H_M)”. Note that the wording “ansatz” means that H_C and H_M consist of parameterized rotational quantum gates of Pauli-Z (RZ) and Pauli-X (RX), respectively [3,4]. Such that H_C consists of a number of RZ(v⋅ɣ), RZZ(v⋅ɣ), RZZZ(v⋅ɣ), and so on, while H_M consists of n numbers of RX(ω⋅β), where (i) v and ω are the coefficients of time evolutions, (ii) ɣ and β are the parameterized angular rotations between the angles of [0, 2π] and [0, π], respectively [3,4], and (iii) n is the number of input qubits for a problem initially set to the states of |0⟩.

In the quantum domain, H_C is the circuit of a problem as the unitary operator $\left({\mathrm{e}}^{ – i\mathsf{\gamma }{H}_{\mathrm{C}}}\right)$, which is a set of non-connected nodes as RZj(v⋅ɣ) and connected nodes as RZjZk(v⋅ɣ), where j and k are the indices of input qubits. While H_M is the circuit for the sum of all n input qubits as the unitary operator $\left({\mathrm{e}}^{ – i\beta H_M}\right)$, which is a set of n RX(ω⋅β). Notice that H_M acts as the diffusion operator of QAOA analogous to the diffusion operator in Grover’s search algorithm [5,6,7,8], and H_M may include other variants and types of gates, not just RX gates, depending on the model of QAOA used [9,10,11,12,13]. To improve the quality of all approximated solutions, H_C and H_M are iterated for a number of repetitions (p), where p ≥ 1. Such that every ${\mathrm{e}}^{ – i{\mathsf{\gamma }}_p{H}_{\mathrm{C}}}$ consists of RZ(v⋅ɣ_p), RZZ(v⋅ɣ_p), etc., and every ${\mathrm{e}}^{ – i{\beta }_p{H}_M}$ consists of RX(ω⋅β_p).

In the classical domain, the numerical values of coefficients (v and ω) are calculated during the construction of H_C and H_M. The numerical values of angles (ɣ and β) are initially randomized as [ɣ₁ … ɣ_p, β₁ … β_p] for H_C and H_M, respectively. Notice that some studies initialized such angles to defined values using machine learning and tensor techniques [9,10,11,12,13]. In general, the circuit of QAOA is executed with a quantum processing unit (QPU), and then measured (in the classical domain) for approximated solutions depending on the chosen values of ɣ and β. The measured solutions (as the energy cost of QAOA [3,4]), the chosen values of ɣ and β (as the optimization parameters of QAOA), and the Hamiltonians (H_C and H_M as an objective function) are fed to a classical optimization minimizer function [14,15,16]. Such a minimizer then recalculates the numerical values of these optimization parameters based on the energy cost from the objective function, and updates H_C and H_M of QAOA with new optimized numerical values of ɣ and β, respectively. For a number of objective function evaluations (nfev), the optimization operational concurrencies between a QPU and a minimizer are repeated, until finding all optimized approximated solutions for a combinatorial optimization problem or stopping based on a pre-defined condition, which is the so-called “halt condition”. For that, the QAOA is considered a variational quantum search algorithm solving combinatorial optimization problems, in the hybrid classical-quantum domain [17,18,19].

In our work [20], we introduced a new methodology for solving arbitrary classical Boolean problems as Hamiltonians (H_C and H_M) using QAOA, and we termed this new variant of QAOA the “Boolean-Hamiltonians Transform for QAOA (BHT-QAOA)”. In general, the BHT-QAOA can be summarized as follows.

• An arbitrary classical Boolean problem is constructed as a quantum Boolean oracle [8,21]. This constructed oracle can be expressed in arbitrary logical structures, such as Product-Of-Sums (POS) [22,23], Sum-Of-Products (SOP) [22,24], Exclusive-or Sum-Of-Products (ESOP) [25,26], XOR-Satisfiability (CNF-XOR SAT and DNF-XOR SAT) [27,28], Algebraic Normal Form (ANF) (or Reed-Muller expansion) [29,30], just to name a few.
• This constructed oracle (in any logical structure) is converted into its equivalent quantum Boolean oracle in ESOP structure, unless it was initially constructed in ESOP structure.
• The quantum Boolean oracle in ESOP structure is transformed into its equivalent quantum Phase oracle [8,21], based on our modified transformation rules originally discussed by Figgatt et al. [21].
• The Hamiltonians (H_C and H_M) of QAOA are then generated from this transformed quantum Phase oracle, based on our modified composition rules originally presented by Hadfield [31].
• The above-mentioned optimization operational concurrencies between a QPU and a minimizer are performed for the generated H_C and H_M, until finding all optimized approximated solutions. Notice that, in [20], the SciPy optimization minimizer [32] is performed using the constrained optimization by linear approximation (COBYLA) algorithm [14,16,32].

The goal of this article is to investigate various approximation algorithms of SciPy optimization minimizer for the BHT-QAOA to find all optimized approximated solutions for arbitrary classical Boolean problems. These optimization approximation algorithms are: (i) Broyden-Fletcher-Goldfarb-Shanno (BFGS) [32,33,34], (ii) limited-memory BFGS with bounds (L-BFGS-B) [35,36], (iii) sequential least squares programming (SLSQP) [37,38], (iv) COBYLA, and (v) constrained optimization by quadratic approximations (COBYQA) [39]. Our investigation is comparing and classifying such approximation algorithms based on our two proposed performance metrics: (i) the final utilization of nfev and (ii) the final quality of qubits measurement as the optimized approximated solutions.

In this article, arbitrary classical Boolean problems (as applications) are expressed as Boolean oracles in various logical structures, and these Boolean oracles are then solved using BHT-QAOA for p repetitions, with an IBM QPU and different algorithms of SciPy optimization minimizer. These applications are: (i) an arbitrary Boolean problem in POS structure, (ii) an arbitrary Boolean problem in SOP structure, (iii) an arbitrary Boolean problem in ESOP structure, (iv) a 2×2 Sudoku game, and (v) a 4-bit conditioned half-adder digital circuit. Eventually, our investigation proves that the BFGS and SLSQP algorithms for the BHT-QAOA successfully find all best-approximated solutions for these arbitrary applications, in the context of fewer nfev and higher quality of qubits measurement.

2. Methods

In quantum computing, a quantum Boolean oracle is an easier and straightforward approach in conceptually expressing an arbitrary classical Boolean problem than using a quantum Phase oracle, because (i) the quantum Boolean-based gates can be easily realized using the truth tables (and De Morgan’s Laws [22]) of their equivalent classical Boolean gates, and (ii) the quantum Boolean-based gates and their qubits can be easily analyzed using classical Boolean logic, such as a Boolean logic of 0 represents a quantum state of |0⟩ and a Boolean logic of 1 represents a quantum state of |1⟩. In this article, for ease of description, the quantum Boolean oracle and the quantum Phase oracle will be simply denoted as the “Boolean oracle” and the “Phase oracle”, respectively.

In BHT-QAOA, converting a Boolean oracle (in any logical structure) into a Phase oracle will (i) remove all ancilla qubits (including the output qubit), i.e., the total number of utilized qubits will be dramatically reduced to the number of input qubits only, and (ii) omit the mirror gates (as the uncomputing part) of an oracle, i.e., the total number of quantum gates will be significantly minimized for the circuit of a Phase oracle, depending on the initial construction of a Boolean oracle that expresses a classical Boolean problem.

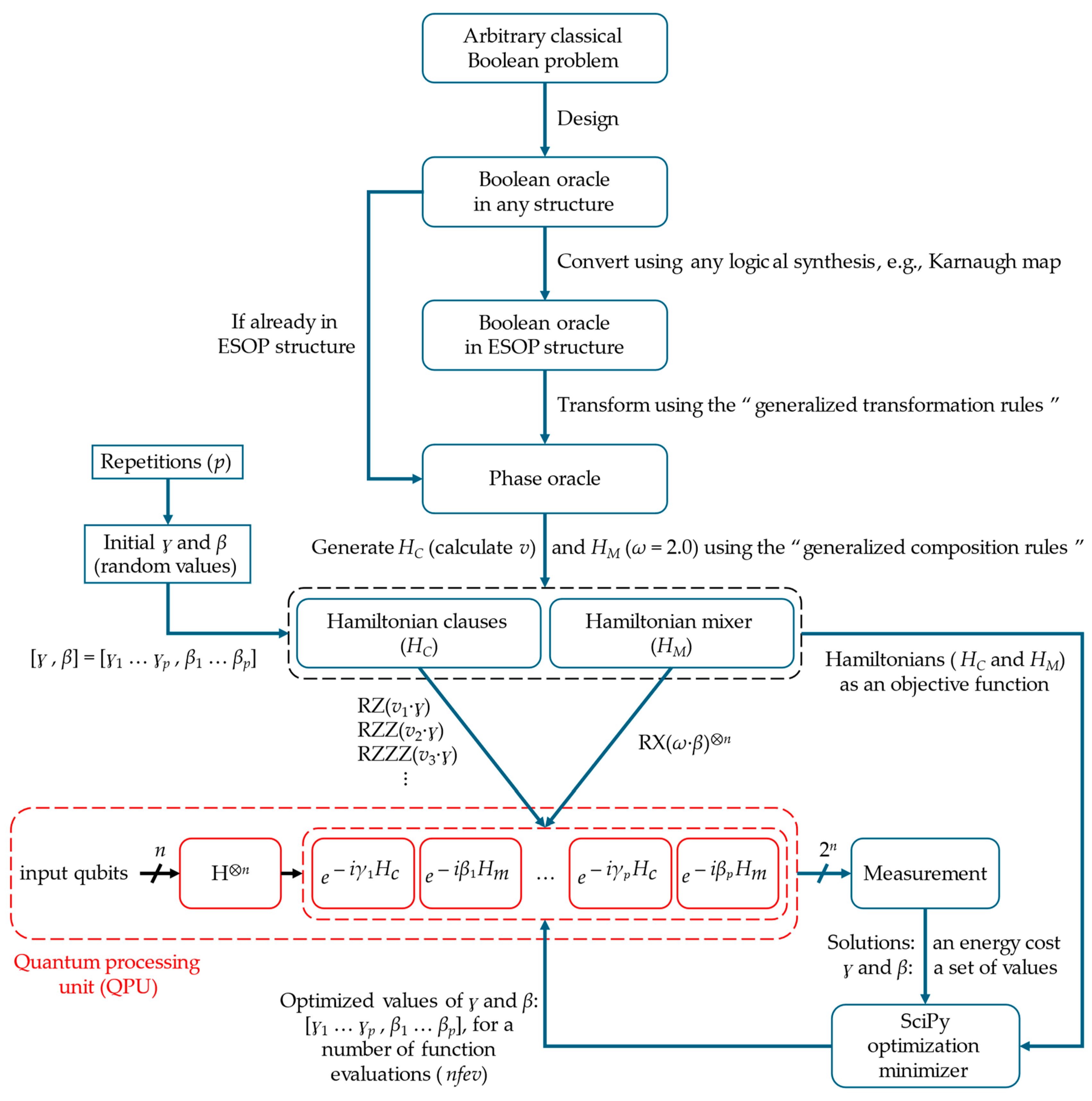
2.1. The Methodology of BHT-QAOA

Our essential methodology [20] of BHT-QAOA for solving arbitrary classical Boolean problems in the hybrid classical-quantum domain can be simply discussed as follows. Firstly, a classical Boolean problem is conceptually designed as a Boolean oracle in any logical structure. Such an oracle may consist of n input qubits (as the literals of a Boolean expression or the variables of a problem), m ancilla qubits (as the auxiliary output qubits) for intermediate quantum operations, and one fqubit (as the functional qubit) for the final quantum output of this oracle, where n ≥ 2 and m ≥ 0.

Secondly, this Boolean oracle in any logical structure is converted into its equivalent Boolean oracle in ESOP structure. There are many synthesis methods to achieve such a conversion, such as ESOP synthesis [25], Karnaugh map synthesis [22], binary decision diagram (BDD) synthesis [40,41], just to name a few. By utilizing any synthesis method, all mirror gates and m ancillae (except fqubit) are removed for the converted Boolean oracle in ESOP structure. Notice that a synthesis method may not generate the minimized ESOP structure; however, the DSOP (Disjoint Sum-Of-Products) structure may be generated, which is an expensive structure as compared to the minimized ESOP structure, depending on the number of n-bit Toffoli gates, where n ≥ 3 qubits.

Thirdly, this Boolean oracle in ESOP (or DSOP) structure is transformed into its equivalent Phase oracle, by utilizing the technique originally discussed by Figgatt et al. [21] for transforming 4-bit Toffoli gates into 3-bit controlled-Z (CCZ) gates, for Grover’s algorithm of single-solution [5,6,7,8]. In [20], we efficiently generalized their technique to include Feynman (CX) and n-bit Toffoli gates as well, and we termed our generalized technique the “generalized transformation rules” as follows.

Rule 1:	A Feynman (CX) gate is transformed into a Pauli-Z (Z) gate, when Equation (1) stated below is a solution-satisfiable, where j is the index of an input qubit (q). The left side of Equation (1) is the Boolean-based output of a CX gate, and its right side is the phase-inverted output of a Z gate.
${\mathrm{q}}_{\mathrm{j}} \oplus \mathit{fqubit} =–{\left(– 1\right)}^{{\mathrm{q}}_{\mathrm{j}}}$		(1)
Rule 2:	A Toffoli gate is transformed into a controlled-Z (CZ) gate, when Equation (2) stated below is a solution-satisfiable, where j and k are the indices of input qubits (q). The left side of Equation (2) is the Boolean-based output of a Toffoli gate, and its right side is the phase-inverted output of a CZ gate.
$\left({\mathrm{q}}_{\mathrm{j}} \wedge {\mathrm{q}}_{\mathrm{k}}\right)\oplus \mathit{fqubit} =– {\left(– 1\right)}^{{\mathrm{q}}_{\mathrm{j}} · {\mathrm{q}}_{\mathrm{k}}}$		(2)
Rule 3:	An n-bit Toffoli gate is transformed into an (n–1)-bit multi-controlled Z (MCZ) gate, when Equation (3) stated below is a solution-satisfiable, where j is the index of an input qubit (q) and n ≥ 3 qubits (q + fqubit). The left side of Equation (3) is the Boolean-based output of an n-bit Toffoli gate, and its right side is the phase-inverted output of an (n–1)-bit MCZ gate.
$\left({\bigwedge }_{ \mathrm{j}=1}^{n–1}{\mathrm{q}}_{\mathrm{j}}\right)\oplus \mathit{fqubit}=– {\left(– 1\right)}^{{\prod }_{ \mathrm{j}=1}^{ n–1}{\mathrm{q}}_{\mathrm{j}}}$		(3)

After applying these generalized transformation rules on the Boolean oracle in ESOP (or DSOP) structure, the resultant circuit of Phase oracle is simply constructed, with the removal of fqubit, i.e., the width of a circuit is reduced, and the significant minimization of multi-controlled quantum gates, i.e., the depth of a circuit is shrunk.

Fourthly, the Hamiltonians (H_C and H_M) of BHT-QAOA are directly generated from the converted Phase oracle, using our four proposed “generalized composition rules (H_g)” stated in Table 1, which are generalized from three Hadfield’s Boolean-based composition rules (H_f) [31] for the quantum Boolean-based gates of Feynman (CX), 3-bit Toffoli (CCX), and n-bit Toffoli (${\mathrm{C}}^{n–1}\mathrm{X}$). In Table 1, four quantum gates are mainly utilized to generate the Hamiltonians (H_C and H_M) from a Phase oracle, using the quantum phase-based gates of Pauli-Z (Z), controlled-Z (CZ), multi-controlled Z (MCZ), and Pauli-X (X).

Finally, based on Table 1, the four generalized composition rules (H_g) will be then directly applied to a Phase oracle to generate H_C and calculate its v coefficient. Because β (as a set of rotational angles of H_M) rotates between [0, π] [3,4], we set its coefficient (ω) to cover all the range between [0, 2π] for possible phase values of RX gates in H_M, to find all optimized approximated solutions for an arbitrary classical Boolean problem. Such that, ω (as the coefficient of β) is initially set to 2 for all n numbers of RX(ω⋅β) gates in H_M, where n is the total number of input qubits.

2.2. The Architecture of BHT-QAOA

After transforming an arbitrary classical Boolean problem to the Hamiltonians (H_C and H_M) and calculating their coefficients (v and ω), respectively, the numerical values of ɣ and β are initially randomized and then plugged into the architecture of BHT-QAOA for first execution, as illustrated in Figure 1. Subsequently, the SciPy optimization minimizer is utilized to optimize these numerical values (ɣ and β) for best-approximated solutions, in a number of function evaluations (nfev), by employing three cofactors as follows.

• H_C and H_M (in a number of p), as the “objective function” needs to be minimized.
• Measured solutions of BHT-QAOA, as the “energy cost” of the objective function.
• Previously calculated ɣ and β, as their “numerical values” need to be optimized.

2.3. The Optimization Approximation Algorithms

In our research of the BHT-QAOA [20], we utilized the SciPy optimization minimizer and COBYLA algorithm with promising optimized approximated solutions for arbitrary classical Boolean problems. However, in this article, we investigate other approximation algorithms for the BHT-QAOA. These optimization approximation algorithms are BFGS, L-BFGS-B, SLSQP, COBYLA, and COBYQA. Our investigation is based on the comparison among these five optimization approximation algorithms using our two performance metrics, which are the final utilization of nfev and the final quality of qubits measurement as the best-approximated solutions. Notice that, after measurement, qubits are converted into bits, and the quality of qubits measurement indicates that the solutions become more distinguishable from the non-solutions.

The Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm [32,33,34] is an iterative quasi-Newton method [38] for solving unconstrained nonlinear optimization problems. The BFGS iteratively approximates the Hessian matrix [38,39] to find the minimum of a function, often requiring fewer iterations than the gradient descent (GD) algorithm [38]. The BFGS is widely used in machine learning (ML) [42] for training models, such as neural networks (NN) [43] and support vector machines (SVM) [44].

The limited-memory BFGS with bounds (L-BFGS-B) algorithm [35,36] is a limited-memory quasi-Newton method to solve large-scale bound-constrained nonlinear optimization problems. The L-BFGS-B is mainly utilized for large dense problems and when there is difficulty in computing the Hessian matrix. The L-BFGS-B extends the standard L-BFGS algorithm [45] by incorporating simple bounds (lower and upper limits) on the variables for a function.

The sequential least squares programming (SLSQP) algorithm [37,38] is a method for solving nonlinear optimization problems with constraints. The SLSQP iteratively solves a sequence of quadratic programming subproblems to find the optimal solutions. The SLSQP is particularly useful for problems with both equality and inequality constraints.

The constrained optimization by linear approximation (COBYLA) algorithm [14,16,32] is a derivative-free optimization algorithm for solving problems with nonlinear inequality and equality constraints. COBYLA works by approximating the objective functions and their constraints using linear models, to find solutions without requiring the derivatives of these functions, where their gradients are difficult to compute.

The constrained optimization by quadratic approximations (COBYQA) algorithm [39] is a derivative-free optimization algorithm for solving general nonlinear optimization problems. COBYQA replaces COBYLA as a general derivative-free optimization solver, since COBYQA can handle unconstrained, bound-constrained, linearly constrained, and nonlinearly constrained problems.

3. Results and Discussion

Arbitrary classical Boolean problems (applications) are designed as Boolean oracles (in different logical structures). These Boolean oracles are solved with the BHT-QAOA for p repetitions, where p ≥ 1. As shown in Figure 1, our experiments have utilized the ibm_brisbane [46] QPU to perform the quantum processing domain of the BHT-QAOA, to execute the quantum circuit of an application, in p. While the SciPy minimizer performs the classical processing domain of the BHT-QAOA, to optimize the numerical values of ɣ and β with the energy cost of their Hamiltonians (H_C and H_M), in nfev. These applications are investigated using five optimization approximation algorithms of SciPy minimizer function, which are BFGS, L-BFGS-B, SLSQP, COBYLA, and COBYQA.

Because of our IBM Quantum Platform account limitations, the complete architecture of BHT-QAOA (shown in Figure 1) is completely simulated in the classical domain using IBM quantum libraries (Qiskit, AerSimulator, and Aer-EstimatorV2 [46,47,48]), for 1024 resampling times, which is the so-called “shots” [49]. After this classically simulated BHT-QAOA, the optimized numerical values of ɣ and β (from the SciPy minimizer with five approximation algorithms) are concurrently plugged into their respective H_C and H_M for an application, using the simulated noisy model of the ibm_brisbane QPU.

Notice that due to the limited physical connectivity of four neighboring qubits for the recent quantum layouts (architectures) of IBM QPUs [50,51], the designed Boolean oracles (in various logical structures) for the following applications must have n input qubits and m ancilla qubits (including fqubit), where 2 ≤ n ≤ 4 and m ≥ 0. Figure 2 demonstrates the circuits of Boolean oracles for these applications as follows.

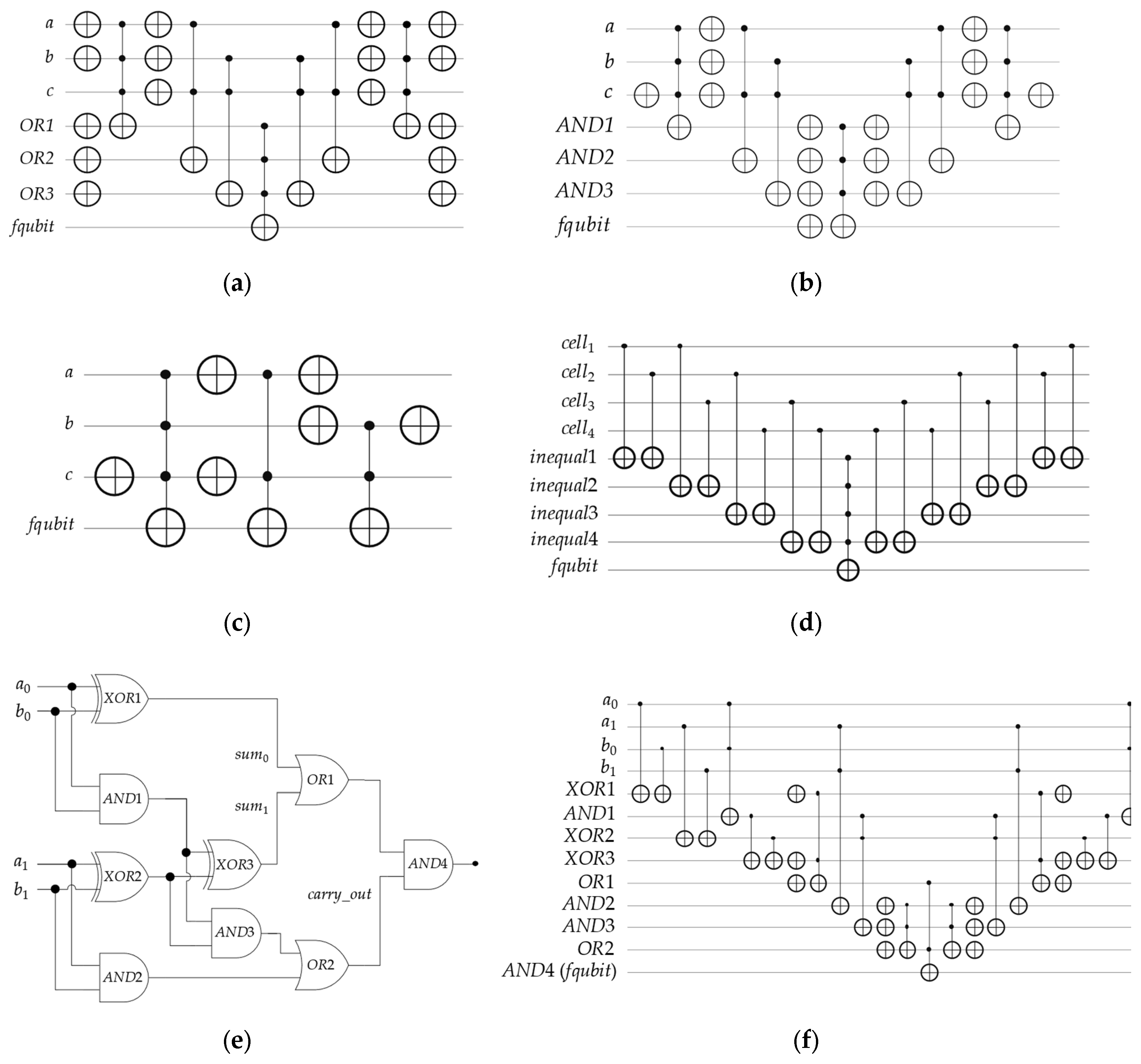
• An arbitrary Boolean problem in POS structure, as stated in Equation (4) and shown in Figure 2a.

(a ∨ b ∨ ¬ c) ∧ (¬ a ∨ c) ∧ (¬ b ∨ c)

(4)

2.

An arbitrary Boolean problem in SOP structure, as stated in Equation (5) and illustrated in Figure 2b.

(a ∧ b ∧ ¬ c) ∨ ( ¬ a ∧ c) ∨ ( ¬ b ∧ c)

(5)

3.

An arbitrary Boolean problem in ESOP structure, as stated in Equation (6) and shown in Figure 2c.

(a ∧ b ∧ ¬ c) ⊕ (¬ a ∧ c) ⊕ (¬ b ∧ c)

(6)

4.

A 2×2 Sudoku game, which is the constraints satisfaction problem – satisfiability (CSP-SAT) [52,53], as stated in Equation (7) and demonstrated in Figure 2d.

(cell₁ ⊕ cell₂) ∧ (cell₁ ⊕ cell₃) ∧ (cell₂ ⊕ cell₄) ∧ (cell₃ ⊕ cell₄)

(7)

5.

A 4-bit conditioned half-adder (HA) digital circuit, which is ORing two 1-bit sums and then ANDing them with one 1-bit carry-out, as stated in Equation (8) and illustrated in Figure 2e,f.

[(a₀ ⊕ b₀) ∨ ((a₀ ∧ b₀) ⊕ (a₁ ⊕ b₁))] ∧ [(a₁ ∧ b₁) ∨ ((a₀ ∧ b₀) ∧ (a₁ ⊕ b₁))]

(8)

For the two performance metrics (the final utilization of nfev and the final quality of qubits measurement), Table 2 states the comparison of the final utilization of nfev for the five optimization approximation algorithms for all applications. While Figure 3 illustrates the final measured solutions (as the quality of qubits measurement) for all applications using the five optimization approximation algorithms.

As illustrated in Figure 3(a–e), the highest bars in the histograms denote the final solutions for all applications using the five optimization approximation algorithms, and each histogram of an application denotes the results of (a) four solutions {$\stackrel{\mathrm{-}}{ a }\stackrel{\mathrm{-}}{ b }\stackrel{\mathrm{-}}{ c }$, $a\stackrel{\mathrm{-}}{ b} c$, $\stackrel{\mathrm{-}}{ a } b c$, $a b c$} for the Boolean oracle in POS structure of Equation (4), (b) four solutions {$a b \stackrel{\mathrm{-}}{ c}$ , $\stackrel{\mathrm{-}}{ a }\stackrel{\mathrm{-}}{ b }c$, $a\stackrel{\mathrm{-}}{ b} c$, $\stackrel{\mathrm{-}}{ a }b c$} for the Boolean oracle in SOP structure of Equation (5), (c) three solutions {$a b \stackrel{\mathrm{-}}{ c}$, $a \stackrel{\mathrm{-}}{ b} c$, $\stackrel{\mathrm{-}}{ a }b c$} for the Boolean oracle in ESOP structure of Equation (6), (d) two permutative solutions {solution 1: cell₁=cell₄=0 and cell₂=cell₃=1; solution 2: cell₁=cell₄=1 and cell₂=cell₃=0} for the 2×2 Sudoku game of Equation (7), and (e) three solutions {$a_0{a}_1\overline{b_0}{b}_1$, $\overline{a_0}{a}_1{b}_0{b}_1$, $a_0{a}_1{b}_0{b}_1$} for the 4-bit conditioned half-adder (HA) circuit of Equation (8).

Notice that, in Figure 3, (i) the first measured bit (the most-right) of a solution is equivalent to the first input qubit, (ii) the last measured bit (the most-left) of a solution is equivalent to the last input qubit, (iii) the higher probability of qubits indicates a solution, and (iv) the lower probability of qubits indicates a non-solution. Table 3 summarizes the final quality of qubits measurement for all optimization approximation algorithms with the BHT-QAOA, as calculated in Equation (9), where N = $2^n$, n is the number of input qubits, S is the probability of a solution, and P is the probability of a solution or non-solution.

$${\mathrm{Quality} \mathrm{of} \mathrm{qubits} \mathrm{measurement}}_{\mathit{algorithm}}={\displaystyle \frac{\sum _{ i=1}^{ N}{ S}_i}{\sum _{ j=1}^{ N}{P}_j}}\times 100$$

(9)

Based on the evaluation of two performance metrics in Table 2 and Table 3, on the one hand, the BHT-QAOA successfully optimizes the numerical values of ɣ and β and finds all approximated solutions for all applications, as a proof of concept for utilizing any optimization approximation algorithm with the BHT-QAOA to solve arbitrary classical Boolean problems. On the other hand, the BFGS and SLSQP are the fastest optimization approximation algorithms for the BHT-QAOA, in the context of fewer utilization of nfev. While the BFGS, L-BFGS-B, and SLSQP are the most accurate optimization approximation algorithms for the BHT-QAOA, in the context of a higher quality of qubits measurement. Broadly, the BFGS and SLSQP algorithms successfully demonstrate their capabilities of optimizing the numerical values of ɣ and β and find all best-approximated solutions for all applications, as compared to the other utilized optimization approximation algorithms.

Accordingly, the BHT-QAOA with the BFGS and SLSQP algorithms will provide broad opportunities in investigating many of classical Boolean problems in the hybrid classical-quantum domain, which are neither designed nor solved using the standard QAOA [3,4]. Therefore, various classical Boolean problems for the applications of digital logic circuits, synthesizers, and machine learning can be realized as Hamiltonians and then solved using BHT-QAOA with these two optimization approximation algorithms.

4. Conclusions

Our previously introduced BHT-QAOA (Boolean-Hamiltonians Transform for Quantum Approximate Optimization Algorithm [20]), to solve arbitrary classical Boolean problems as Hamiltonians in the hybrid classical-quantum domain, is re-investigated with five classical optimization approximation algorithms and two performance metrics. These algorithms are BFGS, L-BFGS-B, SLSQP, COBYLA, and COBYQA. While the two performance metrics are: (i) the final utilization of nfev and (ii) the final quality of qubits measurement for the best-approximated solutions, where nfev is the number of function evaluations for a problem between a quantum processing unit and a classical optimization approximation algorithm.

In this article, arbitrary Boolean applications are constructed as Boolean oracles in various logical structures, and then BHT-QAOA successfully searches for all optimized approximated solutions for these applications using all five optimization approximation algorithms, in the hybrid classical-quantum domain. However, our investigation proved that the BFGS and SLSQP are the fastest optimization approximation algorithms for the BHT-QAOA, in the context of fewer utilization of nfev. While the BFGS, L-BFGS-B, and SLSQP are the most accurate optimization approximation algorithms for the BHT-QAOA, in the context of a higher quality of qubits measurement. Collectively, both BFGS and SLSQP approximation algorithms successfully demonstrate their capabilities in finding all best-approximated solutions for these arbitrary Boolean applications, in the context of both fewer values of nfev and higher quality of qubits measurement.

In conclusion, further classical Boolean problems can be investigated for arbitrary logical structures for the practical engineering applications in the topics of digital logic synthesizers, robotics, machine learning, just to name a few, and the BHT-QAOA with the BFGS and SLSQP algorithms will successfully solve such practical applications effectively in the hybrid classical-quantum domain.