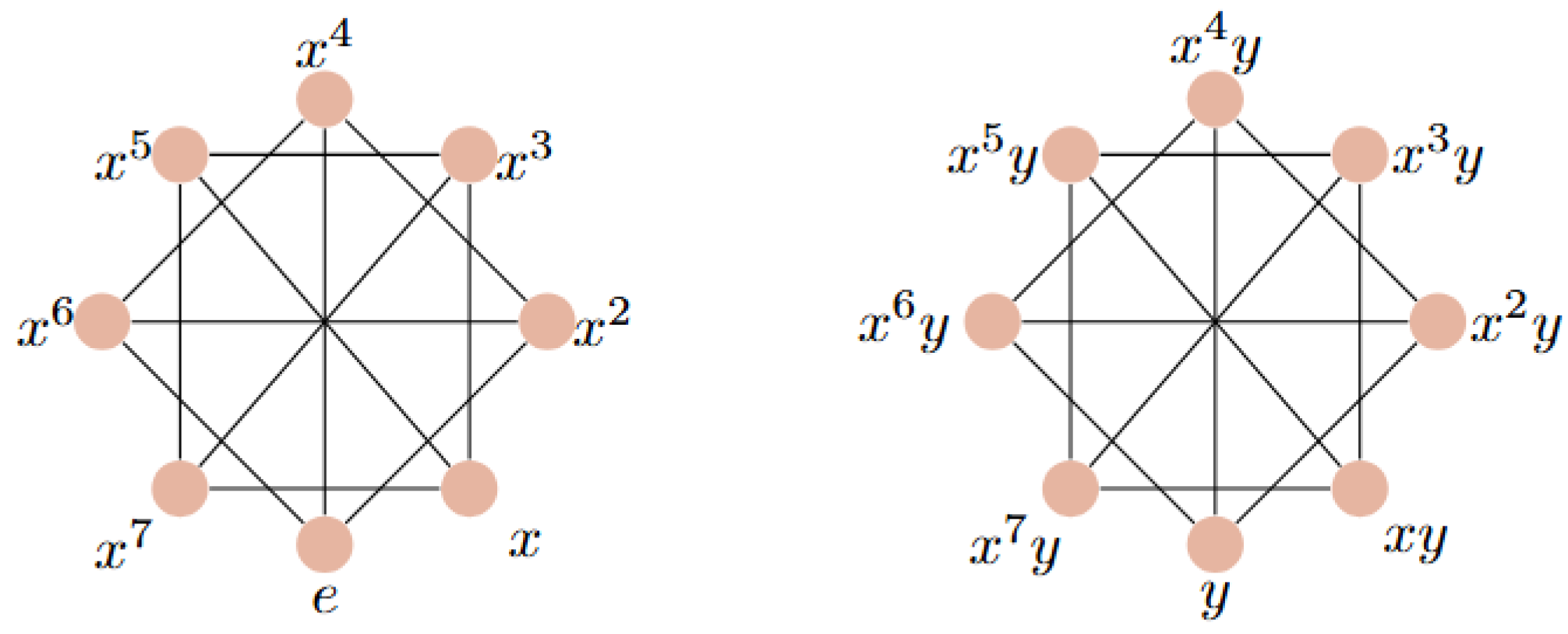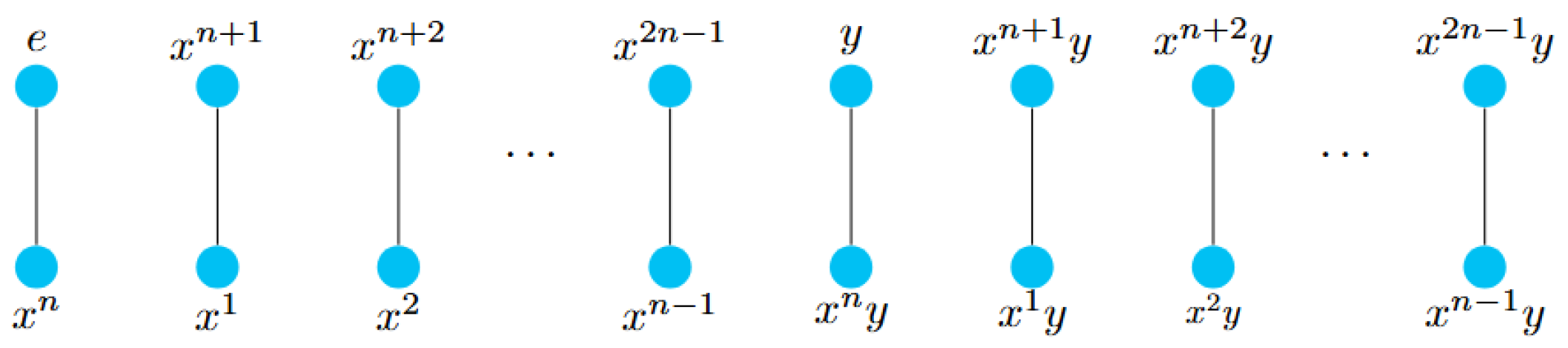The Structure of Cayley Graph of Generalized Quaternion Group of Valency Less than or Equal 3

1. Introduction

A Cayley graph is a graph constructed from a group using a specified subset of its elements. Arthur Cayley introduced the concept of Cayley graph in 1878 [5]. In this paper, all groups are considered finite. In such graphs, the vertices correspond to the elements of the generating group. Two vertices in the Cayley graph will be adjacent if the operations of the corresponding elements belong to a connecting set, which is a subset of the generating group of the graph.

Let G be a group and S be a subset of G, with $e_G\notin S$ and $S^{-1}\subseteq S$. The Cayley graph generated by a group G and a connecting set $S\subseteq G$, denoted by $Cay(G,S)$, is a graph whose vertex set is $V\left(Cay\right(G,S\left)\right)=G$ and two vertices $x,y\in V\left(Cay\right(G,S\left)\right)$ are adjacent if and only if $x{y}^{-1}\in S$ [2]. These conditions, namely $e_G\notin S$ and $S^{-1}\subseteq S$, ensure the resulting Cayley graph is simple and undirected. In this paper, all graphs are assumed to be simple and undirected. It is well-known that the Cayley graph $Cay(G,S)$ is $\left|S\right|$-regular, meaning that every vertex in the graph has the same valency (degree) as the number of elements in a set S. Furthermore, if the connecting set S generates the group G, then the Cayley graph $Cay(G,S)$ is connected [7].

In this paper, we focus on finite groups. A group is a non-empty set equipped with a binary operation satisfying associativity, the existence of an identity element, and the existence of inverses [11]. If the set is finite, the group is referred to as a finite group. Let G be a group and $a\in G$. The order of G is the number of elements in G, denoted by $\left|G\right|$ [11]. Thus, G is a finite group if $\left|G\right|$ is finite. The order of an element a is the smallest positive integer n such that $a^n$ equal to the identity element of G [11]. In this paper, the order of an element a denoted by $o\left(a\right)$. For any group G with binary operation *, a subgroup H in G is a group generated by the set $H\subseteq G$ with the binary operations *. Equivalently, H is a subgroup of G if and only if for all $x,y\in H$, it follows that $x*y^{-1}\in H$ [1]. Let A be a set of a group G. Then $\langle A\rangle$ is an intersection of all subgroups of G that contains A. Furthermore, subgroup $\langle A\rangle$ is called subgroup generated by A [1]. If a group G is equal to $\langle A\rangle$, then G is said to be generated by A. If A is a singleton $\left\{a\right\}$, then $\langle A\rangle =\langle a\rangle$, and G is called cyclic group. From Malik et al.(1997) [11], we use the definition of right cosets and Lagrange theorem that in this paper. Let H be a subgroup of group G and element $a\in G$. The set $Ha=\{ha\mid h\in H\}$ is called right coset of H in G. For H is a subgroup of a finite group G, Lagrange theorem states that order of H divides the order of G.

In 2021, Al-Kaseasbeh and Erfanian [2] investigated the structure of the Cayley graph over the dihedral group with valencies 1, 2, and 3. The dihedral group $D_n$ with $2n$ elements has two generators, x and y, whose order of x is n and the order of y is 2 [4]. On the other hand, there is a group with two generators known as the generalized quaternion group. Let n be a positive integer greater than or equal to 2. The generalized quaternion group with $4n$ elements, denoted by $Q_{4n}$, is a group generated by x and y, represented by the presentation $\langle x,y\mid x^{2n}=y^4=e,x^n=y^2,y^{-1}xy=x^{-1}\rangle$ [12]. For further characteristics of the generalized quaternion group, the author refers to Conrad (2014) [3]. Motivated by these results, this study further investigates the structure of the Cayley graph over the generalized quaternion group with the same valencies.

Let $\mathrm{\Gamma }\left(V\right(\mathrm{\Gamma }),E(\mathrm{\Gamma }\left)\right)$ be a graph, where $V\left(\mathrm{\Gamma }\right)$ denotes the vertex set and $E\left(\mathrm{\Gamma }\right)$ denotes the edge set. In general, $\mathrm{\Gamma }\left(V\right(\mathrm{\Gamma }),E(\mathrm{\Gamma }\left)\right)$ graph is usually written simply as $\mathrm{\Gamma }$. For every $a,b\in \mathrm{\Gamma }$, the vertex a adjacent to vertex b, denoted $\left(a\right)\left(b\right)\in E\left(\mathrm{\Gamma }\right)$. Some basic, well-known graph structures used in this paper are the null graph $N_m$, the path graphs $P_n$, the cycle graph $C_n$, and the complete graph $K_n$ as introduced by Wilson et al.(1996)[14]. Some graph structures, such as the circulant graph $C_n^{s_1{s}_2\dots s_k}$, as defined by Golin et al.(2004)[8] and the Möbius ladder graph $M_n$ as introduced by Guy et al.(1967)[9], are also considered in this paper. Let ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ be a graph such that $V\left({\mathrm{\Gamma }}_2\right)\subseteq V\left({\mathrm{\Gamma }}_1\right)$ and $E\left({\mathrm{\Gamma }}_2\right)\subseteq E\left({\mathrm{\Gamma }}_1\right)$. Then the ${\mathrm{\Gamma }}_2$ is called a subgraph of ${\mathrm{\Gamma }}_1$. For any $S\subseteq V\left({\mathrm{\Gamma }}_1\right)$, the subgraph induced by S, denoted ${\mathrm{\Gamma }}_1\left[S\right]$, is the subgraph with vertex set S, and all edges whose endpoints are contained in S [13]. In other words, for every $x,y\in S$, if $\left(x\right)\left(y\right)\in E\left({\mathrm{\Gamma }}_1\right)$ then $\left(x\right)\left(y\right)\in E\left({\mathrm{\Gamma }}_1\left[S\right]\right)$. Some operations over two graphs used in this research are disjoint union $(+)$ [15] and Cartesian product $(\square )$ [10] of the two graphs. It is also proposed in some theories that two distinct graphs can be isomorphic. Any graphs ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ are isomorphic, denoted by ${\mathrm{\Gamma }}_1\cong {\mathrm{\Gamma }}_2$, if and only if there exists an isomorphism from ${\mathrm{\Gamma }}_1$ to ${\mathrm{\Gamma }}_2$. The isomorphism from ${\mathrm{\Gamma }}_1$ to ${\mathrm{\Gamma }}_2$ is a bijective function $\phi$ from ${\mathrm{\Gamma }}_1$ to ${\mathrm{\Gamma }}_2$, such that for every $x,y\in V\left({\mathrm{\Gamma }}_1\right)$, $\left(x\right)\left(y\right)\in E\left({\mathrm{\Gamma }}_1\right)$ if and only if $\left(\phi \left(x\right)\right)\left(\phi \left(y\right)\right)\in E\left({\mathrm{\Gamma }}_2\right)$ [13].

This research will investigate the isomorphism of the Cayley graph generated by $Q_{4n}$ with valencies less than or equal to 3, with the well-known graph, or those operations.

2. Results

The structure of the Cayley graph over a group is, in general, still an open problem for research. Kaseasbeh et al. (2021) [2] explored the structure of the Cayley graph over the dihedral group with maximal valencies 3. Farhan et al. (2024) [6] utilized computational methods to simulate and analyze the structure of Cayley graphs of the dihedral groups. Motivated by the insights from these studies, we are interested in examining the structure of Cayley graphs over other groups, particularly the generalized quaternion group.

Recall that the generalized quaternion group $Q_{4n}$ is the group defined by the presentation

$$\begin{array}{cc}\hfill Q_{4n}& =\langle x,y|x^{2n}=y^4=e,x^n=y^2,y^{-1}xy=x^{-1}\rangle \hfill \end{array}$$

where the order of x is $2n$ and the order of y is 4. Let $y\in Q_{4n}$. Then $y^{-1}=x^{n}y\in Q_{4n}$. From the fact that $y^{-1}xy=x^{-1}$, we have $yx=x^{2n-1}y$ for $x\in Q_{4n}$. For any $1\le k\le 2n-1$, we can generalize the properties of $y{x}^k$ by using the following proposition.

Proposition 1.

For any k with $1\le k\le 2n-1$, the equality $y{x}^k=x^{2n-k}y$ holds.

We have $x^{-1}=x^{2n-1}$. In general, for every $1\le k\le 2n-1$, we have $x^{-k}=x^{2n-k}$. Clearly, ${\left(xy\right)}^{-1}=x^{n+1}y$. For $x^{k}y$ with $1\le k\le 2n-1$ in general, the inverse of $x^{k}y$ will be provided in the following proposition.

Proposition 2.

For any $1\le k\le 2n-1$, we have ${\left(x^{k}y\right)}^{-1}=x^{n+k}y$.

Using the following proposition, we can determine the orders of various elements in $Q_{4n}$, excluding x and y, in general.

Proposition 3.

The only non-identity element in $Q_{4n}$ with order 2 is $x^n$.

After establishing that $x^n$ is the only non-identity element of order 2 in $Q_{4n}$, we now examine the orders of elements of the form $x^{k}y$, which are essential for understanding the structure of $Q_{4n}$ and its Cayley graphs.

Proposition 4.

For each $1\le k\le 2n$, the order of $x^{k}y$ is 4.

As an illustration of the concepts discussed in this section, the following graph presents an example of the Cayley graph $\mathrm{Cay}(Q_{4n},S)$ with $n=4$ and the generating set $S=\{x^2,x^4,x^6\}$. This example helps visualize the structure and connectivity of the generalized quaternion group through its associated Cayley graph.

Figure 1. $Cay(Q_{16},S)$ with $S=\{x^2,x^4,x^6\}$.

Figure 1. $Cay(Q_{16},S)$ with $S=\{x^2,x^4,x^6\}$.

In the next discussion, we present the structure of the Cayley graph on the generalized quaternion group for valencies 1, 2, and 3. The Cayley graph’s structure on the generalized quaternion group for valencies 1 is shown in the subsequent theorem.

Theorem 1.

For any generator $S\subseteq Q_{4n}$ with $\left|S\right|=1$, we have

$$Cay(Q_{4n},S)\cong 2n{K}_2.$$

Proof. 

Consider any $S=\left\{a\right\}$ with $a=a^{-1}$ for some $a\in Q_{4n}$. By Proposition 3, $S=\left\{x^n\right\}$. Since $\left|S\right|=1$, the Cayley graph $Cay(Q_{4n},S)$ is 1-regular. Now, we determine the pairs of vertices that are connected in $Cay(Q_{4n},S)$. Since $e^{-1}=e$, it follows that $x^n{e}^{-1}=x^{n}e=x^n\in S$, implying that vertex e is connected to vertex $x^n$ in $Cay(Q_{4n},S)$. For the other vertices in $Cay(Q_{4n},S)$, we examine the following cases:

i.

For $x^k$ with $1\le k\le n-1$.

Consider any vertex $p\in Q_{4n}$ such that $x^k{p}^{-1}=x^n$. Then,

$$\begin{array}{c}\hfill x^k{p}^{-1}=x^n\iff p=x^{n+k}.\end{array}$$

This implies $\left(x^k\right)\left(x^{n+k}\right)\in E\left(Cay(Q_{4n},S)\right)$ for $1\le k\le n-1$. In other words, there are $n-1$ edges of the form $\left(x^k\right)\left(x^{n+k}\right)$ for each $1\le k\le n-1$.

ii.

For $x^{n}y$, consider any vertex $s\in Q_{4n}$ such that $x^{n}y{s}^{-1}=x^n$. Then,

$$\begin{array}{c}\hfill x^{n}y{s}^{-1}=x^n\iff s=y.\end{array}$$

Therefore, the $x^{n}y$ is connected by edge to vertex y in $Cay(Q_{4n},S)$.

iii.

For $x^{k}y$ with $1\le k\le n-1$.

Consider any $q\in Q_{4n}$ such that $\left(x^{k}y\right)q^{-1}=x^n$. Then,

$$\begin{array}{c}\hfill x^{k}y{q}^{-1}=x^n\iff q=x^{n+k}y.\end{array}$$

Consequently, $\left(x^{k}y\right)\left(x^{n+k}y\right)\in E\left(Cay(Q_{4n},S)\right)$ for each $1\le k\le n-1$. In other words, there are $n-1$ edges connecting $\left(x^{k}y\right)$ and $\left(x^{n+k}y\right)$ for each $1\le k\le n-1$.

Furthermore, the graph $Cay(Q_{4n},S)$ has $1+(n-1)+1+(n-1)=2n$ edges, and each vertex has degree 1. Therefore, $Cay(Q_{4n},S)\cong 2n{K}_2$.

□

The Cayley graph as given in Theorem 1 can be illustrated in Figure 2.

In the next discussion, we present the structure of the Cayley graph on the generalized quaternion group for valencies 2. We consider $S\subseteq Q_{4n}$ with $\left|S\right|=2$, $e\in S$, and $S^{-1}\subseteq S$. There are two cases, as follows.

• $S=\{a,b\}$ with $a^2=b^2=e$ for some $a,b\in Q_{4n}\setminus \left\{e\right\}$ and $a\ne b$.
• $S=\{a,a^{-1}\}$ for some $a\in Q_{4n}\setminus \left\{e\right\}$ with $a\ne a^{-1}$.

By Proposition 3 we know that in the $Q_{4n}$, the only element of order 2 is $x^n$. Hence, we conclude that the case $S=\{a,b\}$ is invalid. For valency 2, we only observe for $S=\{a,a^{-1}\}$ for some $a\in Q_{4n}\setminus \left\{e\right\}$ with $a\ne a^{-1}$.

There are two possible cases for $S=\{a,a^{-1}\}$. That are when $a=x^k$ for any $1\le k\le 2n-1$ and $k\ne n$, or when $a=x^{k}y$ for any $1\le k\le 2n$. In other words, for valency 2 we will investigate the set $S=\{x^n,x^{2n-k}\}$ for any $1\le k\le 2n-1$ and $k\ne n$, and also $S=\{x^{k}y,x^{n+k}y\}$ for any $1\le k\le 2n$. In the following proposition we consider the case $\{a,a^{-1}\}=\{x^k,x^{2n-k}\}$.

Proposition 5.

For any generator $S_1=\{x^k,x^{2n-k}\}$ with $1\le k\le n-1$ or $n+1\le k\le 2n-1$, we have

$$Cay(Q_{4n},S_1)\cong 2gcd(2n,k)C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}.$$

Proof. 

Let $S_1=\{x^k,x^{2n-k}\}$ for any $1\le k\le 2n-1$ or $n+1\le k\le 2n-1$. Since ${\left(x^k\right)}^{-1}=x^{2n-k}$, it follows that $S_1=S_1^{-1}$. Since the order of x is $2n$, it follows that the order of $x^k$ is ${\displaystyle \frac{2n}{gcd(2n,k)}}$ for some $1\le k\le 2n-1$ or $n+1\le k\le 2n-1$. Thus, we obtain $\langle S_1\rangle =\langle x^k\rangle =\{e,x^k,x^{2k},x^{3k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\}$ with ${\displaystyle \frac{2n}{gcd(2n,k)}}$ elements. Observe that

$${\left(x^k\right)}^i{\left({\left(x^k\right)}^{i+1}\right)}^{-1}=x^{ik}{x}^{-ik}{x}^{-k}=x^{-k}={\left(x^k\right)}^{-1}=x^{2n-k}\in S_1$$

for each $i=1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}$. Thus we have a cycle

$$e-x^k-x^{2k}-x^{3k}-\dots -x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}-x^{{\displaystyle \frac{2n}{gcd(2n,k)}}k}=e$$

of length ${\displaystyle \frac{2n}{gcd(2n,k)}}$. Therefore

$$\{\left(e\right)\left(x^k\right),\left(x^k\right)\left(x^{2k}\right),\left(x^{2k}\right)\left(x^{3k}\right),\dots ,\left(x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\right)\left(e\right)\}\subseteq E\left(Cay(Q_{4n},S_1)\right).$$

Furthermore, let $H_1=\langle x^k\rangle =\{e,x^k,x^{2k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\}$ be a cyclic subgroup of $Q_{4n}$ of order ${\displaystyle \frac{2n}{gcd(2n,k)}}$. Consequently, $[Q_{4n}:H_1]=2gcd(2n,k)$ which means there are exactly $2gcd(2n,k)$ distinct right cosets, namely $H_1{g}_1=H_1,H_1{g}_2,H_1{g}_3,H_1{g}_4,\dots ,H_1{g}_{(2gcd(2n,k\left)\right)}$, where $g_1=e\in H_1$ and $g_2,g_3,g_4,\dots ,$

$g_{(2gcd(2n,k\left)\right)}\in Q_{4n}\setminus H_1$. For each right coset $H_1{g}_j=\{g_j,x^k{g}_j,x^{2k}{g}_j,x^{3k}{g}_j,\dots ,$

$x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}{g}_j\}$, we obtain $2gcd(2n,k)$ cycle of the form

$$g_j-x^k{g}_j-x^{2k}{g}_j-\dots -x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}{g}_j-x^{{\displaystyle \frac{2n}{gcd(2n,k)}}k}{g}_j=g_j$$

for any $j=1,2,\dots ,(2gcd(2n,k\left)\right)$, each of length ${\displaystyle \frac{2n}{gcd(2n,k)}}$.

Let $(2gcd(2n,k))C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$ be $2gcd(2n,k)$ copies of cycle graph with order ${\displaystyle \frac{2n}{gcd(2n,k)}}$. Let $V((2gcd(2n,k))C_{{\displaystyle \frac{2n}{gcd(2n,k)}}})$ be

$$\left\{{\overline{0}}_j,{\overline{1}}_j,{\overline{2}}_j,\dots ,\overline{{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)}_j}\mid j=1,2,\dots ,(2gcd(2n,k))\right\}.$$

It is clear that $V\left(Cay(Q_{4n},{\mathcal{S}}_1)\right)=\bigcup _{j=1}^{2gcd(2n,k)}{H}_1{g}_j$. Construct a function $f_1^{\prime }:V\left(Cay(Q_{4n},{\mathcal{S}}_1)\right)\to V((2gcd(2n,k))C_{{\displaystyle \frac{2n}{gcd(2n,k)}}})$ by

$$f_1^{\prime }\left(x^{ik}{g}_j\right)=\overline{{\left(i(mod{\displaystyle \frac{2n}{gcd(2n,k)}})\right)}_j}$$

for every $x^{ik}{g}_j\in H_1{g}_j$ with $j=1,2,3,\dots ,2gcd(2n,k)$. Then, $f_1^{\prime }$ is an isomorphism. Conversely, for every $x^{i_{1}k}{g}_p\in H_1{g}_p$ and $x^{i_{2}k}{g}_q\in H_1{g}_q$ for some $p,q\in \{1,2,3,\dots ,2gcd(2n,k\left)\right\}$ with $p\ne q$ and for some $i_1,i_2\in \{1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}\}$, thus we have

$$\begin{array}{c}\hfill a{\left(b\right)}^{-1}=\left(x^{i_{1}k}{g}_p\right){\left(x^{i_{2}k}{g}_q\right)}^{-1}=x^{i_{1}k}{g}_p{g}_q^{-1}{x}^{-i_{2}k}\notin S_1.\end{array}$$

In other words, $x^{i_{1}k}{g}_p$ and $x^{i_{1}k}{g}_q$ does not adjacent in $Cay(Q_{4n},S_1)$. Every coset is an independent set, and every coset generates an induced subgraph that is isomorphic to $C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$. Consequently, $Cay(Q_{4n},S_1)\cong 2gcd(2n,k)C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$.

□

In the following proposition, we prove for the case $S=\{x^{k}y,x^{n+k}y\}$ in the Cayley graph over the generalized quaternion group with valency 2.

Proposition 6.

For any generator $S_2=\{x^{k}y,x^{n+k}y\}$ with $1\le k\le 2n$, we have $Cay(Q_{4n},S_2)\cong n{C}_4$.

Proof. 

Given $S_2=\{x^{k}y,x^{n+k}y\}$ with $1\le k\le 2n$. Since ${\left(x^{k}y\right)}^{-1}=x^{n+k}y$, it follows that $S_2^{-1}=S_2$. Furthermore, by Proposition 4, it is known that $o\left(x^{k}y\right)=4$ for every $1\le k\le 2n$, so that

$$\langle x^{k}y\rangle =\{e,x^{k}y,{\left(x^{k}y\right)}^2,{\left(x^{k}y\right)}^3\}=\{e,x^{k}y,x^n,x^{n+k}y\}.$$

Note that for some $e,x^{k}y,x^n,x^{n+k}y\in Q_{4n}$ for each $1\le k\le 2n$, the following hold:

$$\begin{array}{cc}\hfill e{\left(x^{k}y\right)}^{-1}& =x^{n+k}y\in S_2,\hfill \\ \hfill x^{k}y{\left(x^n\right)}^{-1}& =x^{n+k}y\in S_2,\hfill \\ \hfill x^n{\left(x^{n+k}y\right)}^{-1}& =x^{n+k}y\in S_2,\mathrm{and}\hfill \\ \hfill \left(x^{n+k}y\right)e^{-1}& =x^{n+k}y\in S_2.\hfill \end{array}$$

Therefore, we obtain a cycle $e-x^{k}y-x^n-x^{n+k}y-e$ of length 4 for every $1\le k\le 2n$. Thus, $\{\left(e\right)\left(x^{k}y\right),\left(x^{k}y\right)\left(x^n\right),\left(x^n\right)\left(x^{n+k}y\right),\left(x^{n+k}y\right)\left(e\right)\}\subseteq E\left(Cay(Q_{4n},{\mathcal{S}}_2)\right)$ for every $1\le k\le 2n$.

Furthermore, $H_2=\langle x^k\rangle =\{e,x^{k}y,x^n,x^{n+k}y\}$ is a cyclic subgroup of $Q_{4n}$ of order 4. Consequently, $[Q_{4n}:H_2]=n$, which means there are n distinct right cosets: $H_2{p}_1=H_2,H_2{p}_2,H_2{p}_3,\dots ,H_2{p}_n$, where $p_1=e\in H_2$ and $p_2,p_3,p_4,\dots ,p_n\in Q_{4n}\setminus H_2$. For each right coset

$$H_2{p}_j=\{p_j,x^{k}y{p}_j,x^n{p}_j,x^{n+k}y{p}_j\},$$

we can construct n cycles of the form $p_j-x^{k}y{p}_j-x^n{p}_j-x^{n+k}y{p}_j-p_j$ for $j=1,2,\dots ,n$, each of length 4.

Let $n{C}_4$ be n copies of the cycle graph of order 4. Let $V\left(n{C}_4\right)$ be

$\left\{{\overline{i(mod4)}}_u\mid u=1,2,3,\dots ,n,\forall i=0,1,2,3\right\}$. Construct a function

$$f_2^{\prime }:V\left(Cay(Q_{4n},{\mathcal{S}}_2)\right)\to V\left(n{C}_4\right)$$

by $f_2^{\prime }\left({\left(x^{k}y\right)}^i{p}_j\right)={\overline{i(mod4)}}_j$ for every ${\left(x^{k}y\right)}^i{p}_j\in H_2{p}_j$ for some $j=1,2,3,\dots ,n$ and for all $i=0,1,2,3$. The function $f_2^{\prime }$ is an isomorphism. Using the same steps as before, it is clear that cosets are an independent set. In other words, the n distinct cosets are isomorphic to $C_4$. Consequently, $Cay(Q_{4n},S_2)\cong n{C}_4$.

□

By Proposition 5 and Proposition 6, the general property for the Cayley graphs of the generalized quaternion group $Q_{4n}$ with valency 2 can be described as follows.

Theorem 2.

For any generator $S=\{a,a^{-1}\}$ for some $a\in Q_{4n}$, $a\ne a^{-1}$ where $o\left(a\right)=m$, we have $Cay(Q_{4n},S)\cong {\displaystyle \frac{4n}{m}}{C}_m$.

Proof. 

Consider $S\subseteq Q_{4n}$ with $e\notin S$ and $S=\{a,a^{-1}\}$ for some $a\in Q_{4n}$, where $a\ne a^{-1}$. Since $a\ne a^{-1}$, it follows that $o\left(a\right)\ne 2$. Therefore $a\ne x^n$. There are two possible cases for $S=\{a,a^{-1}\}$, as follows.

Case 1.

$S=\{x^k,x^{2n-k}\}$ for each $1\le k\le n-1$ or $n+1\le k\le 2n-1$. If $o\left(x^k\right)={\displaystyle \frac{2n}{gcd(2n,k)}}=m$, then by Proposition 5, it follows that $Cay(Q_{4n},S)\cong (2gcd(2n,k))C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\cong {\displaystyle \frac{4ngcd(2n,k)}{2n}}{C}_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\cong {\displaystyle \frac{4n}{m}}{C}_m$.

Case 2.

$S=\{x^{k}y,x^{n+k}y\}$ for each $1\le k\le 2n$. If $o\left(x^{k}y\right)=4=m$, then by Proposition 6, it follows that $Cay(Q_{4n},S)\cong n{C}_4\cong {\displaystyle \frac{4n}{4}}{C}_4\cong {\displaystyle \frac{4n}{m}}{C}_m$.

It is proven. □

In this subsection, we will present the structure of the Cayley graph on the generalized quaternion group for valency 3. The $Cay(Q_{4n},S)$ has valency 3 if the $\left|S\right|=3$, $e\notin S$, and $S^{-1}\subseteq S$. Two alternative scenarios for the set S that can produce $Cay(Q_{4n},S)$ as a graph with valency 3 are as follows.

• $S=\{a,b,c\}$ with $a^2=b^2=c^2=e$ for some $a,b,c\in Q_{4n}\setminus \left\{e\right\}$ each different.
• $S=\{a,a^{-1},b\}$ with $b^2=e$ for some $a,b\in Q_{4n}\setminus \left\{e\right\}$ and $a\ne b$.

However, the first scenario cannot occur, as demonstrated by the following lemma.

Lemma 1.

Let $n\ge 2$. Then, $\left|S\right|=3$ if and only if S satisfying one of the following conditions :

i.

$S=\{x^k,x^{2n-k},x^n\}$ for some $1\le k<n$ and $n<k\le 2n-1$.

ii.

$S=\{x^{p}y,x^{n+p}y,x^n\}$ for some $1\le p\le 2n$.

Proof. 

It is clear that $\left|S\right|=\left|\right\{x^k,x^{2n-k},x^n\left\}\right|=3$ for some $1\le k<n$ and $n<k\le 2n-1$ or $\left|S\right|=\left|\right\{x^{p}y,x^{n+p}y,x^n\left\}\right|=3$ for some $1\le p\le 2n$. Conversely, we know that the $\left|S\right|=3$. As previously stated, S with 3 elements can occur in the following two scenarios.

Case 1.

$S=\{a,b,c\}$ with $a^2=b^2=c^2=e$ for some 3 difference elements $a,b,c\in Q_{4n}\setminus \left\{e\right\}$. By Proposition 3, we have $a=b=c=x^n$. Thus, $S=\left\{x^n\right\}$ which contradicts to the fact $\left|S\right|=3$. Therefore, this case doesn’t occur.

Case 2.

$S=\{a,a^{-1},b\}$ with $b^2=e$ for some $a,b\in Q_{4n}\setminus \left\{e\right\}$ and $a\ne b$. By Proposition 3, $b\in S$ must be equal to $x^n$. Thus, we have $S=\{a,a^{-1},x^n\}$ for some $a\in Q_{4n}\setminus \{e,x^n\}$. There are only 2 possible cases, as follows.

2.a.

For $a=x^k$ with $1\le k<n$ or $n<k\le 2n-1$, we have ${\left(x^k\right)}^{-1}=x^{2n-k}$, and hence $S=\{x^k,x^{2n-k},x^n\}$.

2.b.

For $a=x^{p}y$ with $1\le p\le 2n$, by Proposition 4, we have ${\left(x^{p}y\right)}^{-1}=x^{n+p}y$, and hence $S=\{x^{p}y,x^{n+p}y,x^n\}$.

This completes the proof.

□

By Lemma 1, to observe the structure of the Cayley graph over the generalized quaternion group with valency 3, we only investigate the set $S=\{x^k,x^{2n-k},x^n\}$ with $1\le k<n$ or $n<k\le 2n-1$ and $S=\{x^{p}y,x^{n+p}y,x^n\}$ with $1\le p\le 2n$.

First, for the case $S=\{x^k,x^{2n-k},x^n\}$ with $1\le k<n$ or $n<k\le 2n-1$, we have 2 possible subgroups generated by S, as follows:

i.

$\langle \mathcal{S}\rangle =\langle x^k\rangle$, when $n=ik$ for some $1\le i\le o\left(x^k\right)$.

ii.

$\langle \mathcal{S}\rangle =\langle x^k,x^n\rangle$, when n is not a multiple of k.

The following lemma provides the reader with the structure of the $Cay(Q_{4n},S)$ with valency 3 for $S=\{x^k,x^{2n-k},x^n\}$ generating the cyclic subgroup in $Q_{4n}$ of order 4.

Lemma 2.

For any generator $S_1=\{x^k,x^{2n-k},x^n\}$ for $1\le k\le 2n$ with $k\ne n$ where the $\langle S_1\rangle =\langle x^k\rangle$ and $o\left(x^k\right)=4$, we have $Cay(Q_{4n},S_1)\cong n{K}_4$.

Proof. 

Clearly $S_1^{-1}\subseteq S_1$. Since $\langle S_1\rangle =\langle x^k\rangle$ for $1\le k\le 2n$ and $k\ne n$, and $o\left(x^k\right)=4$, by Proposition 3 we get $o\left(x^n\right)=2$. Thus $x^n$ must be equal to $x^{2k}$. Therefore ${\left(x^k\right)}^{-1}=x^{2n-k}=x^{3k}$. For every $1\le k\le 2n$, we have

$$\begin{array}{c}\hfill x^k{\left(e\right)}^{-1}=x^{2k}{\left(x^k\right)}^{-1}=x^{3k}{\left(x^{2k}\right)}^{-1}=x^{3k}{\left(e\right)}^{-1}=x^{2n-k}\in S_1.\end{array}$$

Therefore, we get a cycle $e-x^k-x^{2k}-x^{3k}-e$ of length 4, for every $1\le k\le 2n$. Moreover,

$$\begin{array}{c}\hfill e{\left(x^{2k}\right)}^{-1}=x^k{\left(x^{3k}\right)}^{-1}=x^{2k}=x^n\in S_1.\end{array}$$

Thus, $\{\left(e\right)\left(x^k\right),\left(x^k\right)\left(x^{2k}\right),\left(x^{2k}\right)\left(x^{3k}\right),\left(x^{3k}\right)\left(e\right),\left(e\right)\left(x^{2k}\right),\left(x^k\right)\left(x^{3k}\right)\}$ includes in

$E\left(Cay(Q_{4n},S_1)\right)$ for every $1\le k\le 2n$ and $k\ne n$.

Let $K_4$ be the complete graph with 4 vertices and let $V\left(K_4\right)=\{\overline{0},\overline{1},\overline{2},\overline{3}\}$. Construct a function

$$g:\{e,x^k,x^{2k},x^{3k}\}⟶V\left(K_4\right)$$

by $g\left(x^{ik}\right)=\overline{i}$, for every $i=0,1,2,3$ and for every $1\le k\le 2n$. It is easy to prove that the function g is an isomorphism. Thus, $\langle S_1\rangle =\langle x^k\rangle =\{e,x^k,x^{2k},x^{3k}\}$ generates an induced subgraph that is isomorphic to $K_4$.

Furthermore, $H_{S_1}=\langle S_1\rangle =\langle x^k\rangle =\{e,x^k,x^{2k},x^{3k}\}$ is a cyclic subgroup of $Q_{4n}$ of order 4. Consequently, $[Q_{4n}:H_{S_1}]=n$. Thus, there are n different right cosets in $Q_{4n}$. All of the right cosets are as follows

$$H_{S_1}{\gamma }_1=H_{S_1},H_{S_1}{\gamma }_2,H_{S_1}{\gamma }_3,\dots ,H_{S_1}{\gamma }_n,$$

where ${\gamma }_1=e\in H_{S_1}$ and ${\gamma }_2,{\gamma }_3,\dots ,{\gamma }_n\in Q_{4n}\setminus H_{S_1}$. Each right coset $H_{S_1}{\gamma }_j$ is equal to $\{{\gamma }_j,x^k{\gamma }_j,x^{2k}{\gamma }_j,x^{3k}{\gamma }_j\}$ for $j\in \{1,2,\dots ,n\}$. Using the same steps as before, we can construct an isomorphism between the induced subgraph of $Cay(Q_{4n},S_1)$ generated by $\left[H_{S_1}{\gamma }_j\right]$ and the $K_4$ graph for every $j=1,2,3,\dots ,n$. As a result, each of the n distinct right cosets is isomorphic to $K_4$. Thus, we can conclude that $Cay(Q_{4n},S_1)\cong n{K}_4$. □

The structure of the $Cay(Q_{4n},S)$, with $S=\{x^k,x^{2n-k},x^n\}$, which generates the cyclic subgroup in $Q_{4n}$ with order larger than 4, is detailed below.

Lemma 3.

For any generator $S_2=\{x^k,x^{2n-k},x^n\}$ for $1\le k\le 2n$ with $k\ne n$, where the $\langle S\rangle =\langle x^k\rangle$ and $o\left(x^k\right)\ge 6$, we have

$$Cay(Q_{4n},S_2)\cong 2gcd(2n,k)M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}.$$

Proof. 

It is clear that $S_2^{-1}\subseteq S_2$. We have $o\left(x^k\right)={\displaystyle \frac{2n}{gcd(2n,k)}}$. Thus, ${\displaystyle \frac{2n}{gcd(2n,k)}}=o\left(x^k\right)\ge 6$. Since $\langle S_2\rangle =\langle x^k\rangle$ for $1\le k\le 2n$ and $k\ne n$, also ${\displaystyle \frac{2n}{gcd(2n,k)}}=o\left(x^k\right)\ge 6$, we have

$$\langle S_2\rangle =\langle x^k\rangle =\{x^k,x^{2k},x^{3k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k},x^{{\displaystyle \frac{2n}{gcd(2n,k)}}k}=e\}.$$

Since $\langle S_2\rangle =\langle x^k\rangle$ and $x^n\in S_2$, it follows that $x^n$ must be equal to $x^{ik}$ for some $i\in \{1,2,3,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}\}$. Thus, we obtain ${\left(x^{ik}\right)}^2=e=x^{{\displaystyle \frac{2n}{gcd(2n,k)}}}$, which is equivalent to $i={\displaystyle \frac{n}{gcd(2n,k)}}\ge 3$. For every $1\le j\le {\displaystyle \frac{2n}{gcd(2n,k)}}$ and $1\le k\le 2n$, we have

$$\begin{array}{c}\hfill {\left(x^k\right)}^j·{\left({\left(x^k\right)}^{j+1}\right)}^{-1}=x^{2n-k}\in S_2\mathrm{and}{\left(x^k\right)}^j·{\left({\left(x^k\right)}^{j-1}\right)}^{-1}=x^k\in S_2.\end{array}$$

Therefore, we have a cycle $e-x^k-x^{2k}-x^{3k}-\dots -x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}-e$ of length ${\displaystyle \frac{2n}{gcd(2n,k)}}$ for every $1\le k\le 2n$. Furthermore,

$$\begin{array}{cc}\hfill {\left(x^k\right)}^j{\left({\left(x^k\right)}^{j+{\displaystyle \frac{n}{gcd(2n,k)}}}\right)}^{-1}& =x^{-{\displaystyle \frac{n}{gcd(2n,k)}}}=x^{-n}=x^n\in S_2.\hfill \end{array}$$

Thus, the set

$$\begin{array}{cc}\hfill & \left\{\left(x^{jk}\right)\left(x^{(j+1)k}\right)\mid \mathrm{for}\mathrm{all}j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}\cup \hfill \\ \hfill & \left\{\left(x^{jk}\right)\left(x^{(j-1)k}\right)\mid \mathrm{for}\mathrm{all}j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}\cup \hfill \\ \hfill & \left\{\left(x^{jk}\right)\left(x^{(j+{\displaystyle \frac{n}{gcd(2n,k)}})k}\right)\mid \mathrm{for}\mathrm{all}j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}\hfill \end{array}$$

is included in $E(Cay(Q_{4n},S_2)$ for all $1\le k\le 2n$ with $k\ne n$.

Let $M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$ be a Möbius ladder graph of ${\displaystyle \frac{2n}{gcd(2n,k)}}$ vertices with

$$V\left(M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\right)=\left\{\overline{j(mod{\displaystyle \frac{2n}{gcd(2n,k)}})}\mid j=1,2,3,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}\right\}\mathrm{and}$$

$$\begin{array}{cc}\hfill E\left(M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\right)=& \left\{\left(\overline{j(mod{\displaystyle \frac{2n}{gcd(2n,k)}})}\right)\left(\overline{j+1(mod{\displaystyle \frac{2n}{gcd(2n,k)}})}\right)\right.\hfill \\ & \left.\mid j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}\cup \hfill \\ \hfill & \left\{\left(\overline{j(mod{\displaystyle \frac{2n}{gcd(2n,k)}})}\right)\left(\overline{j+{\displaystyle \frac{n}{gcd(2n,k)}}(mod{\displaystyle \frac{2n}{gcd(2n,k)}})}\right)\right.\hfill \\ \hfill & \left.\mid j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}.\hfill \end{array}$$

Construct a function $h:\{e,x^k,x^{2k},x^{3k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\}⟶V\left(M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\right)$ by $h\left(x^{jk}\right)=\overline{j(mod{\displaystyle \frac{2n}{gcd(2n,k)}})}$ for all $j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1$ and for all $1\le k\le 2n$ with $k\ne n$. We obtain

$$\begin{array}{c}\hfill x^{jk}{x}^{(j+1)k}\in E\left(Cay(Q_{4n},S_2)\right)\iff g\left(x^{jk}\right)g\left(x^{(j+1)k}\right)\in E\left(M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\right)\end{array}$$

and

$$\begin{array}{c}\hfill x^{jk}{x}^{(j+{\displaystyle \frac{n}{gcd(2n,k)}})k}\in E\left(Cay(Q_{4n},{\mathcal{S}}_2)\right)\iff g\left(x^{jk}\right)g\left(x^{(j+{\displaystyle \frac{n}{gcd(2n,k)}})k}\right)\in E\left(M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\right)\end{array}$$

for all $j=0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1$. In other words, the function h is an isomorphism. Thus, $\langle S_2\rangle =\langle x^k\rangle =\{e,x^k,x^{2k},x^{3k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\}$ in the $Cay(Q_{4n},S_1)$ generates an induced subgraph that is isomorphic to $M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$.

Furthermore, $H_{S_2}=\langle S_2\rangle =\langle x^k\rangle =\{e,x^k,x^{2k},x^{3k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\}$ is subgroup of $Q_{4n}$ of order ${\displaystyle \frac{2n}{gcd(2n,k)}}$. As a result, $[Q_{4n}:H_{S_2}]=2gcd(2n,k)$ indicates that $Q_{4n}$ contains $2gcd(2n,k)$ unique right cosets. All of the right cosets are as follows

$$H_{S_2}{\theta }_1=H_{S_2},H_{S_2}{\theta }_2,H_{S_2}{\theta }_3,\dots ,H_{S_2}{\theta }_{2gcd(2n,k)}$$

where ${\theta }_1=e\in H_{S_2}$ and ${\theta }_2,{\theta }_3,\dots ,{\theta }_{2gcd(2n,k)}\in Q_{4n}\setminus H_{S_2}$. Each right coset $H_{S_2}{\theta }_p$ equals to $\{{\theta }_p,x^k{\theta }_p,x^{2k}{\theta }_p,x^{3k}{\theta }_p,\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}{\theta }_p\}$ for $p\in \{1,2,\dots ,$

$2gcd(2n,k)\}$. Using the same techniques as before, it is easy to demonstrate the isomorphism between the subgraph of $Cay(Q_{4n},S_2)$ induced by $H_{S_2}{\theta }_p$ and the Möbius ladder graph $M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$ graph for every $p=1,2,3,\dots ,2gcd(2n,k)$. Therefore, each of the $2gcd(2n,k)$ distinct subgraphs is isomorphic to $M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$. Thus, we may conclude that

$$Cay(Q_{4n},S_2)\cong 2gcd(2n,k)M_{{\displaystyle \frac{2n}{gcd(2n,k)}}}.$$

□

In addition to the case $\langle S\rangle =\langle x^k\rangle$, we now consider the scenario where the generating set S gives rise to a subgroup generated by both $x^k$ and $x^n$, leading to a different structural form of the Cayley graph.

Lemma 4.

For any generator $S_3=\{x^k,x^{2n-k},x^n\}$ for some $1\le k\le 2n-1$ with $k\ne n$, and the $\langle S_3\rangle =\langle x^k,x^n\rangle$, we have

$$Cay(Q_{4n},S_3)\cong gcd(2n,k)\left(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2\right).$$

Proof. 

It is clear that $S_3\subseteq S_3^{-1}$. $o\left(x^k\right)={\displaystyle \frac{2n}{gcd(2n,k)}}$ for any $1\le k\le 2n-1$ with $k\ne n$. We have

$$\begin{array}{c}\hfill \langle S_3\rangle =\langle x^k,x^n\rangle =\{x^k,x^{2k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k},e,x^n,x^{n+k},\dots ,x^{n+({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\},\end{array}$$

of ${\displaystyle \frac{4n}{gcd(2n,k)}}$ elements. For every $i\in \{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\}$ holds

$$\begin{array}{c}\hfill x^{ik}{\left(x^{(i+1)k}\right)}^{-1}=x^{-k}=x^{2n-k}\in S_3.\end{array}$$

Therefore, we have a cycle $e-x^k-x^{2k}-x^{3k}-\dots -x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}$ of length ${\displaystyle \frac{2n}{gcd(2n,k)}}$. For every $i\in \{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\}$, we obtain

$$\begin{array}{c}\hfill x^{n+ik}{\left(x^{n+(i+1)k}\right)}^{-1}=x^{-k}=x^{2n-k}\in S_3.\end{array}$$

In the same way, we also have a cycle $x^n-x^{n+k}-x^{n+2k}-\dots -x^{n+({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}-x^n$ of length ${\displaystyle \frac{2n}{gcd(2n,k)}}$. Furthermore, for every $i\in \{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\}$ we have

$$\begin{array}{c}\hfill x^{ik}{\left(x^{n+ik}\right)}^{-1}=x^{ik}{x}^n{x}^{-ik}=x^n\in S_3.\end{array}$$

Thus, the set

$$\begin{array}{cc}\hfill & \left\{x^{ik}{x}^{(i+1)k}\mid \mathrm{for}\mathrm{every}i\in \{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\}\right\}\cup \hfill \\ \hfill & \left\{x^{n+ik}{x}^{n+(i+1)k}\mid \mathrm{for}\mathrm{every}i\in \{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\}\right\}\cup \hfill \\ \hfill & \left\{x^{ik}{x}^{n+ik}\mid \mathrm{for}\mathrm{every}i\in \{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\}\right\}\hfill \end{array}$$

is included in $E\left(Cay(Q_{4n},S_3)\right)$ for every $1\le k\le 2n$ and $k\ne n$.

Let $C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2$ be a cartesian product graph of $C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}$ and $P_2$. Let

$$\begin{array}{cc}\hfill V(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2)=& \left\{(0,1),(1,1),(2,1),(3,1),\dots ,\left({\displaystyle \frac{2n}{gcd(2n,k)}}-1,1\right),(0,2),\right.\hfill \\ \hfill & \left.(1,2),(2,2),(3,2),\dots ,\left({\displaystyle \frac{2n}{gcd(2n,k)}}-1,2\right)\right\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill E(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2)=& \left\{(0,1)(1,1),(1,1)(2,1),(2,1)(3,1),\dots ,\right.\hfill \\ \hfill & \left({\displaystyle \frac{2n}{gcd(2n,k)}}-2,1\right)\left({\displaystyle \frac{2n}{gcd(2n,k)}}-1,1\right),\hfill \\ & \left.\left({\displaystyle \frac{2n}{gcd(2n,k)}}-1,1\right)(0,1)\right\}.\hfill \end{array}$$

Construct a function $l:\langle S_3\rangle \to V(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2)$ by $l\left(x^{ik}\right)=(i,1)$ and $l\left(x^{n+ik}\right)=(i,2)$ for all $i\in \left\{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}$. We obtain

$$\begin{array}{cccccccc}\hfill & x^{ik}{x}^{(i+1)k}\in E\left(Cay(Q_{4n},{\mathcal{S}}_4)\right)\hfill & \hfill & \iff \hfill & \hfill & l\left(x^{ik}\right)l\left(x^{(i+1)k}\right)\in E(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2),\hfill & \hfill & \\ \hfill & x^{n+ik}{x}^{n+(i+1)k}\in E\left(Cay(Q_{4n},{\mathcal{S}}_4)\right)\hfill & \hfill & \iff \hfill & \hfill & l\left(x^{ik}\right)l\left(x^{(i+1)k}\right)\in E(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2),\hfill & \hfill & \\ \hfill & x^{ik}{x}^{n+ik}\in E\left(Cay(Q_{4n},{\mathcal{S}}_4)\right)\hfill & \hfill & \iff \hfill & \hfill & l\left(x^{ik}\right)l\left(x^{n+ik}\right)\in E(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2),\hfill & \hfill \end{array}$$

for all $i\in \left\{0,1,2,\dots ,{\displaystyle \frac{2n}{gcd(2n,k)}}-1\right\}$. In other words, l is an isomorphism. It is easy to verify that $\langle S_3\rangle =\langle x^k,x^n\rangle =\{x^k,x^{2k},\dots ,x^{({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k},e,x^n,x^{n+k},\dots ,$

$x^{n+({\displaystyle \frac{2n}{gcd(2n,k)}}-1)k}\}$ generates an induced subgraph of $Cay(Q_{4n},S_3)$ that is isomorphic to $C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2$.

Moreover, we can construct $gcd(2n,k)$ different right cosets, using the same techniques as Lemma 3. Furthermore, we can verify that every different right coset induces a subgraph that is isomorphic to $C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2$. Thus,

$$Cay(Q_{4n},S_3)\cong gcd(2n,k)\left(C_{{\displaystyle \frac{2n}{gcd(2n,k)}}}\square P_2\right).$$

□

Secondly, we observe for the case $S=\{x^{p}y,x^{n+p}y,x^n\}$ with $1\le p\le 2n$. By Proposition 4, the order of $x^{p}y$ is 4, so that we have

$$\begin{array}{c}\hfill \langle S\rangle =\langle x^{p}y\rangle =\{e,x^{p}y,x^n,x^{n+p}y\}.\end{array}$$

In other words, $\langle S\rangle =\langle x^{p}y\rangle$. In the following lemma, we characterize the structure of the Cayley graph with the connecting set $S=\{x^{p}y,x^{n+p}y,x^n\}$ for $1\le p\le 2n$.

Lemma 5.

For any generator $S=\{x^{p}y,x^{n+p}y,x^n\}$ for some $1\le p\le 2n$, we have $Cay(Q_{4n},S)\cong n{K}_4$.

Proof. 

Clearly $o\left(x^{p}y\right)=4$, thus $\langle S\rangle =\langle x^{p}y\rangle =\{x^{p}y,{\left(x^{p}y\right)}^2,{\left(x^{p}y\right)}^3,{\left(x^{p}y\right)}^4\}=\{e,x^{p}y,x^n,x^{n+p}y\}$. For $i=0,1,2,3$, we have

$${\left(x^{p}y\right)}^i{\left(x^{p}y\right)}^{-(i+1)}={\left(x^{p}y\right)}^{-1}=x^{n+p}y\in S.$$

Thus we have a cycle $e-x^{p}y-x^n-x^{n+p}y-e$ of length 4. Moreover, it holds

$$\begin{array}{cc}\hfill x^n{\left(e\right)}^{-1}& =x^n\in S,\hfill \\ \hfill x^{n+p}y{\left(x^{p}y\right)}^{-1}& =x^{n+p}y{x}^{n+p}y=x^n\in S.\hfill \end{array}$$

Thus, we have $\{\left(e\right)\left(x^{p}y\right),\left(x^{p}y\right)\left(x^n\right),\left(x^n\right)\left(x^{n+p}y\right),\left(x^{n+p}y\right)\left(e\right),\left(e\right)\left(x^n\right),\left(x^{p}y\right)\left(x^{n+p}y\right)\}$ is a subset of $E\left(Cay(Q_{4n},S)\right)$ for every $1\le p\le 2n$.

Let $K_4$ be a complete graph of order 4 and size 6 with $V\left(K_4\right)=\{\overline{0},\overline{1},\overline{2},\overline{3}\}$. Construct a function

$$\alpha :\{e,x^{p}y,x^n,x^{n+p}y\}\to V\left(K_4\right)$$

with $\alpha \left({\left(x^{p}y\right)}^i\right)=\overline{i(mod4)}$ for $i=0,1,2,3$. We obtain

$$\begin{array}{cc}\hfill {\left(x^{p}y\right)}^i{\left(x^{p}y\right)}^{i+1}\in E\left(Cay(Q_{4n},S)\right)& \iff \alpha \left({\left(x^{p}y\right)}^i\right)\alpha \left({\left(x^{p}y\right)}^{i+1}\right)\in E\left(K_4\right)\mathrm{and}\hfill \\ \hfill {\left(x^{p}y\right)}^i{\left(x^{p}y\right)}^{i+2}\in E\left(Cay(Q_{4n},S)\right)& \iff \alpha \left({\left(x^{p}y\right)}^i\right)\alpha \left({\left(x^{p}y\right)}^{i+2}\right)\in E\left(K_4\right).\hfill \end{array}$$

Thus $\alpha$ is an isomorphism. It follows that the subgraph induced by $\langle S\rangle =\{e,x^{p}y,x^n,x^{n+p}y\}$ is isomorphic to $K_4$.

Furthermore, we may construct subgraphs induced by the n right cosets using the same procedure as before. It can be shown that each distinct right coset induces a subgraph isomorphic to $K_4$. Therefore, $Cay(Q_{4n},S)\cong n{K}_4.$ □

All generating sets S that give rise to Cayley graphs with valency 3 have been fully classified. The following theorem characterizes the structure of Cayley graphs over the generalized quaternion group with valency 3 in detail.

Theorem 3.

For any generator $\mathcal{S}=\{a,a^{-1},x^n\}\subseteq Q_{4n}$ for some $a\in Q_{4n}\setminus \{e,x^n\}$. It holds

i.

if $\langle \mathcal{S}\rangle =\langle a\rangle$ and $o\left(a\right)=4$, we have $Cay(Q_{4n},\mathcal{S})\cong n{K}_4$,

ii.

if $\langle \mathcal{S}\rangle =\langle a\rangle$ and $o\left(a\right)=p$ for some $p\in \mathbb{N}$ with $p\ge 6$ we have $Cay(Q_{4n},\mathcal{S})\cong {\displaystyle \frac{4n}{p}}{M}_p$,

iii.

if $\langle \mathcal{S}\rangle =\langle a,x^n\rangle$ and $o\left(a\right)=q$ for some $q\in \mathbb{N}$ then we have $Cay(Q_{4n},\mathcal{S})\cong {\displaystyle \frac{2n}{q}}(C_q\square P_2)$.

3. Conclusion

This paper explores the structure of the Cayley graph over the generalized quaternion group with valencies up to 3. Future work may investigate the structure of the same Cayley graph with valencies greater than or equal to 4.