A Methodology for Quantum Gates Homogenizing using Lie Group Representations

1. Introduction

The advent of quantum computing promises to revolutionize numerous fields, offering unparalleled capabilities for solving complex problems currently intractable for classical machines. At the heart of this revolutionary paradigm are quantum gates, the fundamental unitary operations that manipulate quantum states. As quantum hardware continues its rapid scaling, a rich and increasingly diverse set of these gates has emerged, ranging from universal single-qubit rotations and entangling two-qubit operations like CNOT, and highly specialized multi-qubit constructs, such as Toffoli gates or complex, custom-designed unitary oracles [1,2]. While this inherent diversity in gate types provides flexibility in algorithmic design and reflects the unique native capabilities and physical interaction mechanisms of various quantum hardware platforms (e.g., superconducting circuits, trapped ions, photonic systems), it simultaneously introduces significant complexities in the practical development, analysis, and execution of quantum programs. The proliferation of distinct gate types, each with its own physical realization, error profile, and computational cost, often obscures the underlying mathematical unity of quantum operations and presents formidable challenges for quantum software engineering [3].

This article addresses the critical problem of quantum gate homogenization: the endeavor to establish a unified and consistent mathematical framework for representing, classifying, and manipulating this vast array of quantum operations. We contend that the elegant and powerful theory of Lie groups and their representations offers precisely such a framework. Lie groups, as continuous groups of transformations, naturally describe the smooth and continuous nature of quantum evolution, while their representations provide a systematic way to understand how these transformations act on the Hilbert space of quantum systems. By abstracting away specific physical implementations or conventional naming conventions, Lie theory allows us to view all quantum gates as elements of a continuous mathematical manifold, thereby enabling a truly homogeneous perspective that spans different gate types and even distinct quantum computing paradigms [4,5]. This homogenization is not merely an academic exercise; it offers tangible benefits for addressing the multifaceted challenges facing the field.

The practical implications of this homogenization are far-reaching. By providing a unified mathematical language for quantum operations, the theory of Lie groups simplifies the process of quantum program analysis, allowing for more accurate resource estimation and formal verification [6]. It streamlines quantum program synthesis by offering systematic methods for constructing arbitrary unitary operations from a minimal, universal set of fundamental gates, enhancing automated circuit design [7]. Furthermore, it fundamentally underpins the efficiency of transpilation, enabling compilers to effectively map logical circuits onto diverse hardware architectures with optimized gate counts and depths, regardless of the hardware’s native gate set [8]. This unified framework also guides the design and calibration of quantum hardware itself, as physical control pulses can be precisely tailored to generate desired Lie group elements, leading to higher-fidelity gate operations [9,10]. Ultimately, homogenization fosters greater interoperability, portability, and scalability across the rapidly evolving quantum computing ecosystem.

The structure of this article is designed to progressively build a comprehensive understanding of quantum gate homogenization through the lens of Lie group representations. In Section 2, we elaborate on the practical problem of gate homogenization, surveying its impact across various aspects of quantum computing, including program analysis, synthesis, transpilation, and hardware construction, highlighting contemporary challenges and state-of-the-art solutions. Section 3 lays the theoretical foundations, meticulously detailing the mathematical concepts of Lie groups, Lie algebras, and their representations, complete with explicit examples relevant to quantum systems. We then delve into the application of this theory: Section 4 focuses on single-qubit gates, demonstrating how $SU\left(2\right)$ provides a complete homogenization via the Euler Angle Decomposition and its connection to the Bloch sphere. Building upon this, Section 5 expands to multi-qubit gates, showcasing how universal gate sets (e.g., through the Solovay-Kitaev Theorem) enable homogenization by approximation and how the decomposition of composite Hilbert spaces into irreducible representations (multiplets) offers a profound, symmetry-aware homogenization. Crucially, Section 5 also reinterprets fundamental quantum phenomena like superposition and entanglement through the lens of these irreducible representations. In Section 6, we propose a general methodology for systematically transforming quantum programs into a homogeneous gate set, differentiating between discrete variable systems (qubits/qudits) and more general continuous Lie group-based systems. Finally, Section 7 provides practical demonstrations of this methodology, applying it to well-known quantum algorithms such as Deutsch’s Algorithm, Quantum Teleportation, and Quantum Phase Estimation, using the Qiskit framework to illustrate the transformation from a heterogeneous to a homogeneous gate representation. By demonstrating this unified mathematical framework, this article aims to simplify the conceptualization, development, and deployment of quantum software, ultimately contributing to the advancement of scalable and robust quantum computing.

2. The Problem of Quantum Gate Homogenization

The rapid proliferation of quantum computing paradigms and architectures has led to a rich but often disparate vocabulary of quantum gates. While this diversity allows for specialized optimizations and reflects unique physical capabilities, it simultaneously introduces significant challenges in the design, analysis, and execution of quantum programs. The "homogenization" of quantum gates—that is, finding a unified and consistent framework for representing and manipulating these diverse operations—is therefore a pressing problem that underpins the scalability and practical utility of quantum computing.

2.1. Quantum Program Analysis

Analyzing the behavior, performance, and correctness of quantum programs is paramount for their development and deployment, yet the inherent heterogeneity of gate sets significantly complicates this process. Traditional metrics like simple gate counts and circuit depth often fall short when comparing circuits composed of different types of gates, as the actual "cost" of a gate can vary drastically depending on its type and the underlying hardware. This leads to a lack of a truly unified abstraction, making it challenging to reason about a circuit’s true resource consumption or its inherent quantum complexity [2]. State-of-the-art approaches are moving towards more sophisticated hardware-aware cost models that account for nuanced factors like gate fidelities, execution times, qubit connectivity, and even crosstalk [3]. These models implicitly acknowledge the need for a common denominator (often a universal gate set) against which all operations can be benchmarked, enabling more realistic performance estimations and a clearer understanding of program efficiency.

Furthermore, efforts in quantum circuit characterization involve extracting essential properties of circuits or individual gates that transcend specific gate names, often relying on randomized benchmarking (RB) or gate-set tomography (GST) to characterize gate errors and fidelities. These techniques provide a homogeneous performance metric, allowing for platform-agnostic comparison of gate quality rather than mere gate type [11,12]. The goal is to provide a standardized performance profile for any physically implemented gate, regardless of its logical definition. This homogenization of performance data is critical for accurate error mitigation and effective resource estimation for fault-tolerant quantum computing, allowing for more informed decisions in algorithm design and hardware selection. Moreover, the nascent but growing field of formal verification for quantum programs greatly benefits from a homogeneous gate basis, as it simplifies the definition and verification of primitive logical operations, making the entire process more tractable for complex circuits [6].

Finally, the increasing size and complexity of quantum programs necessitate automated analysis tools. A homogeneous gate set simplifies the input to these tools, allowing them to focus on structural analysis, optimization potential, and property extraction without needing to account for an arbitrary number of gate definitions [13]. This streamlined representation is crucial for developing robust static analysis techniques, identifying common sub-circuits, and performing design-space exploration in a scalable manner. By reducing the problem space to a consistent set of operations, homogenization enables more efficient and reliable analytical methods, contributing directly to the maturation of quantum software engineering.

2.2. Quantum Program Synthesis

The creation of quantum algorithms and their translation into executable circuits (quantum program synthesis) faces a significant hurdle due to gate diversity, particularly when designing novel quantum algorithms or variational Ansätze [14]. Developers are often confronted with an overwhelming choice of gates, lacking systematic methods for constructing complex unitary operations beyond known templates (e.g., quantum adders, multipliers). This intuitive barrier restricts creativity and limits the potential for automated algorithmic discovery, as the process often relies on ad-hoc methods or manual ingenuity rather than systematic generative approaches. Without a clear algebraic roadmap, the synthesis process can be inefficient and suboptimal, making portability across different quantum computing platforms a considerable challenge.

To address this, state-of-the-art synthesis methods increasingly employ optimization solvers and machine learning techniques to search for optimal gate sequences that implement a desired unitary. These methods typically operate within a predefined, homogeneous universal gate set, transforming the problem of arbitrary unitary synthesis into a structured search problem [7]. Examples include reinforcement learning-based approaches that learn to build circuits [15] or methods that leverage satisfiability modulo theories (SMT) solvers for exact synthesis of small circuits [16]. The underlying principle is that by operating on a homogeneous set of elementary gates, the search space becomes well-defined and structured, enabling more efficient exploration and convergence to a solution, thereby automating parts of the quantum software development lifecycle.

Furthermore, advancements in quantum compilation frameworks are extending beyond simple basis translation to include sophisticated synthesis capabilities. These frameworks leverage algebraic decompositions (such as KAK decomposition for two-qubit gates or generalized methods for multi-qubit operations) to systematically break down high-level unitary functions into homogeneous sequences of elementary gates [17]. This automated synthesis, fundamentally grounded in group-theoretical principles, ensures that any desired operation, no matter how complex, can be expressed as a finite composition of a few, well-understood homogeneous primitives. This not only enhances the portability and modularity of quantum programs but also streamlines the development of higher-level quantum software libraries, as complex functions can be defined unitarily and then automatically compiled into a consistent low-level gate set executable on hardware.

2.3. Transpilation

Transpilation, the crucial step of adapting a logical quantum circuit to a specific hardware architecture, is arguably the most direct beneficiary and driver of gate homogenization research. Quantum processors inherently support only a limited set of native gates, which vary significantly across different qubit technologies (e.g., single-qubit rotations and CNOTs for superconducting circuits, Mølmer-Sørensen gates for trapped ions, or specific gates in neutral atom platforms). This inherent heterogeneity creates a fundamental mismatch between the abstract gates in a high-level quantum program and the physical operations available [3]. State-of-the-art transpilers address this by performing a basis transformation, where all gates in the input circuit are converted into the native gate set of the target device. This often involves a multi-stage process of hierarchical decomposition rules (e.g., a Toffoli gate might first decompose into CNOTs, Hadamards, and T gates, which then further decompose into hardware-native single- and two-qubit gates), systematically transforming a heterogeneous logical circuit into a homogeneous hardware-specific one [2].

Beyond simple basis translation, advanced transpilation passes incorporate sophisticated optimization techniques that aim to reduce gate count, circuit depth, or qubit communication (routing) while adhering to the homogeneous target basis [18]. These optimizations are critical for improving circuit fidelity and execution time on noisy intermediate-scale quantum (NISQ) devices, where coherence times are limited and gate errors accumulate quickly. The uniform representation provided by homogenization greatly simplifies the application of graph-theoretic algorithms for qubit routing and scheduling, and allows for more effective application of template matching and peephole optimization techniques. The ongoing development of adaptive transpilers that can respond dynamically to real-time hardware noise profiles, connectivity changes, or specific performance targets further emphasizes the need for a robust, homogeneous gate representation to enable effective, context-aware optimization in a dynamic environment [8].

Ultimately, the drive for homogenization in transpilation is a direct response to the "assembly language" nature of current quantum hardware. Just as classical compilers translate high-level code into machine instructions, quantum transpilers translate high-level quantum logic into a homogeneous set of primitive operations compatible with specific quantum processors. This process streamlines the development pipeline, ensures portability across diverse hardware, and is essential for achieving optimal performance and efficient utilization of quantum resources on current and future quantum computing platforms.

2.4. Quantum Hardware Construction and Calibration

The very design, fabrication, and calibration of quantum hardware are profoundly influenced by the gate set they implement. While some platforms might offer highly optimized, fast implementations of a few specific gates, the overarching goal for universal quantum computers is to achieve universal quantum control – the ability to implement any arbitrary unitary operation with high fidelity. This necessitates a deep understanding of how a homogeneous set of fundamental gates can be precisely realized and calibrated [9]. Research is actively focused on developing universal quantum control techniques that, by meticulously manipulating analog control pulses (e.g., microwave, laser pulses), can generate a wide range of quantum gates, often leveraging insights from Lie theory on the Lie algebra of the system’s Hamiltonian, where control parameters correspond to coefficients of generators in the Lie algebra [10].

The primary challenge lies in achieving high fidelity for these complex, homogeneous gates in the presence of various noise sources and decoherence mechanisms inherent to quantum systems [19]. Advanced calibration techniques are continuously being developed to systematically characterize the exact unitary implemented by physical pulses and to mitigate errors. Methods like Gate Set Tomography (GST) and Randomized Benchmarking (RB) are at the forefront, aiming to verify that the physical gates closely match their ideal homogeneous mathematical counterparts by measuring their average fidelity and error rates [11,12]. These techniques provide a standardized, homogenized view of gate performance across different hardware implementations, allowing for objective comparison and continuous improvement of qubit quality and gate operations.

The pursuit of gate homogenization also drives efforts in control electronics design and pulse sequencing. By having a unified mathematical framework for all gates, engineers can design more efficient and scalable control systems capable of generating the precise waveforms needed to implement any arbitrary unitary transformation using a minimal set of underlying physical interactions. This contributes significantly to the modularity and scalability of quantum hardware, paving the way for larger and more complex quantum processors [19]. The convergence towards a common, homogenous mathematical description for gates thus simplifies not only the design of robust control systems but also the development of automated, on-chip calibration protocols, which are essential for increasing the operational time, reliability, and ultimately, the utility of quantum computers.

2.5. Theoretical Understanding and Generalization

From a theoretical standpoint, the problem of gate homogenization touches upon the very foundations of quantum information science. A homogeneous gate set provides a unified mathematical language for describing computational processes, simplifying the analysis of quantum complexity theory and the fundamental limits of quantum algorithms. It allows researchers to move beyond the specifics of particular gate implementations to reason about the intrinsic computational power of universal gate sets, fostering a deeper understanding of quantum computational capabilities. It is also crucial for the development of fault-tolerant quantum computation, where operations must be realized using a specific set of highly reliable, fault-tolerant gates (often requiring resource-intensive techniques like magic state distillation for non-Clifford operations). The compilation of arbitrary circuits into such fault-tolerant gate sets inherently relies on their decomposition into a homogeneous basis [20].

Furthermore, as quantum computing expands beyond the qubit paradigm, the principles of homogenization become even more pronounced. The exploration of qudits (quantum systems with $d>2$ levels) introduces the need to understand operations within $SU\left(d\right)$, where group theoretical tools become indispensable for classifying gates, determining universality, and identifying elementary operations [21]. Similarly, in continuous variable (CV) quantum computing (systems with infinite-dimensional Hilbert spaces like photonic modes), generalized Lie groups (e.g., the Symplectic group for Gaussian operations) and their representations become the primary tools for classifying operations, understanding entanglement, and determining the universality of gate sets in a continuous space [22]. This generalizability across diverse quantum platforms underscores the power of Lie theory to provide a consistent theoretical framework for all forms of quantum computation, unifying seemingly disparate approaches under a common mathematical umbrella.

In summary, the problem of quantum gate homogenization is not merely an academic exercise but a multifaceted challenge whose solution is essential for the advancement of quantum computing. This article posits that this solution lies deeply rooted in the elegant and powerful mathematics of Lie groups and their representations. By viewing all quantum gates as elements of a continuous mathematical space described by Lie groups, we unlock a systematic approach to classification, decomposition, and synthesis, thereby addressing these critical challenges that are actively being researched in the contemporary quantum landscape.

3. Theoretical Foundations: Lie Groups and Representations

Quantum operations are inherently unitary transformations acting on quantum states within a Hilbert space. The mathematical framework for understanding these transformations with a unified, continuous perspective is provided by the theory of Lie groups and their representations. This section delves into the essential mathematical background required to appreciate how Lie groups homogenize quantum gates.

3.1. Lie Groups and Their Relevance to Quantum Gates

A Lie group G is a mathematical object that simultaneously possesses the structure of a group and a differentiable manifold. This means that its elements can be continuously varied, and the group operations (multiplication and inversion) are smooth functions with respect to this manifold structure. For quantum computing, Lie groups provide the natural mathematical space in which quantum gates reside. Specifically, for a quantum system with a D-dimensional Hilbert space $\mathcal{H}$, the set of all unitary operators acting on $\mathcal{H}$ forms the Unitary Group, $U\left(D\right)$. A crucial subgroup for quantum gates is the Special Unitary Group, $SU\left(D\right)$, which consists of all $D\times D$ unitary matrices with a determinant of +1. The condition of determinant +1 arises from the physical indistinguishability of global phase factors in quantum mechanics; $e^{i\theta }U$ represents the same physical operation as U. Therefore, all quantum gates acting on an N-qubit system (where $D=2^N$) are elements of $SU\left(2^N\right)$ [5,23].

The group structure implies that gates can be composed (multiplied) to form new gates, and every gate has an inverse. The manifold structure signifies that gates can be parameterized continuously. For example, a rotation gate $R_X\left(\theta \right)$ depends continuously on the angle $\theta$. This continuous parametrization is a core aspect of homogenization, allowing for a single mathematical form to describe an infinite family of related operations. The properties of Lie groups allow for the rigorous study of the relationships and transformations between different quantum gates, fundamentally homogenizing what might otherwise appear as a disparate collection of operations [4].

The importance of this continuous structure cannot be overstated. Unlike finite groups, which are relevant for discrete symmetries (e.g., permutation groups for identical particles), Lie groups describe continuous symmetries, such as rotations in space or phase transformations in quantum mechanics. This continuous aspect is precisely what allows for the smooth interpolation between different gates and for the approximation of any complex gate by a sequence of simpler, continuously adjustable gates. This forms the basis for quantum control, where continuous parameters of physical pulses are mapped to specific unitary evolutions, allowing for the precise generation of desired quantum gates [10].

3.2. Lie Algebras: The Generators of Quantum Gates

Intimately connected to every Lie group G is its Lie algebra, denoted $\mathfrak{g}$. The Lie algebra can be intuitively understood as the tangent space of the Lie group at its identity element. It captures the "infinitesimal" transformations that, when continuously applied, generate the finite transformations (elements) of the Lie group. For the special unitary group $SU\left(D\right)$, its Lie algebra $\mathfrak{su}\left(D\right)$ consists of all $D\times D$ anti-Hermitian matrices with a trace of zero. A matrix A is anti-Hermitian if $A^{†}=-A$. This property is crucial because unitary operators U are generated by Hermitian operators H via the exponential map: $U=e^{iH}$[5]. If H is Hermitian, then $iH$ is anti-Hermitian, meaning $iH\in \mathfrak{su}\left(D\right)$.

Theorem 3.1. 

Exponential Map and Unitary Generators For any finite-dimensional Hilbert space, a unitary operator U can always be written in the form $U=e^{iH}$ for some Hermitian operator H. If $U\in SU\left(D\right)$ (i.e., $det\left(U\right)=1$), then the corresponding Hermitian operator H must be traceless.

Proof Sketch. 

• Unitary Condition: If U is unitary, $U{U}^{†}=\mathrm{I}$. Taking the derivative with respect to a parameter t of a path $U\left(t\right)$ with $U\left(0\right)=\mathrm{I}$, we get $\dot{U}\left(0\right)U^{†}\left(0\right)+U\left(0\right){\dot{U}}^{†}\left(0\right)=0$, which simplifies to $\dot{U}\left(0\right)+{\dot{U}}^{†}\left(0\right)=0$. This means $\dot{U}\left(0\right)$ is anti-Hermitian.
• Infinitesimal Generator: Let $A=\dot{U}\left(0\right)$ be an infinitesimal generator. Since A is anti-Hermitian, we can write $A=iH$ where H is Hermitian ($H^{†}=H$).
• Finite Transformation: A finite transformation U can be approximated as $U\approx \mathrm{I}+\delta t·A=\mathrm{I}+i\delta t·H$. Iterating this, $U={lim}_{n\to \infty }{(\mathrm{I}+i(t/n)H)}^n=e^{iHt}$. This is the exponential map from the Lie algebra to the Lie group.
• Determinant Condition: For $U\in SU\left(D\right)$, we require $det\left(U\right)=1$. The property $det\left(e^A\right)=e^{\mathrm{Tr}\left(A\right)}$ implies that if $det\left(U\right)=1$, then $\mathrm{Tr}\left(iH\right)=0$, which in turn means $\mathrm{Tr}\left(H\right)=0$[24]. Thus, Hermitian and traceless operators are the generators for $SU\left(D\right)$.

   □

The elements of the Lie algebra $\mathfrak{su}\left(D\right)$ are often referred to as the "generators" of quantum gates. For example, the Pauli matrices ${\sigma }_x,{\sigma }_y,{\sigma }_z$ are the generators for single-qubit rotations, representing the infinitesimal rotations around the x, y, and z axes on the Bloch sphere, respectively [23]. The ability to express any quantum gate as an exponential of a Hermitian generator is central to quantum control, where precise time-dependent Hamiltonians are engineered to realize target unitary operations. This concept provides a profound homogenization: all gates, regardless of their complexity, emerge from the exponentiation of linear combinations of fundamental, infinitesimal generators [10].

The Lie algebra also defines the structure of the Lie group. The commutation relations between the generators are fundamental invariants of the group, revealing its symmetry properties. For instance, the commutation relations of the Pauli matrices define the $\mathfrak{su}\left(2\right)$ Lie algebra, which governs all single-qubit operations. Understanding these relations allows for predicting how different gates interact and and how they compose. This algebraic perspective simplifies gate synthesis and analysis by reducing the problem to manipulating elements within a linear vector space (the Lie algebra) rather than a curved manifold (the Lie group) [4].

3.3. Representations and the Decomposition of Hilbert Space

A representation of a Lie group G is a mapping (a homomorphism) from the group elements to a set of linear operators on a vector space V. In quantum mechanics, these operators are unitary transformations on a Hilbert space, and V is often the Hilbert space of the quantum system itself. A representation is irreducible (irrep) if the vector space V has no proper non-zero subspaces that are invariant under all operators in the representation. If a representation is reducible, it means the Hilbert space can be decomposed into a direct sum of smaller invariant subspaces, each corresponding to an irreducible representation [5]. This decomposition is denoted by the symbol ⨁. For example, if a space V decomposes into two invariant subspaces $V_1$ and $V_2$, we write $V=V_1⨁V_2$. $V_2$ would be the orthogonal complement of $V_1$ if the subspaces are orthogonal.

The decomposition of a Hilbert space into irreducible representations is a powerful homogenization technique. It means that the total complex system can be broken down into independent "symmetry sectors," where operations respecting that symmetry will only transform states within those sectors, never mixing states between different ones. This simplifies analysis because the full high-dimensional unitary matrix of an operation can become block-diagonal when expressed in a basis aligned with these irreducible subspaces, revealing the inherent symmetries of the system and its operations [24].

Explicit Calculation Example: Single Qubit (Fundamental Representation of SU(2))

The fundamental representation of $SU\left(2\right)$ acts on ${\mathbb{C}}^2$, the Hilbert space of a single qubit. An element $U\in SU\left(2\right)$ is a $2\times 2$ unitary matrix with determinant 1:

$$U=\left(\begin{array}{cc}a& b\\ -b^{*}& a^{*}\end{array}\right){,\left|a\right|}^2+{\left|b\right|}^2=1$$

This is the defining representation of $SU\left(2\right)$, and it is also its simplest non-trivial irreducible representation, corresponding to spin-$1/2$. Any operation on a single qubit, whether a Hadamard, Pauli-X, or an arbitrary rotation, is simply an element of this $2\times 2$ matrix group. There are no invariant subspaces other than the trivial ones ($\left\{0\right\}$ and ${\mathbb{C}}^2$ itself), confirming its irreducibility. All possible pure states of a single qubit, represented as vectors $\left(\begin{array}{c}\alpha \\ \beta \end{array}\right)$ where ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$, live in this 2-dimensional irreducible space.

Explicit Calculation Example: Two Qubits (Tensor Product and Decomposition)

When combining two qubits, their individual Hilbert spaces ${\mathbb{C}}^2$ combine via a tensor product. The total Hilbert space is ${\mathcal{H}}_2={\mathbb{C}}^2\otimes {\mathbb{C}}^2={\mathbb{C}}^4$. Operations on this combined space are elements of $SU\left(4\right)$. A general operator on this composite space, if it acts independently on each qubit (a local operation), would be of the form $U_1\otimes U_2$, where $U_1,U_2\in SU\left(2\right)$.

The theory of representations, specifically the Clebsch-Gordan Theorem, dictates how this tensor product representation of $SU\left(2\right)\times SU\left(2\right)$ can be decomposed into a direct sum of irreducible representations of the total spin $SU\left(2\right)$ group that acts on the combined system.

Theorem 3.2. 

Clebsch-Gordan Theorem for SU(2) - Simplified The tensor product of two irreducible representations of $SU\left(2\right)$ with total angular momentum quantum numbers $j_1$ and $j_2$ decomposes into a direct sum of irreducible representations with total angular momentum J, where J ranges from $|j_1-j_2|$ to $j_1+j_2$ in integer steps.

$${\rho }_{j_1}\otimes {\rho }_{j_2}=\underset{J=|j_1-j_2|}{\overset{j_1+j_2}{⨁}}{\rho }_J$$

The dimension of the irreducible representation ${\rho }_j$ is $2j+1$.

Proof Sketch (Conceptual via Spin Addition). The proof relies on constructing basis states for the coupled system (e.g., $\left|J,M_J\right.〉$ states) from the uncoupled states (e.g., $\left|j_1,m_1\right.〉\left|j_2,m_2\right.〉$) using angular momentum ladder operators $J_{\pm }=J_{1\pm }+J_{2\pm }$. One starts with the state of maximum $M_J=m_1+m_2$, which must belong to the maximum $J=j_1+j_2$ multiplet. Successive applications of $J_{-}$ generate all $2J+1$ states in that multiplet. For each new $J_z$ value created, the remaining linearly independent states form the highest $M_J$ state of a smaller J multiplet, and the process repeats until all basis states are accounted for [23]. This process systematically yields the decomposition into disjoint, invariant subspaces.    □

For two qubits, each is a spin-$1/2$ system ($j_1=1/2,j_2=1/2$). Applying the Clebsch-Gordan rule:

$$1/2\otimes 1/2=0⨁1$$

This means the 4-dimensional Hilbert space of two qubits (${\mathbb{C}}^4$) decomposes into a 1-dimensional irreducible representation (corresponding to $J=0$, a singlet) and a 3-dimensional irreducible representation (corresponding to $J=1$, a triplet). The 1D singlet subspace is the orthogonal complement of the 3D triplet subspace within ${\mathbb{C}}^4$.

The basis states for these irreducible subspaces, expressed in the computational basis ($\left|00\right.〉,\left|01\right.〉,\left|10\right.〉,\left|11\right.〉$), are:

• Singlet ($J=0$, dimension 1):

  $$\left|S\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉-\left|10\right.〉)$$
• Triplet ($J=1$, dimension 3):

  $$\left|T_1\right.〉=\left|00\right.〉$$

  $$\left|T_0\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉+\left|10\right.〉)$$

  $$\left|T_{-1}\right.〉=\left|11\right.〉$$

Here, $T_m$ denotes a triplet state with total spin $J=1$ and $M_J=m$.

This decomposition highlights that a 4-dimensional space can be fundamentally understood not just by its basis states, but by how it transforms under $SU\left(2\right)$ operations. Any operation (gate) that respects the total spin symmetry will be block-diagonal when expressed in this singlet-triplet basis, meaning it will only map states within the singlet subspace to other states within the singlet subspace, and similarly for the triplet. This profound simplification is a direct result of representation theory.

3.4. Examples of Important Lie Groups and Representations for Quantum Computing

Beyond $SU\left(D\right)$ for D-dimensional quantum systems, other Lie groups and their representations are vital:

• $SU\left(2\right)$: As discussed, this is the fundamental group for single-qubit operations. Its irreducible representations (spin-j multiplets, with dimension $2j+1$) directly correspond to the states of single qubits ($j=1/2$, duplet) and the symmetry properties of multi-qubit systems (singlets, triplets, etc., from spin addition) [5].
• $SU\left(2^N\right)$: This is the overarching group for all N-qubit unitary operations. The universal gate set theorems (e.g., Solovay-Kitaev, Section 5.1) essentially state that a finite set of specific gates generates a dense subset of this group, making it accessible for universal quantum computation [24].
• Symplectic Group ($Sp(2n,\mathbb{R})$): This group is crucial for Continuous Variable Quantum Computing (CVQC). It describes linear canonical transformations in phase space, which correspond to Gaussian operations (like squeezing, displacement, and beam splitters) in CVQC. These operations preserve the Gaussian nature of states, making $Sp(2n,\mathbb{R})$ the natural group for understanding a significant class of CVQC algorithms [22].
• Heisenberg Group: Closely related to the Symplectic group, the Heisenberg group encapsulates the canonical commutation relations between position and momentum operators. Its representations are fundamental for describing the quantum states of bosonic modes and for understanding the quantum mechanics of continuous variables.
• Other Lie Groups: Depending on the physical system or the type of symmetry, other Lie groups may become relevant. For example, $SU\left(d\right)$ for qudits, or specific point groups and space groups for analyzing molecular or condensed matter systems that exhibit discrete spatial symmetries within a larger Lie group framework [4,21].

In essence, the theory of Lie groups and their representations provides the deep mathematical language to describe, classify, and homogenize the vast landscape of quantum gates and the states they act upon. It moves beyond specific gate names to reveal the underlying continuous structures and symmetries that govern quantum mechanics, providing indispensable tools for analysis, synthesis, and hardware development in quantum computing.

4. Homogenizing Single-Qubit Gates with SU(2)

A single qubit, the fundamental unit in quantum information, is mathematically represented by a state vector in the 2-dimensional complex Hilbert space ${\mathbb{C}}^2$. Operations on a single qubit are precisely described by elements of the Special Unitary Group $SU\left(2\right)$, which acts on this ${\mathbb{C}}^2$ space. This fundamental correspondence forms the cornerstone of single-qubit gate homogenization.

4.1. The Single Qubit as the Fundamental Representation of SU(2)

The Hilbert space ${\mathbb{C}}^2$ for a single qubit is the fundamental representation (also known as the defining representation) of $SU\left(2\right)$. This is an irreducible representation corresponding to spin $j=1/2$. Any transformation on a single qubit, whether a simple bit flip or a complex rotation, is a unitary operator $U\in SU\left(2\right)$. This establishes a direct and universal mapping: every single-qubit gate, regardless of its traditional name or specific implementation, is an element of $SU\left(2\right)$ [5]. This inherently homogenizes the gate set by placing them all within the same mathematical structure.

The Lie algebra $\mathfrak{su}\left(2\right)$ is the set of all $2\times 2$ anti-Hermitian, traceless matrices. A standard basis for $\mathfrak{su}\left(2\right)$ is $\{i{\sigma }_x,i{\sigma }_y,i{\sigma }_z\}$, where ${\sigma }_x,{\sigma }_y,{\sigma }_z$ are the Pauli matrices:

$${\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),{\sigma }_z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

These satisfy the commutation relations $[{\sigma }_j,{\sigma }_k]=2i{ϵ}_{jkl}{\sigma }_l$[23]. Any element $A\in \mathfrak{su}\left(2\right)$ can be written as $A=i(a_x{\sigma }_x+a_y{\sigma }_y+a_z{\sigma }_z)$ for real $a_x,a_y,a_z$. Any single-qubit gate $U\in SU\left(2\right)$ can be generated by exponentiating a linear combination of these generators. Specifically, a rotation around an axis $\overrightarrow{n}=(n_x,n_y,n_z)$ (a unit vector) by an angle $\theta$ is given by:

$$U=e^{-i{\displaystyle \frac{\theta }{2}}\overrightarrow{n}·\overrightarrow{\sigma }}=cos\left({\displaystyle \frac{\theta }{2}}\right)\mathrm{I}-isin\left({\displaystyle \frac{\theta }{2}}\right)(\overrightarrow{n}·\overrightarrow{\sigma })$$

where $\overrightarrow{n}·\overrightarrow{\sigma }=n_x{\sigma }_x+n_y{\sigma }_y+n_z{\sigma }_z$. This form reveals that all single-qubit rotations are continuously connected and parameterized by $(\theta ,\overrightarrow{n})$. This is a powerful homogenization, as it replaces a myriad of discrete gate definitions with a continuous family parameterized by a few real numbers. For instance, considering Qiskit’s common gate definitions:

• Pauli-X (X): This is a $\pi$-rotation about the x-axis. Here, $\theta =\pi ,\overrightarrow{n}=(1,0,0)$. $X=e^{-i{\displaystyle \frac{\pi }{2}}{\sigma }_x}=cos(\pi /2)\mathrm{I}-isin(\pi /2){\sigma }_x=-i{\sigma }_x=\left(\begin{array}{cc}0& -i\\ -i& 0\end{array}\right)$. Qiskit’s X gate is $\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$. This difference is a global phase of i, which is physically irrelevant.
• Pauli-Z (Z): This is a $\pi$-rotation about the z-axis. Here, $\theta =\pi ,\overrightarrow{n}=(0,0,1)$. $Z=e^{-i{\displaystyle \frac{\pi }{2}}{\sigma }_z}=cos(\pi /2)\mathrm{I}-isin(\pi /2){\sigma }_z=-i{\sigma }_z=\left(\begin{array}{cc}-i& 0\\ 0& i\end{array}\right)$. Qiskit’s Z gate is $\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$. Again, a global phase of i.
• Hadamard (H): The Hadamard gate transforms the basis states as $H\left|0\right.〉=(\left|0\right.〉+\left|1\right.〉)/\sqrt{2}$ and $H\left|1\right.〉=(\left|0\right.〉-\left|1\right.〉)/\sqrt{2}$. Its matrix is ${\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$. This can be expressed as a rotation by $\pi$ around the axis $(1/\sqrt{2},0,1/\sqrt{2})$ (i.e., the axis bisecting X and Z on the Bloch sphere), or as a sequence of rotations: $H=R_Y(\pi /2)R_X\left(\pi \right)$ (up to global phase) [24].

This concept emphasizes that any single-qubit unitary can be constructed by exponentiating a suitable element of the Lie algebra $\mathfrak{su}\left(2\right)$, representing the continuous control over the qubit’s evolution.

4.2. Geometric Homogenization via the Bloch Sphere and SO(3)

The connection between $SU\left(2\right)$ and the rotation group $SO\left(3\right)$ provides an intuitive geometric homogenization for single-qubit operations. The Bloch sphere is a geometrical representation of the pure state space of a single qubit, where any pure state $\left|\psi \right.〉=cos(\theta /2)\left|0\right.〉+e^{i\varphi }sin(\theta /2)\left|1\right.〉$ maps to a unique point on the surface of a unit sphere in ${\mathbb{R}}^3$ with spherical coordinates $(\theta ,\varphi )$. Crucially, $SU\left(2\right)$ is the universal covering group of $SO\left(3\right)$[5]. This means that every rotation in $SO\left(3\right)$ (a rotation of the Bloch sphere) corresponds to precisely two elements in $SU\left(2\right)$ (differing by a global sign, U and $-U$), and every element in $SU\left(2\right)$ corresponds to a unique rotation in $SO\left(3\right)$. This non-trivial 2-to-1 homomorphism $SU\left(2\right)\to SO\left(3\right)$ is formalized by:

Theorem 4.1. 

Isomorphism between $SU\left(2\right)/{\mathbb{Z}}_2$ and $SO\left(3\right)$ The quotient group $SU\left(2\right)/{\mathbb{Z}}_2$ is isomorphic to $SO\left(3\right)$, where ${\mathbb{Z}}_2=\{\mathrm{I},-\mathrm{I}\}$ is the center of $SU\left(2\right)$. This isomorphism provides a direct correspondence between $SU\left(2\right)$ matrices and rotations in 3D space.

Proof Sketch (via Adjoint Representation).

• Vector Space of Hermitian Traceless Matrices: Consider the real vector space $\mathcal{V}=\{M\in M_2\left(\mathbb{C}\right)\mid M=M^{†},\mathrm{Tr}\left(M\right)=0\}$. This space is isomorphic to ${\mathbb{R}}^3$, with a basis given by the Pauli matrices: ${\sigma }_x,{\sigma }_y,{\sigma }_z$. Any vector $\overrightarrow{r}\in {\mathbb{R}}^3$ (representing a point on the Bloch sphere) can be mapped to $M_{\overrightarrow{r}}=r_x{\sigma }_x+r_y{\sigma }_y+r_z{\sigma }_z$.
• Adjoint Action: For any $U\in SU\left(2\right)$, define an action on $\mathcal{V}$ by conjugation: $M_{\overrightarrow{r}}\mapsto U{M}_{\overrightarrow{r}}{U}^{†}$. It can be shown that $U{M}_{\overrightarrow{r}}{U}^{†}$ is also a Hermitian, traceless matrix, so it can be written as $M_{{\overrightarrow{r}}^{\prime }}$ for some new vector ${\overrightarrow{r}}^{\prime }\in {\mathbb{R}}^3$.
• Orthogonal Transformation: The mapping $R_U:\overrightarrow{r}\mapsto {\overrightarrow{r}}^{\prime }$ is a linear transformation that preserves the Euclidean norm $\left|\right|\overrightarrow{r}{\left|\right|}^2={\displaystyle \frac{1}{2}}\mathrm{Tr}\left(M_{\overrightarrow{r}}^2\right)$, and thus $R_U\in O\left(3\right)$. One can further show that $det\left(R_U\right)=1$, so $R_U\in SO\left(3\right)$.
• Homomorphism and Kernel: The map $U\mapsto R_U$ is a group homomorphism from $SU\left(2\right)$ to $SO\left(3\right)$. The kernel of this homomorphism, i.e., the elements U for which $R_U$ is the identity rotation, are precisely I and $-\mathrm{I}$. This establishes the 2-to-1 covering map and the isomorphism $SU\left(2\right)/{\mathbb{Z}}_2\cong SO\left(3\right)$ [4].

   □

This theorem implies that every quantum operation on a single qubit, viewed as an element of $SU\left(2\right)$, can be precisely visualized as a rotation of the Bloch sphere. This geometric interpretation provides a unified language for all single-qubit gates, transforming their effects into understandable spatial rotations. For instance, a Hadamard gate maps $\left|0\right.〉$ to $\left|+\right.〉$ and $\left|1\right.〉$ to $\left|-\right.〉$; on the Bloch sphere, this corresponds to a rotation of $\pi$ around the Y-axis followed by a rotation of $\pi$ around the X-axis (or equivalent combinations), effectively mapping the Z-axis to the X-axis and vice-versa. The $SU\left(2\right)$ group inherently captures all possible ways to transform a single qubit, providing a unified and geometric understanding of its gate set [24]. This homogenization is not merely conceptual; it guides the design of physical control pulses, which typically implement such rotations directly by tuning electromagnetic fields [9].

4.3. Euler Angle Decomposition for Practical Homogenization

The most direct practical application of $SU\left(2\right)$ in homogenizing single-qubit gates is the Euler Angle Decomposition. This theorem asserts that any $SU\left(2\right)$ gate can be expressed as a product of three elementary rotations about fixed axes, typically rotations about the z-axis, y-axis, and z-axis again. This transforms a diverse collection of discrete gate definitions into a single, parameterizable form.

Theorem 4.2. 

Euler Angle Decomposition for SU(2) Any unitary matrix $U\in SU\left(2\right)$ can be expressed (up to a global phase) in terms of three Euler angles $(\theta ,\varphi ,\lambda )$ as:

$$U(\theta ,\varphi ,\lambda )=R_Z\left(\varphi \right)R_Y\left(\theta \right)R_Z\left(\lambda \right)$$

where the rotation matrices are defined as:

$$R_Y\left(\theta \right)=e^{-i{\displaystyle \frac{\theta }{2}}{\sigma }_y}=\left(\begin{array}{cc}cos(\theta /2)& -sin(\theta /2)\\ sin(\theta /2)& cos(\theta /2)\end{array}\right)$$

$$R_Z\left(\lambda \right)=e^{-i{\displaystyle \frac{\lambda }{2}}{\sigma }_z}=\left(\begin{array}{cc}{e}^{-i\lambda /2}& 0\\ 0& e^{i\lambda /2}\end{array}\right)$$

Multiplying these out, we obtain the standardUgate form used in Qiskit (often calledU3in older versions):

$$U(\theta ,\varphi ,\lambda )=\left(\begin{array}{cc}{e}^{-i(\varphi +\lambda )/2}cos(\theta /2)& -e^{i(\varphi -\lambda )/2}sin(\theta /2)\\ e^{i(-\varphi +\lambda )/2}sin(\theta /2)& e^{i(\varphi +\lambda )/2}cos(\theta /2)\end{array}\right)$$

Proof Sketch. As briefly outlined in Section 3.1, the proof involves taking a general $SU\left(2\right)$ matrix, $M=\left(\begin{array}{cc}a& b\\ -b^{*}& a^{*}\end{array}\right)$ with ${\left|a\right|}^2+{\left|b\right|}^2=1$. By judiciously choosing the angles $\theta ,\varphi ,\lambda$ and comparing the elements of M with the product matrix $R_Z\left(\varphi \right)R_Y\left(\theta \right)R_Z\left(\lambda \right)$, one can uniquely solve for these three real parameters (up to $2\pi$ periodicity). For instance, $\theta$ can be determined from $\left|a\right|$ or $\left|b\right|$, while $\varphi$ and $\lambda$ capture the phases of a and b [5]. This mathematical guarantee ensures that any single-qubit unitary operation, no matter how complex its matrix appears, can be fully specified by just three real numbers. This forms the basis for universal single-qubit gates.    □

Initial Situation (Common View)

Quantum programs typically employ distinct gate names like Hadamard (H), Pauli-X (X), Pauli-Y (Y), Pauli-Z (Z), Phase (S), T, and parameterized rotations like RY(theta). Each appears as a unique, pre-defined operation with its own specific matrix representation.

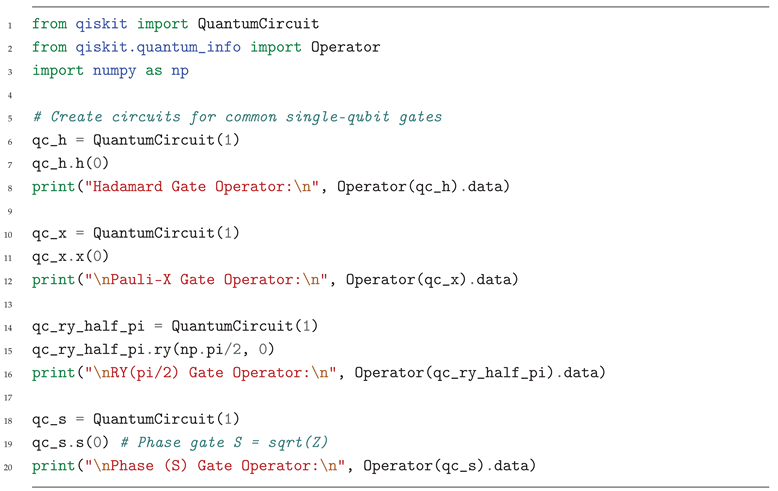
Transformed Situation (SU(2) Homogenization - Euler Angle Decomposition)

The SU(2) framework elegantly unifies all single-qubit operations under the U(theta, phi, lambda) gate, which is the canonical form for single-qubit unitaries.

This transformation clarifies that distinct named gates are merely specific points within the continuous manifold of $SU\left(2\right)$ operations. All single-qubit operations can be generated by a sequence of three elementary rotations, significantly homogenizing their understanding and implementation. The U gate in Qiskit (and equivalent gates in other frameworks) serves as the canonical example of this homogenization, providing a single, universal gate type from which all other single-qubit operations can be constructed, whether by design or through transpiler decomposition [25]. This mathematical unity directly simplifies the design of quantum control systems and the calibration of single-qubit gates, as the objective becomes implementing arbitrary rotations within the $SU\left(2\right)$ manifold with high fidelity. The ability to programmatically decompose any single-qubit unitary into these canonical Euler angles, as demonstrated with OneQubitEulerDecomposer, provides a powerful tool for analyzing, comparing, and compiling single-qubit operations in a universally homogeneous fashion [26]. The precision of these decompositions, crucial for realizing complex algorithms, is a key area of ongoing research in quantum control [10].

5. Homogenizing Multi-Qubit Gates with SU($2^N$)

For N qubits, the Hilbert space is ${\mathcal{H}}^{\otimes N}={\left({\mathbb{C}}^2\right)}^{\otimes N}$, with dimension $D=2^N$. Operations on this high-dimensional space are elements of the Special Unitary Group $SU\left(D\right)$, or $SU\left(2^N\right)$. The homogenization of multi-qubit gates is achieved through two powerful avenues: the concept of universal gate sets, which reduces all complex operations to sequences of a few fundamental ones, and the decomposition of the composite Hilbert space into irreducible representations (multiplets), which reveals inherent symmetries and simplifies analysis.

5.1. Universal Gate Sets: Homogenization by Approximation and Decomposition

The sheer number of possible unitary operations on N qubits ($2^N\times 2^N$ complex unitary matrices) means that enumerating or specifically naming all possible gates is impractical. The concept of a universal gate set elegantly solves this by demonstrating that a small, finite set of gate types is sufficient to approximate any unitary operation in $SU\left(2^N\right)$ to arbitrary precision. This transforms the problem from managing an infinite, diverse array of gates to understanding the composition of a finite, homogeneous set of building blocks.

A commonly accepted universal gate set for qubits includes all single-qubit rotations (which themselves are homogeneous via $SU\left(2\right)$’s Euler Angle Decomposition) and a single entangling two-qubit gate, such as the CNOT (Controlled-NOT) gate. The theoretical basis for this universality is rigorously established, particularly by results like the Solovay-Kitaev Theorem.

Theorem 5.1. 

Solovay-Kitaev Theorem - Formal Statement Sketch Let $\mathcal{G}$ be a finite set of gates that generates a dense subgroup of $SU\left(D\right)$ (i.e., it is universal). Then for any desired unitary $U\in SU\left(D\right)$ and any $ϵ>0$, there exists a sequence of gates $G_1{G}_2\dots G_L$ from $\mathcal{G}$ such that $\left|\right|G_1\dots G_L-U\left|\right|\le ϵ$. Furthermore, the length of this sequence L scales polylogarithmically with the inverse of the error: $L=O\left({log}^c(1/ϵ)\right)$ for some small constant $c\approx 2$ [27,28].

Proof Sketch. 

• Density (Lie Algebra Generation): The initial step involves showing that the given universal gate set $\mathcal{G}$ is "dense" in $SU\left(D\right)$. This is often achieved by demonstrating that the Lie algebra generated by the infinitesimal forms of the gates in $\mathcal{G}$ (i.e., their generators) spans the entire Lie algebra $\mathfrak{su}\left(D\right)$. If the generators of a set of gates span the entire Lie algebra, then any element of the Lie group can be approximated by exponentiating elements from this algebra, which translates to composing the gates [24]. For example, the Lie algebra for N qubits $\mathfrak{su}\left(2^N\right)$ is spanned by all tensor products of Pauli matrices and the identity operator. A universal gate set, such as $\{R_x\left(\theta \right),R_y\left(\theta \right),\mathrm{CNOT}\}$, allows one to effectively generate any element in this Lie algebra through commutators and Lie products (e.g., $[X\otimes \mathrm{I},\mathrm{I}\otimes X]$ or $[R_x(\pi /2),R_y(\pi /2)]\propto Z$), which then can be exponentiated to form any desired unitary [24]. This establishes the algebraic reachability within the Lie group.
• Recursive Approximation (Group Elements): The core of the Solovay-Kitaev algorithm involves a recursive procedure. If we have an approximation $U_k$ to a target unitary U with error ${ϵ}_k$, we aim to find a better approximation $U_{k+1}$ with error ${ϵ}_{k+1}\ll {ϵ}_k$. This is achieved by finding elements $A,B\in \mathcal{G}$ such that their commutator $[A,B]=AB{A}^{-1}{B}^{-1}$ is close to the identity. By carefully selecting $A,B$ and their inverses, one can construct an element ${\left(AB{A}^{-1}{B}^{-1}\right)}^{-1}U$ that is closer to the identity. The theorem then relies on a "balanced product" technique where one approximates $G^{-1}U$ by a product of commutators of elements from $\mathcal{G}$, ensuring that the approximation error decreases quadratically at each recursive step, leading to the efficient polylogarithmic scaling [24].
• Complexity Scaling: The logarithmic scaling of the gate sequence length (L) with inverse error ($ϵ$) is a remarkable feature, guaranteeing efficient approximation. This is a vast improvement over naive approximation strategies which might scale polynomially or exponentially [27,28]. The Solovay-Kitaev algorithm provides not just the existence but a constructive method for this homogenization, making it a cornerstone for efficient compilation strategies.

   □

This theorem provides a powerful conceptual and practical homogenization. It implies that from a compilation perspective, any complex multi-qubit operation (e.g., a multi-controlled gate like Toffoli, or even an entire quantum algorithm’s unitary component) can be systematically decomposed into a sequence of operations drawn from a basic, homogeneous set of single-qubit rotations (Euler angles) and a single two-qubit entangling gate. Modern quantum compilers (transpilers) rely heavily on these decomposition rules to map high-level circuits onto the native gate sets of quantum hardware, which are often universal sets [3]. This process is central to automated quantum program synthesis [7].

Initial Situation (Common View)

Quantum programs often use a wide variety of multi-qubit gates, sometimes custom-defined or high-level abstract operations. SWAP and Toffoli are typical examples of gates often treated as fundamental primitives in circuit diagrams, even though their underlying physical implementation might be complex.

Transformed Situation (SU($2^N$) Homogenization - Universal Gate Decomposition)

The universal gate set framework allows us to homogenize these gates by decomposing them into a common basis. For instance, a SWAP gate can be precisely represented as three CNOT gates (a canonical decomposition), and a Toffoli gate can be decomposed into a sequence of CNOT and single-qubit U gates. This demonstrates that complex, multi-qubit operations are not new fundamental entities, but rather compositions of elementary, homogeneous operations.

This highlights a crucial homogenization: any complex multi-qubit operation, whether a well-known gate like SWAP or a randomly generated unitary element of $SU\left(2^N\right)$, can be effectively expressed as a sequence of simpler, universal gates (U and CNOT). This principle underpins quantum circuit compilation, translating high-level algorithmic concepts into hardware-executable gate sequences, thus providing a homogeneous language for describing quantum programs from abstract logic down to physical execution [2,3]. This systematic decomposition process is essential for achieving portability and optimizing circuits for diverse quantum hardware platforms, as discussed in Section 2.3. The KAK (Khane-Albert-Kitaev) decomposition, a powerful generalization of Euler decomposition for two-qubit gates, provides a canonical way to express any $SU\left(4\right)$ gate as a product of local unitaries and a single parameterized entangling gate, further unifying the understanding of two-qubit operations [17]. This algebraic approach offers exact decomposition methods, complementing the approximation strategies of Solovay-Kitaev for specific gate sizes.

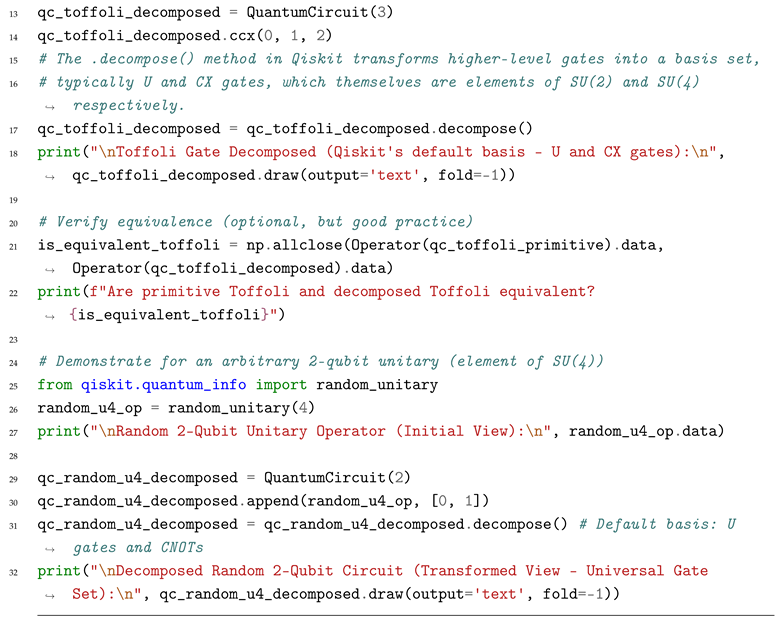
5.2. Multiplets and Symmetry Homogenization (Irreducible Representations)

Beyond decomposition into universal gates, another powerful aspect of Lie group theory for multi-qubit homogenization is the decomposition of the composite Hilbert space itself into irreducible representations (irreps). As discussed in Section 3.3, when combining multiple qubits (each a spin-1/2 system, described by the fundamental representation of $SU\left(2\right)$), the composite Hilbert space ${\mathcal{H}}^{\otimes N}={\left({\mathbb{C}}^2\right)}^{\otimes N}$ can be broken down into a direct sum of irreducible representations of the total spin $SU\left(2\right)$ group that acts on the combined system. These irreps are known as "multiplets" (singlets, triplets, quadruplets, etc.), akin to those found in particle physics. This transformation homogenizes the understanding of quantum states by classifying them according to their fundamental symmetry properties.

For two qubits, the 4-dimensional Hilbert space (${\mathbb{C}}^2\otimes {\mathbb{C}}^2={\mathbb{C}}^4$) decomposes according to the Clebsch-Gordan rule (Theorem 3.3):

$$1/2\otimes 1/2=0⨁1$$

This means ${\mathbb{C}}^4$ can be viewed as the direct sum of a 1-dimensional irreducible representation (corresponding to total spin $J=0$, the singlet subspace, ${\mathcal{H}}_S$) and a 3-dimensional irreducible representation (corresponding to total spin $J=1$, the triplet subspace, ${\mathcal{H}}_T$). These subspaces are orthogonal complements of each other: ${\mathcal{H}}_2={\mathcal{H}}_S⨁{\mathcal{H}}_T$. The specific basis states for these subspaces (as derived in Section 3.3) are:

• Singlet ($J=0$, dimension 1):

  $$\left|S\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉-\left|10\right.〉)$$
• Triplet ($J=1$, dimension 3):

  $$\left|T_1\right.〉=\left|00\right.〉$$

  $$\left|T_0\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉+\left|10\right.〉)$$

  $$\left|T_{-1}\right.〉=\left|11\right.〉$$

Here, $T_m$ denotes a triplet state with total spin $J=1$ and $M_J=m$.

This decomposition is a powerful form of homogenization because it classifies quantum states by their intrinsic symmetry properties under $SU\left(2\right)$ rotations. Crucially, if a quantum gate (or Hamiltonian) commutes with the total spin operators (i.e., it respects the total spin symmetry), then it will not mix states between different irreducible subspaces. When such a symmetry-preserving gate is expressed in a basis adapted to these multiplets, its matrix representation will be block-diagonal. Each block corresponds to an invariant subspace (an irrep), meaning the gate operates independently within each multiplet. This block-diagonalization significantly simplifies the analysis of the gate’s effect by decoupling its action into independent sub-problems. This principle is widely used in quantum chemistry and condensed matter physics simulations to reduce the computational cost by exploiting molecular or crystalline symmetries, effectively reducing the problem space by leveraging a homogeneous symmetry-adapted basis [21].

Initial Situation (Common View)

Quantum gates acting on multiple qubits are typically viewed as dense matrices in the computational basis ($\left|00\right.〉,\left|01\right.〉,\left|10\right.〉,\left|11\right.〉$), making their inherent symmetries, or lack thereof, non-obvious.

Transformed Situation (Multiplet Homogenization - Block-Diagonalization)

We apply a basis transformation to express the gate matrices in the singlet-triplet basis. The transformation matrix P converts from the computational basis to the singlet-triplet basis (ordered as $\left|T_1\right.〉,\left|T_0\right.〉,\left|T_{-1}\right.〉,\left|S\right.〉$). The columns of P are the new basis vectors expressed in the old basis.

$$P=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1/\sqrt{2}& 0& 1/\sqrt{2}\\ 0& 1/\sqrt{2}& 0& -1/\sqrt{2}\\ 0& 0& 1& 0\end{array}\right)$$

(Note: The order of basis vectors for triplet/singlet can vary, but this specific ordering is common. The computational basis states are typically ordered as $\left|00\right.〉,\left|01\right.〉,\left|10\right.〉,\left|11\right.〉$.) The transformation of an operator M to the new basis is given by $M^{\prime }=P^{†}MP$.

The output for the SWAP gate, when represented in the singlet-triplet basis, clearly demonstrates a block-diagonal structure. Specifically, the SWAP operation on the singlet state $\left|S\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉-\left|10\right.〉)$ results in $-\left|S\right.〉$ (a phase, indicating invariance), meaning the singlet subspace is invariant under SWAP (it just acquires a phase). The triplet states $\left|T_1\right.〉,\left|T_0\right.〉,\left|T_{-1}\right.〉$ are either mapped to themselves or permuted/phase-shifted amongst each other strictly within the triplet subspace. This leads to a matrix where a $3\times 3$ block operates on the triplet subspace and a $1\times 1$ block operates on the singlet subspace. This block-diagonal form is a direct manifestation of the group-theoretical homogenization, revealing that SWAP commutes with the total spin operator ${\widehat{J}}^2$, thus preserving the total spin of the system and significantly simplifying its analysis by decoupling its effects on different symmetry sectors.

In contrast, the CNOT gate, a canonical entangling gate, does not preserve the total spin symmetry in the same way. As shown in the output, its matrix in the singlet-triplet basis is not block-diagonal. Instead, it features non-zero elements connecting the singlet and triplet subspaces. This indicates that CNOT actively mixes states between the singlet and triplet subspaces (e.g., transforming a product state, which is a superposition of singlet and triplet components, into a pure Bell state that is an irrep basis state, such as $\left|{\Phi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|00\right.〉+\left|11\right.〉)$ from $\left|00\right.〉$). This non-block-diagonal nature for CNOT directly reflects its role in creating entanglement, which is fundamentally about superposition across different irreducible representations when viewed from this perspective. This analysis provides a homogeneous, symmetry-based understanding of entangling gates.

5.3. Reinterpreting Superposition and Entanglement through Irreducible Representations

The theory of irreducible representations provides a profound lens through which to re-examine the fundamental quantum phenomena of superposition and entanglement. Rather than being abstract concepts, they become concrete properties tied to the structure of the underlying Hilbert space and its decomposition [24]. This reinterpretation offers a deeper, homogenized understanding of these uniquely quantum behaviors.

• Superposition Reinterpreted: For a single qubit, any arbitrary superposition state $\left|\psi \right.〉=\alpha \left|0\right.〉+\beta \left|1\right.〉$ (where ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$) is simply an element within the fundamental (spin-1/2, or duplet) irreducible representation of $SU\left(2\right)$. Geometrically, every pure superposition state maps to a unique point on the Bloch sphere, which is a visual representation of this 2-dimensional irreducible space. The linearity of quantum mechanics naturally means that any superposition of basis states is itself a valid vector within this irreducible representation space. There’s no "mixing" across different irreps in this single-qubit context because the space itself is the fundamental irrep. This provides a homogeneous understanding of all pure single-qubit states, treating them as points in a single, well-defined mathematical space [5].
• Entanglement Reinterpreted: The true power of this reinterpretation becomes profoundly evident with entanglement, particularly when considering multi-qubit systems. As shown in Section 5.2, the 4-dimensional Hilbert space of two qubits, ${\left({\mathbb{C}}^2\right)}^{\otimes 2}$, decomposes into a 1-dimensional singlet (spin-0) and a 3-dimensional triplet (spin-1) irreducible representation of the total spin $SU\left(2\right)$. Crucially, the maximally entangled Bell states directly form a basis for these irreducible subspaces (or are elements within them):

  -

  Singlet (Spin-0, total angular momentum $J=0,M_J=0$):$\left|{\Psi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉-\left|10\right.〉)$

  -

  Triplet (Spin-1, total angular momentum $J=1$):

  • $\left|T_1\right.〉=\left|00\right.〉$ ($J=1,M_J=1$)
  • $\left|T_0\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|01\right.〉+\left|10\right.〉)$ ($J=1,M_J=0$)
  • $\left|T_{-1}\right.〉=\left|11\right.〉$ ($J=1,M_J=-1$)

  While often presented as "the four Bell states," these are directly the singlet and specific triplet states (note: two of the canonical Bell states are actually the $\left|T_0\right.〉$ and $\left|S\right.〉$ states, and the other two, $\left|{\Phi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|00\right.〉+\left|11\right.〉)$ and $\left|{\Phi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|00\right.〉-\left|11\right.〉)$, are linear combinations of $\left|T_1\right.〉$ and $\left|T_{-1}\right.〉$ states, or are related via local operations).
  From this perspective, entanglement is not merely "spooky action at a distance" but rather the manifestation of quantum states belonging to specific irreducible subspaces that cannot be factored into product states. A product state like $\left|00\right.〉$ is an element of the triplet subspace, but a superposition like $\alpha \left|00\right.〉+\beta \left|11\right.〉$ (if not normalized properly) might span multiple irreps. However, a maximally entangled state like $\left|{\mathrm{\Psi }}^{-}\right.〉$ is a pure element of the singlet irrep, meaning no local operation can transform it into a product state. This deep structural property directly leads to entanglement. Product states, conversely, are elements of the composite Hilbert space that can be written as tensor products of individual qubit states; they are typically not pure elements of a single high-dimensional irrep of the total spin group, but rather live in superpositions across multiple irreps or are specific components within them.
  Entangling gates, like the CNOT, gain a deeper meaning when viewed through this lens. They are operations that take product states (or states easily expressed as products) and transform them into states that reside purely within these irreducible entangled subspaces. For instance, CNOT applied to $\left|00\right.〉$ yields $\left|00\right.〉$ (a triplet state). Applying CNOT to a superposition like $H\otimes \mathrm{I}\left|00\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|00\right.〉+\left|10\right.〉)$ then produces the entangled Bell state $\left|{\Phi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}(\left|00\right.〉+\left|11\right.〉)$, which is an element of the triplet subspace. The CNOT matrix’s non-block-diagonal form in the singlet-triplet basis (as seen in the practical example above) directly reflects its ability to mix different components of the Hilbert space that transform differently under total spin symmetry. This mixing capability is precisely what allows CNOT to generate entanglement, creating states that are pure elements of irreducible, inseparable representations of the combined system. This reinterpretation deeply homogenizes our understanding of entanglement, grounding it in the fundamental symmetries of the underlying Lie group and its representation theory.

6. Methodology for Homogenizing Quantum Programs

To systematically transform quantum programs into a homogeneous gate set, we propose the following methodologies, distinguishing between discrete variable systems (qubits/qudits) and more general Lie group-based systems. These methodologies encapsulate the practical application of Lie group theory and its representations to tackle the gate homogenization problem, providing a structured approach for quantum software engineering.

6.1. Discrete Variable (Qubit/Qudit) Systems

This methodology focuses on the homogenization of quantum programs designed for digital quantum computers operating on discrete variable systems (qubits or qudits). The primary goal is to represent any quantum program, which defines a composite unitary operation, using a homogeneous basis of a universal gate set, thereby simplifying its description, enabling hardware compilation, and facilitating performance analysis.

The homogenization process for discrete variable systems begins with the Program-to-Unitary Mapping. This crucial initial step involves mathematically capturing the combined effect of the entire quantum program or a specific complex sub-operation (such as a multi-qubit oracle, a Quantum Fourier Transform block, or a unitary evolution representing a quantum chemistry problem) as a single, abstract unitary matrix $U_{program}$. For an N-qubit system, this unitary matrix will be an element of $SU\left(2^N\right)$, or $SU\left(d^N\right)$ for N qudits of dimension d. This mapping is achieved by taking the ordered product of the matrix representations of all individual gates within the circuit sequence: $U_{program}=U_L{U}_{L-1}\dots U_2{U}_1$, where $U_i$ is the matrix representation of the i-th gate. It is important to note that for circuits including measurements and classical feedback, this mapping typically applies only to the unitary sections of the circuit, as measurements introduce non-unitary state collapses. Computationally, frameworks like Qiskit provide tools such as the Operator class to compute the unitary matrix for a given QuantumCircuit (e.g., Operator(my_circuit).data). However, for larger circuits (e.g., $N\ge 10-15$ qubits), directly computing and storing this $2^N\times 2^N$ matrix becomes intractable due to its exponential scaling, necessitating more sophisticated symbolic, tensor network-based, or approximate methods for abstraction. This initial step is fundamental for homogenization, as it transforms a chronological sequence of heterogeneously named gates and operations into a single, compact mathematical object residing within a specific Lie group, forming the precise "target" for all subsequent homogenization efforts.

Following the unified unitary mapping, the next critical phase is Universal Gate Set Selection. This phase involves choosing a finite, universal gate set $\mathcal{G}$, which will serve as the "homogeneous basis" or the fundamental "alphabet" from which all other operations in the quantum program will be constructed. The chosen set must be implementable on the target quantum hardware; for instance, for superconducting qubits, a common universal choice is the set containing all single-qubit rotations (which are themselves homogeneous via $SU\left(2\right)$’s Euler Angle Decomposition) and a single entangling two-qubit gate, such as the CNOT gate. The mathematical guarantee for the existence of such universal sets is provided by fundamental theorems, such as the Solovay-Kitaev Theorem (Theorem 5.1), which states that these sets generate a dense subgroup of the relevant Lie group ($SU\left(2^N\right)$ for qubits), implying that any unitary operation can be approximated to arbitrary precision. From a practical computational perspective, quantum computing platforms like Qiskit explicitly expose the native gate sets of their backends (e.g., accessible via backend.basis_gates), enabling transpilers to automatically select and work with the appropriate universal sets for a given hardware target. Additionally, custom universal gate sets can be defined programmatically for specialized applications or theoretical explorations. This step is a cornerstone of homogenization as it defines the fundamental, elementary building blocks from which all quantum program complexity ultimately arises, representing a crucial compression of the infinite possibilities of the Lie group $SU\left(2^N\right)$ into a finite, manageable set of primitives.

The core of the homogenization process for discrete variable systems culminates in Unitary Decomposition/Compilation. This step involves applying sophisticated circuit synthesis and decomposition algorithms to express the previously mapped $U_{program}$ using a sequence of gates exclusively from the chosen universal gate set $\mathcal{G}$. For quantum circuits involving a small number of qubits (e.g., $N=2$), exact synthesis methods, such as the KAK decomposition (Khane-Albert-Kitaev decomposition), can be employed. The KAK decomposition factorizes any $SU\left(4\right)$ gate into products of local $SU\left(2\right)$ unitaries and a single parametrized entangling gate, offering an optimal or near-optimal decomposition in terms of two-qubit gates [17]. For larger N, where exact synthesis becomes computationally prohibitive, approximation algorithms based on the Solovay-Kitaev Theorem or iterative numerical methods are employed to break down the complex unitary into a sequence of operations from the universal set. Quantum compilation pipelines, exemplified by Qiskit’s qiskit.transpile() function, automatically perform this decomposition, often integrated seamlessly with other optimization passes like qubit routing and gate scheduling [25]. The QuantumCircuit.decompose() method in Qiskit provides a generic means to convert composite gates or entire circuits into their constituent elementary operations (typically based on a predefined or default basis). This process is a direct computational application of the universal gate theorem, relying on finding an efficient path within the Lie group $SU\left(2^N\right)$ from the identity to $U_{program}$ using compositions of elements from $\mathcal{G}$. Advanced synthesis tools that utilize reinforcement learning or satisfiability modulo theories (as discussed in Section 2.2) also operate primarily by performing this decomposition, albeit with different search strategies [7,16]. This systematic process rigorously expresses the complex $U_{program}$ as a homogeneous sequence of gates, eliminating reliance on a diverse nomenclature and ensuring that any quantum algorithm, regardless of its original logical representation, can be efficiently compiled and executed on a hardware platform supporting the chosen universal gate set, thereby achieving a fully homogenized representation of the program’s unitary evolution.

Finally, an advanced refinement step is Symmetry-Aware Optimization. After the initial homogenization into a universal gate set, further optimization can often be achieved by explicitly leveraging the intrinsic symmetry properties of the quantum system or specific sub-circuits within the program. If certain parts of the program exhibit symmetries (e.g., conservation of total spin, particle number conservation, or permutation symmetry), identifying the corresponding irreducible representations (multiplets) of the relevant Lie group (such as the total spin $SU\left(2\right)$ for multi-qubit systems, as detailed in Section 5.2) becomes highly beneficial. By transforming relevant sections of the circuit into a basis adapted to these irreducible representations, one can reveal block-diagonal structures for operations that respect these symmetries. This decomposition into invariant subspaces allows for significant simplification: gates only act within their respective symmetry sectors, never mixing states between different multiplets. This can potentially reduce the effective dimensionality of the problem or simplify gate counts by avoiding unnecessary entangling operations across symmetry-protected boundaries, leading to more efficient circuit implementations [21]. Computationally, this often requires more specialized libraries or custom transpiler passes that can detect and exploit such symmetries. While not yet standard in all commercial compilers, frameworks like Qiskit’s EquivalenceLibrary allow users to define custom decompositions, which could be designed to be symmetry-aware. Research is actively exploring how to integrate automated symmetry detection and exploitation into quantum compilers to achieve more efficient and robust circuit syntheses, transforming optimization from a purely gate-count-based problem to a symmetry-informed one [13]. This advanced stage of homogenization elevates the process from merely unifying gate names to unifying the structure of interactions based on fundamental physical principles, leading to deeper insights and more effective resource utilization.

6.2. General Lie Group Systems

This methodology extends the concept of homogenization to quantum systems where operations are naturally continuous rather than discrete, or where the quantum information is encoded in continuous variables (e.g., amplitudes and phases of electromagnetic fields in photonic systems, or collective vibrational modes in molecular systems). Here, the focus shifts from sequences of discrete gates to continuous time evolution generated by Hamiltonians, which are fundamental elements of Lie algebras. This approach is particularly relevant for Continuous Variable Quantum Computing (CVQC) and general Quantum Control.

The homogenization process for general Lie group systems commences with System and Operation Identification (Lie Group/Algebra). This crucial first step involves precisely identifying the fundamental Lie group G and its associated Lie algebra $\mathfrak{g}$ that mathematically describe the system’s quantum states and the allowed transformations. For Continuous Variable Quantum Computing (CVQC) using bosonic modes, the primary group governing linear canonical transformations in phase space (such as displacements, squeezing operations, and beam splitters, which preserve the Gaussian nature of quantum states) is the Symplectic group ($Sp(2n,\mathbb{R})$)[22]. The corresponding Lie algebra consists of operators quadratic in the position and momentum operators. For understanding the fundamental commutation relations between these operators, the Heisenberg group is essential. In a broader context of Quantum Control for arbitrary D-level quantum systems, the relevant Lie group remains $SU\left(D\right)$, but the primary interest is in generating a target unitary through precise continuous, time-dependent Hamiltonian evolution rather than assembling it from discrete gate sequences. Computationally, specialized libraries like Strawberry Fields are tailored for CVQC, enabling the precise definition of these systems and their allowed Hamiltonian terms. This step is fundamental for homogenization as it establishes the overarching mathematical space that all continuous operations inhabit, providing a consistent underlying structure for analysis and control, and defining the precise "universe" of possible evolutions for the given physical system.

Once the underlying mathematical structure of the system and its transformations is defined, the next step is to represent the Target Operation as a Group Element or Path. Unlike discrete gate sequences, the desired quantum operation in this continuous domain is typically conceived as a specific element $U\in G$ within the Lie group manifold or, more commonly, as a continuous trajectory (time evolution) within this manifold. This path is governed by a time-dependent Hamiltonian $H\left(t\right)$, which is an element of the Lie algebra $\mathfrak{g}$ (or its complexification, if non-Hermitian dynamics are considered, though not typical for unitary gates). The core problem then becomes finding the appropriate time-dependent control fields that define $H\left(t\right)$ such that the system is steered from an initial state to a target state, or a specific target unitary transformation $U=\mathcal{T}exp(-i{\int }_0^{T}H\left(t^{\prime }\right)d{t}^{\prime })$ is implemented, where $\mathcal{T}$ is the time-ordering operator. Mathematically, this relies heavily on the exponential map (Theorem 3.2), which provides the crucial link between elements of the Lie algebra (infinitesimal generators) and elements of the Lie group (finite transformations). For instance, in CVQC, a desired gate like a two-mode squeezing gate would be directly represented as a specific element of $Sp(4,\mathbb{R})$, obtainable by exponentiating a particular quadratic Hamiltonian. Computational tools at this phase involve quantum simulators capable of propagating quantum states under continuous time evolution, often by numerically solving the Schrödinger equation for time-dependent Hamiltonians [10]. This approach homogenizes desired operations by viewing them as precise mathematical objects (elements or trajectories) within a single, consistent Lie group, thereby enabling unified analytical tools and optimization objectives for continuous quantum processes.

The central homogenization step for continuous systems is Generator-Based Synthesis (Lie Algebra). Here, the objective is to synthesize the target operation by directly controlling the Lie algebra generators, which correspond to physically tunable control parameters (e.g., the amplitudes and phases of microwave pulses in superconducting circuits, or the frequencies and intensities of laser fields in trapped ion systems). This involves finding the optimal time-dependent control fields that generate the desired unitary transformation. This process falls squarely within the domain of quantum optimal control theory, employing advanced algorithms such as GRAPE (Gradient Ascent Pulse Engineering) or Krotov algorithms. These algorithms iteratively refine control pulses to "build" the desired unitary from these infinitesimal generators, effectively finding the most efficient way to navigate the Lie group manifold using its Lie algebra elements [10]. This is often referred to as "compiling" to the pulse level, representing the true native and homogeneous operation on many physical platforms, as the fundamental interactions are continuously controlled. The mathematical basis of this process lies in controllability theory, which determines whether a given set of Lie algebra generators can indeed reach any desired element in the Lie group (i.e., whether the system is "Lie-reachable"). Optimal control theory then extends this to finding the most efficient (e.g., shortest time, lowest power, highest fidelity) path. The Lie bracket operation ($[X,Y]=XY-YX$), fundamental to Lie algebras, signifies how the sequential application of different control fields can generate new effective Hamiltonians (e.g., applying control for X then Y can effectively synthesize an operation proportional to Z), and thus new effective gate operations. Computationally, specialized software packages for quantum optimal control (e.g., QuTiP’s qoc module, or components of Qiskit Pulse for pulse-level control) are used for pulse shaping and optimization, computing the precise analog waveforms required to realize specific quantum gates or transformations with high fidelity [9]. This step provides profound homogenization by ensuring that all operations are understood as being "grown" from the fundamental infinitesimal transformations defined by the Lie algebra, offering a unified origin and a continuous, homogeneous path for all quantum dynamics, effectively eliminating the need for discrete gate names at the lowest level of physical control.

Finally, similar to discrete systems, Symmetry-Aware Basis/Strategy (Advanced) offers a powerful optimization avenue in the continuous domain. This involves explicitly exploiting the representation theory of the relevant Lie group to identify invariant subspaces or to design control strategies that naturally align with the system’s symmetries. For example, in CVQC, representing states and operations in a basis of Fock states (number states) or coherent states can simplify certain problems by leveraging the symmetries inherent in bosonic systems. If the system’s Hamiltonian possesses symmetries, the system’s dynamics will preserve the quantum numbers associated with those symmetries, leading to block-diagonalization of the time-evolution operator (propagator) in the appropriate representation basis [22]. This allows for targeted control only within relevant symmetry sectors, preventing wasteful control efforts in irrelevant subspaces. Mathematically, this leverages the power of group representations to simplify the control problem by reducing its effective dimensionality or by identifying conserved quantities, making the search for optimal control sequences more efficient. Computational tools specific to CVQC (e.g., Strawberry Fields, LightOn) are designed to inherently work within these group-theoretic frameworks. Custom optimal control algorithms can be tailored to exploit these symmetries, potentially leading to more robust or efficient control sequences by avoiding unnecessary mixing of subspaces and focusing computational resources where they are most effective. This advanced stage of homogenization leverages the fundamental structure of the Lie group to guide the optimization and analysis of continuous operations, providing a deeper understanding of the system’s controllability and its inherent limits. It allows for the precise sculpting of quantum states and operations within their native mathematical spaces, rather than forcing them into an approximate, discrete gate set.

7. Examples of Homogenized Quantum Programs

We now illustrate the methodology for discrete variable systems using Qiskit.

7.1. Example 1: Deutsch’s Algorithm

The Deutsch’s algorithm is a foundational quantum algorithm designed to determine a global property of a boolean function $f:\{0,1\}\to \{0,1\}$ (whether it is constant or balanced) with a single query to the function, an exponential speedup over classical deterministic algorithms for this specific problem [24]. This example, while simple, demonstrates the core steps of quantum computation including superposition, oracle interaction, and interference, making it an excellent candidate to illustrate homogenization.

Initial Situation (Common View - Qiskit Program)

In its conventional representation, the Deutsch’s algorithm circuit is built using a sequence of distinct, named gates: Hadamard gates for initial superposition and final measurement basis transformation, a Pauli-X gate for ancilla initialization, and a function-dependent oracle gate. The oracle itself is often a high-level conceptual block or a custom gate, like a Controlled-NOT (CX) for $f\left(x\right)=x$ or an identity gate for $f\left(x\right)=0$. Each of these gates is treated as a separate, pre-defined primitive.

This initial representation, while functionally correct, treats each quantum operation as a distinct logical entity. The process of homogenization aims to transform this diverse set of operations into a unified, minimal basis.

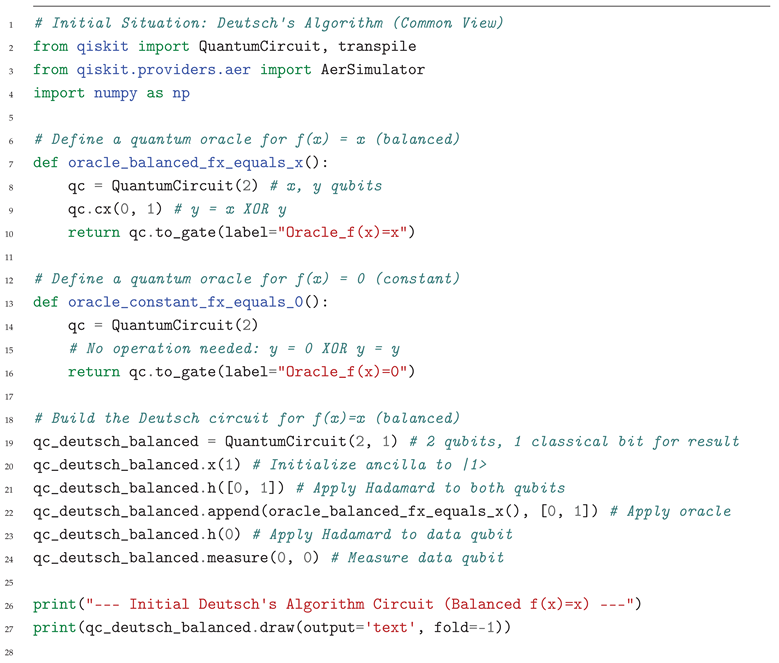
Transformed Situation (SU($2^N$) Homogenization - Universal Gate Decomposition)

The homogenization methodology, specifically steps 1, 2, and 3 from Section 6.1, can be applied to Deutsch’s Algorithm.

First, Program-to-Unitary Mapping (Methodology Step 1) extracts the unitary component of the circuit. In Deutsch’s algorithm, the sequence of Hadamards and the oracle gate, preceding the final measurement, collectively define a single 2-qubit unitary operator $U_{Deutsch}\in SU\left(4\right)$. This unitary encapsulates the entire quantum logic of the algorithm.

Next, Universal Gate Set Selection (Methodology Step 2) is performed. For standard qubit-based computation in Qiskit, the default universal gate set is typically comprised of all single-qubit U gates (which are themselves parameterized rotations in $SU\left(2\right)$) and the CX (Controlled-NOT) gate. This set serves as our homogeneous "alphabet" for representing any multi-qubit unitary.

Finally, Unitary Decomposition/Compilation (Methodology Step 3) is applied. The extracted $U_{Deutsch}$ unitary is then decomposed into a sequence of gates from this chosen universal set. This process effectively rewrites the algorithm using only u and cx gates, thereby achieving a homogeneous representation of the circuit’s quantum logic.

The homogenization of Deutsch’s Algorithm demonstrates that the entire quantum circuit, including the oracle, can be viewed as a single, specific 2-qubit unitary operator within $SU\left(4\right)$. This operator, regardless of the function it implements, is ultimately a composition of a homogeneous set of fundamental u and cx gates. This transforms the problem from a specific algorithm to the synthesis of a particular $SU\left(4\right)$ element using universal building blocks. This process not only provides a uniform representation for hardware compilation but also simplifies the analysis of the algorithm’s complexity by expressing it in a minimal, consistent gate set.

7.2. Example 2: Quantum Teleportation

Quantum teleportation is a key quantum communication protocol that enables the transfer of an unknown quantum state from a sender (Alice) to a receiver (Bob) with the aid of a pre-shared entangled pair and classical communication [24]. This algorithm highlights the interplay between quantum operations, entanglement, and classical information.

Initial Situation (Common View - Qiskit Program)

The quantum teleportation circuit, as commonly depicted, involves a sequence of standard, named gates: Hadamard gates for superposition, CNOT gates for entanglement generation and Bell-state measurement, explicit measurement operations, and classically controlled Pauli gates (X and Z) for state correction. The classical control flow based on measurement outcomes is an integral part of the algorithm’s logical definition.

This circuit, while functionally clear, utilizes a mix of named gates and classical control. The homogenization process, particularly focusing on the unitary part, aims to consolidate these into a unified representation.

Transformed Situation (SU($2^N$) Homogenization - Universal Gate Decomposition)

The homogenization methodology (Section 6.1) can be applied to the quantum teleportation circuit.

The initial step, Program-to-Unitary Mapping (Methodology Step 1), involves identifying the purely unitary segments of the algorithm. In quantum teleportation, the preparation of the Bell pair, followed by Alice’s part of the Bell measurement (the cx and h gates on her qubits), collectively form a specific 3-qubit unitary operation within $SU\left(2^3\right)$. The subsequent measurements and classical feedback loops for Bob’s corrections are non-unitary operations and are outside the scope of direct unitary homogenization, though they are crucial for the algorithm’s completion.

Next, Universal Gate Set Selection (Methodology Step 2) relies on choosing a target homogeneous gate set. For practical purposes in Qiskit, this remains the set of all single-qubit U gates and CX gates, which are native or easily convertible on most quantum hardware.

Finally, Unitary Decomposition/Compilation (Methodology Step 3) is applied to the extracted 3-qubit unitary component. This process systematically decomposes the complex sequence of entanglement generation and Bell state projection into a homogeneous sequence of u and cx gates. This emphasizes that the entire quantum mechanical core of the teleportation protocol is a specific element within the $SU\left(2^3\right)$ manifold, fully expressible through compositions of a minimal universal set.

The homogenization here lies in recognizing that the complex interplay of gates in quantum teleportation, from Alice’s encoding to the pre-measurement Bell state formation, can be represented as a specific multi-qubit unitary operation within $SU\left(2^3\right)$. This complex unitary, despite its algorithmic interpretation, is then systematically expressed through a homogeneous sequence of elementary u gates (from $SU\left(2\right)$) and cx gates (from $SU\left(4\right)$). This abstract perspective homogenizes the entire quantum process into fundamental, hardware-level operations, highlighting the universality of the gate set. Such homogenization is crucial for the efficient compilation of communication protocols onto real quantum hardware and for the theoretical analysis of their resource requirements [3].

7.3. Example 3: Quantum Phase Estimation

Quantum Phase Estimation (QPE) is one of the most significant quantum algorithms, providing the core subroutine for Shor’s factoring algorithm and quantum simulations of molecular and material properties [24]. Its goal is to estimate the phase $\varphi$ of an eigenvalue $e^{2\pi i\varphi }$ of a unitary operator U, given an eigenvector $\left|\psi \right.〉$ (i.e., $U\left|\psi \right.〉=e^{2\pi i\varphi }\left|\psi \right.〉$). This algorithm is complex due to its multi-qubit nature and the dependence on controlled powers of the oracle unitary U.

Initial Situation (Common View - Qiskit Program)

A typical QPE circuit involves: initializing counting qubits in superposition, applying a sequence of controlled-$U^{2^k}$ operations (where U is the unitary whose phase is being estimated, raised to powers of $2^k$), and finally applying an inverse Quantum Fourier Transform (QFT) to the counting qubits. Each Controlled-U^2^k operation can be quite complex itself, and the QFT is a multi-qubit transformation often treated as a high-level primitive.

This initial representation features high-level conceptual gates like Controlled-U^power and QFT, which mask significant underlying complexity. Homogenization reveals the true gate cost and structure.

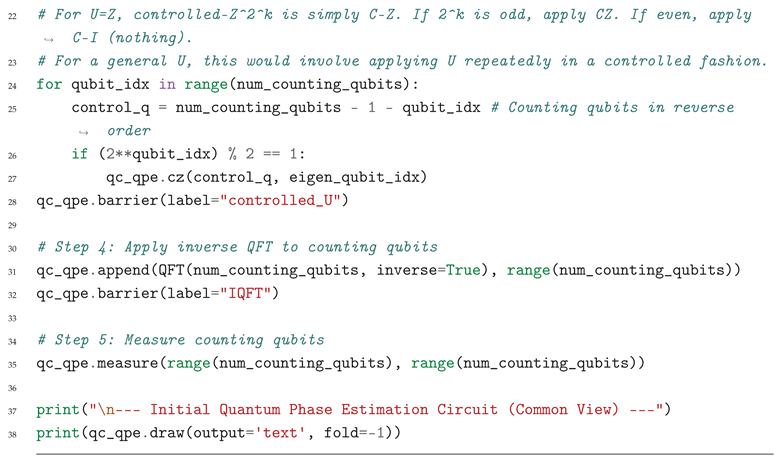
Transformed Situation (SU($2^N$) Homogenization - Universal Gate Decomposition)

The homogenization methodology (Section 6.1) is particularly powerful for an algorithm like QPE. The process begins with Program-to-Unitary Mapping (Methodology Step 1). The entire quantum logic of QPE, comprising the initial Hadamards on counting qubits, the preparation of the eigenvector, all controlled-$U^{2^k}$ operations, and the final inverse QFT, constitutes a single large unitary operator $U_{QPE}\in SU\left(2^{N_c+1}\right)$, where $N_c$ is the number of counting qubits. This unitary fully describes the transformation of the input state to the final state before measurement.

Next, for Universal Gate Set Selection (Methodology Step 2), we again choose the standard Qiskit universal basis of U gates and CX gates. This is the homogeneous target set for all operations in the QPE algorithm.

Finally, Unitary Decomposition/Compilation (Methodology Step 3) is performed. This crucial step systematically decomposes the entire $U_{QPE}$ into a sequence of operations from the chosen universal set. This involves expanding the abstract QFT gate into its constituent Hadamards, Phase, and CNOT gates. Similarly, each Controlled-U^2^k operation, which might involve many repeated applications of U, is itself decomposed into a sequence of U and CX gates. This transformation reveals the true, underlying gate complexity of the QPE algorithm in terms of the fundamental homogeneous primitives.

The homogenization of QPE demonstrates how complex algorithms, defined by specialized gates like Controlled-U^2^k and QFT, are ultimately reducible to a sequence of elementary gates from a universal set. This is achieved by viewing these high-level operations as specific elements of $SU\left(2^N\right)$ which can then be algorithmically decomposed. This process not only clarifies the true gate complexity of the algorithm in terms of fundamental operations (e.g., number of CNOTs and single-qubit rotations) but also enables its compilation onto any universal quantum computer, thereby achieving a homogeneous representation of the program’s unitary evolution.

8. Conclusions

The theory of Lie groups and their representations offers a profoundly elegant and practical framework for homogenizing, simplifying, and generalizing quantum gates. It transforms an ostensibly disparate collection of operations into a structured, unified mathematical entity. We began by highlighting the multifaceted problem of gate heterogeneity across program analysis, synthesis, transpilation, and hardware construction, emphasizing the need for a systematic solution.

From the universal parametrization of single-qubit gates within $SU\left(2\right)$ (exemplified by the Euler Angle Decomposition and Qiskit’s U gate) to the decomposition of complex multi-qubit operations into universal gate sets within $SU\left(2^N\right)$ (as demonstrated by the Solovay-Kitaev Theorem and Qiskit’s decompose() method), this theoretical lens provides unparalleled clarity. These mathematical principles underpin the ability to translate any quantum algorithm into a set of fundamental, uniformly described operations, crucial for interoperability and hardware compatibility.

The power of group theory is further showcased by the decomposition of multi-qubit Hilbert spaces into irreducible representations (multiplets). This intrinsic structuring allows for the block-diagonalization of symmetry-preserving gates, simplifying their analysis and revealing their inherent properties, as explicitly demonstrated with the SWAP gate in the singlet-triplet basis. Crucially, this framework offers a fundamental reinterpretation of core quantum phenomena: superpositions are understood as states residing within specific irreducible representation spaces, and entanglement manifests as states that belong to irreducible subspaces that cannot be factored into independent components. This deeper understanding provides a homogeneous conceptual foundation for quantum information.

The methodology outlined, meticulously separating approaches for discrete and continuous variable systems, provides a systematic approach to homogenizing quantum programs. For discrete systems, it involves mapping programs to unitaries in $SU\left(2^N\right)$ and then systematically decomposing them into a universal gate set. For continuous systems and quantum control, it involves identifying the relevant Lie group/algebra and synthesizing operations using their fundamental generators. The practical Qiskit examples of Deutsch’s Algorithm, Quantum Teleportation, and Quantum Phase Estimation demonstrate how abstract group-theoretic concepts are applied to transform conventional quantum circuits into a homogeneous representation, facilitating compilation and revealing underlying structures. These insights are not merely abstract; they directly inform the design of efficient quantum algorithms, the optimization of circuit compilation for specific hardware, and the development of advanced quantum control strategies. As quantum computing continues its rapid expansion to larger scales and more diverse physical implementations (qudits, CVQC), the language of Lie groups and their representations will remain an indispensable tool for navigating, understanding, and ultimately mastering its complex landscape.