Binary Superposition Algebra: A Hyper Complex, Commutative, and Associative Product

1. Introduction

Hyper-complex algebraic systems are widely used to model non-trivial physical phenomena, particularly in quantum mechanics. However, associativity and commutativity are often lost in classical extensions such as quaternions, octonions, and sedenions. In this work, we introduce a binary superposition structure that enables a stable multiplication operation. This framework combines logical consistency, geometric structure, and algebraic coherence. It provides a pathway for constructing algebraic models that preserve key structural properties essential for advanced applications in quantum theory.

2. Superimposed Hyper-Complex Number of Level 3 1

2.1. Hyperspace $E_{\left(2;2\right)}$

A superimposed hyper complex number is a number representing points in complex hyperspaces of dimension$n\ge 2$.

In hyperspace$E_{\left(2 ; 2\right)}=\left\{\left(v_{r,1} ; v_i\right);(v_{r,2} ; v_j)\right\}$, for any point M there exists a unique superimposed hyper complex number $h\in \mathbb{S}(2 ;2)$such that$h=z_1+z_2$.

■

hyperspace $E_{\left(2 ; 2\right)}$is a space composed of two real dimensions $v_{r,1}$; $v_{r,2}$and two imaginary dimensions $v_i$;$v_j$

■

$z_1$is the complex number that represents a point $M_1$on the plane $\left(O ; v_{r,1} ; v_i\right)$where $(O;v_{r,1})$ is the real axis and $\left(O;v_i\right)$is the imaginary axis of the plane $\left(O ; v_{r,1} ; v_i\right)$such that: $z_1=a_1+bi$.

■

$z_2$is the complex number that represents a point $M_2$on the plane$\left(O ; v_{r,2} ; v_j\right)$ where $\left(O;v_{r,2}\right)$is the real axis and $\left(O;v_j\right)$is the imaginary axis of the plane $\left(O ; v_{r,2} ; v_j\right)$such that:$z_2=a_2+cj$.

We therefore obtain

$$h=a_1+bi+a_2+cj$$

$$h=a_1+a_2+bi+cj$$

By superimposing the real axes $\left(O;v_{r,1}\right)$and $\left(O;v_{r,2}\right)$then posing $a=a_1+a_2$we then have the superimposed hyper-complex number $h=a+bi+cj$which gives us an extension to 3 dimensions denoted ${\mathbb{C}}_{\left(1; 2\right)}$from the set $\mathbb{C}$ of complex numbers.

2.2. Hyperspace $E_{\left(3;3\right)}$

By the same reasoning; we will also have that; for any point M of the hyper-space $E_{\left(3 ; 3\right)}=\left\{\left(v_{r,1} ; v_i\right);(v_{r,2} ; v_j);(v_{r,3} ; v_k)\right\}$, there exists a unique superimposed hyper-complex number $h\in \mathbb{S}(3 ;3)$such that $h=z_1+z_2+z_3$.

$z_1=x_{1,r}{v}_{1,r}+x_{2,r}{v}_{2,r}$; $z_1=x_{3,r}{v}_{3,r}+y_{1,i}{v}_{1,i}$ And $z_1=y_{2,i}{v}_{2,i}+y_{3,i}{v}_{3,i}$

$h=x_{1,r}{v}_{1,r}+x_{2,r}{v}_{2,r}+x_{3,r}{v}_{3,r}+y_{1,i}{v}_{1,i}+y_{2,i}{v}_{2,i}+y_{3,i}{v}_{3,i}$

$h=x_{1,r}{v}_r+x_{2,r}{v}_r+x_{3,r}{v}_r+y_{1,i}{v}_{1,i}+y_{2,i}{v}_{2,i}+y_{3,i}{v}_{3,i}$

$h=\left(x_{1,r}+x_{2,r}+x_{3,r}\right)v_r+y_{1,i}{v}_{1,i}+y_{2,i}{v}_{2,i}+y_{3,i}{v}_{3,i}$

By asking: $x_{1,r}+x_{2,r}+x_{3,r}=x_r$

We obtain: $h=x_r{v}_r+y_{1,i}{v}_{1,i}+y_{2,i}{v}_{2,i}+y_{3,i}{v}_{3,i}$

If now we pose $v_r=1$; $v_{1,i}=i$; $v_{2,i}=j$; and $v_{3,i}=k$.

As well as: $x_r=a$;$y_{1,i}=b;$ $y_{2,i}=c$;$y_{3,i}=d$

We also obtain a writing of the superimposed hyper-complex number: $h=a+bi+cj+dk$

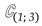Which also gives us an extension to 4 dimensions noted from the set of complex numbers.

3. The Imaginary Product ${⨂}_{\mathit{e}}^{\mathit{i}}$ and the Real Product ${⨂}_{\mathit{e}}^{\mathit{r}}$ 1

3.1. The Rules of the Imaginary Product ${⨂}_{\mathit{e}}^i$ and the Real Product ${⨂}_e^r$

We note that the multiplication of superimposed hyper-complex numbers reveals (as the great Irish mathematician William Rohan Hamilton discovered) additional, hidden, and superimposed dimensions. These additional dimensions form new superimposed spaces.

As clearly stated in the article "Complex Superposition Algebra" the imaginary product of superimposed hyper complex numbers is indeed commutative and associative in the superposition phase. However, the property of associativity is lost in the de-superposition phase of hyper complex numbers. This is mainly due to the appearance of a negative sign for the squares of imaginary numbers. After a year of reflection I noticed that the mixing of negative signs $(-)$ in the imaginary product was the cause of the loss of associativity. This means that, they are also superimposed and must be defined for each rotation plane.

Recall that the multiplication of imaginary bases is defined by the imaginary product noted ${⨂}_e^i$(in the article: Complex Superposition Algebra)1; is associated with the applications $f$and $S_i$; defined as follows:

Let the sets $H=\left\{0+4p;1+4p;2+4p;3+4p\right\}\left(p\in \mathbb{Z}\right)$; $I=\left\{-1;0;1\right\}$and $J=\left\{-1;+1\right\}$ and the applications$f$; $S_i$be defined by:

$$f\left(H\right)=I \mathrm{Such} \mathrm{as}\text{:} \left\{\begin{array}{c}f\left(0+4p\right)=0 \\ f\left(1+4p\right)=1 \\ f\left(2+4p\right)=0 \\ f\left(3+4p\right)=-1\end{array}\right.$$

$S_{n,\pm }=\left(\left\{0+4p;2+4p\right\}\right)=J$such as :$S_{n,\pm }=\left\{\begin{array}{c}{S}_{0,\pm }\left(0+4p\right)=+1\\ S_{2,\pm }\left(2+4p\right)=-1\end{array}\right.$

So the imaginary product application for two hyper-complex numbers

$V_i=e^{{\displaystyle \frac{\pi }{2}}\left({\alpha }_1{v}_{1,i}+{\alpha }_2{v}_{2,i}+{\alpha }_3{v}_{3,i}\right)}$ and $V_i^{\mathrm{\text{'}}}=e^{{\displaystyle \frac{\pi }{2}}\left({{\alpha }_1}^{\mathrm{\text{'}}}{v}_{1,i}+{{\alpha }_2}^{\mathrm{\text{'}}}{v}_{2,i}+{{\alpha }_3}^{\mathrm{\text{'}}}{v}_{3,i}\right)}$is defined by:

${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)=e^{{\displaystyle \frac{\pi }{2}}\left({\alpha }_1{v}_{1,i}+{\alpha }_2{v}_{2,i}+{\alpha }_3{v}_{3,i}\right)}\times e^{{\displaystyle \frac{\pi }{2}}\left({{\alpha }_1}^{\mathrm{\text{'}}}{v}_{1,i}+{{\alpha }_2}^{\mathrm{\text{'}}}{v}_{2,i}+{{\alpha }_3}^{\mathrm{\text{'}}}{v}_{3,i}\right)}$

${⨂}_e^i=S_i\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times S_i\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times S_i\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)e^{{\displaystyle \frac{\pi }{2}}\left(f\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times v_{1,i}+f\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times v_{2,i}+f({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}})\times v_{3,i}\right)}$

If we note ${\prod }_i=S_i\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times S_i\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times S_i\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)$

So we have ${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)={\prod }_i\times e^{{\displaystyle \frac{\pi }{2}}\left(f\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times v_{1,i}+f\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times v_{2,i}+f({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}})\times v_{3,i}\right)}$

3.2. New Rules and Notations

To maintain associativity let's make the following changes:

We will modify: $f\left(3+4p\right)=-1$ by $f\left(3+4p\right)=1$

We will use the signs: $S_{1,\pm }\left(1+4p\right)=+1$ and $S_{3,\pm }\left(3+4p\right)=-1$; each in its plane of rotation.

Which logically, changes nothing; because this is an inversion of the sign of:

$f\left(3+4p\right)=-1$ towards $S_{3,\pm }\left(3+4p\right)=-1$ and $S_{1,\pm }\left(1+4p\right)=+1$ is positive, so there is no change.

Finally let's add an index notation to $f$ what we get $f_n$ and replace the notation $S_{n,\pm }$ with $S_n$. Which corresponds the positions of $f_n$ to those of $S_n$.

This means that it will no longer be necessary to raise the sign $\left(-\right)$ in the imaginary exponential, but leave it in front. We just want to adapt the imaginary product to a notation of superimposed hyper complex numbers that offers associativity.

So the applications associated with the imaginary product will now be:

$f_n\left(H\right)=I$ such that: $f_n=\left\{\begin{array}{c}f\left(0+4p\right)=0 \\ f\left(1+4p\right)=1 \\ f\left(2+4p\right)=0 \\ f\left(3+4p\right)=1 \end{array}\right.$; and $S_n\left(H\right)=J$ such that: $S_n=\left\{\begin{array}{c}S\left(0+4p\right)=+1\\ S\left(1+4p\right)=+1 \\ S\left(2+4p\right)=-1\\ S\left(3+4p\right)=-1\end{array}\right.$

We will also change the sign ${\prod }_i=S_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times S_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times S_3\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)$ and define as a superposition of signs; in their rotation planes. We will use the following superimposed notation:

$${\prod }_i=⟨S_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)|S_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)|S_3\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)⟩$$

This allows us to maintain the rules of signs of multiplication in each plane of rotation. This superposition allows us to avoid multiplying signs that are not in the same plane of rotation. I remind you that; the fact that multiplication is linked to rotation in the plane defined by Jean Robert Argan among others. 2

We will define the modified imaginary product as follows:

Let the sets $H=\left\{0+4p;1+4p;2+4p;3+4p\right\}\left(p\in \mathbb{Z}\right)$; $I=\left\{0;1\right\}$ and $J=\left\{-\mathit{1} ;+\mathit{1}\right\}$ and applications ${ f}_n$; $S_i$ defined by:

$f_n\left(H\right)=I$ such that: $\left\{\begin{array}{c}f\left(0+4p\right)=0 \\ f\left(1+4p\right)=1 \\ f\left(2+4p\right)=0 \\ f\left(3+4p\right)=1 \end{array}\right.$; and $S_n\left(H\right)=J$ such that: $\left\{\begin{array}{c}S\left(0+4p\right)=+1\\ S\left(1+4p\right)=+1 \\ S\left(2+4p\right)=-1\\ S\left(3+4p\right)=-1\end{array}\right.$

Then the imaginary product application is defined by:

${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)=e^{{\displaystyle \frac{\pi }{2}}\left({\alpha }_1{v}_{1,i}+{\alpha }_2{v}_{2,i}+{\alpha }_3{v}_{3,i}\right)}\times e^{{\displaystyle \frac{\pi }{2}}\left({{\alpha }_1}^{\mathrm{\text{'}}}{v}_{1,i}+{{\alpha }_2}^{\mathrm{\text{'}}}{v}_{2,i}+{{\alpha }_3}^{\mathrm{\text{'}}}{v}_{3,i}\right)}$

${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)=⟨S_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)|S_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)|S_2\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)⟩e^{{\displaystyle \frac{\pi }{2}}\left(f_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times v_{1,i}+f_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times v_{2,i}+f_3({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}})\times v_{3,i}\right)}$

If we note ${\prod }_i=⟨S_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)|S_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)|S_3\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)⟩$ this on the assumption that the signs were positive to begin with.

Taking into account the previous signs we will have:

${\prod }_i=⟨S_1\left({\alpha }_1\right)\times S_1\left({{\alpha }_1}^{\mathrm{\text{'}}}\right)\times S_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\right]|S_2\left({\alpha }_2\right)\times S_2\left({{\alpha }_2}^{\mathrm{\text{'}}}\right)\times S_2\left[f_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\right]|S_3\left({\alpha }_3\right)\times S_3\left({{\alpha }_3}^{\mathrm{\text{'}}}\right)\times S_3\left[f_3\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)\right]⟩$

We once again obtain a long notation:

This is why we will also note: $\left\{\begin{array}{c}{\prod }_1=S_1\left({\alpha }_1\right)\times S_1\left({{\alpha }_1}^{\mathrm{\text{'}}}\right)\times S_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\right]\\ {\prod }_2=S_2\left({\alpha }_2\right)\times S_2\left({{\alpha }_2}^{\mathrm{\text{'}}}\right)\times S_2\left[f_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\right]\\ {\prod }_3=S_3\left({\alpha }_3\right)\times S_3\left({{\alpha }_3}^{\mathrm{\text{'}}}\right)\times S_3\left[f_3\left({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}}\right)\right]\end{array}\right.$

So we have ${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)={\prod }_i\times e^{{\displaystyle \frac{\pi }{2}}\left(f_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)\times v_{1,i}+f_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)\times v_{2,i}+f_3({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}})\times v_{3,i}\right)}$

$${⨂}_e^i\left(V_i ; V_i^{\text{'}}\right)=⟨ {\prod }_1 |{ \prod }_2 |{ \prod }_3⟩\times e^{{\displaystyle \frac{\pi }{2}}\left(f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\times v_{1,i}+f_2\left({\alpha }_2+{{\alpha }_2}^{\text{'}}\right)\times v_{2,i}+f_3({\alpha }_3+{{\alpha }_3}^{\text{'}})\times v_{3,i}\right)}$$

If we note

$$e^{{\displaystyle \frac{\pi }{2}}\left(f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\times v_{1,i}+f_2\left({\alpha }_2+{{\alpha }_2}^{\text{'}}\right)\times v_{2,i}+f_3({\alpha }_3+{{\alpha }_3}^{\text{'}})\times v_{3,i}\right)}=⟨f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)|f_2\left({\alpha }_2+{{\alpha }_2}^{\text{'}}\right)|f_3({\alpha }_3+{{\alpha }_3}^{\text{'}})⟩$$

We will have ${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)=⟨{\prod }_1|{\prod }_2|{\prod }_3⟩\times ⟨f_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)|f_2\left({\alpha }_2+{{\alpha }_2}^{\mathrm{\text{'}}}\right)|f_3({\alpha }_3+{{\alpha }_3}^{\mathrm{\text{'}}})⟩$

Since this notation can be long, we will propose a simpler notation of the imaginary product as follows:

$${⨂}_e^i\left(V_i ; V_i^{\text{'}}\right)=⟨\begin{array}{c}{f}_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\\ {\prod }_1\end{array}|\begin{array}{c}{f}_2\left({\alpha }_2+{{\alpha }_2}^{\text{'}}\right)\\ {\prod }_2\end{array}|\begin{array}{c}{f}_3\left({\alpha }_3+{{\alpha }_3}^{\text{'}}\right)\\ {\prod }_3\end{array}⟩$$

Each hyper complex unit is defined by a pair of overlapping values:

(i) A logical component resulting from a binary function $f_n$

(ii) A phase component associated with ${\prod }_n$, representing the sign resulting from the superposition and desuperposition phases.

These two values are encoded in overlapping lines. The imaginary product is defined by the rule:

$${⨂}_e^i\left(V_i ; V_i^{\text{'}}\right)=⟨\begin{array}{c}{f}_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\\ {\prod }_1\end{array}|\begin{array}{c}{f}_2\left({\alpha }_2+{{\alpha }_2}^{\text{'}}\right)\\ {\prod }_2\end{array}|\begin{array}{c}{f}_3\left({\alpha }_3+{{\alpha }_3}^{\text{'}}\right)\\ {\prod }_3\end{array} ⟩$$

This rating $⟨\begin{array}{c}\dots \\ \dots \end{array}|\begin{array}{c}\dots \\ \dots \end{array}|\begin{array}{c}\dots \\ \dots \end{array}⟩$ indicates an overlapping concatenation.

3.3. Demonstration of Commutativity and Associativity

Let us try to show that imaginary product is commutative and associative.

To begin, let's note that the applications:

• $f_1$; $f_2$; $f_3$…… $f_n$are equivalent; the index notation is there to specify that each application $f_n$is associated with a base $v_{i,n}$.
• $S_1$; $S_2$; $S_3$…… $S_n$are equivalent; the index notation is there to specify that each application $S_n$is associated with the application $f_n$and therefore with the base $v_{i,n}$.
• We will generalize the notation for a level superposition $n$with the notation:
• $V_i=\underset{n}{\underbrace{⟨\begin{array}{c}{\alpha }_1\\ S_1\left({\alpha }_1\right)\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{\alpha }_n\\ S_n\left({\alpha }_n\right)\end{array}⟩}}$; where ${\alpha }_n\in \left\{0;1\right\}$and$n\in \mathbb{N}$

3.3.1. Commutativity

For commutativity we have:

$${⨂}_e^i\left(V_i ; V_i^{\text{'}}\right)=\underset{n}{\underbrace{⟨\begin{array}{c}{f}_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\\ {\prod }_1\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left({\alpha }_n+{{\alpha }_n}^{\text{'}}\right)\\ {\prod }_n\end{array}⟩}}$$

Addition and multiplication being commutative we have:

$$⟨\begin{array}{c}{f}_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\\ {\prod }_1\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left({\alpha }_n+{{\alpha }_n}^{\text{'}}\right)\\ {\prod }_n\end{array}⟩=⟨\begin{array}{c}{f}_1\left({{\alpha }_1}^{\text{'}}+{\alpha }_1\right)\\ {\prod }_1\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left({{\alpha }_n}^{\text{'}}+{\alpha }_n\right)\\ {\prod }_n\end{array}⟩$$

We can then conclude that:${⨂}_e^i\left(V_i;V_i^{\mathrm{\text{'}}}\right)={⨂}_e^i\left(V_i^{\mathrm{\text{'}}};V_i\right)$

Therefore the imaginary product is commutative for all levels of superposition.

3.3.2. Associativity

For associativity we have:

$${⨂}_e^i\left[\left(V_i ; V_i^{\text{'}}\right);V_i^{\text{'}\text{'}}\right]=⟨\begin{array}{c}{f}_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)\\ {\prod }_1\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left({\alpha }_n+{{\alpha }_n}^{\text{'}}\right)\\ {\prod }_n\end{array}⟩⟨\begin{array}{c}{{\alpha }_1}^{\text{'}\text{'}}\\ S_1\left({{\alpha }_1}^{\text{'}\text{'}}\right)\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{{\alpha }_n}^{\text{'}\text{'}}\\ S_n\left({{\alpha }_n}^{\text{'}\text{'}}\right)\end{array}⟩$$

$${⨂}_e^i\left[\left(V_i ; V_i^{\text{'}}\right);V_i^{\text{'}\text{'}}\right]=⟨\begin{array}{c}{f}_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)+{{\alpha }_1}^{\text{'}\text{'}}\right]\\ {\prod }_1\times S_1\left({{\alpha }_1}^{\text{'}\text{'}}\right)\times S_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)+{{\alpha }_1}^{\text{'}\text{'}}\right]\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left[f_n\left({\alpha }_n+{{\alpha }_n}^{\text{'}}\right)+{{\alpha }_n}^{\text{'}\text{'}}\right]\\ {\prod }_1\times S_n\left({{\alpha }_n}^{\text{'}\text{'}}\right)\times S_n\left(f_n\left({\alpha }_n+{{\alpha }_n}^{\text{'}}\right)+{{\alpha }_n}^{\text{'}\text{'}}\right)\end{array}⟩$$

Then we have:

$${⨂}_e^i\left[V_i ;\left( V_i^{\text{'}} ;V_i^{\text{'}\text{'}}\right)\right]=⟨\begin{array}{c}{\alpha }_1\\ S_1\left({\alpha }_1\right)\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{\alpha }_n\\ S_n\left({\alpha }_n\right)\end{array}⟩⟨\begin{array}{c}{f}_1\left({{\alpha }_1}^{\text{'}}+{{\alpha }_1}^{\text{'}\text{'}}\right)\\ {\prod }_1\text{'}\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left({{\alpha }_n}^{\text{'}}+{{\alpha }_n}^{\text{'}\text{'}}\right)\\ {\prod }_n\text{'}\end{array}⟩$$

$${⨂}_e^i\left[V_i ;\left( V_i^{\text{'}} ;V_i^{\text{'}\text{'}}\right)\right]=⟨\begin{array}{c}{f}_1\left[{{\alpha }_1+f}_1\left({{\alpha }_1}^{\text{'}}+{{\alpha }_1}^{\text{'}\text{'}}\right)\right]\\ S_1\left({\alpha }_1\right)\times {\prod }_1\text{'}\times S_1\left[{{\alpha }_1+f}_1\left({{\alpha }_1}^{\text{'}}+{{\alpha }_1}^{\text{'}\text{'}}\right)\right]\end{array}|\begin{array}{c}\dots \dots \\ \dots \dots \end{array}|\begin{array}{c}{f}_n\left[{{\alpha }_n+f}_n\left({{\alpha }_n}^{\text{'}}+{{\alpha }_n}^{\text{'}\text{'}}\right)\right]\\ S_n\left({\alpha }_n\right)\times {\prod }_n\text{'}\times S_n\left[{{\alpha }_n+f}_n\left({{\alpha }_n}^{\text{'}}+{{\alpha }_n}^{\text{'}\text{'}}\right)\right]\end{array}⟩$$

To say that: ${⨂}_e^i\left[V_i;\left(V_i^{\mathrm{\text{'}}};V_i^{\mathrm{\text{'}}\mathrm{\text{'}}}\right)\right]={⨂}_e^i\left[V_i;\left(V_i^{\mathrm{\text{'}}};V_i^{\mathrm{\text{'}}\mathrm{\text{'}}}\right)\right]$; is equivalent to having the following two equalities:

$$\left\{\begin{array}{c}{f}_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)+{{\alpha }_1}^{\text{'}\text{'}}\right]=f_1\left[{{\alpha }_1+f}_1\left({{\alpha }_1}^{\text{'}}+{{\alpha }_1}^{\text{'}\text{'}}\right)\right] \\ {\prod }_1\times S_1\left({{\alpha }_1}^{\text{'}\text{'}}\right)\times S_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)+{{\alpha }_1}^{\text{'}\text{'}}\right]=S_1\left({\alpha }_1\right)\times {\prod }_1\text{'}\times S_1\left[{{\alpha }_1+f}_1\left({{\alpha }_1}^{\text{'}}+{{\alpha }_1}^{\text{'}\text{'}}\right)\right]\end{array}\right.$$

We will try to test all possible cases. The three elements${\alpha }_1$;${{\alpha }_1}^{\text{'}}$; ${{\alpha }_1}^{\text{'}\text{'}}$belong to the binary set$\left\{0;1\right\}$, and the set of arrivals is also binary; so the number of possibilities is $2^3=8$. We will study this equality in the form of a table.

Let us remember that the applications$f_1$;$f_2$; $f_3$…… $f_n$are equivalent and so are the applications$S_1$; $S_2$; $S_3$…… $S_n$. So we will limit the comparison to the application $f_1$and the application$S_1$.

➢

Let's start with the application$f_1$

We can deduce from this table that: $f_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\mathrm{\text{'}}}\right)+{{\alpha }_1}^{\mathrm{\text{'}}\mathrm{\text{'}}}\right]=f_1\left[{{\alpha }_1+f}_1\left({{\alpha }_1}^{\mathrm{\text{'}}}+{{\alpha }_1}^{\mathrm{\text{'}}\mathrm{\text{'}}}\right)\right]$

➢

Let's finish with the application $S_1$

We can deduce from this second table that:

$${\prod }_1\times S_1\left({{\alpha }_1}^{\text{'}\text{'}}\right)\times S_1\left[f_1\left({\alpha }_1+{{\alpha }_1}^{\text{'}}\right)+{{\alpha }_1}^{\text{'}\text{'}}\right]=S_1\left({\alpha }_1\right)\times {\prod }_1\text{'}\times S_1\left[{{\alpha }_1+f}_1\left({{\alpha }_1}^{\text{'}}+{{\alpha }_1}^{\text{'}\text{'}}\right)\right]$$

From the results of Table 1 and Table 2: the equality ${⨂}_e^i\left[V_i;\left(V_i^{\mathrm{\text{'}}};V_i^{\mathrm{\text{'}}\mathrm{\text{'}}}\right)\right]={⨂}_e^i\left[V_i;\left(V_i^{\mathrm{\text{'}}};V_i^{\mathrm{\text{'}}\mathrm{\text{'}}}\right)\right]$is true

Therefore the imaginary product is associative for all levels of superposition.

3.3.3. The Actual Product ${⨂}_{\mathrm{e}}^{\mathrm{r}}$

For the real product ${⨂}_e^r$to multiply two real parts together; we will no longer need a transformation (rotation and a transformation from imaginary to real writing as proposed in the first article). This is for two reasons: the first because all the real axes are united on a single one and second the new rules (new notation) allow the de-superposition. Thus the basis of the real part for a superimposed hyper-complex number for a level superposition $n$is written as follows:

$$h_r=\underset{n}{\underbrace{⟨ \begin{array}{c}0\\ \pm 1\end{array} |\begin{array}{c}\dots . \dots \\ \dots . \dots \end{array}| \begin{array}{c}0\\ \pm 1\end{array} ⟩}}$$

4. Notation and Structure of Algebraic Spaces ${\mathbb{S}}_{(2;2)}$ and ${\mathbb{S}}_{(3;3)}$

4.1. Algebraic Space ${\mathbb{S}}_{(2;2)}$

The set of complex numbers $\mathbb{C}$ and its 3D extension ${\mathbb{C}}_{(1;2)}$ as defined in the article “Complex Superposition Algebra” 1 are subsets of the algebraic space ${\mathbb{S}}_{(2;2)}$. Here is the commutative table of ${\mathbb{C}}_{(1;2)}$:

Table 3. Commutative table in ${\mathbb{C}}_{(1;2)}$1.

$\times$	1	$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$
1	1	$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$
$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} i}$	-1	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	-$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$
$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	-1	-$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} i}$
$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	-$e^{ {\displaystyle \frac{\pi }{2}} j}$	-$e^{ {\displaystyle \frac{\pi }{2}} i}$	-1	-1
$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}} i}$	-1	-1

Table 3. Commutative table in ${\mathbb{C}}_{(1;2)}$1.

$\times$	1	$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$
1	1	$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$
$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} i}$	-1	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	-$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$
$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	-1	-$e^{ {\displaystyle \frac{\pi }{2}} i}$	$e^{ {\displaystyle \frac{\pi }{2}} i}$
$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$	-$e^{ {\displaystyle \frac{\pi }{2}} j}$	-$e^{ {\displaystyle \frac{\pi }{2}} i}$	-1	-1
$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$	$e^{ {\displaystyle \frac{\pi }{2}} j}$	$e^{ {\displaystyle \frac{\pi }{2}} i}$	-1	-1

The imaginary numbers $i=e^{ {\displaystyle \frac{\pi }{2}} i}$ and $j=e^{ {\displaystyle \frac{\pi }{2}} j}$are the primary bases.

Here we note the appearance of new superimposed imaginary numbers $e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$and$e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$.

To simplify their representation we will note:

➢

$s$ the first superimposed imaginary number $s=e^{ {\displaystyle \frac{\pi }{2}}\left(i+j\right)}$

➢

$t$ the second imaginary superimposed number $t=e^{ {\displaystyle \frac{\pi }{2}}\left(i-j\right)}$.

This will allow us to give the superimposed notation of the imaginary product and consequently of the hyper-complex numbers in

$i=⟨\begin{array}{c}1 \\ 1 \end{array}|\begin{array}{c} 0\\ 1\end{array}⟩$; $j=⟨\begin{array}{c}0 \\ 1 \end{array}|\begin{array}{c} 1\\ 1\end{array}⟩$ ; $s=⟨\begin{array}{c}1 \\ 1\end{array}|\begin{array}{c} 1\\ 1\end{array}⟩$ and $t=⟨\begin{array}{c}1 \\ 1 \end{array}|\begin{array}{c} 1\\ -1\end{array}⟩$

For real numbers we have

Unity $1=⟨\begin{array}{c}0 \\ 1 \end{array}|\begin{array}{c} 0\\ 1\end{array}⟩$ and its opposite $-1=⟨\begin{array}{c} 0 \\ -1 \end{array}|\begin{array}{c} 0\\ 1\end{array}⟩=⟨\begin{array}{c}0 \\ 1 \end{array}|\begin{array}{c} 0\\ -1\end{array}⟩=⟨\begin{array}{c} 0 \\ -1 \end{array}|\begin{array}{c} 0\\ -1\end{array}⟩$

So some will think that it is multiplying the signs – to obtain the number 1; in the writing of the number$⟨\begin{array}{c} 0 \\ -1 \end{array}|\begin{array}{c} 0\\ -1\end{array}⟩$.

What we need to understand here is that this number is the square of the imaginary numbers of level 2, so it is logically negative. This being the very definition of an imaginary number.

Let's note here that this looks a lot like binary code. Some people, like myself, will wonder what binary code is doing in a geometric structure. I keep thinking, dear Euler, how did you discover the imaginary exponential?

But we will come back to this later to give a logical and geometric explanation but above all its possible applications.

In the meantime, let's give an example of calculation

$$i\times j=⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 0\\ 1\end{array} ⟩\times ⟨ \begin{array}{c}0 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array} ⟩$$

$$i\times j=⟨ \begin{array}{c}{f}_1\left(1+0\right) \\ S_1\left(1\right)\times S_1\left(0\right)\times S_1\left(1+0\right)\end{array} | \begin{array}{c} f_2\left(0+1\right)\\ S_2\left(0\right)\times S_2\left(1\right)\times S_2\left(0+1\right)\end{array} ⟩$$

$$i\times j=⟨\begin{array}{c}{f}_1\left(1\right) \\ S_1\left(1\right)\times S_1\left(0\right)\times S_1\left(1\right) \end{array}|\begin{array}{c} f_2\left(1\right)\\ S_2\left(0\right)\times S_2\left(1\right)\times S_2\left(1\right) \end{array}⟩=⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩=s$$

Let us try to calculate the applications $f$and$S$ directly.

$$\left(i\times j\right)\times s=\left(⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 0\\ 1\end{array}⟩\times ⟨ \begin{array}{c}0 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩\right)\times ⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩=⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩\times ⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩=⟨\begin{array}{c} 0 \\ -1 \end{array}|\begin{array}{c} 0\\ -1\end{array}⟩=-1$$

$$i\times \left(j\times s\right)=⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 0\\ 1\end{array}⟩\left(⟨ \begin{array}{c}0 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩\times ⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 1\\ 1\end{array}⟩\right)=⟨ \begin{array}{c}1 \\ 1 \end{array}| \begin{array}{c} 0\\ 1\end{array}⟩\times ⟨ \begin{array}{c}1 \\ 1 \end{array}|\begin{array}{c} 0\\ -1\end{array}⟩=⟨\begin{array}{c} 0 \\ -1 \end{array}|\begin{array}{c} 0\\ -1\end{array}⟩=-1$$

The imaginary product is a binary code generator

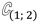
4.2. Algebraic Space ${\mathbb{S}}_{(3;3)}$

To simplify their representation we will note:

❖

Real numbers superposition level 3

➢

$v_r=1=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩$: the real number$v_r$

❖

Its opposite is:

• $-1=⟨ \begin{array}{c} 0\\ -1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩=⟨ \begin{array}{c} 0\\ 1\end{array}|\begin{array}{c} 0\\ -1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ -1\end{array}⟩$: Superposition of level 1
  $-1=⟨ \begin{array}{c} 0\\ -1\end{array}| \begin{array}{c} 0\\ -1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩=⟨ \begin{array}{c} 0\\ -1\end{array}| \begin{array}{c} 0\\ 1\end{array}|\begin{array}{c} 0\\ -1\end{array}⟩=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c} 0\\ -1\end{array}|\begin{array}{c} 0\\ -1\end{array}⟩$: Superposition of level 2
  $-1=⟨ \begin{array}{c} 0\\ -1\end{array}| \begin{array}{c} 0\\ -1\end{array}| \begin{array}{c} 0\\ -1\end{array}⟩$: Superposition of level 3

❖

Imaginary numbers

■

Superposition of level 1

➢

$i_{1;1}=v_{1,i}=e^{ {\displaystyle \frac{\pi }{2}} i_{1;1}}=⟨ \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩$: the first primary imaginary number

➢

$i_{2;1}=v_{2,i}=e^{ {\displaystyle \frac{\pi }{2}} i_{2;1}}=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩$: the second primary imaginary number

➢

$i_{3;1}=v_{3,i}=e^{ {\displaystyle \frac{\pi }{2}} i_{3;1}}=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$: the third primary imaginary number

■

Superposition of level 2

➢

$i_{1;2}=s_{1,i}=e^{ {\displaystyle \frac{\pi }{2}}\left(i_{3;1}+i_{1;1}\right)}=⟨ \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$: the first superimposed imaginary number of level 2

➢

$i_{2;2}=s_{2,i}=e^{ {\displaystyle \frac{\pi }{2}}\left(i_{1;1}+i_{2;1}\right)}=⟨ \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩$: the second superimposed imaginary number of level 2

➢

$i_{3;2}=s_{3,i}=e^{ {\displaystyle \frac{\pi }{2}}\left(i_{2;1}+i_{3;1}\right)}=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$: the third superimposed imaginary number of level 2

➢

$i_{4;2}=s_{4,i}=e^{ {\displaystyle \frac{\pi }{2}}\left(i_{3;1}-i_{1;1}\right)}=⟨ \begin{array}{c} 1\\ -1\end{array}| \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$: the fourth superimposed imaginary number of level 2

➢

$i_{5;2}=s_{5,i}=e^{ {\displaystyle \frac{\pi }{2}}\left(i_{1;1}-i_{2;1}\right)}=⟨ \begin{array}{c}1\\ 1\end{array}|\begin{array}{c} 1\\ -1\end{array}| \begin{array}{c}0\\ 1\end{array}⟩$: the fifth superimposed imaginary number of level 2

➢

$i_{6;2}=s_{6,i}=e^{ {\displaystyle \frac{\pi }{2}}\left(i_{2;1}-i_{3;1}\right)}=⟨ \begin{array}{c}0\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}| \begin{array}{c} 1\\ -1\end{array}⟩$: the sixth superimposed imaginary number of level 2:

■

Superposition of level 3

➢

$i_{1;3}=u_{2,i}=e^{{\displaystyle \frac{\pi }{2}}\left(i_{\mathrm{1,1}}+i_{\mathrm{2,1} }+i_{\mathrm{3,1}}\right)}=⟨ \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$ the first superimposed imaginary number of level 3

➢

$i_{2;3}=u_{1,i}=e^{{\displaystyle \frac{\pi }{2}}\left(i_{\mathrm{3,1}}+i_{\mathrm{1,1}}-i_{\mathrm{2,1} }\right)}=⟨ \begin{array}{c}1\\ 1\end{array}|\begin{array}{c} 1\\ -1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$ the second superimposed imaginary number of level 3

➢

$i_{3;3}=u_{3,i}=e^{{\displaystyle \frac{\pi }{2}}\left(i_{\mathrm{1,1}}+i_{\mathrm{2,1}}-i_{\mathrm{3,1}}\right)}=⟨ \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}|\begin{array}{c} 1\\ -1\end{array}⟩$the third superimposed imaginary number of level 3

➢

$i_{4;3}=u_{4,i}=e^{{\displaystyle \frac{\pi }{2}}\left(i_{\mathrm{2,1}}+i_{\mathrm{3,1}}-i_{\mathrm{1,1}}\right)}=⟨\begin{array}{c} 1\\ -1\end{array}| \begin{array}{c}1\\ 1\end{array}| \begin{array}{c}1\\ 1\end{array}⟩$the fourth superimposed imaginary number of level 3

The imaginary number $i_{n;p}$will designate the nth superimposed imaginary number of level p

Calculation example:

$$i_{2;2}\times i_{3;3}=⟨ \begin{array}{c}1\\ 1\end{array} | \begin{array}{c}1\\ 1\end{array} | \begin{array}{c}0\\ 1\end{array} ⟩\times ⟨ \begin{array}{c}1\\ 1\end{array} | \begin{array}{c}1\\ 1\end{array} |\begin{array}{c} 1\\ -1\end{array}⟩=⟨ \begin{array}{c} 0\\ -1\end{array} | \begin{array}{c} 0\\ -1\end{array} |\begin{array}{c} 1\\ -1\end{array}⟩=-i_{3;1}$$

Here we must note that the result is level 1 superposition. The associated negative real number of$⟨ \begin{array}{c}0\\ 1\end{array} | \begin{array}{c}0\\ 1\end{array} |\begin{array}{c} 1\\ -1\end{array}⟩$is$⟨\begin{array}{c} 0\\ -1\end{array} |\begin{array}{c} 0\\ -1\end{array} |\begin{array}{c} 0\\ 1\end{array} ⟩$; so we have:

$$-1\times i_{3;1}=⟨\begin{array}{c} 0\\ -1\end{array} |\begin{array}{c} 0\\ -1\end{array} |\begin{array}{c} 0\\ 1\end{array} ⟩\times ⟨ \begin{array}{c}0\\ 1\end{array} | \begin{array}{c}0\\ 1\end{array} |\begin{array}{c} 1\\ -1\end{array}⟩=⟨ \begin{array}{c} 0\\ -1\end{array} | \begin{array}{c} 0\\ -1\end{array} |\begin{array}{c} 1\\ -1\end{array} ⟩$$

Which means that in the table established in the article "Complex Superposition Algebra" 1; we must make some modification related to the rules of superposition of signs. However this table is indeed commutative; the negative signs have been multiplied between them so in some related to the de-superposition we will have an inversion of the sign. The new rules established show that the imaginary product is commutative and associative. So there is no longer the need to establish a table related to commutativity or associativity for real and imaginary products.

5. Logical and Physical Interpretation:

This superimposed binary product models a regular logical operator in a leveled superposition space. The preservation of fundamental algebraic properties opens a path towards a representation of qbits and tbits in a discrete geometric structure, where each level encodes an extended binary logic.

6. Conclusion

We have introduced a superimposed hyper-complex multiplication that maintains the essential algebraic properties of commutativity and associativity, even in higher-dimensional settings. This advancement lays the groundwork for a logical and geometric formalization of quantum operators beyond the traditional complex state space. The proposed structure bridges binary logic and geometric representation in a unified framework.

7. Perspectives

Future work will explore how this algebraic framework naturally integrates quantum concepts such as superposition, spin, and dynamic evolution. By extending the current structure, we aim to develop a more comprehensive model of quantum systems rooted in discrete geometric and logical operations.