Submitted:
09 June 2025
Posted:
10 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Background of the Study
2. Literature Review
2.1. Integration Market
2.2. Cryptocurrencies as a Safe Haven and Hedging
2.3. Risk Spillover
3. Methodology of the study
3.1. ARFIRMA-EGARCH
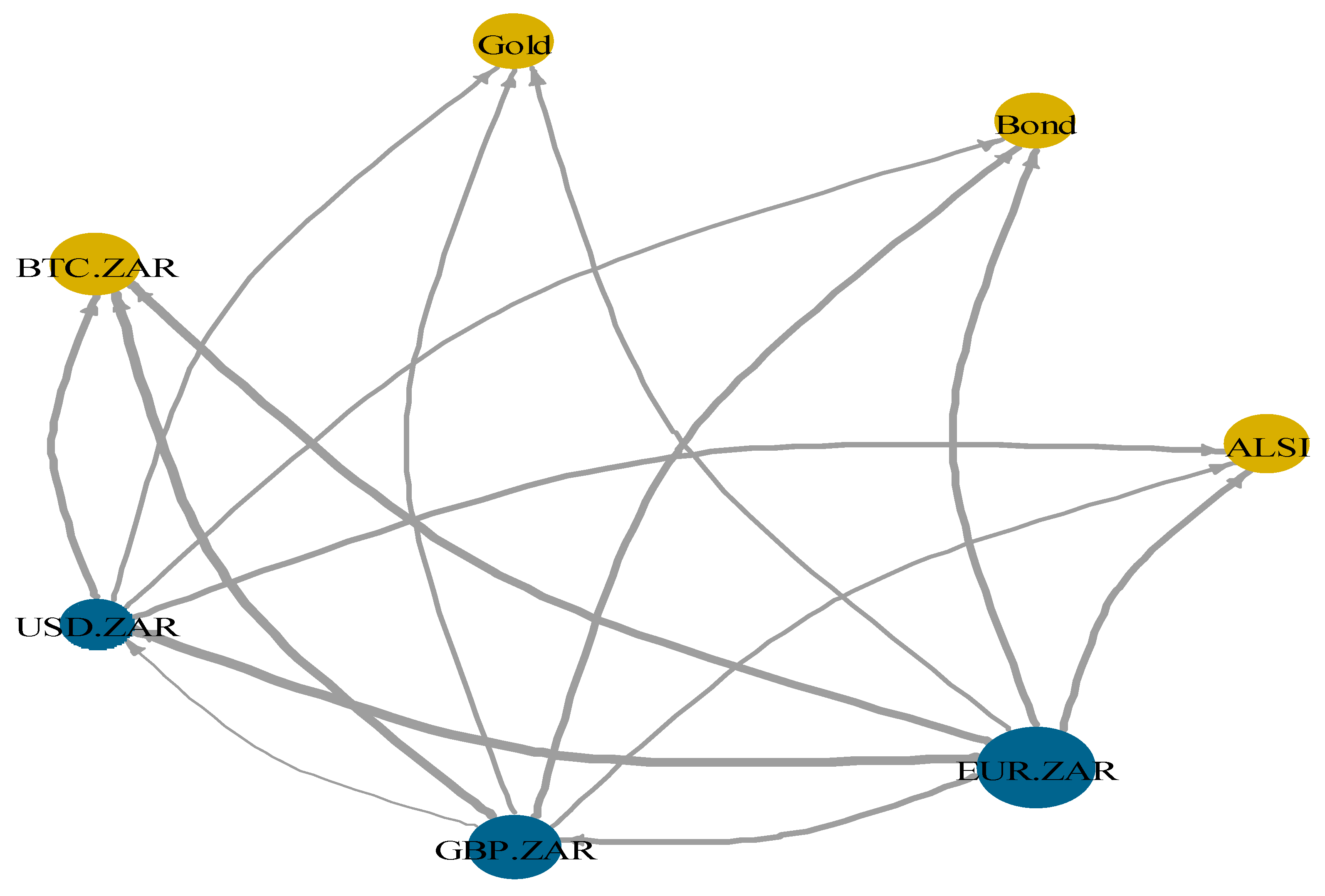
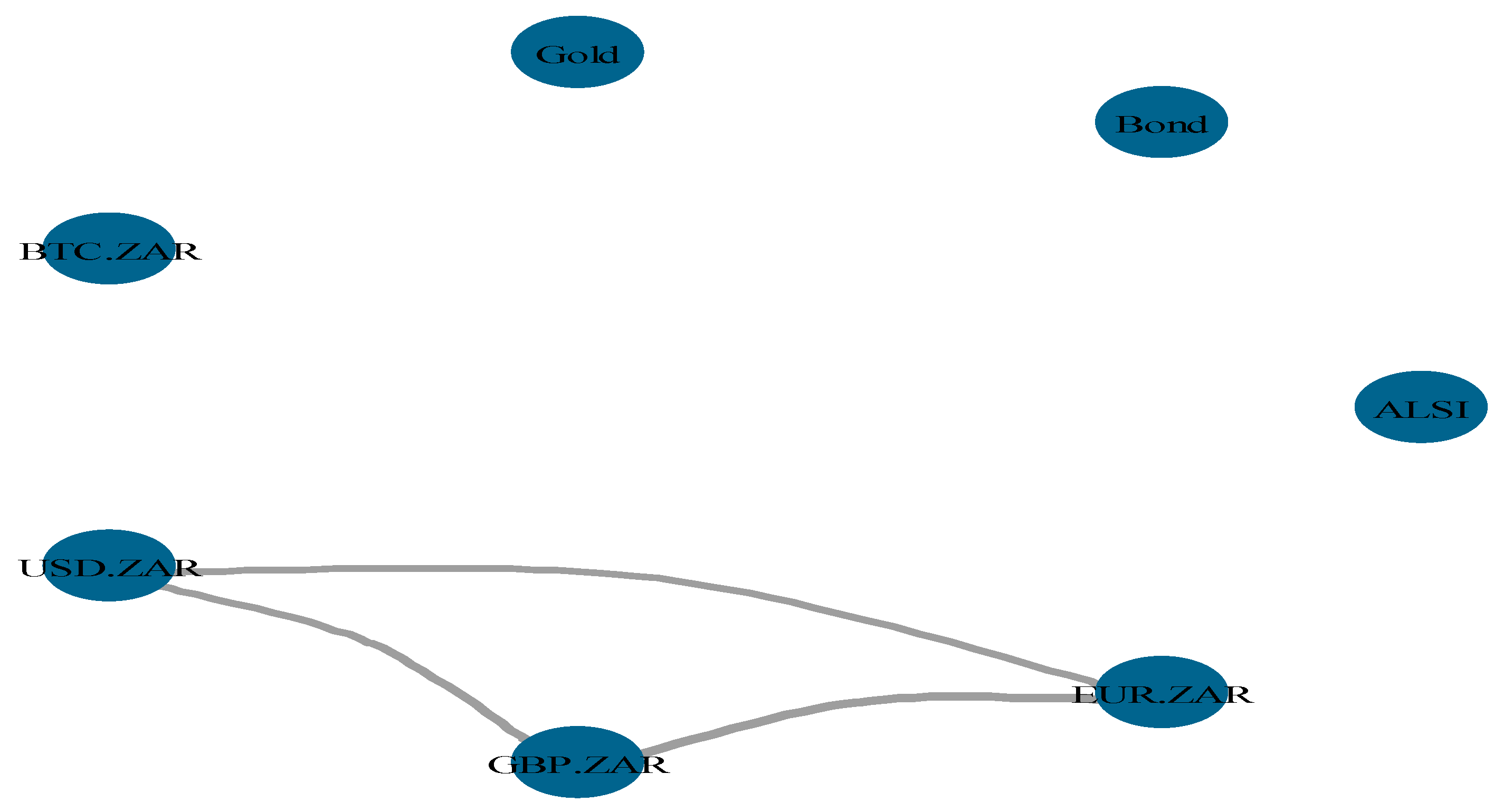
3.2. Measuring Connectedness
3.3. Connectedness Network Measures
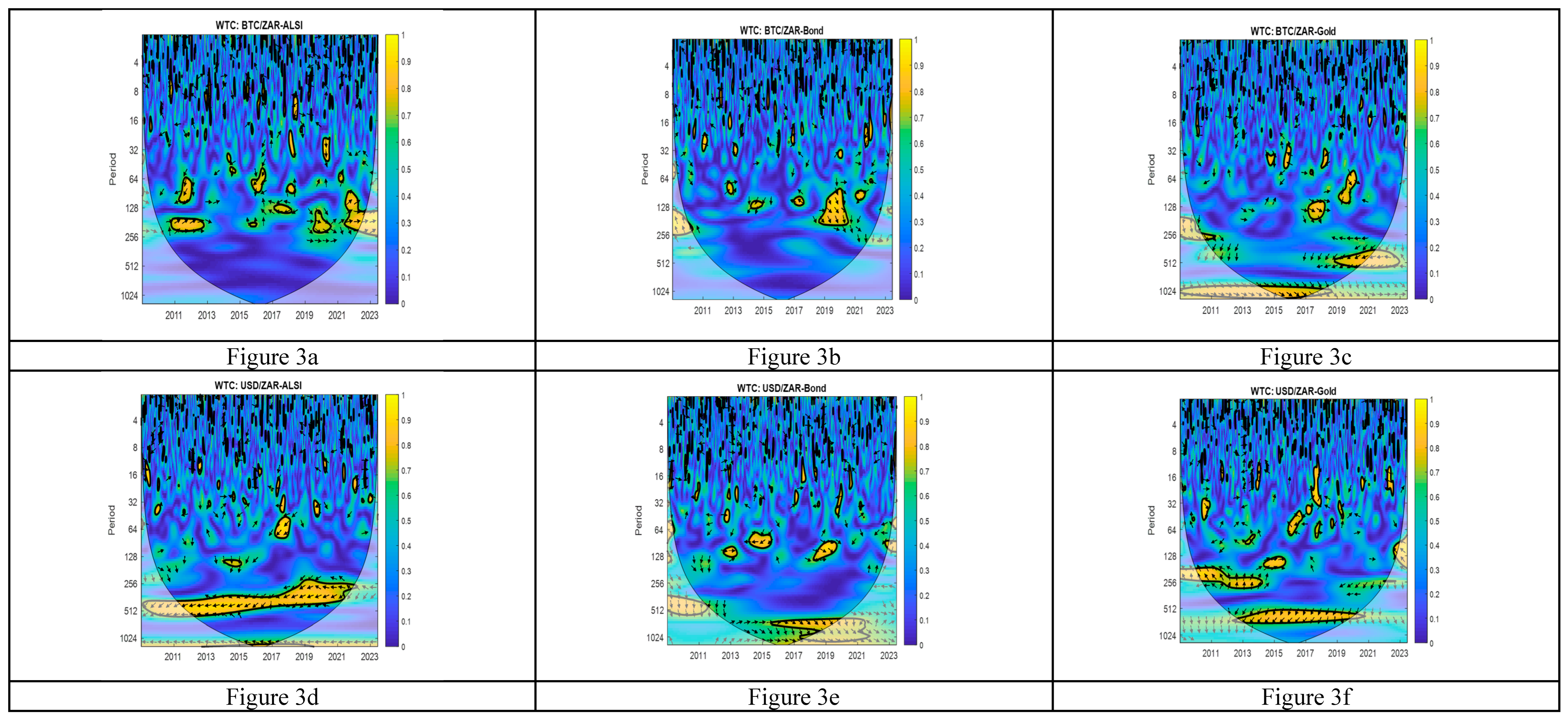
3.4. Wavelet-Squared Coherence
3.5. Wavelet Transform Coherence (WTC)
4. Empirical Results and Discussion
4.1. Data Analysis
4.2. Statistic Descriptive Results
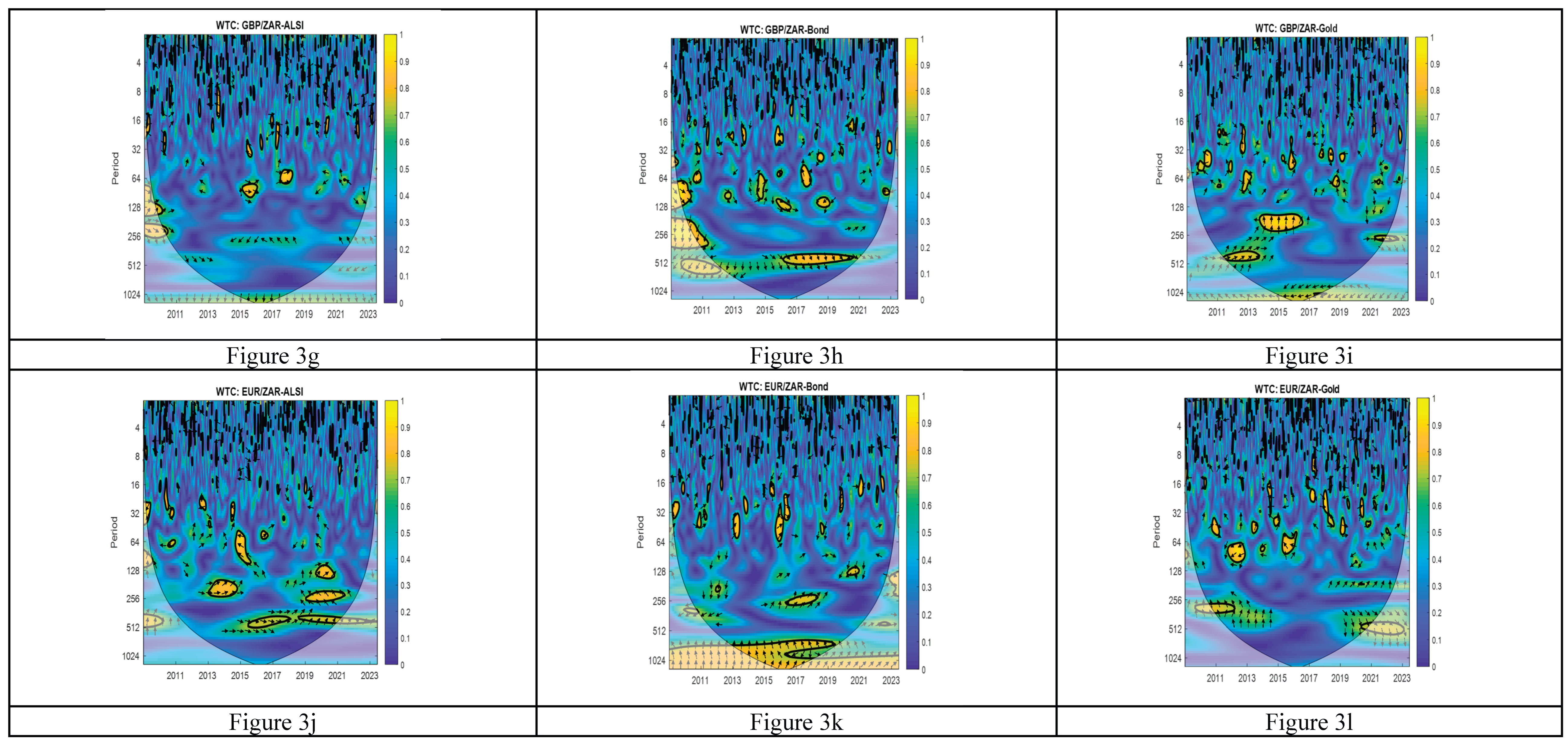
5. Conclusion and Policy Recommendations
| 1 | USD/ZAR, GBP/ZAR, and EUR/ZAR |
| 2 | All share index (ALSI), bonds, and gold |
| 3 | ALSI, Bond, Gold, USD/ZAR, EUR/ZAR, GBP/ZAR |
References
- (Adelowotan, 2024) Adelowotan, M. (2024). Exploring the development of regulatory framework for crypto assets in South Africa. The Business and Management Review, 15, p.75. [CrossRef]
- (Akhtaruzzaman et al., 2022) Akhtaruzzaman, M., Boubaker, S., Nguyen, D.K. and Rahman, M.R. (2022). Systemic risk-sharing framework of cryptocurrencies in the COVID–19 crisis. Finance Research Letters, 47, p.102787. [CrossRef]
- (Alvarez-Ramirez & Rodriguez, 2021) Alvarez-Ramirez, J. and Rodriguez, E. (2021). A singular value decomposition approach for testing the efficiency of Bitcoin and Ethereum markets. Economics Letters, 206, p.109997. [CrossRef]
- (Andrada-Félix et al., 2020) Andrada-Félix, J., Fernandez-Perez, A. and Sosvilla-Rivero, S. (2020). Distant or close cousins: Connectedness between cryptocurrencies and traditional currencies' volatilities. Journal of International Financial Markets, Institutions and Money, 67, p.101219. [CrossRef]
- (Antonakakis et al., 2020) Antonakakis, N., Chatziantoniou, I. and Gabauer, D. (2020). Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. Journal of Risk and Financial Management, 13(4), p.84. [CrossRef]
- (Arouri et al., 2011) Arouri, M. E. H., Jouini, J. & Nguyen, D. K., (2011). Volatility spillovers between oil prices and stock sector returns: Implications for portfolio management. Journal of International Money and Finance, Volume 30, p. 1387–1405. [CrossRef]
- (Baur & Dimpfl, 2021) Baur, D.G. and Dimpfl, T. (2021). The volatility of Bitcoin and its role as a medium of exchange and a store of value. Empirical Economics, 61(5), pp.2663-2683. [CrossRef]
- (Bhuiyan et al., 2023) Bhuiyan, R.A., Husain, A. and Zhang, C. (2023). Diversification evidence of Bitcoin and Gold from wavelet analysis. Financial Innovation, 9(1), p.100. [CrossRef]
- (Bloomfield et al., 2004) Bloomfield, D. Shaun, RT James McAteer, Bruce W. Lites, Philip G. Judge, Mihalis Mathioudakis, and Francis P. Keenan. (2004). Wavelet Phase Coherence Analysis: Application to a Quiet-Sun Magnetic. The Astrophysical Journal 617: 623–32.
- (Bonga-Bonga & Khalique, 2023) Bonga-Bonga, L. and Khalique, M. (2023). The dynamic relationship between digital currency and other financial markets in developed and emerging markets. Available at SSRN 4790892.
- (Bouri et al., 2020) Bouri, E., Shahzad, S.J.H. and Roubaud, D. (2020). Cryptocurrencies as hedges and safe-havens for US equity sectors. The Quarterly Review of Economics and Finance, 75, pp.294-307. [CrossRef]
- (Chang et al., 2013) Chang, C.-L., McAleer, M. & Tansuchat, R. (2013). Conditional correlations and volatility spillovers between crude oil and stock index returns. The North American Journal of Economics and Finance, Volume 25, pp. 116-138. [CrossRef]
- (Chatziantoniou & Gabauer, 2021) Chatziantoniou, I. and Gabauer, D. (2021). EMU risk-synchronisation and financial fragility through the prism of dynamic connectedness. The Quarterly Review of Economics and Finance, 79, pp.1-14. [CrossRef]
- (Chen & Sun, 2024) Chen, B.X. and Sun, Y.L. (2024). Risk characteristics and connectedness in cryptocurrency markets: New evidence from a non-linear framework. The North American Journal of Economics and Finance, 69, p.102036. [CrossRef]
- (Corbet et al., 2020) Corbet, S., Larkin, C. and Lucey, B. (2020). The contagion effects of the COVID-19 pandemic: Evidence from Gold and cryptocurrencies. Finance Research Letters, 35, p.101554. [CrossRef]
- (Diebold & Yilmaz, 2012) Diebold, F.X. and Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting, 28(1), pp.57-66. [CrossRef]
- (Diebold & Yilmaz, 2014) Diebold, F.X. and Yılmaz, K. (2014). On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics, 182(1), pp.119-134. [CrossRef]
- (Engle & Granger, 1987) Engle, R.F. and Granger, C.W. (1987). Co-integration and error correction: representation, estimation, and testing. Econometrica: journal of the Econometric Society, pp.251-276. [CrossRef]
- (Gajardo et al., 2018) Gajardo, G., Kristjanpoller, W.D. and Minutolo, M., (2018). Does Bitcoin exhibit the same asymmetric multifractal cross-correlations with crude oil, Gold and DJIA as the Euro, Great British Pound and Yen?. Chaos, Solitons & Fractals, 109, pp.195-205. [CrossRef]
- (Giannellis, 2022) Giannellis, N. (2022). Cryptocurrency market connectedness in Covid-19 days and the role of Twitter: Evidence from a smooth transition regression model. Research in International Business and Finance, 63, p.101801. [CrossRef]
- (Gil-Alana et al., 2020) Gil-Alana, L.A., Abacha, E.J.A. and Rojo, M.F.R. (2020). Cryptocurrencies and stock market indices. Are they related?. Research in International Business and Finance, 51, p.101063.
- (Gopane, 2022) Gopane, T.J. (2022). Volatility behaviour of Bitcoin as a digital asset: evidence of shock transmission dynamics from the South African financial markets. Journal of Telecommunications and the Digital Economy, 10(2), pp.195-213.
- (Granger & Joyeux, 1980) Granger, C.W. and Joyeux, R., (1980). An introduction to long-memory time series models and fractional differencing. Journal of time series analysis, 1(1), pp.15-29. [CrossRef]
- (Granger, 1980) Granger, C.W. (1980). Long memory relationships and the aggregation of dynamic models. Journal of Econometrics, 14(2), pp.227-238.
- (Greeff, 2019) Greeff, C. (2019). An investigation into the output tax consequences of Bitcoin transactions for a South African value-added tax vendor. South African Journal of Economic and Management Sciences, 22(1), pp.1-9. [CrossRef]
- (Grubel, 1968) Grubel, H.G. (1968). Internationally diversified portfolios: welfare gains and capital flows. The American Economic Review, pp.1299-1314.
- (Harwick, 2016) Harwick, C. (2016). Cryptocurrency and the problem of intermediation. The Independent Review, 20(4), pp.569-588.
- (Hoque et al., 2023) Hoque, M.E., Soo-Wah, L., Tiwari, A.K. and Akhter, T. (2023). Time and frequency domain connectedness and spillover among categorical and regional financial stress, Gold and Bitcoin market. Resources Policy, 85, p.103786. [CrossRef]
- (Hosking, 1981) Hosking, J.R.M., (1981). Equivalent forms of the multivariate portmanteau statistic. Journal of the Royal Statistical Society Series B: Statistical Methodology, 43(2), pp.261-262.
- (Hsu et al., 2021) Hsu, S.H., Sheu, C. and Yoon, J. (2021). Risk spillovers between cryptocurrencies and traditional currencies and Gold under different global economic conditions. The North American Journal of Economics and Finance, 57, p.101443. [CrossRef]
- (Hung, 2022) Hung, N.T. (2022). Asymmetric connectedness among S&P 500, crude oil, Gold and Bitcoin. Managerial Finance, 48(4), pp.587-610.
- (Ibrahim et al., 2024) Ibrahim, B.A., Elamer, A.A., Alasker, T.H., Mohamed, M.A. and Abdou, H.A. (2024). Volatility contagion between cryptocurrencies, Gold and stock markets pre-and-during COVID-19: evidence using DCC-GARCH and cascade-correlation network. Financial Innovation, 10(1), p.104. [CrossRef]
- (Jankeeparsad & Tewari, 2022) Jankeeparsad, R.W. and Tewari, D. (2022). Bitcoin: an exploratory study investigating adoption in South Africa. Interdisciplinary Journal of Information, Knowledge & Management, 17. [CrossRef]
- (Jeleskovic et al., 2023) Jeleskovic, V., Latini, C., Younas, Z.I. and Al-Faryan, M.A. (2023). Optimization of portfolios with cryptocurrencies: Markowitz and GARCH-Copula model approach. arXiv preprint arXiv:2401.00507.
- (Jeribi & Fakhfekh, 2021) Jeribi, A. and Fakhfekh, M. (2021). Portfolio management and dependence structure between cryptocurrencies and traditional assets: evidence from FIEGARCH-EVT-Copula. Journal of Asset Management, 22(3), pp.224-239. [CrossRef]
- (Ji et al., 2019) Ji, Q., Bouri, E., Lau, C.K.M. and Roubaud, D. (2019). Dynamic connectedness and integration in cryptocurrency markets. International Review of Financial Analysis, 63, pp.257-272. [CrossRef]
- (Kang et al., 2019) Kang, S.H., McIver, R.P. and Hernandez, J.A. (2019). Co-movements between Bitcoin and Gold: A wavelet coherence analysis. Physica A: Statistical Mechanics and its Applications, 536, p.120888. [CrossRef]
- (Katsiampa et al., 2019) Katsiampa, P., Corbet, S. and Lucey, B. (2019). High frequency volatility co-movements in cryptocurrency markets. Journal of International Financial Markets, Institutions and Money, 62, pp.35-52. [CrossRef]
- (Koop et al., 1996) Koop, G., Pesaran, M.H. and Potter, S.M. (1996). Impulse response analysis in nonlinear multivariate models. Journal of econometrics, 74(1), pp.119-147. [CrossRef]
- (Koutmos et al., 2021) Koutmos, D., King, T. and Zopounidis, C. (2021). Hedging uncertainty with cryptocurrencies: Is Bitcoin your best bet?. Journal of Financial Research, 44(4), pp.815-837. [CrossRef]
- (Kumah & Odei-Mensah, 2021) Kumah, S.P. and Odei-Mensah, J. (2021). Are Cryptocurrencies and African stock markets integrated?. The Quarterly Review of Economics and Finance, 81, pp.330-341. [CrossRef]
- (Kumah et al., 2022) Kumah, S.P., Odei-Mensah, J. and Baaba Amanamah, R. (2022). Co-movement of cryptocurrencies and African stock returns: A multiresolution analysis. Cogent Business & Management, 9(1), p.2124595. [CrossRef]
- (Li et al., 2020) Li, Z., Wang, Y. and Huang, Z. (2020). Risk connectedness heterogeneity in the cryptocurrency markets. Frontiers in Physics, 8, p.243. [CrossRef]
- (Lose & Kalitanyi, 2025) Lose, A. and Kalitanyi, V. (2025). Regulating and Monitoring Challenges in Compliance of Cryptocurrencies in South Africa. The Journal of Developing Areas, 59(2), pp.291-299. [CrossRef]
- (Maghyereh & Abdoh, 2022) Maghyereh, A. and Abdoh, H. (2022). COVID-19 and the volatility interlinkage between Bitcoin and financial assets. Empirical Economics, 63(6), pp.2875-2901. [CrossRef]
- (Maiti et al., 2020) Maiti, M., Vukovic, D., Krakovich, V. and Pandey, M.K. (2020). How integrated are cryptocurrencies. International Journal of Big Data Management, 1(1), pp.64-80.
- (Mariana et al., 2021) Mariana, C.D., Ekaputra, I.A. and Husodo, Z.A. (2021). Are Bitcoin and Ethereum safe-havens for stocks during the COVID-19 pandemic?. Finance research letters, 38, p.101798. [CrossRef]
- (Mensi et al., 2019) Mensi, W., Rehman, M.U., Al-Yahyaee, K.H., Al-Jarrah, I.M.W. and Kang, S.H. (2019). Time frequency analysis of the commonalities between Bitcoin and major Cryptocurrencies: Portfolio risk management implications. The North American Journal of Economics and Finance, 48, pp.283-294. [CrossRef]
- (Milne & Lawack, 2024) Milne, A. and Lawack, V. (2024). Digital assets in payments and transaction banking (No. 11073).
- (Milunovich, 2018) Milunovich, G. (2018). Cryptocurrencies, mainstream asset classes and risk factors: A study of connectedness. Australian Economic Review, 51(4), pp.551-563. [CrossRef]
- (Msomi & Nyandeni, 2025) Msomi, S. and Nyandeni, A. (2025). Spillover effects and hedging abilities of cryptocurrencies: a case of the South African market. International Journal of Blockchains and Cryptocurrencies, 6(1), pp.42-68.
- (Naeem et al., 2021) Naeem, M.A., Farid, S., Balli, F. and Hussain Shahzad, S.J. (2021). Hedging the downside risk of commodities through cryptocurrencies. Applied Economics Letters, 28(2), pp.153-160. [CrossRef]
- (Nakamoto, 2008) Nakamoto, S. (2008). A peer-to-peer electronic cash system. Bitcoin.–URL: https://Bitcoin. Org/Bitcoin. Pdf, 4(2), p.15.
- (Ndlovu & Chikobvu, 2023) Ndlovu, T. and Chikobvu, D. (2023). A Wavelet-Decomposed WD-ARMA-GARCH-EVT Model Approach to Comparing the Riskiness of the Bitcoin and South African Rand Exchange Rates. Data, 8(7), p.122. [CrossRef]
- (Nelson, 1991) Nelson, D.B. (1991). Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the Econometric Society, pp.347-370.
- (Okonkwo et al., 2021) Okonkwo, C., Osu, B.O., Chighoub, F. and Oruh, B.I. (2021). The co-movement of Bitcoin and some African currencies–A wavelet analysis. Journal of Research in Emerging Markets. [CrossRef]
- (Pesaran & Shin, 1998) Pesaran, H.H. and Shin, Y., (1998). Generalized impulse response analysis in linear multivariate models. Economics Letters, 58(1), pp.17-29. [CrossRef]
- (Pukthuanthong & Roll, 2009) Pukthuanthong, K. and Roll, R. (2009). Global market integration: An alternative measure and its application. Journal of Financial Economics, 94(2), pp.214-232. [CrossRef]
- (Sebastião & Godinho, 2020) Sebastião, H. and Godinho, P. (2020). Bitcoin futures: An effective tool for hedging cryptocurrencies. Finance Research Letters, 33, p.101230. [CrossRef]
- (Shahzad et al., 2022) Shahzad, S.J.H., Balli, F., Naeem, M.A., Hasan, M. and Arif, M. (2022). Do conventional currencies hedge cryptocurrencies? The Quarterly Review of Economics and Finance, 85, pp.223-228.
- (Shahzad et al., 2019) Shahzad, S.J.H., Bouri, E., Roubaud, D., Kristoufek, L. and Lucey, B. (2019). Is Bitcoin a better safe-haven investment than Gold and commodities?. International Review of Financial Analysis, 63, pp.322-330. [CrossRef]
- (Shahzad et al., 2021) Shahzad, S.J.H., Naeem, M.A., Peng, Z. and Bouri, E. (2021). Asymmetric volatility spillover among Chinese sectors during COVID-19. International Review of Financial Analysis, 75, p.101754. [CrossRef]
- (Shahzad et al., 2023) Shahzad, U., Mohammed, K.S., Tiwari, S., Nakonieczny, J. and Nesterowicz, R. (2023). Connectedness between geopolitical risk, financial instability indices and precious metals markets: Novel findings from Russia Russia-Ukraine conflict perspective. Resources Policy, 80, p.103190.
- (Reddy & Lawack, 2019 ) Reddy, E. and Lawack, V. (2019). An overview of the regulatory developments in South Africa regarding the use of cryptocurrencies. SA Mercantile Law Journal, 31(1), pp.1-28.
- (Rehman et al., 2024) Rehman, S.U., Ahmad, T., Desheng, W.D. and Karamoozian, A. (2024). Analyzing selected cryptocurrencies' spillover effects on global financial indices: Comparing risk measures using conventional and eGARCH-EVT-Copula approaches. arXiv preprint arXiv: 2407.15766.
- ((Tiwari et al., 2013) Tiwari, A.K., Dar, A.B., Bhanja, N. and Shah, A. (2013). Stock market integration in Asian countries: Evidence from wavelet multiple correlations. Journal of Economic Integration, pp.441-456. [CrossRef]
- (Torrence & Webster, 1999) Torrence, Christopher, and Peter J. Webster. (1999). Interdecadal Changes in the ENSO–Monsoon System. Journal of Climate 12: 2679–90.
- (Urquhart & Zhang, 2019) Urquhart, A. and Zhang, H., 2(019). Is Bitcoin a hedge or safe haven for currencies? An intraday analysis. International Review of Financial Analysis, 63, pp.49-57. [CrossRef]
- (Wang & Wang, 2011) Wang, P. and Wang, P. (2011). Asymmetry in return reversals or asymmetry in volatilities?—New evidence from new markets. Quantitative finance, 11(2), pp. 271-285.
- (Wang et al., 2019) Wang, P., Zhang, W., Li, X. and Shen, D., 2019. Is cryptocurrency a hedge or a safe-haven for international indices? A comprehensive and dynamic perspective. Finance Research Letters, 31, pp.1-18. [CrossRef]
- (Wątorek et al., 2023) Wątorek, M., Kwapień, J. and Drożdż, S. (2023). Cryptocurrencies are becoming part of the world global financial market. Entropy, 25(2), p.377. [CrossRef]
- (Wiesen et al., 2018) Wiesen, T.F., Beaumont, P.M., Norrbin, S.C. and Srivastava, A. (2018). Are generalized spillover indices overstating connectedness?. Economics Letters, 173, pp.131-134. [CrossRef]
- (Wu , 2021) Wu, S. (2021). Co-movement and return spillover: Evidence from Bitcoin and traditional assets. SN Business & Economics, 1(10), p.122. [CrossRef]
- (Wu et al., 2019) Wu, S., Tong, M., Yang, Z. and Derbali, A. (2019). Does Gold or Bitcoin hedge economic policy uncertainty? Finance Research Letters, 31, pp.171-178.
- (Xu et al., 2021) Xu, Q., Zhang, Y. and Zhang, Z. (2021). Tail-risk spillovers in cryptocurrency markets. Finance Research Letters, 38, p.101453. [CrossRef]
- (Yi et al., 2018) Yi, S., Xu, Z. and Wang, G.J. (2018). Volatility connectedness in the cryptocurrency market: Is Bitcoin a dominant cryptocurrency? International Review of Financial Analysis, 60, pp.98-114.
- (Zeng & Ahmed, 2023) Zeng, H. and Ahmed, A.D. (2023). Market integration and volatility spillover across major East Asian stock and Bitcoin markets: an empirical assessment. International Journal of Managerial Finance, 19(4), pp.772-802. [CrossRef]
- (Zięba et al., 2019) Zięba, D., Kokoszczyński, R. and Śledziewska, K. (2019). Shock transmission in the cryptocurrency market. Is Bitcoin the most influential?. International Review of Financial Analysis, 64, pp.102-125. [CrossRef]
| ALSIr | Bondr | Goldr | BTC/ZARr | GBP/ZARr | USD/ZARr | EUR/ZARr | |
| Mean | 0.000323 | -1.22E-05 | 0.000230 | 0.002483 | 0.000177 | 0.000254 | 0.000177 |
| Median | 0.000479 | 0.000000 | 0.000307 | 0.001866 | -0.000207 | -0.000105 | -0.000154 |
| Std. Dev. | 0.010269 | 0.009241 | 0.009969 | 0.049487 | 0.008919 | 0.009580 | 0.008792 |
| Skewness | -0.119433 | 0.732539 | -0.307999 | -0.273970 | 0.214797 | 0.263403 | 0.372391 |
| Kurtosis | 4.571204 | 12.16870 | 6.593023 | 11.66077 | 4.247051 | 3.988566 | 4.783945 |
| Jarque-Bera | 380.1235 | 12974.84 | 2000.035 | 11334.03 | 261.8231 | 188.8456 | 562.4425 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Variables | ARCH (3) | |||||||
| ALSI | -0.0002 (0.0001) |
0.0687*** (0.0154) |
-0.4370*** (0.0198) |
0.0322** (0.0126) |
0.9542*** (0.0020) |
0.16014*** (0.0201) |
4.9954*** (0.4071) |
0.1081 [0.7423] |
| Bond | 0.0003*** (0.0001) |
-0.0384** (0.0150) |
-0.0892*** (0.0066) |
0.0181** (0.0089) |
0.9703*** (0.0007) |
0.0849** (0.0365) |
4.0719*** (0.5057) |
0.3670 [0.5446] |
| Gold | 0.0020*** (0.0005) |
0.0090 (0.0163) |
-1.4517*** (0.1263) |
0.0348*** (0.0040) |
0.7436*** (0.0209) |
0.6231*** (0.0708) |
2.5390*** (0.1399) |
0.0003 [0.9851] |
| BTC/ZAR | 0.0003** (0.0001) |
-0.0054 (0.0168) |
-0.1237*** (0.0012) |
0.0429*** (0.0080) |
0.9868*** (0.0004) |
0.0758*** (0.0023) |
13.7971*** (2.5556) |
0.4051 [0.5245] |
| USD/ZAR | 0.0021*** (0.0002) |
-0.0012 (0.0169) |
-0.2315*** (0.0005) |
0.0278*** (0.0096) |
0.9756*** (0.0002) |
0.1025*** (0.0054) |
8.8175*** (1.1316) |
3.1200 [0.0773] |
| GBP/ZAR | 0.0004*** (0.0001) |
0.0119 (0.0173) |
-0.3521*** (0.0066) |
0.0391*** (0.0109) |
0.9632*** (0.0007) |
0.1274*** (0.0127) |
8.4339*** (1.0224) |
0.1555 [0.693] |
| EUR/ZAR | 0.0003*** (0.0001) |
0.9165*** (0.0015) |
-0.9265*** (0.0055) |
0.0525*** (0.0053) |
0.9590*** (0.0023) |
0.0460*** (0.0090) |
14.9380*** (3.3820) |
0.4625 [0.4964] |
| ALSI | Bond | Gold | BTC/ZAR | USD/ZAR | GBP/ZAR | EUR./ZAR | FROM | |
| ALSI | 94.49 | 0.95 | 0.96 | 1.15 | 0.88 | 0.71 | 0.85 | 5.51 |
| Bond | 0.78 | 93.96 | 1.21 | 0.83 | 0.95 | 1.13 | 1.13 | 6.04 |
| Gold | 0.99 | 1.36 | 94.33 | 0.97 | 0.82 | 0.77 | 0.76 | 5.67 |
| BTC/ZAR | 1.08 | 0.82 | 0.93 | 93.75 | 1.07 | 1.15 | 1.21 | 6.25 |
| USD/ZAR | 0.36 | 0.50 | 0.44 | 0.52 | 42.12 | 27.28 | 28.78 | 57.88 |
| GBP/ZAR | 0.31 | 0.52 | 0.37 | 0.44 | 26.97 | 41.72 | 29.68 | 58.28 |
| EUR/ZAR | 0.34 | 0.54 | 0.42 | 0.43 | 28.00 | 29.21 | 41.05 | 58.95 |
| TO | 3.86 | 4.69 | 4.33 | 4.35 | 58.69 | 60.26 | 62.41 | 198.59 |
| TCI | ||||||||
| NET | -1.66 | -1.35 | -1.34 | -1.90 | 0.81 | 1.98 | 3.46 | 28.37 |
| NPT | 1.00 | 2.00 | 0.00 | 3.00 | 4.00 | 5.00 | 6.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





