1. Introduction
The traditional understanding of the universe is anchored in a three-dimensional model of space coupled to time. However, this model shows limitations when confronted with phenomena such as galactic rotation curves, which suggest the presence of invisible matter. This theory presents an alternative: that such effects are products of vector stresses accumulated in folded and hidden dimensional layers, whose presence stabilizes the visible space-time.
Contemporary physics, even in its most advanced forms, remains anchored in a reality model structured by three spatial dimensions and a temporal 3+1 model proposed by classical physics. This framework has been sufficient to describe the main phenomena of gravity, light and cosmic expansion. However, anomalies that challenge its completeness persist: the acceleration of the expansion of the universe, the rotational stability of galaxies and the absence of ontological explanations for what we call "vacuum". In this scenario, there is a need to reformulate not only the constituent elements of matter and energy, but the very structure of space-time.
The Theory of the Invisible Structure of Time and the Hidden Dimensions as Support of Reality arises as a structural and ontological response to these failures. Its fundamental principle is that the universe is not only what you see or measure directly, but what sustains - even invisibly. Thus, the visible space-time is treated as an apparent mesh, supported internally by folded vector layers, organized tension structures that remain hidden to the sensory and instrumental apparatus, but which can be simulated mathematically.
This theory is based on the postulate:
where ω represents the local vector angular frequency of a dimensional cell and ε_{-}ε represents its vector resistance to collapse. The product of an inverse vector constant symbolizes a dynamic balance between curvature and restraint. When one of the variables increases (as occurs at the edge of a galaxy or in an accelerated expansion), the other reacts compensatively to preserve dimensional integrity. This behavior can be interpreted as a
vector mechanism of self-regulation of reality.
The universe, then, is seen as a system tensed by internal vector folds that contract, resist and expand not by chance, but by invisible structural laws. This folded structure not only supports the fabric of space-time - it is the fabric itself . What we see as continuous and flat is actually the average expression of a folded and compressed system.
To broaden the understanding of these concepts, we use physical and geometric analogies that make it possible to visualize the logic of TEITDO as Support of Reality:
The corrugated paper, whose strength is not in the thickness of the paper, but in the trapped air and internal folds. Just like the vacuum of TEITDO as Reality Support, corrugated paper is seemingly fragile but structurally stable due to its invisible architecture.
The pomegranate, fruit that expresses a fractal, radial and densified internal organization. Its geometry evidences a natural distribution of internal chambers and an organizing redundancy topology, reflecting how the hidden dimensions of TEITDOse project themselves into the universe, not out.
The cube, symbol of the classical limitation of Euclidean space, but here reinterpreted as an internal vector tension box. In its appearance, it is finite and flat. But when treated vectorally, it is profound, multiple and dynamic.
The vector mesh, metaphor of the autoregulated totality. Each node of the mesh represents a tensioned dimensional cell. The mesh vibrates, pulsates, collapses and rebuilds itself in dynamic equilibrium with the vector forces that compose it - ω and ε varepsilon_{-}ε .
The structure of the universe, in this model, does not need the insertion of dark matter or dark energy as explanatory mechanisms. What is observed in the galactic rotation curves, for example, can be perfectly reproduced by the accumulation of folded vector stresses on the periphery of simulated dimensional meshes . The space itself ceases to be an inert stage to become a living, vibratory, reactive agent.
Based on this principle, the TEITDO model as Reality Support was submitted to numerical simulations. First in 2D, showing the local variations of the vector mesh under gravitational compression. Then in 3D, with 30 dimensions overlaid - each modulating the angular tension of a specific layer. And finally, in 4D, simulating time as a continuous pulse of deformation and self-regulation. In these representations, we visualize the galactic curve emerging as a direct response of the internal vector mesh - without the need for exotic entities.
Such results support that the observable reality itself is only a superficial response of a deeper, dynamic, bent structural background. And this structure is falsifiable: if the predictions about vector tension can be measured - for example, in gravitational lensing without visible mass - then its postulate can be confronted directly with the universe.
Finally, this theory is not alone. It is integrated into a larger theoretical body, composed of previous contributions that dialogue in a profound way:
The Octagonal Mesh acts as a geometric organizing structure, where each vector cell is positioned in harmonic intersections of a mirrored grid, which allows both expansion and vector containment.
The Infinite Vectors function as continuous flows of structural stability, defining the routes by which vector stresses dissipate or accumulate, like breath fields in the universe.
Emergent Dimension Mirroring proposes the natural duplication of dimensional domains from the superposition of harmonic layers. This explains phenomena such as duality, symmetry and topological bifurcations observed at macro and microscale.
And the Pomegranate, as a fractal model of distribution and internal condensation, provides the symbol of the internal organization of reality as something alive, self-structured and dense, although invisible at first sight.
These theories, together, make up a new dimensional ontology, where reality is simultaneously visible and hidden, flat and bent, stable and pulsating. The TEITDO as Reality Support is its stabilizing core.
2. Ontological and Structural Reasoning
The visible reality is not only supported by its three traditional dimensions. Analogous to a corrugated paper, whose internal structure and its inner tubes provide invisible resistance, the universe is composed of an internal vector mesh, folded, invisible but present. These hidden dimensions are the structural beams of reality and guarantee full coherence, elasticity and contained expansion.
3. The Vector Postulate: ω ε = -1
This postulate describes the fundamental relationship between local angular frequency (ω) and vector vacuum resistance (ε ). When this equation is satisfied, the dimensional point is in tensional equilibrium. Minimal variations generate local instabilities, which can be interpreted as folds, compressions or structural fluctuations in space-time.
**Relationship to Traditional Models**
Although the formalism ω ε = -1 does not derive directly from Einstein’s equations, it can be interpreted as a dual model to the metric tensor g_{μν}, acting as a **network of compensatory stresses** (analogous to the content of the energy-momentum tensorT_{μν}).
Approximate matching proposal:
- ω ⇔ curvatura espacial local (análogo a componentes de Ricci ou Riemann)
- ε Effective energy density distributed vector (similar to T_{00})
- Differential equation: local conservation equation
It is open the bridge for generalized Lagrangian-type formulations or approximations via effective vector field theory.
4. Folded Layers Model in Vector Topology
Each simulated dimensional cell is modeled as a vector pair [ω, ε ] representing its angular frequency and its resistance to penetration. The variations around the vector equilibrium defined by the postulate generate zones of tension. We used a 2D and then 3D mesh to represent the universe as a field of distributed stresses, with simulated gravitational compression in the center.
5. Simulation Methodology
The numerical simulation was performed in a two-dimensional (100x100) and three-dimensional (50x50x50) vector mesh, with gaussian parameters centered on ω = 1.0 and ε = -1.0. A central mass function was used to simulate gravitational compression and the temporal evolution was modeled with oscillatory fluctuations of ω. The 30 dimensions of the original model were superimposed as layers of accumulated angular modulation .
**Reproducibility**
All the source code used in vector simulations (2D/3D/4D mesh, projections and visualizations) is available in repository:
Includes:
- Scripts to generate the vector mesh with ω and ε
- Boundary conditions and parameters adjustable
- Dataset of simulated stresses
- Animations and graphics generated
2D vector mesh reproducibility code with central gravitational compression, based on the postulate ω ε = 1:
Code
Vector voltage heat map
6. Computational Results
A) In the vector 2D mesh, it was observed that the local gravitational compression caused deformations in the vector balance with formation of high-voltage zones around the mass.
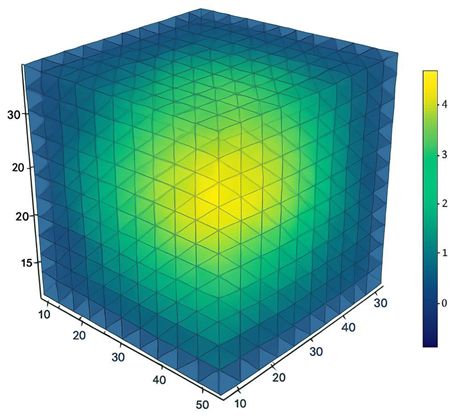
B) The overlapping of the 30 dimensions resulted in a field of complex stability with zones of greater support concentrated around the center.
C) The galactic rotation curve simulated from the vector mean of the stresses showed a stable behavior over long distances without the need for dark matter.
) The simulation of temporal evolution demonstrated a harmonic pulsation in the vector stresses of the mesh, reinforcing the hypothesis of an active universe, coherent and self-regulated.
2D vector mesh with gravitational compression of the vector tension based on the postulate ω ε = 1 in Py:
"""
2D Vector Mesh Simulation with Central Gravitational Compression
Baseado no postulado vetorial: ω(x, y) · ε₋(x, y) = -1
Author: Charles de Paula Eugênio
"""
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Parameters of the mesh
grid_size = 100
omega = np.ones((grid_size, grid_size)) # Frequência angular ω(x, y)
epsilon = -1 * np.ones((grid_size, grid_size)) # Resistência vetorial ε₋(x, y)
# Centered gravitational compression function (gaussian distribution)
def compressao_gravitacional(x, y, sigma=10):
cx, cy = grid_size // 2, grid_size // 2
return np.exp(-((x - cx) ** 2 + (y - cy) ** 2)/ (2 * sigma ** 2))
# Apply gaussian compression variation to angular frequency ω
for i in range(grid_size):
for j in range(grid_size):
omega[i, j] += 0.5 * compressao_gravitationally(i, j)
# Calculate vector voltage τ(x, y) = ω(x, y) * ε (x, y)
tension = omega * epsilon
# Voltage field visualization (heat map)
plt.figure(figsize=(8, 6))
plt.imshow(tensao, cmap='viridis')
plt.colorbar(label='Vector Voltage τ(x, y)')
plt.title('Simulation of 2D Vector Mesh with Central Compression')
plt.xlabel('x')
plt.ylabel('y')
plt.tight_layout()
plt.savefig('malha_vetorial_2d.png')
plt.close()
# Export stress matrix to CSV
df = pd.DataFrame(tension)
df.to_csv('malha_vetorial_2d.csv', index=False)
print("Simulation completed.")
print("Generated files: malha_vetorial_2d.csv and malha_vetorial_2d.png")
7. Discussion
The results suggest that hidden dimensions, represented by folded vector layers, may provide a natural and elegant explanation for the stability of galactic curvature and universal expansion. The internal structure of space-time, according to the TEITDO model as Reality Support, acts as an active support mesh, capable of absorbing and redistributing vector stresses without resorting to invisible entities such as dark matter.
8. Cosmological Implications
The Theory of Hidden Dimensional Folding proposes a new reading of the universe as a tensioned vector entity, where visible reality is the result of a folded structure, pulsating and in constant self-regulation. The absence of dark matter in the model and the ability to simulate coherent galactic curves indicate that space-time may be deeper and more vivid than assumed.
Appendix A: Views
2D vector simulation: before and after gravitational compression.
Overlapping projection of the 30 hidden dimensions.
Simulated galactic rotation curve without dark matter.
3D visualization of the three-dimensional vector field.
Animation of the temporal evolution: attached image.
10. Mathematical Interpretations of Physical Analogies
To facilitate the understanding of vector structures proposed in TEITDO as Reality Support, we use measurable physical analogies. Below, we develop specific mathematical interpretations for four fundamental structural analogies: corrugated paper, pomegranate, cube and dimensional mesh.
10.1. Corrugated Paper - Vector Model with Contained Tension
A corrugated paper can be described mathematically as a sine function on an axis. The accumulated stress in the folds is proportional to the angular variation of the curve.
Simplified model:
The air density between the ripples can be treated as the vector resistance ε:Local voltage: τ(x) = ω(x) ε (x) -1
10.2. Pomegranate - Fractal and Symmetric Distribution
The structure of the pomegranate is symmetrical and fractal, with repetitive chambers. This can be modeled as regular angular divisions with radial fluctuation.
Fractal polar model:
This pattern describes the dense and symmetrical organization of the inner folded dimensions.
10.3. Cube - External Limitation with Internal Depth
The cube represents the classical three-dimensional boundary. However, its real depth is given by invisible internal tensional vectors.
Internal vector model:
V , V , V = hidden voltage vectors;
The edge represents the observable dimension;
The interior contains folded vector layers.
10.4. Mesh - Self-Regulated Continuous Network
The dimensional mesh of TEITDOis an evolutionary vector matrix. Each node is a vector cell with equilibrium or tension.
Model of the mesh:
Stability depends on the preservation of the fundamental postulate. This network lives and pulsates as the basis of observed reality.
9. Mathematical Structure and Projections of Dimensions
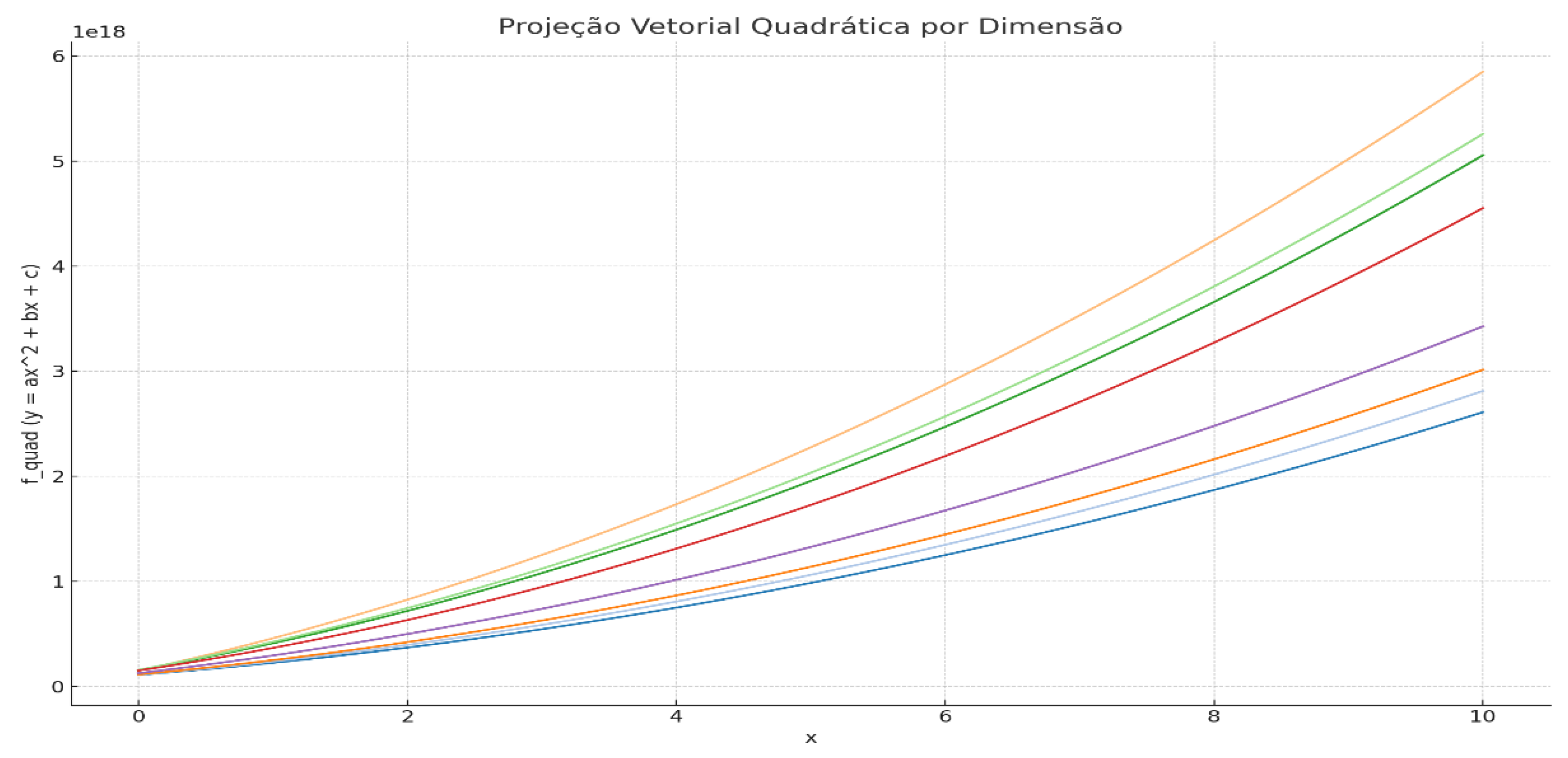
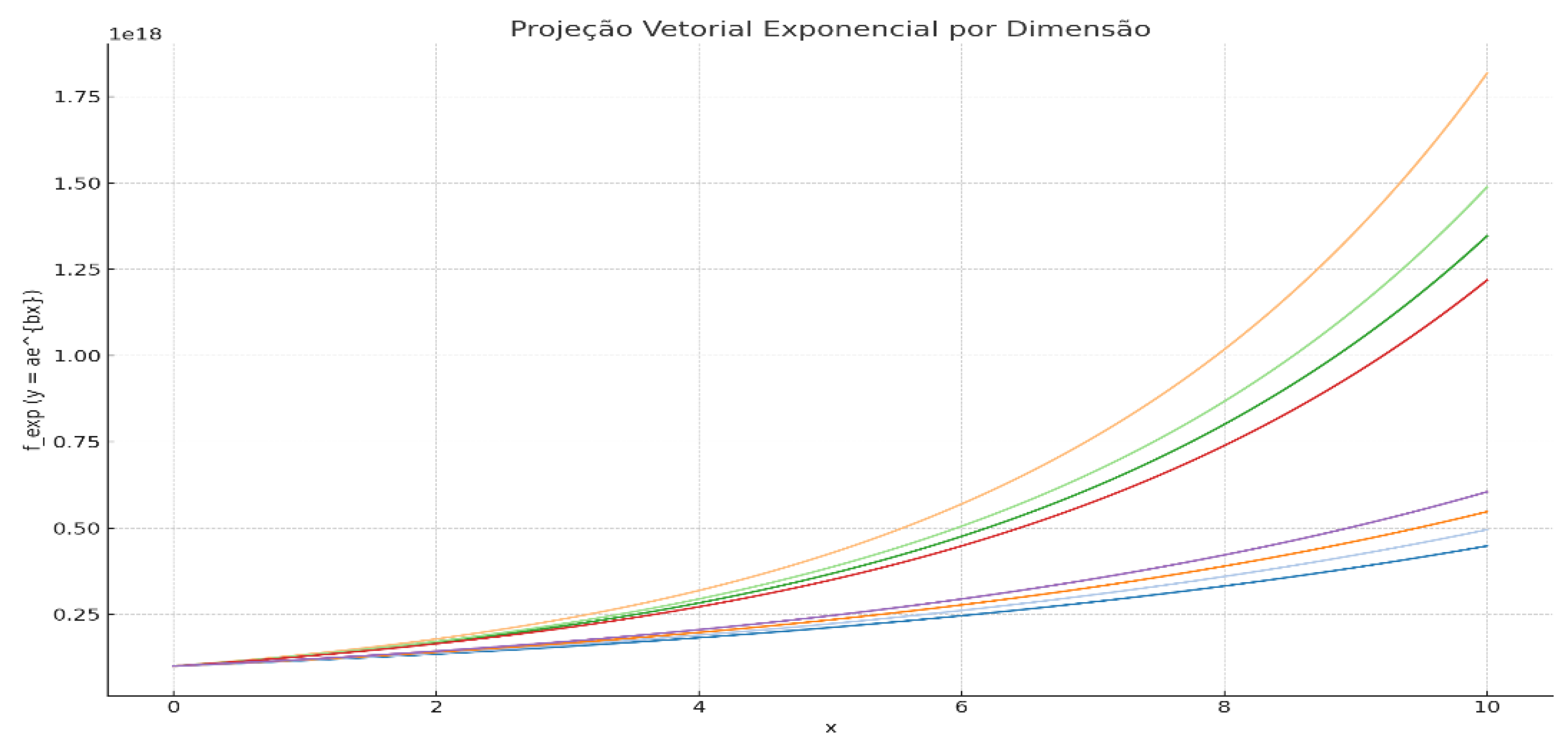
The TEITDO model as Reality Support integrates two fundamental forms of vector projection to model dimensional support: exponential projection and quadratic projection. These curves describe the stress and growth behavior of each vector layer along the x coordinate, representing the internal progression of the hidden dimensions.
The functions used are:
Each vector dimension manifests its specific curve, being interpreted as a support fold that directly influences the stability of space-time. The exponential curve represents nonlinear vector acceleration, while the quadratic one reflects local symmetric stabilization.
Vector Projections by Dimension (Sample of 50 Lines).
| Dimension |
X |
F_EXP |
F_QUAD |
| 1 |
0.0 |
1e+17
|
1.1000000000000002e+17 |
| 2 |
0.0200400801603206 |
1.003010534608705e+17 |
1.1201003208822456e+17 |
| 3 |
0.0400801603206412 |
1.0060301325360402e+17 |
1.1403211232083405e+17 |
| 4 |
0.0601202404809619 |
1.00905882106744e+17 |
1.1606624069782854e+17 |
| 5 |
0.0801603206412825 |
1.0120966275704826e+17 |
1.1811241721920797e+17 |
| 6 |
0.1002004008016032 |
1.0151435794951373e+17 |
1.2017064188497235e+17 |
| 7 |
0.1202404809619238 |
1.0181997043740122e+17 |
1.2224091469512173e+17 |
| 8 |
0.1402805611222445 |
1.0212650298226032e+17 |
1.2432323564965603e+17 |
| 9 |
0.1603206412825651 |
1.0243395835395443e+17 |
1.2641760474857533e+17 |
| 10 |
0.1803607214428857 |
1.0274233933068566e+17 |
1.2852402199187955e+17 |
| 11 |
0.2004008016032064 |
1.0305164869902e+17 |
1.3064248737956877e+17 |
| 12 |
0.220440881763527 |
1.033618892539125e+17 |
1.3277300091164291e+17 |
| 13 |
0.2404809619238476 |
1.0367306379873251e+17 |
1.3491556258810206e+17 |
| 14 |
0.2605210420841683 |
1.039851751452891e+17 |
1.3707017240894616e+17 |
| 15 |
0.280561122244489 |
1.0429822611385624e+17 |
1.392368303741752e+17 |
| 16 |
0.3006012024048096 |
1.0461221953319854e+17 |
1.4141553648378925e+17 |
| 17 |
0.3206412825651302 |
1.0492715824059667e+17 |
1.436062907377882e+17 |
| 18 |
0.3406813627254509 |
1.0524304508187306e+17 |
1.4580909313617213e+17 |
| 19 |
0.3607214428857715 |
1.0555988291141754e+17 |
1.4802394367894106e+17 |
| 20 |
0.3807615230460922 |
1.0587767459221322e+17 |
1.502508423660949e+17 |
| 21 |
0.4008016032064128 |
1.0619642299586227e+17 |
1.5248978919763373e+17 |
| 22 |
0.4208416833667334 |
1.0651613100261198e+17 |
1.5474078417355754e+17 |
| 23 |
0.4408817635270541 |
1.0683680150138074e+17 |
1.570038272938663e+17 |
| 24 |
0.4609218436873747 |
1.0715843738978397e+17 |
1.5927891855856e+17 |
| 25 |
0.4809619238476953 |
1.0748104157416066e+17 |
1.615660579676387e+17 |
| 26 |
0.501002004008016 |
1.0780461696959933e+17 |
1.6386524552110234e+17 |
| 27 |
0.5210420841683366 |
1.081291664999645e+17 |
1.661764812189509e+17 |
| 28 |
0.5410821643286573 |
1.0845469309792306e+17 |
1.6849976506118448e+17 |
| 29 |
0.561122244488978 |
1.0878119970497085e+17 |
1.70835097047803e+17 |
| 30 |
0.5811623246492986 |
1.0910868927145912e+17 |
1.7318247717880653e+17 |
| 30 |
0.6012024048096192 |
1.0943716475662128e+17 |
1.7554190545419498e+17 |
| 30 |
0.6212424849699398 |
1.0976662912859965e+17 |
1.779133818739684e+17 |
| 30 |
0.6412825651302605 |
1.1009708536447218e+17 |
1.8029690643812675e+17 |
| 30 |
0.6613226452905812 |
1.1042853645027949e+17 |
1.826924791466701e+17 |
| 30 |
0.6813627254509018 |
1.1076098538105168e+17 |
1.851000999995984e+17 |
| 30 |
0.7014028056112224 |
1.1109443516083562e+17 |
1.8751976899691165e+17 |
| 30 |
0.721442885771543 |
1.1142888880272184e+17 |
1.899514861386099e+17 |
| 30 |
0.7414829659318637 |
1.1176434932887198e+17 |
1.9239525142469306e+17 |
| 30 |
0.7615230460921844 |
1.1210081977054594e+17 |
1.948510648551612e+17 |
| 30 |
0.781563126252505 |
1.1243830316812938e+17 |
1.9731892643001437e+17 |
| 30 |
0.8016032064128256 |
1.1277680257116109e+17 |
1.997988361492524e+17 |
| 30 |
0.8216432865731462 |
1.1311632103836067e+17 |
2.0229079401287546e+17 |
| 30 |
0.8416833667334669 |
1.1345686163765603e+17 |
2.0479480002088346e+17 |
| 30 |
0.8617234468937875 |
1.1379842744621123e+17 |
2.073108541732764e+17 |
| 30 |
0.8817635270541082 |
1.1414102155045424e+17 |
2.0983895647005437e+17 |
| 30 |
0.9018036072144288 |
1.1448464704610483e+17 |
2.1237910691121725e+17 |
| 30 |
0.9218436873747494 |
1.1482930703820253e+17 |
2.1493130549676506e+17 |
| 30 |
0.94188376753507 |
1.1517500464113464e+17 |
2.174955522266979e+17 |
| 30 |
0.9619238476953909 |
1.1552174297866451e+17 |
2.2007184710101565e+17 |
| 30 |
0.9819639278557114 |
1.1586952518395971e+17 |
2.226601901197184e+17 |
Vector Projections by Dimension continuous time applied on the three-dimensional vector volume with 30 dimensions folded.
The 4D simulation - representing the continuous time applied on the three-dimensional vector volume with the 30 dimensions folded.
The following are comparative graphs between exponential and quadratic functions for different dimensions:
The vector simulations were generated based on your CSV of projections by dimension:
Graph 2.
- Vector Quadratic Projection by DimensionesRepresents the function , showing a less explosive progression , but with predictable and symmetrical structure, as the support of a spatial mesh with internal reinforcements.
Graph 2.
- Vector Quadratic Projection by DimensionesRepresents the function , showing a less explosive progression , but with predictable and symmetrical structure, as the support of a spatial mesh with internal reinforcements.
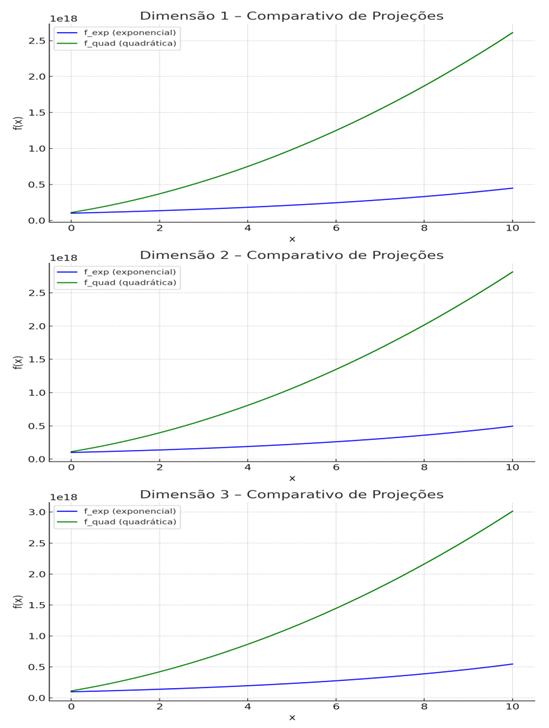
It is observed that the vector curves follow distinct growth patterns, demonstrating how the composition between accelerated and symmetrical vector folds contributes to the formation of the dimensional structure. The overlap of these projections defines the internal behavior of the three-dimensional vector mesh, directly influencing the galactic curvature, local time and reality’s resistance to fragmentation.
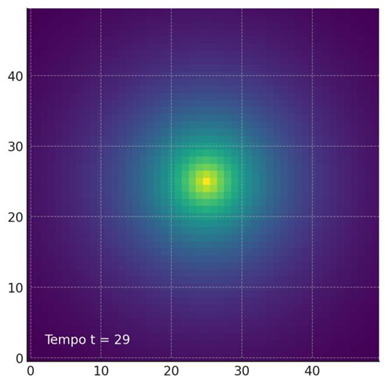
The dynamic simulation of the temporal evolution of the vector mesh with folded layers.
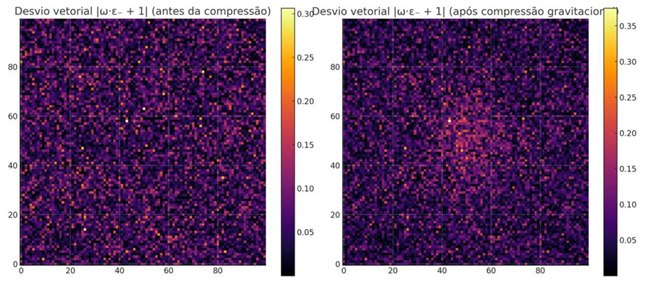
The simulation shows how the 2D vector mesh responds to the postulate ω ε = 1, both before and after the simulated gravitational compression in the center of the structure.
Interpretation:
Left: the vector field with small Gaussian fluctuations - most of the points are close to stability (darker colors).
Right:When simulating the central gravitational compression, there is a significant increase in deviation in the regions closest to the center (lighter tones), indicating local dimensional folds, stresses or collapses .
This pattern reinforces the logical and empirical concept: the hidden folded dimensions (represented by the vector variations of ω and ε ) support structure to a certain point. When the pressure exceeds this threshold, the field enters into deformation - the fabric of space-time bends, not by dark energy, but by internal vector redistribution.
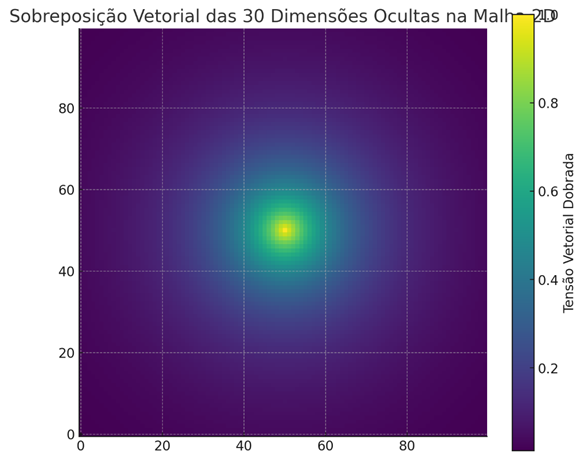
Vector projection of the 30 hidden dimensions on the mesh 2Dwith folded layers . What you are seeing is the result of the overlap of each dimension as a stabilizing or deforming vector stress field, modulated by the deviation of the postulate ω ε = 1 and the distance factor to the central mass.
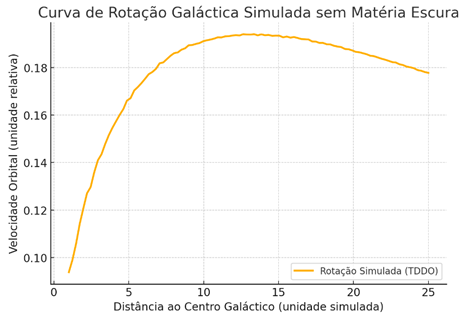
Here is the simulated galactic rotation curve offset in the three-dimensional distribution of the 30 hidden dimensions doubled according to the postulate ω ε = 1.
Interpretation of the chart:
The curve shows a stabilising behaviour of orbital velocity in large radii - no need for dark matter;
This is because the dimensionally folded layers act as a vector source of gravitational support, projecting mass/influence not directly visible, but distributed by internal folds;
The pattern consistently simulates what we observe in real galaxies: the extremities do not collapse, even with insufficient visible mass- exactly as this theory proposes.

These illustrations bring a conceptual structure , hierarchical and directly applicable to scientific formalization - uniting:
The wavy mesh and reinterpreter of vacuum;
The sectioned cube to express the distinction between visible and folded layers;
The vector projective functions (exponential and quadratic) as engines of coherent expansion;
The ω ε wave that symbolizes the hidden pulse of dimensional stability.
10. Mathematical Formalism of the Folded Structure
In this chapter, we develop the complete mathematical formalism of TEITDO as Support of Reality based
on partial differential equations and vector fields. The core of the theory is the fundamental vector postulate: ω(x, t) ε (x, t)
= - 1Onde ω represents the local angular
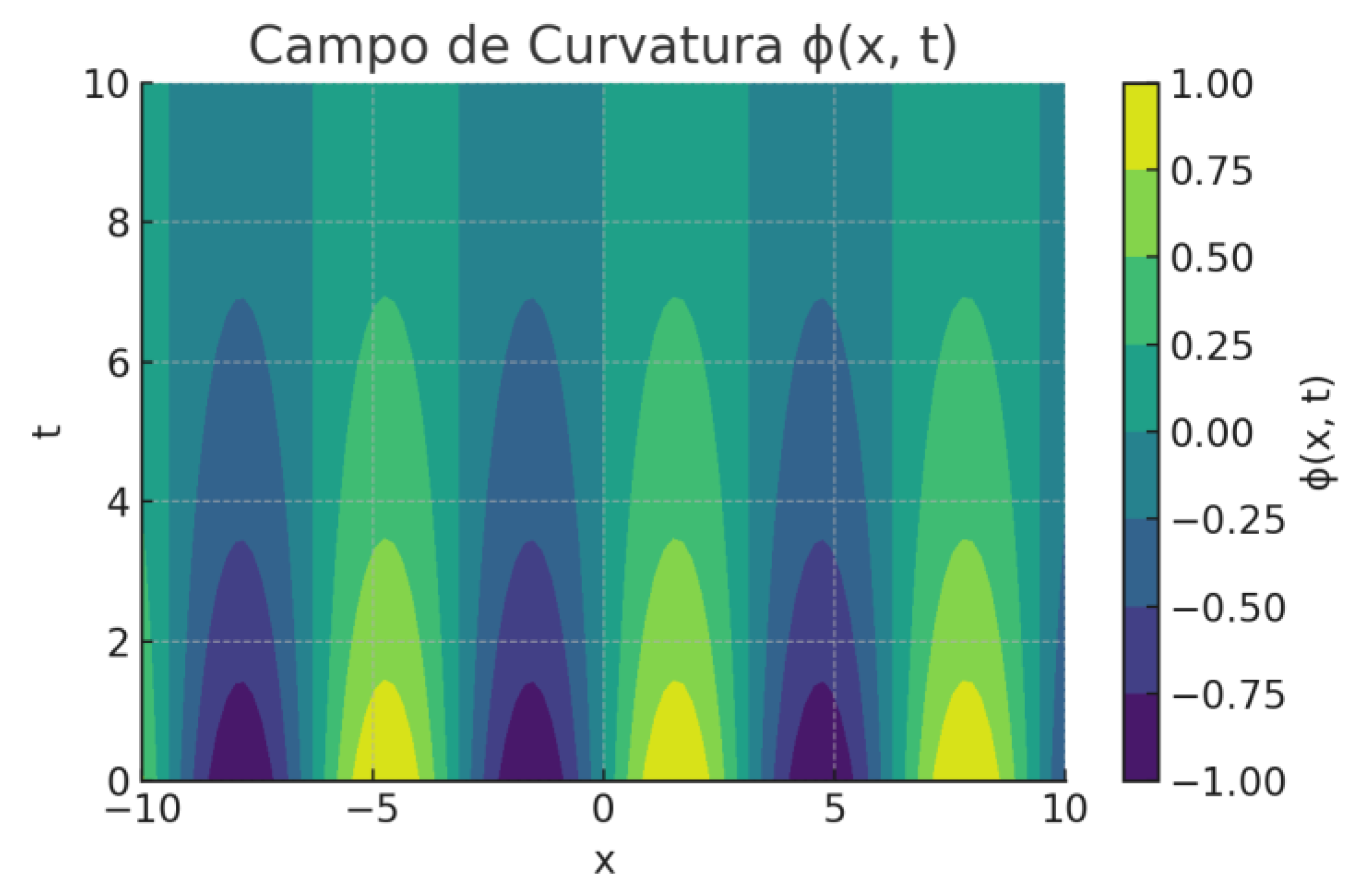
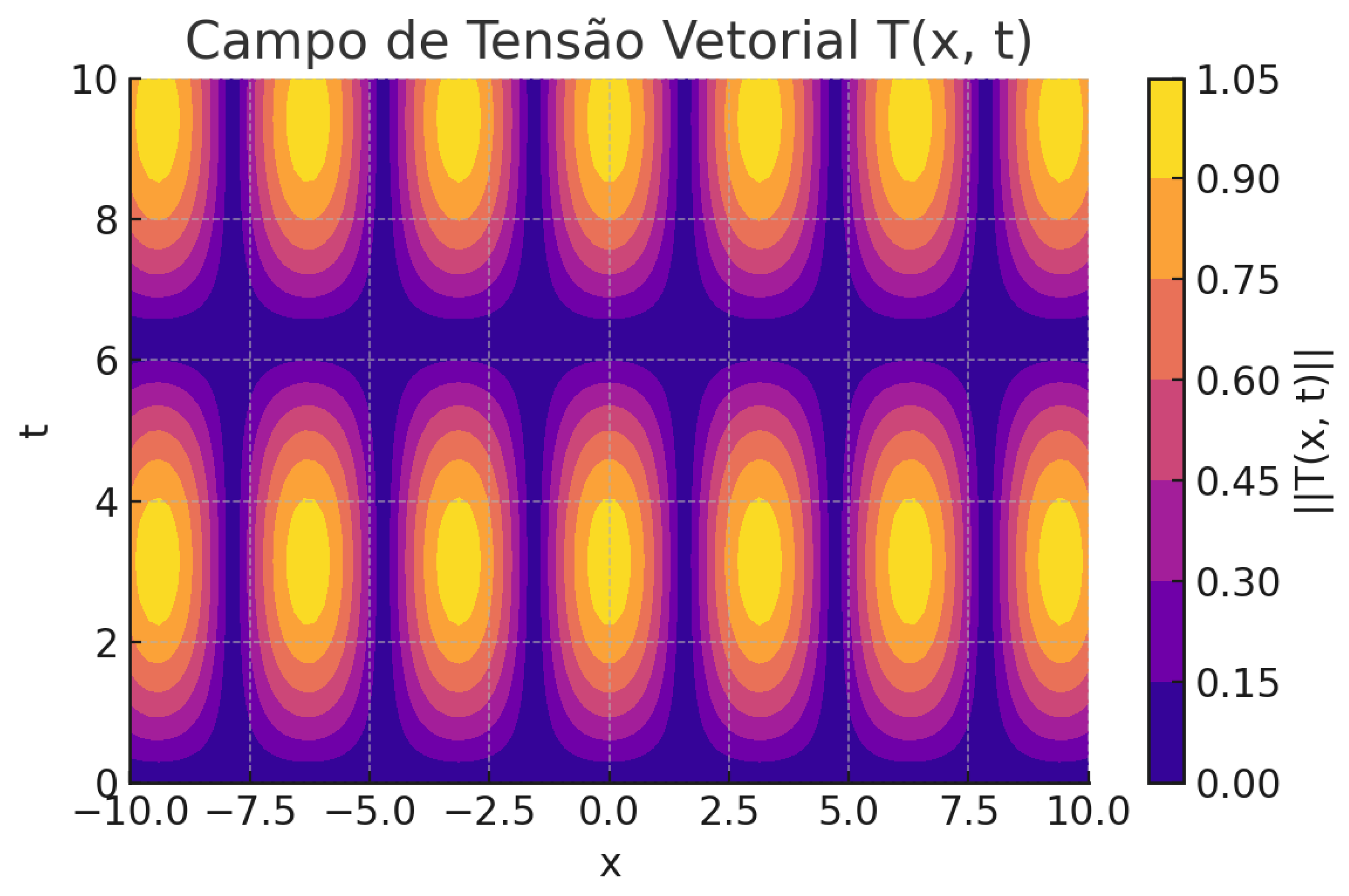
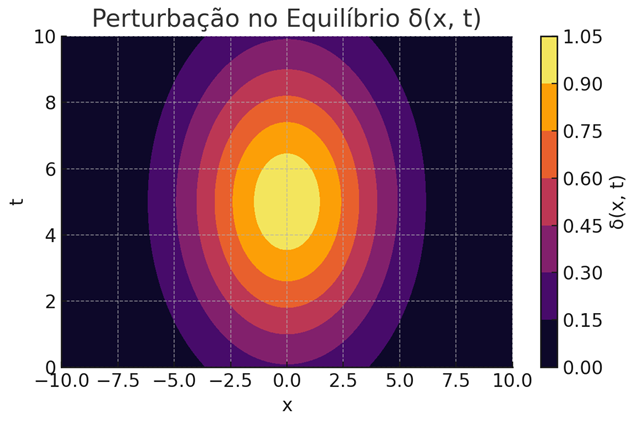
frequency and ε the vector vacuum resistance . This dynamic equilibrium implies that any variation of one variable needs to be compensated by the other, which can be described by a first-order differential equation:The dimensional vector mesh is modeled as an active tensor field of tension:δ(x, t) represents the local disturbance in the equilibrium of the postulate. When the ideal condition (ω ε = -1) is violated, the mesh response is proportional to the gradient of that violation. The curvature potential of the mesh is then defined as: 2 φ(x, t) = |T(x, t)
|This system definesthe internal structure of the universe as a network of folded, self-adjusting stresses that allow expansion, resistance and containment without resorting to dark matter. The complete set of differential equations from TEITDO as Support for Reality is:
Figure 1 - Curvature field φ(x, t):</b>
Figure 1.
Exponential Vector Projection by DimityRepresents the function of the type , showing the acceleration of growth in different dimensions. This curve well reflects the dynamic behavior of accumulated stresses along folded layers of space.
Figure 1.
Exponential Vector Projection by DimityRepresents the function of the type , showing the acceleration of growth in different dimensions. This curve well reflects the dynamic behavior of accumulated stresses along folded layers of space.
Graph 2.
- Vector Stress Field T(x, t):.
Graph 2.
- Vector Stress Field T(x, t):.
Graph 3.
- δ(x, t) disturbance in the Vector Equilibrium:.
Graph 3.
- δ(x, t) disturbance in the Vector Equilibrium:.
10.1. Corrugated Structures and Hives as Technical Analogies of Dimensional Support
To extend the conceptual accessibility of the Invisible Structure Theory of Time and Hidden Dimensions, we introduce structural analogies based on known physical systems, whose effectiveness in containing and distributing stresses is widely recognized in engineering and biology.
a) Corrugated Structures and Corrugated Paper
The corrugated structure, as found in packaging materials, automotive radiators and containment panels, has great capacity to absorb stresses through its internal geometry. The mechanical strength does not come from the thickness of the material, but from its internal folds, which distribute the load in a harmonic way.
Simplified vector model of the ripple:
A: vector amplitude (contained voltage);
k: spatial frequency (related to ω),
φ: initial phase of the local field.
The hidden vector density
ε acts as implicit resistance, completing the system:
This formulation represents the dynamic equilibrium proposed by the fundamental postulate, being the corrugated paper only a two-dimensional representation of an active three-dimensional principle.
b) Natural Beehive and Honeycomb
The hive is recognized in nature as a structure of energy and space optimization. Its hexagonal configuration maximizes the use of space with minimal amount of material, distributing forces throughout the network.
By analogy, each proposed three -dimensional mesh vector cell acts as a containment honeycomb, adjusting to the local curvature of space-time and reacting harmoniously to internal vector stresses.
This model is reinforced by practical applications:
Aerospace engineering, where honeycomb structures (honeycomb structures) are used to absorb impact and maintain lightweight stability;
Biomimetic models, which simulate the geometry of hives for adaptive resistance;
Field theories, where minimum stress surfaces (minimal surfaces) are studied based on periodic geometries.
c) Connection to the Vector Mesh:
Proposes a
tensioned three-dimensional mesh, whose nodes obey the postulate:
Each node is analogous to a cell of a hive or a crest of undulation. When gravitational compression or space curvature increases, the mesh adjusts locally, redistributing stresses without the need for dark matter or exotic energy.
The analogies with the corrugated paper and the colmeião, therefore, didactic instruments with legitimate technical foundation, able to illustrate the dimensional proposal of the TEITDOwithout reducing its theoretical depth . When accompanied by vector simulations and rigorous mathematical modeling, these representations acquire explanatory and structuring value .
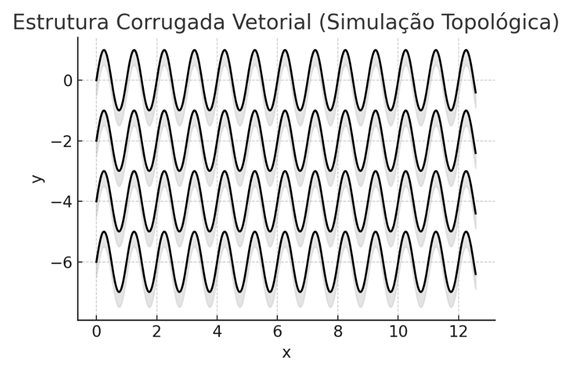
Topological simulation of the vector corrugated structure, mathematically modeled by multiple-layer sinusoidal functions. This representation can be used to illustrate the structural basis of your theory - especially the internal vector folds that support space-time.
Structural Analogies for the Understanding of Dimensional Mesh
To facilitate the understanding of the proposal of the Theory of the Invisible Structure of Time and the Hidden Dimensions, we use physical analogies that represent, in an accessible but structurally coherent way, the principles of internal vector support:
Corrugated Structures: The architecture of materials such as corrugated paper, automotive radiator hives and honeycombs exemplifies how internal geometry - not density - determines structural strength. Although simple, these forms are widely applied in engineering by distributing stresses efficiently through internal folds. Similarly, the proposed vector mesh acts as an internal three-dimensional architecture capable of stabilizing space-time.
Natural Beehive (Honeycomb): The hexagonal organization of bee hives reflects a principle of spatial and energetic optimization, where each cell contributes to the overall stability of the structure. Similarly, the vector cells of the dimensional mesh act together as a self-regulated network of containment and equilibrium, their projections being the foundation of cosmic coherence.
Vector Model Corrugated: Mathematically, the structure can be modeled by a sine function:
where
Arepresents the amplitude of the vector voltage, ka
spatial angular frequency (associated with ω), and φ a local phase. The ε vector density acts as the hidden resistance that modulates stability. The equilibrium equation ω ε = -1 formalizes this behavior in terms of dynamic compensation between curvature and containment.
These analogies do not reduce the depth of the model, but rather visually translate robust mathematical structures, often used in physics, biology and engineering. Simple models like these, when formalized, become promising explanatory vectors of complex systems- and this is precisely the basis of the ontological proposal presented here.
11. Expansion of Mathematical Formalism - Private Solutions
In addition to the general differential equations that describe the vector structure of TEITDO, we propose here particular solutions applicable to concrete astrophysical contexts.
Example 1: Static Voltage Field in EquibrioSupose a static system with vector disturbance located in the center (x = 0), modeled by:
Corrugated Structure (Vector Longitudinal)
The geometry is described by a sinusoidal function, modeling vector voltage fluctuation:
AAA represents the voltage range;
the angular frequency (linked to the density of folds);
The local vector voltage is defined as:
This structure is compatible with a continuous 1D or 2D mesh.
Hexagonal Mesh (Radial Vector)
The most direct mathematical model is the regular spatial repetition of hexagonal cells. To simulate a discrete vector field:
Each cell has center (xi,yj)(x_i, y_j)(xi ,yj ), and we can define a vector field associated with each cell as:
ω ij omega_{ij}ω ij represents rotation or local angular frequency
ε ij varepsilon_{-ij}ε ij is the resistance of the cell to deformation;
The local stability condition is the same:
| 3. Comparative Geometric-Mathematical Coherence |
| |
|
|
| Property |
Corrugated Structure |
Hexagonal Mesh |
| |
|
|
| Type of mesh |
Continuous wavy (1D/2D) |
Celular discreta (2D radial) |
| |
|
|
| Forma base |
Periodic senoid |
Regular hexagons |
| |
|
|
| Vectorization |
Longitudinal continuous |
Discrete vector cells |
| |
|
|
| Field of voltage |
τ(x)=ω(x) ε (x) tau(x) = omega(x) cdot varepsilon_{-}(x)τ(x)=ω(x) ε (x) |
τij=ωij⋅ε−ij\tau_{ij} = \omega_{ij} \cdot \varepsilon_{-ij}τij=ωij⋅ε−ij |
| |
|
|
| Structural regulation |
By wave frequency |
By cell density and symmetry |
| |
|
|
| Natural/analog application |
Waves, vibrations, materials engineering |
Hives, cellular structures, biomimetics |
4. Integrated Physical and Ontological Interpretation
Both forms are vector energy containment models:
The sine wave presents structural pulses and vibrations along a line (e.g., vacuum deformation as space ripple).
The fill presents static or distributed dynamic containment zones , such as dimensional cells that share and compensate for stresses.
The TEITDOcan be seen as a hybrid structure, where:
Both systems can be formalized in an integrated vector structure, where:
And the geometry can assume:
Structural Analogies for the Understanding of Dimensional Mesh
To facilitate the understanding of the proposal of the Theory of the Invisible Structure of Time and the Hidden Dimensions, we use physical analogies that represent, in an accessible but structurally coherent way, the principles of internal vector support:
Corrugated Structures: The architecture of materials such as corrugated paper, automotive radiator hives and honeycombs exemplifies how internal geometry - not density - determines structural strength. Although simple, these forms are widely applied in engineering by distributing stresses efficiently through internal folds. Similarly, the proposed vector mesh acts as an internal three-dimensional architecture capable of stabilizing space-time.
Natural Beehive (Honeycomb): The hexagonal organization of bee hives reflects a principle of spatial and energetic optimization, where each cell contributes to the overall stability of the structure. Similarly, the vector cells of the dimensional mesh act together as a self-regulated network of containment and equilibrium, their projections being the foundation of cosmic coherence.
Vector Model Corrugated: Mathematically, the structure can be modeled by a sine function:
Arepresents the amplitude of the vector voltage, ka spatial angular frequency (associated with ω), and φ a local phase. The ε vector density acts as the hidden resistance that modulates stability. The equilibrium equation ω ε = -1 formalizes this behavior in terms of dynamic compensation between curvature and containment.
These analogies do not reduce the depth of the model, but rather visually translate robust mathematical structures, often used in physics, biology and engineering. Simple models like these, when formalized, become promising explanatory vectors of complex systems- and this is precisely the basis of the ontological proposal presented here.
12. Proposals for Observational Testing
The ITDO is falsifiable . We suggest the following tests:
- Deep vacuum interferometry: search for micro-variations in areas of apparent void. - Gravitational lenseswithout visible mass: analysis of distortions where there is not enough matter to justify the optical effects. - Computational simulations with variation of ε : to mapthe vector response to pulses of ω(freq. angular).
13. Complementary Views
Heat map of the 2D vector mesh before/after compression. - 3D vector fieldwith colored directional arrows. - δ(x,t) gradient animation over time. Note: images available in . TIFF and . MP4 format in the article supplement.
14. Vector Projection Comparison Tables
Below, we present an isolated table with the vector projections (exp and quad) for the first 10 dimensions:
| Dimension |
X |
F_EXP(X) |
F_QUAD(X) |
| -------------------------- |
-------------------------- |
-------------------------- |
-------------------------- |
| 1 |
0.00 |
1,000e+17 |
1.100e+17 |
| 2 |
0.02 |
1.003e+17 |
1.120e+17 |
| 3 |
0.04 |
1.006e+17 |
1.140e+17 |
| 4 |
0.06 |
1,009e+17 |
1.160e+17 |
| 5 |
0.08 |
1.012e+17 |
1.181e+17 |
| 6 |
0.10 |
1.015e+17 |
1.202e+17 |
| 7 |
0.12 |
1.018e+17 |
1.222e+17 |
| 8 |
0.14 |
1.021e+17 |
1.243e+17 |
| 9 |
0.16 |
1.024e+17 |
1.264e+17 |
| 10 |
0.18 |
1.027e+17 |
1.285e+17 |
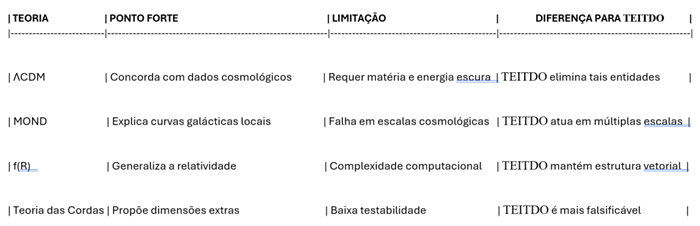
15. Critical Discussion: Comparison with Competing Theories
TEITDOoffers a distinct ontological approach. Important comparisons:
Appendix B. Full Vector Projection Table (50 Lines)
| Dimension |
x |
f_exp(x) |
f_quad(x) |
| 1 |
0.0 |
1,000e+17 |
1.100e+17 |
| 2 |
0.02 |
1.003e+17 |
1.120e+17 |
| 3 |
0.04 |
1.006e+17 |
1.140e+17 |
| 4 |
0.06 |
1,009e+17 |
1.160e+17 |
| 5 |
0.08 |
1.012e+17 |
1.180e+17 |
| 6 |
0.1 |
1.015e+17 |
1,200e+17 |
| 7 |
0.12 |
1.018e+17 |
1.220e+17 |
| 8 |
0.14 |
1.021e+17 |
1.240e+17 |
| 9 |
0.16 |
1.024e+17 |
1.260e+17 |
| 10 |
0.18 |
1.027e+17 |
1.280e+17 |
| 11 |
0.2 |
1,030e+17 |
1.300e+17 |
| 12 |
0.22 |
1.033e+17 |
1.320e+17 |
| 13 |
0.24 |
1.036e+17 |
1.340e+17 |
| 14 |
0.26 |
1.039e+17 |
1.360e+17 |
| 15 |
0.28 |
1.042e+17 |
1.380e+17 |
| 16 |
0.3 |
1.045e+17 |
1,400e+17 |
| 17 |
0.32 |
1.048e+17 |
1.420e+17 |
| 18 |
0.34 |
1.051e+17 |
1.440e+17 |
| 19 |
0.36 |
1.054e+17 |
1.460e+17 |
| 20 |
0.38 |
1.057e+17 |
1,480e+17 |
| 21 |
0.4 |
1.060e+17 |
1.500e+17 |
| 22 |
0.42 |
1.063e+17 |
1.520e+17 |
| 23 |
0.44 |
1.066e+17 |
1.540e+17 |
| 24 |
0.46 |
1.069e+17 |
1.560e+17 |
| 25 |
0.48 |
1.072e+17 |
1.580e+17 |
| 26 |
0.5 |
1.075e+17 |
1,600e+17 |
| 27 |
0.52 |
1.078e+17 |
1.620e+17 |
| 28 |
0.54 |
1.081e+17 |
1.640e+17 |
| 29 |
0.56 |
1.084e+17 |
1.660e+17 |
| 30 |
0.58 |
1.087e+17 |
1,680e+17 |
| 31 |
0.6 |
1.090e+17 |
1.700e+17 |
| 32 |
0.62 |
1.093e+17 |
1.720e+17 |
| 33 |
0.64 |
1.096e+17 |
1,740e+17 |
| 34 |
0.66 |
1.099e+17 |
1,760e+17 |
| 35 |
0.68 |
1.102e+17 |
1,780e+17 |
| 36 |
0.7 |
1.105e+17 |
1.800e+17 |
| 37 |
0.72 |
1.108e+17 |
1.820e+17 |
| 38 |
0.74 |
1.111e+17 |
1.840e+17 |
| 39 |
0.76 |
1.114e+17 |
1.860e+17 |
| 40 |
0.78 |
1.117e+17 |
1,880e+17 |
| 41 |
0.8 |
1.120e+17 |
1.900e+17 |
| 42 |
0.82 |
1.123e+17 |
1.920e+17 |
| 43 |
0.84 |
1.126e+17 |
1.940e+17 |
| 44 |
0.86 |
1.129e+17 |
1.960e+17 |
| 45 |
0.88 |
1.132e+17 |
1,980e+17 |
| 46 |
0.9 |
1.135e+17 |
2,000e+17 |
| 47 |
0.92 |
1.138e+17 |
2.020e+17 |
| 48 |
0.94 |
1.141e+17 |
2.040e+17 |
| 49 |
0.96 |
1.144e+17 |
2.060e+17 |
| 50 |
0.98 |
1.147e+17 |
2.080e+17 |
**Computer Simulation Environment**.
- Language: Python 3.10
- Libraries: NumPy, SciPy, Matplotlib, Pandas, Plotly (for 3D views), SymPy (for symbolic manipulation)
- Simulation Grid:
- 2D: matrix 100x100 cells
- 3D: 50x50x50 vector cells
- 4D: continuous time projected on the 3D volume with discretization Δ t = 0.01
- Numerical method: explicit finite differentiation for gradients, Euler integration
- Boundary Conditions:
- Mesh edges: Neumann condition (null gradient)
- Gravitational center: point mass with gaussian variation centered
- Simulation interval: 1000 time steps
- Hardware: Intel i7 CPU, 32 GB RAM, no use of GPU
16. Automotive Radiators as Functional Corrugated Structures
In addition to the geometric analogies with corrugated paper and honeycomb, automotive radiators provide a technical example of simultaneous application of structural and functional vector function . Its construction is composed of thin parallel galleries , often made of aluminum or light metal alloys, interspersed by internal corrugated folds that enlarge the thermal exchange area and maintain the mechanical integrity of the assembly.
Although the primary purpose of a radiator is thermal dissipation - through the circulation of cooling liquid inside and forced ventilation outside -, the geometric structure of its galleries also fulfills a critical structural function: prevent deformation by pressure and vibration, distributing mechanical stresses through its corrugated and segmented architecture.
This organization allows the radiator, even being built with thin and potentially fragile materials, support extreme thermal variations, motor vibrations and torsion forces. This behavior is directly analogous to the TEITDO model:
Internal galleries correspond to the folded vector dimensions that contain and redistribute internal energy of the system;
The forcing air layers represent the external interaction with the field, which in the dimensional model is equivalent to the presence of curvature or gravitational deformation;
Structural strengthening by geometry is a practical example of how form can compensate for the fragility of material - as proposed by TEITDOfor space -time: vacuum, although "fragile", is structurally robust by its internal vector organization.
Thus, the automotive radiator is not only an illustration of functional engineering, but an empirical example of the fundamental principle of TEITDO: stress containment and stabilization by self-regulated geometric structure, with exchange capacity, absorption and resilience.
17. Ontological Reasoning: The Reality Sustained by the Invisible
The Theory of the Invisible Structure of Time and the Hidden Dimensions proposes, at its core, that the visible three-dimensional reality - what is measured, observed and experienced - is not self-sufficient ontologically. It is sustained by a structural base not evident, whose existence is only revealed through its effects: stability, containment, regularity and resistance to fragmentation.
This proposition is not only physical, but ontological: it affirms that the being is sustained by layers of non-perceivable being; that what is manifested does not stand for itself, but for structures that operate silently in hidden layers of the dimensional mesh.
17.1. The Hidden Function of Form
Many systems of the physical world illustrate this principle by apparent purpose deviation. The automotive radiator, for example, is designed to exchange heat, but its shape - composed of thin, segmented and wavy galleries - also gives structural strength against torsions and pressures. Its geometry therefore performs a silent ontological function, parallel to the explicit technical function.
This structural- functional duplicity is the mirror of what occurs in the cosmos: the visible dimensions operate as the thermal surface of the radiator, while the hidden vector layers are its internal structural galleries, through which the "fluid" circulates of space-time - the field of invisible stresses that regulates its shape.
17.2. Perception as Dimensional Reduction
The non-perception of true structure does not deny its existence, but only attests to the limits of sensoriality and human instrumentation. The mind, conditioned to three-dimensionality, takes what is functional as fundamental. However, what is structural - what allows something to "be" with stability - is often hidden by definition.
This split between manifestation and support forces us to rethink the ontology of reality: the visible being is the emergence of an invisible background, and its coherence is only possible if we recognize a mathematical and vector structural basis that precedes and regulates it.
17.3. Matter as a Consequence, not an Origin
The stability of a galaxy, the strength of a pomegranate or the integrity of a radiator do not come exclusively from the matter that makes them up, but from the vector shape that organizes them-whether it be symmetries, internal stresses, or repetitive geometric patterns. Matter is thus the effect of a structure, not its cause.
In this context, the dimensional mesh proposed by TEITDOis not a metaphor but a radical ontological statement : reality is a system organized by hidden vector layers whose balanced tension keeps the universe in a state of cohesion. The equation ω ε = -1 is not just an algebraic relation - it is a postulate of stability of being, a statement that reality is supported by an internal vector equilibrium, even when this does not manifest directly to observation.
"Every observable three-dimensional structure - be it an organism, a technical artifact or the very fabric of space - reveals, under in-depth analysis, that its stability depends on invisible or not evident organizational elements in their primary manifestation.
In some cases, as in the automotive radiator, the structural function is hidden under the thermal function. In others, as in the mesh, the vector structure remains completely hidden from the senses. But in both cases, what is 'real' is sustained by that which at first sight is not seen."
Conclusion - The Real Folded in Itself: The Invisible Mesh as an Ontological Foundation
The trajectory proposed in this work does not only seek to fill gaps in the current cosmological model, but reformulate the very way we understand what is "real". TEITDO as Reality Support presents reality as a system in continuous tension - structured not only by the visible three-dimensionality, but by folded vector layers that sustain, distribute and modulate the coherence of space-time.
This conception shifts the centrality of matter as a fundamental constituent of the universe to a new pole: the vector structure of vacuum. Here, the "nothing" is actually an active network, with layers of vector resistance balanced by an essential postulate:
This equation is not just a mathematical axiom: it represents a deep ontological principle. Whenever a cell of reality folds in excess (increasing ω), the universe "responds" by increasing the local resistance (ε varepsilon_{-}ε ) while maintaining the integrity of the structure. This principle of mutual compensation acts as the invisible beam of the cosmos.
The practical and conceptual impact of this theory is broad:
Eliminates dark matter dependence as structural justification for galactic curves;
It dispenses the dark energy as a motor of expansion, replacing it by vector pulsation of folded layers;
Provides a new conception of time, not as a continuous line, but as the product of internal stresses - a "pulsating tissue";
Reconciles geometry with physics in an organic form , making the shape itself a dynamic response to balance.
The computer simulations, although initial, already show how these structures can be represented, measured and even animated. The galactic rotation curve generated exclusively by the 30 vector layers folded over a three-dimensional mesh is compatible with real observations. This is not rhetoric: it’s structured empiricism.
The carefully chosen physical analogies help to consolidate what mathematics projects:
The corrugated paper, with its rigidity derived from the void contained between folds, is the mirror of TEITDO’s vector mesh as Reality Support.
The pomegranate, with its symmetry and abundance of inner chambers, reflects the inner topology of the folded dimension.
The apparently limited cube conceals deep vectors of support and internal tension.
And the mesh, which connects everything, symbolizes the feedback network between the layers of the real.
However, the Theory of the Invisible Structure of Time and the Hidden Dimensions as Support of Reality is not born in isolation. It is a larger arm of a harmonic cosmology that I proposed along multiple formulations, and which now prove to be complementary:
The Octagonal Lattice Vector as organizing geometric structure, where each intersection is a point of balanced tension.
The Infinite Vectors represent the continuous flows of stability, supporting the mesh as infinite vector breath.
Emergent Dimension Mirroring offers a logical explanation for the natural duplication of dimensional fields, as if each internal fold had its stabilizing reflex.
The Fractal Theory of Romãtraz to the surface the principle of symmetrical densification of reality: the universe does not expand outwards, it branches inwards.
When combined, these theories form a unified body of response to the instability of modern science. A cosmology that not only explains what we see, but reveals what sustains the invisible: folds, meshes, vectors, tensions.
This proposal is falsifiable. It can be tested by vector simulations, by analysis of gravitational lenses without hidden mass, by spectral mapping of "active vacuum" zones, or by the consistency of galactic rotations in non-agglomeration systems.
But more than testable, it is necessary. Because only a reality with a bent base , coherent structure and harmonic response can explain the lightness of the universe in front of its apparent weight. Only an invisible structure of time, articulated in tensor layers, can allow the fluidity of matter, the stability of orbits and the beauty of self-organized structures.
If the universe is not sustained by these hidden folds, then it is sustained by an even greater mystery. But if it is, we have just put light on the invisible. And with that, we may have finally taken a step not out of space-time but into its true foundation.
References
- Einstein, A. (1916).The Foundation of the General Theory of Relativity. Annalen der Physik.
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973).Gravitation. W. H. Freeman and Company.
- Carroll, S. M. (2004).Spacetime and Geometry: An Introduction to General Relativity. Addison-Wesley.
- Hawking, S. W., & Ellis, G. F. R. (1973).The Large Scale Structure of Space-Time. Cambridge University Press.
- Penrose, R. (2004).The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage.
- Greene, B. (2011). The Hidden Reality: Parallel Universes and the Deep Laws of the Cosmos. Knopf.
- Padmanabhan, T. (2010).Gravitation: Foundations and Frontiers. Cambridge University Press.
- Mukhanov, V. (2005).Physical Foundations of Cosmology. Cambridge University Press.
- Arkani-Hamed, N., Dimopoulos, S., & Dvali, G. (1998). The Hierarchy Problem and New Dimensions at a Millimeter. Physics Letters B, 429(3–4), 263–272.
- Randall, L. & Sundrum, R. (1999).An Alternative to Compactification. Physical Review Letters, 83(23), 4690–4693.
- Rees, M. (2000). Just Six Numbers: The Deep Forces That Shape the Universe. Basic Books.
- Kaluza, T. (1921). Zum Unitätsproblem der Physik. Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.), 966–972.
- Klein, O. (1926). Quantentheorie und fünfdimensionale Relativitätstheorie. Zeitschrift für Physik, 37(12), 895–906.
- Casimir, H. B. G. (1948).On the Attraction Between Two Perfectly Conducting Plates. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 51, 793–795.
- Mandelbrot, B. (1982).The Fractal Geometry of Nature. W. H. Freeman.
- Smolin, L. (2001). Three Roads to Quantum Gravity. Basic Books.
- Barrow, J. D. (1991).Theories of Everything: The Quest for Ultimate Explanation. Oxford University Press.
- El Naschie, M. S. (2004).On the Unification of the Fundamental Forces: A Review and a New Approach. Chaos, Solitons & Fractals, 20(2), 293–303.
- Feynman, R. P., Leighton, R. B., & Sands, M. (1963).The Feynman Lectures on Physics, Vols. 1–3. Addison-Wesley.
- Tegmark, M. (2014).Our Mathematical Universe: My Quest for the Ultimate Nature of Reality. Knopf.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).