The Persistent Mysteries: Foundational and Philosophical Problems with Infinity in Science and Mathematics

1. Introduction: The Ubiquity and Unease of Infinity

From the infinite spans of space to the minute subdivisions of time, infinity permeates our knowledge of the cosmos. Underlining set theory, calculus, and topology, it is a notion firmly woven into the tapestry of current mathematics. Georg Cantor’s revolutionary work in the late 19th century exposed a hierarchy of infinities, showing that some infinities are bigger than others and so establishing infinity as a topic of intense mathematical investigation (Fieker & Horn, 2024). Still, infinity has always been a source of anxiety, posing philosophical riddles and contradictions that question our intuition and the very boundaries of human understanding (Davis, 2024), notwithstanding its formal grace and undoubtable usefulness.

The anxiety with infinity is not novel. Ancient Greek philosophers, especially Zeno of Elea, enunciated paradoxes challenging the possibility of infinite division or infinite processes, such Achilles and the Tortoise, therefore bringing forth the logical absurdities resulting from supposing infinite divisibility of space and time (Pemberton, 2022). Early obstacles set the ground for a continuing philosophical conflict: is infinity merely a potentiality, a process that may be carried out indefinitely but never completed (potential infinity), or does it exist as an actual entity (actual infinity)? Aristotle championed this difference, which has significantly shaped later mathematical and philosophical thinking (de Oliveira, 2022).

This article reveals that though infinity is a necessary tool, its unthinking adoption as a description of reality demands more investigation. Among the several aspects of this continuing enigma, we will examine the historical and philosophical objections, the development of alternate mathematical systems, and the contemporary problems infinity in physics presents. Rather than disproving infinity in a strictly mathematical sense—its mathematical existence is axiomatic in some systems—the goal is to inspire fresh food for scientific thinking by considering the limits and consequences of its use.

2. Historical Roots of Skepticism: From Zeno to Hilbert’s Hotel

Deep historical roots have produced the doubt around infinity, often expressed as contradictions that reveal the counterintuitive nature of infinite sets. Perhaps the most well-known ancient difficulties are Zeno’s paradoxes—the Dichotomy and Achilles and the Tortoise in particular. According to the Dichotomy paradox, traversing any distance entails first traversing half of it, then half of the remaining half, and so on—that is, an infinite number of steps must be accomplished in a finite time, which seems impossible (Bierdz, 2024). Though calculus offers a mathematical basis to solve these contradictions by showing that an infinite series can converge to a finite sum, the fundamental philosophical conflict regarding the completion of an infinite process persists (Allison, 2024).

Hilbert’s Hotel, another good example, a thought experiment suggested by David Hilbert in 1924, shows the counterintuitive characteristics of real infinities, as depicted by Figure 1 (Kumar et al., 2023).

By just moving present guests to higher numbered rooms, a hotel with an infinite number of rooms, all taken, can still fit fresh visitors—even an infinite number of new ones. Though mathematically appropriate within set theory, this thought experiment emphasizes how characteristics that apply to finite groups do not always apply to infinite ones, therefore creating absurdity for those who fight with the idea of real infinity (Herberg-Rothe, 2024).

These historical difficulties emphasize a basic philosophical division: the difference between actual and possible infinity. Actual infinity is a finished, existing infinite set or amount—for instance, the set of all natural numbers. Conversely, possible infinity describes a process that can go on forever without stopping but never achieves a finished infinite state (e.g., counting numbers). Many mathematicians and philosophers have claimed that only potential infinity is conceptually consistent or physically feasible (Scholz, 2023). Debates regarding the ontological nature of infinite mathematical objects are still driven by the strain between these two viewpoints.

3. Mathematical Alternatives: Finitism, Ultrafinitism, and Constructivism

The unease with real infinity has prompted the creation of other mathematical theories aimed at establishing mathematics on more positive or finite bases. These schools of thought frequently contradict the classical principles of set theory and the law of excluded middle, which are essential for proving the existence of infinite sets and for several nonconstructive proofs in mathematics (Fisher & Maurin, 2024).

3.1. Finitism

Finitism argues, in its most basic form, that only finite mathematical items are relevant or exist. It denies that infinite sets as complete totalities are possible. For a strict finitist, even the set of all natural numbers is not a completed entity but rather a potentiality; one can always generate another natural number, but the collection itself never reaches an end (Ernest, 2023). From this point of view, mathematical objects should be graspable or constructible using finite means. While finiters could embrace the notion of arbitrarily big numbers, they wouldn’t accept infinitely large numbers. Strict finitism has far-reaching consequences because many of current mathematics—notably analysis and set theory—depends greatly on infinite ideas (Van Atten, 2023).

3.2. Ultrafinitism

Asserting that not only are infinite sets non-existent but also there is an upper bound on the size of numbers or mathematical objects that can be meaningfully considered, ultrafinitism is a still more extreme form of finitism. Though frequently unsaid, this upper boundary is indirectly related to what is computationally possible or physically realizable (e.g., the quantity of particles in the cosmos or the greatest number of computations a computer might execute within the lifetime of the world) (Anel & Carten, 2021). Ultrafinitists may contend that since 10100 (a googol) cannot be physically represented or modified in any actual way, it is not really a number in the same sense as tiny integers. This radical perspective questions the basic underpinnings of mathematics and begs serious issues about the nature of mathematical existence (Hansson, 2023).

3.3. Intuitionism and Constructivism

A bigger philosophy that stresses the need for constructive proofs (Skovsmose, 2024), constructivism especially as seen in Brouwer’s intuitionism. To demonstrate the existence of a mathematical object in constructivist mathematics, one has to offer a means of construction. In classical mathematics, existence can be proven by contradiction (e.g., assuming an object doesn’t exist and deriving a contradiction, without building the object), which stands in contrast.

Applied to infinite sets, intuitionism, a potent form of constructivism, resists the law of excluded middle—that a statement is either true or untrue—as one cannot constructively verify the truth of a statement about an infinite collection (McCarty, 2021). For intuitionists, infinite sets are considered as possibilities rather than as actual entities. The actual numbers, for instance, are regarded as a process of producing ever more accurate approximations (Ishihara, 2023), rather than as a terminated infinite set. Though not rejecting the notion of infinite extensibility, these ideologies radically change the terrain of what counts as a legitimate mathematical proof and which mathematical entities are regarded as real.

Though not generally used, these alternative systems underline the ongoing philosophical issues about infinity and show how math may be built on different foundational assumptions to generate different conclusions about the nature of mathematical truth and existence (Hartimo et al., 2024)

4. Infinity in Physics: From Cosmology to Quantum Mechanics

The difficulties brought on by infinity go beyond abstract mathematical theory; they infuse the whole cloth of our physical ideas. From the cosmological level to the quantum world, infinities usually arise as signs of theoretical failures or conceptual challenges (León, 2024).

4.1. Cosmological Infinities

Questions concerning the spatial and temporal extent of the cosmos immediately challenge the notion of infinity in cosmology. Is the universe spatially finite but unbounded (like the surface of a sphere) or infinite? Will time have a beginning (the Big Bang) and an end or will it span eternally backward and ahead? Although the Big Bang hypothesis proposes a finite past, the possibility of an unbounded future or an infinite huge universe is still up for discussion (Fletcher, 2021). Further complicating these issues is the notion of a multiverse, where countless worlds could coexist, therefore pushing the limits of what is empirically verifiable (de Adana, 2024).

Another well-known example are singularities, which are points where physical parameters become infinite. Often considered to be restrictions of our present physical theories (Maltsev, 2023), the singularity at the heart of a black hole—where spacetime curvature grows infinite—and the original singularity of the Big Bang—where density and temperature were infinite. Although mathematically obtained, these infinities are mostly seen as signs that our models are deficient and need a more basic theory—for example, quantum gravity—to solve them (Rovelli, 2020).

4.2. Infinities in Quantum Field Theory

The most successful theory to define basic particles and forces, Quantum Field Theory (QFT), is afflicted with infinity. Calculating in QFT often causes integrals to diverge, which produces infinite values for measurable properties such electron mass or charge (Halimeh et al., 2022). Developed to address these infinities by absorbing them into a redefinition of fundamental constants was the method of renormalization. Although very good at making precise forecasts, renormalization is seen by some as a sleight of hand, a practical workaround rather than a genuine resolution of the underlying infinities (FIELD & HARTZ, 2022). This brings up philosophical issues about whether these infinities are manifestations of a deeper, unresolved physical reality or artifacts of our mathematical theories.

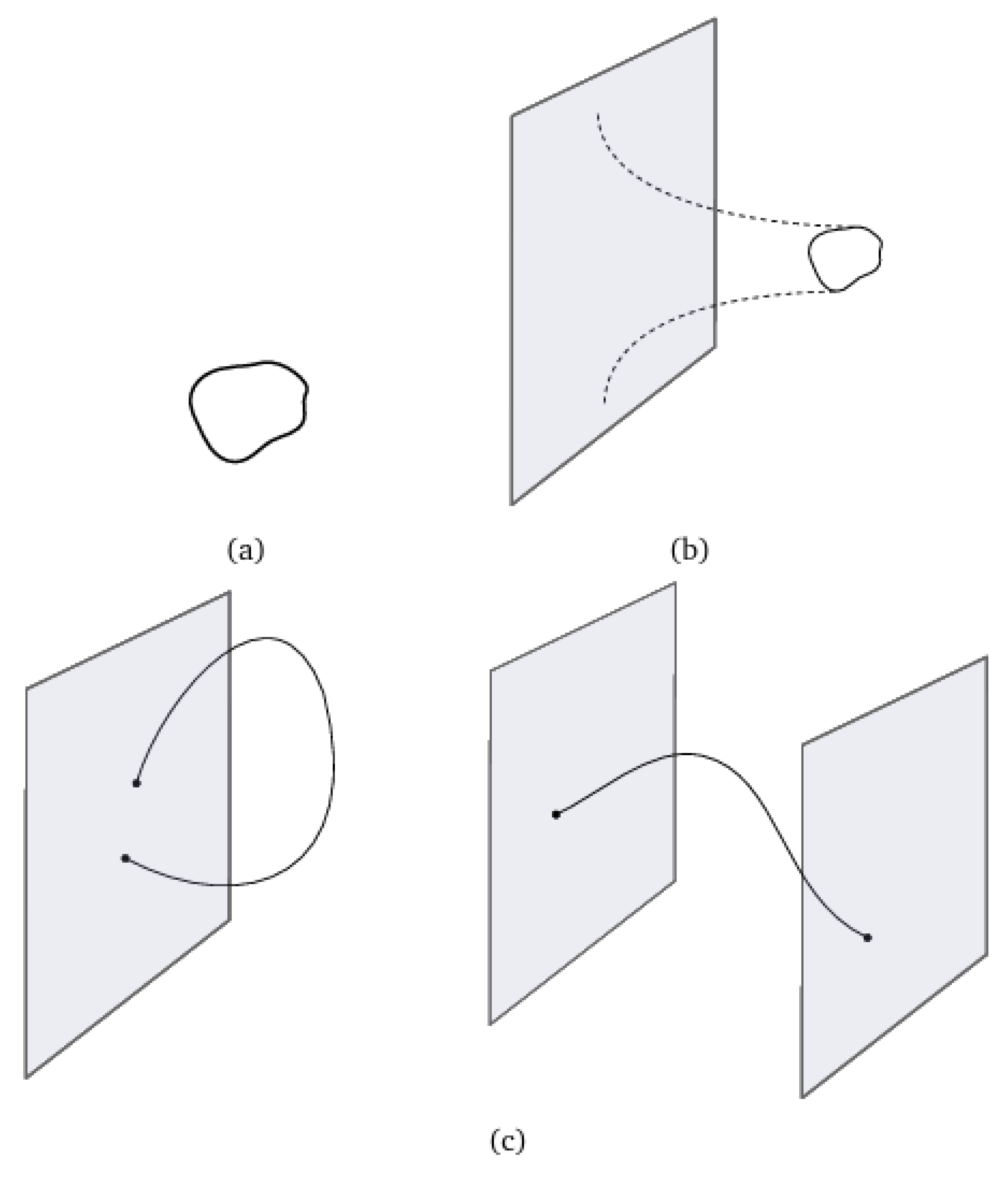
In QFT, the issue of ultraviolet divergences (infinities originating from very short distances/high energies) and infrared divergences (infinities stemming from very long distances/low energies) is still a dynamic field of study. Some physicists argue that the presence of infinities in modern theories points to their incompleteness, therefore suggesting that a truly basic theory of everything like string theory or loop quantum gravity should naturally be free of such infinities (Gil Hernández, 2023) , as simply demonstrated by Figure 2 (c.f., Maccaferri et al., 2025).

4.3. The Continuum in Physics

General relativity and traditional field theories depend on the hypothesis of a continuous spacetime, a manifold of infinitely divisible points. At the Planck scale—the smallest possible distances and times—quantum gravity models, however, propose that spacetime may be made up of fundamental quanta (Vladimir, 2024) rather than continuous. Should spacetime be truly discrete, then the infinite divisibility assumed in classical physics would break down, hence changing our understanding of space and time and eliminating infinities arising from continuous structures at the most basic level (Cinti et al., 2025). This marks a significant perspective change from a continuum model toward a more granular, finite portrayal of reality.

5. Open Problems and New Food for Scientific Thought

Infinity presents persistent difficulties that might lead in many directions for fresh philosophical and scientific investigation. These open difficulties are basic concerns that might fundamentally alter our conception of mathematics, physics, and the nature of reality itself—not only technical obstacles.

5.1. The Character of Mathematical Existence

Among the most significant unresolved issues is the nature of mathematical existence. Mathematical objects—especially infinite ones—exist independently of human thought (Platonism) or are mental constructs (constructivism, intuitionism) or merely useful fictions (formalism). The ontological issues we must face are raised by the arguments over infinity. Should infinity only be a potentiality, what consequences for theories depending on actual infinities—such as classical set theory—arise? (Landry, 2022). Exploring nonclassical logics and foundational systems that do not rely on the axiom of infinity might lead to novel mathematical paradigms (Dybjer & Setzer, 2022).

5.2. Resolving Physical Infinity

Many people think the infinities found in quantum field theory and cosmology are indications of unfinished science. For example, the search for a theory of quantum gravity is mostly motivated by the need to reconcile QFT’s divergences with general relativity’s singularities (Kiefer, 2023). At the most basic levels, new ideas—string theory, loop quantum gravity, and causal set theory—provide alternative views on how these infinities might be avoided or naturally normalized (Franklin & Robertson, 2024). Achievement in this project would not just unify physics but also give a clearer picture of whether infinity is a trait of actual reality or a byproduct of our present-day descriptive instruments.

5.3. The Function of Finitude and Computation

The practical constraints of infinite processes have received fresh respect as computational models and complexity theory have developed. Fundamentally a computational system, or if our ability to observe and interact with it is limited, then what are the implications for the idea of infinity? (Feri, 2025). Though extreme, ultrafinitism stresses the practical limitations on what can be known or calculated within a finite universe. This viewpoint promotes the creation of mathematics more in line with physical limits and computational feasibility, therefore possibly generating fresh numerical techniques and algorithms (Miller, 2023).

5.4. Revisiting the Continuum

Classical physics is deeply rooted in the idea of a continuous spacetime and continuous quantities. Conversely, the prospect of a discrete spacetime at the Planck scale—or the intrinsic discreteness of quantum events—indicates that the continuum may be an emergent property instead than a fundamental one (Etingof, 2024). An active field of research is developing mathematical models that either provide a smooth transition between discrete and continuous descriptions or do not depend on the continuum. (Van Suijlekom, 2025) suggests several approaches to calculus, noncommutative geometry, or novel kinds of discrete mathematics.

5.5. Philosophical Implications for Human Cognition

At last, the battle with infinity highlights also the limitations of human intuition and understanding. Our experience is based in a limited world, and our minds are naturally limited. Infinite sets and processes have counterintuitive characteristics that imply our intuitive grasp of numbers and amounts may collapse at extreme scales (Lakoff & Núñez, 2000). Investigating the cognitive origins of mathematical ideas such as infinity may help to highlight how we build our mathematical reality and where our intuitive biases might lie (Dehaene et al., 2025).

6. Conclusion: Infinity as a Frontier of Knowledge

The idea of infinity is anything but straightforward; it’s a lively and complex area of intellectual exploration. While we’ve made great strides in mathematically defining it, the philosophical and physical implications of infinity still raise deep and thought-provoking questions. The presence of infinities in our most advanced physical theories, historical scepticism, and the growth of competing mathematical viewpoints such as constructivism and finitism all hint to ongoing intellectual debate. These are more than just academic quandaries; they are significant unresolved questions that could lead to new insights into philosophy, physics, and mathematics. Its enduring mystery forces us to reassess our most fundamental assumptions about numbers, space, time, and the underlying nature of reality, regardless of whether we see infinity as a real phenomenon, a helpful metaphor, or a symbol of the limits of our current understanding. We enable ourselves to investigate new lines of scientific inquiry by facing the discomfort and conflicts that infinity presents. This broadens the boundaries of knowledge and fosters a deeper, more complex comprehension of the cosmos in which we exist. A true reflection of the boundless curiosity that characterises the human soul is the quest to understand infinity, or even to contemplate its absence.