Exploring Depth Estimation Algorithms with Light Fields for Image Segmentation

I. Introduction

II. Motivation and Objective

III. Related Works

IV. Methods

Dataset

We are using the 4D Light Field Benchmark Dataset to the experiments is the development of a dataset that can be used for training the depth estimation method and the background estimation method. We make modifications to a well-known light field dataset to make it suitable for image segmentation applications. The dataset has only a small number of training and test images, but the images are high quality and contain challenging occlusion and foreground-background geometry. In order to provide ground truth depth images, we use the segmentation information available with the original dataset, which is constructed by human operators. Only the global segmentation information is used; at each pixel, labels available with the dataset indicate whether the pixel is known and belongs to the foreground or the background. These labels can be directly assigned to the known pixels in an image, while the unknown pixels are filled in by open-inpainting methods. The 4D Light Field Benchmark consists of a grid of 9 × 9 angular views, with each view captured at a spatial resolution of 512 × 512 pixels. We evaluated quantity based on three data points the Pascal VOC and Filter dataset light field object detection and segmentation with 17×17 views and 960 × 1280 resolution [6].

A. Least Squares Gradient (LSG) Method

Now, we present a brief summary of LSG solutions in the case of the RoI problem when using the disparity degree image. Consider the correspondence energy function, which is minimized over the pulse interval in a various particular way. Namely, different smoothness and data terms are applied. If the energy function does not contain discontinuity-preserving terms, the straightforward application of the RoI method results in the double local integrals, which gives several pixels satisfying. Thus, the output is interconnected subpixel accurate [7]. Such a RoI method that is independent of the determination of the neighboring pixels of the problem pixel does not belong to the app-fragment class of sound pixels interpolation methods. When a point of view is shifted, an image patch is also displaced as $d{∆}_x$ and $d{∆}_y$. However, the lead's equation is the following equality:

L(x, y, u, v) = L(x − d∆x, y − d∆y, u + ∆x, v + ∆y)

We can use one additional term to obtain the app-square method, which is one among those having a much wider application area for light field sensors, including also non-planar ones. It does not modify the delta sensitivity at turning points and preserves the delta magnitude sensitivity at them. We modified the parameters of the L interpolation method; another derivative sensitivity in the simple turning points can also be preserved. Some other 3D sensor models based on RoI or Culmann integration methods were in the state of patent applications or patents describing the device construction. This connection has been restructured and reinterpreted for all picture patches as a squared error E, which will be reduced in proportion to d.

$$E={\int }_{\alpha }\sum _p\left[L\left(x,y,u,v\right)-L\left(x-d{\Delta }_x, y-d{\Delta }_y, u+{\Delta }_x, v+{\Delta }_y\right)\right]$$

$$d^{*}=\arg \underset{d}{\min }E$$

Consequently, by resolving the above optimization issue, we get the following conclusion:

$$d^{\mathrm{*}}={\displaystyle \frac{{\sum }_p\left(L_x{L}_u+L_y{L}_v\right)}{{\sum }_p\left(L_x^2+L_y^2\right)}}$$

The displacement between the object's image across all light field images is denoted by $d^{\mathrm{*}}$. In the context of light field analysis, spatial intensity variations are denoted x by $I_x$ and $I_y$for the horizontal and vertical axes, respectively, whereas $I_u$and $I_v$ correspond to gradients along the angular dimensions, capturing directional changes across different viewpoints.

B. Plane Sweeping Method

We applied another commonly used cost-volume creation method, the plane-sweeping algorithm. This leads to dense depth estimation given the set of multi-view images. The algorithm is designed to identify correspondences between the images, improve on epipolar scan-line correspondence techniques, and use the strength of cues such as inter-image color gradients and inter-image gradient pair changing trends. Based on the significant depth inconsistency regions of subsequent frames starting with a small number of frames, we present the concept of local planes to identify the relevant corresponding features [8]. Additionally, the performance will be enhanced with many points corrected. The light-field data undergoes 4D shearing to refocus each view to the center view, as demonstrated in the formula.

$$Ld\left(x, y, u, v\right)=L\left(x+ud, y+vd, u, v\right)$$

Let $L_d$ represent the disparity-adjusted light field view and L the original light field. The light field is parameterized using spatial coordinates ( x , y ) and angular coordinates ( u , v ), which are used to achieve horizontal and vertical alignment of the views. Following this alignment process, the images are stacked together, and a cost volume C is constructed. The cost is computed based on the variance across views, serving as the matching function for disparity estimation.

$$\overline{L_d}\left(x,y,u,v\right)={\displaystyle \frac{1}{\left|U\right|\left|V\right|}}\sum _{u\exists U}\sum _{v\exists V}{L}_d\left(x,y,u,v\right)$$

$$C\left(x,y,d\right)={\displaystyle \frac{1}{\left|U\right|\left|V\right|}}\sum _{u\in U}\sum _{v\in V}{\left(L_d\left(x,y,u,v\right)-\overline{L_d}\left(x,y,u,v\right)\right)}^2$$

Here, $\overline{L_d}\left(x,y\right)$denotes the mean of $L_d\left(x,y,u,v\right)$ computed over all angular views, where U and V represent the complete sets of discrete angular coordinates in the light field. The terms $\left|U\right|$ and $\left|V\right|$ correspond to the cardinalities of these sets, indicating the number of angular samples along each dimension. The cost volume is filtered using a 3 x 3 box filter to create a visually appealing result and remove noise. The optimal disparity, denoted as $d^{*}$, is obtained after constructing and refining the cost volume, and it serves as the resulting disparity map.

$$d^{*}=\arg \underset{d}{\min }C\left(x,y,d\right)$$

The method of plane sweeping receives relatively sparse and irregular points using a triplet and motion vector in a forward and backward direction it subsequently produces a dense disparity map by utilizing the matching cost based on pixel correspondence. Since the features of the multi-view images are aligned on the plane of the epipole line, the basic premise is that the local epipole plane of the feature point can be identified. By regarding the feature detected in the keyframe as the midpoint of the local plane, it is matched in pairs with the matching cost to generate the disparity at the corresponding feature point. For the feature points with no estimate, the multi-view matching cost corresponding to the sparse points is observed over a wide range of points, and the disparity estimate relies on the smoothness constraint. Using the wide motion vector provides a larger amount of matching between the wide point cloud than that of the epipolar scan line. The experiment displays that the disparity image obtained should be increasingly accurate when monitoring the wide range of 3D areas [9].

C. Epipolar-Plane and Fine-to-Coarse Refinement Method

The goal of image segmentation in dept map light field is to label each pixel with its semantic context. State-of-the-art 3D segmentation algorithms struggle with segmenting objects not visible in the input, and in some applications, an accurate depth map can alleviate the problem. Depth information can be acquired through a variety of techniques, but none are as universal and common as a simple RGB camera. We experiment with Multiview 3D reconstruction algorithms that utilize light fields to generate the depth map. We present a novel technique that combines a generic method of creating foam segments from depth and uses the corresponding color information to refine edges and fill holes. In this section, we present an epipole-plane image (EPI), then explain how it can be generated and mapped bilaterally for increased resolution and finally detail the fine-to-coarse estimation process. We used high-resolution photos to generate a depth map from a dense 3D light field [10]. However, there is no global optimization method for every pixel handled in parallel GPU efficiency. In this project, the approach is a somewhat more straightforward variation of obtaining the depth map in the central view. We disregard the propagation portion of this process. We have extended our 3D technique to 4D [14]. First, we compute Edge Confidence Ce as:

$$C_e\left(x,y\right)=\sum _{\left(x^{\text{'}},y^{\text{'}}\right)\in N\left(x,y\right)}|I\left(x,y\right)-I\left(x^{\text{'}},y^{\text{'}}\right)|$$

Where the central view image $I$ is displayed in a 3 x 7 window, with a threshold of 0.05 in level 0 and 0.1 in every other level in our fine-to-coarse procedure. Secondly, for each pixel $(x,y)$ in $I$, we sampled a collection of radiance R from various perspectives $R\left(x,y,u,v,d\right)=L\left(x+\left(\widehat{u}-u\right)d,y+\left(\widehat{v}-v\right) d,s,t\right)|s=1..n, t=1..m$where n denotes the number of horizontal views and m the number of vertical views. The color density score (S) can be calculated as follows:

$$S\left(x,y,d\right)={\displaystyle \frac{1}{R\left(x,y,u,v,d\right)}}\sum _{r\in R\left(x,y,u,v,d\right)}K\left(r-\overline{r}\right)$$

Where K denotes a kernel $K\left(x\right)=1-\parallel {\displaystyle \frac{h}{x}}$ when $\parallel {\displaystyle \frac{h}{x}}\parallel \le 1$ and 0 otherwise. We set h = 0.1 in here. Firstly$, \bar{r}$ is the radiance corresponding to the pixel which is calculating S. To emphasize r more robust, we will update$\bar{r}$ iteration by mean-shift algorithm as:

$$\overline{r}\leftarrow {\displaystyle \frac{\sum K\left(r-\overline{r}\right)r}{\sum K\left(r-\overline{r}\right)}}$$

Thus, we select the disparity $d^{*}$ that maximizes the score function S denoted $d^{*}=\arg \underset{d}{\max }S\left(x,y,d\right).$We only keep the value of $d^{*}$with Depth Confidence $C_d$higher than ε = 0.03. We can compute $C_d$as below:

$$C_d\left(x,y\right)=C_e\left(x,y\right)\left|\right|S_{max}-\overline{S}\left|\right|$$

We will generate the disparity map $D(x, y)$and denoise it uses a 3 × 3 median filter. We will save this map for the fine-to-coarse step. We will refine the disparity bound of unassigned $d^{*}$ pixels. Finally, we will initiate the fine-to-coarse process to interpolate low $Cd$ disparity map pixels. The central view picture $I$ is initially subjected to a Gaussian filter with a kernel size of 7 × 7 and a standard deviation $\left(\sigma \right)=\sqrt{0.}5.$At last, after Gaussian blurring, we down-sample $I$ by a factor of 0.5. We start with the computation of $C_e$. This iterative process continues until the size of I is reduced to fewer than 10 pixels. Then, we up-sample the disparity maps from the course to densest level for filling-up all the pixels without disturbing the $d^{*}$ that we computed for finer levels and combined them all as the final disparity map D.

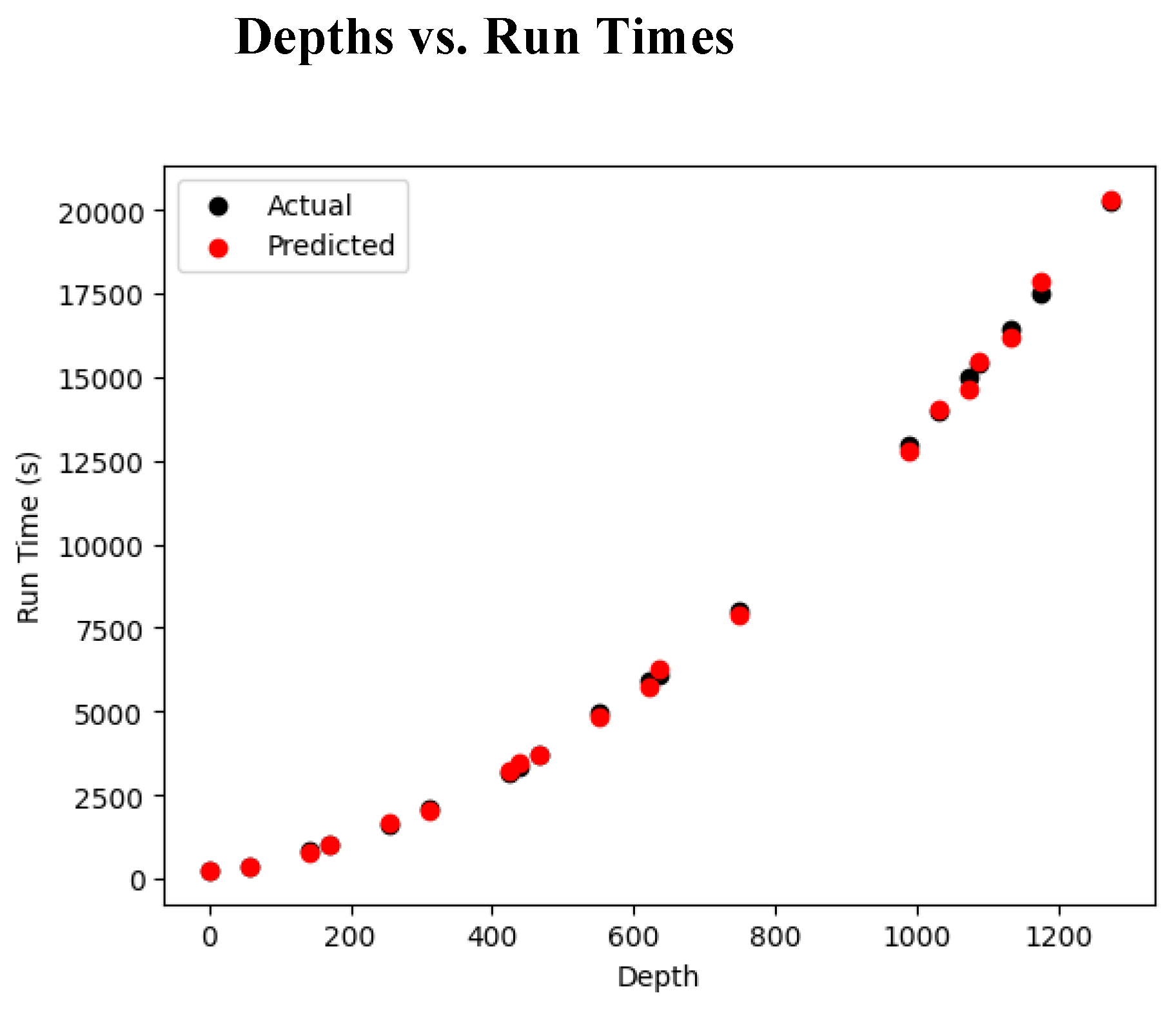
Figure 1. Depths vs. Run Times (in seconds).

Figure 1. Depths vs. Run Times (in seconds).

The depth estimation method utilizes multiple images of the scene to estimate the depth for every pixel. A unique characteristic of light fields and the lens arrangement we utilize in the applicable algorithms is to synthesize the epipole-plane image (EPI). The patch-based method refines depth variations present in the scene slice parallel to the lenslet array by utilizing the adjacent texture information in the input. Depth can be used to identify thin to moderate foam segments [11]. The characteristic cushion and porous foam segments can be identified using depth, color, and edge information only. The EPI image can be synthesized at a much higher resolution than the original placed texture data, increasing the quality of the estimated depth. By refining the depth variations present in the EPI, missing spatial pixels are estimated with increased accuracy.

V. Results

C. Plane Sweeping Method

The plane sweeping method also requires the rectified light field as input and the depth map produced as output. Thus, though it can only estimate disparities between neighboring views, we are unable to obtain both a smooth depth map and accurate disparities simultaneously in this way. However, we use an integral line within the camera for the reaction. A greater span of the integral line indicates a larger spatial separation between neighboring points both of these competing requirements produce a significant disparity. The output of this method is a smooth, complete, and largely accurate depth map [15]. Preview the proposed algorithm below.

Algorithm 1: The algorithm depicted, titled depth estimation from light field, outlines a multi-stage approach to generate a refined disparity or depth map from a 4D light field image. It begins with preprocessing steps including segmentation and normalization. The core depth estimation involves computing local structure gradients (LSG), plane sweeping using disparity hypotheses, and EPI-based fine-to-coarse estimation leveraging epipolar plane image structures. Post-processing includes median filtering and iterative refinement steps such as Gaussian blurring, down sampling, and up sampling to progressively enhance the resolution and accuracy of the disparity map. The final output is a high-quality, refined depth estimation.Algorithm

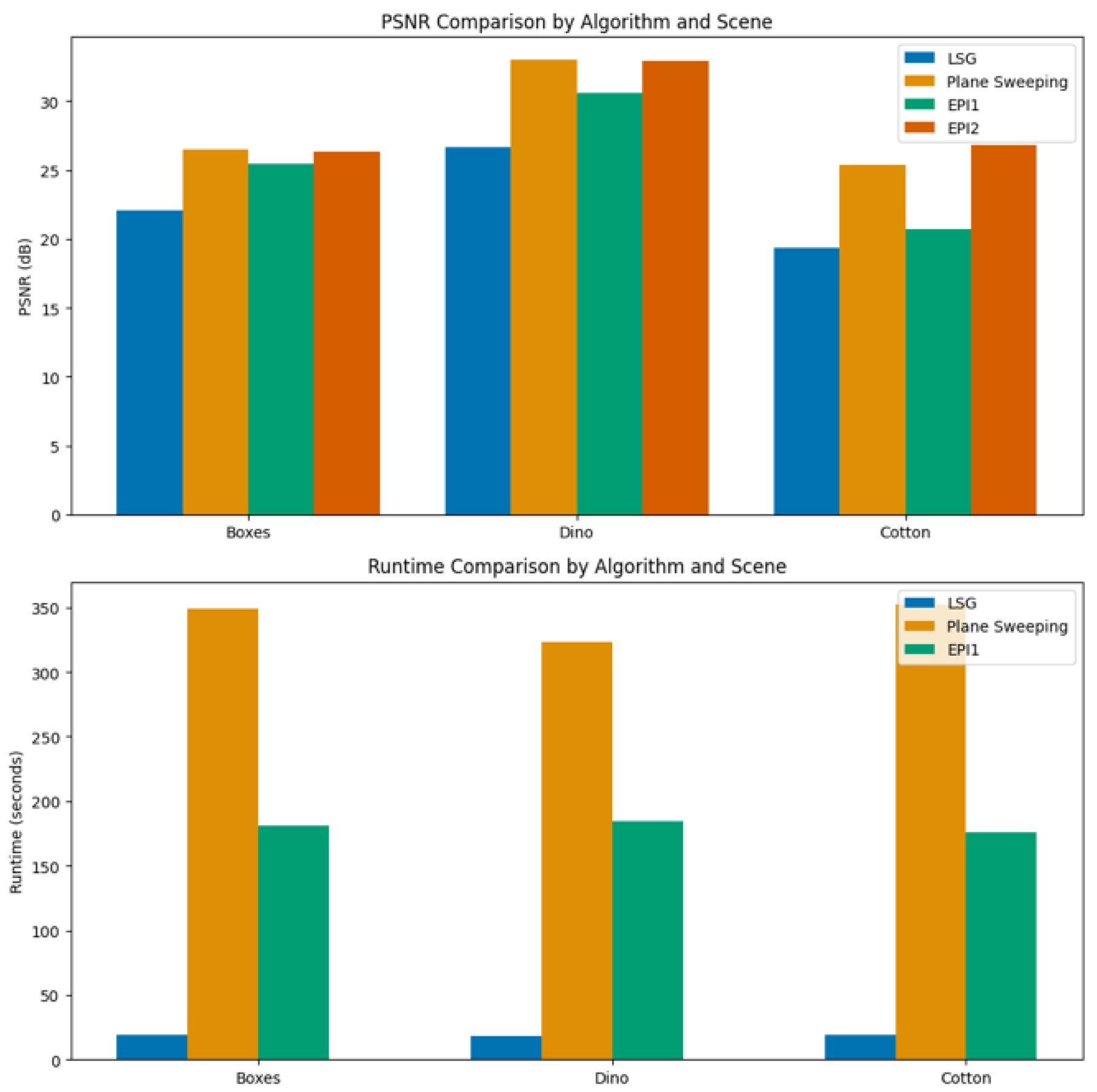
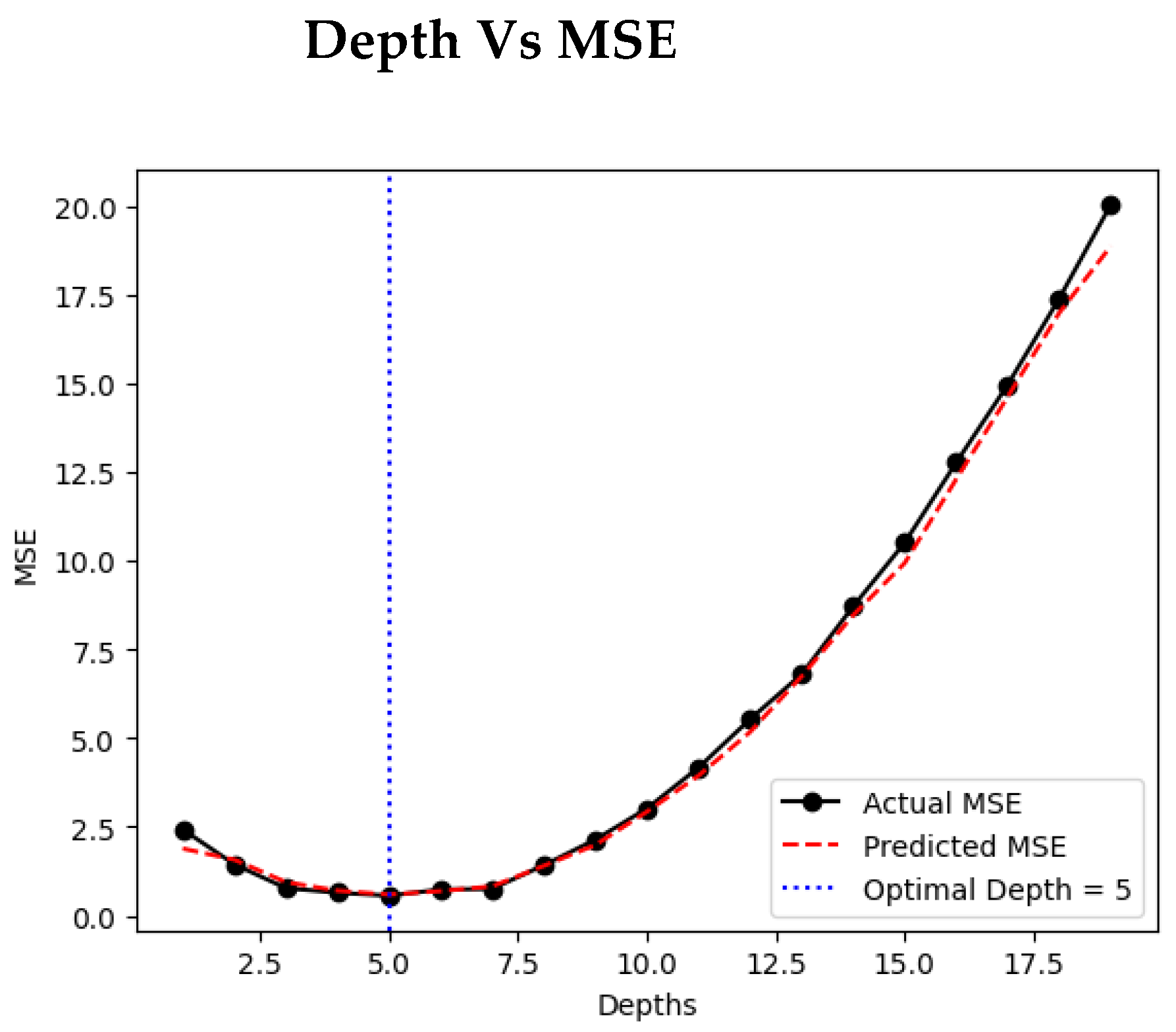
Increasing the number of depth samples allows the algorithm to examine a broader range of disparity values, improving the precision in selecting the most accurate match. This pattern is observable in Figure 3, which illustrates a decline in Mean Squared Error (MSE) as depth granularity increases. Given the current disparity range of -2 to 2, this result aligns with expectations. However, the reduction in MSE remains minimal, with differences on the scale of ${10}^{-4}$, suggesting diminishing returns with further depth subdivisions. Consequently, the main experiments were carried out using 11 discrete depth layers to balance accuracy with computational cost. From a visual standpoint, the reconstructed outputs show a strong resemblance to the ground truth images, as evidenced by results in Table 2 and Table 3. The quantitative evaluation further supports this observation: PSNR values (Table 4) are notably high, indicating effective reconstruction fidelity relative to competing techniques. Additionally, Table 3’s error visualizations reveal that the 'boxes' and 'cotton' datasets exhibit minor foreground errors (seen in darker pixel regions), while the 'dino' dataset shows more pronounced differences, particularly in the foreground, where higher pixel intensity implies greater disparity from the ground truth.

Figure 2. Comparison of PSNR and Runtime for Different Algorithm.

Figure 2. Comparison of PSNR and Runtime for Different Algorithm.

Figure 3. Relationship Between Number of Depth Planes and Mean Squared Error (MSE). This figure illustrates the inverse relationship between the number of sampled depth planes and the corresponding MSE during disparity estimation. As the number of depths increases, the algorithm can better approximate true disparities, resulting in improved accuracy. However, the rate of MSE reduction diminishes beyond a certain point, suggesting limited performance gains at the cost of increased computation. Semantic segmentation assigns a semantic label to every pixel in the image, grouping pixels with similar categories. Instance segmentation extends this by reflects both object identity and its corresponding depth [21,22].

VI. Conclusion and Future Work

References

1. Leistner, T., Mackowiak, R., Ardizzone, L., Köthe, U., & Rother, C. (2022). Towards multimodal depth estimation from light fields. https://arxiv.org/pdf/2203.16542. [CrossRef]
2. Jin, J. & Hou, J. (2021). Occlusion-aware Unsupervised Learning of Depth from 4-D Light Fields. https://arxiv.org/pdf/2106.03043. [CrossRef]
3. Anisimov, Y., Wasenmüller, O., & Stricker, D. (2019). Rapid Light Field Depth Estimation with Semi- Global Matching. https://arxiv.org/pdf/1907.13449. [CrossRef]
4. Lahoud, J., Ghanem, B., Pollefeys, M., & R. Oswald, M. (2019). 3D instance segmentation via multitask metric learning. https://arxiv.org/pdf/1906.08650. [CrossRef]
5. Petrovai, A. & Nedevschi, S. (2022). MonoDVPS: A Self-Supervised Monocular Depth Estimation Approach to Depth-aware Video Panoptic Segmentation. https://arxiv.org/pdf/2210.07577. [CrossRef]
6. Anisimov, Y. & Stricker, D. (2018). Fast and Efficient Depth Map Estimation from Light Fields. https://arxiv.org/pdf/1805.00264. [CrossRef]
7. R, A. & Sinha, N. (2021). SSEGEP: Small SEGment Emphasized Performance Evaluation Metric for Medical Image Segmentation. https://arxiv.org/pdf/2109.03435. [CrossRef]
8. Schröppel, P., Bechtold, J., Amiranashvili, A., & Brox, T. (2022). A benchmark and a baseline for robust multi-view depth estimation. https://arxiv.org/pdf/2209.06681. [CrossRef]
9. de Silva, R., Cielniak, G., & Gao, J. (2021). Towards agricultural autonomy: crop row detection under varying field conditions using deep learning. https://arxiv.org/pdf/2109.08247. [CrossRef]
10. Cakir, S., Gauß, M., Häppeler, K., Ounajjar, Y., Heinle, F., & Marchthaler, R. (2022). Semantic Segmentation for Autonomous Driving: Model Evaluation, Dataset Generation, Perspective Comparison, and Real-Time Capability. https://arxiv.org/pdf/2207.12939. [CrossRef]
11. Honauer, K., Johannsen, O., Kondermann, D., & Goldlüecke, B. (2017). A dataset and evaluation methodology for depth estimation on 4D light fields. Lecture Notes in Computer Science, 19-34. [CrossRef]
12. Wikipedia contributors. (2018, November 18). Focus stacking. Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/Focus_stacking.
13. Wikipedia contributors. (2017, August 28). Shift-and-add. Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/Shift-and-add.
14. Kim, C., Zimmer, H., Pritch, Y., Sorkine-Hornung, A., Gross, M., & Sorkine, O. (2013). Scene reconstruction from high spatio-angular resolution light fields. https://dl.acm.org/doi/10.1145/2461912.2461926. [CrossRef]
15. Yucer, K., Sorkine-Hornung, A., Wang, O., & Sorkine-Hornung, O. (2016). Efficient 3D object segmentation from densely sampled light fields with applications to 3D reconstruction. ACM Transactions on Graphics, 35(3), Article 22. [CrossRef]
16. Y. Anisimov and D. Stricker, "Fast and Efficient Depth Map Estimation from Light Fields," 2017 International Conference on 3D Vision (3DV), Qingdao, China, 2017, pp. 337-346. [CrossRef]
17. Zhang, Z., & Chen, J. (2020). Light-field-depth-estimation network based on epipolar geometry and image segmentation. Journal of the Optical Society of America A, 37(7), 1236-1244. [CrossRef]
18. Gao, M., Deng, H., Xiang, S., Wu, J., & He, Z. (2022). EPI Light Field Depth Estimation Based on a Directional Relationship Model and Multiview point Attention Mechanism. Sensors, 22(16), 6291. [CrossRef]
19. Zhang, S., Liu, Z., Liu, X., Wang, D., Yin, J., Zhang, J., Du, C., & Yang, B. (2025). A Light Field Depth Estimation Algorithm Considering Blur Features and Prior Knowledge of Planar Geometric Structures. Applied Sciences, 15(3), 1447. [CrossRef]
20. Kamal Nasrollahi and Thomas B. Moeslund. 2014. Super-resolution: a comprehensive survey. Mach. Vision Appl. 25, 6 (August 2014), 1423–1468. [CrossRef]
21. Kong, Y., Liu, Y., Huang, H., Lin, C.-W., & Yang, M.-H. (2023). SSegDep: A simple yet effective baseline for self-supervised semantic segmentation with depth. arXiv preprint arXiv:2308.12937. https://arxiv.org/abs/2308.12937. [CrossRef]
22. Cheng, B., Collins, M. D., Zhu, Y., Liu, T., Huang, T. S., Adam, H., & Chen, L.-C. (2020). Panoptic-DeepLab: A simple, strong, and fast baseline for bottom-up panoptic segmentation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 12475–12485. [CrossRef]