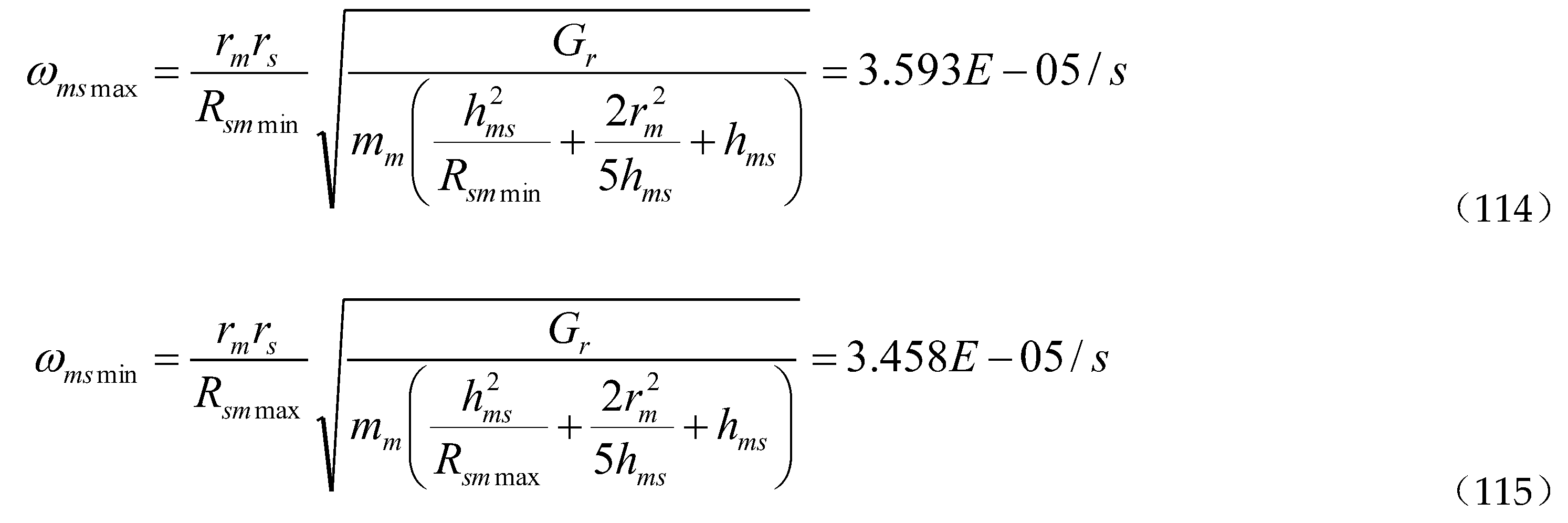1. Introduction
In 1609, Kepler [
1] published his first and second laws of planetary motion. The first law states that the orbit of a planet is an ellipse, with the sun at one focus of the ellipse; the second law states that lines connecting the planet and the sun sweep out equal areas in equal intervals of time. The essence of Kepler's second law is the law of conservation of angular momentum in planetary motion [
2]. In 1687, Isaac Newton stated the law of universal gravitation in "Mathematical Principles of Natural Philosophy" [
3]. The law of universal gravitation states that there is a gravitational force between any two objects in the universe, and its magnitude is proportional to their masses and inversely proportional to the square of the distance between them. Newton's universal gravitation provides the centripetal force for planets to move and explains the source of power for planets to move in elliptical orbits.
This article analyzes the gravitational force between planets, successfully simulates the elliptical orbit of the planet, and analyzes the causes of related gravitational coefficients, planetary precession and precession, the tumbling of 'Oumuamua and artificial satellites, seasonal changes and cyclical changes in the Earth's rotation, the long-term slowdown of the Earth's rotation speed, changes in the Earth's rotation rate are strongly related to the orbital motion of the sun, the rapid reverse rotation of the Earth's core, and the synchronous rotation of the planet.
2. The Equivalent Spherical Surface of the Planet Emitting Gravitons
The article "Gravity, Gravitational Field and Gravitons - Inference on the Frequency of Gravitational Energy Waves" [
4] believes that the most basic unit of matter is the nucleon (the collective name for protons and neutrons), and all nucleons emit gravitons, which carry The energy of is Planck's constant h, with a value of 6.626×10^(-34) J·s. Gravitons propagate in space as gravitational energy waves. When the gravitational energy waves encounter other nucleons, they resonate with them and transfer energy to form gravity. The deflected gravity theory [
5] believes that the gravitons emitted by the cores inside the planet interact with other nuclei inside the planet to form the cohesion of the planet. Some of the gravitons emitted by the cores in the shell near the outside of the planet are emitted outside the sphere and propagate in space as gravitational energy waves. When the gravitational energy waves encounter the nuclei of other planets, they resonate with them and transfer energy to form the gravitational force between the planets.
Figure 1 is a schematic diagram of the equivalent sphere of the planet emitting gravitons. In the figure, rs is the radius of the planet, and rso is the thickness of the graviton shell sent by the planet to the outside of the sphere. There should be a sphere rse in the middle. It can be considered that all the gravitons of the planet are emitted by this sphere. If this sphere is used as the equivalent sphere of the planet's graviton emission, in general, this sphere can be considered to be in the middle of the planet's graviton emission shell. The article "On the Nuclear Force is the Manifestation of Gravity at Microscopic Distances" [
6] calculated the number of gravitons emitted by a single nucleon based on the binding energy of hydrogen. The article "On the Relationship between Atomic Structure and Basic Forces" [
7] based on the analysis that the resonance of gravitational energy waves and nucleons conforms to the normal distribution, corrected the number of gravitons emitted by a single nucleon per second as:
The proportion of gravitons passing through a nucleon that can be absorbed by the nucleon is:
The article "An attempt to correct the formula of universal gravity based on the proportion of gravitons emitted by the planet to the outside of the sphere - the proportion of gravitons outside the sphere in the theory of deflected gravity" [
8] calculated the number of gravitons sent from the planet to the outside of the sphere. Among them, the thickness of the outer layer of the planet that can emit gravitons outside the sphere is:
In the formula, kng is the proportion of gravitons passing through the nucleon that can be absorbed by the nucleon, m0 is the nucleon mass, r0 is the nucleon radius, ρs is the density of the planet shell material, and the corrected value after bringing in the data is:
The number of gravitons sent from the planet to the outside is:
In the formula, ngo is the number of gravitons sent out of the planet by the planet, nng is the number of gravitons emitted by a single nucleon in one second, ko is the proportion of the outward facing part of the nucleon to the total surface area, kng is the proportion of gravitons passing through the nucleon that can be absorbed by the nucleon, r0 is the nucleon radius, rs is the planet radius, m0 is the mass of a single nucleon, and ρs is the density of the planet's shell material. After substituting constants and calculating:
When the planet is relatively large, the above formula is approximately:
Table 1 is a statistical table of the number of gravitons emitted by planets in the solar system to the outside of the sphere. The first column in the table is the name of the planet, the second column is the mass of the planet, the third column is the radius of the planet, the fourth column is the density of the planet's shell, the sun is the density of the photosphere, the earth is the density of the crust, the fifth column is the thickness of the shell that the planet can send out of the sphere, and the sixth column is the ratio of the thickness of the shell that can be sent out of the sphere to the radius of the planet. It can be seen that this The ratio is on the order of 10^-6. Column 7 is the number of gravitons sent out of the sphere calculated according to the above equation (6). Column 8 is the number of gravitons sent out of the sphere calculated based on the above equation (7). It can be seen that the simplified formula has no effect on the calculation of the number of gravitons sent out of the sphere. The last column is several commonly used constants. It can be seen from the above analysis that the thickness of the shell of the planet that emits gravitons is too small compared to the radius of the planet and can be ignored. Therefore, the equivalent shell radius of the planet that emits gravitons is approximately equal to the radius of the planet.
3. The Center of Mass of the Planet and the Point of Gravity Action
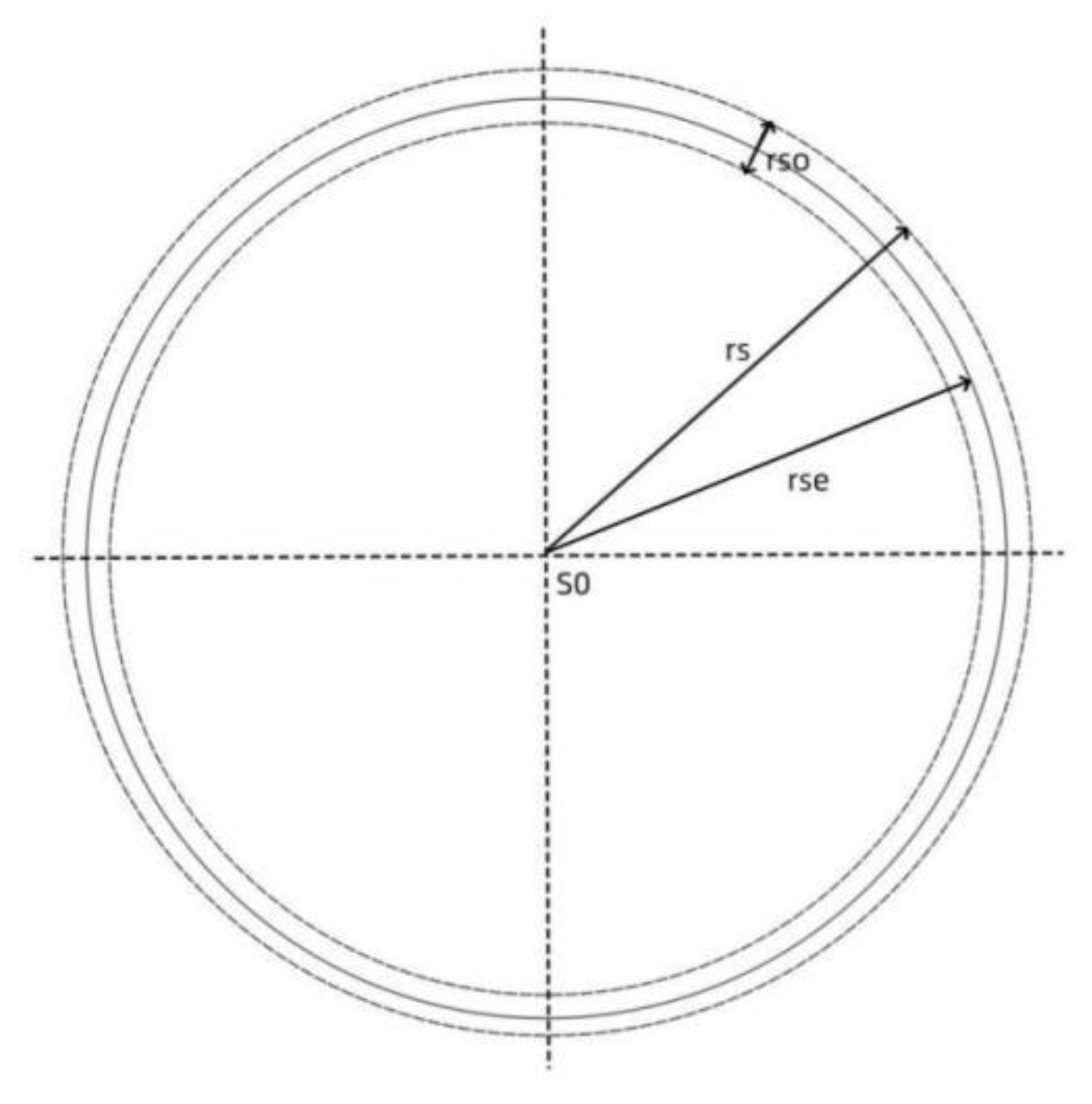
Figure 2 is an analysis diagram of the gravitational interaction between the two planets. In the picture, planet E rotates around planet S. The center of mass of the central planet S is S0, the radius is rs, and the mass is ms. The center of mass of the planet E is E0, the radius is re, and the mass is me. The distance between the centers of mass of the planets is R0. Now analyze the effect of planet S on planet E. In the figure, only the gravitons emitted by the nuclei on the spherical surface of planet S facing planet E can form a gravitational force on the shell nuclei of planet E facing planet S. This phenomenon can be demonstrated by the basic principles of gravity formation and the gravitational double valley phenomenon during solar eclipses [
9]. Before a solar eclipse occurs, objects on the ground are subject to the dual gravity of the sun and the moon, and the gravity of the earth will decrease. During the solar eclipse, the gravity of objects on the ground is measured, and the results show that the gravity of objects on the ground is the same as when there is only the sun, which means that the gravitons received by the sun on the ground are blocked by the moon.
To accurately calculate the effect of the gravitons emitted by planet S on planet E, we should calculate the gravitational force of each surface element on the spherical surface of planet S to each surface element on the spherical surface of planet E. When the distance between the planets is much larger than the planet radius, it can be approximately considered that the energy transferred between the spherical surface elements of the two planets is equal, so that the energy transmitted from the spherical surface of planet S to the spherical surface of planet E is proportional to the spherical area.
The calculation formula for the surface area of the spherical crown is S=2πRh. Obviously, the equivalent center of the nucleon that acts on the spherical surface of planet S is on the line connecting the centers of mass of the two planets, such as the Sg point in the figure. Suppose the distance between the center of gravity action and the center of mass S0 of planet S is hs, Ss1 is the area of the spherical crown above the point of gravity action, and Ss2 is the area of the entire spherical crown that emits gravitons, as follows:
For planet E, the area affected by planet S is larger than half a sphere. Therefore, the equivalent center of gravitational action is closer to the center of mass of planet E, as shown in Eg in the figure. Let the distance between the center of gravity and the center of mass be he, the area of the spherical crown below the point of gravity action of planet E is Se1, and the area of the entire spherical crown that can receive gravitons is Se2:
Assume that the distance between the equivalent gravitational centers of the two planets is Rg, and the gravitational action distance is
The gravitons emitted by all the nuclei on planet S facing planet E can reach planet E, and all the nuclei on planet E facing planet S can receive gravitons. Therefore, the energy transferred from planet S to planet E is:
The first term in the formula is the number of nucleons that can be distributed on the spherical surface of planet S facing planet E. The second term is the number of nucleons that can be distributed on the spherical surface of planet E facing planet S. The third term is the number of gravitons emitted by a single nucleon on spherical S and reaching a single nucleon on spherical E. nng is the number of gravitons emitted by a single nucleon. kse is the interaction probability between gravitons and nucleons. h is the energy exchanged between gravitons and nucleons. The above formula is simplified to:
in:
Generally, hs=0.5rs, he=0.5re, R>>hs, R>>he. After entering into formula 26 and modifying Gr, it becomes:
Here Gr is the gravitational coefficient, kse is the probability of interaction between the gravitons emitted by planet S and the nucleons of planet E, and h is Planck's constant. From the above analysis, it can be concluded that the energy (gravity) transferred by nuclei between planets is proportional to the surface area of the planet, not the mass of the planet. The gravity in Newton's universal gravitation is proportional to the mass of the planet is only an approximation for small objects.
4. Analysis of the Role of Gravity on the Movement of the Planet
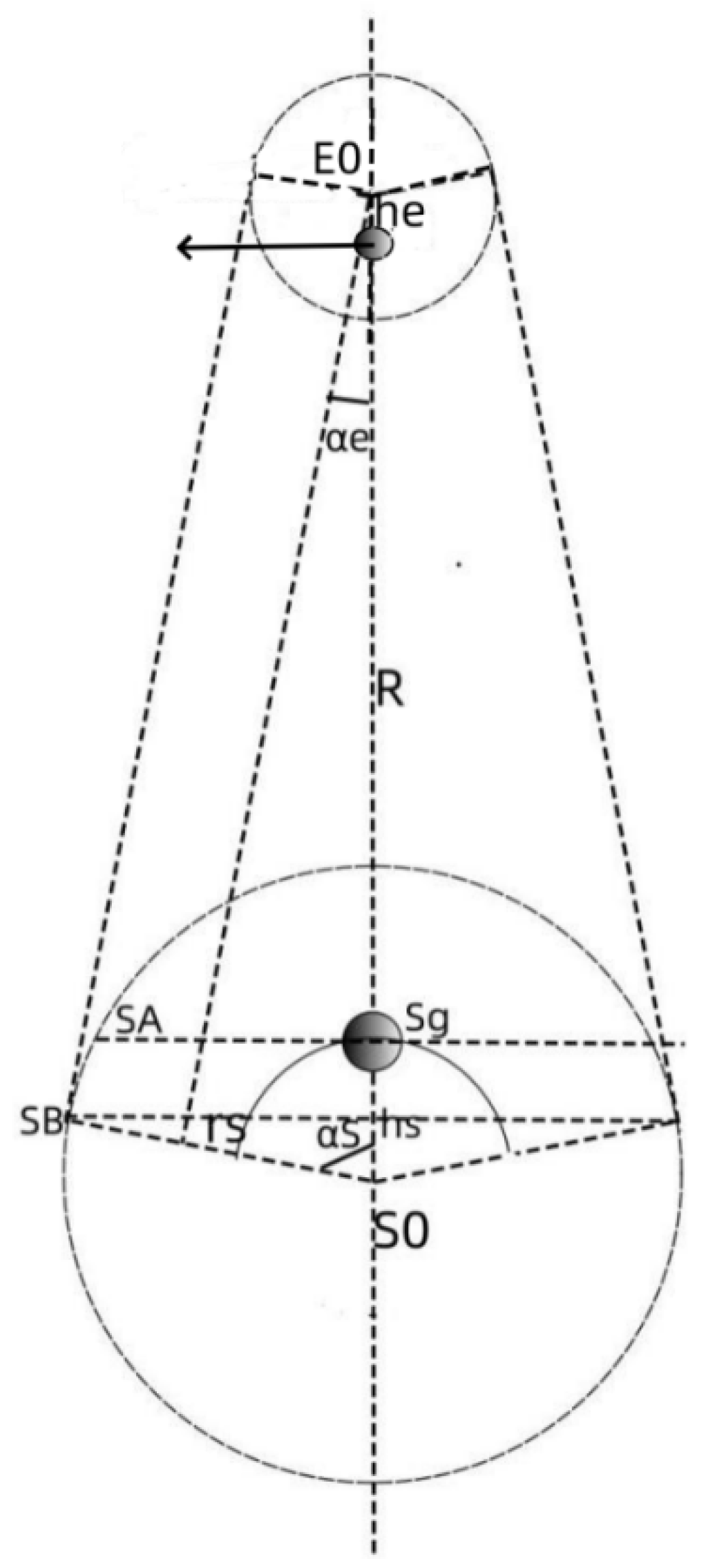
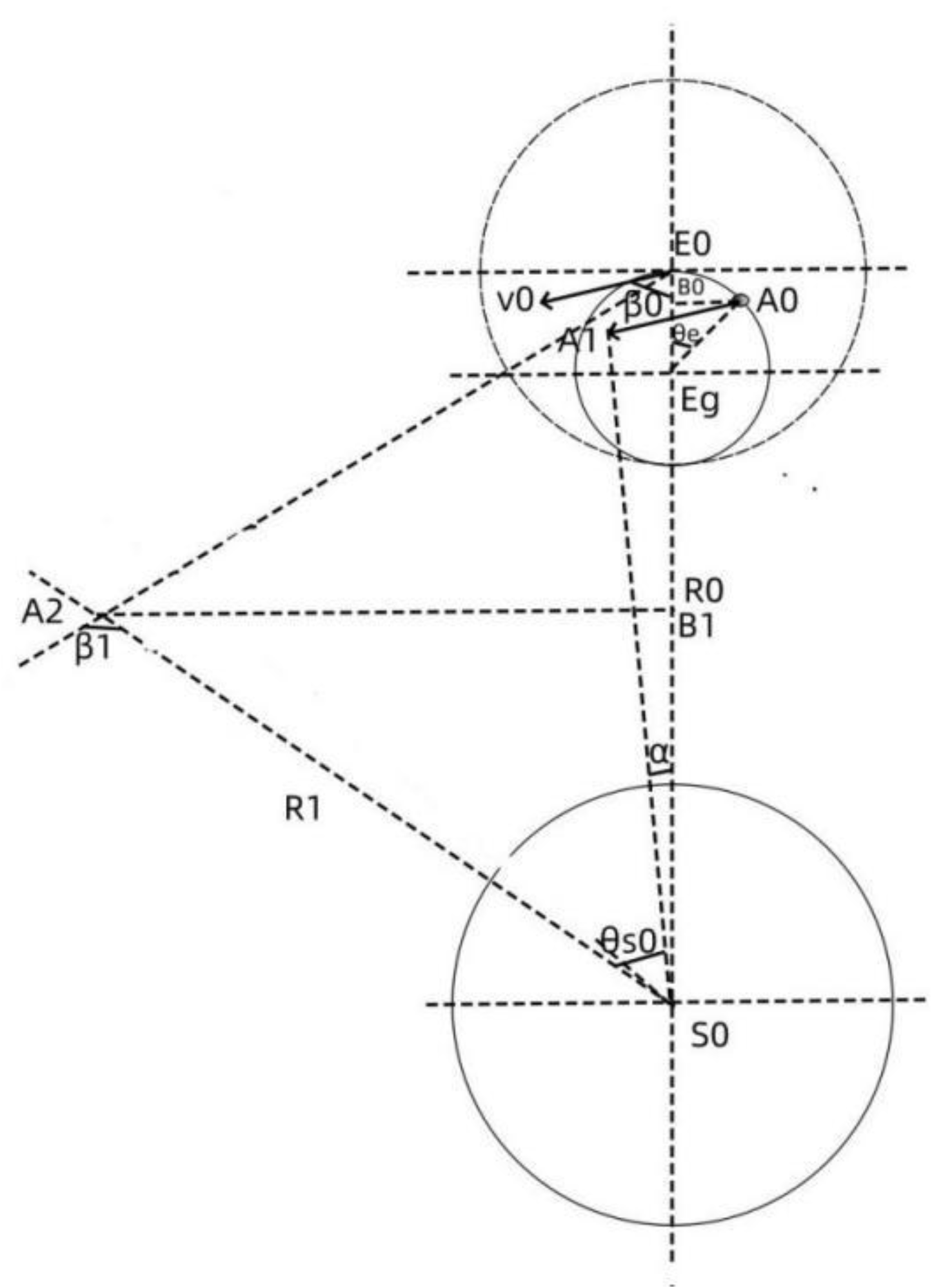
Figure 3 is an analysis diagram of the revolution and rotation of the planet caused by the gravity of the planet. In the figure, S0 is the center of mass of the central planet S, and E is the planet orbiting the central planet S. When the planet E is at the position E0, the gravitational effect point of the planet S on the planet E is Eg0. Since the gravitational point is separated from the center of mass of the planet, the gravity is divided into Fs0 related to the central planet S and Fe0 related to the planet E. When the same planet E is at the position E1, the gravitational force is divided into Fs1 and Fs1 related to the central planet S. Fe1 related to the planet E. When the planet E is at the position E2, the gravity is divided into Fs2 related to the central planet S and Fe2 related to the planet E. It can be seen that Fs0, Fs1, and Fs2 related to the central planet S all act on the gravitational point Eg of the planet, forming the driving force for the movement of the planet E around the planet S. In effect, Fs forms the centripetal force for the planet E to orbit the planet S.
Since the gravitational point Eg is separated from the center of mass of the planet, another effect of the gravitational force on the gravitational point Eg is to drag the planet E. Generally, the external force rotates around the center of the sphere. Without considering the movement of the planet E around the center planet S, it can be considered that the planet E has always been affected by a gravitational force Fe, and this point of action is fixed at the gravitational point Eg, so this is not The external force rotates around the planet. In contrast, the center of mass of the planet rotates around the point of gravity Eg. At the initial position E0, the center of mass of the planet has a tendency to move toward A0. As time goes by, the angle at which the center of mass of the planet rotates around the point of gravity Eg increases. Under the combined action of the two components of gravity, when the planet is at position E1, the center of mass moves to point A1. When the planet is at position E2, the center of mass moves to point A2.
According to the above analysis, the total gravity Fse of the planet is:
The components related to the revolution of planet E are:
In the formula, gravity causes the linear speed of planet E to orbit the central planet S as vs, unit m/s, the angular speed of revolution is Ωs, unit radians/s, and me is the mass of the object (unit kg).
For a rotating body, the moment of inertia is a physical quantity that describes the amount of inertia of an object when it rotates around a certain axis. For a uniform sphere, its moment of inertia is:
Among them, m is the mass of the sphere, r is the radius of the sphere, and ki is the moment of inertia coefficient. Generally, ki=0.4.
For a rotating body whose axis of rotation does not coincide with the center of mass, the parallel axis theorem states that the moment of inertia is:
Here m is the mass of the rigid body, Ic is the moment of inertia about the axis of rotation passing through the center of mass, and d is the distance between the axis of rotation and the center of mass.
It can be seen from this that the moment of inertia of the planet E rotating around the gravitational point Eg is:
In the formula, me is the mass of planet E, re is the radius of planet E, and he is the distance between the gravity point Eg and the center of mass of planet E.
According to the law of rotation of a rigid body on a fixed axis:
Where Mz represents the total external moment about a certain fixed axis, I represents the moment of inertia of the rigid body around a given axis, and α represents the angular acceleration. Here the torque is the component of gravity and the rotation of the planet. The moment arm is the distance he between the gravity point Eg and the center of mass of the planet. According to the definition of angular acceleration:
At this time, the fixed-axis rotation law of a rigid body can be written as:
Regarding the rotation of the planet, this refers to the component of rotation in the plane of the planet's revolution, which is generally not in the same plane as the actual rotation of the planet. Therefore, the angular speed of the planet's rotation here is not the angular speed of the planet's rotation that is usually observed.
For an object in circular motion, the relationship between its linear velocity and angular velocity is as follows:
According to the law of conservation of momentum, momentum cannot be created and destroyed out of thin air. For planet E, the revolution of the planet produces a positive momentum, and the rotation of planet E around the center of mass Eg produces a reverse momentum. The two should be equal:
Put the above result into equation 30:
Bring the 26 formula into:
Since the mass of the planet cannot be accurately measured, here is:
The above formula can be simplified to:
The ratio of the component force used for the planet's rotation to the entire gravitational force is:
It can be seen from this that almost all of the planet's gravity is used for the rotation of the planet, and only a little bit is used for the revolution of the planet. Here, it can also be considered that at the point of gravity, the torque of the planet's revolution is equal to the torque of the planet's rotation. Since the moment arm of the planet's revolution is much larger than the moment arm of the planet's rotation, the force used for the planet's revolution is much smaller than the force of the planet's rotation.
The movement of the planet is not a simple force-free system. It is affected by gravity at any time. Therefore, the angular momentum of the planet's revolution at any point includes: the angular momentum of the planet's initial velocity relative to the central planet. Gravity forms the angular momentum of the planet's revolution. Gravity forms the angular momentum of the planet's rotation reflected on the orbiting sphere:
Since vs is equal to ve, after bringing it into the above formula
The angular momentum of the planet's revolution is only the angular momentum caused by the initial speed. It can be seen that the mutual cancellation of the angular momentum of the planet's revolution caused by gravity is the fundamental reason for the conservation of angular momentum in the planet's revolution system.
For different positions, according to the law of conservation of angular momentum:
In the formula, L is the angular momentum, R0, v0, and β0 are the distance between the planet and the central planet at the initial position, the linear velocity of the planet, and the angle between the gravitational line and the linear velocity. R1, v1, and β1 are the distance between the planet and the central planet after the position changes, the linear velocity of the planet, and the angle between the gravitational line and the linear velocity. Obtained from the above formula:
For planets whose minimum and maximum revolution speeds cannot be found, Kepler's area law is used to estimate the maximum speed at perihelion of the planet. Assume that the semi-major axis of planet E's orbit is a and the semi-minor axis is b, then the elliptical area of planet E's orbit is:
According to Kepler's area law, when the planet E moves in an elliptical orbit, the line connecting it to the sun sweeps out equal areas in equal time. Divide the running period of planet E into n parts, then divide the ellipse area into n parts. Let the unit area be Sn, let the linear speed of planet E be v0, the angle between planet E and the gravitational line be β0, the distance between planet E and the central planet S be R0, and the time interval be Δt:
The initial linear velocity of the planet at perihelion is:
Figure 4 is a planet operation analysis diagram. Here, the operation cycle of planet E is divided into n equal parts according to time, and the unit time is Δt. In the figure, the center S0 of the central planet S is used as the coordinate origin. R0 is the distance between the initial position of the planet and S0, v0 is the initial running speed of planet E, β0 is the angle between the initial running direction of the planet and the gravitational line, and θe is The angle at which the center of mass of planet E rotates around the gravitational point Eg in unit time Δt. θs is the angle at which planet E rotates around the central planet S due to the gravitational component. Translate v0 to point A0, and its end point is A1. Then rotate A1 by θs angle to position A2. A2 is the end position of the center of mass of planet E after Δt time. here:
The coordinates of point A1 are:
The distance from point A1 to S0 is:
The angle α between point A1 and the initial position of planet E satisfies:
When the planet E rotates by an angle θs to the position A2 after Δt time under the action of the gravitational component Fs, the distance between the planet E and S0 remains R1, and the angle between the position A2 of the planet E and the initial position increases to:
It can be seen that the rotation of the planet balances the inertia of the planet's movement.
5. Simulation of Planet’s Elliptical Orbit
The relevant parameters between the Earth and the Sun [
10] are as follows: The Earth’s revolution period is 365.256363004 days (solar day), and its average radius is approximately 6371.0 km, the orbital semi-major axis is 1.49598023×10^8km, the aphelion distance is 1.52097597×10^8km, the perihelion distance is 1.47098450×10^8km, the oblateness is 3.35128×10^-3, and the solar radius is 6.955×10^5km.
Based on the above derivation, the Earth's orbit can be simulated.
Table 2 is a partial screenshot of the simulation data table of the Earth's orbit around the sun. The last column in the table is the relevant constants, re is the radius of the earth, rs is the radius of the sun, Rmin is the perihelion distance, Rmax is the aphelion distance, Grm is the ratio of the gravitational constant to the mass, ki is the rotational inertia coefficient, T is the revolution period, n is the number of equal divisions of the period, here we take 10000, and
Table 1 above is only a small part of the data. Δt is the unit time, S is the orbital area calculated based on the Earth's semi-major axis and oblateness, which is used to calculate the initial velocity of the Earth's perigee, and Sn is the unit area. In
Table 2, the first column R is the distance between the earth and the sun when the earth is at different positions. The initial value is perihelion. The second column is the distance interpolation of the distance in the first row minus the distance in the second row. The third column hs is the distance from the gravitational point where the sun emits gravitons to the center of mass of the sun. The fourth column he is the distance from the gravitational point Eg of the sun acting on the earth to the center of mass of the earth. The fifth column is the angle between the direction of the earth's motion and the gravitational line. The sixth column is the earth's center of mass. The speed of the ball and the initial velocity at perihelion are calculated using Kepler's area law. The seventh column ωe is the angular velocity produced by the earth's autorotation due to gravity. The eighth column Ωs is the angular velocity produced by the force used for the earth's revolution. The ninth column α is the angle at which the earth is deflected by the combined motion of the earth's initial inertia v0 and the earth's rotation caused by gravity. The tenth column θc is the actual angular displacement of the earth per unit time, which is the sum of θs and α. The eleventh column θ is the accumulation of angular displacement per unit time, and the twelfth to thirteenth columns are the rectangular coordinates used when drawing simulation data.
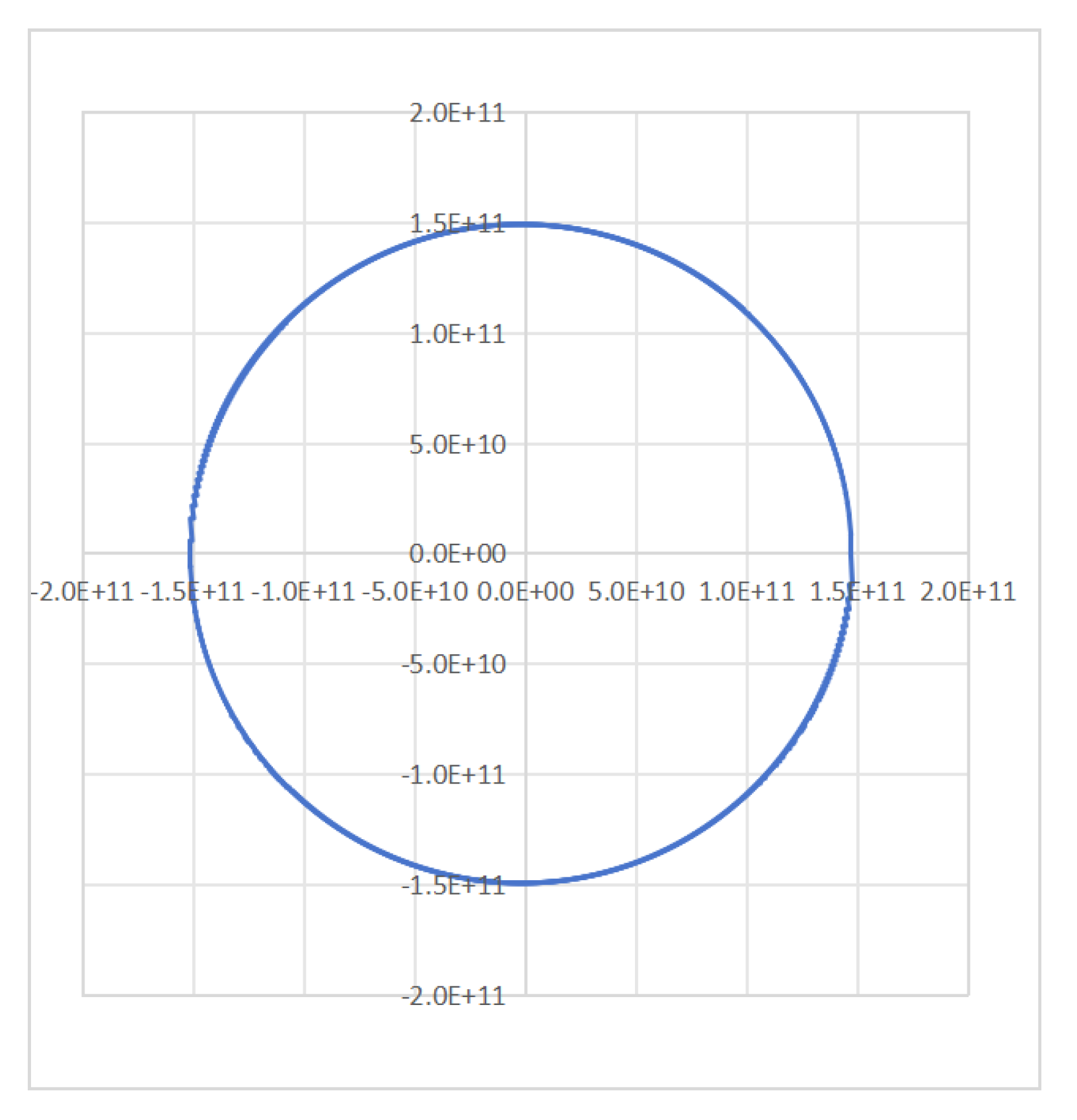
Figure 5 is the earth orbit simulation diagram generated directly from
Table 2. The perihelion point is 1.47098E+11m, which is given by the simulation initial value. Today's return point is 1.47500E+11m. Here E is the power base commonly used in the table. 1.47098E+11m is the same as 1.47098×10^11m. It can be seen that there is a difference between the return point and the initial given value.
The orbit of Mercury around the sun can also be simulated. Mercury[
11] has a diameter of 4880km, a semi-major axis of 0.3871 astronomical units, an eccentricity of 0.205630, a revolution period of 87.9691 days, a perihelion of 0.307499 astronomical units, aphelion of 0.466697 astronomical units, a solar radius of 6.955×10^8m, and the rotational inertia coefficient (dimensionless rotational inertia) of Mercury is about 0.325.
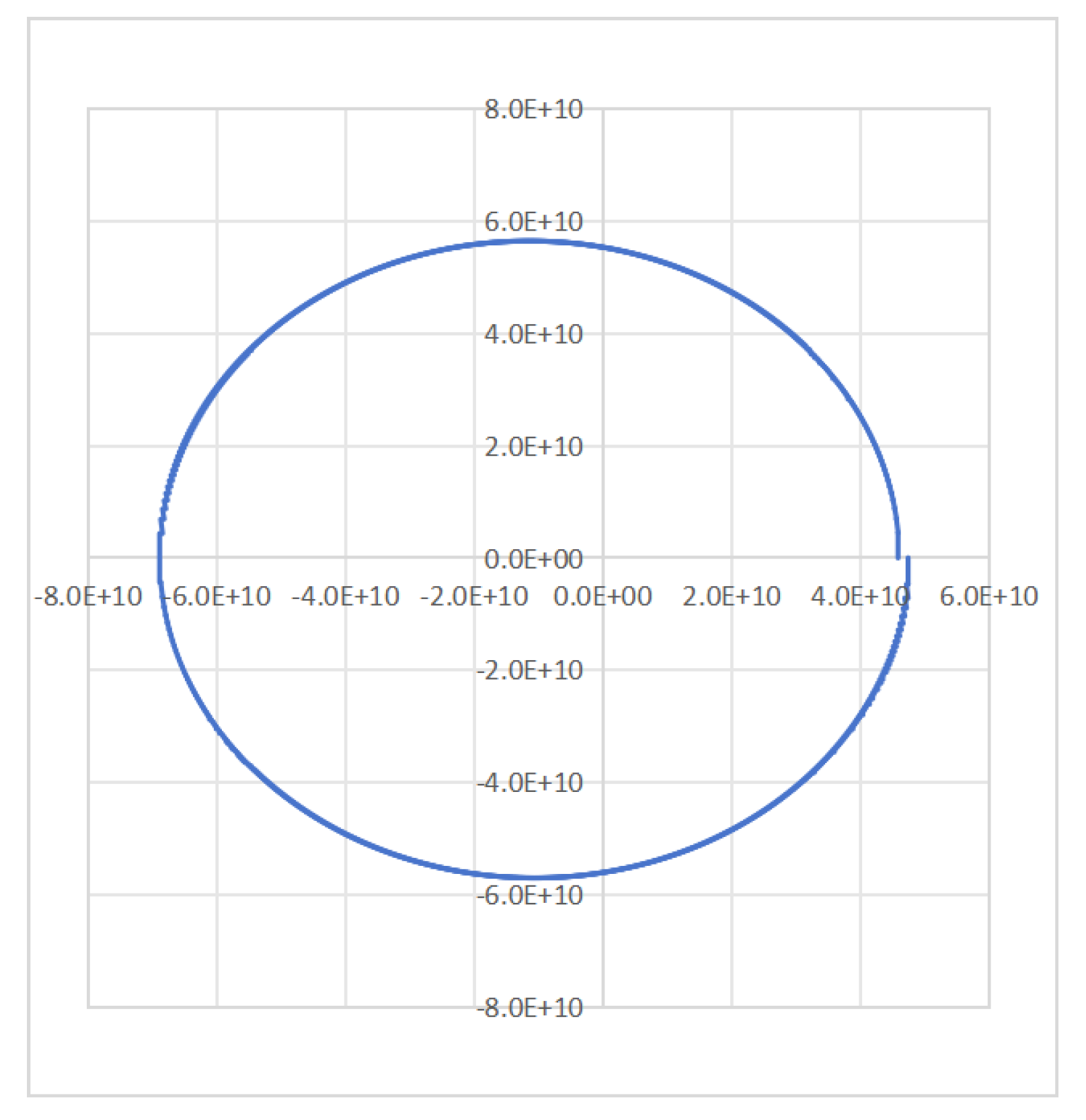
Figure 6 is a Mercury orbit simulation diagram generated directly from the Mercury orbit data simulation table. The perihelion point is 4.600124E+10m, which is given by the simulation initial value, and the perihelion return point is 4.757547E+10m. The difference between the two may be large.
6. Gravity Coefficient
The basic information about the eight planets in the solar system is as follows:
The average radius of the Earth is 6.371×10^6m, the mass of the Earth is 5.972×10^24kg, the radius of the Sun is 6.955×10^8m, the Earth’s revolution period is 365.256363 days (sidereal days), 2 days per day 3 hours, 56 minutes and 4.100 seconds (sidereal time) (sidereal day), aphelion distance 1.52097597×10^11m, perihelion distance 1.4709845×10^11m, average revolution speed 29783 m/s, the maximum revolution speed is 30287 m/s, the minimum revolution speed is 29291 m/s, the semi-major axis of the orbit is 1.49598×10^11m, and the semi-minor axis is 1.4958×10^11m.
Mercury has a mass of 3.3011×10^23kg, a diameter of 4880km, a semi-major axis of 0.3871 AU, an eccentricity of 0.205630, a revolution period of 87.9691 days, a perihelion of 0.307499 AU, and aphelion of 0.466697 AU.
Venus has a mass of 4.8675×10^24kg, a diameter of 12103.6 km, a semi-major axis of 0.723332 AU, an eccentricity of 0.006772, a revolution period of 224.701 days, a perihelion of 0.718440 AU, and aphelion of 0.728213 AU.
Mars has a mass of 6.4171×10^23kg, a diameter of 6779km, a semi-major axis of 1.523679 astronomical units, an eccentricity of 0.09341233, a revolution period of 686.971 days, perihelion of 1.382 astronomical units, and aphelion of 1.666 astronomical units.
Jupiter has a mass of 1.8982×10^27kg, a diameter of 139822 km (average diameter), a rotation period of 9 hours, 55 minutes and 30 seconds, a semi-major axis of 5.2044 AU, an eccentricity of 0.0489, a revolution period of 11.862 years, an aphelion of 5.4588 AU, and a perihelion of 4.9501 AU.
Saturn has a mass of 5.6834×10^26kg, a diameter of 116464 km, a semi-major axis of 9.5826 AU, an eccentricity of 0.0565, a revolution period of 29.4571 years, a perihelion of 9.0412 AU, and aphelion of 10.1238 AU.
Uranus has a mass of 8.681×10^25kg, a diameter of 50724km, a semi-major axis of 19.2184 AU, an eccentricity of 0.046381, a revolution period of 84.0205 years, a perihelion of 18.33 AU, and aphelion of 20.11 AU.
Neptune has a mass of 1.0241×10^26kg, a diameter of 49244km, a semi-major axis of 30.07 AU, an eccentricity of 0.008678, a revolution period of 164.8 years, an aphelion of 30.33 AU, and a perihelion of 29.81 AU.
Based on the above analysis, data simulation is performed on the orbits of the planets in the solar system, and the gravitational coefficient is adjusted to achieve a good closure of the elliptical orbit of the planet.
Table 3 is a statistical table of the gravitational coefficients corresponding to the planets in the solar system.
In the table, rs is the radius of the central planet, re is the radius of the planet or moon, Rm is the distance to the near-central planet, RM is the distance to the far-central planet, m is the mass of the planet, T is the revolution period, S is the area of the orbital ellipse, and Gi is the gravity coefficient obtained from data simulation. It can be seen that the gravitational coefficient is not a fixed value.
In the discussion in the above section, we only focused on the number of gravitons sent by the central star to the planets, that is, we only focused on the number of gravitational lines sent by the central star to the planets. In fact, we also focused on the probability of interaction between each gravitational line and the planet's nuclei.
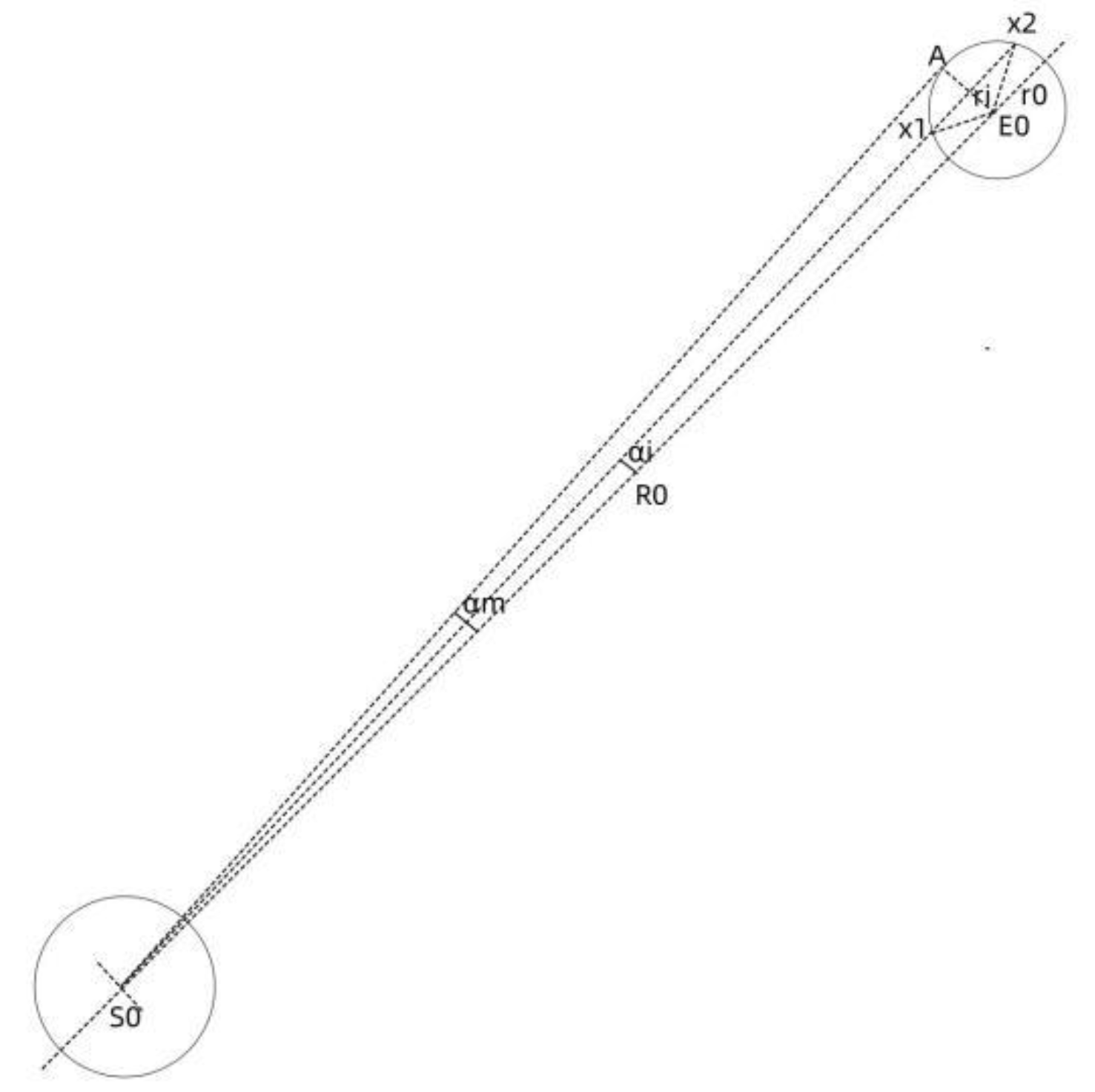
Figure 7 is a schematic diagram of a gravitational line passing through a nucleus. In the figure, S0 is the center of mass of the central planet, E is a nucleon on planet E, R0 is the distance between the two planets, r0 is the radius of the nucleon, αi is the angle between the gravitational line passing through the nucleon and the line connecting the nucleon to the center of mass of the central planet, and αM is its maximum angle.
In the figure, in the triangle x1x2E0, the gravitational line passes through the length of the nucleon:
The length of a general gravity line passing through a nucleon and the interaction probability of a nucleon conform to the normal distribution or Rayleigh distribution. Here we only discuss the interaction probability between a single gravity line and a nucleon. The normal distribution should be chosen, and its probability is:
Here x is the length of the gravitational line passing through the nucleon, μ is the expected value, and σ is the variance. For the gravitons emitted by the central planet, the peak probability of action is 1 when x=2r0 (nucleon radius), so the probability of action when the length of the gravitational line passing through the nucleus is x is:
Bringing into equation (37):
Combine the constants into b1:
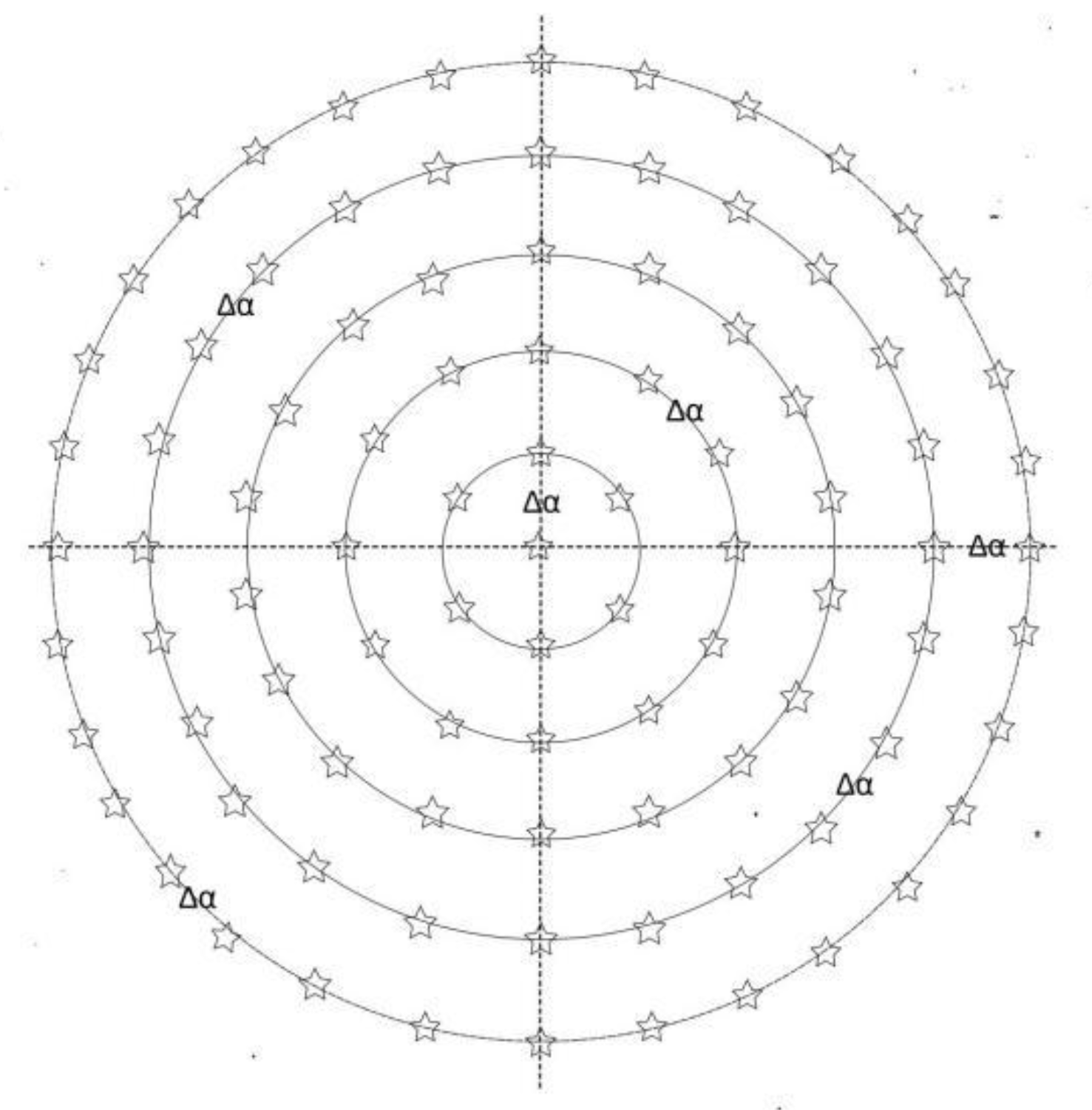
Figure 8 is a probability analysis diagram of the interaction between gravitational lines and nucleons. The five-pointed star in the diagram represents the possible location of gravitational lines. Divide the nucleon into circles with a spacing of Δα. The spacing between possible positions of gravitational lines on each circle is also Δα. At this time, in addition to the possibility of the center of the nucleon on the planet E, a circle of possible gravitational line action points will be formed around the center. The angle of view of this circle is Δα. There should be 2π possible gravitational line action points in a circle according to the minimum spacing. In this circle, the probability of interaction between a gravitational line and the nucleon is equal. The sum of the probabilities is:
The average probability of a single gravity line is:
At this time, in addition to the possible points of action of the gravitational line at the center of the nucleon on planet E, there will also be two circles of possible points of action of the gravitational line formed around the center. The radii of this circle are Δr and 2Δr, and the corresponding points of possible action of the gravitational line are 2π and 2×2π. The probability magnitude of the interaction between the gravitational line and the nucleon in the same circle, the average probability of the gravitational line at this time is:
At this time, in addition to the possible points of action of the gravitational line at the center of the nucleon on planet E, n circles of possible points of action of the gravitational line will be formed around the center. The radius of this circle is Δr to nΔr, and the corresponding points of possible action of the gravitational line are 2π to n×2π. The probability magnitude of the interaction between the gravitational line and the nucleon in the same circle, the average probability of the gravitational line at this time is:
It is very difficult to sum up this formula. If we adjust the constant b1 to b2, we should be able to find an exponential function that makes all exponential functions equal. Obviously this exponential function is related to n. At this time, the total average probability of a single gravity line remains unchanged:
here:
Bringing the above formula into the equation and incorporating the constant b, the probability of a single gravity line acting is
This is the probability of a gravitational line on planet S resonating with a nucleon on planet E.
At this time, the gravity formula (25) can be modified as:
The gravitational coefficient Gi between different planets is:
Gr, Gi and b in the formula are all constants.
Taking the moon's orbit around the earth as the first group and the earth's orbit around the sun as the second group, and bringing in the data, the constant b can be calculated:
By adding the gravitational coefficients of the eight planets in the solar system and the moon, the gravitational coefficient Gr can be obtained:
List the data of the eight planets and the moon in the solar system, and make appropriate adjustments to b to minimize the deviation between the calculated gravity coefficient and the gravity coefficient obtained by orbit simulation.
Table 4 is the gravity coefficient calculation table. Here are only the gravitational coefficients fitted based on the planets in the solar system. They may not be applicable when the distance is too small or too large.
The first column in the table is some constants, the second column is the name of the planet, the third column is the radius of the central planet, and the fourth column is the radius of the planet or moon.
The fifth column is the average distance between the planet and the central planet, the sixth column is the gravity coefficient Gi obtained during orbit simulation, the seventh column is the exponential part when the gravity coefficient is calculated, the eighth column is the gravity coefficient calculated through formula (87), and the last column is the difference between the calculated gravity coefficient and the simulated gravity coefficient. The last line below is the total of some items. Through list calculation and adjustment, the final gravitational coefficient is:
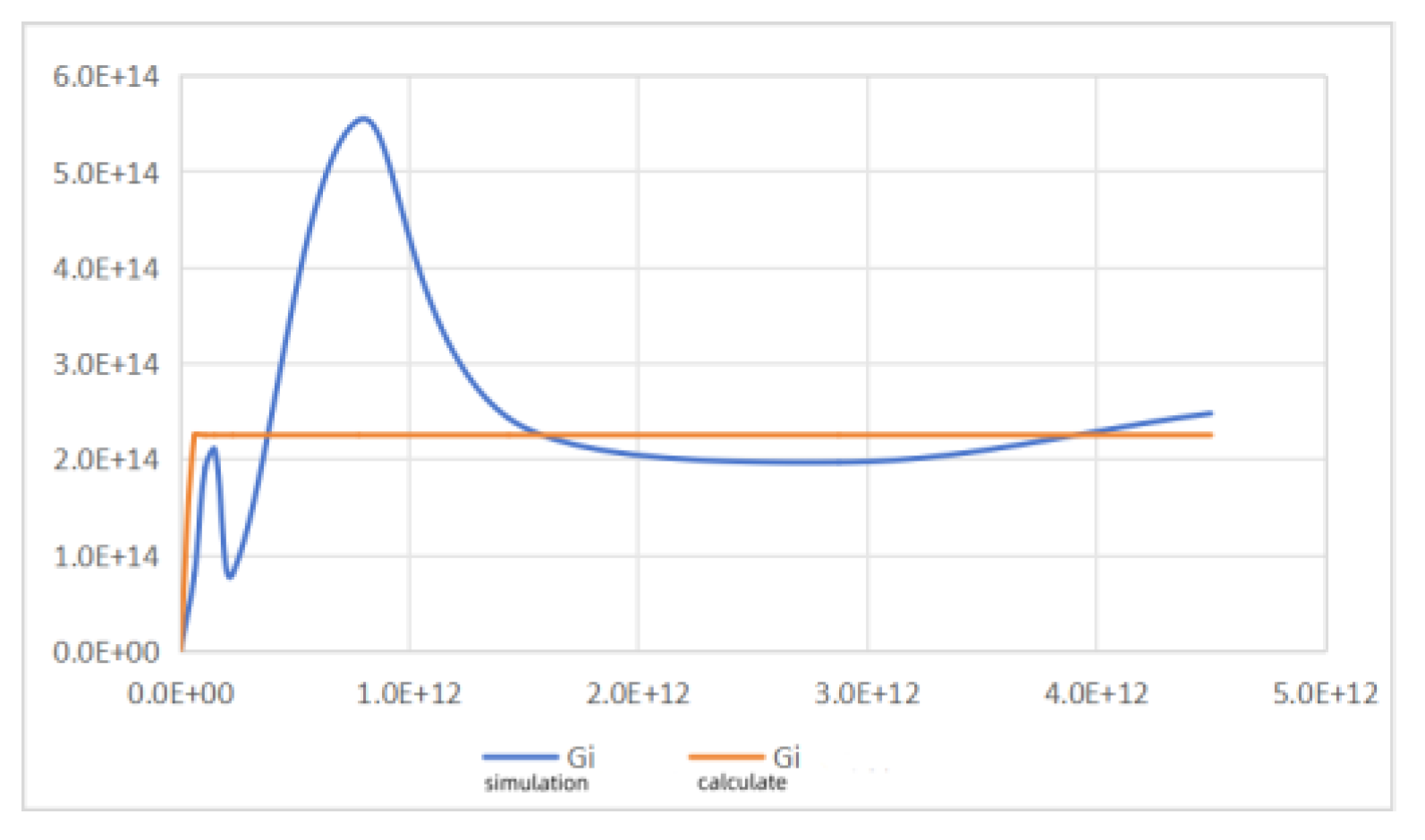
Figure 9 is a graph of the relationship between the old and new gravitational coefficients and distances generated directly from
Table 4. The abscissa in the graph is the distance between the planets, in meters; the ordinate is the gravity coefficient. The blue in the graph is the gravitational coefficient obtained from the planet orbit simulation, and the orange is the gravitational coefficient calculated through the gravity formula. In fact, it should change according to an exponential relationship. Since the distance on the abscissa is not uniform, it looks like a broken line.
According to the new gravity coefficient formula, the data of the planet's orbit is simulated again, and the planet's mass is adjusted. The adjusted planet's mass is as shown in
Table 5:
In the lunar orbit simulation in the table, the gravitational coefficient index part is not brought into the gravity calculation, but the gravitational coefficient is uniformly adjusted. In other planet orbit simulations, the gravitational coefficient index part is directly brought into the gravity calculation. In the table, m (original) is the mass before adjustment, m (new) is the mass after adjustment, and Δm is the ratio of mass differences. It can be seen that Mercury and Venus have increased more in mass, while Jupiter and Neptune have decreased more in mass. It should be noted that here is the gravitational coefficient adjusted based on the minimum total difference in the gravitational coefficients of the planets in the solar system. If there is sufficient evidence to prove that the mass of a certain planet (such as the Earth) is very accurate, the gravitational coefficient and planet mass can also be adjusted based on the parameters of a certain planet. In addition, the mass of the central planet cannot be determined with this method.
7. Precession of Planetary Perihelion
Scientists have long discovered the phenomenon of "precession" ("orbital precession") in which a planet cannot return to its initial point after one revolution. The specific manifestation is that the position of the perihelion (or ascending node) of the planet's orbit in space will slowly move, resulting in a slight deviation between the starting point and the end point of each revolution. The traditional view is that the main causes of precession or orbital precession are: a. Gravitational perturbation: The gravitational perturbation of other celestial bodies (such as the influence of Jupiter on Mercury) will change the shape and direction of the planet's orbit. b. Relativistic effect: According to the general theory of relativity, the gravitational field of the sun will cause precession of planetary orbits, such as the precession of Mercury’s perihelion. c. Long-term perturbation: Orbital elements (such as ascending node longitude, perihelion longitude) will continue to change due to the interaction of celestial bodies in the solar system.
This article analyzes the gravitational force between planets and successfully simulates the elliptical orbit of the planets. Through the simulation of the planet's elliptical orbit, it is shown that the planet's orbit itself has a "precession" (orbital precession) phenomenon that cannot return to the initial point after one revolution. We performed orbit simulations for the eight major planets in the solar system and calculated the differences in perihelion points. The results are as follows in
Table 6:
In the table, Rs is the radius of the sun, Re is the radius of the planet, Rmin is the perihelion distance of the planet, ki is the rotational inertia coefficient, T is the period, a is the semi-major axis, e is the eccentricity (oblateness), S is the elliptical orbit area, and β0 is the planetary motion. The angle between the traveling direction and the line connecting the planet's sun, Rn is the distance to the return point after the planet orbits for one week, ΔR is the distance between the return point and the initial point, arc seconds is the ratio of the distance difference to the initial perihelion point, multiplied by 3600 to convert it into arc seconds. It can be seen from the above statistical table that the order from largest to smallest is: Mercury 123.2, Mars 93.6, Uranus 59.6, Saturn 36.5, Jupiter 21.9, Neptune 13.9, Earth 9.8, Venus 3.9. The orbit simulation of the planet is only related to the radius of the sun and the orbital parameters of the planet. Therefore, the precession (orbital precession) of the planet that cannot return to the initial perihelion in one cycle is only related to the parameters of the planet's orbit itself. It can also be said that the planet's orbit itself has a certain precession (orbital precession).
In the above table, β0 is the angle between the direction of the planet and the line connecting the planet and the sun. The traditional view is that this value should be 90 degrees at perihelion. From the planetary orbit simulation, it can be seen that in order to ensure that the distance of the planet continues to increase after perihelion, the value at perihelion is close to 90°, but it cannot be 90°.
8. Oumuamua and Satellite Tumbling
With the rapid development of science and technology, humans have launched more and more artificial satellites. In the operation of many satellites, failures occasionally occur, especially after attitude control fails, artificial satellites often roll.
In 1958, the first U.S. satellite "Explorer 1" dissipated a lot of energy due to the vibration of its four whip antennas. After working normally for a period of time, the satellite unexpectedly tumbled, causing the mission to fail.
On April 3, 1973, the Soviet Union launched the Salyut 2 space station. Shortly after the space station entered orbit, the attitude control system malfunctioned, causing the space station to roll and eventually explode into 25 pieces.
In January 1989, after 165 days of normal operation, the Fengyun-1B satellite lost control of its attitude due to a sudden failure of the onboard computer. It was later rescued and returned to normal operation.
On May 19, 1998, the Galaxy-4 communications satellite located above the equator at 99 degrees west longitude in North America suddenly experienced a serious failure. The attitude control system control processor on the satellite failed, causing the satellite to roll and stop working.
On February 17, 2016, Japan successfully launched the Astro-H (Astro-H, also known as "Hitomi") satellite from the Tanegashima Space Center in Japan using an H-2A-30 rocket. It is the eighth X-ray astronomy satellite launched by Japan. It is used to investigate the formation and evolution of the universe and study physical phenomena hidden in space. However, on March 27, the Japan Aerospace Exploration Agency (JAXA) confirmed that they were unable to obtain the satellite’s signal on March 26. On April 8, JAXA held a second press conference and pointed out that at 03:01 on March 26, shortly after adjusting the satellite control direction, the satellite control system was abnormal, and then the satellite was in a tumbling state, and the solar cell wing could not provide power. After gradually reducing the rotational speed, the solar cell wing can provide part of the electrical energy, and the satellite returns to steady-state operation.
On October 19, 2017, Oumuamua, the first interstellar object confirmed to pass through the solar system, was discovered. The object is cigar-shaped, about 400 meters long and 40 meters wide, with a red surface and unknown solid composition. It cuts vertically into the ecliptic plane from the direction of Lyra at a speed of 26 kilometers per second, with an orbital eccentricity of 1.19951, the highest value observed in the solar system. Observations in 2018 showed that there are deviations in its trajectory that cannot be explained by gravity. In fact, this is a problem with traditional gravity theory [
13]. Oumuamua has a rolling phenomenon during operation.
So why does the tumbling phenomenon occur after the satellite's attitude is out of control? From the above analysis, it can be seen that after the satellite's attitude is out of control, under the action of gravity, the orbital plane will rotate in the opposite direction to the revolution direction. It is really due to this rotation that the satellite tumbles. This is also the case for the interstellar object 'Oumuamua.
9. Earth’s Rotation
For the entire earth, the gravitational point of the sun forms a circle with a radius of 3.171E+06m. From
Table 1, it can be seen that the gravitational point (circle) of the sun on the earth falls into the liquid layer. On the circle of the sun's gravity, the earth's average rotation angular speed caused by the sun's gravity is 6.118E-05 rad/s, and the linear speed is: 194m/s. In recent years, seismic science has developed rapidly. Through the study of the abrupt interface of seismic wave propagation velocity, it is confirmed that the earth is composed of crust, mantle and core[
14], as shown in
Table 7.
Crust: The crust is the outermost solid lithosphere of the earth, with an average thickness of about 17 kilometers, but it is unevenly distributed. The continental crust is thick (average 33 kilometers, the Qinghai-Tibet Plateau can reach 60-70 kilometers), mainly composed of granite (silicon-aluminum layer) and basalt (silicon-magnesium layer); the oceanic crust is thin (average 6 kilometers), with almost no granite and mainly basalt.
Mantle: divided into upper mantle and lower mantle, with a total thickness of about 2900 kilometers. There is an asthenosphere at the top of the upper mantle (depth of about 60-250 kilometers), which is the origin of magma; the material in the lower mantle is plastic and solid, and the density and pressure increase with depth. The upper mantle is dominated by peridotite, and the part near the core contains iron and nickel oxides.
Earth's core: divided into outer core and inner core. The outer core (depth 2900-5100 kilometers) is liquid iron-nickel alloy, and the inner core (5100 kilometers to the center of the earth) is solid iron-nickel. Seismic wave evidence: Transverse waves (S waves) cannot pass through the outer core, confirming its liquid nature.
In recent years, Chinese-American scientist Song Xiaodong and others have discovered through observation and research of seismic waves [15-23] that the rotation direction of the earth's core is opposite to the rotation direction of the earth, with an angle of 10° from the rotation axis, and the rotation speed of the core is about 1.1° faster than the rotation speed of the earth itself.
In recent years, scientific researchers have shown through long-term observations [24-26] that the earth's rotation speed slows down in spring and speeds up in autumn, with the annual cycle amplitude being about 20-25 milliseconds. The traditional view is that the reason is mainly related to seasonal changes in atmospheric circulation, especially the redistribution of the earth's angular momentum caused by wind system activities.
In recent years, scientific researchers have shown through long-term observations [
27] that the Earth's rotation speed is gradually slowing down, causing the day length to increase by about 12 milliseconds per century. The traditional view is that the Earth's tidal friction is the main reason for long-term changes in the rotation speed.
In recent years, scientific researchers have shown through long-term observations [
28]: "The correlation between the sun's orbital motion and the changes in the earth's rotation rate reaches 0.9994."
This article believes that the above phenomena are related to the separation of the sun's gravitational force on the earth from the earth's center of mass, and the fact that 99.99% of the sun's gravitational force on the earth is used for the earth's rotation.
9.1. Reverse rotation of the Earth’s core
Since the earth is affected by the gravitational force of the sun, the spherical surface of the earth sets into the liquid layer of the earth. It is very difficult to calculate the rotation speed of the inner sphere caused by gravity from the spherical surface of the gravitational force. Only a qualitative inference can be made here: the earth's core has a rotation that is opposite to the movement of the earth around the sun. Since the distance from the gravitational circle to the solid inner sphere is small and the density of liquid material is high, the rotation speed of the earth caused by the gravity of the gravitational circle will drive the inner sphere to rotate faster than the rotation speed of the earth's crust.
9.2. Reasons for the slowdown of the Earth’s rotation
From the sun's gravitational circle outward, the earth's rotation speed caused by gravity decays rapidly until the solid matter in the earth's crust stops attenuating. At this time, in the earth's revolution plane (ecliptic plane), the gravity on the earth's crust will produce a rotation speed opposite to the earth's revolution speed. This can only be a qualitative inference. It is very difficult to calculate the speed of crustal rotation caused by gravity from the spherical surface on which gravity acts. Here we can infer the proportional coefficient of the rotation of the earth's crust driven by the earth's rotation speed on the gravitational action circle.
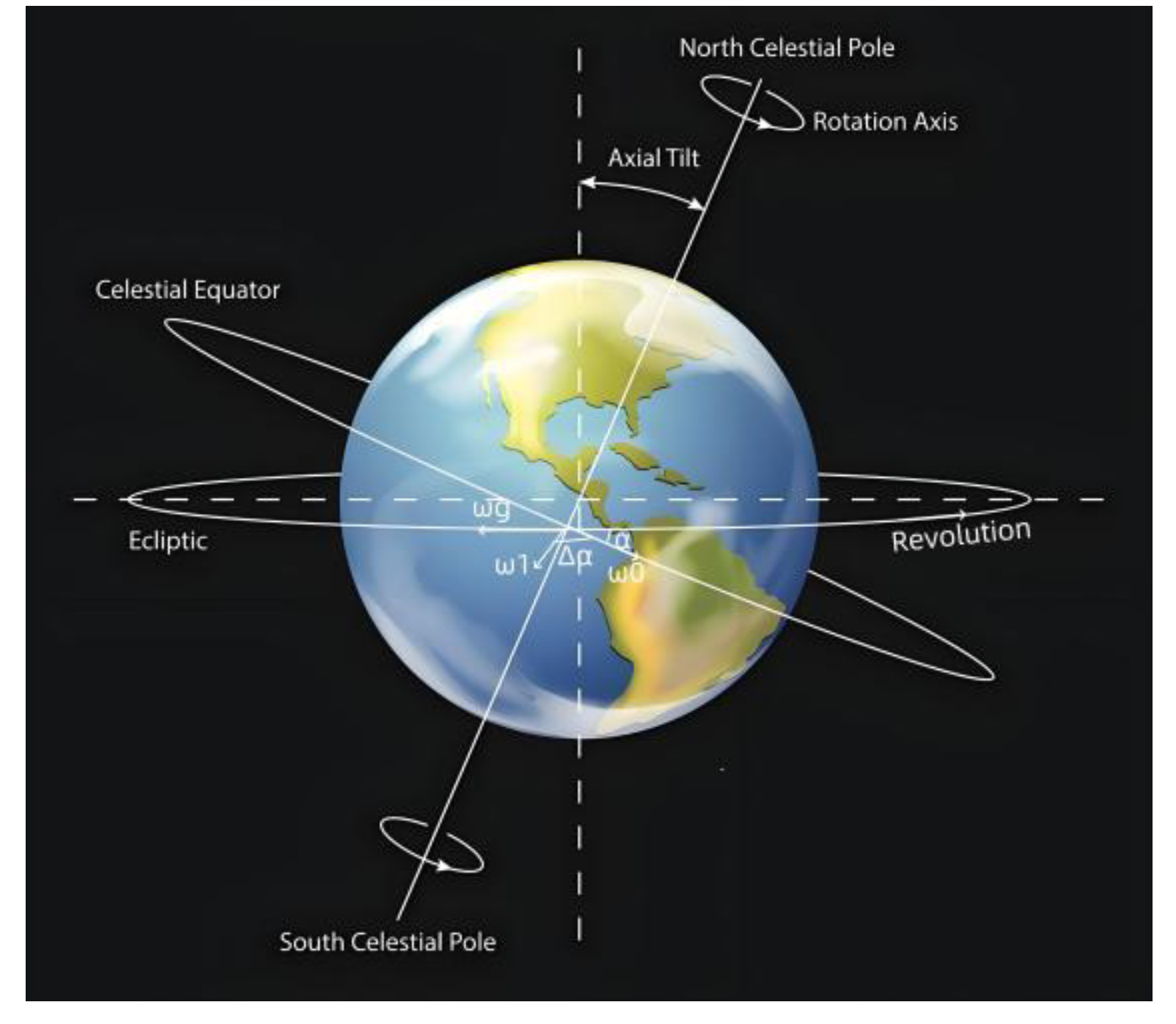
The earth revolves around the sun in a counterclockwise direction, and the angle between its orbital plane (ecliptic plane) and the earth's equator is 23.439281° (0.40909 radians).
This angle is also the angle between the rotation axis and the revolution axis, as shown in
Figure 10. The Earth's rotation period is: 23 hours, 56 minutes and 4 seconds (sidereal day). The average angular velocity is:
The linear velocity at the equator is approximately 465 meters/second.
Data shows that the earth's rotation slows down by an average of about 0.00015 seconds per year. Average daily slowdown:
Assume that the angular velocity of rotation caused by gravity is ωg, and the angular velocity of the earth after one rotation is ω1
Bring in the numerical value and get a reasonable value:
The ratio of the rotation angular velocity of the earth's crust caused by gravity to the rotation angular velocity on the circle of gravity is:
It can be seen that since the point of gravity falls into the liquid layer, the angular speed of the earth's rotation caused by gravity has been greatly reduced.
9.3. Seasonal and cyclical changes in the Earth’s rotation
Seasonal and cyclical changes in the Earth's rotation are related to the Earth's position in its orbit, and the Earth's position in its orbit is reflected in the Earth's gravitational pull from the sun. The gravitational force of the earth on the ecliptic plane conforms to formula (6). The reverse rotation angular velocity of the earth caused by the gravitational force of the sun on the ecliptic plane conforms to the formula (22). The angular velocity of the earth's rotation caused by the gravitational force of the sun on the ecliptic plane is:
In the formula, ωe is the reverse rotation angular velocity of the earth formed by the point where the sun's gravity acts on the ecliptic plane, re is the radius of the earth, rs is the radius of the sun, R0 is the distance between the sun and the earth, Gi is the gravitational constant, me is the mass of the earth, and he is the distance from the point of gravity to the center of the earth. Since he<R0,Assume that the coupling coefficient of the angular velocity of the point of gravity coupled to the earth's crust to form the crust's rotation is kω, and the angular velocity of the reverse rotation of the earth's crust caused by gravity is:
It can be seen from this: If the distance between the sun and the earth changes by 5%, the angular speed of the earth's rotation caused by gravity will change by approximately 5%, and the angular speed of the earth's rotation reflected in the crust will change by 5%. In other words, changes in the distance (gravity) between the sun and the earth can be 100% reflected in the earth's rotation speed caused by the gravity of the earth's ecliptic plane.
The Earth's rotation angular velocity caused by gravity and the Earth's own angular velocity are superimposed to form a new Earth's rotation angular velocity that conforms to formula (36). Therefore, the crust's rotation angular velocity caused by ωg1 is:
The angular velocity of crustal rotation caused by ωg2 is:
The change in crustal rotation speed caused by the change in ωg2-ωg1 is:
The change in the rotation speed of the Earth's crust caused by this gravity determines the change in the Earth's rotation speed. To sum up: the position of the earth in its orbit changes seasonally and with half-year and annual cycles. Therefore, the sun-earth gravity will change seasonally and change with half-year and annual cycles. The changes in the sun-earth gravity determine the changes in the rotation of the earth's crust. In the end, it must be manifested as changes in the earth's rotation speed with seasonal changes and changes with half-year and annual cycles.
9.4. Changes in the Earth’s rotation speed are strongly related to the sun’s gravity
According to many years of research by scholars such as Teng Yongfu, Liu Fugang, Luo Jinming, and Berlin from the School of Science of Qiqihar University: the correlation between the sun's orbital movement and changes in the earth's rotation rate reaches 0.9994. The orbital motion of the sun actually reflects the change in the distance between the sun and the earth. The change in the distance between the sun and the earth determines the change in the gravity of the sun and the earth. According to the derivation and calculation in the previous section, the change in the gravity of the sun and the earth determines the change in the earth's rotation. Therefore, it is inevitable that the change in the earth's rotation speed is strongly related to the orbital motion of the sun.
9.5. The influence of the moon, Jupiter and Saturn on changes in the earth’s rotation speed
In the solar system, due to the gravitational pull of the sun on the earth, the earth revolves around the sun; due to the gravitational pull of the earth on the moon, the moon revolves around the earth; while the earth exerts a gravitational pull on the moon, the moon also exerts a gravitational pull on the earth. The gravitational pull of the moon on the earth will also cause the earth to produce a reverse rotation angular speed at the point where the moon-earth gravitational force acts, so that the rotation of the earth is affected by changes in the distance (gravity) between the earth and the moon. Jupiter, Saturn, etc. are larger in size and will also exert a certain gravitational pull on the Earth. As the distance between Jupiter, Saturn and the Earth changes, their gravitational pull on the Earth will change. These changes in gravity will also affect the Earth's rotation speed, but the magnitude of the impact is different.
10. Synchronous Rotation of the Moon
10.1. Synchronous rotation of the moon
Many scholars have expressed their opinions on the moon's synchronous rotation [29-32]. Scholars generally believe that the reason for the moon's synchronous rotation is mainly the result of the tidal locking effect. The Earth's gravitational pull on the Moon is stronger on the end closer to the Earth than on the end farther away from the Earth. This gravitational difference causes the Moon's spherical shell to bulge. The continuous pull eventually slows down the Moon's rotation speed until it reaches a state that is synchronized with the orbital period. Does the tidal locking effect really have such a big effect? This view is questionable.
From the analysis in
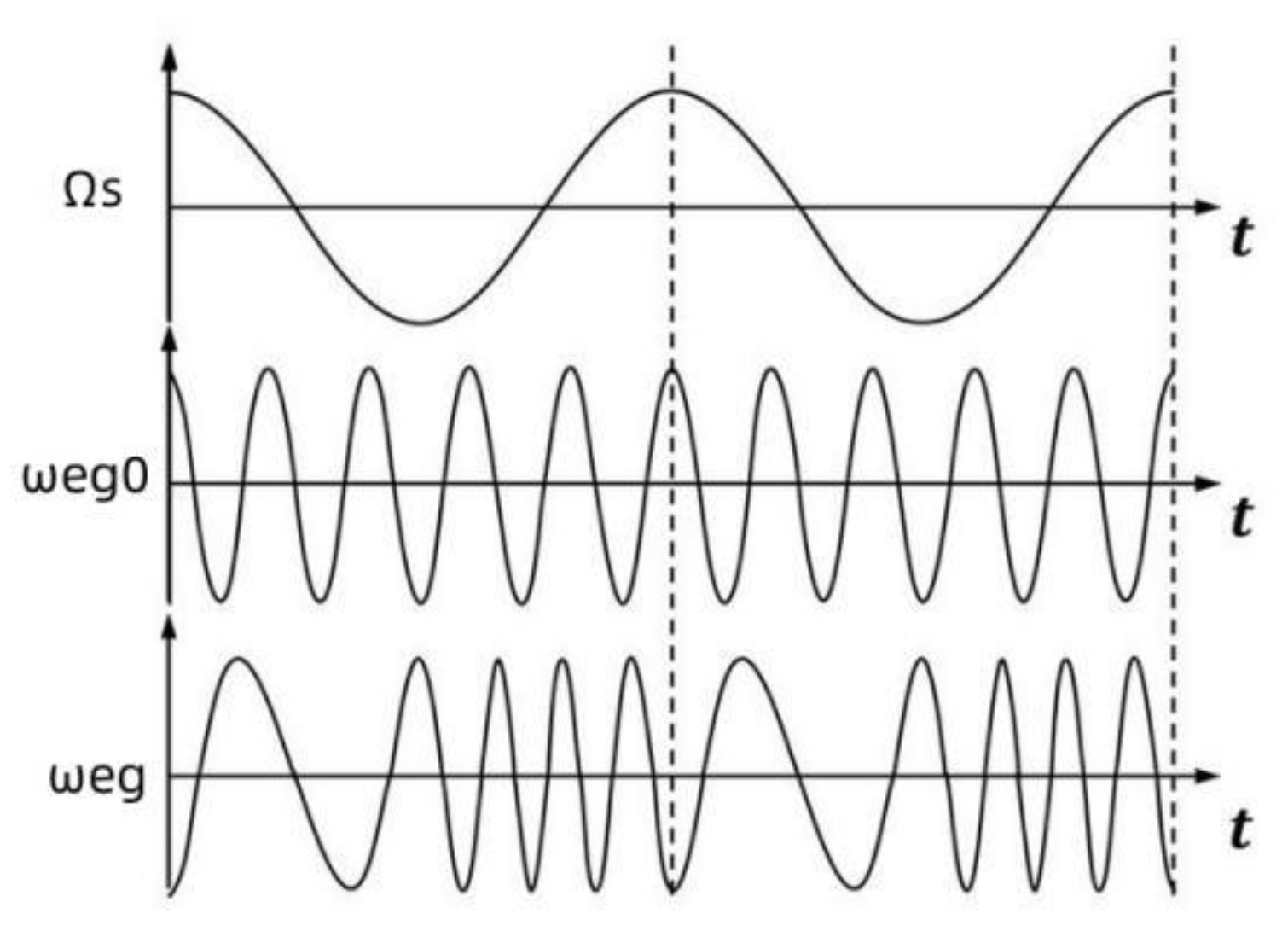
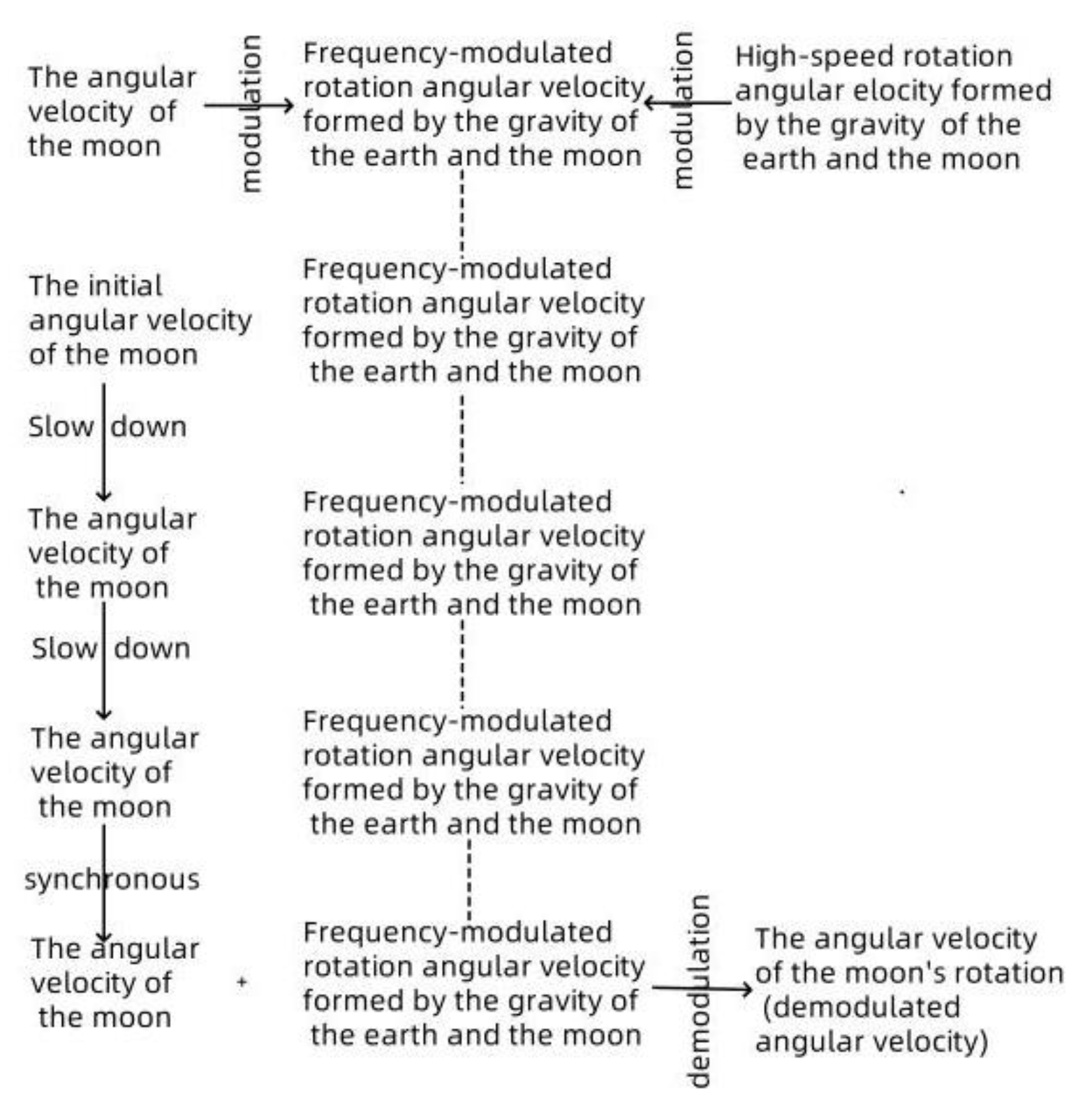
Section 6, it can be seen that the moon is affected by the gravitational pull of the earth and will form a rotation on the equinox plane opposite to the direction of revolution, and its rotation angular speed is ωe. The gravitational force exerted by the moon on the earth is consistent with the above equation (25). The moon's rotation angular velocity conforms to the above equation (43). It can be seen from the lunar elliptical orbit simulation table that the angular rotation speed of the moon ωe caused by the gravity of the earth and the moon is about 30 times the actual angular rotation speed of the moon. At the same time, ωe is affected by the distance between the earth and the moon, and its size is proportional to the angular speed of the moon Ωs. Therefore, the gravity of the earth and the moon causes The lunar rotation angular velocity ωe can be seen as the lunar revolution angular velocity Ωs and a relatively high-speed angular velocity ωeg0. That is to say, the moon's rotation angular velocity ωeg is modulated by the moon's revolution angular velocity Ωs at the angular velocity ωeg0. As shown in
Figure 11.
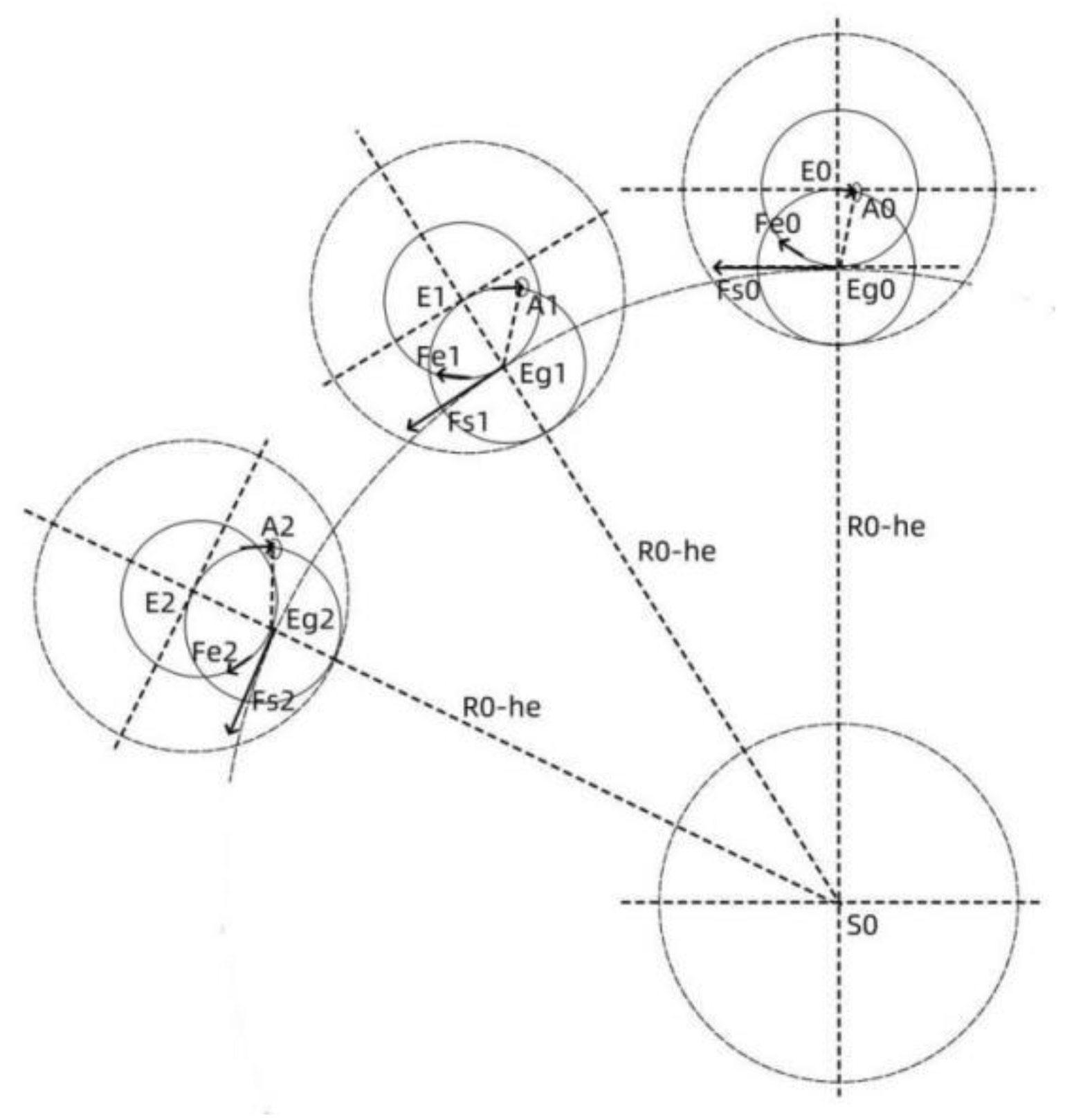
The moon is affected by the angular velocity ωeg generated by the gravity of the earth. The initial angular rotation velocity of the moon ωc0 will be superimposed into a new angular velocity of the moon ωc1. The superposition of themoon. The initial angular velocity of the moon will gradually decrease, and the angle between the lunar rotation angular velocity and the equinox will also change. Due to the long-term existence of the Earth-Moon gravity, the Moon's initial rotation angular velocity will gradually converge with the Moon's rotation angular velocity caused by the Sun-Earth gravity. The Moon's initial rotation angular velocity will eventually be the same as the Moon's rotation angular velocity ωeg caused by the Earth-Moon gravity. At this time, this rotation angular velocity will be superimposed with the Moon's rotation angular velocity ωeg caused by the Earth-Moon gravity, which is equivalent to the demodulation process of frequency modulation waves. The demodulated waveform is the moon's revolution angular velocity waveform modulated on the moon's rotation angular velocity caused by the gravity of the earth and moon. This rotation angular speed is the final rotation angular speed of the moon, which is the same as the moon's revolution angular speed. From the results, the moon is rotating synchronously. It can be seen from the wave superposition data simulation diagram that when the frequencies of the two waves are similar, a flat curve with a very small amplitude will appear. At this time, the moon's rotation plane is perpendicular to the moon's equinox plane. The entire modulation and demodulation process of the moon's rotation is shown in
Figure 12.
10.2. Changes in the angle between the lunar equatorial plane and the equatorial plane
After the moon achieves synchronous rotation, regardless of the influence of other factors, the angle between the moon's rotation surface and the equinox surface will be 90°. The rotation speed of the moon is the demodulated rotation speed of the moon around the earth Ωme. The minimum value is 2.386E-06 rad/s, the average value is 2.662E-06 rad/s, and the maximum value is 2.979E-06 rad/s. The average radius of the moon is 1737.10km, and its rotation period is 27.32 days (rotating counterclockwise from west to east). The angle between the moon's axis of rotation and the ecliptic plane will also vary between 6.69° (i.e. 5.15°+1.54°) and 3.60° (i.e. 5.15°-1.54°).
The moon is a satellite of the earth. While the moon orbits the earth, it also orbits the sun together with the earth.
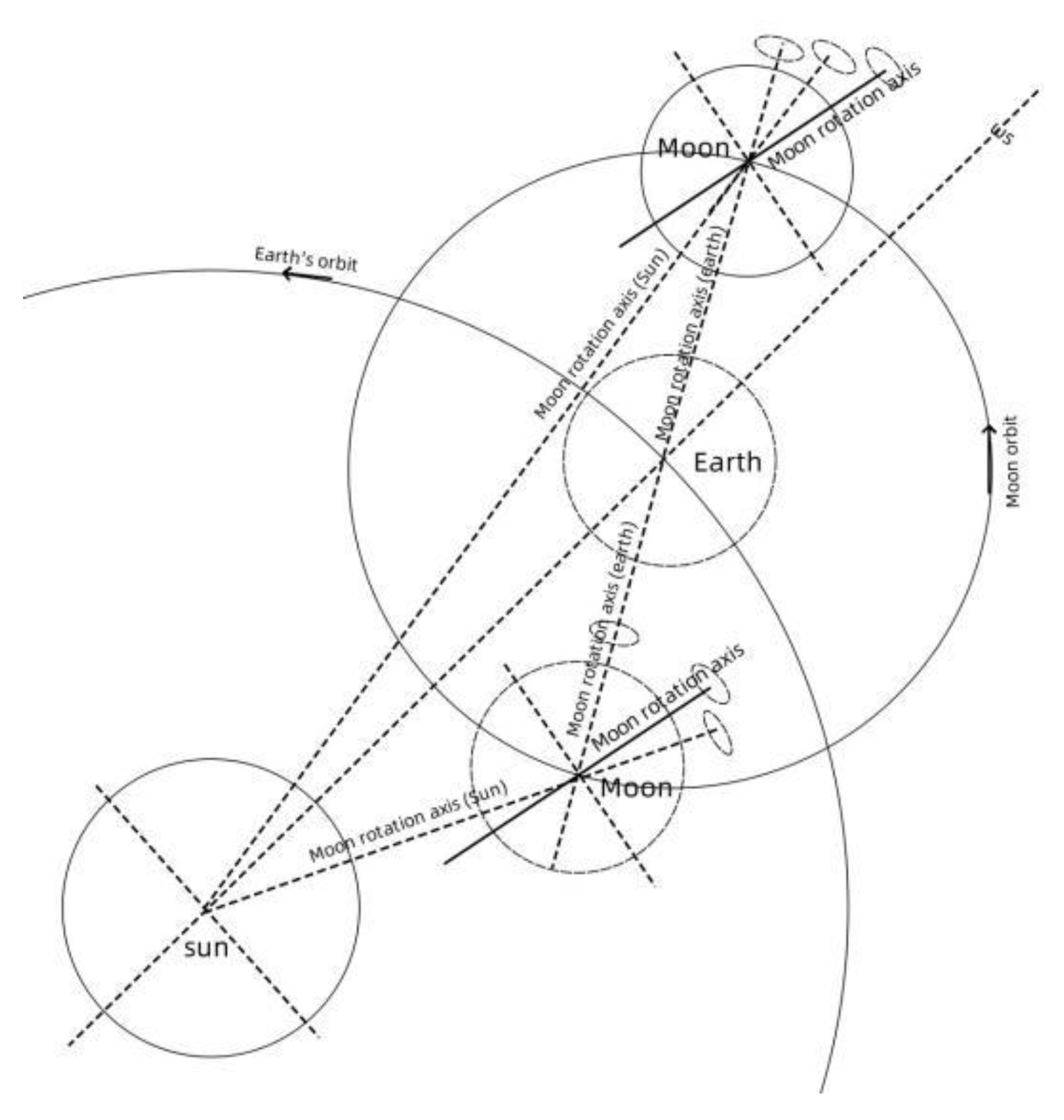
Figure 13 is a schematic diagram of the moon and the earth orbiting the sun. In the figure, S0 is the center of mass of the sun, E0 is the center of mass of the earth, and M0 is the center of mass of the moon. The line connecting S0E0 is the axis of rotation of the Earth that rotates in the ecliptic plane opposite to the direction of the Earth's revolution under the gravity of the sun. The line connecting E0M0 is the axis of rotation of the moon that rotates in the ecliptic plane opposite to the direction of the moon's revolution under the gravity of the Earth. The line connecting S0M0 is the axis of rotation that forms the rotation of the moon under the gravity of the sun. When the moon and the earth achieve synchronous rotation, the moon's rotation plane is perpendicular to the ecliptic plane, and the rotation plane of the moon's rotation formed by the sun's gravity is perpendicular to the line connecting S0M0. The synchronous rotation angular speed of the moon and the earth and the moon's rotation angular speed formed by the sun's gravity are finally superimposed to form the observable rotation angular speed of the moon. The final observable rotation angular velocity plane of the Moon forms an angle α with the equinox plane.
Assuming the synchronous angular rotation speed of the moon and the earth ωme, the angular rotation speed of the moon ωms caused by the gravity of the sun, and assuming that the angle between the earth-moon line and the sun-moon line is δ, then the synthetic lunar rotation angular speed ωm is:
Here, the synchronous rotation angular velocity of the moon and the earth ωeg is the demodulated rotation speed of the moon around the earth Ωs. The minimum value is 2.386E-06 rad/s, the average value is 2.662E-06 rad/s, and the maximum value is 2.979E-06 rad/s.
Since the distance between the moon and the earth is much smaller than the distance between the sun and the earth, the moon's orbit around the sun can be approximated as the earth's orbit around the sun. The moon's rotation angular speed caused by the sun's gravity is:
The minimum distance between the earth and the moon is 3.631E+08m, the maximum distance is 4.057E+08m, the minimum distance between the sun and the earth is 1.471E+11m, the maximum distance between the sun and the earth is 1.521E+11m, the minimum distance between the sun and the earth - the maximum distance between the earth and the moon is the minimum distance between the sun and the moon. The distance is 1.467E+11m. The maximum distance between the sun and the earth + the maximum distance between the earth and the moon is the maximum distance between the sun and the moon. The maximum distance between the sun and the moon is 1.525E+11m. The gravitational coefficient Gr is the constant 1.210E+12N/m^2 used in the earth-moon gravity simulation, and other constants are added to get:
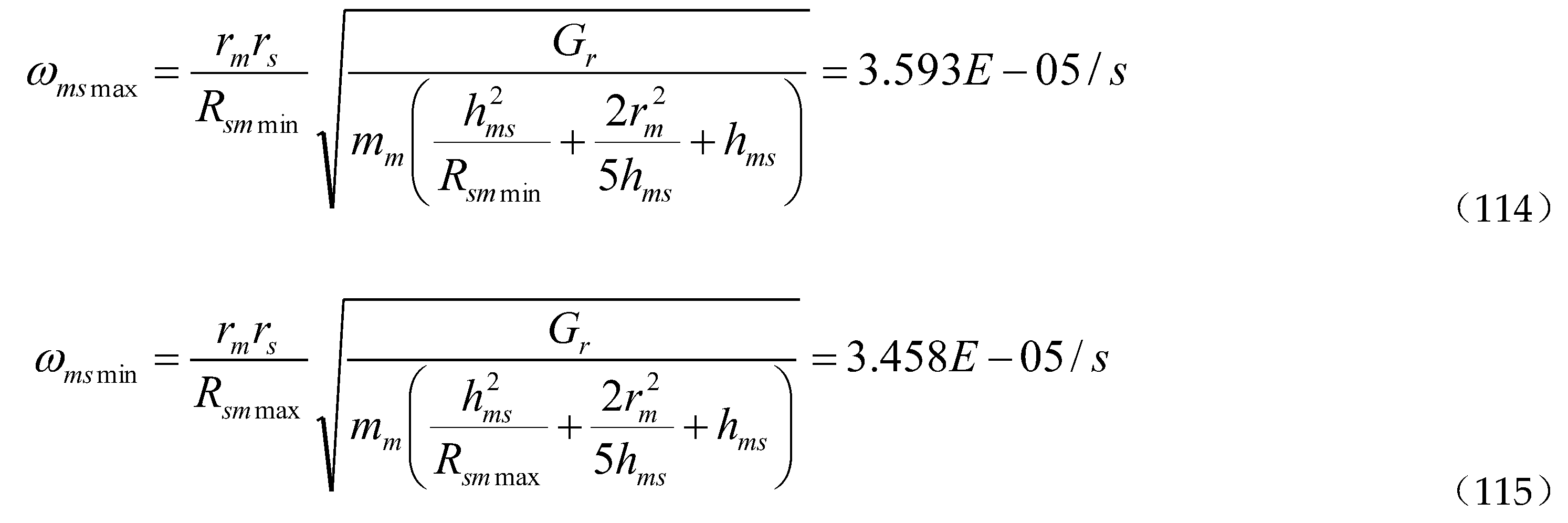
The minimum value of the angle δ between the line connecting the earth and the moon and the line connecting the sun and the moon is when the sun, earth, and moon are on the same line (solar or lunar eclipse). At this time, the angle δ=0, and the maximum value is when the earth and moon are both on the ecliptic plane. At this time, δ is consistent with:
The angle α between the equatorial plane and the equatorial plane of the moon can be calculated from the above data.
Since the moon's rotational angular velocity ωms due to the gravity of the sun involves a three-body problem, it is more complicated. Here, ωms can also be deduced from the angle between the moon's equatorial plane and the equatorial plane.
The angular rotation speed ωms of the moon produced by the gravity of the sun is in the same order of magnitude as the angular rotation speed ωms of the moon produced by the gravity of the sun estimated above. The calculated angular velocity falls within the range of the angular velocity of the reverse projection. However, the calculation range of the calculation is small, while the calculation range of the calculation of the reverse projection is large. This should be related to the frequency broadening after the rotation angular velocity modulation and demodulation of the calculation of the moon's revolution. Further accounting and research are needed.
11. Verification Method
The rotation of the planet caused by gravity can be verified by launching a solid rigid body artificial satellite. After the solid rigid body satellite enters the orbit, no power or adjustment is added. At this time, the artificial satellite is only affected by the gravity of the earth. Then it is tested whether the artificial satellite rotates and whether the rotation direction is opposite to the direction of revolution. The speed of rotation can also be tested. The artificial satellite here will be affected by the sun and other planets.
12. Conclusions
Gravity is a process in which nuclei emit gravitons, the gravitons propagate in space as gravitational energy waves, and the gravitational energy waves resonate with other nuclei when they encounter them, resulting in energy transfer. For the planet, the gravitons emitted by the nuclei inside the planet interact with other nuclei inside the planet to form the cohesion of the planet. Some of the gravitons emitted by the nuclei on the surface of the planet are emitted outside the sphere. These gravitons emitted outside the sphere encounter the nuclei of other planets. Its resonance forms an energy transfer. This transferred energy will cause the resonant nuclei to produce a displacement perpendicular to the gravitational line, forming a force vertical to the gravitational line. For a planet orbiting the central planet S, only the spherical nuclei facing the central planet S can receive the center. The gravitons emitted by the central planet S, and the nuclei of the planet facing away from the central planet S, will not receive the gravitons emitted by the central planet S. In this way, for the entire planet, the equivalent gravitational point Eg is not at the center of mass of the planet, but at the center of mass close to the central planet S. A spherical surface with a radius of about 0.5 on one side, so that the central planet S will have two effects on the planet E rotating around it. One is the centripetal force rotating around the central planet S, and the other is the planet's rotation force when the center of mass of the planet rotates around the gravitational point Eg. Within a certain time Δt, the initial speed of planet E will cause the planet to produce a linear displacement at a uniform speed. The component Fs of the gravity of the central planet S will cause the planet E to move a certain distance on the arc. The other component Fe of the gravity of the central planet S will cause the center of mass of the planet E to move backward on the arc for a certain distance around the point of gravity. Under the combined action of these three, the planet E will form a standard elliptical orbit. According to the law of conservation of momentum, the linear velocity of a planet formed by gravity around the central planet is equal to and opposite to the linear velocity of the planet's rotation. The angular velocity of a planet formed by gravity around the central planet is equal to and opposite to the angular velocity reflected from the planet's rotation to the central planet. At this time, for the revolution of the planet, the angular momentum generated by gravity cancels each other out, leaving only the angular momentum formed by the initial speed of the planet. This is the fundamental reason why the angular momentum of the planet's revolution under the action of gravity is conserved. After derivation calculations and data simulation, more than 99.9% of the gravity of the central planet is used for the rotation of the planet. It can also be said to balance the inertia of the planet's operation. It can also be considered that at the point of gravity, the torque of the planet's revolution is equal to the torque of the planet's rotation. Since the moment arm of the planet's revolution is much larger than the moment arm of the planet's rotation, the force used for the planet's revolution is much smaller than the force of the planet's rotation. The gravitational force between planets is not only related to the number of gravitational lines (gravitons) between the planets, but also related to the probability of interaction between gravitational lines and nucleons. The probability of interaction between gravitational lines and nucleons is exponentially related to the distance. The probability is small when the distance is small, and the probability is high when the distance is large. The gravitational coefficient between planets consists of a fixed part and an exponential part related to the distance. The fixed part reflects the number of gravitational lines between planets, and the exponential part reflects the probability of interaction between gravitational lines and nucleons. Through the simulation of the orbits of the eight planets in the solar system, this article found that none of them can return to the precession (orbital precession) phenomenon at the initial point, especially Mercury. Similarly, as an earth satellite, an artificial satellite is orbiting the earth. It is affected by the earth's gravity and forms a force of reverse rotation in its orbit. Under normal circumstances, the artificial satellite is controlled by the attitude control system, which balances the satellite rotation caused by the earth's gravity. When the attitude control fails, the satellite rolls under the influence of the earth's gravity, which is a normal manifestation of the satellite's rotation. For the Earth, the rotation speed on the sun's gravitational circle is reflected in the Earth's crust, and superimposes with the Earth's initial rotation angular speed, forming a phenomenon in which the Earth's rotation angular speed slowly decreases. This speed is reflected in the Earth's core, causing the Earth's core to rotate in the opposite direction to the Earth's current rotation, and this rotation speed is greater than the rotation speed of the Earth's crust. The changes in the earth's four seasons and the annual cycle are closely related to the position of the earth in its orbit. The position of the earth in its orbit reflects the changes in the earth's gravity from the sun. 99.99% of the sun's gravity is used for the earth's rotation, so the changes in the sun's gravity determine It determines the changes in the earth's rotation speed on the gravitational circle, determines the change in the earth's rotation speed coupled to the crust, and also determines the actual earth's rotation speed after the superposition of the earth's rotation speed caused by gravity and the earth's own rotation speed. To sum up, the seasonal periodic changes in the Earth's rotation and long-term slowdown are strongly related to changes in the sun's orbit. The reverse and rapid rotation of the Earth's core are all related to the separation of the sun's gravity point from the Earth's center. They are the inevitable result of almost all of the sun's gravity being used for the Earth's rotation. For the moon, the moon's rotation speed caused by the earth's gravity is much faster than the actual rotation speed, and this speed is affected by the moon's revolution speed. Therefore, it can be considered that the rotation speed generated by the earth's gravity on the moon is a frequency modulation wave modulated by the moon's revolution speed. The initial rotation speed of the moon is the same as the moon's rotation speed generated by the earth's gravity. Continuously superimposed, the initial rotation speed of the moon will approach the moon's rotation speed generated by the earth's gravity. When the two speeds are similar, the superposition of the two speeds will demodulate the revolution speed modulated on the moon's rotation speed generated by the earth's gravity. From the results, the demodulated speed is the same as the moon's revolution speed, which means that the moon is rotating synchronously. The moon revolves around the earth and at the same time the earth revolves around the sun. While the moon is subject to the gravity of the earth, it is also subject to the gravity of the sun. The gravity of the sun will cause the moon to rotate in the opposite direction to the revolution in the moon's orbit around the sun. When the moon rotates synchronously with the earth, The demodulated rotation plane is perpendicular to the moon's equinox plane. The lunar rotation generated by the sun's gravity is superimposed on the angular velocity of the Earth-Moon synchronous rotation to form the moon's observable rotation angular velocity. The angle between the moon's observable angular velocity rotation plane and the equinox plane will change within a certain range. From the above analysis, it can be seen that the solid structure that is integrated from the 0.5 radius of the planet to the spherical surface is a necessary condition for the synchronous rotation of the planet. The synchronous rotation of the planet is the ultimate return path of the planet.
References
- Wu Yeming. Mathematical explanation and modern proof of Kepler's laws [J]. Practice and Understanding of Mathematics, 2005, 35(12)5.DOI10.3969j.issn.1000-0984.2005.12.038.
- Wang Chuyun, Gan Shangpeng. Application of the law of conservation of angular momentum [J]. University Physics, 1988, 1(5): 12-12.
- "Mathematical Principles of Natural Philosophy" Newton PDF (full version). https://zhuanlan.zhihu.com/p/675301592.
- Chen Junli, Kang Yaohui. Gravity, gravitational field and gravitons—inference about the frequency of gravitational energy waves [J]. Astronomy and Astrophysics, 2022, 10(1): 1-10. [CrossRef]
- Chen Junli, Deflected Gravity Theory, Hanspub Publishing House, 2024-06-24. https://www.hanspub.org/books/BookManage?BookID=308, ISBN: 978-1-64997-896-7.
- Chen Junli, on nuclear force as the manifestation of gravity at microscopic distances [J]. Modern Physics, 2023, 13(5): 113-124. [CrossRef]
- Chen Junli. On the relationship between atomic structure and fundamental forces [J]. Astronomy and Astrophysics, 2024, 12(4): 57-71. [CrossRef]
- Chen Junli, Kang Yaohui. An attempt to correct the universal gravitation formula based on the proportion of gravitons emitted from the planet to the extrasphere—the proportion of extraspherical gravitons in the deflected gravity theory [J]. Astronomy and Astrophysics, 2023, 11(3): 27-39. [CrossRef]
- Chen Junli. Analysis of the causes of the formation of the Allais effect and gravity valley [J]. Astronomy and Astrophysics, 2023, 11(2): 13-26. [CrossRef]
- Baidu Encyclopedia. Earth [EB/OL]. https://baike.baidu.com/item/%E5%9C%B0%E7%90%83/6431, 2025-11-02.
- Baidu Encyclopedia. Mercury [EB/OL]. https://baike.baidu.com/item/%E6%B0%B4%E6%98%9F/135917, 2025-11-02.
- Baidu Encyclopedia. Oumuamua [EB/OL]. https://baike.baidu.com/item/%E5%A5%A5%E9%99%8C%E9%99%8C/22223109.
- Chen Junli. On the causes of 'Oumuamua's abnormal acceleration and orbital deviation: solar repulsion [J]. Astronomy and Astrophysics, 2023, 11(1): 1-11. [CrossRef]
- Earth structure (geographical noun) - Baidu Encyclopedia. https://baike.baidu.com/item/%E5%9C%B0%E7%90%83%E7%BB%93%E6%9E%84/10631795.
- AMDziewonski, R.Jeanloz, Ding Zhifeng. Rotation of the Earth's core in planets within planets [J]. World Earthquake Translation Series, 1997(6)5.DOICNKISUNDZYC.0.1997-06-000.
- Yang Kuiyi. The earth’s core rotates faster than the earth [J]. Science and Technology Trends, 1997(6)1.DOICNKISUNKJIC.0.1997-06-019.
- M.Carlowicz, Xiao Chunyan, Teng Yuntian. Observation results reveal that the earth’s core rotates faster than the earth itself [J]. World Earthquake Translation Series, 1997(4)2.DOICNKISUNDZYC.0.1997-04-016.
- Li Le, Zhou Huilan, Chen Qifu. Progress in seismological research on the Earth's inner core [J]. Progress in Geophysics, 2004, 19(2). DOI10.3969j.issn.1004-2903.2004.02.006.
- Zhang Weiwei, Xu Houze, Wang Aisheng. Research on the rotational motion of the inner core Earth and the fixed reference frame of the Earth [J]. Progress in Geophysics, 2005, 20(003)712-717. DOI10.3969j.issn.1004-2903.2005.03.022.
- Zhiyan. The direction of rotation of the earth’s core [J]. A must-read for junior high school students, 2016(10)1.
- Yang Xuexiang. A surprising discovery of the rapid rotation of the earth's solid core [J]. Earth, 1997, 01(No.97)7-8.DOICNKISUNDIQU.0.1997-01-001.
- Yang Xuexiang, Chen Dianyou. Dynamic effects of the earth's core [J]. Progress in Geophysics, 1996, 11(1)3. DOICNKISUNDQWJ.0.1996-01-005.
- Zhu Tao. Differential rotation of the Earth [J]. Progress in Geophysics, 2003, 18(2)247-255. DOI10.3969j.issn.1004-2903.2003.02.011.
- Yang Donghong, Yang Xuexiang. Research and calculation model of changes in the earth's rotation speed [J]. Progress in Geophysics, 2013(1)13. DOI10.6038pg20130107.
- Song Guanyi. Analysis of the main causes of seasonal changes in the earth's rotation speed [J]. Progress in Geophysics, 2011, 26(2):450-455. DOI:10.3969/j.issn.1004-2903.2011.02.008.
- Song Guanyi. Analysis of some major remaining problems in the subject of earth rotation [J]. Progress in Geophysics, 2014, 29(1):4-14. DOI:10.6038/pg20140102.
- Baidu Encyclopedia, Earth’s rotation. https://baike.baidu.com/item/%E5%9C%B0%E7%90%83%E8%87%AA%E8%BD%AC/799188.
- Teng Yongfu, Liu Fugang, Luo Jinming, et al. A response mechanism of long-term changes in the earth's rotation angular velocity to the characteristics of the sun's orbital motion [J]. Progress in Geophysics, 2019, 34(5)8. DOI10.6038pg2019CC0548.
- Huang Yuan. Discussion on the rotation of Venus [J]. Journal of Earth Science and Environment, 1997(S1)33-36.
- Gao Buxi. Rotation, shape and gravitational field of the moon and giant satellites [C] Proceedings of the 10th National Academic Symposium on Lunar Science and Comparative Planetology, Meteoriteology and Astrochemistry. 2012.
- Tian Shuqin. Derivation of stellar rotational force [J]. Science and Technology Information, 2012(35)4. DOI10.3969j.issn.1672-3791.2012.35.003.
- Uncovering the "mystery" of the moon's synchronous rotation. https://zhuanlan.zhihu.com/p/25325495.
Figure 1.
The equivalent spherical surface of the planet emitting gravitons.
Figure 1.
The equivalent spherical surface of the planet emitting gravitons.
Figure 2.
Schematic diagram of separation of gravity action point and center of mass.
Figure 2.
Schematic diagram of separation of gravity action point and center of mass.
Figure 3.
Planetary revolution and rotation caused by gravity.
Figure 3.
Planetary revolution and rotation caused by gravity.
Figure 4.
Planet Operation Analysis Chart.
Figure 4.
Planet Operation Analysis Chart.
Figure 5.
Earth orbit simulation diagram.
Figure 5.
Earth orbit simulation diagram.
Figure 6.
Mercury orbit simulation diagram.
Figure 6.
Mercury orbit simulation diagram.
Figure 7.
Schematic diagram of calculation of probability of gravity line and nucleon interaction.
Figure 7.
Schematic diagram of calculation of probability of gravity line and nucleon interaction.
Figure 8.
Calculation of probability of graviton nucleon interaction.
Figure 8.
Calculation of probability of graviton nucleon interaction.
Figure 9.
Relationship between old and new gravitational coefficients and distance.
Figure 9.
Relationship between old and new gravitational coefficients and distance.
Figure 10.
Ball rotation analysis diagram.
Figure 10.
Ball rotation analysis diagram.
Figure 11.
Moon rotation speed modulation and demodulation process.
Figure 11.
Moon rotation speed modulation and demodulation process.
Figure 12.
Composite diagram of the moon’s rotation caused by gravity.
Figure 12.
Composite diagram of the moon’s rotation caused by gravity.
Figure 13.
Schematic diagram of the movement of the sun, earth and moon.
Figure 13.
Schematic diagram of the movement of the sun, earth and moon.
Table 1.
The number of gravitons emitted by planets in the solar system to the outside of the sphere.
Table 1.
The number of gravitons emitted by planets in the solar system to the outside of the sphere.
planet
name |
ms
(kg) |
rs
(m) |
ρs
(kg/m^3) |
rso
(m) |
k |
nso |
nso
(rs) |
r0(m) |
| sun |
1.99E+30 |
6.96E+08 |
10 |
4145.00 |
5.96E-06 |
7.75E+72 |
7.75E+72 |
8.00E-16 |
| Mercury |
3.30E+23 |
2.44E+06 |
5425 |
7.64 |
3.13E-06 |
9.52E+67 |
9.52E+67 |
m0(kg) |
| Venus |
4.87E+24 |
6.05E+06 |
5242.3 |
7.91 |
1.31E-06 |
5.86E+68 |
5.86E+68 |
1.67E-27 |
| Earth |
5.97E+24 |
6.37E+06 |
2800 |
14.80 |
2.32E-06 |
6.49E+68 |
6.49E+68 |
nng |
| Mars |
6.42E+23 |
3.39E+06 |
3934.1 |
10.54 |
3.11E-06 |
1.84E+68 |
1.84E+68 |
2.23E+22 |
| Jupiter |
1.90E+27 |
6.99E+07 |
1326.2 |
31.25 |
4.47E-07 |
7.81E+70 |
7.81E+70 |
ko |
| saturn |
5.68E+26 |
5.82E+07 |
687.1 |
60.33 |
1.04E-06 |
5.42E+70 |
5.42E+70 |
0.55 |
| Uranus |
8.68E+25 |
2.54E+07 |
1270.4 |
32.63 |
1.29E-06 |
1.03E+70 |
1.03E+70 |
kng |
| Neptune |
1.02E+26 |
2.46E+07 |
1637.9 |
25.31 |
1.03E-06 |
9.69E+69 |
9.69E+69 |
0.378 |
Table 2.
Simulation table of Earth’s revolution data around the sun.
Table 2.
Simulation table of Earth’s revolution data around the sun.
re
(m) |
R
(m) |
ΔR
(m) |
Hs
(m) |
He
(m) |
β0 |
v0
(m/s) |
ωe |
ωs |
α |
θc |
θ |
X
(m) |
Y
(m) |
| 6.371E+06 |
1.47098E+11 |
|
3.494E+08 |
3.171E+06 |
1.5711105 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00065 |
1.471E+11 |
9.528E+07 |
rs
(m) |
1.47098E+11 |
-1.7E+00 |
3.494E+08 |
3.171E+06 |
1.5711202 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00130 |
1.471E+11 |
1.906E+08 |
| 6.955E+08 |
1.47098E+11 |
-9.3E+02 |
3.494E+08 |
3.171E+06 |
1.5711299 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00194 |
1.471E+11 |
2.858E+08 |
Rmin
(m) |
1.47098E+11 |
-1.8E+03 |
3.494E+08 |
3.171E+06 |
1.5711396 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00259 |
1.471E+11 |
3.811E+08 |
| 1.471E+11 |
1.47098E+11 |
-2.8E+03 |
3.494E+08 |
3.171E+06 |
1.5711493 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00324 |
1.471E+11 |
4.764E+08 |
Rmax
(m) |
1.47098E+11 |
-3.7E+03 |
3.494E+08 |
3.171E+06 |
1.5711590 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00389 |
1.471E+11 |
5.717E+08 |
| 1.521E+11 |
1.47098E+11 |
-4.6E+03 |
3.494E+08 |
3.171E+06 |
1.5711687 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00453 |
1.471E+11 |
6.669E+08 |
| Grm |
1.47098E+11 |
-5.5E+03 |
3.494E+08 |
3.171E+06 |
1.5711784 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00518 |
1.471E+11 |
7.622E+08 |
| 1.2464E-10 |
1.47098E+11 |
-6.5E+03 |
3.494E+08 |
3.171E+06 |
1.5711881 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00583 |
1.471E+11 |
8.575E+08 |
| ki |
1.47098E+11 |
-7.4E+03 |
3.494E+08 |
3.171E+06 |
1.5711977 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00648 |
1.471E+11 |
9.528E+08 |
| 0.3307 |
1.47098E+11 |
-8.3E+03 |
3.494E+08 |
3.171E+06 |
1.5712074 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00712 |
1.471E+11 |
1.048E+09 |
T
(s) |
1.47099E+11 |
-9.2E+03 |
3.494E+08 |
3.171E+06 |
1.5712171 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00777 |
1.471E+11 |
1.143E+09 |
| 3.156E+07 |
1.47099E+11 |
-1.0E+04 |
3.494E+08 |
3.171E+06 |
1.5712268 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00842 |
1.471E+11 |
1.239E+09 |
| n |
1.47099E+11 |
-1.1E+04 |
3.494E+08 |
3.171E+06 |
1.5712365 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00907 |
1.471E+11 |
1.334E+09 |
| 10000 |
1.47099E+11 |
-1.2E+04 |
3.494E+08 |
3.171E+06 |
1.5712462 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.00972 |
1.471E+11 |
1.429E+09 |
Δt
(s) |
1.47099E+11 |
-1.3E+04 |
3.494E+08 |
3.171E+06 |
1.5712559 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.01036 |
1.471E+11 |
1.524E+09 |
| 3156 |
1.47099E+11 |
-1.4E+04 |
3.494E+08 |
3.171E+06 |
1.5712656 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.01101 |
1.471E+11 |
1.620E+09 |
S
(m^2) |
1.47099E+11 |
-1.5E+04 |
3.494E+08 |
3.171E+06 |
1.5712753 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.01166 |
1.471E+11 |
1.715E+09 |
| 7.007E+22 |
1.47099E+11 |
-1.6E+04 |
3.494E+08 |
3.171E+06 |
1.5712850 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.01231 |
1.471E+11 |
1.810E+09 |
Sn
(m^2) |
1.47099E+11 |
-1.7E+04 |
3.494E+08 |
3.171E+06 |
1.5712946 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.01295 |
1.471E+11 |
1.905E+09 |
| 7.007E+18 |
1.47099E+11 |
-1.8E+04 |
3.494E+08 |
3.171E+06 |
1.5713043 |
3.019E+04 |
6.194E-05 |
1.335E-09 |
6.435E-04 |
6.477E-04 |
0.01360 |
1.471E+11 |
2.001E+09 |
Table 3.
Gravity coefficient statistical table.
Table 3.
Gravity coefficient statistical table.
| Planet name |
rs(m) |
re(m) |
Rm(m) |
RM(m) |
m(kg) |
T(s) |
S(m^2) |
Gr(N/m^2) |
| Moon |
6.371E+06 |
1.737E+06 |
3.631E+08 |
4.057E+08 |
7.342E+22 |
2.354E+06 |
4.635E+17 |
1.1995E+12 |
| Mercury |
6.955E+08 |
2.440E+06 |
4.600E+10 |
6.982E+10 |
3.301E+23 |
7.580E+06 |
1.031E+22 |
8.0110E+13 |
| Venus |
6.955E+08 |
6.052E+06 |
1.075E+11 |
1.089E+11 |
4.868E+24 |
1.936E+07 |
3.678E+22 |
1.9119E+14 |
| Earth |
6.955E+08 |
6.371E+06 |
1.471E+11 |
1.521E+11 |
5.972E+24 |
3.147E+07 |
7.007E+22 |
2.1055E+14 |
| Mars |
6.955E+08 |
3.390E+06 |
2.067E+11 |
2.492E+11 |
6.417E+23 |
5.919E+07 |
1.625E+23 |
8.0780E+13 |
| Jupiter |
6.955E+08 |
6.991E+07 |
7.405E+11 |
8.166E+11 |
1.898E+27 |
3.733E+08 |
1.902E+24 |
5.5409E+14 |
| saturn |
6.955E+08 |
5.823E+07 |
1.353E+12 |
1.514E+12 |
5.683E+26 |
9.271E+08 |
6.446E+24 |
2.4310E+14 |
| Uranus |
6.955E+08 |
2.536E+07 |
2.742E+12 |
3.008E+12 |
8.681E+25 |
2.644E+09 |
2.594E+25 |
1.9715E+14 |
| Neptune |
6.955E+08 |
2.462E+07 |
4.460E+12 |
4.537E+12 |
1.024E+26 |
5.187E+09 |
6.357E+25 |
2.4816E+14 |
Table 4.
Gravity coefficient calculation table.
Table 4.
Gravity coefficient calculation table.
| e |
name |
rs(m) |
re(m) |
Ra(m) |
Gi(simulation) |
exponential part |
Gi(calculation) |
ΔG |
| 2.71828 |
Moon |
6.371E+06 |
1.737E+06 |
3.844E+08 |
1.200E+12 |
0.00532 |
1.200E+12 |
0.00000000 |
| b |
Mercury |
6.955E+08 |
2.440E+06 |
6.108E+10 |
8.011E+13 |
0.99979 |
2.256E+14 |
1.81617289 |
| 7.73848853E+17 |
Venus |
6.955E+08 |
6.052E+06 |
1.082E+11 |
1.912E+14 |
0.99993 |
2.256E+14 |
0.18016370 |
| Gr |
Earth |
6.955E+08 |
6.371E+06 |
1.496E+11 |
2.106E+14 |
0.99997 |
2.256E+14 |
0.07168182 |
| 2.25650410E+14 |
Mars |
6.955E+08 |
3.390E+06 |
2.280E+11 |
8.078E+13 |
0.99999 |
2.256E+14 |
1.79335294 |
| |
Jupiter |
6.955E+08 |
6.991E+07 |
7.786E+11 |
5.541E+14 |
1.00000 |
2.257E+14 |
0.59275547 |
| |
saturn |
6.955E+08 |
5.823E+07 |
1.434E+12 |
2.431E+14 |
1.00000 |
2.257E+14 |
0.07177982 |
| |
Uranus |
6.955E+08 |
2.536E+07 |
2.875E+12 |
1.972E+14 |
1.00000 |
2.257E+14 |
0.14456195 |
| |
Neptune |
6.955E+08 |
2.462E+07 |
4.498E+12 |
2.482E+14 |
1.00000 |
2.257E+14 |
0.09070599 |
| total |
|
|
|
|
1.806E+15 |
8.00499 |
|
4.76117458 |
Table 5.
Planet Mass Adjustment Table.
Table 5.
Planet Mass Adjustment Table.
| name |
rs(m) |
re(m) |
Ra(m) |
Gi (simulation) |
Gi (calculation) |
m (kg original) |
m (kg new) |
Δm |
| Moon |
6.371E+06 |
1.737E+06 |
3.844E+08 |
1.200E+12 |
1.200E+12 |
7.342E+22 |
7.3420E+22 |
0.00000 |
| Mercury |
6.955E+08 |
2.440E+06 |
6.108E+10 |
8.011E+13 |
2.256E+14 |
3.301E+23 |
9.2978E+23 |
1.81658 |
| Venus |
6.955E+08 |
6.052E+06 |
1.082E+11 |
1.912E+14 |
2.256E+14 |
4.868E+24 |
5.7446E+24 |
0.18020 |
| Earth |
6.955E+08 |
6.371E+06 |
1.496E+11 |
2.106E+14 |
2.256E+14 |
5.972E+24 |
6.4006E+24 |
0.07174 |
| Mars |
6.955E+08 |
3.390E+06 |
2.280E+11 |
8.078E+13 |
2.256E+14 |
6.417E+23 |
1.7925E+24 |
1.79332 |
| Jupiter |
6.955E+08 |
6.991E+07 |
7.786E+11 |
5.541E+14 |
2.257E+14 |
1.898E+27 |
7.7304E+26 |
-0.59275 |
| Saturn |
6.955E+08 |
5.823E+07 |
1.434E+12 |
2.431E+14 |
2.257E+14 |
5.683E+26 |
5.2755E+26 |
-0.07177 |
| Uranus |
6.955E+08 |
2.536E+07 |
2.875E+12 |
1.972E+14 |
2.257E+14 |
8.681E+25 |
9.9358E+25 |
0.14455 |
| Neptune |
6.955E+08 |
2.462E+07 |
4.498E+12 |
2.482E+14 |
2.257E+14 |
1.898E+27 |
9.312E+25 |
-0.95094 |
Table 6.
Statistical table of solar system planetary precession (orbital precession).
Table 6.
Statistical table of solar system planetary precession (orbital precession).
| name |
Rs
(m) |
Re
(m) |
Rmin
(m) |
ki |
T
(s) |
a
(m) |
e |
S
(m^2) |
β0 |
Rn
(m) |
ΔR
(m) |
angle second |
| Mercury |
6.955E+08 |
2.440E+06 |
4.600E+10 |
0.3250 |
7.601E+06 |
5.791E+10 |
0.20563 |
1.031E+22 |
1.5711128 |
4.75755E+10 |
1.574E+09 |
123.2 |
| Venus |
6.955E+08 |
6.052E+06 |
1.075E+11 |
0.3350 |
1.941E+07 |
1.082E+11 |
0.00677 |
3.678E+22 |
1.5711105 |
1.07595E+11 |
1.175E+08 |
3.9 |
| Earth |
6.955E+08 |
6.371E+06 |
1.471E+11 |
0.3307 |
3.156E+07 |
1.496E+11 |
0.00335 |
7.007E+22 |
1.5711105 |
1.47500E+11 |
4.012E+08 |
9.8 |
| Mars |
6.955E+08 |
3.390E+06 |
2.067E+11 |
0.3660 |
5.935E+07 |
2.279E+11 |
0.09341 |
1.625E+23 |
1.5711102 |
2.12119E+11 |
5.374E+09 |
93.6 |
| Jupiter |
6.955E+08 |
6.991E+07 |
7.405E+11 |
0.4000 |
3.743E+08 |
7.786E+11 |
0.04890 |
1.902E+24 |
1.5711110 |
7.45021E+11 |
4.496E+09 |
21.9 |
| saturn |
6.955E+08 |
5.823E+07 |
1.353E+12 |
0.4000 |
9.296E+08 |
1.434E+12 |
0.05650 |
6.446E+24 |
1.5711107 |
1.36626E+12 |
1.372E+10 |
36.5 |
| Uranus |
6.955E+08 |
2.536E+07 |
2.742E+12 |
0.4000 |
2.652E+09 |
2.875E+12 |
0.04638 |
2.594E+25 |
1.5711092 |
2.78753E+12 |
4.540E+10 |
59.6 |
| Neptune |
6.955E+08 |
2.462E+07 |
4.460E+12 |
0.4000 |
5.201E+09 |
4.498E+12 |
0.00868 |
6.357E+25 |
1.5711101 |
4.47674E+12 |
1.722E+10 |
13.9 |
Table 7.
Solid Earth Structure Table.
Table 7.
Solid Earth Structure Table.
| The Earth's Circle Name |
Depth
(km) |
radius
(km) |
earthquake
P-wave velocity(km/s) |
earthquake
shear velocity(km/s) |
Density(grams / cubic centimeter) |
State of matter |
| First level layering |
second level
layering |
traditional layering |
| Outer sphere |
crust |
crust |
0~33 |
6338-6371 |
5.6~7.0 |
3.4~4.2 |
2.6~2.9 |
Solid state substance |
| Outer transition layer |
Outer transition layer (Above) |
Upper mantle |
33~980 |
5391-6338 |
8.1~10.1 |
4.4~5.4 |
3.2~3.6 |
Partially melted substance |
| Outer transition layer (Below) |
Lower mantle |
980~2900 |
3471-5391 |
12.8~13.5 |
6.9~7.2 |
5.1~5.6 |
Liquid-solid state substance |
| Liquid layer |
Liquid layer |
outer core |
2900~4700 |
1671-3471 |
8.0~8.2 |
cannot pass through |
10.0~11.4 |
Liquid state substance |
| Inner sphere |
Internal transition layer |
transition layer |
4700~5100 |
1271-1671 |
9.5~10.3 |
|
12.3 |
Liquid -solid state substance |
| The earth's core |
inner core |
5100~6371 |
0-1271 |
10.9~11.2 |
|
12.5 |
solid state substance |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).