Submitted:
02 June 2025
Posted:
04 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Primordial Universe
2.1. Cosmological Model
2.1.1. The Probable Origin of the Expansion of the Universe
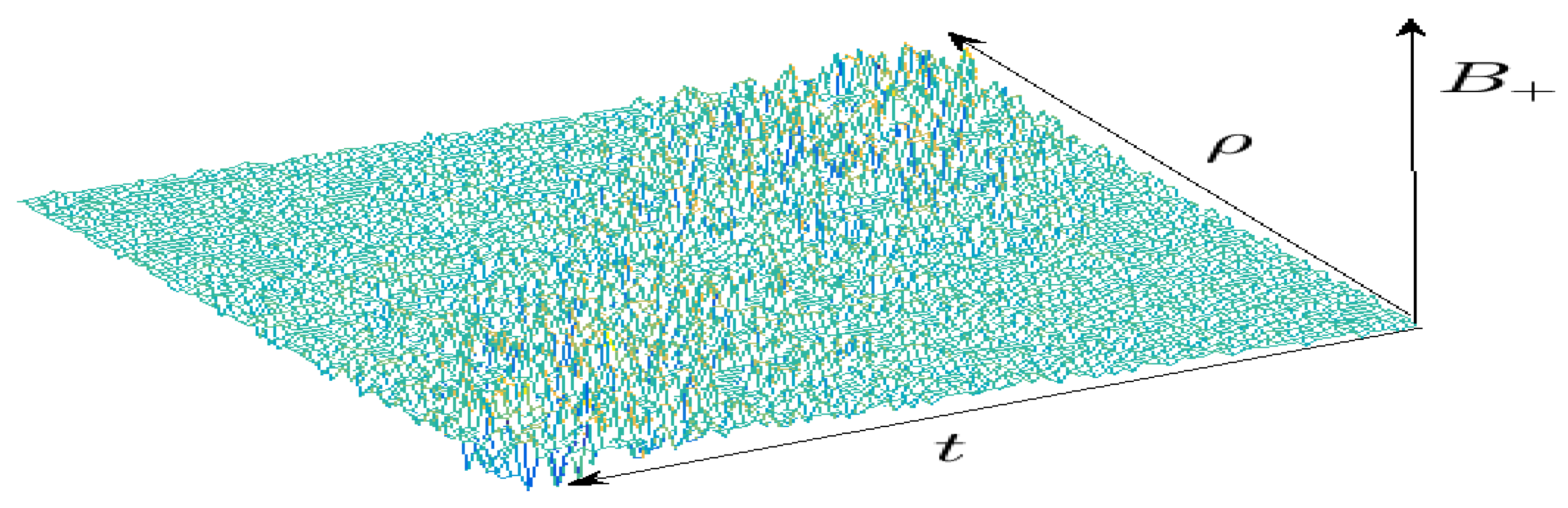
3. Conclusion and Perspectives
References
- M. Clifford, Living Rev. Relativity.174 (2014).
- B. P. Abbott and al., LIGO-Virgo scientific collaboration, Phys. Rev. Lett.116061102 (2016).
- B. P. Abbott and al., LIGO-Virgo scientific collaboration, Classical Quantum Gravity.37055002 (2020).
- A. Nischizawa and al, Phys. Rev. D.79082002 (2019).
- S. Farnes, Astronomy.And. Astrophysics.620A92 (2018) .
- M. Corredoira, Foundations. of. Physics.47, 711–768, (2017).
- M. Krauss and S. Turner, Gen. Relativ. Grav.271137–1144 (1995).
- Reiss et al, The. Astrophysical. Journal. Letters.934:L7(52pp) (2022).
- D, Merrit arxiv.org/pdf/1703.02389.
- A. Pomeransky, Phys. Rev. D73044004 (2006).
- J. Defo and K. Kuetche, JETP.1353 (2022).
- V. Belinskii and V. Zakharov, Sov. Phys. JETP48985 (1978).
- V. A. Belinski and E. Verdaguer, Gravitational soliton (Cambridge University Press, Cambridge, 2001).
- V. A. Belinsky and D. Fargion, IL NUOVO CIMENTO591 (1980).
- V. Belinski and G. Vereshchagin Phys. Lett. B778332-338 (2017).
- T. Matos and al, arxiv.org/abs/2309.09989.
- M. Carmeli and C. Charach, Foundations. of. Physics.14, 10, (1984).
- F. Dyson, Int. J. Mod. Phys. A.2825 (2013).
- M. Parikh, F. Wilczek, and G. Zahariade, arXiv:2005.07211.
- E. Tauber, Foundations. of. Physics.14, 10, (1984).
- T. Piran, P. N. Sarfier and R. F. Stark, Phys. Rev. D323101 (1985).
- A. Sakharov, Sov. Phys. JETP523 (1980).
- A. Sakharov, Phys. Lett. USSR 5 24 (1967).
- Y. Hadad and V. Zakharov, arxiv.org/abs/1401.7251.
- J. Weber and J. A. Wheeler, Rev. Mod. Phys.29509 (1957).
- D. Kennefick, Phys. Today. 9 43 (2005).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



