1. Introduction
There are many forms in the natural world that resist basic geometric explanation. Mandelbrot(Mageed 2024 a), noted that clouds are not spheres, mountains are not cones, and coastlines are not circles. With its emphasis on smooth, uniform forms, Euclidean geometry has been the most often used framework for scientific investigation throughout ages. But with the introduction of fractal geometry in the middle of the 20th century (Mageed, 2024 a), our capacity to measure and understand the intrinsic irregularity and complexity present in nature was transformed. Fundamentally, a fractal (Mageed, 2024a) is a rough or broken geometric form that can be broken down into parts, each of which is (at least roughly) a lesser replica of the whole. Together with a fractal dimension often greater than its topological dimension, this quality—known as self-similarity—reveals a more fundamental order inside seeming anarchy.
Given their prevalence, fractal patterns seem not only to be coincidences but also emergent characteristics of basic physical and biological mechanisms (Mageed & Mohamed, 2023; Mageed, 2024b). From the efficient transport networks inside living organisms to the enormous, filamentary structures of the cosmic web, fractals offer best answers for maximizing surface area, lowering energy use, or enabling sophisticated interactions across ranges (Mageed, 2025). The manifestation and importance of fractal geometry across an astonishing array of scales and spheres will be thoroughly explored in this paper: the complex biological systems of humans(Mageed & Mohamed, 2023), birds, and animals; the dynamic geological characteristics of Earth; and the awe-inspiring, large-scale constructions of space, the universe(Mageed, 2025), and galaxies. By looking at these different instances, we hope to highlight the unifying power of fractal mathematics in revealing the underlying structure of our universe.
2. Fractals in Humans
A wonder of biological engineering, the human body shows fractal features at several levels, therefore highlighting the efficacy and strength of fractal designs in biological systems. The lungs' bronchial tree is perhaps the most striking illustration. Following a self-similar pattern as in
Figure 1 (c.f., Mageed & Mohamed, 2023), this complex network of airways splits repeatedly from the trachea down to the small alveoli. Though on a lesser scale, each branching generation reflects the last one. Maximizing the surface area accessible for gas exchange, this fractal branching enables efficient oxygen intake and carbon dioxide removal in a small volume (Ortiz-Puerta, 2023) suggests that the fractal dimension of the human lung is roughly 2.7-2.9, hence indicating its space-filling efficiency.
In a same vein, the human circulatory system is a textbook case of a fractal network. Arteries branch into arterioles, which further divide into capillaries, therefore creating a large, self-similar tree that permeates every tissue and cell (Poole & Musch, 2023; Johannes, 2025). This fractal design guarantees effective delivery of blood, oxygen, and nutrients to every part of the body as well as thorough removal of metabolic waste products. (Žnidarič et al., 2023) argues that the fractal character of the vascular system minimizes the energy needed for circulation and maximizes flow resistance. Reflecting its capacity to occupy a three-dimensional environment (Grosu et al., 2023), studies have proved that the fractal dimension of the human vascular tree is around 3.
Particularly in its complex neural networks and the complex surface of the cerebral cortex, the human brain exhibits fractal characteristics. (Maryenko, 2024) The cortex's folding, which enables a great surface area to be packed into a constrained cranial volume, shows fractal characteristics. Believed to maximize the merging of synaptic inputs (Guidolin et al., 2024), the receptive extensions of neurons also display fractal geometry in their branching patterns. According to (Kv et al., 2024), the fractal dimension of dendritic trees has been related with neuronal complexity and functional efficiency. Moreover, suggesting scale-invariant processes underlying cognitive activities are the temporal dynamics of brain activity, measured by electroencephalography (EEG), often show fractal fluctuations (Morales et al., 2023).
Beyond these internal systems, even the human skin can show fractal patterns, especially in the arrangement of pores or the complex lines of fingerprints (Roy & Vemaganti, 2024). Less obviously fractal than the lung or circulatory system, the micro-architecture of skin can reveal self-similar roughness at several magnifications. These biological systems' fractal characteristic emphasizes their evolutionary optimization for function, resilience, and adaptability (West, 2022). Knowing these fractal dimensions can also have important consequences for medical diagnostics, for example in detecting aberrant tissue structure or physiological rhythms (Catrambone et al., 2021).
3. Fractals in Birds and Animals
From the minute patterns within single cells to the more extensive groupings of species, the animal kingdom offers a great canvas of fractal representations. Classic examples of fractal development, the branching patterns of antlers in deer or moose maximize surface area and strength for fighting or display Di Guida et al., 2025). Every branch reflects the general structure, so fostering an elegant but effective composition. Likewise adapting to mechanical stresses (Innocenti et al., 2022), the skeletal structures of several species—especially the trabecular bone within joints—exhibit a fractal-like porous architecture offering greatest strength with least material. According to (Eser & Sarıbaş, 2024), weight bearing and shock absorption depend on this self-similar configuration of bone struts.
Like those of humans, the nervous systems of several creatures show fractal branching of neurons and their dendritic trees, therefore enhancing connectivity and signal processing (Kunasegaran et al. 2023). Remarkably maximizing their reach within the soil (Weigelt et al., 2021), the complex network of roots in plants—essential for nutrient and water uptake—also follows fractal patterns. Although not living, the ideas pertain to biological development.
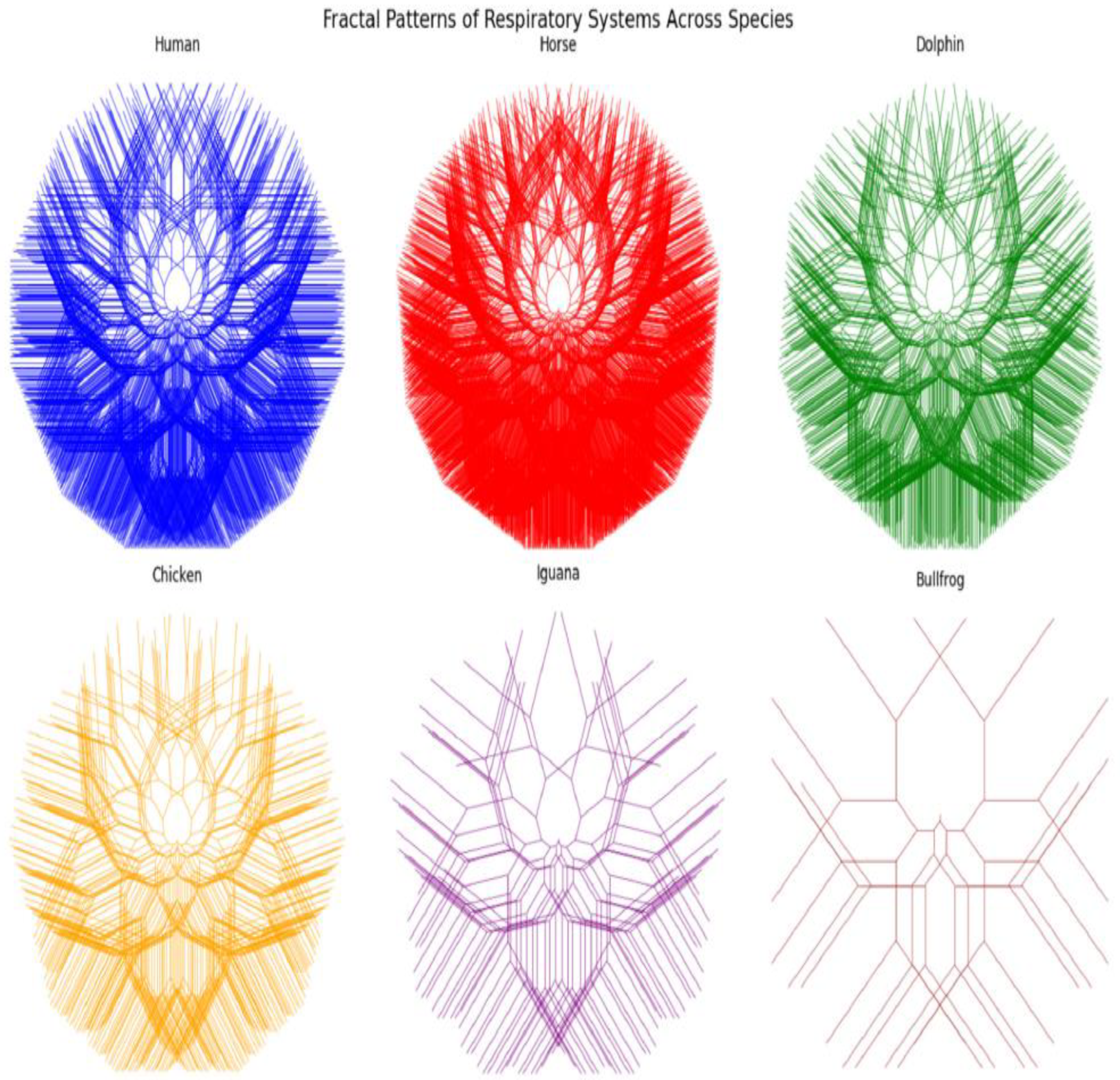
Feather structure in birds can show fractal features. According to (Xu & Barrett, 2025, the barbules branching off barbs, which then branch off the main rachis, create a hierarchical, self-similar structure that enhances the feather's strength, lightness, and aerodynamic qualities. This complex structure insulates and enables quick flight. Additionally, emergent fractal patterns can occasionally be seen in the swarming of insects or fish or in the flocking of birds (Caprini et al., 2020). Although not a fixed fractal, the dynamic collective motion can show scale-invariant correlations, where the patterns of movement at one scale resemble those at another, therefore reflecting complex interactions between people (Gómez-Nava et al., 2022). Often highly effective group reactions to predators or habitat changes result from this self-organisation. For a fascinating visualisation, see
Figure 2 (c.f., Montgomery, 2024).
Similar as those in people, the circulatory and respiratory systems of animals are therefore obvious instances of fractal networks (Ghanbari et al., 2020). Adhering to fractal principles for best transport (Maina, 2023), these systems range from the gills of fish to the tracheae of insects maximize surface area for exchange within a limited volume. Though seeming hexagonal, the honeycomb pattern produced by bees may be seen as a packing problem solution contributing to the general fractal-like efficiency of the hive's organization at a bigger scale (Shoemaker et al., 2021).
Sometimes even the patterns on animal coats—such as the stripes of a zebra or the spots of a leopard—can be defined using reaction-diffusion models generating fractal-like patterns (Yang et al., 2021). Though not mathematically self-similar, these patterns often show scale-invariance in their statistical characteristics, therefore reflecting the underlying developmental processes. Emphasizing their function as basic blueprints for biological complexity and functional optimization, fractals are extensively seen in animal morphology and behavior (Karperien & Jelinek, 2024).
4. Fractals on Earth
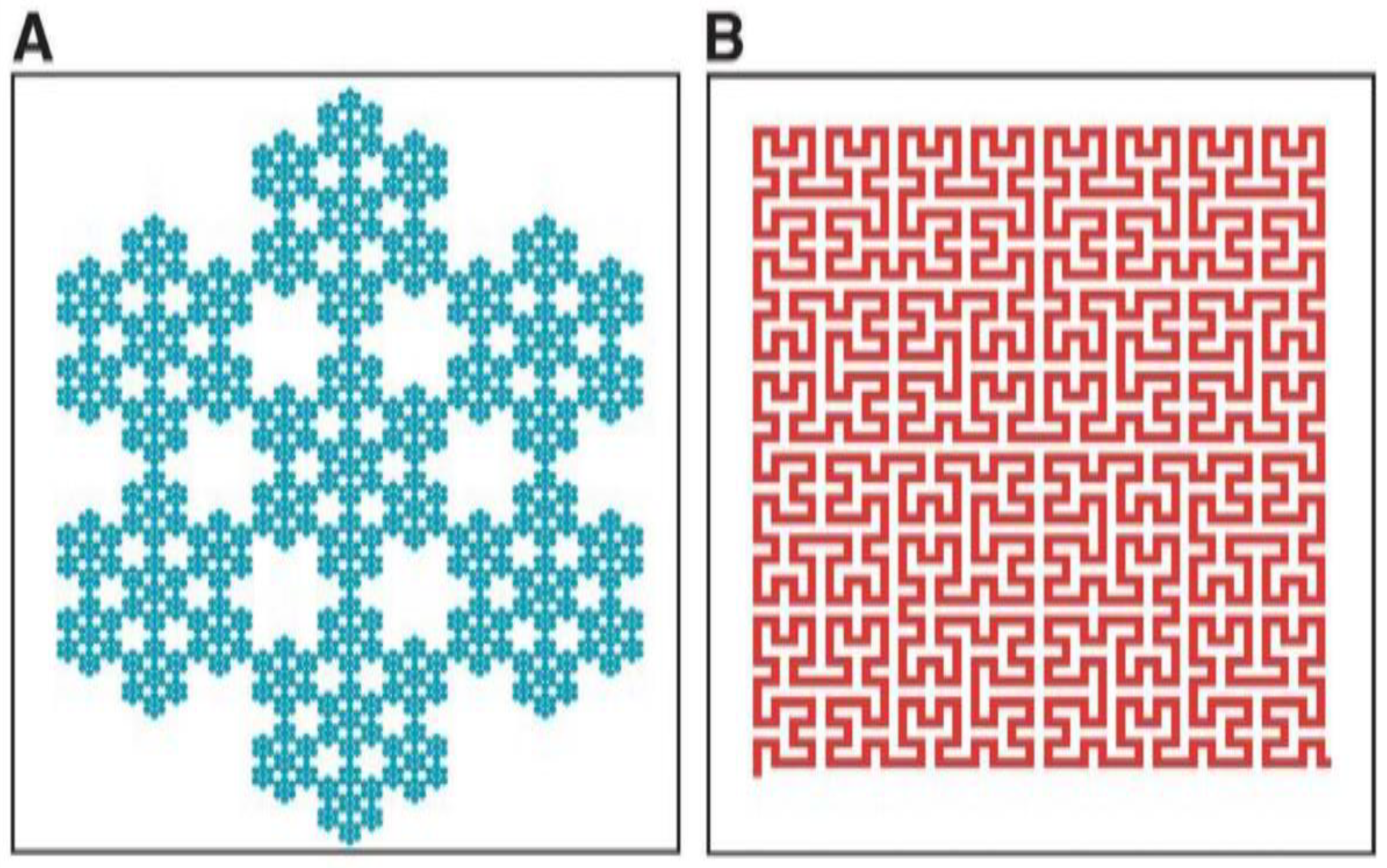
From large geologic features to microscopic mineral structures, our dynamic canvas, Earth, is etched in many forms by fractal geometry(Bhat & Mageed, 2023; Mageed, 2023c; Mageed, 2024d). The coastline is maybe the most well-known instance. As Mandelbrot so expertly showed, the length of a coastline varies with the length of the measuring instrument applied (Bhat & Mageed, 2023; Mageed, 2023c; Mageed, 2024d). Looking closer reveals more complex details—bays within bays, coves inside coves—showing a self-similar pattern across scales. Coastlines have a fractal dimension usually between 1 and 2 because of this intrinsic oddity, which reflects their roughness and space-filling qualities (Mageed, 2024 a, Bhat & Mageed, 2023; Mageed, 2023c; Mageed, 2024d), as depicted in
Figure 3 (c.f., Mageed, 2024 a).The fractal dimension of a coastline reflects the interplay of geological processes like erosion, sedimentation, and tectonic activity.
Another classic instance of fractal geometry on Earth are river networks. From big rivers to little streams, the bifurcation patterns of rivers and their tributaries create very effective drainage systems (Bhat & Mageed, 2023; Mageed, 2023c; Mageed, 2024d).
This structured branching helps to reduce the total length of the river channels while maximising the area drained, therefore improving water flow and sediment transport. Often, the fractal dimension of river networks is found to be around 2, which suggests their space-filling effectiveness in two dimensions (Bhat & Mageed,2023;Mageed,2023c; Mageed, 2024d).Energy dissipation and hydrological efficiency ideas generate this fractal arrangement.
Fractal features may also be found in mountain ranges and topographic surfaces. Fractal dimensions can help to characterize the toughness of mountains, whose peaks and valleys show at different scales (Srivastava et al., 2021). Under great timescales, geologic processes such faulting, folding, and erosion combine to produce this scale-invariant roughness. Reflecting the variating slopes of complexity and erosion (El-Nabulsi & Anukool, 2022), topographic fractal dimension can span 2.0 to 2.5.
Moreover, patterns of clouds show fractal qualities. From little cumulus to large storm systems, the erratic, wispy forms of clouds often show self-similarity at several magnifications (Fleischmann, et al., 2014). Reflecting the turbulent processes of atmospheric dynamics (Barnsley & Demko, 2014), clouds usually have a fractal dimension of around 2.35. Understanding atmospheric transport and climate modeling depends on this fractal character.
Even on a tiny scale, rock fractures and geologic fault lines can show fractal designs (Yang & Liu, 2022). Cracks in rocks often obey fractal scaling rules in their geometry and distribution, therefore affecting the mechanical characteristics of the crust of the Earth and the propagation of earthquakes (Li et al., 2025). Influenced by the fractal distribution of fuel and wind patterns (Qin et al., 2024), the fractal character of forest fires and their spreading patterns also shows self-organization and scale-invariance. (Milovanov & Iomin, 2023) argued that the ubiquitous occurrence of fractals on Earth highlights the basic function of scale-invariance and self-organization in determining the physical environment and dynamic processes of our planet.
5. Fractals in Space, the Universe, and Galaxies
From our solar system to the whole observable universe(Teles et al., 2022), the largest scales of the cosmos unexpectedly show fractal-like patterns that challenge established cosmological theories and provide fresh insights on the distribution of matter. Although celestial bodies like planets and stars are usually spherical(Teles et al., 2022), their distribution and the greater constructions they create sometimes show fractal features, as in
Figure 4 and
Figure 5 (c.f., Puetz, 2022).
Although not exactly fractal(Teles et al., 2022), some events inside our solar system can be examined from a viewpoint of scale-invariance. For example, the distribution of craters on planetary surfaces sometimes reflects power-law distributions, which may be suggestive of fractal processes of impact and erosion (Lagain et al., 2022). Though their fractal dimension is debated (Tiscareno & Murray, 2018), the ring systems of gas giants like Saturn, with their complex substructures and gaps, can show complex patterns that, at certain resolutions, might suggest self-organization driven by gravitational interactions.
Beyond our close surroundings(Teles et al., 2022), the arrangement of galaxies in the cosmos offers one of the most convincing large-scale instances of fractal geometry. Galaxy surveys show that galaxies are grouped into large, filamentary constructions, walls, and voids rather than evenly dispersed, hence forming the cosmic web (Norris et al., 2021; Vogelsberger et al., 2020).
Cosmology has long argued over the idea of a fractal universe. Though the standard cosmological model typically assumes homogeneity on very large scales, the observed fractal clustering of galaxies up to hundreds of megaparsecs implies that fractal geometry might be a more precise depiction of the universe's structure over a wide range of scales (Peebles, 2020) Some theories (Pössel, 2020) provide an alternative explanation for the observed large-scale structure without calling for exotic dark material or dark energy. According to theory, the hierarchical clustering (Cassey et al., 2023) resulting from the gravitational collapse of primordial density perturbations gives rise to the fractal character of the cosmic web.
Additionally studied for fractal characteristics is the distribution of quasars and gamma-ray bursts, so exposing maybe new understanding about the greatest structures and most energetic occurrences in the cosmos (Gaite, 2019; Giovanelli, 2025).
Conclusion
Fractal geometry's investigation across many fields—from the complex biological architectures within living entities to the huge, hierarchical structures of the cosmos—reveals its great and pervasive impact on the natural environment. Far from being just mathematical curiosities, fractals provide a strong lens via which to grasp the basic rules controlling growth, efficiency, and organization in nature. While the fractal designs of animal antlers and bone structures show effective material use and strength, the self-similar branching of human lungs and circulatory systems maximizes transport and exchange. The rough coastlines, complicated river systems, and dense mountain ranges that adorn our planet are clear evidence of the scale-invariant processes of rock formation and erosion.
Most notably, the cosmic web with its filamentary arrangement of galaxies questions our conventional ideas of cosmic homogeneity, implying that the universe itself may show fractal characteristics over great distances. This fractal model offers a strong basis for grasping how straightforward, repetitive rules generate complexity from simple beginnings, resulting in emergent patterns that are functionally optimized and aesthetically appealing.
Beyond simple description, fractal geometry has use in fields as diverse as medicine (diagnosing disease based on changes in fractal dimensions of tissues) to environmental science (modeling forest fire spread or river basin hydrology) and cosmology (understanding the evolution of large-scale structure). Though the exact fractal dimension and the scope of scales over which self-similarity holds true might vary, the basic concept is constant: nature usually creates intricate forms by repeating basic patterns at several magnifications.
Fractal geometry offers in essence a graceful and unifying mathematical language for capturing the intrinsic irregularity and hierarchical organization of the cosmos. It exposes a hidden order underlying the observed anarchy of natural events by connecting the microscopic and the macroscopic. Fractal geometric provides insights that will certainly be essential in unravelling the deep riddles of our universe, from the smallest biological structures to the vastest galactic tapestries, as our knowledge of complicated systems keeps growing.
References
- Barnsley, M.F. and Demko, S.G. eds., 2014. Chaotic dynamics and fractals. Academic Press.
- Bhat, A.H. and Mageed, I.A., 2023. Generalised Z-Entropy (Gze) and Fractal Dimensions (FDs). In Fractal Analysis-Applications and Updates. IntechOpen. [CrossRef]
- Caprini, L. , Marini Bettolo Marconi, U. and Puglisi, A., 2020. Spontaneous velocity alignment in motility-induced phase separation. Physical review letters, 124(7), p.078001. [CrossRef]
- Casey, C.M. , Kartaltepe, J.S., Drakos, N.E., Franco, M., Harish, S., Paquereau, L., Ilbert, O., Rose, C., Cox, I.G., Nightingale, J.W. and Robertson, B.E., 2023. COSMOS-Web: an overview of the JWST Cosmic Origins Survey. The Astrophysical Journal, 954(1), p.31. [CrossRef]
- Catrambone, V. , Barbieri, R., Wendt, H., Abry, P. and Valenza, G., 2021. Functional brain–heart interplay extends to the multifractal domain. Philosophical Transactions of the Royal Society A, 379(2212), p.20200260. [CrossRef]
- Di Guida, N.S. and Cassini, G.H., 2025. Fractal Dimension and Suture Complexity During Postnatal Ontogeny in Neotropical Deer in Relation to Sexual Dimorphism and Other Biological Features. Journal of Experimental Zoology Part B: Molecular and Developmental Evolution. [CrossRef]
- El-Nabulsi, R.A. and Anukool, W., 2022. Fractal dimension modeling of seismology and earthquakes dynamics. Acta Mechanica, 233(5), pp.2107-2122. [CrossRef]
- Eser, S. and Sarıbaş, E., 2024. Anatomical assessment of the trabecular structure of the alveolar bone in periodontal disease by fractal analysis method. Folia Morphologica, 83(1), pp.157-167. [CrossRef]
- Fleischmann, M. , Tildesley, D.J. and Ball, R.C. eds., 2014. Fractals in the natural sciences. Princeton University Press.
- Gaite, J. , 2019. The fractal geometry of the cosmic web and its formation. Advances in Astronomy, 2019(1), p.6587138. [CrossRef]
- Ghanbari, B. , Günerhan, H. and Srivastava, H.M., 2020. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos, Solitons & Fractals, 138, p.109910. [CrossRef]
- Giovannelli, F. , 2025. Gamma-Ray Bursts: The Energy Monsters of the Universe. Galaxies, 13(2), p.16. [CrossRef]
- Gómez-Nava, L. , Bon, R. and Peruani, F., 2022. Intermittent collective motion in sheep results from alternating the role of leader and follower. Nature Physics, 18(12), pp.1494-1501. [CrossRef]
- Grosu, G.F. , Hopp, A.V., Moca, V.V., Bârzan, H., Ciuparu, A., Ercsey-Ravasz, M., Winkel, M., Linde, H. and Mureșan, R.C., 2023. The fractal brain: scale-invariance in structure and dynamics. Cerebral Cortex, 33(8), pp.4574-4605. [CrossRef]
- Guidolin, D. , Tortorella, C., De Caro, R. and Agnati, L.F., 2024. A Self-Similarity Logic May Shape the Organization of the Nervous System. In The Fractal Geometry of the Brain (pp. 203-225). Cham: Springer International Publishing. [CrossRef]
- Innocenti, B. , Bori, E., Armaroli, F., Schlager, B., Jonas, R., Wilke, H.J. and Galbusera, F., 2022. The use of computational models in orthopedic biomechanical research. In Human orthopaedic biomechanics (pp. 681-712). Academic Press. [CrossRef]
- Johannes, F. , 2025. Allometric scaling of somatic mutation and epimutation rates in trees. Evolution, 79(1), pp.1-5. [CrossRef]
- Karperien, A.L. and Jelinek, H.F., 2024. Morphology and fractal-based classifications of neurons and microglia in two and three dimensions. The Fractal Geometry of the Brain, pp.149-172. [CrossRef]
- Kunasegaran, K. , Ismail, A.M.H., Ramasamy, S., Gnanou, J.V., Caszo, B.A. and Chen, P.L., 2023. Understanding mental fatigue and its detection: a comparative analysis of assessments and tools. PeerJ, 11, p.e15744. [CrossRef]
- Kv, R. , Prasad, K. and Peralam Yegneswaran, P., 2023. Segmentation and classification approaches of clinically relevant curvilinear structures: A review. Journal of Medical Systems, 47(1), p.40. [CrossRef]
- Lagain, A. , Kreslavsky, M., Baratoux, D., Liu, Y., Devillepoix, H., Bland, P., Benedix, G.K., Doucet, L.S. and Servis, K., 2022. Has the impact flux of small and large asteroids varied through time on Mars, the Earth and the Moon?. Earth and Planetary Science Letters, 579, p.117362. [CrossRef]
- Li, D. , Gong, H., Ru, W. and Luo, P., 2025. Study on the macro-mechanical behavior and micro-structure evolution law of broken rock mass under triaxial compression. Computational Particle Mechanics, 12(1), pp.509-525. [CrossRef]
- Mageed, I.A. and Mohamed, M., 2023. Chromatin can speak Fractals: A review.
- Mageed, I.A. , 2023a, November. Fractal Dimension (Df) of Ismail’s Fourth Entropy with Fractal Applications to Algorithms, Haptics, and Transportation. In 2023 international conference on computer and applications (ICCA) (pp. 1-6). IEEE. [CrossRef]
- Mageed, I.A. , 2024a. The Fractal Dimension Theory of Ismail's Third Entropy with Fractal Applications to CubeSat Technologies and Education. Complexity Analysis and Applications, 1(1), pp.66-78.
- Mageed, I.A. , 2024b. Fractal Dimension of the Generalized Z-Entropy of The Rényian Formalism of Stable Queue with Some Potential Applications of Fractal Dimension to Big Data Analytics. [CrossRef]
- Mageed, I.A. , 2024c. Fractal Dimension (Df) Theory of Ismail’s Entropy (IE) with Potential Df Applications to Structural Engineering. Journal of Intelligent Communication, 3(2), pp.111-123. [CrossRef]
- Mageed, I.A. , 2024d. A Theory of Everything: When Information Geometry Meets the Generalized Brownian Motion and the Einsteinian Relativity. J Sen Net Data Comm, 4(2), pp.01-22.
- Maina, J.N. , 2023. Structure of the avian respiratory system. In Current perspectives on the functional design of the avian respiratory system (pp. 191-267). Cham: Springer International Publishing. [CrossRef]
- Maryenko, N.I. , 2024. Applications of fractal analysis techniques in magnetic resonance imaging and computed tomography for stroke diagnosis and stroke-related brain damage: a narrative review. Advanced Technology in Neuroscience, 1(1), pp.105-122. [CrossRef]
- Milovanov, A.V. and Iomin, A., 2023. Dynamical chaos in nonlinear Schrödinger models with subquadratic power nonlinearity. Physical Review E, 107(3), p.034203. [CrossRef]
- Montgomery, R. , 2024. Fractal Geometry in Vertebrate Respiratory Systems: A Comparative Analysis of Branching Patterns Across Species. [CrossRef]
- Morales, G.B. , Di Santo, S. and Muñoz, M.A., 2023. Quasi universal scaling in mouse-brain neuronal activity stems from edge-of-instability critical dynamics. Proceedings of the National Academy of Sciences, 120(9), p.e2208998120. [CrossRef]
- Norris, R.P. , Marvil, J., Collier, J.D., Kapińska, A.D., O’Brien, A.N., Rudnick, L., Andernach, H., Asorey, J., Brown, M.J., Brueggen, M. and Crawford, E., 2021. The Evolutionary Map of the Universe pilot survey. Publications of the astronomical society of Australia, 38, p.e046. [CrossRef]
- Ortiz-Puerta, D. , 2023. Formulation and implementation of flexible surface models for the representation and morphological analysis of the respiratory airways in human lungs (Doctoral dissertation, Pontificia Universidad Catolica de Chile (Chile)). [CrossRef]
- Peebles, D.J. ., 2020. The large-scale structure of the universe (Vol. 96). Princeton university press.
- Poole, D.C. and Musch, T.I., 2023. Capillary-mitochondrial oxygen transport in muscle: paradigm shifts. Function, 4(3), p.zqad013. [CrossRef]
- Pössel, M. , 2020. Interpretations of cosmic expansion: anchoring conceptions and misconceptions. Physics Education, 55(6), p.065006. [CrossRef]
- Puetz, S.J. , 2022. The infinitely fractal universe paradigm and consupponibility. Chaos, Solitons & Fractals, 158, p.112065. [CrossRef]
- Qin, Z. , Wang, H., He, A., Sun, Y., Li, J., Zhang, Y. and Zhang, Q., 2024. Backscattering linear depolarization ratio of smoke aerosols from biomass burning. Journal of Geophysical Research: Atmospheres, 129(19), p.e2024JD041276. [CrossRef]
- Roy, A. and Vemaganti, K., 2024. Fractal surface-based three-dimensional modeling to study the role of morphology and physiology in human skin friction. Surface Topography: Metrology and Properties, 12(1), p.015006. [CrossRef]
- Shoemaker, L.G. , Walter, J.A., Gherardi, L.A., DeSiervo, M.H. and Wisnoski, N.I., 2021. Writing mathematical ecology: A guide for authors and readers. Ecosphere, 12(8), p.e03701. [CrossRef]
- Srivastava, R.P. , Vedanti, N. and Dimri, V.P., 2021. Fractals and chaos. In Encyclopedia of Solid Earth Geophysics (pp. 405-412). Cham: Springer International Publishing. [CrossRef]
- Teles, S. , Lopes, A.R. and Ribeiro, M.B., 2022. Galaxy distributions as fractal systems. The European Physical Journal C, 82(10), p.896. [CrossRef]
- Tiscareno, M.S. and Murray, C.D. eds., 2018. Planetary ring systems: properties, structure, and evolution. Cambridge University Press. [CrossRef]
- Vogelsberger, M. , Marinacci, F., Torrey, P. and Puchwein, E., 2020. Cosmological simulations of galaxy formation. Nature Reviews Physics, 2(1), pp.42-66. [CrossRef]
- Weigelt, A. , Mommer, L., Andraczek, K., Iversen, C.M., Bergmann, J., Bruelheide, H., Fan, Y., Freschet, G.T., Guerrero-Ramírez, N.R., Kattge, J. and Kuyper, T.W., 2021. An integrated framework of plant form and function: the belowground perspective. New Phytologist, 232(1), pp.42-59. [CrossRef]
- West, B.J. , 2022. The fractal tapestry of life: II entailment of fractional oncology by Physiology networks. Frontiers in Network Physiology, 2, p.845495. [CrossRef]
- Xu, X. and Barrett, P.M., 2025. The origin and early evolution of feathers: implications, uncertainties and future prospects. Biology Letters, 21(2), p.20240517. [CrossRef]
- Yang, B. and Liu, Y., 2022. Application of fractals to evaluate fractures of rock due to mining. Fractal and Fractional, 6(2), p.96. [CrossRef]
- Yang, F.Y. , Fuller, C.A., McGuire, M.K., Glaser, R., Smith, N.J., Manz, N. and Lindner, J.F., 2021. Disruption and recovery of reaction–diffusion wavefronts interacting with concave, fractal, and soft obstacles. Physica A: Statistical Mechanics and its Applications, 565, p.125536. [CrossRef]
- Žnidarič, M. , Škrinjar, D. and Kapel, A., 2023. Electrodermal activity and heart rate variability for detection of peripheral abnormalities in type 2 diabetes: A review. Biomolecules and Biomedicine, 23(5), p.740. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).