On the Enthalpy-Entropy Compensation Characterizing Processes in Aqueous Solution

1. Introduction

The expression enthalpy-entropy compensation means that the enthalpy change and the entropy change associated with a given process can be individually large, but, on the strength of the fundamental thermodynamic relationship ΔG = ΔH - T⋅ΔS, the variation of these two state functions produces a small change in the Gibbs free energy [1]. A simple explanation of the phenomenon can be that a strengthening of energetic interactions among molecules leads to a negative enthalpy change, but also to a decrease in the degrees of freedom and, therefore, to a negative entropy change. Despite the validity of the previous sentence, it does not provide a useful rationalization of the phenomenon of enthalpy-entropy compensation. In the past, there was debate about the real occurrence of the phenomenon in light of the procedures adopted to arrive at the thermodynamic values starting from the experimental data [2,3,4,5]; however, this debate now seems to have reached a conclusion [6].

Enthalpy-entropy compensation is widely associated with processes occurring in water or aqueous solutions, as pointed out by Lumry and Rajender in a pioneering article published in 1970 [7]. Since then, the scenario has not changed, confirming that water plays a pivotal role in the phenomenon of enthalpy-entropy compensation [8,9,10,11,12]. For instance, the temperature-induced unfolding of small globular proteins in aqueous solutions is usually a reversible process characterized by both large positive enthalpy changes and large positive entropy changes around the denaturation temperature, and, for the same reasons, the Gibbs free energy change associated with denaturation, evaluated around room temperature, is modest (look at Figure 2 and Figure 4 in the Cooper’s review [9]) [13,14,15,16,17]. Indeed, the native state of small globular proteins is considered to be marginally more stable than the denatured state [18,19]. Similarly, careful investigations on the thermodynamic consequences of both point mutations of residues lining the binding cleft of several enzymes and of various structural modifications of several substrates and inhibitors have recorded large enthalpy and entropy changes, but always of the same sign, so that the effect on the Gibbs free energy change associated with binding has turned out to be small (i.e., the binding constant was little affected) [20,21,22,23,24,25,26,27,28,29]. It should not be hard to imagine the frustration experienced by scientists trying to increase the affinity of an inhibitor for a given binding cleft because of the occurrence of enthalpy-entropy compensation.

Over the years, several authors have formulated several theoretical rationalizations of enthalpy-entropy compensation [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44], each of which has strengths and weaknesses. In the present review, we would like to show how a general theory of hydration, originally devised by Lee [45,46,47,48] and then widely applied and strengthened by one of us [49,50,51,52,53], can rationalize, at the molecular level, the widespread diffusion of the phenomenon in processes occurring in water.

2. Theoretical Considerations

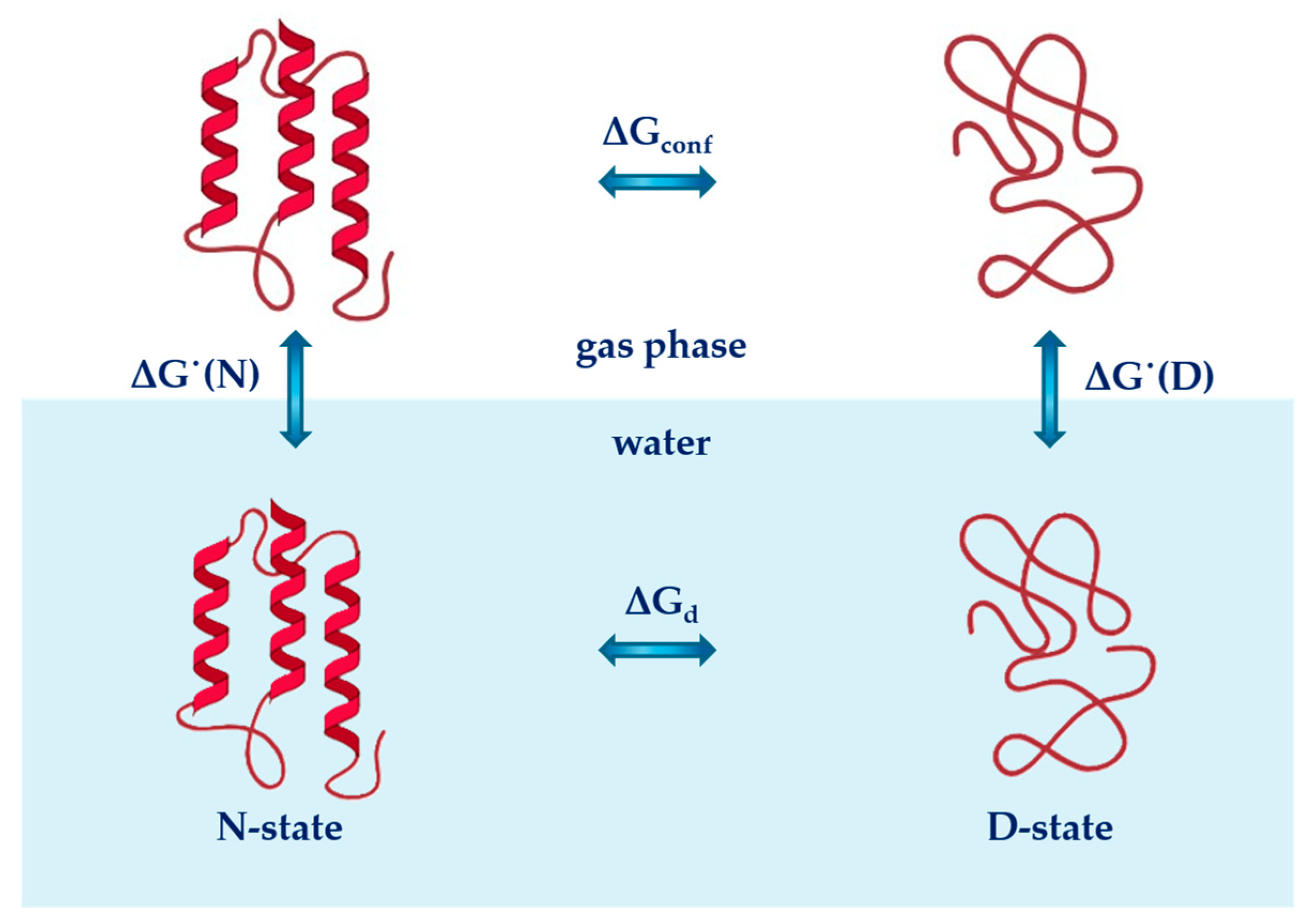
The conformational stability of globular proteins in water (in the assumption that only two macroscopic states, the native state N-state, and the denatured state D-state, are populated by polypeptide chains) can be analysed by means of the thermodynamic cycle reported in Figure 1 [51,52]. The cycle leads to the following relationship:

$${\mathsf{\Delta }\mathbf{G}}_{\mathbf{d}}={\mathsf{\Delta }\mathbf{G}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{f}}+\mathsf{\Delta }\mathbf{G}\dot{}\left(\mathbf{D}\right)-\mathsf{\Delta }\mathbf{G}\dot{}\left(\mathbf{N}\right),$$

(1)

where ${\mathsf{\Delta }\mathbf{G}}_{\mathbf{d}}$ is the Gibbs free energy change associated with protein unfolding in water or aqueous solution; ${\mathsf{\Delta }\mathbf{G}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{f}}$ is the Gibbs free energy change associated with protein unfolding in the ideal gas phase; and ΔG˙(D) and ΔG˙(N) are the Gibbs free energy changes associated with the hydration (i.e., ideal gas-to-water transfer) of the D-state and N-state, respectively.

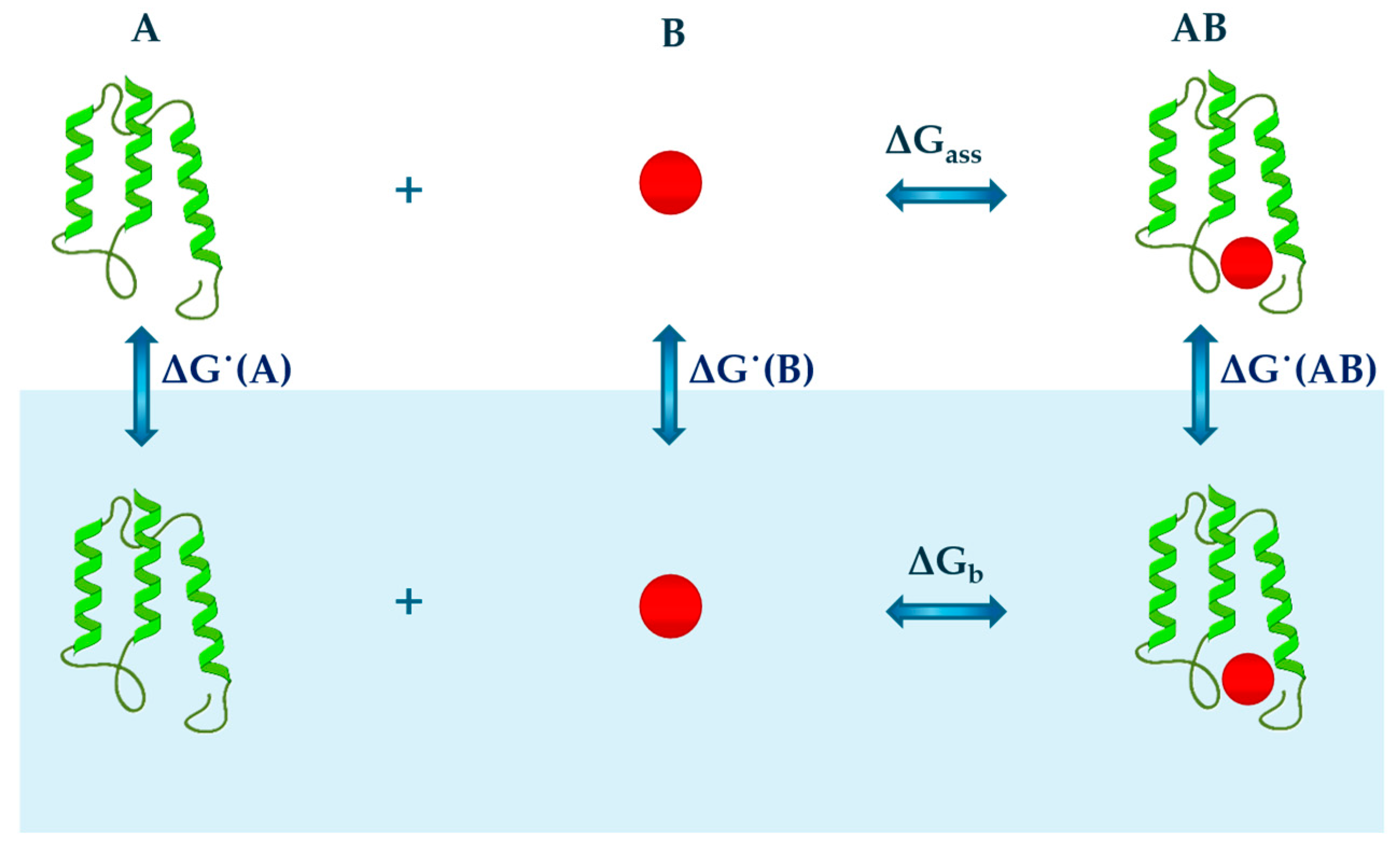
On the other hand, a bimolecular association in water between the A and B molecules can be analysed according to the thermodynamic cycle reported in Figure 2 and described by the following relationship:

$${\mathsf{\Delta }\mathbf{G}}_{\mathbf{b}}={\mathsf{\Delta }\mathbf{G}}_{\mathbf{a}\mathbf{s}\mathbf{s}}+\mathsf{\Delta }\mathbf{G}\dot{}\left(\mathbf{A}\mathbf{B}\right)-\mathsf{\Delta }\mathbf{G}\dot{}\left(\mathbf{A}\right)-\mathsf{\Delta }\mathbf{G}\dot{}\left(\mathbf{B}\right),$$

(2)

where ${\mathsf{\Delta }\mathbf{G}}_{\mathbf{b}}$is the Gibbs free energy change associated with the binding process in water or aqueous solution; ${\mathsf{\Delta }\mathbf{G}}_{\mathbf{a}\mathbf{s}\mathbf{s}}$ is the Gibbs free energy change associated with the binding process in the ideal gas phase; and ΔG˙(AB), ΔG˙(A) and ΔG˙(B) are the Gibbs free energy changes associated with the hydration of the formed complex AB, the molecule A and the molecule B, respectively. A similar thermodynamic cycle can be used to analyse other processes that occur in water, such as the formation of micelles. These exempla highlight how hydration is an unavoidable step in the analysis of the processes occurring in water and, as such, requires a precise definition and particular attention. The statistical mechanical analysis done by Ben-Naim indicates that hydration must be defined as the transfer of a solute molecule, at constant temperature and pressure, from a fixed position in the ideal gas phase to a fixed position in liquid water [54].

By using the Widom’s potential distribution theorem [55,56,57], hydration can be treated as the action of an external perturbation on liquid water, Ψ(X), where X represents a multidimensional vector accounting for one of the possible configurations of water molecules in the system. The Ben-Naim standard hydration Gibbs free energy change is given by [45]:

$$\mathsf{\Delta }\mathrm{G}\dot{}={-\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<e^{-{\displaystyle \frac{\psi \left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_p,$$

(3)

where the subscript p means that the ensemble average is done over the pure liquid configurations. The related probability density function, assuming an NPT ensemble, is given by the following relationship:

$${\rho }_p\left(X\right) = {\displaystyle \frac{e^{-\frac{H\left(X\right)}{RT}}}{\int e^{-\frac{H\left(X\right)}{RT}}dX}},$$

(4)

where H(X) = U(X) + P⋅V(X) is the enthalpy function of one of the possible configurations, U(X) and V(X) are the corresponding intermolecular interaction energy and volume, respectively, and the denominator is the isobaric-isothermal configurational partition function of the pure liquid. The ensemble average of Eq. (3) is taken over the water configurations before the action of the perturbation (i.e., the Boltzmann weights in the average do not include Ψ(X), which acts as a ghost).

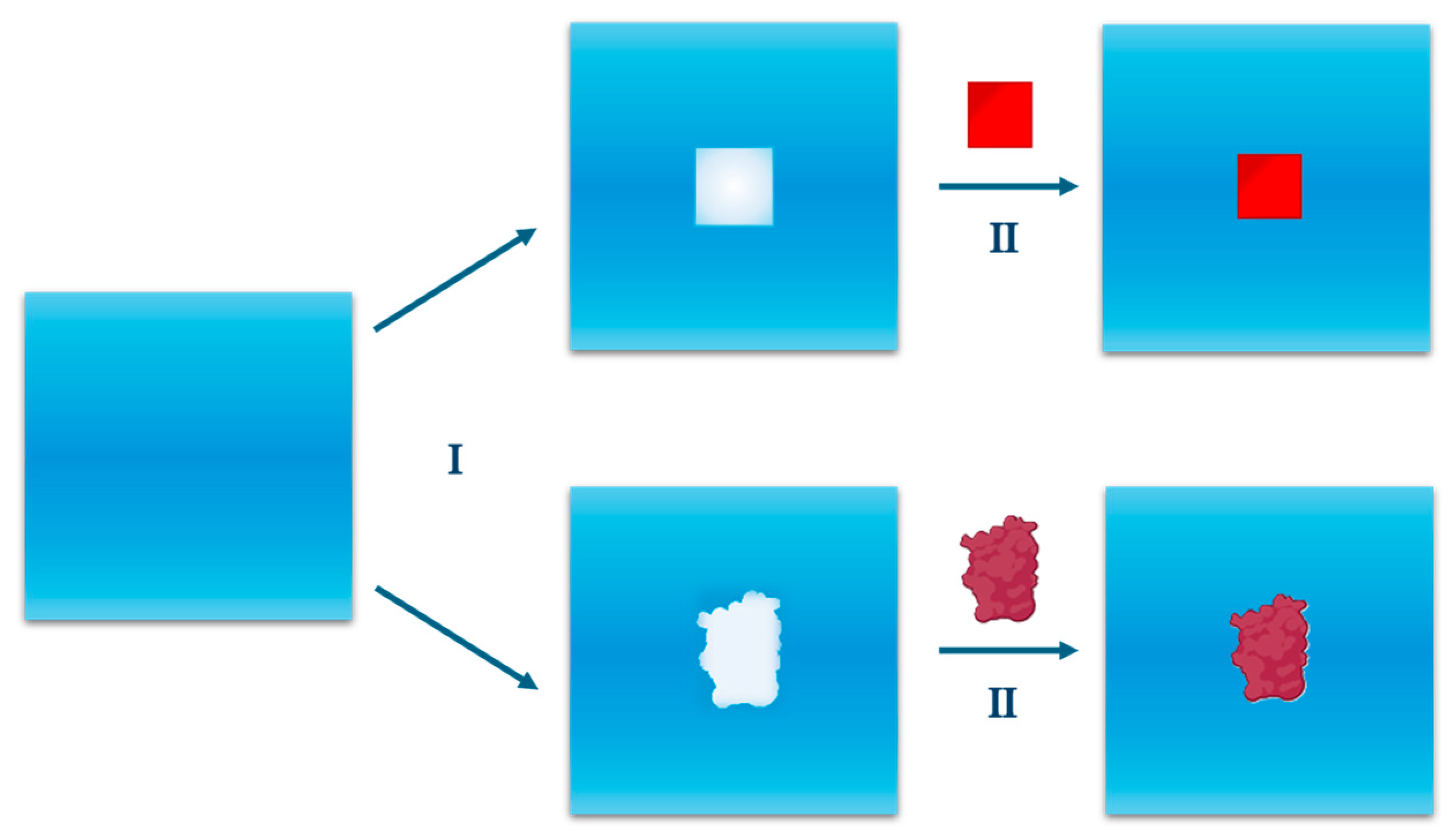
To shed light on the thermodynamics of hydration at the molecular level, it is advisable to break down the process into several steps that must have a clear physical meaning. Liquids are a condensed state of the matter, and the insertion of a solute molecule into water requires the exclusion of water molecules from the region of space that will be occupied by the solute. So, the first necessary step of hydration is the creation, at a fixed position in water, of a cavity suitable to be occupied by the solute molecule. Cavity creation is a theoretical process that cannot be investigated by means of experimental measurements; however, it is necessary to take into account the consequences of a simple but fundamental fact: each molecule has its own body. Following the cavity formation, a solute molecule interacts with water molecules by means of van der Waals attractions and/or H-bonds, depending on its chemical nature; it follows that the second step of hydration is the turning on the attractive potential. On the basis of these considerations, Lee suggested that the perturbation potential should be factorized in the following way [45,46]:

$$e^{-{\displaystyle \frac{\psi \left(X\right)}{\mathrm{R}\mathrm{T}}}}=\mathsf{\zeta }(X)·e^{-{\displaystyle \frac{{\psi }_a\left(X\right)}{\mathrm{R}\mathrm{T}}}},$$

(5)

where $\mathsf{\zeta }\left(X\right)$ is a counting function, whose value is 1 when in a given water configuration there is a cavity suitable to be occupied by the solute molecule or is 0 when such a cavity does not exist in that configuration; and ${\psi }_a\left(X\right)$ represents the attractive potential between the solute molecule and the surrounding water molecules. By using Eq. (5), with a few straightforward passages, Eq. (3) becomes:

$$\mathsf{\Delta }\mathrm{G}\dot{}={-\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<\mathsf{\zeta }\left(X\right)>}_p {-\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<e^{-{\displaystyle \frac{{\psi }_a\left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_c,$$

(6)

where the subscript c indicates that the ensemble average is done over the liquid configurations containing a cavity suitable to be occupied by the solute molecule. The related probability density function is given by:

$${\rho }_c\left(X\right) ={\displaystyle \frac{ \mathsf{\zeta }\left(X\right)·e^{-\frac{H\left(X\right)}{RT}}}{\int {\mathsf{\zeta }\left(X\right)·e}^{-\frac{H\left(X\right)}{RT}}dX}}.$$

(7)

According to Eq. (6), $\mathsf{\Delta }\mathrm{G}\dot{}$is the sum of two terms: (a) the reversible work to create the cavity, ${\mathsf{\Delta }\mathrm{G}}_c$, and (b) the reversible work to turn on the attractive solute-water interactions, ${\mathsf{\Delta }\mathrm{G}}_a$. It does not imply the addition of independent contributions, since intermolecular attractions are turned on after the cavity has already been created.

The so-called Widom’s inverse relationship [56] allows a modification of Eq. (3), which becomes [45,46]:

$$\mathsf{\Delta }\mathrm{G}\dot{}={-\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<e^{-{\displaystyle \frac{\psi \left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_p {=\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<e^{{\displaystyle \frac{\psi \left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_s,$$

(8)

where the subscript s signifies that the ensemble average is computed over the solution configurations that possess the cavity occupied by the solute molecule interacting with the surrounding solvent molecules. In this ensemble, the solute molecule does not act as a ghost, but interacts with water molecules; and the corresponding probability density function becomes:

$${\rho }_s\left(X\right) ={\displaystyle \frac{ \mathsf{\zeta }(X)·e^{-\frac{{\psi }_a\left(X\right)+H\left(X\right)}{RT}}}{\int {\mathsf{\zeta }\left(X\right)·e}^{-\frac{{\psi }_a\left(X\right)+H\left(X\right)}{RT}}dX}}.$$

(9)

The general caveat is that the Widom’s inverse relationship holds only if the perturbation Ψ(X), required to create a cavity at a fixed position in a liquid, is not infinite [46,56], which is the case when the position is occupied by liquid molecules (i.e., for most liquid configurations). This mathematical condition and the physical considerations above imply that cavity creation is a particularly important process, which must constitute the starting point of any theoretical treatment of the hydration phenomenon. The two steps described, shown in Figure 3, will be analysed in detail below.

2.1. Cavity Creation

The reversible work of cavity creation is the reversible work required to pick out the configurations containing the cavity in the overall set of the pure liquid configurations (please note: the spatial homogeneity of the liquid renders un-necessary to define an exact position of the cavity, except for the surface regions) [58]:

$${\mathsf{\Delta }G}_c={-\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<\mathsf{\zeta }\left(X\right)>}_p .$$

(10)

Molecular-sized cavities occur in a liquid as a consequence of molecular-scale density fluctuations at equilibrium (such fluctuations can be studied by Monte Carlo or Molecular Dynamics computer simulations [59,60,61,62,63,64]). Density fluctuations cannot be studied on a lattice and, to use the cavity concept in lattice models, the reversible work of cavity creation must be associated with the energetic breaking of intermolecular bonds, the number of which depends on the lattice geometry [65]. Unfortunately, this energetic description of the reversible work of cavity creation is simply not correct.

Direct application of equilibrium statistical mechanics leads to the following expressions for the enthalpy change, ${\mathsf{\Delta }H}_c$, and the entropy change, ${\mathsf{\Delta }S}_c$, associated with cavity creation:

$${\mathsf{\Delta }H}_c=\int H\left(X\right)·[{\rho }_c\left(X\right)-{\rho }_p\left(X\right)]dX = {<H\left(X\right)>}_c-{<H\left(X\right)>}_p$$

(11)

and

$${\mathsf{\Delta }S}_c=-R·\int [{\rho }_c\left(X\right)·ln{\rho }_c\left(X\right)-{\rho }_p\left(X\right)·ln{\rho }_p\left(X\right)]dX=$$

(12)

$$=R·ln{\mathsf{\zeta }\left(X\right)}_p+{\displaystyle \frac{{<H\left(X\right)>}_c-{<H\left(X\right)>}_p}{T}}={\mathsf{\Delta }S}_x+{\displaystyle \frac{{\mathsf{\Delta }H}_c}{T}}.$$

By inserting the relationships of Eq. (4) and Eq. (7) in the integral of the first line of Eq. (12), it is not difficult to get to the expression in the second line. The difference in the average ensemble enthalpy between the liquid configurations possessing the desired cavity and the total liquid configurations gives rise to ${\mathsf{\Delta }H}_c$. The change in the entropy associated with the cavity formation ${\mathsf{\Delta }S}_c$ consists of two contributions: (a) the solvent-excluded volume contribution ${\mathsf{\Delta }S}_x$ due to a loss in the number of configurations, which loss, since the liquid configurations containing the desired cavity represent a roughly infinitesimal fraction of the total liquid configurations, causes a large negative contribution to the entropy in any liquid, but especially in water by virtue of its large number density and the small size of its molecules [45,48,53], two characteristics that overwhelm the small volume packing density of water; (b) a difference in the two ensembles of liquid configurations as those containing the cavity would have a different distribution of energy levels, whose contribution is distinct from that of the solvent-excluded volume and is totally compensated by the enthalpy change since the liquid configurations possessing the desired cavity are a subset of the total configurations of the pure liquid [58].

Therefore, Equations (11) and (12) show that: (a) ${\mathsf{\Delta }H}_c$ is totally compensated by the entropy contribution of the non-solvent-excluded volume upon the cavity creation; (b) ${\mathsf{\Delta }G}_c$ has an entropic origin, since it arises from the effect of the solvent-excluded volume associated with the reduction in the size of the configuration space accessible to the solvent molecules:

$${\mathsf{\Delta }G}_c = -T·{\mathsf{\Delta }\mathrm{S}}_x.$$

(13)

At this point a detailed explanation of the solvent-excluded volume effect is necessary. Holding the temperature and pressure fixed, liquid configurations having the suitable cavity will have a volume greater than the mean volume by an amount equal to the van der Waals volume of the cavity. This increase in liquid volume does not cancel the solvent-excluded volume effect for two closely related reasons: (a) the cavity must remain empty at the given fixed position to be occupied by the solute molecule; (b) this requirement implies that the centre of all liquid molecules cannot fit into the shell existing between the van der Waals surface of the cavity and the water-accessible surface of the cavity itself (the condition is shown in Figure 4 for a spherical cavity). The geometric constraint holds for all liquid molecules since they are in continuous translational motion in the system volume (i.e., it does not exclusively affect the liquid molecules lining the surface of the cavity) and is strictly related to the fixed position of the cavity. This result has general validity given that each molecule has its own body, even though hard sphere fluid theories, such as classic scaled particle theory [48,53,66], are exploited to perform analytic calculations.

2.2. Turning on the Attractive Solute-Water Interactions

The reversible work to turn on the attractive solute-water van der Waals potential is given by [45]:

$${\mathsf{\Delta }G}_a={-\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}<e^{-{\displaystyle \frac{{\psi }_a\left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_c.$$

(14)

The application of the Gibbs-Helmholtz equation leads to:

$${{\mathsf{\Delta }H}_a= {<{\psi }_a\left(X\right)>}_c+[<H(X)+{\psi }_a(X)>}_s-{<H\left(X\right)+{\psi }_a\left(X\right)>}_c={<{\psi }_a\left(X\right)>}_c+{\mathsf{\Delta }H}_{ar}.$$

(15)

The enthalpy change consists of two parts: the first is the average attractive solute-water van der Waals potential, excluding the effect of any solvent reorganization; the second is the enthalpy contribution arising from water reorganization upon the turning on the attractive solute-water van der Waals potential [46,48].

The entropy change is given by the following:

$${\mathsf{\Delta }S}_a={\mathrm{R}\mathrm{l}\mathrm{n}<e^{-{\displaystyle \frac{{\psi }_a\left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_c+{\displaystyle \frac{{<{\psi }_a\left(X\right)>}_c}{\mathrm{T}}}+{\displaystyle \frac{{\mathsf{\Delta }H}_{ar}}{T}}.$$

(16)

By setting ${\kappa =\psi }_a\left(X\right)-{<{\psi }_a\left(X\right)>}_c$, expanding in power series the exponential function and recognizing that ${<\kappa >}_c \equiv 0$, one obtains:

$${\mathrm{R}\mathrm{l}\mathrm{n}<e^{-{\displaystyle \frac{{\psi }_a\left(X\right)}{\mathrm{R}\mathrm{T}}}}>}_c\approx -{\displaystyle \frac{{<{\psi }_a\left(X\right)>}_c}{\mathrm{T}}}+{\displaystyle \frac{{<{\kappa }^2>}_c}{{2RT}^2}};$$

(17)

and the entropy change becomes:

$${\mathsf{\Delta }S}_a\approx {\displaystyle \frac{{\mathsf{\Delta }H}_{ar}}{T}}+{\displaystyle \frac{{<{\kappa }^2>}_c}{{2RT}^2}}.$$

(18)

The Gibbs free energy change is as follows:

$${\mathsf{\Delta }G}_a\approx {<{\psi }_a\left(X\right)>}_c-{\displaystyle \frac{{<{\kappa }^2>}_c}{2RT}}.$$

(19)

The attractive solute-water van der Waals potential ${\psi }_a\left(X\right)$ is weak compared to the energetic strength of the tetrahedral H-bonding network of water, as well as the fluctuations in the value of ${<{\psi }_a\left(X\right)>}_c$ prove to be small. This implies that the second term on the right-hand side of Eq. (19) can be neglected and, hence, that the reorganization of water molecules associated with the turning on the attractive solute-water van der Waals potential is a compensatory process [46,48]. Indeed, in line with the expectations for a spontaneous process, this reorganization is characterized by a negative change in Gibbs free energy, albeit small [50]. Therefore, ${<{\psi }_a\left(X\right)>}_c$ is almost equal to the attractive solute-water van der Waals energy, and the Gibbs free energy change results to be:

$${\mathsf{\Delta }G}_a\approx {<{\psi }_a\left(X\right)>}_c \approx { <{\psi }_a\left(X\right)>}_s = E_a.$$

(20)

The overall change in Gibbs free energy due to hydration is:

$${\mathsf{\Delta }G}^{·} \approx {\mathsf{\Delta }G}_c+E_a.$$

(21)

Equation (21), although not exact, allows for direct calculations to test its validity. Its first application, by Pierotti in 1965 [67], to the hydration of nonpolar species provided a remarkable agreement with experimental values of the Gibbs free energy change. This result was not expected at that time, when the dominant idea was that the poor solubility in water of nonpolar species was due to the formation of icebergs (see the famous pictorial iceberg model devised by Frank and Evans [68,69]). In reality, the success was a simple consequence of the enthalpy-entropy compensation that characterizes the structural reorganization of water-water H-bonds following the insertion of the solute. The analogue fortune of the integral equation theory devised by Pratt and Chandler in 1977 [70] can be rationalized along the same lines.

The hydration enthalpy change is:

$${\mathsf{\Delta }H}^{·}\approx E_a+{\mathsf{\Delta }H}_c+{\mathsf{\Delta }H}_{ar}=E_a+{\mathsf{\Delta }H}^h,$$

(22)

where ${\mathsf{\Delta }H}^h$represents the enthalpy contribution due to the overall structural reorganization of the water-water H-bonds upon solute insertion, including both the cavity creation and the turning on the attractive solute-water van der Waals potential. The hydration entropy change is given by:

$${\mathsf{\Delta }S}^{·}\approx {\mathsf{\Delta }S}_x+{\displaystyle \frac{{\mathsf{\Delta }H}_c+{\mathsf{\Delta }H}_{ar}}{T}}={\mathsf{\Delta }S}_x+{\mathsf{\Delta }S}^h,$$

(23)

where ${\mathsf{\Delta }S}^h$ is the entropy contribution due to the overall structural reorganization of the water-water H-bonds upon solute insertion. It represents the water response to the external perturbation and is characterized by an almost complete enthalpy-entropy compensation, so it is possible approximate that:

$${\mathsf{\Delta }H}^h\approx T·{\mathsf{\Delta }S}^h.$$

(24)

This analysis highlights how the structural reorganization of water-water H-bonds is a compensatory process, provided that the attractive solute-water potential is weak compared to the energetic strength of the tetrahedral H-bonding network of water [42,43,44,45,46]. This is a clear physical condition fulfilled by the hydration of noble gases, alkanes, benzene and toluene, but also by the hydration of n-alcohols (note that the perturbation produced by a single OH group is not so strong, according to the available structural and thermodynamic data [71,72]). The condition is also satisfied in the binding of substrates and inhibitors to proteins, since the burial of small surfaces by contact with water cannot produce a strong perturbation of water-water H-bonds. The situation does not change in the case of protein-protein association when large surfaces are buried, because of the presence in these of both polar and nonpolar groups, both positive and negative charges, whose overall effect on the structure of the water results to be not so strong due to balancing effects.

One last point deserves attention. The hydration heat capacity change ${\mathsf{\Delta }C}_p^{·}$, based on Eq. (22), results to be:

$${\mathsf{\Delta }C}_p^{·}={\displaystyle \frac{\partial E_a}{\partial T}}+{\displaystyle \frac{\partial {\mathsf{\Delta }H}^h}{\partial T}}.$$

(25)

Since the temperature dependence of $E_a$ is small [73], the large positive ${\mathsf{\Delta }C}_p^{·}$ associated with several processes occurring in water (e.g., hydration of non-charged species, unfolding of small globular proteins) is mainly caused by the structural reorganization of water-water H-bonds [45,46,47,48,74,75,76,77]. This clarifies why the temperature dependence of the enthalpy and entropy changes associated with such processes is almost entirely compensatory [9,46].

3. Structural Analysis

The thermodynamic functions associated with the reorganization of water-water H-bonds can be calculated by means of a model based on the structural and energetic features of water-water H-bonds. Long ago, Pauling [78] provided an estimate of the energy required to break a H-bond in water, E(H-bond) = 20.9 kJ mol^-1. This estimate can be used to arrive at the corresponding vibration frequency. In the harmonic approximation, the force constant k can be calculated from the relationship: k = 2⋅β²⋅E(H-bond), where β is the constant occurring in the Morse potential [79]. Using the customary value β = 2⋅10¹⁰ m^-1, it turns out that k = 27.8 N m^-1, ω = 162 cm^-1 and ν = 4.86⋅10¹² Hz [35]. The THz frequency, inserted into the statistical mechanical expression of the entropy associated with the energy levels of the harmonic oscillator (HO) [79], leads to S(HO) = 10.6 J K^-1mol^-1 at 300 K. Dunitz [35] assumed that the three degrees of freedom corresponding to the intramolecular vibrational modes of a water molecule are not excited at room temperature (because their frequencies are too high), whereas the other six degrees of freedom can be described as vibrational modes of the 3D H-bonded lattice constituted by all the water molecule, which modes are all characterized by the same entropy calculated above. Therefore, the overall entropy contribution, at 300 K, would be 6⋅T⋅S(HO) = 19.1 kJ mol^-1 and would almost compensate for the energetic term E(H-bond) = 20.9 kJ mol^-1. Dunitz used this calculation to provide a rationalization of the enthalpy-entropy compensation detected for bimolecular association processes occurring in water [35], which has been widely accepted [10,29].

In contrast, we think that the meaning of this simple exercise could be different: a structural reorganization of water-water H-bonds (associated with any processes that occurs in water) would cause a small modification in both the energy levels and their relative population, leading to a large enthalpy-entropy compensation. Actually, it has been shown long time ago, by Lee and Graziano for the hydration of alkanes [47] and by Graziano for the hydration of noble gases [80] and n-alcohols [81], that a properly modified version of the two-state model developed by Muller to describe the structural reorganization of water-water H-bonds [82], by distinguishing the hydration shell water from the bulk water, is able to provide compensatory changes in enthalpy and entropy. The reliability of this model has been confirmed by its ability to reproduce a temperature dependence of the hydration heat capacity change in line with experimental data [83,84].

The rightness of our interpretation is supported by the Ford’s analysis [85]. Ford showed that enthalpy-entropy compensation is not a general feature of bimolecular associations in the gas phase, suggesting that the real cause is not the weakness of intermolecular interactions, but the characteristics of the structural reorganization of water-water H-bonds.

However, it is important to emphasize that the exercise devised by Dunitz [35], although simple, is more accurate than one might imagine at first glance. Raman spectra of liquid water in the THz frequency region show the presence of a band centred at 60 cm^-1 and another wide band centred at 175 cm^-1 [86,87]. Walrafen assigned the first band to the transverse acoustic modes and the second band to the longitudinal acoustic modes of the 3D H-bonded (and disordered) lattice of liquid water, which “behaves like a moderately rigid, isotropic, elastic solid at THz frequencies” [86]. The frequency range covered by these two bands corresponds to the various estimates of the H-bond energy strength existing in the literature [47,82,83,88,89] and indicates that the structural reorganization of water-water H-bonds associated with the hydration step of processes occurring in water should be characterized by an almost complete enthalpy-entropy compensation.

4. Conclusions

Enthalpy-entropy compensation is a phenomenon that characterizes most processes occurring in water and aqueous solutions. In order to provide a rationalization, in this work we have shown that: (a) hydration must always be a step of thermodynamic cycles that can be used to analyse the process of interest; (b) a general theory of hydration, already widely accepted, indicates that the structural rearrangement of water-water H-bonds (i.e., the response of water to the perturbation caused by solute insertion) is compensatory, as long as the energetic strength of the solute-water attraction is weak compared to the energetic strength of water-water H-bonds; (c) a modified version of the Muller’s model is able to describe the structural reorganization of water-water H-bonds, reproducing compensatory enthalpy and entropy changes; (d) water is special with respect to enthalpy-entropy compensation, because the cooperativity of its 3D H-bonded network is such that even solute-water attractions, consisting of H-bonds, result to be weak.