Analysis of Semi-Global Factors Influencing the Prediction of Accident Severity

1. Introduction

With the growing diversity of road users and transport systems in Germany, it is becoming increasingly important to better understand the causes and influencing factors of accidents (Lord & Mannering, 2010). Although traffic is becoming increasingly complex, the number of fatal road accidents in Germany has been falling for several years. According to the German Federal Statistical Office (Statistisches Bundesamt, 2025), this is due to the introduction of new regulations and improved vehicle technology. Nevertheless, the factors influencing accidents need to be further analyzed in order to improve road safety. This applies not only to fatal accidents, but also to minor accidents. Identifying the influencing factors can provide very useful information for infrastructure planners.

Since each accident is highly dependent on individual external factors, it is necessary to work out these influences for each accident individually. As these influences are often highly interdependent and influence each other, new methods must be found to isolate the interdependencies. Only then is a large-scale and empirical analysis possible.

The complexity of influences in an accident can be represented, for example, by weather conditions, the state and condition of the road, the traffic situation and the people involved. Due to the complexity of accident data, patterns and correlations are not immediately apparent. Even small changes, such as the time of day or the types of people and vehicles involved, can determine whether an accident at the same location results in minor or serious injuries. For some years now, machine learning (ML) approaches have been used to classify the severity of accidents (Abdulhafedh, A. (2017), Satu et al. (2018), Parsa et al. (2020) (Shaik et al., 2021), (Pourroostaei Ardakani et al., 2023)). The aim is to automatically learn and map the correlations between the details of a real accident and the severity of the accident. The advantage of this approach is that very few assumptions need to be made in advance in order to classify a wide variety of data. This ensures a high degree of flexibility, especially with more complex ML models, with respect to a wide variety of accidents and their outcomes. This approach is widely used in accident research to extract influences from large amounts of data.

However, this approach has some limitations: So-called decision rules can be derived from simpler ML models such as decision trees or random forests, which are able to identify correlations between individual influences. The problem with these decision rules is, that they are not capable of identifying local factors of individual accidents. An alternative is the widespread use of feature importance for more complex ML models. These are also unsuitable for analyzing individual accidents because they cannot identify local effects or whether the effect is negative or positive.

Although complex ML models, such as neural networks, have been shown to be better at predicting the severity of accidents based on given information, it is much more difficult to derive and interpret the influencing factors. Explainable AI (XAI) methods are increasingly being used to reveal the decision-making process of these ’black box’ models.

In addition to the explicability of the decision process of an ML model, the geospatial reference of the data must also be taken into account. There is a large research gap in this area, especially when analyzing accident data. Currently, there are not many studies applying what is known as geospatial explainable artificial intelligence (Roussel 2023). In geospatial XAI, geospatial information should be integrated into the analysis and communication of ML results.

The aim of this work is to demonstrate that the use of geospatial XAI can also be used to determine factors influencing accident severity. An additional challenge is the interpretation and visualization of these complex results. So, another goal of this study is to develop a concept that uses geospatial areas at different scales to enable the study of global accident factors, influencing factors in a geospatial region and local influencing factors. A similar approach has been developed by Roussel (2025) and is called ’Geo-Glocal XAI’. From this we define the following research questions:

• How can geospatial XAI and glocal explanations be used to identify the factors influencing the decision to classify accident severity?
• How can these global, glocal and local influencing factors be visualized in a simplified way with maps and plots to improve interpretability?

The study is structured as follows: In Chapter 2, we present a comprehensive overview of the current approaches in research to determine accident severity using ML models. We present the missing explanatory approaches in research and give an introduction to geospatial XAI. In Chapter 3, we present the newly developed method to derive and map complex influencing factors together with the ML quality. In Chapter 4 we apply the developed concept to our selected use case of accident analysis in Germany and present and discuss the results in Chapter 5. In Chapter 6, we conclude the results of the study and point out future directions.

2. State of the Art

In this chapter, we present current research using ML approaches to predict accident severity. Specifically, we will show studies in this research area that use some XAI approaches. We also provide general information on the research field of geospatial XAI.

Accident severity classification using machine learning has become increasingly important in recent years. Numerous studies have looked at data-based prediction of accident severity using different data sources, models and analysis methods. In the past, the focus has been on identifying the best ML model for such classification tasks.

The study of Pradhan and Sameen (2020) highlights the advantages of using complex ML models such as neural networks (NNs) over linear models. They confirm that the relationships between features and outputs in accident severity prediction are non-linear, and therefore best represented by a NN. The study of Abdulhafedh (2017) also proves that the use of a NN is promising for predicting accident severity. However, these studies also point to the risk that increasing complexity can reduce the comprehensibility of the model, without presenting solutions to make the model transparent. This research gap is also highlighted in the review by Shaik et al. (2021), which presents an extensive list of data-based analysis approaches for accident severity. This study also focuses on the performance of each ML model. Accuracy measures such as F1 score, recall, precision or accuracy are compared. The study highlights the difficulties in predicting accident severity with ML approaches, as well as possible solutions to achieve better results. One challenge that often arises in this use case is that the accident data is often very unbalanced. There are many more accidents of minor severity compared to fatal accidents, which poses a challenge for machine learning models. Possible sampling methods to overcome this challenge and increase the accuracy of the models are presented. Feature selection and preprocessing are also discussed to improve the quality of the training data. While these methods can improve performance, they can also make the predictability of the prediction more difficult. For example, encoding features can potentially complicate interpretation. The diversity of features is also essential for the quality of machine learning predictions. Studies such as Abdulhafedh (2017) have demonstrated a correlation between road characteristics (e.g., road class, number of lanes, and speed limit) and accident severity, suggesting that a broad range of accident-related features can improve predictive performance.

Further Abdulhafedh (2017) emphasizes that the model should be selected according to the data base, but that NNs offer the greatest variety of applications due to their great adaptability. Tambouratzis (2010) shows that the performance and accuracy of accident data classification results can be improved by combining NNs and decision trees. However, it is also important that the decisions made by ML models are transparent and fully disclosed so that people can understand the influences on the model, especially for sensitive predictions such as accident severity. Tambouratzis (2010) identifies two benefits of transparency: First, model biases due to missing and biased data can be identified. Second, confidence in the prediction can be increased by communicating the rationale for the decision in a human-readable way.

The work of Zeng & Huang (2014) also demonstrates the strength of an NN based on a practical dataset. They used 53,732 accidents from Florida in 2006, each with 17 descriptive features and four accident classes. They achieved an accuracy of 54.84% for the test dataset, which is comparable to other studies. In addition, they performed sensitivity tests on the trained ML model to make the decision making more comprehensible. Approaches such as these are the first step in analyzing the factors influencing predicted accident severity. However, this approach can only identify influences globally. Correlations and effects of individual characteristics cannot be covered.

To better understand the decision making of an ML model, some studies have specialized in using decision trees, such as decision trees, random forests or other combinations instead of an NN. The strength of these models is that they can cover non-linear problems and can be explained with little effort (Abellán et al. 2013). The quickest way to do this is to derive so-called decision rules. These can provide a meaningful insight into the decision making of the ML model, as they are based entirely on the trained model. The model’s decisions can be read directly in the form of rules. However, to obtain a comprehensive statement about the influences, it may be necessary to train many trees. To obtain an unbiased and comprehensive picture of the most influential attributes, the individual decision rules of each tree need to be combined and normalized (Satu et al, 2018). However, the work of Satu et al. (2018) proves that the explanatory power of the decision rules is not sufficient to determine the factors influencing the decision of accident severity. They called these influencing factors "risk combinations". Working with decision rules also presents several challenges. Normalized influences are only available globally, and the derived rules only apply to part of the trained model. It is not possible to output the influences for individual instances. In addition, only the importance of a feature can be specified, but not whether the given value of the feature had a positive or negative influence on the decision. Furthermore, a large number of decision trees are required to cover the influences of all factors.

Roussel and Böhm (2023) emphasize that XAI techniques are primarily used in geospatial use cases to improve ML models, rather than using the influencing factors as interpretable domain information for domain experts. This can be seen, for example, in the work of Amorim et al. (2023). They predict the severity of traffic accidents on Brazilian highways. To reduce the complexity of the data, they use the XAI technique local interpretable model-agnostic explanations (LIME) to identify the features that have the least influence on the prediction. They then remove them from the entire data set for a new model training. This improved the prediction quality of the model. However, this study again shows that the potential of the influencing factors is greatly underestimated and not used for deeper knowledge transfer or subsequent data analysis. Especially for geospatial use cases, XAI techniques can add significant value and provide new insights for decision making. According to Roussel and Böhm (2023), the most common models used in conjunction with XAI are boosting algorithms such as extreme gradient boosting (XGBoost). It should be emphasized that the lower the model accuracy, the lower the explanatory power of a model ex-planation; XAI can only reveal the results of an ML model, but cannot evaluate or modify them (Roussel, 2024).

By far the most widely used XAI technique is the SHAP method (Lundberg & Lee, 2017). SHAP is model agnostic and can be applied to any ML model to reveal the decision-making process of a classification. A key advantage of SHAP is its ability to provide both global and local explanations. Global explanations are obtained by aggregating the local SHAP values over the entire dataset and provide an overview of which features have the greatest influence on the model predictions. These global results can be presented in different types of plots to visualize the average contributions of all features. Local explanations, on the other hand, show how individual features influence specific predictions and are often visualized in waterfall plots, which show the contribution of individual features to a specific prediction step by step.

In addition to the traditional visualization of SHAP values, the work of Roussel (2024) deals with the geovisualization of these values. The paper emphasizes that SHAP is a good way to identify influencing factors in an ML model, but that the geospatial representation of these influencing factors has not been sufficiently explored. Two approaches are presented to visualize these factors using geographic maps. A point visualization and an area visualization of the SHAP values are presented. In the punctual visualization, the influencing factors can be represented by color and the characteristic values by size on a map with an exact spatial coordinate. It has been shown that this can reveal spatial patterns that cannot be visualized using the familiar plots. In the area-wide visualization, the SHAP values or the features with the highest SHAP values were visualized with a Voronoi diagram. After intersection with the road network, this can be used to visualize actual geospatial areas of influence across the whole area.

When analyzing accident data, previous research has used ML models to accurately predict accident severity. Only a few studies have used a trained ML model to evaluate factors influencing the prediction. So far, decision rules or feature combinations have mainly been used to identify the risk factors of a serious accident. The interpretation of influencing factors is not widely used in accident analysis but has great potential. The calculated influencing factors can not only make the decision processes of ML models transparent and thus provide important information for subsequent investigations. Influencing factors can also be used to improve ML models and make them more robust. Furthermore, there is still a lack of modern visualization approaches to display accident data. Accident data can be geospatially localized, providing the opportunity to perform geospatial analysis, which can help to identify patterns in the data.

The study by Roussel (2025) provides the first outlines of a global-local explainability approach, which is a scalable explanatory approach for geospatial use cases. This glocal XAI method is also tested in this study to determine the influencing factors and the subsequent geospatial information. The next chapter presents a concept that performs a geospatial scaling of the SHAP values in order to present ML predictions.

3. Concept

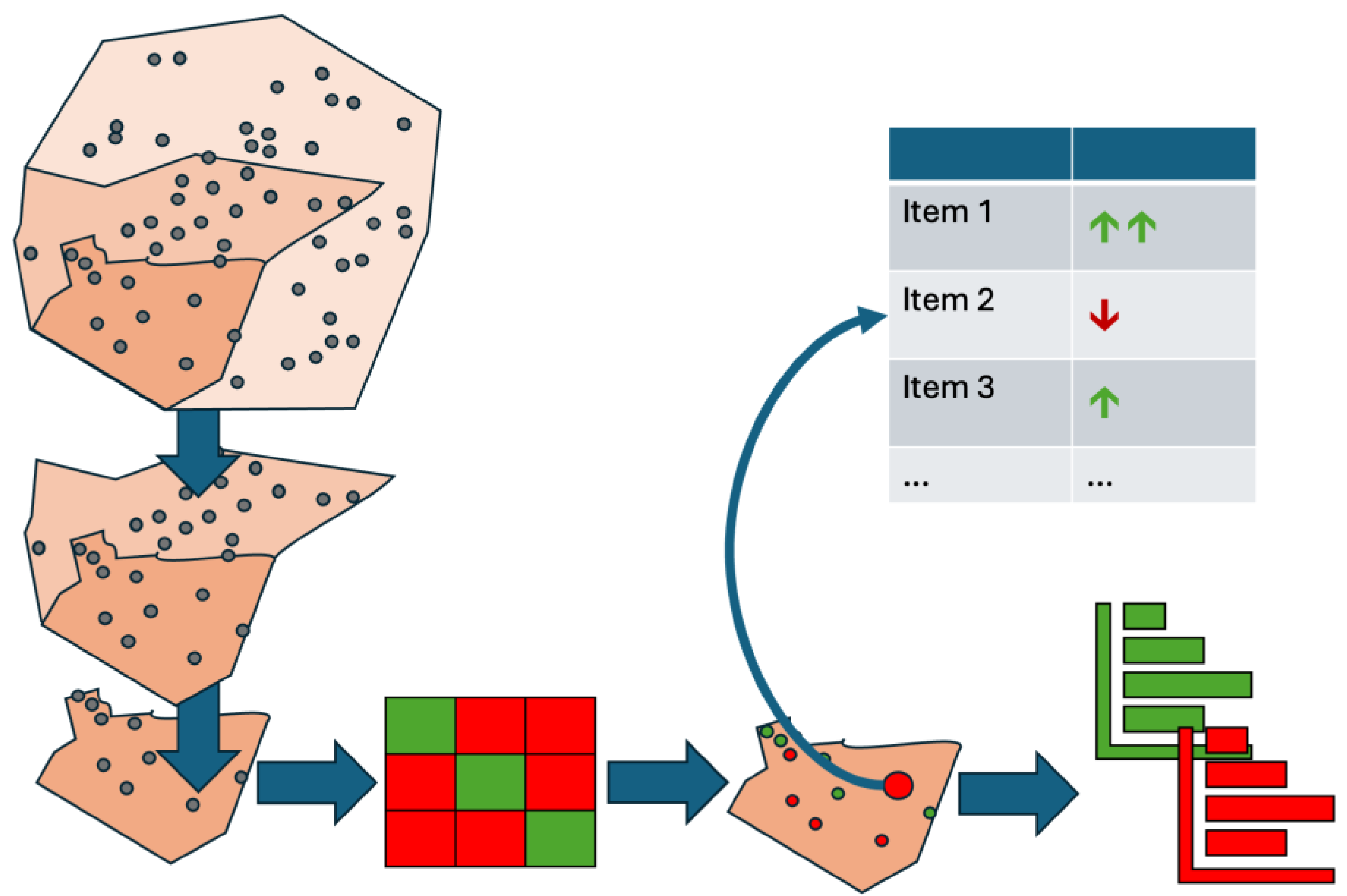
This chapter introduces a developed concept that can calculate the influencing factors of an ML classification not only locally for individual datasets or globally for all predictions but also scaled and taking the predicted classes into account. The concept of semi-global influence factors aims to represent extensive influencing variables in a generalized way without distorting them. Combining these two requirements has not yet been investigated; the present concept addresses this research gap.

To this end, two types of data segmentation are employed: First, the data points are spatially segmented, and then they are assigned to the cells of the confusion matrix. The first segmentation is used for geographical classification, and the second segmentation enables a differentiated analysis of the ML model’s decision-making process depending on the target class and the predicted class. The influencing factors of this twofold-segmented data can then be aggregated to make statements about the effect of individual features on specific cells of the confusion matrix within spatial areas.

Figure 1. Novel Concept zur Ableitung von semi-gloablen Einflussfaktoren.

Figure 1. Novel Concept zur Ableitung von semi-gloablen Einflussfaktoren.

The first step is spatial segmentation. With geographic data in particular, it is essential to recognize and analyze spatial patterns and relationships. The challenge lies in structuring the data in a meaningful way to make semi-global statements, especially when the data is distributed irregularly in space. Therefore, the data set is first divided into clearly definable geographical areas. These areas can be administrative boundaries, such as federal states, counties, or city districts. Alternatively, sub-areas based on social, infrastructural, or climatic criteria, such as forest, urban, and rural areas, are also possible. The choice of segmentation depends on the available data and the respective use case.

The larger the selected areas, the more generalized the subsequent statement about the influencing factors will be. Conversely, smaller segments enable a more precise derivation of spatial patterns. The presented concept uses scalable analysis to examine both small-scale structures with low point density and large-scale areas with aggregated influencing factors. Thus, it is possible to conduct an area-related analysis of the influencing variables at different spatial scales. The predictions generated by the ML model can also be localized semi-globally through this segmentation.

The ML model calculates a probability for each target class, so the sum of all the probabilities is always 100%. XAI methods, such as SHAP, allow us to analyze these probabilities in detail to determine the influence of individual features. The resulting local influencing factors depend on the instance and target class under consideration.

A common mistake when deriving global influencing factors is aggregating all local influences on a target class y_i. This is problematic if it is calculated regardless of whether the model correctly predicted the target class. This procedure can lead to distortions because it includes incorrect predictions. To avoid this, a second classification of the data is performed after spatial segmentation based on the initial classification. The predictions are then assigned to cells of a confusion matrix that compares the actual classes with those predicted by the model.

This division allows for dynamic analysis of predictions based on the respective spatial unit. An interactive dashboard visually presents the results, allowing complex influencing factors to be explored in a user-friendly, low-threshold manner.

The confusion matrix also facilitates targeted aggregation. Influencing factors per target class are calculated based exclusively on instances correctly classified by the model. This avoids distortions due to misclassification. Additionally, incorrect predictions can be analyzed to identify the responsible features. Classifying the data as true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) enables a structured and cumulative representation of the influencing factors. This approach provides a robust basis for analyzing model decisions, especially wrong ones.

Combining spatial and classification-based segmentation provides a more detailed view of the classification results. This approach is particularly effective when using XAI methods, such as SHAP. It goes beyond classic SHAP diagrams, such as beeswarm or summary plots, by offering alternative, visually prepared display options.

The visualization uses simplified symbols to depict individual feature flows without altering the underlying numerical values. For each target class, it is clear which features have increased or decreased the prediction probability. The intensity of influence can also be displayed symbolically, enabling a diverse user group to understand the semi-global influencing factors.

Additionally, the interactive dashboard allows users to dynamically adjust the target class, leading to different influences on the target class. This allows for a targeted analysis of the features that led to the inclusion or exclusion of certain classes. Even in cases of misclassification, the features that caused the model to make an incorrect prediction can be quickly identified. The dashboard offers a transparent and comprehensible representation of the factors influencing the model prediction thanks to the dynamic visualization of local SHAP values using waterfall and decision plots. The combination of interactive analysis options, user-centered design, and a comparative presentation of all target classes strengthens understanding of the model’s internal decision-making processes. This creates a sound basis for further interdisciplinary analyses.

This concept is suitable for any use case involving the classification of highly spatially distributed data with a trained ML model, followed by analysis using XAI methods.

4. Implementation

Das folgende Kapitel zeigt die Umsetzung des beschriebenen Konzeptes aus dem Kapitel 3. Es wird ein Prozessablauf aufgezeigt, mit denen aus Unfalldaten die Einflussfaktoren auf die Unfallschwere mittels XAI abgeleitet werden sollen. Hierbei soll die Stadt Mainz als Untersuchungsgebiet exemplarisch analysiert werden.

Data

Zu Beginn wird der verwendete Datensatz vorgestellt. Die in dieser Arbeit verwendeten Unfalldaten stammen aus dem Unfallatlas der statistischen Ämtern des Landes und des Bundes1. In diesem frei verfügbaren Datensatz werden alle von der Polizei aufgenommen Verkehrsunfälle auf deutschen Straßen aufgeführt, bei denen ein Personenschaden vorlagt. Die Daten werden jährlich zur Verfügung gestellt, hierbei können jedoch Lücken bei der Abgabe mancher Bundesländer auftreten (Mecklenburg-Vorpommern ist erst seit 2021 vertreten). Die durch die Polizei aufgenommenen Unfälle werden mit geografischen Koordinaten versehen und sind somit räumlich darstellbar und analysierbar.

Der Untersuchungszeitraum umfasst die Jahre 2016 – 2022. In diesem Zeitraum wurden 1,396,570 Unfälle in Deutschland registriert und im Unfallatlas zur Verfügung gestellt. Hiervon sind 1,118,604 (80%) Unfälle mit Leichtverletzten, 263,664 (19%) Unfälle mit Schwerverletzten und 14,316 (1%) Unfälle mit tödlich verletzten Verkehrsteilnehmern. Wie die Arbeiten von Pourroostaei Ardakani et al. (2023) oder Pradhan & Ibrahim Sameen (2020) bereits aufgezeigt haben, sind auch hier die Unfalldaten stark unbalanciert.

Die Unfalldaten der einzelnen Bundesländer werden durch die statistischen Ämtern des Landes und des Bundes zusammengeführt und generalisiert. Zu jedem Unfall werden 13 Features geführt. Diese geben räumliche, zeitliche, atmosphärische und situative Auskünfte und sind in Error! Reference source not found. aufgelistet. Dies sind weniger umfangreich als in Datensätzen vergleichbarer Arbeiten. Die Beschreibung der Features stammt aus der Datensatzbeschreibung Unfallatlas (Statistische Ämter des Bundes und der Länder, 2021) und aus der Erläuterung der Grundbegriffe der Verkehrsunfallstatistik (Statistisches Bundesamt, 2022).

Table 1. Auflistung der Features in dem standardisierten Format der Unfalldaten, welche durch die statistischen Ämter zur Verfügung gestellt wurden.

Beschreibung	Wertebereich
Servity	Kategorial (1-3)
Accident with Bicycle	Binär
Accident with Car (PKW)	Binär
Accident with Pedestrian	Binär
Accident with Motorcycle	Binär
Accident with Other Vehicle	Binär
Day of Week	Kategorial (1-7)
Month	Kategorial (1-12)
Hour	Kategorial (0-23)
Accident type	Kategorial (0-9)
Accident category	Kategorial (1-7)
Lighting condition	Kategorial (0-2)
Road condition	Kategorial (0-2)
Road type	Kategorial (1-11)

Table 1. Auflistung der Features in dem standardisierten Format der Unfalldaten, welche durch die statistischen Ämter zur Verfügung gestellt wurden.

Beschreibung	Wertebereich
Servity	Kategorial (1-3)
Accident with Bicycle	Binär
Accident with Car (PKW)	Binär
Accident with Pedestrian	Binär
Accident with Motorcycle	Binär
Accident with Other Vehicle	Binär
Day of Week	Kategorial (1-7)
Month	Kategorial (1-12)
Hour	Kategorial (0-23)
Accident type	Kategorial (0-9)
Accident category	Kategorial (1-7)
Lighting condition	Kategorial (0-2)
Road condition	Kategorial (0-2)
Road type	Kategorial (1-11)

Die von den statistischen Ämtern herausgegebenen Verkehrsunfälle wurde in der Datenaufbereitung georeferenziert. In diesem Schritt wurde der genaue Unfallort auf die nächstgelegene Straßenachse bezogen. Jedoch enthält der Datensatz nur eine räumliche Koordinate und keine Auskunft über die Straßeneigenschaften. Um nun die Unfalldaten mit zusätzlichen Straßeninformationen anzureichern, ist ein automatisierbarer Ansatz gefordert.

Um die Eigenschaften der jeweiligen Straße einem Unfall anzuhängen, wurden die frei zur Verfügung stehenden Daten von OpenStreetMap (OSM)2 als zusätzliche Datengrundlage genutzt. Bei der Datenanreicherung wurde sich exemplarisch also nur auf die Straßenklasse als zusätzliches Attribut bezogen, da Angaben zur Straßenbreite, der Anzahl der Spuren oder der Höchstgeschwindigkeiten nicht flächendeckend vorlagen. Es wurde die Einschränkung vorgenommen, dass nur Straßen aus OSM berücksichtigt werden, auf denen ein Verkehrsunfall stattfinden kann.

Data Engineering

Auffällig bei der Betrachtung der Datentypen der Features in Error! Reference source not found. ist, dass diese primär als kategoriale Werte angegeben werden. Hierbei wird für jedes Feature ein Wert aus einer von den Statistische Ämter des Bundes und der Länder definierten Liste angegeben. Diese Werte sind oftmals nicht miteinander vergleichbar oder sortierbar. Damit jedoch eine modellagnostische Auswertung der Unfallschwere anhand dieser Features möglich ist, müssen diese durch Transformationen und Encoding in eine Modell-lesbare Struktur überführt werden. Durch Sampling-Methoden müssen die unbalancierten Unfallangaben ebenfalls angepasst werden.

Zeitangaben wie Stunden und Monate sind zyklisch, sodass eine rein numerische Darstellung benachbarte Werte wie 23:00 und 01:00 Uhr verzerrt abbildet.

Zur korrekten Erfassung dieser zyklischen Natur werden Sinus- und Kosinus-Transformationen angewendet, was sich in der Praxis bewährt hat (London, 2016; Cédric et al., 2023). Die neuen kontinuierlichen Werte werden als Features gespeichert.

Die kategorialen, nominalskalierten Features Unfallart, Unfalltyp, Lichtverhältnisse, Straßenzustand und Straßenklasse sind Angaben, die keine natürliche Reihenfolge haben und nicht direkt vergleichbar sind. Es wird auf das One-Hot-Encoding zurückgegriffen, um eine unabhängige Betrachtung der einzelnen Feature-Klassen durch das ML-Modell zu gewährleisten. Das One-Hot-Encoding ermöglicht zwar die modellagnostische Bearbeitung von kategorialer Daten, führt aber auch zu einer starken Merkmalsvermehrung und damit zum „Fluch der Dimensionalität“ (Bellman, 1961). Im vorliegenden Fall wuchs die Anzahl der Features infolge der Transformationen von 13 auf 52, was höhere Modellkomplexität und mehr Trainingsdaten erforderlich macht.

Es wird ein eigenständiger Sampling-Ansatz verwendet, um ein ML-Modell zu trainieren, welches im ersten Schritt eine Klassifikation der Unfallschwere anhand der Features vornimmt. Mit einem Testdatensatz soll im Nachhinein die Qualität des Modells überprüft werden und die Grundlage für die Visualisierung der semi-globalen Einflussfaktoren sein. Um ein aussagekräftiges ML-Modell zu trainieren, werden gleichverteilte, heterogene und vor allem viele Unfalldaten benötigt. Die Trainingsdaten werden dabei unabhängig von spezifischen geografischen Regionen zusammengestellt, um Verzerrungen zu vermeiden und die Leistungsfähigkeit des Modells über durch ein möglichst variablen Trainingsdatensatz zu maximieren. Dennoch sind im angereicherten Datensatz die Verteilungen der einzelnen Unfallschweren immer noch sehr unausgeglichen. Amorim et al. (2023) hatten in ihrer Arbeit dieses Problem ebenfalls aufgezeigt. Es wurden ML-Modelle mit einem balanciertem beziehungsweise mit einem unausgeglichenem Datensatz trainiert. Hierbei wurde festgestellt, dass Zusammenhänge zwischen den Eingabefeatures und den Zielvariablen nur bei balancierten Datensätzen vorlagen. Das Finden der unterbesetzten Klasse in einem unausgeglichen Datensatz war kaum möglich und die Qualität der Klassifizierung anhand der Fehlermaße um über 10% schlechter (Untersucht wurden NN, Entscheidungsbäume, SVM und Naive Bayes). Es muss entweder auf Undersampling oder Oversampling zurückgegriffen werden. Ein Nachteil beim Undersampling ist, dass wichtige Informationen, welche in den zufällig gelöschten Instanzen liegen könnten, nicht vom ML-Modell gesehen und adaptiert werden können. In der Forschung wird aus diesem Grund oftmals auf das Oversampling zurückgegriffen. Vor allem die Synthetic Minority Over-sampling TEchnique (SMOTE) ist weit verbreitet. Anstatt Instanzen der unterrepräsentierten Klasse einfach zu kopieren, bis die Klassenverteilung gleich ist, werden hier synthetische Instanzen gebildet. Das Kopieren der Daten würde zu Overfitting führen, da hier immer wieder dieselben Fälle für das Training benutzt werden würden. Bei SMOTE werden die Instanzen neu gebildet, die Feature-Werte orientieren sich hier an den nächsten Instanzen und haben somit individuelle Werte. Bei umfangreichen Neuerzeugungen und wenigen Ausgangsdaten kann ebenfalls Overfitting auftreten. Amorim et al. (2023) oder Parsa et al. (2020) verwendeten SMOTE, um die von Natur aus unausgeglichen Unfalldaten anzupassen. Diese bewährte Sampling-Methode wird deswegen auch im neuen Sampling-Ansatz verwendet.

Auffällig bei der Durchführung von SMOTE an den deutschen Unfalldaten war das darauffolgende zu starke Berücksichtigen der zuvor unterrepräsentierten Unfallschwere-Klassen. Da sowohl Undeersampling als auch SMOTE keine zufriedenstellenden Ergebnisse lieferten wurden die Stärken der beiden Methoden in einem eigenen Ansatz verbunden. Zunächst wurde die Menge der tödlichen Unfälle mit SMOTE auf 160,000 erweitert, das entspricht eine Verzehnfachung der Unfälle. Die Unfälle mit leichten und schweren Unfallausgang werden nun auf die Menge der tödlich Verunglückten reduziert. Durch diesen Ansatz werden nicht zu viele Instanzen synthetisch erzeugt, was zu Overfitting führen könnte und gleichzeitig werden weniger Daten der überrepräsentierten Klassen gelöscht, was einen Informationssicherung gewährleistet. Um später die Klassifizierung zu bewerten, wurden die Unfälle aus Mainz aus dem Trainingsdatensatz entfernt und als Testdaten verwendet. Diese wurden nicht ausgeglichen, da sie die genauen Verhältnisse repräsentieren sollen.

Klassifizierung

Die vorbereiteten Unfalldaten sollen genutzt werden, um ein ML-Modell zu trainieren, welches die Unfallschwere anhand der einzelnen Features vorhersagen kann. Hierbei wird eine Mehrklassen-Klassifikation durchgeführt. Die im Kapitel 2 vorgestellten Arbeiten greifen dabei vor allem auf Baumstrukturen, wie dem XGBoost, Decision Trees, oder Random Forst oder auf Neuronale Netze, wie dem MLP oder auch PNN zurück. Aus beiden Gruppen sollen die weitverbreiteten Modelle MLP und XGBoost gegenübergestellt werden, wobei der Fokus der Arbeit nicht in der Bestimmung des bestgeeigneten Modell liegen soll, sondern viel mehr das aufgestellte Konzept praktisch beweisen soll. Die beiden Modelle sind hierbei von Ihrem Aufbau und ihren Trainingsansätzen grundsätzlich verschieden. Die ableitbaren Genauigkeiten können für eine unabhängige Bestätigung des Trainings herangezogen werden.

Table 2. Fehlermaße des MLP-NN und des XGBoost mit und ohne Berücksichtigung des Sampling-Ansatzes und der zusätzlichen Straßenklasse.

Klassifikator	Balancierte Daten?	Mit Straßenklasse?	Genauigkeit	F1-Score	Recall	Precision
XGBoost	Nein	Nein	85%	30,6%	33,2%	28,4%
MLP-NN	Nein	Nein	85%	30,6%	33,3%	28,4%
XGBoost	Ja	Nein	63%	36,4%	58,9%	38,3%
MLP-NN	Ja	Nein	64%	37,5%	59,9%	39,7%
XGBoost	Ja	Ja	65%	37,2%	59,6%	38,7%
MLP-NN	Ja	Ja	59%	35,3%	51,9%	38,5%

Table 2. Fehlermaße des MLP-NN und des XGBoost mit und ohne Berücksichtigung des Sampling-Ansatzes und der zusätzlichen Straßenklasse.

Klassifikator	Balancierte Daten?	Mit Straßenklasse?	Genauigkeit	F1-Score	Recall	Precision
XGBoost	Nein	Nein	85%	30,6%	33,2%	28,4%
MLP-NN	Nein	Nein	85%	30,6%	33,3%	28,4%
XGBoost	Ja	Nein	63%	36,4%	58,9%	38,3%
MLP-NN	Ja	Nein	64%	37,5%	59,9%	39,7%
XGBoost	Ja	Ja	65%	37,2%	59,6%	38,7%
MLP-NN	Ja	Ja	59%	35,3%	51,9%	38,5%

Das erste Training des XGBoost-Klassifikators und des MLP-NN wurde mit den zusammengefassten Unfalldaten aus Deutschland durchgeführt. Hierbei wurde auf das Sampling der Daten verzichtet. Anschließend wurde das Training mit den angeglichenen Unfallschwere-Klassen wiederholt. Das dritte Modelltraining der beiden ML-Ansätze wurde mit den balancierten Unfalldaten und Berücksichtigung der Straßenklasse durchgeführt. Diese Datenanreicherung konnte nur beim XGBoost zu Modellverbesserungen führen. Die Ergebnisse der Mehrklassen-Klassifikation lassen sich Error! Reference source not found. ablesen.

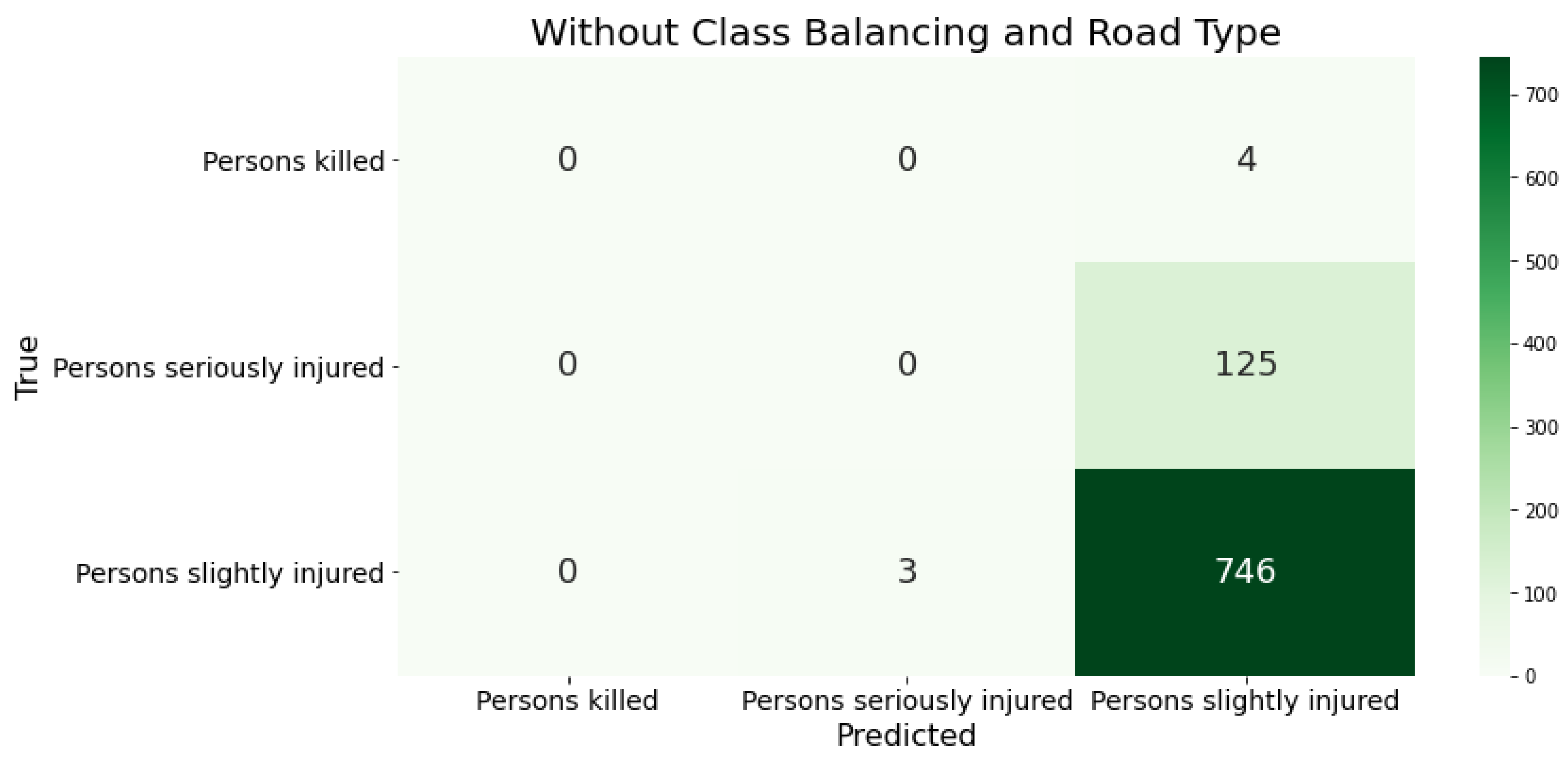
Bei der Betrachtung der Konfusion-Matrix der Klassifikationsergebnisse des XGBoost-Klassifikators bei unausgeglichen Trainingsdaten fällt auf, dass das Modell alle Unfälle als leichte Unfälle klassifiziert (siehe Error! Reference source not found.). Der Umfang dieser Unfallschwere überwiegt die anderen beiden Klasse so sehr, dass das Modell nicht genügend Daten der unterrepräsentierten Klasse hat, um diese Unfallklassen zu identifizieren. Dieser Sachverhalt bestätigt die Notwendigkeit der im Pre-Processing durchgeführte Sampling-Methode.

Figure 2. Klassifizierungsergebnisse des XGBoost mit den deutschen Daten als Trainingsgrundlage durch Konfusion-Matrizen. Ohne Berücksichtigung der Klassenverteilung und der Straßenklassen.

Figure 2. Klassifizierungsergebnisse des XGBoost mit den deutschen Daten als Trainingsgrundlage durch Konfusion-Matrizen. Ohne Berücksichtigung der Klassenverteilung und der Straßenklassen.

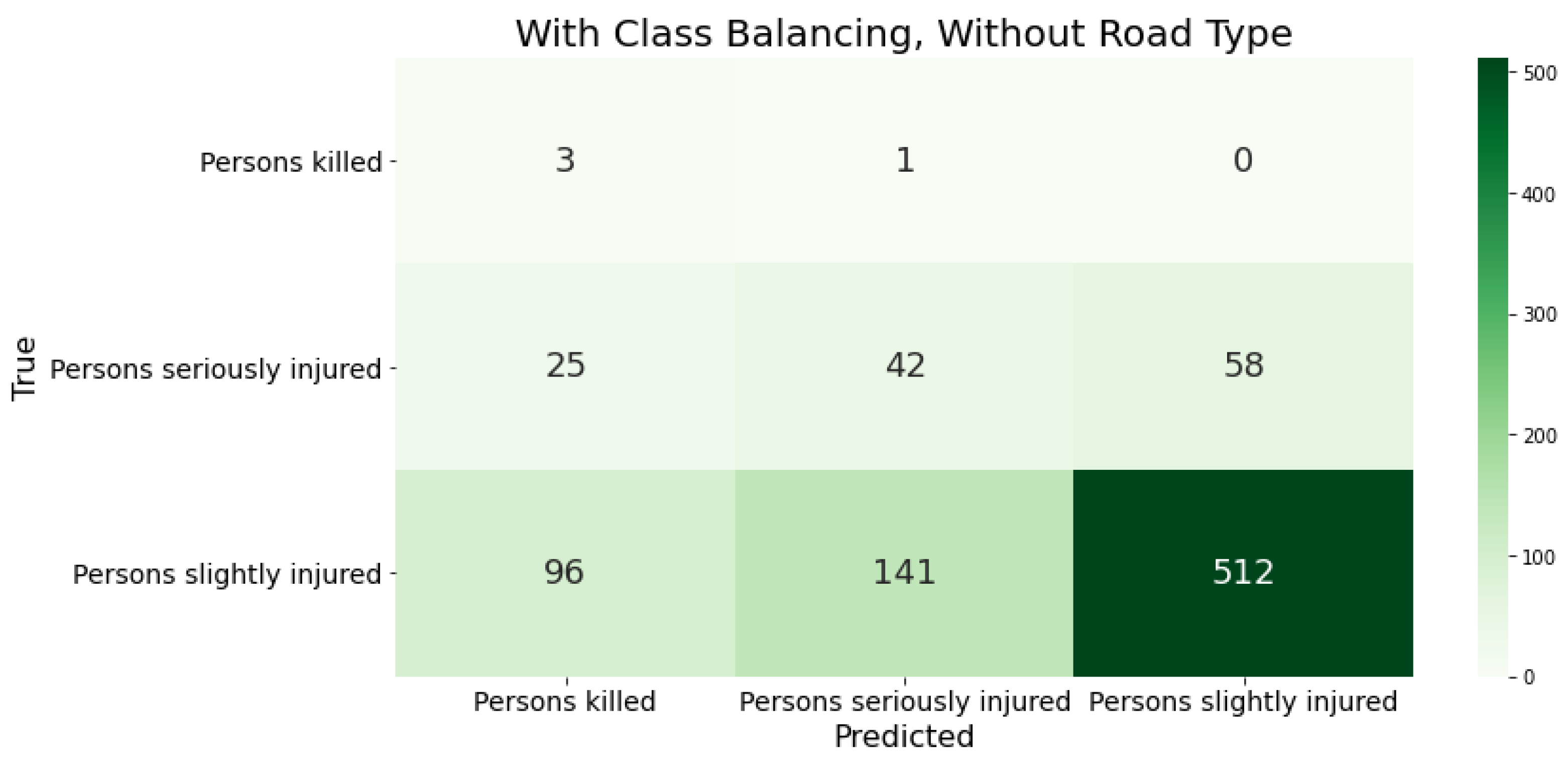
Figure 3. Klassifizierungsergebnisse des XGBoost mit den deutschen Daten als Trainingsgrundlage durch Konfusion-Matrizen. Nach Anpassung der Klassenverteilung in den Trainingsdaten. Ohne Straßenklasse.

Figure 3. Klassifizierungsergebnisse des XGBoost mit den deutschen Daten als Trainingsgrundlage durch Konfusion-Matrizen. Nach Anpassung der Klassenverteilung in den Trainingsdaten. Ohne Straßenklasse.

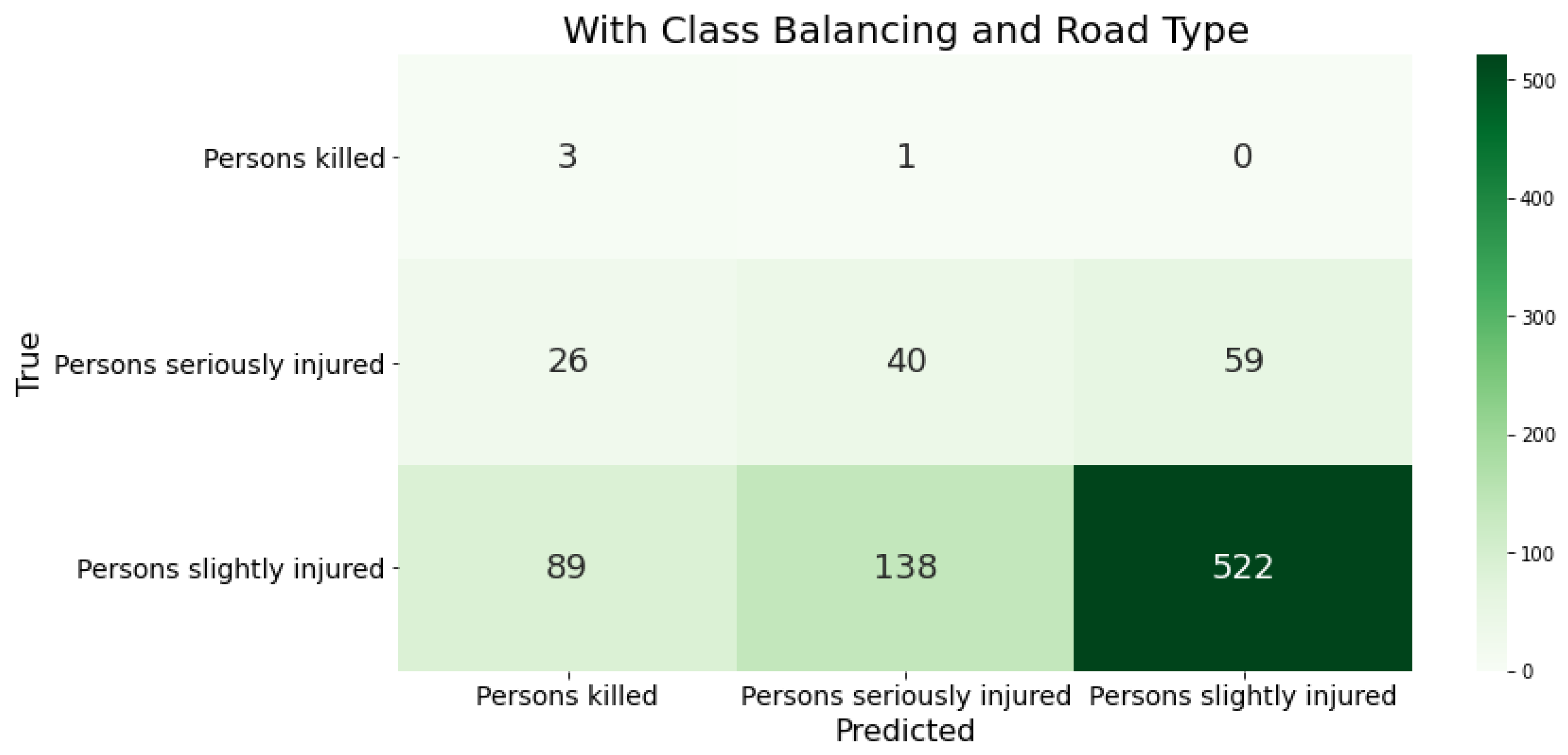
Figure 4. Klassifizierungsergebnisse des XGBoost mit den deutschen Daten als Trainingsgrundlage durch Konfusion-Matrizen. Nach Anpassung der Klassenverteilung in den Trainingsdaten. Angereichert mit der Straßenklasse.

Figure 4. Klassifizierungsergebnisse des XGBoost mit den deutschen Daten als Trainingsgrundlage durch Konfusion-Matrizen. Nach Anpassung der Klassenverteilung in den Trainingsdaten. Angereichert mit der Straßenklasse.

Nach dem Angleichen der Klassenhäufigkeiten in den Trainingsdaten verbessern sich fast alle Fehlermaße, da nun mehr schwere und tödliche Unfälle korrekt klassifiziert werden können (siehe Error! Reference source not found.). Die Recall-Werte dieser Klassen betragen 75% bzw. 38%. Jedoch werden jetzt auch mehr leichte Unfälle in den Testdatensatz als Unfälle mit tödlichem Unfallausgang vorhergesagt. Sichtbar wird das durch einen geringen Precision-Wert für diese Unfallklasse von 3% und einem Rückgang des Recall-Wertes auf 70% für die leichtverletze Unfallklasse. Dies kann auf Overfitting der Modelle hinweisen und muss genauer untersucht werden. Auch die Genauigkeit der Klassifikation wird geringer. Sie fiel um 20% auf 65%. Dies hängt damit zusammen, dass die überrepräsentierten leichten Unfälle nun öfter in andere Unfallschweren vorhergesagt werden. Die Steigerung des Gesamt-Recall-Wertes um 26% verdeutlichen aber auch, dass das korrekte Zuordnen der Unfallschwere vor allem in den unterrepräsentierten Klassen verbessert werden konnte. Hier wurden von 4 tatsächlichen Unfällen mit tödlichem Unfallausgang 3 korrekt klassifiziert. Jedoch wurden 26 schwere Unfälle und 89 leichte Unfälle als tödliche Unfälle vorhersagt, was unter anderem in einem geringen Gesamt-Precision-Wert von 38,7% resultiert.

Die beiden untersuchten Modelle XGBoost und MLP-NN weisen in den Fehlermaßen ähnliche Werte auf. Hierdurch wird die Klassifikation durch diese zwei unabhängigen und unterschiedlichen ML-Modelle qualitativ bestätigt. Vergleichbar mit dem XGBoost-Klassifikator werden für das MLP-NN auch schwere und tödliche Unfälle erst nach dem Anpassen der Klassenhäufigkeiten vorhergesagt. Auch hier führt dies aber auch zu einem möglichen Overfitting des Modells, was an den nun falsch klassifizierten leichten Unfällen liegt. Dennoch weist das MLP-NN leicht bessere Ergebnisse in allen Fehlermaßen nach (1%-3%), da dieses Modell mehr Unfälle mit einer leichten Unfallschwere korrekt vorhergesagt hat.

Das Hinzufügen eines weiteren Features, der Straßenklasse, macht die Datengrundlage komplexer. Somit ist auch ein Modell gefordert, welches die gestiegene Komplexität richtig abbilden kann. Nur der XGBoost-Algorithmus war in der Lage die Qualität der Klassifikationsergebnisse noch zu steigern (siehe Error! Reference source not found.). Das MLP-NN verlor an allen Fehlermaßen. Mehr Unfälle mit Leichtverletzten wurden den Unfällen mit schwer oder tödlich Verletzten zugeordnet, dies ist im Recall-Wert der Klasse von 34% abzulesen. Darüber hinaus wurden weniger tatsächliche Unfälle mit einer tödlichen Unfallschwere identifiziert. Das Modell hat nach der Anreicherung der Daten mit der Straßenklasse fälschlicherweise mehr Unfälle als schwere Unfälle vorhergesagt.

Der XGBoost-Klassifikator soll als primäres Modell bei der weiteren Bearbeitung verwendet werden, da dieser neben einer starken Performance auch nicht lineare Sachverhalte gut abbilden kann. Durch verschiedene Beschleunigungsmechanismen können XAI-Methoden wie SHAP effizienter mit Baumstrukturen, wie dem XGBoost berechnet werden, dies ist ein großer Vorteil im Vergleich zum MLP-NN.

Darüber hinaus wurde anschließend mithilfe von Kreuz-Validierungen eine Hyperparametertuning zur Identifizierung der besten Modellparameter vorgenommen. Das Modell ist für ein Mehrklassenklassifikationsproblem mit einer softmax-Zielfunktion konfiguriert und besteht aus 500 Entscheidungsbäumen mit einer maximalen Tiefe von vier Ebenen. Zur Reduktion von Überanpassung wird bei der Konstruktion jedes Baums jeweils nur eine Stichprobe von 80 % der Trainingsdaten sowie 60 % der Merkmale verwendet. Zusätzlich werden L1- und L2-Regularisierung eingesetzt, um die Modellkomplexität zu begrenzen. Die Lernrate ist mit 0,015 bewusst niedrig gewählt, um eine stabile und schrittweise Konvergenz zu fördern. Durch ein zusätzliches Finetuning konnten die Fehlermaße erneut verbessert werden (2% in allen Fehlermaßen).

XAI

Um die semi-globale Einflussfaktoren des XGBoost-Modells transparent darzustellen, wird Explainable AI (XAI) eingesetzt, wobei SHAP aufgrund seiner Modellagnostik sowie der Möglichkeit zur gleichzeitigen lokalen und globalen Interpretation der Modellentscheidungen verwendet wird (Lundberg et al., 2020). Im Vergleich zu alternativen Ansätzen wie LIME, das primär lokale Erklärungen liefert, erlaubt SHAP eine konsistentere Bewertung der Einflussfaktoren über viele Instanzen hinweg. Für das XGBoost-Modell wird der speziell angepasste TreeExplainer genutzt, der die SHAP-Werte effizient und modellintern berechnet und somit eine performante Analyse großer Datensätze ermöglicht3.

Ziel ist es, alle Unfälle der Testdaten aus Mainz mithilfe von SHAP-Werten zu erklären. Insgesamt wurden 878 Instanzen analysiert, für die je ein SHAP-Wert pro Feature und pro Zielklasse berechnet wurde – also 52 Merkmale über drei Klassen hinweg, was in Summe 136,968 einzelnen SHAP-Werte ergibt.

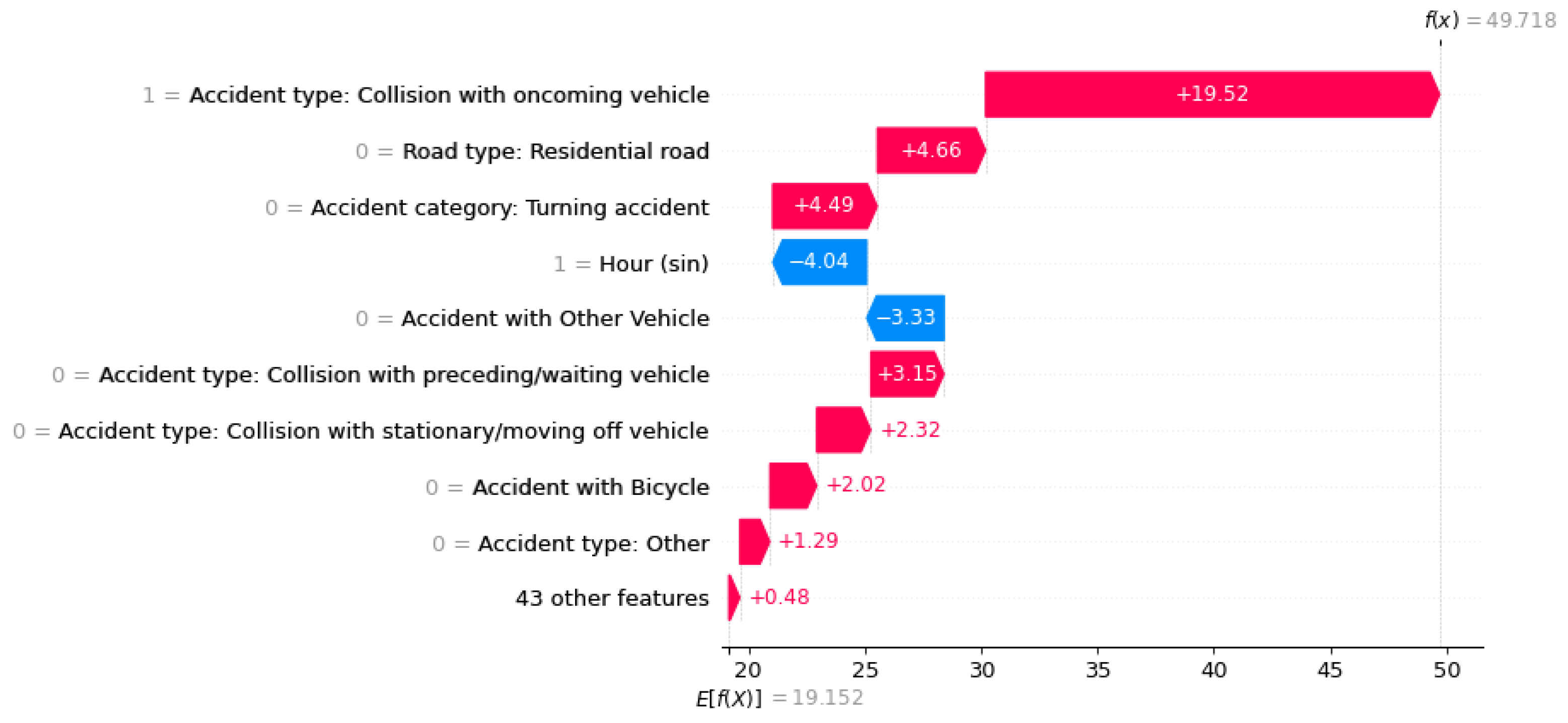
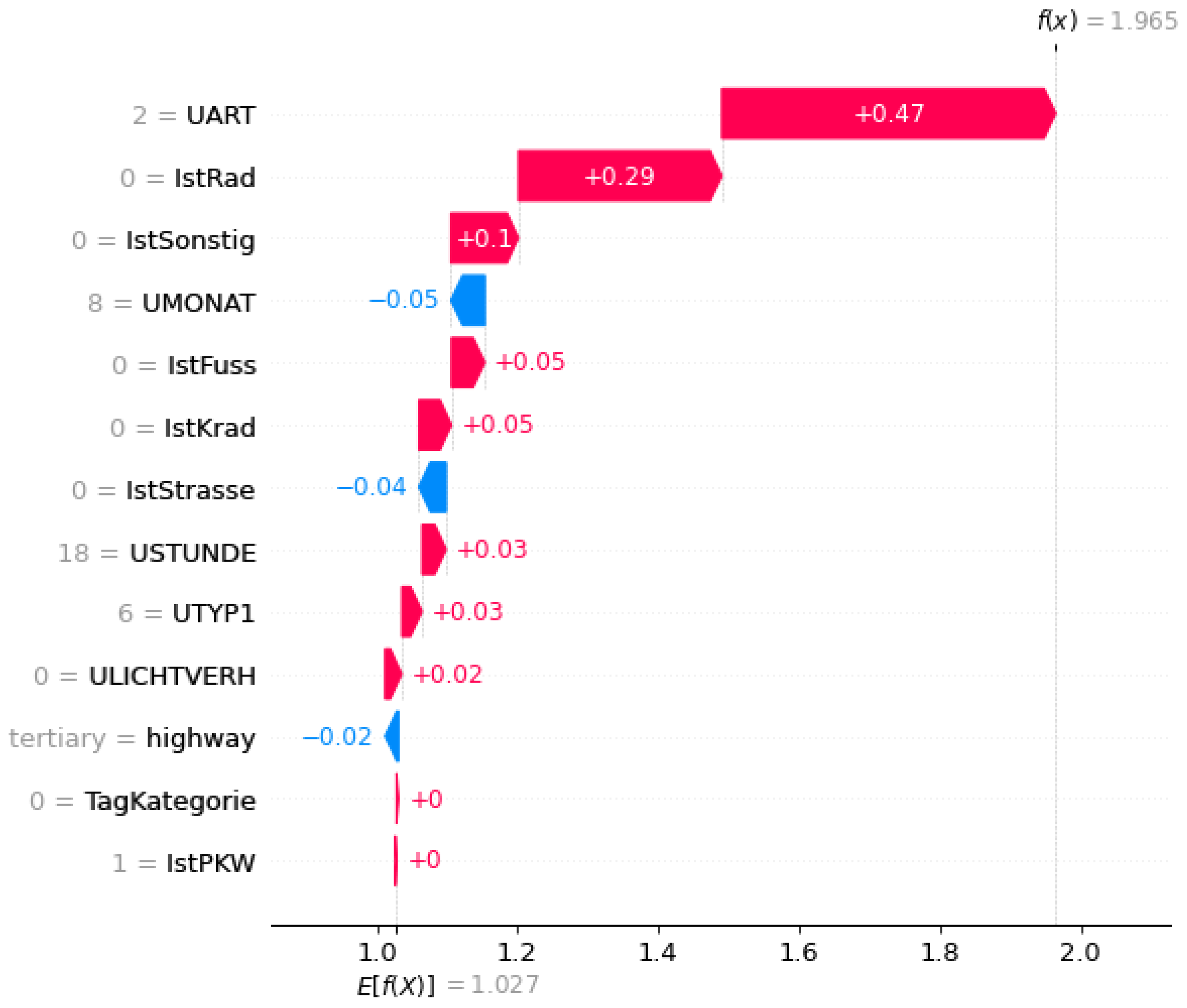
Die Einflussfaktoren je Zielklasse können für jede Instanz beispielsweise mithilfe eines Waterfall-Plots lokal visualisiert werden, wie in Error! Reference source not found.-Error! Reference source not found. dargestellt.

Figure 5. Waterfall-Plots der drei Unfallschwere “Persons killed“ zur Visualisierung der Einflussfaktoren auf eine ML-Vorhersage.

Figure 5. Waterfall-Plots der drei Unfallschwere “Persons killed“ zur Visualisierung der Einflussfaktoren auf eine ML-Vorhersage.

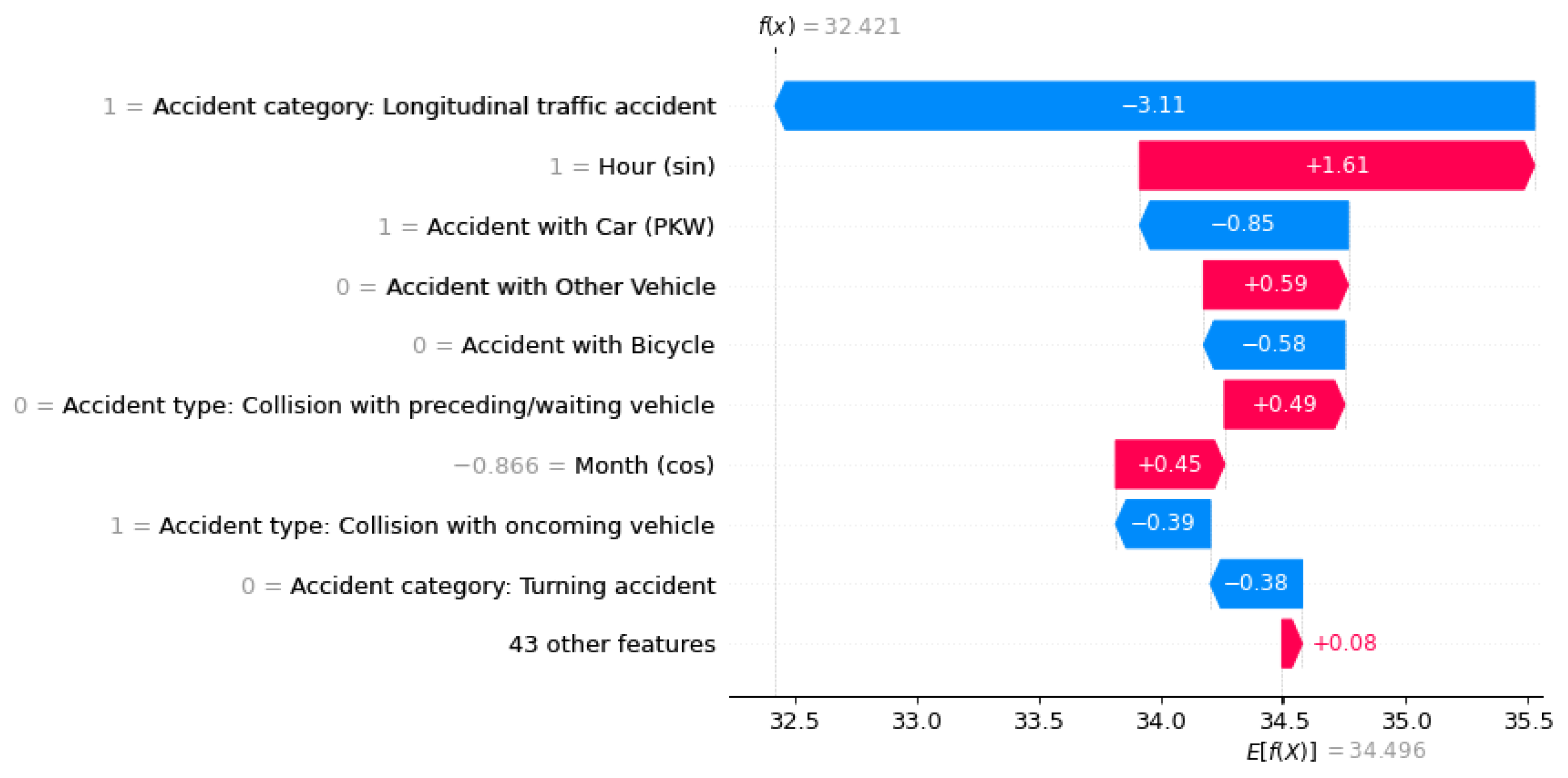
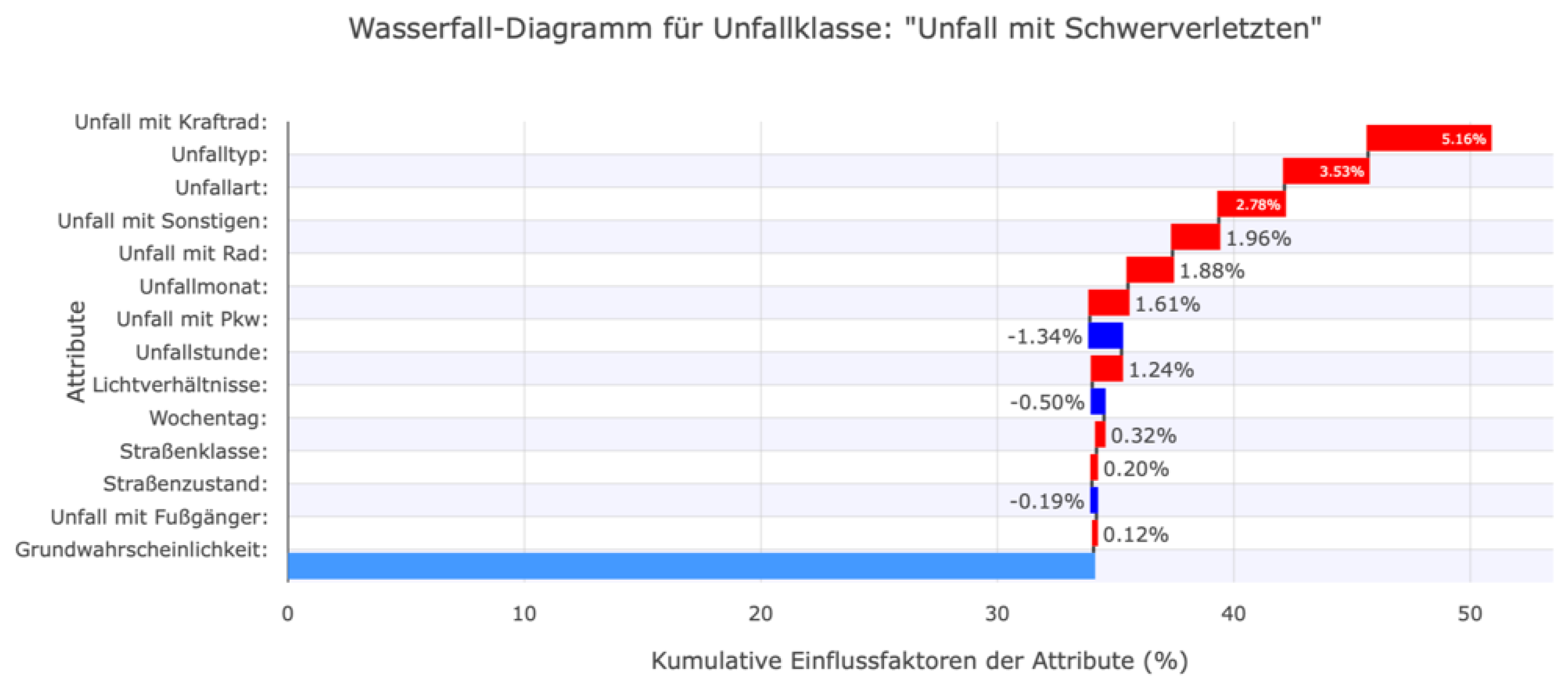
Figure 6. Waterfall-Plots der drei Unfallschwere “Persons seriously injured“ zur Visualisierung der Einflussfaktoren auf eine ML-Vorhersage.

Figure 6. Waterfall-Plots der drei Unfallschwere “Persons seriously injured“ zur Visualisierung der Einflussfaktoren auf eine ML-Vorhersage.

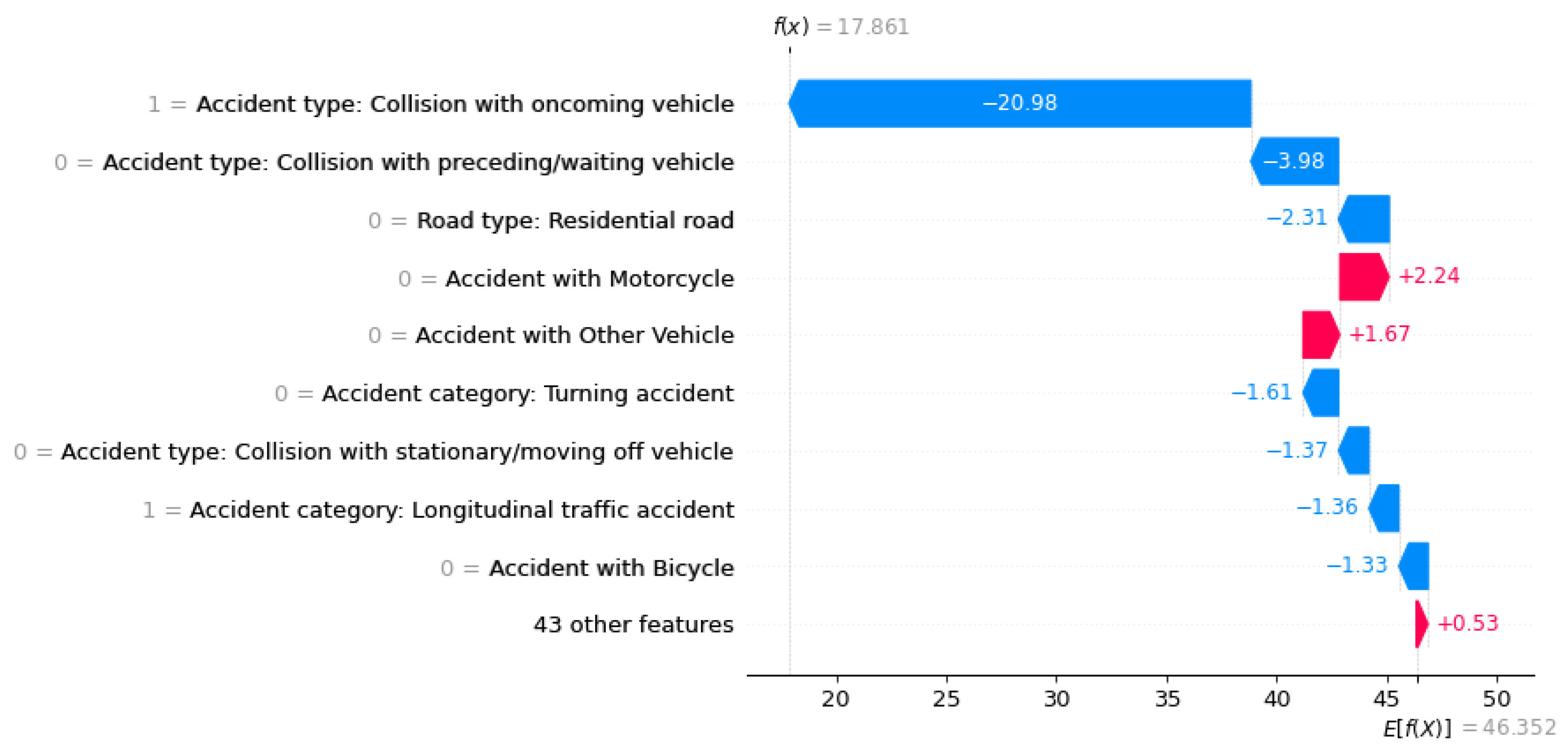
Figure 7. Waterfall-Plots der drei Unfallschwere “Persons sligthly injured“ zur Visualisierung der Einflussfaktoren auf eine ML-Vorhersage.

Figure 7. Waterfall-Plots der drei Unfallschwere “Persons sligthly injured“ zur Visualisierung der Einflussfaktoren auf eine ML-Vorhersage.

Neben den SHAP-Werten wird für jede Klasse ein Basiswert (E(f(x))) berechnet. Dieser drückt bei unausgeglichen Datensätzen die Grundwahrscheinlichkeit der einzelnen Klasse aus. Das bedeutet, dass diese Wahrscheinlichkeit das Vorkommen einer Klasse ohne die Betrachtung der individuellen Features einer Instanz beschreibt. Bei gleichem Vorkommen aller Zielklassen ist der Basiswert ebenfalls gleich. Da die Einflussfaktoren durch SHAP-Werte auf die unausgeglichen Testdaten bezogen werden sollen, wurde dem Tree-Explainer neben dem trainierten ML-Modell ebenfalls die Klassenverhältnisse im Testdatensatz übergeben. Die Vorhersagen der Unfallschwere und deren Einflussfaktoren können somit auf einen neuen unausgeglichenen Datensatz angewendet werden. Die berechneten Grundwahrscheinlichkeiten der Klassen im Testdatensatz spiegeln die unterschiedlichen Häufigkeiten der Unfallschwere wider, wobei leichte Verletzungen am häufigsten vorkommen. Diese Basiswerte dienen als Referenzpunkt für die Berechnung der SHAP-Werte und berücksichtigen das Klassenungleichgewicht im Datensatz.

Die SHAP-Werte werden von der Bibliothek im Logit-Raum ausgegeben und für die Interpretation mithilfe der Softmax-Funktion in Wahrscheinlichkeiten umgerechnet:

$$p={\displaystyle \frac{e^{{logit}_k}}{{\sum }_{j=1}^K{e}^{{logit}_j}}}$$

Die Softmax-Funktion ist ein gängiges Verfahren zur Transformation von Logits in Wahrscheinlichkeiten bei Klassifikationsaufgaben (Goodfellow et al., 2016).

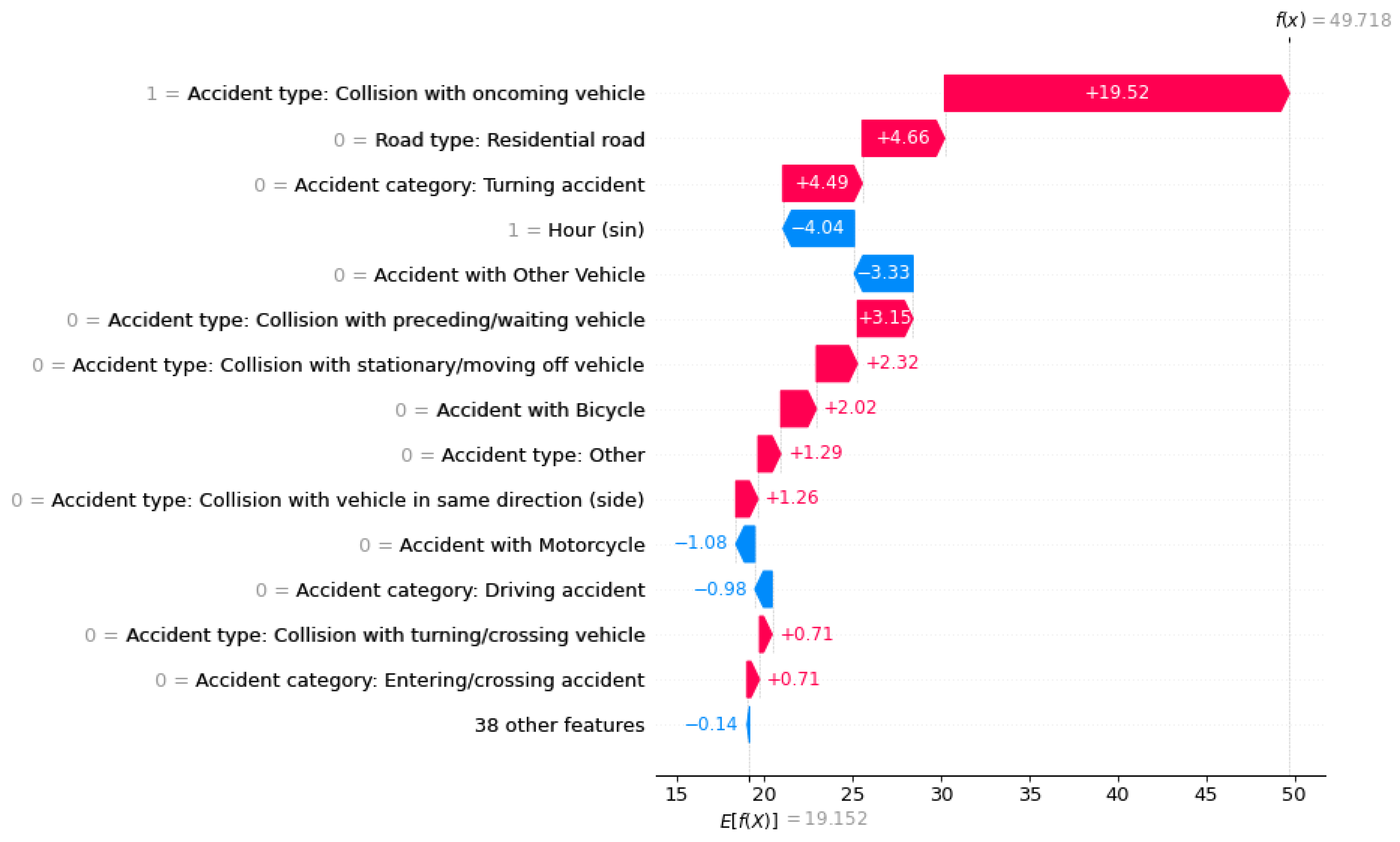
Die SHAP-Werte der kategorialen Features mussten nachbearbeitet werden, da diese in der Vorverarbeitung durch One-Hot-Encoding in mehrere binäre Variablen aufgeteilt wurden (z. B. Unfallart, Unfalltyp, Lichtverhältnis). Dadurch wurde jedem ursprünglichen Feature eine Gruppe einzelner SHAP-Werte zugeordnet – jeweils einer pro Feature-Klasse (siehe Error! Reference source not found.). Das erschwert die Erklärbarkeit, da für ein ursprüngliches Feature nun mehrere Einflussfaktoren vorliegen.

Um dies zu beheben, wurden die SHAP-Werte für jedes ursprüngliche Feature gruppiert und aufsummiert. Dieser Schritt ist aufgrund der Additivitätseigenschaft der SHAP-Werte mathematisch zulässig. Die Zuordnung der Gruppen erfolgte basierend auf der bekannten Kodierungsstruktur und der Reihenfolge der Feature-Matrix. So konnte jedem ursprünglichen kategorialen Feature wieder ein einziger Einflusswert pro Instanz und Zielklasse zugewiesen werden (siehe Error! Reference source not found.).

Die Gesamtsumme aller SHAP-Werte bleibt durch diese Aggregation unverändert und entspricht weiterhin der vorhergesagten Wahrscheinlichkeit. Wichtig ist jedoch, dass der resultierende SHAP-Wert eines Merkmals das Zusammenspiel aller zugehörigen Kategorien abbildet – sowohl deren Vorhandensein als auch das Fehlen der übrigen.

Figure 8. Waterfall-Plot mit Logit-Werten. Vor dem Bearbeitungsschritt der Feature-Addition der kategorialen Features.

Figure 8. Waterfall-Plot mit Logit-Werten. Vor dem Bearbeitungsschritt der Feature-Addition der kategorialen Features.

Figure 9. Waterfall-Plot mit Logit-Werten. Nach dem Bearbeitungsschritt der Feature-Addition der kategorialen Features.

Figure 9. Waterfall-Plot mit Logit-Werten. Nach dem Bearbeitungsschritt der Feature-Addition der kategorialen Features.

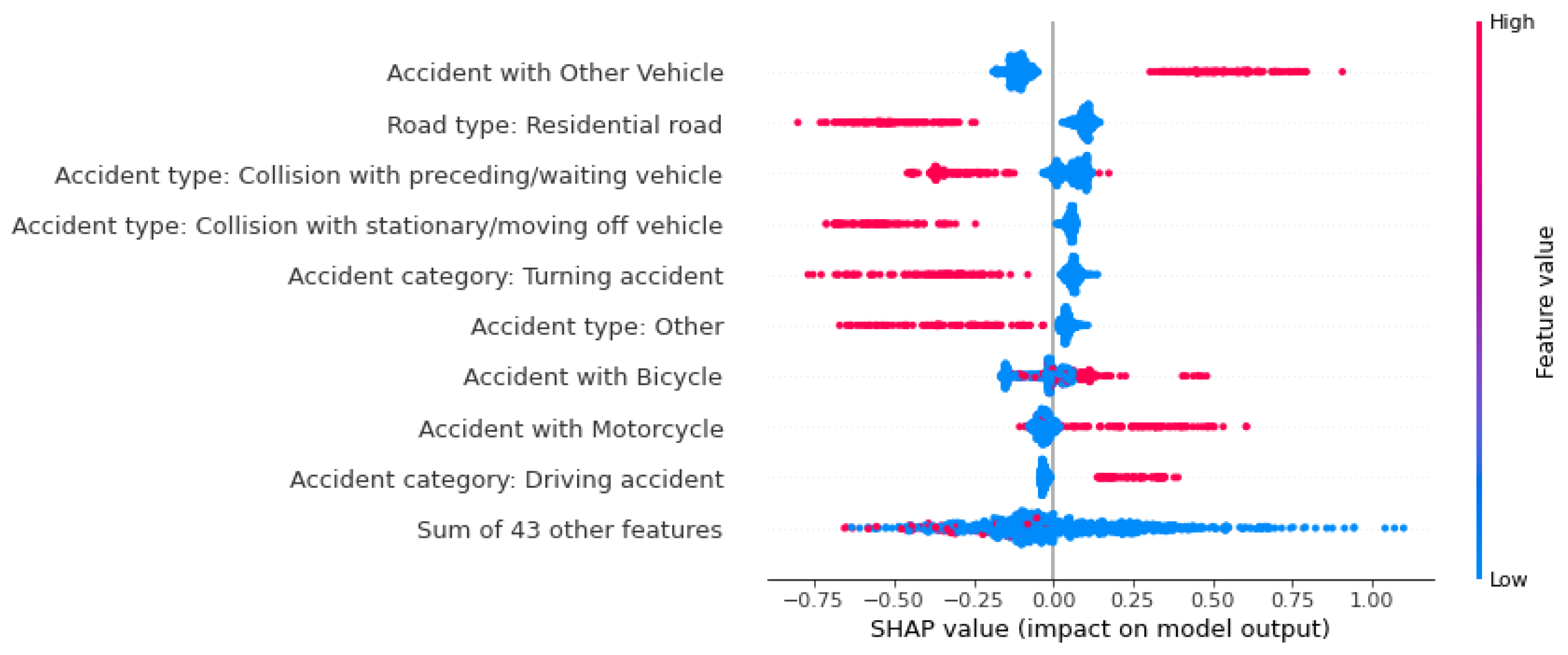
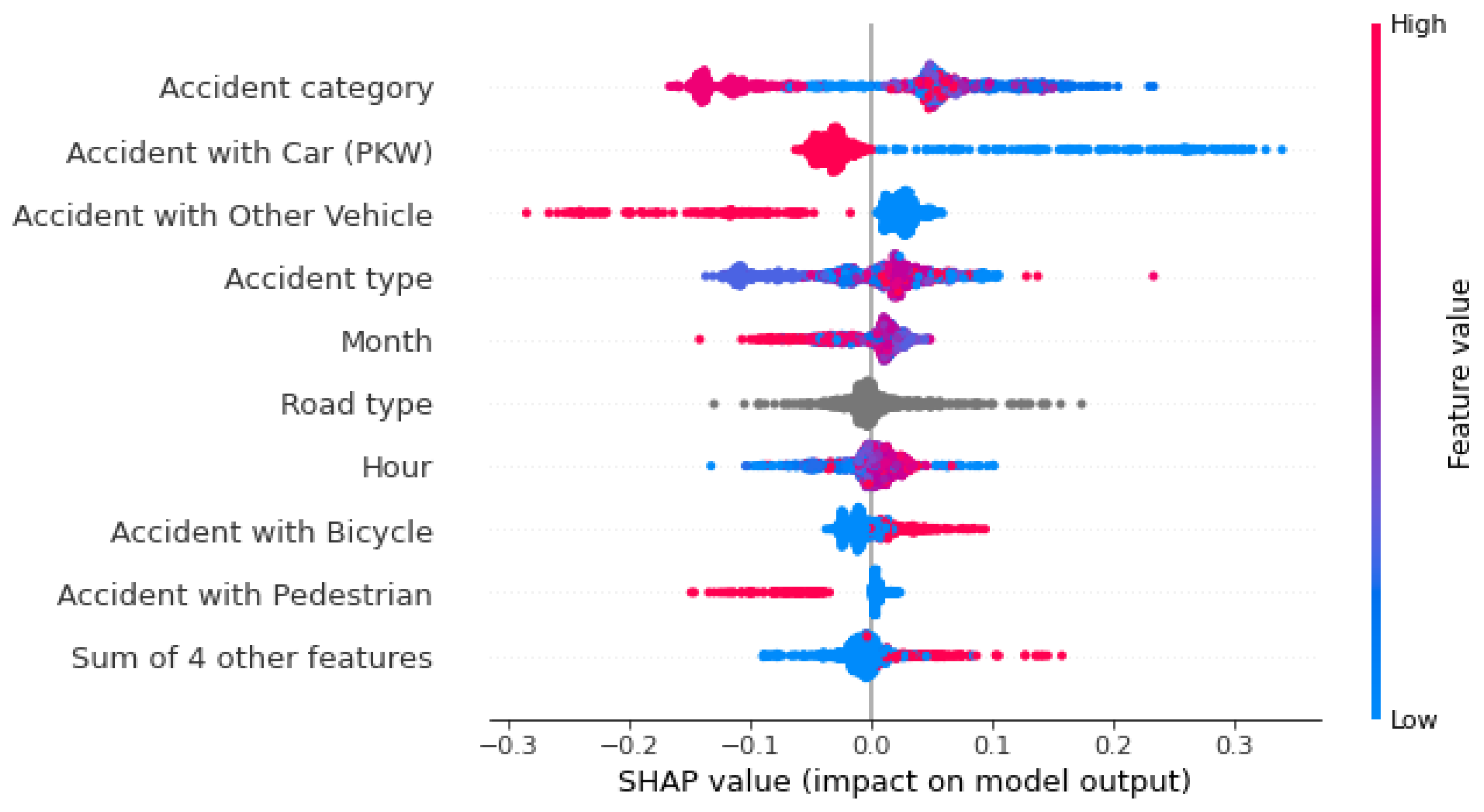
Eine weitere Möglichkeit, die Einflussfaktoren mithilfe der SHAP-Bibliothek zu visualisieren, ist mit dem Beeswarm-Plot. Im Vergleich zu den vorangegangenen Darstellungen handelt es sich hierbei um eine globale Betrachtung der Einflüsse. SHAP kann auch zur globalen Analyse eingesetzt werden, etwa über den Beeswarm-Plot. In Error! Reference source not found., Error! Reference source not found. und Error! Reference source not found. ist jeweils ein Beeswarm-Plot für die drei Unfallschwereklassen dargestellt. Es fällt auf, dass „Unfall mit Sonstigen” das wichtigste Feature für das Modell zur Vorhersage von tödlichen Unfällen ist. Liegt für dieses Feature ein Wert von eins vor, also eine Beteiligung von dem Fahrzeugtyp, wird die Wahrscheinlichkeit für diese Klasse immer erhöht. Dies ist ebenfalls bei einer Fußgängerbeteiligung zu erkennen. Die Straßenklasse „Straße im Wohngebiet“ senkt die Wahrscheinlichkeit dieser Klasse, genauso wie der Feature-Wert der Unfallart von 2 („Zusammenstoß mit vorausfahrendem/ wartendem Fahrzeug“).

Figure 10. Beeswarm-Plot zur globalen Betrachtung von Einflussfaktoren auf die Vorhersage: “Persons killed“.

Figure 10. Beeswarm-Plot zur globalen Betrachtung von Einflussfaktoren auf die Vorhersage: “Persons killed“.

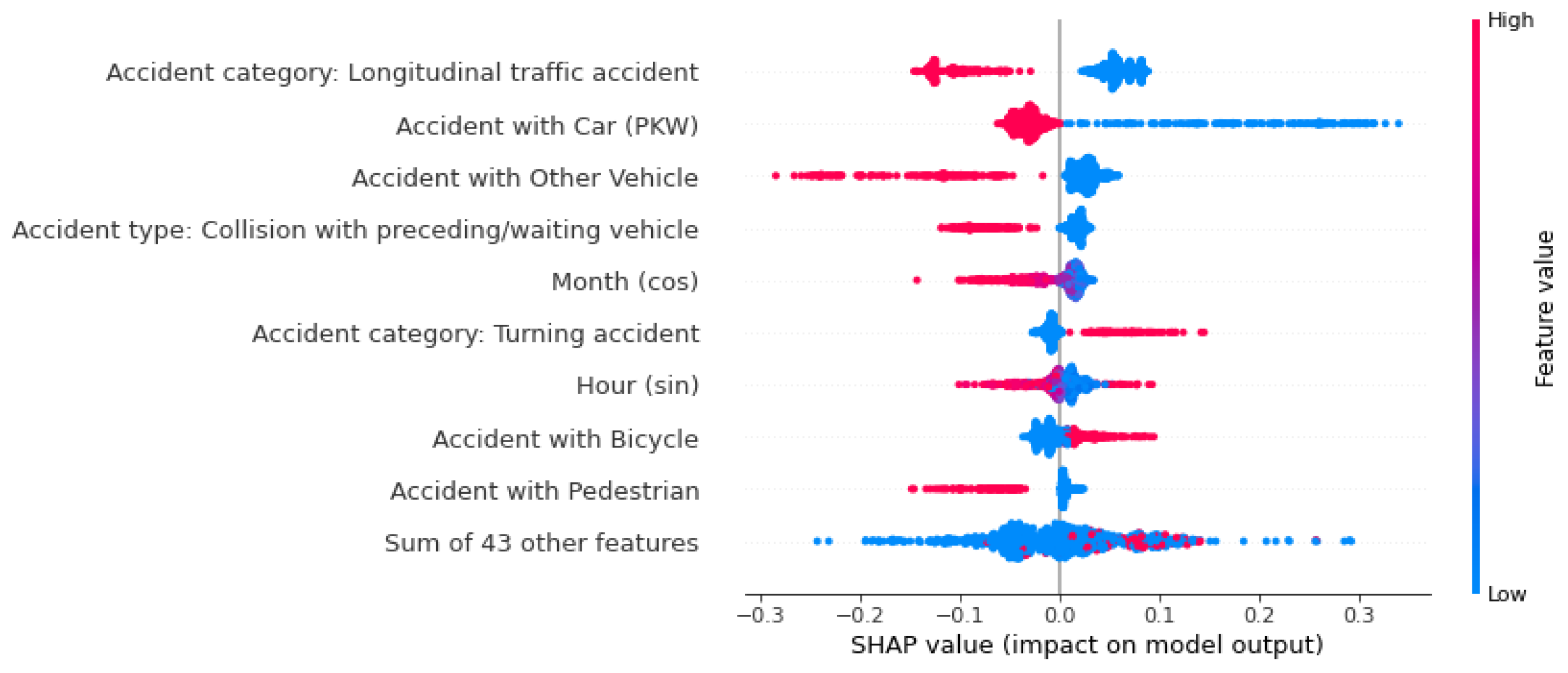
Figure 11. Beeswarm-Plot zur globalen Betrachtung von Einflussfaktoren auf die Vorhersage: Persons seriously injured.

Figure 11. Beeswarm-Plot zur globalen Betrachtung von Einflussfaktoren auf die Vorhersage: Persons seriously injured.

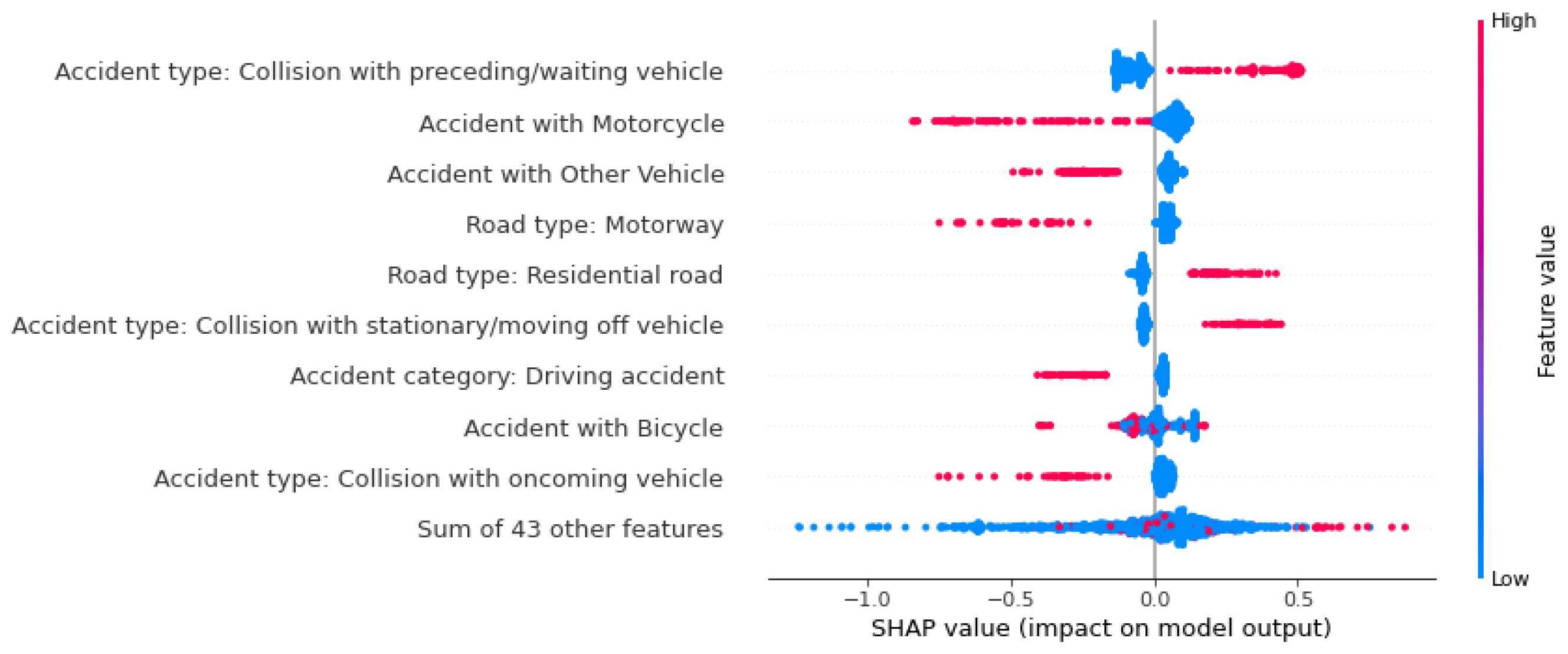
Figure 12. Beeswarm-Plot zur globalen Betrachtung von Einflussfaktoren auf die Vorhersage: Persons slightly injured.

Figure 12. Beeswarm-Plot zur globalen Betrachtung von Einflussfaktoren auf die Vorhersage: Persons slightly injured.

Die Wahrscheinlichkeit, dass ein Unfall als schwerer Unfall vorhergesagt wird, wird vor allem von den Feature-Werten des Unfalltyps 6 („Unfall im Längsverkehr“) und einer Autobeteiligung beeinflusst. Anders als bei den als tödlich vorhergesagten Unfällen ist hier das Nicht-Vorliegen dieser Features für eine Erhöhung der Wahrscheinlichkeit dieser Klasse verantwortlich. In anderen Worten: Ist an einem Unfall kein Auto beteiligt gewesen, erhöht das Modell die Vorhersage-Wahrscheinlichkeit für einen schweren Unfall. Die beteiligten Fahrzeuge beeinflussen vor allem die Vorhersage-Wahrscheinlichkeit für Unfälle mit einem leichten Ausgang. Die Beteiligung von einem Fahrrad, einem Fußgänger, einem Motorrad, oder einem sonstigen Fahrzeug haben alle einen negativen Einfluss auf die Vorhersagewahrscheinlichkeit, genauso wie die Straßenklasse „Autobahn“. Die Unfallart 2 („Zusammenstoß mit vorausfahrendem/ wartendem Fahrzeug“), hat die Wahrscheinlichkeit eines tödlichen Unfalls gesenkt. Für die Vorhersage eines Unfalls mit Leichtverletzten hat dieses Feature den größten positiven Einfluss auf die ML-Modell.

Mit dem Beeswarm-Plot lassen sich somit die Einflussfaktoren in einem ML-Modell gut abbilden. Neben dem absoluten Einfluss wird zusätzlich angegeben, ob ein Feature die Wahrscheinlichkeit nun gesenkt oder erhöht hat. Auch der jeweilige Wert des Features wird hierbei berücksichtigt, was den Vorteil eines Beeswarm-Plots gegenüber einer klassischen Bar-Plot ausdrückt. Denn hier können nur die Wichtigkeit der einzelnen Features für das Modell dargestellt werden, nicht aber der Betrag, der Einfluss des jeweiligen Wertes und die klassenabhängige Einflüsse.

Bei der Betrachtung der Beeswarm-Plots in Error! Reference source not found. fällt jedoch auch auf, dass die vorher angesprochene Zusammenführung der kategorialen Features nicht durchgeführt wurde. Dies hängt damit zusammen, dass das Aufsummieren der SHAP-Werte der einzelnen Feature-Klassen die Betrachtung generalisiert. Manche Feature-Klassen erhöhen die Vorhersage-Wahrscheinlichkeit, andere senken sie. Darüber hinaus sind die Feature-Klassen nominalskaliert, was bedeutet, dass sie keine natürliche Reihenfolge besitzen. Eine höhere Unfalltyp-Klasse muss nicht zwingend einen höheren oder niedrigeren Einfluss auf die Vorhersage haben. Werden die SHAP-Werte der Features mit mehreren Klassen zusammengefasst, hat das zur Folge, dass die Einflüsse der Features nicht mehr durch einen Beeswarm-Plot interpretiert werden können.

Figure 13. Schwierigkeiten die Einflüsse aus einem Beeswarm-Plot auf die tödliche Unfallvorhersage abzulesen, nachdem die SHAP-Werte von einigen Features zusammengefasst wurden.

Figure 13. Schwierigkeiten die Einflüsse aus einem Beeswarm-Plot auf die tödliche Unfallvorhersage abzulesen, nachdem die SHAP-Werte von einigen Features zusammengefasst wurden.

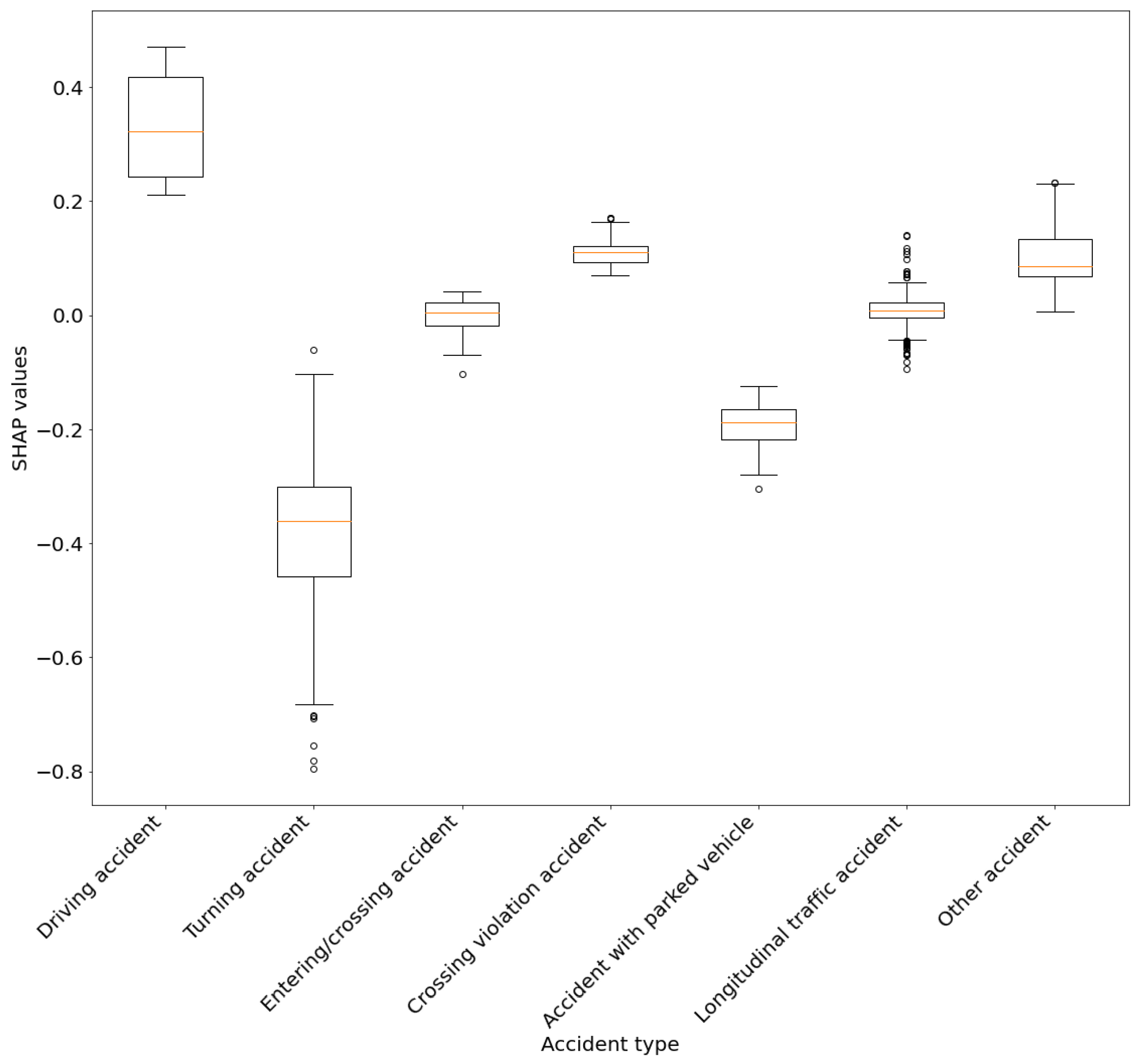
Figure 14. Vergleich der Einflüsse der Klassen des Features Unfalltyp auf die Vorhersagewahrscheinlichkeit von tödlichen Unfällen.

Figure 14. Vergleich der Einflüsse der Klassen des Features Unfalltyp auf die Vorhersagewahrscheinlichkeit von tödlichen Unfällen.

Um die Einflüsse der Feature-Klassen auf eine Unfallklasse zu visualisieren, kann eine Boxplot-Ansicht verwendet werden (siehe Error! Reference source not found.). Hierbei werden beispielsweise die einzelnen Unfalltyp-Kategorien betrachtet und deren durchschnittlicher Einfluss auf die Vorhersagewahrscheinlichkeit, ob ein Unfall als tödlich vorhergesagt wird. Diese Darstellung erlaubt die Einflussfaktoren der Klassen eines einzelnen Features miteinander zu vergleich. Es muss jedoch beachtet werden, dass hier alle Instanzen betrachtet wurden, auch diese, welche von dem Modell nicht als tödliche Unfälle vorhergesagt wurden. Der Ansatz zum Umgang mit kategorialen Features und derer Visualisierung basiert auf den Arbeiten von O’Sullivan (2022).

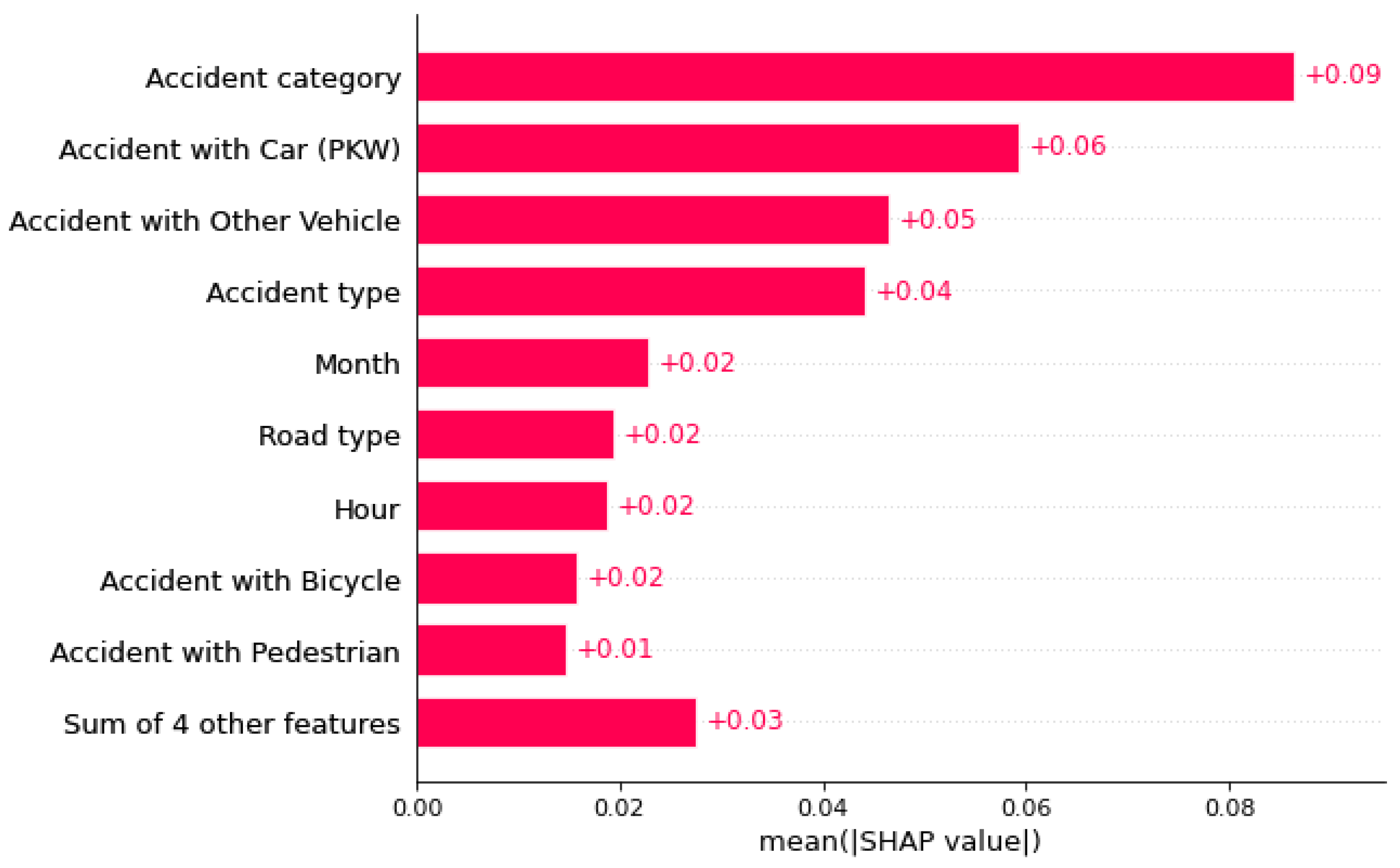
Da der Beeswarm-Plot nach der Zusammenführung der SHAP-Werte nicht mehr sinnvoll interpretierbar ist, wird stattdessen ein Bar-Plot genutzt (siehe Error! Reference source not found.), der die durchschnittlichen absoluten SHAP-Werte je Feature und Unfallklasse übersichtlich darstellt. Diese Darstellung ist weniger detailliert, dafür leichter verständlich.

Im nächsten Kapitel wird ein Ansatz vorgestellt, mit dem semi-globale Einflussfaktoren unter anderem mithilfe von Bar-Plots visualisiert werden. Hierbei soll die Datenmenge unterteilt werden, sodass Bar-Plots für bestimmte Vorhersagen gebildet werden können. Damit können beispielsweise Nutzerfragen beantwortet werden, wie: Welches Feature hat durchschnittlich den größten Einfluss auf das ML-Modell, wenn dieses leichte Unfälle als tödliche Unfälle identifiziert? Dadurch können Klassifikationsergebnisse und Fehlklassifikationen anhand von vielen Instanzen bewertet werden.

Figure 15. Ein Bar-Plot als vereinfachte Darstellung der Wichtigkeiten der Features in der Vorhersage einer Unfallschwere.

Figure 15. Ein Bar-Plot als vereinfachte Darstellung der Wichtigkeiten der Features in der Vorhersage einer Unfallschwere.

5. Results and Discussion

Das erarbeite Konzept soll die im Kapitel 1 aufgestellten Forschungsfragen beantworten. Ziel soll es sein, eine Lösung zu präsentieren, um semi-globale Einflussfaktoren zu berechnen und im nächsten Schritt niedrigschwellig zu vermitteln. Diese Forschungslücke tritt bei der Vermittlung von räumlichen Einflussfaktoren auf. Die prototypische Umsetzung in Form eines Dashboards soll eine mögliche Lösung hierfür präsentieren. Übertragen auf den Use Case sollen die Unfalldaten, die ML-Ergebnisse und die Einflussfaktoren dynamisch für eine tiefergehende Analyse zusammengefasst werden um beispielsweise Fachanwendern wie Straßenplaner, Unfallforscher, ML-Experten oder Verkehrsteilnehmer die Möglichkeit zu eröffnen, die riesige Menge an individuellen ML-Vorhersagen explorativ zu untersuchen oder die Qualität des ML-Modells zu bewerten. Die Vorteile der Georeferenzierung der Unfälle soll genutzt werden, um räumliche Muster aufzuzeigen. Das Dashboard wurde prototypisch für deutsche Analysten entwickelt. Deswegen wird aufkommenden Screenshots nur eine deutsche Version zu sehen sein.

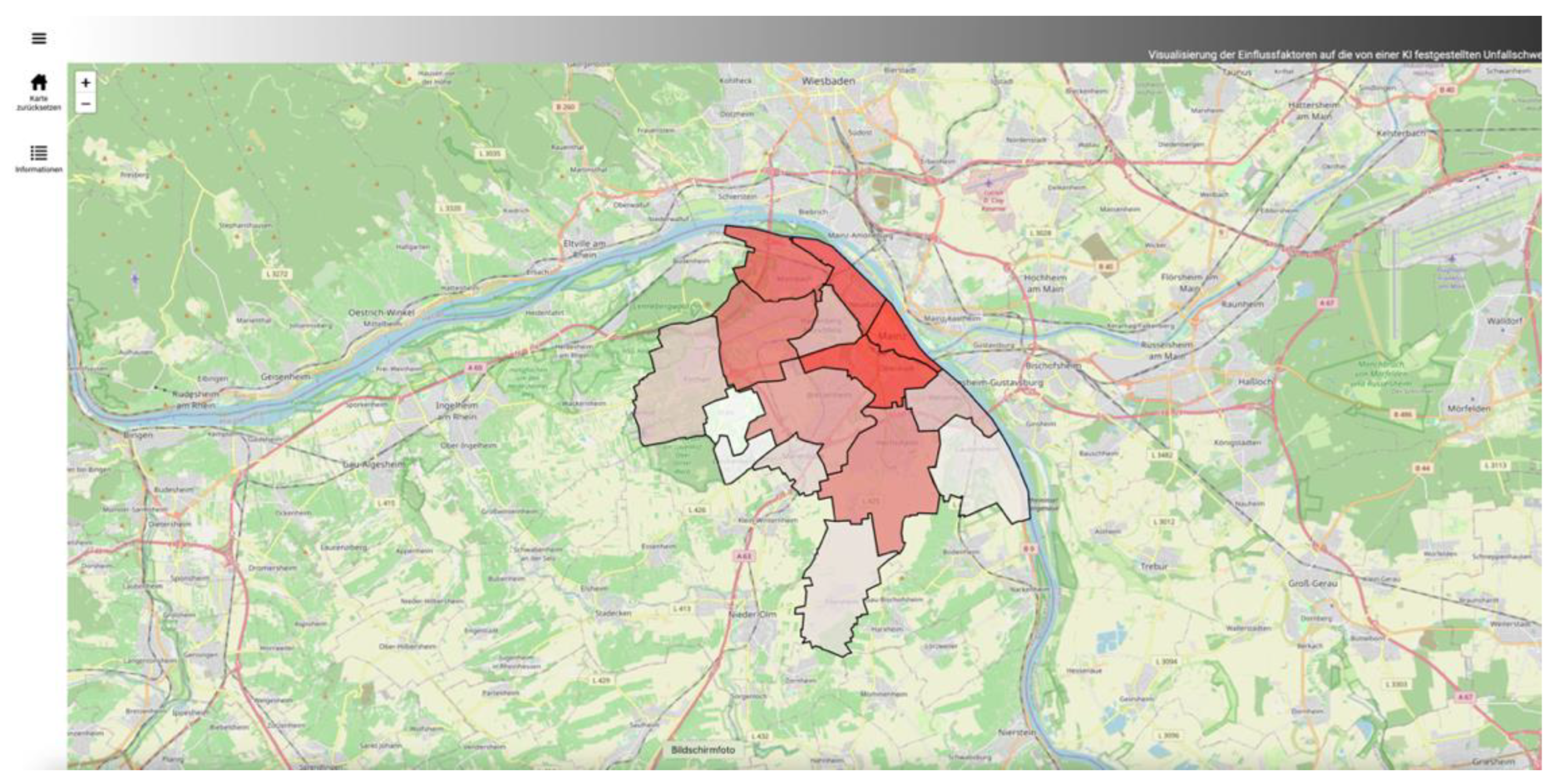
Figure 16. Übersichtskarte im Web-Dashboard. Zu Beginn werden die Mainzer Stadtteile auf einer Karte angezeigt. Durch ein ausklapbares Menü kann ein Nutzer die Daten filtern.

Figure 16. Übersichtskarte im Web-Dashboard. Zu Beginn werden die Mainzer Stadtteile auf einer Karte angezeigt. Durch ein ausklapbares Menü kann ein Nutzer die Daten filtern.

Wie in den Konzept aufgezeigt, werden die Mainzer Unfalldaten nach ihrer räumlichen Lage sortiert. Exemplarisch wurden hierbei die Mainzer Stadtteile verwendet. Weitergehend können auch größere und kleinere Verwaltungseinheiten oder andere sozio-räumliche Begrenzungen verwendet werden, um die Unfalldaten weiter zu unterteilen. Diese räumlichen Einheiten wurden in der Arbeit nicht tiefergehend untersucht, wodurch kleinmaßstäbige Einflüsse, wie gefährliche Verkehrskreuzungen nicht festgestellt werden können. Die aufgeteilten punktuellen Daten können nun auf einer Karte durch flächenhafte Darstellungen visualisiert werden (siehe Error! Reference source not found.). Hierbei können außerdem weiterführende Visualisierungskonzepte genutzt werden, um die Unterschiede in den einzelnen Stadtteilen grafisch herauszustellen. Es wurde in der Arbeit die Anzahl der Unfälle pro Stadtteil und die Vorhersagequalität des Modells anhand von Fehlermaßen pro Stadtteil durch Einfärbungen dargestellt. Hier könnten auch andere Einfärbungen in Abhängigkeit der speziellen Einflussfaktoren denkbar sein, um noch bessere räumliche Vergleiche mithilfe von Karten zu erreichen. Es fällt bei dem Vergleich der Stadtteile auf, dass die im Innenstadtbereich liegenden Gebiete eine weitaus höhere Anzahl an Unfällen vorweisen, dies hat vielmehr mit einem größeren Verkehrsaufkommen, anstatt einer erhöhten Unfallgefahr zu tun. Die Unfallfrequenz sollte als weitere Zielvariable in einem ML-Modell aufgenommen werden, um die Unfallhäufigkeit zusätzlich zu der Unfallschwere angeben zu können. Die Stadtteile sind somit nur bedingt anhand ihrer Anzahl vergleichbar. Darüber hinaus sind die Einflussfaktoren abhängig vom Stadtteil unterschiedlich. Durch die Nutzung eines einzigen ML-Modells werden stadtteilbezogene Eigenschaften nicht berücksichtigt.

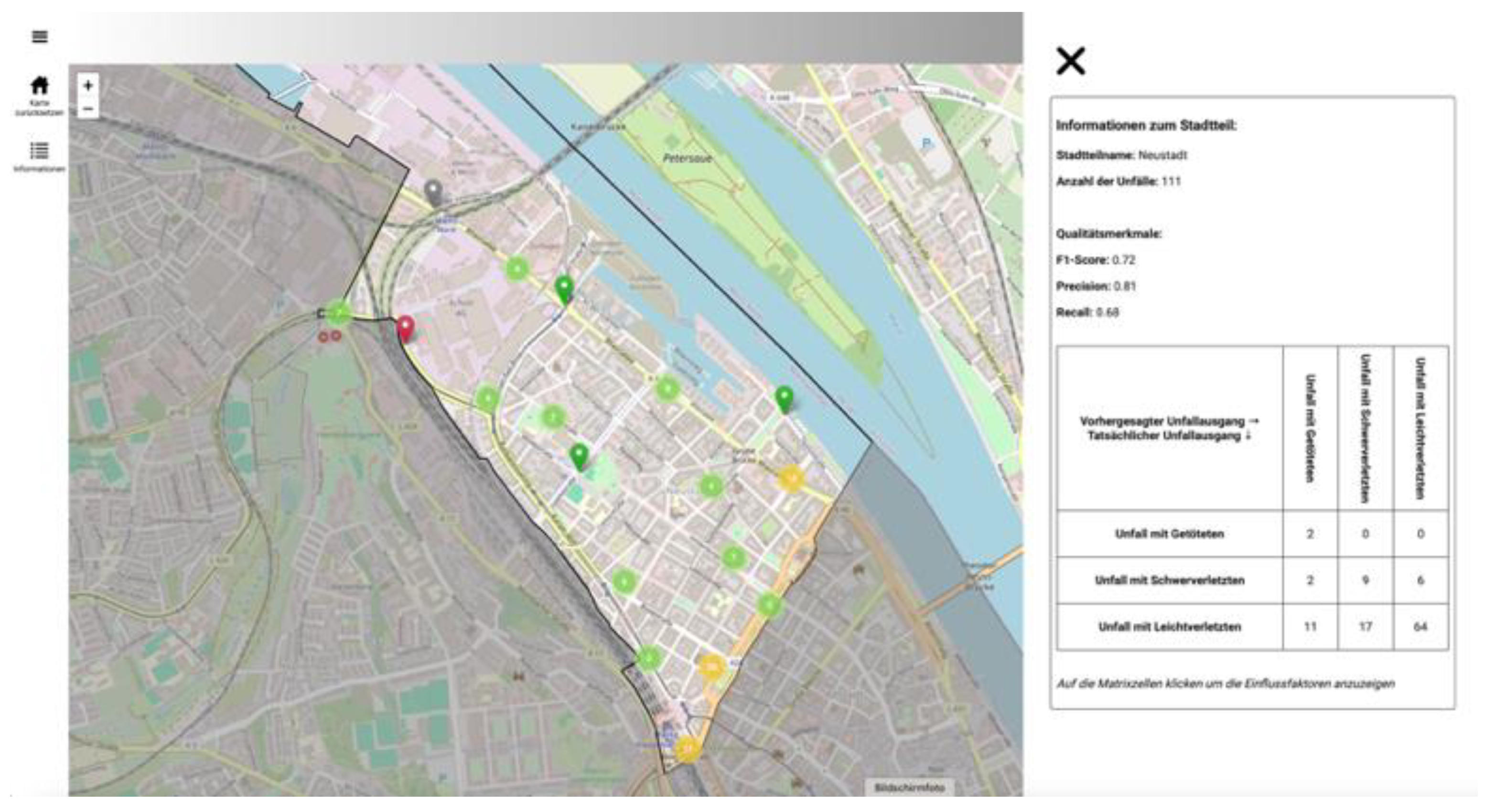
Durch das Klicken auf einen Stadtteil, kann eine dynamische und interaktive Konfusion-Matrix für die ML-Vorhersagen der Unfallschwere der Unfälle im jeweiligen Stadtteil angezeigt werden. Hier werden die vorhergesagten Unfallschweren mit den tatsächlichen Unfallschweren in diesem Stadtteil gegenübergestellt. Somit kann ein Nutzer sich leicht ein Bild machen, wie die Fehlermaße zustande kommen und welche Klassifizierungsfehler das Modell womöglich hat. Eine Stadtteilübersicht aus dem Web-Dashboard ist in Error! Reference source not found. dargestellt.

Figure 17. Die Stadtteilübersicht fasst alle Unfälle in einem Gebiet zusammen (hier Stadtteil Neustadt). Zusätzlich zu der räumlichen Verteilung können die Fehlermaße der im Stadtteil liegenden Unfälle betrachtet werden. Die interaktive Konfusion-Matrix dient zru weiteren Navigation.

Figure 17. Die Stadtteilübersicht fasst alle Unfälle in einem Gebiet zusammen (hier Stadtteil Neustadt). Zusätzlich zu der räumlichen Verteilung können die Fehlermaße der im Stadtteil liegenden Unfälle betrachtet werden. Die interaktive Konfusion-Matrix dient zru weiteren Navigation.

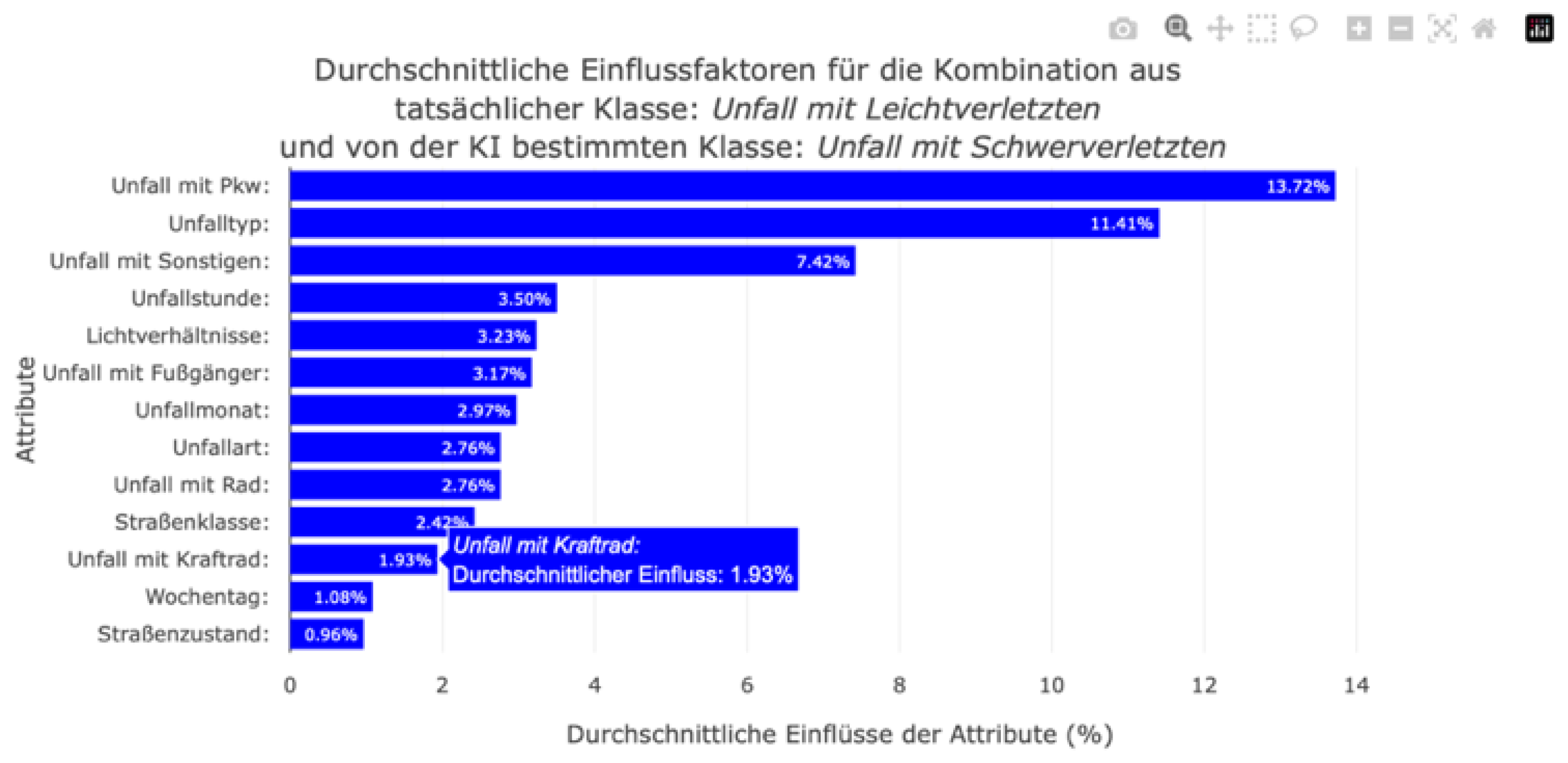
Figure 18. Bar-Plot der Einflussfaktoren im Stadtteil Neustadt für Fehlklassifizierung von Unfällen mit Leichtverletzten, welche jedoch als Unfälle mit Schwerverletzten vorhergesagt wurden.

Figure 18. Bar-Plot der Einflussfaktoren im Stadtteil Neustadt für Fehlklassifizierung von Unfällen mit Leichtverletzten, welche jedoch als Unfälle mit Schwerverletzten vorhergesagt wurden.

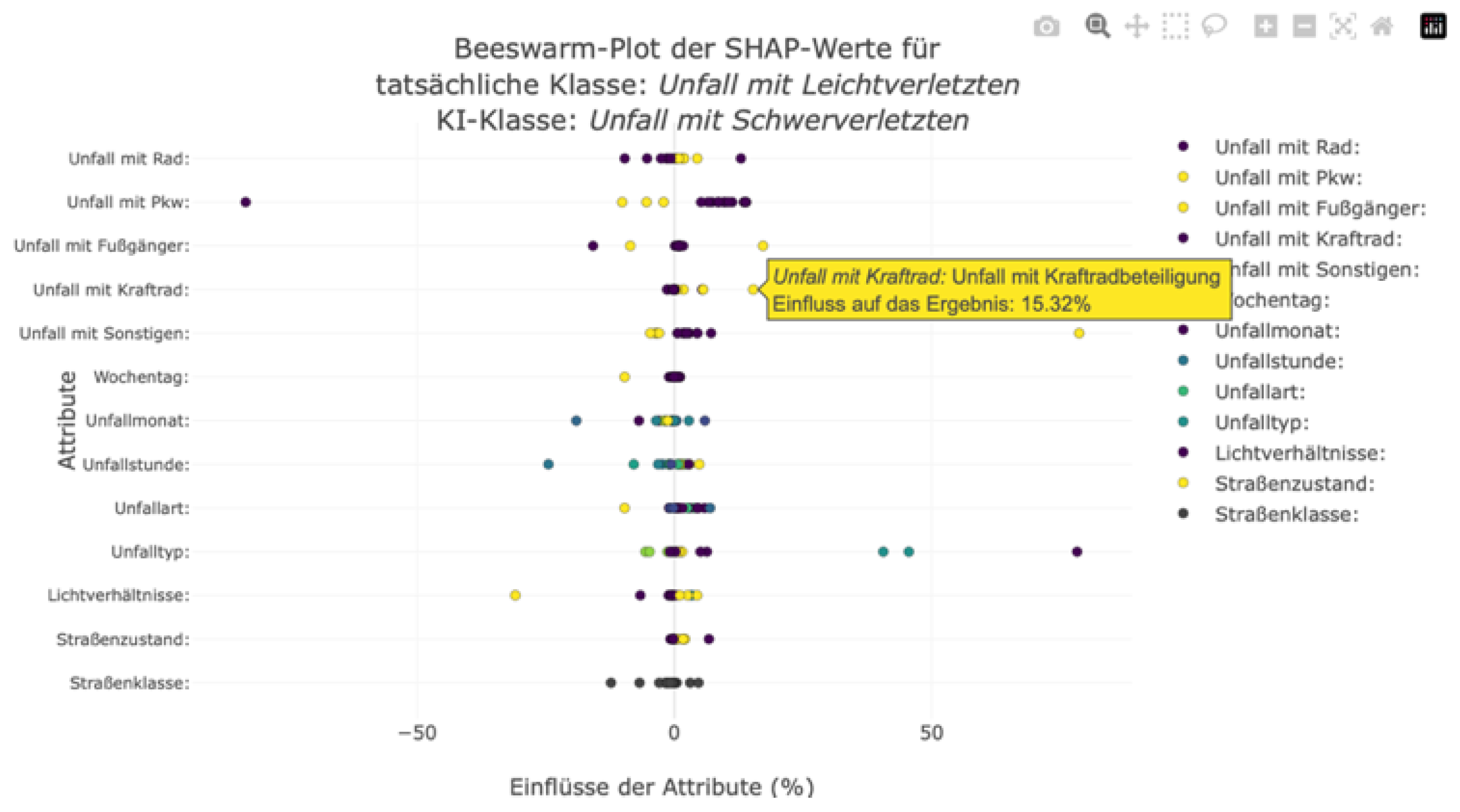
Figure 19. Visualisierung der individuellen Einflussfaktoren im Stadtteile Neustadt mit einem Beeswarm-Plot. Hierbei werden ebenfalls die tatsächlichen und vorhergesagten Klassen berücksichtigt.

Figure 19. Visualisierung der individuellen Einflussfaktoren im Stadtteile Neustadt mit einem Beeswarm-Plot. Hierbei werden ebenfalls die tatsächlichen und vorhergesagten Klassen berücksichtigt.

Mit dem Klicken in eine Zelle der Konfusion-Matrix wird ein Bar-Plot erzeugt, welcher die durchschnittlichen absoluten SHAP-Werte für diese Unfallschwere darstellt. Ein großer Nachteil des Bar-Plots aus der SHAP-Bibliothek war die starke Generalisierung der Daten. Wurde für eine Unfallschwere-Klasse ein Bar-Plot erzeugt, so wurden der durchschnittliche SHAP-Wert eines Features aus allen Instanzen berechnet, selbst wenn der Klassifikator die zu untersuchende Klasse als unwahrscheinlichste Klasse einer Instanz vorhergesagt hat. Darüber hinaus wurden sowohl richtig als auch falsch klassifizierte Instanzen gemeinsam betrachtet. Die Ergebnisse im Bar-Plot wurden also verzerrt dargestellt. Eine differenzierte Untersuchung, welche Features die größten Einflüsse bei fehlerhaften Klassifizierungen hatten, war nicht möglich. Durch das dynamische Berechnen der durchschnittlichen absoluten Einflussfaktoren abhängig von der tatsächlichen und der vorhergesagten Unfallschwere im Web-Dashboard kann ein Nutzer nun die Einflussfaktoren spezifisch abrufen (siehe Error! Reference source not found.). Somit konnten die Nachteile des globalen Bar-Plots entfernt und ein genaueres Bild über die ML-Vorhersage und die Einflussfaktoren gebildet werden. Die durchschnittlichen absoluten SHAP-Werte, welche durch den Bar-Plot dargestellt werden, bilden jedoch nicht ab, ob ein Feature die Vorhersagewahrscheinlichkeit einer Unfallschwere gesenkt oder gestiegen hat. Somit drückt der Bar-Plot vielmehr die Wichtigkeit eines Features in der ML-Vorhersage aus, anstatt eine Auskunft darüber zu geben, wie eine Feature-Wert die individuelle Unfallschwere-Vorhersage beeinflusst hat. Darüber hinaus können die durchschnittlichen Angaben durch sehr große, oder sehr kleine SHAP-Werte in einzelnen Fällen stark verzerrt werden.

Um Nutzern mit einem tieferen Verständnis für die Einflussfaktoren und deren Zusammenhänge eine genauere Betrachtung der Zusammensetzung der im Bar-Plot dargestellten durchschnittlichen absoluten SHAP-Werte geben zu können, wurde zusätzlich ein Beeswarm-Plot integriert. Dieser zeigt die individuellen SHAP-Werte der Instanzen an. Hierbei wird für jedes Feature eine Achse erzeugt, auf der die SHAP-Werte als Punkte markiert werden. Durch das Interagieren mit den einzelnen Punkten kann der jeweilige SHAP-Wert und der ausschlaggebende Feature-Wert angezeigt werden. Somit kann der Nutzer auch die Richtung der Wichtigkeit und die Zusammensetzung der SHAP-Werte nachvollziehen. Die einzelnen Punkte werden, wie in einem typischen Beeswarm-Plot, abhängig von ihrem Feature-Wert farblich markiert. Hierbei wurde auf einen kontinuierlichen Farbverlauf verzichtet, da die nominalskalierten Features keine Sortierung und somit keinen Verlauf aufweisen. Nichtsdestotrotz kann der Nutzer durch diese Hervorhebung mögliche Zusammenhänge zwischen Feature-Wert und SHAP-Wert erkennen. Ein Beispiel ist in Error! Reference source not found. dargestellt. In diesem Diagramm werden die Einflussfaktoren der leichten Unfälle in einem Stadtteil angezeigt, welche fälschlicherweise als schwere Unfälle klassifiziert worden sind. Durch die gemeinsame Betrachtung der Feature-Werte und SHAP-Werte können Muster identifiziert werden, welche das ML-Modell dazu bewegt haben, diese Unfälle falsch zu klassifizieren. Hier ist zu erkennen, dass die Beteiligung eines Kraftfahrrad in einen Unfall die Wahrscheinlichkeit eines schweren Unfalls gesteigert hat. Die fehlende Beteiligung eines Kraftrads in einem Unfall hat die Vorhersagewahrscheinlichkeit dieser Unfallschwere minimal gesenkt. Im Bar-Plot konnte dieser Zusammenhang nicht abgeleitet werden, außerdem war in diesem Diagramm nicht ablesbar, ob die Angabe zur Kraftradbeteiligung die Wahrscheinlichkeit gesenkt oder gestiegen hat (vgl. Error! Reference source not found.). Somit lässt sich aus der Visualisierung der einzelnen SHAP-Werte durch den Beeswarm-Plot ableiten, dass die Beteiligung eines Kraftrades die Vorhersagewahrscheinlichkeit eines schweren Unfalls in diesem Stadtteil steigert. Andere Einflüsse und Zusammenhänge lassen sich analog aus den Diagrammen der Konfusion-Matrix ableiten.

Das entwickelte Konzept ermöglicht eine gezielte Analyse von Unfallmustern auf Stadtteilebene, reduziert die angezeigten Datenmengen und kombiniert interaktive Visualisierungen mit differenzierter Modellbewertung. Durch die Trennung korrekt und falsch klassifizierter Unfälle sowie den Einsatz gängiger Diagrammtypen wird eine transparente und zugleich niedrigschwellige Interpretation der Einflussfaktoren unterstützt.

Neben der Stadtteilbetrachtung der Unfallschweren und deren Einflussfaktoren, können auch die einzelnen Unfälle ebenfalls frei untersucht werden. Somit wird auf die Entdeckungslust des Nutzers gesetzt, sich mit den einzelnen Unfällen zu beschäftigen. Das Dashboard dient bei der Betrachtung der lokalen Einflussfaktoren vielmehr als Visualisierungs- und Navigationswerkzeug, um die Ergebnisse der einzelnen Berechnung darzustellen, anstatt dass es Analysemöglichkeiten bietet.

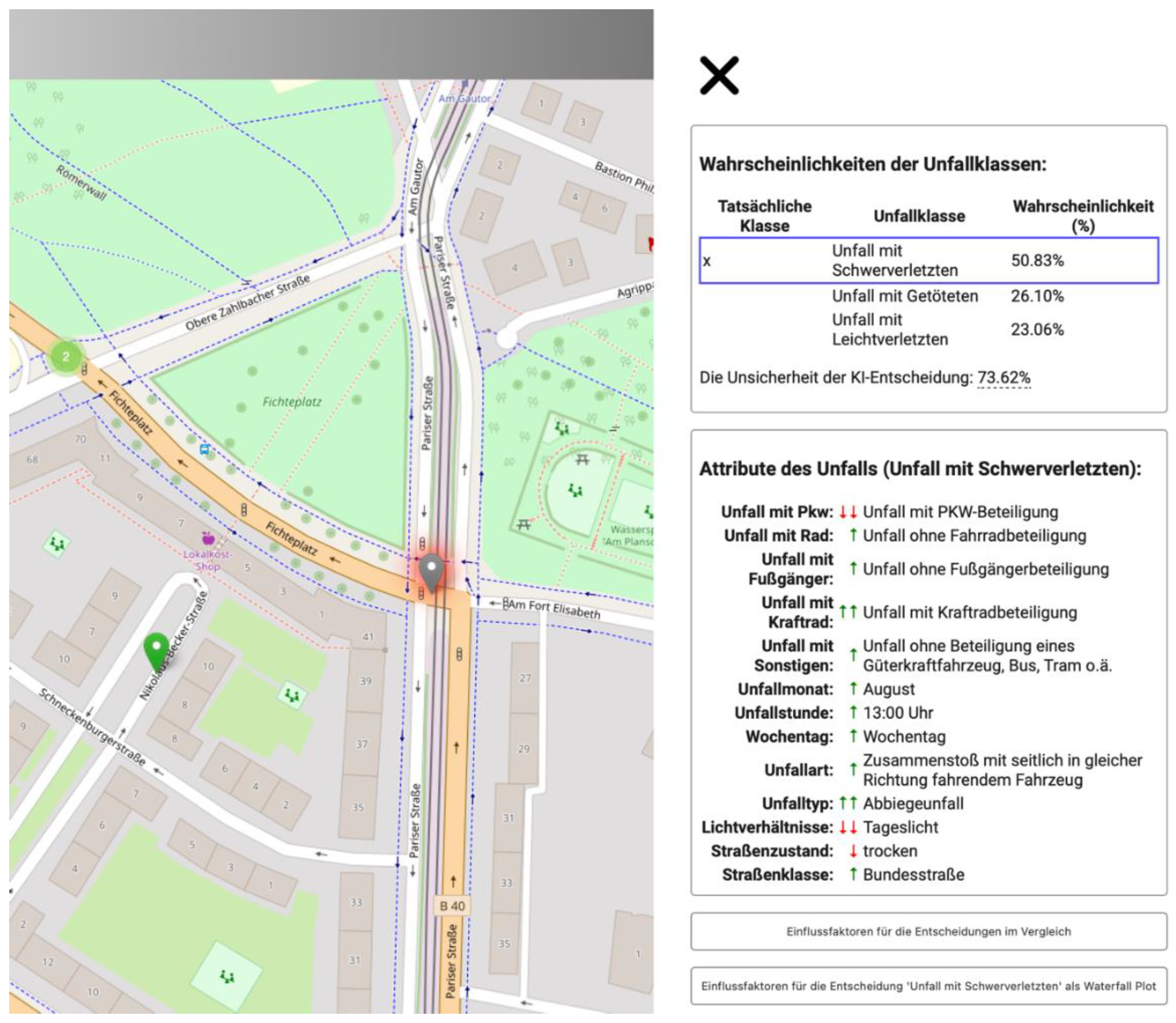
Der entwickelte Prozessablauf zur Ableitung der Einflussfaktoren kann unfallabhängige Aussagen zur Wahrscheinlichkeitsbildung eines ML-Modells geben. Somit enthält jeder Unfall individuelle Angaben, wobei alle Unfälle auf der gleichen Struktur basieren. Hierfür werden die Unfälle eines Stadtteils farblich markiert als Marker dargestellt. Roussel, et al. (2024) haben die Möglichkeiten der kartenbasierten Vermittlung von Einflussfaktoren beschäftigt. Neben der Unfallklasse könnten auf der Karten auch zusätzliche Angaben wie dem einflussreichsten Feature auf die Entscheidung, dem Vergleich zwischen tatsächlicher und vorhergesagter Unfallschwere, oder die Unsicherheit der Vorhersage den Informationsgehalt erhöhen. Durch das Interagieren mit einem Marker lassen sich somit die individuellen Angaben zu einem Unfall anzeigen. Hierbei ist die Unfallschwere als Hauptuntersuchungsmerkmal die wichtigste Angabe. Der Nutzer bekommt in dem Informationsfenster die vom Klassifikator bestimmten Wahrscheinlichkeiten der einzelnen Unfallklassen angezeigt. Neben der Wahrscheinlichkeit der Vorhersage wird hier auch eine Gegenüberstellung mit der tatsächlichen Klasse der Unfallschwere vorgenommen und die Unsicherheit der Vorhersage angegeben. Die umfangreichen Informationen werden tabellenförmig für den angeklickten Marker angezeigt, somit wird die Karte nicht komplexen Informationsvisualisierungen überfrachtet. Trotzdem können die Karte und unfallabhängige Informationen gleichzeitig verwendet und betrachtet werden. Außerdem werden im Informationsfenster die in der Klassifikation verwendeten Features mit ihren jeweiligen Werten aufgelistet. Dadurch kann der Nutzer sich leicht einen Überblick über den Unfall machen. Es können die jeweiligen Angaben aus der Datengrundlage betrachtet werden, somit können Unfälle leicht rekonstruiert werden. Die kodierten Werte in der Datengrundlage wurden durch aussagekräftige Beschreibungen ersetzt, um somit auch Nutzern, die die Unfallstatistik der statistischen Ämter nicht kennen, die Möglichkeit zu geben die unfallbeschreibenden Angaben nachvollziehen zu können.

Figure 20. Visualisierung eines Unfalls mittels Karte und Informationsfenster im Web-Dashboard.

Figure 20. Visualisierung eines Unfalls mittels Karte und Informationsfenster im Web-Dashboard.

Eine weitere Schwierigkeit lag in der niedrigschwelligen Vermittlung der Einflüsse dieser Unfallangaben. Es wurde ein Konzept entwickelt, welches die beispielhafte analysierende Nutzerfrage beantworten sollte: Welchen Einfluss hatten die Lichtverhältnisse zum Unfallzeitpunkt auf die Wahrscheinlichkeit, dass der Unfall mit Schwerverletzten endet?

Einflussfaktoren beschreiben, wie die einzelnen Features die Wahrscheinlichkeit einer Klasse bei der Klassifizierung beeinflusst haben. Diese Einflussfaktoren können positiv oder negativ sein, je nachdem ob sie die Wahrscheinlichkeit einer Unfallschwere für das Modell erhöht oder gesenkt haben. Der Betrag dieser Einflussfaktoren bestimmt, in welchem Maße die Vorhersage beeinflusst wurde. Um den Nutzer niedrigschwellig an die Einflussfaktoren heranzuführen, wurden diese in Form von Symbolen in der Auflistung der Angaben zu einem Unfall neben jedem Feature angegeben. Anstatt den Einfluss in Prozent anzugeben, wurden Pfeile zur Visualisierung der Einflussrichtung genutzt (↓ drückt einen negativen Einfluss auf die Vorhersage aus; ↑ drückt einen positiven Einfluss auf die Vorhersage aus). Diese relative Angabe der Einflüsse vereinfacht die Nachvollziehbarkeit von Einflüssen auf eine ML-Klassifikation. Darüber hinaus werden die Features mit den größten SHAP-Werten, also mit dem betragsmäßig größten Einfluss, mit einem doppelten Pfeil angegeben. Dadurch kann auch ohne Betrachtung der genauen SHAP-Werte ein Nutzer die einflussreichsten Features erkennen.

Dank des dynamische Dashboard können klassenabhängigen lokalen SHAP-Werte vom Nutzer selbst ausgewählt und analysiert werden. Durch die Auswahl einer anderen Unfallklasse werden die Symbole und die Diagramme automatisch aktualisiert. Die Zusammensetzung der Einflussfaktoren des Modells lassen sich somit direkt ablesen und vergleichen. Ein Screenshot aus dem Dashboard ist in Error! Reference source not found. dargestellt.

Figure 21. Waterfall-Plot im Web-Dashboard zur Visualisierung der lokalen Einflussfaktoren auf die Vorhersage: Persons seriously injured.

Figure 21. Waterfall-Plot im Web-Dashboard zur Visualisierung der lokalen Einflussfaktoren auf die Vorhersage: Persons seriously injured.

Figure 22. Decision-Plot im Web-Dashboard zum Vergleich der Einflussfaktoren auf die Unfallklassen.

Figure 22. Decision-Plot im Web-Dashboard zum Vergleich der Einflussfaktoren auf die Unfallklassen.

Die schrittweise Heranführung der Nutzer an immer detaillierte und Umfangreichere Information zu einer lokalen ML-Entscheidung endet in der Vollständigen Darstellung der Waterfall- und Decision-Plots (siehe Error! Reference source not found. und Error! Reference source not found.). Hier können nun alle Werte gleichzeitig betrachtet werden. Hierbei ist jedoch darauf zu achten, dass ein potenzieller Nutzer keine Vorkenntnisse zu Klassifikationen mittels ML hat und deswegen die angegebenen Klassenwahrscheinlichkeiten sowie die SHAP-Werte nicht nachvollziehen kann. Dies könnte im äußersten Fall dazu führen, dass der Nutzer die angegebenen Einflussfaktoren als Wichtigkeit eines Features auf die Unfallschwere in der echten Welt interpretiert. Es wird nicht ausreichend vermittelt, dass die berechneten Einflussfaktoren ausschließlich einen Einfluss auf eine ML-Vorhersage haben, nicht jedoch auf den tatsächlichen Unfallgrund.

Die Arbeit hat sich vorrangig mit der Erstellung eines Konzeptes zur Berechnung und Visualisierung von semi-globalen Einflussfaktoren von räumlichen Datensätzen beschäftigt. Hierbei wurde das Konzept durch einen praktischen Anwendungsfall bestätigt. Durch das Konzept konnten Fehlklassifizierungen leicht identifiziert werden und separate semi-globale Einflussfaktoren berechnet werden. Durch das Dashboard konnte somit analysiert werden, wie die ML-Entscheidung zustande gekommen ist. Dies ermöglicht viele anschließende Untersuchungen, wie die der von den statistischen Ämter des Bundes und der Länder zur Verfügung gestellter Unfalldaten. Es ist durch die im Kapitel 2 vorgestellten Arbeiten bekannt, dass die Unfälle durch relevante Eigenschaften beschrieben werden müssen. Im Zuge der Veröffentlichung wurden Informationen wie beispielsweise das vollständige Datum, Angaben zu den beteiligten Personen (Alter, Geschlecht, Fahrerfahrung) oder mögliche Drogen-/Alkoholeinflüsse entfernt. Andere Angaben wie die Witterungsbedingungen, Anzahl der Beteiligten, Geschwindigkeiten und Straßendaten wurden generalisiert oder zusammengefasst zur Verfügung gestellt. Das Fehlen dieser durch zahlreiche Arbeiten als relevant bewiesenen Einflussfaktoren kann zu einem einfacheren und dadurch auch weniger aussagekräftigeren Modell führen. Wichtige Unfalleigenschaften konnten im Training des ML-Modells nicht beachtet werden. Dadurch entstanden fehlerhafte Zusammenhänge zwischen den Unfalldaten oder Informationslücken in der Unfallbeschreibung. Diese fehlerhaften Zusammenhänge fallen bei der Analyse des Modells mittels SHAP auf. Fehlklassifizierte Unfälle, deren Unfallschwere als tödlich anstatt als leicht angegeben wurden, hatten beispielsweise einen überproportionalen Einfluss des Features „Beteiligung eines sonstigen Verkehrsmittels“ (LKW, Bus, Tram) da überwiegend Kraftfahrzeuge in tödlichen Unfällen beteiligt waren (vgl. Error! Reference source not found.a). Das Modell, welches mit den deutschen Unfalldaten trainiert wurde, kann die Unfallschwere nur anhand der 13 Features zu einem Unfall vorhersagen, somit entstanden Informationslücken in den Daten. Das hatte zur Folge, dass Unfälle mit Schwerverletzten dieselben Features wie Unfälle mit Leichtverletzten hatten. Das Modell war nicht in der Lage mit der geringen Anzahl an Features den Unfall der richtigen Unfallschwere zuzuordnen. Dies konnte durch die hohen Fehlklassifikationen des trainierten ML-Modells nachgewiesen werden. Auch eine Anreicherung mit den frei verfügbaren OSM-Daten muss in diesem Zusammenhang kritisch betrachtet werden. Da OSM auf die Freiwilligkeit der Datenerhebung durch seine Nutzer setzt, ist die Vollständigkeit und Aktualität der Daten nicht qualitativ gesichert. Dies bezieht sich primär auf die Vollständigkeit der Eigenschaften einer Straße, nicht auf das Straßennetz. Es muss genauer untersucht werden, ob weitere Angaben die Qualität noch weiter verbessern können. Hierbei zählen neben zusätzlichen Straßeneigenschaften vor allem Wetterdaten und Angaben zu den Unfallbeteiligten. Hierbei müssen ebenfalls effiziente Ansätze zur Datenanreicherung entwickelt und neue Informationsquellen erschlossen werden. Außerdem muss überprüft werden, ob ein ML-Modell die größer Datenkomplexität abdecken kann, denn es wurde festgestellt, dass das MLP-NN keine verbesserten Vorhersagen mit der zusätzlichen Straßenklasse als Feature im Training mit sich brachte. Gegebenenfalls müssen andere ML-Modelle auf ihre Nutzbarkeit zur Vorhersage der Unfallschwere untersucht werden.

Das Verwenden der unausgeglichenen Unfalldaten führte schnell zu der Notwendigkeit nach einem Sampling-Ansatzes. Im Vergleich zu anderen Arbeiten wurde hier eine Kombination aus Under- und Oversampling verwendet. Zwar konnte erst dadurch eine Unterscheidung zwischen den einzelnen Unfallklassen vorgenommen werden, das Zusammenspiel aus den wenigen kategorialen Features und der Ungelichverteilung führt trotzdem noch zu schlechteren Ergebnissen als andere Arbeiten, wie Satu et al. (2018) oder (Pourroostaei Ardakani et al., 2023). Dies könnte auch mit dem konservativen „macro Averaging” zusammenhängen das als Berechnungsgrundlage angenommen wurde.

Dank des Dashboard ist es möglich tiefere Untersuchungen zu Einflussfaktoren auf ML-Entscheidungen festzustellen. Hierbei ermöglichten die räumlichen und thematischen Aufteilungen der Daten eine hochwertige Untersuchung der Unfalldaten und des Klassifikators.

6. Conclusions and Future Work

In diesem Kapitel fasst die Ergebnisse der Arbeit zusammen und ein Ausblick auf die kommenden darauf aufbauenden arbeiten gegeben.

Conclusion

In dieser Arbeit wurde ein Konzept vorgestellt, mit der es ermöglicht werden sollte tiefergehende Einblicke in räumliche Einflussfaktoren zu erhalten. Mit den sogenannten semi-globalen Einflussfaktoren können auf einfache Weise die Entscheidungsfindung von ML-Modellen offengelegt werden. Mit dem Konzept sollte eine Möglichkeit eröffnet werden, räumliche Daten mithilfe von Geo-Glocal XAI-Techniken untersuchbar zu machen.

Das Konzept wurde an einem praktischen Anwendungsfall getestet. Dieser hat sich mit der datenbasierten Analyse von Unfalldaten beschäftigt. Das Ziel war das Ableiten von Einflussfaktoren, welche die Schwere von Verkehrsunfällen verändern. Diese komplexen Informationen zu einem Unfall sind stark voneinander abhängig. Zusammenhänge zwischen den Unfallangaben und der Unfallschwere sind nur schwer abzuleiten. Diese Datengrundlage eignete sich optimal, um das Konzept anzuwenden.

Ein XGBoost-Klassifikator wurde trainiert, um die Unfallschwere auf Basis der Unfallangaben vorherzusagen. ML-Modelle erkennen datenbasiert Muster, die menschlichen Analysen bislang entgangen sein könnten. Um die komplexen Zusammenhänge dieser ML-Entscheidungen anschließend nachvollziehbar zu machen, kam der XAI-Ansatz SHAP zum Einsatz. Die daraus abgeleiteten semi-globalen Einflussfaktoren ermöglichten die Identifikation räumlicher Muster. Eine interaktive Konfusionsmatrix half dabei, die typischen Schwächen globaler SHAP-Visualisierungen zu umgehen. Die detaillierten Einflussfaktoren liefern die Grundlage für Unfallforscher, Stadt- und Verkehrsplaner sowie ML-Experten für zukünftige Analysen und Modellverbesserungen. Ein Dashboard mit intuitiven Visualisierungen und Kartenintegration stellt die Ergebnisse nutzerfreundlich dar und erlaubt eine transparente Navigation durch die Einflussfaktoren.

Future Work

Die Arbeit beschäftigte sich mit der räumlichen Visualisierung der semi-globalen Einflussfaktoren in Form von Diagrammen. Eine dynamische Karte in Verbindung mit einer interaktiven Konfusion-Matrix ermöglichten hierbei die Analyse. In zukünftigen Arbeiten sollten weitere Möglichkeiten untersucht werden, wie Einflussfaktoren für komplexe Vorhersagen wie die der Unfallschwere räumlich dargestellt werden könnten. Hierbei müssen die Vorteile einer kartengestützten Visualisierung identifiziert und Konzepte der Visualisierung erstellt werden. Somit können die umfangreichen Daten auch flächendeckend und leicht verständlich mit Karten dargestellt werden. Hierbei könnten beispielweise die lokalen SHAP-Wert eines Features beziehungsweise die Features mit dem größten Einfluss auf eine ML-Vorhersage auf ein Straßennetz bezogen werden. Dieses kodierte Straßennetz kann für weitere Analysen genutzt werden, da die darin enthaltenen Informationen eine Grundlage bieten würden, um räumliche Verteilungen von Einflussfaktoren zu identifizieren. Neben der Verteilung könnten somit auch die regionale Einflüsse einzelner Features räumlich dargestellt werden. Dadurch können weitere Untersuchungen durchgeführt werden: „In welchen Teilen der Stadt wir die Wahrscheinlichkeit eines schweren Unfall durch eine Fahrradbeteiligung gesteigert, in welchen wird sie verringert?“. Die Übertragbarkeit dieser Ansätze auf die Unfallschwere in Mainz war in dieser Arbeit jedoch nur bedingt umsetzbar. Die größte Schwierigkeit war die räumliche Verteilung der Unfälle in Mainz. Bereiche in der Innenstadt werden sehr stark von vielen Unfällen beeinflusst, wohingegen Unfälle im Außenbereich der Stadt einen sehr großen Einflussradius besitzen würden.