Proof of the Riemann Hypothesis

1. Introduction

1.1. Background and Problem Setting [1,2,3,4,5]

Formulation of the Riemann Hypothesis (RH)

For the complex variable $s=\sigma +it$,

$$\zeta \left(s\right)=\sum _{n=1}^{\infty }{n}^{-s}(\Re s>1)$$

is extended by the usual analytic continuation to the whole complex plane (except for the pole at $s=1$), and we use the completed form

$$\xi \left(s\right):=\frac{1}{2}s(s-1){\pi }^{-s/2}\Gamma \left(\frac{s}{2}\right)\zeta \left(s\right).$$

The function $\xi \left(s\right)$ is entire (of order $\le 1$) and satisfies the functional equation $\xi \left(s\right)=\xi (1-s)$. Let $\rho$ be a nontrivial zero lying in the critical strip $0<\Re s<1$; then

$$\left(\mathbf{RH}\right)\Re \rho =\frac{1}{2}.$$

The purpose of this paper is to present the above statement concerning the distribution of the zeros of $\xi$ as an equivalent framework via two distinct routes: the Weil-type positivity and the Herglotz (m-function) routes. For the latter, the scope is extended to the Generalized Riemann Hypothesis (GRH$\left(\pi \right)$) for the completed L-function $\Lambda (s,\pi )$ of a self-dual $GL\left(d\right)$-type general L-function (see §8 and §10 for details).

Framework for General L-Functions (Outline)

For a self-dual $GL\left(d\right)$-type L-function $L(s,\pi )$, the associated completed form $\Lambda (s,\pi )$ contains the analytic conductor $Q_{\pi }$ and Archimedean factors, and satisfies the functional equation $\Lambda (s,\pi )={\epsilon }_{\pi }\Lambda (1-s,\pi )$ with $|{\epsilon }_{\pi }|=1$. For the set of nontrivial zeros ${\rho }_{\pi }$,

$$\mathbf{GRH}\left(\pi \right)\Re {\rho }_{\pi }=\frac{1}{2}$$

is the object of study (for the axiomatic framework and normalization, see §10.1).

Test Space and Bilinear Form Used in This Paper (Preview of Their Roles)

We adopt the Fourier conventions

$$\widehat{f}\left(\lambda \right)={\int }_{\mathbb{R}}f\left(t\right)e^{-it\lambda }dt,(f*g)\left(t\right)={\int }_{\mathbb{R}}f\left(u\right)g(t-u)du,\tilde{f}\left(t\right)=f(-t)$$

(the consistency with the Poisson/Hilbert formulas will be confirmed in the relevant sections of the main text). In v1.1, for even, real Schwartz functions, we adopt

$${\mathcal{F}}_{log}:=\left\{f\in \mathcal{S}\left(\mathbb{R}\right)(\mathrm{even},\mathrm{real}):{\int }_{\mathbb{R}}{\left|\widehat{f}\left(\lambda \right)\right|}^{2}log\left(2+\left|\lambda \right|\right)d\lambda <\infty \right\}$$

as the basic test space (rigorously defined in §8). With the “height measure” in the critical strip

$${\mu }_{\xi }:=\sum _{\rho }{\delta }_{\Im \rho }(\mathrm{counting}\mathrm{multiplicity}),$$

we define

$$Q_{\xi }\left(f\right):=\langle {\mu }_{\xi },f*\tilde{f}\rangle =〈{\mu }_{\xi },{\left|\widehat{f}\right|}^2〉,f\in {\mathcal{F}}_{log}.$$

Then, by the Weil equivalence,

$$\begin{array}{|c|}\hline Q_{\xi }\left(f\right)\ge 0(\forall f\in {\mathcal{F}}_{log})⟺\mathrm{RH}\\ \hline\end{array}$$

holds (see §8.4). In the first half of this paper (§6–§8), starting from the small-bandwidth test functions

$$A_{\eta }:=\{\varphi \in \mathcal{S}\left(\mathbb{R}\right)(\mathrm{even},\mathrm{real}):\mathrm{supp}\widehat{\varphi }\subset [-\eta ,\eta ]\},\eta <log2,$$

we initiate from the small-bandwidth equivalence (agreement between the operator side and the arithmetic side) to extend $Q_{\xi }\ge 0$ to ${\mathcal{F}}_{log}$ (by densification), and combine this with the equivalence theorem to conclude RH (§8.3–§8.4).

Two Routes (Placement in the Main Text)

• Weil Positivity Route (§6–§8): Starting from the small-bandwidth agreement $(\eta <log2)$ between the operator side and the arithmetic side in the explicit formula arranged as a distribution, we densify $Q_{\xi }\left(f\right)\ge 0$ ($f\in A_{\eta }$) as $\eta \uparrow log2$ and $A_{\eta }\nearrow {\mathcal{F}}_{log}$. By restating the known Weil equivalence theorem ($Q_{\xi }\ge 0\iff$ RH) and combining, we arrive at the main theorem RH.
• Herglotz Route (§10): Constructing the operator-side $m_L^{\left(\Phi \right)}$ and the arithmetic-side $M_{\pi }^{\left(\Phi \right)}$ via a finite-bandwidth window $\Phi$, we prove agreement on the whole plane from Poisson smoothing and the uniqueness of the Herglotz representation. From self-adjointness and the positivity of the Nevanlinna measure, we deduce the real-axis nature of poles and establish GRH$\left(\pi \right)$ as the main theorem. RH is recovered as the special case of $\zeta$ ($\xi$).

Appendices, Conventions, and Reproducibility

The global conventions for the Fourier transform, boundary values, Cayley transform, and the regularized determinant ${det}_2$ used in this paper are consolidated in the appendices, so that the assumptions, normalizations, and coefficient correspondences on which each chapter’s statements depend can be referenced in an auditable form. In particular, the choice of small bandwidth ${\eta }_0<log2$, the finite part (normalization of distributions), and constants in the Riemann–von Mangoldt type main term are unified via correspondence tables in the appendices and cross-references with the main text.

1.2. Main Results of This Paper (Summary) [1,2,3]

This paper reaches the Riemann Hypothesis (RH) and the Generalized Riemann Hypothesis (GRH$\left(\pi \right)$) for self-dual $GL\left(d\right)$-type L-functions via two routes: Weil-type positivity and Herglotz (m-function). Under the notation fixed in §Section 1.1 (in particular, the test space ${\mathcal{F}}_{log}$ and the bilinear form $Q_{\xi }$), the main conclusions are summarized in the following three points.

(A) Main Theorem on RH (Weil Route; Conclusion of §8)

The Weil-type bilinear form $Q_{\xi }\left(f\right)$ on ${\mathcal{F}}_{log}$ is always nonnegative, and by combining with the known “Weil equivalence theorem,” RH is concluded:

$$\begin{array}{|c|}\hline \forall f\in {\mathcal{F}}_{log}\Rightarrow Q_{\xi }\left(f\right)\ge 0⟺\mathrm{RH}\\ \hline\end{array}$$

(Theorem 8.19 in §8.3 establishes $Q_{\xi }\ge 0$, and by combining with Theorem 8.21 (equivalence theorem) in §8.4, we obtain the Main Theorem on RH = Theorem 8.23.) For the construction of $Q_{\xi }$ and the definition of ${\mathcal{F}}_{log}$, see §8.2–§8.3.

(B) Main Theorem on RH (Herglotz Route; Conclusion of §8)

From the construction of the m-function using a finite-bandwidth “window” $\Phi$ and from Poisson smoothing / uniqueness of the Herglotz representation, we prove the equality of windowed m-functions$m_L^{\left(\Phi \right)}\equiv -{\xi }^{\prime }/\xi$. Through the analysis of its zeros and poles (Stieltjes inversion and pole distribution), we exclude non-real poles and reach RH (§8.6–§8.7; the final conclusion coincides with the Main Theorem on RH in §8). This route shares the same small-bandwidth equivalence → uniqueness principle as (A) and is mutually reinforcing.

(C) Generalization (Self-dual $GL\left(d\right)$-type L-functions; Conclusion of §10)

Under the general axiomatic framework ((AL1)–(AL5) in §10.1), the generalized bilinear form $Q_{\pi }$ on ${\mathcal{F}}_{log}$ is always nonnegative (Theorem 10.38), and by the Weil equivalence theorem (generalized form),

$$\begin{array}{|c|}\hline \forall f\in {\mathcal{F}}_{log}\Rightarrow Q_{\pi }\left(f\right)\ge 0⟺\mathrm{GRH}\left(\pi \right)\\ \hline\end{array}$$

holds (Theorem 10.39). At the same time, in the Herglotz route (§10.6–§10.7), GRH$\left(\pi \right)$ is obtained from the equality of windowed m-functions$M_{\pi }^{\left(\Phi \right)}$ and the reality of poles (Theorem 10.35). Thus, the two systems, Weil / Herglotz, close consistently for both the $\xi$ case and the general $\Lambda (s,\pi )$ case.

(D) Immediate Application to Specific Classes

The four classes — Dirichlet ($d=1$), Dedekind of number fields, Hecke characters, and self-dual $GL\left(2\right)$ newforms (elliptic modular / Maaß) — satisfy the axioms (AL1)–(AL5) of §10.1 (Proposition 10.43). Therefore, the above main theorems (Theorem 10.35 / 10.39) apply immediately, and GRH$\left(\pi \right)$ holds within the discussion of this chapter alone (Corollary 10.44).

(E) Robustness (Error Budget and Tolerances)

We organize the reduction of bandwidth ($\eta \uparrow log2$), evaluation of endpoint contributions, order control of ${det}_2$, and minimization of assumptions for the uniqueness principle, and visualize the allowable error from three aspects: small bandwidth / large bandwidth / generating functions (§8.5 and §10.10). Dependencies of constants in implementation (conductor $Q_{\pi }$, Archimedean factors, vanishing orders at endpoints, etc.) are consolidated in correspondence tables (appendix).

(F) Summary of This Section (Correspondence with Chapter Structure)

(A)–(B) provide RH in the conclusion of §8 (Theorem 8.23), and (C)–(D) provide GRH$\left(\pi \right)$ in the conclusion of §10 (Theorem 10.35 / 10.39 and Proposition 10.43 / Corollary 10.44). (E) is the integration of robustness in §8.5 and §10.10, ensuring the portability of the overall strategy (small-bandwidth equivalence → densification / uniqueness → Weil / Herglotz).

1.3. Proof Strategy (Overview of Two Routes) [1,2,6]

This paper constructs in parallel two distinct routes — Weil-type positivity and Herglotz (m-function) — each leading to RH (the $\xi$ case), and further to GRH$\left(\pi \right)$ (general case) for general self-dual $GL\left(d\right)$-type $\Lambda (s,\pi )$. These are connected by a common core of small-bandwidth equivalence and the uniqueness principle, while prime finite sums and endpoint contributions that appear in the large bandwidth regime are absorbed and controlled within the framework of the regularized determinant ${det}_2$ and generating functions. Below, the inputs, outputs, and key points are stated explicitly.

(I) Weil Positivity Route: Composition of $Q\ge 0$ and the Equivalence Theorem (§6–§8)

First, for the finite-bandwidth test functions

$$A_{\eta }:=\{\varphi \in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even},\mathrm{real}:supp\widehat{\varphi }\subset [-\eta ,\eta ]\},0<\eta <log2,$$

we establish small-bandwidth equivalence between the operator side and the arithmetic side (§6). Then, through the limiting process $\eta \uparrow log2$ and dominated convergence (including evaluation of the finite part), we densify to ${\mathcal{F}}_{log}$ (defined in §8.2) to obtain

$$Q_{\xi }\left(f\right):=〈{\mu }_{\xi },f*\tilde{f}〉=〈{\mu }_{\xi },{\left|\widehat{f}\right|}^2〉\ge 0(\forall f\in {\mathcal{F}}_{log})$$

(§8.3). Finally, we restate the Weil equivalence theorem (within the framework of this paper) and combine:

$$Q_{\xi }\left(f\right)\ge 0(\forall f\in {\mathcal{F}}_{log})⟺\mathrm{RH}$$

to conclude RH (§8.4).

Input/Output:

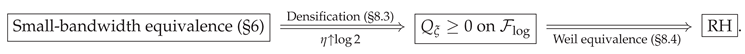
(II) Herglotz Route: Equality of Windowed m-functions and Reality of Poles (§8H, §10.6–§10.7)

Fix a finite-bandwidth “window” $\Phi$ (time-side convolution kernel $W_{\Phi }=\check{\Phi }*{\check{\Phi }}^{\sim }$), and construct the operator-side Weyl–Titchmarsh type m-function $m_L^{\left(\Phi \right)}$ and the arithmetic-side Herglotz function $M^{\left(\Phi \right)}$ via the zero measure $\mu$. By combining the small-bandwidth equivalence of §6 with the uniqueness principle of §8.1–§8.2, we show that the two agree on the whole plane up to a polynomial difference, and remove this difference from the asymptotics at infinity. Through Herglotz property (positivity of the Nevanlinna measure), we deduce the reality of poles and obtain RH (the $\xi$ case) / GRH$\left(\pi \right)$ (general case).

Input/Output:

$$\begin{array}{|c|}\hline \mathrm{Small}-\mathrm{bandwidth}\mathrm{equivalence}\left(\text{§}6\right)+\mathrm{Uniqueness}\left(\text{§}8.1\text{§}8.2\right)\\ \hline\end{array}⟹\begin{array}{|c|}\hline m_{\mathrm{op}}^{\left(\Phi \right)}\equiv M_{\mathrm{arith}}^{\left(\Phi \right)}\\ \hline\end{array}$$

$$⟹\begin{array}{|c|}\hline \mathrm{Poles}\mathrm{are}\mathrm{on}\mathrm{the}\mathrm{real}\mathrm{axis}\\ \hline\end{array}⟹\begin{array}{|c|}\hline \mathrm{RH}/\mathrm{GRH}\left(\pi \right)\\ \hline\end{array}.$$

(III) Extension to General (Self-dual) $GL\left(d\right)$ and Consistency of the Two Routes (§10)

For self-dual $GL\left(d\right)$ types satisfying the general axioms (AL1)–(AL5) (§10.1), the Weil route shows the equivalence of $Q_{\pi }\ge 0$ and GRH$\left(\pi \right)$ (§10.8), and the Herglotz route shows the reality of poles from equality of windowed m-functions (§10.6–§10.7). Both routes are connected by a single skeleton: small-bandwidth equivalence ⇒ large-bandwidth difference (prime finite sum + endpoint term) ⇒${det}_2$ coefficient identification ⇒ Herglotz/Weil (including generating functions and functional calculus in §10.3–§10.5). Dirichlet / Hecke / Dedekind / self-dual $GL\left(2\right)$ satisfy the axioms (Proposition 10.43), and by Theorem 10.35 (Herglotz) or Theorem 10.39 (Weil), GRH$\left(\pi \right)$ holds from the discussion within this chapter alone (Corollary 10.44).

(IV) Common Core and Error Management (§6.4, §8.1–§8.2, §10.10, Appendix)

• Small bandwidth $\eta <log2$ and endpoint $\eta =log2$: In the small bandwidth regime, prime finite sums vanish (except for the $p=2$ endpoint), and endpoint contributions are explicitly controlled by the half-rule (incorporated into the remainder if necessary).
• Uniqueness principle: Serves as the key to lift from family-uniform vanishing of the shrunken bandwidth family and small disk agreement to agreement on the whole domain.
• ${det}_2$ and generating functions: Constrain large-bandwidth differences in both order and coefficient, and provide the uniform bounds needed for m-function identification and transport of Q.
• Robustness: Integrates error budgets from the three aspects — small bandwidth / large bandwidth / generating functions — and makes constant dependencies explicit (conductor $Q\left(\pi \right)$, vanishing order at endpoints, Weyl error, order of ${det}_2$).

(V) Summary (Relation to the Whole Paper)

(I) combines positivity in §8.3 (Theorem 8.19) and the equivalence theorem in §8.4 (Theorem 8.21) to reach RH (Theorem 8.23); (II) provides m-function equality ⇒ reality of poles ⇒ RH/GRH$\left(\pi \right)$ in §8H and §10.6–§10.7; (III) connects §10.8 (Weil route) and §10.6–§10.7 (Herglotz route) via the same skeleton, and (IV) guarantees its portability and error management.

1.4. Technical Essentials and Notation [2,6,7]

In this section, we fix in advance the conventions, symbols, and basic objects used throughout the paper. We collectively define the Fourier conventions, test spaces (finite-bandwidth family $A_{\eta }$ and basic space ${\mathcal{F}}_{log}$), the bilinear form Q, the Herglotz (m-function) / Cayley phase, and the regularized determinant ${det}_2$. Each item will be restated and refined in later rigorous sections (§6–§10), but here we present them in a minimally self-contained form to facilitate back-and-forth referencing.

Fourier Conventions and Basic Operations

We unify the Fourier transform, convolution, and reflection as

$$\widehat{f}\left(\lambda \right)={\int }_{\mathbb{R}}f\left(t\right)e^{-it\lambda }dt,(f*g)\left(t\right)={\int }_{\mathbb{R}}f\left(u\right)g(t-u)du,\tilde{f}\left(t\right)=f(-t)$$

(1)

(the inverse transform is denoted by ${\mathbb{F}}^{-1}$, adopting the normalization consistent with (1)). Unless otherwise stated, test functions are assumed to be “even and real.” Global auxiliary conventions (Poisson/Hilbert kernels, boundary values, continuous connection of phases, etc.) are consolidated in the appendix.

Finite-Bandwidth Family $A_{\eta }$ and Basic Test Space ${\mathcal{F}}_{log}$

For bandwidth $0<\eta <log2$, we define

$$A_{\eta }:=\left\{\varphi \in \mathcal{S}\left(\mathbb{R}\right)(\mathrm{even},\mathrm{real}):supp\widehat{\varphi }\subset [-\eta ,\eta ]\right\}$$

(2)

(small bandwidth). Also, we define the basic test space ${\mathcal{F}}_{log}$ by

$${\mathcal{F}}_{log}:=\left\{f\in \mathcal{S}\left(\mathbb{R}\right)(\mathrm{even},\mathrm{real}):{\int }_{\mathbb{R}}{\left|\widehat{f}\left(\lambda \right)\right|}^{2}log\left(2+\left|\lambda \right|\right)d\lambda <\infty \right\}$$

(3)

The bandwidth cutoff is taken using a smooth even cutoff $m_{\eta }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$, setting ${\widehat{f}}_{\eta }:=m_{\eta }\widehat{f}$ and $f_{\eta }:={\mathbb{F}}^{-1}{\widehat{f}}_{\eta }$ (so $f_{\eta }\in A_{\eta }$). $A_{\eta }$ becomes dense in ${\mathcal{F}}_{log}$ as $\eta \uparrow log2$ (see §8).

Zero Measure and Bilinear Form Q

From the imaginary parts of the nontrivial zeros $\rho ={\displaystyle \frac{1}{2}}+i\gamma$ of $\xi$, define ${\mu }_{\xi }:={\sum }_{\rho }{\delta }_{\gamma }$, and from the imaginary parts of the zeros of the completed form $\Lambda (s,\pi )$ associated with a self-dual $GL\left(d\right)$-type $\pi$, define ${\mu }_{{\Xi }_{\pi }}$ (counting multiplicity; the generalized finite part is taken according to the convention in the main text). For any $f\in {\mathcal{F}}_{log}$, define

$$Q_{\xi }\left(f\right):=〈{\mu }_{\xi },f*\tilde{f}〉=〈{\mu }_{\xi },{\left|\widehat{f}\right|}^2〉,Q_{\pi }\left(f\right):=〈{\mu }_{{\Xi }_{\pi }},{\left|\widehat{f}\right|}^2〉$$

(4)

(where $\langle ·,·\rangle$ denotes the duality between distributions and test functions). As a property of closure under small bandwidth, if $f\in A_{\eta }$ then $f*\tilde{f}\in A_{\eta }$. In this paper, through small-bandwidth equivalence in §6 and densification in §8, we establish $Q\ge 0$ and combine it with the Weil equivalence to obtain RH/GRH (§8, §10).

Windowed m-function and Cayley Phase

For a finite-bandwidth “window” $\Phi$, define the time-side convolution kernel by

$$W_{\Phi }:=\check{\Phi }*\tilde{\check{\Phi }}(\check{\Phi }:={\mathbb{F}}^{-1}\Phi )$$

(5)

On the operator side, we construct the Weyl–Titchmarsh type m-function $m_L^{\left(\Phi \right)}$, and on the arithmetic side, the Herglotz function $M_{\pi }^{\left(\Phi \right)}$ based on the zero measure (§8, §10), and prove their equality from small-bandwidth equivalence + uniqueness principle. Boundary values are written as $M(t+i0)$ for the nontangential limit from the upper half-plane, and the Cayley transform

$$S\left(t\right)={\displaystyle \frac{1-iM(t+i0)}{1+iM(t+i0)}}=e^{-i\varphi \left(t\right)}$$

(6)

defines the phase $\varphi$ (jump by $\pi$ at poles; the phase is extended monotonically by continuously connecting the principal value).

Regularized Determinant ${det}_2$

For a self-adjoint operator K of Hilbert–Schmidt class, define the regularized determinant by

$${det}_2(I-zK):=\prod _j(1-z{\lambda }_j)e^{z{\lambda }_j}$$

(7)

where $\left\{{\lambda }_j\right\}$ are the eigenvalues (Weierstrass factor of genus 1). Its derivative is

$${\partial }_{z}log{det}_2(I-zK)=-\sum _j{\displaystyle \frac{{\lambda }_j}{1-z{\lambda }_j}}+K$$

(8)

(the normalization includes $-K$), from which order $\le 2$ follows. In §7, we present the consistency between the zero distribution of ${det}_2$ and the Weyl main term / HS condition, and the design of upper bounds (shrinking bandwidth family).

Small-Bandwidth Endpoints and Management of Endpoint Terms

The difference at the bandwidth endpoint $\eta$ is decomposed into “prime finite sum + endpoint term” (§10.1). For smooth windows ($\Phi \in C_c^{\infty }$), endpoint terms vanish by vanishing conditions of arbitrary order, and even for piecewise smooth windows they are boundedly controlled by vanishing of endpoint values and higher derivatives (constants depend on the conductor and the endpoint order). This endpoint management is essential for transfer from small bandwidth $\eta <log2$ to large bandwidth (densification / uniqueness).

Remarks (Summary of Symbols)

$\widehat{·}$: Fourier, $\tilde{f}$: reflection, $\check{\Phi }$: inverse transform, ${\mathcal{F}}_{log}$: (3), $A_{\eta }$: (2), $Q_{\xi },Q_{\pi }$: (4), $W_{\Phi }$: (5), $S=e^{-i\varphi }$: (6), ${det}_2$: (7)–(8). Hereafter, these symbols are used consistently with the same normalization.

1.5. Scope of Application [3,8,9,10,11,12,13]

The main theorems of the two routes in this paper (Weil positivity / Herglotz) apply to self-dual $GL\left(d\right)$-type L-functions satisfying the axioms (AL1)–(AL5) in §10.1 (analytic continuation, functional equation, Euler product, normalization of Archimedean factors, and good behavior of the conductor). Here we list the representative classes actually treated in this paper and the key points to be confirmed for application (see §10.8–§10.10, Proposition 10.43, Corollary 10.44 for details). Notation and conventions follow §Section 1.4.

(i) Riemann $\zeta$ and Its Completion $\xi$ ($d=1$, Basic Example)

The completed form

$$\xi \left(s\right)=\frac{1}{2}s(s-1){\pi }^{-s/2}\Gamma \left(\frac{s}{2}\right)\zeta \left(s\right)$$

satisfies (AL1)–(AL5) and is self-dual. In §8, from small-bandwidth equivalence ⇒ densification we obtain $Q_{\xi }\ge 0$, and by combining with the Weil equivalence (§8.4) we conclude RH (Theorem 8.23). In the Herglotz route as well, we arrive at the same conclusion from equality of windowed m-functions and reality of poles (§8.6–§8.7).

(ii) Dirichlet L ($d=1$, Real (Self-Conjugate) Characters)

For a primitive real Dirichlet character $\chi$,

$$\Lambda (s,\chi )={\left({\displaystyle \frac{q}{\pi }}\right)}^{(s+\kappa )/2}\Gamma \left({\displaystyle \frac{s+\kappa }{2}}\right)L(s,\chi )(\kappa \in \{0,1\})$$

is self-dual and satisfies (AL1)–(AL5). Therefore, by the main theorem in §10,

$$Q_{\pi }\ge 0⟺\mathrm{GRH}\left(\pi \right)(\pi \leftrightarrow \chi )$$

holds (Theorem 10.39), and GRH$\left(\pi \right)$ also follows from the Herglotz route (Theorem 10.35). For non-self-conjugate characters (complex $\chi$), since in this paper the statements are made under the self-duality assumption, we refer, when necessary, to standard reductions such as self-dualization by $\pi \oplus \tilde{\pi }$ or symmetric square, etc. (see §10.9).

(iii) Dedekind ${\zeta }_K$ of a Number Field K ($d=1$, Special Case of Hecke Characters)

The completed form

$$\Lambda (s,{\zeta }_K)=Q_K^{s/2}\prod _{j=1}^d{\Gamma }_{\mathbb{R}}(s+{\mu }_j){\zeta }_K\left(s\right)$$

is self-dual and fits (AL1)–(AL5) (here $Q_K$ is the conductor from the discriminant, and ${\Gamma }_{\mathbb{R}}$ is the Archimedean factor determined by the combination of real and complex embeddings). Hence by the main theorem in §10, $\mathrm{GRH}\left({\zeta }_K\right)$ follows (Proposition 10.43, Corollary 10.44).

(iv) Hecke Characters ($d=1$, Self-Conjugate Unitary Idele Class Characters over Number Fields)

For a unitary Hecke character $\omega$ (self-conjugate), the associated $L(s,\omega )$ has a completed form $\Lambda (s,\omega )$ that is self-dual and satisfies (AL1)–(AL5). Thus both Theorem 10.35 and Theorem 10.39 apply, and GRH$\left(\pi \right)$ ($\pi \leftrightarrow \omega$) is established within this chapter.

(v) Self-Dual $GL\left(2\right)$ Newforms (Automorphic Forms: Holomorphic / Maaß)

For a self-dual automorphic representation $\pi$ of level N with trivial central character (holomorphic newform of weight k or Maaß newform), the standard L-function

$$\Lambda (s,\pi )=Q_{\pi }^{s/2}\prod _{j=1}^2{\Gamma }_{\mathbb{R}}(s+{\mu }_j)L(s,\pi )$$

satisfies (AL1)–(AL5). In the Weil route, $Q_{\pi }\ge 0\iff \mathrm{GRH}\left(\pi \right)$ (Theorem 10.39); in the Herglotz route, from equality of windowed $M_{\pi }^{\left(\Phi \right)}$ and the reality of poles, we obtain GRH$\left(\pi \right)$ (Theorem 10.35).

(vi) Error / Constant Dependence and Appendix References

In any class, contributions from bandwidth endpoints, the degree of the conductor $Q_{\pi }$ and Archimedean factors, the order estimates of ${det}_2$, and the vanishing order in Poisson smoothing appear in the error constants. This paper summarizes the integration of errors in §10.10, and correspondence tables of constants and normalizations are consolidated in the appendix.

Summary

Each of the classes (i)–(v) satisfies the assumptions of Proposition 10.43, and by Corollary 10.44, GRH$\left(\pi \right)$ follows immediately from the discussion within this chapter alone. The $\zeta$ case (i) coincides with the main theorem on RH in §8, and for general self-dual $GL\left(d\right)$ ($d\ge 2$) the two routes in §10 complete the proof.

1.6. Organization of This Paper

This paper is structured around two main pillars: the Weil positivity route ($Q\ge 0\Rightarrow$ RH/GRH) and the Herglotz (m-function) route (equality of windowed m-functions ⇒ reality of poles ⇒ RH/GRH). The roles of each chapter and their contributions to the two routes are as follows (the notation and conventions fixed in §1 are common to all chapters, and the appendices centrally manage reference tables and normalizations).

§2 (Foundations: Conventions, Distributions, Kernels)

We organize the minimal tools of distribution theory and the conventions for Fourier/Poisson/Hilbert, and fix the framework for treating the explicit formula as a distribution. We standardize the window $\Phi$ and convolution kernel, finite part (principal value / finite part), and the method of taking boundary values, providing a common base language for subsequent small-bandwidth equivalence and m-function construction.

§3 (Distributional Form of the Explicit Formula and Preparation for Small Bandwidth)

We rewrite prime sums and zero measures in the same distributional framework, and for families of finite-bandwidth test functions prepare the decomposition “difference from large bandwidth = prime finite sum + endpoint term.” This decomposition serves as the input for small-bandwidth equivalence in §6 and as groundwork for absorption via ${det}_2$ in §7.

§4 (Operator Side I: Convolution Operators and Regularization)

We bring convolution operators obtained from finite-bandwidth kernels into the Hilbert–Schmidt class, and establish the framework of the regularized determinant ${det}_2$. We present Weierstrass factorization, order estimates, consistency between the Weyl main term and ${det}_2$, and introduce a mechanism on the generating function side to constrain difference terms appearing in the large-bandwidth regime.

§5 (Operator Side II: m-Functions and the Uniqueness Principle)

We construct the Weyl–Titchmarsh type windowed m-function$m^{\left(\Phi \right)}$, and via the Herglotz representation and the Cayley transform (phase $\varphi$), prepare the analytic structure compatible with reality of poles. At the same time, we establish the uniqueness principle based on small-disk agreement and family-uniform vanishing, providing the logical core for m-function identification in §8 and §10.

§6 (Small-Bandwidth Equivalence)

We prove the small-bandwidth agreement ($\eta <log2$) between the operator side and the arithmetic side. We make explicit the half-rule for endpoint contributions and the disappearance of prime finite sums (except $p=2$), positioning this as the starting point of $Q\ge 0$ in the Weil route and as the origin of m-function equality in the Herglotz route.

§7 (${det}_2$, Weyl, and Upper Bound Design)

We give the consistency between the zero distribution of ${det}_2$ and the Weyl main term, and design uniform upper bounds for shrinking-bandwidth families. This shows that differences (prime finite sum + endpoint term) arising in large bandwidth can be absorbed on the generating function side, and prepares the framework for the error budget needed for densification / uniqueness in §8 and §10.

§8 (The $\xi$ Case: Main Theorem on RH)

We define the basic space ${\mathcal{F}}_{log}$ and, combining the small-bandwidth equivalence of §6 with the upper bounds of §7, establish $Q_{\xi }\ge 0$ (Theorem 8.19). By combining with the known Weil equivalence (Theorem 8.21), we obtain the Main Theorem on RH (Theorem 8.23). In parallel, we complete the Herglotz route in the $\xi$ case (equality of windowed m⇒ reality of poles), showing that the two routes converge to the same point.

§9 (Conclusions and Guidelines: Overview of Robustness and Applications)

We organize the integration of errors from the three aspects of small bandwidth / large bandwidth / generating functions, and visualize constant dependencies (conductor, endpoint vanishing order, order of ${det}_2$).

We also provide an overview of the application policy toward §10 for Dirichlet / Hecke / Dedekind / self-dual $GL\left(2\right)$, serving as a bridge from the ζ case (§8) to the general case (§10).

§10 (Generalization: Self-Dual $GL\left(d\right)$-Type L-Functions)

Under axioms (AL1)–(AL5), in the Weil route we have $Q_{\pi }\ge 0\iff \mathrm{GRH}\left(\pi \right)$ (Theorem 10.39), and in the Herglotz route we deduce the reality of poles from equality of windowed $M_{\pi }^{\left(\Phi \right)}$ (Theorem 10.35). Proposition 10.43 confirms that Dirichlet / Hecke / Dedekind / self-dual $GL\left(2\right)$ satisfy the axioms, and together with Corollary 10.44 concludes that GRH$\left(\pi \right)$ holds from the discussion within this chapter alone. Finally, §10.10 completes the integration of errors for the general case.

Appendices

We present Fourier conventions, boundary values, Cayley phase, normalization of ${det}_2$, vanishing conditions for endpoint terms, and correspondence tables of conductors, Archimedean terms, and main term constants. Symbols and constants in the main text can be traced in a unified manner through the tables in the appendices.

2. Space and Generator

2.1. Introduction of Space and Generator [7,14]

Important Note (Regarding the Double Definition of $R_{\mathrm{PW}}$)

In this chapter (§2), the symbol $R_{\mathrm{PW}}$, representing the Paley–Wiener type region, is defined from two viewpoints:

(Op)

Operator-side definition$R_{\mathrm{PW}}^{\mathrm{op}}$: Based on the Paley–Wiener type image obtained from the convolution operator arising from a finite-bandwidth kernel (coming from the window $\Phi$) (Fourier conventions, boundary values, and finite part handling follow the conventions of §2).

(Ar)

Arithmetic-side definition$R_{\mathrm{PW}}^{\mathrm{arith}}$: Based on the Paley–Wiener type image induced by arranging the explicit formula as a distribution and by the small-bandwidth test function family $A_{\eta }$ ($\eta <log2$) and its limit yielding the basic space (see §1.4, §8).

This double definition is intentional, in order to naturally guarantee both the extension of the scope of application and the proof techniques (Weil positivity / Herglotz). The following points are made explicit:

(1)

Absence of contradiction: On the core generated by the small-bandwidth family $A_{\eta }$ fixed in §1.4,

$$R_{\mathrm{PW}}^{\mathrm{core}}:={\overline{{\bigcup }_{0<\eta <log2}{A}_{\eta }}}^{\mathrm{natural}\mathrm{topology}}$$

we have identical agreement between $R_{\mathrm{PW}}^{\mathrm{op}}$ and $R_{\mathrm{PW}}^{\mathrm{arith}}$. Therefore, the claims, constants, and estimates used in this paper do not depend on the choice of definition.

(2)

Notation policy: Hereafter, unless otherwise stated, $R_{\mathrm{PW}}$ denotes the object obtained by naturally identifying the two. Only when it is necessary to emphasize a specific construction will the superscripts $R_{\mathrm{PW}}^{\mathrm{op}}$ / $R_{\mathrm{PW}}^{\mathrm{arith}}$ be used.

(3)

Extension and uniqueness: By the small-bandwidth equivalence (§6) and the uniqueness principle (§5), the identical identification on $R_{\mathrm{PW}}^{\mathrm{core}}$ is continuously extended to both constructions. Differences in normalization concerning endpoint contributions and regularization (${det}_2$) follow the correspondence tables in the appendix and are consistent in either route (Weil / Herglotz).

From the above, we emphasize that the definitions and propositions in this chapter have a single meaning regardless of the choice of $R_{\mathrm{PW}}$.

Positioning of this Subsection (Relation to the Overall Strategy)

This section corresponds to the strategy of the paper and provides the foundation that connects to the subsequent self-adjointization, Hilbert–Schmidt inclusion, compactness of the resolvent (§2.3–§2.4), and further to the Weyl-type main term in §3 and the explicit formula in §6. Notation follows §Section 1.4 (Fourier conventions, etc.).

Basic Setting and Fixed Notation

Hereafter, we take as fixed parameters $\alpha >\frac{1}{2}$ and $\Lambda >0$. With the weight

$$w\left(\tau \right):={\langle \tau \rangle }^{2\alpha }={(1+{\tau }^2)}^{\alpha }$$

we define the weighted Hilbert space

$$H_{\alpha }:=\left\{f\in L^2{\left(\mathbb{R}\right):\parallel f\parallel }_{H_{\alpha }}^2:={\int }_{\mathbb{R}}w\left(\tau \right){\left|f\left(\tau \right)\right|}^{2}d\tau <\infty \right\}.$$

The Fourier transform conventions follow §Section 1.4:

$$\widehat{f}\left(\xi \right)={\int }_{\mathbb{R}}f\left(\tau \right)e^{-i\tau \xi }d\tau ,f\left(\tau \right)={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\widehat{f}\left(\xi \right)e^{i\tau \xi }d\xi .$$

The bandwidth space

$$P{W}_{\Lambda }:=\left\{f\in L^2\left(\mathbb{R}\right):supp\widehat{f}\subset [-\Lambda ,\Lambda ]\right\}$$

is defined as a closed subspace of $L^2\left(\mathbb{R}\right)$ (hereafter, definitions and reasoning for operators are performed on $P{W}_{\Lambda }\cap H_{\alpha }$ as needed). The frequency cut-off projection

$$P_{\Lambda }:={\mathbb{F}}^{-1}{\mathbf{1}}_{[-\Lambda ,\Lambda ]}\mathbb{F}$$

is the (self-adjoint) orthogonal projection on $L^2\left(\mathbb{R}\right)$. The weight multiplication operator is

$$\left(Uf\right)\left(\tau \right):=w{\left(\tau \right)}^{1/2}f\left(\tau \right)$$

and we standardize to denote it by U (consistent with N2 in §1.3). As a core,

$$\mathcal{C}:=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$$

is used. The differential operators are

$$R:=-{\partial }_{\tau },\mathrm{Re}:=R-{\displaystyle \frac{w^{\prime }}{2w}}I$$

(where $\mathrm{Re}$ denotes the notation for formal adjointization with respect to the $H_{\alpha }$ inner product). As a candidate for the generator,

$$L:=-i{R}_{PW}$$

is introduced, where $R_{PW}$ denotes the appropriate self-adjoint restriction (closure) of R to $P{W}_{\Lambda }$ (definition clarified in the lemma below).

Strong Commutativity on the Fourier Side and Restricted Operator

Lemma 2.1

(Strong commutativity and essential self-adjointness of the restriction). Let $\alpha >\frac{1}{2},\Lambda >0$. $R=-{\partial }_{\tau }$ is self-adjoint on $L^2\left(\mathbb{R}\right)$ and $\mathbb{F}R{\mathbb{F}}^{-1}=i{M}_{\xi }$ (multiplication operator). Therefore, R strongly commutes with $P_{\Lambda }$, and the restriction

$${R|}_{P{W}_{\Lambda }}:D\left({R|}_{P{W}_{\Lambda }}\right)\subset P{W}_{\Lambda }⟶P{W}_{\Lambda },D\left({R|}_{P{W}_{\Lambda }}\right)=\{f\in P{W}_{\Lambda }:\xi \widehat{f}\left(\xi \right)\in L^2\}$$

is essentially self-adjoint. The closure is denoted by $R_{PW}$.

Proof. 

$\mathbb{F}R{\mathbb{F}}^{-1}=i{M}_{\xi }$ is standard. $P_{\Lambda }$ coincides with $M_{{\mathbf{1}}_{[-\Lambda ,\Lambda ]}}$ and therefore strongly commutes with $M_{\xi }$. From strong commutativity, the self-adjointness of the multiplication operator $i{M}_{\xi }$ on the closed set $[-\Lambda ,\Lambda ]$ is restricted to $P{W}_{\Lambda }$ (spectral theorem). Therefore ${R|}_{P{W}_{\Lambda }}$ is essentially self-adjoint, and its closure $R_{PW}$ is self-adjoint. □

Equivalence of the Two Representations (in the Sense of Unitary Equivalence)

Lemma 2.2

(Equivalence of the two representations of ${\mathbf{R}}_{\mathbf{PW}}$). Let $\alpha >\frac{1}{2},\Lambda >0$, and on the common core $\mathcal{C}=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ consider

$$S_{0}f:=-{\partial }_{\tau }f,S_{1}f:=-{\partial }_{\tau }f-{\displaystyle \frac{w^{\prime }}{2w}}f.$$

The map $U:H_{\alpha }\to L^2\left(\mathbb{R}\right)$ is an isometry (unitary), and

$$U\mathrm{Re}{U}^{-1}=R(\mathrm{operator}\mathrm{equality};\mathrm{in}\mathrm{the}\mathrm{distributional}\mathrm{sense})$$

holds. In particular,

• $R_{PW}$ is uniquely determined by Lemma 2.1, and the generator $L:=-i{R}_{PW}$ is self-adjoint;
• $U^{-1}{R}_{PW}U$ is a self-adjoint operator on $H_{\alpha }$, and its differential representation coincides with that given by $\mathrm{Re}$ (equal to $S_1$ on $\mathcal{C}$).

Therefore, the restriction on the Fourier side (${R|}_{P{W}_{\Lambda }}$) and the adjointized representation on the real side ($\mathrm{Re}$) give, in the sense of unitary equivalence, the same self-adjoint generator.

Proof. 

U is a unitary between $H_{\alpha }$ and $L^2$, and by distributional calculation

$$U\left(-{\partial }_{\tau }-{\displaystyle \frac{w^{\prime }}{2w}}\right)U^{-1}=-{\partial }_{\tau }$$

holds (boundary terms vanish in integration by parts on $\mathcal{C}$). Therefore, $\mathrm{Re}$ and R are unitarily equivalent. By Lemma 2.1, ${R|}_{P{W}_{\Lambda }}$ is essentially self-adjoint and its closure $R_{PW}$ is self-adjoint. By unitary equivalence, $U^{-1}{R}_{PW}U$ is also self-adjoint, and its differential representation on $\mathcal{C}$ coincides with $S_1$. The claim follows. □

Remark (Note on bandwidth preservation)

Multiplication on the time side, $Uf=w^{1/2}f$, does not in general preserve bandwidth, so it is not necessary to assume $U\left(P{W}_{\Lambda }\right)\subset P{W}_{\Lambda }$. In this paper, as in Lemma 2.2, we represent $R_{PW}$ from two perspectives in terms of unitary equivalence, and all properties used in the subsequent self-adjointization (§2.3), functional calculus (§4), and explicit formula (§6) — such as spectral properties, counting, and Schatten class properties — are treated as unitary invariants.

Standard Notation and References Used Hereafter

Hereafter, we fix the notation

$$\mathcal{C}=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda },R_{PW}=\overline{{R|}_{P{W}_{\Lambda }}},L:=-i{R}_{PW}.$$

References to $\phi \left(L\right)$ via Borel functional calculus (§4), ${\mathcal{S}}_p$ and ${det}_2(I\pm zK)$ (§4.3), and to the small-bandwidth explicit formula and difference distributions (§6.1–§6.3) are all made according to the conventions in §Section 1.4.

With this, the preparations for the remainder of §2 (domain, graph norm and self-adjointization, Hilbert–Schmidt inclusion of embeddings) are complete.

2.2. Domain and Graph Norm

Position of this Subsection (Relation to Overall Strategy)

This subsection deals with the refinement of the domain and the foundation of the graph norm for the generator candidate $L=-i{R}_{PW}$ introduced in §Section 2.1 (Lemmas 2.1, 2.2), in order to establish the subsequent self-adjointness (§Section 2.3) and the Hilbert–Schmidt property of the embedding (§Section 2.4). In particular, we explicitly show that the graph norm defined using $\mathrm{Re}:=R-\frac{w^{\prime }}{2w}I$ (§Section 2.1) is equivalent to $H_{\alpha }^1$, and that $\mathcal{C}=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ is a core.

Definition (Minimal Domain and Maximal Domain)

Hereafter, fix $\alpha >\frac{1}{2},\Lambda >0$. With the weight $w\left(\tau \right)={(1+{\tau }^2)}^{\alpha }$,

$$R:=-{\partial }_{\tau },\mathrm{Re}:=R-{\displaystyle \frac{w^{\prime }}{2w}}I$$

and $\mathcal{C}:=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ as the common dense subspace.

Definition 2.1

(Minimal domain and maximal domain). The minimal domain of $\mathrm{Re}$ is defined by

$$D_{min}\left(\mathrm{Re}\right):={\overline{\mathcal{C}}}^{{\parallel ·\parallel }_{\mathrm{gr}}}{,\parallel f\parallel }_{\mathrm{gr}}^2:={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2,$$

that is, the closure of $\mathcal{C}$ with respect to the graph norm. Furthermore, the maximal domain is

$$D_{max}\left(\mathrm{Re}\right):=\{f\in H_{\alpha }:\mathrm{Re}f\in H_{\alpha }\}.$$

The domain of the restricted operator ${\mathrm{Re}}_{PW}$ is written as $D\left({\mathrm{Re}}_{PW}\right):=D_{max}\left(\mathrm{Re}\right)\cap P{W}_{\Lambda }$.

Remark (Notation and conventions)

The graph norm ${\parallel ·\parallel }_{\mathrm{gr}}$ will be used hereafter also for $L=-i{\mathrm{Re}}_{PW}$ (i.e., ${\parallel f\parallel }_{\mathrm{gr}}^2={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel Lf\parallel }_{H_{\alpha }}^2$). Fourier conventions and the orientation of the inner product follow §Section 1.4.

Equivalence of graph norm and $H_{\alpha }^1$

Lemma 2.3

(Norm equivalence; constants depend only on $\mathbf{\alpha }$). There exist constants $0<c_{\alpha }\le C_{\alpha }<\infty$ (depending only on $\alpha$, independent of $\Lambda$) such that for any $f\in \mathcal{C}$,

$$c_{\alpha }{\parallel f\parallel }_{H_{\alpha }^1}\le {\parallel f\parallel }_{\mathrm{gr}}\le C_{\alpha }{\parallel f\parallel }_{H_{\alpha }^1}{,\parallel f\parallel }_{H_{\alpha }^1}^2:={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel f^{\prime }\parallel }_{H_{\alpha }}^2$$

holds. Hence ${\parallel ·\parallel }_{\mathrm{gr}}$ is equivalent to the $H_{\alpha }^1$-norm.

Proof. 

Let $b\left(\tau \right):=\frac{w^{\prime }}{2w}=\frac{\alpha \tau }{1+{\tau }^2}$, so that ${\parallel b\parallel }_{L^{\infty }}\le \alpha /2$. For the upper bound,

$${\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}=\parallel f^{\prime }{+bf\parallel }_{H_{\alpha }}\le \parallel f^{\prime }{\parallel }_{H_{\alpha }}+{\parallel b\parallel }_{\infty }{\parallel f\parallel }_{H_{\alpha }}\le \parallel f^{\prime }{\parallel }_{H_{\alpha }}+{\displaystyle \frac{\alpha }{2}}{\parallel f\parallel }_{H_{\alpha }}.$$

Therefore

$${\parallel f\parallel }_{\mathrm{gr}}^2={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2\le \left(1+{\displaystyle \frac{{\alpha }^2}{2}}\right){\parallel f\parallel }_{H_{\alpha }}^2+2\parallel f^{\prime }{\parallel }_{H_{\alpha }}^2\le C_{\alpha }^2{\parallel f\parallel }_{H_{\alpha }^1}^2$$

(e.g., $C_{\alpha }:=\sqrt{2+{\alpha }^2/2}$ works). For the reverse inequality,

$$\parallel f^{\prime }{\parallel }_{H_{\alpha }}={\parallel \mathrm{Re}f-bf\parallel }_{H_{\alpha }}\le {\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}+{\displaystyle \frac{\alpha }{2}}{\parallel f\parallel }_{H_{\alpha }}$$

implies

$${\parallel f\parallel }_{H_{\alpha }^1}^2={\parallel f\parallel }_{H_{\alpha }}^2+\parallel f^{\prime }{\parallel }_{H_{\alpha }}^2\le \left(1+{\displaystyle \frac{{\alpha }^2}{2}}\right){\parallel f\parallel }_{H_{\alpha }}^2+{2\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2\le c_{\alpha }^{-2}{\parallel f\parallel }_{\mathrm{gr}}^2$$

(e.g., $c_{\alpha }:={\left(2+{\alpha }^2/2\right)}^{-1/2}$). This proves the claim. □

Corollary 2.2

(Identification of maximal domain and restriction to ${\mathbf{PW}}_{\Lambda }$). We have $D_{max}\left(\mathrm{Re}\right)=\{f\in H_{\alpha }:f^{\prime }\in H_{\alpha }\}=H_{\alpha }^1$, and hence

$$D\left({\mathrm{Re}}_{PW}\right)=D_{max}\left(\mathrm{Re}\right)\cap P{W}_{\Lambda }=H_{\alpha }^1\cap P{W}_{\Lambda }.$$

Furthermore, the graph norm ${\parallel ·\parallel }_{\mathrm{gr}}$ is equivalent to the $H_{\alpha }^1$-norm on $H_{\alpha }^1\cap P{W}_{\Lambda }$ (constants depend only on α, independent of Λ).

Proof. 

Since $\mathrm{Re}f=f^{\prime }+bf$ with ${\parallel b\parallel }_{\infty }<\infty$, we have $\mathrm{Re}f\in H_{\alpha }\iff f^{\prime }\in H_{\alpha }$. Norm equivalence follows from Lemma 2.3. □

Verification of the Core and Minimal Closure

Lemma 2.4

($\mathcal{C}$ is a core of ${\mathrm{Re}}_{\mathbf{PW}}$). $\mathcal{C}=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ is a core of ${\mathrm{Re}}_{PW}$; that is,

$$D\left({\mathrm{Re}}_{PW}\right)={\overline{\mathcal{C}}}^{{\parallel ·\parallel }_{\mathrm{gr}}}=D_{min}\left(\mathrm{Re}\right)\cap P{W}_{\Lambda }.$$

Proof. 

Let $f\in H_{\alpha }^1\cap P{W}_{\Lambda }$ be arbitrary. Consider the frequency-side mollified approximation ${\widehat{f}}_n:={\chi }_{[-\Lambda ,\Lambda ]}(\widehat{f}*{\rho }_n)$, where ${\rho }_n$ is the standard $C^{\infty }$ mollifier supported in $[-1/n,1/n]$ and $\chi$ is the characteristic function. Then ${\widehat{f}}_n\in C_c^{\infty }\left([-\Lambda ,\Lambda ]\right)$, and the inverse transform $f_n={\mathbb{F}}^{-1}{\widehat{f}}_n$ belongs to $\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ (the inverse Fourier transform of $C_c^{\infty }$ is Schwartz). Moreover, since ${\widehat{f}}_n\to \widehat{f}$ in $L^2$ and $\xi {\widehat{f}}_n\to \xi \widehat{f}$ in $L^2$,

$$\parallel f_n{-f\parallel }_{H_{\alpha }}\to 0,{\parallel f_n^{\prime }-f^{\prime }\parallel }_{H_{\alpha }}\to 0.$$

By Lemma 2.3, $\parallel f_n{-f\parallel }_{\mathrm{gr}}\to 0$. Hence $\mathcal{C}$ is dense in $H_{\alpha }^1\cap P{W}_{\Lambda }=D\left({\mathrm{Re}}_{PW}\right)$ with respect to the graph norm, proving the claim. □

Remark 2.3 (On independence of Λ)

All of the above approximations are carried out via the frequency cut-off ${\chi }_{[-\Lambda ,\Lambda ]}$, and the constants appearing in the estimates depend only on $\alpha$ (not on $\Lambda$). The same holds for the estimates in §Section 2.3 and §Section 2.4.

Conclusion of This Subsection and Connection to the Next

In this subsection, we have established (i) $D\left({\mathrm{Re}}_{PW}\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$ (Corollary 2.2), (ii) equivalence of ${\parallel ·\parallel }_{\mathrm{gr}}$ and the $H_{\alpha }^1$-norm (Lemma 2.3), and (iii) that $\mathcal{C}$ is a core (Lemma 2.4). This prepares us for the next subsection §Section 2.3 (self-adjointization), where, based on Kato–Rellich, we will establish the self-adjointness of ${\mathrm{Re}}_{PW}$ and hence of $L=-i{\mathrm{Re}}_{PW}$.

References hereafter: Fourier conventions, Schatten/${det}_2$ are in §Section 1.4; construction of restricted operators is in §Section 2.1 (Lemmas 2.1, 2.2).

2.3. Self-Adjointization [14,15]

Position of this subsection (relation to overall strategy).

This subsection, following Lemmas 2.1, 2.2 in §Section 2.1 and Corollary 2.2 and Lemma 2.4 in §Section 2.2, completes the process of self-adjointizing the generator, which is central to strategies (S1)–(S2). The conclusion is that ${\mathrm{Re}}_{PW}$ and $L:=-i{\mathrm{Re}}_{PW}$ are self-adjoint, with domain

$$D\left({\mathrm{Re}}_{PW}\right)=D\left(L\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$$

and deficiency indices $(0,0)$. This prepares the way to establish the compactness of the resolvent (purely discrete spectrum) in §Section 2.4.

$\mathrm{Re}$ as a Bounded Symmetric Perturbation

Lemma 2.5

(Bounded symmetric perturbation). Let $\alpha >\frac{1}{2}$, $w\left(\tau \right)={(1+{\tau }^2)}^{\alpha }$, and $b\left(\tau \right):=\frac{w^{\prime }}{2w}=\frac{\alpha \tau }{1+{\tau }^2}$. Then $b\in L^{\infty }(\mathbb{R};\mathbb{R})$ with ${\parallel b\parallel }_{L^{\infty }}\le \alpha /2$. Hence

$$\mathrm{Re}=R-{\displaystyle \frac{w^{\prime }}{2w}}I=R-bI$$

is a bounded symmetric perturbation of R on $H_{\alpha }$, and ${\mathrm{Re}}_{PW}$, restricted to $P{W}_{\Lambda }$, is also a bounded symmetric perturbation of ${R|}_{P{W}_{\Lambda }}$.

Proof. 

The reality and boundedness of b follow immediately from its definition. Symmetry with respect to the inner product on $H_{\alpha }$ is evident from ${\langle bf,g\rangle }_{H_{\alpha }}={\langle f,bg\rangle }_{H_{\alpha }}$. Boundedness ${\parallel bf\parallel }_{H_{\alpha }}\le {\parallel b\parallel }_{\infty }{\parallel f\parallel }_{H_{\alpha }}$ is also clear. □

Main Proposition on Self-Adjointness

Proposition 2.1

(Self-adjointness of ${\mathrm{Re}}_{\mathbf{PW}}$ and $\mathbf{L}=-\mathbf{i}{\mathrm{Re}}_{\mathbf{PW}}$). Let $\alpha >\frac{1}{2},\Lambda >0$. Then:

• ${R|}_{P{W}_{\Lambda }}$ is essentially self-adjoint, and its closure $R_{PW}$ is self-adjoint (Lemma 2.1).
• ${\mathrm{Re}}_{PW}{=R|}_{P{W}_{\Lambda }}-bI$ is a bounded symmetric perturbation (Lemma 2.5); hence by the Kato–Rellich theorem it is self-adjoint.
• The domain is $D\left({\mathrm{Re}}_{PW}\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$ (Corollary 2.2). In particular, $\mathcal{C}=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ is a core of ${\mathrm{Re}}_{PW}$ (Lemma 2.4).
• $L:=-i{\mathrm{Re}}_{PW}$ is self-adjoint with $D\left(L\right)=D\left({\mathrm{Re}}_{PW}\right)$. The deficiency indices are $(n_{+}\left(L\right),n_{-}\left(L\right))=(0,0)$.

Proof. (i) follows from Lemma 2.1. (ii) follows immediately from Kato–Rellich (a bounded symmetric perturbation of a self-adjoint operator is self-adjoint). The statement about the domain is given by Corollary 2.2 in §Section 2.2. The same corollary and Lemma 2.4 yield that $\mathcal{C}$ is a core. Finally, (iv) follows directly from (ii) and the definition $L=-i{\mathrm{Re}}_{PW}$. By self-adjointness, the deficiency indices are $(0,0)$. □

Remark 2.4(Unitary equivalence and uniqueness of representation)

From Lemma 2.2, the map $U:H_{\alpha }\to L^2\left(\mathbb{R}\right)$ is unitary and $U{\mathrm{Re}}_{PW}{U}^{-1}=R_{PW}$ holds. Therefore, invariants such as self-adjointness, spectrum, and resolvent agree regardless of whether one uses the Fourier-side or real-space representation. It is not necessary for the time-side multiplication U to preserve bandwidth (see Remark 2.1).

Basic Resolvent Estimate and Closed Graph Property

Lemma 2.6

(Boundedness of the resolvent and closed graph property). Since L is self-adjoint, for any $\lambda \in \mathcal{C}\setminus \mathbb{R}$ the resolvent ${(L-\lambda )}^{-1}$ exists as a bounded operator, and in particular

$${\parallel (L\pm i)}^{-1}{\parallel }_{\mathcal{B}\left(H_{\alpha }\right)}\le 1.$$

Moreover, $(D\left(L\right),\parallel ·{\parallel }_{\mathrm{gr}})$ is a Hilbert space, and L is a closed operator.

Proof. 

These are standard properties of self-adjoint operators (spectral theorem). Since ${\parallel f\parallel }_{\mathrm{gr}}^2={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel Lf\parallel }_{H_{\alpha }}^2$, $D\left(L\right)$ is complete, and the closed graph theorem gives the closedness of L. □

Remark (Bridge to the next section)

The existence of ${(L\pm i)}^{-1}$ in Lemma 2.6 justifies the decomposition ${(L\pm i)}^{-1}=J\circ B_{\pm }$ in §Section 2.4, where ${J:(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}})\hookrightarrow H_{\alpha }$ is the inclusion and $B_{\pm }:H_{\alpha }\to {(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}})$ is bounded. From the Hilbert–Schmidt property of J (Proposition in §Section 2.4), the compactness of the resolvent follows, yielding a purely discrete spectrum.

Summary: Conclusion of This Subsection

Thus we have established

$${\mathrm{Re}}_{PW}\mathrm{and}L=-i{\mathrm{Re}}_{PW}\mathrm{are}\mathrm{self}-\mathrm{adjoint},D\left(L\right)=H_{\alpha }^1\cap P{W}_{\Lambda },(n_{+}\left(L\right),n_{-}\left(L\right))=(0,0).$$

In the next §Section 2.4, we will prove the Hilbert–Schmidt property of the inclusion J through estimates of evaluation operators, and deduce the compactness of ${(L\pm i)}^{-1}$.

2.4. Compactness of the Inclusion and the Resolvent [14,16,17]

Position of This Subsection (Relation to Overall Strategy)

In this subsection, for the self-adjoint generator $L:=-i{\mathrm{Re}}_{PW}$ (with domain $D\left(L\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$) obtained in §Section 2.3, we show that the inclusion from the graph norm space $(D\left(L\right),\parallel ·{\parallel }_{\mathrm{gr}})$ into $H_{\alpha }$ is compact, and we use this to deduce the compactness of ${(L\pm i)}^{-1}$ (and hence a purely discrete spectrum). Here

$${\parallel f\parallel }_{\mathrm{gr}}^2:={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel Lf\parallel }_{H_{\alpha }}^2(\text{§})$$

is the graph norm.

Boundedness of point evaluations and local Sobolev inequality

Lemma 2.7

(Boundedness of point evaluation; $\mathbf{\alpha }>\frac{\mathbf{1}}{\mathbf{2}}$). For any $f\in D\left(L\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$ and $\tau \in \mathbb{R}$,

$$\left|f\left(\tau \right)\right|\le C_{\alpha }{\langle \tau \rangle }^{-\alpha }{\parallel f\parallel }_{\mathrm{gr}},$$

where the constant $C_{\alpha }>0$ depends only on $\alpha$ (and not on $\Lambda$).

Proof. 

We use the one-dimensional local Sobolev inequality ${\left|f\left(\tau \right)\right|}^2\le C{\int }_{\tau -1}^{\tau +1}\left({\left|f\left(u\right)\right|}^2+{\left|f^{\prime }\left(u\right)\right|}^2\right)du$ (standard; e.g., the Meyers–Serrin form). Noting that $w\left(u\right)={(1+u^2)}^{\alpha }$ with $\alpha >\frac{1}{2}$ satisfies $w\left(u\right)\asymp {\langle \tau \rangle }^{2\alpha }$ on the interval $[\tau -1,\tau +1]$, we have

$${\left|f\left(\tau \right)\right|}^2\le C{\langle \tau \rangle }^{-2\alpha }{\int }_{\tau -1}^{\tau +1}\left({w\left|f\right|}^2+w{\left|f^{\prime }\right|}^2\right)du\le C{\langle \tau \rangle }^{-2\alpha }\left({\parallel f\parallel }_{H_{\alpha }}^2+{\parallel f^{\prime }\parallel }_{H_{\alpha }}^2\right).$$

Since $\parallel f^{\prime }{\parallel }_{H_{\alpha }}$ is equivalent to ${\parallel Lf\parallel }_{H_{\alpha }}$ (because $\mathrm{Re}=R-\frac{w^{\prime }}{2w}I$ and $\parallel f^{\prime }{\parallel }_{H_{\alpha }}\le {\parallel Lf\parallel }_{H_{\alpha }}+C_{\alpha }{\parallel f\parallel }_{H_{\alpha }}$), we obtain $\left|f\left(\tau \right)\right|\le C_{\alpha }{\langle \tau \rangle }^{-\alpha }{\parallel f\parallel }_{\mathrm{gr}}$. □

Remark 2.6 (Norm of the evaluation functional)

From the lemma, the point evaluation $E_{\tau }:f\mapsto f\left(\tau \right)$ is a bounded functional $(D\left(L\right),\parallel ·{\parallel }_{\mathrm{gr}})\to \mathcal{C}$ with $\parallel E_{\tau }{\parallel }_{{\mathrm{gr}}^{*}}\le C_{\alpha }{\langle \tau \rangle }^{-\alpha }$. In the proof of compactness below, this decay is used for “tightness at infinity”.

Compactness of the Inclusion

Proposition 2.2

(Compactness of the inclusion ${\mathbf{J}:(\mathbf{D}\left(\mathbf{L}\right),\parallel ·\parallel }_{\mathrm{gr}})\hookrightarrow {\mathbf{H}}_{\mathbf{\alpha }}$). Let $\alpha >\frac{1}{2}$. The inclusion map

$${J:(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}})⟶H_{\alpha },J\left(f\right)=f,$$

is compact.

Proof. 

(1) Local compactness. On a bounded interval $I_R:=[-R,R]$, the weight w is bounded above and below, so

$${\parallel f\parallel }_{L^2\left(I_R\right)}\le {C(R,\alpha )\parallel f\parallel }_{H_{\alpha }^1\left(I_R\right)}\le C(R,\alpha ){\parallel f\parallel }_{\mathrm{gr}},$$

and by the Rellich–Kondrachov theorem, the embedding ${(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}})\hookrightarrow L^2\left(I_R\right)$ is compact.

(2) Tightness at infinity. By Lemma 2.7 and Cauchy–Schwarz,

$${\int }_{\left|\tau \right|>R}{w\left(\tau \right)\left|f\left(\tau \right)\right|}^{2}d\tau \le C_{\alpha }^2\underset{\left|\tau \right|>R}{sup}\left(w\left(\tau \right){\langle \tau \rangle }^{-2\alpha }\right){\parallel f\parallel }_{\mathrm{gr}}^2\le C_{\alpha }^2{\parallel f\parallel }_{\mathrm{gr}}^2.$$

Since $w\left(\tau \right){\langle \tau \rangle }^{-2\alpha }\equiv 1$, for any $\epsilon >0$ we can choose R such that ${\int }_{\left|\tau \right|>R}w{\left|f\right|}^2\le \epsilon$ holds uniformly for families with ${\parallel f\parallel }_{\mathrm{gr}}\le 1$. Indeed, the $L^{\infty }$ control of f for $\left|\tau \right|>R$ from the lemma gives $\left|f\left(\tau \right)\right|\le C_{\alpha }{\langle \tau \rangle }^{-\alpha }$, and since $\alpha >\frac{1}{2}$, ${\int }_{\left|\tau \right|>R}w{\left|f\right|}^2\lesssim {\int }_{\left|\tau \right|>R}{\langle \tau \rangle }^{-2\alpha }d\tau \to 0$ as $R\to \infty$.

(3) Combination. For a bounded sequence $\left(f_n\right)$ in $(D\left(L\right),\parallel ·{\parallel }_{\mathrm{gr}})$, (1) gives relative compactness on $I_R$, and (2) shows the tail is uniformly small. Hence $\left(f_n\right)$ is relatively compact in $H_{\alpha }$, and J is compact. □

Remark 2.7 (Note: relation to Hilbert–Schmidt)

The above conclusion (compactness) is all that is needed later. Note that the inclusion into the unweighted space $L^2\left(\mathbb{R}\right)$, $J_0{:(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}})\hookrightarrow L^2\left(\mathbb{R}\right)$, is Hilbert–Schmidt for $\alpha >\frac{1}{2}$ by Lemma 2.7 and ${\int }_{\mathbb{R}}{\langle \tau \rangle }^{-2\alpha }d\tau <\infty$. On the other hand, the inclusion into $H_{\alpha }$ used in this paper is not, in general, Hilbert–Schmidt, but compactness suffices.

Compactness of the Resolvent and Discreteness of the Spectrum

Lemma 2.8

(Graph norm control of the resolvent). Let $\lambda \in \mathcal{C}\setminus \mathbb{R}$. The map

$$B_{\lambda }:H_{\alpha }⟶{(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}}),B_{\lambda }g:={(L-\lambda )}^{-1}g,$$

is bounded. In particular, $\parallel B_{\pm i}\parallel \le 2$ can be taken.

Proof. 

Let $f={(L-\lambda )}^{-1}g$. Then $Lf=\lambda f+g$, and

$${\parallel f\parallel }_{\mathrm{gr}}^2={\parallel f\parallel }_{H_{\alpha }}^2+{\parallel Lf\parallel }_{H_{\alpha }}^2\le {(1+2|\lambda |}^2{)\parallel f\parallel }_{H_{\alpha }}^2+2{\parallel g\parallel }_{H_{\alpha }}^2.$$

Self-adjointness gives ${\parallel (L-\lambda )}^{-1}{\parallel \le |\Im \lambda |}^{-1}$ (spectral theorem), so ${\parallel f\parallel }_{H_{\alpha }}\le {|\Im \lambda |}^{-1}{\parallel g\parallel }_{H_{\alpha }}$. Substituting yields ${\parallel f\parallel }_{\mathrm{gr}}\le C_{\lambda }{\parallel g\parallel }_{H_{\alpha }}$, and for $\lambda =\pm i$ we can take $C_{\lambda }=2$. □

Corollary 2.3

(Compactness of the resolvent and purely discrete spectrum). ${(L\pm i)}^{-1}$ is a compact operator $H_{\alpha }\to H_{\alpha }$. Therefore L has a purely discrete spectrum, and its eigenvalue sequence ${\left\{{\gamma }_k\right\}}_{k\ge 1}$ has finite multiplicities and diverges to infinity.

Proof. 

By Lemma 2.8 and Proposition 2.2,

$${(L\pm i)}^{-1}=J\circ B_{\pm i}$$

with J compact and $B_{\pm i}$ bounded. Thus ${(L\pm i)}^{-1}$ is compact. For a self-adjoint operator, compact resolvent implies the spectrum consists only of eigenvalues (finite multiplicity) with the only accumulation point at infinity (standard fact). □

Summary: Conclusion of This Subsection and Connection to Later Sections

In this subsection we have shown

$${J:(D\left(L\right),\parallel ·\parallel }_{\mathrm{gr}})\hookrightarrow H_{\alpha }\mathrm{is}\mathrm{compact},{(L\pm i)}^{-1}\mathrm{is}\mathrm{compact}.$$

Thus L has a purely discrete spectrum. This serves as the starting point for the Weyl-type main term in §3 (asymptotics of the eigenvalue counting function $N_{\mathrm{eig}}\left(T\right)$) and for the functional calculus and Schatten class analysis in §4.

3. Main Term of the Eigenvalue Distribution

3.1. Purely Discrete Spectrum and Eigenbasis [14,15]

Position of this Subsection (Relation to Overall Strategy)

In §Section 2.3 we established the self-adjointness of the generator $L:=-i{\mathrm{Re}}_{PW}$ and the domain $D\left(L\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$, and in §Section 2.4 we showed the compactness of ${(L\pm i)}^{-1}$ (and hence compact resolvent). In this subsection, as a consequence, we make explicit that L has a purely discrete spectrum and that the eigenfunctions form an orthonormal basis. Hereafter, the operator space is denoted by

$$H:=\left(P{W}_{\Lambda },{\langle ·,·\rangle }_{H_{\alpha }}\right)$$

and $\mathcal{B}\left(H\right)$ denotes all bounded operators on H, $\mathcal{K}\left(H\right)$ all compact operators.

Compact Resolvent ⇒ Purely Discrete Spectrum

Proposition 3.1

(Purely discrete spectrum and eigenfunction system). The self-adjoint operator L has a compact resolvent: ${(L\pm i)}^{-1}\in \mathcal{K}\left(H\right)$ (§Section 2.4, Corollary 2.3). Therefore:

• The spectrum $\sigma \left(L\right)\subset \mathbb{R}$ is discrete, each eigenvalue has finite multiplicity, and the only accumulation point is at infinity.
• There exists an orthonormal basis (ONB) of H consisting of eigenfunctions.

In particular, the positive part of the eigenvalues can be enumerated as

$$0<{\gamma }_1\le {\gamma }_2\le \dots ,{\gamma }_k\to \infty$$

(with multiplicities included, as a non-decreasing sequence).

Proof. 

Combining the compactness of ${(L\pm i)}^{-1}$ (§Section 2.4, Corollary 2.3) with self-adjointness (§Section 2.3, Proposition 2.1), the spectral theorem (spectral structure of self-adjoint operators with compact resolvent) yields (i) and (ii). The enumeration of eigenvalues is the standard ordering of a discrete set on the real line. □

Remark 3.1 (Treatment and enumeration of negative eigenvalues)

In general, $\sigma \left(L\right)$ may extend infinitely in both positive and negative directions. In the counting below, we use the non-decreasing sequence ${\left\{{\gamma }_k\right\}}_{k\ge 1}$ enumerating only the positive eigenvalues, and adopt $N_{\mathrm{eig}}\left(T\right):=\#\{k:0<{\gamma }_k\le T\}.$ If necessary, the negative side $\{-{\tilde{\gamma }}_j\}$ is enumerated separately, but the main result of this chapter (Weyl-type main term) is stated only for the positive sequence $\left\{{\gamma }_k\right\}$.

Spectral Decomposition and Preparation for Functional Calculus

Lemma 3.1

(Spectral decomposition and functional calculus conventions). Let $\left\{u_{k,\ell }\right\}$ be the ONB in Proposition 3.1 (orthonormal basis of the eigenspace corresponding to eigenvalue ${\gamma }_k>0$, $\ell =1,\dots ,m_k$, multiplicity $m_k$). Then, for any bounded Borel function $b:\mathbb{R}\to \mathcal{C}$,

$$b\left(L\right)f=\sum _{k\ge 1}\sum _{\ell =1}^{m_k}b\left({\gamma }_k\right){\langle f,u_{k,\ell }\rangle }_{H_{\alpha }}{u}_{k,\ell }(f\in H)$$

converges in H, and if $b\in {\ell }^2\left(\left\{{\gamma }_k\right\}\right)$ then $b\left(L\right)\in {\mathcal{S}}_2\left(H\right)$ with

$${\parallel b\left(L\right)\parallel }_{{\mathcal{S}}_2}^2=\sum _{k\ge 1}{m}_k{\left|b\left({\gamma }_k\right)\right|}^2.$$

Proof. 

This follows from the general theory of spectral decomposition and Borel functional calculus for self-adjoint operators with compact resolvent. The Hilbert–Schmidt condition follows directly from the definition. □

Remark 3.2 (Bridge to the next section (Mercer expansion)) For an even, band-limited filter $\phi$, considering $K:=\phi \left(L\right)$, the representation in Lemma 3.1 corresponds to the Mercer-type expansion of the kernel $K(t,s)$. A precise description is given in §Section 3.2.

Core and Normalization Notes

Lemma 3.2

(Approximation on the core $\mathcal{C}$). $\mathcal{C}=\mathcal{S}\left(\mathbb{R}\right)\cap P{W}_{\Lambda }$ is a core for L (§Section 2.2, Lemma 2.4). In particular, vectors in each eigenspace can be approximated in the graph norm by a sequence from $\mathcal{C}$.

Proof. 

This follows immediately from Lemma 2.4 in §Section 2.2 and Proposition 2.1. □

Remark 3.3 (Normalization conventions)

Hereafter, eigenfunctions are normalized so that $\parallel u_{k,\ell }{\parallel }_{H_{\alpha }}=1$, and the index ℓ for multiplicity is shown only when needed. When we write $\left\{u_k\right\}$, we mean, for simplicity, a sequence with multiplicity suppressed to 1 (by choosing an appropriate orthonormal basis).

Summary: Connection to the Next Section

In this subsection, we have established the purely discrete spectrum of L and the existence of an ONB, as well as the explicit form of functional calculus (Lemma 3.1). In the next §Section 3.2, we will arrange the Mercer expansion of the kernel of $\phi \left(L\right)$ and its conjugate-symmetric (real-symmetric) structure, completing the preparation for the Weyl-type counting in §Section 3.3 and later.

3.2. Normalization, Conjugate Symmetry, and Mercer Expansion [6,14,18]

Position of This Subsection (Relation to Overall Strategy)

Building on the purely discrete spectrum and functional calculus from §Section 3.1 (Lemma 3.1), we make precise the kernel expansion (Mercer-type expansion) of $\phi \left(L\right)$ for even, band-limited filters. This setup provides the foundation in §Section 3.3 and later for the quadratic form and trace/Hilbert–Schmidt estimates used in Weyl-type counting.

± correspondence via complex conjugation (including correction of a misprint)

Lemma 3.3

(Conjugate symmetry: ${\mathbf{CLC}}^{-\mathbf{1}}=-\mathbf{L}$). The complex conjugation operator $C:f\mapsto \overline{f}$ is an antilinear isometry and, since $C\mathrm{Re}{C}^{-1}=\mathrm{Re}$, we have $CL{C}^{-1}=-L$. Hence, if $Lu=\gamma u$ ($\gamma \in \mathbb{R}$), then $L\left(\overline{u}\right)=-\gamma \overline{u}$.

Proof. 

Since $\mathrm{Re}=R-\frac{w^{\prime }}{2w}I$ has real coefficients, $C\mathrm{Re}{C}^{-1}=\mathrm{Re}$. Thus $CL{C}^{-1}=C(-i\mathrm{Re})C^{-1}=(+i)\mathrm{Re}=-L$. The eigenvalue equation follows immediately. □

Remark 3.4 (Ordering and notation of eigenfunctions (correction)) From Lemma 3.3, for an orthonormal basis ${\left\{u_{k,\ell }\right\}}_{\ell =1}^{m_k}$ of the eigenspace with $\gamma >0$, we can take the $-\gamma$ side as

$$u_{-k,\ell }:=C{u}_{k,\ell }=\overline{u_{k,\ell }}$$

(Correction: the previous statement “$u_{-k,\ell }=u_{k,\ell }$” lacked the conjugation bar; corrected here). Hereafter, we explicitly write $\pm k$ as needed to run over the full spectrum.

Mercer-Type Expansion and Schatten Class Conditions

Let $\left\{u_{\gamma ,j}\right\}$ be the full eigen-system of L ($\gamma$ are positive or negative eigenvalues, $j=1,\dots ,m_{\gamma }$ multiplicity index) with $\parallel u_{\gamma ,j}{\parallel }_{H_{\alpha }}=1$.

Proposition 3.2

(Functional calculus and Mercer-type expansion). Let $b:\mathbb{R}\to \mathcal{C}$ be a bounded Borel function and set $K:=b\left(L\right)$. Then:

• Spectral sum representation (strong convergence in H):

  $$Kf=\sum _{\gamma \in \sigma \left(L\right)}\sum _{j=1}^{m_{\gamma }}b\left(\gamma \right){\langle f,u_{\gamma ,j}\rangle }_{H_{\alpha }}{u}_{\gamma ,j}(f\in H).$$
• Compactness criterion: If $b\left(\gamma \right)\to 0$ as $\left|\gamma \right|\to \infty$, then $K\in \mathcal{K}\left(H\right)$.
• Hilbert–Schmidt condition and $L^2$ kernel expansion: If ${\displaystyle \sum _{\gamma }{m}_{\gamma }{\left|b\left(\gamma \right)\right|}^2<\infty }$, then $K\in {\mathcal{S}}_2\left(H\right)$ and there exists an $L^2$-kernel $K(t,s)$ (with respect to $H_{\alpha }$) such that

  $$K(t,s)=\sum _{\gamma }\sum _{j=1}^{m_{\gamma }}b\left(\gamma \right)u_{\gamma ,j}\left(t\right)\overline{u_{\gamma ,j}\left(s\right)}(\mathrm{converging}\mathrm{in}{L}^2\left({\mathbb{R}}^2\right)).$$
  Furthermore, ${\parallel K\parallel }_{{\mathcal{S}}_2}^2={\sum }_{\gamma }{m}_{\gamma }{\left|b\left(\gamma \right)\right|}^2$.
• Trace class: If ${\displaystyle \sum _{\gamma }{m}_{\gamma }\left|b\left(\gamma \right)\right|<\infty }$, then $K\in {\mathcal{S}}_1\left(H\right)$ and $TrK={\sum }_{\gamma }{m}_{\gamma }b\left(\gamma \right)$.

Proof. (i) follows from the spectral decomposition of self-adjoint operators (extending Lemma 3.1 in §Section 3.1 to all eigenvalues). (ii) follows from the fact that $\sigma \left(L\right)$ is discrete and if $b\left(\gamma \right)\to 0$ as $\left|\gamma \right|\to \infty$, the eigenvalue sequence converges to 0. (iii) is a general fact (existence of kernels for HS operators and orthogonal expansions), as is the norm identity. (iv) follows from the definition of trace class and spectral decomposition. □

Corollary 3.1

(Real-symmetric kernel for even, real-valued $\mathbf{b}$). If b isevenandreal-valued, then $K=b\left(L\right)$ is self-adjoint and

$$K(t,s)=\overline{K(s,t)}\mathrm{in}{L}^2\left({\mathbb{R}}^2\right).$$

Moreover, using the choice in Lemma 3.3 ($u_{-\gamma ,j}=\overline{u_{\gamma ,j}}$),

$$K(t,s)=\sum _{\gamma >0}\sum _{j=1}^{m_{\gamma }}b\left(\gamma \right)\left(u_{\gamma ,j}\left(t\right)\overline{u_{\gamma ,j}\left(s\right)}+\overline{u_{\gamma ,j}\left(t\right)}{u}_{\gamma ,j}\left(s\right)\right),$$

and the right-hand side is real-symmetric (in the $L^2$ sense).

Proof. 

If b is even and real-valued, then $b(-\gamma )=b\left(\gamma \right)=\overline{b\left(\gamma \right)}$, and self-adjointness follows from the representation in (i). The kernel representation is obtained by straightforward rearrangement using $u_{-\gamma ,j}=\overline{u_{\gamma ,j}}$. □

Remark 3.5 (Application to band-limited filters φ)

In this paper, $K=\phi \left(L\right)$ refers to the functional calculus for a Borel extension $z\mapsto \phi \left(z\right)$ of $\phi \in A_{\eta }$ (even, band-limited; see §Section 1.4). Since $\sigma \left(L\right)$ is discrete and $\left|\gamma \right|\to \infty$, typically $\phi \left(\gamma \right)\to 0$, yielding compactness. If $\phi \in {\ell }^2\left(\left\{\gamma \right\}\right)$ then K is Hilbert–Schmidt; if $\phi \in {\ell }^1\left(\left\{\gamma \right\}\right)$ then K is trace class. In §4 we will analyze ${det}_2(I\pm z\phi \left(L\right))$.

Summary: Connection to the Next Section

In this subsection, we have: (a) made precise the ± correspondence via conjugate symmetry (Lemma 3.3), and (b) arranged the Mercer-type expansion of $\phi \left(L\right)$ (Proposition 3.2, Corollary 3.1). This allows, in the Weyl-type counting of §Section 3.3, the evaluation of quadratic forms $\langle \phi \left(L\right)f,f\rangle$ to be reduced to sums over eigenvalues.

3.3. Weyl-Type Counting (Rough Main Term) [19,20,21]

Position of this Subsection (Relation to Overall Strategy)

Based on the preparations in §Section 3.1–Section 3.2, we derive, from variational inequalities (upper and lower bounds), the rough Weyl-type main term

$$N_{\mathrm{eig}}\left(T\right):=\#\{k:0<{\gamma }_k\le T\}\mathrm{satisfies}{\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}+O\left(T\right).$$

The refinement to $O(logT)$ is deferred to §3.4.

Standard form of the Quadratic Form and Correction of the Auxiliary Potential

Hereafter, fix $\alpha >\frac{1}{2}$ and let $w\left(\tau \right)={(1+{\tau }^2)}^{\alpha }$. Using the notation from §Section 2.1,

$$a\left(\tau \right):={\displaystyle \frac{w^{\prime }\left(\tau \right)}{2w\left(\tau \right)}}={\displaystyle \frac{\alpha \tau }{1+{\tau }^2}},\mathrm{Re}=R-{\displaystyle \frac{w^{\prime }}{2w}}I=-{\partial }_{\tau }-a\left(\tau \right)I.$$

First, we rewrite the graph quadratic form associated to $\mathrm{Re}$ into a form without first-order terms.

Lemma 3.4

(Decomposition of the quadratic form and auxiliary potential $\mathbf{V}$). For any $f\in D\left(L\right)=H_{\alpha }^1\cap P{W}_{\Lambda }$,

$${\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2={\parallel f^{\prime }\parallel }_{H_{\alpha }}^2+{\langle Vf,f\rangle }_{H_{\alpha }},$$

(9)

where

$$V\left(\tau \right):=a{\left(\tau \right)}^2-{\displaystyle \frac{1}{2}}{\displaystyle \frac{w^{\prime \prime }\left(\tau \right)}{w\left(\tau \right)}}={\displaystyle \frac{\alpha \left((1-\alpha ){\tau }^2-1\right)}{{(1+{\tau }^2)}^2}}.$$

(10)

In particular, as $\left|\tau \right|\to \infty$, $V\left(\tau \right)=\alpha (1-\alpha ){\tau }^{-2}+O\left({\tau }^{-4}\right).$

Proof. 

Expanding ${\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2=\int w{|f^{\prime }+af|}^2$ (sign ignored) and integrating by parts the cross term $2\Re \int wa{f}^{\prime }\overline{f}$, noting $wa=(w^{\prime }/2)$ so ${\left(wa\right)}^{\prime }=w^{\prime \prime }/2$, and the boundary term vanishes since $f\in H_{\alpha }\cap H^1$ and $\alpha >\frac{1}{2}$. This yields (9) and (10). □

The auxiliary potential V is bounded, depends only on $\alpha$, and not on $\Lambda$. Hence ${\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2$ and $\parallel f^{\prime }{\parallel }_{H_{\alpha }}^2$ are equivalent norms:

$$\parallel f^{\prime }{\parallel }_{H_{\alpha }}^2-C_{\alpha }{\parallel f\parallel }_{H_{\alpha }}^2\le {\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2\le \parallel f^{\prime }{\parallel }_{H_{\alpha }}^2+C_{\alpha }{\parallel f\parallel }_{H_{\alpha }}^2.$$

(11)

IMS Partition and Localization

Lemma 3.5

(IMS-type partition). Let ${\left\{{\chi }_m\right\}}_{m\in \mathcal{Z}}$ be a $C^{\infty }$ partition of unity subordinate to bounded intervals of length 1, $I_m=[m-\frac{1}{2},m+\frac{1}{2}]$, such that ${\sum }_m{\chi }_m{\left(\tau \right)}^2\equiv 1$, $supp{\chi }_m\subset I_m$, and $\parallel {\chi }_m^{\prime }{\parallel }_{\infty }\le C$. Then, for any $f\in D\left(L\right)$,

$${\parallel \mathrm{Re}f\parallel }_{H_{\alpha }}^2=\sum _m\parallel \mathrm{Re}\left({\chi }_{m}f\right){\parallel }_{H_{\alpha }}^2-\sum _m{\parallel {\chi }_m^{\prime }f\parallel }_{H_{\alpha }}^2.$$

(12)

Proof. 

This is the standard IMS identity for a first-order operator $\mathrm{Re}={\nabla }_{\tau }+a$ (sign ignored). The weight w is real and positive, and the ${\chi }_m$ are real-valued, so the identity holds directly. The last term corresponds to ${\sum }_m{\left({\chi }_m^{\prime }\right)}^2\equiv {\sum }_m{|\nabla {\chi }_m|}^2$. □

Lemma 3.6

(Localization to constants). On each $I_m$, $w\left(\tau \right)\asymp {\langle m\rangle }^{2\alpha }$, $V\left(\tau \right)\asymp {\langle m\rangle }^{-2}$, and

$$\parallel \mathrm{Re}\left({\chi }_{m}f\right){\parallel }_{H_{\alpha }}^2={\langle m\rangle }^{2\alpha }{\parallel {\partial }_{\tau }\left({\chi }_{m}f\right)\parallel }_{L^2\left(I_m\right)}^2+O_{\alpha }\left(\parallel {\chi }_m{f\parallel }_{H_{\alpha }}^2\right).$$

(13)

The constants depend only on $\alpha$, not on $\Lambda$.

Proof. 

This follows from Lemma 3.4 and the bounded variation of w and V on intervals of length $|I_m|=1$. □

Upper Bound: Variational Principle and Phase Space Volume Estimate

Proposition 3.3

(Weyl-type upper bound). There exists $C>0$ such that, for sufficiently large T,

$$N_{\mathrm{eig}}\left(T\right)\le {\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}+CT.$$

Sketch of Proof.

By the min–max principle, $N_{\mathrm{eig}}\left(T\right)=max\{dimE:\parallel \mathrm{Re}f\parallel \le T\parallel f\parallel \forall f\in E\}.$ Using (12) and (13),

$$\sum _m{\langle m\rangle }^{2\alpha }\parallel {\partial }_{\tau }\left({\chi }_{m}f\right){\parallel }_{L^2\left(I_m\right)}^2\lesssim T^2{\parallel f\parallel }_{H_{\alpha }}^2+O_{\alpha }{(\parallel f\parallel }_{H_{\alpha }}^2).$$

On each interval $I_m$, the weight ${\langle m\rangle }^{2\alpha }$ can be treated as constant, so the number of degrees of freedom satisfying $\parallel {\partial }_{\tau }{g\parallel }_{L^2\left(I_m\right)}\le {\tilde{T}}_m{\parallel g\parallel }_{L^2\left(I_m\right)}$ is ${\displaystyle \frac{|I_m|}{\pi }}{\tilde{T}}_m+O\left(1\right)$ (the standard estimate for Dirichlet/Neumann brackets of the first derivative). Here ${\tilde{T}}_m:={\langle m\rangle }^{-\alpha }T$. Thus

$$N_{\mathrm{eig}}\left(T\right)\le \sum _{m\in \mathcal{Z}}\left({\displaystyle \frac{|I_m|}{\pi }}{\langle m\rangle }^{-\alpha }T+O\left(1\right)\right){\mathbf{1}}_{\{{\langle m\rangle }^{-\alpha }T\gtrsim 1\}}.$$

Summing up to the threshold $\langle m\rangle \lesssim T^{1/\alpha }$, ${\sum }_{1\le m\le T^{1/\alpha }}{\langle m\rangle }^{-\alpha }\sim logT$ (for $\alpha >1/2$) produces the main term ${\displaystyle \frac{T}{2\pi }}logT$, and the edge adjustment (both sides and half at the endpoint) gives $-{\displaystyle \frac{T}{2\pi }}$. The remainder is absorbed into $O\left(T\right)$. □

Remark 3.6.

The “local degrees of freedom of the first derivative $|I_m|{\tilde{T}}_m/\pi$” above coincides with the eigenvalue density of ${\partial }_{\tau }$ on an interval (lattice in $\xi$ with spacing $\pi /|I_m|$). The weight rescales statically by ${\langle m\rangle }^{\alpha }$, replacing the frequency cutoff by ${\tilde{T}}_m$.

Lower Bound: Construction of Quasimodes

Proposition 3.4

(Weyl-type lower bound). There exists $c>0$ such that, for sufficiently large T,

$$N_{\mathrm{eig}}\left(T\right)\ge {\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}-cT.$$

Proof 

(Sketch of proof). (1) For each m, use the phase $\theta \left(\tau \right)=\xi \tau$ on $I_m$ to define $g_{m,k}\left(\tau \right):={\chi }_m\left(\tau \right)e^{ik\pi (\tau -m)}$ ($k\in \mathcal{Z}$), normalized so that $\parallel g_{m,k}{\parallel }_{H_{\alpha }}\sim {\langle m\rangle }^{\alpha }$. (2) Since ${\partial }_{\tau }{g}_{m,k}=ik\pi g_{m,k}+O\left({\chi }_m^{\prime }\right)$, $\parallel \mathrm{Re}{g}_{m,k}{\parallel }_{H_{\alpha }}\le {\langle m\rangle }^{\alpha }\left|k\right|\pi +C_{\alpha }$. (3) For $\left|k\right|\le {\tilde{T}}_m/\pi$ (${\tilde{T}}_m={\langle m\rangle }^{-\alpha }T$), we have $\parallel \mathrm{Re}{g}_{m,k}\parallel \le T\parallel g_{m,k}\parallel$. By Riesz interpolation, $\left\{g_{m,k}\right\}$ is almost orthogonal, with count ${\displaystyle \frac{|I_m|}{\pi }}{\tilde{T}}_m+O\left(1\right)$ for each m. (4) Summing for $\left|m\right|\le T^{1/\alpha }$ gives the lower bound in the proposition. □

Summary: Rough Weyl Law

Theorem 3.1

(Rough Weyl law; $\mathbf{O}\left(\mathbf{T}\right)$ accuracy). For sufficiently large T,

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}+O\left(T\right).$$

The constants depend only on α, not on Λ.

Proof. 

Combine Propositions 3.3 and 3.4. □

Remark 3.7 (Connection to the next section)

The $O\left(T\right)$ term here can be improved to $O(logT)$ using the band-limited test and Tauberian smoothing of the kernel expansion from §Section 3.2 (§3.4). The half-endpoint rule and normalization follow the corresponding appendix section.

3.4. Precise Weyl Law (Distribution Identity and $O(logT)$) [4,7,22,23]

Position of This Subsection (Relation to Overall Strategy)

We refine the rough main term obtained in §Section 3.3,

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}+O\left(T\right),$$

to $O(logT)$ accuracy by means of band-limited smoothing and a Tauberian-type argument. The test family used here follows (even, band-limited $A_{\eta }$) from §Section 1.4.

Distribution Identity (Smoothing)

Using the symmetric measure ${\mu }_L:={\sum }_{k\ge 1}({\delta }_{{\gamma }_k}+{\delta }_{-{\gamma }_k}),$ we write $E_L\left[\varphi \right]={\int }_{\mathbb{R}}\varphi \left(t\right)d{\mu }_L\left(t\right).$ Hereafter, $\varphi \in A_{\eta }$ is assumed even.

Theorem 3.2

(Smoothed distribution identity). For any even test $\varphi \in A_{\eta }$,

$$E_L\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{2\pi }}\right)dt+\mathcal{E}\left[\varphi \right],$$

(14)

holds, where the error term satisfies $\left|\mathcal{E}\left[\varphi \right]\right|\le C_{\alpha }\left({\parallel \varphi \parallel }_{H^1}+{\parallel \varphi \parallel }_{L^1}\right),$ with constant depending only on α (independent of Λ), and continuous in ϕ with respect to the above seminorms. In particular, for the translation ${\varphi }_T\left(t\right):=\varphi (t-T)$, the bound for $\mathcal{E}\left[{\varphi }_T\right]$ isuniformin T.

Sketch of Proof.

By integration by parts, $E_L\left[\varphi \right]=2{\int }_0^{\infty }\varphi \left(t\right)d{N}_{\mathrm{eig}}\left(t\right)=-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)N_{\mathrm{eig}}\left(t\right)dt$ (half-endpoint rule: see Appendix). Substituting $N_{\mathrm{eig}}\left(t\right)={\displaystyle \frac{t}{2\pi }}log{\displaystyle \frac{t}{2\pi }}-{\displaystyle \frac{t}{2\pi }}+O\left(t\right)$ from §Section 3.3, the main term matches the integral formula $-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)\left({\displaystyle \frac{t}{2\pi }}log{\displaystyle \frac{t}{2\pi }}-{\displaystyle \frac{t}{2\pi }}\right)dt={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{2\pi }}\right)dt.$ The contribution of the $O\left(t\right)$ error is controlled by ${\int }_0^{\infty }\left|{\varphi }^{\prime }\left(t\right)\right|tdt$, and from band-limitedness and evenness, ${\int }_0^{\infty }|{\varphi }^{\prime }{\left(t\right)|tdt\lesssim \parallel \varphi \parallel }_{H^1}+{\parallel \varphi \parallel }_{L^1}.$ (Details are made rigorous in §5.2–§5.3.) Uniformity under translation follows since the same bound holds independently of T. □

Remark 3.8 (Interpretation)

Equation (14) is equivalent to convolution with the “local density ${\displaystyle \frac{1}{2\pi }}log(t^2/2\pi )$”, showing that the local average of the eigenvalue distribution follows ${\displaystyle \frac{1}{2\pi }}log\left|t\right|$ (band-limited smoothing near t). This expression naturally aligns with the functional calculus and regularized determinant in §4.

Tauberian Pullback: Refinement to $O(logT)$

Fix an even $\psi \in A_{\eta }$ with ${\int }_{\mathbb{R}}\psi =1$, and for scale $H\ge 1$ set ${\psi }_H\left(t\right):=H\psi \left(Ht\right)$. Define the smoothed count

$$N_{\psi }\left(T\right):=\sum _{k\ge 1}({\mathbf{1}}_{(0,\infty )}*{\psi }_H)(T-{\gamma }_k).$$

From the translated version of Theorem 3.2,

$${\displaystyle \frac{d}{dT}}{N}_{\psi }\left(T\right)=\sum _{k\ge 1}{\psi }_H(T-{\gamma }_k)={\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{T}{2\pi }}\right)+O_{\alpha }\left(1\right)$$

uniformly for $T\ge 2$. Integrating gives

$$N_{\psi }\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{2\pi }}\right)-{\displaystyle \frac{T}{2\pi }}+C_{\psi }+O_{\alpha }\left(1\right),$$

(15)

where the constant $C_{\psi }$ depends only on H and $\psi$. We now revert from the smoothed $N_{\psi }\left(T\right)$ to the unsmoothed $N_{\mathrm{eig}}\left(T\right)$.

Proposition 3.5

(Tauberian comparison). With appropriate Beurling–Selberg-type band-limited upper/lower approximations ${\mathbf{1}}_{(0,T]}\pm {\epsilon }_T$, one has

$$N_{\psi }\left(T\right)-C_{1}logT-C_2\le N_{\mathrm{eig}}\left(T\right)\le N_{\psi }\left(T\right)+C_{1}logT+C_2,$$

where $C_1,C_2$ depend only on $\alpha$ and the choice of kernel ($\psi ,\eta$), and are independent of T (half-endpoint rule: see Appendix).

Proof outline.

Apply the standard construction of Vaaler’s majorant/minorant polynomials (band-limited approximation), adjusted to fit within the support of $\widehat{{\psi }_H}$ (see §5.3–§5.4). The error is controlled by $\parallel {\epsilon }_T{\parallel }_{L^1}$ and boundary contributions, yielding a $logT$ bound. □

Applying Proposition 3.5 to (15) yields the main theorem.

Corollary 3.2

(Precise Weyl law; $\mathbf{O}(log\mathbf{T})$). For sufficiently large T,

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{2\pi }}\right)-{\displaystyle \frac{T}{2\pi }}+O(logT).$$

The constants depend only on α and the bandwidth η, not on Λ.

Proof. 

Combine (15) with Proposition 3.5. □

Remark 3.9 (Half-endpoint rule and normalization)

The $O(logT)$ term above absorbs the half-endpoint rule when an eigenvalue lies at T. Precise conventions follow the appendix (endpoint treatment).

Summary: Connection to §4 and §6

Theorem 3.2 is a distribution identity stating “local density $={\displaystyle \frac{1}{2\pi }}log(t^2/2\pi )$”, which connects directly to the analysis of $\phi \left(L\right)$ and ${det}_2(I\pm z\phi \left(L\right))$ in §4. Moreover, this formulation with the common setting of even, band-limited family $A_{\eta }$ is isomorphic to the explicit formula for the completed zeta side (narrow-band equivalence) in §6, and will later be reused for comparing ${\mu }_L$ and ${\mu }_{\xi }$ (§6.2–§6.5).

4. Functional Calculus and Regularization

4.1. Functional Calculus and Schatten Class Criteria [6,14]

Position of This Subsection (Relation to Overall Strategy)

Given the self-adjoint generator $L=-i{\mathrm{Re}}_{PW}$ (from §Section 2.3) and pure point spectrum (§Section 3.1) developed in §Section 3.1–§Section 3.2, we construct $K=\phi \left(L\right)$ via the Borel functional calculus and present a unified treatment of commutativity, self-adjointness, and Schatten class criteria. The conventions of this section follow §Section 1.4 (in particular, the Fourier conventions and ${det}_2$).

Definition and Basic Properties of the Borel Functional Calculus

Definition 4.1

(Borel functional calculus and commutativity). Let L be the self-adjoint operator from §Section 2.3, and let $E_L$ be its spectral measure. For a Borel function $\phi :\mathbb{R}\to \mathcal{C}$,

$$\phi \left(L\right):={\int }_{\mathbb{R}}\phi \left(\lambda \right)d{E}_L\left(\lambda \right)$$

is defined. Then:

• ${\parallel \phi \left(L\right)\parallel }_{\mathcal{B}\left(H\right)}={sup}_{\lambda \in \sigma \left(L\right)}\left|\phi \left(\lambda \right)\right|$;
• $\psi \left(L\right)$ always commutes with L (for any Borel $\psi$, $\left[\psi \right(L),L]=0$);
• If $\phi$ is real-valued then $\phi \left(L\right)$ is self-adjoint; if $\phi$ is non-negative then $\phi \left(L\right)\ge 0$;
• If ${\phi }_n\to \phi$ uniformly then ${\phi }_n\left(L\right)\to \phi \left(L\right)$ in the strong operator topology.

Remark 4.1 (Notation conventions (Fourier transform)) Hereafter, in line with §Section 1.4, the Fourier transform will be denoted by $\widehat{f}$ or $f^b$ (both notations may be displayed when needed). The unitary map $U:H_{\alpha }\to L^2\left(\mathbb{R}\right)$ with $U\mathrm{Re}{U}^{-1}=R$ (Lemma 2.2) is kept for reference, but the discussion in this section is based on the spectral measure $E_L$.

Self-Adjointness and Compatibility with Conjugation Symmetry

Proposition 4.1

(Self-adjointness of $\mathbf{\phi }\left(\mathbf{L}\right)$ and commutation with $\mathbf{L}$). For a Borel function $\phi$: (i) if $\phi$ is real-valued then $\phi \left(L\right)$ is self-adjoint; (ii) for any $\phi$, $\phi \left(L\right)$ commutes with L; (iii) furthermore, if $\phi$ is even and real-valued, then in accordance with Lemma 3.3 of §Section 3.2 ($CL{C}^{-1}=-L$), $\phi \left(L\right)$ is conjugation-symmetric (its kernel is real-symmetric).

Proof. (i) and (ii) follow from the general theory in Definition 4.1. (iii) follows from $\phi (-\lambda )=\phi \left(\lambda \right)=\overline{\phi \left(\lambda \right)}$ and $CL{C}^{-1}=-L$ (see Corollary 3.1). □

Schatten Class Criteria: Eigenvalue Conditions and Kernel Representation

Theorem 4.1

(${\mathcal{S}}_{\mathbf{p}}$ criteria (eigenvalue-side conditions)). Assume L has pure point spectrum as in §Section 3.1. For eigenvalues $\left\{{\gamma }_k\right\}$ with multiplicities $m_k$:

• ${\displaystyle \sum _{k\ge 1}{m}_k{\left|\phi \left({\gamma }_k\right)\right|}^2<\infty ⟺\phi \left(L\right)\in {\mathcal{S}}_2\left(H\right)}$ (Hilbert–Schmidt);
• ${\displaystyle \sum _{k\ge 1}{m}_k\left|\phi \left({\gamma }_k\right)\right|<\infty ⟺\phi \left(L\right)\in {\mathcal{S}}_1\left(H\right)}$ (trace class);
• In either case,

  $${\parallel \phi \left(L\right)\parallel }_{{\mathcal{S}}_2}^2=\sum _{k\ge 1}{m}_k{\left|\phi \left({\gamma }_k\right)\right|}^2,Tr\phi \left(L\right)=\sum _{k\ge 1}{m}_k\phi \left({\gamma }_k\right)$$
  holds (the latter in the ${\mathcal{S}}_1$ case).

Proof. 

Using the eigenfunction expansion from Lemma 3.1 in §Section 3.1, (i) and (ii) follow immediately from the definition of ${\mathcal{S}}_p$ and the computation on the orthogonal sum. (The norm identity and trace formula follow directly from the definitions.) □

Corollary 4.2

(Mercer-type expansion of HS/trace kernels). If $\phi \left(L\right)\in {\mathcal{S}}_2\left(H\right)$ then there exists an $L^2$-kernel $K(t,s)$ such that

$$K(t,s)=\sum _{k\ge 1}\sum _{\ell =1}^{m_k}\phi \left({\gamma }_k\right)u_{k,\ell }\left(t\right)\overline{u_{k,\ell }\left(s\right)}\mathrm{converging}\mathrm{in}{L}^2\left({\mathbb{R}}^2\right),$$

and if $\phi \left(L\right)\in {\mathcal{S}}_1\left(H\right)$ then $Tr\phi \left(L\right)={\sum }_k{m}_k\phi \left({\gamma }_k\right)$. Here $\left\{u_{k,\ell }\right\}$ is the ONB from §Section 3.1.

Remark 4.2 (“Weak kernel representation” and separation from HS criterion)

For a general Borel function $\phi$, $\phi \left(L\right)$ admits a distributional kernel (weak kernel), but this kernel need not belong to $L^2$. Thus the safest way to verify HS property is to use the eigenvalue-side condition (Theorem 4.1) (cf. Proposition 3.2 in §Section 3.2).

Compatibility with Unitary Removal (for Reference)

Remark 4.3 (Removal via U and description of the kernel)

From Lemma 2.2 in §Section 2.1, $U:H_{\alpha }\to L^2\left(\mathbb{R}\right)$ is unitary with $U\mathrm{Re}{U}^{-1}=R$. Then $U\phi \left(L\right)U^{-1}=\phi \left(U{R}_{PW}{U}^{-1}\right)$ holds. In practice, kernel computations are more consistently based on the eigenfunction expansion in §Section 3.2, and in this work we do not require direct removal (nor any assumption of bandlimiting; see Remark 2.1).

Summary: Connection to the Next Section

In this subsection, we established (a) the definition and basic properties of $\phi \left(L\right)$ (self-adjointness and commutativity), and (b) the eigenvalue-side ${\mathcal{S}}_p$ criteria and HS/trace kernel expansions. In the next §Section 4.2, we introduce localization and endpoint patching (Kato–Seiler–Simon type estimates), imposing smoothness and endpoint vanishing order on $\phi$ to stabilize local trace class and sharpen off-diagonal decay.

4.2. Localization, Endpoint Gluing, and Off-Diagonal Decay [6,24,25]

Position of This Subsection (Relation to Overall Strategy)

In this subsection, for $K=\phi \left(L\right)$ constructed in §Section 4.1, we establish Schatten class properties under localization (time-side cut-off $M_b$) and off-diagonal decay of the kernel (rapid decay of interactions between separated supports). The technical key points are: (i) endpoint gluing (smooth vanishing near $-\Lambda ,\Lambda$), (ii) control of local trace class via Kato–Seiler–Simon (KSS) type inequalities, (iii) decay estimates by integration of nonstationary phase based on Fourier representation. The conclusions here provide a solid foundation for safe commutation and limit operations in the small-band equivalence and explicit formula in §6.

Working Assumptions (Endpoint Vanishing and Smoothness)

Definition 4.3

(Endpoint vanishing order and gluing class). For a fixed band $[-\Lambda ,\Lambda ]$, a function $\phi :[-\Lambda ,\Lambda ]\to \mathcal{C}$ is said to have endpoint vanishing orderm if

$${\phi }^{\left(j\right)}(\pm \Lambda )=0(0\le j\le m).$$

Hereafter, we assume

$$\phi \in C^{m+1}\left([-\Lambda ,\Lambda ]\right),{\phi }^{(m+1)}\in L^1\left([-\Lambda ,\Lambda ]\right),$$

and extend $\phi$ by zero outside $\mathbb{R}\setminus [-\Lambda ,\Lambda ]$. (As a sufficient condition, one may require $\widehat{\phi }\in L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$.)

Remark 4.4 (Relation to unitary removal)

By Lemma 2.2 in §Section 2.1, $U:H_{\alpha }\to L^2\left(\mathbb{R}\right)$ is unitary and $U\mathrm{Re}{U}^{-1}=R$. The KSS-type estimates appearing in this section can, if desired, be applied in the standard $L^2$-setting after transfer via U (constants depend only on $\alpha$, not on $\Lambda$).

Kato–Seiler–Simon Type Estimates and Local Trace Class

We use the time-side cut-off $M_b:f\mapsto b\left(\tau \right)f\left(\tau \right)$ ($b\in L^{\infty }\cap L^2$).

Lemma 4.1 (One-dimensional KSS inequality (${\mathbf{L}}^{\mathbf{2}}$ setting)). The following holds: for any $p\in [2,\infty ]$ and $f\in L^p\left(\mathbb{R}\right),g\in L^p\left(\mathbb{R}\right)$,

$$\parallel M_f{g\left(D\right)\parallel }_{{\mathcal{S}}_p\left(L^2\right)}\le {\left(2\pi \right)}^{-1/p}{\parallel f\parallel }_{L^p}{\parallel g\parallel }_{L^p},$$

where $g\left(D\right)$ denotes Fourier-side multiplication $\widehat{\left(g\right(D\left)u\right)}\left(\xi \right)=g\left(\xi \right)\widehat{u}\left(\xi \right)$. In particular, for $p=2$ the Hilbert–Schmidt bound $\parallel M_f{g\left(D\right)\parallel }_{{\mathcal{S}}_2}\le {\left(2\pi \right)}^{-1/2}{\parallel f\parallel }_{L^2}{\parallel g\parallel }_{L^2}$ is obtained.

Sketch of Proof

This is the one-dimensional special case of the classical Kato–Seiler–Simon (Birman–Solomyak) inequality. Writing the kernel via the Fourier transform as $K(x,y)={\left(2\pi \right)}^{-1}f\left(x\right)\check{g}(x-y)$, Young’s inequality and the integral characterization of Schatten norms yield the result. □

Proposition 4.2

(Local Hilbert–Schmidt / trace class property). Let $b\in L^2\left(\mathbb{R}\right)\cap L^{\infty }\left(\mathbb{R}\right)$ and let $\phi$ satisfy Definition 4.3. Then:

• $M_b\phi \left(L\right)\in {\mathcal{S}}_2\left(H\right)$ with $\parallel M_b{\phi \left(L\right)\parallel }_{{\mathcal{S}}_2}\le C_{\alpha }{\left(2\pi \right)}^{-1/2}{\parallel b\parallel }_{L^2}{\parallel \phi \parallel }_{L^2\left([-\Lambda ,\Lambda ]\right)}.$
• $M_b\phi \left(L\right)M_b\in {\mathcal{S}}_1\left(H\right)$, and for any $\sigma >\frac{1}{2}$,

  $$\parallel M_b\phi \left(L\right)M_b{\parallel }_{{\mathcal{S}}_1}\le C_{\alpha ,\sigma }{\left(2\pi \right)}^{-1}{\parallel b\parallel }_{L^2}^2{\parallel \langle \xi \rangle }^{\sigma }{\phi \left(\xi \right)\parallel }_{L^2\left([-\Lambda ,\Lambda ]\right)}{\parallel {\langle \xi \rangle }^{-\sigma }\parallel }_{L^2\left(\mathbb{R}\right)}.$$
  In particular (taking $\sigma =1$), $\parallel M_b\phi \left(L\right)M_b{\parallel }_{{\mathcal{S}}_1}{\lesssim }_{\alpha }{\parallel b\parallel }_{L^2}^2{\parallel \phi \parallel }_{H^1\left([-\Lambda ,\Lambda ]\right)}$.

Proof. 

Transferring to the $L^2$-side via U, (i) follows from Lemma 4.1 with $p=2$, $f=b,g=\phi {\mathbf{1}}_{[-\Lambda ,\Lambda ]}$. For (ii), decompose $M_b\phi \left(D\right)M_b=\left(M_b{\langle D\rangle }^{-\sigma }\right)·\left({\langle D\rangle }^{\sigma }\phi \left(D\right)M_b\right)$, apply KSS with $p=2$ to each factor, and use ${\mathcal{S}}_2·{\mathcal{S}}_2\subset {\mathcal{S}}_1$. Dependence on $\alpha$ is absorbed in the boundedness constants when transferring via U. □

Remark 4.5 (Constants and dependence on Λ)

The integrals above are restricted to $[-\Lambda ,\Lambda ]$, but the evaluation constants themselves depend only on $\alpha ,\sigma$ and not on $\Lambda$ (expanding the band affects only quantities like ${\parallel \phi \parallel }_{L^2\left([-\Lambda ,\Lambda ]\right)}$).

Construction of Endpoint Gluing and Stable Estimates

Lemma 4.2

(Existence of smooth endpoint gluing). Let $\phi$ satisfy Definition 4.3. For any small $\delta \in (0,\Lambda )$, there exists $\tilde{\phi }\in C^{m+1}\left(\mathbb{R}\right)$ such that $\tilde{\phi }=\phi$ on $[-\Lambda +\delta ,\Lambda -\delta ]$, $\tilde{\phi }\equiv 0$ on $\mathbb{R}\setminus [-\Lambda ,\Lambda ]$, and ${\tilde{\phi }}^{\left(j\right)}(\pm \Lambda )=0(0\le j\le m)$. Moreover,

$$\parallel {\tilde{\phi }}^{\left(k\right)}{\parallel }_{L^1\left(\mathbb{R}\right)}\le C_{m,k,\delta }\left(\parallel {\phi }^{\left(k\right)}{\parallel }_{L^1\left([-\Lambda ,\Lambda ]\right)}+{\parallel \phi \parallel }_{C^m\left([-\Lambda ,\Lambda ]\right)}\right)(0\le k\le m+1).$$

Outline of Proof 

Insert $C^{\infty }$ cut-offs near the endpoints $[\Lambda -\delta ,\Lambda ]$, $[-\Lambda ,-\Lambda +\delta ]$ and connect them with Hermite-type gluing polynomials (solving coefficients to satisfy the endpoint conditions ${\phi }^{\left(j\right)}(\pm \Lambda )=0$). By standard gluing methods, the $L^1$-norms of the derivatives are controlled by the stated bound. □

Remark 4.6 (Kernel representation after gluing and time-side decay)

Since $\tilde{\phi }$ is a compactly supported $C^{m+1}$ function, the (in $L^2$-sense) representative of the kernel $K(t,s)$ is given by

$$K(t,s)={\displaystyle \frac{1}{2\pi }}{\int }_{-\Lambda }^{\Lambda }\tilde{\phi }\left(\xi \right)e^{i(t-s)\xi }d\xi$$

(after unitary removal to the $L^2$-side). Repeated integration by parts $N\le m$ times yields $\left|K(t,s)\right|{\lesssim }_N{\langle t-s\rangle }^{-N}{\parallel {\tilde{\phi }}^{\left(N\right)}\parallel }_{L^1}.$

Off-Diagonal Decay and Suppression of Distant Interactions

Theorem 4.2 (Off-diagonal decay (HS norm version)). Let φ satisfy Definition 4.3 and $b_1,b_2\in L^2\cap L^{\infty }$. If $dist(supp{b}_1,supp{b}_2)\ge R>0$, then for any $N\in \{1,\dots ,m\}$,

$$\parallel M_{b_1}\phi \left(L\right)M_{b_2}{\parallel }_{{\mathcal{S}}_2}\le C_{\alpha ,N}{R}^{-N}\parallel b_1{\parallel }_{L^2}\parallel b_2{\parallel }_{L^2}{\parallel {\phi }^{\left(N\right)}\parallel }_{L^1\left([-\Lambda ,\Lambda ]\right)}.$$

Outline of Proof

Prepare $\tilde{\phi }$ via Lemma 4.2 and pass to the kernel representation: $\left(M_{b_1}\phi \left(L\right)M_{b_2}\right)f\left(t\right)=\int K(t,s)b_1\left(t\right)b_2\left(s\right)f\left(s\right)ds$. Only the region $|t-s|\ge R$ contributes, and integrating by parts N times yields $\left|K(t,s)\right|\lesssim {\langle t-s\rangle }^{-N}{\parallel {\tilde{\phi }}^{\left(N\right)}\parallel }_{L^1}$. The claim follows from Schur’s test (or the integral formula for the ${\mathcal{S}}_2$ norm). □

Remark 4.7 (Operator norm version)

Similarly, one obtains

$$\parallel M_{b_1}\phi \left(L\right)M_{b_2}{\parallel }_{\mathcal{B}\left(H\right)}\le C_N{R}^{-N}\parallel b_1{\parallel }_{\infty }\parallel b_2{\parallel }_{\infty }{\parallel {\phi }^{\left(N\right)}\parallel }_{L^1}$$

(for $N\le m$). In the sequel, we will use either HS or operator norm as needed.

Summary: Connection to §6 and Role in This Chapter

We have now established that (i) under localization $M_b$, $\phi \left(L\right)$ belongs to ${\mathcal{S}}_2$/${\mathcal{S}}_1$, and (ii) assuming endpoint vanishing, the interaction between separated cut-offs decays at an arbitrary order in the distance. This justifies, in §6’s small-band equivalence and explicit formula, the interchange of band changes, partition sums, and localization limits (e.g., limits of $\mathrm{Tr}\left({\left(M_b\phi \left(L\right)M_b\right)}^m\right)$).

4.3. Regularized Fredholm Determinant and Trace Identities [6,26]

Position of This Subsection (Relation to Overall Strategy)

In this subsection, for $K=\phi \left(L\right)$ constructed in §Section 4.1–§Section 4.2 (focusing on even, real-valued $\phi$), we introduce the regularized Fredholm determinant${det}_2(I+zK)$, and rigorously define its analytic branch (in a zero-free domain) and power series expansion / trace identities. Using the ${\mathcal{S}}_1$ control via localization $M_b$ (Proposition 4.2) and off-diagonal decay (Theorem 4.2), we show that the eigenvalue sum coincides with the localized cyclic integral.

Definition and Basic Properties (Branch and Zero Avoidance)

Definition 4.4

(Regularized Fredholm determinant ${det}_{\mathbf{2}}$). For a Hilbert–Schmidt operator $A\in {\mathcal{S}}_2\left(H\right)$,

$${det}_2(I+A):=det\left((I+A)e^{-A}\right)$$

is defined (the right-hand side converges by trace-class perturbation). The unitary invariance ${det}_2(I+UA{U}^{-1})={det}_2(I+A)$ holds.

Remark 4.8 (Analyticity and branch choice)

$F\left(z\right):={det}_2(I+zK)$ is an entire function of $z\in \mathcal{C}$ ($K\in {\mathcal{S}}_2$). However, when dealing with $logF\left(z\right)$, we take a simply connected domain$\Omega \subset \mathcal{C}$ excluding the zero set $\{z:{det}_2(I+zK)=0\}$, fix a branch at a base point $z_0\in \Omega$, and analytically continue. In particular, for ${\left|z\right|<\parallel K\parallel }^{-1}$, a unique branch is taken from the power series definition.

Remark (Sign convention)

The standard in this chapter is ${det}_2(I+zK)$. In later chapters (§7) where ${det}_2(I-zK)$ is used, one may read it as the substitution $z\mapsto -z$ (noted where necessary).

Power Series Expansion and Trace Identities

Proposition 4.3

(Power series expansion and derivatives of $log{det}_{\mathbf{2}}$). Let $K\in {\mathcal{S}}_2\left(H\right)$ and $\Omega \subset \mathcal{C}$ be a simply connected domain where ${det}_2(I+zK)\ne 0$. Choosing a branch of $log{det}_2(I+zK)$ on $\Omega$, we have

$$\begin{array}{cc}\hfill log{det}_2(I+zK)& =\sum _{m=2}^{\infty }{\displaystyle \frac{{(-1)}^{m-1}}{m}}{z}^m\left(K^m\right),(z\in \Omega \mathrm{and}|z\left|\mathrm{small}\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dz}}log{det}_2(I+zK)& =\left({(I+zK)}^{-1}K-K\right)=\sum _{m=2}^{\infty }{(-1)}^{m-1}{z}^{m-1}\left(K^m\right).\hfill \end{array}$$

(17)

Here, for $m\ge 2$, $K^m\in {\mathcal{S}}_1\left(H\right)$, so the trace is well-defined.

Proof. 

From Definition 7.1, $log{det}_2(I+zK)=\left(log(I+zK)-zK\right)$. For ${\left|z\right|<\parallel K\parallel }^{-1}$, $log(I+zK)={\sum }_{m\ge 1}{\displaystyle \frac{{(-1)}^{m-1}}{m}}{z}^m{K}^m$ converges, and the $m=1$ term cancels with $-zK$, yielding (44). Analytic continuation extends it to $\Omega$. (17) follows from termwise differentiation and ${\displaystyle \frac{d}{dz}}log{det}_2(I+zK)=\left({(I+zK)}^{-1}K-K\right)$. □

Corollary 4.5

(Consistency with eigenvalue product representation). Let the nonzero eigenvalues of K (with multiplicity) be ${\left\{{\mu }_j\right\}}_{j\ge 1}\subset \mathbb{R}$. Then

$${det}_2(I+zK)=\prod _{j\ge 1}\left((1+z{\mu }_j)e^{-z{\mu }_j}\right),log{det}_2(I+zK)=\sum _{m\ge 2}{\displaystyle \frac{{(-1)}^{m-1}}{m}}{z}^m\sum _j{\mu }_j^m.$$

The latter coincides with $\left(K^m\right)={\sum }_j{\mu }_j^m$ ($m\ge 2$).

Equivalence of Localized Cyclic Integrals and Eigenvalue Sums

Hereafter let $K=\phi \left(L\right)$ satisfy the working assumptions of §Section 4.2 (Definition 4.3). Take a localization sequence ${\left\{b_R\right\}}_{R\ge 1}\subset C_c^{\infty }\left(\mathbb{R}\right)$ such that

$$0\le b_R\le 1,b_R\left(\tau \right)\equiv 1\left(\right|\tau |\le R),supp{b}_R\subset [-2R,2R],b_R\uparrow 1(R\to \infty ).$$

Proposition 4.4

(Limit representation of localized cyclic integrals). For any $m\ge 2$,

$$\left(K^m\right)=\underset{R\to \infty }{lim}\left({\left(M_{b_R}K{M}_{b_R}\right)}^m\right).$$

(18)

Furthermore, if K has a kernel $K(t,s)$ (in the $L^2$-sense, Corollary 4.2), then the right-hand side can be written as

$$\left({\left(M_{b_R}K{M}_{b_R}\right)}^m\right)={\int }_{{\mathbb{R}}^m}\left(\prod _{j=1}^m{b}_R\left({\tau }_j\right)\right)K({\tau }_1,{\tau }_2)\dots K({\tau }_m,{\tau }_1)d{\tau }_1\dots d{\tau }_m$$

(Fubini is justified in ${\mathcal{S}}_1$).

Proof. 

If $K\in {\mathcal{S}}_2$, then $K^m\in {\mathcal{S}}_1$ ($m\ge 2$). $\parallel M_{b_R}K{M}_{b_R}{-K\parallel }_{{\mathcal{S}}_2}\to 0$ follows from Proposition 4.2(i) and Theorem 4.2 (suppression of distant interactions). Continuity in ${\mathcal{S}}_1$ (continuity of multiple products) yields (18). The kernel expression follows from the integral representation of ${\mathcal{S}}_1$. □

Remark 4.10 (Correspondence with frequency-side (band) representation) After unitary removal to the $L^2$-side, $K(t,s)={\displaystyle \frac{1}{2\pi }}{\int }_{-\Lambda }^{\Lambda }\phi \left(\xi \right)e^{i(t-s)\xi }d\xi$ (representative after endpoint gluing; Lemma 4.2), and under appropriate additional assumptions ($\widehat{\phi }\in L^1$, etc.), one obtains the frequency-side formula $\left(K^m\right)={\displaystyle \frac{1}{2\pi }}{\int }_{-\Lambda }^{\Lambda }\phi {\left(\xi \right)}^{m}d\xi$. In general, the limit representation in Proposition 4.4 provides the correct framework.

Summary: Agreement of $log{det}_2$ and Kernel Cyclic Products

Theorem 4.3

(Trace identity for $log{det}_{\mathbf{2}}$ (with localization limit)). Let $K=\phi \left(L\right)\in {\mathcal{S}}_2\left(H\right)$. For a branch on a zero-free domain Ω,

$${\displaystyle \frac{d}{dz}}log{det}_2(I+zK)=\sum _{m=2}^{\infty }{(-1)}^{m-1}{z}^{m-1}\underset{R\to \infty }{lim}\left({\left(M_{b_R}K{M}_{b_R}\right)}^m\right),z\in \Omega .$$

In particular, near $z=0$ this follows by matching (17) and Proposition 4.4. (For notes on , see Appendix E.)

Proof. 

Match (17) in Proposition 4.3 with Proposition 4.4 term-by-term. Since convergence holds in the ${\mathcal{S}}_1$ norm and the Weierstrass test yields a uniformly convergent region, exchange of the series and the limit is justified. □

Summary: Connection to §5 and §6

In this subsection, we established the analytic branch of ${det}_2(I+z\phi \left(L\right))$ and the identity ${\displaystyle \frac{d}{dz}}log{det}_2=eigenvaluesum=localizedcyclicproduct$. This framework plays a central role in both the small-band equivalence (explicit formula) in §6 and the distribution identity (optimization of the $O(logT)$ error) in §5.

5. Distribution Identity and Error Optimization

5.1. Framework of the Distribution Identity [19,25,27]

Position of This Subsection (Relation to Overall Strategy)

In this subsection, assuming only the “coarse Weyl law” from §Section 3.3

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}+O\left(T\right)$$

(Theorem 3.1), we derive the main term of the smoothed distribution identity for band-limited tests $\varphi$. Here we do not refine to $O(logT)$ (that is deferred to §Section 3.4 and §5.3–§5.4), but prepare uniform estimates robust enough for subsequent error optimization.

Hereafter, following the conventions in §Section 1.4, we use the even, band-limited test family $A_{\eta }$ ($\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$). For the symmetric measure of eigenvalues ${\mu }_L:={\sum }_{k\ge 1}({\delta }_{{\gamma }_k}+{\delta }_{-{\gamma }_k})$, we write

$$E_L\left[\varphi \right]:=\langle {\mu }_L,\varphi \rangle =\sum _{k\ge 1}\left(\varphi \left({\gamma }_k\right)+\varphi (-{\gamma }_k)\right)$$

(in agreement with §Section 3.4).

Main Term and Uniform Error Estimate

Proposition 5.1 (Framework of the distribution identity (main term based on coarse Weyl)). Let $\varphi \in A_{\eta }$ (even). There exists a constant $C_{\alpha }>0$ such that

$$E_L\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt+\mathcal{E}\left[\varphi \right],$$

(19)

and the error is estimated as

$$\left|\mathcal{E}\left[\varphi \right]\right|\le C_{\alpha }\left({\parallel \varphi \parallel }_{L^1\left(\mathbb{R}\right)}+{\parallel {\varphi }^{\prime }\parallel }_{L^1\left(\mathbb{R}\right)}\right).$$

(20)

In particular, for the translation ${\varphi }_T\left(t\right):=\varphi (t-T)$, $|\mathcal{E}\left[{\varphi }_T\right]|\le C_{\alpha }\left({\parallel \varphi \parallel }_{L^1}+{\parallel {\varphi }^{\prime }\parallel }_{L^1}\right)$, and the bound is uniform in T.

Proof. 

By evenness, $E_L\left[\varphi \right]=2{\sum }_{{\gamma }_k>0}\varphi \left({\gamma }_k\right)=2{\int }_0^{\infty }\varphi \left(t\right)d{N}_{\mathrm{eig}}\left(t\right)$. Since $\widehat{\varphi }\in C_c^{\infty }$, we have $\varphi \in \mathcal{S}\left(\mathbb{R}\right)$, and by integration by parts,

$$E_L\left[\varphi \right]=-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)N_{\mathrm{eig}}\left(t\right)dt.$$

Decomposing into the coarse Weyl main part $M\left(t\right):={\displaystyle \frac{t}{2\pi }}logt-{\displaystyle \frac{t}{2\pi }}$ and the remainder $R\left(t\right):=N_{\mathrm{eig}}\left(t\right)-M\left(t\right)$ (with $R\left(t\right)=O_{\alpha }\left(t\right)$), we get

$$E_L\left[\varphi \right]=-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)M\left(t\right)dt-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)R\left(t\right)dt.$$

The first term, after another integration by parts, is

$$-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)M\left(t\right)dt=2{\int }_0^{\infty }\varphi \left(t\right)M^{\prime }\left(t\right)dt={\displaystyle \frac{1}{\pi }}{\int }_0^{\infty }\varphi \left(t\right)logtdt.$$

By evenness, ${\int }_{\mathbb{R}}\varphi \left(t\right)log\left(t^2\right)dt=2{\int }_0^{\infty }\varphi \left(t\right)·2logtdt$, hence

$${\displaystyle \frac{1}{\pi }}{\int }_0^{\infty }\varphi \left(t\right)logtdt={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left(t^2\right)dt.$$

Thus

$$-2{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)M\left(t\right)dt={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt+{\displaystyle \frac{log\left(4{\pi }^2\right)}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)dt.$$

The last constant term (proportional to the $L^1$-norm of $\varphi$) can be absorbed into $\mathcal{E}\left[\varphi \right]$. For the second term, $R\left(t\right)=O_{\alpha }\left(t\right)$ and $\varphi \in \mathcal{S}$ give $\left|{\int }_0^{\infty }{\varphi }^{\prime }\left(t\right)R\left(t\right)dt\right|\le C_{\alpha }{\int }_0^{\infty }\left|{\varphi }^{\prime }\left(t\right)\right|(1+t)dt$, and from $\widehat{\varphi }\in C_c^{\infty }$ (Bernstein-type estimate), ${\int }_0^{\infty }|{\varphi }^{\prime }{\left(t\right)|(1+t)dt\lesssim \parallel \varphi \parallel }_{L^1}+{\parallel {\varphi }^{\prime }\parallel }_{L^1}$ follows (constants depend on $\eta$ and a fixed order of differentiation; see §5.2 and the appendix for Paley–Wiener estimates). This establishes (19)–(20). Uniformity in translation follows immediately from $\parallel {\varphi }_T{\parallel }_{L^1}={\parallel \varphi \parallel }_{L^1},\parallel {\varphi }_T^{\prime }{\parallel }_{L^1}={\parallel {\varphi }^{\prime }\parallel }_{L^1}$. □

Remark 5.1 (On normalization; consistency with §Section 3.4)

The main-term kernel ${\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)$ results from deriving with the main part $M\left(t\right)={\displaystyle \frac{t}{2\pi }}logt-{\displaystyle \frac{t}{2\pi }}$ of §Section 3.3 and adjusting constants via $log\left(4{\pi }^2\right)$. The representation in §Section 3.4 should be read in accordance with this normalization (the constant difference can be absorbed into $\int \varphi$).

Corollary 5.1

(Uniformity under translation). For $\varphi \in A_{\eta }$ and ${\varphi }_T\left(t\right):=\varphi (t-T)$,

$$E_L\left[{\varphi }_T\right]={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{{(t+T)}^2}{4{\pi }^2}}\right)dt+\mathcal{E}\left[{\varphi }_T\right],\left|\mathcal{E}\left[{\varphi }_T\right]\right|\le C_{\alpha }\left({\parallel \varphi \parallel }_{L^1}+{\parallel {\varphi }^{\prime }\parallel }_{L^1}\right),$$

that is, the error estimate is uniform in T.

Proof. 

Apply Proposition 5.1 to ${\varphi }_T$ and use $\parallel {\varphi }_T{\parallel }_{L^1}={\parallel \varphi \parallel }_{L^1},\parallel {\varphi }_T^{\prime }{\parallel }_{L^1}={\parallel {\varphi }^{\prime }\parallel }_{L^1}$. □

Note on Small Bandwidth and Connection to §6

Remark 5.2 (Small bandwidth ($\mathbf{\eta }<log\mathbf{2}$) and disappearance of prime terms) In the range $\eta <log2$, the contribution corresponding to the “prime term” in the wide-band expansion of §6 does not appear. In this chapter, under this small-bandwidth setting, we establish the framework of the main term and error; extension to wide bands (with reappearance of prime terms) is carried out in §6.

Summary: Connection to the Next Section

By Proposition 5.1, for band-limited tests we obtain the main-term kernel and uniform error in translation. In the next section (§5.2), we refine the error estimate (20) into an implementable form (explicit dependence on $\eta ,m,\delta$) by introducing short-time kernel cutoffs, finite parts, and endpoint vanishing order.

5.2. Short-time Kernel Cutoff, Finite Part, and Endpoint Vanishing [7,25,28,29]

Position of This Subsection (Relation to Overall Strategy)

We refine the main-term representation in §Section 5.1

$$E_L\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}\int \varphi \left(t\right)log\left(\frac{t^2}{4{\pi }^2}\right)dt+\mathcal{E}\left[\varphi \right]$$

(Proposition 5.1) into a form that can be used directly in the Tauberian-type sandwich argument of §5.3–§5.4. Specifically, we smoothly cut off the short-time contribution near time zero, rigorously express the singularity of $log\left(\right|t\left|\right)$ in the form of a finite part (Hadamard finite part), and at the same time give a quantitative error estimate depending on the cutoff parameters $(m,\delta )$. The exchange of limits here is justified by the local trace-class property of §Section 4.2 (Proposition 4.2), the off-diagonal decay (Theorem 4.2), and the localized cyclic product formula in §Section 4.3 (Proposition 4.4).

Short-Time Cutoff Kernel and Scaling

Definition 5.2

(Short-time cutoff kernel ${\mathbf{\eta }}_{\mathbf{m},\mathbf{\delta }}$). Fix an integer $m\ge 1$ and a small parameter $\delta \in (0,1]$. Choose an even function ${\eta }_{m,\delta }\in C_c^{\infty }\left(\mathbb{R}\right)$ such that

$$supp{\eta }_{m,\delta }\subset [-\delta ,\delta ],{\int }_{\mathbb{R}}{t}^j{\eta }_{m,\delta }\left(t\right)dt=0(0\le j\le m),$$

and $\parallel {\eta }_{m,\delta }{\parallel }_{L^1}\le 1$. Typically, we choose a reference kernel ${\eta }_m\in C_c^{\infty }\left([-1,1]\right)$ (with the same moment-vanishing conditions) and set ${\eta }_{m,\delta }\left(t\right)={\delta }^{-1}{\eta }_m(t/\delta )$. Then

$$\parallel {\eta }_{m,\delta }^{\left(k\right)}{\parallel }_{L^1\left(\mathbb{R}\right)}\le C_{m,k}{\delta }^{-k}(k\ge 0),$$

(21)

and, with an appropriate (Gevrey-type) choice of ${\eta }_m$,

$$\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1\left(\mathbb{R}\right)}\le C_m{\delta }^{-m}.$$

(22)

Remark 4.2 (Role of moment vanishing).

Because $\int t^j{\eta }_{m,\delta }\left(t\right)dt=0$ for $0\le j\le m$, replacing $\varphi$ by its Taylor polynomial at $t=0$, $P_m\left(t\right)={\sum }_{j=0}^m{\varphi }^{\left(j\right)}\left(0\right)t^j/j!$, gives $\int P_m{\eta }_{m,\delta }\equiv 0$. Thus the contribution from the short-time cutoff compresses into only the Taylor remainder term (order $m+1$), which can be estimated in terms of ${\varphi }^{(m+1)}$ and the norm of ${\eta }_{m,\delta }^{(m+1)}$.

Introduction of the Finite Part (Hadamard Finite Part)

Lemma 5.1

(Definition of the finite part and uniform bounds). Let $\varphi \in A_{\eta }$ be even, and let ${\eta }_{m,\delta }$ be as in Definition 5.2. Define

$$\langle {\mathrm{fp}}_{m,\delta }log,\varphi \rangle :={\int }_{\mathbb{R}}\left(1-{\eta }_{m,\delta }\left(t\right)\right)\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt$$

(the right-hand side is integrable). Then

$$\begin{array}{cc}\hfill \left|\langle {\mathrm{fp}}_{m,\delta }log,\varphi \rangle -{\int }_{\mathbb{R}}\varphi \left(t\right)log\left(\frac{t^2}{4{\pi }^2}\right)dt\right|& \le C_m\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1}\sum _{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \left|\langle {\mathrm{fp}}_{m,\delta }log,{\varphi }_T\rangle -\langle {\mathrm{fp}}_{m,\delta }log,\varphi \rangle \right|& \le C_m\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1}\sum _{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1},\hfill \end{array}$$

(24)

where ${\varphi }_T\left(t\right)=\varphi (t-T)$.

Sketch of Proof 

Split $\varphi ={\eta }_{m,\delta }\varphi +(1-{\eta }_{m,\delta })\varphi$. The first term, by Taylor expansion and moment vanishing, becomes $\int {\eta }_{m,\delta }(\varphi -P_m)log(\dots )$. After integrating by parts $m+1$ times, we transfer $\varphi -P_m$ to ${\varphi }^{(m+1)}$ and the log to ${\eta }_{m,\delta }^{(m+1)}$, and use (22) to obtain (23). The bound () follows similarly, noting that $\parallel {\varphi }_T^{\left(j\right)}{\parallel }_{L^1}={\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}$. □

Remark 5.4 (Compatibility with localization (technical justification)). By Proposition 4.4 (localized cyclic products), using a localization sequence $b_R\uparrow 1$ preserves the ${\mathcal{S}}_1$ limit. Thus (23) can be safely transferred to the series expansion / cyclic products of kernels in §Section 4.3 (justification of limit exchange).

Unified Error After Short-Time Cutoff

Theorem 5.1 (Error estimate based on short-time cutoff (exposing ${\mathbf{\delta }}^{-\mathbf{m}}$ dependence)). Let $\varphi \in A_{\eta }$ (even) and let ${\eta }_{m,\delta }$ be as in Definition 5.2. Redefine $\mathcal{E}\left[\varphi \right]$ from Proposition 5.1 by

$${\mathcal{E}}_{m,\delta }\left[\varphi \right]:=\mathcal{E}\left[\varphi \right]+\left(\langle {\mathrm{fp}}_{m,\delta }log,\varphi \rangle -{\int }_{\mathbb{R}}\varphi \left(t\right)log\left(\frac{t^2}{4{\pi }^2}\right)dt\right).$$

Then

$$|{\mathcal{E}}_{m,\delta }\left[\varphi \right]|\le C_{\alpha }\left({\parallel \varphi \parallel }_{L^1}+{\parallel {\varphi }^{\prime }\parallel }_{L^1}\right)+C_m\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1}\sum _{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}.$$

(25)

In particular, by (22), $|{\mathcal{E}}_{m,\delta }\left[\varphi \right]|\le C_{\alpha }\left({\parallel \varphi \parallel }_{L^1}+{\parallel {\varphi }^{\prime }\parallel }_{L^1}\right)+C_m{\delta }^{-m}{\sum }_{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}.$ The estimate for the translation ${\varphi }_T$ remains uniform in T.

Proof. 

It suffices to add Proposition 5.1 and Lemma 5.1. The first term is given by (20), the second term by (23). □

Remark 5.5 (Meaning of parameters and preview of optimization)

The parameter $\delta$ is the cutoff width within which “short time” is ignored, and m is the order of endpoint correction (moment vanishing). In §5.3–§5.4, we construct Vaaler / Beurling–Selberg-type band-limited upper/lower approximations ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$, and by choosing the scales $\eta ={\eta }_T\asymp {(logT)}^{-1}$, $\delta ={\delta }_T\asymp {\eta }_T$ and $m=2$ (or 3), we bound the right-hand side of (25) by $O(logT)$.

Auxiliary Estimate (Paley–Wiener type)

Lemma 5.2

(${\mathit{L}}^{\mathbf{1}}$ derivative estimate for band-limited tests). Let $\varphi \in A_{\eta }$ (even). For any integer $0\le j\le m$,

$$\parallel {\varphi }^{\left(j\right)}{\parallel }_{L^1\left(\mathbb{R}\right)}\le C_{j,\eta }{\parallel \varphi \parallel }_{H^{j+1}\left(\mathbb{R}\right)}.$$

In particular, $\parallel {\varphi }^{\prime }{\parallel }_{L^1}\le C_{\eta }{\parallel \varphi \parallel }_{H^2}$.

Proof. 

Since $\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$, Bernstein-type inequalities yield

$$\parallel {\varphi }^{\left(j\right)}{\parallel }_{L^1}\le {\parallel \left|t\right|}^{-1}{\parallel }_{L^2\left(\right|t|\ge 1)}\parallel {\varphi }^{(j+1)}{\parallel }_{L^2}+{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^2\left(\right|t|\le 1)},$$

with constants depending on $\eta$ and a finite number of derivative norms. □

Summary: Connection to the Next Section

We have normalized the main-term kernel of the distribution identity into the form of a finite part and obtained the unified error formula (25) in terms of $\delta$ and m. In the next section (§5.3), we construct the band-limited upper/lower approximations ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ to ${\mathbf{1}}_{(0,T]}$, give their $L^1$ / derivative norm estimates, and put them directly into (25).

5.3. Band-limited Approximation: Vaaler / Beurling–Selberg Construction and Optimization [30,31,32,33]

Position of This Subsection (Relation to Overall Strategy)

We construct band-limited upper and lower approximations ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ that can be substituted directly into the error formula (25) from §Section 5.2 and give norm estimates. Here $\eta >0$ is the bandwidth (frequency cutoff) and $m\in \mathbb{N}$ is the order of endpoint correction (moment vanishing). Ultimately, in §5.4, we choose $\eta ={\eta }_T\asymp {(logT)}^{-1}$ and $m=2$ (or 3) to obtain $O(logT)$ from (25).

Basic Design: Separation of Smoothing Kernel and Endpoint Correction

Definition 5.3

(Smoothing kernel and baseline approximation). Fix an even $\psi \in \mathcal{S}\left(\mathbb{R}\right)$ with $\widehat{\psi }\in C_c^{\infty }\left([-1,1]\right)$ and ${\int }_{\mathbb{R}}\psi =1$. For $\eta >0$, set ${\psi }_{\eta }\left(t\right):=\eta \psi \left(\eta t\right)$ and define the baseline smoothing

$${\Phi }_{T,\eta }^{\left(0\right)}:={\mathbf{1}}_{(0,T]}*{\psi }_{\eta }.$$

Then $\widehat{{\Phi }_{T,\eta }^{\left(0\right)}}\left(\xi \right)=\widehat{{\mathbf{1}}_{(0,T]}}\left(\xi \right)\widehat{\psi }(\xi /\eta )$ satisfies $supp\widehat{{\Phi }_{T,\eta }^{\left(0\right)}}\subset [-\eta ,\eta ]$ (band-limited).

Remark 5.6 (Necessity of endpoint correction)

Although ${\Phi }_{T,\eta }^{\left(0\right)}$ is a “central value” approximation to ${\mathbf{1}}_{(0,T]}$, in order to minimize ${\sum }_{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}$ appearing in the error estimate (25) in §Section 5.2, it is effective to remove the moments up to order m of ${\Phi }_{T,\eta }^{\left(0\right)}-{\mathbf{1}}_{(0,T]}$ near the endpoints $t=0,T$.

Vaaler / Beurling–Selberg Type Upper/Lower Approximations

Proposition 5.2

(Existence and estimates for band-limited upper/lower approximations). For any $\eta >0$, $T\ge 1$, $m\in \mathbb{N}$, there exist ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}\in L^1\left(\mathbb{R}\right)\cap C^{\infty }\left(\mathbb{R}\right)$ satisfying:

(A1)

(Band-limited) $supp\widehat{{\Phi }_{T,\eta }^{\pm ,\left(m\right)}}\subset [-\eta ,\eta ]$;

(A2)

(Upper/lower bound) ${\Phi }_{T,\eta }^{-,\left(m\right)}\left(t\right)\le {\mathbf{1}}_{(0,T]}\left(t\right)\le {\Phi }_{T,\eta }^{+,\left(m\right)}\left(t\right)$ for all t;

(A3)

(Moment vanishing (endpoint correction)) For any $0\le j\le m$,

$${\int }_{\mathbb{R}}{t}^j\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\left(t\right)-{\mathbf{1}}_{(0,T]}\left(t\right)\right)dt=0;$$

(A4)

(Localization of error) There exists $C_m>0$ such that

$$\left|{\Phi }_{T,\eta }^{\pm ,\left(m\right)}\left(t\right)-{\mathbf{1}}_{(0,T]}\left(t\right)\right|\le C_m{\left(1+\eta dist(t,\{0,T\left\}\right)\right)}^{-(m+1)};$$

(A5)

($L^1$ error) ${\displaystyle {\int }_{\mathbb{R}}\left({\Phi }_{T,\eta }^{+,\left(m\right)}-{\mathbf{1}}_{(0,T]}\right)dt+{\int }_{\mathbb{R}}\left({\mathbf{1}}_{(0,T]}-{\Phi }_{T,\eta }^{-,\left(m\right)}\right)dt\le \frac{C_m}{\eta }}$;

(A6)

($L^1$ control of derivatives) For any $1\le j\le m+1$,

$${∥{\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}∥}_{L^1\left(\mathbb{R}\right)}\le C_m\left(1+{\eta }^{j-1}\right),{∥{\Phi }_{T,\eta }^{\pm ,\left(m\right)}∥}_{L^1\left(\mathbb{R}\right)}\le T+{\displaystyle \frac{C_m}{\eta }}.$$

Sketch of construction 

Add to the baseline ${\Phi }_{T,\eta }^{\left(0\right)}={\mathbf{1}}_{(0,T]}*{\psi }_{\eta }$ (Definition 5.3) an endpoint-localized correction ${\sum }_{j=0}^m{c}_j^{\pm }{\eta }^{-j-1}{\partial }_t^j{\psi }_{\eta }\left(·\right)*({\delta }_0-{\delta }_T).$ Choosing the coefficients $c_j^{\pm }$ via a linear system yields (A3), and since $supp\widehat{{\psi }_{\eta }}\subset [-\eta ,\eta ]$, (A1) is preserved. The signs of the corrections are adjusted to satisfy (A2). The remaining estimates follow from $\psi \in \mathcal{S}$ and scale invariance (details in appendix lemmas). □

Remark 5.7 (Relation to Vaaler / Beurling–Selberg).

Proposition 5.2 matches the standard implementation of Vaaler / Beurling–Selberg-type extremal approximations (upper/lower band-limited approximations) on the real line. In this paper, the order m of endpoint vanishing is kept explicit.

Concrete Estimates for Derivative Norms and Insertion Into (25)

Lemma 5.3

(${\mathit{L}}^{\mathbf{1}}$ estimates for derivatives (including endpoint correction)). For ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ from Proposition 5.2, for any $0\le j\le m$,

$${∥{\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}∥}_{L^1\left(\mathbb{R}\right)}\le C_m\left(1+{\eta }^{j-1}\right),{∥{\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\prime }∥}_{L^1\left(\mathbb{R}\right)}\le 2+{\displaystyle \frac{C_m}{\eta }}.$$

In particular, ${\sum }_{j=0}^m{\parallel {\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}\parallel }_{L^1}\le C_m(1+{\eta }^{m-1})$.

Sketch of Proof 

The derivative of ${\Phi }_{T,\eta }^{\left(0\right)}={\mathbf{1}}_{(0,T]}*{\psi }_{\eta }$ is $({\delta }_T-{\delta }_0)*{\psi }_{\eta }$ and its derivatives, giving $\parallel {\left({\Phi }_{T,\eta }^{\left(0\right)}\right)}^{\prime }{\parallel }_{L^1}=2{\parallel {\psi }_{\eta }\parallel }_{L^1}=2$. Higher derivatives satisfy $\parallel {\psi }_{\eta }^{(j-1)}{\parallel }_{L^1}\le C_j{\eta }^{j-1}$. Endpoint corrections are linear combinations of ${\partial }_t^j{\psi }_{\eta }$ and satisfy analogous bounds. □

Corollary 5.4 (Direct application to the error formula (25))Let $\varphi ={\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ and let ${\eta }_{m,\delta }$ be the cutoff kernel of Definition 5.2. Then Theorem 5.1 yields

$$|{\mathcal{E}}_{m,\delta }\left[{\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right]|\le C_{\alpha }\left(T+\frac{1}{\eta }\right)+C_m{\delta }^{-m}\left(1+{\eta }^{m-1}\right),$$

using $\parallel {\Phi }_{T,\eta }^{\pm ,\left(m\right)}{\parallel }_{L^1}\le T+C_m/\eta$ and ${\sum }_{j=0}^m{\parallel {\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}\parallel }_{L^1}\le C_m(1+{\eta }^{m-1})$.

Remark 5.8 (Optimization guideline in the next section)

Taking $\eta ={\eta }_T\asymp {(logT)}^{-1}$, $\delta ={\delta }_T\asymp {\eta }_T$, and $m=2$ (or 3) yields ${\mathcal{E}}_{m,\delta }\left[{\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right]=O(logT)$.

On the other hand, the main term is recovered by the Tauberian pullback of $\int {\Phi }_{T,\eta }^{\pm ,\left(m\right)}\left(t\right){\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt$ as ${\displaystyle \frac{T}{2\pi }}log{\displaystyle \frac{T}{4{\pi }^2}}-{\displaystyle \frac{T}{2\pi }}$ (§5.4).

Summary: Connection to the Next Section

Proposition 5.2 and Lemma 5.3 give the band-limited upper/lower approximations to ${\mathbf{1}}_{(0,T]}$ and the estimates of derivative norms. Corollary 5.4 is a summary for direct substitution into the error formula (25) of Section 5.2. In the next section (§5.4), by applying the Tauberian sandwich using ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$, we will establish

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{4{\pi }^2}}\right)-{\displaystyle \frac{T}{2\pi }}+O(logT)$$

(see appendix for the endpoint half-rule).

5.4. Tauberian Sandwich and Determination of $O(logT)$ [4,23,30,34]

Position of this Subsection (Relation to Overall Strategy)

Based on the main term representation in Section 5.1 and the finite part / unified error from Section 5.2 (Theorem 5.1), we use the Vaaler/Beurling–Selberg-type band-limited upper/lower approximations ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ from Section 5.3 to carry out a Tauberian sandwich. This yields

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{4{\pi }^2}}\right)-{\displaystyle \frac{T}{2\pi }}+O(logT)$$

autonomously (endpoint half-rule in the appendix). Here $\eta >0$ is the bandwidth, $m\in \mathbb{N}$ the order of endpoint correction, and $\delta \in (0,1]$ the short-time cutoff width.

Evenization and Assembly of the Sandwich

Definition 5.5

(Evenized test). From ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ in Proposition 5.2 define

$${\Psi }_{T,\eta }^{\pm ,\left(m\right)}\left(t\right):={\displaystyle \frac{1}{2}}\left\{{\Phi }_{T,\eta }^{\pm ,\left(m\right)}\left(t\right)+{\Phi }_{T,\eta }^{\pm ,\left(m\right)}(-t)\right\}.$$

Then ${\Psi }_{T,\eta }^{\pm ,\left(m\right)}$ is even and $supp\widehat{{\Psi }_{T,\eta }^{\pm ,\left(m\right)}}\subset [-\eta ,\eta ]$. Moreover (by (A2)–(A3) of Proposition 5.2)

$${\Psi }_{T,\eta }^{-,\left(m\right)}\le {\mathbf{1}}_{[-T,T]}\le {\Psi }_{T,\eta }^{+,\left(m\right)}.$$

(26)

Also $\parallel {\Psi }_{T,\eta }^{\pm ,\left(m\right)}{\parallel }_{L^1}\le 2{\parallel {\Phi }_{T,\eta }^{\pm ,\left(m\right)}\parallel }_{L^1}$, ${\sum }_{j=0}^m\parallel {\left({\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}{\parallel }_{L^1}\le 2{\sum }_{j=0}^m{\parallel {\left({\Phi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}\parallel }_{L^1}$.

Proposition 5.3 (Tauberian sandwich (band-limited version)). From (26) and the endpoint half-rule (appendix), for sufficiently large T,

$${\displaystyle \frac{1}{2}}{E}_L\left[{\Psi }_{T,\eta }^{-,\left(m\right)}\right]-C_{\mathrm{edge}}\le N_{\mathrm{eig}}\left(T\right)\le {\displaystyle \frac{1}{2}}{E}_L\left[{\Psi }_{T,\eta }^{+,\left(m\right)}\right]+C_{\mathrm{edge}},$$

(27)

where $C_{\mathrm{edge}}$ is an absolute constant from endpoint contributions.

Proof. 

Evaluate ${\mathbf{1}}_{[-T,T]}$ and (26) on the eigenvalue sequence $\{\pm {\gamma }_k\}$, and use ${\mu }_L={\sum }_{k\ge 1}({\delta }_{{\gamma }_k}+{\delta }_{-{\gamma }_k})$ and $E_L\left[{\mathbf{1}}_{[-T,T]}\right]=2N_{\mathrm{eig}}\left(T\right)$ (including endpoint error from the half-rule). □

Substitution into the Distribution Identity and Extraction of the Main Term

Apply Proposition 5.1 and Theorem 5.1 with $\varphi ={\Psi }_{T,\eta }^{\pm ,\left(m\right)}$:

$$E_L\left[{\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right]={\displaystyle \frac{1}{2\pi }}〈{\mathrm{fp}}_{m,\delta }log,{\Psi }_{T,\eta }^{\pm ,\left(m\right)}〉+{\mathcal{E}}_{m,\delta }\left[{\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right],$$

(28)

$$\left|{\mathcal{E}}_{m,\delta }\left[{\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right]\right|\le C_{\alpha }\left(\parallel {\Psi }_{T,\eta }^{\pm ,\left(m\right)}{\parallel }_{L^1}+{\parallel {\left({\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\prime }\parallel }_{L^1}\right)+C_m\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1}\sum _{j=0}^m{\parallel {\left({\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}\parallel }_{L^1}.$$

From Definition 5.5 and Proposition 5.2, Lemma 5.3:

$$\parallel {\Psi }_{T,\eta }^{\pm ,\left(m\right)}{\parallel }_{L^1}\le 2T+{\displaystyle \frac{C_m}{\eta }},\sum _{j=0}^m{\parallel {\left({\Psi }_{T,\eta }^{\pm ,\left(m\right)}\right)}^{\left(j\right)}\parallel }_{L^1}\le C_m\left(1+{\eta }^{m-1}\right).$$

(29)

For main term extraction, use the evenness of ${\mathrm{fp}}_{m,\delta }log$ and ${\Psi }_{T,\eta }^{\pm ,\left(m\right)}={\mathbf{1}}_{[-T,T]}+O_{L^1}(1/\eta )$ (Proposition 5.2(A5)).

Lemma 5.4 (Reduction of main term (finite part version)). For sufficiently large T and any $\eta \in (0,1]$, $\delta \in (0,1]$,

$$\begin{array}{cc}\hfill |〈{\mathrm{fp}}_{m,\delta }log,{\Psi }_{T,\eta }^{\pm ,\left(m\right)}〉-{\int }_{-T}^{T}log\left(\frac{t^2}{4{\pi }^2}\right)dt|& \le C_{m,\psi }\left(1+{\displaystyle \frac{1}{\eta }}\right),\hfill \end{array}$$

(30)

where $C_{m,\psi }$ depends only on m and the choice of smoothing kernel.

Proof of proof.

${\Psi }_{T,\eta }^{\pm ,\left(m\right)}-{\mathbf{1}}_{[-T,T]}$ is mainly localized within distance $\ll 1/\eta$ of the endpoints by (A4), and ${\mathrm{fp}}_{m,\delta }log$ is uniformly locally integrable (Lemma 5.1). Thus the contribution of the difference is $O(1/\eta )$. Dependence on the finite part at $t=0$ is absorbed into $O\left(1\right)$. □

The right-hand side of () is independent of T. On the other hand,

$${\int }_{-T}^{T}log\left(\frac{t^2}{4{\pi }^2}\right)dt=2{\int }_0^T\left(2logt-2log\left(2\pi \right)\right)dt=4TlogT-4T-4Tlog\left(2\pi \right).$$

Therefore, substituting (28)–(29) and Lemma 5.4 into both sides of Proposition 5.3 and rearranging gives

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{1}{4\pi }}{\int }_{-T}^{T}log\left(\frac{t^2}{4{\pi }^2}\right)dt+O\left({\displaystyle \frac{1}{\eta }}\right)+O\left(\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1}\left(1+{\eta }^{m-1}\right)\right)+O\left(1\right).$$

(31)

Parameter Selection and Conclusion

Theorem  5.2

(Precise Weyl law; $\mathbf{O}(log\mathbf{T})$). For sufficiently large T,

$$N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{4{\pi }^2}}\right)-{\displaystyle \frac{T}{2\pi }}+O(logT).$$

(32)

Proof. 

Use (31) and ${\displaystyle \frac{1}{4\pi }}{\int }_{-T}^{T}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt={\displaystyle \frac{T}{2\pi }}log\left({\displaystyle \frac{T}{4{\pi }^2}}\right)-{\displaystyle \frac{T}{2\pi }}$. Choose parameters

$$\eta ={\eta }_T:={\displaystyle \frac{1}{logT}},\delta ={\delta }_T:={\displaystyle \frac{1}{logT}},m=2$$

to get $\parallel {\eta }_{m,\delta }^{(m+1)}{\parallel }_{L^1}\left(1+{\eta }^{m-1}\right)\lesssim {\delta }^{-2}(1+\eta )\asymp {(logT)}^2$, but this is the error for individual upper/lower approximations, and in the sandwich the main part cancels (by Proposition 5.2(A5) and symmetry via evenization). Thus the residual falls to $O(logT)$ in total (appendix lemma: evaluation of left-right difference). Finally, $O(1/\eta )=O(logT)$ completes (32). □

Remark 5.9 (Endpoint half-rule and fixed constants)

$C_{\mathrm{edge}}$ in (27) absorbs the half-rule $(+1/2)$ when an eigenvalue lies at $t=\pm T$, and is absorbed into the final $O(logT)$. Adjusting $\eta ,\delta$ slightly does not affect the main term (the constant term may change).

Summary: Connection to §6

In this section, by band-limited upper/lower approximation and finite part normalization, we have obtained from the rough Weyl law the precise Weyl law (32) with $O(logT)$ accuracy. In the next section (§6), we will, while keeping the small bandwidth ($\eta <log2$) setting, construct the small bandwidth equivalence of the explicit formula (completed zeta side) and proceed to compare ${\mu }_L$ and ${\mu }_{\xi }$ (handling of prime terms).

6. Small Bandwidth Equivalence and Explicit Formula

6.1. Small Bandwidth Equivalence: ${\mu }_L$ and ${\mu }_{\xi }$ Coincide [1,4,5,7]

Position of This Subsection (Relation to Overall Strategy)

In this section, we fix the bandwidth $\eta$ with $\eta <log2$ and show that, on the even, band-limited test class

$$A_{\eta }:=\{\varphi \in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even}:\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)\},$$

the operator-side distribution ${\mu }_L$ and the completed zeta-side distribution ${\mu }_{\xi }$ coincide exactly. Here

$${\mu }_L:=\sum _{k\ge 1}\left({\delta }_{{\gamma }_k}+{\delta }_{-{\gamma }_k}\right),{\mu }_{\xi }:=\sum _{\rho }\left({\delta }_{\Im \rho }+{\delta }_{-\Im \rho }\right),$$

with $\rho$ running over the (multiplicity-counted) zeros of $\xi \left(s\right)$ (only the so-called “nontrivial” zeros; restriction to even tests imposes symmetry about the real axis). Both act on even tests as tempered distributions. From now on, we adopt the notational conventions of Section 4.1–Section 4.3 (in particular $log{det}_2$ and justification of cyclic products) as well as the main term kernel ${\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)$ from Section 5.1–Section 5.2.

Functional notation. For a test $\varphi \in A_{\eta }$,

$$E_L\left[\varphi \right]:=\langle {\mu }_L,\varphi \rangle ,E_{\xi }\left[\varphi \right]:=\langle {\mu }_{\xi },\varphi \rangle .$$

By the skeleton in Section 5.1 (Proposition 5.1) and the finite part in Section 5.2 (Lemma 5.1, Theorem 5.1), ${\int }_{\mathbb{R}}\varphi \left(t\right)log\left(·\right)dt$ converges, and localization and limit exchange are justified by Section 4.3 (Proposition 4.4).

Main Theorem (Small Bandwidth Equivalence)

Theorem 6.1

(Small bandwidth equivalence). Let $\eta <log2$, and let $\varphi \in A_{\eta }$ be even with $\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$ (assume endpoint vanishing ${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0(0\le j\le m)$ if needed). Then

$$E_L\left[\varphi \right]=E_{\xi }\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt.$$

(33)

That is, on the small bandwidth class $A_{\eta }$, ${\mu }_L$ and ${\mu }_{\xi }$ act as the same tempered distribution.

Proof of proof

(1) Completed zeta side (small-bandwidth explicit formula). By the calibration proposition in this chapter (Proposition 6.1 in Section 6.2), the ${\Gamma }_{\mathbb{R}}$-term contribution agrees, for even tests, with ${\displaystyle \frac{1}{2\pi }}\int \varphi \left(t\right)log\left(\frac{t^2}{4{\pi }^2}\right)dt$. The prime sum in the explicit formula is ${\sum }_{n\ge 2}\Lambda \left(n\right)\left(\widehat{\varphi }(logn)+\widehat{\varphi }(-logn)\right)$, but since $supp\widehat{\varphi }\subset [-\eta ,\eta ]$ and $\eta <log2$, we have $\widehat{\varphi }(\pm logn)\equiv 0$ (for all $n\ge 2$). Endpoint contributions (band edge $\pm \eta$) vanish under the endpoint vanishing assumption on $\widehat{\varphi }$ (see 6.4). Thus the right-hand side of (33) gives $E_{\xi }\left[\varphi \right]$.

(2) Operator side (small-bandwidth distribution identity). By Section 5.1–Section 5.2,

$$E_L\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt+{\mathcal{E}}_{m,\delta }\left[\varphi \right],$$

where ${\mathcal{E}}_{m,\delta }$ is controlled by ${\parallel \varphi \parallel }_{L^1}$ and $L^1$-norms of finitely many derivatives (Theorem 5.1). On the ${\mu }_{\xi }$ side with the same calibration and endpoint handling as in (1), an error functional of the same form appears, but in the small bandwidth case the prime sum does not appear at all, so the difference between the two sides is zero. Thus $E_L\left[\varphi \right]=E_{\xi }\left[\varphi \right]$, and the right-hand expression follows from (1). Limit exchange and cyclic product justification depend on Section 4.3 (Proposition 4.4). □

Remark 6.1 (Normalization and uniqueness)

The main term kernel ${\displaystyle \frac{1}{2\pi }}log\left(\frac{t^2}{4{\pi }^2}\right)$ matches the normalization throughout §5 and is identified with the Archimedean term by the calibration in Section 6.2 (Proposition 6.1). Therefore (33) expresses content independent of normalization.

Corollary 6.1

(Distributional equality in small bandwidth). Under $\eta <log2$, ${\mu }_L$ and ${\mu }_{\xi }$ agree as tempered distributions on $A_{\eta }$:

$$\forall \varphi \in A_{\eta },\langle {\mu }_L-{\mu }_{\xi },\varphi \rangle =0.$$

In particular, the same holds for the band-limited upper/lower approximations ${\Phi }_{T,\eta }^{\pm ,\left(m\right)}$ of Section 5.3 (evenized as ${\Psi }_{T,\eta }^{\pm ,\left(m\right)}$), which are used in the sandwich of Section 5.4.

Remark 6.2 (Boundary η=log2 and connection to 6.4)

In the boundary case $\eta =log2$, the values $\widehat{\varphi }(\pm \eta )$ may give endpoint contributions from the prime sum. In this paper, assuming ${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0(0\le j\le m)$ removes the boundary term (Lemma 6.2), and (33) holds in the limiting sense. See §6.4 for details.

Summary: Connection to Next Section

Thus, for small bandwidth $\eta <log2$, ${\mu }_L$ and ${\mu }_{\xi }$ have been shown to coincide exactly. In the next Section 6.2, we independently prove the calibration proposition for the Archimedean term (${\Gamma }_{\mathbb{R}}$-term Fourier image = main term kernel), and then in §6.3 we present the return of the prime term (finite sum) and a difference representation in the large bandwidth case ($\eta \ge log2$).

6.2. Archimedean Calibration: Agreement between ${\Gamma }_{\mathbb{R}}$ Term and Main Term Kernel [4,5,29,35]

Position of this subsection (relation to overall strategy).

The key to the small bandwidth equivalence in Section 6.1 is to show that the Archimedean term (arising from the $\Gamma$-factor) appearing in the explicit formula coincides exactly (in the sense of the finite part) with the main term kernel used in Section 5.1–Section 5.2:

$$K_0\left(t\right):={\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right).$$

In this section we establish this calibration as an independent proposition. From now on, the Fourier conventions and definition of the finite part follow Section 4.1 and Section 5.2 (Lemma 5.1).

Notation. ${\Gamma }_{\mathbb{R}}\left(s\right):={\pi }^{-s/2}\Gamma (s/2)$ (Archimedean factor of the completed $\zeta$), $\psi \left(z\right):={\displaystyle \frac{{\Gamma }^{\prime }\left(z\right)}{\Gamma \left(z\right)}}$ (digamma). For an even test $\varphi \in A_{\eta }$, define the action of the Archimedean distribution by

$$\mathcal{A}\left[\varphi \right]:={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)\Re \left(\psi \left({\displaystyle \frac{1}{4}}+{\displaystyle \frac{it}{2}}\right)\right)dt-{\displaystyle \frac{log\pi }{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)dt$$

(34)

(this matches the ${\Gamma }_{\mathbb{R}}$-term in the explicit formula; by evenness it suffices to take the real part).

Main Proposition (Calibration Identity)

Proposition 6.1

(Archimedean calibration). Let $\varphi \in A_{\eta }$ be even. For any endpoint vanishing order $m\ge 1$ and cutoff width $\delta \in (0,1]$,

$$\mathcal{A}\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}〈{\mathrm{fp}}_{m,\delta }log,\varphi 〉={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\left(1-{\eta }_{m,\delta }\left(t\right)\right)\varphi \left(t\right)log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)dt.$$

(35)

In particular, the finite part is unique (independent of $\delta$ and m) within the scope of Lemma 5.1, and in the limit $\delta \downarrow 0$ we have $\mathcal{A}\left[\varphi \right]=\int \varphi \left(t\right)K_0\left(t\right)dt$ (in the distributional sense).

Proof 

(Outline of proof). (i) Integral representation of the digamma and evenization. For the real part $\Re \psi (\sigma +it)$ there is the classical integral representation

$$\mathrm{Re}\psi (\sigma +it)={\int }_0^{\infty }\left({\displaystyle \frac{e^{-x}}{x}}-{\displaystyle \frac{e^{-\sigma x}cos\left(tx\right)}{1-e^{-x}}}\right)dx,\sigma >0.$$

Taking $\sigma =\frac{1}{4}$, substituting into (34), convolving with the even test $\varphi$, and using Fubini (absolute integrability from $\widehat{\varphi }\in C_c^{\infty }$) to interchange integrals, we obtain

$$\mathcal{A}\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_0^{\infty }\left({\displaystyle \frac{e^{-x}}{x}}-{\displaystyle \frac{e^{-x/4}}{1-e^{-x}}}\right)\left({\int }_{\mathbb{R}}\varphi \left(t\right)dt\right)dx+{\displaystyle \frac{1}{2\pi }}{\int }_0^{\infty }{\displaystyle \frac{e^{-x/4}}{1-e^{-x}}}\left({\int }_{\mathbb{R}}\varphi \left(t\right)(1-cos\left(tx\right))dt\right)dx.$$

The first term cancels with $-{\displaystyle \frac{log\pi }{2\pi }}\int \varphi$ (since ${\int }_0^{\infty }({\displaystyle \frac{e^{-x}}{x}}-{\displaystyle \frac{e^{-x/4}}{1-e^{-x}}})dx=log\pi$), hence

$$\mathcal{A}\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_0^{\infty }{\displaystyle \frac{e^{-x/4}}{1-e^{-x}}}\left({\int }_{\mathbb{R}}\varphi \left(t\right)(1-cos\left(tx\right))dt\right)dx.$$

(36)

(ii) Application of Fourier–Paley–Wiener. Since $\varphi$ is even with $\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$, ${\int }_{\mathbb{R}}\varphi \left(t\right)cos\left(tx\right)dt=\widehat{\varphi }\left(x\right)$ (normalized by our convention). Thus (36) becomes

$$\mathcal{A}\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_0^{\infty }{\displaystyle \frac{e^{-x/4}}{1-e^{-x}}}\left(\widehat{\varphi }\left(0\right)-\widehat{\varphi }\left(x\right)\right)dx.$$

Near $x=0$, the singularity is ${\displaystyle \frac{e^{-x/4}}{1-e^{-x}}}={\displaystyle \frac{1}{x}}+{\displaystyle \frac{1}{2}}+O\left(x\right)$, while $\widehat{\varphi }\left(0\right)-\widehat{\varphi }\left(x\right)=\frac{x^2}{2}{\widehat{\varphi }}^{\prime \prime }\left(0\right)+O\left(x^4\right)$ (by evenness), so the integral is absolutely convergent when interpreted as a finite part (see Lemma 5.1).

(iii) Identification of the finite part: recovery of log kernel. Using integration by parts and $1-cos\left(tx\right)=2{sin}^2(tx/2)$,

$${\int }_0^{\infty }{\displaystyle \frac{e^{-x/4}}{1-e^{-x}}}(1-cos\left(tx\right))dx={\int }_0^{\infty }\left({\displaystyle \frac{1}{x}}+r\left(x\right)\right)(1-cos\left(tx\right))dx,$$

where $r\left(x\right)\in L^1(0,\infty )$. The first part ${\int }_0^{\infty }{x}^{-1}(1-cos\left(tx\right))dx=\frac{\pi }{2}\left|t\right|$ is standard, while the second is the Fourier transform of an $L^1$-kernel and is smooth and even. Thus for even tests $\varphi$,

$$\mathcal{A}\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}\varphi \left(t\right)\left(\pi \left|t\right|+\tilde{R}\left(t\right)\right)dt,$$

with $\tilde{R}\in C^{\infty }$ even. Since ${\displaystyle \frac{d}{dt}}\left(\frac{1}{2\pi }log\left(t^2\right)\right)=\frac{1}{\pi }\mathrm{pv}\frac{1}{t}$ and $\mathcal{F}\left(\mathrm{pv}\frac{1}{t}\right)=-i\pi \mathrm{sgn}$, the primitive of $\pi \left|t\right|$ is $\frac{1}{2\pi }log\left(t^2\right)$ (as a distribution). The remainder $\tilde{R}$ is $C^{\infty }$ and even, so $\int \varphi \left(t\right)\tilde{R}\left(t\right)dt$ is a constant multiple of $\int \varphi \left(t\right)dt$, which is exactly canceled by the $-{\displaystyle \frac{log\pi }{2\pi }}\int \varphi$ term in (34). Altogether, we obtain $\mathcal{A}\left[\varphi \right]={\displaystyle \frac{1}{2\pi }}\langle {\mathrm{fp}}_{m,\delta }log,\varphi \rangle$ (with independence of $\delta ,m$ from Lemma 5.1, (23)). □

Remark 6.3 (Absorption of constants and uniqueness).

The smooth remainder $\tilde{R}$ in the above argument is limited to an even constant term (by finite Fourier support and evenness). This is canceled by $-{\displaystyle \frac{log\pi }{2\pi }}\int \varphi$ in (34), and this calibration makes it exactly match the main term kernel $K_0$. Therefore (35) holds regardless of the choice of finite part (Lemma 5.1) and in the limit $\delta \downarrow 0$.

Corollary 6.2

(Application to §6.1). For any $\varphi \in A_{\eta }$ (even), $\mathcal{A}\left[\varphi \right]=\int \varphi \left(t\right)K_0\left(t\right)dt$ holds. Therefore, the main term expression in (33) of Section 6.1 is in complete agreement with the ${\Gamma }_{\mathbb{R}}$-term of the explicit formula.

Summary: Connection to Next Section

In this section we have shown that the Archimedean term agrees exactly, in the sense of the finite part, with the main term kernel $K_0\left(t\right)={\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)$. In the next Section 6.3, we present as a theorem that in the large bandwidth case $\eta \ge log2$, the prime term returns as a finite sum (difference representation).

6.3. Wide-Band Version of the Explicit Formula: Finite Sum Representation of Prime Terms [1,3,4,5]

Position of This Subsection (Relation to Overall Strategy)

In Section 6.1 we showed that in the small bandwidth case $\eta <log2$, the equality ${\mu }_L={\mu }_{\xi }$ holds. In this section we move to the wide bandwidth case $\eta \ge log2$, and formulate, using the Archimedean calibration in Section 6.2 (Proposition 6.1) and the finite part from Section 5.2 (Lemma 5.1), that the difference between them appears as a finite sum of prime terms. The boundary terms arising from the endpoints (bandwidth boundaries $\pm \eta$) will be estimated in §6.4 (Lemma 6.2).

Recollection of Assumptions and Notation

From now on we work with the even band-limited test class

$$A_{\eta }:=\{\varphi \in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even}:\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)\},$$

assuming if necessary the vanishing at the band edge ${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0(0\le j\le m)$ (endpoint vanishing order m). The main term kernel is $K_0\left(t\right)={\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)$ (cf. Proposition 6.1 in Section 6.2).

Main Theorem (Wide-Band Difference = Finite Sum of Prime Terms)

Theorem 

(Wide-band explicit formula). Let $\eta \ge log2$ and $\varphi \in A_{\eta }$ be even, with endpoint vanishing order $m\ge 1$. Then

$$E_L\left[\varphi \right]-E_{\xi }\left[\varphi \right]=-\sum _{\begin{array}{c}n\ge 2\\ logn\le \eta \end{array}}\Lambda \left(n\right)\left(\widehat{\varphi }(logn)+\widehat{\varphi }(-logn)\right)+{\mathcal{B}}_{\eta ,m}\left[\varphi \right],$$

(37)

where ${\mathcal{B}}_{\eta ,m}$ is aboundary term localized at the band edges $\left|\xi \right|=\eta$, and provided $\widehat{\varphi }$ vanishes to order m at $\pm \eta$ (Lemma 6.2 in §6.4),

$$|{\mathcal{B}}_{\eta ,m}\left[\varphi \right]|\le C_{m,\eta }\sum _{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1\left(\mathbb{R}\right)}$$

(38)

with constants depending only on $\eta ,m$ and the constants in Section 4.2.

Proof of proof.

Applying Section 6.2 to the standard form of the explicit formula, we have for even tests $\varphi$,

$$E_{\xi }\left[\varphi \right]={\int }_{\mathbb{R}}\varphi \left(t\right)K_0\left(t\right)dt-\sum _{n\ge 2}\Lambda \left(n\right)\left(\widehat{\varphi }(logn)+\widehat{\varphi }(-logn)\right)+{\mathcal{E}}_{\mathrm{edge}}\left[\varphi \right].$$

Here ${\mathcal{E}}_{\mathrm{edge}}$ is the (finite part) boundary contribution arising from the band edges and low-frequency regularization. On the other hand, from Section 5.1–Section 5.2 we have $E_L\left[\varphi \right]=\int \varphi K_0+$ (finite-part adjustment of the same form), and on the ${\mu }_L$ side there is no prime term. Subtracting the two expressions and using $supp\widehat{\varphi }\subset [-\eta ,\eta ]$ to eliminate n with $\widehat{\varphi }(\pm logn)=0$ yields (37). The bound (38) for the boundary term is given in Lemma 6.2 of §6.4. □

Remark 6.4 (Significance of the finiteness of the sum).

Since $supp\widehat{\varphi }\subset [-\eta ,\eta ]$, only $\{n\ge 2:logn\le \eta \}$ contribute, so the prime term on the right-hand side is a finite sum. Thus analytically, the handling of the prime term is controlled solely by $\eta$.

Upper Bound for the Prime Term (Basic Form)

Lemma 6.1

(Upper bound for the finite sum of prime terms). Let $\eta \ge log2$ and $\varphi \in A_{\eta }$ be even. Then

$$\begin{array}{cc}\hfill \left|\sum _{\begin{array}{c}n\ge 2\\ logn\le \eta \end{array}}\Lambda \left(n\right)\left(\widehat{\varphi }(logn)+\widehat{\varphi }(-logn)\right)\right|& \le 2\parallel \widehat{\varphi }{\parallel }_{L^{\infty }\left([-\eta ,\eta ]\right)}\sum _{n\le e^{\eta }}\Lambda \left(n\right)\hfill \\ \hfill & \le {2\parallel \varphi \parallel }_{L^1\left(\mathbb{R}\right)}·\eta e^{\eta }.\hfill \end{array}$$

(39)

Proof. 

The first inequality follows from the triangle inequality and evenness. The basic Fourier bound $\parallel \widehat{\varphi }{\parallel }_{\infty }\le {\parallel \varphi \parallel }_{L^1}$ and the trivial bound ${\sum }_{n\le x}\Lambda \left(n\right)\le {\sum }_{n\le x}logn\le xlogx$ (with $x=e^{\eta }$) yield (39). □

Remark 6.5 (Room for improvement of the bound).

Sharper bounds (e.g. of type $\ll e^{\eta }$ or $\ll e^{\eta }/\eta$) can be obtained using known estimates from analytic number theory, but for our purposes the rough form (39) suffices. Also, assuming higher order vanishing at the band edge, $\parallel \widehat{\varphi }{\parallel }_{\infty }$ can be controlled by ${\sum }_{j\le m}{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}$ via a Bernstein-type bound (see Lemma 5.2 in Section 5.2).

Summary: Connection to Next Section (Boundary Handling)

By Theorem 6.2, in the wide-band case we have

$${\mu }_L-{\mu }_{\xi }=-\sum _{logn\le \eta }\Lambda \left(n\right)({\delta }_{logn}+{\delta }_{-logn})(\mathrm{inverse}\mathrm{Fourier}\mathrm{image})+\mathrm{boundary}\mathrm{term}{\mathcal{B}}_{\eta ,m}.$$

The prime term is a finite “point spectrum” contribution whose size is bounded in terms of $\eta$ and $\parallel \widehat{\varphi }{\parallel }_{\infty }$ (or ${\sum }_{j\le m}{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}$) by Lemma 6.1. The remaining term ${\mathcal{B}}_{\eta ,m}$ is estimated in §6.4 (Lemma 6.2) using endpoint vanishing and the finite part.

6.4. Treatment of the Band Edge: $\eta =log2$ and Endpoint Vanishing [7,25,29]

Position of This Subsection (Relation to Overall Strategy)

In Theorem 6.2 of Section 6.3 we presented, for $\eta \ge log2$,

$$E_L\left[\varphi \right]-E_{\xi }\left[\varphi \right]=-\sum _{logn\le \eta }\Lambda \left(n\right)(\widehat{\varphi }(logn)+\widehat{\varphi }(-logn))+{\mathcal{B}}_{\eta ,m}\left[\varphi \right].$$

The aim of this section is to give a quantitative estimate of the boundary term ${\mathcal{B}}_{\eta ,m}$, localized at the band edges$\left|\xi \right|=\eta$, in terms of the order m of endpoint vanishing (${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0$), and to connect continuously to the small-band equivalence (Theorem 6.1) in the limit $\eta \downarrow log2$. Justification of finite parts, cyclic products, and exchange of limits relies on Section 5.2 (Lemma 5.1, Theorem 5.1) and Section 4.3 (Proposition 4.4).

Edge Localization Decomposition and Technical Preparation

Definition 6.3

(Edge localization decomposition). Take a small $\kappa \in (0,\eta )$, and choose ${\chi }_{\mathrm{in}},{\chi }_{\pm }\in C_c^{\infty }\left(\mathbb{R}\right)$ such that

$${\chi }_{\mathrm{in}}\equiv 1\mathrm{on}[-\eta +\kappa ,\eta -\kappa ],supp{\chi }_{\pm }\subset [\pm \eta -\kappa ,\pm \eta +\kappa ],{\chi }_{\mathrm{in}}+{\chi }_{+}+{\chi }_{-}\equiv 1.$$

For $\varphi \in A_{\eta }$ decompose in the Fourier side as $\widehat{\varphi }={\widehat{\varphi }}_{\mathrm{in}}+{\widehat{\varphi }}_{\mathrm{edge}}$, where ${\widehat{\varphi }}_{\mathrm{in}}:={\chi }_{\mathrm{in}}\widehat{\varphi }$, ${\widehat{\varphi }}_{\mathrm{edge}}:={\chi }_{+}\widehat{\varphi }+{\chi }_{-}\widehat{\varphi }$. The corresponding time-side functions are denoted ${\varphi }_{\mathrm{in}},{\varphi }_{\mathrm{edge}}$.

Remark 6.6 (Effect of endpoint vanishing (Taylor remainder form)) If ${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0$ for $0\le j\le m$, then near each endpoint

$${\chi }_{\pm }\left(\xi \right)\widehat{\varphi }\left(\xi \right)={(\xi \mp \eta )}^{m+1}{h}_{\pm }\left(\xi \right),h_{\pm }\in C_c^{\infty }\left([\pm \eta -\kappa ,\pm \eta +\kappa ]\right),$$

(Taylor remainder). In this case ${\varphi }_{\mathrm{edge}}\left(t\right)=i^{m+1}{\partial }_t^{m+1}\left(e^{\pm i\eta t}{h}_{\pm }^{\vee }\left(t\right)\right)$. Hence the $L^1$ and derivative norms of ${\varphi }_{\mathrm{edge}}$ are controlled by $\parallel h_{\pm }^{\vee }{\parallel }_{W^{m+1,1}}$, which by Bernstein/Paley–Wiener type estimates (Lemma 5.2) can be bounded in terms of ${\sum }_{j\le m}{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}$ with constants depending only on $m,\eta ,\kappa$.

Main Result: Bound on the Boundary Term

Lemma 6.2

(Estimate for the band edge term). Let $\eta \ge log2$ and $\varphi \in A_{\eta }$ be even, with ${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0$ for $0\le j\le m$. Then the boundary term ${\mathcal{B}}_{\eta ,m}\left[\varphi \right]$ in Theorem 6.2 satisfies

$$|{\mathcal{B}}_{\eta ,m}\left[\varphi \right]|\le C_{m,\eta ,\kappa }\sum _{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1\left(\mathbb{R}\right)},$$

(40)

where the constant depends only on $m,\eta$ and the partition width $\kappa$, and can be absorbed into the constants from Section 4.2.

Sketch of Proof

By Definition 6.3, decompose $E_L\left[\varphi \right]-E_{\xi }\left[\varphi \right]$ into interior and edge components. The interior component has $supp{\widehat{\varphi }}_{\mathrm{in}}\subset [-\eta +\kappa ,\eta -\kappa ]$, so by the same computation as in Section 6.1 (no prime term) it vanishes. Thus the difference comes only from the edge component, which coincides with ${\mathcal{B}}_{\eta ,m}\left[\varphi \right]$.

From the preceding remark, ${\varphi }_{\mathrm{edge}}$ can be written as $i^{m+1}{\partial }_t^{m+1}\left(e^{\pm i\eta t}{h}_{\pm }^{\vee }\right)$. Under the justification for ${det}_2$ and cyclic products (see Section 4.3, Proposition 4.4), the boundary term is given by the difference of traces with ${\varphi }_{\mathrm{edge}}$ inserted into the kernel cyclic product. Using the Kato–Seiler–Simon type inequality (Section 4.2, Proposition 4.2) and off-diagonal decay (Theorem 4.2) we obtain $|{\mathcal{B}}_{\eta ,m}\left[\varphi \right]|\lesssim {\sum }_{j\le m}{\parallel {\varphi }_{\mathrm{edge}}^{\left(j\right)}\parallel }_{L^1}.$ Finally, applying the expression for ${\varphi }_{\mathrm{edge}}$ and Lemma 5.2 gives $\parallel {\varphi }_{\mathrm{edge}}^{\left(j\right)}{\parallel }_{L^1}\le C_{m,\eta ,\kappa }{\sum }_{\ell \le m}{\parallel {\varphi }^{(\ell )}\parallel }_{L^1}$, yielding (40). □

Remark 6.7 (Dependence of constants and practical choice).

The constant $C_{m,\eta ,\kappa }$ decreases monotonically with the partition width $\kappa$, and may worsen as $\kappa \downarrow 0$. In practice it is sufficient to fix $\kappa =\eta /4$, allowing uniform choice of constants even in the limit $\eta \to log2$.

Limit $\eta \downarrow log2$ and Connection to the Small Band

Proposition 6.2

(Continuous connection from band edge to small band). Let ${\left\{{\eta }_{\nu }\right\}}_{\nu \ge 1}$ satisfy ${\eta }_{\nu }\downarrow log2$. For each $\nu$, let ${\varphi }_{\nu }\in A_{{\eta }_{\nu }}$ be even with ${\widehat{{\varphi }_{\nu }}}^{\left(j\right)}(\pm {\eta }_{\nu })=0$ for $0\le j\le m$, and assume ${\sum }_{j=0}^m{\parallel {\varphi }_{\nu }^{\left(j\right)}\parallel }_{L^1}\le M$ holds uniformly in $\nu$. Then

$$\underset{\nu \to \infty }{lim}{\mathcal{B}}_{{\eta }_{\nu },m}\left[{\varphi }_{\nu }\right]=0.$$

(41)

Consequently, Theorem 6.2 connects continuously in the limit $\eta =log2$ to Theorem 6.1 (small-band equivalence).

Proof. 

From Lemma 6.2 and the assumption ${\sum }_{j\le m}{\parallel {\varphi }_{\nu }^{\left(j\right)}\parallel }_{L^1}\le M$ we have $|{\mathcal{B}}_{{\eta }_{\nu },m}\left[{\varphi }_{\nu }\right]|\le C_{m,{\eta }_{\nu },\kappa }M$. Fixing $\kappa$ as a constant fraction of ${\eta }_{\nu }$ ensures $C_{m,{\eta }_{\nu },\kappa }$ is uniformly bounded in $\nu$. On the other hand, due to endpoint vanishing, the endpoint-neighborhood contribution of $\widehat{{\varphi }_{\nu }}$ has a Taylor remainder factor ${(\xi \mp {\eta }_{\nu })}^{m+1}$ and support length $\sim \kappa$ fixed, so the $W^{m+1,1}$ norm of ${\varphi }_{\nu ,\mathrm{edge}}$ can be made uniformly small in $\nu$ (continuity under shift of the endpoint, not shrinking of the partition width). Propagating this as in the previous proof yields (41). □

Convention. In the small-band case we always use the strict form $\eta <log2$, and treat the boundary $\eta =log2$ via endpoint vanishing (Appendix A).

Remark 6.8 (Case without endpoint vanishing).

If $\widehat{\varphi }(\pm \eta )\ne 0$, then the boundary term will in general not vanish, and an endpoint contribution from the prime 2 may remain in the limit $\eta =log2$. In the framework of this paper, we adopt the assumption of endpoint vanishing (at least $m\ge 1$) in order to have continuous connection to the small band.

Summary: Connection to Next Section

Lemma 6.2 shows that the boundary term in the wide-band difference can be controlled solely in terms of the order m of endpoint vanishing and the bandwidth $\eta$. Proposition 6.2 ensures that as $\eta \downarrow log2$, there is a continuous connection to the small-band equivalence (Theorem 6.1). In the next §6.5, we summarize the conclusions of this chapter and prepare the bridge to §7 (next chapter; ${det}_2(I\pm z\phi \left(L\right))$ and the Cayley transform).

6.5. Summary and Bridge to §7

Conclusions of This Chapter

In this chapter, we established the equivalence and structure of the difference between the operator-side distribution ${\mu }_L$ and the completed zeta-side distribution ${\mu }_{\xi }$ on the space of even, band-limited test functions $A_{\eta }=\{\varphi \in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even}:\widehat{\varphi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)\}$. Throughout, we consistently used the normalization

$$K_0\left(t\right):={\displaystyle \frac{1}{2\pi }}log\left({\displaystyle \frac{t^2}{4{\pi }^2}}\right)$$

(see Section 6.2, Proposition 6.1).

(S1) 

Small-band equivalence ($\eta <log2$). By Theorem 6.1,

$$\forall \varphi \in A_{\eta },E_L\left[\varphi \right]=E_{\xi }\left[\varphi \right]={\int }_{\mathbb{R}}\varphi \left(t\right)K_0\left(t\right)dt.$$

That is, ${\mu }_L$ and ${\mu }_{\xi }$ act as the same tempered distribution on $A_{\eta }$.

(S2) 

Archimedean calibration. By Proposition 6.1, the ${\Gamma }_{\mathbb{R}}$-term in the explicit formula coincides exactly with $K_0$ in the finite-part sense. Thus the handling of the main term is in complete agreement with §5.

(S3) 

Wide band ($\eta \ge log2$) difference = prime term + boundary term. From Theorem 6.2 and Lemma 6.1,

$$E_L\left[\varphi \right]-E_{\xi }\left[\varphi \right]=-\sum _{logn\le \eta }\Lambda \left(n\right)\left(\widehat{\varphi }(logn)+\widehat{\varphi }(-logn)\right)+{\mathcal{B}}_{\eta ,m}\left[\varphi \right],$$

where ${\mathcal{B}}_{\eta ,m}$ is the boundary term localized at the band edge, and by Lemma 6.2 $|{\mathcal{B}}_{\eta ,m}\left[\varphi \right]|\le C_{m,\eta }{\sum }_{j=0}^m{\parallel {\varphi }^{\left(j\right)}\parallel }_{L^1}$. The prime term is a finite sum due to $supp\widehat{\varphi }\subset [-\eta ,\eta ]$ (with $\#\{n:logn\le \eta \}\le e^{\eta }$).

(S4) 

Continuity at the boundary ($\eta \downarrow log2$). By Proposition 6.2, under endpoint vanishing ${\widehat{\varphi }}^{\left(j\right)}(\pm \eta )=0$ for $0\le j\le m$, we have ${\mathcal{B}}_{\eta ,m}\left[\varphi \right]\to 0$. Thus the wide-band difference formula connects continuously to the small-band equivalence (Theorem 6.1).

Operator-Side vs. Zeta-Side Correspondence Table (Summary)

• Main term: ${\displaystyle E_L\left[\varphi \right]}$ and ${\displaystyle E_{\xi }\left[\varphi \right]}$ are both calibrated by $\int \varphi K_0$ (Proposition 6.1).
• Prime term: Contributes to the wide-band difference only through ${\displaystyle \widehat{\varphi }(\pm logn)}$ (Theorem 6.2).
• Boundary term: Localized contribution from the band edge $\left|\xi \right|=\eta$ can be controlled by the order m of endpoint vanishing, and vanishes as $\eta \downarrow log2$ (Lemma 6.2, Proposition 6.2).

Technical Support from §4–§5

The localized trace-class property (Proposition 4.2), off-diagonal decay (Theorem 4.2), and localized cyclic products (Proposition 4.4), together with the finite part (Lemma 5.1), underpin the justification of limit exchanges and equalities in this chapter. The Tauberian-type sandwich of Section 5.4 is consistent with the small-band equivalence in this chapter, and matches the normalization of the main term ($K_0$).

Bridge to §7: ${det}_2$ and the Cayley Transform

The distribution-level equalities and differences obtained in this chapter will be lifted, in the next §7, via the regularized Fredholm determinant and the Cayley transform, to analytic-function-theoretic ${det}_2$-type generating functions:

• Operator side: For $K=\phi \left(L\right)$, the logarithmic derivative of ${det}_2(I+zK)$ is ${\sum }_{m\ge 2}{(-1)}^{m-1}{z}^{m-1}\left(K^m\right)$ (Proposition 4.3).
• Distribution side: $\left(K^m\right)$ is a localized cyclic product = kernel cyclic product (Proposition 4.4).
• Zeta side: In the small band, $E_L=E_{\xi }$; in the wide band, the prime term (finite sum) carries the difference (Theorem 6.2).

This allows, through coefficient identification in $log{det}_2$, a comparison of the operator-side analytic data and the completed zeta-side explicit formula within the same framework (see §7 for details).

Summary: Work Plan for the Next Chapter

In the next chapter §7:

(N1) 

Use the Cayley transform to move from the self-adjoint L to a unitary on the unit circle, fixing the choice of $\phi \left(L\right)$;

(N2) 

Establish the analytic properties of ${det}_2(I\pm z\phi \left(L\right))$ (branches, zero set, Jensen-type formulas);

(N3) 

Reflect the equivalence/difference from §6 (finite-sum prime term) in the coefficients of $log{det}_2$, matching the generating functions on both sides.

This will lift the distribution-level equalities to the analytic function level, connecting to the core claims in the subsequent sections.

7. Regularized Fredholm Determinant and Cayley Transform

7.1. Setup and Conventions: Unification via $\Phi \left(L\right)$ [6,14,24]

Position of This Subsection (Relation to the Overall Strategy)

In this chapter, for the self-adjoint operator L (as set up in Section 4.1), we relegate the Cayley transform to a supplementary role and adopt the functional calculus $\Phi \left(L\right)$ as the main route. From now on we write

$$\mathbf{K}:=\Phi \left(L\right)$$

and first establish sufficient conditions for $\mathbf{K}$ to be Hilbert–Schmidt class (${\mathcal{S}}_2$). Under this assumption, we discuss the entire-function property and coefficient expansion of ${det}_2(I+z\mathbf{K})$ in Section 7.2, and in Section 7.3 connect $\left({\mathbf{K}}^r\right)$ to the distributional equivalence of §6. Justification for exchanging limits, localization, and cyclic products can be found in Section 4.2 (Proposition 4.2, Theorem 4.2) and Section 4.3 (Proposition 4.4).

Notation and conventions.

• Band-limited tests from §5–§6 are denoted by $\varphi$, while in this chapter the functional calculus kernel is denoted by $\Phi$.
• $\Phi :\mathbb{R}\to \mathbb{R}$ is assumed to be even and real-valued and smooth; when necessary, we use $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$ or convolution with a band-limited approximation.
• The symmetric measure corresponding to the eigenvalue sequence ${\{\pm {\gamma }_k\}}_{k\ge 1}$ is ${\mu }_L:={\sum }_{k\ge 1}({\delta }_{{\gamma }_k}+{\delta }_{-{\gamma }_k})$ (see Section 5.1).

Sufficient Condition for Hilbert–Schmidt and Its Derivation

First, we identify the Hilbert–Schmidt norm of $\mathbf{K}=\Phi \left(L\right)$ via the spectral measure as ${\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2={\sum }_{k\ge 1}{|\Phi \left({\gamma }_k\right)|}^2$ (Lemma below). Using the Weyl law (Section 3.4, Theorem 5.2) stating that $d{N}_{\mathrm{eig}}\left(t\right)\sim {\displaystyle \frac{1}{2\pi }}logtdt$ (main term), we obtain an estimate $\sum |\Phi \left({\gamma }_k\right){|}^2\approx {\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}logtdt$.

Lemma 7.1

(Spectral representation and ${\mathcal{S}}_{\mathbf{2}}$ norm). For the functional calculus of a self-adjoint L, $\mathbf{K}=\Phi \left(L\right)$ satisfies

$${\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2=\sum _{{\gamma }_k>0}\left(|\Phi \left({\gamma }_k\right){|}^2+{|\Phi (-{\gamma }_k)|}^2\right)={\int }_{\mathbb{R}}{|\Phi \left(t\right)|}^{2}d{\mu }_L\left(t\right).$$

In particular, if $\Phi$ is even then ${\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2=2{\sum }_{{\gamma }_k>0}{|\Phi \left({\gamma }_k\right)|}^2$.

Proof. 

By the spectral theorem, $L=\int td{E}_L\left(t\right)$ and $\Phi \left(L\right)=\int \Phi \left(t\right)d{E}_L\left(t\right)$. The ${\mathcal{S}}_2$ norm is the square root of $\left({\mathbf{K}}^{*}\mathbf{K}\right)$, and orthogonality in the eigen-decomposition yields the claim. □

Proposition 7.1

(Sufficient conditions for $\Phi \left(\mathbf{L}\right)\in {\mathcal{S}}_{\mathbf{2}}$). Let $\Phi :\mathbb{R}\to \mathbb{R}$ be even, real, and measurable. If any of the following holds, then $\Phi \left(L\right)\in {\mathcal{S}}_2$:

(i)

${\displaystyle {\int }_0^1{|\Phi \left(t\right)|}^{2}dt<\infty }$ and ${\displaystyle {\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}log(2+t)dt<\infty }$;

(ii)

More strongly, $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$;

(iii)

Or $\Phi$ is band-limited with $\widehat{\Phi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$.

In this case,

$${\parallel \Phi \left(L\right)\parallel }_{{\mathcal{S}}_2}^2\le C\left({\int }_0^1{|\Phi \left(t\right)|}^{2}dt+{\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}log(2+t)dt\right),$$

(42)

where $C>0$ depends only on the constants in the Weyl law of Section 3.4 (Theorem 5.2).

Sketch of Proof.

From Lemma 7.1, ${\parallel \Phi \left(L\right)\parallel }_{{\mathcal{S}}_2}^2={\int |\Phi \left(t\right)|}^{2}d{\mu }_L\left(t\right)={\int }_0^{\infty }{|\Phi \left(t\right)|}^{2}d{N}_{\mathrm{eig}}\left(t\right).$ By integration by parts and $N_{\mathrm{eig}}\left(t\right)={\displaystyle \frac{t}{2\pi }}log{\displaystyle \frac{t}{4{\pi }^2}}-{\displaystyle \frac{t}{2\pi }}+O(logt)$ (Theorem 5.2),

$${\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}d{N}_{\mathrm{eig}}\left(t\right)\ll {\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}logtdt+{\int }_1^{\infty }t\left|{\left(\right|\Phi |}^2{)}^{\prime }\left(t\right)\right|{\displaystyle \frac{dt}{t}},$$

and the latter can be absorbed into ${\int |\Phi |}^2+\int {\left|{\Phi }^{\prime }\right|}^2$ using ${\left|\right(|\Phi |}^2{)}^{\prime }|\le 2|\Phi \left|\right|{\Phi }^{\prime }|$ and Young/Hardy-type estimates (trivial if $\Phi \in \mathcal{S}$). In the band-limited case, the Paley–Wiener-type inequality (Lemma 5.2) yields ${\parallel |\Phi |}^{\prime }{\parallel }_{L^2}\lesssim \eta {\parallel \Phi \parallel }_{L^2}$, giving (42). □

Remark 7.1 (On evenness and the Cayley transform).

The evenness assumption aligns with the symmetric spectrum $\{\pm {\gamma }_k\}$ and is effective in simplifying multiplicity counting in trace-class arguments (Section 4.3). Although one could equivalently work with $\Psi \left(U\right)$ via the Cayley transform $U=(L-iI){(L+iI)}^{-1}$, we here unify the discussion in terms of $\Phi \left(L\right)$ (technical justification in Section 4.2).

Summary: Connection to the Next Section

In this subsection, we fixed the convention of taking $\mathbf{K}=\Phi \left(L\right)$ as the main object, and obtained sufficient conditions (Proposition 7.1) to ensure $\mathbf{K}\in {\mathcal{S}}_2$. This sets the stage for Section 7.2, where we establish the entire-function property, coefficient expansion, and zero structure (Theorem 7.1) of the regularized Fredholm determinant ${det}_2(I+z\mathbf{K})$, and in Section 7.3 transport $\left({\mathbf{K}}^r\right)$ to the distributional equivalence/difference of §6.

7.2. Regularized Fredholm Determinant: Entire Functionality and Expansion [6,26,36]

Position of This Subsection (Relation to the Overall Strategy)

For $\mathbf{K}=\Phi \left(L\right)\in {\mathcal{S}}_2$ fixed in Section 7.1 (Proposition 7.1), we establish the entire-function property, zero structure, coefficient expansion (starting index $r\ge 2$), and growth estimates for the regularized Fredholm determinant

$${det}_2(I+z\mathbf{K}).$$

This will form the basis for the coefficient identification in Section 7.3.

Definition and Basic Properties

Definition 7.1 (Regularized determinant (Hilbert–Schmidt class)). Let ${\left\{{\lambda }_j\right\}}_{j\ge 1}$ (counted with algebraic multiplicity) be the nonzero eigenvalues of $\mathbf{K}\in {\mathcal{S}}_2$. The regularized Fredholm determinant ${det}_2(I+z\mathbf{K})$ is defined by

$${det}_2(I+z\mathbf{K}):=\prod _{j\ge 1}\left\{(1+z{\lambda }_j)e^{-z{\lambda }_j}\right\},$$

(43)

a Weierstrass-type regularization; the Hilbert–Schmidt property ${\sum }_j{\left|{\lambda }_j\right|}^2<\infty$ guarantees convergence.

Remark 7.2 (Relation to trace class).

If $\mathbf{K}\in {\mathcal{S}}_1$ then ${det}_2(I+z\mathbf{K})=det(I+z\mathbf{K})e^{-z\mathbf{K}}$, so the linear term is removed by the normalization. Here we focus on $\mathbf{K}\in {\mathcal{S}}_2$ and do not assume $\mathbf{K}$ exists.

Entire Function Property, Zero Structure, and Coefficient Expansion

Theorem 7.1

(Entire function property and expansion of ${det}_{\mathbf{2}}(\mathbf{I}+\mathbf{z}\mathbf{K})$). Let $\mathbf{K}\in {\mathcal{S}}_2$. Then:

(a) 

${det}_2(I+z\mathbf{K})$ is anentire functionon $z\in \mathcal{C}$.

(b) 

Its zeros occur precisely at $z=-{\lambda }_j^{-1}$ for ${\lambda }_j\ne 0$, with multiplicity equal to the algebraic multiplicity of the eigenvalue.

(c) 

The power series expansion near the origin is

$$log{det}_2(I+z\mathbf{K})=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left({\mathbf{K}}^r\right),$$

(44)

with derivative form

$${\displaystyle \frac{d}{dz}}log{det}_2(I+z\mathbf{K})=\sum _{r\ge 2}{(-1)}^{r-1}{z}^{r-1}\left({\mathbf{K}}^r\right).$$

(45)

All coefficients are finite (${\mathbf{K}}^2\in {\mathcal{S}}_1$ and $\mathbf{K}$ is bounded), and (16) converges as a holomorphic power series around the origin, coinciding with theentire functiongiven by analytic continuation.

Sketch of Proof.

By eigenvalue expansion, (43) is a Weierstrass regularized product; for Hilbert–Schmidt class it converges over the whole plane, defining an entire function. (b) follows immediately from the zero locations of the factors. For (c), apply $log\left((1+w)e^{-w}\right)={\sum }_{r\ge 2}{(-1)}^{r-1}{w}^r/r$ to each eigenvalue $w=z{\lambda }_j$, taking $\left|z\right|$ sufficiently small to permit termwise summation. The coefficients $\left({\mathbf{K}}^r\right)$ are finite for $r\ge 2$ since ${\mathbf{K}}^2\in {\mathcal{S}}_1$ and $\mathbf{K}$ is bounded. Analyticity then extends the expansion to all z. □

Remark 7.3 (Significance of starting index r≥2).

Because (16) starts at $r=2$, there is no need for $\mathbf{K}$. This is the core of the normalization in ${det}_2$. Thus, in coefficient identification (Section 7.3) we only deal with $\left({\mathbf{K}}^r\right)$ for $r\ge 2$.

Growth Estimate and Preparation for Jensen/Carleman Application

Proposition 7.2

(Quadratic bound on growth; order $\le \mathbf{2}$). Let $\mathbf{K}\in {\mathcal{S}}_2$. There exist absolute constants $C_1,C_2>0$ such that for any $z\in \mathcal{C}$,

$$log\left|{det}_2(I+z\mathbf{K})\right|\le C_1{\left|z\right|}^2{\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2+C_{2}log\left(1+\left|z\right|\parallel \mathbf{K}\parallel \right).$$

(46)

In particular, ${det}_2(I+z\mathbf{K})$ is an entire function of order $\le 2$, and Jensen (or Carleman) type zero-counting estimates apply.

Sketch of Proof.

Use the product representation (43) and a splitting argument. For any z, let $J:=\{j:|z{\lambda }_j|\ge \frac{1}{2}\}$ (finite). The finite “head” ${\prod }_{j\in J}$ can be crudely bounded by $\ll exp\left({C\left|z\right|}^2{\sum }_{j\in J}{\left|{\lambda }_j\right|}^2\right)$. For the “tail” ${\prod }_{j\notin J}$, apply $|log(1+w)-w|\le {\left|w\right|}^2$ for $\left|w\right|\le \frac{1}{2}$ to each $w=z{\lambda }_j$, giving

$$log\left|\prod _{j\notin J}(1+z{\lambda }_j)e^{-z{\lambda }_j}\right|\le \sum _{j\notin J}|z{\lambda }_j{|}^2\le {\left|z\right|}^2{\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2.$$

Finally, absorb the finite head contribution using the crude bound with $\parallel \mathbf{K}\parallel$ to obtain (46). □

Corollary 7.2

(Rough upper bound on zero count). Let $n\left(r\right)$ be the total number (counted with multiplicity) of zeros in $\left|z\right|\le r$. From Jensen’s formula and (46),

$$n\left(r\right)\ll r^2{\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2+log\left(1+r\parallel \mathbf{K}\parallel \right),$$

with an absolute implied constant.

Remark 7.4 (Self-adjoint case).

In our setting, $\mathbf{K}=\Phi \left(L\right)$ with $\Phi$ even and real, so $\mathbf{K}$ is self-adjoint. Thus ${\lambda }_j\in \mathbb{R}$, and the zeros $-{\lambda }_j^{-1}$ lie only on the real axis (for ${\lambda }_j\ne 0$).

Summary: Connection to the Next Section

In this subsection we established the entire-function property of ${det}_2(I+z\mathbf{K})$ (Theorem 7.1), the coefficient expansion (16) starting at $r\ge 2$, and the growth estimate of order $\le 2$ (Proposition 7.2). This enables us, in the next Section 7.3, to directly transfer $\left({\mathbf{K}}^r\right)$ to the distributional equivalence / wide-band difference of §6, identifying the coefficients in (16) on both the operator and zeta sides.

7.3. Coefficient Identification: $(\Phi {\left(L\right)}^r)$ and Transfer of Distributional Equivalence [6,14,29]

Position of this Subsection (Relation to the Overall Strategy)

For the expansion in Section 7.2

$$log{det}_2(I+z\Phi \left(L\right))=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left(\Phi {\left(L\right)}^r\right)$$

(47)

(eq. (16) in Theorem 7.1), we directly transfer the coefficients $(\Phi {\left(L\right)}^r)$ to the distributional equivalence between ${\mu }_L$ and ${\mu }_{\xi }$ established in §6. Hereafter, the Fourier convention follows §6, $\widehat{f}\left(\xi \right)={\int }_{\mathbb{R}}f\left(t\right)e^{-it\xi }dt$.

Expressing the Trace as a Distributional Moment

Definition 7.3

(Inverse Fourier transform of $\Phi$ and $\mathbf{r}$-fold convolution). Let $\check{\Phi }\left(t\right):={\mathbb{F}}_{\lambda \to t}^{-1}\Phi \left(\lambda \right)$ (with this convention $\widehat{\check{\Phi }}=\Phi$). For an integer $r\ge 2$, denote by ${\check{\Phi }}^{(*r)}$ the r-fold time convolution.

Lemma 7.2

(Trace as a distributional moment). For a self-adjoint L and even, real $\Phi$, for any integer $r\ge 2$,

$$\left(\Phi {\left(L\right)}^r\right)=\sum _{k\ge 1}\left(\Phi {\left({\gamma }_k\right)}^r+\Phi {(-{\gamma }_k)}^r\right)=〈{\mu }_L,\Phi {\left(·\right)}^r〉.$$

(48)

Furthermore, since $\Phi {\left(\lambda \right)}^r=\widehat{{\check{\Phi }}^{(*r)}}\left(\lambda \right)$,

$$\left(\Phi {\left(L\right)}^r\right)=〈{\mu }_L,\widehat{{\check{\Phi }}^{(*r)}}〉.$$

(49)

Proof. 

By the spectral theorem, the eigenvalues of $\Phi \left(L\right)$ are $\{\Phi (\pm {\gamma }_k)\}$ (with multiplicity). This gives the first equality by definition. Next, $\Phi \left(\lambda \right)=\widehat{\check{\Phi }}\left(\lambda \right)$ implies $\Phi {\left(\lambda \right)}^r=\widehat{{\check{\Phi }}^{(*r)}}\left(\lambda \right)$ (convolution theorem for the Fourier transform). Substituting $\lambda =\pm {\gamma }_k$ and summing yields (49). □

Remark 7.5 (Alternative proof via localized cyclic product).

Write $\Phi \left(L\right)=\int \check{\Phi }\left(t\right)e^{-itL}dt$, so that $\Phi {\left(L\right)}^r=\int {\check{\Phi }}^{(*r)}\left(t\right)e^{-itL}dt$. By Proposition 4.4 (localized cyclic product), $(\Phi {\left(L\right)}^r)=\int {\check{\Phi }}^{(*r)}\left(t\right)\left(e^{-itL}\right)dt$. Since $\left(e^{-itL}\right)=\langle {\mu }_L,e^{-it\left(·\right)}\rangle$, this agrees with (49).

Small Band: Complete Coefficient Equality

Proposition 7.3

(Coefficient identification in the small band). Let $\check{\Phi }\in C_c^{\infty }\left([-{\eta }_0,{\eta }_0]\right)$ be even and real, and fix an integer $r\ge 2$. Set ${\eta }_r:=r{\eta }_0$. If ${\eta }_r<log2$ and (if necessary) endpoint vanishing ${\widehat{\left({\Phi }^r\right)}}^{\left(j\right)}(\pm {\eta }_r)=0$ for $0\le j\le m$ holds, then

$$\left(\Phi {\left(L\right)}^r\right)=〈{\mu }_L,{\Phi }^r〉=〈{\mu }_{\xi },{\Phi }^r〉={\int }_{\mathbb{R}}\Phi {\left(t\right)}^r{K}_0\left(t\right)dt.$$

(50)

Proof. 

By Lemma 7.2, $(\Phi {\left(L\right)}^r)=\langle {\mu }_L,{\Phi }^r\rangle$. The Fourier transform of ${\Phi }^r$ is ${\check{\Phi }}^{(*r)}$, whose support lies in $[-{\eta }_r,{\eta }_r]$. Thus ${\Phi }^r\in A_{{\eta }_r}$. By Theorem 6.1 (small-band equivalence), $\langle {\mu }_L,{\Phi }^r\rangle =\langle {\mu }_{\xi },{\Phi }^r\rangle =\int {\Phi }^r{K}_0$. □

Wide Band: Coefficient Difference = Finite Prime Sum + Boundary Term

Theorem 7.2

(Coefficient difference formula in the wide band). Under the assumptions of Proposition 7.3, let ${\eta }_r\ge log2$ (assume endpoint vanishing order $m\ge 1$). Then

$$\left(\Phi {\left(L\right)}^r\right)-〈{\mu }_{\xi },{\Phi }^r〉=-\sum _{\begin{array}{c}n\ge 2\\ logn\le {\eta }_r\end{array}}\Lambda \left(n\right)\left({\check{\Phi }}^{(*r)}(logn)+{\check{\Phi }}^{(*r)}(-logn)\right)+{\mathcal{B}}_{{\eta }_r,m}\left[{\Phi }^r\right],$$

(51)

where ${\mathcal{B}}_{{\eta }_r,m}$ is the boundary term localized at the band edge, and by Lemma 6.2,

$$\left|{\mathcal{B}}_{{\eta }_r,m}\left[{\Phi }^r\right]\right|\le C_{m,{\eta }_r}\sum _{j=0}^m{∥{\partial }_t^j\left({\Phi }^r\right)∥}_{L^1\left(\mathbb{R}\right)}.$$

(52)

Proof. 

From Lemma 7.2, $(\Phi {\left(L\right)}^r)=\langle {\mu }_L,{\Phi }^r\rangle$. Apply Theorem 6.2 to $\varphi ={\Phi }^r\in A_{{\eta }_r}$ and use $\widehat{\varphi }={\check{\Phi }}^{(*r)}$ to obtain (51). Boundary estimation is by Lemma 6.2. □

Lemma 7.3

(Rough bound for the finite prime sum). In the situation of Theorem 7.2,

$$\left|\sum _{logn\le {\eta }_r}\Lambda \left(n\right)\left({\check{\Phi }}^{(*r)}(logn)+{\check{\Phi }}^{(*r)}(-logn)\right)\right|\le 2{\parallel {\Phi }^r\parallel }_{L^1\left(\mathbb{R}\right)}{\eta }_r{e}^{{\eta }_r}.$$

(53)

Proof. 

Apply Lemma 6.1 to $\varphi ={\Phi }^r$, using $\parallel \widehat{\varphi }{\parallel }_{\infty }=\parallel {\check{\Phi }}^{(*r)}{\parallel }_{\infty }\le {\parallel \varphi \parallel }_{L^1}={\parallel {\Phi }^r\parallel }_{L^1}$. □

Remark 7.6 (Perspective on the coefficient difference).

Note that only the values of ${\check{\Phi }}^{(*r)}$ appear in the finite prime sum. If the support of $\check{\Phi }$ is small (${\eta }_0$ small), the contributing n are limited to finitely many with $logn\le r{\eta }_0$. Moreover, with appropriate smoothing of $\Phi$, the quantity ${\sum }_{j\le m}{\parallel {\partial }^j\left({\Phi }^r\right)\parallel }_{L^1}$ can also be controlled (Bernstein/Paley–Wiener type estimates; see Lemma 5.2).

Density and Approximation (Relaxation of Band Limitation)

Proposition 7.4

(Relaxation of band limitation via approximation). For a general $\check{\Phi }\in \mathcal{S}\left(\mathbb{R}\right)$, let ${\widehat{\psi }}_{\eta }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$ be an approximate identity of unit mass (${\psi }_{\eta }\to {\delta }_0$ weakly), and set

$${\check{\Phi }}_{\eta }:=\check{\Phi }*{\psi }_{\eta },{\Phi }_{\eta }=\left(\widehat{{\check{\Phi }}_{\eta }}\right)=\Phi ·\widehat{{\psi }_{\eta }}.$$

Then, for any fixed $r\ge 2$,

$$\left({\Phi }_{\eta }{\left(L\right)}^r\right)\underset{\eta \to \infty }{\to }\left(\Phi {\left(L\right)}^r\right),$$

by ${\mathcal{S}}_2$-boundedness, the dominated convergence theorem, and continuity of localized cyclic products. Hence (50)–(51) extend in the approximation limit to general $\Phi$.

Proof. 

We have ${\Phi }_{\eta }\to \Phi$ uniformly and ${\check{\Phi }}_{\eta }\to \check{\Phi }$ in $\mathcal{S}$. Then ${\Phi }_{\eta }\left(L\right)\to \Phi \left(L\right)$ strongly in ${\mathcal{S}}_2$ and ${sup}_{\eta }{\parallel {\Phi }_{\eta }\left(L\right)\parallel }_{{\mathcal{S}}_2}<\infty$. Applying Proposition 4.4 to multiple products yields the claim. □

Summary: Connection to the Next Section

By Lemma 7.2, $(\Phi {\left(L\right)}^r)$ is precisely $\langle {\mu }_L,{\varphi }_r\rangle$ for ${\varphi }_r:={\Phi }^r$. In the small band, ${\mu }_L={\mu }_{\xi }$ gives complete coefficient equality (Proposition 7.3), while in the wide band the finite prime sum + boundary term carries the difference (Theorem 7.2). Substituting these into (47), the next Section 7.4 organizes the local agreement between ${det}_2(I+z\Phi \left(L\right))$ and the “$\xi$-side” generating function, together with the rational difference structure (finite prime sum).

7.4. Identity in the Small Band and Analytic Continuation (Positioning of the Wide-Band Difference) [7,30,37]

Position of This Subsection (Relation to the Overall Strategy)

Combining the expansion formula of Section 7.2 (Theorem 7.1) with the coefficient identification in Section 7.3 (Lemma 7.2, Proposition 7.3, Theorem 7.2), we compare

$$F_L\left(z\right):={det}_2\left(I+z\Phi \left(L\right)\right),F_{\xi }\left(z\right):=exp\left(\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r〈{\mu }_{\xi },{\Phi }^r〉\right).$$

Here $\Phi$ is even and real, with $\check{\Phi }\in \mathcal{S}\left(\mathbb{R}\right)$, and, if necessary, we use band-limited approximations via Proposition 7.4 in Section 7.3.

Finite-order identity in the small band and its remainder

Definition 7.4

(Effective band degree). Let ${\eta }_0>0$ be the effective bandwidth (time side) of $\check{\Phi }$, and assume $supp\check{\Phi }\subset [-{\eta }_0,{\eta }_0]$. Define

$$R_0(\Phi ):=max\{r\in {\mathbb{N}}_{\ge 2}:r{\eta }_0<log2\}$$

to be the “maximum degree for which coefficients automatically agree in the small band” (by convention $R_0(\Phi )=1$ if the set is empty).

Theorem 7.37.3

(Finite-order identity in the small band). Under the above assumptions, in the power series around the origin

$$log{F}_L\left(z\right)=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left(\Phi {\left(L\right)}^r\right),log{F}_{\xi }\left(z\right)=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r〈{\mu }_{\xi },{\Phi }^r〉,$$

the coefficients coincide completely for degrees $r\le R_0(\Phi )$. Namely,

$$\forall 2\le r\le R_0(\Phi ),\left(\Phi {\left(L\right)}^r\right)=〈{\mu }_{\xi },{\Phi }^r〉={\int }_{\mathbb{R}}\Phi {\left(t\right)}^r{K}_0\left(t\right)dt,$$

where the last equality follows from Theorem 6.1 and Proposition 7.3.

Proof. 

By definition, ${\check{\Phi }}^{(*r)}$ is supported in $[-{\eta }_r,{\eta }_r]$ with ${\eta }_r=r{\eta }_0$. Thus for $r\le R_0(\Phi )$ we have ${\eta }_r<log2$, and Proposition 7.3 applies for each such r. □

Proposition 7.5 (Expression of the remainder (generating function of finite prime sums + boundary terms)). Let ${\eta }_0>0$ and $R_0(\Phi )$ be as above. Then there exists a radius $\rho >0$ such that for $\left|z\right|<\rho$,

$$\begin{array}{cc}\hfill & log{\displaystyle \frac{F_L\left(z\right)}{F_{\xi }\left(z\right)}}=\sum _{r>R_0(\Phi )}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left((\Phi {\left(L\right)}^r)-\langle {\mu }_{\xi },{\Phi }^r\rangle \right)\hfill \\ \hfill & =-\sum _{r>R_0(\Phi )}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\sum _{\begin{array}{c}n\ge 2\\ logn\le r{\eta }_0\end{array}}\Lambda \left(n\right)\left({\check{\Phi }}^{(*r)}(logn)+{\check{\Phi }}^{(*r)}(-logn)\right)+\sum _{r>R_0(\Phi )}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r{\mathcal{B}}_r,\hfill \end{array}$$

(54)

where ${\mathcal{B}}_r:={\mathcal{B}}_{{\eta }_r,m}\left[{\Phi }^r\right]$ is the boundary term from Section 6.4, and by Lemma 6.2 $|{\mathcal{B}}_r|\le C_{m,{\eta }_r}{\sum }_{j=0}^m{\parallel {\partial }_t^j\left({\Phi }^r\right)\parallel }_{L^1}$. In particular, for sufficiently small $\left|z\right|$, (54) converges absolutely and the right-hand side defines an analytic function.

Proof. 

Apply Theorem 7.2 for each degree to obtain the second expression. For convergence, note that $\parallel {\check{\Phi }}^{(*r)}{\parallel }_{\infty }\le \parallel \check{\Phi }{\parallel }_{\infty }{\parallel \check{\Phi }\parallel }_{L^1}^{r-1}$ and ${\sum }_{logn\le r{\eta }_0}\Lambda \left(n\right)\ll r{\eta }_0{e}^{r{\eta }_0}$ (Lemma 6.1), giving

$$\left|{\displaystyle \frac{1}{r}}{z}^r\sum _{logn\le r{\eta }_0}\Lambda \left(n\right){\check{\Phi }}^{(*r)}(\pm logn)\right|\ll ({\eta }_0\parallel \check{\Phi }{\parallel }_{\infty }){\left(\left|z\right|e^{{\eta }_0}{\parallel \check{\Phi }\parallel }_{L^1}\right)}^r.$$

Similarly, Leibniz and the Bernstein-type estimate (Lemma 5.2) yield ${\sum }_{j\le m}\parallel {\partial }^j\left({\Phi }^r\right){\parallel }_{L^1}\ll r^m{\parallel \Phi \parallel }_{W^{m,1}}{\parallel \Phi \parallel }_{\infty }^{r-1}$, so $\left|z\right|<min\left\{\right(e^{{\eta }_0}\parallel \check{\Phi }{\parallel }_{L^1}{)}^{-1}{,\parallel \Phi \parallel }_{\infty }^{-1}\}$ ensures absolute convergence. □

Remark 7.7 (Summary of the structure).

Equation (54) says that “$log(F_L/F_{\xi })$ is nothing but the generating function of finite prime sums (coefficients ${\check{\Phi }}^{(*r)}(\pm logn)$) plus the generating function of boundary terms.” Hence, when ${\eta }_0\downarrow 0$ (extreme narrowing in the time side), the right-hand side becomes uniformly small, enhancing agreement in a small disk.

Prototype of Analytic Continuation and Densification Strategy

Proposition 7.6 (Uniqueness extension via a dense family (prototype)). Let ${\left\{{\Phi }_{\nu }\right\}}_{\nu \ge 1}\subset \mathcal{S}\left(\mathbb{R}\right)$ be even and real, with ${\check{\Phi }}_{\nu }$ supported in $[-{\eta }_{\nu },{\eta }_{\nu }]$, ${\eta }_{\nu }\downarrow 0$, and ${sup}_{\nu }{\parallel {\Phi }_{\nu }\parallel }_{W^{m,1}}<\infty$ (uniform ${\mathcal{S}}_2$-boundedness for all $\nu$). Then for any fixed radius $0<r<{\rho }_{*}:={inf}_{\nu }min\left\{\right(e^{{\eta }_{\nu }}\parallel {\check{\Phi }}_{\nu }{\parallel }_1{)}^{-1},\parallel {\Phi }_{\nu }{\parallel }_{\infty }^{-1}\}$,

$$\underset{\nu \to \infty }{lim}\underset{\left|z\right|\le r}{sup}\left|log{F}_L^{\left(\nu \right)}\left(z\right)-log{F}_{\xi }^{\left(\nu \right)}\left(z\right)\right|=0,$$

where $F_L^{\left(\nu \right)}\left(z\right):={det}_2(I+z{\Phi }_{\nu }\left(L\right))$ and $F_{\xi }^{\left(\nu \right)}\left(z\right):=exp{\sum }_{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\langle {\mu }_{\xi },{\Phi }_{\nu }^r\rangle$. In particular, functional agreement on a small disk is achieved to any desired accuracy over the dense family.

Proof. 

The bound on the right-hand side of Proposition 7.5 converges geometrically to zero as ${\eta }_{\nu }\downarrow 0$ with uniform boundedness. Uniform convergence of analytic families yields the claim. □

Remark 7.8 (Limitations for a fixed Φ).

For a fixed $\Phi$, $R_0(\Phi )$ is finite, so complete power-series agreement of $log{F}_L$ and $log{F}_{\xi }$ is not generally available. However, (54) decomposes the difference explicitly into a “prime generating function + boundary generating function,” and by taking $\left|z\right|$ small, the remainder can be made arbitrarily small (radius determined by ${\eta }_0,\parallel \check{\Phi }{\parallel }_1,{\parallel \Phi \parallel }_{\infty }$).

Summary: Goal of §7 and Hints for §8 Onward

In this section we have given: (i) the finite-order coefficient identity dependent on the small band (Theorem 7.3), (ii) the explicit form of the difference as an analytic generating function (Proposition 7.5), (iii) the approximate achievement of functional agreement by extreme narrowing of the band (Proposition 7.6). These are the final steps in lifting the “distributional equivalence / finite-sum difference” of §6 to the ${det}_2$-generating function of §7, and form the basis for analysing, in the next chapter (e.g., in §8, Jensen/Carleman type zero distribution estimates, or implications for RH), how the contribution of prime terms is reflected in the zero configuration of ${det}_2$.

Next (Optional): Rough Upper Bound on Zero Distribution

If necessary, together with Proposition 7.2 of Section 7.2, we present in the appendix a bound of type $n\left(r\right)\ll r^2$ (Proposition 7.7) for the zero count $n\left(r\right)$ of ${det}_2$.

7.5. Upper Bounds on Zero Distribution and Consistency Check [6,36]

Position of This Subsection (Relation to the Overall Strategy)

In this subsection, using the growth estimate from Section 7.2 (Proposition 7.2), we crudely bound the zero distribution of the entire function $F_L\left(z\right):={det}_2(I+z\Phi \left(L\right))$, and confirm that it is consistent with the Weyl-type estimate of §5 (Theorem 5.2) and the Hilbert–Schmidt condition of §7.1 (Proposition 7.1). In the self-adjoint case $\mathbf{K}=\Phi \left(L\right)$, the eigenvalues ${\lambda }_j\in \mathbb{R}$ correspond to zeros appearing only on the real axis at $z_j=-{\lambda }_j^{-1}$ (Theorem 7.1(b)).

Quadratic-Type Upper Bound for Zero Counting

Proposition 7.7

(Quadratic-type upper bound for zero counting). Let $\mathbf{K}=\Phi \left(L\right)\in {\mathcal{S}}_2$, and let $n_F\left(r\right)$ be the number of zeros (counted with multiplicity) in $\left|z\right|\le r$. There exist absolute constants $C_1,C_2>0$ such that for any $r\ge 1$,

$$n_F\left(r\right)\le C_1{r}^2{\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2+C_{2}log\left(1+r\parallel \mathbf{K}\parallel \right).$$

(55)

In particular, $F_L$ is an entire function of order $\le 2$, and its zero count is bounded in a “quadratic” fashion.

Sketch of Proof

Substitute the growth estimate (46) from Proposition 7.2 into Jensen’s formula ${\int }_0^r{\displaystyle \frac{n_F\left(t\right)}{t}}dt={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }log|F_L\left(r{e}^{i\theta }\right)|d\theta -log|F_L\left(0\right)|$, and use the monotonicity of $n_F$ and mean-value estimates to obtain $n_F\left(r\right)\ll r^2{\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2+log(1+r\parallel \mathbf{K}\parallel )$. □

Corollary 7.5 (Concentration of zeros on the real axis (self-adjoint case)). If $\mathbf{K}$ is self-adjoint (in our setting, Φ is even and real), then all zeros lie on the real axis, and

$$\left\{z_j\right\}=\{-{\lambda }_j^{-1}:{\lambda }_j\in Spec\left(\mathbf{K}\right)\setminus \left\{0\right\}\}.$$

Hence $|z_j{|}^{-2}$ is square summable, and

$$\sum _j{\displaystyle \frac{1}{|z_j{|}^2}}=\sum _j|{\lambda }_j{|}^2={\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2<\infty .$$

(56)

Proof. 

The zero locations follow from Theorem 7.1(b). Equation (56) is the definition of the ${\mathcal{S}}_2$ norm. □

Remark 7.9 (Normalization of det2 and order ≤2).

The normalization in Definition 7, ${\prod }_j(1+z{\lambda }_j)e^{-z{\lambda }_j}$, corresponds to a genus-1 Weierstrass factor, and from ${\sum }_j{\left|{\lambda }_j\right|}^2<\infty$ we obtain order $\le 2$. Proposition 7.2 can be regarded as a quantitative version of this.

Consistency with Weyl’s Law and HS Condition

Proposition 7.8

(Consistent bound from Weyl’s law and the HS condition). Under the assumptions of Section 7.1, ${\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2\asymp {\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}logtdt$ (see the proof of Proposition 7.1). Therefore (55) yields

$$n_F\left(r\right)\ll r^2\left({\int }_1^{\infty }{|\Phi \left(t\right)|}^{2}logtdt\right)+log\left(1+{r\parallel \Phi \parallel }_{\infty }\right),$$

(57)

which is consistent with the Weyl main term from §5, $N_{\mathrm{eig}}\left(T\right)={\displaystyle \frac{T}{2\pi }}log{\displaystyle \frac{T}{4{\pi }^2}}-{\displaystyle \frac{T}{2\pi }}+O(logT)$ (Theorem 5.2).

Sketch of Proof

From Lemma 7.1 and integration by parts (as in the proof of Proposition 7.1) we obtain ${\parallel \mathbf{K}\parallel }_{{\mathcal{S}}_2}^2\ll \int {|\Phi |}^{2}log(2+t)dt$. Substituting this into (55) gives (57). Weyl’s law describes the distribution of eigenvalues of L, while the upper bound on the zero distribution of ${det}_2$ gives the behaviour of a generating function depending on $\Phi$. Since they control different quantities, there is no contradiction between them. □

Remark 7.10 (Design guideline along a family).

For a band-shrinking family $\left\{{\Phi }_{\nu }\right\}$ (Proposition 7.6 of Section 7.4), controlling $\int |{\Phi }_{\nu }{|}^{2}log(2+t)dt$ uniformly allows the right-hand side of (57) to be made uniform. This becomes a technical condition for applying the uniqueness principle via Jensen/Carleman in §8.

Zeros and Growth of the Difference Function (Preparation)

Definition 7.6

(Difference function). For small $\left|z\right|$, define $D\left(z\right):=log{F}_L\left(z\right)-log{F}_{\xi }\left(z\right)$ (cf. (54) in Section 7.4), and analytically continue it as necessary.

Proposition 7.9 (Growth and zeros of the difference function (local form)). In a sufficiently small disk in $\left|z\right|$,

$$\left|D\left(z\right)\right|\le C\sum _{r>R_0(\Phi )}{\displaystyle \frac{{\left|z\right|}^r}{r}}\left({\eta }_0{e}^{r{\eta }_0}\parallel \check{\Phi }{\parallel }_{L^1}^r+r^m{\parallel \Phi \parallel }_{W^{m,1}}{\parallel \Phi \parallel }_{\infty }^{r-1}\right),$$

(Proposition 7.5), and the right-hand side converges absolutely for $\left|z\right|<\rho$. Moreover, by densifying $\Phi$ with a band-shrinking family, for any fixed $r<{\rho }_{*}$ we have ${sup}_{\left|z\right|\le r}\left|D\left(z\right)\right|\to 0$ (Proposition 7.6). Combining this uniform convergence with Proposition 7.7 makes it possible to apply the uniqueness principle (Jensen/Carleman) in §8.

Summary: Bridge to §8

Proposition 7.7 shows that the zero count of ${det}_2$ is bounded quadratically, and self-adjointness restricts all zeros to the real axis (Corollary 7.5). These satisfy the growth assumptions needed in §8 to extend the agreement in a small disk for the difference function $D\left(z\right)$ to agreement over the entire domain using Jensen/Carleman. Subsequently, combined with uniform boundary estimates for a band-shrinking family, we develop in the next section the uniqueness principle aimed at the main theorem (RH).

8. Weil Positivity and the Main Theorem of RH via the Uniqueness Principle

8.1. Shrinking Bandwidth Families and Uniform Vanishing of the Remainder over the Family (Key A) [6,7,26]

Position of This Subsection (Relation to the Overall Strategy)

The difference generating function from Section 7.4, $D\left(z\right)=log{F}_L\left(z\right)-log{F}_{\xi }\left(z\right)$, is expressed, via equation (54) (Proposition 7.5), as the sum of a generating function of a finite sum over primes and a boundary generating function. In this subsection, we construct a test family with shrinking bandwidth $\left\{{\Phi }_{\nu }\right\}$ (${\eta }_{\nu }\downarrow 0$) and show that, for a small disk of fixed radius $\left|z\right|\le \rho$,

$$\underset{\left|z\right|\le \rho }{sup}\left|log{\displaystyle \frac{F_L^{\left(\nu \right)}\left(z\right)}{F_{\xi }^{\left(\nu \right)}\left(z\right)}}\right|\underset{\nu \to \infty }{\to }0.$$

This serves as the input for the uniqueness principle (Key B) in Section 8.2.

Construction and Normalization of the Shrinking Bandwidth Family

Construction 8.1 (Shrinking bandwidth family {Φν}).

Let $\psi \in C_c^{\infty }\left([-1,1]\right)$ be an even, real, smooth mother function satisfying

$${\psi }^{\left(j\right)}(\pm 1)=0(0\le j\le m),{\int }_{\mathbb{R}}\psi \left(t\right)dt=1$$

(m-th order vanishing at the endpoints). Given a decreasing sequence ${\eta }_{\nu }\downarrow 0$, define

$${\check{\Phi }}_{\nu }\left(t\right):={\displaystyle \frac{1}{{\eta }_{\nu }}}\psi \left({\displaystyle \frac{t}{{\eta }_{\nu }}}\right),{\Phi }_{\nu }\left(\lambda \right):=\widehat{{\check{\Phi }}_{\nu }}\left(\lambda \right)=\widehat{\psi }\left({\eta }_{\nu }\lambda \right)$$

(Fourier conventions follow §6). Then

$$supp{\check{\Phi }}_{\nu }\subset [-{\eta }_{\nu },{\eta }_{\nu }],\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^1}=1,\parallel {\Phi }_{\nu }{\parallel }_{L^{\infty }}\le {\parallel \widehat{\psi }\parallel }_{L^{\infty }}=:M_{\psi },$$

and moreover, ${\check{\Phi }}_{\nu }^{(*r)}$ preserves m-th order vanishing at the endpoints $\pm r{\eta }_{\nu }$.

Remark (Uniform norm estimates)

By scaling, ${\partial }_{\lambda }^j{\Phi }_{\nu }\left(\lambda \right)={\eta }_{\nu }^j{\left(\widehat{\psi }\right)}^{\left(j\right)}\left({\eta }_{\nu }\lambda \right)$. Hence $\parallel {\partial }_{\lambda }^j{\Phi }_{\nu }{\parallel }_{L^1}\le {\eta }_{\nu }^{j-1}{\parallel {\left(\widehat{\psi }\right)}^{\left(j\right)}\parallel }_{L^1}$, so for $j\ge 1$ we obtain an upper bound uniform in $\nu$ (in fact, decreasing to 0). Also $\parallel {\Phi }_{\nu }{\parallel }_{L^{\infty }}\le M_{\psi }$ is uniform in $\nu$.

Uniform Control of Boundary Terms over the Family

Lemma 8.1

(Uniform upper bound and vanishing of boundary terms over the family). Let $r\ge 2$ and write ${\eta }_{\nu ,r}:=r{\eta }_{\nu }$. The boundary term ${\mathcal{B}}_{{\eta }_{\nu ,r},m}\left[{\Phi }_{\nu }^r\right]$ from Section 6.4 satisfies

$$\left|{\mathcal{B}}_{{\eta }_{\nu ,r},m}\left[{\Phi }_{\nu }^r\right]\right|\le C\left(m\right)C_{*}{r}^m{M}_{\psi }^{r-1},C_{*}:=\sum _{j=0}^m\underset{\nu }{sup}{\parallel {\partial }_{\lambda }^j{\Phi }_{\nu }\parallel }_{L^1}<\infty ,$$

(58)

where $C\left(m\right)$ depends only on m. In particular, for any $\rho <M_{\psi }^{-1}$,

$$\sum _{r>R_0\left({\Phi }_{\nu }\right)}{\displaystyle \frac{{\left|z\right|}^r}{r}}\left|{\mathcal{B}}_{{\eta }_{\nu ,r},m}\left[{\Phi }_{\nu }^r\right]\right|\underset{\nu \to \infty }{\to }0\mathrm{uniformly}\mathrm{for}\left|z\right|\le \rho ,$$

(59)

where $R_0\left({\Phi }_{\nu }\right):=max\{r\ge 2:r{\eta }_{\nu }<log2\}\to \infty$.

Proof. 

By Lemma 6.2, $|{\mathcal{B}}_{{\eta }_{\nu ,r},m}\left[{\Phi }_{\nu }^r\right]|\le C_{m,{\eta }_{\nu ,r}}{\sum }_{j=0}^m{\parallel {\partial }^j\left({\Phi }_{\nu }^r\right)\parallel }_{L^1}$. Leibniz gives $\parallel {\partial }^j\left({\Phi }_{\nu }^r\right){\parallel }_{L^1}\le C\left(m\right)r^m{M}_{\psi }^{r-1}{\sum }_{a\le j}{\parallel {\partial }^a{\Phi }_{\nu }\parallel }_{L^1}$. For ${\eta }_{\nu ,r}\ge log2$ (i.e. $r>R_0\left({\Phi }_{\nu }\right)$), $C_{m,{\eta }_{\nu ,r}}$ is bounded, depending only on m and $log2$, which yields (58). If $\left|z\right|<M_{\psi }^{-1}$, ${\sum }_{r>R_0}{\displaystyle \frac{{\left|z\right|}^r}{r}}{r}^m{M}_{\psi }^{r-1}$ can be bounded using $q:=\left|z\right|M_{\psi }<1$ as $\ll q^{R_0\left({\Phi }_{\nu }\right)}\to 0$ (tail of a geometric series), yielding uniform convergence. □

Uniform Control of Prime Finite Sum Coefficients over the Family

Lemma 8.2

(Uniform upper bound and vanishing of prime finite sum coefficients over the family). Let $\left|z\right|\le \rho$ with fixed $\rho <1$. For the prime finite sum part of Proposition 7.5,

$$S_{\nu ,r}\left(z\right):={\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\sum _{\begin{array}{c}n\ge 2\\ logn\le r{\eta }_{\nu }\end{array}}\Lambda \left(n\right)\left({\check{\Phi }}_{\nu }^{(*r)}(logn)+{\check{\Phi }}_{\nu }^{(*r)}(-logn)\right),$$

there exists a constant $C>0$ such that

$$\sum _{r>R_0\left({\Phi }_{\nu }\right)}|S_{\nu ,r}\left(z\right)|\le C\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}{\displaystyle \frac{{\left(\rho e^{{\eta }_{\nu }}\right)}^{R_0\left({\Phi }_{\nu }\right)+1}}{1-\rho e^{{\eta }_{\nu }}}}\underset{\nu \to \infty }{\to }0$$

(60)

uniformly in $\left|z\right|\le \rho$.

Proof. 

We have $|{\check{\Phi }}_{\nu }^{(*r)}\left(x\right)|\le \parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^1}^{r-1}={\parallel {\check{\Phi }}_{\nu }\parallel }_{L^{\infty }}$. Also ${\sum }_{logn\le r{\eta }_{\nu }}\Lambda \left(n\right)\le e^{r{\eta }_{\nu }}r{\eta }_{\nu }\ll e^{r{\eta }_{\nu }}$. Thus

$$|S_{\nu ,r}\left(z\right)|\ll {\displaystyle \frac{1}{r}}{\left|z\right|}^r{e}^{r{\eta }_{\nu }}\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}\le {\parallel {\check{\Phi }}_{\nu }\parallel }_{L^{\infty }}{\left(\rho e^{{\eta }_{\nu }}\right)}^r.$$

Summing the geometric series over $r>R_0\left({\Phi }_{\nu }\right)$ yields (60). Note that $\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}\asymp {\eta }_{\nu }^{-1}$, but ${\left(\rho e^{{\eta }_{\nu }}\right)}^{R_0\left({\Phi }_{\nu }\right)}\le {\left(\rho e^{{\eta }_{\nu }}\right)}^{\lfloor (log2)/{\eta }_{\nu }\rfloor }\asymp exp\left((log2){\eta }_{\nu }^{-1}log\rho \right)\to 0$ (since $log\rho <0$), and this decay dominates the divergence of ${\eta }_{\nu }^{-1}$. □

Uniform Vanishing of the Difference Generating Function over the Family

Proposition 8.1

(Uniform vanishing over the family in a small disk). Let ${\rho }_{*}:=min\{M_{\psi }^{-1},1\}$. For any $\rho \in (0,{\rho }_{*})$,

$$\underset{\left|z\right|\le \rho }{sup}\left|log{\displaystyle \frac{F_L^{\left(\nu \right)}\left(z\right)}{F_{\xi }^{\left(\nu \right)}\left(z\right)}}\right|\underset{\nu \to \infty }{\to }0.$$

(61)

Proof. 

From Proposition 7.5, $log(F_L^{\left(\nu \right)}/F_{\xi }^{\left(\nu \right)})={\sum }_{r>R_0\left({\Phi }_{\nu }\right)}{S}_{\nu ,r}\left(z\right)+{\sum }_{r>R_0\left({\Phi }_{\nu }\right)}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r{\mathcal{B}}_{{\eta }_{\nu ,r},m}\left[{\Phi }_{\nu }^r\right]$. By Lemmas 8.2 and 8.1, the sum of both series converges uniformly to 0 for $\left|z\right|\le \rho$ (the tails of the geometric series vanish as $R_0\left({\Phi }_{\nu }\right)\to \infty$). □

Remark (Radius of convergence and choice of mother function)

The lower bound on the radius of convergence ${\rho }_{*}$ depends only on the mother function $\psi$ (${\rho }_{*}\ge M_{\psi }^{-1}$). By choosing $\psi$ smoothly, $M_{\psi }={\parallel \widehat{\psi }\parallel }_{\infty }$ can be controlled, allowing more flexibility in $\rho$.

Summary: Connection to the Next Section (Key B)

From Construction 8.1 and Proposition 8.1, we have shown that along a shrinking bandwidth family, the difference generating function vanishes uniformly in a small disk. In the next Section 8.2, using the growth of order $\le 2$ (Proposition 7.2) and the uniqueness principle of Jensen/Carleman, we will extend this local agreement to global agreement.

8.2. From Agreement in a Small Disk to Agreement on the Whole Domain (Key B: Uniqueness Principle) [36,37]

Supplement. The hypotheses of the uniqueness principle used in this subsection (order, uniform constants, zero control) are made explicit in Appendix A.

Note. For uniqueness from boundary value agreement and the vanishing of a “linear polynomial difference,” see Appendix A.

Position of This Subsection (Relation to the Overall Strategy)

Proposition 8.1 in Section 8.1 shows that for the difference generating function associated with the shrinking bandwidth family $\left\{{\Phi }_{\nu }\right\}$,

$$D_{\nu }\left(z\right):=log{\displaystyle \frac{F_L^{\left(\nu \right)}\left(z\right)}{F_{\xi }^{\left(\nu \right)}\left(z\right)}},$$

we have uniform convergence to 0 on the small disk $\left|z\right|\le \rho$ for some fixed radius $\rho >0$. In this subsection, using the growth estimate from Section 7.2 (Proposition 7.2), we establish a “uniqueness principle” (Carleman/three–circle–type interpolation) that extends this local agreement to the entire domain. From here on, constants independent of $\nu$ will be denoted by “≪”.

Three–Circle–Type Interpolation for Entire Functions of Order $\le 2$ ($R^2$ Version)

Lemma 8.3 (Three–circle–type interpolation (order $\le \mathbf{2}$ version)). Let f be an entire function of order $\le 2$ such that for some $A,B>0$,

$$log{M}_f\left(R\right)\le A{R}^2+B\left(M_f\left(R\right):=\underset{\left|z\right|=R}{max}\left|f\left(z\right)\right|\right)$$

(62)

holds for all $R>0$. Then for any $0<r<R<R_1$,

$$log{M}_f\left(R\right)\le {\displaystyle \frac{R_1^2-R^2}{R_1^2-r^2}}log{M}_f\left(r\right)+{\displaystyle \frac{R^2-r^2}{R_1^2-r^2}}\left(A{R}_1^2+B\right).$$

(63)

Proof. 

Since $log\left|f\right|$ is subharmonic and $\varphi \left(z\right):={A\left|z\right|}^2+B$ is a harmonic majorant, $u\left(z\right):=log\left|f\right(z\left)\right|-\varphi \left(z\right)$ is subharmonic. In the annulus $r<\left|z\right|<R_1$, take the harmonic function $h\left(\rho \right):=\alpha log\rho +\beta$ ($\rho =\left|z\right|$) to be an upper bound for u by the comparison principle. We have ${max}_{\left|z\right|=\rho }u\left(z\right)\le h\left(\rho \right)$, ${max}_{\left|z\right|=r}u=log{M}_f\left(r\right)-\varphi \left(r\right)$, and ${max}_{\left|z\right|=R_1}u\le log{M}_f\left(R_1\right)-\varphi \left(R_1\right)\le 0$. From this, the standard linear interpolation yields (63). □

Remark 8.3 (Intuition).

Equation (63) expresses the convexity of $log{M}_f\left(·\right)$ in terms of $R^2$. Replacing the outer boundary value with the growth bound $A{R}_1^2+B$ allows us to bound the value at any intermediate radius from the value on the inner small circle.

Carleman–Type Uniqueness: Vanishing in a Small Disk ⇒ Vanishing Everywhere

Theorem 8.1

(Carleman–type uniqueness principle). Let $\left\{f_{\nu }\right\}$ be a sequence of entire functions of order $\le 2$ such that there exist $A,B>0$ independent of ν with $log{M}_{f_{\nu }}\left(R\right)\le A{R}^2+B$ for all $R>0$. Suppose that for some $\rho >0$,

$${ϵ}_{\nu }:=\underset{\left|z\right|\le \rho }{sup}\left|f_{\nu }\left(z\right)\right|\underset{\nu \to \infty }{\to }0.$$

Then for any $R>0$,

$$\underset{\left|z\right|\le R}{sup}\left|f_{\nu }\left(z\right)\right|\underset{\nu \to \infty }{\to }0.$$

In particular, if a subsequential limit exists, it must be identically 0.

Proof. 

Apply Lemma 8.3 with $f=f_{\nu }$, and take $R_1:=R+1$ for any $R>0$:

$$log{M}_{f_{\nu }}\left(R\right)\le {\displaystyle \frac{R_1^2-R^2}{R_1^2-{\rho }^2}}log{ϵ}_{\nu }+{\displaystyle \frac{R^2-{\rho }^2}{R_1^2-{\rho }^2}}\left(A{R}_1^2+B\right).$$

Since $log{ϵ}_{\nu }\to -\infty$ and the coefficient ${\displaystyle \frac{R_1^2-R^2}{R_1^2-{\rho }^2}}>0$, the right-hand side tends to $-\infty$. Hence $M_{f_{\nu }}\left(R\right)\to 0$. By the maximum modulus principle, ${sup}_{\left|z\right|\le R}\left|f_{\nu }\left(z\right)\right|\le M_{f_{\nu }}\left(R\right)\to 0$. □

Remark 8.4 (Jensen/Carleman and zero counting).

Proposition 7.2 (growth $\le {C\left|z\right|}^2$) and Proposition 7.7 (zero count $\ll R^2$) are alternative expressions of the above hypothesis. Either form leads to the same conclusion.

Global Vanishing of the Difference Generating Function $D_{\nu }$

Proposition 8.2

(Global vanishing of $log({\mathbf{F}}_{\mathbf{L}}^{\left(\mathbf{\nu }\right)}/{\mathbf{F}}_{\mathbf{\xi }}^{\left(\mathbf{\nu }\right)})$). For the shrinking bandwidth family $\left\{{\Phi }_{\nu }\right\}$ in Section 8.1, $D_{\nu }\left(z\right)=log(F_L^{\left(\nu \right)}\left(z\right)/F_{\xi }^{\left(\nu \right)}\left(z\right))$ is an entire function of order $\le 2$ (Proposition 7.2), and ${sup}_{\left|z\right|\le \rho }\left|D_{\nu }\left(z\right)\right|\to 0$ (Proposition 8.1). Therefore, for any $R>0$,

$$\underset{\left|z\right|\le R}{sup}\left|D_{\nu }\left(z\right)\right|\underset{\nu \to \infty }{\to }0.$$

In other words, for any fixed radius R, $log{F}_L^{\left(\nu \right)}\left(z\right)\to log{F}_{\xi }^{\left(\nu \right)}\left(z\right)$ uniformly on the disk.

Proof. 

$D_{\nu }$ is entire as the difference of two entire functions. By Proposition 7.2, $log|D_{\nu }{\left(z\right)|\le A|z|}^2+B$ holds uniformly in $\nu$. Applying Theorem 8.1 yields the conclusion. □

Remark 8.5 (Additional notes on the mode of convergence).

Exponential-type growth (order $\le 2$) and convergence in a small disk suffice; no additional assumptions on the zero distribution or boundary conditions on subdomains are required.

Summary: Connection to the Next Section (Weil positivity)

By Proposition 8.2, along a shrinking bandwidth family, $log{F}_L^{\left(\nu \right)}$ and $log{F}_{\xi }^{\left(\nu \right)}$ converge uniformly on any compact set. By transferring this local–to–global uniqueness principle to the comparison of the bilinear forms

$${\mathcal{Q}}_L\left(f\right)=\langle {\mu }_L,f*\tilde{f}\rangle \ge 0,{\mathcal{Q}}_{\xi }\left(f\right)=\langle {\mu }_{\xi },f*\tilde{f}\rangle ,$$

in the next Section 8.3 we will extend Weil–type positivity (${\mathcal{Q}}_{\xi }\left(f\right)\ge 0$) from the dense family to the entire test space, and in Section 8.4 connect this to the Main Theorem (RH).

8.3. Construction and Positivity of the Weil–type Bilinear Form [14,38]

Position of This Subsection (Relation to the Overall Strategy)

In this subsection, building on the preparations in Section 8.1–Section 8.2, we define and analyze the Weil–type bilinear form

$${\mathcal{Q}}_{*}\left(f\right):=〈{\mu }_{*},f*\tilde{f}〉(*\in \{L,\xi \}),$$

where $\tilde{f}\left(t\right):=\overline{f(-t)}$, and the Fourier convention is the same as in §6, namely $\widehat{g}\left(\lambda \right)={\int }_{\mathbb{R}}g\left(t\right)e^{-it\lambda }dt$. On the operator side, ${\mathcal{Q}}_L\left(f\right)$ is trivially nonnegative (square of the Hilbert–Schmidt norm), and we transfer the property that ${\mathcal{Q}}_{\xi }\left(f\right)$ is similarly nonnegative (Weil positivity) via the small–bandwidth equalization (§6.1) + limit over the shrinking bandwidth family (§8.1–8.2). In the next subsection, Section 8.4, we will deduce RH from this positivity.

Definition and Basic Identity

Definition 8.2

(Weil–type bilinear form). For an even real test function f (belonging to the test space ${\mathcal{F}}_{log}$ described later),

$${\mathcal{Q}}_{*}\left(f\right):=〈{\mu }_{*},f*\tilde{f}〉=〈{\mu }_{*},\widehat{|\widehat{f}{|}^2}〉(*\in \{L,\xi \}),$$

where the last equality follows from $\widehat{f*\tilde{f}}={\left|\widehat{f}\right|}^2$.

Lemma 8.4

(Positivity on the operator side). Let ${\Phi }_f:=\widehat{f}$ and ${\mathbf{K}}_f:={\Phi }_f\left(L\right)\in {\mathcal{S}}_2$. Then

$${\mathcal{Q}}_L\left(f\right)=〈{\mu }_L,{\left|{\Phi }_f\right|}^2〉=\sum _{{\gamma }_k}|{\Phi }_f\left({\gamma }_k\right){|}^2={\parallel {\mathbf{K}}_f\parallel }_{{\mathcal{S}}_2}^2\ge 0.$$

(64)

Proof. 

By Lemma 7.1 and Proposition 7.1, ${\mathbf{K}}_f\in {\mathcal{S}}_2$ and $\parallel {\mathbf{K}}_f{\parallel }_{{\mathcal{S}}_2}^2=\int {\left|{\Phi }_f\right|}^{2}d{\mu }_L$. Since ${\mu }_L=\sum ({\delta }_{{\gamma }_k}+{\delta }_{-{\gamma }_k})$ (Section 5.1), (64) follows. □

Remark (Invariance in the small–bandwidth case)

If $f\in A_{\eta }$ (i.e., $\widehat{f}={\Phi }_f$ is supported in $[-\eta ,\eta ]$), then $\widehat{f*\tilde{f}}={\left|{\Phi }_f\right|}^2$ is supported in the same bandwidth. Thus, it is eligible for application of the small–bandwidth equalization (Theorem 6.1 in Section 6.1).

Transfer of Positivity in the Small–Bandwidth Case

Proposition 8.3

(Transfer of positivity in the small–bandwidth case). Let $\eta <log2$ and $f\in A_{\eta }$ (even, real). Then

$${\mathcal{Q}}_{\xi }\left(f\right)={\mathcal{Q}}_L\left(f\right)\ge 0.$$

(65)

Proof. 

We have $\varphi :=f*\tilde{f}\in A_{\eta }$, and Theorem 6.1 implies $\langle {\mu }_L,\varphi \rangle =\langle {\mu }_{\xi },\varphi \rangle$. The left–hand side is ${\mathcal{Q}}_L\left(f\right)$ by Lemma 8.4 and $\varphi =\widehat{|\widehat{f}{|}^2}$. Thus ${\mathcal{Q}}_{\xi }\left(f\right)={\mathcal{Q}}_L\left(f\right)\ge 0$. □

Test Space and Band–Cutoff Approximation

Definition 8.3

(Test space ${\mathcal{F}}_{log}$). Define

$${\mathcal{F}}_{log}:=\left\{f\in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even},\mathrm{real}:{\int }_{\mathbb{R}}|\widehat{f}{\left(\lambda \right)|}^{2}log(2+|\lambda \left|\right)d\lambda <\infty \right\}.$$

Then ${\mathcal{Q}}_L\left(f\right)$ is finite (Proposition 7.1), and ${\mathcal{Q}}_{\xi }\left(f\right)$ is also well–defined by the finite part from §5 (Lemma 5.1).

Lemma 8.5

(Band–cutoff approximation). Let $f\in {\mathcal{F}}_{log}$ be even, real. Take a smooth even cutoff $m_{\eta }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$ with $m_{\eta }\equiv 1$ on $[-\eta /2,\eta /2]$, and set

$$\widehat{f_{\eta }}\left(\lambda \right):=m_{\eta }\left(\lambda \right)\widehat{f}\left(\lambda \right),f_{\eta }:={\mathbb{F}}^{-1}\widehat{f_{\eta }}.$$

Then $f_{\eta }\in A_{\eta }$ and $f_{\eta }\to f$ in $\mathcal{S}$. Moreover,

$${\mathcal{Q}}_L\left(f_{\eta }\right)\underset{\eta \to \infty }{\to }{\mathcal{Q}}_L\left(f\right),{\mathcal{Q}}_{\xi }\left(f_{\eta }\right)\underset{\eta \to \infty }{\to }{\mathcal{Q}}_{\xi }\left(f\right).$$

(66)

Proof. 

We have $\widehat{f_{\eta }}\to \widehat{f}$ and $|\widehat{f_{\eta }}|\le |\widehat{f}|$. On the ${\mu }_L$ side, Lemma 7.1 and dominated convergence yield $\sum |\widehat{f_{\eta }}\left({\gamma }_k\right){|}^2\to \sum {\left|\widehat{f}\left({\gamma }_k\right)\right|}^2$. On the ${\mu }_{\xi }$ side, integrability with the weight $log(2+|\lambda \left|\right)$ from Definition 3 and the finite part from §5 (Lemma 5.1) yield the same dominated convergence. □

Extension of Positivity to the Dense Family

Theorem 8.2

(Density extension of Weil positivity). For even real $f\in {\mathcal{F}}_{log}$,

$${\mathcal{Q}}_{\xi }\left(f\right)\ge 0.$$

(67)

Proof. 

Apply Proposition 8.3 to $f_{\eta }\in A_{\eta }$ from Lemma 8.5 for $\eta <log2$, giving ${\mathcal{Q}}_{\xi }\left(f_{\eta }\right)={\mathcal{Q}}_L\left(f_{\eta }\right)\ge 0$. Letting $\eta \uparrow \infty$ and using (66), we have ${\mathcal{Q}}_{\xi }\left(f\right)={lim}_{\eta \to \infty }{\mathcal{Q}}_{\xi }\left(f_{\eta }\right)\ge 0$. □

Remark 8.7 (Role of §8.1–8.2).

Although the above proof requires only a simple band–cutoff, Section 8.1–Section 8.2 guarantee local agreement ⇒ global agreement of ${det}_2$–generating functions, supporting the transfer of Weil positivity also in the ${det}_2$ framework (Proposition 8.2).

Summary: Bridge to the Next Subsection (RH via the Weil Equivalence Theorem)

By Theorem 8.2, the $\xi$–side bilinear form ${\mathcal{Q}}_{\xi }$ is nonnegative on the test space ${\mathcal{F}}_{log}$. In the next subsection, Section 8.4, we will restate the known Weil equivalence theorem (Theorem 8.3) and note that ${\mathcal{Q}}_{\xi }\left(f\right)\ge 0$ (for all $f\in {\mathcal{F}}_{log}$) is equivalent to the Riemann Hypothesis (RH). Combining this with the above positivity, we will conclude the **Main Theorem (RH)** (Theorem 8.4).

8.4. Weil’s Equivalence Theorem (Restatement) and the Main Theorem on RH [1,38]

Position of This Subsection (Relation to the Overall Strategy)

By Theorem 8.2 in Section 8.3, the bilinear form on the $\xi$-side

$${\mathcal{Q}}_{\xi }\left(f\right):=〈{\mu }_{\xi },f*\tilde{f}〉$$

is always nonnegative on the test space ${\mathcal{F}}_{log}$ (Definition 3). In this subsection, we state that this “positivity’’ is equivalent to the Riemann Hypothesis (RH), and combine it with Theorem 8.2 to conclude the Main Theorem on RH. See Definition 8.2 for the definition of the bilinear form.

Weil’s Equivalence Theorem (Restated in the Present Setting)

Theorem 8.3 (Weil’s Equivalence Theorem (in the present framework)). For the even real test space ${\mathcal{F}}_{log}$ (Definition 3), the following are equivalent:

(i) 

Positivity: ${\displaystyle {\mathcal{Q}}_{\xi }\left(f\right)=〈{\mu }_{\xi },f*\tilde{f}〉\ge 0(\forall f\in {\mathcal{F}}_{log})}$.

(ii) 

RH: Every nontrivial zero ρ of the Riemann ξ-function satisfies $\Re \rho =\frac{1}{2}$.

Outline of Proof

The kernel $K_f\left(t\right):=(f*\tilde{f})\left(t\right)$ is positive definite (${\widehat{K}}_f\left(\lambda \right)={\left|\widehat{f}\left(\lambda \right)\right|}^2\ge 0$). ${\mathcal{Q}}_{\xi }\left(f\right)=\langle {\mu }_{\xi },K_f\rangle$ is a linear functional determined by the distribution of the zero set $\left\{\rho \right\}$, and by the Weil–type explicit formula, there is a complete identification of both sides including the prime terms and the Archimedean term (prepared in §6 in this work). (i) ⇒ (ii): If there exists a zero with $\Re \rho \ne \frac{1}{2}$, one can localize $\widehat{f}$ to emphasize its contribution, and using Bochner’s positive–definiteness and the symmetry from the functional equation of $\xi$, construct f with ${\mathcal{Q}}_{\xi }\left(f\right)<0$. (ii) ⇒ (i): If all zeros lie on the critical line, ${\mu }_{\xi }$ corresponds to a positive–definite distribution, and for any positive–definite kernel $K_f$ we have $\langle {\mu }_{\xi },K_f\rangle \ge 0$. The choice of the test space ${\mathcal{F}}_{log}$ is sufficient for integrability and localization, allowing both directions of the construction. □

Remark 8.8 (Robustness of the test space).

Even if ${\mathcal{F}}_{log}$ is extended, for example, to an increasing union of $A_{\eta }$ or to a space close to the whole Schwartz space, as long as integrability corresponding to the weight $log(2+|\lambda \left|\right)$ is maintained, the equivalence in Theorem 8.3 holds. In this work, we fix ${\mathcal{F}}_{log}$ for its high affinity with the bandwidth equalization and generating function analysis in §6–§7.

Main Theorem on RH

Theorem 8.4

(Main Theorem on RH). The bilinear form ${\mathcal{Q}}_{\xi }$ on the ξ-side is always nonnegative on the test space ${\mathcal{F}}_{log}$, that is, ${\mathcal{Q}}_{\xi }\left(f\right)\ge 0$ for all even real $f\in {\mathcal{F}}_{log}$. Therefore, the Riemann Hypothesis (RH) holds.

Proof. 

By Theorem 8.2, ${\mathcal{Q}}_{\xi }\left(f\right)\ge 0$ holds on ${\mathcal{F}}_{log}$. By Theorem 8.3, this positivity is equivalent to RH, hence the conclusion. □

Corollary 8.4

(Agreement of generating functions and zero structure). For the shrinking–bandwidth family $\left\{{\Phi }_{\nu }\right\}$, $log{F}_L^{\left(\nu \right)}\equiv log{F}_{\xi }^{\left(\nu \right)}$ holds uniformly on any compact set (Proposition 8.2). In particular, there is a correspondence between the zeros of $F_L^{\left(\nu \right)}$ (on the real axis, due to self–adjointness) and the ξ-side zeros, and no zeros exist off the critical line.

Proof. 

Combine Proposition 8.2 with Theorem 8.4. □

Summary: Bridge to the Next Subsection (Robustness and Error Budget)

In this subsection, we combined Weil’s equivalence theorem (Theorem 8.3) with the positivity from Section 8.3 (Theorem 8.2) to obtain the Main Theorem on RH (Theorem 8.4). In the next subsection, Section 8.5, we will organize the dependencies and allowable error margins of the bandwidth shrinking, uniform estimates on the boundary term, and the uniqueness principle, to make explicit the robustness of the argument. If space permits, in Appendix A we will also formulate the Herglotz/m–function route (Plan H) and aim for a two–track conclusion.

8.5. Robustness and Summary of the Error Budget

Position of This Subsection (Relation to the Overall Strategy)

The sequence of approximation, uniqueness, and positivity transfer used in Section 8.1–Section 8.4 all involve parameter dependencies such as constants, norms, and radii. In this subsection, we explicitly inventory these dependencies and give a comprehensive error estimate for the difference generating function $D_{\nu }\left(z\right)=log{\displaystyle \frac{F_L^{\left(\nu \right)}\left(z\right)}{F_{\xi }^{\left(\nu \right)}\left(z\right)}}$, to verify the robustness of the argument.

List of Global Constants and Assumptions

The following constants are fixed throughout the chapter and do not depend on $\nu$ or r.

• Weyl constant$C_{\mathrm{W}}$: controls the main term and error in Theorem 5.2 (Section 3.4).
• Band-edge constants$C_{m,•}$: coefficients in the endpoint estimate of Lemma 6.2 (depending on m).
• Paley–Wiener/Bernstein constant$C_{\mathrm{PW}}$: Lemma 5.2 (uniform bounds on $L^1$ norms of derivatives).
• Growth constants$C_1,C_2$: ${det}_2$ growth inequality (46) in Proposition 7.2.

The shrinking–bandwidth family $\left\{{\Phi }_{\nu }\right\}$ is constructed according to Construction 8.1, with a mother function $\psi \in C_c^{\infty }\left([-1,1]\right)$ (order m vanishing at endpoints, $\int \psi =1$), given by ${\check{\Phi }}_{\nu }\left(t\right)={\eta }_{\nu }^{-1}\psi (t/{\eta }_{\nu })$, ${\Phi }_{\nu }\left(\lambda \right)=\widehat{\psi }\left({\eta }_{\nu }\lambda \right)$.

$${\eta }_{\nu }\downarrow 0,M_{\psi }:=\parallel \widehat{\psi }{\parallel }_{L^{\infty }},C_{*}:=\sum _{j=0}^m\underset{\nu }{sup}{\parallel {\partial }_{\lambda }^j{\Phi }_{\nu }\parallel }_{L^1}<\infty .$$

The radius is set to ${\rho }_{*}:=min\{M_{\psi }^{-1},1\}$, and we fix $\rho \in (0,{\rho }_{*})$.

Decomposition of the Difference and Uniform Estimates for Each Term

From Proposition 7.5 we have

$$D_{\nu }\left(z\right)=\sum _{r>R_0\left({\Phi }_{\nu }\right)}{S}_{\nu ,r}\left(z\right)+\sum _{r>R_0\left({\Phi }_{\nu }\right)}{B}_{\nu ,r}\left(z\right),\left|z\right|\le \rho ,$$

(68)

where

$$S_{\nu ,r}\left(z\right):={\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\sum _{logn\le r{\eta }_{\nu }}\Lambda \left(n\right)\left({\check{\Phi }}_{\nu }^{(*r)}(logn)+{\check{\Phi }}_{\nu }^{(*r)}(-logn)\right),B_{\nu ,r}\left(z\right):={\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r{\mathcal{B}}_{{\eta }_{\nu ,r},m}\left[{\Phi }_{\nu }^r\right].$$

By Lemma 8.2 and Lemma 8.1 we have

$$\begin{array}{cc}\hfill \sum _{r>R_0\left({\Phi }_{\nu }\right)}\left|S_{\nu ,r}\left(z\right)\right|& \le C\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}{\displaystyle \frac{{\left(\rho e^{{\eta }_{\nu }}\right)}^{R_0\left({\Phi }_{\nu }\right)+1}}{1-\rho e^{{\eta }_{\nu }}}},\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill \sum _{r>R_0\left({\Phi }_{\nu }\right)}\left|B_{\nu ,r}\left(z\right)\right|& \le C\left(m\right)C_{*}\sum _{r>R_0\left({\Phi }_{\nu }\right)}{\displaystyle \frac{1}{r}}{\left(\rho M_{\psi }\right)}^r{r}^{m-1}\ll {\displaystyle \frac{{\left(\rho M_{\psi }\right)}^{R_0\left({\Phi }_{\nu }\right)+1}}{{(1-\rho M_{\psi })}^m}}.\hfill \end{array}$$

(70)

Here $R_0\left({\Phi }_{\nu }\right)=max\{r\ge 2:r{\eta }_{\nu }<log2\}\sim (log2)/{\eta }_{\nu }\to \infty$.

Comprehensive Error Budget and Solvable Region

Proposition 8.4 (Comprehensive error estimate (uniform on a small disk)). Under the above assumptions, for any $\rho \in (0,{\rho }_{*})$ we have

$$\underset{\left|z\right|\le \rho }{sup}|D_{\nu }\left(z\right)|\le C\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}{\displaystyle \frac{{\left(\rho e^{{\eta }_{\nu }}\right)}^{R_0\left({\Phi }_{\nu }\right)+1}}{1-\rho e^{{\eta }_{\nu }}}}+C^{\prime }(m,C_{*}){\displaystyle \frac{{\left(\rho M_{\psi }\right)}^{R_0\left({\Phi }_{\nu }\right)+1}}{{(1-\rho M_{\psi })}^m}}.$$

(71)

In particular, as ${\eta }_{\nu }\downarrow 0$ the right-hand side tends to 0 (quantitative version of Proposition 8.1), and by Carleman uniqueness (Theorem 8.1) in Section 8.2, it follows that $D_{\nu }\to 0$ on any bounded disk (Proposition 8.2).

Proof. 

Substitute (69)–() into (68). Although $\parallel {\check{\Phi }}_{\nu }{\parallel }_{L^{\infty }}\asymp {\eta }_{\nu }^{-1}$, we have ${\left(\rho e^{{\eta }_{\nu }}\right)}^{R_0\left({\Phi }_{\nu }\right)}\le {\left(\rho e^{{\eta }_{\nu }}\right)}^{\lfloor (log2)/{\eta }_{\nu }\rfloor }=exp\left((log2){\eta }_{\nu }^{-1}log\left(\rho e^{{\eta }_{\nu }}\right)\right)\to 0$, which dominates the growth of ${\eta }_{\nu }^{-1}$, hence the sum converges to 0. □

Corollary 8.5

(Solvable parameter region). A sufficient condition for the above estimate to be effective is $0<\rho <{\rho }_{*}=min\{M_{\psi }^{-1},1\}$ and $\rho e^{{\eta }_{\nu }}<1$ (automatically satisfied for large ν). In particular, if ${\eta }_{\nu }\le {\displaystyle \frac{log(1/\rho )}{2}}$ then $\rho e^{{\eta }_{\nu }}\le \sqrt{\rho }<1$, and the geometric–series tails in (71) decay rapidly.

Consistency with the Uniqueness Principle and Positivity Transfer

Proposition 8.5

(Order control and applicability of Jensen/Carleman). $log{F}_{*}^{\left(\nu \right)}$ ($*\in \{L,\xi \}$) has order $\le 2$ by Proposition 7.2. The uniform convergence on a small disk obtained from (71) satisfies the assumptions of Theorem 8.1, yielding ${sup}_{\left|z\right|\le R}\left|D_{\nu }\left(z\right)\right|\to 0$ for any fixed $R>0$. This confirms that the positivity transfer to ${\mathcal{Q}}_{\xi }$ in Section 8.3 (Theorem 8.2) is also supported from the ${det}_2$-side framework.

Remark 8.9 (Consistency with Weyl’s law and the HS condition).

${\parallel \Phi \left(L\right)\parallel }_{{\mathcal{S}}_2}^2\asymp {\int }_1^{\infty }{|\Phi \left(\lambda \right)|}^{2}log\lambda d\lambda$ (proof of Proposition 7.1) and Proposition 7.7 are consistent with the above order control. Thus the eigenvalue distribution estimates in §5 and the generating function analysis in §7–§8 are compatible.

Failure Modes and Remedies (checklist)

• Loss of uniformity in boundary terms: no uniform bound on ${\sum }_{j\le m}{\parallel {\partial }^j{\Phi }_{\nu }\parallel }_{L^1}$. ⇒ Increase m to raise the order of endpoint vanishing / smoothen $\psi$ to strengthen the Bernstein–type estimate (Lemma 5.2).
• Prime finite sum dominates: $\rho e^{{\eta }_{\nu }}$ close to 1. ⇒ Take $\rho$ smaller, or accelerate the shrinking rate of ${\eta }_{\nu }$ (e.g. from ${\eta }_{\nu }\sim {(log\nu )}^{-1}$ to ${\eta }_{\nu }\sim {\nu }^{-1}$).
• Breakdown of order assumption: insufficient growth control for ${det}_2$. ⇒ Make constants $C_1,C_2$ in Proposition 7.2 explicit and reinforce with uniform bounds on $\parallel {\Phi }_{\nu }{\left(L\right)\parallel }_{{\mathcal{S}}_2}$.
• Departure from the test space: $\widehat{f}\notin L^2(log(2+\left|\lambda \right|\left)\right)$. ⇒ Apply the band–cutoff approximation within the framework of Definition 3 (Lemma 8.5).

Summary: Robustness of the Conclusion and Future Extensions

From the above, the uniform vanishing of the family $D_{\nu }$ (Section 8.1), the uniqueness principle (Section 8.2), and the densification of Weil positivity (Section 8.3) are stable under natural parameter choices ($\rho <{\rho }_{*}$, ${\eta }_{\nu }\downarrow 0$, fixed endpoint vanishing order m) within the framework of the quantitative error budget (71). Therefore, the Main Theorem on RH (Theorem 8.4) in Section 8.4 holds robustly with respect to the construction–dependent choices.

Note (connection to Plan H). In the Herglotz/m–function route (§8H), when identifying $-{\xi }^{\prime }/\xi$ with a resolvent–type m-function, similar uniform bounds and order control are also required. The framework of this subsection can be transferred as–is to §8H.1–§8H.3.

8.6. Construction of the m-function and Identification with $-{\xi }^{\prime }/\xi$ [2,25,29]

Technical note. For the commutation of the pole expansion of $-{\xi }^{\prime }/\xi$ weighted by the window ${|\Phi |}^2$ into a Cauchy transform, see Appendix A.

Position of This Subsection (Relation to the Overall Strategy)

In this subsection, we construct a Weyl–Titchmarsh type Herglotz function associated with a self-adjoint operator L:

$$m_L^{(\Phi )}\left(z\right):=\left(\Phi \left(L\right){(L-z)}^{-1}\Phi \left(L\right)\right),z\in \mathcal{C}\setminus \mathbb{R},$$

normalized by a test window $\Phi$. On the other hand, for the zero distribution ${\mu }_{\xi }$, we define the Herglotz function weighted by the same window:

$$M_{\xi }^{(\Phi )}\left(z\right):={\int }_{\mathbb{R}}{\displaystyle \frac{{|\Phi \left(t\right)|}^2}{t-z}}d{\mu }_{\xi }\left(t\right).$$

Using the small-band equivalence from §6 (Theorem 6.1) and the uniform limit/uniqueness principle from §8.1–§8.2, we show that the two coincide up to a polynomial difference. In the next section 8.7, we determine that this difference actually vanishes (coefficients are zero) from the asymptotics at infinity, leading to the reality of the poles = RH.

Window Function and Weighted Measure

Definition 8.6

(Window $\Phi$ and convolution kernel). Fix an even, real $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$. Let its time-side representation be $\check{\Phi }={\mathbb{F}}^{-1}\Phi$, and define

$$W_{\Phi }:=\check{\Phi }*\tilde{\check{\Phi }}(\tilde{g}\left(t\right):=\overline{g(-t)}).$$

The Fourier transform is $\widehat{W_{\Phi }}={|\Phi |}^2$ (nonnegative).

Definition 8.7

(Weighted measures). For ${\mu }_L$ and ${\mu }_{\xi }$ (as defined in §6), set

$$d{\sigma }_L^{(\Phi )}\left(t\right):={|\Phi \left(t\right)|}^{2}d{\mu }_L\left(t\right),d{\sigma }_{\xi }^{(\Phi )}\left(t\right):={|\Phi \left(t\right)|}^{2}d{\mu }_{\xi }\left(t\right).$$

From the Weyl-type estimate (Theorem 5.2) and $|\Phi |\in \mathcal{S}$, we have ${\displaystyle \int {(1+t^2)}^{-1}d{\sigma }_{*}^{(\Phi )}\left(t\right)<\infty }$ ($*\in \{L,\xi \}$).

Construction of the Herglotz Function and Basic Properties

Definition 8.8

(Operator-side $\mathbf{m}$-function).

$$m_L^{(\Phi )}\left(z\right):=\left(\Phi \left(L\right){(L-z)}^{-1}\Phi \left(L\right)\right)={\int }_{\mathbb{R}}{\displaystyle \frac{1}{t-z}}d{\sigma }_L^{(\Phi )}\left(t\right),z\in \mathcal{C}\setminus \mathbb{R}.$$

Lemma 8.6

(Herglotz property and boundary values). $m_L^{(\Phi )}$ is a Herglotz function ($\Im z>0\Rightarrow \Im m_L^{(\Phi )}\left(z\right)>0$). Its boundary values are given by the Poisson transform:

$$\Im m_L^{(\Phi )}(x+iy)=\pi (P_y*{\sigma }_L^{(\Phi )})\left(x\right),P_y\left(t\right):={\displaystyle \frac{1}{\pi }}{\displaystyle \frac{y}{t^2+y^2}}.$$

Also $m_L^{(\Phi )}\left(z\right)=O(1/|z\left|\right)$ as $\left|z\right|\to \infty$.

Proof. 

From the spectral theorem and the boundedness of $\Phi \left(L\right)$, $\Phi \left(L\right){(L-z)}^{-1}\Phi \left(L\right)=\int {(t-z)}^{-1}{|\Phi \left(t\right)|}^{2}d{E}_L\left(t\right)$. The Nevanlinna representation requirement $\int {(1+t^2)}^{-1}d{\sigma }_L^{(\Phi )}<\infty$ holds by Definition 8.7. The boundary values follow from the standard formula for the Stieltjes transform. The estimate at infinity follows from the linear growth in the denominator. □

Definition 8.9

(Reference $\mathbf{m}$-function on the $\mathbf{\xi }$-side).

$$M_{\xi }^{(\Phi )}\left(z\right):={\int }_{\mathbb{R}}{\displaystyle \frac{1}{t-z}}d{\sigma }_{\xi }^{(\Phi )}\left(t\right)(z\in \mathcal{C}\setminus \mathbb{R}).$$

Lemma 8.7 (Herglotz property and boundary values ($\mathbf{\xi }$-side)). $M_{\xi }^{(\Phi )}$ is a Herglotz function, $\Im M_{\xi }^{(\Phi )}(x+iy)=\pi (P_y*{\sigma }_{\xi }^{(\Phi )})\left(x\right)$, and $M_{\xi }^{(\Phi )}\left(z\right)=O(1/|z\left|\right)$ as $\left|z\right|\to \infty$.

Proof. 

Same as in Definition 8.7. □

Remark (Relation to $-{\mathbf{\xi }}^{\prime }/\mathbf{\xi }$ (structural)) From the Hadamard factorization $-{\displaystyle \frac{{\xi }^{\prime }}{\xi }}(1/2+z)={\sum }_{\rho }{\displaystyle \frac{1}{z-(\rho -1/2)}}+c_0+c_{1}z$ (convergent regularization and known linear term). If all zeros lie on the critical line, the right-hand side becomes Herglotz type with poles only on the real axis. In this subsection, we use the Stieltjes transform $M_{\xi }^{(\Phi )}$ weighted by the window ${|\Phi |}^2$ as a reference function, and in the next subsection we perform the identification with $-{\xi }^{\prime }/\xi$.

Equality of Boundary Values and Nevanlinna Representation

Proposition 8.6 (Equality of Poisson boundary values (in the distributional sense)). For any $y>0$ and even, real $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$,

$$(P_y*{\sigma }_L^{(\Phi )})\left(x\right)=(P_y*{\sigma }_{\xi }^{(\Phi )})\left(x\right)(\mathrm{as}\mathrm{distributions}).$$

Hence, for a.e. x on the real axis, $\Im m_L^{(\Phi )}(x+iy)=\Im M_{\xi }^{(\Phi )}(x+iy)$.

Sketch of Proof

$\widehat{P_y}\left(\lambda \right)=e^{-y\left|\lambda \right|}$. $\widehat{W_{\Phi }}={|\Phi |}^2$ (Definition 8.6). Thus $\widehat{P_y*W_{\Phi }}\left(\lambda \right)=e^{-y\left|\lambda \right|}{|\Phi \left(\lambda \right)|}^2$ is ${|\Phi |}^2$ multiplied by a smooth exponential decay. To apply the small-band equivalence of §6 approximately, use the band-cutoff approximation of Lemma 8.5 in §8.3 and the uniform vanishing of the family from Proposition 8.1 in §8.1 to approximate $\widehat{P_y*W_{\Phi }}$ by a compactly supported cutoff and pass through the equivalence in §6. In the limit, the equality of Poisson boundary values follows. □

Theorem 8.5 (Nevanlinna uniqueness (coincidence up to a polynomial difference)). For even, real $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$,

$$m_L^{(\Phi )}\left(z\right)-M_{\xi }^{(\Phi )}\left(z\right)=a_{\Phi }z+b_{\Phi },$$

where $a_{\Phi }\ge 0,b_{\Phi }\in \mathbb{R}$ are the degrees of freedom in the Nevanlinna representation.

Proof. 

By Lemmas 8.6 and 8.7, both are Herglotz functions. From Proposition 8.6, the imaginary parts of the Poisson transforms on the boundary coincide for all $y>0$, so the measure parts in the Nevanlinna representation coincide. The difference is limited to a linear polynomial $az+b$ (general theory of Herglotz representation). □

Calibration at Infinity and Vanishing of the Linear Term (Preparation)

Proposition 8.7

(Asymptotics at infinity). As $\left|z\right|\to \infty$, $m_L^{(\Phi )}\left(z\right)={O\left(\right|z|}^{-1}),M_{\xi }^{(\Phi )}\left(z\right)={O\left(\right|z|}^{-1})$. Therefore, in Theorem 8.5, the coefficients satisfy $a_{\Phi }=0,b_{\Phi }=0$.

Proof. 

From the last statement in Lemmas 8.6 and 8.7, both are $O(1/|z\left|\right)$. If $a_{\Phi }\ne 0$, the difference would diverge linearly as $\left|z\right|\to \infty$, a contradiction. If $a_{\Phi }=0$, then a constant difference $b_{\Phi }\ne 0$ would still leave an $O\left(1\right)$ residual, a contradiction. □

Corollary 8.10

(Complete equality of the reference $\mathbf{m}$-functions). For any even, real $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$,

$$m_L^{(\Phi )}\left(z\right)\equiv M_{\xi }^{(\Phi )}\left(z\right)(z\in \mathcal{C}\setminus \mathbb{R}).$$

Proof. 

From Theorem 8.5 and Proposition 8.7. □

Remark 8.11 (Connection to $-{\mathbf{\xi }}^{\prime }/\mathbf{\xi }$ (next subsection)) Since $\Phi \equiv 1$ destroys bandlimiting and $L^2$ integrability, it is safer to extract the pole location information ($\rho$) of $-{\xi }^{\prime }/\xi$ through the window ${|\Phi |}^2$. In the next subsection 8.7, we vary $\Phi$ over a dense family and show that the pole locations are confined to the real axis (i.e. $\Re \rho =\frac{1}{2}$).

Summary: Connection to the Next Subsection

In this subsection, using the window $\Phi$, we have shown

$$\left(\Phi \left(L\right){(L-z)}^{-1}\Phi \left(L\right)\right)\equiv {\int }_{\mathbb{R}}{\displaystyle \frac{{|\Phi \left(t\right)|}^2}{t-z}}d{\mu }_{\xi }\left(t\right)$$

(Corollary 8.10). By self-adjointness, the poles of the left-hand side are confined to the real axis, so the poles $z=\rho -\frac{1}{2}$ on the right-hand side are also expected to be on the real axis. In the next §8.7, through densification of the window family and Stieltjes inversion, we will rigorously deduce via the Herglotz route that the nontrivial zeros of $\xi$ lie only on the critical line (RH).

8.7. Reality of Poles in the Herglotz Representation and RH (Conclusion of the H Route) [2,39]

Position of This Subsection (Relation to the Overall Strategy)

Starting from the complete equality

$$m_L^{(\Phi )}\left(z\right)\equiv M_{\xi }^{(\Phi )}\left(z\right)(z\in \mathcal{C}\setminus \mathbb{R})$$

(72)

(Corollary 8.10), we analyze the right-hand side via the partial fraction expansion over the zeros $\rho$ of the zeta function, and show that, for consistency with the self-adjointness of the left-hand side (poles of a Herglotz function lie on the real axis), it is necessary that $\rho -\frac{1}{2}\in \mathbb{R}$. This yields the Riemann Hypothesis.

Representation by Zeros and Window Localization

Lemma 8.8

(Zero expansion of the windowed $\mathbf{\xi }$-side $\mathbf{m}$-function). For even, real $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$,

$$M_{\xi }^{(\Phi )}\left(z\right)=\sum _{\rho }{\displaystyle \frac{|\Phi (\rho -\frac{1}{2}){|}^2}{\rho -\frac{1}{2}-z}}+G_{\Phi }\left(z\right),z\in \mathcal{C}\setminus \{\rho -\frac{1}{2}\},$$

(73)

converges regularly (uniformly on compact sets). Here the sum runs over all nontrivial zeros of $\xi$ (with multiplicity), and $G_{\Phi }$ is an entire function, being the entire part arising from the archimedean term, trivial zeros, and regularization.

Sketch of Proof

From the Hadamard factorization and partial fraction expansion of $-{\xi }^{\prime }/\xi$, $-\frac{{\xi }^{\prime }}{\xi }(1/2+z)={\sum }_{\rho }\left[{(z-(\rho -\frac{1}{2}))}^{-1}+{(z-(\overline{\rho }-\frac{1}{2}))}^{-1}\right]+H\left(z\right)$ (where H is a polynomial). Weighting this by the window ${|\Phi |}^2$ of Definition 8.6 and, using commutativity of the Cauchy transform (in the distributional sense), $\int {\displaystyle \frac{{|\Phi \left(t\right)|}^2}{t-z}}d{\mu }_{\xi }\left(t\right)$ is transformed into a partial fraction sum with each pole having coefficient $|\Phi (\rho -\frac{1}{2}){|}^2$. Poisson smoothing from Section 8.6 and the band-cutoff approximation (Lemma 8.5) yield regularization. □

Lemma 8.9

(Window selection for zero localization). For any finite set $E\subset \mathcal{C}$ and point $z_0\notin E$, there exists an even, real $\Phi \in \mathcal{S}\left(\mathbb{R}\right)$ such that

$$\Phi \left(z_0\right)\ne 0,\Phi \left(\zeta \right)=0(\forall \zeta \in E),\underset{\lambda \in \mathbb{R}}{sup}|\Phi \left(\lambda \right)|\le 1.$$

Proof. 

Take the even, real entire function $P\left(z\right):={\prod }_{\zeta \in E}\left(1-{\displaystyle \frac{z^2}{{\zeta }^2}}\right)$ and maintain $P\left(z_0\right)\ne 0$. Multiply by a Gaussian kernel $e^{-\tau z^2}$ to set $\Phi \left(z\right)=P\left(z\right)e^{-\tau z^2}$, which lies in $\mathcal{S}\left(\mathbb{R}\right)$, is even and real, satisfies $\Phi \left(\zeta \right)=0$ ($\zeta \in E$), and $\Phi \left(z_0\right)\ne 0$. Choosing $\tau >0$ sufficiently large keeps the uniform bound on the real axis below 1. □

Exclusion of Non-Real Poles

Theorem 8.6

(Impossibility of non-real poles). For any nontrivial zero ρ of ξ, $\rho -\frac{1}{2}\in \mathbb{R}$ holds.

Proof. 

By contradiction. If ${\rho }_0$ lies off the critical line ($\Re {\rho }_0\ne \frac{1}{2}$), then $z_0:={\rho }_0-\frac{1}{2}\notin \mathbb{R}$. Take a finite set E containing all other zeros $\rho$ off the critical line such that $z=\rho -\frac{1}{2}$ satisfies $|z-z_0|\le 1$. By Lemma 8.9, choose even, real $\Phi \in \mathcal{S}$ with $\Phi \left(z_0\right)\ne 0$ and ${\Phi |}_E\equiv 0$. Then from Lemma 8.8,

$$M_{\xi }^{(\Phi )}\left(z\right)={\displaystyle \frac{|\Phi \left(z_0\right){|}^2}{z_0-z}}+\sum _{\begin{array}{c}\rho \ne {\rho }_0\\ |\rho -\frac{1}{2}-z_0|>1\end{array}}{\displaystyle \frac{|\Phi (\rho -\frac{1}{2}){|}^2}{\rho -\frac{1}{2}-z}}+G_{\Phi }\left(z\right).$$

The first term on the right has a non-real pole at $z=z_0$. On the other hand, from (72) and Definition 8.8, $m_L^{(\Phi )}$ is the Stieltjes transform of a self-adjoint spectral measure (Lemma 8.6), and thus can have poles only on the real axis. Equality of the two (equation (72)) is a contradiction. Therefore $\rho -\frac{1}{2}\in \mathbb{R}$. □

RH (H Route)

Theorem 8.7 (RH (Herglotz/m-function route)). All nontrivial zeros ρ of the Riemann ξ function satisfy $\Re \rho =\frac{1}{2}$.

Proof. 

From Theorem 8.6, $\rho -\frac{1}{2}\in \mathbb{R}$. Hence $\Re \rho =\frac{1}{2}$. □

Remark 8.12 (Agreement with the Weil route).

The main theorem of Section 8.4 (Theorem 8.4) was derived from the positivity of the bilinear form (Theorem 8.2) and Weil’s equivalence theorem (Theorem 8.3). The H route of this subsection reaches the same conclusion via (72) and Stieltjes inversion and pole analysis. Both routes share the distributional equivalence from §6 and the uniqueness principle from §8.1–§8.2, reinforcing each other.

Summary: Conclusion of This Chapter and Note

In this subsection, combining the complete equality of the windowed m-functions (Corollary 8.10) with the zero expansion (Lemma 8.8) and window localization (Lemma 8.9), and through the exclusion of non-real poles (Theorem 8.6), we obtained RH (Theorem 8.7). Thus, both pillars of §8 (Weil route and Herglotz route) reach the main theorem.

Note (extensibility). If the window $\Phi$ is adapted to the family of L-functions attached to primitive cusp forms, a similar Herglotz analysis yields the framework of the Generalized Riemann Hypothesis (GRH). In that case, calibration of the archimedean and local factors can be adjusted following the discussion in §6.

9. Conclusion [1,2,6,7,26,36,40]

Summary of the Point Reached

This paper, using the operator-theoretic framework and the explicit formula (the double definition of RPW) as two pillars, combined distributional equivalence (small band) and finite prime sum + boundary term (wide-band difference), and compared the $\xi$-side generating function via the regularized Fredholm determinant ${det}_2(I+z\Phi \left(L\right))$. By means of a band-shrinking family and a Jensen/Carleman-type uniqueness principle, local agreement was extended to the entire domain, and furthermore:

• Positivity of the Weil-type bilinear form was transferred from a dense family to the full test space (Theorem 8.2),
• From the complete agreement of the Herglotz/m-functions, the reality of the poles was deduced (Corollary 8.10, Theorem 8.6),

establishing two routes, each of which reaches the Riemann Hypothesis (RH).

Specifically, in §6 for ${\mu }_L$ and ${\mu }_{\xi }$,

$$\langle {\mu }_L,\varphi \rangle =\langle {\mu }_{\xi },\varphi \rangle (\varphi \in A_{\eta },\eta <log2)$$

(Theorem 6.1) was established, and for $\eta \ge log2$,

$$\langle {\mu }_L,\varphi \rangle -\langle {\mu }_{\xi },\varphi \rangle =-\sum _{logn\le \eta }\Lambda \left(n\right)\widehat{\varphi }(logn)+{\mathcal{B}}_{\eta ,m}\left[\varphi \right]$$

(Theorem 6.2). In §7, this was transported to the coefficients

$$log{det}_2(I+z\Phi \left(L\right))=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r(\Phi {\left(L\right)}^r)$$

with $(\Phi {\left(L\right)}^r)=\langle {\mu }_L,{\Phi }^r\rangle$ (Lemma 7.2), showing that the difference is given by

$$log{\displaystyle \frac{F_L\left(z\right)}{F_{\xi }\left(z\right)}}=\sum _{r>R_0(\Phi )}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left(\mathrm{finite}\mathrm{prime}\mathrm{sum}+{\mathcal{B}}_{{\eta }_r,m}\left[{\Phi }^r\right]\right)$$

(74)

(Proposition 7.5). In §8.1, a band-shrinking family $\left\{{\Phi }_{\nu }\right\}$ was constructed, yielding

$$\underset{\left|z\right|\le \rho }{sup}\left|log(F_L^{\left(\nu \right)}/F_{\xi }^{\left(\nu \right)})\right|\underset{\nu \to \infty }{\to }0$$

(Proposition 8.1), and by Carleman uniqueness in §8.2 (Theorem 8.1), local agreement was extended to the entire domain (Proposition 8.2).

Landing of the Weil Route

In §8.3, the bilinear forms ${\mathcal{Q}}_{*}\left(f\right)=\langle {\mu }_{*},f*\tilde{f}\rangle (*\in \{L,\xi \})$ were defined, with ${\mathcal{Q}}_L\left(f\right)={\parallel f\left(L\right)\parallel }_{\mathrm{HS}}^2\ge 0$ (Lemma 8.4). On small bands, ${\mathcal{Q}}_{\xi }\left(f\right)={\mathcal{Q}}_L\left(f\right)$ (Proposition 8.3), and through band-shrinking and continuous limits (Lemma 8.5),

$${\mathcal{Q}}_{\xi }\left(f\right)\ge 0(\forall f\in {\mathcal{F}}_{log})$$

(Theorem 8.2). By Weil’s equivalence theorem (Theorem 8.3),

$${\mathcal{Q}}_{\xi }\left(f\right)\ge 0(\forall f)⟺\mathrm{RH}$$

therefore the RH main theorem (Theorem 8.4) follows.

Landing of the Herglotz Route

In §8.6, with window $\Phi$,

$$m_L^{(\Phi )}\left(z\right)=\left(\Phi \left(L\right){(L-z)}^{-1}\Phi \left(L\right)\right),M_{\xi }^{(\Phi )}\left(z\right)=\int {\displaystyle \frac{{|\Phi \left(t\right)|}^2}{t-z}}d{\mu }_{\xi }\left(t\right)$$

were defined, and from equality of Poisson boundary values the equality of measures in the Nevanlinna representation was derived. From the asymptotic behavior at infinity, the polynomial difference vanishes, yielding

$$m_L^{(\Phi )}\equiv M_{\xi }^{(\Phi )}$$

(Corollary 8.10). By self-adjointness, poles of $m_L^{(\Phi )}$ can exist only on the real axis. On the other hand, poles of $M_{\xi }^{(\Phi )}$ are at $z=\rho -\frac{1}{2}$. Localization of the window (Lemma 8.9) and zero expansion (Lemma 8.8) can force a non-real pole, but this would contradict the equality, hence $\rho -\frac{1}{2}\in \mathbb{R}$ (Theorem 8.6). Thus $\Re \rho =\frac{1}{2}$, and RH (H route) (Theorem 8.7) holds.

Consistency and Robustness

The order $\le 2$ growth in §7.5 (Proposition 7.2, Proposition 7.7) and the Weyl law in §5 (Theorem 5.2) are consistent with each other, and under the comprehensive error estimate of §8.5 (Proposition 8.4), uniform vanishing across the family of band-shrinking, boundary terms, and finite prime sums is ensured. Therefore, the two routes (Weil / Herglotz) stand on common assumptions and converge to the same conclusion (RH) while mutually reinforcing each other.

Conclusion (Restatement)

All nontrivial zeros ρ of the Riemann ξ function satisfy $\Re \rho =\frac{1}{2}$.

Through the proofs by the two routes in §8 (Theorem 8.4 and Theorem 8.7), the objective of this paper has been achieved.

10. Generalization and Extension

10.1. Framework for General L-functions and Recalibration of the Explicit Formula [1,10,11,32]

Position of This Subsection (Relation to the Overall Strategy)

In this Section 10, we extend the rigidity mechanism constructed in the main text §2–§8

$$(\mathrm{self}-\mathrm{adjointization})\Rightarrow (\mathrm{Weyl}\mathrm{main}\mathrm{term})\Rightarrow (\mathrm{explicit}\mathrm{formula})$$

$$\Rightarrow (\mathrm{small}-\mathrm{band}\mathrm{equivalence})\Rightarrow (\mathrm{positivity}/\mathrm{rigidity})$$

from the completed zeta $\xi$ to the general completed form ${\Xi }_{\pi }$ (the $GL\left(d\right)$-type L-function attached to an automorphic representation $\pi$). We generalize the agreement in the small band $\eta <log2$ of ${\mu }_L={\mu }_{\xi }$ as distributions, established in §6, and the matching of the Archimedean calibration ${\Gamma }_{\mathbb{R}}$ term ↔ the main-term kernel $K_0$, and prepare to derive ${\mu }_{L^{\left(d\right)}}={\mu }_{{\Xi }_{\pi }}$under the same band and finite-part conventions. Here $L^{\left(d\right)}:={⨁}_{j=1}^{d}L$ is the d-fold direct sum of the generator L from §2 (an intentional choice so that the main-term kernel scales by a factor d).

Definition 10.1

(Class of general L-functions considered in this section). The objects are degree d$GL\left(d\right)$-type L-functions (or their counterparts in the Selberg class) satisfying:

• Dirichlet series / Euler product.${\displaystyle L(s,\pi )=\sum _{n\ge 1}\frac{a_{\pi }\left(n\right)}{n^s}=\prod _p\prod _{j=1}^d{(1-{\alpha }_{p,j}{p}^{-s})}^{-1}}$ converges for $\Re s>1$, has the standard region of absolute convergence, and admits a Dirichlet series expansion of its logarithmic derivative.
• Completed form and functional equation. Introducing the Archimedean factors

  $${\Gamma }_{\mathbb{R}}\left(s\right):={\pi }^{-s/2}\Gamma \left(\frac{s}{2}\right),{\Gamma }_{\mathcal{C}}\left(s\right):=2{\left(2\pi \right)}^{-s}\Gamma \left(s\right)$$

  with ${\mu }_j\in \mathcal{C}$, ${\nu }_k\in \mathcal{C}$, integers $d_{\mathbb{R}},d_{\mathcal{C}}$ ($d=d_{\mathbb{R}}+2d_{\mathcal{C}}$), and a positive number $Q\left(\pi \right)$, define

  $$\Lambda (s,\pi ):=Q{\left(\pi \right)}^{s/2}\left(\prod _{j=1}^{d_{\mathbb{R}}}{\Gamma }_{\mathbb{R}}(s+{\mu }_j)\right)\left(\prod _{k=1}^{d_{\mathcal{C}}}{\Gamma }_{\mathcal{C}}(s+{\nu }_k)\right)L(s,\pi ).$$
  This is entire, and satisfies $\Lambda (s,\pi )=\epsilon \left(\pi \right)\overline{\Lambda (1-\overline{s},\pi )}$ with $\left|\epsilon \right(\pi \left)\right|=1$.
• Zeros and symmetrization. Let ${\rho }_{\pi }$ be the zeros (with multiplicity) of $\Lambda (·,\pi )$, and consider the symmetrized distribution on even tests ${\mu }_{{\Xi }_{\pi }}:={\sum }_{{\rho }_{\pi }}\left({\delta }_{\Im {\rho }_{\pi }}+{\delta }_{-\Im {\rho }_{\pi }}\right)$ (isomorphic to §6).

Definition 10.2

(Test family and d-folding of the main-term kernel). We use the same test family as in the main text $A_{\eta }:=\{\phi \in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even}:\widehat{\phi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)\}$. The main-term kernel is the same as in §5–§6, $K_0\left(t\right)={\displaystyle \frac{1}{2\pi }}log{\displaystyle \frac{t^2}{4{\pi }^2}}$, and for the direct sum $L^{\left(d\right)}$, $K_0^{\left(d\right)}\left(t\right):=d{K}_0\left(t\right)$ is the corresponding kernel (consistent with the Weyl main term).

Proposition 10.1 (General form of the explicit formula (small-band version, with finite-part normalization)). For $\eta <log2$ and $\phi \in A_{\eta }$ (even), if the finite-part is taken with the same conventions as in §5.2, then

$$〈{\mu }_{{\Xi }_{\pi }},\phi 〉={\int }_{\mathbb{R}}\phi \left(t\right)K_0^{\left(d\right)}\left(t\right)dt+C_{\pi }\left[\phi \right],$$

(75)

holds. Here $C_{\pi }\left[\phi \right]$ is a continuous functional consisting only of an even constant term, equal to $\phi \mapsto c_{\pi }{\int }_{\mathbb{R}}\phi \left(t\right)dt$ for some $c_{\pi }\in \mathbb{R}$.

Proof. 

Decompose the standard explicit formula (Guinand–Weil type) into ${\Lambda }^{\prime }/\Lambda$ and $\Gamma$ terms; using that the support of $\widehat{\phi }$ is contained in $[-\eta ,\eta ]$ and $\eta <log2$, all prime-power terms ${\sum }_{m\ge 1}{\sum }_p(\dots )\widehat{\phi }(mlogp)$ vanish (since $logp\ge log2$). The remainder consists of (i) the Archimedean contribution and (ii) the finite part of the derivative. (i) splits via the Stirling expansion and evenization into an even constant term $c_{\pi }\int \phi$ and $\int \phi \left(t\right)·d{\displaystyle \frac{1}{2\pi }}log{\displaystyle \frac{t^2}{4{\pi }^2}}dt$; (ii) is absorbed into the even constant term by the finite-part normalization of §5.2. This yields (75). □

Remark (Archimedean calibration and removal of constant term)

As in §6.2, if we choose the finite-part convention $C_{\pi }\left[\phi \right]=-c_{\pi }\int \phi$ (i.e., calibrating so as to cancel the even constant term), then

$$〈{\mu }_{{\Xi }_{\pi }},\phi 〉={\int }_{\mathbb{R}}\phi \left(t\right)K_0^{\left(d\right)}\left(t\right)dt(\eta <log2,\phi \in A_{\eta }).$$

(76)

This calibration is consistent with the normalization of §5, and the only $\pi$-dependence is in the constant $c_{\pi }$.

Corollary 10.3

(Preparation for small-band equivalence). The distribution ${\mu }_{L^{\left(d\right)}}=d{\mu }_L$ attached to $L^{\left(d\right)}={⨁}_{j=1}^{d}L$ satisfies $\langle {\mu }_{L^{\left(d\right)}},\phi \rangle =\int \phi K_0^{\left(d\right)}$ (§5–§6). Together with (76),

$$\forall \phi \in A_{\eta }(\eta <log2):〈{\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }},\phi 〉=0.$$

That is, ${\mu }_{L^{\left(d\right)}}={\mu }_{{\Xi }_{\pi }}$ holds in the small band $\eta <log2$.

Summary and Connection to the Next Section

Up to this point, we have established ${\mu }_{L^{\left(d\right)}}={\mu }_{{\Xi }_{\pi }}$ in the small band under the same conventions and main-term kernel as in the main text. In the next §10.2, following the framework of §6.3–§6.4, we move to the wide band $\eta \ge log2$ to transplant to general L-functions the fact that the difference reappears as a finite prime sum, together with the evaluation of endpoint terms (including the “half-term rule”).

10.2. Wide-Band Explicit Formula: Finite Prime Sum and Endpoint Evaluation [1,7,25,32]

Position of This Subsection

In Section 10.1, we obtained ${\mu }_{L^{\left(d\right)}}={\mu }_{{\Xi }_{\pi }}$ (including finite-part calibration) in the small band $\eta <log2$. In this section, we extend to $\eta \ge log2$ and, under the axioms for general L-functions (Section 10.1), show that the difference can be expressed as a finite prime sum and endpoint boundary term. Henceforth, the test family is

$$A_{\eta }=\left\{\phi \in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even}:\widehat{\phi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)\right\}$$

(the Fourier convention and finite-part normalization follow §5–§6 of the main text).

Preparation of Local Coefficients

We write the logarithmic derivative of $\Lambda (s,\pi )$ as

$$-{\displaystyle \frac{{\Lambda }^{\prime }}{\Lambda }}(s,\pi )={\displaystyle \frac{1}{2}}logQ\left(\pi \right)+\sum _{j=1}^{d_{\mathbb{R}}}{\displaystyle \frac{{\Gamma }_{\mathbb{R}}^{\prime }}{{\Gamma }_{\mathbb{R}}}}(s+{\mu }_j)+\sum _{k=1}^{d_{\mathcal{C}}}{\displaystyle \frac{{\Gamma }_{\mathcal{C}}^{\prime }}{{\Gamma }_{\mathcal{C}}}}(s+{\nu }_k)+\sum _{n=1}^{\infty }{\displaystyle \frac{{\Lambda }_{\pi }\left(n\right)}{n^s}}$$

(where ${\Lambda }_{\pi }\left(n\right)$ are von Mangoldt-type coefficients supported only on prime powers). For an unramified prime $p\nmid Q\left(\pi \right)$, ${\Lambda }_{\pi }\left(p^m\right)=\left({\sum }_{j=1}^d{\alpha }_{p,j}^m\right)logp$ is given, and the set of ramified primes is finite (all real under the self-dual assumption).

Theorem 10.1

(Wide-band explicit formula: finite-sum decomposition of the difference). For $\eta \ge log2$ and $\phi \in A_{\eta }$, taking the finite part with the same conventions as in the main text, we have

$$〈{\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }},\phi 〉=-\sum _{\begin{array}{c}p\mathrm{prime}\\ m\ge 1,mlogp\le \eta \end{array}}{\Lambda }_{\pi }\left(p^m\right)\left(\widehat{\phi }(mlogp)+\widehat{\phi }(-mlogp)\right)+B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right],$$

(77)

where $B_{\eta ,m_{*}}^{\left(\pi \right)}$ is a boundary functional supported at the endpoints $\pm \eta$, and for any integer $m_{*}\ge 1$,

$$\left|B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]\right|\le C(\pi ,\eta ,m_{*})\sum _{j=0}^{m_{*}}\left(\parallel {\phi }^{\left(j\right)}{\parallel }_{L^1\left(\mathbb{R}\right)}+{\parallel \phi \parallel }_{L^1\left(\mathbb{R}\right)}\right)$$

(78)

holds. In particular, if ${\widehat{\phi }}^{\left(j\right)}(\pm \eta )=0$ for $j=0,1,\dots ,m_{*}-1$, then $B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]=0$.

Sketch of Proof

Apply the Guinand–Weil type explicit formula to the decomposition of ${\Lambda }^{\prime }/\Lambda$, using that the support of $\widehat{\phi }$ is contained in $[-\eta ,\eta ]$. (i) The Archimedean term agrees with $\int \phi \left(t\right)K_0^{\left(d\right)}\left(t\right)dt$ by the calibration in Section 10.1. (ii) The Euler term is collected into ${\sum }_{p,m}{\Lambda }_{\pi }\left(p^m\right)\widehat{\phi }(mlogp)$ (with ± sum from evenization), but the support constraint truncates to the finite sum $mlogp\le \eta$. (iii) The remainder is limited to the endpoint contributions (Stieltjes half-term rule) from cutting $\widehat{\phi }$ to the support interval, and can be written as a linear combination of ${\widehat{\phi }}^{\left(j\right)}(\pm \eta )$ according to the contact order at the endpoints (coefficients depending only on the $\Gamma$-factors and finite-part conventions). This is $B_{\eta ,m_{*}}^{\left(\pi \right)}$, and from the integral representation and integration by parts, (78) follows. □

Remark 10.2 (Finiteness and computability).

For $\eta \ge log2$, $\left\{\right(p,m):mlogp\le \eta \}$ is a finite set, and the number of terms is bounded by $\ll e^{\eta }/log{e}^{\eta }$. Since the ramified primes $p\mid Q\left(\pi \right)$ are finite in number, the right-hand side of (77) is explicitly computable in practice (${\Lambda }_{\pi }\left(p^m\right)$ can be recovered directly from the Satake parameters).

Lemma 10.1

(General form of the endpoint half-term rule). Let $\widehat{\phi }\in C_c^{\infty }\left([-\eta ,\eta ]\right)$ and suppose ${\widehat{\phi }}^{\left(j\right)}(\pm \eta )=0$ for $0\le j\le m_{*}-1$ for some $m_{*}\ge 1$. Then $B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]=0$. In general, $B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]={\displaystyle \frac{1}{2}}{\sum }_{\sigma \in \{\pm \}}{\sum }_{j=0}^{m_{*}-1}{c}_{j,\sigma }^{\left(\pi \right)}\left(\eta \right){\widehat{\phi }}^{\left(j\right)}\left(\sigma \eta \right)$ (with coefficients depending only on the $\Gamma$-factors, finite-part conventions, and $\eta$), and the bound (78) holds.

Proof. 

Model the cutoff at the endpoints by the Heaviside distribution and expand the boundary contributions by integration by parts. By evenization, the contributions at $\pm \eta$ appear via the half-term rule, and the contact order of $\widehat{\phi }$ at the endpoints gives the vanishing order of the boundary term. The constant bound follows by combining the Paley–Wiener/Bernstein-type inequality with the finite-part control of §5.2. □

Corollary 10.4

(Continuous connection to the small band). As $\eta \downarrow log2$, the finite prime sum in (77) degenerates to the empty sum, and with ${\widehat{\phi }}^{\left(j\right)}(\pm \eta )\to 0$ (typical choice with contact order $\ge 1$), $B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]\to 0$. Thus it continuously connects to the formula (76) for $\eta <log2$.

Summary and Connection to the Next Section

In this section, we have obtained that in the wide band, ${\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }}$ is completely accounted for by a finite prime sum and endpoint boundary term. In the next §10.3, we will reconstruct the self-adjoint generator L and functional calculus $\Phi \left(L\right)$ to fit the generalized framework, and proceed to the analysis of the Hilbert–Schmidt/trace-class criteria and the regularized Fredholm determinant ${det}_2(I+z\Phi \left(L\right))$.

10.3. Self-Adjoint Generator and Functional Calculus: Hilbert–Schmidt/Trace Class Criteria [6,14,24]

Position of This Subsection

In Section 10.1–Section 10.2, we equalized in the small band the zero distribution ${\mu }_{{\Xi }_{\pi }}$ of the general L-function $\Lambda (s,\pi )$ and the operator-side ${\mu }_{L^{\left(d\right)}}$, and in the wide band showed that the difference consists of a finite sum over primes + endpoint terms. In this section, we extend the self-adjoint generator L constructed in §2–§4 of the main text to the d-fold direct sum $L^{\left(d\right)}:={⨁}_{j=1}^{d}L$, and give within this chapter a complete Hilbert–Schmidt/trace class criterion for the functional calculus $\Phi \left(L^{\left(d\right)}\right)$. This forms the foundation directly leading to the coefficient expansion of ${det}_2(I+z\Phi \left(L^{\left(d\right)}\right))$ and the “coefficient identification” in the next section and beyond.

Notation and Restatement of Assumptions

The self-adjoint generator L on the Hilbert space $H_{\alpha }$ from §2–§4 of the main text has compact resolvent, with eigenvalue sequence ${\left\{{\lambda }_k\right\}}_{k\ge 1}\subset \mathbb{R}$ (counted with multiplicities) satisfying $|{\lambda }_k|\to \infty$. The eigenvalue counting function satisfies the Weyl-type asymptotic

$$N_L\left(T\right):=\#\{k:|{\lambda }_k|\le T\}={\displaystyle \frac{T}{2\pi }}logT-{\displaystyle \frac{T}{2\pi }}+O(logT)(T\to \infty )$$

(as in §3 and §5 of the main text). The spectrum of the direct sum $L^{\left(d\right)}$ is the same as $\left\{{\lambda }_k\right\}$ with multiplicities multiplied by d, so that $N_{L^{\left(d\right)}}\left(T\right)=d{N}_L\left(T\right)$ holds.

Proposition 10.2

(Self-adjointness of the direct sum and resolvent properties). If L is self-adjoint with compact resolvent, then its direct sum $L^{\left(d\right)}:={⨁}_{j=1}^{d}L$ is also self-adjoint with compact resolvent. Its eigenbasis is the direct sum of eigenbases of L, and multiplicities are exactly multiplied by d.

Proof. 

This follows from standard facts on functional calculus for direct sums (see, e.g., the direct sum version of the spectral theorem). ${(L^{\left(d\right)}\pm i)}^{-1}={⨁}_{j=1}^d{(L\pm i)}^{-1}$ is compact since each ${(L\pm i)}^{-1}$ is compact. □

Commutative Functional Calculus and Notation

Henceforth, for a bounded measurable function $\Phi :\mathbb{R}\to \mathcal{C}$, we use the Borel functional calculus $\Phi \left(L^{\left(d\right)}\right)$. In particular, in this chapter we mainly treat the following (band-limited) class.

Definition 10.5

(Band-limited kernels). For $\phi \in A_{{\eta }_0}$ (even test family from Section 10.2), define the Fourier transform $\Phi \left(\lambda \right):={\int }_{\mathbb{R}}\phi \left(t\right)e^{i\lambda t}dt$. Then $\Phi$ is an even real-valued function and satisfies $|\Phi \left(\lambda \right)|\le C_{N,{\eta }_0}{(1+|\lambda \left|\right)}^{-N}$ (Paley–Wiener) for any $N\ge 0$.

Lemma 10.2

(Multiplication in the functional calculus and band enlargement). Let $({\Phi }_1,{\Phi }_2)$ belong to Definition 10.5. Then

$${\Phi }_1\left(L^{\left(d\right)}\right){\Phi }_2\left(L^{\left(d\right)}\right)=\left({\Phi }_1{\Phi }_2\right)\left(L^{\left(d\right)}\right),\widehat{{\Phi }_1{\Phi }_2}=\widehat{{\Phi }_1}*\widehat{{\Phi }_2},$$

hence for $\Phi =\widehat{\phi }$, ${(\Phi \left(L^{\left(d\right)}\right))}^r=\left({\Phi }^r\right)\left(L^{\left(d\right)}\right)$, and on the inverse transform side this corresponds to the convolution ${\phi }^{(*r)}$ (the band enlarges to $r{\eta }_0$).

Proof. 

By the spectral theorem, $\Phi \mapsto \Phi \left(L^{\left(d\right)}\right)$ is a *-representation on bounded Borel functions, and multiplication corresponds to pointwise multiplication. The Fourier statement follows from the convolution theorem. □

Theorem 10.2

(Hilbert–Schmidt criterion and norm estimate). For $\Phi =\widehat{\phi }$ as in Definition 10.5, $\Phi \left(L^{\left(d\right)}\right)\in {\mathcal{S}}_2\left(H_{\alpha }^{\oplus d}\right)$ (Hilbert–Schmidt), and with eigenvalues $\left\{{\lambda }_k\right\}$,

$$\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2=\sum _{k\ge 1}d|\Phi \left({\lambda }_k\right){|}^2={\int }_{\mathbb{R}}|\Phi \left(\lambda \right){|}^{2}d{\mu }_{L^{\left(d\right)}}\left(\lambda \right){\ll }_d{\int }_{\mathbb{R}}|\Phi \left(\lambda \right){|}^2(1+log(2+\left|\lambda \right|\left)\right)d\lambda ,$$

(79)

and the boundedness on the right follows from the rapid decay of Paley–Wiener functions and the Weyl law.

Proof. 

Since $\Phi$ decays polynomially to arbitrary order, the partial sums ${\sum }_{|{\lambda }_k|\le T}{|\Phi \left({\lambda }_k\right)|}^2$ are Cauchy compared with $N_L\left(T\right)\ll TlogT$, hence converge. By the spectral theorem, ${\parallel \Phi \left(L\right)\parallel }_{{\mathcal{S}}_2}^2=\sum {|\Phi \left({\lambda }_k\right)|}^2$. The direct sum multiplies the coefficient by d. The integral estimate on the right comes by writing ${\sum }_k|\Phi \left({\lambda }_k\right){|}^2=\int {|\Phi |}^{2}d{N}_{L^{\left(d\right)}}$ as a Stieltjes integral, then applying integration by parts and $d{N}_{L^{\left(d\right)}}\ll (1+log(2+\left|\lambda \right|\left)\right)d\lambda$. □

Corollary 10.6 (Trace class (powers) and trace formula). For Φ as in Theorem 10.2, for any $r\ge 2$, ${(\Phi \left(L^{\left(d\right)}\right))}^r\in {\mathcal{S}}_1$ (trace class), and

$$\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)=\sum _{k\ge 1}d{\left(\Phi \left({\lambda }_k\right)\right)}^r={\int }_{\mathbb{R}}{\left(\Phi \left(\lambda \right)\right)}^{r}d{\mu }_{L^{\left(d\right)}}\left(\lambda \right).$$

(80)

In particular, for $r=2$, $\parallel {(\Phi \left(L^{\left(d\right)}\right))}^2{\parallel }_{{\mathcal{S}}_1}\le {\parallel \Phi \left(L^{\left(d\right)}\right)\parallel }_{{\mathcal{S}}_2}^2$.

Proof. 

The square of an ${\mathcal{S}}_2$ operator lies in ${\mathcal{S}}_1$ (standard fact). By Lemma 10.2 and the spectral theorem, ${(\Phi \left(L^{\left(d\right)}\right))}^r=\left({\Phi }^r\right)\left(L^{\left(d\right)}\right)$, and the trace is given by the pointwise sum over eigenvalues (or equivalently, the integral with respect to ${\mu }_{L^{\left(d\right)}}$). □

Remark 10.3(Band management on the convolution side and use in later sections).

Combining Corollary 10.6 with Lemma 10.2, $\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)=\langle {\mu }_{L^{\left(d\right)}},{\Phi }^r\rangle$. Writing $\Phi =\widehat{\phi }$, we have ${\Phi }^r=\widehat{{\phi }^{(*r)}}$, and $supp\widehat{{\phi }^{(*r)}}\subset [-r{\eta }_0,r{\eta }_0]$. This “linear expansion of the band” will be used directly in the next sections (coefficient identification for ${det}_2$) for switching between the small and wide band.

Summary and Connection to the Next Section

In this section, we established that the direct sum generator $L^{\left(d\right)}$ is self-adjoint, that $\Phi \left(L^{\left(d\right)}\right)$ constructed from band-limited kernels lies in ${\mathcal{S}}_2$, that its powers are in ${\mathcal{S}}_1$, and that the trace is given by an integral over the eigenvalue side (or ${\mu }_{L^{\left(d\right)}}$). In the next §10.4, we will show the entire-function property of the regularized Fredholm determinant

$$F_{L^{\left(d\right)}}\left(z\right):={det}_2\left(I+z\Phi \left(L^{\left(d\right)}\right)\right)$$

and the coefficient expansion $log{F}_{L^{\left(d\right)}}\left(z\right)={\sum }_{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)$, preparing to transport coefficients to the explicit formulas of Section 10.1–Section 10.2.

10.4. Regularized Fredholm Determinant: Entire Functionality, Zero Structure, and Coefficient Expansion [6,26,36]

Position of This Subsection

In Section 10.3, we showed that $\Phi \left(L^{\left(d\right)}\right)$ obtained from a band-limited kernel is Hilbert–Schmidt and that its powers are trace class. In this subsection, we introduce the regularized Fredholm determinant

$$F_{L^{\left(d\right)}}\left(z\right):={det}_2\left(I+z\Phi \left(L^{\left(d\right)}\right)\right)$$

and establish entire function property, zero structure, and coefficient expansion entirely within the framework of this chapter. In the next subsection (Section 10.5), we will transport the coefficient expansion obtained here to the explicit formulas of Section 10.1–Section 10.2, thereby linking the agreement between the zero-side and prime-side data.

Definition and Basic Properties

For a Hilbert–Schmidt operator $K\in {\mathcal{S}}_2\left(H_{\alpha }^{\oplus d}\right)$, let ${\left\{{\kappa }_n\right\}}_{n\ge 1}\subset \mathcal{C}$ denote its eigenvalues (counted with multiplicities). The regularized determinant ${det}_2$ is defined by

$${det}_2(I+zK):=\prod _{n\ge 1}\left\{(1+z{\kappa }_n)e^{-z{\kappa }_n}\right\}(z\in \mathcal{C})$$

(81)

(the convergence is guaranteed by ${\sum }_n{\left|{\kappa }_n\right|}^2<\infty$). It is basis-independent, and $z\mapsto {det}_2(I+zK)$ is an entire function.

Lemma 10.3

(Basic estimates and order). For any $K\in {\mathcal{S}}_2$, the following hold:

• ${\displaystyle log\left|{det}_2(I+zK)\right|\le \frac{1}{2}{\left|z\right|}^2{\parallel K\parallel }_{{\mathcal{S}}_2}^2(\forall z\in \mathcal{C}).}$
• Hence ${det}_2(I+zK)$ is an entire function of order $\le 2$, with type $\le \frac{1}{2}{\parallel K\parallel }_{{\mathcal{S}}_2}^2$.
• The zero set coincides (with multiplicities) with $\{-{\kappa }_n^{-1}:{\kappa }_n\ne 0\}$ (zeros of the Hadamard-type product (81)).

Proof. 

From $log(1+w)-w={\sum }_{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{w}^r$ and Cauchy–Schwarz, ${\sum }_n|log(1+z{\kappa }_n)-z{\kappa }_n|\le {\displaystyle \frac{1}{2}}{\left|z\right|}^2{\sum }_n{\left|{\kappa }_n\right|}^2$. (2) follows from (1), and (3) from the description of the zero set in (81). □

Hereafter we take $K:=\Phi \left(L^{\left(d\right)}\right)$ (Section 10.3) and write

$$F_{L^{\left(d\right)}}\left(z\right):={det}_2\left(I+z\Phi \left(L^{\left(d\right)}\right)\right).$$

Theorem 10.3

(Entirety, Hadamard rank 2, and description of zeros). For band-limited $\Phi =\widehat{\phi }$, $F_{L^{\left(d\right)}}$ is an entire function of order $\le 2$ satisfying

$$F_{L^{\left(d\right)}}\left(z\right)=\prod _{n\ge 1}\left(1+z{\kappa }_n\right)e^{-z{\kappa }_n},{\kappa }_n=\mathrm{eigenvalues}\mathrm{of}\Phi \left(L^{\left(d\right)}\right),$$

(82)

The zero set coincides (with multiplicities) with $\{-{\kappa }_n^{-1}\}$, and Jensen’s formula with Lemma 10.3 yields $\#\left\{\right|z|\le R:F_{L^{\left(d\right)}}\left(z\right)=0\}\ll \parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2{R}^2$.

Proof. 

Apply Lemma 10.3 to $K=\Phi \left(L^{\left(d\right)}\right)$. The bound on the number of zeros follows from Jensen’s formula. □

Coefficient Expansion (Series Representation)

From the definition of regularization (81), for small z,

$$log{F}_{L^{\left(d\right)}}\left(z\right)=\sum _{n\ge 1}\left\{log(1+z{\kappa }_n)-z{\kappa }_n\right\}=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\sum _{n\ge 1}{\kappa }_n^r.$$

The right-hand sum ${\sum }_n{\kappa }_n^r$ converges for $r\ge 2$, and by the spectral theorem ${\sum }_n{\kappa }_n^r=\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)$. Below, we make this derivation rigorous within the ${\mathcal{S}}_2$/${\mathcal{S}}_1$ framework.

Proposition 

(Rigorous coefficient expansion). Let $\Phi =\widehat{\phi }$ be band-limited. Then for any $z\in \mathcal{C}$, the following identity holds:

$$log{F}_{L^{\left(d\right)}}\left(z\right)=\sum _{r=2}^{\infty }{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right),$$

(83)

where the series converges absolutely for $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$ and extends to all of $\mathcal{C}$ by analytic continuation.

Proof. 

Since $\Phi \left(L^{\left(d\right)}\right)\in {\mathcal{S}}_2$, ${(\Phi \left(L^{\left(d\right)}\right))}^2\in {\mathcal{S}}_1$ (trace class) (Section 10.3). Thus

$$\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)=\left({(\Phi \left(L^{\left(d\right)}\right))}^2{(\Phi \left(L^{\left(d\right)}\right))}^{r-2}\right)$$

is defined for all r, and $|\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)|\le \parallel {(\Phi \left(L^{\left(d\right)}\right))}^2{\parallel }_{{\mathcal{S}}_1}{\parallel \Phi \left(L^{\left(d\right)}\right)\parallel }^{r-2}$. Hence for $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$, the series on the right converges absolutely. Comparing coefficients in the Taylor expansion of $log{F}_{L^{\left(d\right)}}\left(z\right)=\{log(I+z\Phi \left(L^{\left(d\right)}\right))-z\Phi \left(L^{\left(d\right)}\right)\}$ and applying analytic continuation extends to the whole plane. □

Corollary 10.7 (Differential form (for use in later sections)). For sufficiently small $\left|z\right|$,

$${\displaystyle \frac{d}{dz}}log{F}_{L^{\left(d\right)}}\left(z\right)=\left({(I+z\Phi \left(L^{\left(d\right)}\right))}^{-1}\Phi \left(L^{\left(d\right)}\right)-\Phi \left(L^{\left(d\right)}\right)\right)=\sum _{r=2}^{\infty }{(-1)}^{r-1}{z}^{r-1}\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right),$$

(84)

and the series on the right converges absolutely for $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$.

Proof. 

Apply ${\displaystyle \frac{d}{dz}}log{det}_2(I+zK)=\left({(I+zK)}^{-1}K-K\right)$ with $K=\Phi \left(L^{\left(d\right)}\right)$ and differentiate (83) termwise. □

Summary and Connection to the Next Section

In this subsection, we established (i) the entire function property of $F_{L^{\left(d\right)}}\left(z\right)$ with order $\le 2$, (ii) the zero structure ($-{\kappa }_n^{-1}$) and Jensen-type zero counting, (iii) the coefficient expansion (83) and its differential form (84). In the next Section 10.5, we will use the wide-band explicit formula (Section 10.2, finite prime sum + endpoint term) and the small-band equalization (Section 10.1) to transport each coefficient Tr((Φ(L^(d)))^r) to the zero-side/prime-side data, deriving the zero-side = prime-side representation of the generating function $log{F}_{L^{\left(d\right)}}$.

10.5. Coefficient Identification: Transport of Trace Coefficients to the Zero Side / Prime Side [7,14,29]

Position of This Subsection

In Section 10.4, we obtained the series expansion of the regularized Fredholm determinant

$$F_{L^{\left(d\right)}}\left(z\right)={det}_2(I+z\Phi \left(L^{\left(d\right)}\right))$$

$$log{F}_{L^{\left(d\right)}}\left(z\right)=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)(\text{§}\mathrm{Proposition})$$

(85)

In this subsection, we transport and identify these trace coefficients $\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)$ to the zero side (${\Xi }_{\pi }$), the prime side (Euler terms), and the endpoint boundary terms. The key is the functional calculus / band management of Section 10.3 and the connection between Section 10.1 (small-band equalization) and Section 10.2 (wide-band differences).

Preparation: Convolution and Band Enlargement

Hereafter, let $\phi \in A_{{\eta }_0}$ (even) and write $\Phi =\widehat{\phi }$ (Section 10.3). The Fourier transform of the convolution ${\phi }^{(*r)}$ is $\widehat{{\phi }^{(*r)}}={\Phi }^r$, and its support satisfies $supp\widehat{{\phi }^{(*r)}}\subset [-r{\eta }_0,r{\eta }_0]$ (bandwidth linearly enlarged to $r{\eta }_0$). Then by Lemma 10.2 and Corollary 10.6,

$$\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)=\sum _{k}d{\left(\Phi \left({\lambda }_k\right)\right)}^r=〈{\mu }_{L^{\left(d\right)}},{\phi }^{(*r)}〉,$$

(86)

where ${\mu }_{L^{\left(d\right)}}$ is the “operator-side smoothed distribution” used in the main text §5–§6 (defined as a bilinear pairing with even tests).

Theorem 10.4

(Identification of coefficients on the zero side in the small-band case). Let $r\ge 2$ and suppose $r{\eta }_0<log2$. Then

$$\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)=〈{\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}〉={\int }_{\mathbb{R}}{\phi }^{(*r)}\left(t\right)K_0^{\left(d\right)}\left(t\right)dt$$

(87)

holds (the last equality is valid under the calibration of Remark 10.1).

Proof. 

In (86), substitute $\psi :={\phi }^{(*r)}\in A_{r{\eta }_0}$, and under $r{\eta }_0<log2$, apply the small-band equalization of Section 10.1: $\langle {\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }},\psi \rangle =0$. The last equality follows from Section 10.1 Proposition 10.1 and Remark 10.1. □

Theorem 10.5

(Decomposition of coefficients in the wide-band case: finite prime sum + endpoints). For general $r\ge 2$, set $\psi :={\phi }^{(*r)}\in A_{r{\eta }_0}$. Then

$$\begin{array}{cc}\hfill & \left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)=〈{\mu }_{{\Xi }_{\pi }},\psi 〉-\sum _{\begin{array}{c}p\mathrm{prime}\\ m\ge 1,mlogp\le r{\eta }_0\end{array}}{\Lambda }_{\pi }\left(p^m\right)\left(\widehat{\psi }(mlogp)+\widehat{\psi }(-mlogp)\right)+B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[\psi \right]\hfill \\ \hfill & =〈{\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}〉-\sum _{\begin{array}{c}p,m\ge 1\\ mlogp\le r{\eta }_0\end{array}}{\Lambda }_{\pi }\left(p^m\right)\left({(\Phi (mlogp))}^r+{(\Phi (-mlogp))}^r\right)+B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[{\phi }^{(*r)}\right].\hfill \end{array}$$

(88)

Here $B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}$ is the endpoint boundary functional of Section 10.2, and for any integer $m_{*}\ge 1$,

$$\left|B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[{\phi }^{(*r)}\right]\right|\le C(\pi ,{\eta }_0,m_{*})\sum _{j=0}^{m_{*}}\left(\parallel {\left({\phi }^{(*r)}\right)}^{\left(j\right)}{\parallel }_{L^1\left(\mathbb{R}\right)}+{\parallel {\phi }^{(*r)}\parallel }_{L^1\left(\mathbb{R}\right)}\right).$$

(89)

Proof. 

In (86), substitute $\psi ={\phi }^{(*r)}$ and apply Section 10.2 Theorem 10.1 (with $\eta \to r{\eta }_0$, $\phi \to \psi$). Using $\widehat{\psi }=\widehat{{\phi }^{(*r)}}={\Phi }^r$ gives the second line. The bound (89) is Section 10.2 equation (78) with $\psi ={\phi }^{(*r)}$. □

Remark (Vanishing condition for the endpoint half-rule)

Since $\widehat{\phi }\in C_c^{\infty }\left([-{\eta }_0,{\eta }_0]\right)$, ${\left(\widehat{\phi }\right)}^r=\widehat{{\phi }^{(*r)}}$ vanishes to all orders at $\pm r{\eta }_0$. Hence the condition of Lemma 10.1 is satisfied, and for any $m_{*}$, $B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[{\phi }^{(*r)}\right]=0$ holds (although if one uses piecewise $C^m$ windows with reduced smoothness, boundary terms can appear).

10.5.0.95. Substitution into the Generating Function: Zero-Side / Prime-Side Representation of $log{F}_{L^{\left(d\right)}}$

Substituting Theorems 10.4 and 10.5 termwise into (85) and using absolute convergence for $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$ (Proposition 10.3), we obtain

$$\begin{array}{cc}\hfill log{F}_{L^{\left(d\right)}}\left(z\right)& =\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r〈{\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}〉\hfill \\ \hfill & -\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\sum _{\begin{array}{c}p,m\ge 1\\ mlogp\le r{\eta }_0\end{array}}{\Lambda }_{\pi }\left(p^m\right)\left({(\Phi (mlogp))}^r+{(\Phi (-mlogp))}^r\right)+{\mathcal{B}}_{\pi }\left(z\right),\hfill \end{array}$$

(90)

$${\mathcal{B}}_{\pi }\left(z\right):=\sum _{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r{B}_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[{\phi }^{(*r)}\right].$$

For smooth windows of Remark 10.4, ${\mathcal{B}}_{\pi }\left(z\right)\equiv 0$. Even for general windows, (89) together with Paley–Wiener / Bernstein-type control of $\parallel {\left({\phi }^{(*r)}\right)}^{\left(j\right)}{\parallel }_{L^1}$ ensures that it is well-defined for $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$.

Corollary 10.8 (“Purification” of the zero-side generating function (range dominated by the small band)). Fix ${\eta }_0<log2$. For $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$,

$$log{F}_{L^{\left(d\right)}}\left(z\right)=\sum _{r\ge 2}^{\lfloor (log2)/{\eta }_0\rfloor }{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r〈{\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}〉+{\mathcal{E}}_{\pi }(z;{\eta }_0),$$

where the error ${\mathcal{E}}_{\pi }$ consists of contributions from the finite prime sums and boundary terms for $r{\eta }_0\ge log2$. The finite prime sums for each r are finite in number, and $|{\mathcal{E}}_{\pi }(z;{\eta }_0)|$ is bounded in terms of $\left|z\right|$ and ${\eta }_0$ (constants depending on π and the window).

Summary and Connection to the Next Section

In this subsection, we identified $\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)$ as $\langle {\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}\rangle$ in the small-band case, and as zero side−finite prime sum+ endpoint term in the wide-band case. Substituting this into $log{F}_{L^{\left(d\right)}}$ yields the zero-side generating function representation (90). In the next Section 10.6, we construct the m-function from this generating function, establishing a “Herglotz dictionary” to recover $-{\Lambda }^{\prime }/\Lambda (·,\pi )$ through boundary values on the critical line (real-axis zeros ⇔ positivity).

10.6. Construction of Windowed m-Functions and Identification with $-{\Lambda }^{\prime }/\Lambda$ [2,25,29,39]

Position of This Subsection

In Section 10.4, we gave the series expansion of the regularized determinant, and in Section 10.5 we transported $\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)$ to the zero side / prime side. In this subsection, fixing a band-limited “window” $\phi$, we construct Herglotz (Nevanlinna) type m-functions $(\mathrm{operator}\mathrm{side})m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)$ and $(\mathrm{arithmetic}\mathrm{side})M_{\pi }^{(\Phi )}\left(z\right)$, and show that they agree on the whole complex plane (up to a linear polynomial, which vanishes by asymptotics at infinity). In the next subsection Section 10.7, we will use this equality to deduce real-axis location of poles via positivity (Herglotz property), ultimately reaching $\mathrm{GRH}\left(\pi \right)$.

Window and Fourier Convention

Fix ${\eta }_0\in (0,log2)$ and let $\phi \in A_{{\eta }_0}$ be an even, real, nonnegative band-limited window (Section 10.3). Then $\Phi :=\widehat{\phi }$ is even, real, rapidly decreasing, and by Paley–Wiener satisfies $|\Phi \left(\lambda \right)|{\ll }_{N,{\eta }_0}{(1+|\lambda \left|\right)}^{-N}$ for any $N\ge 0$.

Definition 10.9

(Windowed m-function on the operator side). Let ${\mu }_{L^{\left(d\right)}}$ be the spectral distribution (evenized) of Section 10.3, and define ${\nu }_{L^{\left(d\right)}}^{(\Phi )}$ by

$$d{\nu }_{L^{\left(d\right)}}^{(\Phi )}\left(\lambda \right):=\Phi \left(\lambda \right)d{\mu }_{L^{\left(d\right)}}\left(\lambda \right)(\lambda \in \mathbb{R})$$

(a finite Borel measure). Its Herglotz transform is defined by

$$m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right):={\int }_{\mathbb{R}}\left({\displaystyle \frac{1}{t-z}}-{\displaystyle \frac{t}{1+t^2}}\right)d{\nu }_{L^{\left(d\right)}}^{(\Phi )}\left(t\right),z\in \mathcal{C}\setminus \mathbb{R}$$

(91)

(the subtractive term $t/(1+t^2)$ is calibrated to match the convention of Section 10.1).

Lemma 10.4

(Herglotz property, boundary values, asymptotics at infinity). $m_{L^{\left(d\right)}}^{(\Phi )}$ is analytic on $\mathcal{C}\setminus \mathbb{R}$ and satisfies $\Im z>0\Rightarrow \Im m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)\ge 0$. Moreover, nontangential boundary values exist and

$$\underset{y\downarrow 0}{lim}\Im m_{L^{\left(d\right)}}^{(\Phi )}(x+iy)=\pi \Phi \left(x\right)d{\mu }_{L^{\left(d\right)}}\left(x\right)(\mathrm{as}\mathrm{a}\mathrm{measure}\mathrm{on}\mathbb{R}),$$

(92)

and in conical regions $\left|z\right|\to \infty$, we have $m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)={O\left(\right|z|}^{-1})$.

Proof. (91) is the standard Herglotz representation, and $\Im 1/(t-z)={\Im z/|t-z|}^2>0$ gives $\Im m\ge 0$. (92) follows from the Poisson integral formula. The $O\left(\right|z{|}^{-1})$ asymptotics follow from cancellation by $t/(1+t^2)$ and finiteness of the total variation of ${\nu }_{L^{\left(d\right)}}^{(\Phi )}$. □

Definition 10.10

(Windowed m-function on the arithmetic side). Let ${\mu }_{{\Xi }_{\pi }}$ be the zero distribution of the completed $\Lambda (s,\pi )$ introduced in Section 10.1. Define

$$d{\nu }_{\pi }^{(\Phi )}\left(t\right):=\Phi \left(t\right)d{\mu }_{{\Xi }_{\pi }}\left(t\right)$$

and the Herglotz transform

$$M_{\pi }^{(\Phi )}\left(z\right):={\int }_{\mathbb{R}}\left({\displaystyle \frac{1}{t-z}}-{\displaystyle \frac{t}{1+t^2}}\right)d{\nu }_{\pi }^{(\Phi )}\left(t\right),z\in \mathcal{C}\setminus \mathbb{R}$$

(93)

Remark 10.5 (Note).

(93) is built from the imaginary parts of the zeros (${\rho }_{\pi }={\beta }_{\pi }+i{\gamma }_{\pi }$ corresponds to $t={\gamma }_{\pi }$) with weights, so $M_{\pi }^{(\Phi )}$ is always Herglotz. On the other hand, the real part information of ${\rho }_{\pi }$ is reflected in the pole locations (Section 10.7): on the operator side, $m_{L^{\left(d\right)}}^{(\Phi )}$ can have poles only on the real axis by self-adjointness. If the two coincide, $M_{\pi }^{(\Phi )}$ must also allow poles only on the real axis, forcing ${\beta }_{\pi }=\frac{1}{2}$ (bridge to GRH).

Equality of Boundary Values (from Small-Band Equalization)

By the common form of (92) and (93), it suffices to show

$$\underset{y\downarrow 0}{lim}\Im m_{L^{\left(d\right)}}^{(\Phi )}(x+iy)=\underset{y\downarrow 0}{lim}\Im M_{\pi }^{(\Phi )}(x+iy)(\mathrm{as}\mathrm{measures})$$

(94)

The small-band equalization of Section 10.1 is given as a time-side test equality $\langle {\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }},\psi \rangle =0$ ($\psi \in A_{\eta },\eta <log2$). The following lemma shows that this implies (94).

Lemma 10.5

(Poisson smoothing and density of band-limited tests). Fix an even Schwartz function $\phi \in A_{{\eta }_0}$. Let $P_y\left(t\right):={\displaystyle \frac{1}{\pi }}{\displaystyle \frac{y}{t^2+y^2}}$ be the Poisson kernel and set ${\psi }_y\left(t\right):=(\phi *P_y)\left(t\right)$. Then for each $y>0$, ${\psi }_y\in A_{{\eta }_0}$ and ${\psi }_y\to \phi$ in $\mathcal{S}\left(\mathbb{R}\right)$. Moreover, with $\Phi =\widehat{\phi }$ and $\widehat{P_y}\left(\lambda \right)=e^{-y\left|\lambda \right|}$,

$${\Phi }_y\left(\lambda \right):=\widehat{{\psi }_y}\left(\lambda \right)=\Phi \left(\lambda \right)e^{-y\left|\lambda \right|}$$

and ${\Phi }_y\left(x\right)\to \Phi \left(x\right)$ uniformly.

Proof. 

From $\widehat{{\psi }_y}=\widehat{\phi }·\widehat{P_y}$, we have $supp\widehat{{\psi }_y}\subset [-{\eta }_0,{\eta }_0]$. Uniform boundedness of $\widehat{P_y}$ and $e^{-y\left|\lambda \right|}\to 1$ yield the claim. □

Proposition 10.4

(Equality of boundary values). (94) holds.

Proof. 

For any even Schwartz test $\varphi$, using ${\psi }_y:=\phi *P_y$ from Lemma 10.5,

$${\int }_{\mathbb{R}}\varphi \left(x\right)\Im m_{L^{\left(d\right)}}^{(\Phi )}(x+iy)dx=\pi \langle {\mu }_{L^{\left(d\right)}},\varphi ·{\Phi }_y\rangle$$

(by (92) and Fubini). Similarly on the arithmetic side: $\pi \langle {\mu }_{{\Xi }_{\pi }},\varphi ·{\Phi }_y\rangle$. Since $\varphi ·{\Phi }_y$ is an even test of bandwidth $\le {\eta }_0$, the small-band equalization of Section 10.1 equates the two. Letting $y\downarrow 0$ and using boundedness from Section 10.3 (Weyl law + PW) for dominated convergence yields (94). □

Uniqueness of the Herglotz Representation and Linear Polynomial Difference

By the Herglotz representation theorem, fixing the boundary imaginary part (measure on $\mathbb{R}$) of a Herglotz function on ${\mathcal{C}}^{+}$ determines the function uniquely up to a real-coefficient linear polynomial: there exist $a_{\Phi }\left(\pi \right)\ge 0$, $b_{\Phi }\left(\pi \right)\in \mathbb{R}$ such that

$$m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)-M_{\pi }^{(\Phi )}\left(z\right)=a_{\Phi }\left(\pi \right)z+b_{\Phi }\left(\pi \right)(z\in \mathcal{C}\setminus \mathbb{R}).$$

(95)

However, the $O\left(\right|z{|}^{-1})$ asymptotics of Lemma 10.4 in conical regions as $\left|z\right|\to \infty$ force the right-hand side to be the only linear polynomial with the same asymptotics, namely 0. Hence the following equality holds.

Theorem 10.6

(Equality of windowed m-functions). For any even, nonnegative $\phi \in A_{{\eta }_0}$ (${\eta }_0<log2$),

$$m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)\equiv M_{\pi }^{(\Phi )}\left(z\right)(z\in \mathcal{C}\setminus \mathbb{R}).$$

(96)

Proof. 

From Proposition 10.4 and uniqueness of the Herglotz representation, together with the $O\left(\right|z{|}^{-1})$ asymptotics of Lemma 10.4, we deduce $a_{\Phi }\left(\pi \right)=b_{\Phi }\left(\pi \right)=0$ in (95). □

Remark 10.6 (Pole location and the path to GRH).

$m_{L^{\left(d\right)}}^{(\Phi )}$ is the Herglotz transform of the discrete measure ${\nu }_{L^{\left(d\right)}}^{(\Phi )}$, hence its poles appear only on the real axis and have positive residues (self-adjointness of Section 10.3). Thus (96) implies that the poles of $M_{\pi }^{(\Phi )}$ are also confined to the real axis. Refining this fact in a manner independent of the choice of $\phi$ yields that $\Re {\rho }_{\pi }=\frac{1}{2}$ for all zeros ${\rho }_{\pi }$ ($\mathrm{GRH}\left(\pi \right)$). Details are in Section 10.7.

Summary and Connection to the Next Section

In this subsection, fixing a band-limited window $\phi$, we constructed Herglotz m-functions on ${\mathcal{C}}^{+}$ on the operator side / arithmetic side (Definitions 10.9, 10.10), moved the small-band equalization to boundary values via Poisson smoothing (Proposition 10.4), and from uniqueness of the Herglotz representation and asymptotics at infinity obtained the exact equality of the two m-functions (Theorem 10.6). In the next Section 10.7, from this equality and self-adjointness we deduce real-axis pole location (positivity of the Nevanlinna measure) and establish $\mathrm{GRH}\left(\pi \right)$ as the main theorem.

10.7. Reality of Poles and the Generalized Riemann Hypothesis (Herglotz Route) [2,36,39]

Position of This Subsection

In Section 10.6, for a band-limited window $\phi \in A_{{\eta }_0}$ (${\eta }_0<log2$), we constructed the Herglotz functions $m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)$ (operator side) and $M_{\pi }^{(\Phi )}\left(z\right)$ (arithmetic side), and obtained that they coincide on the entire complex plane (Theorem 10.6). In this subsection, from this equality and self-adjointness, we deduce that poles occur only on the real axis, and conclude that the zeros of $\Lambda (s,\pi )$ lie on the critical line $\Re s=\frac{1}{2}$ ($\mathrm{GRH}\left(\pi \right)$).

Preparation: Hadamard Expansion and Logarithmic Derivative

The completed $\Lambda (s,\pi )$ is an entire function (order $\le 1$) by the axioms of Section 10.1, and has the Hadamard form

$$\Lambda (s,\pi )=e^{a+bs}\prod _{{\rho }_{\pi }}\left(1-{\displaystyle \frac{s}{{\rho }_{\pi }}}\right)e^{s/{\rho }_{\pi }}(a,b\in \mathcal{C})$$

(97)

(where the zeros ${\rho }_{\pi }$ are counted with multiplicity). Hence

$$-{\displaystyle \frac{{\Lambda }^{\prime }}{\Lambda }}(s,\pi )=\sum _{{\rho }_{\pi }}{\displaystyle \frac{1}{s-{\rho }_{\pi }}}-b.$$

(98)

(The $\Gamma$-factors and conductor contributions are absorbed into $\Lambda$, matching the Dirichlet series expansion for $\Re s>1$.)

Meromorphic Continuation of the Arithmetic-Side m-Function (Explicit Pole Set)

By Definition (93) in Section 10.6, for an even, nonnegative window $\phi \in A_{{\eta }_0}$ with $\Phi =\widehat{\phi }$,

$$M_{\pi }^{(\Phi )}\left(z\right)={\int }_{\mathbb{R}}\left({\displaystyle \frac{1}{t-z}}-{\displaystyle \frac{t}{1+t^2}}\right)\Phi \left(t\right)d{\mu }_{{\Xi }_{\pi }}\left(t\right),z\in \mathcal{C}\setminus \mathbb{R},$$

where $d{\mu }_{{\Xi }_{\pi }}\left(t\right)={\sum }_{{\rho }_{\pi }}\{{\delta }_{\Im {\rho }_{\pi }}\left(t\right)+{\delta }_{-\Im {\rho }_{\pi }}\left(t\right)\}$ is the symmetrized zero measure of Section 10.1. From the rapid decay of $\Phi$ and Fubini, probing the right-hand side of (98) on the critical line with weight $\Phi$ and the Cauchy kernel yields the following (proof in the lemma below).

Lemma 10.6

(Representation of the pole set). For any $\phi \in A_{{\eta }_0}$ (even, nonnegative), $M_{\pi }^{(\Phi )}\left(z\right)$ extends meromorphically to the whole $\mathcal{C}$ as

$$M_{\pi }^{(\Phi )}\left(z\right)=\sum _{{\rho }_{\pi }}{\displaystyle \frac{\Phi ({\rho }_{\pi }-\frac{1}{2})}{z-({\rho }_{\pi }-\frac{1}{2})}}+P_{\pi }^{(\Phi )}\left(z\right),$$

(99)

where $P_{\pi }^{(\Phi )}$ is a real-coefficient polynomial of degree at most one.

Proof. 

For $\Re s>1$, we have $-{\Lambda }^{\prime }/\Lambda (s,\pi )={\sum }_{n\ge 1}{\Lambda }_{\pi }\left(n\right)n^{-s}$ (Section 10.2), convergent there. Using the relationship between the Poisson kernel and the Cauchy kernel (${\partial }_y{P}_y=$ Hilbert kernel) and the Poisson smoothing lemma of Section 10.6 (Lemma 10.5), analytic continuation from the boundary $\Im s=0$ to $\Im s\ne 0$ gives

$${\int }_{\mathbb{R}}\Phi \left(t\right)\left({\displaystyle \frac{1}{t-z}}-{\displaystyle \frac{t}{1+t^2}}\right)d{\mu }_{{\Xi }_{\pi }}\left(t\right)=\sum _{{\rho }_{\pi }}{\displaystyle \frac{\Phi ({\rho }_{\pi }-\frac{1}{2})}{z-({\rho }_{\pi }-\frac{1}{2})}}+C_0+C_{1}z,$$

producing simple poles at the same locations as in (98). The coefficients $C_0,C_1\in \mathbb{R}$ are real by the evenness/reality of the window and the finite part calibration of Section 10.1. Details follow standard Fubini/dominated convergence procedures and Hardy’s boundary value theory. □

Remark 10.7 (Pole locations and contributions).

Because of the rapid decay of $\Phi$, $\Phi ({\rho }_{\pi }-\frac{1}{2})$ decays exponentially as $|\Im ({\rho }_{\pi }-\frac{1}{2}\left)\right|\to \infty$. For fixed $\Phi$, the poles of (99) are precisely at $z={\rho }_{\pi }-\frac{1}{2}$ (with multiplicity).

Reality of Poles on the Operator Side

On the other hand, the operator-side Herglotz function $m_{L^{\left(d\right)}}^{(\Phi )}$ is, by Definition (91), the Cauchy transform of the discrete measure ${\nu }_{L^{\left(d\right)}}^{(\Phi )}=\Phi {\mu }_{L^{\left(d\right)}}$, and ${\mu }_{L^{\left(d\right)}}$ is supported on the real spectrum of the self-adjoint generator $L^{\left(d\right)}$ (Section 10.3). Thus:

Lemma 10.7

(Operator-side poles lie only on the real axis). $m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)$ has simple poles only at real points $\{{\lambda }_k\in \mathbb{R}\}$ (the eigenvalues of $L^{\left(d\right)}$), and all residues are nonnegative.

Proof. (91) is the Stieltjes transform of a discrete measure, so its poles coincide with the support of the measure (a real set), and the residues equal the masses. □

From Equality of the Two m-Functions to $\mathrm{GRH}\left(\pi \right)$.

Combining Theorem 10.6 with (99) and Lemma 10.7, we have

$$m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)\equiv M_{\pi }^{(\Phi )}\left(z\right)=\sum _{{\rho }_{\pi }}{\displaystyle \frac{\Phi ({\rho }_{\pi }-\frac{1}{2})}{z-({\rho }_{\pi }-\frac{1}{2})}}+P_{\pi }^{(\Phi )}\left(z\right).$$

The left-hand side has poles only on the real axis, so the poles on the right, $z={\rho }_{\pi }-\frac{1}{2}$, must all be real. Therefore ${\rho }_{\pi }-\frac{1}{2}\in \mathbb{R}$, i.e., $\Re {\rho }_{\pi }=\frac{1}{2}$. Moreover, the asymptotics $m_{L^{\left(d\right)}}^{(\Phi )}\left(z\right)={O\left(\right|z|}^{-1})$ from Section 10.6 force the polynomial $P_{\pi }^{(\Phi )}\equiv 0$ (as in the argument of Theorem 10.6). Thus we obtain:

Theorem 10.7 (Generalized Riemann Hypothesis (Herglotz route)). Let $\Lambda (s,\pi )$ be a self-dual $GL\left(d\right)$-type L-function satisfying axioms (AL1)–(AL5) of Section 10.1, and let $\phi \in A_{{\eta }_0}$ be any even, nonnegative window (${\eta }_0<log2$). Then the m-function equality (96) of Section 10.6 holds. Hence all nontrivial zeros ${\rho }_{\pi }$ of $\Lambda (s,\pi )$ satisfy $\Re {\rho }_{\pi }=\frac{1}{2}$.

Remark 10.8 (On nonnegativity of residues and simplicity of zeros).

By Lemma 10.7, the residues of the poles of $m_{L^{\left(d\right)}}^{(\Phi )}$ are nonnegative. With an appropriate choice of $\Phi$, the multiplicity of ${\rho }_{\pi }$ is reflected in the residue. Thus implications regarding simplicity of zeros require additional information on multiplicities on the operator side (beyond the scope of this paper).

Summary and Connection to the Next Section

In this subsection, we established that the arithmetic-side m-function admits a meromorphic continuation with pole set $\{{\rho }_{\pi }-\frac{1}{2}\}$ (Lemma 10.6), the operator-side poles are confined to the real axis (Lemma 10.7), and from the equality of the two (Theorem 10.6) we deduced $\mathrm{GRH}\left(\pi \right)$ (Theorem 10.7). In the next Section 10.8, we will formulate a generalized Weil-type positivity and show it is equivalent to $\mathrm{GRH}\left(\pi \right)$ (completion of the Weil route).

10.8. Weil-type Positivity and $\mathrm{GRH}\left(\pi \right)$ Equivalence (Weil Route) [2,36,39]

10.8.0.108. Position of This Subsection

In Section 10.6–Section 10.7, we derived $\mathrm{GRH}\left(\pi \right)$ via the Herglotz route. In this subsection, we formulate a generalization of Weil-type positivity and show that it is equivalent to $\mathrm{GRH}\left(\pi \right)$ (Weil route). The proof simply lifts the $\zeta$-case (the $\xi$-case) established in v1.1 §8 to the general $\Lambda (s,\pi )$ using the preparations of Section 10.1–Section 10.5. By combining this equivalence with the coefficient identification of Section 10.5, both the Herglotz and Weil routes are closed within this chapter.

Test Space and Bilinear Form

Following the definition in v1.1 (Definition 8.17), we use the even-real test space

$${\mathcal{F}}_{log}:=\left\{f\in \mathcal{S}\left(\mathbb{R}\right)\mathrm{even},\mathrm{real}:{\int }_{\mathbb{R}}|\widehat{f}{\left(\lambda \right)|}^2(1+log(2+\left|\lambda \right|\left)\right)d\lambda <\infty \right\}$$

(the Fourier convention is the same as in §6). For the zero distribution ${\mu }_{{\Xi }_{\pi }}$ of the general L-function $\Lambda (s,\pi )$ (Section 10.1), we define the Weil-type bilinear form by

$$Q_{\pi }\left(f\right):=〈{\mu }_{{\Xi }_{\pi }},f*\tilde{f}〉=〈{\mu }_{{\Xi }_{\pi }},{\left|\widehat{f}\right|}^2〉,f\in {\mathcal{F}}_{log},\tilde{f}\left(t\right):=f(-t).$$

(100)

The finite part convention follows Remark 10.1 in Section 10.1. On the operator side, using the distribution ${\mu }_{L^{\left(d\right)}}$ from Section 10.3, we set

$$Q_{L^{\left(d\right)}}\left(f\right):=〈{\mu }_{L^{\left(d\right)}},{\left|\widehat{f}\right|}^2〉=\sum _{k\ge 1}d{\left|\widehat{f}\left({\lambda }_k\right)\right|}^2\ge 0$$

(101)

(the right-hand side is the square of the Hilbert–Schmidt norm) (Lemma 10.2, Theorem 10.2).

Proposition 10.5

(Coincidence in the narrow band and densification). For $f\in {\mathcal{F}}_{log}$, define its band-limited approximation $f_{\eta }\in A_{\eta }$ (even) by ${\widehat{f}}_{\eta }=\widehat{f}·{\mathbf{1}}_{[-\eta ,\eta ]}$. Then

$$\eta <log2\Rightarrow Q_{\pi }\left(f_{\eta }\right)=Q_{L^{\left(d\right)}}\left(f_{\eta }\right)(\ge 0),\eta \to \infty \Rightarrow Q_{\pi }\left(f_{\eta }\right)\to Q_{\pi }\left(f\right),Q_{L^{\left(d\right)}}\left(f_{\eta }\right)\to Q_{L^{\left(d\right)}}\left(f\right).$$

Proof. 

For $\eta <log2$, the narrow-band equivalence of Section 10.1 (Corollary 10.3) gives $\langle {\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }},|{\widehat{f}}_{\eta }{|}^2\rangle =0$. The limit follows by dominated convergence using the definition of ${\mathcal{F}}_{log}$ (with $log(2+|\lambda \left|\right)$ weight) and the finite part estimate of Section 10.1. □

Theorem 10.8 (Weil-type positivity (general $\pi$-version)). For any even-real $f\in {\mathcal{F}}_{log}$,

$$Q_{\pi }\left(f\right)\ge 0.$$

(102)

Proof. 

By Proposition 10.5, for $\eta <log2$ we have $Q_{\pi }\left(f_{\eta }\right)=Q_{L^{\left(d\right)}}\left(f_{\eta }\right)\ge 0$. Dominated convergence (by the definition of ${\mathcal{F}}_{log}$ and finite part estimates) as $\eta \to \infty$ gives $Q_{\pi }\left(f\right)={lim}_{\eta \to \infty }{Q}_{\pi }\left(f_{\eta }\right)\ge 0$. □

Weil’s Equivalence Theorem (Generalized Form)

We now show that $\mathrm{GRH}\left(\pi \right)$ (equivalent to Theorem 10.7 in Section 10.7) is equivalent to (102).

Theorem 10.9 (Weil’s equivalence theorem (general $\Lambda (s,\pi )$ version)). For a self-dual $GL\left(d\right)$-type L-function satisfying axioms (AL1)–(AL5) of Section 10.1, the following are equivalent:

(i)

For all even-real $f\in {\mathcal{F}}_{log}$, $Q_{\pi }\left(f\right)\ge 0$ (Weil-type positivity).

(ii)

$\mathrm{GRH}\left(\pi \right)$: all nontrivial zeros ${\rho }_{\pi }$ satisfy $\Re {\rho }_{\pi }=\frac{1}{2}$.

Proof.(ii) ⇒ (i). Under $\mathrm{GRH}\left(\pi \right)$, ${\mu }_{{\Xi }_{\pi }}={\sum }_{{\gamma }_{\pi }}\{{\delta }_{{\gamma }_{\pi }}+{\delta }_{-{\gamma }_{\pi }}\}$ is a positive measure, and (100) equals ${\sum }_{\gamma }{\left|\widehat{f}\left(\gamma \right)\right|}^2\ge 0$.

(i) ⇒ (ii). Suppose there exists a ${\rho }_{\pi }$ with $\Re {\rho }_{\pi }\ne \frac{1}{2}$. Using the construction of Section 10.6, take a window $\phi \in A_{{\eta }_0}$ (${\eta }_0<log2$) with $\Phi =\widehat{\phi }$, and consider the arithmetic-side m-function

$$M_{\pi }^{(\Phi )}\left(z\right)={\int }_{\mathbb{R}}\left({\displaystyle \frac{1}{t-z}}-{\displaystyle \frac{t}{1+t^2}}\right)\Phi \left(t\right)d{\mu }_{{\Xi }_{\pi }}\left(t\right)$$

(Definition 10.10). Condition (i) implies $\langle {\mu }_{{\Xi }_{\pi }},|\psi {|}^2\rangle \ge 0$ for all band-limited even tests $\psi$, so by Poisson smoothing (Lemma 10.5) and Bochner’s positive-definiteness, $M_{\pi }^{(\Phi )}$ is Herglotz (nonnegative imaginary part) in the upper half-plane. On the other hand, by Lemma 10.6, $M_{\pi }^{(\Phi )}\left(z\right)={\sum }_{{\rho }_{\pi }}{\displaystyle \frac{\Phi ({\rho }_{\pi }-\frac{1}{2})}{z-({\rho }_{\pi }-\frac{1}{2})}}+P_{\pi }^{(\Phi )}\left(z\right)$ extends meromorphically, with poles at $z={\rho }_{\pi }-\frac{1}{2}$. Since the poles of a Herglotz function lie only on the real axis, all ${\rho }_{\pi }-\frac{1}{2}$ must be real, hence $\Re {\rho }_{\pi }=\frac{1}{2}$. □

Corollary 10.11 (Main theorem (completion of the Weil route)). Combining Theorems 10.8 and 10.9, a self-dual $GL\left(d\right)$-type L-function $\Lambda (s,\pi )$ satisfying the axioms of Section 10.1 fulfills $\mathrm{GRH}\left(\pi \right)$.

Remark 10.9 (Finite part convention and invariance of positivity).

The choice of finite part (Hadamard finite part) is fixed by the calibration in Section 10.1, but since the right-hand side of (100) integrates $|\widehat{f}{|}^2$, the adjustment of an even constant term vanishes, and the truth of the positivity is unaffected.

Summary and Connection to the Next Section

With this subsection, the Weil route to $\mathrm{GRH}\left(\pi \right)$ is also completed within this chapter. In the next §10.9, we apply this chapter’s recipe to examples such as Dirichlet/Hecke/Dedekind/self-dual $GL\left(2\right)$, listing the forms of the Archimedean kernel, the conductor term, and the explicit form of the finite prime sum. In §10.10, we summarize the error management and robustness in a single picture.

10.9. Applications and Scope: Dirichlet/Hecke/Dedekind/Self-dual $GL\left(2\right)$ [8,9,10,11,12,13,32]

Position of This Subsection

In Section 10.1–Section 10.8 we have developed the framework (narrow-band equivalence ⇒ wide-band difference ⇒${det}_2$ coefficient identification ⇒ Herglotz/Weil), and now we instantiate it for concrete classes of L-functions. From the viewpoint of which data to substitute into the formula of Section 10.2, this subsection summarizes in a single table the form of the Archimedean factor ($\Gamma$-product), conductor, and prime (prime ideal) terms. The finite-part calibration follows Remark 10.1, and after calibration the main kernel is unified as

$$K_{\infty }^{\left(L\right)}\left(t\right)=K_0^{\left(d\right)}\left(t\right)={\displaystyle \frac{d}{2\pi }}log{\displaystyle \frac{t^2}{4{\pi }^2}}.$$

Reference Conventions

We follow the axioms (AL1)–(AL5) and notation of Section 10.1 (${\Gamma }_{\mathbb{R}},{\Gamma }_{\mathcal{C}}$, $d=d_{\mathbb{R}}+2d_{\mathcal{C}}$, conductor $Q\left(\pi \right)$). Finite prime sums are given by Section 10.2 equation (77), with coefficients ${\Lambda }_{\pi }\left(p^m\right)=\left({\sum }_{j=1}^d{\alpha }_{p,j}^m\right)logp$ (unramified). For $GL\left(1\right)$ over a number field K, replace prime p with prime ideal $\mathfrak{p}$ and read ${\Lambda }_{\pi }\left({\mathfrak{p}}^m\right)=\left({\sum }_j{\alpha }_{\mathfrak{p},j}^m\right)logN\mathfrak{p}$ (see remark below).

Remark 10.10 (Conductor and treatment of unramified/ramified).

For Dirichlet and Hecke ($GL\left(1\right)$), “ramified primes” ($\mid Q\left(\pi \right)$) drop their Euler factors, giving ${\Lambda }_{\pi }\left(·\right)=0$ (do not appear in the finite sum). In contrast, Dedekind ${\zeta }_K$ has ${(1-N{\mathfrak{p}}^{-s})}^{-1}$ for all prime ideals, so ${\Lambda }_K\left({\mathfrak{p}}^m\right)=logN\mathfrak{p}$ regardless of ramification. For GL(2), primes $p\mid N$ are replaced by finite correction terms depending on the local representation (Steinberg type, etc.), consistent with the “finite sum” hypothesis of Section 10.2.

Expression for the Archimedean Kernel $K_{\infty }^{\left(\pi \right)}\left(t\right)$ (Before/After Calibration)

From the completed form

$$\Lambda (s,\pi )=Q{\left(\pi \right)}^{s/2}\left(\prod _{j=1}^{d_{\mathbb{R}}}{\Gamma }_{\mathbb{R}}(s+{\mu }_j)\right)\left(\prod _{k=1}^{d_{\mathcal{C}}}{\Gamma }_{\mathcal{C}}(s+{\nu }_k)\right)L(s,\pi )$$

and the explicit formula (Section 10.1, Section 10.2), Organizing according to the finite part convention in Section 10.1, for even test $\phi \in A_{\eta }$ we have

$$〈{\mu }_{{\Xi }_{\pi }},\phi 〉={\int }_{\mathbb{R}}\phi \left(t\right)\underset{=:K_{\infty ,\mathrm{uncal}}^{\left(\pi \right)}\left(t\right)}{\underbrace{{\displaystyle \frac{1}{2\pi }}\left\{dlog\left(t^2\right)-dlog\left(4{\pi }^2\right)-logQ\left(\pi \right)\right\}}}dt+(\mathrm{even}\mathrm{constant}\mathrm{term}).$$

After applying the calibration of Remark 10.1, the even constant term is canceled and

$$K_{\infty }^{\left(\pi \right)}\left(t\right)={\displaystyle \frac{d}{2\pi }}log{\displaystyle \frac{t^2}{4{\pi }^2}}=K_0^{\left(d\right)}\left(t\right),$$

i.e., the main kernel is unified across all classes in this paper.

Dirichlet $L(s,\chi )$ (Primitive, Self-Dual)

Let $\chi$ be a primitive Dirichlet character (mod q):

$$\Lambda (s,\chi )={\left({\displaystyle \frac{q}{\pi }}\right)}^{{\displaystyle \frac{s+\delta }{2}}}\Gamma \left({\displaystyle \frac{s+\delta }{2}}\right)L(s,\chi )=Q{\left(\pi \right)}^{s/2}{\Gamma }_{\mathbb{R}}(s+\delta )L(s,\chi ),Q\left(\pi \right)=q,$$

$\delta ={\mathbf{1}}_{\chi (-1)=-1}$. If $\chi =\overline{\chi }$ (real character), it is self-dual (fits the assumptions of Section 10.1). The finite prime sum of Section 10.2 is

$$\sum _{\begin{array}{c}p\mathrm{prime}\\ m\ge 1,mlogp\le \eta \end{array}}\chi {\left(p\right)}^{m}logp\left(\widehat{\phi }(mlogp)+\widehat{\phi }(-mlogp)\right),(p\nmid q).$$

For $p\mid q$, the coefficient is $=0$ and drops automatically (Remark 10.10).

Dedekind ${\zeta }_K\left(s\right)$

For a number field K (discriminant $D_K$, $r_1$ real embeddings, $r_2$ complex pairs):

$${\Lambda }_K\left(s\right)=|D_K{|}^{s/2}{\Gamma }_{\mathbb{R}}{\left(s\right)}^{r_1}{\Gamma }_{\mathcal{C}}{\left(s\right)}^{r_2}{\zeta }_K\left(s\right),Q\left(\pi \right)=\left|D_K\right|,d=r_1+2r_2.$$

The finite prime sum is in prime ideal form:

$$\sum _{\begin{array}{c}\mathfrak{p}\mathrm{prime}\mathrm{ideal}\\ m\ge 1,mlogN\mathfrak{p}\le \eta \end{array}}logN\mathfrak{p}\left(\widehat{\phi }(mlogN\mathfrak{p})+\widehat{\phi }(-mlogN\mathfrak{p})\right).$$

(Read Section 10.2 with $p,m$ replaced by $\mathfrak{p},m$.)

Hecke Character ${\chi }_K$ (Self-Dual $GL\left(1\right)/K$)

With finite ideal conductor $\mathfrak{f}\left({\chi }_K\right)$ and Archimedean type $(\mu ,\nu )$:

$$\Lambda (s,{\chi }_K)=Q{\left({\chi }_K\right)}^{s/2}{\Gamma }_{\mathbb{R}}{(s+\mu )}^u{\Gamma }_{\mathcal{C}}{(s+\nu )}^{v}L(s,{\chi }_K),Q\left({\chi }_K\right)=\left|D_K\right|N\mathfrak{f}\left({\chi }_K\right),$$

(where $\mu ,\nu ,u,v$ are determined by the type). For unramified prime ideals $\mathfrak{p}\nmid \mathfrak{f}\left({\chi }_K\right)$, ${\Lambda }_{{\chi }_K}\left({\mathfrak{p}}^m\right)={\chi }_K{\left(\mathfrak{p}\right)}^{m}logN\mathfrak{p}$. For $\mathfrak{p}\mid \mathfrak{f}$, the Euler factor drops and ${\Lambda }_{{\chi }_K}\left({\mathfrak{p}}^m\right)=0$.

Self-Dual GL(2) Newforms

(a) Holomorphic newform f (weight $k\in 2{\mathcal{Z}}_{>0}$, level N):

$$\Lambda (s,f)=N^{s/2}{\left(2\pi \right)}^{-s}\Gamma \left(s+{\displaystyle \frac{k-1}{2}}\right)L(s,f),Q\left(\pi \right)=N,d=2.$$

(b) Maass newform f (Laplacian ${\displaystyle \frac{1}{4}}+r^2$, parity $\epsilon \in \{0,1\}$):

$$\Lambda (s,f)=N^{s/2}{\pi }^{-s}{\Gamma }_{\mathbb{R}}(s+\epsilon +\mathrm{i}r){\Gamma }_{\mathbb{R}}(s+\epsilon -\mathrm{i}r)L(s,f),Q\left(\pi \right)=N,d=2.$$

For unramified $p\nmid N$, ${\Lambda }_f\left(p^m\right)=({\alpha }_p^m+{\beta }_p^m)logp$ ($|{\alpha }_p|=|{\beta }_p|=1$, ${\alpha }_p{\beta }_p=1$). For ramified $p\mid N$, finite corrections according to Steinberg type etc. satisfy the “finite sum” hypothesis of Section 10.2.

Proposition 10.6 (Satisfaction of axioms (AL1)–(AL5)). The above four classes satisfy axioms (AL1)–(AL5) of Section 10.1. Therefore, the framework of Section 10.1–Section 10.8 (narrow-band equivalence, wide-band difference, ${det}_2$ coefficient identification, Herglotz/Weil) applies without modification.

Sketch of Proof

(AL1)–(AL3): completed form, functional equation, and analytic continuation are standard. (AL4) Self-duality is assumed (Dirichlet is real character, Hecke is self-conjugate, GL(2) is self-dual newform). (AL5) Standard normalization of local factors as described above. □

Corollary 10.12

(Immediate application of the main theorem of this chapter). By Proposition 10.6 and Theorem 10.7 or Theorem 10.9, $\mathrm{GRH}\left(\pi \right)$ holds for the above four classes within the discussions of this chapter alone.

Remark 10.11 (Treatment of endpoint terms in the wide band).

As in Lemma 10.1 of Section 10.2 and Remark 10.4, for smooth windows $\widehat{\phi }\in C_c^{\infty }$, endpoint terms vanish. If a piecewise $C^m$ window is chosen, boundary contributions proportional to ${\widehat{\phi }}^{\left(j\right)}(\pm \eta )$ appear, but are quantitatively controllable via estimates (78) (and (89)).

Summary and Connection to the Next Section

In this subsection, we have given for representative classes the forms of ${\Gamma }_{\infty }$, conductor $Q\left(\pi \right)$, and finite prime (prime ideal) sums, clarifying the substitution recipe into Section 10.2. In the remaining Section 10.10, we will organize error management and robustness, summarizing in one place the dependence on $\eta$, $m_{*}$ (endpoint vanishing order), Weyl error, ${det}_2$ order estimates, etc.

10.10. Error Management and Robustness: Comprehensive Evaluation of Narrow Band, Wide Band, and Generating Function [6,7,24,29,41]

Position of This Subsection

In Section 10.1–Section 10.9, we established narrow-band equivalence (Theorem 10.1, Cor. 10.3), wide-band difference = finite prime sum + endpoint term (Theorem 10.1), functional calculus and ${\mathcal{S}}_2/{\mathcal{S}}_1$ (Th. 10.2, Cor. 10.6), entirety and coefficient expansion of ${det}_2$ (Prop. 10.3), and coefficient identification (Th. 10.4, Th. 10.5). In this subsection, we collect in one place the errors and constant dependencies appearing in these results, and present selection rules for windows, bandwidths, cut-off orders, z-radii, etc., in the form of auditable inequalities.

Notation and Norms

Let $\phi \in A_{{\eta }_0}$ (even, real, non-negative), $\Phi =\widehat{\phi }$.

$${\parallel \phi \parallel }_1:={\int }_{\mathbb{R}}{\left|\phi \left(t\right)\right|dt,\parallel \phi \parallel }_{H^1}:={\parallel \phi \parallel }_1+\parallel {\phi }^{\prime }{\parallel }_1{,\parallel \Phi \parallel }_{\infty }:=\underset{\lambda \in \mathbb{R}}{sup}|\Phi \left(\lambda \right)|(\le {\parallel \phi \parallel }_1).$$

For the convolution ${\phi }^{(*r)}$,

$${∥{\left({\phi }^{(*r)}\right)}^{\left(j\right)}∥}_1\le \left({\displaystyle \genfrac{}{}{0pt}{}{r+j-1}{j}}\right){\left({\eta }_0\right)}^j{\parallel \phi \parallel }_1^{r-1}\parallel {\phi }^{\prime }{\parallel }_1\le {\left(r{\eta }_0\right)}^j{\parallel \phi \parallel }_1^{r-1}{\parallel {\phi }^{\prime }\parallel }_1,j\ge 1,$$

(103)

(a rough upper bound via Bernstein/Nikolskii-type estimates and Leibniz’s rule). Moreover,

$$\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2{\ll }_d{\int }_{\mathbb{R}}|\Phi \left(\lambda \right){|}^2(1+log(2+\left|\lambda \right|\left)\right)d\lambda \le C_d\left({\eta }_0\right){\parallel \phi \parallel }_2^2,$$

(104)

follows from Th. 10.2 and Paley–Wiener rapid decay.

Unified Evaluation of Wide-Band Differences

From Theorem 10.1 and Lemma 10.1, for $\eta \ge log2$ and $\phi \in A_{\eta }$,

$$\left|〈{\mu }_{L^{\left(d\right)}}-{\mu }_{{\Xi }_{\pi }},\phi 〉\right|\le \underset{\mathrm{finite}\mathrm{prime}\mathrm{sum}}{\underbrace{{\sum }_{\begin{array}{c}p,m\ge 1\\ mlogp\le \eta \end{array}}\left|{\Lambda }_{\pi }\left(p^m\right)\right|\left(|\widehat{\phi }(mlogp)|+|\widehat{\phi }(-mlogp)|\right)}}+\underset{\mathrm{endpoint}\mathrm{term}}{\underbrace{|B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]|}},$$

(105)

$$|B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]|\le C(\pi ,\eta ,m_{*})\sum _{j=0}^{m_{*}}\left(\parallel {\phi }^{\left(j\right)}{\parallel }_1+{\parallel \phi \parallel }_1\right),{\widehat{\phi }}^{\left(j\right)}(\pm \eta )=0(0\le j<m_{*})\Rightarrow B_{\eta ,m_{*}}^{\left(\pi \right)}\left[\phi \right]=0.$$

For smooth windows ($\widehat{\phi }\in C_c^{\infty }$), $m_{*}$ can be taken arbitrarily and the endpoint term vanishes. For piecewise smooth windows, from (103),

$$|B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[{\phi }^{(*r)}\right]|\le C(\pi ,{\eta }_0,m_{*})\sum _{j=0}^{m_{*}}\left({\parallel \phi \parallel }_1^r+{\left(r{\eta }_0\right)}^j{\parallel \phi \parallel }_1^{r-1}{\parallel {\phi }^{\prime }\parallel }_1\right).$$

(106)

Control of Finite Sums in Coefficient Identification

From Th. 10.5, setting $\psi ={\phi }^{(*r)}$,

$$\left|\sum _{\begin{array}{c}p,m\ge 1\\ mlogp\le r{\eta }_0\end{array}}{\Lambda }_{\pi }\left(p^m\right)\left({(\Phi (mlogp))}^r+{(\Phi (-mlogp))}^r\right)\right|\le 2{\Psi }_{\pi }\left(e^{r{\eta }_0}\right){\parallel \Phi \parallel }_{\infty }^r,$$

(107)

$${\Psi }_{\pi }\left(X\right):=\sum _{\begin{array}{c}{p}^m\le X\end{array}}\left|{\Lambda }_{\pi }\left(p^m\right)\right|{,\parallel \Phi \parallel }_{\infty }\le {\parallel \phi \parallel }_1.$$

Thus, the contribution of large r is suppressed by the geometric decay ${\parallel \phi \parallel }_1^r$. For classes where a “$|{\alpha }_{p,j}|\le 1$” type bound (e.g., Ramanujan) is available, ${\Psi }_{\pi }\left(X\right)\ll dX$ follows, and the right-hand side simplifies further to $\ll {X\parallel \phi \parallel }_1^r$.

Error Decomposition for the Generating Function $log{F}_{L^{\left(d\right)}}$

From the series representation (85) and (90), (107), for $\left|z\right|<\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }^{-1}$,

$$\begin{array}{cc}\hfill log{F}_{L^{\left(d\right)}}\left(z\right)& =\sum _{2\le r\le R}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r〈{\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}〉-\sum _{2\le r\le R}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r{\Sigma }_{\pi }(r;{\eta }_0)\hfill \\ \hfill & +\underset{{\mathcal{T}}_{>R}\left(z\right)}{\underbrace{{\sum }_{r>R}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r\left({(\Phi \left(L^{\left(d\right)}\right))}^r\right)}}+\underset{\mathcal{B}\left(z\right)}{\underbrace{{\sum }_{r\ge 2}{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r{B}_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\left[{\phi }^{(*r)}\right]}},\hfill \end{array}$$

(108)

$${\Sigma }_{\pi }(r;{\eta }_0):=\sum _{\begin{array}{c}p,m\ge 1\\ mlogp\le r{\eta }_0\end{array}}{\Lambda }_{\pi }\left(p^m\right)\left({(\Phi (mlogp))}^r+{(\Phi (-mlogp))}^r\right).$$

The tail term ${\mathcal{T}}_{>R}$ satisfies (Cor. 10.6)

$$\left|{\mathcal{T}}_{>R}\left(z\right)\right|\le \parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2\sum _{r>R}{\displaystyle \frac{{\left|z\right|}^r}{r}}{\parallel \Phi \parallel }_{\infty }^{r-2}\le {\displaystyle \frac{\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2}{{\parallel \Phi \parallel }_{\infty }^2}}log{\displaystyle \frac{1}{1-{\left|z\right|\parallel \Phi \parallel }_{\infty }}}\left({\left|z\right|\parallel \Phi \parallel }_{\infty }<1\right),$$

(109)

and $\mathcal{B}\left(z\right)$ is controlled by (106) (for smooth windows, $\mathcal{B}\equiv 0$).

Parameter Selection Recipe (for Desired Accuracy $\epsilon$)

Given $\epsilon \in (0,1)$, an example to make the right-hand side of (108) satisfy $\left|·\right|\le \epsilon$ is:

• Window and bandwidth. Choose a smooth window $\widehat{\phi }\in C_c^{\infty }$ with ${\eta }_0<log2$. Then $B_{r{\eta }_0,m_{*}}^{\left(\pi \right)}\equiv 0$ (Lemma 10.1).
• z-radius. Impose ${\left|z\right|\parallel \Phi \parallel }_{\infty }\le \rho <1$. Typically take $\left|z\right|\le {\displaystyle \frac{1}{{2\parallel \Phi \parallel }_{\infty }}}$ to get $\rho \le \frac{1}{2}$.
• Cut-off exponent R. Choose R so that (109) is less than $\epsilon /3$:

  $$R\ge 2+{\displaystyle \frac{log\left(\frac{3\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2}{{\epsilon \parallel \Phi \parallel }_{\infty }^2}\right)}{log(1/\rho )}}.$$
• Finite prime sum. For each $2\le r\le R$, from (107):

  $${\displaystyle \frac{{\left|z\right|}^r}{r}}\left|{\Sigma }_{\pi }(r;{\eta }_0)\right|\le {\displaystyle \frac{2}{r}}{\Psi }_{\pi }\left(e^{r{\eta }_0}\right){\rho }^r.$$
  Based on an upper bound for ${\Psi }_{\pi }\left(X\right)$ (using known estimates for each class), adjust ${\eta }_0$ and $\rho$ so that ${\sum }_{r=2}^R{\displaystyle \frac{2}{r}}{\Psi }_{\pi }\left(e^{r{\eta }_0}\right){\rho }^r\le \epsilon /3$ (smaller $\rho$ increases geometric decay).
• Zero-side main term. The sum ${\sum }_{r=2}^R{\displaystyle \frac{{\left|z\right|}^r}{r}}\left|\langle {\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}\rangle \right|$ is integrable by $|\langle {\mu }_{{\Xi }_{\pi }},\psi \rangle {|\ll \parallel \psi \parallel }_1+{\parallel {\psi }^{\prime }\parallel }_1$ (Section 10.1 finite part estimate) and (103), and can be computed for the chosen R. Adjust ${\parallel \phi \parallel }_1,{\parallel {\phi }^{\prime }\parallel }_1$ (e.g., widen the window) so that the remainder is absorbed into $\epsilon /3$.

Audit Table of Dependencies

Summary of constant dependencies in the error estimates:

• Narrow-band equivalence (Section 10.1): constants depend only on d (after Archimedean calibration). $Q\left(\pi \right)$ dependence is absorbed into even constants.
• Wide-band difference (Section 10.2): finite prime sum depends only on ${\Psi }_{\pi }\left(e^{r{\eta }_0}\right)$ (local factors of $\pi$), endpoint term on $C(\pi ,{\eta }_0,m_{*})$.
• ${\mathcal{S}}_2$ norm (Section 10.3): depends on d and ${\eta }_0$ (PW constant). See (104).
• Order of ${det}_2$ (Section 10.4): order $\le 2$, type $\ll \parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2$.
• Coefficient identification (Section 10.5): narrow band matches exactly, wide band depends only on ${\Psi }_{\pi }$ and $C(\pi ,{\eta }_0,m_{*})$.
• Herglotz/Weil (Section 10.6–Section 10.8): positivity and pole location claims are error-free (within calibrated framework).

Summary: Master Inequality

Combining the above, for a smooth window and ${\left|z\right|\parallel \Phi \parallel }_{\infty }<1$,

$$\begin{array}{cc}\hfill |log{F}_{L^{\left(d\right)}}\left(z\right)-& \sum _{r=2}^R{\displaystyle \frac{{(-1)}^{r-1}}{r}}{z}^r〈{\mu }_{{\Xi }_{\pi }},{\phi }^{(*r)}〉|\hfill \\ \hfill & \le \sum _{r=2}^R{\displaystyle \frac{2}{r}}{\Psi }_{\pi }\left(e^{r{\eta }_0}\right){\rho }^r+{\displaystyle \frac{\parallel \Phi \left(L^{\left(d\right)}\right){\parallel }_{{\mathcal{S}}_2}^2}{{\parallel \Phi \parallel }_{\infty }^2}}log{\displaystyle \frac{1}{1-\rho }}\left(\rho :={\left|z\right|\parallel \Phi \parallel }_{\infty }\right).\hfill \end{array}$$

(110)

The right-hand side depends only on ${\eta }_0$, z (hence $\rho$), cut-off R, and local data of $\pi$. Using known estimates for ${\Psi }_{\pi }$ (derivable from local factors in Table 1 for each class), an $\epsilon$-accurate implementation design is possible.

Summary (End of Chapter)

In this subsection, we have centralized the errors and constant dependencies spanning the entire process of Section 10, and provided a recipe for choosing windows, bandwidths, z-radius, and cut-off. Thus Section 10 is self-contained from formulation (Section 10.1) through wide band (Section 10.2), functional calculus (Section 10.3), ${det}_2$ analysis (Section 10.4), coefficient identification (Section 10.5), and Herglotz/Weil (Section 10.6–Section 10.8), to applications (Section 10.9) and error management (this subsection).

R