Submitted:
19 May 2025
Posted:
20 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Observations and Data Reduction
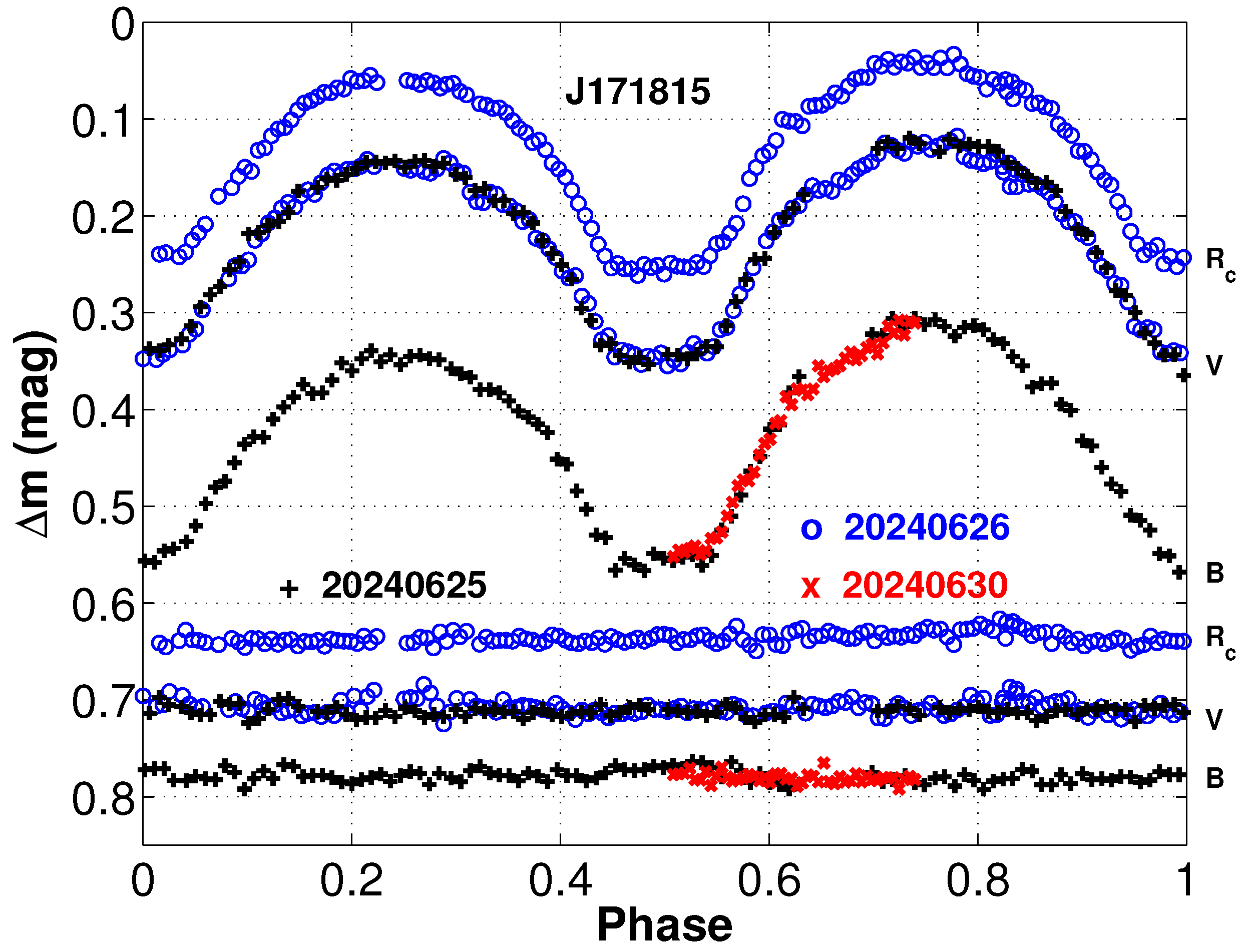
2.1. Ground Based Observation
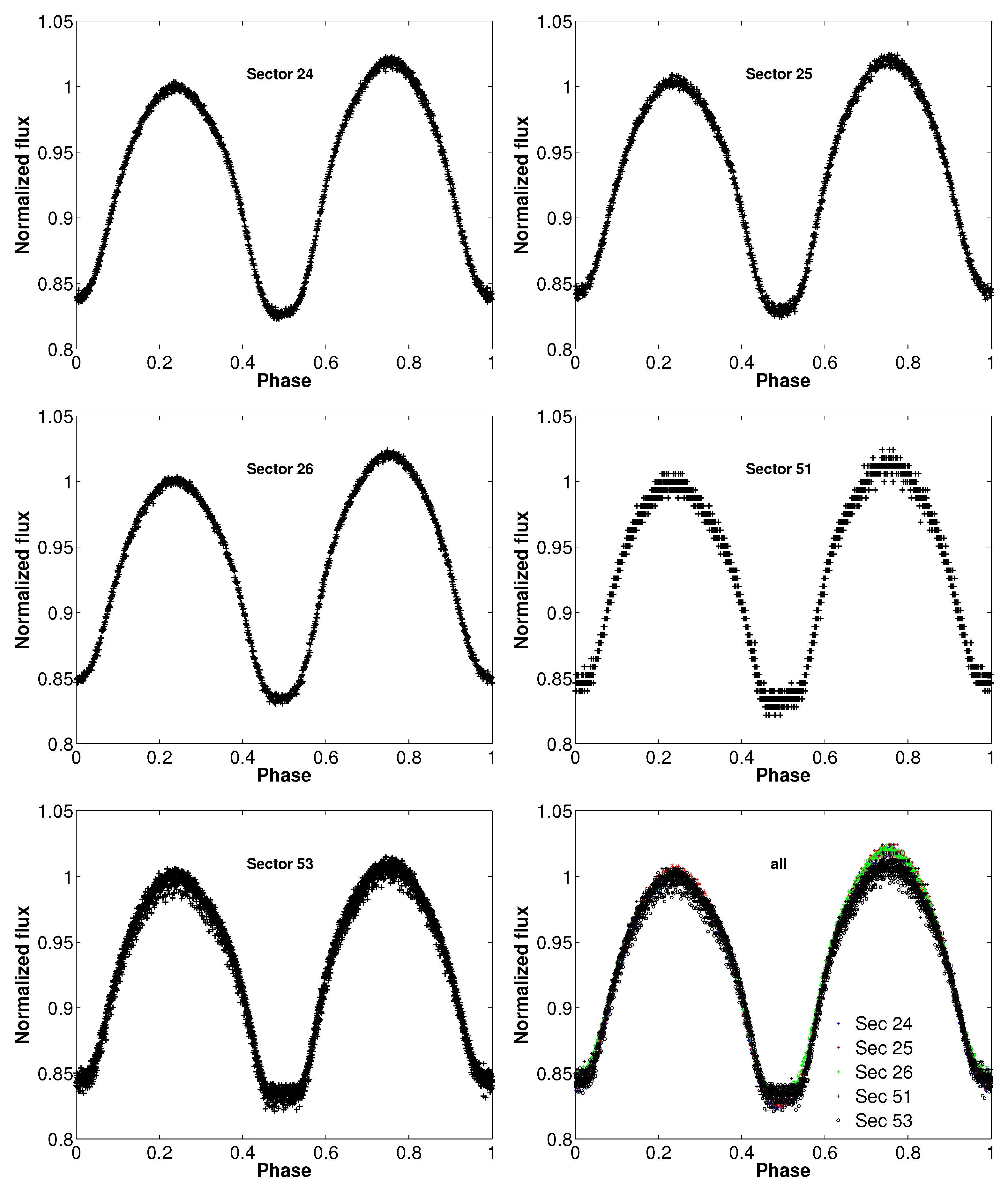
2.2. TESS Observation
3. Orbital Period Investigation
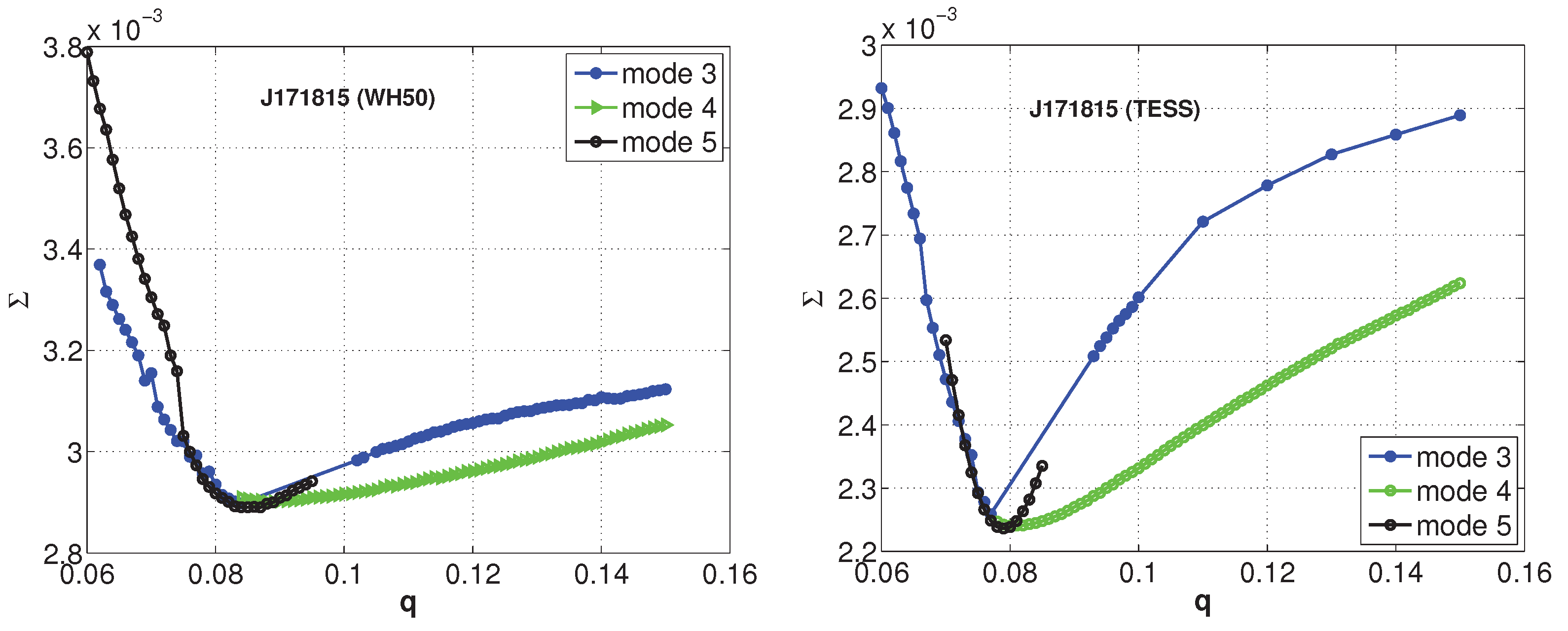
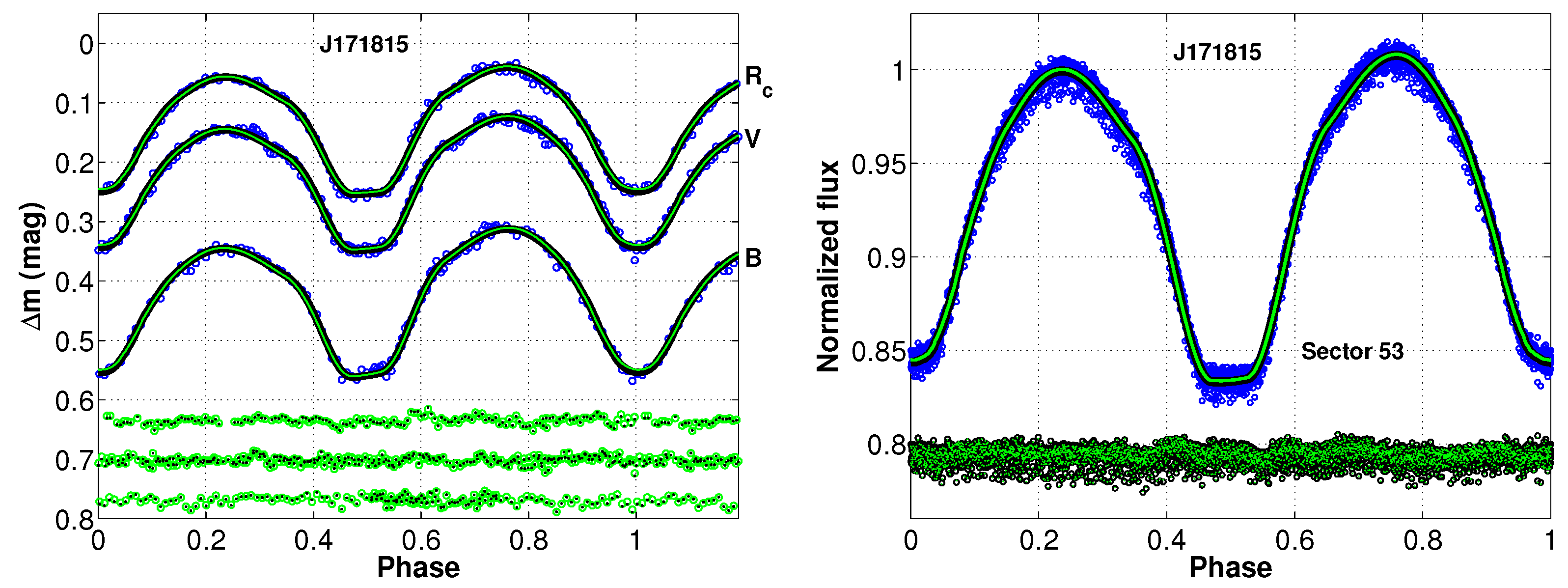
4. Photometric Solutions
5. Discussions and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shaw, J.S. Near-Contact Binary Stars. In Proceedings of the Active Close Binaries Proceedings, NATO Advanced Study Institute, Vol. 319, NATO Advanced Study Institute (ASI) Series C; 1990; p. 241. [Google Scholar]
- Zhu, L.; Qian, S.; Liu, L.; Liao, W.P.; He, J.J.; Li, L.J.; Zhao, E.G.; Dai, Z.B.; Zhang, J.; Li, K. A Preliminary Photometric Study of the HW Vir-like Binary NSVS14256825. In Proceedings of the 9th Pacific Rim Conference on Stellar Astrophysics; Qain, S.; Leung, K.; Zhu, L.; Kwok, S., Eds., Vol. 451, Astronomical Society of the Pacific Conference Series; 2011; p. 155. [Google Scholar]
- Zhu, L.; Qian, S. BL Andromedae and GW Tauri: close binary stars in a key evolutionary stage. Monthly Notices of the Royal Astronomical Society 2006, 367, 423–432. [Google Scholar] [CrossRef]
- Meng, Z.B.; Wang, H.W.; Yu, Y.X.; Hu, K.; Xiang, F.Y. HT Lyn and IR Lyn: Two Semi-detached-type Near-contact Binaries with Stable Orbital Period. Research in Astronomy and Astrophysics 2022, 22, 115015. [Google Scholar] [CrossRef]
- Darwin, G.H. The Determination of the Secular Effects of Tidal Friction by a Graphical Method. Proceedings of the Royal Society of London Series I 1879, 29, 168–181. [Google Scholar]
- Hut, P. Stability of tidal equilibrium. Astronomy & Astrophysics 1980, 92, 167–170. [Google Scholar]
- Yang, Y.G.; Qian, S.B. Deep, Low Mass Ratio Overcontact Binary Systems. XIV. A Statistical Analysis of 46 Sample Binaries. Astronomical Journal 2015, 150, 69. [Google Scholar] [CrossRef]
- Pešta, M.; Pejcha, O. Mass-ratio distribution of contact binary stars. Astronomy & Astrophysics 2023, arXiv:astro-ph.SR/2212.02553]672, A176. [Google Scholar] [CrossRef]
- Arbutina, B.; Wadhwa, S. The Critical Mass Ratio for W-UMa-Type Contact Binary Sytems. Serbian Astronomical Journal 2024, arXiv:astro-ph.SR/2404.03821]208, 1–15. [Google Scholar] [CrossRef]
- Wadhwa, S.S.; Landin, N.R.; Arbutina, B.; Tothill, N.F.H.; De Horta, A.Y.; Filipović, M.D.; Petrović, J.; Djurašević, G. Low-mass contact binaries: orbital stability at extreme low mass ratios. Monthly Notices of the Royal Astronomical Society 2024, arXiv:astro-ph.SR/2411.02020]535, 2494–2502. [Google Scholar] [CrossRef]
- Cheng, Q.; Xiong, J.; Ding, X.; Ji, K.; Li, J.; Liu, C.; Li, J.; Luo, J.; Lyu, X.; Han, Z.; et al. The First Photometric Analysis of Two Low-mass-ratio Contact Binary Systems in TESS Survey. Astronomical Journal 2024, arXiv:astro-ph.SR/2405.19841]167, 148. [Google Scholar] [CrossRef]
- Guo, D.F.; Li, K.; Liu, F.; Li, H.Z.; Xia, Q.Q.; Gao, X.; Gao, X.; Chen, X.; Gao, D.Y.; Sun, G.Y. The first photometric and orbital period investigation of an extremely low mass ratio contact binary with a sudden period change TYC 4002-2628-1. Monthly Notices of the Royal Astronomical Society 2022, arXiv:astro-ph.SR/2209.15175]517, 1928–1936. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Guo, D.F.; Gao, D.Y.; Chen, X.; Wang, L.H.; Xin, Y.X.; Han, Y.X.; Kim, C.H.; Jeong, M.J. Detection of the lowest mass ratio contact binary in the universe: TYC 3801-1529-1. Astronomy & Astrophysics 2024, arXiv:astro-ph.SR/2411.12132]692, L4. [Google Scholar] [CrossRef]
- Drake, A.J.; Graham, M.J.; Djorgovski, S.G.; Catelan, M.; Mahabal, A.A.; Torrealba, G.; García-Álvarez, D.; Donalek, C.; Prieto, J.L.; Williams, R.; et al. The Catalina Surveys Periodic Variable Star Catalog. Astrophysical Journal Supplement Series 2014, arXiv:astro-ph.SR/1405.4290]213, 9. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). Journal of Astronomical Telescopes, Instruments, and Systems 2015, 1, 014003. [Google Scholar] [CrossRef]
- Li, K.; Kim, C.H.; Xia, Q.Q.; Michel, R.; Hu, S.M.; Gao, X.; Guo, D.F.; Chen, X. The First Light Curve Modeling and Orbital Period Change Investigation of Nine Contact Binaries around the Short-period Cutoff. Astronomical Journal 2020, arXiv:astro-ph.SR/2003.02377]159, 189. [Google Scholar] [CrossRef]
- Li, K.; Xia, Q.Q.; Kim, C.H.; Gao, X.; Hu, S.M.; Guo, D.F.; Gao, D.Y.; Chen, X.; Guo, Y.N. Photometric Study and Absolute Parameter Estimation of Six Totally Eclipsing Contact Binaries. Astronomical Journal 2021, arXiv:astro-ph.SR/2104.13759]162, 13. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Liu, X.Y.; Gao, X.; Li, L.Z.; Chen, X.; Sun, G.Y. Extremely Low Mass Ratio Contact Binaries. I. The First Photometric and Spectroscopic Investigations of Ten Systems. Astronomical Journal 2022, arXiv:astro-ph.SR/2209.03653]164, 202. [Google Scholar] [CrossRef]
- Eastman, J.; Siverd, R.; Gaudi, B.S. Achieving Better Than 1 Minute Accuracy in the Heliocentric and Barycentric Julian Dates. Publications of the Astronomical Society of the Pacific 2010, arXiv:astro-ph.IM/1005.4415]122, 935. [Google Scholar] [CrossRef]
- Wilson, R.E.; Devinney, E.J. Realization of Accurate Close-Binary Light Curves: Application to MR Cygni. Astrophysical Journal 1971, 166, 605. [Google Scholar] [CrossRef]
- Wilson, R.E.; Van Hamme, W.; Terrell, D. Flux Calibrations from Nearby Eclipsing Binaries and Single Stars. Astrophysical Journal 2010, 723, 1469–1492. [Google Scholar] [CrossRef]
- Wilson, R.E. Accuracy and Efficiency in the Binary Star Reflection Effect. Astrophysical Journal 1990, 356, 613. [Google Scholar] [CrossRef]
- Wilson, R.E. Spotted Star Light Curves with Enhanced Precision. Astronomical Journal 2012, 144, 73. [Google Scholar] [CrossRef]
- Wilson, R.E. Eclipsing Binary Solutions in Physical Units and Direct Distance Estimation. Astrophysical Journal 2008, 672, 575–589. [Google Scholar] [CrossRef]
- Van Hamme, W.; Wilson, R.E. Third-Body Parameters from Whole Light and Velocity Curves. Astrophysical Journal 2007, 661, 1129–1151. [Google Scholar] [CrossRef]
- Gaia Collaboration. ; Prusti, T.; de Bruijne, J.H.J.; Brown, A.G.A.; Vallenari, A.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; Biermann, M.; Evans, D.W.; et al. The Gaia mission. Astronomy & Astrophysics 2016, arXiv:astro-ph.IM/1609.04153]595, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration. ; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Bailer-Jones, C.A.L.; Biermann, M.; Evans, D.W.; Eyer, L.; et al. Gaia Data Release 2. Summary of the contents and survey properties. Astronomy & Astrophysics 2018, arXiv:astro-ph.GA/1804.09365]616, A1. [Google Scholar] [CrossRef]
- Andrae, R.; Fouesneau, M.; Creevey, O.; Ordenovic, C.; Mary, N.; Burlacu, A.; Chaoul, L.; Jean-Antoine-Piccolo, A.; Kordopatis, G.; Korn, A.; et al. Gaia Data Release 2. First stellar parameters from Apsis. Astronomy & Astrophysics 2018, arXiv:astro-ph.SR/1804.09374]616, A8. [Google Scholar] [CrossRef]
- Lucy, L.B. Gravity-Darkening for Stars with Convective Envelopes. Zeitschrift für Astrophysik 1967, 65, 89. [Google Scholar]
- Ruciński, S.M. The Proximity Effects in Close Binary Systems. II. The Bolometric Reflection Effect for Stars with Deep Convective Envelopes. Acta Astronomica 1969, 19, 245. [Google Scholar]
- Terrell, D.; Wilson, R.E. Photometric Mass Ratios of Eclipsing Binary Stars. Astrophysics and Space Sciences 2005, 296, 221–230. [Google Scholar] [CrossRef]
- Li, K.; Xia, Q.Q.; Kim, C.H.; Hu, S.M.; Guo, D.F.; Jeong, M.J.; Chen, X.; Gao, D.Y. Two Contact Binaries with Mass Ratios Close to the Minimum Mass Ratio. Astrophysical Journal 2021, arXiv:astro-ph.SR/2109.02923]922, 122. [Google Scholar] [CrossRef]
- Zhu, L.Y.; Qian, S.B.; Zola, S.; Kreiner, J.M. Near-Contact Binaries with Mass Transfer: V473 Cassiopeiae and II Persei. Astronomical Journal 2009, 137, 3574–3580. [Google Scholar] [CrossRef]
- Tian, X.M.; Chang, L.F. Investigation on the mass transferring near-contact binary TT Cet. Publication of the Astronomical Society of Australia 2020, 37, e031. [Google Scholar] [CrossRef]
- Chang, L.F.; Zhu, L.Y. V505 Cyg: A Mass-transferring Marginal Contact Binary. Publications of the Astronomical Society of the Pacific 2022, 134, 054202. [Google Scholar] [CrossRef]
- Zhang, J.; Qian, S.B.; Han, Z.T.; Wu, Y. Two W-subtype contact binaries: GQ Boo and V1367 Tau. Monthly Notices of the Royal Astronomical Society 2017, 466, 1118–1126. [Google Scholar] [CrossRef]
- Pecaut, M.J.; Mamajek, E.E. Intrinsic Colors, Temperatures, and Bolometric Corrections of Pre-main-sequence Stars. Astrophysical Journal Supplement Series 2013, arXiv:astro-ph.SR/1307.2657]208, 9. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 |
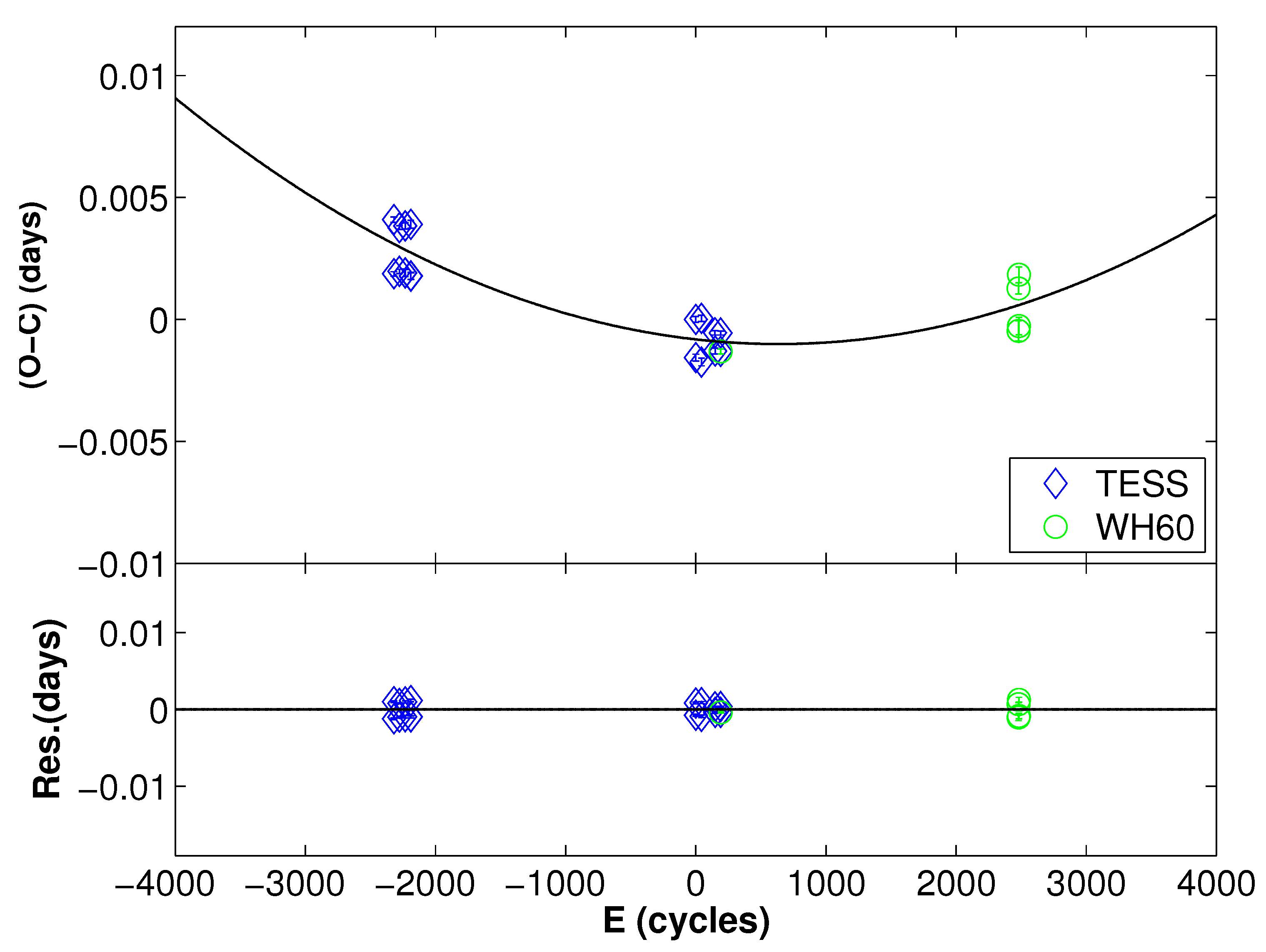
| BJD +2450000 | Error (days) | Min. | E | O-C(day) | BJD +2450000 | Error (days) | Min. | E | O-C(day) |
|---|---|---|---|---|---|---|---|---|---|
| 8961.15962 a | I | -2320.0 | 0.00409 | 9698.69977 a | I | 0.0 | 0.00000 | ||
| 8961.31635 a | II | -2319.5 | 0.00187 | 9698.85715 a | II | 0.5 | -0.00157 | ||
| 8974.51138 a | I | -2278.0 | 0.00376 | 9712.36981 a | I | 43.0 | 0.00004 | ||
| 8974.66855 a | II | -2277.5 | 0.00197 | 9712.52697 a | II | 43.5 | -0.00175 | ||
| 8988.81727 a | I | -2233.0 | 0.00383 | 9745.74946 a | I | 148.0 | -0.00055 | ||
| 8988.97430 a | II | -2232.5 | 0.00191 | 9745.90766 a | II | 148.5 | -0.00130 | ||
| 9002.48734 a | I | -2190.0 | 0.00390 | 9759.41945 a | I | 191.0 | -0.00056 | ||
| 9002.64418 a | II | -2189.5 | 0.00179 | 9759.57765 a | II | 191.5 | -0.00131 | ||
| 8988.81728 a | I | -2233.0 | 0.00384 | 10487.11039 b | I | 2480.0 | 0.00127 | ||
| 8988.97429 a | II | -2232.5 | 0.00190 | 10487.26761 b | II | 2480.5 | -0.00047 | ||
| 9002.48734 a | I | -2190.0 | 0.00390 | 10488.06468 b | I | 2483.0 | 0.00183 | ||
| 9002.64416 a | II | -2189.5 | 0.00177 | 10488.22153 b | II | 2483.5 | -0.00027 |
| Parameters | () | () | () | () |
|---|---|---|---|---|
| 5495 | 5495 | 5495 | 5495 | |
| 5632(9) | 5754(4) | 5612(9) | 5738(4) | |
| q() | 0.081(1) | 0.077(1) | 0.084(1) | 0.079(1) |
| 69.7(2) | 69.8(1) | 70.3(3) | 70.0(1) | |
| 1.897 | 1.885 | 1.908 | 1.891 | |
| ) | 1.844 | 1.834 | 1.853 | 1.839 |
| 1.896(1) | 1.885(1) | 1.919(3) | 1.895(1) | |
| 1.896 | 1.885 | 1.908 | 1.891 | |
| f | 1(2)% | 1(1)% | ||
| 99(1)% | 100(1)% | |||
| 100% | 100% | |||
| 0.598(1) | 0.601(1) | 0.589(1) | 0.597(1) | |
| 0.192(1) | 0.189(1) | 0.194(1) | 0.191(1) | |
| (rad) | 0.3466 | 0.4532 | 0.3466 | 0.3384 |
| (rad) | 1.6796 | 1.7660 | 1.7190 | 1.7597 |
| (rad) | 0.2096 | 0.2077 | 0.2089 | 0.2073 |
| 1.1673 | 1.0891 | 1.1673 | 1.1164 | |
| 0.001769 | 0.001899 | 0.001605 | 0.001738 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





