Submitted:
29 April 2025
Posted:
19 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Robust Statistical Analysis of Results by Means of the Q/Hampel Method in a Staggered-Nested Design with Two Factors
2.1. Determination of the Robust Reproducibility Standard Deviation
2.2. Determination of the Robust Intermediate Standard Deviation Using the Q Method
2.3. Determination of the Robust Repeatability Standard Deviation
2.4. Determination of the Robust Mean
3. Conclusion
Conflicts of Interest
References
- ISO 5725-2, Accuracy (trueness and precision) of measurement methods and results — Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method.
- ISO 5725-3, Accuracy (trueness and precision) of measurement methods and results — Part 3: Intermediate measures of the precision of a standard measurement method. -.
- ISO 5725-5, Accuracy (trueness and precision) of measurement methods and results — Part 5: Alternative methods for the determination of the precision of a standard measurement method.
- ISO 13528, Statistical methods for use in proficiency testing by interlaboratory comparisons.
- Müller, C.H. Müller C.H. and Uhlig S., Estimation of variance components with high breakdown point and high efficiency; Biometrika; 88: Vol. 2, pp. 353-366, 2001.
- Uhlig S., Robust estimation of variance components with high breakdown point in the 1-way random effect model. In: Kitsos, C.P. and Edler, L.; Industrial Statistics; Physica, S. 65-73, 1997.
- Uhlig S., Robust estimation of between and within laboratory standard deviation measurement results below the detection limit, Journal of Consumer Protection and Food Safety, 2015.
- Rousseeuw, P.J. and Croux, C., Alternatives to the Median Absolute Deviation. Journal of the American Statistical Association, 88, 1273-1283, 1993.
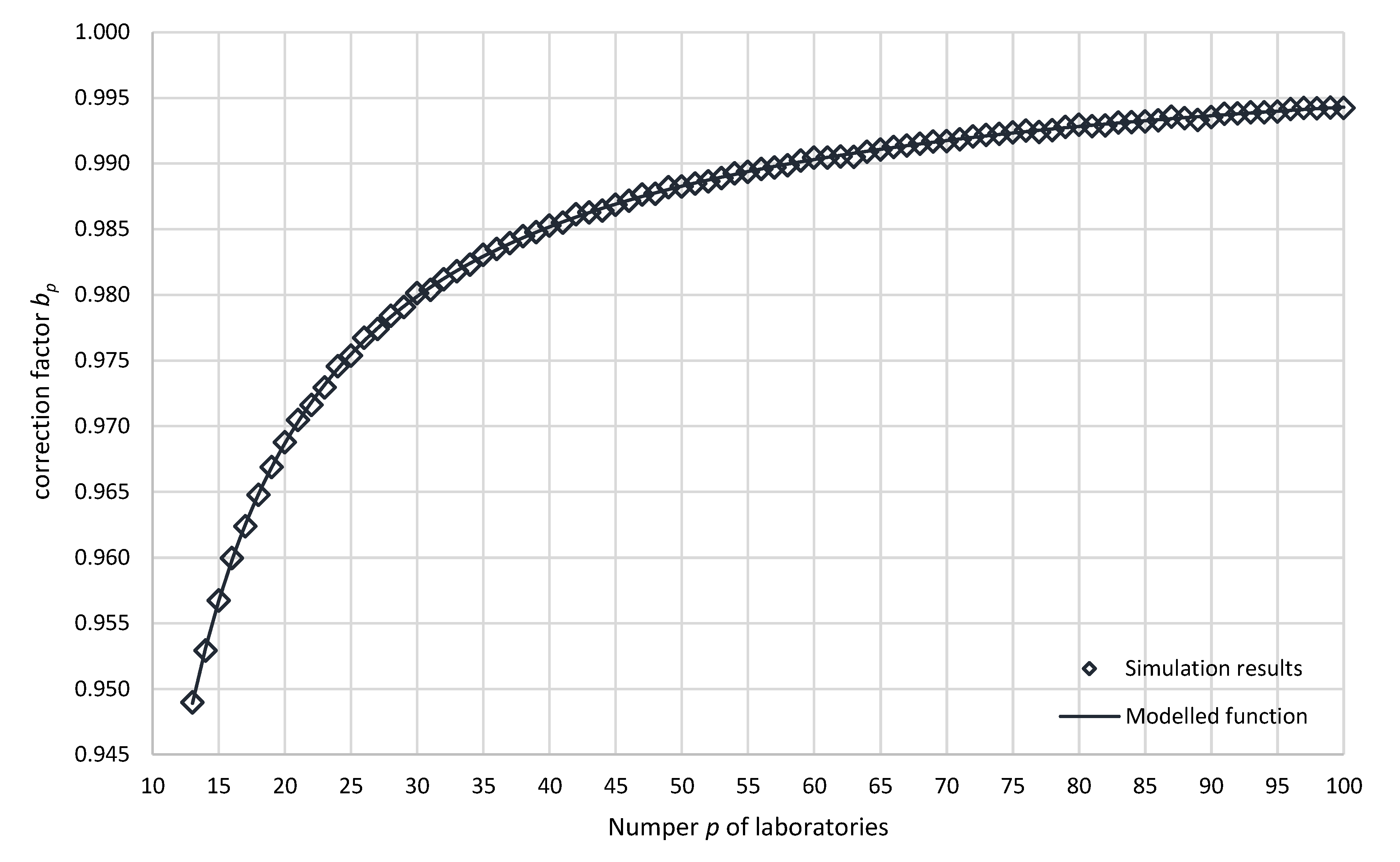

| ) | ) | ) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 1.3212 | 0.058% | 0.7569 | 37 | 1.0163 | 0.014% | 0.9839 | 70 | 1.0084 | 0.010% | 0.9917 |
| 5 | 1.1864 | 0.054% | 0.8429 | 38 | 1.0158 | 0.014% | 0.9845 | 71 | 1.0082 | 0.010% | 0.9919 |
| 6 | 1.1490 | 0.044% | 0.8703 | 39 | 1.0154 | 0.014% | 0.9848 | 72 | 1.0080 | 0.010% | 0.9921 |
| 7 | 1.1173 | 0.041% | 0.8950 | 40 | 1.0149 | 0.013% | 0.9853 | 73 | 1.0079 | 0.010% | 0.9922 |
| 8 | 1.1001 | 0.036% | 0.9090 | 41 | 1.0147 | 0.013% | 0.9855 | 74 | 1.0078 | 0.009% | 0.9922 |
| 9 | 1.0857 | 0.034% | 0.9211 | 42 | 1.0140 | 0.013% | 0.9861 | 75 | 1.0077 | 0.009% | 0.9924 |
| 10 | 1.0737 | 0.032% | 0.9313 | 43 | 1.0139 | 0.013% | 0.9863 | 76 | 1.0075 | 0.009% | 0.9925 |
| 11 | 1.0657 | 0.030% | 0.9384 | 44 | 1.0138 | 0.013% | 0.9864 | 77 | 1.0077 | 0.009% | 0.9924 |
| 12 | 1.0586 | 0.028% | 0.9446 | 45 | 1.0133 | 0.013% | 0.9869 | 78 | 1.0075 | 0.009% | 0.9925 |
| 13 | 1.0538 | 0.027% | 0.9490 | 46 | 1.0130 | 0.012% | 0.9872 | 79 | 1.0073 | 0.009% | 0.9928 |
| 14 | 1.0494 | 0.026% | 0.9529 | 47 | 1.0125 | 0.012% | 0.9876 | 80 | 1.0071 | 0.009% | 0.9930 |
| 15 | 1.0452 | 0.024% | 0.9568 | 48 | 1.0124 | 0.012% | 0.9877 | 81 | 1.0072 | 0.009% | 0.9928 |
| 16 | 1.0417 | 0.023% | 0.9600 | 49 | 1.0119 | 0.012% | 0.9882 | 82 | 1.0071 | 0.009% | 0.9929 |
| 17 | 1.0391 | 0.022% | 0.9624 | 50 | 1.0119 | 0.012% | 0.9883 | 83 | 1.0069 | 0.009% | 0.9931 |
| 18 | 1.0365 | 0.022% | 0.9648 | 51 | 1.0117 | 0.012% | 0.9885 | 84 | 1.0069 | 0.009% | 0.9931 |
| 19 | 1.0342 | 0.021% | 0.9669 | 52 | 1.0115 | 0.012% | 0.9886 | 85 | 1.0068 | 0.009% | 0.9932 |
| 20 | 1.0322 | 0.020% | 0.9688 | 53 | 1.0112 | 0.011% | 0.9889 | 86 | 1.0067 | 0.009% | 0.9933 |
| 21 | 1.0304 | 0.020% | 0.9705 | 54 | 1.0109 | 0.011% | 0.9892 | 87 | 1.0065 | 0.009% | 0.9936 |
| 22 | 1.0292 | 0.019% | 0.9716 | 55 | 1.0107 | 0.011% | 0.9894 | 88 | 1.0066 | 0.009% | 0.9935 |
| 23 | 1.0278 | 0.019% | 0.9730 | 56 | 1.0105 | 0.011% | 0.9896 | 89 | 1.0067 | 0.009% | 0.9933 |
| 24 | 1.0261 | 0.018% | 0.9746 | 57 | 1.0104 | 0.011% | 0.9897 | 90 | 1.0065 | 0.009% | 0.9935 |
| 25 | 1.0252 | 0.018% | 0.9754 | 58 | 1.0102 | 0.011% | 0.9899 | 91 | 1.0063 | 0.008% | 0.9938 |
| 26 | 1.0238 | 0.017% | 0.9768 | 59 | 1.0099 | 0.011% | 0.9902 | 92 | 1.0062 | 0.008% | 0.9938 |
| 27 | 1.0231 | 0.017% | 0.9774 | 60 | 1.0096 | 0.011% | 0.9905 | 93 | 1.0061 | 0.008% | 0.9939 |
| 28 | 1.0221 | 0.017% | 0.9784 | 61 | 1.0096 | 0.011% | 0.9905 | 94 | 1.0061 | 0.008% | 0.9939 |
| 29 | 1.0214 | 0.016% | 0.9791 | 62 | 1.0095 | 0.010% | 0.9905 | 95 | 1.0061 | 0.008% | 0.9939 |
| 30 | 1.0203 | 0.016% | 0.9801 | 63 | 1.0096 | 0.010% | 0.9905 | 96 | 1.0059 | 0.008% | 0.9941 |
| 31 | 1.0200 | 0.016% | 0.9804 | 64 | 1.0092 | 0.010% | 0.9909 | 97 | 1.0058 | 0.008% | 0.9942 |
| 32 | 1.0192 | 0.015% | 0.9812 | 65 | 1.0090 | 0.010% | 0.9911 | 98 | 1.0058 | 0.008% | 0.9942 |
| 33 | 1.0185 | 0.015% | 0.9818 | 66 | 1.0088 | 0.010% | 0.9913 | 99 | 1.0058 | 0.008% | 0.9943 |
| 34 | 1.0180 | 0.015% | 0.9823 | 67 | 1.0087 | 0.010% | 0.9914 | 100 | 1.0058 | 0.008% | 0.9942 |
| 35 | 1.0172 | 0.014% | 0.9830 | 68 | 1.0086 | 0.010% | 0.9915 | ||||
| 36 | 1.0168 | 0.014% | 0.9835 | 69 | 1.0084 | 0.010% | 0.9917 |
| ) | ) | ) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 1.0855 | 0.046% | 0.9212 | 37 | 1.0081 | 0.019% | 0.9920 | 70 | 1.0043 | 0.014% | 0.9957 |
| 5 | 1.0561 | 0.046% | 0.9469 | 38 | 1.0080 | 0.018% | 0.9920 | 71 | 1.0041 | 0.014% | 0.9959 |
| 6 | 1.0550 | 0.040% | 0.9479 | 39 | 1.0077 | 0.018% | 0.9924 | 72 | 1.0043 | 0.014% | 0.9957 |
| 7 | 1.0409 | 0.040% | 0.9607 | 40 | 1.0077 | 0.018% | 0.9923 | 73 | 1.0040 | 0.014% | 0.9960 |
| 8 | 1.0410 | 0.036% | 0.9606 | 41 | 1.0074 | 0.018% | 0.9927 | 74 | 1.0041 | 0.013% | 0.9959 |
| 9 | 1.0324 | 0.036% | 0.9686 | 42 | 1.0073 | 0.018% | 0.9928 | 75 | 1.0039 | 0.013% | 0.9961 |
| 10 | 1.0321 | 0.033% | 0.9689 | 43 | 1.0072 | 0.017% | 0.9929 | 76 | 1.0040 | 0.013% | 0.9960 |
| 11 | 1.0272 | 0.033% | 0.9735 | 44 | 1.0068 | 0.017% | 0.9932 | 77 | 1.0038 | 0.013% | 0.9963 |
| 12 | 1.0270 | 0.031% | 0.9737 | 45 | 1.0064 | 0.017% | 0.9936 | 78 | 1.0040 | 0.013% | 0.9960 |
| 13 | 1.0233 | 0.031% | 0.9772 | 46 | 1.0068 | 0.017% | 0.9933 | 79 | 1.0039 | 0.013% | 0.9961 |
| 14 | 1.0231 | 0.029% | 0.9774 | 47 | 1.0066 | 0.017% | 0.9935 | 80 | 1.0038 | 0.013% | 0.9962 |
| 15 | 1.0206 | 0.029% | 0.9798 | 48 | 1.0064 | 0.016% | 0.9937 | 81 | 1.0039 | 0.013% | 0.9962 |
| 16 | 1.0200 | 0.027% | 0.9804 | 49 | 1.0064 | 0.016% | 0.9937 | 82 | 1.0034 | 0.013% | 0.9966 |
| 17 | 1.0178 | 0.027% | 0.9825 | 50 | 1.0063 | 0.016% | 0.9937 | 83 | 1.0035 | 0.013% | 0.9965 |
| 18 | 1.0173 | 0.026% | 0.9830 | 51 | 1.0057 | 0.016% | 0.9943 | 84 | 1.0037 | 0.013% | 0.9963 |
| 19 | 1.0157 | 0.026% | 0.9846 | 52 | 1.0059 | 0.016% | 0.9941 | 85 | 1.0035 | 0.013% | 0.9965 |
| 20 | 1.0157 | 0.025% | 0.9845 | 53 | 1.0058 | 0.016% | 0.9942 | 86 | 1.0036 | 0.012% | 0.9964 |
| 21 | 1.0147 | 0.025% | 0.9855 | 54 | 1.0055 | 0.016% | 0.9946 | 87 | 1.0034 | 0.012% | 0.9966 |
| 22 | 1.0140 | 0.024% | 0.9862 | 55 | 1.0053 | 0.016% | 0.9947 | 88 | 1.0036 | 0.012% | 0.9964 |
| 23 | 1.0131 | 0.024% | 0.9870 | 56 | 1.0055 | 0.015% | 0.9946 | 89 | 1.0035 | 0.012% | 0.9965 |
| 24 | 1.0134 | 0.023% | 0.9867 | 57 | 1.0052 | 0.015% | 0.9948 | 90 | 1.0036 | 0.012% | 0.9964 |
| 25 | 1.0122 | 0.023% | 0.9880 | 58 | 1.0054 | 0.015% | 0.9946 | 91 | 1.0033 | 0.012% | 0.9967 |
| 26 | 1.0121 | 0.022% | 0.9880 | 59 | 1.0050 | 0.015% | 0.9950 | 92 | 1.0034 | 0.012% | 0.9966 |
| 27 | 1.0109 | 0.022% | 0.9893 | 60 | 1.0051 | 0.015% | 0.9949 | 93 | 1.0031 | 0.012% | 0.9969 |
| 28 | 1.0112 | 0.021% | 0.9889 | 61 | 1.0052 | 0.015% | 0.9948 | 94 | 1.0032 | 0.012% | 0.9968 |
| 29 | 1.0102 | 0.021% | 0.9899 | 62 | 1.0050 | 0.015% | 0.9950 | 95 | 1.0031 | 0.012% | 0.9969 |
| 30 | 1.0102 | 0.021% | 0.9899 | 63 | 1.0048 | 0.015% | 0.9952 | 96 | 1.0031 | 0.012% | 0.9969 |
| 31 | 1.0099 | 0.020% | 0.9902 | 64 | 1.0051 | 0.014% | 0.9949 | 97 | 1.0031 | 0.012% | 0.9969 |
| 32 | 1.0095 | 0.020% | 0.9906 | 65 | 1.0046 | 0.014% | 0.9954 | 98 | 1.0031 | 0.012% | 0.9969 |
| 33 | 1.0091 | 0.020% | 0.9909 | 66 | 1.0048 | 0.014% | 0.9952 | 99 | 1.0029 | 0.012% | 0.9971 |
| 34 | 1.0092 | 0.019% | 0.9909 | 67 | 1.0046 | 0.014% | 0.9954 | 100 | 1.0032 | 0.012% | 0.9968 |
| 35 | 1.0084 | 0.019% | 0.9917 | 68 | 1.0044 | 0.014% | 0.9956 | ||||
| 36 | 1.0088 | 0.019% | 0.9913 | 69 | 1.0043 | 0.014% | 0.9958 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




