Fractal-Derivative Cosmology: Time, Gravity, and Structure from a Single Scalar Field

1. Introduction

The quest for a unified theory that reconciles General Relativity and Quantum Mechanics remains one of the most fundamental open problems in physics. Although various approaches—such as String Theory, Loop Quantum Gravity, and Causal Set Theory—have been explored, they still face unresolved conceptual limitations or rely on assumptions lacking experimental support.

In this work, I present an alternative framework in which time, gravity, and gauge fields are not fundamental entities, but rather emergent properties of a single scalar field $\mathrm{\Phi }(\chi ,x^{\mu })$, defined over a fractal extension of spacetime. The additional variable $\chi$ is a discrete, log-periodic scale dimension with no classical metric, introducing a nested vibrational structure across scales. This proposal, which I call the DIM theory (Infinitesimal Dynamics of the Spacetime Matrix), is grounded in the hypothesis that successive derivatives of $\mathrm{\Phi }$ generate the physical content of the universe:

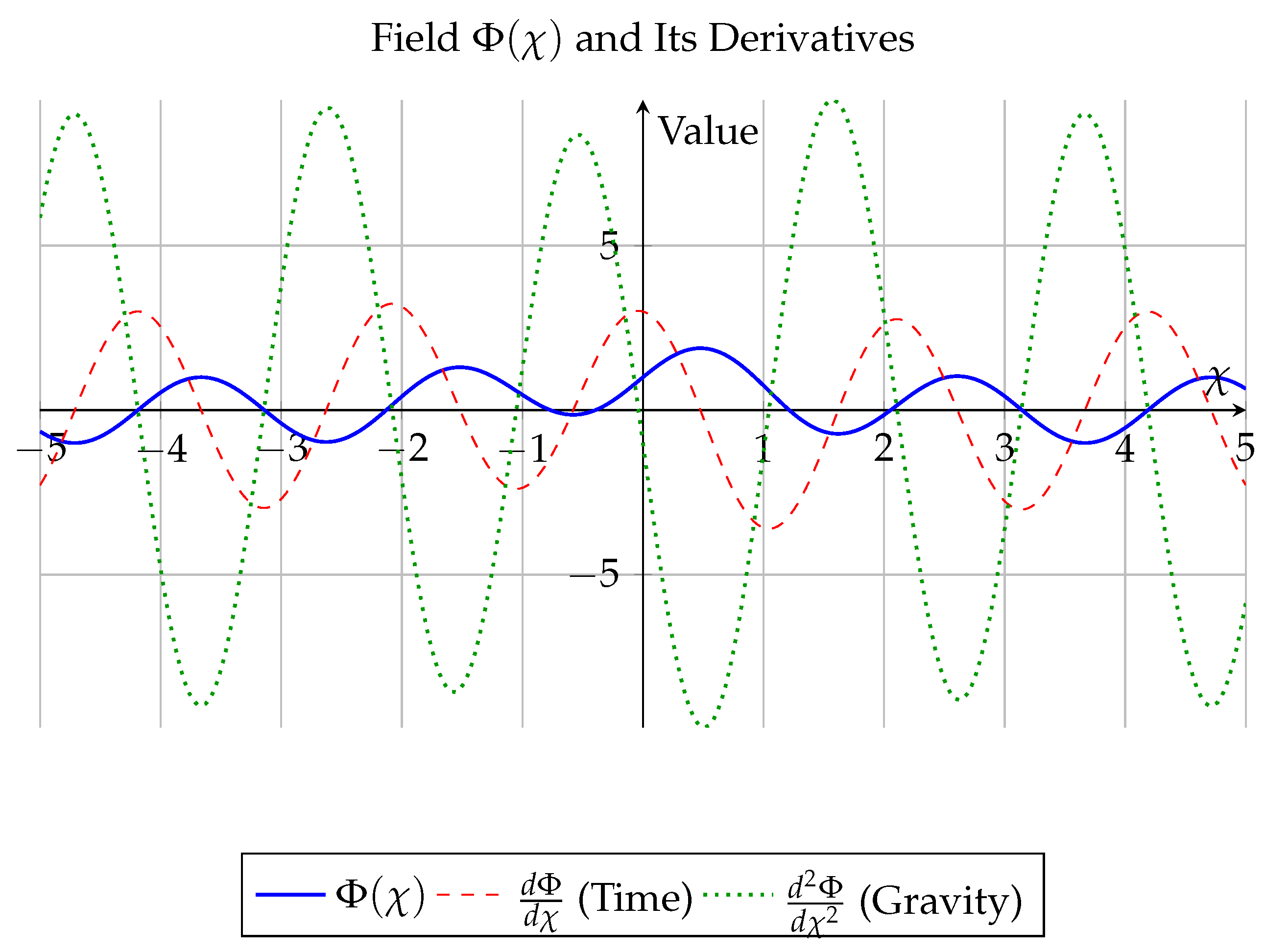
• Time emerges as the first derivative with respect to $\chi$.
• Gravity arises from the second derivative.
• Gauge fields and fermions appear through higher-order harmonics and modal projections.

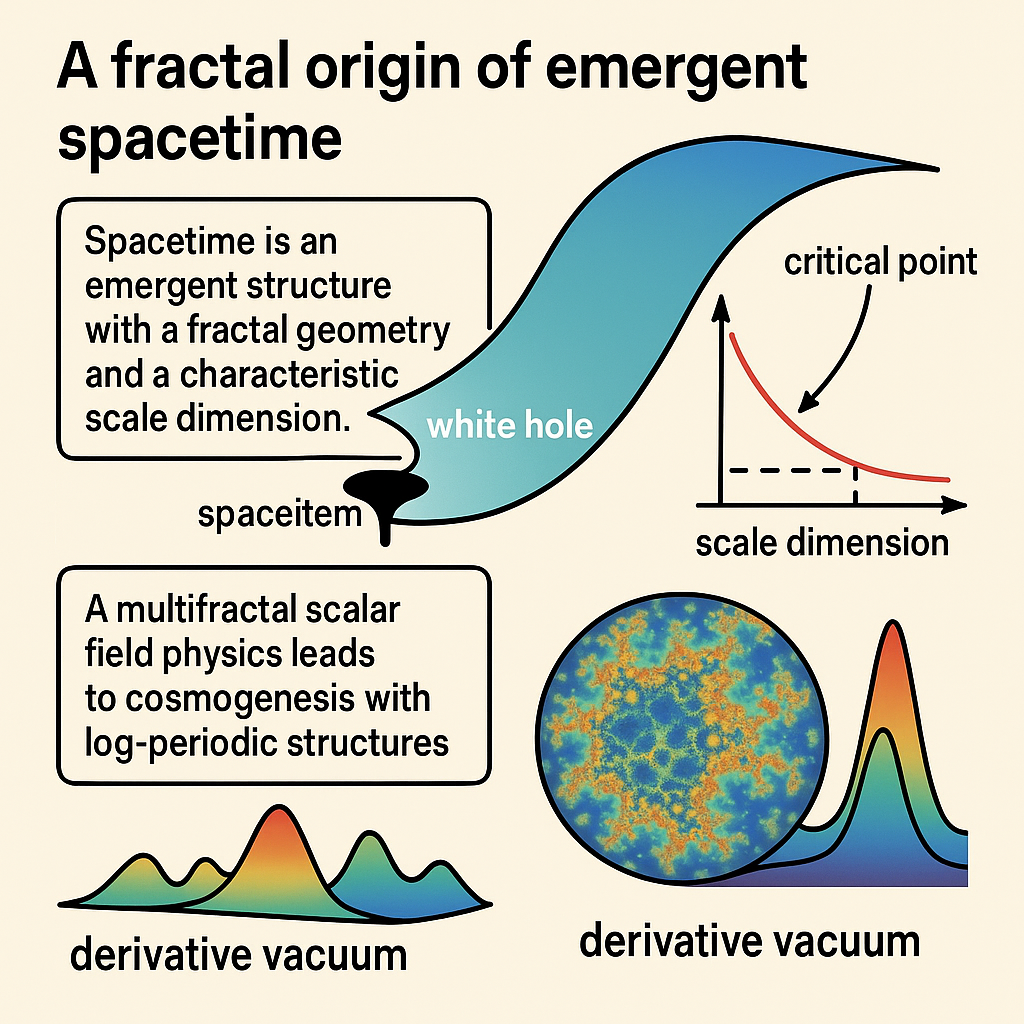
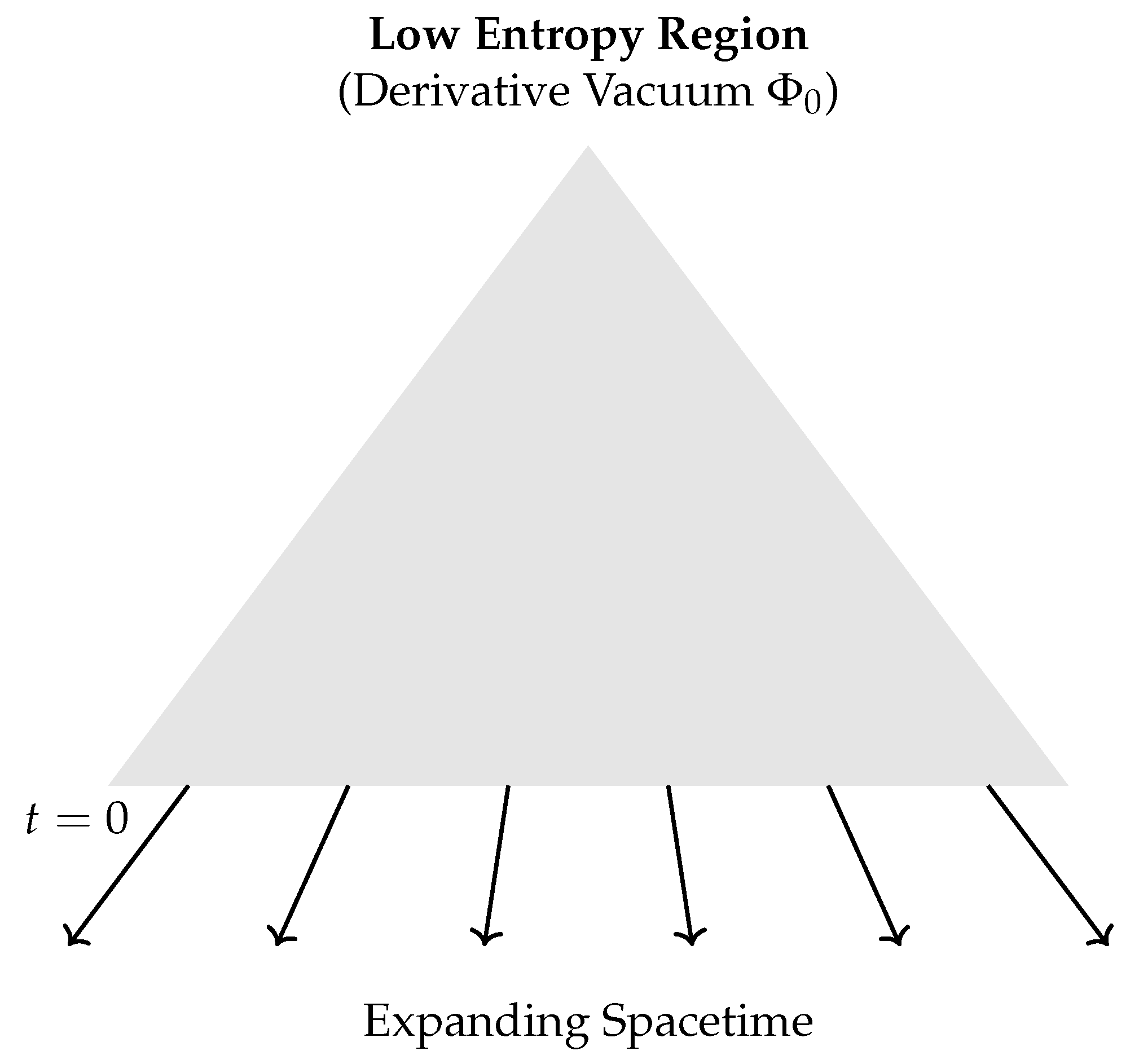
The universe is thus understood as an unfolding process from a maximally symmetric informational state—called the Derivative Vacuum ${\mathrm{\Phi }}_0$—toward structured phenomena. Unlike traditional unification attempts, this framework suggests that physical laws are not imposed externally but emerge from the internal structure of $\mathrm{\Phi }$.

The theory is formalized using a five-dimensional Klein-Gordon equation and a renormalization group approach adapted to fractal geometries, showing asymptotic safety via a non-Gaussian fixed point and infrared stabilization back to ${\mathrm{\Phi }}_0$. A dimensional reduction yields modified Friedmann equations and an effective metric with log-periodic corrections, compatible with standard cosmology at large scales.

Numerical simulations support the spontaneous emergence of large-scale structures, vibrational condensates, and multifractal organization. Furthermore, the theory leads to concrete, falsifiable predictions: deviations from Newtonian gravity at submillimeter scales, exotic modes in gravitational waves, and fractal signatures in the Cosmic Microwave Background (CMB). It also reinterprets the Big Bang not as a singularity but as a low-entropy white hole ejection, preserving thermodynamic consistency.

The goal of this paper is to present this unified framework and to outline a concrete validation program. DIM offers a mathematically consistent and ontologically grounded pathway for rethinking the foundations of cosmology and quantum gravity.

2. Theoretical Framework and Literature Review

2.1. Additional Dimensions and Unification Attempts

Efforts to unify the fundamental forces through additional dimensions go back to the early 20th century, starting with the Kaluza-Klein theory, and later extending into modern String Theory and M-theory. These approaches postulate compactified or extended extra dimensions to account for gauge symmetries and gravity within a single framework. However, empirical validation of such extra dimensions remains elusive, and the tension between General Relativity and Quantum Mechanics is still unresolved.

2.2. Fractal Geometry in Physics

Fractal geometry, originally developed by Mandelbrot, has provided a powerful language for describing self-similarity and scale invariance across physical systems. In cosmology, some models have proposed that the large-scale structure of the universe—including galaxy distributions, filaments, and voids—exhibits fractal features. The use of log-periodic modulations in the spacetime metric, as introduced in this theory, offers a potential explanation for these structures without invoking non-baryonic dark matter.

2.3. White Holes and Cosmology

White holes appear in General Relativity as time-reversed solutions of black holes. While no direct observational evidence exists for their physical realization, various speculative frameworks—especially in quantum cosmology—have suggested that the early universe may have emerged from a white-hole-like process. This interpretation provides a possible resolution to the low-entropy initial condition problem and aligns with the second law of thermodynamics.

2.4. Dimensional Projections and Mathematical Background

Derivatives and integrals are understood in this framework as projection operators from the higher-dimensional $\chi$ space to the four observable dimensions. This idea is reminiscent of Weyl’s early attempts to relate scale, geometry, and physical laws. Here, we define a unified potential $\mathrm{\Phi }\left(\chi \right)$ whose successive derivatives give rise to time and gravity, while its log-periodic fractal structure modulates the observable spacetime geometry.

3. Development of the Unified Theory

3.1. Unified Potential Function

The central element of the theory is a real scalar potential $\mathrm{\Phi }\left(\chi \right)$, defined over a higher-dimensional scale coordinate $\chi$. A representative form of the potential is:

$$\mathrm{\Phi }\left(\chi \right)=Asin\left(k\chi \right)+B{e}^{-\lambda {\chi }^2},$$

(3.1)

which combines oscillatory behavior (via the sine term) with localization (through the Gaussian decay). This structure reflects both periodicity and amplitude damping across $\chi$.

3.2. Time as the First Derivative of $\mathrm{\Phi }\left(\chi \right)$

Time is hypothesized to emerge from the first derivative of $\mathrm{\Phi }$ with respect to the extra dimension $\chi$:

$$t\left(\chi \right)={\displaystyle \frac{d\mathrm{\Phi }}{d\chi }}.$$

(3.2)

In this view, time is not fundamental but the result of a projection from higher-dimensional dynamics.

3.3. Gravity as the Second Derivative

Gravitational effects emerge from the second derivative of $\mathrm{\Phi }$:

$$g\left(\chi \right)={\displaystyle \frac{d^2\mathrm{\Phi }}{d{\chi }^2}}.$$

(3.3)

In regions where $g\left(\chi \right)<0$, the model suggests the possibility of local gravitational repulsion, which could have implications for structure formation or early-universe dynamics.

3.4. Fractal Structure of Spacetime

To explain cosmic structure and certain large-scale anomalies, a log-periodic fractal correction is introduced in the spacetime metric:

$$d{s}^2=-f(r,\chi )d{t}^2+g(r,\chi )d{r}^2+r^{2}d{\mathrm{\Omega }}^2,$$

(3.4)

with

$$f(r,\chi ),g(r,\chi )\propto 1+\alpha cos(\beta logr+\gamma \chi ).$$

(3.5)

The $logr$ term introduces scale repetitions that can replicate filamentary structures without invoking dark matter.

3.5. Reinterpretation of the Big Bang as a White Hole

In this framework, the Big Bang is reinterpreted not as a singularity but as the “mouth” of a white hole, ejecting energy and matter from a low-entropy initial state. This aligns with the second law of thermodynamics and avoids the infinite-entropy paradox of conventional models.

3.6. Derivatives and Integrals Between Dimensions

Derivatives act as projection operators: the dynamics in $\chi$ project down as physical magnitudes such as time and curvature. Integrals serve to accumulate energy and structure from the 5D manifold into effective 4D observables.

3.7. Integration of the Hypotheses

The theory is based on four core hypotheses:

• A higher-dimensional scale coordinate $\chi$ exists.
• Time and gravity emerge as successive derivatives of a unified potential $\mathrm{\Phi }\left(\chi \right)$.
• Spacetime exhibits a log-periodic fractal structure.
• The Big Bang corresponds to a white-hole-like ejection from a low-entropy origin.

As summarized in Figure 1, time, gravity, gauge fields, and fermionic structures emerge from successive projections of the scalar field $\mathrm{\Phi }\left(\chi \right)$.

4. Formal Mathematical Framework

4.1. Five-Dimensional Field Equation

The scalar potential $\mathrm{\Phi }(\chi ,t,x^i)$ satisfies a five-dimensional Klein-Gordon-type equation:

$${\square }_5\mathrm{\Phi }-m^2\mathrm{\Phi }=0,$$

(4.1)

where the 5D d’Alembertian operator is defined as:

$${\square }_5=-{\displaystyle \frac{{\partial }^2}{\partial {\chi }^2}}+{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^2}{\partial t^2}}-{\nabla }^2.$$

(4.2)

Figure 2 shows the behavior of a representative solution $\mathrm{\Phi }\left(\chi \right)$ and its first and second derivatives, which correspond to emergent time and gravitational curvature.

4.2. Separation of Variables

We consider a separation of variables of the form:

$$\mathrm{\Phi }(\chi ,t,x^i)={\mathrm{\Phi }}_{\chi }\left(\chi \right)·{\mathrm{\Phi }}_t\left(t\right)·{\mathrm{\Phi }}_x\left(x^i\right),$$

(4.3)

where each factor satisfies its corresponding differential equation:

• Kaluza-Klein modes in $\chi$,
• Temporal oscillations in t,
• Spatial wave solutions in $x^i$.

4.3. Forces and Projections from Derivatives

Time and gravity arise as projections of $\mathrm{\Phi }\left(\chi \right)$:

$$\begin{array}{cc}\hfill t\left(\chi \right)& ={\displaystyle \frac{d\mathrm{\Phi }}{d\chi }},\hfill \end{array}$$

(4.4)

$$\begin{array}{cc}\hfill g_{\mu \nu }& ={\eta }_{\mu \nu }+{\displaystyle \frac{d^2\mathrm{\Phi }}{d{\chi }^2}}{\eta }_{\mu \nu }.\hfill \end{array}$$

(4.5)

4.4. Spacetime Metric and White Hole Geometry

Starting from the classical FLRW metric:

$$d{s}^2=-c^{2}d{t}^2+a{\left(t\right)}^2\left({\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\mathrm{\Omega }}^2\right),$$

(4.6)

we introduce:

• Fractal perturbations to the metric,
• A reinterpretation of the initial cosmological condition as a white hole.

4.5. Entropy Evolution and White Hole Thermodynamics

Entropy evolves from an initially low state. The white hole expels matter and energy in a direction consistent with the arrow of time and the second law of thermodynamics, avoiding the paradox of infinite entropy at the Big Bang.

4.6. Modified Friedmann Equations

The Friedmann equations are modified to incorporate both the $\chi$ dimension and fractality:

$$\begin{array}{cc}\hfill {\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2& ={\displaystyle \frac{8\pi G}{3}}(\rho +{\rho }_{\mathrm{\Phi }}+{\rho }_{\mathrm{fractal}})-{\displaystyle \frac{k}{a^2}}+\Lambda ,\hfill \end{array}$$

(4.7)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\ddot{a}}{a}}& =-{\displaystyle \frac{4\pi G}{3}}(\rho +{\rho }_{\mathrm{\Phi }}+{\rho }_{\mathrm{fractal}}+3p+3p_{\mathrm{\Phi }})+\Lambda .\hfill \end{array}$$

(4.8)

4.7. Derivatives and Integrals in the Multidimensional Context

• Derivatives with respect to $\chi$ define physical magnitudes such as time and gravity.
• Integrals allow the conversion of energy and structure from 5D to 4D, incorporating fractal effects into observable dynamics.

5. Physical Implications and Observational Predictions

5.1. Weakness of Gravity Under Normal Conditions

Since gravity emerges as the second derivative of the potential $\mathrm{\Phi }\left(\chi \right)$, it is naturally attenuated compared to other interactions. This attenuation may explain the relative weakness of gravity without requiring compactification or suppression mechanisms.

5.2. Black Holes and White Holes: Gravity Dominates Time

In regions of extreme curvature, higher-order derivatives of $\mathrm{\Phi }\left(\chi \right)$ become dominant. This allows for the existence of exotic solutions such as:

• Black holes: local temporal collapse,
• White holes: matter/energy ejection with entropy asymmetry.

5.3. Dark Matter and Dark Energy

The log-periodic fractality and the extra dimension $\chi$ introduce additional gravitational effects. These can reproduce:

• Flat galactic rotation curves,
• Accelerated cosmic expansion,

without the need to invoke unknown forms of matter or energy.

As illustrated in Figure 3, the Big Bang is reinterpreted as an entropic ejection from a white hole-like state ${\mathrm{\Phi }}_0$.

5.4. Small-Scale Modifications of Newtonian Gravity

The theory predicts oscillatory deviations from Newton’s law at submillimeter scales:

$$F\left(r\right)\cancel{\propto }{\displaystyle \frac{1}{r^2}}.$$

(5.1)

These anomalies could be detectable in high-precision microgravity experiments.

5.5. Gravitational Waves with Extra Modes

The interaction between $\mathrm{\Phi }\left(\chi \right)$ and the fractal geometry may induce additional polarization modes in gravitational waves, detectable in observatories such as:

• LIGO,
• Virgo,
• LISA.

5.6. Anisotropies in the Cosmic Microwave Background (CMB)

The fractal structure of the metric leaves signatures in the CMB:

• Log-periodic modulations at intermediate and small angular scales,
• Potential correlations with anomalies observed in Planck and WMAP data.

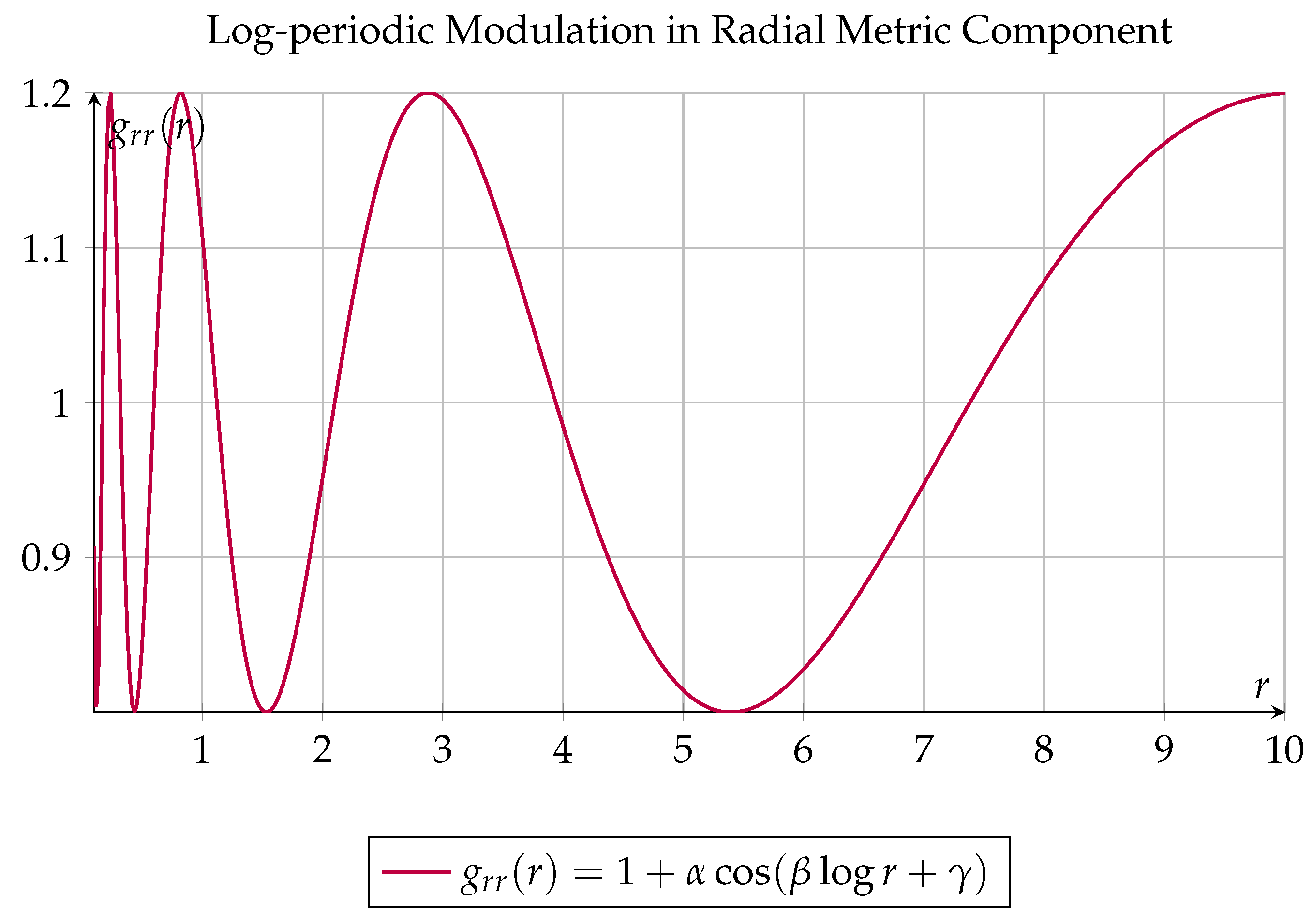
The radial metric component $g_{rr}\left(r\right)$ exhibits oscillations in $logr$ as shown in Figure 4, which may underlie observed anisotropies in the CMB.

5.7. Main Results Summary

The main predictions and conclusions of the theory can be summarized as:

• The Big Bang is reinterpreted as a white hole, consistent with low initial entropy.
• Cosmic structure arises from log-periodic fractal modulation of spacetime.
• Time and gravity emerge as successive derivatives of the scalar potential $\mathrm{\Phi }\left(\chi \right)$.
• Observable signatures include:
  • Deviations in Newtonian gravity at short distances,
  • Additional modes in gravitational waves,
  • Fractal anisotropies in the CMB.
• General Relativity is recovered in the limit of negligible fractality.

6. Numerical Simulations and Validation

6.1. Simulation Setup

The initial state is defined by low entropy and a high expansion rate, consistent with a white hole scenario. Adjustable parameters include:

• $\alpha$, $\beta$, $\gamma$ — fractal metric modulation,
• A, B, k, $\lambda$ — parameters of the potential $\mathrm{\Phi }\left(\chi \right)$.

These are calibrated to match cosmological observations such as the CMB and large-scale structure.

6.2. Simulation Results

2D and 3D numerical experiments reveal:

• Emergence of fractal patterns,
• Reproduction of filamentary structures,
• Partial consistency with CMB anisotropy data.

A representative parameter set:

$$A=1,B=1,k=3,\lambda =0.5,\alpha =0.2,\beta =5,\gamma =2$$

(6.1)

yields:

• $\mathrm{\Phi }\left(\chi \right)$: oscillatory behavior with exponential decay,
• $t\left(\chi \right)=d\mathrm{\Phi }/d\chi$: alternating sign, suggesting regions of temporal inversion,
• $g\left(\chi \right)=d^2\mathrm{\Phi }/d{\chi }^2$: zones of negative curvature, possibly gravitational repulsion.

6.3. Comparison with Observational Data

CMB (Planck, WMAP):

• Matches at medium angular scales,
• Discrepancies at small scales, tunable via $\alpha$ and $\beta$.

Galactic Distribution (SDSS):

• Statistical self-similarity in real data aligns with the log-periodic modulation of the model.

6.4. Computational Tools and Visualization

Simulations were performed using environments such as:

• Wolfram Language,
• Python with NumPy.

They show:

• Density ridges and valleys in $\rho (\chi ,r)$,
• Oscillatory modes in $\mathrm{\Phi }\left(\chi \right)$ potentially corresponding to quantum fluctuations.

6.5. Interpretation and Significance

The emergent patterns support the theory’s central ideas:

• Log-periodic fractality may mimic dark matter effects,
• The $\chi$ dimension induces scale-dependent density variations,
• Time and gravity are not fundamental but emergent from deeper structure.

Despite this preliminary coherence, further steps are needed:

• Experimental tests in microgravity,
• Gravitational wave signal analysis,
• Detailed spectral analysis of the CMB.

7. Compatibility with Existing Theories

7.1. Recovery of General Relativity at Large Scales

In the limit where fractal modulation vanishes ($\alpha \to 0$), the theory converges to the standard Friedmann-Lemaître-Robertson-Walker (FLRW) cosmology:

$$d{s}^2=-c^{2}d{t}^2+a{\left(t\right)}^2\left({\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\mathrm{\Omega }}^2\right).$$

(7.1)

Time and curvature behave classically when $\mathrm{\Phi }\left(\chi \right)$ becomes smooth and its derivatives are regular.

7.2. Consistency with Quantum Field Theory

The scalar field $\mathrm{\Phi }$ evolves according to a Klein-Gordon equation in five dimensions. In the low-energy limit, the extra dimension $\chi$ decouples and the theory reduces to a four-dimensional scalar field theory:

$${\square }_4\varphi -m^2\varphi =0.$$

(7.2)

Gauge interactions can be interpreted as effective modulations of $\mathrm{\Phi }$ across $\chi$, analogous to extra-dimensional modes in Kaluza-Klein theory.

7.3. Integration with Thermodynamics

By reinterpreting the Big Bang as a white hole, the model preserves the second law of thermodynamics and avoids the paradox of infinite entropy. Entropy increases monotonically as $\mathrm{\Phi }\left(\chi \right)$ differentiates.

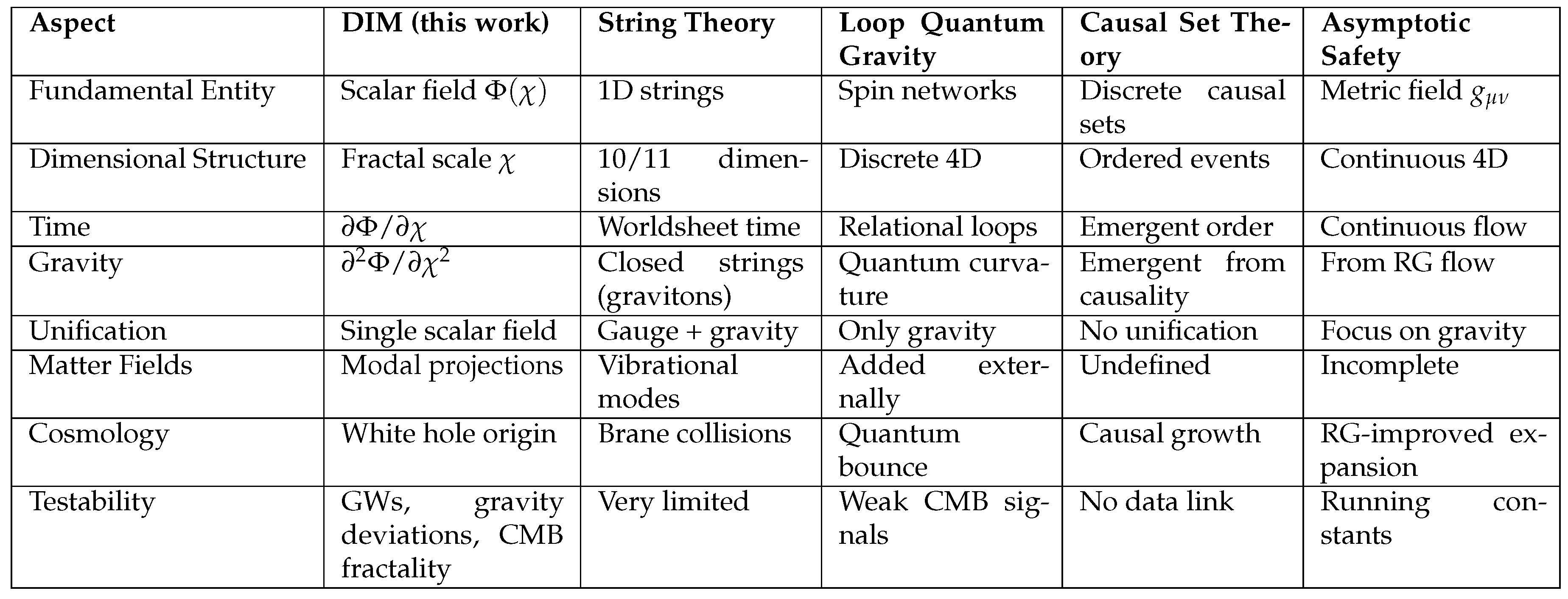
7.4. Comparison with Other Theoretical Frameworks

• String Theory: The role of $\chi$ resembles a compactified dimension but lacks supersymmetry or string tension.
• Loop Quantum Gravity: While LQG quantizes spacetime geometry, DIM proposes geometry as an emergent feature from field derivatives.
• Causal Set Theory: Both share a discrete and scale-sensitive structure, but DIM operates in continuous spacetime with log-periodic features.
• Asymptotic Safety: DIM achieves UV completion via a non-Gaussian fixed point under functional renormalization, consistent with asymptotic safety goals.

7.5. Limits of Applicability

The theory assumes a continuous $\chi$ parameter. If future data confirm that nature is fundamentally discrete or that higher-order derivatives break down, the model would require adaptation.

7.6. Summary of Compatibility

• The model reduces to General Relativity and standard QFT in appropriate limits.
• It respects the second law of thermodynamics.
• It is compatible with known symmetries and cosmological observations.
• It diverges from existing theories by deriving geometry and interactions from a single scalar source.

8. Conclusions and Future Work

8.1. Summary of the Proposal

This work introduces a unified framework in which time, gravity, gauge fields, and matter emerge from successive derivatives of a single scalar field $\mathrm{\Phi }(\chi ,x^{\mu })$ defined on a log-periodic fractal extension of spacetime.

The theory presents four central hypotheses:

• The existence of an additional fractal dimension $\chi$.
• Time and gravity emerge as derivatives of a unified field.
• The Big Bang corresponds to a white hole with low entropy.
• Spacetime exhibits log-periodic fractal modulation.

These assumptions lead to:

• A 5D Klein-Gordon-type equation with fractal corrections,
• Emergence of cosmic structures from self-organization,
• Predictive capacity for deviations in gravity and wave phenomena.

8.2. Original Contributions

• Ontological reinterpretation of physical magnitudes as derivative projections.
• Mathematical unification of spacetime, gravity, and interactions via a single scalar source.
• A falsifiable, non-perturbative renormalization structure with asymptotic safety.
• Numerical simulations supporting self-organization and multifractality.

8.3. Future Work

• Formal quantization of $\mathrm{\Phi }(\chi ,x^{\mu })$ and study of modal interference.
• Development of observational strategies to detect log-periodic gravitational anomalies.
• Study of entropy flow and thermalization in white hole scenarios.
• Extension of simulations to include fermionic structures and gauge fields.
• Comparative analysis with CMB and large-scale distribution data.

8.4. Final Remarks

The DIM framework aims to bridge mathematical structure and ontological clarity, proposing that time, gravity, and structure are not fundamental but emergent. If correct, this perspective could offer new tools to interpret the universe’s origin and dynamics from a deeper informational substrate.