1. Introduction
There are many interpretations of Quantum Mechanics (QM) and the Handbook edited by Olival Freire [
1] is probably the most up to date textbook. In it, one can find the early history of QM, the controversies (starting with the famous Bohr-Einstein debate), the historical development of QM as well as many interpretations. An interpretation is in fact a full-size theory; about 15 theories compete. The de Broglie-Bohm theory seems to be the most compatible with this work and, on this subject, Goldstein’s Bohmian Mechanics [
2] is an interesting read.
“Quantum Physics is on the Wrong Track, Says Breakthrough Prize Winner Gerard t’Hooft”. Such is the title of an article interviewing t’Hooft [
3]. For t’Hooft, superposition and non-locality seem to be the main problem; this work hopefully sheds some light on this problem.
This work, like the 15 theories, is trying to make sense of QM; but this approach is different as it uses the consequence of a new idea on special relativity.
2. New Idea on Special Relativity
This section 2 is a condensed presentation of a previous study [
4].
2.1. Simultaneity
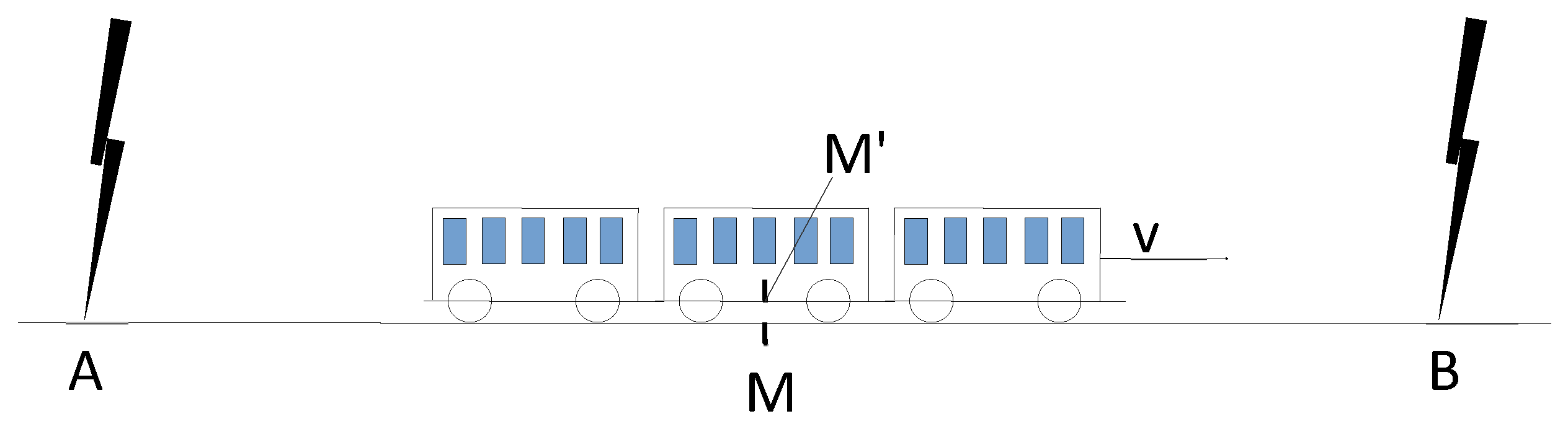
Figure 1 is the example that Einstein gave us in his Relativity [
5] to show the loss of simultaneity. Lightning bolts A and B are simultaneous and for Einstein, only observer M can detect the simultaneity. But M and M’ are both inertial observers. M’ has the right to think (s)he is immobile. M and M’ both observe simultaneity. Reducing the bolt to a single photon, photons A and B go at the speed of light for M and for M’ whatever v speed is. That is what special relativity is telling us, and it is another way to reach the conclusion that both M and M’ observe simultaneity.
The return of simultaneity has been presented in a previous peer-reviewed study [
4]. In the previous study, the loss of simultaneity would be correct in a quantum world (i.e. atomic or subatomic scale). This example and others show that special relativity is applied differently in the quantum and macroscopic worlds. The return of simultaneity in our macro-world has an important effect on spacetime diagrams.
2.2. Spacetime Diagrams
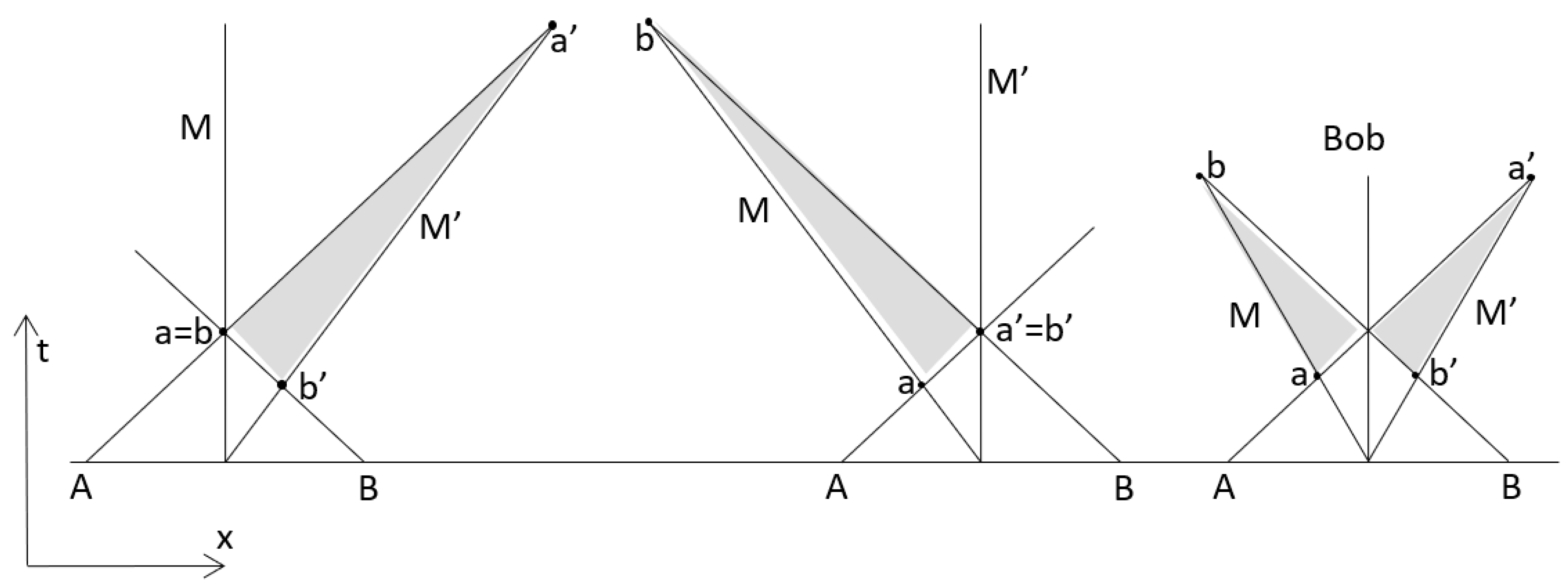
If we draw the spacetime diagram corresponding to
Figure 1 we obtain the diagram on the left of
Figure 2. On that figure, photon A reaching M is denoted by dot a, and by dot a’ for M’; similarly for photon B with dots b and b’. But we have just seen that photons A and B reach M' at the same time. So, if for M, time is running from b’ to a’, for M’ it is just one instant.
Similarly with the diagram in the middle, we have seen that photons A and B reach M at the same time. If time is running from a to b for M’, for M it is just one instant.
So even if in the diagram, a, b, a’ and b’ are not at the same position, they represent a single instant: a=b=a’=b’. The diagram on the right is simply a combination of both diagrams with an extra observer (Bob) who is the immobile observer and sees M’ moving towards B and M moving towards A. In [
4] those grey areas have been interpreted as local and temporal superposition.
3. The EPR Paradox
The original motivation of this paper was to use the superpositions obtained with the new insight of section 2 to solve the EPR paradox.
3.1. Review of the Paradox
The EPR paper [
6] is the first paper on “the spooky action at a distance”. The inspiration for the EPR paper dated from the Solvay V conference [
7]. Einstein presented a thought experiment in which an electron passes through a small aperture and diffracts, producing a wave. The electron would be in a superposition state until it reaches a screen; the wave function collapses in the position where the electron shows itself. The EPR paper moves from the philosophical problem of Solvay to a physical (testable) problem as it uses the entanglement phenomenon and two particles. The problem is the collapse of the wave function with the instantaneous materialisation of the electron for the Solvay’s problem.
The EPR paper shows that, under some special conditions, two particles may have a special link between them (the entanglement). By measuring the property of one particle, the property of the other particle will “collapse” instantaneously, whatever the distance that separates them. For Einstein, as nothing can go faster than light, how can information travel instantaneously? The conclusion of the EPR paper is that “the description of reality as given by the wave function is not complete”.
The interesting point of the EPR paper is the demonstration of non-locality as described above. QM and the entanglement were doing something impossible. If experiment shows the impossible, an explanation is needed for Einstein who suggested some hidden parameters as an explanation. Bohr couldn’t falsify the demonstration of non-locality. So he conceded that the wave function was symbolic, but he maintained that QM did not need the hidden variables or further explanation [
8].
About 60 years ago, John Bell showed that a test is possible [
9]. He had the same problem as Einstein, the lack of rigour of Copenhagen’s interpretation was bothersome but Bell had more information available. So, he added in some missing maths and arrived at an interesting suggestion: the Bell inequality. A violation of Bell’s inequality would show there is something non-local like the fact that to observe one photon would affect instantly the other photon which would be miles away. If the Bell inequality is violated, then Bohr is correct, if not then Einstein is correct with his hidden variables. So far, all experiments have shown a violation of Bell’s inequality [
10]; Bohr would be correct and there are no hidden parameters. It seems the question is closed.
Despite the Nobel prize having been awarded to Aspect/Clauser/Zeilinger in 2022, there are still many papers about the EPR paradox [
11,
12].
In the introduction, we have seen that the non-locality is a problem for t’Hooft; indeed it seems incompatible with relativity, and it seems that most of the 15 interpretations of QM are trying to solve that problem [
1]. As there are no hidden parameters, Einstein would say that another explanation is needed and, in a way, this is what physicists are trying to do with their interpretations of QM.
3.2. What Counts Is the Initial State
Here is a short sentence from section 10 of [
4]: “Interesting to see that the starting point is what counts for special relativity…”. It is a very important observation for the EPR paradox. Indeed, the experiment starts when the bolts of lightning strike.
Figure 1 represents the initial state when the lightning strikes; M and M’ are at the same point and that is why both observe simultaneity. When the observation is made, M and M’ are at different points which cause the illusion of non-simultaneity for the other observer. So what counts is the initial state, the t=0.
“What counts is the initial state” could become a new law and physicists have become very good at changing things between that initial state and the observation. That ability was essential to close loopholes in experimental tests of Bell’s inequality; so far it seems that this new law would be correct but probably needs to be expressed in careful terms.
3.3. Superposition
We have seen that the grey areas of the diagrams of
Figure 2 are where M and M’ observe simultaneity. As the areas extend in the x direction there is a superposition (of position). Bob cannot tell exactly when and where M and M’ observe simultaneity; the only possible statement is that it is in the grey areas. Not knowing “where” (until an observation) is typical of QM. The “when” is the ‘novelty’, those grey areas are one instant for M or M’; time doesn’t flow for them, but flows for Bob; therefore the idea of a temporal superposition. Contrary to [
4], the idea of temporal superposition is not new, Tumulka [
13] would have reached an identical suggestion with a totally different approach (maths on GRW theory), but he didn’t use the term “temporal superposition”.
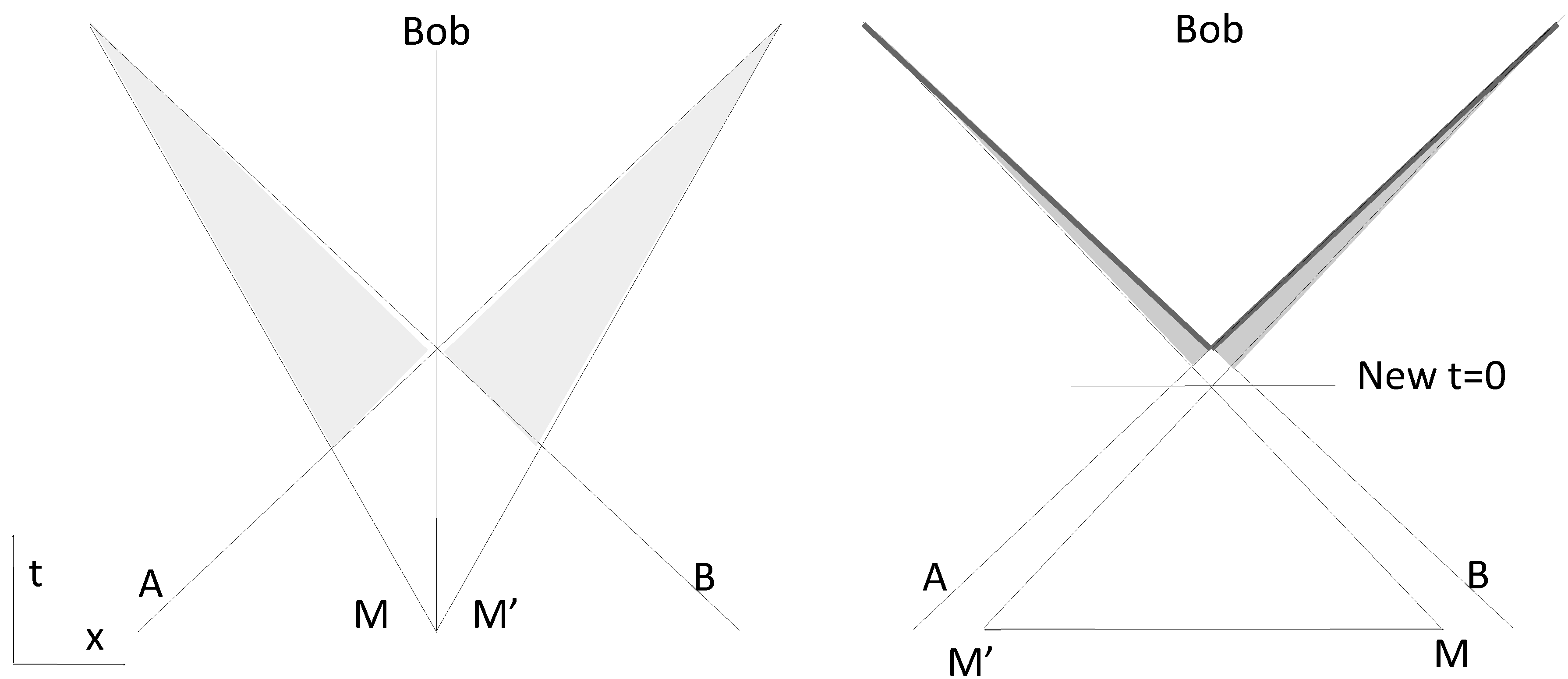
Left of
Figure 3, there is the spacetime diagram which was on the right of
Figure 2 with the light grey areas. From left to right of
Figure 3, the starting position for M has been moved towards B and M’ towards A; they also travel much faster. The consequence is a smaller darker grey area. Now, let’s imagine a further move where M’ is travelling with A and M travelling with B. The grey area would be reduced to a line for each, a line as long as needed, a line where there would be superposition.
The change from the lightning strikes on a railway to the entanglement experiment needs that move of the original position of M and M’. Two photons of the experiment are generated at the same points and travel in opposite directions. Another “new t=0” is where photons “cross” Bob on the figure. The photons of the experiment are not crossing but are generated at a single point. We have just seen that the two lines corresponding to the trajectory of the photons are lines where there is superposition. So, as soon as a measurement is made, as the photon is everywhere on the line at the same time, it is also in contact with the other photon which is also everywhere on the line at the same time. The information “a measurement has been made” can be transmitted to the other photon. Local realism defended by Einstein becomes plausible.
The idea of “what counts is the initial state” would simplify the picture. Two entangled photons are emitted and go in opposite directions. When the photons are away from each other, there is an observation of one photon; observation of the other photon confirms the violation of Bell's inequality. But if “what counts is the initial state”, as the initial moment (t=0) is the emission; at that point, the photons are together, there is locality.
3.4. Discussion
This work gives a totally different interpretation to Bell’s inequality. Bell's reasoning is correct if Einstein’s reasoning is correct. Einstein based his reasoning on the fact that information cannot travel instantaneously from photon A to photon B without breaking the laws of physics. If this paper is correct, it would mean that, in a special state (of superposition) information can travel instantaneously from photon A to photon B without breaking the laws of physics. It wouldn’t break the law of physics because the photons are in a temporal (as well as local) superposition. When one photon is observed, the information can travel along this superposition line and reach the other photon in a way that will seem instantaneous to Bob. This is something currently considered impossible, but if in the future information is transmitted over a long distance instantaneously, it will be proof that this idea is correct.
If we can determine whether a photon is in a state of superposition or not, there is a way. A measurement device can “measure” or “not measure” the property of one photon, leaving the other photon is a state of superposition or not. Another device measures whether that other photon is in a state of superposition or not; information would be transmitted instantaneously. Observing the collapse of a wave function would be similar. But I can’t see how those tests would be possible. Probably another “John Bell” would be needed to transmit information instantly.
4. The Double-Slit Experiment and the Wave-Particle Duality
The double-slit experiment is the typical example of QM because of the wave-particle duality.
4.1. History
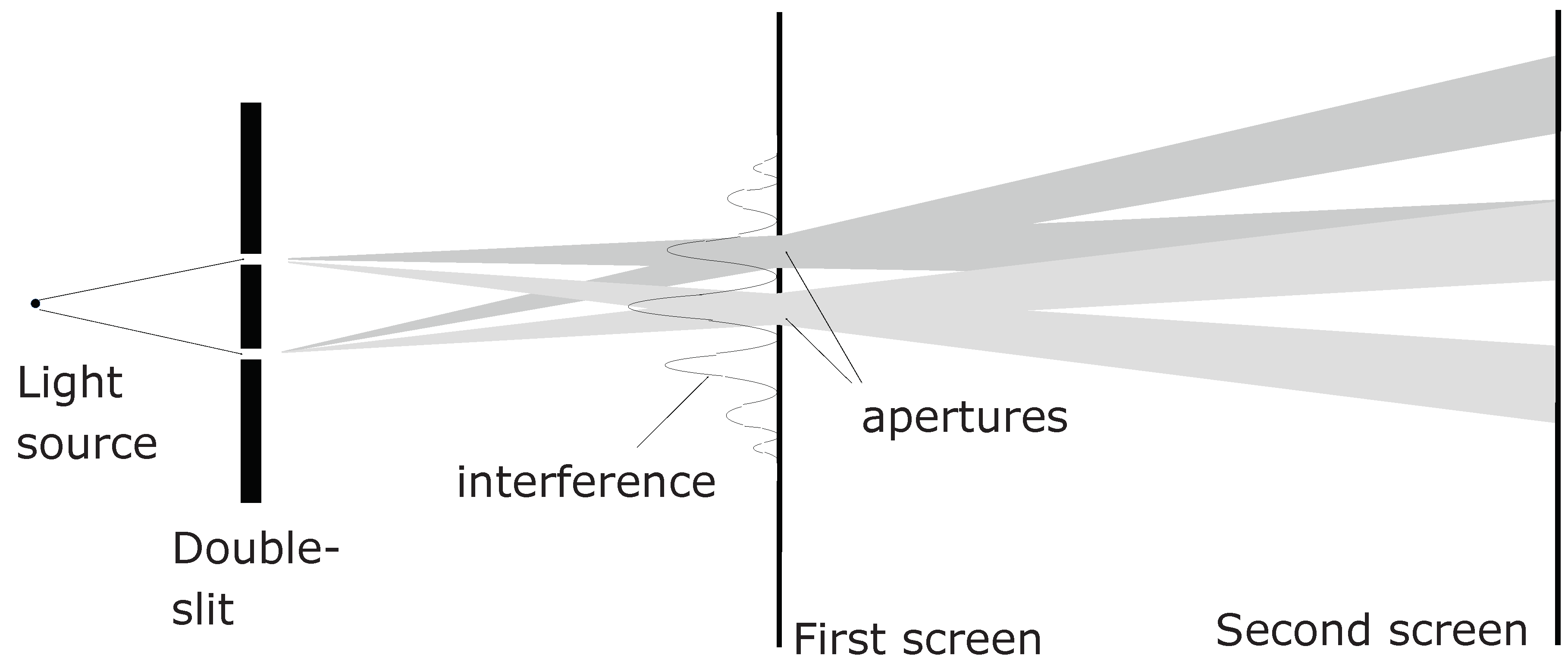
Figure 4 represents the double-slit experiment with a small addition explained later; that experiment is about light. Newton thought light was a particle while Descartes thought of it as vibration. In 1801, Thomas Young carried out the first double-slit experiment as a demonstration of the wave behaviour. The double-slit experiment is now described as a double-path experiment. A difference in the path-lengths results in a phase shift, creating an interference pattern. It shows that light is a wave.
Then Planck explained some results with the idea that light would be a particle [
14] and Einstein used the photoelectric effect to confirm that light is a particle [
15]. With the de Broglie hypothesis [
16], every object in the universe would be associated with a wave; therefore the duality wave-particle. In 1927, two experiments demonstrated that electrons show the same behaviour as photons in a double-slit experiment, which was later extended to atoms and molecules. So photons, electrons, atoms and molecules possess that duality wave-particle.
Following the de Broglie hypothesis, wave-particle duality became an important concept in QM: a wave cannot exist without a particle and a particle always has a wave attached. That is not currently the case in classical physics. Schrödinger developed de Broglie’s wave equations to reach his famous equation and the wave function. Somehow that wave function became associated with the particle, probably because of that duality. Remember that the wave function originates from de Broglie’s wave equations, not directly related to particles per se.
On this duality wave-particle, Bohr added the idea of complementarity. For Bohr, it is not possible to know at the same time which slit the photon has been through and to observe the interference. In other terms, either we observe the wave characteristic of a particle or we observe the particle; but we can’t observe both at the same time. So with the double-slit experiment, if we observe which slit a photon uses, what should happen is decoherence, the interference pattern would be lost.
Obviously, physicists tried to observe both wave and particle by putting a detector near the slits; it is called a “which way” experiment. Before the slit, the current theory tells us that the photon is in a superposition; the superposition that Einstein complained about in Solvay V [
7]. Superposition is very fragile, and the Qubit of quantum computers are based on a coherent superposition of multiple states. Qubit functions only at low temperature because that is the only way to preserve that superposition. When physicists carried out their “which way” experiment, they obtained the information about the slit, but the interference is disturbed as in Mittelstaedt [
17]. Probably the detector near the slit disturbs the superposition which is so fragile. The point is that wave and particle has been observed at the same time. Physicists are now talking about a “wave-particle trade-off” to avoid rejecting complementarity.
4.2. A New “Which Way” Experiment
The schematic of the new experiment is presented
Figure 4.
It is a typical double-slit experiment which could use a laser as a light source. On the first screen, there are some apertures letting the photons pass through and reach a second screen. Only two apertures are drawn on the figure for clarity. For the experiment, maybe only one aperture should be open at a time. As photons travel in a straight line, the observation on the second screen will be able to tell which slit has been used.
Because I believe the disturbed interference observed by Mittelstaedt is explained, I believe that wave (undisturbed interference) and particle behaviour will be observed at the same time with this new experiment. The complementarity principle wouldn’t be correct, and Copenhagen’s interpretation would be incorrect as the complementary principle has been described by Bohr as an essential feature of QM [
18] (for Bohr, QM equals Copenhagen’s interpretation). But nobody understands QM and can predict the outcome, therefore the test needs to be done.
If the interference disappears, then the complementarity principle is respected, and current QM is safe. But that would be extraordinary; how does the wave function know that opening an aperture will allow us to determine which slit the photon used? The wave function will then use that knowledge to erase the interference. But there is no logic with QM, therefore this is possible.
Another possibility: on that second screen, photons could be detected where none are expected (if respecting the straight trajectory as on the figure), the complementarity principle is respected, and current QM is safe because we won’t be able to determine where the photon is coming from.
So there are three possible outcomes: which one is correct?
5. Superposition
Common sense tells me that undisturbed interference will be observed, and which slit was used will be determined. I would interpret the result as if superposition is only possible with the wave, because clearly the photon would have used one slit or the other so is not in superposition. Remembering the origin of the wave function (from de Broglie’s wave equations) becomes important. The wave function shouldn’t be applied to the particle. The photon would show classical behaviour which would satisfy Einstein’s question of Solvay.
Now the EPR paradox. At first, I believed the justification with superposition would only be valid with photons because of the speed of light and the corresponding Lorentz factor that "stops" the flow of time. As time doesn’t flow for the photons, information is free to travel on those superposition lines. But M and M’ could be two entangled particles; those particles won’t be travelling at the speed of light, time would flow.
There are papers on entanglement with different objects (quarks, etc.), the EPR paper is about particles, not about light. So my idea of time not flowing could be too simple.
Two entangled electrons would go their way. If the electron is also in superposition, to occupy the dark grey areas of
Figure 3, electrons would travel straight but could also suddenly turn at a right angle when they dematerialize to occupy the grey area of superposition. Electrons are made of matter; they are not ghosts. Because of electrons, I realized that I cannot see a photon being at the same time near the point of observation and near the point of emission. A photon has a speed observed by Bob, it cannot travel from the emission to the observation point in zero time (time of Bob). That is another reason why superposition is only applicable to a wave, not to a particle.
Please note that even with particles (the dark grey areas) there is a common point, a locality. The superposition area is also a temporal superposition, time is not flowing for the particle. So, for an electron, information carried by the wave in superposition, could “come back in time seen by Bob” and use the locality point. So the ghost would be the wave; locality is back for a particle as well.
Here is a new experiment that could prove that only the wave is in superposition and not the particle. The setup will be the same as an experiment to observe Bell’s inequality. In addition, there will be a shutter on the path of the first photon. The shutter will be open so the photon can run towards the detector. Then the shutter closes before the photon reaches the detector. Will the photon reach the detector? If the photon is everywhere at the same time, the shutter may catch it before the detector. It would be an observation of superposition of the photon. But I believe the photon will reach the detector all the time. Will entanglement be observed? In other words, will the shutter stop information coming back? The wave cannot be without a particle, so the shutter would cut the wave. My belief is that entanglement won’t be observed because it is the wave that carries information. Mr Aspect, pouvez-vous reproduire votre expérience et ajouter cet obturateur ? (Prof Aspect, could you test that idea?)
This new experiment would test the “what counts is the initial state”. Would the information travel back in time to the open shutter (initial state)?
6. Further Discussion
Because in classical physics, something cannot be at two places at once, I assumed that superposition applies only to the wave. I am not unifying classical and quantum physics but in classical physics, a boat is at one place, but the wave is at many places at once. Similarly, the photon would be at one place and the wave everywhere at once. That similarity is pleasing because it would be easier to unify the two physics.
I now believe that temporal superposition and local superposition are the same phenomenon.
This work is not a theory but could complete the de Broglie-Bohm theory. Please do read Goldstein’s booklet [
2]. This work explains what superposition could be and helps with maintaining locality with the EPR paradox.
Because complementarity would be in doubt, is Heisenberg’s uncertainty principle correct? Does it apply only to a wave or also to a particle?
Can Wheeler's delayed-choice experiments [
19] be explained with this work?
Can this work explain the double-slit experiment on time [
20]?
It would be interesting to find out if this work is compatible with Tumulka’s paper [
13].
I hope that other scientists will join the debate and answer these questions; each question may require a lot of work.
On a different note: is there a different time for QM as suggested in [
4]? The time dilation described with special relativity is good enough, and no other consideration is needed.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Einstein-Podolsky-Rosen |
EPR |
| Quantum Mechanics |
QM |
References
- Freire O. (ed.) “The Oxford Handbook of the History of Quantum Interpretations” Oxford Academic (2022).
- Goldstein, S. "Bohmian Mechanics", The Stanford Encyclopedia of Philosophy (Summer 2024 Edition), Edward N. Zalta & Uri Nodelman (eds.), URL = https://plato.stanford.edu/archives/sum2024/entries/qm-bohm/.
- Billings, L “Quantum Physics is on the Wrong Track, Says Breakthrough Prize Winner Gerard t’Hooft”, Scientific American, April 7, 2025.
- Danis, F. “Limit and potentials of Special Relativity”. Applied Physics Research; 2024 Vol. 16, No. 2, p.112. [CrossRef]
- Einstein A. 1916. “Relativity: The Special and the General Theories.” The folio society, London, 2004.
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality be Considered Complete? Physical Review. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Einstein A. in Sovay V, 1927, pp. 254-6.
- Baggot J. and Heilbron J. “Quantum Drama. From the Bohr-Einstein debate to the riddle of entanglement”. Oxford University Press 2024.
- Bell, J.S. On the Einstein Podolsky Rosen Paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Aspect, A. Bell's inequality test: more ideal than ever. Nature 1999, 398, 189–90. [Google Scholar] [CrossRef]
- Pignard, O. Quantum entanglement of photons explained by a superluminal influence. Physics Essays 2025, 38, 2. [Google Scholar]
- Tononi A and Lewenstein M “Temporal Bell inequalities in non-relativistic many-body physics” 2025 Quantum Sci. Technol. 10 03LT01.
- Tumulka, R. On spontaneous wave function collapse and quantum field theory. Proc. R. Soc. A. 2006, 462, 1897–1908. [Google Scholar] [CrossRef]
- Planck, M. Über das Gesetz der Energieverteilung im Normalspektrum. Annalen der Physik. 1901, 4, 553–563. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Annalen der Physik 1905, 17, 891. [Google Scholar] [CrossRef]
- de Broglie, L. " Recherches sur la théorie des quanta". Foundation of Louis de Broglie (English translation by A.F. Kracklauer, 2004. ed.).
- Mittelstaedt, P.; Prieur, A.; Schieder, R. Unsharp particle-wave duality in a photon split-beam experiment. Foundations of Physics. 1987, 17, 891–903. [Google Scholar] [CrossRef]
- Don, H. Who invented the Copenhagen Interpretation? A study in mythology. Philosophy of Science 2004, 71, 669–682. [Google Scholar]
- Ma, X.; Kofler, J.; Zeilinger, A. Delayed-choice gedanken experiments and their realizations. Reviews of Modern Physics. 88 (1): 015005. arXiv:1407.2930. 2016.
- Castelvecchi, D. Light waves squeezed through 'slits in time'. Nature 2023, 616, 230. [Google Scholar] [CrossRef] [PubMed]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).