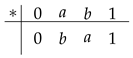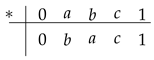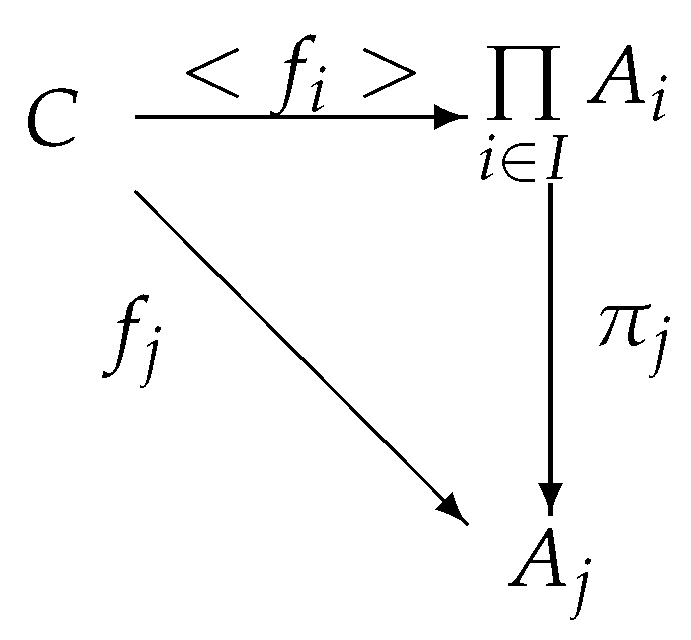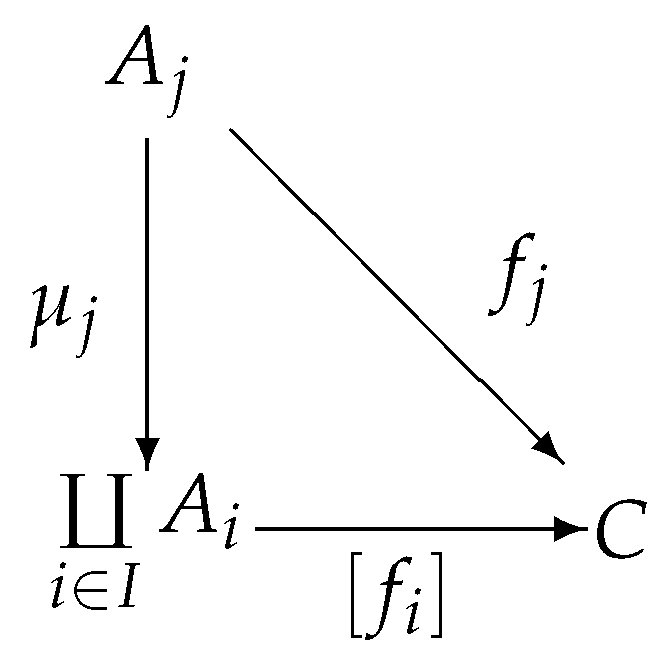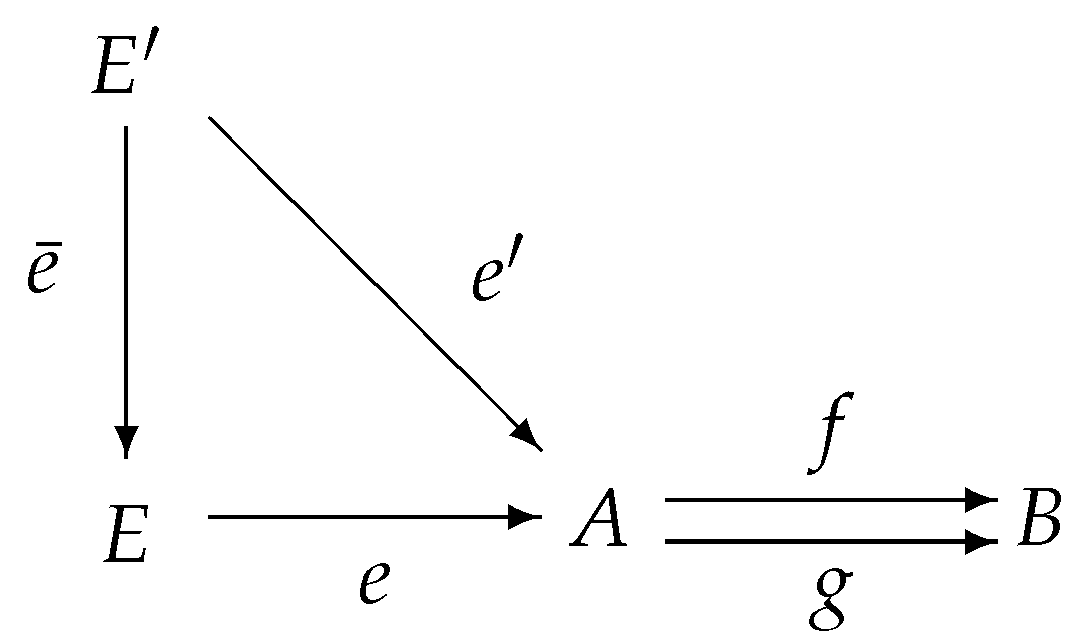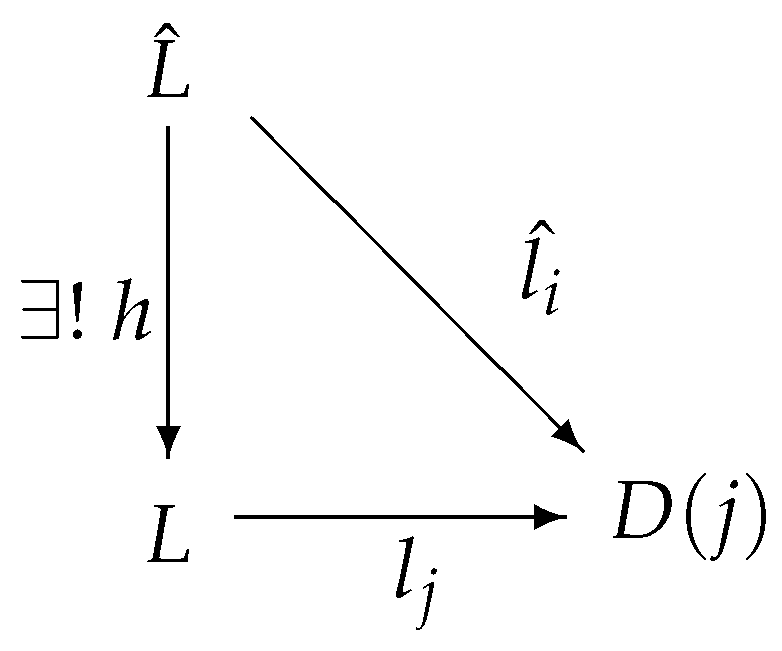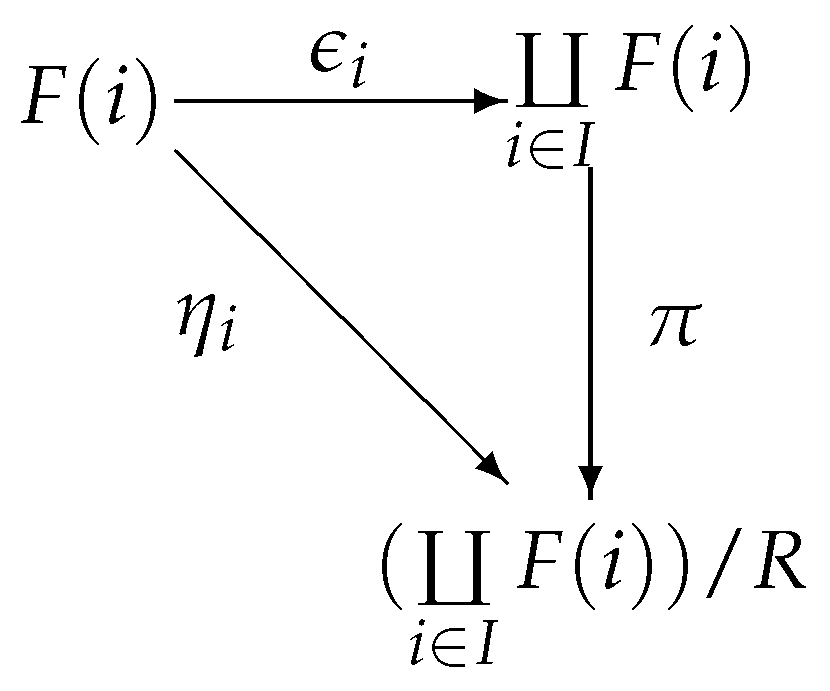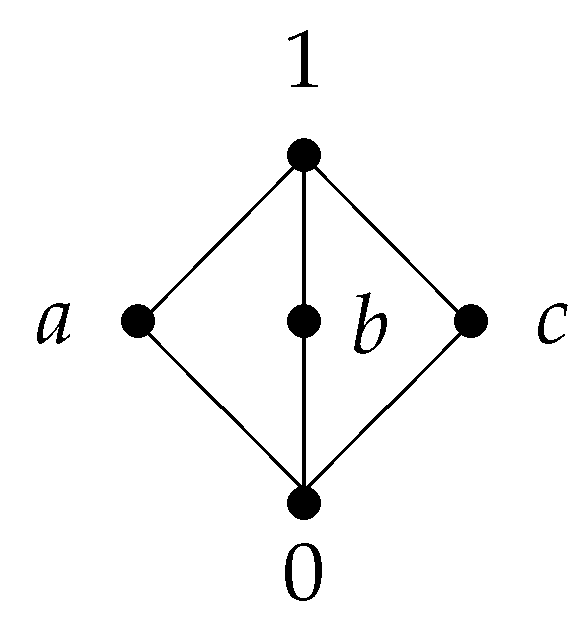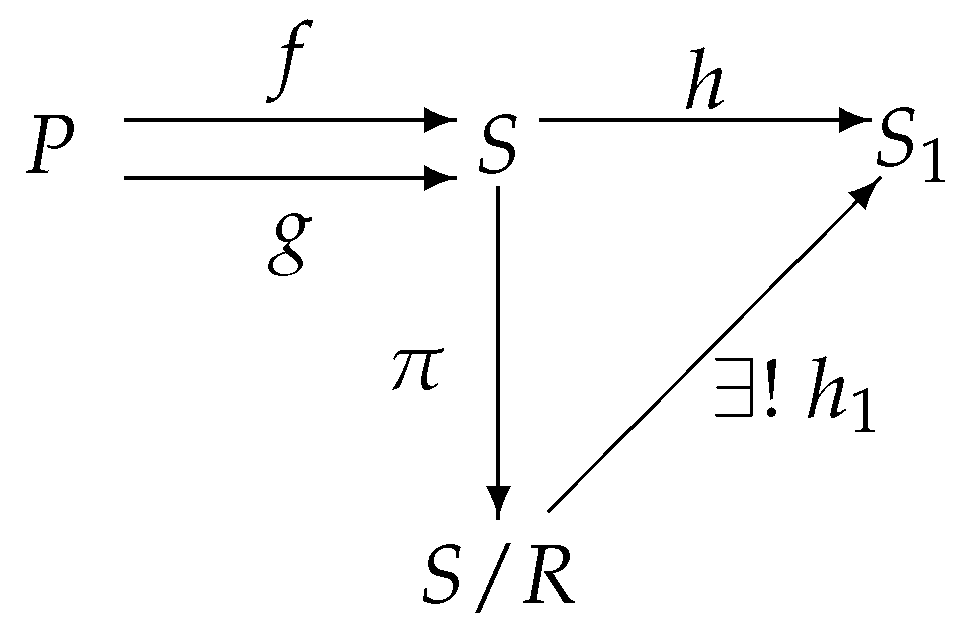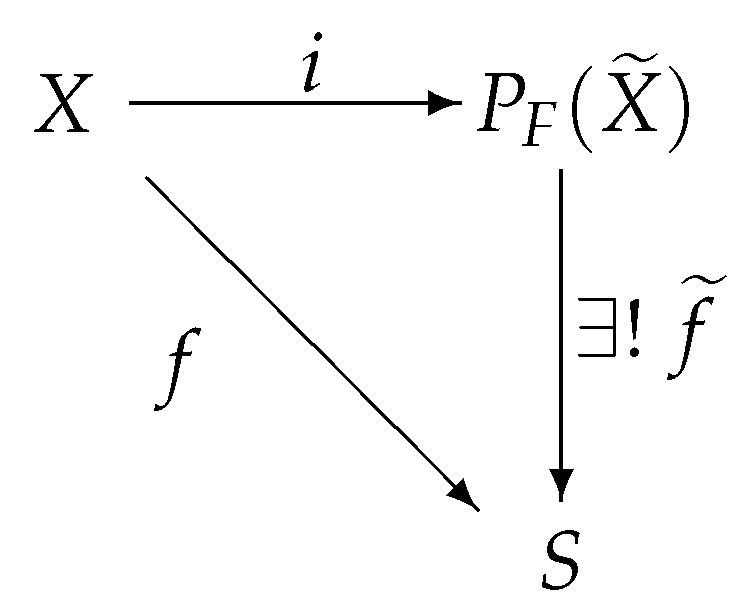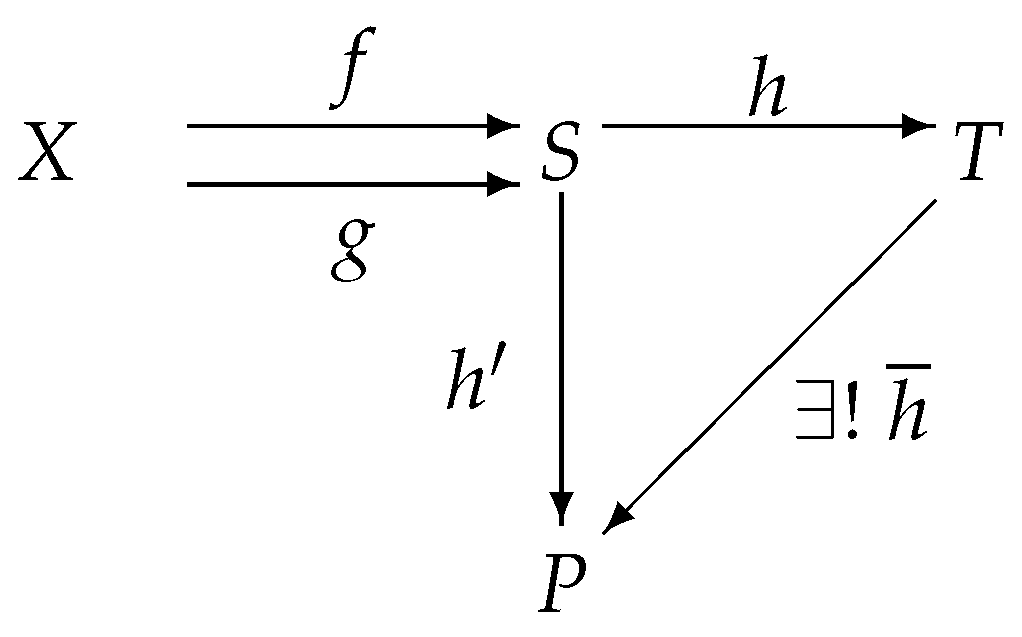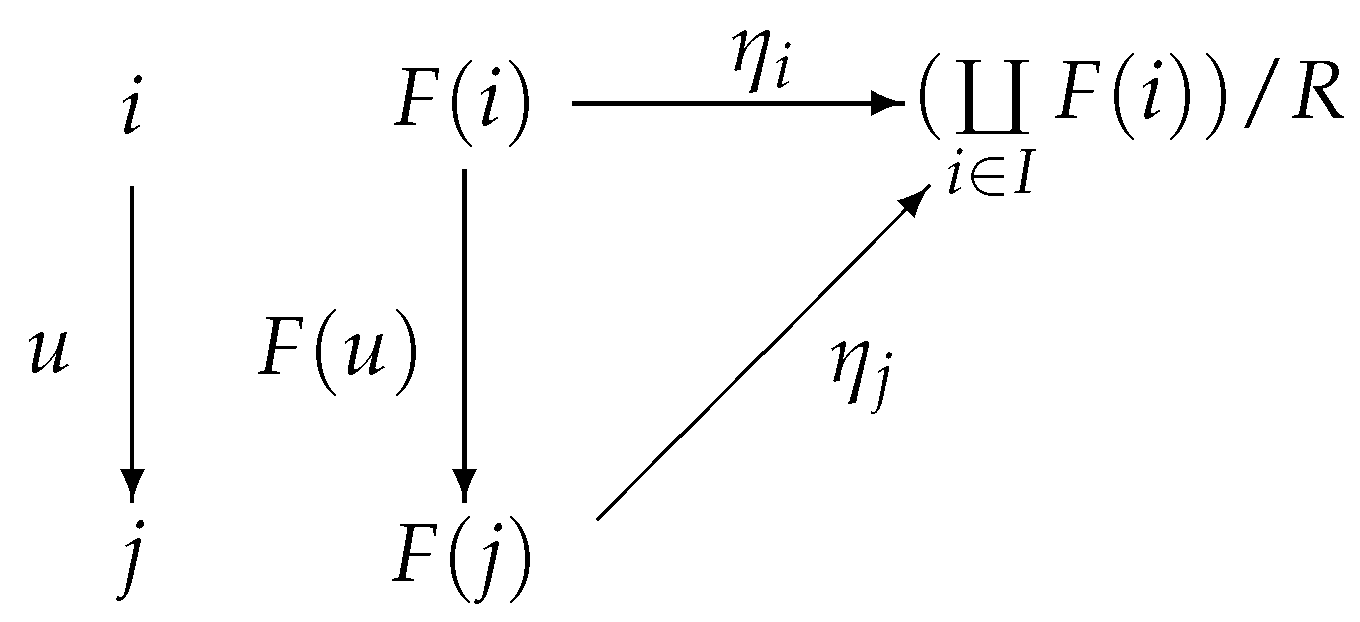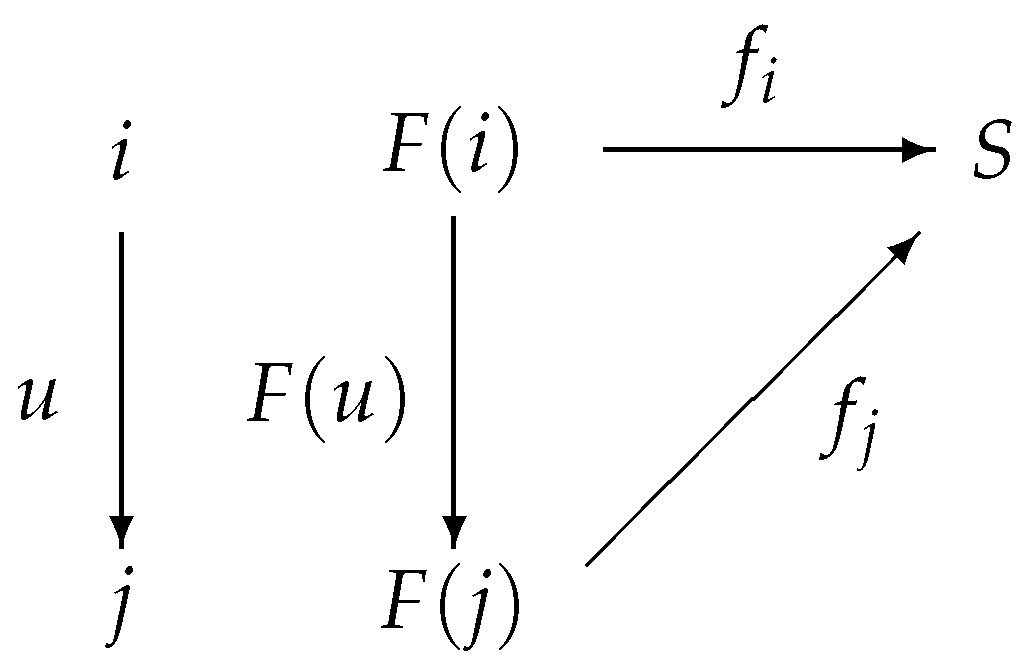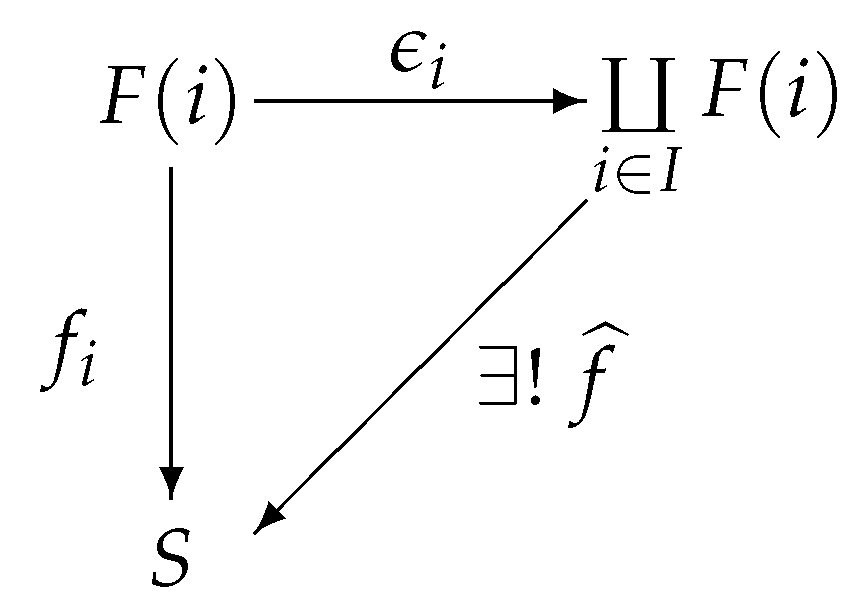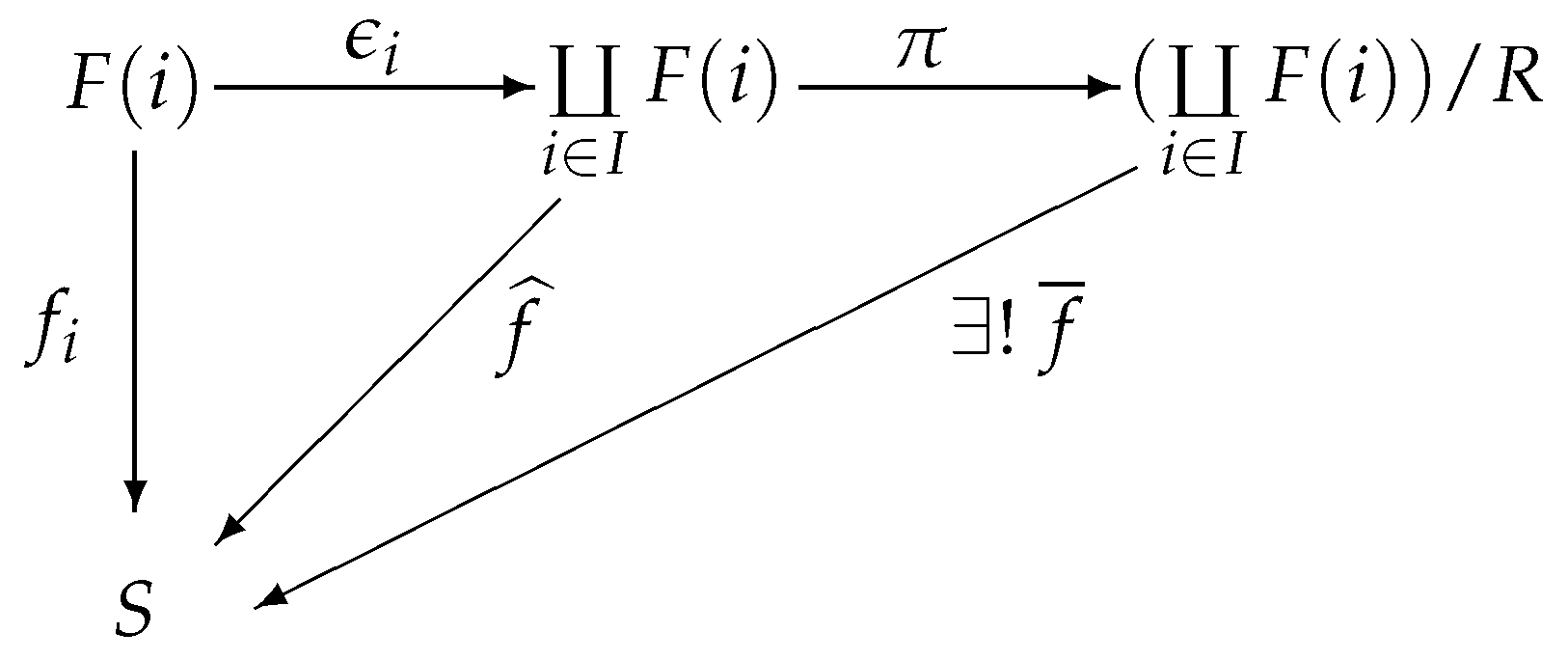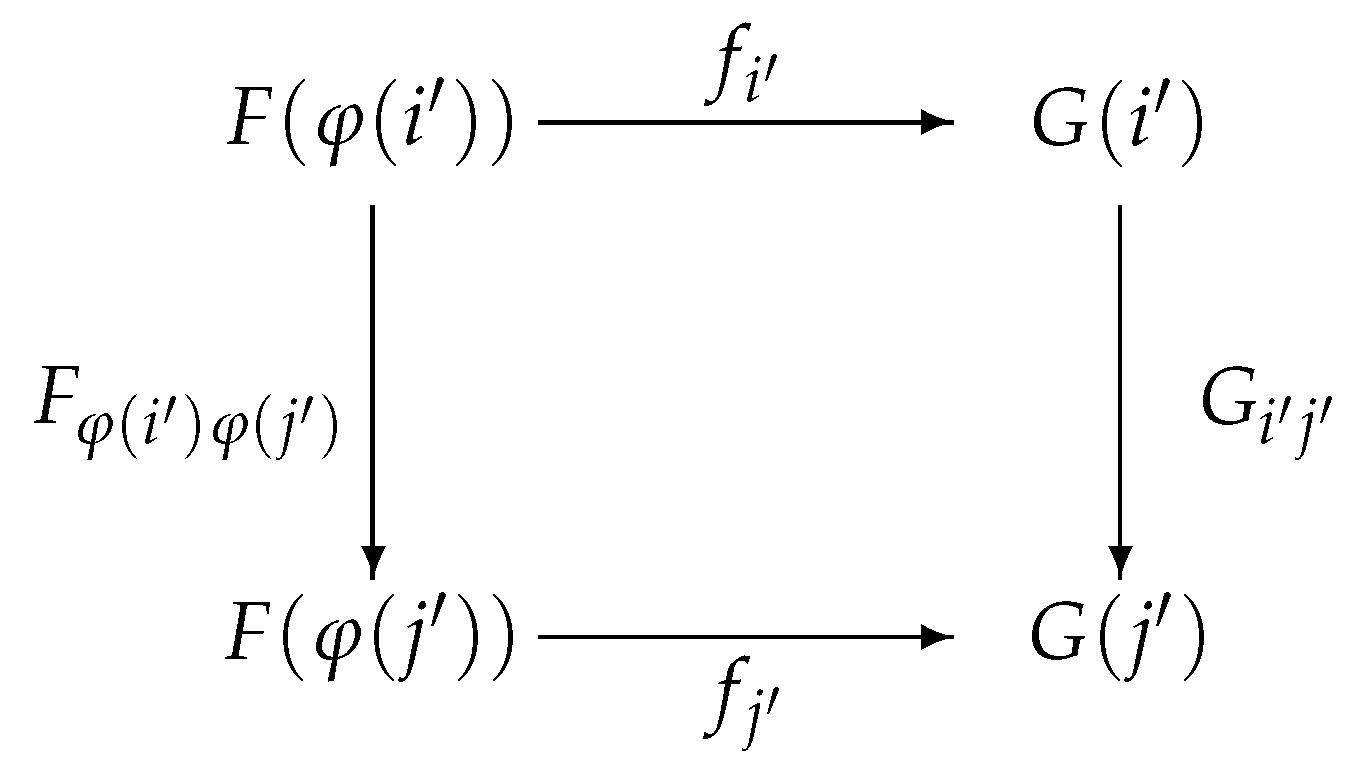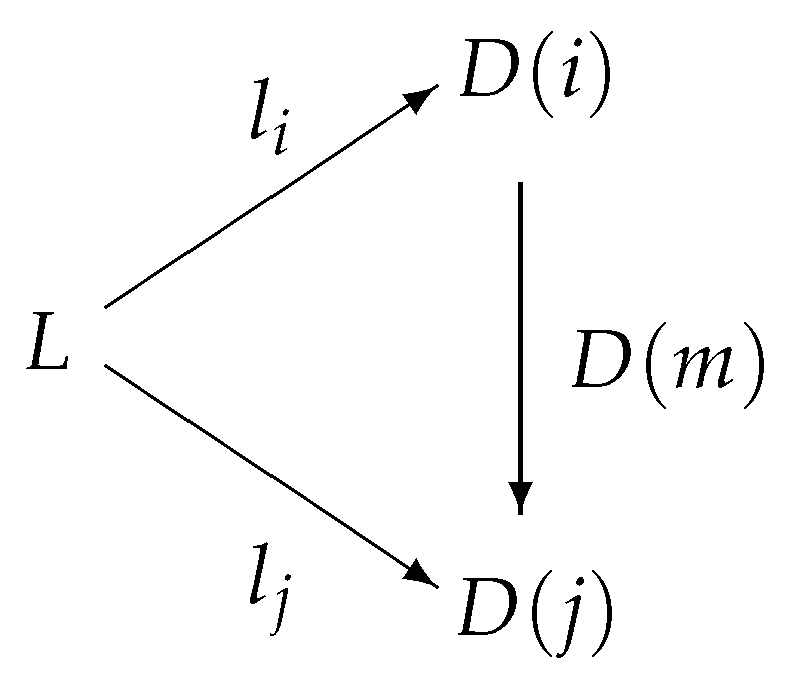Algebraic Properties of Category of Involutive M-Semilattices and Its Limits

1. Introduction

Quantale was proposed by Mulvey in 1986. The term quantale was coined as a combination of quantum logic and locale by Mulvey in [1]. Since quantale theory provides a powerful tool in studying non-commutative structure and a new mathematicial model for quantum mechanics. Hence, the theory of quantales has attracted the attention of many scholars. Quantale theory has a wide range of applications, especially in studying non-commutative structures [2], linear logic [3,4,5], C*-algebras [6], topological space [7,8,9], category [10,11,12], roughness theory [13], and so on. A systematic introduction of quantale theory can be found in [14] written by Rosenthal in 1990.

The m-semilattices is an important related structure of quantale. Rosenthal has proved that each coherent quantale is isomorphic to a quantale consisting of all ∨-semilattice ideals of an m-semilattice with a top element. Since m-semilattices connect the structures of ∨-semilattices with the multiplications of semigroups, hence m-semilattices can be regarded as generalizations of residual lattices, lattice-ordered semigroups, quantales and frames. The m-semilattices theory has aroused great interests of many scholars. In [15], By using the fuzzy set method, the concept of (prime) idals of an m-semilattice was introduced. Equivalent characterzations of (prime) ideals and (prime) ideas were given. In [16], Zhou and Zhao proposed the congruences induced by fuzzy (prime) ideals of an m-semilattice, studied the properties of the upper (lower) rough fuzzy approximation operators with respect to these congruence, and introduced the notions of rough fuzzy (prime) ideal of m-semilattices. In [17], the minmal neighborthood approximation operator on m-semilattice was studied and introduce the definition of fuzzy rought sets based on fuzzy coverings of m-semilattices. In [18], Su and Zhao introduced the concept of filers in m-semilattice and the filer topology on m-semilattices was constructed. A series of properties of filters spaces were studied. In [19], Pan and Han proved that the category of coheren quantales is a reflective subcategory of the category of m-semilattices. Based on the definition of m-semilattices, the concept of involutive m-semilattices was given. A series of important properties of involutive m-semilattices were studied and proved that the category of involutive m-semilattices is complete ([20]). In [21], The definiton of generalized M-P inverse of m-semilattice matrix was introduced. The necessary and sufficient condition for the existence of generalized M-P inverse of m-semilattice matrix was obtained. There are also some scholars who have provided different definitions of m-semilattices from various research backgrounds([22,23,24,25]).

The category theory provides a new language that affords economy of thought and expression as well as allowing easier communication among investigators in different areas. The algebric properties and limit structures of a category are important research focuses. If the algebraic properties of a category are proven and its limit structures are provided, then many categorical properties are naturally hold. This paper researches the algebraic properties of the category of involutive m-semilattices, as well as the structures of colimit, direct limit, and inverse limit. In the following, some simple concepts of category theory are referred to references [26].

This paper is organized as follows. In section 1, we show some basic concepts and results neeed in this article. In section 2, the concepts of nucleus and congruence are introduced. We prove that the category of involutive m-semilattices is algebraic. In section 3, we discuss the structure of coproduct and colimit in the category of involutive m-semilattices. In section 4, we study the inverse limit and direct limit in the category of involutive m-semilattices. The properties between inverse limits are discussed.

2. Preliminaries

Definition 1

([20]). Let$(S,\vee )$ be a ∨-semilattice, $(S,·)$ be a semigroup, and * is a unary operation on S satisfying:

(1) $a·(b\vee c)=(a·b)\vee (a·c),(b\vee c)·a=(b·a)\vee (c·a)$ for all $a,b\in S$.

(2) $a^{**}=a$ for all $a\in S$.

(3) ${(a·b)}^{*}=b^{*}·a^{*}$ for all $a,b\in S$.

(4) ${(a\vee b)}^{*}=a^{*}\vee b^{*}$ for all $a,b\in S$.

(5) There is a maximum element in S.

Then $(S,\vee ,·,*)$ is called an involutive m-semilattice.

Example 1.

(1) Let $(B,\wedge ,\vee ,\neg )$ be a Boolean algebra. We define a semigroup multiplication · on B and an involution operation * on B as follows

$$\forall a,b\in S,a·b=a\wedge b,a^{*}=a.$$

It is easy to verify that $(B,\vee ,·,*)$ is an involutive m-semilattice.

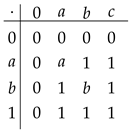
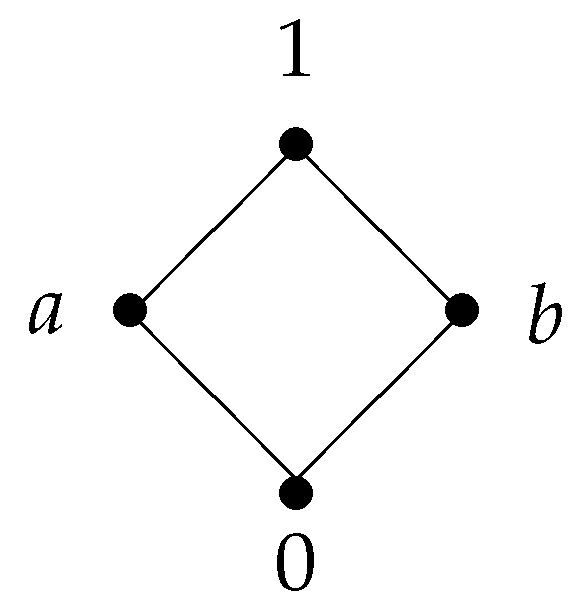
(2) Let $S=\{0,a,b,1\}$ be a lattice determined by Figure 1. A semigroup multplication on S and an involution operation on S are detemined by the tables below.

It can be verified that $(S,·,*)$ is an involutive m-semilattice.

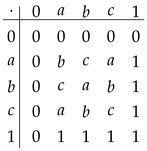
(3) Let $S=\{0,a,b,c,1\}$ be a lattice determined by Figure 2. A semigroup multplication on S and an involution operation on S are detemined by the tables below.

Then $(S,·,*)$ be an involutive m-semilattice.

Definition 2

([20]). Let $S_1$ and $S_2$ be two involutive m-semiattices. A mapping $f:S_1\to S_2$ is said to be involutive m-semilattice homomorphism if satisfying:

(1) $f(a·b)=f\left(a\right)·f\left(b\right)$;

(2) $f(a\vee b)=f\left(a\right)\vee f\left(b\right)$;

(3) $f\left(a^{*}\right)={\left(f\left(a\right)\right)}^{*}$.

Definition 3

([26]). A category is a quintuple $\mathcal{C}=(\mathcal{O},\mathcal{M},dom,cod,\circ )$ where

(1) $\mathcal{O}$ is a class whose members are called $\mathcal{C}$-objects,

(2) $\mathcal{M}$ is a class whose members are called $\mathcal{C}$-morphisms,

(3) $dom$ and $cod$ are functions from $\mathcal{M}$ to $\mathcal{O}$ ($dom\left(f\right)$) is called the domain of f and $cod\left(f\right)$ is called the codomain of f,

(4) ∘ is a function from $D=\left\{\right(f,g\left)\right|f,g\in \mathcal{M},dom\left(f\right)=cod\left(g\right)\}$ into $\mathcal{M}$, called the composition law of $\mathcal{C}(\circ (f,g\left)\right)$ is usually written $f\circ g$ and we say that $f\circ g$ is defined if and only if c$(f,g)\in D$; such that the following condition are satisfied:

(i) Matching Condition: If $f\circ g$ is defined, then $dom(f\circ g)=dom\left(g\right)$ and $cod(f\circ g)=cod\left(f\right)$;

(ii) Associativity Condition: If $f\circ g$ and $h\circ f$ are defined, then $h\circ (f\circ g)=(h\circ f)\circ g$;

(iii) Identity Existence Condition: For each $\mathcal{C}$-object A there exists a $\mathcal{C}$-morphism e such that $dom\left(e\right)=A=cod\left(e\right)$ and

(a) $f\circ e=f$ whenever $f\circ e$ is defined, and

(b) $e\circ g=g$ whenever $e\circ g$ is defined.

(iv) Smallness of Morphism Class Condition: For any pair $(A,B)$ of $\mathcal{C}$-object, the class

$ho{m}_{\mathcal{C}}(A,B)=\left\{f\right|f\in \mathcal{M},dom\left(f\right)=A$ and $cod\left(f\right)=B\}$

is a set.

For a give category $\mathcal{C}$, the class of $\mathcal{C}$-objects will be denonted by $Ob\left(\mathcal{C}\right)$, whereas, $Mor\left(\mathcal{C}\right)$ will stand for the class of $\mathcal{C}$-morphisms.

Example 2

([26]). The category Set whose class of objects is the class of all sets; whose morphisms sets $hom(A,B)$ are all functions from A to B, and whose composition law is the usual composition of functions. Set is commonly called the category of sets.

Definition 4

([26]). A category $\mathcal{C}$ is said to be:

(1) small provided that $\mathcal{C}$ is a set;

(2) discrete provided that all of its morphisms are identities;

(3) connected provided that for each pair $(A,B)$ of $\mathcal{C}$-objects, $ho{m}_{\mathcal{C}}(A,B)\ne \varnothing$.

Definition 5

([26]). Let $\mathcal{C}$ and $\mathcal{D}$ be categories, A functor from $\mathcal{C}$ to $\mathcal{D}$ is a triple $(\mathcal{D},F,\mathcal{D})$ where is a function from the class of morphisms of to the class of morphisms of $\mathcal{D}$ (i.e., $F:Mor\left(\mathcal{C}\right)\to Mor\left(\mathcal{D}\right))$ satisfying the following conditions:

(1) F preserves identities, i.e., if e is a $\mathcal{D}$-identity, then $F\left(e\right)$ is a $\mathcal{D}$-identity.

(2) F preserves composition; $F(f\circ g)=F\left(f\right)\circ F\left(g\right)$, i.e., whenever $dom\left(f\right)=cod\left(g\right)$, then $dom\left(F\right(f\left)\right)=cod\left(F\right(g\left)\right)$ and the above equality holds.

For any concrete category $\mathcal{C}$, there is a functor $U:\mathcal{C}\to Set$ that assigns to any object A, the underlying set $U\left(A\right)$ and to any morphism, the corresponding function on the underlying sets. U is called the forgetful functor on $\mathcal{C}$.

Definition 6

([26]). A product of a family ${\left(A_i\right)}_{i\in I}$ of $\mathcal{C}$-objects is a pair $(\prod _{i\in I}{A}_i,{\left(\pi \right)}_{i\in I})$ satisfying the following properties:

(1) $\prod _{i\in I}{A}_i$ is a $\mathcal{C}$-object.

(2) for each $j\in J$, ${\pi }_j:\prod _{i\in I}{A}_i\to A_j$ is a $\mathcal{C}$-morphism (called the projection from $\prod _{i\in I}{A}_i$ to $A_j$).

(3) for each pair $(C,{\left(f_i\right)}_{i\in I})$, (where C is a $\mathcal{C}$-object and for each $j\in J$, $f_j:C\to \prod _{i\in I}{A}_i$) there exists a unique $\mathcal{C}$-morphism $<f_i>:C\to \prod _{i\in I}{A}_i$ such that for each $j\in J$, the triangle

Figure 3.

Figure 3.

commutes.

Definition 7

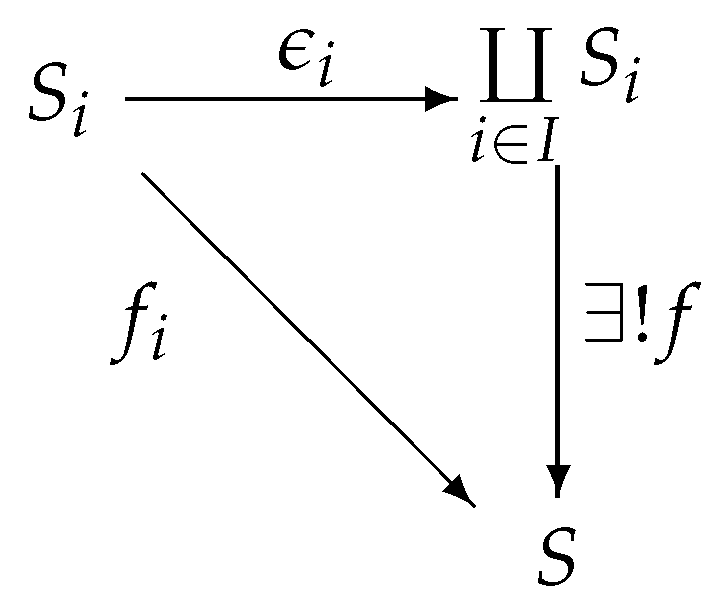
([26]). A coproduct of a family ${\left(A_i\right)}_{i\in I}$ of $\mathcal{C}$-objects is a pair $({\left({\mu }_i\right)}_{i\in I},\coprod _{i\in I}{A}_i)$ satisfying the following properties:

(1) $\coprod _{i\in I}{A}_i$ is a $\mathcal{C}$-object.

(2) For each $j\in J$, ${\mu }_j:A_j\to \coprod _{i\in I}{A}_i$ is a $\mathcal{C}$-morphism (called the injection from$A_j$ to $\coprod _{i\in I}{A}_i$).

(3) For each pair $({\left(f_i\right)}_{i\in I},C)$, (where C is a $\mathcal{C}$-object and for each $j\in J$, $f_j:A_j\to C$) there exists a unique $\mathcal{C}$-morphism $\left[f_i\right]:\coprod _{i\in I}{A}_i\to C$ such that for each $j\in J$, the triangle

Figure 4.

Figure 4.

commutes.

Definition 8

([26]). Let $A\stackrel{f}{\underset{g}{\rightrightarrows }}B$ be a pair of $\mathcal{C}$-morphisms. A pair $(E,e)$ is called an equalizer in $\mathcal{C}$ of f and g provided that the following hold:

(1) $e:E\rightrightarrows A$ is a $\mathcal{C}$-morphism;

(2) $f\circ e=g\circ e$;

(3) For any $\mathcal{C}$-morphism $e^{\prime }:E^{\prime }\to A$ such that $f\circ e^{\prime }=g\circ e^{\prime }$, there exists a unique $\mathcal{C}$-morphism $\overline{e}:E^{\prime }\to E$ such that the triangle

Figure 5.

Figure 5.

commutes.

Dually: If $c:B\to \mathcal{C}$, then $(c,\mathcal{C})$ is called a coequalizer in $\mathcal{C}$ of a pair $A\stackrel{f}{\underset{g}{\rightrightarrows }}B$ if and only if $c\circ f=c\circ g$ and each morphism $c^{\prime }$ with the property that $c^{\prime }\circ f=c^{\prime }\circ g$ can be uniquely factored through c.

Definition 9

([26]). A category $\mathcal{C}$ is called algebraic provied that is satisfies the following conditions:

(1) The category $\mathcal{C}$ has coequalizers;

(2) The forgetful functor $U:\mathcal{C}\to Set$ has a left adjoint;

(3) The forgetful functor $U:\mathcal{C}\to Set$ preserves and reflects regular epimorphisms.

3. The Category of Involutive M-Semilattices is Algebraic

Definition 10.

Let S be an involutive m-semiattices. A closure (coclosure) operator is an order preserving increasing (decreasing), idempotent map $j:S\to S$. If j is a closure (coclosure) operator on S, then $a\le j\left(b\right)\left(j\right(a)\le b)$ if and only if $j\left(a\right)\le j\left(b\right)$ for all $a,b\in S$.

Definition 11.

Let S be an involutive m-semiattices. A involutive m-semilattice nucleus on S is a closure operator j such that $j\left(a\right)·j\left(b\right)\le j(a·b)$ and $j\left(a^{*}\right)={\left(j\left(a\right)\right)}^{*}$ for all $a,b\in S$. Let $N\left(S\right)$ denote the set of all involutive m-semilattice nuclei on S.

Lemma 1.

Let j is an involutive m-semilattice nucleus on S, then $j(a·b)=j(a·j(b\left)\right)=j\left(j\right(a)·b)=j\left(j\right(a\left)j\right(b\left)\right)$ for all $a,b\in S$.

Definition 12.

Let S be an involutive m-semilattice with a maximum element 1. $\forall j\in N\left(S\right)$.

(1) j is right-sided(left-sided) if and only if $j(a·1)=j\left(a\right)$ for all $a\in S$.

(2) j is commutative if and only if $j(a·b)=j(b·a)$ for all $a,b\in S$.

(3) j is idmpotent if and only if $j\left(a^2\right)=j\left(a\right)$ for all $a\in S$.

(4) Let $S_j$ be the set of all fixed points of j, then $S_j=\{a\in S|j\left(a\right)=a\}$ is called a quotient of S.

Theorem 1.

Let S be an involutive m-semilattice, $\forall j\in N\left(S\right)$, then

(1) j is right-sided(left-sided) if and only if $S_j$ is right-sided(left-sided).

(2) j is commutative if and only if $S_j$ is commutative.

(3) j is idmpotent if and only if $S_j$ is idmpotent.

Proof. 

It is easy to be verified by Definition 11 and Lemma 1. □

Definition 13.

Let S be an involutive m-semilattice and the relation $R\subseteq S\times S$ satisfying:

(1) $(a,b),(c,d)\in R$ implies $(a\vee c,b\vee d)\in R$ for all $a,b,c,d\in S$;

(2) $(a,b),(c,d)\in R$ implies $(a·c,b·d)\in R$ for all $a,b,c,d\in S$;

(3) If $(a,b)\in R$, then $(a^{*},b^{*})\in R$.

Then R is called an involutive m-semilattice congruence on S.

For any $x\in S$, let ${\left[x\right]}_R$ denote the congruence class of x, and $Con\left(S\right)$ denote the set of all congruences on S. Then $Con\left(S\right)$ is a complete lattice with respect to the inclusion order.

Theorem 2.

Let S be an involutive m-semilattice and j be a nucleus on S. Then $(S_j,{\vee }_j,{·}_j,{*}_j)$ is an involutive m-semilattice and $j:S\to S_j$ is an involutive m-semilattice homomorphism, where $\forall a,b\in S_j$, $a{·}_{j}b=j(a·b),a{\vee }_{j}b=j(a\vee b),a^{{*}_j}=j\left(a^{*}\right)$.

Proof. 

It is easy to prove that the three operations mentioned above are well-defined and $(S_j,{\vee }_j)$ is a join semilattice with a maximum element.

We will show that $(S_j,{\vee }_j,{·}_j,{*}_j)$ is an involutive m-semilattice. For any $a,b\in S$, by the Definition of ${·}_j$ and Lemma 1, we have $\left(a{·}_{j}b\right){·}_{j}c=j(a·b){·}_{j}c=j(j(a·b)·c)=j((a·b)·j\left(c\right))=j(a·(b·j\left(c\right)))=j(a·(j\left(b\right)·j\left(c\right)))=j(a·\left(b{·}_{j}c\right))=a{·}_j\left(b{·}_{j}c\right)$. Thus the associativity of ${·}_j$ is valid.

Next, we will show that the distributive law is valid. For any $a,b,c\in S_j$, then

(1) $a{·}_j\left(b{\vee }_{j}c\right)\ge \left(a{·}_{j}b\right){\vee }_j\left(a{·}_{j}c\right)$.

(2) by Lemma 1, we have $a{·}_j\left(b{\vee }_{j}c\right)=j(a·j(b\vee c))=j(a·(b\vee c))=j((a·b)\vee (c·d))\le j(j(a·b)\vee j(a·c))=j(\left(a{·}_{j}b\right)\vee \left(a{·}_{j}c\right))=\left(a{·}_{j}b\right){\vee }_j\left(a{·}_{j}c\right)$.

Hence, $a{·}_j\left(b{\vee }_{j}c\right)=\left(a{·}_{j}b\right){\vee }_j\left(a{·}_{j}c\right)$. Similarly, it can be proven that the right distributive law $\left(b{\vee }_{j}c\right)·a_j=\left(b{·}_{j}a\right){\vee }_j\left(c{·}_{j}a\right)$ is hold.

Finally, we will prove that ${*}_j$ is an involutive operation on $S_j$.

For any $a,b\in S_j$, then

(1) ${\left(a^{{*}_j}\right)}^{{*}_j}={\left(j\left(a^{*}\right)\right)}^{{*}_j}={\left({\left(j\left(a\right)\right)}^{*}\right)}^{{*}_j}=j{\left({\left(j\left(a\right)\right)}^{*}\right)}^{*})=j\left({\left(j\left(a\right)\right)}^{*}\right)={\left(j\left(j\left(a\right)\right)\right)}^{*}={\left(j\left(a\right)\right)}^{*}=j\left(a^{*}\right)=a^{{*}_j}$.

(2) ${\left(a{·}_{j}b\right)}^{{*}_j}={\left(j(a·b)\right)}^{{*}_j}=j\left({\left(j(a·b)\right)}^{*}\right)=j\left(j\left({(a·b)}^{*}\right)\right)=j\left(j(b^{*}·a^{*})\right)=j(b^{*}·a^{*})$. By the Lemma 1 it follows that $b^{{*}_j}{·}_j{a}^{{*}_j}=j(b^{{*}_j}·a^{{*}_j})=j(j\left(b^{*}\right)·j\left(a^{*}\right))=j(b^{*}·a^{*})$. Thus ${\left(a{·}_{j}b\right)}^{{*}_j}=b^{{*}_j}{·}_j{a}^{{*}_j}$.

(3) ${\left(a{\vee }_{j}b\right)}^{{*}_j}={\left(j(a\vee b)\right)}^{{*}_j}=j\left({\left(j(a\vee b)\right)}^{*}\right)=j(j\left(a^{*}\right)\vee j\left(b^{*}\right))=j\left(a^{*}\right){\vee }_{j}j\left(b^{{*}_j}\right)=a^{{*}_j}{\vee }_j{b}^{{*}_j}$.

Therefore ${*}_j$ is an is an involutive operation on $S_j$.

For any $a,b\in S$, then

(1) $j(a\vee b)\le j(j\left(a\right)\vee j\left(b\right))=j\left(a\right){\vee }_{j}j\left(b\right)$. By the definition of j it follows that $j(a\vee b)=j\left(j(a\vee b)\right)\ge j(j\left(a\right)\vee j\left(b\right))=j\left(a\right){\vee }_{j}j\left(b\right)$. Thus $j(a\vee b)=j\left(a\right){\vee }_{j}j\left(b\right)$.

(2) From Lemma 1 it follows that $j\left(a\right){·}_{j}j\left(b\right)=j(j\left(a\right)·j\left(b\right))=j(a·b)$, thus j preserves operation ${·}_j$.

(3) $j\left(a^{*}\right)=a^{{*}_j}\le {\left(j\left(a\right)\right)}^{{*}_j}$, but ${\left(j\left(a\right)\right)}^{{*}_j}=j\left({\left(j\left(a\right)\right)}^{*}\right)\ge j\left(a^{*}\right)$, thus $j\left(a^{*}\right)={\left(j\left(a\right)\right)}^{{*}_j}$.

From (1),(2),(3) we know that mapping $j:S\to S_j$ is an involutive m-semilattice homomorphism. □

Theorem 3.

Let S be an involutive m-semilattice. $\forall j\in N\left(S\right)$, an equivalence R is defined as follows: $(a,b)\in R$ if and only if $j\left(a\right)=j\left(b\right)$ for all $a,b\in S$. Then R is a congruence on S.

Theorem 4.

Let S be an involutive m-semilattice, and R is a congrence of S. For all $a,b,c\in S$, define $\left[a\right]\le \left[b\right]\iff [a\vee b]=\left[b\right]$; $\left[a\right]\vee \left[b\right]=[a\vee b]$; $\left[a\right]·\left[b\right]=[a·b]$; ${\left(\left[a\right]\right)}^{*}=\left[a^{*}\right]$. The mapping $\pi :S\to S/R$ such that $\pi \left(a\right)=\left[a\right]$. Then $(S/R,·,*)$ is an involutive m-semilattice, and the mapping π is an involutive m-semilattice homomorphism.

Proof. 

We first show that ≤ is a parital order on $S/R$.

For any $\left[a\right],\left[b\right],\left[c\right]\in S/R$, then

(1) It’s clear that $\left[a\right]\le \left[a\right]$.

(2) If $\left[a\right]\le \left[b\right]$ and $\left[b\right]\le \left[a\right]$, then $[a\vee b]=\left[b\right]$ and $[b\vee a]=\left[a\right]$, thus $\left[a\right]=\left[b\right]$.

(3) If $\left[a\right]\le \left[b\right]$ and $\left[b\right]\le \left[c\right]$, then $[a\vee c]=[a\vee (b\vee c\left)\right]=\left[\right(a\vee b)\vee (b\vee c\left)\right]=[b\vee c]=\left[c\right]$, i.e., $\left[a\right]\le \left[c\right]$.

It is easy verified that the above operations $·,\vee ,$and * are well defined, and $(S/R,\vee )$ is a semilattice with a maximum element $\left[1\right]$.

Next, for any $\left[a\right],\left[b\right],\left[c\right]\in S/R$, we have

(1) $\left(\right[a]·[b\left]\right)·\left[c\right]=[a·b]·\left[c\right]=\left[\right(a·b)·c)]=[a·(b·c)]=[a]·(\left[b\right]·\left[c\right])$.

(2) $\left[a\right]·\left(\right[b]\vee [c\left]\right)=\left[a\right]·[b\vee c]=[a·(b\vee c\left)\right]=\left[\right(a·b)\vee (a·c\left)\right]=[a·b]\vee [a·c]=\left(\right[a]·[b\left]\right)\vee \left(\right[a]·[c\left]\right)$. Similarly, it can be proven that $\left(\right[b]\vee [c\left]\right)·\left[a\right]=\left(\right[b]·[a\left]\right)\vee \left(\right[c]·[a\left]\right)$ also hold.

(3) we verify that * is an involution operation on $S/R$.

(i) ${\left(\left[a\right]\right)}^{**}=\left[a^{**}\right]=\left[a^{*}\right]={\left[a\right]}^{*}$.

(ii) ${\left([a·b]\right)}^{*}=\left[{(a·b)}^{*}\right]=[b^{*}·a^{*}]={\left(\left[b\right]\right)}^{*}·{\left(\left[a\right]\right)}^{*}$.

(iii) ${\left([a\vee b]\right)}^{*}=\left[{(a\vee b)}^{*}\right]=[a^{*}\vee b^{*}]={\left(\left[a\right]\right)}^{*}\vee {\left(\left[b\right]\right)}^{*}$.

Therefor $(S/R,·,*)$ is an involutive m-semilattice.

Finally, we will prove that the mapping $\pi :S\to S/R$ is an involutive m-semilattice homomorphism.

For any $\left[a\right],\left[b\right]\in S/R$, then

(1) $\pi (a\vee b)=[a\vee b]=\left[a\right]\vee \left[b\right]=\pi \left[a\right]\vee \pi \left[b\right]$.

(2) $\pi (a·b)=[a·b]=\left[a\right]·\left[b\right]=\pi \left(a\right)·\pi \left(b\right)$.

(3) $\pi \left(a^{*}\right)=\left[a^{*}\right]={\left[a\right]}^{*}={\left[\pi \left(a\right)\right]}^{*}$. □

Definition 14.

Let $IMSLatt$ be the category whose objects are the involutive m-semilattices, and whose morphisms are the involutive m-semilattice homomorphisms. Obviously, the category $IMSLatt$ is a concrete category.

Lemma 2.

Let $f:S\to P$ be an involutive m-semilattice homomorphism, then $f^{-1}(△)=\{(x,y)\in S\times S|f\left(x\right)=f\left(y\right)\}$ is an involutive m-semilattice congrence on S.

Let S be an involutive m-semilattice, and R is a binary relation on S. There exists the smallest congrence containing R, which is the intersection all the involutive m-semilattice congrence containing R on S. We said this congrence is generated by R, denoted by $<R>$.

Theorem 5.

$IMSLatt$ has coequalizer.

Proof. 

Let S and P be two involutive m-semilattices, $f,g:S\to P$ be two involutive m-semilattice homomorphisms, and R is the smallest congrence, which contain $\left\{\right(f\left(a\right),g\left(a\right)|a\in P\}$.

Suppose that $\pi :S\to S/R$ is the canonical mapping, then the mapping $\pi$ is an involutive m-semilattice homomorphism by Theorem 4. We will show that $(\pi ,S/R)$ is the coequalier of f and g.

(1) Let $a\in P$, then $(\pi \circ f)\left(a\right))=\pi (f\left(a\right))=[f\left(a\right)]$ and $(\pi \circ g)\left(a\right))=\pi (g\left(a\right))=[g\left(a\right)]$. Since $\left(f\right(a),g(a\left)\right)\in R$, this imples that $\left[f\right(a\left)\right]=\left[g\right(a\left)\right]$, i.e., $\pi \circ f=\pi \circ g$.

(2) Let $h:S\to S_1$ be an involutive m-semilattice homomorphism such that $h\circ f=h\circ g$. Let $R_1={\left(h\right)}^{-1}(▵)$ and $▵=\left\{(x,x)\right|x\in S_1\}$. By the Lemma 2 it follows that $R_1$ is a congrence of S. $\forall a\in P$, then $h\left(f\right(a\left)\right)=h\left(g\right(a\left)\right)$. This implies that $(f\left(a\right),g\left(a\right))\in R_1$, thus $R\subseteq R_1$.

Define a mapping $h_1:S/R\to S$ such that $h_1\left(\left[a\right]\right)=h\left(a\right)$ for all $\left[a\right]\in S/R$. Let $(a,b)\in R$, then $(a,b)\in R_1$, i.e., $h_1\left(a\right)=h_1\left(b\right)$. This means that $h_1$ is well defined.

Let $\left[a\right],\left[b\right]\in S/R$, then

(1) $h_1(\left[a\right]·\left[b\right])=h_1\left([a·b]\right)=h(a·b)=h\left(a\right)·h\left(b\right)=h_1\left(\left[a\right]\right)·h_1\left(\left[b\right]\right)$.

(2) $h_1(\left[a\right]\vee \left[b\right])=h_1\left([a\vee b]\right)=h(a\vee b)=h\left(a\right)\vee h\left(b\right)=h_1\left(\left[a\right]\right)\vee h_1\left(\left[b\right]\right)$.

(3) $h_1\left({\left(\left[a\right]\right)}^{*}\right)=h_1\left(\left[a^{*}\right]\right)=h\left(a^{*}\right)={\left(h\left(a\right)\right)}^{*}={\left[h_1\left(\left[a\right]\right)\right]}^{*}$.

Hence the mapping $h_1:S/R\to S$ an involutive m-semilattice homomorphism.

Let $x\in S$, then $h_1\circ \pi \left(x\right)=h_1\left(\left[x\right]\right)=h\left(x\right)$, i.e., $h_1\circ \pi =h$. Thus Figure 6 commutes.

Let $h_2:S/R\to S$ such that $h_2\circ \pi =h$, then $h_2\left(\left[x\right]\right)=(h_2\circ \pi )\left(x\right)=(h_1\circ \pi )\left(x\right)=h_1\left(\left[x\right]\right)$, i.e., $h_2=h_1$. Therefore $(\pi ,S/R)$ is the coequalizer of f and g. □

The problem of free generation plays a crucial role in algebra, and free generation of some mathematical structures have been widely studied ([27,28]). Next, we will discuss the structure of free involutive m-semilattices in detail.

Let X be a set, use $\tilde{X}=\{x_1{x}_2\dots x_n|x_n\in X,n\in Z^{+}\}$ to denote the set of all finite strings composed of elements from X. A binary operation ★ is defined as follows:

$\forall x_1{x}_2\dots x_n,y_1{y}_2\dots y_m\in \tilde{X}$,

$(x_1{x}_2\dots x_n)★(y_1{y}_2\dots y_m)=x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m$.

It is easy to verify that the binary operation ★ satisfies associative law. $(\tilde{X},★)$ is called the free semigroup generated by the set X.

Let $P_F\left(\tilde{X}\right)$ denote the set of all finite subsets of the set $\tilde{X}$. Two binary operations are defined on the set $P_F\left(\tilde{X}\right)$ as follows: $\forall A,B\in P_F\left(\tilde{X}\right)$,

$A•B=\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B,n,m\in Z^{+}\}$,

$A^{*}=\{x_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A,n\in Z^{+}\}$.

Theorem 6.

The triple $(P_F\left(\tilde{X}\right),•,*)$ is an involutive m-semilattice with respect to the set inclusion order.

Proof. 

It is easy to prove that $((P_F\left(\tilde{X}\right),\subseteq )$ is a lattice.

For any $A,B,C\in P_F\left(\tilde{X}\right)$, then

(1) $A•(B\cup C)=(A•B)\cup (A•C)$ and $(B\cup C)•A=(B•A)\cup (C•A)$ are obviously valid.

(2) $(A•B)•C=\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\}•C$

$=\{(x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m)★(z_1{z}_2\dots z_s)|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m$

$\in B,z_1{z}_2\dots z_s\in C\}$

$=\{(x_1{x}_2\dots x_n)★(y_1{y}_2\dots y_m{z}_1{z}_2\dots z_s)|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m$

$\in B,z_1{z}_2\dots z_s\in C\}$

$=A•(B•C)$.

(3) ${\left(A^{*}\right)}^{*}={\left(\{x_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A\}\right)}^{*}=\{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\}=A$.

${(A•B)}^{*}={\left(\{x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\}\right)}^{*}$

$=\{y_m{y}_{m-1}\dots y_1{x}_n{x}_{n-1}\dots x_1|x_1{x}_2\dots x_n\in A,y_1{y}_2\dots y_m\in B\}$

$=\{y_m{y}_{m-1}\dots y_1{x}_n{x}_{n-1}\dots x_1|x_n{x}_{n-1}\dots x_1\in A^{*},y_m{y}_{m-1}\dots y_1\in B^{*}\}$

$=B^{*}•A^{*}$.

Obviously, ${(A\cup B)}^{*}=A^{*}\cup B^{*}$. From the above proof, it can be seen that $(P_F\left(\tilde{X}\right),•,*)$ is an involutive m-semilattice. □

Theorem 7.

There is a functor $P_F:Set\to IMSLatt$ which is left adjint to the forgetful functor $U:IMSLatt\to Set$.

Proof. 

Let X and Y be nonempty sets and $f:X\to Y$ be a mapping. By Theorem 6 it follows that $P_F\left(\tilde{X}\right)$ and $P_F\left(\tilde{Y}\right)$ are involutive m-semilattices. Define $P_F\left(f\right):P_F\left(\tilde{X}\right)\to P_F\left(\tilde{Y}\right)$ such that $P_F\left(f\right)\left(A\right)=\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$ for all $A\in P_F\left(\tilde{X}\right)$, then the mapping $P_F\left(f\right)$ is well defined.

Next, we will prove that the mapping $P_F\left(f\right)$ is an involutive m-semilattice homomorphism. For any $A,B\in P_F\left(\tilde{X}\right)$, then

(1) $P_F\left(f\right)(A\cup B)=\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\cup B\}$

$=\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A$ or $x_1{x}_2\dots x_n\in B\}$

$=P_F\left(f\right)\left(A\right)\cup P_F\left(f\right)\left(B\right)$.

Therefore, the mapping f preserves the union of sets.

(2) $P_F\left(f\right)(A•B)=\{f\left(x_1\right)\dots f\left(x_n\right)f\left(y_1\right)\dots f\left(y_m\right)|x_1{x}_2\dots x_n{y}_1{y}_2\dots y_m\in A•B\}$

$=\{f\left(x_1\right)\dots f\left(x_n\right)f\left(y_1\right)\dots f\left(y_m\right)|x_1\dots x_n\in A,y_1\dots y_m\in B\}$

$=\{f\left(x_1\right)\dots f\left(x_n\right)|x_1\dots x_n\in A\}$$•\{f\left(y_1\right)\dots f\left(y_m\right)|y_1\dots y_m\in B\}$

$=P_F\left(f\right)\left(A\right)•P_F\left(f\right)\left(B\right)$.

Therefore, the mapping $P_F\left(f\right)$ preserves the operation •.

(3) $P_F\left(f\right){\left(A\right)}^{*}=\{f\left(x_n\right)f\left(x_{n-1}\right)\dots f\left(x_1\right)|x_n{x}_{n-1}\dots x_1\in A^{*}\}$

$=\left\{{(f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right))}^{*}\right|x_1{x}_2\dots x_n\in A\}$

$={\left(\{f\left(x_1\right)f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\right)}^{*}$

$={\left(P_F\left(f\right)\left(A\right)\right)}^{*}$.

Hence, the mapping $P_F\left(f\right)$ preserves the involutive operation *.

From the above proof, it can be concluded that the mapping $P_F\left(f\right)$ is an involutive semilattice homomorphism.

Next, we will check $P_F:Set\to IMSLatt$ is a functor.

Define a mapping $i_X:X\to X$ such that $i_X\left(x\right)=x$ for all $x\in X$. For any $A\in P_F\left(\tilde{X}\right)$, then

(1) $P_F\left(i_X\right)\left(A\right)=\{i_X\left(x_1\right)i_X\left(x_2\right)\dots i_X\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$

$=\{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\}$

$=A$

$=i_{P_F\left(X\right)}\left(A\right)$.

This means that the functor $P_F$ preserves identity mappings.

(2) Let $f:X\to Y$, $g:Y\to Z$, then

$P_F(f\circ g)\left(A\right)=\{(f\circ g)\left(x_1\right)(f\circ g)\left(x_2\right)\dots (f\circ g)\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$

$=\left\{(f\circ g)(x_1{x}_2\dots x_n)\right|x_1{x}_2\dots x_n\in A\}$

$=\left\{f\left(g(x_1{x}_2\dots x_n)\right)\right|x_1{x}_2\dots x_n\in A\}$

$=\left\{f(g\left(x_1\right)g\left(x_2\right)\dots g\left(x_n\right))\right|x_1{x}_2\dots x_n\in A\}$

$=P_F\left(f\right)\left(\{g\left(x_1\right)g\left(x_2\right)\dots g\left(x_n\right)|x_1{x}_2\dots x_n\in A\}\right)$

$=(P_F\left(f\right)\circ P_F\left(g\right))\left(A\right).$

Thus the functor $P_F$ preservers composition of f and g.

Finally, we will prove that $P_F:Set\to IMSLatt$ is the left adjoint to the forgetful functor $U:IMSLatt\to Set$.

Let X be a non-empty set, define a mapping $i:X\to P_F\left(\tilde{X}\right)$ such that $i\left(x\right)=x$ for all $x\in X$. Let S be an involutive semilattice and mapping $f:X\to S$, we define a mapping $\tilde{f}:P_F\left(\tilde{X}\right)\to S$ such that $\tilde{f}\left(A\right)=\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_1\dots x_n\in A)\}$ for all $A\in P_F\left(\tilde{X}\right)$. Since $\{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_1\dots x_n\in A\left)\right\}$ is a finite set, then $\tilde{f}\left(A\right)\in S$. This show that the mapping $\tilde{f}$ is well defined.

For any $A,B\in P_F\left(\tilde{X}\right)$, then

(1) $\tilde{f}(A\cup B)=\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\cup B\}$

$=(\bigvee \{f\left(y_1\right)·f\left(y_2\right)\dots f\left(y_m\right)|y_1{y}_2\dots y_m\in A\})$

$\vee (\bigvee \{f\left(z_1\right)·f\left(z_2\right)\dots f\left(z_s\right)|z_1{z}_2\dots z_s\in B\})$

$=\tilde{f}\left(A\right)\vee \tilde{f}\left(B\right)$.

(2) $\tilde{f}(A•B)=\bigvee \{f\left(y_1\right)·f\left(y_2\right)\dots f\left(y_n\right)·f\left(z_1\right)·f\left(z_2\right)\dots f\left(z_s\right)|y_1{y}_2\dots y_m\in A,$

$z_1{z}_2\dots z_s\in B\left)\right\}$

$=(\bigvee \{f\left(y_1\right)·f\left(y_2\right)\dots f\left(y_m\right)|y_1{y}_1\dots y_m\in A\})$

$·(\bigvee \{f\left(z_1\right)·f\left(z_2\right)\dots f\left(z_s\right)|z_1{z}_2\dots z_s\in B\})$

$=\tilde{f}\left(A\right)·\tilde{f}\left(B\right)$.

(3) $\tilde{f}\left(A^{*}\right)=\bigvee \{f\left(x_n\right)·f\left(x_{n-1}\right)\dots f\left(x_1\right)|x_n{x}_{n-1}\dots x_1\in A^{*})\}$

$=\bigvee \left(\{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A)\right\}{)}^{*}$

$=(\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A)\}{)}^{*}$

$={\left(\tilde{f}\left(A\right)\right)}^{*}$.

Hence the mapping $P_F\left(f\right)$ is an involutive semilattices homomorphism.

For any $x\in X$, then $(\tilde{f}\circ i)\left(x\right)=\tilde{f}\left(\left\{x\right\}\right)=f\left(x\right)$, i.e., $\tilde{f}\circ i=f$, hence Figure 7 commutes.

Suppose that $\widetilde{f^{\prime }}:P_F\left(f\right)\to S$ is another homomorphism such that $\widetilde{f^{\prime }}\circ i=f$.

Then $\tilde{f}\left(\left\{x\right\}\right)=(\tilde{f}\circ i)\left(x\right)=f\left(x\right)=(\widetilde{f^{\prime }}\circ i)\left(x\right)=\widetilde{f^{\prime }}\left(\left\{x\right\}\right)$, i.e., $\tilde{f}\left(\left\{x\right\}\right)=\widetilde{f^{\prime }}\left(\left\{x\right\}\right)$.

For any $A\in P_F\left(\tilde{X}\right)$, then

$\tilde{f}\left(A\right)=\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$

$=\bigvee \{\widetilde{f^{\prime }}\left(\left\{x_1\right\}\right)·\widetilde{f^{\prime }}\left(\left\{x_2\right\}\right)\dots \widetilde{f^{\prime }}\left(\left\{x_n\right\}\right)|x_1{x}_2\dots x_n\in A\}$

$=\bigvee \left\{\widetilde{f^{\prime }}(\left\{x_1\right\}•\left\{x_2\right\}\dots •\left\{x_n\right\})\right|x_1{x}_2\dots x_n\in A\}$

$=\bigvee \left\{\widetilde{f^{\prime }}(x_1{x}_2\dots x_n)\right|x_1{x}_2\dots x_n\in A\}$

$=\widetilde{f^{\prime }}(\bigcup \{x_1{x}_2\dots x_n|x_1{x}_2\dots x_n\in A\})$

$=\widetilde{f^{\prime }}\left(A\right)$.

Thus $\tilde{f}=\widetilde{f^{\prime }}$. This means that $\tilde{f}$ is an unique involutive m-semilattice homomorphism, and satisfies the commutativity of Figure 7.

The above proof shows that the functor $P_F$ is left adjoint to the forgetful functor U. □

Definition 15

([26]). A morphism $f:A\to B$ is said to be a monmorphism in $\mathcal{C}$ provided that for all $\mathcal{C}$-morphisms h and k such that $f\circ h=f\circ k$, it follows that $h=k$ (i.e., f is left-cancellable with respect to composition in $\mathcal{C}$).

Dual: A morphism $f:A\to B$ is said to be a epimorphism in $\mathcal{C}$ provided that for all $\mathcal{C}$-morphisms h and k such that $h\circ f=k\circ f$, it follows that $h=k$ (i.e., f is right-cancellable with respect to composition in $\mathcal{C}$).

Every morphism in a concrete category that is an injective function on underlying sets is a monomorphism; Every morphism in a concrete category that is an surjective function on underlying sets is an epiomorphism.

Theorem 8.

In IMSLatt the monomorphisms are precisely the morphisms which are injective on the underlying sets and the epimorphisms are precisely the morphisms which are surjective on the underlying sets.

Proof. 

The proof is straightforward by Definition 15. □

Definition 16

([26]). If $e:E\to A$ is a $\mathcal{C}$-morphism, then e is called a regular monomorphism if and only if there are $\mathcal{C}$-morphisms f and g such that $(E,e)$ is the equalizer of f and g.

Dual: If $e:A\to E$ is a $\mathcal{C}$-morphism, then e is called a regular epimorphism if and only if there are $\mathcal{C}$-morphisms f and g such that $(e,E)$ is the coequalizer of f and g.

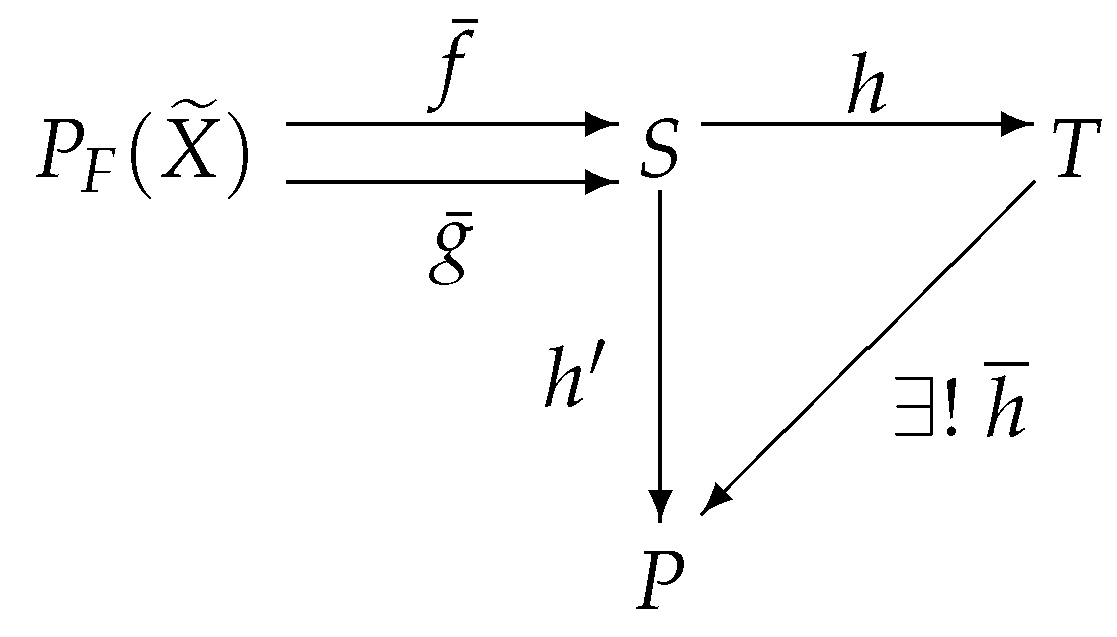
Theorem 9.

The forgetful functor $U:IMSLatt\to Set$ preserves and reflects regular epimorphisms.

Proof. 

Obviously, the forgetful functor $U:IMSLatt\to Set$ preserves regular epimorphisms. We will prove that forgetful functor $U:IMSLatt\to Set$ reflects regular epimorphisms, which requires proving that the epimorphisms are precisely the regular epimorphisms in the category IMSLatt.

Let $h:S\to T$ be an epimorphism in the category IMSLatt. Since the surjective is an regular epimorphism in the category Set, then the mapping h is a regular epimorphism in the category Set. It means that there is a set X and the mappings $f,g:X\to S$ such that $(h,T)$ is the coequalizer of f and g. Then Figure 8 commutes:

For any $A\in P_F\left(\tilde{X}\right)$, define two mappings $\tilde{f}:P_F\left(\tilde{X}\right)\to S$ and $\tilde{g}:P_F\left(\tilde{X}\right)\to S$ as follows:

$\tilde{f}\left(A\right)=\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$,

$\tilde{g}\left(A\right)=\bigvee \{g\left(x_1\right)·g\left(x_2\right)\dots g\left(x_n\right)|x_1{x}_2\dots x_n\in A\}$.

By the proof of Theorem 6, we know that mappings $\tilde{f}$ and $\tilde{g}$ are the involutive m-semilattice homomorphisms. Since $h\circ f=h\circ g$, then

$h\circ \tilde{f}\left(A\right)=h(\bigvee \{f\left(x_1\right)·f\left(x_2\right)\dots f\left(x_n\right)|x_1{x}_2\dots x_n\in A\})$

$=\bigvee \{(h\circ f)\left(x_1\right)·(h\circ f)\left(x_2\right)\dots (h\circ f)\left(x_n\right)|x_1{x}_2\dots x_n\in A\left\}\right)$

$=\bigvee \{(h\circ g)\left(x_1\right)·(h\circ g)\left(x_2\right)\dots (h\circ g)\left(x_n\right)|x_1{x}_2\dots x_n\in A\left\}\right)$

$=h(\bigvee \{g\left(x_1\right)·g\left(x_2\right)\dots g\left(x_n\right)|x_1{x}_2\dots x_n\in A\})$,

hence $h\circ \tilde{f}=h\circ \tilde{g}$.

Let mapping $h^{\prime }:S\to P$ such that $h^{\prime }\circ \tilde{f}=h^{\prime }\circ \tilde{g}$, then $h^{\prime }\circ f=h^{\prime }\circ g$. Since $(h,T)$ is the coequalizer of f and g. This shows that there exists a unique mapping $\overline{h}:T\to P$ such that $h^{\prime }=\overline{h}\circ h$.

For any $x,y\in S$, since h is a surjective function, then there are $x_1,y_1\in S$ such that $h\left(x_1\right)=x$ and $h\left(y_1\right)=y$. We have

(1) $\overline{h}(x·y)=\overline{h}(h\left(x_1\right)·h\left(y_1\right))$ $=(\overline{h}\circ h)(x_1·y_1)=h^{\prime }(x_1·y_1)$ $=h^{\prime }\left(x_1\right)·h^{\prime }\left(y_1\right)$ $=(\overline{h}\circ h)\left(x_1\right)·(\overline{h}\circ h)\left(y_1\right)$ $=\overline{h}\left(h\left(x_1\right)\right)·\overline{h}\left(h\left(y_1\right)\right)$ $=\overline{h}\left(x\right)·\overline{h}\left(y\right)$.

(2) $\overline{h}(x\vee y)=\overline{h}(h\left(x_1\right)\vee h\left(y_1\right))=\left((\overline{h}\circ h)\left(x_1\right)\right)\vee \left((\overline{h}\circ h)\left(y_1\right)\right)=h^{\prime }\left(x_1\right)\vee h^{\prime }\left(y_1\right)=\overline{h}\left(h\left(x_1\right)\right)\vee \overline{h}\left(h\left(y_1\right)\right)=\overline{h}\left(x\right)\vee \overline{h}\left(y\right)$.

(3) $\overline{h}\left(x^{*}\right)=\overline{h}\left({\left(h\left(x_1\right)\right)}^{*}\right)=\overline{h}\left(h\left(x_1^{*}\right)\right)=(\overline{h}\circ h)\left(x_1^{*}\right)=h^{\prime }\left(x_1^{*}\right)={\left(h^{\prime }\left(x_1\right)\right)}^{*}={\left((\overline{h}\circ h)\left(x_1\right)\right)}^{*}={\left(\overline{h}\left(x\right)\right)}^{*}$.

Thus the mapping $\overline{h}$ is an involutive m-semilattice homomorphism.

The above proof shows that $(h,T)$ is a coequalizer of f and g in the category IMSLatt. Then Figure 9 commutes:

Therefore the mapping h is a regular epimorphism in IMSLatt. □

By the theorem 5, theorem 7, and theorem 9, we can obtain the theorem 10.

Theorem 10.

The category $IMSLatt$ is algebraic.

4. The Colimit of Funtor in ${\mathbf{IMCSLatt}}_{\mathbf{0}}$

The limit of a functor, which is a generalization of each of the notions "terminal object", "equalizer","product", and "intersection". Therefore, the study of limits is very important for a category. Colimits are the dual definition of limits. The limits and colimits in some categories have been systematically studied ([29,30,31,32]). It is well known that to prove a category is cocomplete, one must verify that the colimit of a functor from a small category to this category exists, and the construction of colimits relies on coproducts. Building coproducts in the involutive m-semilattice category is a complex and difficult task. In this article, we prove that a full subcategory of involutive m-semilattices is cocomplete, providing some insights for the proof of cocompleteness in the category of involutive m-semilattices.

Definition 17

([26]). If I and $\mathcal{C}$ are categories and $D:I\to \mathcal{C}$ is a functor, then a natural source for D is a source $(L,{\left(l_i\right)}_{i\in Ob\left(I\right)})$ in $\mathcal{C}$ such that for each $i\in Ob\left(I\right)$, $l_i:L\to D\left(i\right)$ and for all morphisms $m:i\to j$, the triangle

commutes.

Figure 10.

Figure 10.

Dually: A natural sink for D is a sink $({\left(k_i\right)}_{i\in Ob\left(I\right)},K)$ where ${\left(k_i\right)}_{i\in Ob\left(I\right)}$ is natural transformation from D to the constant functor $K:I\to \mathcal{C}$.

Definition 18

([26]). If $D:I\to \mathcal{C}$ is a functor, then a natural source $(L,l_i)$ for D is called a limit of D provided that if $(\widehat{L},\widehat{l_i})$ is any natural source for D, then there is a unique morphism $h:\widehat{L}\to L$ such that for each $j\in Ob\left(I\right)$, the triangle

Figure 11.

Figure 11.

commutes.

Dually: A natural sink $({\left(k_i\right)}_{i\in Ob\left(I\right)},K)$ is called a colimit of D provied that every natural sink for D factors uniquely through it.

Definition 19.

Let S be an involutive m-semilattice. $\forall \left\{a_i\right\},\left\{b_i\right\}\subseteq S$, and I is a finite set. If S satisfies condition: (CD) $\underset{i\in I}{\vee }(a_i·b_i)=\left(\underset{i\in I}{\vee }{a}_i\right)·\left(\underset{i\in I}{\vee }{b}_i\right)$. Then $(S,\vee ,·,*)$ is called an involutive mc-semilattice. It is clear that if S satisfies (CD), then S satisfies Definition 1(1).

Theorem 11.

Let S be an involutive mc-semilattice, and R is a congrence of S. For any $a,b,c\in S$, define $\left[x\right]\le \left[y\right]\iff [a\vee b]=\left[b\right]$; $\left[a\right]\vee \left[b\right]=[a\vee b]$; $\left[a\right]·\left[b\right]=[a·b]$; ${\left(\left[a\right]\right)}^{*}=\left[a^{*}\right]$. The mapping $\pi :S\to S/R$ such that $\pi \left(a\right)=\left[a\right]$. Then $(S/R,·,*)$ is an involutive mc-semilattice, and the mapping π is an involutive m-semilattice homomorphism.

Proof. 

The proof of Theorem 11 is similar to the proof of Theorem 4. □

Definition 20.

Let ${\left\{S_i\right\}}_{i\in I}$ be a family of involutive mc-semilattices with minimum element, and $\prod _{i\in I}{S}_i$ is the cartesian product of ${\left\{S_i\right\}}_{i\in I}$. For any $i\in S$, define a mapping ${ϵ}_i:S_i\to \prod _{i\in I}{S}_i$ by $\forall x\in I$, ${\left({ϵ}_i\left(x\right)\right)}_j=\left\{\begin{array}{c}x,i=j,\hfill \\ 0_i,i\ne j,\hfill \end{array}\right.$ where $0_i$ denotes the minimal element of $S_i$. Then mapping ${ϵ}_i$ is called a standard injection.

Lemma 3

([20]). Let ${\left\{S_i\right\}}_{i\in I}$ be a family of involutive m-semilattices, and $\prod _{i\in I}{S}_i$ is the cartesian product of ${\left\{S_i\right\}}_{i\in I}$. $\forall s={\left(s_i\right)}_{i\in I},t={\left(t_i\right)}_{i\in I}\prod _{i\in I}{S}_i$, we define a semigroup multiplication "·" and an involutiveoperation on $\prod _{i\in I}{S}_i$ as follows: $s·t={(s_i·t_i)}_{i\in I},s^{*}={\left(s_i^{*}\right)}_{i\in I}.$ Then $(\prod _{i\in I}{S}_i,·,*)$ is an involutive m-semilattice.

Theorem 12.

Let $\coprod _{i\in I}{S}_i=\{x={\left(x_i\right)}_{i\in I}\in \prod _{i\in I}{S}_i|\{i\in I|x_i\ne 0_i\}$ is a finite set }. $\forall s={\left(s_i\right)}_{i\in I},t={\left(t_i\right)}_{i\in I}\subseteq \coprod _{i\in I}{S}_i$, $s·t={(s_i·t_i)}_{i\in I},s^{*}={\left(s_i^{*}\right)}_{i\in I}.$ Then$(\coprod _{i\in I}{S}_i,·,*)$ is an involutive mc-semilattice under the pointwise order of cartesian product.

Proof. 

The proof is similar to the proof of Lemma 3. □

Definition 21.

Let $IMCSLat{t}_0$ be the category whose objects are the involutive mc-semilattices with minimum element, and whose morphisms are the involutive m-semilattice homomorphisms. Obviously, the category $IMCSLat{t}_0$ is a full subcategory of $IMSLatt$.

Theorem 13.

Let ${\left\{S_i\right\}}_{i\in I}$ be a family of involutive mc-semilattices with minimum element, then $(\coprod _{i\in I}{S}_i,{\left\{{ϵ}_i\right\}}_{i\in I})$ is the coproduct of ${\left\{S_i\right\}}_{i\in I}$ in $IMCSLat{t}_0$, where $\forall i\in I$, the mapping ${ϵ}_i:S_i\to \coprod _{i\in I}{S}_i$ is injection.

Proof. 

We shall show that ${ϵ}_i$ is an involutive m-semilattice homomorphism.

$\forall i\in I,\forall x,y\in S_i$, then

(1) ${\left({ϵ}_i(x\vee y)\right)}_i=x\vee y={\left({ϵ}_i\left(x\right)\right)}_i\vee ({ϵ}_i{\left(y\right)}_i={({ϵ}_i\left(x\right)\vee {ϵ}_i\left(y\right))}_i$.

$\forall j\in I$, if $i\ne j$, ${\left({ϵ}_i(x\vee y)\right)}_j=0_j={\left({ϵ}_i\left(x\right)\right)}_j\vee {\left({ϵ}_i\left(y\right)\right)}_j={({ϵ}_i\left(x\right)\vee {ϵ}_i\left(y\right))}_j$.

Thus ${ϵ}_i(x\vee y)={ϵ}_i\left(x\right)\vee {ϵ}_i\left(y\right)$.

(2) ${\left({ϵ}_i(x·y)\right)}_i=x·y={\left({ϵ}_i\left(x\right)\right)}_i·{\left({ϵ}_i\left(y\right)\right)}_i={({ϵ}_i\left(x\right)·{ϵ}_i\left(y\right))}_i$.

$\forall j\in I$, if $i\ne j$, ${\left({ϵ}_i(x·y)\right)}_j=0_j={\left({ϵ}_i\left(x\right)\right)}_j·{\left({ϵ}_i\left(y\right)\right)}_j={({ϵ}_i\left(x\right)·{ϵ}_i\left(y\right))}_j$.

Thus ${ϵ}_i(x·y)={ϵ}_i\left(x\right)·{ϵ}_i\left(y\right)$.

(3) ${\left({ϵ}_i\left(x^{*}\right)\right)}_i=x^{*}={\left({\left({ϵ}_i\left(x\right)\right)}_i\right)}^{*}$.

$\forall j\in I$, if $i\ne j$, ${\left({ϵ}_i\left(x^{*}\right)\right)}_j=0_j={\left(0_j\right)}^{*}={\left({\left({ϵ}_i\left(x\right)\right)}_j\right)}^{*}$.

Thus ${ϵ}_i\left(x^{*}\right)={\left({ϵ}_i\left(x\right)\right)}^{*}$.

Therefore ${ϵ}_i$ is an involutive m-semilattice homomorphism.

Let S be an arbitrary involutive mc-semilattice with minimum element 0. $\forall i\in I$, mapping $f_i:S_i\to S$ is an involutive m-semilattice homomorphism. Define $f:\coprod _{i\in I}{S}_i\to S$ by $\forall x={\left(x_i\right)}_{i\in I}\in \coprod _{i\in I}{S}_i$, $f\left(x\right)=\underset{i\in I}{\bigvee }\left\{f_i\left(x_i\right)\right|x_i\ne 0_i\}$. We first show that f is well defined. For any $x={\left(x_i\right)}_{i\in I}\in \coprod _{i\in I}{S}_i$. By the definition of $\coprod _{i\in I}{S}_i$ it follow that $\{i\in I|x_i\ne 0_i\}$ is a finite set. Since $\forall i\in I$, mapping $f_i:S_i\to S$ is an involutive m-semilattice homomorphism, then $f\left(0_i\right)=0$ (i.e., $f_i$ preserves the minimum element). Thus the set $\{i\in I|f_i\left(x_i\right)\ne 0\}$ is finite. Therefore, the supremum of the set $\{i\in I|f_i\left(x_i\right)\ne 0\}$ in the semilattice S exists. This show that f is well defined.

Next, we prove that f is an involutive m-semilattice homomorphisms.

$\forall a={\left(a_i\right)}_{i\in I},b={\left(b_i\right)}_{i\in I},c={\left(c_i\right)}_{i\in I}\in \coprod _{i\in I}{S}_i$, then

(1) $f(a\vee b)=\underset{i\in I}{\bigvee }{f}_i\left({(a\vee b)}_i\right)=\underset{i\in I}{\bigvee }(f_i\left(a_i\right)\vee \left(f_i\left(b_i\right)\right)=\left(\underset{i\in I}{\bigvee }{f}_i\left(a_i\right)\right)\vee \left(\underset{i\in I}{\bigvee }{f}_i\left(b_i\right)\right)=f\left(a\right)\vee f\left(b\right)$.

(2) $f(a·b)=\underset{i\in I}{\bigvee }\left(f_i\left({(a·b)}_i\right)\right)=\underset{i\in I}{\bigvee }(f_i\left(a_i\right)·f_i\left(b_i\right))$, by Definition 19 it follows that $\underset{i\in I}{\bigvee }(f_i\left(a_i\right)·f_i\left(b_i\right))=\left(\underset{i\in I}{\bigvee }{f}_i\left(a_i\right)\right)·\left(\underset{i\in I}{\bigvee }{f}_i\left(b_i\right)\right)=f\left(a\right)·f\left(b\right)$. then $f(a·b)=f\left(a\right)·f\left(b\right)$.

(3) $f\left(c^{*}\right)=\underset{i\in I}{\bigvee }{f}_i\left({\left(c^{*}\right)}_i\right)$ $=\underset{i\in I}{\bigvee }{f}_i\left(c_i^{*}\right)$ $=\underset{i\in I}{\bigvee }{\left(f_i\left(c_i\right)\right)}^{*}$ $={\left(\underset{i\in I}{\bigvee }{f}_{i\in I}\left(c_i\right)\right)}^{*}={\left(f\left(x\right)\right)}^{*}$.

In the following, we prove that $f_i=f\circ {ϵ}_i$ for all $i\in I$. $\forall x\in S_i$, $(f\circ {ϵ}_i)\left(x\right)=\underset{i\in I}{\bigvee }{f}_i\left({\left({ϵ}_i\right)}_i\right)=f_i\left(x_i\right)$. Then Figure 12 commutes:

Finally, we prove the uniqueness of the involutive m-semilattice homomorphism f that satisfies the conditions $f_i=f\circ {ϵ}_i$.

Assuming g is another involutive m-semilattice homomorphism that satisfies the above condition, i.e., $\forall i\in I$, $f_i=g\circ {ϵ}_i$. Then $\forall x\in \coprod _{i\in I}{S}_i$, we have

$$g\left(x\right)=g\left(\underset{i\in I}{\bigvee }{ϵ}_i\left(x_i\right)\right)=\underset{i\in I}{\bigvee }g\left({ϵ}_i\left(x_i\right)\right)=\underset{i\in I}{\bigvee }(g\circ {ϵ}_i)\left(x_i\right)=\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)=f\left(x\right).$$

Therefore $(\coprod _{i\in I}{S}_i,{\left\{{ϵ}_i\right\}}_{i\in I})$ is the coproduct of ${\left\{S_i\right\}}_{i\in I}$ in $IMCSLat{t}_0$. □

Definition 22

([26]). A category $\mathcal{C}$ is said to be small provided that $\mathcal{C}$ is a set.

Theorem 14.

Let I be a small category, $F:I\to IMCSLat{t}_0$ be a functor, then the colimit of F is $({\left({\eta }_i\right)}_{i\in I},\left(\coprod _{i\in I}F\left(i\right)\right)/R)$, where R is the smallest involutive m-semilattice congruence relation that contains the set $\bigcup \left\{({ϵ}_i\left(a\right),{ϵ}_j\left(F\left(u\right)\left(a\right)\right))\right|u:i\to j\in Mor\left(I\right),a\in D\left(i\right)\}$, $\forall i\in I$, ${ϵ}_i:F\left(i\right)\to \coprod _{i\in I}F\left(i\right)$ is an injection, and $\pi :\coprod _{i\in I}F\left(i\right)\to \left(\coprod _{i\in I}F\left(i\right)\right)/R$ is a projection.

Proof. 

(1) We first show that $({\left({\eta }_i\right)}_{i\in I},\left(\coprod _{i\in I}F\left(i\right)\right)/R)$ is the natural sink of the functor F.

By the Theorem 11 and Theorem 13, it follows that projection $\pi$ and injection ${ϵ}_i$ are both involutive m-semilattice homomorphisms. Then the mapping ${\eta }_i=\pi \circ {ϵ}_i$ is also an involutive m-semilattice homomorphism.

Figure 13.

Figure 13.

$\forall u:i\to j\in MOr\left(I\right)$, $\forall x\in F\left(i\right)$. Because R is the smallest involutive m-semilattice congruence relation that contains the set $\tilde{R}=\bigcup \left\{({ϵ}_i\left(a\right),{ϵ}_j\left(F\left(u\right)\left(a\right)\right))\right|u:i\to j\in Mor\left(I\right),a\in F\left(i\right)\}$, and $\forall i\in I$, then $({ϵ}_i\left(x\right),{ϵ}_j\left(F\left(u\right)\left(x\right)\right)\in R$, thus $({\eta }_j\circ F\left(u\right))\left(x\right)=(\pi \circ {ϵ}_j)\left(F\left(u\right)\left(x\right)\right)=\pi \left({ϵ}_j\left(F\left(u\right)\left(x\right)\right)\right)=[{ϵ}_j\circ F\left(u\right)\left(x\right)]=\left[{ϵ}_i\left(x\right)\right]=\left[(\pi \circ {ϵ}_i)\left(x\right)\right]={\eta }_i\left(x\right)$, then Figure 14 commutes:

Therefore $({\left({\eta }_i\right)}_{i\in I},\left(\coprod _{i\in I}F\left(i\right)\right)/R)$ is the natural sink of the functor F.

(2) Let S be an involutive mc-semilattices with minimum element, $\left\{f_i\right|F\left(i\right)\to S,i\in I\}$ be a family of involutive m-semilattice homomorphisms, and $({\left(f_i\right)}_{i\in I},S)$ is the natural sink of the functor F, then $f_i=f_j\circ \left(F\left(u\right)\right)$, i.e., Figure 15 commutes:

$\forall x={\left(x_i\right)}_{i\in I}\in \coprod _{i\in I}F\left(i\right)$, define $\overline{f}:\left(\coprod _{i\in I}F\left(i\right)\right)/R\to S$ such that $\overline{f}\left(\left[x\right]\right)=\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)$. Since $\left\{f_i\left(x_i\right)\right|i\in I,x_i\ne 0\}$ is a finte set, then $\underset{i\in I}{\bigvee }\left\{f_i\left(x_i\right)\right|i\in I,x_i\ne 0\}\in S$, thus the mapping is well defined.

From the Theorem 13 we know that $(\coprod _{i\in I}F\left(i\right),{\left\{{ϵ}_i\right\}}_{i\in I})$ is the coproduct of ${\left\{F\left(i\right)\right\}}_{i\in I}$ in $IMCSLat{t}_0$, there exists a unique involutive m-semilattice homomorphism $\widehat{f}:\coprod _{i\in I}F\left(i\right)\to S$ satisfying $f_i=\widehat{f}\circ {ϵ}_i$, then Figure 16 commutes:

Let $△=\left\{\right(y,y\left)\right|y\in S\}$, $\forall u:i\to j\in Mor\left(I\right)$, $\forall x\in F\left(i\right)$, then $\widehat{f}\left({ϵ}_i\left(x\right)\right)=f_i\left(x\right)=f_j\left(F\left(u\right)\left(x\right)\right)=(\widehat{f}\circ {ϵ}_i)\left(F\left(u\right)\left(x\right)\right)=\widehat{f}\left(({ϵ}_i\circ F\left(u\right))\left(x\right)\right)$, i.e., $({ϵ}_i\left(x\right),{ϵ}_j\left(F\left(u\right)\left(x\right)\right))\in f^{-1}(△)$. Hence $\tilde{R}=\bigcup \left\{({ϵ}_i\left(a\right),{ϵ}_j\left(F\left(u\right)\left(a\right)\right))\right|u:i\to j\in Mor\left(I\right),a\in D\left(i\right)\}\subseteq f^{-1}(△)$. Since R is the smallest involutive m-semilattice congruence relation that contains the set $\tilde{R}$, therefore $R\subseteq f^{-1}(△)$.

$\forall x={\left(x_i\right)}_{i\in I},y={\left(y_i\right)}_{i\in I}\in \coprod _{i\in I}{F}_i$, if $(x,y)\in R$, then $(x,y)\in f^{-1}(△)$, hence $\widehat{f}\left(x\right)=\widehat{f}\left(y\right)$, therefore $\underset{i\in I}{\bigvee }{f}_i\left(y_i\right)=\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)$, which implies that $\overline{f}\left(\left[x\right]\right)=\overline{f}\left(\left[y\right]\right)$. Thus the mapping $\overline{f}$ is well defined. $\forall i\in I$, $\forall z_i\in F\left(i\right)$, then $\overline{f}\left({\eta }_i\left(z_i\right)\right)=\overline{f}\left((\pi \circ {ϵ}_i)\left(z_i\right)\right)=\overline{f}\left(\left[{ϵ}_i\left(z_i\right)\right]\right)=\underset{j\in I}{\bigvee }{f}_j\left({\left({ϵ}_i\left(z_i\right)\right)}_j\right)=f_i\left(z_i\right)$. Thus $\overline{f}\circ {\eta }_i=f_i$, then Figure 17 commutes:

(3) We shall show that the mapping $\overline{f}:\left(\coprod _{i\in I}F\left(i\right)\right)/R\to S$ is an involutive m-semilattice homomorphism. $\forall x,y\in \left(\coprod _{i\in I}F\left(i\right)\right)/R$, we have

(i) $\overline{f}(\left[x\right]\vee \left[y\right])=\overline{f}\left([x\vee y]\right)=\underset{i\in I}{\bigvee }{f}_i\left({(x\vee y)}_i\right)=\underset{i\in I}{\bigvee }(f_i\left(x_i\right)\vee f_i\left(y_i\right))=\left(\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)\right)\vee \left(\underset{i\in I}{\bigvee }{f}_i\left(y_i\right)\right)=\overline{f}\left(\left[x\right]\right)\vee \overline{f}\left(\left[y\right]\right)$, then $\overline{f}(\left[x\right]\vee \left[y\right])=\overline{f}\left(\left[x\right]\right)\vee \overline{f}\left(\left[y\right]\right)$.

(ii) $\overline{f}(\left[x\right]·\left[y\right])=\overline{f}\left([x·y]\right)=\underset{i\in I}{\bigvee }{f}_i\left({(x·y)}_i\right)=\underset{i\in I}{\bigvee }{f}_i(x_i·y_i)=\underset{i\in I}{\bigvee }(f_i\left(x_i\right)·f_i\left(y_i\right))$. By the Definition 19, we know that $\underset{i\in I}{\bigvee }(f_i\left(x_i\right)·f_i\left(y_i\right))=\left(\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)\right)·\left(\underset{i\in I}{\bigvee }{f}_i\left(y_i\right)\right)=\overline{f}\left(\left[x\right]\right)·\overline{f}\left(\left[y\right]\right)$. Hence $\overline{f}(\left[x\right]·\left[y\right])=\overline{f}\left(\left[x\right]\right)·\overline{f}\left(\left[y\right]\right)$.

(iii) $\overline{f}\left(\left[x^{*}\right]\right)=\underset{i\in I}{\bigvee }{f}_i\left({\left(x^{*}\right)}_i\right)=\underset{i\in I}{\bigvee }{f}_i\left(x_i^{*}\right)=\underset{i\in I}{\bigvee }{\left(f_i\left(x_i\right)\right)}^{*}={\left(\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)\right)}^{*}={\left(\overline{f}\left(\left[x\right]\right)\right)}^{*}$, then $\overline{f}\left(\left[x^{*}\right]\right)={\left(\overline{f}\left(\left[x\right]\right)\right)}^{*}$.

(4) We will prove the uniqueness of the involutive m-semilattice homomorphism $\overline{f}:(\coprod _{i\in I}F\left(i\right)/R\to S$ that satisfies the conditions $f_i=\overline{f}\circ {\eta }_i$. Assuming $\tilde{f}:\left(\coprod _{i\in I}F\left(i\right)\right)/R\to S$ is another involutive m-semilattice homomorphism that satisfies $f_i=\tilde{f}\circ {\eta }_i$, then $\tilde{f}\left(\left[x\right]\right)=\tilde{f}\left(\pi \left(x\right)\right)=\tilde{f}\left(\pi \left(\underset{i\in I}{\bigvee }{ϵ}_i\left(x_i\right)\right)\right)=\tilde{f}\left(\underset{i\in I}{\bigvee }\left(\pi \left({ϵ}_i\left(x_i\right)\right)\right)\right)=\tilde{f}\left(\underset{i\in I}{\bigvee }\left[x_i\right]\right)=\underset{i\in I}{\bigvee }\tilde{f}\left(\left[x_i\right]\right)=\underset{i\in I}{\bigvee }\tilde{f}\left((\pi \circ {ϵ}_i)\left(x_i\right)\right)=\underset{i\in I}{\bigvee }\tilde{f}\left({\eta }_i\left(x_i\right)\right)=\underset{i\in I}{\bigvee }(\tilde{f}\circ {\eta }_i)\left(x_i\right)=\underset{i\in I}{\bigvee }{f}_i\left(x_i\right)=\overline{f}\left(\left[x\right]\right)$. Hence $\tilde{f}=\overline{f}$.

From (1), (2), (3), and (4), it can be concluded that$({\left({\eta }_i\right)}_{i\in I},\left(\coprod _{i\in I}F\left(i\right)\right)/R)$ is the colimit of the functor F. □

Corollary 1.

$IMCSLat{t}_0$ is cocomplete.

5. The Inverse Limit and Direct Limit in $\mathbf{IMSLatt}$

Definition 23.

Let I be a downward-directed set, then I can be taken for a category, where its objects is the elements in I. Let $i,j\in I$, if $i\le j$, then a morphism $u_{ij}:i\to j$ is taken naturally in the category I.

A functor $F:I\to IMSLatt$ is called an inverse system in the category of involutive m-semilattices. An inverse system in IMSLatt can be described by the following satements without using the notion of functor. Let I be a downward-directed set. For any $i,j\in I$ and $i\le j$, there exists an involutive m-semilattice homomorphism $f_{ij}:S_i\to S_j$. And further that $f_{ij}=f_{jk}·f_{ik}$ for all $i,j,k\in I$ satisfing $i\le j\le k,f_{ii}=i{d}_{S_i}:S_i\to S_i$. The triple $(S_i,f_{ij},I)$ is called an inverse system in IMSLatt.

Definition 24.

Let I be a downward-directed set, and $F:I\to IMSLatt$ be an inverse system in IMSLatt. Then the limit of F is called the inverse limit of inverse system $F:I\to IMSLatt$.

Dual: upward-directed set; direct system; direct limit.

From the definitions of the inverse limit and direct limit in IMSLatt. It is clear that the inverse limits are defined to be particular limits and direct limits are particular colimits. Inverse limits and directed limits in some categories have been extensively studied([33,34,35,36,37,38]). The following will give the inverse limit and direct limit in the IMSLatt.

5.1. The Inverse Limit of the Inverse System in $IMSLatt$

Theorem 15

([20]). Let I be a small category, $F:I\to IMSLatt$ be a functor, then the limit of F is $(L,{\left(p_i\right)}_{i\in I})$, where $L=\{f\in \prod _{i\in I}F\left(i\right)|\forall u:i\to j\in Mor\left(I\right)$ such that $f\left(j\right)=F\left(u\right)\left(f\right(i\left)\right)\}$. $\forall i\in I$, $f\in \prod _{i\in I}F\left(i\right)$, the mapping $p_i:\prod _{i\in I}F\left(i\right)\to F\left(i\right)$ is projection, and $p_i\left(f\right)=f\left(i\right)$.

Theorem 16.

Let I be a downward-directed set, and $F:I\to IMSLatt$ be an inverse system in IMSLatt. Then the inverse limit of inverse system F is $(T,{\left(p_i\right)}_{i\in I})$, where $T=\{{\left\{x_i\right\}}_{i\in I}\in \prod _{i\in I}F\left(i\right)|\forall i,j\in I,$if $i\le j,$ then $\exists f_{ij}:F\left(i\right)\to F\left(j\right)\in Mor\left(IMSLatt\right)$ such that $f_{ij}\left(x_i\right)=x_j\}$, and $\forall i\in I$, $\forall x={\left(x_i\right)}_{i\in I}\in \prod _{i\in I}F\left(i\right)$, $p_i:\prod _{i\in I}F\left(i\right)\to F\left(i\right)$ is a projection (i.e., $p_i\left({\left(x_i\right)}_{i\in I}\right)=x_i$).

Proof. 

The proof of Theorem 16 is similar to the proof of Theorem 15 in Reference [20]. □

Suppose $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ are two inverse systems in IMSLatt. Let $(T,{\left(p_i\right)}_{i\in I})$ and $(T^{\prime },{\left(p_i^{\prime }\right)}_{i\in I})$ be the inverse limits of inverse systems F and G, respectively, where I and $I^{\prime }$ are downward-directed sets.

$\forall i,j\in I$, $\forall i^{\prime },j^{\prime }\in I^{\prime }$, $F\left(i\right)=S_i$, $F\left(i^{\prime }\right)=S_{i^{\prime }}$ are involutive m-semilattices. If $i\le j$ and $i^{\prime }\le j^{\prime }$, then $F(i\to j)=F_{ij}:F\left(i\right)\to F\left(j\right)$ and $G(i^{\prime }\to j^{\prime })=G_{i^{\prime }{j}^{\prime }}:F\left(i^{\prime }\right)\to F\left(j^{\prime }\right)$ are involutive m-semilattice homomorphisms. $\forall i,j,k\in I$, $\forall i^{\prime },j^{\prime },k^{\prime }\in I^{\prime }$, if $i\le j\le k$ and $i^{\prime }\le j^{\prime }\le k^{\prime }$, the $F_{jk}·F_{ij}=F_{ik}$, $G_{j^{\prime }{k}^{\prime }}·G_{i^{\prime }{j}^{\prime }}=G_{i^{\prime }{k}^{\prime }}$, $F_{ii}=i{d}_{F\left(i\right)}$, $G_{i^{\prime }{i}^{\prime }}=i{d}_{G\left(i^{\prime }\right)}$. The homomorphisms $F_{ij}$ and $G_{i^{\prime }{j}^{\prime }}$ are called the bonding mapping of inverse systems F and G, respectively.

Definition 25

($\left[36\right]$). Let I be a downward-directed set, and $I^{\prime }\subseteq I$. If $\forall i\in I$, there is a $i^{\prime }\in I^{\prime }$ such that $i^{\prime }\le i$, the set $I^{\prime }$ is called a downward cofinal subset of I.

Based on Definition 3.1 in reference [36], the definition of the mapping between two inverse systems can be given as follows:

Definition 26.

Let $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ be two inverse systems in IMSLatt. $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ is called the mapping from inverse system F to inverse system G if it satisfies the following conditions:

(1) $\phi :I^{\prime }\to I$ is an order preserving mapping and $\phi \left(I^{\prime }\right)$ is a downward cofinal subset of I.

(2) $\forall i^{\prime }\in I^{\prime }$, $f_{i^{\prime }}:F\left(\phi \left(i^{\prime }\right)\right)\to G\left(i^{\prime }\right)$ is an involutive m-semilattice homomorphism, and $\forall i^{\prime },j^{\prime }\in I^{\prime }$, if $i^{\prime }\le j^{\prime }$, then $G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }}=f_{j^{\prime }}\circ F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)}$, i.e., Figure 18 commutes:

Theorem 17.

Let $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ be two inverse systems in IMSLatt. $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ is the mapping from inverse system F to inverse G. Then the mapping $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ induces an involutive m-semilattices homomorphism $f:T\to T^{\prime }$, where $\forall x={\left(x_i\right)}_{i\in I}\in T$, $f\left(x\right)=f\left({\left(x_i\right)}_{i\in I}\right)={\left(x_{i^{\prime }}^{\prime }\right)}_{i^{\prime }\in I^{\prime }}=x^{\prime }\in T^{\prime }$, $x_{i^{\prime }}^{\prime }=(f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)$, and $p_i:\prod _{i\in I}F\left(i\right)\to F\left(i\right)$ is a projection (i.e., $p_i\left({\left(x_i\right)}_{i\in I}\right)=x_i$).

Proof. 

$\forall i^{\prime },j^{\prime }\in I^{\prime }$, if $i^{\prime }\le j^{\prime }$, then $\phi \left(i^{\prime }\right)\le \phi \left(j^{\prime }\right)$. $\forall x={\left(x_i\right)}_{i\in I}\in T$, by Definintion 26(2) and Theorem 16, we know that $(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }})\left(x_{\phi \left(i^{\prime }\right)}\right)=(f_{j^{\prime }}\circ F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)})\left(x_{\phi \left(i^{\prime }\right)}\right)$, then $F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)}\left(x_{\phi \left(i^{\prime }\right)}\right)=x_{\phi \left(j^{\prime }\right)}=p_{\phi \left(j^{\prime }\right)}\left({\left(x_i\right)}_{i\in I}\right)$. Thus $G_{i^{\prime }{j}^{\prime }}\left(x_{i^{\prime }}^{\prime }\right)=G_{i^{\prime }{j}^{\prime }}\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)\right)=(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)=(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }})\left(p_{\phi \left(i^{\prime }\right)}{\left(x_i\right)}_{i\in I}\right)=(G_{i^{\prime }{j}^{\prime }}\circ f_{i^{\prime }})\left(x_{\phi \left(i^{\prime }\right)}\right)=(f_{j^{\prime }}\circ F_{\phi \left(i^{\prime }\right)\phi \left(j^{\prime }\right)})\left(x_{\phi \left(i^{\prime }\right)}\right)=(f_{j^{\prime }}\circ p_{\phi \left(j^{\prime }\right)})\left({\left(x_i\right)}_{i\in I}\right)=x_{j^{\prime }}^{\prime }$. This implies that there exists an involutive m-semilattice homomorphism $G_{i^{\prime }{j}^{\prime }}:G_{i^{\prime }}\to G_{j^{\prime }}$ such that $G_{i^{\prime }{j}^{\prime }}\left(x_{i^{\prime }}^{\prime }\right)=x_{j^{\prime }}^{\prime }$. From Theorem 16 it follows that $x^{\prime }={\left(x_{i^{\prime }}^{\prime }\right)}_{i^{\prime }\in I^{\prime }}\in T^{\prime }$. Hence f is well defined.

$\forall x={\left(x_i\right)}_{i\in I},y={\left(y_i\right)}_{i\in I},z={\left(z_i\right)}_{i\in I}\in T$, $\forall i\in I^{\prime }$, then

(1) ${\left(f(x\vee y)\right)}_{i^{\prime }}=(f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})(x\vee y)=f_{i^{\prime }}{\left((x\vee y)\right)}_{\phi \left(i^{\prime }\right)})=\left(f_{i^{\prime }}\left(x_{\phi \left(i^{\prime }\right)}\right)\right)\vee \left(f_{i^{\prime }}\left(y_{\phi \left(i^{\prime }\right)}\right)\right)=\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(x\right)\right)\vee \left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(y\right)\right)={\left(f\left(x\right)\right)}_{i^{\prime }}\vee {\left(f\left(y\right)\right)}_{i^{\prime }}={(f\left(x\right)\vee f\left(y\right))}_{i^{\prime }}$. This implies that $f(x\vee y)=f\left(x\right)\vee f\left(y\right)$. Thus f preserves union.

(2) ${\left(f(h_1·h_2)\right)}_{i^{\prime }}=(f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})(x·y)={\left(f_{i^{\prime }}(x·y)\right)}_{\phi \left(i^{\prime }\right)}=\left({\left(f_{i^{\prime }}\left(x\right)\right)}_{\phi \left(i^{\prime }\right)}\right)·\left({\left(f_{i^{\prime }}\left(y\right)\right)}_{\phi \left(i^{\prime }\right)}\right)=\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(x\right)\right)·\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(y\right)\right)={(f\left(x\right)·f\left(y\right))}_{i^{\prime }}$. This shows that $f(x·y)=f\left(x\right)·f\left(y\right)$. Thus f preserves semigroup operation ·.

(3) ${\left(f\left(z^{*}\right)\right)}_{i^{\prime }}={\left(f_{i^{\prime }}\left(z^{*}\right)\right)}_{\phi \left(i^{\prime }\right)}={\left({\left(f_{i^{\prime }}\left(z\right)\right)}_{\phi \left(i^{\prime }\right)}\right)}^{*}={\left((f_{i^{\prime }}\circ p_{\phi \left(i^{\prime }\right)})\left(z\right)\right)}^{*}={\left({\left(f\left(z\right)\right)}_{i^{\prime }}\right)}^{*}={\left({\left(f\left(z\right)\right)}^{*}\right)}_{i^{\prime }}$. Thus f preserves involution operation *.

Therefore the mapping f is an involutive m-semilattice homomorphism. □

Definition 27.

Let $F:I\to IMSLatt$ and $G:I^{\prime }\to IMSLatt$ be two inverse systems in IMSLatt. $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ be a mapping from the inverse F to the inverse G. Then above induced morphism $f:T\to T^{\prime }$ is called the limit mapping. It can be denoted by $lim(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$.

Theorem 18.

Let $(\phi ,{\left\{f_{i^{\prime }}\right\}}_{i^{\prime }\in I^{\prime }})$ be a mapping from the inverse F to the inverse G. For any $i^{\prime }\in I^{\prime }$, if $f_{i^{\prime }}$ is a monomorphism, then the induced mapping $f:T\to T^{\prime }$ is also monomorphism.

5.2. The direct limit of the direct system on IMSLatt

Definition 28

([26]). Let I be a set, if the every subset of I have upper bound, then I is called upward-bound.

Definition 29.

Let I be a upward-bound set. The functor $D:I\to IMSLatt$ is called a direct system in IMSLatt, where $\forall i,j\in I$, $D\left(i\right)=S_i$ and $D\left(j\right)=S_j$, if $i\le j$, then $D(i\to j):S_i\to S_j$ is an involutive m-semilattice homomorphism. For the convenience of the following description, let $f_{ij}$ denote the mapping $D(i\to j):S_i\to S_j$.

Lemma 4.

Let $U:IMSLatt\to Set$ be the forgetful functor, and $(u_i,S)$ is the coproduct of ${\left\{U\left(S_i\right)\right\}}_{i\in I}$ in the category of sets (i.e., the disjoint union of sets ${\left\{U\left(S_i\right)\right\}}_{i\in I}$). The binary relation $"\sim "$ on S is defined by the following: $x,y\in S,$ such that $x\in U\left(S_i\right)$, $y\in U\left(S_j\right)$, $x\sim y$ if and only if there is a $k\in K$, such that $i\le k,j\le k$ and $f_{ik}\left(x\right)=f_{jk}\left(x\right)$. Let $\overline{S}=S/\sim$ represents the equivalence class of S under relation "∼", order relation and three operations on S are defined by the following:

$\forall \left[x\right],\left[y\right]\in \overline{S}$, such that $x\in S_i$ and $y\in S_j$, then

(1) $\left[x\right]\le \left[y\right]$ if and only if there is a $k\in I$ satisfies $i,j\le k$ and $f_{ik}\left(x\right)\le f_{jk}\left(x\right)$.

(2) $\left[x\right]\vee \left[y\right]=[f_{ik}\left(x\right)\vee f_{jk}\left(y\right)]$.

(3) $\left[x\right]·\left[y\right]=[f_{ik}\left(x\right)·f_{jk}\left(y\right)]$.

(4) ${\left(\left[x\right]\right)}^{*}=\left[f_{ik}\left(x^{*}\right)\right]$.

Then $(\overline{S},\vee ,·,*)$ is an involution m-semilattice.

Proof. 

It’s easy to prove that the above definitions are well defined, and the set $(\overline{S},\vee ,·,*)$ is an involution m-semilattice. □

Theorem 19.

Let I be a upward-bound set, and $D:I\to IMSLatt$ be a direct system in IMSLatt. $\forall i,j\in I$, if $i\le j$, and $D(i\to j)=f_{ij}:S_i\to S_j$ is an involutive m-semilattice homomorphism, then the direct limit of direct system D is $(l_i,\overline{S})$, where $\overline{S}$ is defined above in the lemma 5, $l_i=\pi \circ u_i:A_i\to S_i$, and the mapping $\pi :S\to S/\sim$ represents the projection from S to its equivalence class $S/\sim$.

Proof. 

The proof of this theorem is similar to the proof of the Theorem 14. □

Corollary 2.

IMSLAtt is directed complete.

Theorem 20.

Let I be a upward-bound set, functor $D:I\to IMSLatt$ is a direct system in IMSLatt, and $(l_i,\overline{S})$ is the direct limit of direct system D. $\forall i,j\in I$, if $i\le j$, mapping $f_{ij}=D(i\to j):S_i\to S_j$ is a monomorphism, then $l_i$ is also a monomorphism.

Proof. 

Proof is straightforward. □