1. Introduction
Cross-site scripting (XSS) attacks remain a persistent security threat due to their widespread occurrence and ease of exploitation [
8]. Machine learning-based detection, including reinforcement learning [
7,
17] and ensemble learning [
6,
38], has advanced significantly, with earlier studies [
4,
6,
12] and more recent works [
1,
3,
5,
10,
38] focusing on improving model architectures and feature extraction.
However, many methods still face generalisation issues due to the highly distributed data structure and privacy concerns. Federated Learning (FL) has emerged as a privacy-preserving alternative, allowing collaborative training without exposing raw data. This study explores the use of FL for XSS detection, addressing key challenges such as non-independent and identically distributed (non-IID) data, heterogeneity and out-of-distribution (OOD). While FL has been applied in cybersecurity [
11,
18], its role in XSS detection remains underexplored. Most prior works focus on network traffic analysis, rather than text-based XSS payloads.
This study presents the first systematic application of federated learning to XSS detection under text-based XSS threat scenarios. Our key contributions are.
We design a federated learning (FL) framework for XSS detection under structurally non-IID client distributions, incorporating diverse XSS types, obfuscation styles, and attack patterns. This setup reflects real-world asymmetry, where some clients contain partial or ambiguous indicators and others contain clearer attacks. Importantly, structural divergence also affects negatives, whose heterogeneity is a key yet underexplored factor in generalisation failure. Our framework enables the study of bidirectional OOD, where fragmented negatives cause high false positive rates under distribution mismatch.
Unlike prior work that mixes lexical or contextual features across splits, we maintain strict structural separation between training and testing data. By using an external dataset [
57] as an OOD domain, we isolate bidirectional distributional shifts across both classes under FL. Our analysis shows that generalisation failure is can also be driven by structurally complicated benign samples not only by rare or obfuscated attacks, emphasizing the importance of structure-aware dataset design.
We compare three embedding models (GloVe [
24], CodeT5 [
26], GraphCodeBERT [
25]) in centralised and federated settings, showing that generalisation depends more on embedding compatibility with class heterogeneity than on model capacity. Using divergence metrics and ablation studies, we demonstrate that structurally complex and underrepresented negatives lead to severe false positives. Static embeddings like GloVe show more robust generalisation under structural OOD, indicating that stability relies more on representational resilience than expressiveness.
2. Related Work
Existing research on federated learning (FL) for XSS detection remains scarce. The most relevant work by Jazi & Ben-Gal [
2] investigated FL’s privacy-preserving properties using simplified setups and traditional models (e.g., MLP, KNN). Their non-IID configuration assumes an unrealistic “all-malicious vs. all-benign” client split, and evaluation is conducted separately on a handcrafted text-based XSS dataset [
57] and the CICIDS2017 intrusion dataset [
28]. However, they do not consider data heterogeneity or OOD generalisation. Still, the dataset [
57] they selected is structurally rich and thus serves as a suitable OOD test dataset in our experiments (see
Section 3.2).
Heterogeneity in datasets remains a significant challenge for XSS detection [
14,
15,
39,
61]. The absence of standardized datasets, particularly in terms of class variety and sample volume, can have a substantial impact on the decision boundaries learned by detection models [
60,
64]. Most existing studies, including [
3,
4,
5,
10], attempt to address this issue through labor-intensive manual processing, aiming to ensure strict control over data quality, feature representation, label consistency, and class definitions.
However, we argue that complete reliance on manual curation often fails to reflect real-world conditions. In practical cybersecurity scenarios, data imbalance is both common and inevitable, especially regarding the ratio and diversity of attack versus non-attack samples [
60,
61,
62]. This often results in pronounced structural and categorical divergence between positive and negative classes. For example, commonly used XSS filters frequently over-filter benign inputs [
63], indicating a mismatch between curated datasets and actual deployment environments.
In light of these challenges, federated learning demonstrates strong potential. It enables models to share decision boundaries through privacy-preserving aggregation [
33,
56], offering an effective alternative to centralized data collection and manual intervention.
Meanwhile, we argue that findings from FL research on malicious URL detection [
9,
37] are partially transferable to XSS detection. Although some malicious URLs may embed XSS payloads, the two tasks differ in semantic granularity, execution contexts, and structural variability. Given their shared challenges like class imbalance, distribution shift, and non-IID data, we think FL techniques proven effective for URL detection offer a reasonable foundation for XSS adaptation.
The high sensitivity of XSS-related information such as emails or session tokens, makes sharing difficult without anonymisation. Yet studies [
53,
54] show that anonymisation often introduces significant distributional shifts due to strategy-specific biases. Disparities in logging, encoding, and user behaviour further distort data distributions, compromising generalisation [
53,
54].
For example, strings embedded in polyglot-style payloads are hard to anonymise, as minor changes may affect execution. Consider the following sample:
<javascript:/*-><img/src='x'onerror=eval(unescape(/%61%6c%65%72%74%28%27%45%78%66%69%6c%3A%20%2b%20%27%2b%60test@example.com:1849%60%29/))>
Naively replacing "test@example.com" with an unquoted *** breaks JavaScript syntax, rendering the sample invalid and misleading detectors. While AST-based desensitisation can preserve structure, it is complex, labour-intensive, and lacks scalability [
52].
To address these challenges, this study introduces a federated learning (FL) framework to enhance XSS detection while preserving data privacy, especially under an OOD scenario. FL enables collaborative training without exposing raw data [
11,
56], mitigating distributional divergence and improving robustness [
56,
59]. More importantly, our approach leverages structurally well-aligned, semantically coherent clients to anchor global decision boundaries, allowing their generalisation capabilities to be implicitly shared across clients with fragmented, noisy, or ambiguous data distributions. In doing so, we avoid the need for centralised, large-scale anonymisation or sanitisation, and instead provide low-quality clients with clearer classification margins without direct data sharing or manual intervention. This decentralised knowledge transfer mechanism forms the basis of our FL framework, detailed in
Section 5, and evaluated under dual OOD settings across three embedding models.
Section 4 will explain the Centralized OOD testing,
4. Independent Client Testing with OOD Distributed Data
In the first part of our evaluation, we trained on Dataset 1 and tested on Dataset 2, then reversed the setup. While both datasets target reflected XSS, they differ in structural and lexical characteristics, as detailed in
Section 3.1. This asymmetry, present in both positive and negative samples, led to significant generalisation gaps. In particular, models trained on one dataset exhibited lower precision and increased false positive rates when tested on the other, reflecting the impact of data divergence under OOD settings.
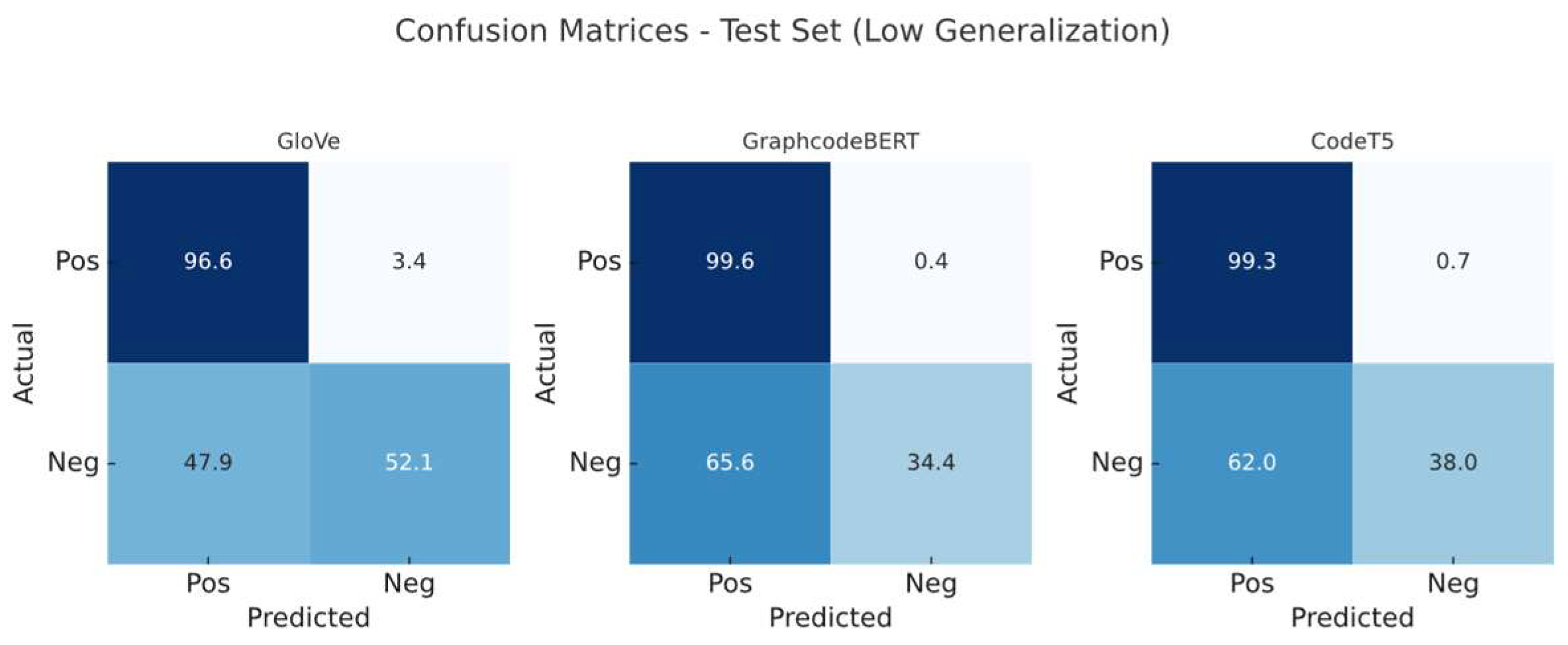
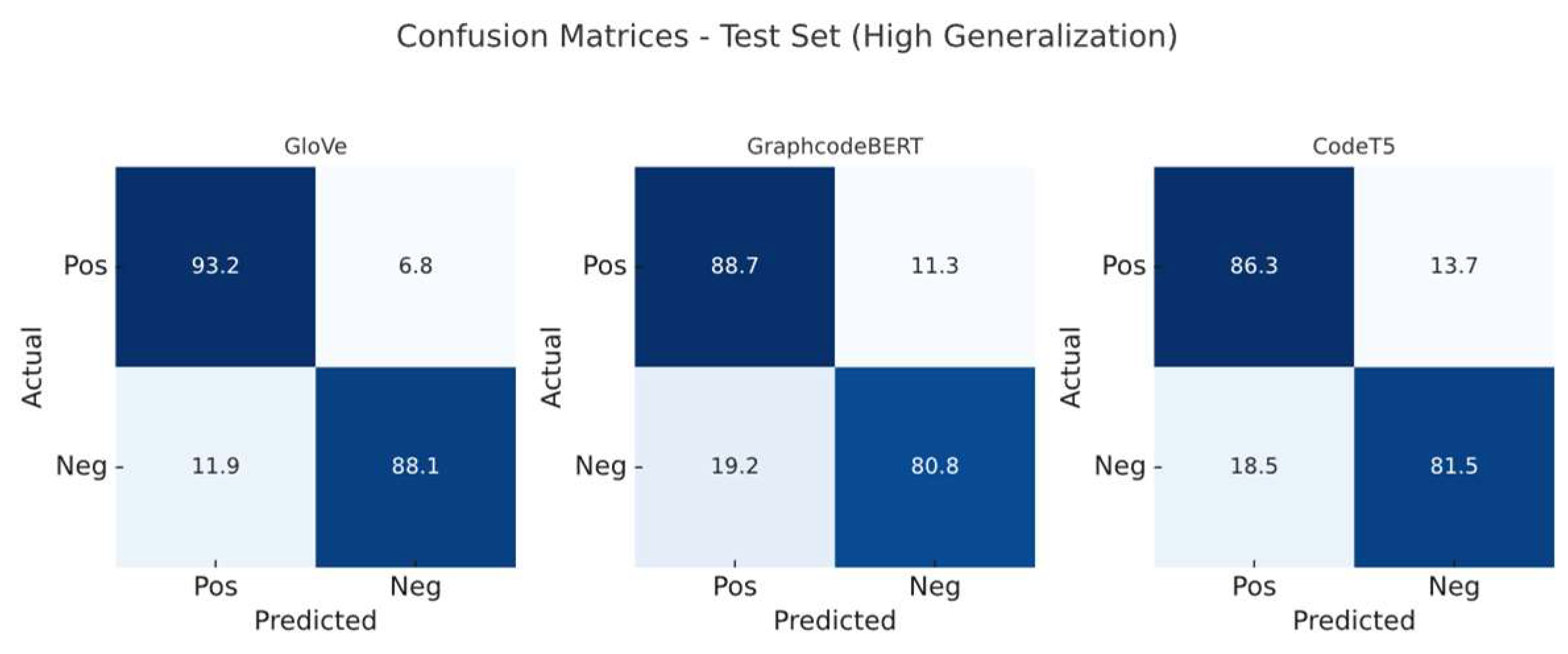
We evaluated all three embedding models under both configurations. Confusion matrices (
Figure 4 and
Figure 5) illustrate the classification differences when trained on low- versus high-generalisation data, respectively. Before this, we established performance baselines via 20% splits on the original training set to rule out overfitting (
Table 3).
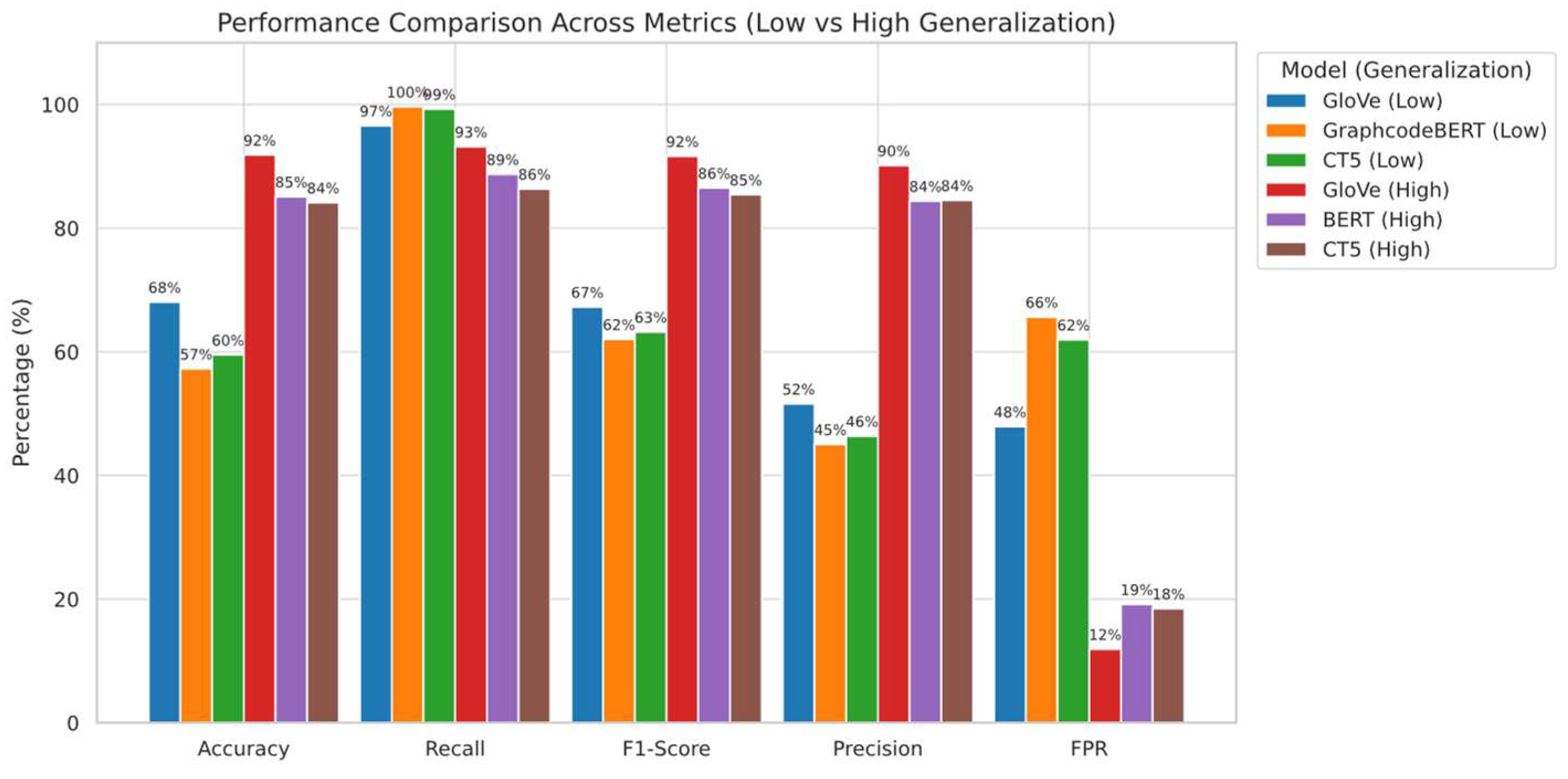
Figure 6 summarises cross-distribution performance under each model, and
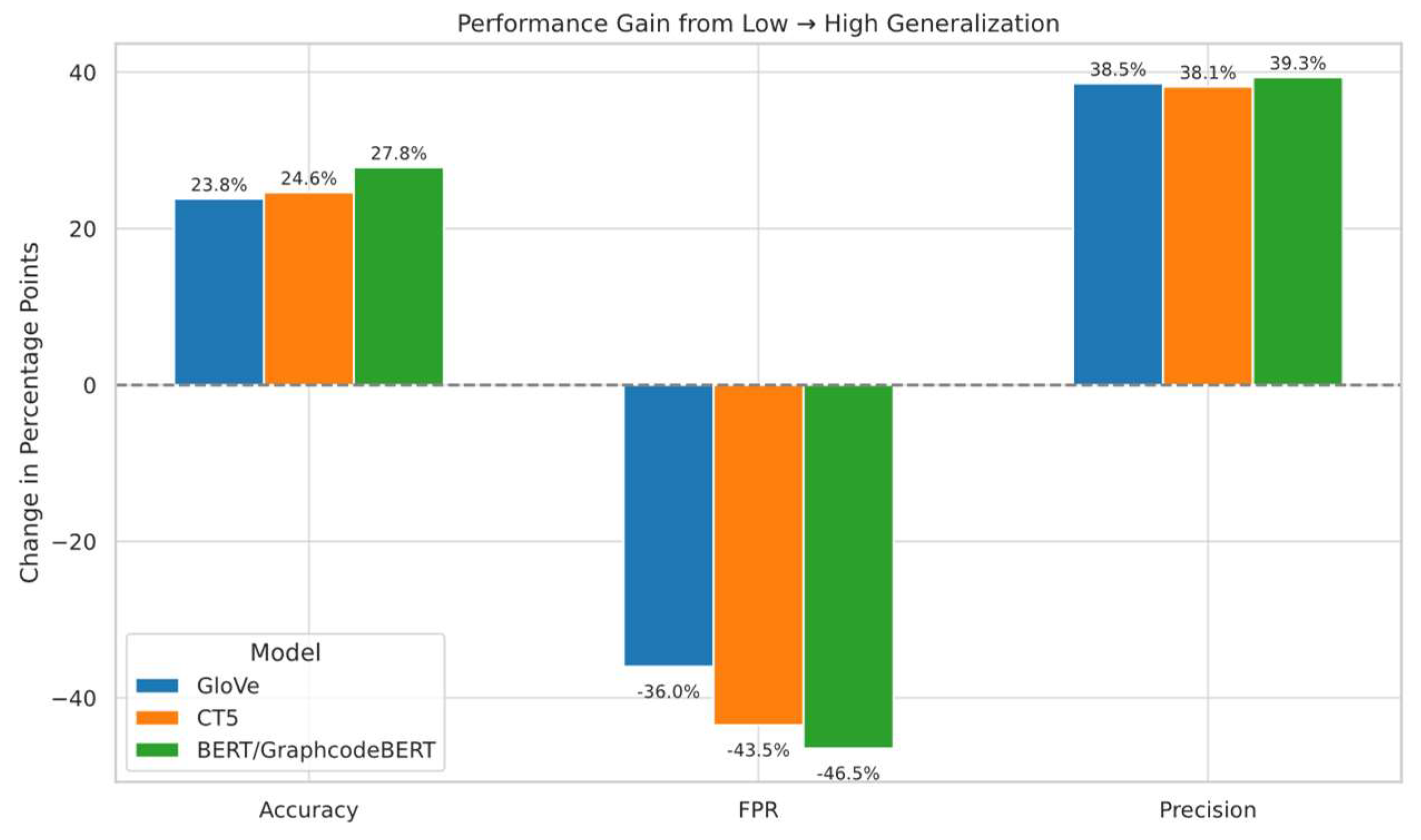
Figure 7 highlights the extent of performance shifts under structural OOD. These results confirm that both positive and negative class structures play a critical role in the generalisation performance of XSS detectors
To isolate the impact of positive sample structure, we conducted cross-set training where the training positives originated from the high-generalisation Dataset2 while retaining fragmented negatives from Dataset1 on the most structure sensitive model GraphcodeBERT. Compared to the baseline trained entirely on Dataset1, this setup substantially improved Accuracy (from 56.80% to 71.57%) and precision (from 44.82% to 68.39%), with Recall slightly increased to 99.70%. These findings highlight that structural integrity in positive samples enhances model confidence and generalisability even under noisy negative supervision. Conversely, negatives primarily increase false positives (FPR 68.19%). See
Table 4.
4.1. Generalisation Performance Analysis
When We evaluate the generalisation ability of GloVe, GraphCodeBERT, and CodeT5 embeddings by testing on the high-generalisation dataset (Dataset 2) and training on the structurally diverse and fragmented Dataset 1. All models experience a significant drop in performance, particularly in precision and false positive rate (FPR), indicating high sensitivity to structural shifts across datasets.
GraphCodeBERT shows the most severe performance degradation, with precision dropping from 84.38% to 45.03% (−39.35%), and FPR increasing from 19.16% to 65.62% (+46.46%). Despite maintaining nearly perfect recall (99.63%), it heavily overpredicts positives when faced with unfamiliar structures, suggesting poor robustness to syntactic variance due to its code-centric pretraining.
CodeT5 suffers slightly less, but still significant degradation: precision drops from 84.50% to 46.36% (-38.14%), and FPR rises from 18.47% to 61.95% (+43.48%). This suggests that while its span-masked pretraining aids structural abstraction, it still fails under negative class distribution shift.
GloVe demonstrates the most stable cross-dataset performance, with a precision decline from 90.13% to 51.58% (−38.55%), and FPR increasing from 11.90% to 47.90 (+36.00%). Although static and context-agnostic, GloVe is less vulnerable to structural OOD, likely due to its reliance on global co-occurrence statistics rather than positional or syntactic features.
These results support that structural generalisation failure arises from both positive class fragmentation and negative class dissimilarity. Models relying on local syntax (e.g., GraphCodeBERT) are more prone to false positives, while those leveraging global distributional features (e.g., GloVe) exhibit relatively better robustness under extreme OOD scenarios.
Sensitivity of Embeddings to Regularization Under OOD
Under structural OOD conditions, CodeT5 achieved high recall (≥99%) but suffered from low precision and high FPR, indicating overfitting to local patterns. Stronger regularization (dropout = 0.3, lr = 0.0005) led to improved precision (+4.73%) and reduced FPR (−10.89%), showing modest gains in robustness. GloVe benefited the most from regularization, with FPR dropping to 29.49% and precision rising to 63.41%. In contrast, GraphCodeBERT remained not very sensitive to regularization, with relatively smaller change across settings. These results suggest that structure-sensitive embeddings require tuning to remain effective under structural shift, while static embeddings like GloVe offer more stable performance.
Notably, we also observed that stronger regularization on dropout tends to widen the performance gap between best and worst OOD scenarios, especially for GloVe (4%~9%). These results suggest that structure-sensitive embeddings require tuning to remain effective under distributional shift. See
Table 5.
4.2. Embedding Level Analysis
To assess whether embedding similarity correlates with generalisation, we computed pairwise Jensen-Shannon Divergence (JSD) [
49] and Wasserstein distances (WD) [
50] across models on both datasets.
and
: Probability distributions of two embedding sets,
: Mean distribution.
: Kullback–Leibler divergence from one distribution to another.
:Cumulative distribution functions.
reflects a symmetric, smoothed divergence metric capturing the balanced difference between
and
.
As shown in
Table 6, the three embedding models respond differently to structural variation. GraphCodeBERT has the lowest JSD (0.2444) but the highest WD (0.0758), suggesting its embeddings shift more sharply in space despite low average token divergence. This sensitivity leads to poor generalisation, with false positive rates exceeding 65% under OOD tests. GloVe shows the highest JSD (0.3402) and moderate WD (0.0562), indicating broader but smoother distribution changes. It performs most stably in OOD scenarios, likely due to better tolerance of structural drift. CodeT5 has the lowest WD (0.0237), meaning its embeddings change little across structure shifts. However, this low sensitivity results in degraded precision, especially for negative-class drift.
Kernel-Based Statistical Validation of OOD Divergence
While metrics like JSD and Wasserstein quantify distributional shifts, they do not assess statistical significance. To address this, we compute the Maximum Mean Discrepancy (MMD) between Dataset 1 and Dataset 2 using Random Fourier Features (RFF) for efficiency, with 40,000 samples per set, for details.
- 4.
score scope for different models embedding in all samples: 0.001633 (GraphcodeBERT) - 0.082517 (GloVe) - 0.118169 (CodeT5).
- 5.
In positive samples: 0.000176 (GloVe) - 0.000853(GraphcodeBERT) - 0.106470 (CodeT5).
- 6.
In negative samples: 0.004105(GraphcodeBERT) - 0.007960 (CodeT5) - Glove (0.517704)
- 7.
All Embeddings’ < 0.001(refers to a distinct OOD)
These data confirmed a statistically significant distributional shift and semantic OOD in negative samples. For formulation, please see below.
,
refers to the set of different embeddings.
means the kernel feature mapping approximated via Random Fourier Features (RFF). For
,
is the observed MMD score,
represents the number of permutations,
is the MMD value obtained for the
i permutation.
The unusually high negative-class MMD of GloVe largely arises from lexical-surface drift along dimensions that have negligible classifier weights. Suggesting the decision boundary learned during hard-negative mining is far from benign regions in these dimensions, the model maintains a low false-positive rate under OOD settings despite the apparent distribution gap. Conversely, contextual models display smaller overall MMD yet place their boundary closer to benign clusters, yielding higher FPR. This suggests that absolute MMD magnitude is not a sufficient indicator of OOD robustness; alignment between drift directions and decision-relevant subspaces is critical.
These results, supported by lexical analysis (
Section 3.2) indicate that the observed generalisation gap is attributable to systematic data divergence, particularly in negative sample distributions, rather than random fluctuations.
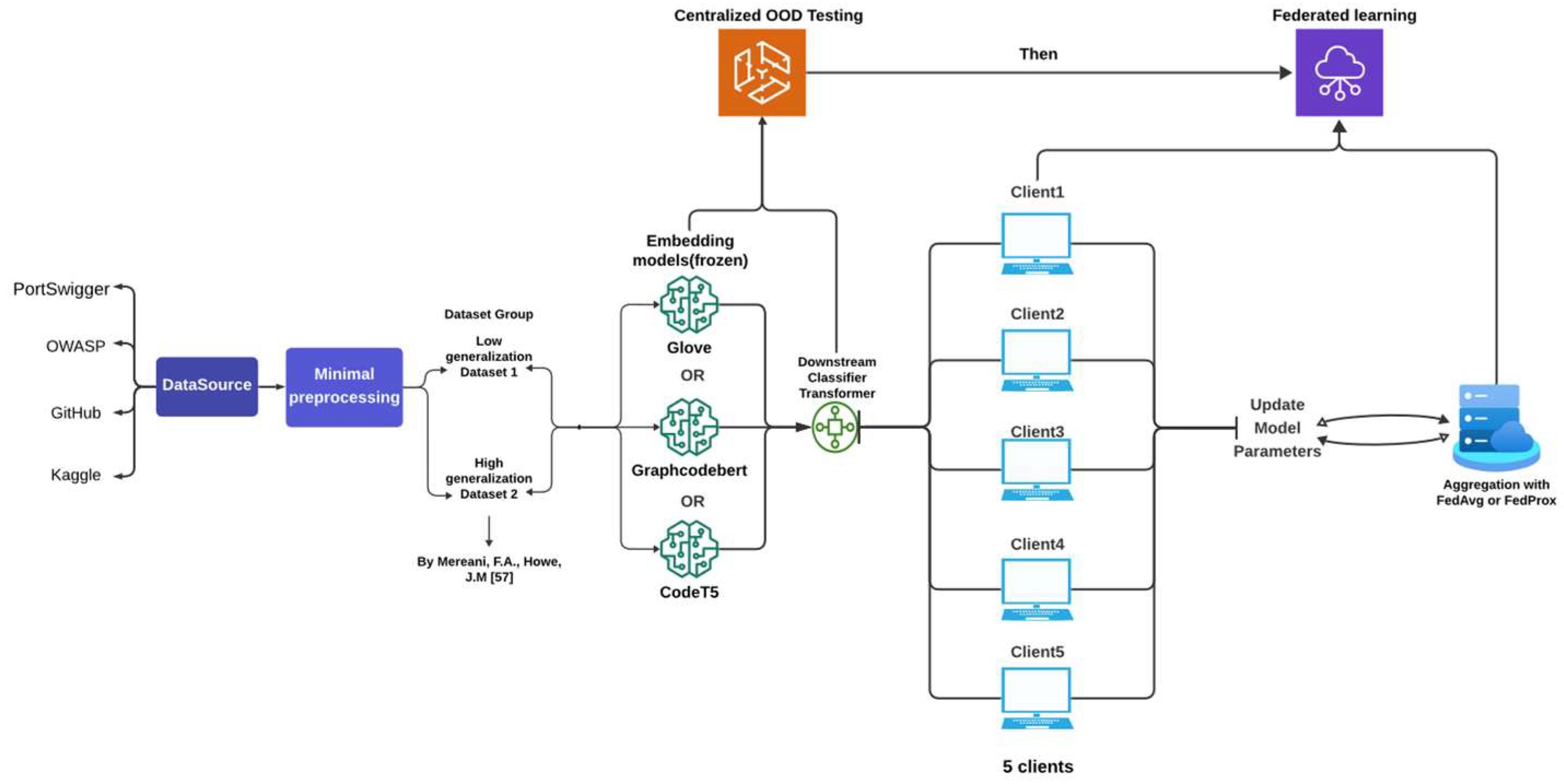
Figure 1.
Project Pipeline.
Figure 1.
Project Pipeline.
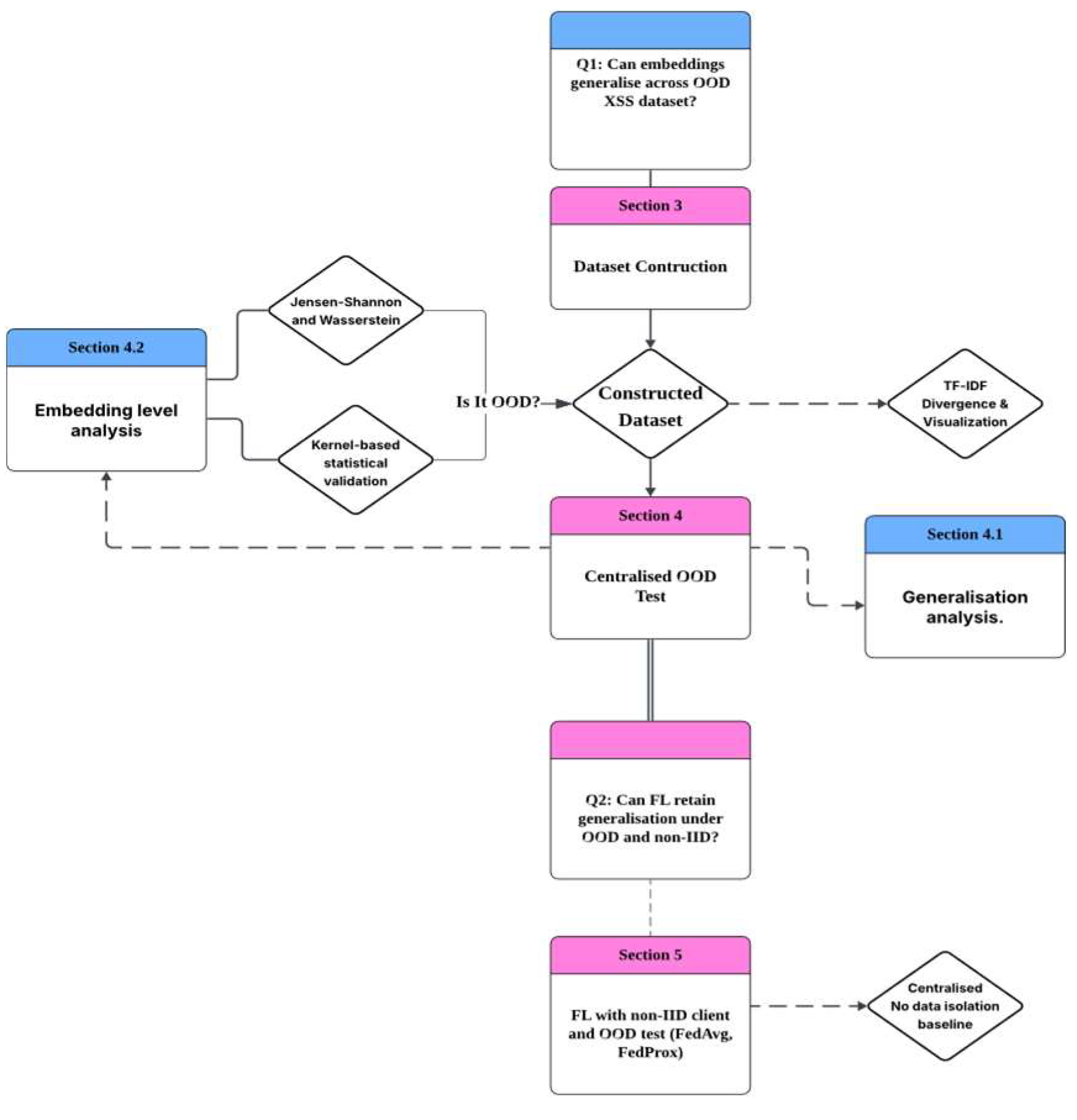
Figure 2.
Paper Logic flow.
Figure 2.
Paper Logic flow.
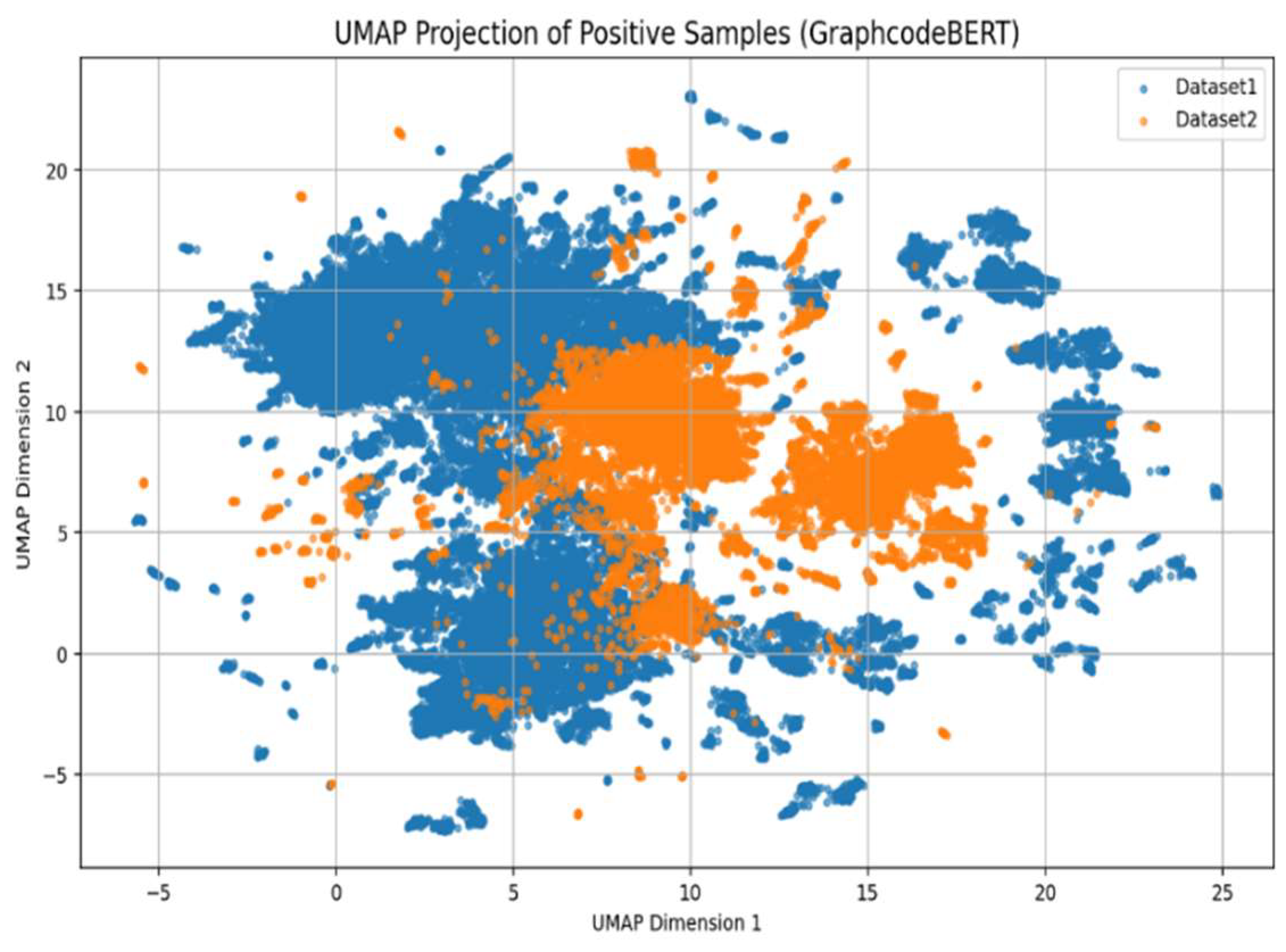
Figure 3.
UMAP of GraphcodeBERT’s embedding positive samples distributions between two datasets.
Figure 3.
UMAP of GraphcodeBERT’s embedding positive samples distributions between two datasets.
Figure 4.
Confusion matrices (per-class normalised, percentage) of the classifier trained on dataset 1.
Figure 4.
Confusion matrices (per-class normalised, percentage) of the classifier trained on dataset 1.
Figure 5.
Confusion matrices (per-class normalised, percentage) of the classifier trained on dataset 2.
Figure 5.
Confusion matrices (per-class normalised, percentage) of the classifier trained on dataset 2.
Figure 6.
Cross-Dataset Classification Performance across Embedding Models. (CT5 refers to CodeT5).
Figure 6.
Cross-Dataset Classification Performance across Embedding Models. (CT5 refers to CodeT5).
Figure 7.
Classifier’s performance change under OOD scenarios.
Figure 7.
Classifier’s performance change under OOD scenarios.
Figure 8.
Train data distribution strategy and sample numbers.
Figure 8.
Train data distribution strategy and sample numbers.
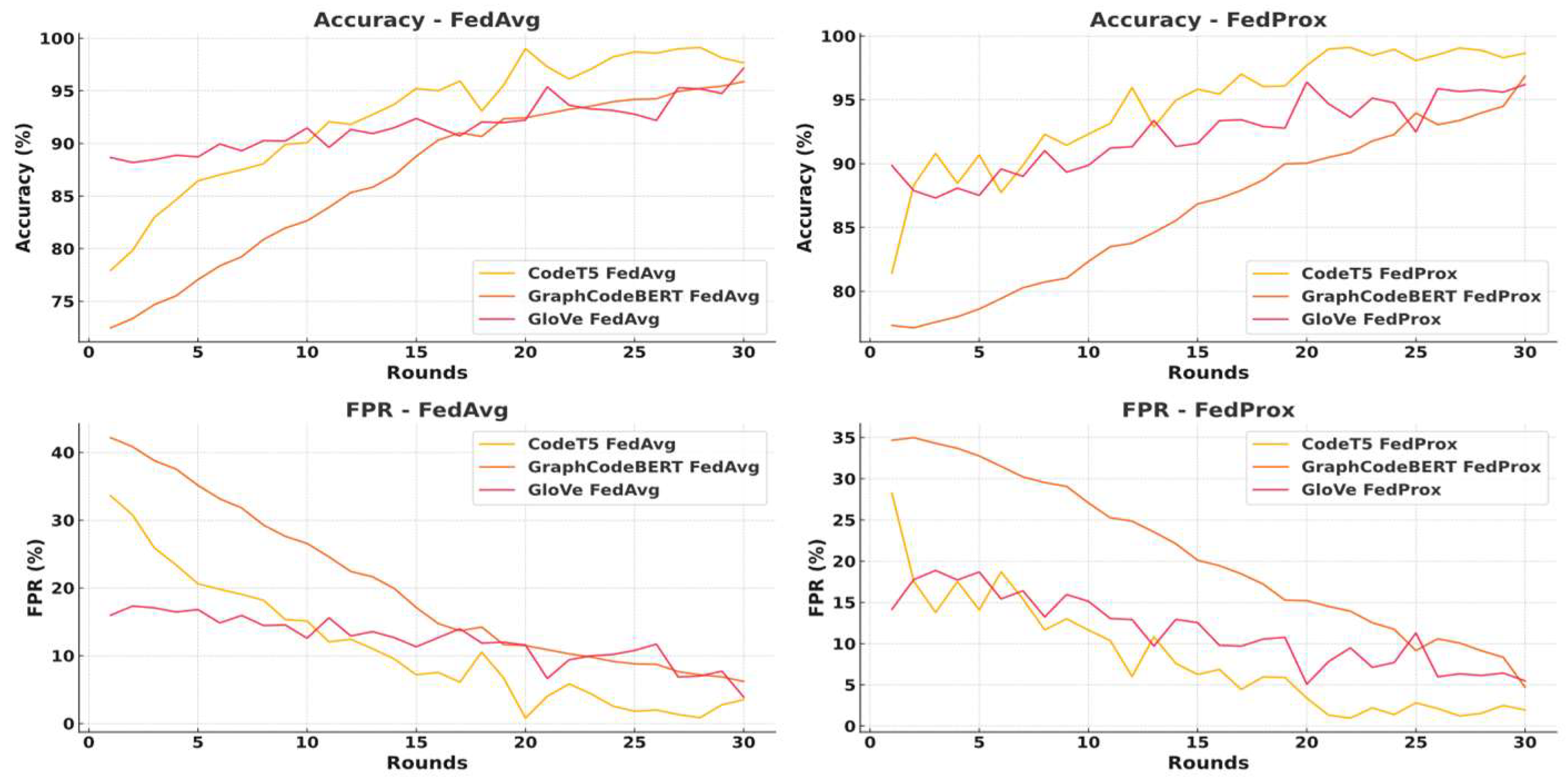
Figure 9.
Classifier convergence curve with GloVe-6b-300d embeddings under FedAvg and FedProx with learning rate, 0.001 or 0.005, aggregation rounds = 50 or 30.
Figure 9.
Classifier convergence curve with GloVe-6b-300d embeddings under FedAvg and FedProx with learning rate, 0.001 or 0.005, aggregation rounds = 50 or 30.
Figure 10.
Classifier convergence comparison under FedAvg and FedProx aggregation with different embedding models, aggregation rounds = 30, learning rate 0.005.
Figure 10.
Classifier convergence comparison under FedAvg and FedProx aggregation with different embedding models, aggregation rounds = 30, learning rate 0.005.
Figure 11.
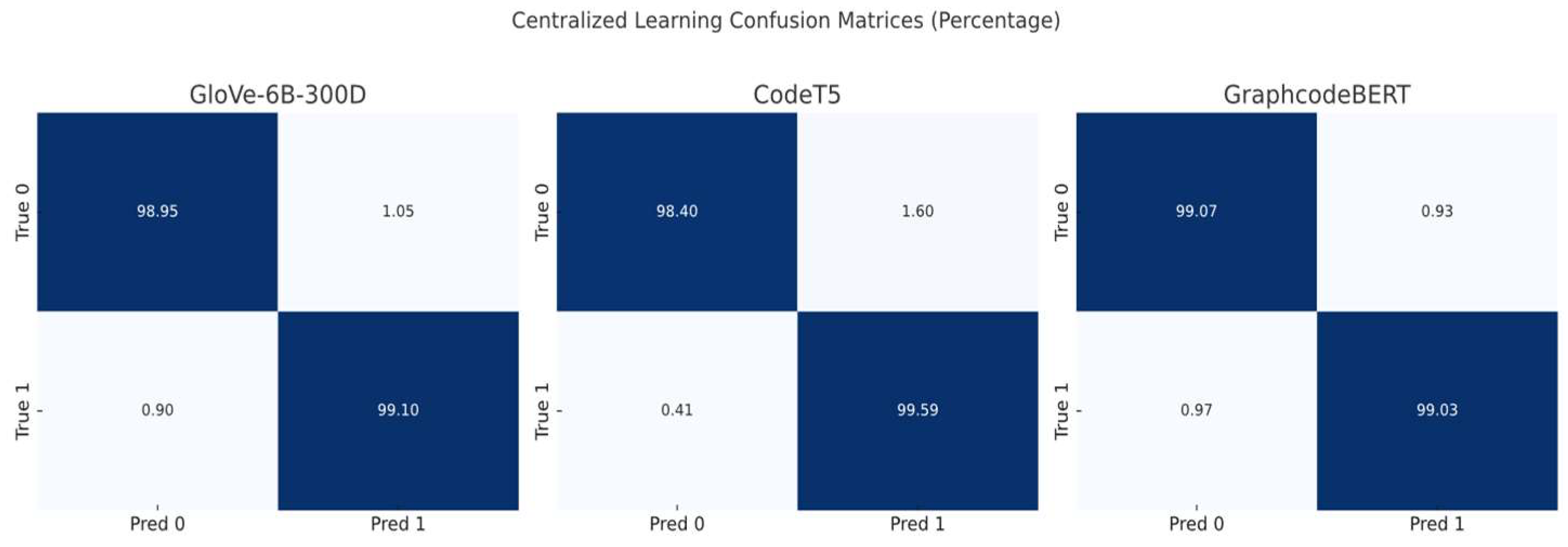
Confusion matrices (per-class normalised, percentage) under centralised training without data isolation.
Figure 11.
Confusion matrices (per-class normalised, percentage) under centralised training without data isolation.
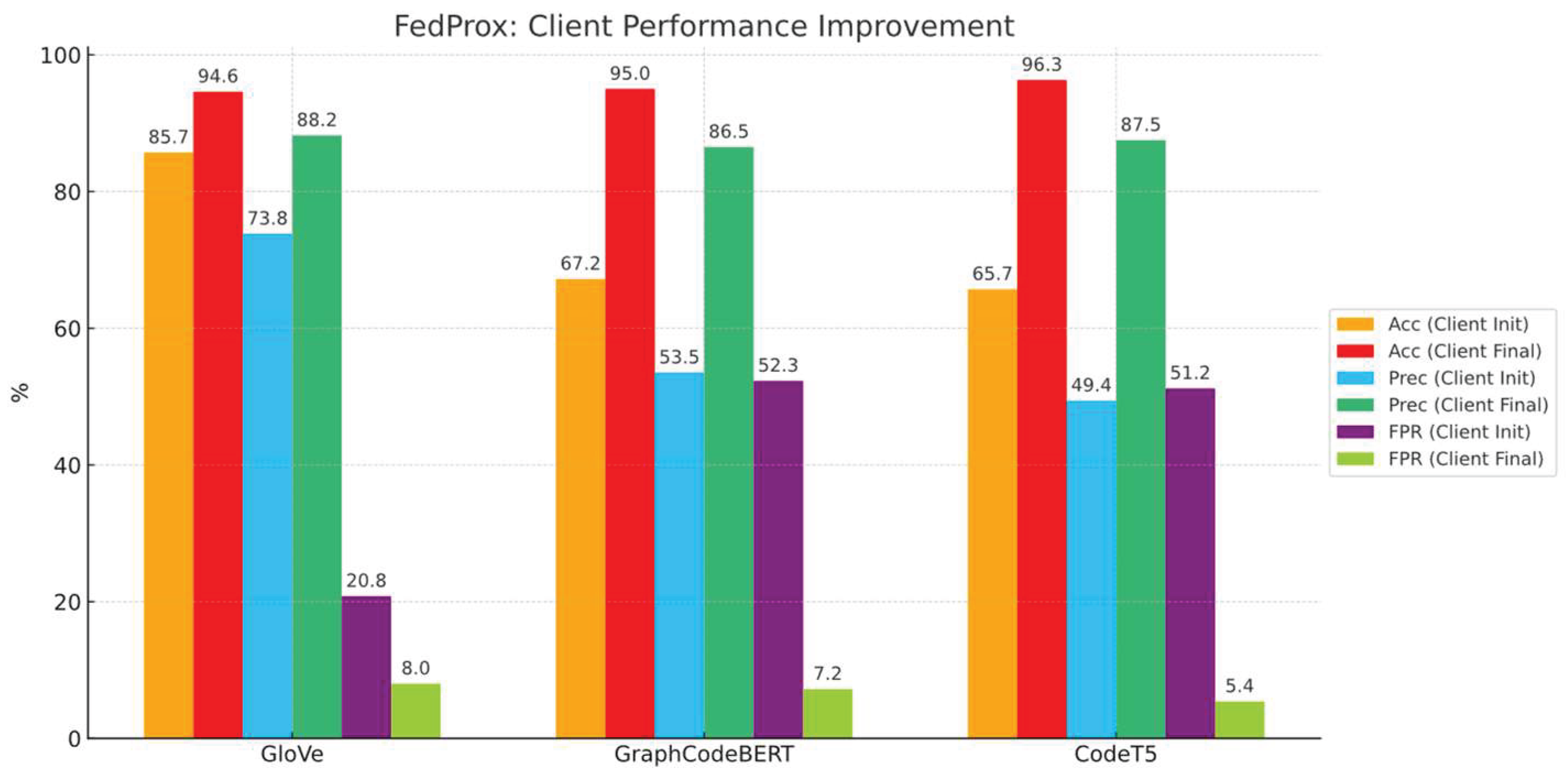
Figure 12.
A single client's best performance improvement comparison with different embedding models. The initial testing is the first round, and the final results are tested in 30 rounds.
Figure 12.
A single client's best performance improvement comparison with different embedding models. The initial testing is the first round, and the final results are tested in 30 rounds.
Table 1.
High-frequency pattern replacements.
Table 1.
High-frequency pattern replacements.
| Function Name Examples |
Rationale |
| Console.error |
Outputs an error message to the console. |
| confirm |
Displays a confirmation dialog asking the user to confirm an action. |
| prompt |
Displays a prompt to input information. |
Table 2.
Quantitative feature-level analysis.
Table 2.
Quantitative feature-level analysis.
| Metrics |
Baseline (IID) |
Negative samples |
Positive Samples |
| Top-100 TF-IDF |
70-90 |
20 ± 1 |
63 ± 1 |
| Jaccard similarity |
70-90% |
10.50% ± 1 |
45.98% ± 1 |
| cosine similarity |
0.85-0.95 |
0.2230 ± 0.01 |
0.4988 ± 0.01 |
Table 3.
Overfitting validation on same dataset.
Table 3.
Overfitting validation on same dataset.
| Embedding Model |
Accuracy |
FPR |
Recall |
Precision |
Test Dataset Type |
| GloVe-6B-300d |
98.12±1% |
1.31±1% |
98.45±1% |
98.29±1% |
20% of Same dataset |
| CodeT5 |
98.30±1% |
2.21±2% |
98.31±1% |
98.16±1% |
20% of Same dataset |
| GraphcodeBERT |
99.24±0.5% |
0.87±2% |
99.40±0.5% |
99.02±0.5% |
20% of Same dataset |
Table 4.
Exchanged positive samples in dataset 2 (As a test dataset) performance comparison.
Table 4.
Exchanged positive samples in dataset 2 (As a test dataset) performance comparison.
| Embedding Model |
Accuracy |
FPR |
Precision |
Recall |
Positive Sample |
| GraphcodeBERT |
56.80% |
66.22% |
44.82% |
99.69% |
Dataset 1 |
| 71.57% |
68.19% |
68.39% |
99.70% |
Dataset 2 |
Table 5.
Regurgitation of two embedding model, downstream Average (5times) performance comparison.
Table 5.
Regurgitation of two embedding model, downstream Average (5times) performance comparison.
| Embedding Model |
Accuracy |
Recall |
Precision |
FPR |
Classifier Hyperparameters |
| GloVe-6B-300d |
65.84% |
98.53% |
50.65% |
51.79% |
Lr = 0.005, drop out = 0.1 |
| 69.31% |
98.08% |
53.38% |
46.21% |
Lr = 0.001, drop out = 0.1 |
| 79.00% |
94.74% |
63.41% |
29.49% |
Lr = 0.001, drop out = 0.5 |
| GraphcodeBERT |
56.80% |
99.69% |
44.82% |
66.22% |
Lr = 0.001, drop out = 0.1 |
| 57.25% |
99.63% |
45.03% |
65.24% |
Lr = 0.0005, drop out = 0.3 |
| CodeT5 |
59.50% |
99.26% |
46.36% |
61.95% |
Lr = 0.001, drop out = 0.1 |
| 66.42% |
97.86% |
51.09% |
51.06% |
Lr = 0.0005, drop out = 0.3 |
Table 6.
Jensen-Shannon and Wasserstein divergence between Dataset 1 and Dataset 2 across different embedding models.
Table 6.
Jensen-Shannon and Wasserstein divergence between Dataset 1 and Dataset 2 across different embedding models.
| Comparison |
JSD |
WD |
| GraphCodeBERT |
0.2444 |
0.0758 |
| GloVe |
0.3402 |
0.0562 |
| CodeT5 |
0.3008 |
0.0237 |
Table 7.
Global Classifier’s performance records under FedProx with different embedding models after 30 rounds of aggregation.
Table 7.
Global Classifier’s performance records under FedProx with different embedding models after 30 rounds of aggregation.
| Embedding Model |
Accuracy |
FPR |
Precision |
Recall |
F-1 |
| GraphcodeBERT |
99.92 / 95.02% |
0.69 / 6.76% |
99.94 / 86.48% |
99.94 / 99.49% |
99.94 / 92.86% |
| GloVe-6b-300d |
98.63 / 94.06% |
1.35 / 9.69% |
99.69 / 86.84% |
99.61 / 98.87% |
99.65 / 93.25% |
| Code T5 |
99.64 / 96.13% |
0.31 / 3.19% |
99.70 / 94.48% |
99.74 / 99.04% |
99.04 / 96.77% |
Table 8.
No data isolation scenario: Classifier performance results.
Table 8.
No data isolation scenario: Classifier performance results.
| Embedding model |
Accuracy |
FPR |
Precision |
Recall |
F1-Score |
| GloVe-6B-300d |
99.01%±1.2 |
1.05%±1.4 |
98.56%±1.5 |
99.10%±1.5 |
98.83%±1.1 |
| CodeT5 |
98.90%±0.5 |
1.60%±1.1 |
97.83%±0.5 |
99.59%±0.3 |
98.70%±1.4 |
| GraphcodeBERT |
99.05%±0.7 |
0.93%±1.2 |
98.72%±1.5 |
99.03%±0.5 |
98.87%±1.2 |