Algorithmic Techniques for GPU Scheduling: A Comprehensive Survey

1. Introduction

Over the past decade, graphics processing units (GPUs) have matured from niche graphics accelerators into general-purpose, high-throughput computing engines, fundamentally altering how we approach data- and compute-intensive tasks. As their use has proliferated beyond rendering—spanning scientific simulation, deep learning, and real-time analytics — traditional CPU-focused schedulers have struggled to balance the massive parallelism and unique memory hierarchies of modern GPU workloads.

This survey brings together findings from across the GPU-scheduling literature to map out both established methods and the latest innovations. We review a spectrum of algorithmic strategies—starting with classic formulations such as bin-packing and priority-queue approaches, and moving toward contemporary, data-driven schemes that employ machine learning for adaptive decision making. For each class of algorithm, we discuss its impact on key performance metrics (e.g., throughput, latency, and utilization) and identify the workload or cluster environments in which it excels. Our goal is twofold: to give researchers a clear picture of the current state of the art and emerging directions in GPU scheduling, and to furnish practitioners with practical guidance for tailoring schedulers to their specific data-center architectures and workload profiles.

1.1. The History and Evolution of GPUs

Originally conceived for real-time graphics rendering, GPUs have since outgrown their narrow origins to become indispensable engines for a wide spectrum of compute-intensive tasks. Their story begins in 1968 with the founding of Evans & Sutherland Computer Corporation to build custom graphics hardware [1]. A defining moment arrived in 1999 when NVIDIA introduced the GeForce 256—often credited as the first “modern” GPU, which established the benchmark for future GPU designs and capabilities [2].

Over the following decades, GPU architectures have seen dramatic enhancements, most notably in programmability, allowing developers to exploit massive parallelism for non-graphical workloads [3]. Today, GPUs drive applications across gaming, professional visualization, high-performance scientific computing, machine learning, and even cryptocurrency mining [4,5,6]. The market has diversified into several segments—consumer and gaming GPUs, professional and workstation cards, data-center artificial intelligence (AI) accelerators, and mobile/embedded solutions — each optimized for distinct performance, power, and feature requirements [7,8,9].

A pivotal milestone arrived in 2006 with NVIDIA’s unveiling of the Tesla architecture, which for the first time incorporated unified shader functionality [3]. Shaders—small programs executed on the GPU to manipulate graphics data—had until then been processed through distinct vertex and pixel pipelines [10]. By unifying these pipelines, every core gained the ability to execute any shader type, vastly increasing both flexibility and programmability. This architectural evolution laid the groundwork for general-purpose GPU computing frameworks such as CUDA (compute unified device architecture) [3,11].

In the years since, GPUs have become omnipresent, powering devices from high-end desktop workstations to smartphones [2,12]. High-performance systems typically employ dedicated GPUs, whereas integrated GPUs (iGPUs)—embedded within the CPU and sharing system memory—are widespread in entry- to mid-level consumer hardware [2,13]. Although iGPUs offer advantages in cost and energy efficiency, they lag significantly in raw compute power: for example, a consumer-grade dedicated GPU of a given generation can deliver between four and twenty-three times the single-precision floating-point throughput of its integrated counterpart [13,14].

1.2. GPU vs CPU: Similarities and Differences in Architecture and Fundamentals

A meaningful comparison between CPUs and GPUs spans architectural design, performance characteristics, memory hierarchy, and resource management. Traditional CPUs prioritize sequential instruction throughput and general-purpose flexibility, whereas modern GPUs consist of thousands of smaller, specialized cores engineered for massive data parallelism [15,16,17,18]. For instance, while a high-end server CPU may reach roughly 192 cores, the NVIDIA A100 GPU boasts 6,912 cores, dramatically illustrating the divergent scaling strategies of these platforms [19,20]. CPUs often encounter diminishing returns from core count increases—constrained by Amdahl’s law and the overhead of sequential resource management—whereas GPUs excel at scheduling and executing thousands of parallel threads with minimal latency [18,21,22,23,24]. Consequently, for highly parallelizable workloads such as scientific simulations and deep learning, GPUs can achieve speedups ranging from 55 × to over 100 × compared to CPUs, a performance gap that further widens with larger model sizes and batch dimensions [25,26,27].

Memory architecture further accentuates the contrast between CPUs and GPUs. GPU workloads—particularly in graphics rendering and deep learning—rely on extremely high memory bandwidth to sustain their massive parallel operations [28]. To meet these demands, GPUs employ specialized on-board memory (e.g., VRAM) and allocate a much larger proportion of registers relative to main memory than CPUs do [29,30]. Consequently, modern data-center GPUs can deliver up to 54 × the memory bandwidth of comparable CPUs, highlighting a profound disparity in data-movement capability [27].

Resource management also diverges sharply between the two architectures. In standalone systems, the GPU driver orchestrates memory allocation, context switching, and command handling, serving as the critical interface between the operating system and the hardware [31,32]. Meanwhile, runtime frameworks such as CUDA and OpenCL furnish low-level scheduling and execution controls [33,34]. At scale, high-performance computing clusters layer in sophisticated orchestration platforms—SLURM, Borg, Yarn, and Kubernetes—to allocate GPU resources, track utilization, and optimize throughput across nodes [35,36,37,38,39]. These systems enforce workload isolation, priority policies, and cluster-wide performance tuning [40], yet the GPU driver remains indispensable for fine-grained, device-level control of the hardware [41].

The performance of GPUs is typically evaluated across several key metrics. Floating-point operations per second (FLOPs) measure raw arithmetic throughput and are broken out by precision—16-bit (half), 32-bit (single), 64-bit (double), and, more recently, 8-bit operations [42,43,44,45]. Tensor performance, reported in TOPS (tera operations per second), reflects the capabilities of specialized tensor cores for AI/ML (machine learning) workloads (e.g., INT8 TOPS for inference or FP16 TFLOPS for training) [46]. Memory bandwidth, in GB/s or TB/s, gauges how quickly data can be moved on and off the GPU—an essential factor for large-scale deep learning [45]. The number of CUDA cores (Nvidia) or stream processors (AMD) indicates parallelism potential [19,47], while VRAM capacity determines the size of models and datasets that can be held in memory [45]. Additionally, clock speed (MHz/GHz) impacts per-core instruction throughput [48], PCIe bandwidth governs CPU–GPU data transfer rates [49], and power consumption (Watts) affects overall energy efficiency and cooling requirements [45,48].

Beyond raw numbers, a GPU’s compute capability defines its supported feature set—such as specific CUDA compute capability levels on Nvidia hardware [45]. Modern data-center GPUs like the Nvidia A100 illustrate these principles in practice: they pack 6,912 cores, 40 GB or 80 GB of VRAM, and 54.2 billion transistors, delivering up to 624 TFLOPS in half-precision or 312 TFLOPS in single-precision workloads [42,43,44]. As machine-learning demands continue to grow, architectures such as the A100 are specifically engineered to optimize both scalability and efficiency for large-scale AI training and inference [1,50].

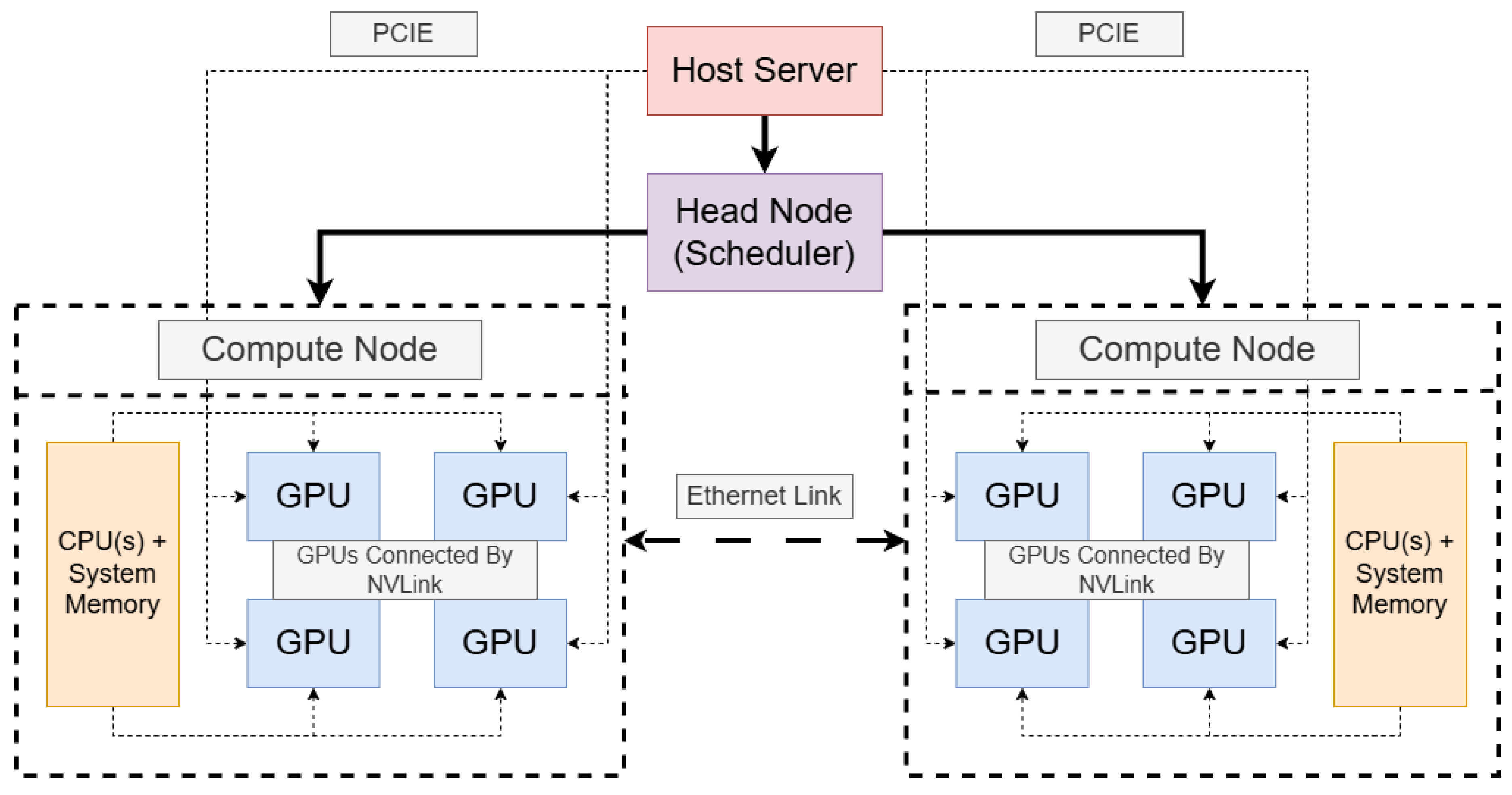
1.3. Cluster Computing and the Necessity of GPU Scheduling Algorithms

Cluster computing has undergone significant evolution over the past few decades. The initial drive for greater computational throughput gave rise to CPU clusters composed of a small number of high-performance cores [51]. However, as machine learning (ML) and deep learning (DL) workloads surged, GPUs have become an indispensable element of modern infrastructure. Large-scale GPU clusters—once the domain of specialized scientific centers—are now commonplace in academic, industrial, and cloud environments [52,53,54]. These systems comprise interconnected nodes, each hosting one or more GPUs, and often feature heterogeneous hardware configurations that integrate diverse CPU architectures, memory hierarchies, and GPU generations [44,55,56,57]. To support the high data rates demanded by ML/DL workloads, GPU clusters employ high-speed interconnects—such as PCIe, NVLink, and InfiniBand—to facilitate rapid data exchange both within and across nodes [58,59]. Figure 1 depicts a representative GPU cluster architecture.

In modern GPU clusters, the high capital and operational costs of GPU hardware and supporting infrastructure demand sophisticated scheduling strategies. High-end GPUs such as the Nvidia A100 80 GB can cost nearly $15 000 [60], and utilization rates in large-scale deployments can plummet to 50 % [44,61]. Such underutilization reflects not a shortage of demand but suboptimal resource allocation. Critical resources—including GPU and CPU compute units, memory bandwidth, and interconnect bandwidth—are both scarce and expensive [36,56,62,63]. Advanced scheduling algorithms that optimize across these dimensions are therefore essential to minimize idle time, balance operator and user objectives, and achieve substantial cost efficiencies in large-scale environments.

Several intertwined factors exacerbate scheduling challenges in these clusters. Heterogeneity extends beyond hardware to encompass a wide spectrum of job profiles: from training workloads that run for days [64] to latency-sensitive inference tasks that complete in milliseconds [65]. Uncertainty in execution times further complicates allocation decisions, as does the diversity of resource requests—ranging from fractional GPUs to multi-GPU or CPU-only configurations. Consequently, simple heuristics such as first-fit or bin-packing fail to capture the multi-dimensional nature of GPU cluster scheduling [36].

Scheduling challenges are also exacerbated by conflicting objectives between cluster operators and users. Operators typically aim to optimize GPU and resource utilization while minimizing job completion times [56,66,67,68], while users prioritize job accuracy and fairness in allocation [62,69,70]. As a result, no single scheduling solution is universally applicable. Algorithmic scheduling techniques have already shown impressive performance, with one algorithm reducing unallocated GPUs by up to 49% [36]. Such improvements could result in significant cost savings, particularly in large-scale data centers with thousands of GPUs. For instance, Helios, operated by SenseTime, manages four clusters with a total of 6,416 GPUs [64].

Building on the challenges outlined above, large language models (LLMs) further amplify the scale and complexity of GPU cluster scheduling. In certain LLM configurations, GPU utilization can dip below 50%, and decreases further as model parameter counts grow—despite proposed methods that can boost utilization to over 75% [61]. Resource allocation for LLM training brings additional difficulties not encountered in standard deep learning workloads, since most existing schedulers were not designed to handle the vast scale, heterogeneity, and dynamic demands of LLMs. Overcoming these challenges will require more sophisticated scheduling strategies.

1.4. Paper Overview

This survey is structured as follows. Section 2 reviews a range of scheduling models and algorithmic paradigms, grouping them into heuristic-based, optimization-based, learning-driven, and queuing-theoretic approaches. Section 3 offers a comparative analysis of these methods, highlighting their respective strengths and weaknesses, the objectives they target, and practical considerations for real-world deployment. Finally, Section 4 identifies open challenges in GPU resource management and proposes promising directions for future research.

Throughout the paper, we introduce GPU-specific terminology as it becomes relevant. For standard scheduling concepts not covered here, we refer the reader to Pinedo’s comprehensive treatment [71].

2. Models

Accurate modeling is the foundation of modern GPU cluster scheduling, allowing us to capture intricate real-world constraints and objectives. A formal model provides a principled framework for reasoning about resource allocation, assessing trade-offs, and guaranteeing desired service levels. Without such models, simplistic schedulers may leave GPUs idle, violate fairness criteria, or fail to meet QoS and SLO targets. For instance, a cluster hosting long-running ML training workloads must allocate GPUs judiciously to prevent both idle hardware and excessive queuing delays [43,72].

In this section, we survey the key modeling techniques used in GPU cluster scheduling. We begin by identifying the core components present in most models, then present a taxonomy of modeling approaches. Afterward, we review the metrics commonly employed to evaluate scheduler performance, and conclude with a comparative discussion of each approach’s strengths and weaknesses.

By casting objectives — such as minimizing job completion time or maximizing throughput — into precise mathematical formulations, these models directly inform the design of efficient scheduling algorithms.

2.1. Components of a Model

GPU cluster architecture. Models typically represent the cluster as a set of compute nodes, each equipped with one or more GPUs, along with CPUs, memory, and high-speed network interfaces. Within a node, GPUs communicate over a fast interconnect, while nodes themselves are linked by a high-speed network, enabling workloads to span multiple machines [73,74]. A central scheduler or cluster manager receives user submissions and determines how to assign GPUs to each job [75]. Jobs may demand fractions of a GPU, a single GPU, or multiple GPUs. Unless stated otherwise, we assume jobs arrive online and wait in a queue until sufficient resources become available.

Jobs and GPU requirements. We model three primary entities: jobs, resources, and queues. Let $J=\{1,2,\dots ,n\}$ denote the set of jobs to be scheduled. Each job $j\in J$ is characterized by:

• GPU demand $g_j$ (which may be fractional or span multiple GPUs),
• estimated runtime $p_j$,
• release time $r_j$ (for online arrivals),
• optional priority or weight.

The cluster provides m GPU slots, which may be homogeneous or heterogeneous across nodes. Scheduling systems may use a single global queue or multiple queues (e.g., to separate jobs by GPU type or priority) [76]. Some models allow preemption, while others assume jobs run non-preemptively to completion [77,78]. In offline formulations, job runtimes may be known or stochastic; in online settings, runtimes are unknown and decisions must be made with incomplete information [79,80]. Gang scheduling is often assumed for multi-GPU jobs, meaning a job requiring $g_j$ GPUs only starts when all $g_j$ GPUs are free, and those GPUs remain dedicated until the job finishes [44,81,82,83]. Some models ignore inter-GPU communication overhead, whereas others explicitly optimize job placement to minimize it [84,85]. Finally, models differ in whether they assume cluster homogeneity or account for mixed GPU types and generations [44,55].

Scheduling timeline. Scheduling models vary in their representation of time, adopting either discrete or continuous frameworks. Discrete-time formulations divide the schedule into uniform slots, which are well suited to Markov decision processes and dynamic programming approaches [77]. Continuous-time models, by contrast, treat job arrivals and completions as asynchronous events, capturing finer temporal dynamics. Many models further simplify by assuming non-preemptive execution, where jobs run to completion once scheduled. Preemptive models—used for GPU time-sharing or when supporting checkpoint–and–restart—must quantify preemption overheads [86]. Finally, time-sharing frameworks introduce a time quantum, the fixed interval for which GPUs are leased to jobs before the scheduler reevaluates resource allocations [87].

Objectives. Let the system state be defined by the set of pending jobs and available GPUs. A scheduling model then specifies an objective function to optimize and a set of constraints to enforce. At a high level, the scheduler must decide which jobs to run, when, and on which GPUs to optimize metrics such as completion time or throughput. Formally, this becomes a combinatorial optimization problem: for example, binary variables $x_{j,k,t}\in \{0,1\}$ can indicate whether job j starts on GPU k at time t. Constraints ensure each GPU runs at most one job at a time, that job j occupies $g_j$ GPUs for its processing time $p_j$, and that allocations respect job demands and hardware limits (e.g., preventing over-allocation under multi-instance virtualization). Even simple objectives — such as minimizing makespan $C_{max}$ on m identical machines (problem $P\Vert C_{max}$) — are NP-hard for $m\ge 2$ [88]. Similarly, minimizing total completion time ${\sum }_j{C}_j$ or average waiting time is NP-hard [89,90]. Consequently, exact optimization is intractable at scale, and most models instead provide a formal foundation for developing and analyzing heuristics and approximation algorithms [91]. A summary of common scheduling objectives appears in Table 1.

Beyond the core objectives defined in Table 1, scheduling models often refine or combine multiple performance metrics. Many objectives are functions of a job’s completion time $C_j$, or related measures such as waiting time $W_j=C_j-r_j-p_j$. Common examples include minimizing average waiting time,

$${\displaystyle \frac{1}{n}}\sum _{j\in J}{W}_j,$$

or maximizing throughput, i.e., the number of jobs completed per unit time [92]. Alternative objectives target the makespan ${max}_j{C}_j$, deadline compliance, or fairness metrics like slowdown — the ratio of a job’s response time to its processing time — to prevent excessive delays for any job [76,93].

Fairness is a central concern in many models. Schedulers may minimize the maximum slowdown across all jobs or ensure that each job’s performance is at least as good as if it ran in isolation on an equal share of the cluster. Mechanisms such as Dominant Resource Fairness (DRF) and its variants (e.g., implemented in Dorm) aim to allocate the dominant resource — GPUs — equitably among users over time [94,95].

Energy efficiency is another critical objective. Some formulations incorporate constraints or multi-objective functions that trade off performance and power consumption. Techniques like dynamic voltage and frequency scaling (DVFS) or powering down idle GPUs can be modeled to minimize total energy usage [96,97,98,99,100]. Energy-aware schedulers seek to reduce GPU power draw while still meeting performance SLOs [101,102,103].

In clusters dominated by ML workloads, scheduling metrics often extend beyond runtime. For example, SLAQ evaluates performance based on the final model accuracy or training loss, rather than just job duration. Other models incorporate job-specific deadlines or accuracy targets directly into the objective function [104].

In summary, a rigorous scheduling model precisely defines (1) what constitutes a feasible schedule—through resource and timing constraints—and (2) what constitutes a good schedule—through one or more explicitly stated objective functions. This formalism underpins the systematic design and analysis of effective scheduling algorithms.

2.2. Categorization of Models

GPU scheduling problems can be modeled in various ways, each capturing different assumptions about job arrivals, system information, and analysis techniques. We categorize these models along several key dimensions and highlight their respective strengths and weaknesses.

Offline and online scheduling models. A fundamental distinction is whether all jobs are known in advance (offline scheduling) or arrive over time (online scheduling). Offline models assume a fixed set of jobs $J=\{1,2,\dots ,n\}$ with known runtimes and resource requirements. The goal is to compute a schedule—an assignment of start times and GPUs to each job—that optimizes a chosen objective (e.g., minimizing total completion time or the makespan). Offline scheduling can be formulated as a deterministic optimization problem, often reducing to NP-hard variants of classic machine scheduling problems [105]. With complete information, near-optimal or optimal schedules can be obtained for moderate-sized instances via integer programming or exhaustive search; however, these approaches do not scale to the large, dynamic workloads observed in real GPU clusters [106].

In contrast, online models treat scheduling as an ongoing process in which jobs arrive according to some distribution and decisions are made without knowledge of future arrivals. The scheduler reacts in real time to job arrivals and completions. Online algorithms are commonly evaluated via competitive analysis, proving performance bounds relative to an offline optimum — for example, guaranteeing a completion time at most c times the optimal (c-competitive) [107,108]. Strong worst-case guarantees are often elusive for complex objectives, and without resource augmentation the competitive ratio may be unbounded. To obtain more meaningful metrics, many analyses instead assume stochastic workloads (e.g., Poisson arrivals with rate $\lambda$, job sizes drawn from known distributions), which enables optimization of expected performance or derivation of steady-state results via queueing theory [109]. Classical queueing models such as the $M/G/k$ system (Poisson arrivals, general service times, k servers) yield predictions for waiting times and queue lengths, and form the basis for many practical online GPU schedulers that serve jobs submitted unpredictably by users [79]. Some recent models further incorporate limited lookahead or predictions — using, for instance, user-provided runtime estimates or historical profiles—to blend online reactivity with partial future knowledge [110].

Queueing-theory based models. Queueing-theoretic abstractions treat each GPU—or collection of GPUs—as a server and model jobs as customers, yielding analytic expressions for performance metrics such as mean waiting time or slowdown. Classical results underpin several scheduling policies: when job sizes are known, the shortest remaining processing time (SRPT) discipline minimizes mean completion time; when sizes are unknown, the Gittins index policy achieves optimal mean slowdown. Likewise, least attained service (LAS)—implemented in Tiresias via a time-slicing scheme—draws directly on these theoretical insights and operates effectively without explicit size estimates.

At the scale of multi-GPU clusters, systems are often represented as an $M/G/k$ queue with a central dispatcher [81]. Such models, however, typically abstract away critical factors like placement constraints and inter-GPU communication overheads. In real-world setups, jobs may require data locality or specialized hardware features (e.g., tensor cores) and can suffer performance degradation if spread across distant nodes—issues that a simple $M/G/k$ framework cannot capture.

To address these limitations, more sophisticated queueing formulations introduce multi-class networks: separate queues represent different GPU types or workload classes, and additional parameters model network delays in distributed training or inference. While these extensions better capture heterogeneity and locality, they trade off analytical tractability. Nonetheless, even simplified queueing approaches remain valuable for informing scheduler design — for instance, by quantifying the impact of FCFS versus priority-based service disciplines on average waiting times under varying load conditions [111].

Optimization-based models. A prevalent approach formulates GPU scheduling as a mixed-integer optimization problem. In time-indexed MILP formulations, binary variables $x_{j,k,t}$ indicate whether job j runs on GPU k at time t; alternative formulations introduce assignment variables $x_{j,k}$ and ordering variables $y_{j,j^{\prime }}$ to capture both placement and sequencing decisions [112,113]. Common objectives include minimizing total (weighted) completion time or maximizing fairness, subject to constraints that enforce at most one job per GPU at any time and any job precedence relations. While these models afford exactness, their variable count grows with the product of jobs, GPUs, and time slots, making them computationally expensive for large instances. Consequently, MILP-based methods are most appropriate in offline settings for small to medium clusters or as benchmarks for heuristic algorithms, where modest problem sizes can often be solved to optimality [91].

To extend optimization into dynamic environments, some systems employ a rolling-horizon strategy: they repeatedly solve an MILP over the current queue or a short future window, then enact the resulting allocation before re-optimizing as new jobs arrive. For example, TetriSched (not GPU-specific) uses an MILP to allocate resources based on learned inference models [106], and Gavel recasts various scheduling policies into optimization problems tailored for heterogeneous clusters [57]. Alternatively, hybrid frameworks like Cynthia formulate a cost-minimization problem with performance guarantees and then apply a bounded-search heuristic guided by lightweight runtime predictions to efficiently discover near-optimal resource configurations in cloud-based DDNN provisioning [114].

Optimization-inspired heuristics. Production GPU schedulers often employ simple, fast heuristics that support real-time decision making and ease of deployment [74]. A canonical example is a shortest-job-first greedy policy, which assigns the smallest pending job to any free GPU immediately upon becoming available. While such rules do not guarantee global optimality, they offer high responsiveness and lend themselves to probabilistic analysis. For instance, modeling GPUs as bins and arriving jobs as items enables evaluation of first-fit and best-fit decreasing placement heuristics:

• First-fit: assign each job to the first available GPU or time slot.
• Best-fit: assign each job to the GPU or slot that minimizes leftover capacity.

Despite their simplicity, these heuristics draw on combinatorial optimization principles and are straightforward to simulate and analyze.

Backfilling is a more advanced heuristic that boosts utilization by opportunistically scheduling smaller jobs ahead of larger, blocked jobs [115]. When the head-of-line job requires multiple GPUs and must wait, backfilling fills idle resources with shorter jobs, thereby reducing overall idle time. This approach is ubiquitous in HPC schedulers [116,117] and has been effectively adapted for GPU clusters.

Dynamic programming (DP) can solve certain simplified scheduling problems exactly via state-space recurrences, where each state encodes the set of completed and running jobs. However, the exponential growth of the state space renders DP infeasible at cluster scale. The heterogeneous earliest-finish-time (HEFT) algorithm offers a practical compromise: it applies DP-inspired analysis to a DAG of tasks, prioritizing and mapping jobs onto heterogeneous processors based on estimated finish times, yielding near-optimal schedules without exhaustive enumeration [118,119].

Hybrid methods combine optimization models with efficient combinatorial algorithms to balance solution quality and scalability. Allox, for example, constructs a bipartite graph at each scheduling interval—pending jobs on one side, available resources on the other—with edge weights reflecting estimated completion times, and solves a minimum-cost matching to assign jobs so as to minimize overall delay [120]. By leveraging specialized matching algorithms rather than brute-force searches, these hybrid heuristics achieve practical performance at scale.

Learning-based models. Recent scheduling frameworks leverage machine learning to predict job characteristics or adaptively optimize decisions. These learning-based models are typically classified into three categories: ML-assisted prediction models, reinforcement learning (RL) models, and hybrid learning models.

ML-assisted prediction models employ learned estimators to predict key job parameters — such as runtime or resource requirements — before scheduling. For each job j, a predictor $\widehat{p_j}=f\left(\mathrm{job}\mathrm{features}\right)$ (e.g., a linear regression, a neural network trained on historical logs, or user-provided estimates) approximates the true value $p_j$ [121]. By incorporating $\widehat{p_j}$ into placement and ordering decisions, schedulers can significantly improve backfilling efficiency and reduce queueing delays in HPC clusters [122]. For example, Optimus probes performance across varying GPU counts to build an online throughput model, dynamically allocating GPUs to maximize aggregate throughput [66], while AlloX performs brief profiling runs on CPU and GPU, fits a linear per-iteration time model, and selects the optimal platform for each job [120]. Robust implementations must also include mechanisms to tolerate or adapt to prediction errors.

Reinforcement learning (RL) models frame scheduling as a Markov decision process (MDP), where states encode resource utilization and queue lengths, actions correspond to dispatch or prioritization decisions, and rewards reflect metrics such as throughput or slowdown. An RL agent learns a dispatch policy by interacting with a simulated cluster or replaying historical traces. DeepRM, for instance, embeds both current and queued jobs in its state representation and dispatches batches to minimize average slowdown [77], while Decima incorporates a graph neural network to capture DAG-structured workloads and learns execution orderings that minimize end-to-end runtime [123]. These models can balance multi-objective goals—efficiency, fairness, QoS—through reward shaping, but their performance often hinges on the fidelity of the training environment. Recent multi-agent RL approaches extend this paradigm by treating GPUs or individual jobs as agents that coordinate to improve global performance [124].

Hybrid learning models combine the adaptability of ML with the predictability of classical heuristics. In these layered systems, ML components tune critical heuristic parameters — such as time-slicing intervals — while the final scheduling decisions rely on traditional rule-based mechanisms. Themis, for example, augments an auction-based scheduler by optimizing bid values through ML-driven models [81], and Pollux continuously adjusts per-job resource allocations (batch size and GPU count) based on observed throughput to steer training workloads toward optimal efficiency [68].

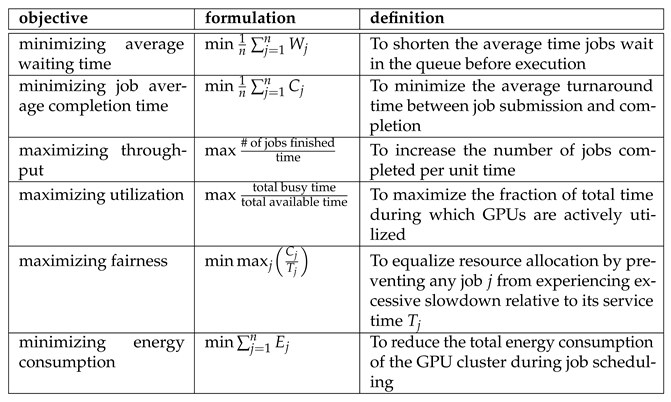
2.3. Evaluation Metrics and Validation Methods for Scheduling Models

Measuring the effectiveness of a scheduling model — and any algorithms it inspires — relies on well-defined metrics that capture both system efficiency and user-centric outcomes. Beyond the objectives listed in Table 1, scheduling for ML workloads introduces an important additional dimension: model quality. Optimizing solely for execution time can be misleading if, for example, resource allocations that minimize runtime degrade the final accuracy of a trained model. To address this, researchers have proposed ML-specific performance metrics. SLAQ assesses schedulers by the final training loss or accuracy achieved under a fixed resource budget, ensuring that faster completions do not come at the expense of model fidelity [104]. Pollux, on the other hand, defines goodput as the count of training samples that genuinely contribute to convergence, filtering out those wasted by suboptimal settings (e.g., excessively large batch sizes) [68]. These metrics are crucial whenever the ultimate goal of scheduling is not just speed but also the quality of the ML outcome.

After establishing appropriate metrics, scheduling models are typically validated through a combination of:

• Theoretical analysis, which proves bounds on performance or fairness under idealized assumptions;
• Simulation, which enables controlled studies—often using trace-driven or synthetic workloads—to compare designs across diverse scenarios;
• Real-world experiments, which deploy schedulers on actual clusters to evaluate behavior under production traffic and uncover practical considerations such as implementation overhead or robustness to unexpected load spikes. Together, these methods provide a comprehensive picture of a model’s strengths, limitations, and applicability.

Theoretical Analysis. After selecting appropriate performance metrics, one method for evaluating a scheduling model or policy is through theoretical analysis. This approach entails proving bounds or optimality guarantees under the model’s simplifying assumptions. For instance, one might show that a scheduling algorithm yields a makespan no greater than 1.5 × OPT (i.e., a 1.5-approximation) on any input, or that under a given stochastic workload model, a policy minimizes expected response time. When models are sufficiently constrained—say, by assuming independent jobs or exact knowledge of runtimes—tools from classical scheduling theory or queueing theory can be applied to derive these results. Such proofs lend confidence by demonstrating, for example, that a new strategy enjoys strictly better worst-case performance or fairness properties than existing approaches. That said, these guarantees often depend on idealized conditions—e.g., IID job sizes or negligible context-switch overhead—that real GPU clusters may violate [125]. Consequently, theoretical insights are most compelling when paired with empirical validation.

Simulation. To assess scheduling models in settings closer to real-world deployments, researchers employ event-driven simulators that model a GPU cluster’s behavior: jobs arrive, are queued, and then dispatched to virtual GPUs according to the scheduling policy, with completions and resource usage tracked precisely. Simulations may use synthetic workloads—drawn from statistical distributions—or replay traces of actual job arrivals and runtimes collected from production clusters [36,126]. Throughout each run, key metrics such as average job completion time, waiting-time distributions, GPU utilization over time, and fairness indices (e.g., Jain’s index or the proportion of jobs meeting specified SLOs) are recorded [113]. By stress-testing algorithms under diverse conditions—such as workload surges or heavy-tailed job sizes—simulation reveals behavior that analytic methods cannot easily capture. Simulators vary in fidelity, from lightweight discrete-event frameworks that abstract away low-level details to comprehensive cluster emulators incorporating network topology and GPU memory contention [127]. Many studies feed in production traces to ensure their experiments mirror operational realities. Comparing strategies side by side in simulation highlights each approach’s strengths and weaknesses (for example, excelling under high load but degrading when job sizes are unpredictable) and often drives further model refinement—such as adjusting assumed workload distributions to better fit observed data.

The most definitive validation of a scheduling model comes from deploying the scheduler on an actual GPU cluster and observing its performance under real workloads. Research prototypes are often tested on hardware ranging from small academic setups (tens of GPUs) to slices of production systems (hundreds of GPUs). For instance, the Tiresias scheduler was evaluated on a 60-GPU production testbed and demonstrated substantial reductions in median job completion time compared to the existing policy [79]. By running experiments on real clusters, one captures all the operational details and overheads that models and simulators may omit—including OS and driver overheads, resource-sharing effects, job startup latencies, and unpredictable user behavior. In these studies, new algorithms are typically benchmarked against standard baselines such as FIFO (first-in-first-out), Dominant Job First (DJF—a parallel-job variant of shortest-job-first), default Kubernetes or Slurm schedulers, and simple backfilling policies [36]. Researchers report not only average improvements but also gains at various percentiles (e.g., tail latency reductions) and analyze potential side effects—such as whether optimizing for mean JCT disproportionately penalizes the longest jobs. These real-world experiments provide the strongest evidence that modeling and algorithmic innovations deliver tangible benefits in production environments.

In summary, validating GPU-scheduling models requires a three-pronged approach — proofs for ideal guarantees, simulations for controlled exploration, and real deployments for production realism—together providing the strongest evidence of practical utility.

2.4. Comparative Analysis of Models

No single modeling approach is universally superior; each entails its own set of trade-offs. In what follows, we contrast the different models in terms of their information requirements, computational tractability, and practical applicability.

Offline models vs. online models. Offline models assume full knowledge of the workload in advance and can, at least in principle, compute schedules that are near-optimal for that fixed job set. They shine in static or batch-processing contexts (for example, nightly jobs), where one can afford to spend significant computation time to derive an optimal plan. However, these approaches often struggle with both scalability and adaptability: a schedule that is optimal for a predetermined collection of jobs may perform poorly when faced with unexpected arrivals or delays.

By contrast, online models make decisions as jobs arrive, eschewing any prescience of future workloads [128]. Their primary goal is to sustain high utilization and low latency in dynamic environments. Lacking complete information, they typically employ heuristics or approximation algorithms; truly optimal online policies exist only under highly idealized assumptions. In practice, systems adopt robust “good-enough” rules that deliver reliable average performance. The strength of online models lies in their realism and flexibility—qualities essential for perpetually running services such as shared GPU clusters—although this comes at the expense of weaker theoretical guarantees.

In short, offline models are most valuable for controlled experiments or as benchmarking baselines, whereas online models are indispensable for real-time scheduling, trading some optimality for responsiveness and robustness in the face of uncertainty.

Queueing-theory-based models vs. optimization-based models. Queueing-theoretic approaches provide elegant analytical insights under stochastic assumptions (e.g., Poisson arrivals and exponential service times) [79,109]. In these simplified settings, they can identify optimal policies—such as SRPT or the Gittins index in an $M/G/1$ queue—and offer probabilistic performance guarantees (for example, bounds on average delay or queue-overflow probability). However, the very abstractions that enable tractability often overlook key complexities: multi-GPU coordination, non-negligible setup times, and the heavy-tailed service distributions typical of ML training workloads.

By contrast, optimization-based models (e.g., MILPs or min-cost flow formulations) can encode detailed system characteristics without relying on simple stochastic assumptions. Taking deterministic inputs—whether point estimates or worst-case values—they capture GPU memory constraints, precedence relations in multi-stage jobs, fairness budgets, energy caps, and more. Their chief limitation is computational: they rarely scale to large, dynamic workloads without heuristic approximations or periodic re-solving, which may be impractical for real-time decision making.

In essence, queueing models excel at providing probabilistic guarantees within idealized frameworks, while optimization models deliver high-fidelity scheduling at the expense of scalability. Many production systems therefore combine both: leveraging queueing theory to establish high-level priority rules and employing optimization solvers to handle subproblems (such as packing jobs onto GPUs) at discrete intervals.

Heuristic approaches vs. formal methods. In practice, many GPU schedulers rely on fast, rule-based heuristics—such as greedy allocation to the best-fitting job or backfilling small jobs into idle slots—to make scheduling decisions with minimal overhead and implementation complexity [129]. These methods can be tuned via parameters (e.g., backfill aggressiveness or priority weightings) to match specific workload patterns or policy goals. Their main drawback is the absence of worst-case performance guarantees: under adversarial or highly skewed arrivals, a naive greedy policy may repeatedly starve large jobs or incur significant delays for certain job classes if fairness constraints are not carefully enforced.

By contrast, formal methods (e.g., integer linear programming or dynamic programming) can compute provably optimal schedules under a given model, ensuring that no better solution exists within the specified assumptions. However, their exponential time complexity generally precludes application to large or highly dynamic clusters except in offline calibration or small subproblem contexts. Furthermore, an “optimal” schedule derived from a simplified model may falter in practice if it omits factors such as communication overhead or variability in service times.

Consequently, state-of-the-art GPU schedulers often adopt a hybrid design: lightweight heuristics handle real-time, large-scale decision-making, while occasional formal optimizations tune parameters or solve constrained subproblems. This blended approach preserves the speed and robustness of heuristics—ensuring, for example, that GPUs are never oversubscribed and no job is indefinitely starved—while leveraging formal analyses to verify and improve the scheduler’s performance in controlled scenarios.

Learning-based models vs. rule-based models. A growing trend is to infuse schedulers with machine learning — for instance, via reinforcement-learning–derived policies or predictive models that estimate job runtimes and performance across GPU types. Such learning-based schedulers can adapt automatically to workload dynamics and capture complex, nonlinear interactions (e.g., shifting bottlenecks between CPU, network, and GPU) that static heuristics often miss. In principle, as they accrue experience or improve their predictive accuracy, these models can converge toward near-optimal scheduling decisions.

However, learning-based approaches introduce significant overheads and operational challenges. Training an RL agent or regression model demands large historical datasets and substantial compute for simulation or model fitting, and there is frequently a cold-start phase during which performance may lag behind established baselines [130]. In production contexts, this initial underperformance can be unacceptable. Learned policies also tend to be opaque, making them difficult to interpret, debug, or formally verify—factors that can undermine operator trust in high-stakes environments. Moreover, without careful regularization or retraining, models risk overfitting to past patterns and may fail to generalize when workloads or hardware configurations evolve (e.g., when new job types or GPU architectures are introduced).

By contrast, traditional rule-based schedulers—simple heuristics or parameterized policies—require no training data, are immediately operational, and degrade predictably only if their underlying assumptions are violated. They are straightforward to debug and tune by human operators and offer stable behavior even under unanticipated conditions.

Recognizing the strengths and weaknesses of both paradigms, recent work often adopts hybrid strategies: using ML to fine-tune heuristic parameters (such as backfill thresholds or time quanta) or delegating only specific subdecisions (e.g., selecting an optimal GPU type via a performance predictor) to learned components, while retaining overall rule-based control. Such hybrids aim to harness the adaptability of learning-based methods without surrendering the reliability and interpretability of established heuristics.

Model selection. Scheduling models are most effective when aligned with the characteristics of their target environment. In batch-oriented HPC clusters—where hardware is homogeneous and throughput dominates—simple priority queues and backfilling heuristics remain the de facto standard. Cloud AI platforms, by contrast, must accommodate elastic scaling [131,132], heterogeneous GPU types, and multi-tenant fairness; here, optimization-based and learning-augmented approaches can yield substantial gains [133]. Real-time inference services impose strict SLOs and deadline guarantees, dictating the use of real-time systems theory—deadline-driven scheduling and preemptive policies—to ensure timely responses under all load conditions [80,134].

Each paradigm offers distinct trade-offs:

• Queueing models – Pros: Analytically tractable; provide closed-form performance bounds and optimal policies under stochastic assumptions. Cons: Scale poorly to large systems without relaxation or decomposition; approximations may sacrifice true optimality.
• Optimization models – Pros: Express rich constraints and system heterogeneity; deliver provably optimal schedules within the model’s scope. Cons: Become intractable for large, dynamic workloads without heuristic shortcuts or periodic re-solving; deterministic inputs may not capture runtime variability.
• Heuristic methods – Pros: Extremely fast and scalable; simple to implement and tune for specific workloads; robust in practice. Cons: Lack formal performance guarantees; require careful parameterization to avoid starvation or unfairness.
• Learning-based approaches – Pros: Adapt to workload patterns and capture complex, nonlinear interactions (e.g., resource interference) that fixed rules miss. Cons: Incur training overhead and cold-start penalties; produce opaque policies that demand extensive validation to prevent drift and ensure reliability.

Because no single approach suffices for all scenarios, production GPU schedulers typically adopt a hybrid strategy: employing ILP or matching solvers for small-scale assignment tasks, relying on heuristics for real-time dispatch, and leveraging learning models for runtime and resource-usage prediction. This blend of methods — grounded in robustness, simplicity, and targeted optimization — enables high performance across diverse, large-scale workloads.

3. Scheduling Algorithms and Their Performance

With GPU-cluster scheduling formalized in Section 2, we now turn to the concrete algorithms that bring those models to life. This section surveys the primary algorithmic strategies for making scheduling decisions in GPU clusters. We organize our discussion into three broad families—classical optimization methods, queueing-theoretic techniques, and learning-based adaptive algorithms—each grounded in different modeling assumptions and offering distinct trade-offs. We then conclude by highlighting practical implementation challenges and presenting a comparative evaluation of their performance.

While models define objectives, constraints, and high-level frameworks, it is the algorithms that carry out the step-by-step assignment of jobs to GPUs. For example, an integer-linear-programming (ILP) formulation may be solved exactly with a MILP solver or approximately via greedy heuristics, whereas a Markov decision process (MDP) model can be tackled with a reinforcement-learning (RL) agent. Hybrid approaches — combining rule-based heuristics with machine-learning predictors — have also gained traction [135]. In the subsections that follow, we analyze each algorithm class in terms of design methodology, computational complexity, and their ability to address the unique challenges of GPU cluster scheduling.

3.1. Classical Optimization Algorithms

Classical schedulers rely on deterministic rules or mathematical optimization, without any learning component. We begin with the simplest and still most widely deployed—family.

Greedy algorithms. Greedy algorithms make locally optimal choices — such as scheduling the “best” job first according to a specific heuristic — to drive strong overall performance. A canonical example is shortest-job-first (SJF), which prioritizes jobs with the smallest runtimes. For a job set J with known processing times $\left\{p_j\right\}$ on a single GPU, SJF orders jobs by non-decreasing $p_j$. Denote by $C_j\left(\sigma \right)$ the completion time of job j under schedule $\sigma$. It is well known that SJF minimizes the sum of completion times, ${\sum }_{j\in J}{C}_j$, on a single GPU [136]. Despite its optimality for average completion time, SJF can starve long jobs [137]. Production systems typically counteract this by applying aging or enforcing a cap on maximum waiting time.

Backfilling. First-come-first-served (FCFS) with backfilling preserves arrival order for the head-of-queue job but allows smaller jobs to leapfrog when resources are idle [115]. If the front job h is blocked by insufficient GPUs, the scheduler reserves resources for h at its earliest start time, then scans the queue for a shorter job j that can complete before h’s reservation. This eliminates idle gaps while ensuring h is never delayed.

Packing on multiple GPUs. When $m>1$ identical GPUs are available, placement reduces to a bin-packing problem. Two classic heuristics are:

• First-Fit (FF). Scan the queue and assign the first job whose demand $g_j$ fits the current free set B of GPUs.
• Best-Fit (BF). Among jobs that fit, choose the one minimizing the leftover capacity $\left|B\right|-g_j$.

Both run in $O\left(\right|J|log|J\left|\right)$ time using a heap. Their theoretical performance follows from Graham’s bound: for identical machines, list-scheduling FF achieves a $\left(2-\frac{1}{m}\right)$-approximation for makespan, and BF attains the same ratio by domination [138].

Heterogeneous clusters. On clusters with diverse GPU types $T=\{{\tau }_1,\dots ,{\tau }_s\}$, naïve FF/BF degrade because a job’s throughput varies by device. Gavel [57] addresses this by probing each job’s per-device throughput ${\varphi }_{j,\tau }$ and scheduling in the transformed space of effective GPU-seconds, thereby extending classical packing heuristics while preserving fairness.

Scalability. All above heuristics maintain a priority queue or balanced tree, incurring $O(log|J\left|\right)$ overhead per scheduling event. This yields sub-millisecond decision latencies even with hundreds of queued jobs — critical for environments with frequent arrivals and completions. Their main limitation is the lack of worst-case guarantees beyond Graham’s bound and potential starvation under pathological workloads. Nevertheless, empirical studies show that well-tuned greedy rules strike a favorable balance between utilization and responsiveness in production clusters 1.

Recent advances also target multi-GPU deep-learning workloads in HPC settings. For example, MARBLE [139] dynamically determines the optimal number of GPUs per job—based on pre-profiled scalability curves—and employs suspend/resume operations to co-schedule multiple jobs on the same node, exploiting non-linear scaling to reduce overall completion times on systems like Summit.

Dynamic programming. When local heuristics are insufficient, researchers have also explored exact but costlier methods such as dynamic programming. Dynamic programming (DP) computes exact schedules for a variety of small-scale subproblems, at the cost of exponential or high-polynomial time. Consider a job set J with release times $r_j$, deadlines $d_j$, and processing times $p_j$ on a single GPU. The feasibility problem $1\mid r_j,d_j\mid {\sum }_j{U}_j$ — selecting the largest subset of jobs that meet their deadlines — admits an $O(2^{\left|J\right|},|J\left|\right)$ state-space DP, while its non-preemptive and preemptive generalizations can be solved in $O\left(n^7\right)$ and $O\left(n^{10}\right)$ time respectively [140]. When deadlines and processing times are small integers, a time-indexed DP yields a pseudo-polynomial algorithm, making it practical for moderate-scale instances.

Although full DP is often infeasible at large scale, it is optimal for key cases. For example, earliest-deadline-first (EDF) is provably optimal for preemptive scheduling with deadlines on a single machine [141]. In the non-preemptive setting, DP can enumerate subsets in increasing order of $d_j$ to maximize throughput exactly, but its exponential term confines its use to small job sets. Beyond ordering, DP also applies to resource-allocation subproblems: it can jointly optimize GPU-count assignments, batch sizes, or parallelization granularity for individual jobs by exploring all allocation states [133].

In production GPU schedulers, DP is often invoked selectively within hybrid frameworks. For instance, OASiS embeds a polynomial-time DP inside an online primal–dual algorithm to determine worker/parameter-server allocations that maximize aggregate utility under time-varying capacities [142]. The DP runs only for a small set of high-priority jobs, while lower-priority jobs revert to greedy heuristics. This “bounded DP + greedy” approach achieves near-optimal throughput with per-decision latencies below 100 ms on real cluster traces.

ILP/MILP formulations and solvers. Mixed-integer linear programming (MILP) offers a general framework: introduce a binary decision variable $x_{j,k,t}$ for each job j, GPU k, and start time t, add linear constraints for assignment, capacity, and makespan, and let a MILP solver search for an optimum. For identical GPUs and makespan minimization $P\Vert C_{max}$, define

$$\begin{array}{ccc}\hfill J=\{1,\dots ,n\}& G=\{1,\dots ,m\}& T=\{0,\Delta ,2\Delta ,\dots ,H\},\hfill \end{array}$$

and

$$x_{j,k,t}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{job}j\mathrm{starts}\mathrm{on}\mathrm{GPU}k\mathrm{at}\mathrm{time}t\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Then the time-indexed MILP is

This formulation uses $O(n,m,|T\left|\right)$ binary variable and is strongly NP-hard even for $m=2$ [143]. Generic branch-and-bound solvers (Gurobi, CPLEX) typically handle up to $\sim 50$ jobs and $\sim 10$ GPUs before runtimes become prohibitive. Two common relax-and-round strategies mitigate this:

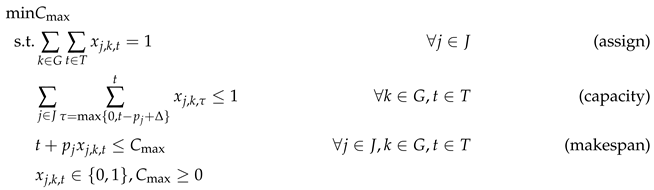
• Continuous relaxation. Replace $x_{j,k,t}\in \{0,1\}$ with $0\le x_{j,k,t}\le 1$, solve the LP, then round the fractional solution.
• List-scheduling rounding. Sort jobs by LP-derived completion times $\widehat{C_j}$ and assign greedily to the earliest available GPU.

When release times are present, online list-scheduling variants achieve a 2-competitive ratio [144,145]. Although full MILP is rarely used online, it serves as a ground-truth oracle for benchmarking heuristics under simplified assumptions [57].

Structure-exploiting solvers. Special cases admit faster combinatorial algorithms. If preemption is allowed and communication costs are ignored, each scheduling epoch reduces to a bipartite matching problem, solvable via the Hungarian algorithm in $O\left(n^3\right)$ time [120]. For single-node multi-GPU placement with memory constraints, column-generation generates only profitable assignment patterns, closing much of the optimality gap while keeping per-decision latency under one second for up to 200 jobs [146].

In summary, ILP/MILP provides a rigorous benchmark and a foundation for principled approximation schemes (LP-rounding, list scheduling), though direct deployment at cluster scale is limited by computational cost.

Heuristic and meta-heuristic approaches. Beyond simple greedy rules, meta-heuristics such as genetic algorithms (GA), simulated annealing (SA), Tabu search, and particle-swarm optimization (PSO) have been explored for GPU scheduling, especially in heterogeneous environments. These methods encode a complete schedule (or resource allocation) as a candidate solution and iteratively refine it.

In a GA, for instance, each chromosome may represent an assignment of jobs to time slots or GPUs. An initial population of random schedules undergoes crossover and mutation, guided by a fitness function aligned with objectives like minimizing makespan or maximizing throughput. GAs have been applied to CPU–GPU cluster scheduling to optimize multiple criteria simultaneously — such as makespan, energy efficiency, and fairness [103].

SA, by contrast, perturbs a current schedule with local random moves and accepts changes according to a temperature-driven probability: uphill moves are occasionally allowed to escape local optima, with the acceptance probability decreasing over time. Similar strategies underlie Tabu search and PSO.

Strengths and limitations: Meta-heuristics excel at exploring large, complex search spaces and can produce high-quality schedules given sufficient runtime. However, like MILP solvers, they incur significant computational overhead—often seconds to minutes per schedule—making them unsuitable for online scheduling, where decisions must occur within milliseconds. As a result, their use is generally confined to offline or semi-offline settings (e.g., precomputing schedules for known workloads or tuning parameters for lighter-weight heuristics). Furthermore, they lack optimality guarantees, and their performance hinges on careful parameter tuning, which itself can be costly [147]. Empirical studies show that GA and SA may slightly outperform greedy heuristics in heterogeneous clusters, but at the expense of minutes of computation time per run.

Despite these drawbacks, meta-heuristics offer valuable insights for policy design. For example, one could run a GA offline on historical traces to optimize scheduling-policy parameters, then deploy the tuned heuristic for real-time decisions. In practice, many production-grade managers—such as Slurm and Kubernetes—rely on simple heuristics augmented with tunable weights or priorities, striking a balance between responsiveness and solution quality [148].

3.2. Queueing-Theoretic Approaches

Queueing-theoretic scheduling algorithms draw on analytical results from classical queueing models to assign each job a dynamic priority. Instead of solving a global optimization, these policies maintain a simple “index” or rank for every job—based on its service history or statistical characteristics—and always dispatch the job with the highest priority. Below, we outline four influential families of queue-based strategies.

Index policies (e.g., Gittins index). Index policies compute a per-job score that balances fairness and efficiency by considering both attained service and the likelihood of short remaining work. The Gittins index is a canonical example: for an $M/G/1$ queue, a job with attained service v receives

$$\mathcal{G}\left(v\right)=\underset{\tau >0}{sup}{\displaystyle \frac{Pr\{S_j\le v+\tau \mid S_j>v\}}{\mathbb{E}min(\tau ,S_j-v)\mid S_j>v]}},$$

the highest reward-to-completion-time ratio achievable by a probing experiment of length $\tau$. While exact computation can be complex, practical implementations rely on approximations that retain near-optimal mean-slowdown performance when job sizes are unknown [149].

Least attained service (LAS) / foreground–background (FB). A simpler offshoot of the Gittins family sets $\mathcal{G}\left(v\right)=-v$, yielding the LAS/FB rule: always run the job with the smallest accumulated service. Under heavy-tailed service distributions, LAS incurs at most a $25\%$ penalty over SRPT for mean slowdown—the information-theoretic lower bound [150]. New arrivals preempt longer-served jobs immediately, mimicking multi-level feedback. In GPU clusters, full preemption is often too costly, so systems like Tiresias use fixed-length leases: after each time slice, the job with least total GPU-time may preempt the current one. By tracking both time and GPU count (2D-LAS), Tiresias avoids starvation with minimal overhead. E-LAS further extends this by incorporating real-time epoch progress rates into the priority, improving job-completion times without runtime profiling [151].

Multi-class priority queues. Queueing theory also motivates dividing work into several priority classes — e.g., “urgent,” “standard,” and “background.” Strict priority in an $M/M/1$ system guarantees minimal response for the top class, though lower classes suffer increased delays. GPU schedulers often emulate SRPT by maintaining, say, short-job and long-job queues: serve all jobs with estimated runtime $<X$ seconds first, then switch to longer tasks. Thresholds are set based on historical job-size distributions, and user-provided estimates can refine class assignments [152].

Processor sharing (PS) approximations. Ideal processor sharing divides capacity equally among active jobs, preventing starvation and smoothing progress. GPUs cannot preempt at the granularity PS demands, but features like NVIDIA A100’s MIG partitions approximate independent instances. Alternatively, coarse time slicing or round-robin dispatchers (e.g., Themis’s finish-time equalization) reassign GPUs periodically to equalize job progress—capturing PS’s fairness spirit while limiting I/O and checkpointing overhead [81].

It is worth noting that these policies are derived under single-server assumptions. In multi-GPU clusters, naïvely applying them per GPU may break global optimality. Practical extensions either decentralize the policy (one index per GPU) or coordinate across servers to generalize index and priority rules to the multi-machine setting.

Practical applicability of queueing models. Queueing-based algorithms come with strong theoretical guarantees under idealized models, but real GPU clusters demand careful approximations and tuning. For example, LAS requires choosing a lease duration: if leases are too long, short jobs lose their responsive service; if too short, preemption overhead grows. A concrete instantiation — “preempt every 30 s to rebalance toward least-attained service” — captures LAS behavior in practice and can be tuned analytically or via empirical evaluation [81]. Likewise, Gittins-style policies rely on accurate size distributions; misestimating a job as short may cause it to monopolize GPUs. Tiresias experiments show that both partially informed (Gittins-like) and agnostic (LAS-style) schemes outperform classical heuristics, suggesting that even simplified index rules can realize much of the theoretical benefit in realistic workloads.

Predictive admission and QoS control. Beyond scheduling, queueing theory’s formulas can drive admission control and service-level guarantees. A scheduler that estimates, say, a one-hour wait for newly submitted work can use that prediction to deny, defer, or reprioritize jobs based on user deadlines or QoS contracts. Simple metrics — Little’s Law ($L=\lambda W$), mean response-time bounds, or $M/M/1$ approximations — can trigger autoscaling or more aggressive preemption when saturation looms, helping to balance cluster utilization against developer expectations.

Trade-offs versus optimization-based methods. Queueing policies like LAS and Gittins Index optimize user-centric metrics (mean response time, slowdown) at the expense of additional preemption and decision overhead. In contrast, optimization-based schedulers typically focus on system-centric objectives (throughput, GPU utilization), often allowing long jobs to finish uninterrupted to avoid migration or checkpoint costs. For instance, an MILP solver may keep a nearly completed job running, boosting overall throughput but delaying short arrivals — precisely the opposite of SRPT-like fairness.

Hybrid designs and practical deployment. Most production schedulers blend both worlds: they pack GPUs efficiently and layer in preemption or time-slicing to prevent starvation. Gandiva, for example, uses placement-optimization via migration while time-slicing hyperparameter searches for rapid feedback [56]. A common pattern is to treat each allocated GPU as a “service chunk” when computing priorities, enabling index or LAS heuristics to work atop any resource-packing framework.

In summary, queueing-theoretic approaches bring a rich repertoire of priority rules, fairness guarantees, and predictive insights. Their core strength lies in optimizing responsiveness and equity—qualities highly valued by ML practitioners — while their main challenge is controlling overhead and ensuring system-wide efficiency. As demonstrated by Tiresias and Themis, with careful adaptation and cluster-specific enhancements, queueing-inspired schedulers can substantially reduce average completion times and deliver fair, predictable GPU allocation in multi-tenant environments [79,81].

3.3. Learning-Based Adaptive Algorithms

Learning-based algorithms harness machine learning — via supervised prediction or reinforcement learning — and adapt over time using feedback from historical logs or live system metrics [153,154,155]. Rather than relying on fixed rules, these methods continually refine their policies as workload patterns evolve.

Supervised prediction models. Predictive models are trained on job features — such as neural network architecture, input size, and user identity — to forecast metrics like runtime, memory footprint, or scaling behavior. A scheduler can then implement a data-driven SJF by ordering jobs according to predicted runtimes. To mitigate mispredictions, jobs that exceed their expected duration are demoted to a lower-priority queue, preserving fairness and robustness.

In heterogeneous GPU clusters, models estimate performance across hardware types. Gavel benchmarks workloads to derive throughput estimates for A100 versus V100 GPUs, adapting classical policies to maximize efficiency in mixed environments [57]. Likewise, GENIE uses lightweight profiling to predict deep learning job latencies and throughputs, enabling a QoS-aware scheduler that meets latency and throughput targets [156].

Interference prediction further enhances sharing. Co-scheML profiles ML applications offline to learn co-location slowdown patterns and predicts whether a new job can safely share a GPU without degrading performance [157]. Remaining-time predictors leverage in-flight metrics—epochs completed or loss curves—to decide if a job should be allowed to finish or be preempted, as in SLAQ’s loss-gradient prioritization [104]. Forecasting tools like Bamboo and Parcae anticipate spot-instance revocations, adjusting parallelism ahead of interruptions to maintain throughput [158].

By replacing conservative or user-provided estimates with learned predictions, supervised methods often outperform traditional backfilling—moderate accuracy alone can yield significant reductions in waiting time and improved resource utilization.

Reinforcement learning–based scheduling. Reinforcement learning (RL) casts scheduling as a sequential decision problem: the scheduler (agent) observes the cluster state (job queue, GPU availability), takes actions (dispatch or preempt jobs), and receives rewards reflecting metrics like negative waiting time, throughput, or fairness. Over repeated interactions, the agent refines its policy to maximize cumulative reward.

Early systems such as DeepRM [77] tame the combinatorial state by limiting the number of waiting jobs and discretizing time and resource slots. They encode the cluster as an “image” of resource occupancy plus job demands and train a neural network to output a scheduling distribution. Decima extends this idea to DAG-structured workloads: a graph neural network embeds each job’s task graph and a policy network selects which task or workflow to advance next, outperforming heuristics like SRTF and fair sharing under variable load [123]. Likewise, HeteroG applies a GNN-based RL agent to jointly learn device placement, parallelism, and communication strategies for DNN training DAGs [159]. RL’s flexibility also enables multi-objective rewards—for example, minimizing average slowdown minus a fairness penalty—which can reveal nuanced trade-offs beyond fixed heuristics. Ryu et al. [160] demonstrate this by training an LLM scheduler to avoid co-scheduling network-heavy jobs on the same switch, reducing contention and boosting throughput.

However, RL in production faces four key challenges:

• Exploration vs. exploitation.
  Learning demands trying suboptimal actions, which in live clusters can degrade performance. Most systems therefore train offline on simulators or historical traces, but must retrain or fine-tune when workloads or hardware change.
• State-space explosion.
  Real clusters host hundreds of jobs, blowing up the state. Abstractions—DeepRM’s image grid, Decima’s graph embeddings, or transformer/attention mechanisms [161]—are essential to focus on relevant features.
• Stability and safety.
  Unconstrained RL policies may starve jobs or violate service guarantees. Hybrid designs combine learned policies with hard constraints (e.g., maximum wait time or GPU caps) to enforce correctness.
• Interpretability.
  RL models are often opaque, making it hard to diagnose why a particular scheduling decision occurred. This opacity can hinder trust in mission-critical environments [162].

Despite these hurdles, industry interest is rising: internal teams at Alibaba and elsewhere have begun prototyping deep RL for resource management and job scheduling based on promising early results from research systems.

Adaptive scheduling via feedback control. Not all adaptive scheduling approaches rely on machine learning; some use principles from feedback control systems [163,164,165]. These methods continuously monitor system metrics and adjust scheduling behavior in response, forming a closed-loop system. For instance, a basic feedback-driven scheduler might monitor average GPU utilization over the last minute: if it falls below a predefined threshold, the system could respond by increasing GPU packing density (e.g., enabling more aggressive time-sharing) or by admitting more jobs from the queue. Conversely, if the average job slowdown rises above a target, the scheduler could throttle job admissions or boost the priority of small or short jobs. Such strategies can be viewed as control systems: monitor a key performance indicator, and if it deviates from the target, adjust a parameter in the scheduling policy accordingly.

Similarly, Elan [165] provides efficient elastic scaling for deep learning jobs by combining a hybrid batch size scaling mechanism with asynchronous coordination and topology-aware state replication. Unlike checkpoint-based systems, Elan allows jobs to scale out, scale in, and migrate without restarting, minimizing disruption and achieving sub-second elasticity with negligible overhead. By balancing training efficiency and model convergence during resource changes, Elan enables higher GPU utilization and faster job completion in production-scale clusters.

A more sophisticated example of feedback control in GPU scheduling is incremental job scaling, as implemented by systems like Pollux and AntMan [68,164]. Pollux uses an online feedback loop per job to monitor its goodput (effective throughput in terms of training progress per unit time) and adapt GPU allocations accordingly. If additional GPUs do not significantly improve goodput (i.e., the job hits diminishing returns), the system reduces its GPU share and reallocates resources to other jobs. Conversely, if a job scales efficiently, more GPUs are allocated up to the point of diminishing returns. This feedback-driven adjustment occurs periodically and adapts to the evolving performance characteristics of each job. AntMan adopts a similar philosophy but extends it by modifying the underlying deep learning frameworks to allow fine-grained, real-time scaling of both GPU memory and compute resources. By continuously monitoring mini-batch performance and dynamically adjusting resource allocation without requiring job restarts, AntMan opportunistically improves GPU utilization and cluster throughput under multi-tenant workloads. Both systems exemplify adaptive behavior based on online measurements — a form of reinforcement through iterative performance feedback—positioning them between classical control and learning-based approaches, and leveraging empirical tuning without requiring offline model training.

Another direction is predictive queueing control, where the scheduler uses observations of job inter-arrival and service times to anticipate load patterns and adjust parameters preemptively. For example, if high-priority jobs begin arriving more frequently, the scheduler might increase the time-slice frequency to enhance multitasking capability or temporarily preempt low-priority jobs to make room. These techniques combine elements of prediction and feedback, aiming to dynamically stabilize key system metrics (e.g., response time, fairness) under workload fluctuations.

Scalability and practical deployment of learning-based scheduling. Once trained, learning-based schedulers can make decisions in milliseconds—often accelerated further on GPUs—easily keeping pace with the few dozen scheduling events per second typical in production clusters. The principal overhead lies in training these models and in collecting representative data that captures the full variability of the target environment. A major scaling challenge is handling a dynamic and potentially very large job set: some designs address this by truncating inputs to a fixed-size “window” of the most urgent or largest jobs and summarizing the remainder, while others employ flexible architectures—such as transformers that natively accept variable-length sequences [166]—or iterative decision loops that process one job at a time. In clusters on the order of 10,000 GPUs, even these techniques can strain centralization; multi-agent reinforcement learning (MARL), in which each agent oversees a rack or node group and coordinates via shared rewards or a meta-policy, offers one promising path toward decentralized, scalable control.

Several RL-based prototypes have validated this approach in simulation. DeepRM and Decima showed that learned policies can surpass classical heuristics under complex constraints like DAG dependencies and heterogeneous job mixes [77,123]. More recently, HeterPS employed an LSTM-based RL scheduler to allocate tasks across CPUs and GPUs in heterogeneous clusters, achieving faster end-to-end training times [167]. These studies demonstrate that, when properly trained, RL can internalize intricate scheduling dynamics and adapt to shifting workloads more effectively than static rules.

Despite these advances, industrial uptake remains cautious. Scheduling is mission-critical, and missteps risk severe performance degradation or outages. Consequently, most production systems employ ML components in a hybrid fashion — using learned models for parameter tuning or runtime prediction, but retaining proven control logic as the primary decision maker — and incorporate extensive safety checks, fallback paths, and human-in-the-loop oversight before permitting fully autonomous operation.

3.4. Comparative Analysis

In this subsection, we evaluate the major categories of scheduling algorithms according to four key dimensions: computational complexity, performance characteristics, scalability, and the environments in which they excel.

Complexity and decision speed. Classical heuristics—such as greedy or rule-based methods—offer extremely low decision latency, often operating in $O(logn)$ time when using priority queues. Consequently, they can react to job arrivals and completions almost instantaneously relative to typical runtime durations. By contrast, ILP- and MILP-based approaches incur substantially greater computational cost: solving a moderately sized MILP can require seconds or even minutes, rendering these methods impractical for real-time scheduling events. Nevertheless, they remain viable for coarse-grained optimization tasks — for example, computing an optimal allocation hourly. Metaheuristics like genetic algorithms (GA) and simulated annealing (SA) similarly demand considerable time to converge, making them better suited for offline analysis or periodic batch scheduling rather than real-time decision-making. Queueing-theoretic policies (e.g., LAS or Gittins index) perform lightweight per-job updates — such as tracking cumulative service—at negligible expense. Likewise, reinforcement learning (RL) policies, once trained, execute scheduling decisions with minimal overhead: neural network inference or table lookups typically complete in milliseconds or less on contemporary hardware. Overall, heuristics, queueing strategies, and trained RL models scale efficiently to thousands of jobs with low runtime overhead, whereas ILP formulations and iterative optimization techniques struggle to scale beyond a few hundred jobs without substantial simplification. For instance, DynamoML integrates fractional GPU sharing, workload-aware gang scheduling, and SLA-driven auto-scaling as Kubernetes operators, yet still achieves per-event decision times under $100ms$ while managing hundreds of concurrent jobs in real clusters [168].

Quality of schedule. When ranked by theoretical proximity to optimal performance, exact ILP solutions are unsurpassed within their model constraints. However, these formulations often abstract away critical system-level factors — such as preemption costs and job heterogeneity. Reinforcement learning (RL) approaches, given ample training data and sufficiently expressive architectures, can empirically approximate optimal schedules, though formal convergence guarantees are scarce and heavily dependent on the training regime and environment. Greedy heuristics, while computationally lightweight and offering strong average-case performance, may deviate substantially from optimality under worst-case inputs. Queueing-theoretic policies —exemplified by the Gittins index — provide provable optimality for specific objectives under simplified assumptions (e.g., minimizing mean slowdown in a single-server queue), yet they can underperform on other metrics such as utilization or strict fairness. Empirical studies underscore inherent trade-offs: schedulers that aggressively pack GPUs to maximize utilization often increase waiting times for small jobs, whereas LAS-like policies optimize responsiveness at the expense of resource efficiency. Hybrid methods seek to reconcile these goals by mitigating resource underutilization while preserving fairness and responsiveness. The choice of algorithm family typically aligns with the target metric:

• Minimizing average job completion time (JCT).
  Theoretically, SRPT and Gittins-index scheduling are optimal when job sizes or distributions are known [79]. In practice, shortest-job-first (SJF) with accurate runtime predictions yields strong results.
• Maximizing utilization.
  Packing heuristics, best-fit allocation, and non-preemptive strategies (e.g., FCFS or backfilling) maintain high GPU occupancy and minimize idle intervals.
• Ensuring fairness.
  Time-sharing mechanisms such as LAS or round-robin prevent job starvation. Cluster-level extensions — like Themis’s auction-based allocation — provide explicit fairness guarantees at the cost of added coordination overhead [81].
• Multi-objective optimization.
  To balance responsiveness, fairness, and efficiency, heuristic frameworks often employ weighted-sum priority scores (e.g., blending estimated slowdown with job importance). RL policies can natively address multiple objectives through reward shaping, dynamically discovering trade-offs via techniques like the “power-of-two-choices.”

Scalability and heterogeneity. Lightweight scheduling algorithms naturally scale to large clusters, since event rates — job arrivals, completions, and preemptions — are typically limited by job runtimes. Even in a busy 1,000-GPU deployment, only tens of scheduling events occur per second, allowing a single-threaded priority–queue or placement update to keep pace. At web-scale (e.g., Google’s Borg, managing millions of jobs), however, centralized schedulers become a throughput bottleneck, prompting distributed or hierarchical designs that partition the cluster into independently managed cells. Most academic proposals assume one scheduler handling a few hundred to a few thousand machines, a regime where heuristics and RL policies remain practical; by contrast, ILP and metaheuristic methods incur prohibitive computation at this scale.

Reinforcement learning (RL) approaches can scale in principle, but only if the policy efficiently summarizes system state. Naïvely encoding all jobs and resources leads to state-space explosion. To mitigate this, many RL schedulers use fixed-size job subsets, recurrent or attention-based networks, or other compact representations. Some systems train on small clusters and transfer policies to larger ones, though such generalization often demands careful architecture design and retraining.

Heterogeneity in GPU types, network bandwidths, and workload characteristics further complicates scaling. Heuristics and queueing frameworks adapt readily — by maintaining per-resource queues or weighting priorities by expected slowdown on each GPU class. ILP formulations can model heterogeneity via extra constraints, but at the cost of larger variable counts and slower solves. RL methods can encode resource types directly in the state, yet typically require retraining to master a heterogeneous environment. Notwithstanding this engineering overhead, recent work — such as HeterPS — demonstrates that RL can effectively learn in diverse cluster settings [167]. Overall, simple heuristics offer the greatest flexibility for rapid deployment, while RL and optimization-based techniques, once tuned or trained, can yield superior performance in large, heterogeneous clusters.

Other performance metrics: fault tolerance, interpretability, explainability, and transparency. Simpler scheduling algorithms are inherently easier to make fault-tolerant. For example, after a crash or restart, a greedy or rule-based scheduler can rebuild its internal state—essentially a queue of pending jobs—by querying the current cluster status. Reinforcement learning (RL) agents, by contrast, do not carry over internal state between decisions (beyond what the environment encodes); their policies must simply be persisted to avoid retraining, which is generally straightforward since they remain static during deployment.

Optimization-based methods (ILP/MILP) present greater recovery challenges. Any change in system state may force the solver to restart from scratch to compute a new solution, a process that can be time-consuming. In the event of infrastructure failures—such as a GPU or node outage—most schedulers treat these incidents as preemptions: the affected job is re-queued or scheduled elsewhere. Heuristic approaches often include built-in fallback rules (e.g., deprioritizing unreliable nodes), whereas learning-based methods can fold failure events into their training or apply online policy updates to adapt over time.

Interpretability and transparency are also critical in multi-tenant clusters, where users’ trust depends on understanding scheduling decisions. Rule-based and heuristic policies are simple to explain — “short jobs first,” “equal GPU shares per user” — enabling clear mental models and reducing frustration. In contrast, ML-driven schedulers, especially RL policies, can exhibit behavior that is hard to trace back to explicit rules. Even when optimizing a well-defined multi-objective function, their decisions may seem arbitrary, which can undermine user confidence when one job is delayed while another proceeds.

3.5. Summary of Scheduling Algorithms and Their Applicability Concerns

We conclude by summarizing which classes of scheduling algorithms are best suited to different operating conditions, and then discuss the practical challenges of deploying custom policies in real-world GPU clusters.

Applicability by scenario. The applicability scenarios of scheduling algorithms can be classified as follows.

• Offline deterministic scenarios.
  When job characteristics are fully known in advance, ILP or dynamic programming (DP) formulations yield optimal schedules, whereas simple greedy heuristics can perform very poorly.
• Online workloads with heavy-tailed jobs.
  In cases where job sizes are unknown and heavy-tailed distributions prevail—typical of many training workloads—queueing-theoretic policies such as Gittins or LAS effectively balance fairness and mean slowdown [79].
• Online workloads with predictable jobs.
  If runtimes are periodic or otherwise predictable, static reservations or simple rules (e.g., SJF) often suffice, although dynamic SJF still performs near-optimally when predictions are accurate.
• Heterogeneous resources.
  For clusters with diverse GPU types, algorithms like Gavel normalize throughput across devices [169]. A two-stage approach—first matching jobs to resource classes (e.g., via ML or bipartite matching) and then applying standard scheduling within each class—can also be effective.
• Multi-tenant cloud environments.
  Fairness and isolation are paramount. Partial-auction mechanisms (e.g., Themis) or fair-share frameworks (e.g., DRF) are widely adopted, often supplemented by inner-loop policies like SJF to optimize per-job latency.

Practical integration and operational challenges. Deploying a custom GPU scheduler requires seamless integration with resource managers (e.g., Kubernetes, Slurm, Yarn) and cluster telemetry. Key considerations include:

• Resource-manager interfacing.
  Obtaining real-time availability requires communicating with the cluster’s control plane or writing scheduler extenders/plugins (e.g., for Kubernetes) [170].
• Distributed and batch workloads.
  Handling multi-node jobs and systems like Slurm, which lack fine-grained preemption support, complicates dynamic rescheduling.
• Framework coordination.
  Deep learning libraries (TensorFlow, PyTorch) expect stable allocations; introducing preemption demands tight coupling to checkpointing hooks and iteration boundaries for “graceful” pause–resume [171,172].
• GPU-specific interfaces.
  Scheduler plugins may need to invoke NVIDIA APIs to manage MIG partitions or query per-device utilization.

In addition to integration challenges, three other dimensions merit attention

• Scheduler overhead and latency.
  Advanced policies — such as AlloX’s $O\left(n^3\right)$ matching [120] or Decima’s neural-policy evaluation [123] — can introduce noticeable decision latency. Amortizing this cost (e.g. by only reevaluating every minute) trades responsiveness for efficiency, but in practice most systems lean heavily on heuristics that make sub-millisecond decisions.
• Preemption, checkpointing, and oversubscription.
  While many fairness-driven and queueing models employ preemption, writing GPU state to disk remains expensive. Techniques like graceful preemption at iteration boundaries mitigate impact [171]. Alternatively, oversubscription with throttling (e.g., SALUS) multiplexes GPU memory and streams to avoid full context switches, at the expense of reduced per-job throughput [173].
• Monitoring and adaptivity.
  Adaptive schedulers require fine-grained telemetry (via node agents or in-band probes) so that migration and admission controls are based on up-to-date data. This monitoring itself adds overhead and must be designed carefully to avoid stale data or oscillatory scheduling behavior.

Beyond per-node telemetry,multi-tenancyadds a cluster-wide layer of complexity. Multi-tenant GPU clusters bring unique scheduling challenges due to interference on shared resources. Co-locating jobs can induce contention not only on CPU cores — leading to context-switching overhead — but also on memory bandwidth, PCIe bus, and disk I/O when GPUs reside on the same node [174,175]. Distributed training workloads further exacerbate contention by saturating network links, potentially throttling performance across tenant jobs [176,177].

To mitigate these issues, modern schedulers incorporate resource topology and affinity into placement decisions. For example, awareness of NVLink connectivity or rack-level bandwidth can lead a scheduler to favor slightly less balanced but network-friendly allocations, reducing contention [127,163,178]. Parrot’s coflow-aware framework dynamically adjusts bandwidth allocations during distributed machine learning, improving average job completion time by up to $18.2\%$ in multi-tenant clusters [179].

Security and isolation are also critical. Without strong tenant separation, one job may leak information or disrupt another via GPU side channels or crashes [180]. Hardware-level isolation mechanisms such as NVIDIA’s Multi-Instance GPU (MIG) partitions are often required to enforce tenant boundaries safely.

A concrete example of system-level complexity is AlloX’s integration with Kubernetes. Implemented as a scheduling extender, it spanned thousands of lines of Go and Python code to manage containers, sample job runtimes on CPU versus GPU, and ultimately allocate whole GPUs — since current clusters lack support for arbitrary GPU time-slicing [120]. This experience highlights that many theoretically optimal strategies (e.g., splitting a GPU) must be abandoned or adapted due to system limitations.

Taken together, these integration and multi-tenancy obstacles reinforce a final lesson: Successful GPU scheduling balances algorithmic elegance with engineering practicality. Designers must iterate between prototype implementation and algorithm refinement, addressing integration, monitoring, preemption, and telemetry overhead to ensure that theory translates into real-world performance improvements.

4. Conclusions

This survey maps the rapidly evolving landscape of GPU-cluster scheduling onto a single, coherent taxonomy. By grouping the literature into four algorithmic lineages — greedy/heuristic packing, exact optimization (DP and MILP), queueing-theoretic policies, and learning-augmented hybrids — we expose the common design levers that underlie seemingly disparate systems. For each lineage we traced how core objectives—low completion time, high utilization, fairness, and energy efficiency—translate into concrete mechanisms and where the inevitable trade-offs surface when workloads vary in scale, heterogeneity, or preemption cost. The analysis shows that no one paradigm dominates; instead, the highest-performing schedulers blend the predictability of formal methods with the adaptability of learning, often moderated by queueing insights for fairness.

Looking forward, three research frontiers stand out. First, the rise of trillion-parameter LLM training threatens to overwhelm current gang-scheduling and placement heuristics; scalable intra-model parallelism and topology-aware network scheduling remain an active area of investigation. Second, dependable runtime predictors remain the linchpin for backfilling, elastic scaling, and RL reward shaping—yet accuracy degrades in the long tail of novel models and data regimes. Third, operators increasingly demand multi-objective guarantees that reconcile cost, carbon footprint, and user-level SLOs; principled methods for navigating that Pareto surface are sparse. Progress on these fronts will require tighter collaboration between systems, ML, and networking communities.

Ultimately, effective GPU scheduling is an exercise in systems synthesis: marrying elegant algorithms with the messy realities of drivers, containers, telemetry, and multi-tenant isolation. The field’s future breakthroughs will come from solutions that respect this duality — algorithms that are not just provably good or empirically fast, but also deployable in production clusters at planetary scale.