Physics-Informed Neural Networks (PINN) for Advanced Thermal Management in Electronics and Battery System: A Review of Recent Developments and Future Prospects

1. Introduction

Electronics and battery systems, which stand out as the two primary contributors to power consumption and heat generation in modern devices, drives the need for advanced thermal management solutions [1,2]. Effective thermal management is essential for maintaining the long-term performance and reliability of electronics and battery systems, particularly as modern devices continue to shrink in size while increasing in power, presenting significant challenges. Consequently, evaluating the thermal performance of these systems during the early design phase is critical, as pre-screening design parameters and manufacturing processes can demand substantial resources [3]. Achieving rapid and precise thermal predictions for various design parameter combinations is thus a key priority. Historically, finite element method (FEM) and computational fluid dynamics (CFD) have been employed, leveraging computational resources to conduct numerical analyses of temperature profiles and fluid flow based on the fundamental equations governing mass, momentum, and energy conservation [4,5,6,7]. The finite volume method or finite element method, common numerical techniques, address partial differential equations (PDEs) by dividing the domain into discrete control volumes or elements and integrating the governing equations across them [8]. This process requires a deep understanding of the underlying physics and the creation of control volumes or meshes, which is critical for obtaining accurate results while managing computational resource demands. However, this approach is often slow and inefficient. With the evolution of electronic systems—from individual chips to packages and full systems, from single battery cell to battery pack and large-scale battery system—featuring billions of transistors and high thermal design power. The next-generation power density system can reach over 100W/cm² [9,10,11], CFD is becoming increasingly impractical for addressing the thermal simulation needs of today’s advanced and rapid technologies.

As machine learning becomes more popular, benefiting from advancements in algorithms and GPU-based parallel solvers, its integration with thermal management has emerged as a growing trend [12,13]. Typically, machine learning has found widespread application in areas like generative AI [14,15], image processing [16,17,18,19] and content creation [20,21,22]. However, in the realm of physics, even when a machine learning model is developed, it often operates as a "black box", lacking clear physical interpretation of the parameters it produces [23,24]. Deep Learning (DL) is a subset of machine learning which has superior performance in physics-related problems by efficiently modeling complex, non-linear physical processes and optimizing system designs through rapid data-driven predictions [25]. For typical DL techniques, constructing an effective model generally demands extensive datasets to optimize its core neural networks structures, which, in turn, often necessitates resource-heavy CFD simulations to generate the required data [26,27].

Physics-Informed Neural Networks (PINNs), on the other hand, overcome this limitation by embedding governing physical principles, typically in the form of PDEs, directly into the training process [28]. The Physics-Informed technique can participate in the stages of initialization, loss function calculation, design of architecture, or hybridized with conventional DL models. This approach enables PINNs to deliver accurate predictions even with limited data, making them well-suited for thermal management tasks governed by established physical laws, such as Fourier’s law of heat conduction or the Navier-Stokes equations for fluid dynamics [29,30,31,32]. Unlike conventional neural networks, PINNs are trained not only on observational data but also on the underlying physics, which serves as a regularization mechanism, narrowing the range of possible solutions and improving their ability to generalize. This makes PINNs particularly advantageous in situations where traditional numerical methods are too slow or computationally demanding, such as real-time thermal regulation or solving inverse problems like parameter estimation.

Recent research has demonstrated the versatility of PINNs across various thermal management domains. For instance, in building thermal modeling, PINNs have been used to develop control-oriented models that combine the interpretability of physical laws with the expressive power of neural networks, as seen in studies like Gokhale et al.’s work on control-oriented thermal models for buildings [33]. Similarly, Wang et al.’s research on heat transfer in porous media using PINNs demonstrated their ability to predict temperature and heat flux fields accurately without labeled data, achieving computation accelerations of five orders of magnitude compared to numerical methods [34]. More examples are discussed in Chapter 2 and 3. These efforts suggest that PINNs could revolutionize thermal management in electronics, though the field is still emerging, with fewer direct studies compared to other areas.

In this review paper, we will discuss the applications of PINN in electronics and battery systems. We will begin by explaining the foundational working principles of PINN and its variants in Chapter 2. In Chapter 3, we will explore PINNs research conducted in electronics thermal management at different scale, from chip to board to system. In Chapter 4, following the same scale category, we describe the PINNs research conducted in battery thermal management from single cell to battery pack to battery system. Within these chapters, based on this understanding of challenges in different-scale thermal management in electronics and battery, we will then evaluate the integration of PINNs with other machine learning techniques and explore variations of the PINN framework. Lastly, we will outline potential future opportunities and prospects for leveraging PINNs in these domains.

2. PINNs and Variations

PINNs represent a significant paradigm shift in scientific machine learning, particularly in solving PDEs governing heat transfer, fluid dynamics, and Multiphysics problems. Unlike conventional deep learning models, which require extensive labeled datasets, PINNs embed physical laws—such as energy conservation and material properties—directly into the training process. This hybrid approach enables PINNs to generate accurate, physically consistent solutions even with limited experimental or simulated data, making them highly valuable for thermal modeling in electronics and battery systems.

2.1. Mathematical Formulation of PINNs

PINNs approximate the solutions of PDEs, which can be generally expressed as:

$$\mathcal{N}\left[\mathit{u}\right(\mathbf{x},t\left)\right]=0, \mathbf{x}\in \mathsf{\Omega }, t\in \left[0, T\right]$$

(1)

where $\mathcal{N}$ represents a differential operator that encodes the governing physics, $\mathsf{\Omega }$ is the computational domain; $\mathit{u}(\mathbf{x},t)$ is the solution of the PDE. For example, in heat conduction simulation, $\mathcal{N}$ is defined according to the Fourier’s law [35]:

$$\mathcal{N}=\nabla ·\left(k\nabla T\right)+\dot{q}-\rho c{\displaystyle \frac{\partial T}{\partial t}}$$

(2)

where $T$ is the temperature, $k$ is the thermal conductivity, $\rho$ is the density, $c$ is the specific heat capacity, and $\dot{q}$ is the energy generated per unit volume.

Similarly, in 3D incompressible flow dynamics simulation, $\mathcal{N}$ consist of two components based on Navier–Stokes equations [36]:

$${\mathcal{N}}_1={\displaystyle \frac{\partial \mathbf{u}}{\partial t}}+\left(\mathbf{u}·\nabla \right)\mathbf{u}+\nabla \mathrm{p}-{\displaystyle \frac{1}{Re}}{\nabla }^2\mathbf{u}$$

(3)

$${\mathcal{N}}_2=\nabla \mathbf{u}$$

where $\mathbf{u}, t, p$ are the fluid velocity, time, and pressure. $Re$ is the Reynolds number.

In a force convection problem, a common heat management scenario, the heat conduction and the fluid dynamics are coupled, hence the PDEs will be defined as follows [37]:

$$\begin{gathered} {\mathcal{N}}_1={\displaystyle \frac{\partial T}{\partial t}}+\left(\mathbf{u}·\nabla \right)T-{\displaystyle \frac{1}{Pe}}{\nabla }^{2}T \\ {\mathcal{N}}_2={\displaystyle \frac{\partial \mathbf{u}}{\partial t}}+\left(\mathbf{u}·\nabla \right)\mathbf{u}+\nabla \mathrm{p}-{\displaystyle \frac{1}{Re}}{\nabla }^2\mathbf{u}+RiT \end{gathered}$$

(4)

$${\mathcal{N}}_3=\nabla \mathbf{u}$$

where $Pe$ and $Ri$ denote the Peclet and Richardson numbers, respectively.

Meanwhile, PDE problems usually include boundary and initial conditions:

$$\mathit{u}\left(\mathbf{x},0\right)=\mathit{h}\left(\mathbf{x}\right), \mathbf{x}\in \mathsf{\Omega }$$

(5)

$$\mathit{u}\left(\mathbf{x}, t\right)=\mathit{g}\left(\mathbf{x},t\right),\mathbf{x}\in \partial \mathsf{\Omega }, t\in [0,T]$$

where $\mathsf{\Omega }$ and $\partial \mathsf{\Omega }$ are the computational domain and boundary, $\mathit{h}\left(\mathbf{x}\right)$ is the initial condition, and $\mathit{g}\left(\mathbf{x},t\right)$ is the boundary conditions. The backbone of PINN is usually a deep neural network (DNN), which takes $\mathbf{x}$ and $t$ as inputs and output the approximated solution of the PDE.

To calculate the solution, PINN minimizes the non-negative residual error associated with equations (1) and (5).

$$\begin{gathered} {\mathcal{L}}_N={\int }_{\left[0,T\right]\times \mathsf{\Omega }}{\left(\mathcal{N}\left[\mathit{u}\left(\mathbf{x},t\right)\right]\right)}^{2}dtd\mathbf{x} \\ {\mathcal{L}}_I={\int }_{\mathsf{\Omega }}{(\mathit{u}\left(\mathbf{x},0\right)-\mathit{h}\left(\mathbf{x}\right))}^{2}d\mathbf{x} \end{gathered}$$

(6)

$${\mathcal{L}}_B={\int }_{\left[0,T\right]\times \partial \mathsf{\Omega }}{(\mathit{u}\left(\mathbf{x}, t\right)-\mathit{g}\left(\mathbf{x},t\right))}^{2}dtd\mathbf{x}$$

PINNs leverage automatic differentiation (AD) from deep learning frameworks to compute the derivatives required for the residual calculation. Unlike finite difference or finite element methods, AD avoids numerical discretization errors. Since evaluating the full integral in residual loss can be computationally expensive, PINNs often employ Monte Carlo sampling [38]. A subset of points $({\mathbf{x}}^i,t^i)$ is randomly sampled from the computational domain, and the mini-batch training algorithm is used to iteratively update the neural network parameters [39].

$$\begin{gathered} {\mathcal{L}}_N={\displaystyle \frac{1}{N_N}}\sum {\left(\mathcal{N}\left[\mathit{u}\left({\mathbf{x}}^{\mathit{i}},t^i\right)\right]\right)}^2 \\ {\mathcal{L}}_I={\displaystyle \frac{1}{N_I}}\sum {(\mathit{u}\left({\mathbf{x}}^i,0\right)-\mathit{h}\left({\mathbf{x}}^i\right))}^2 \end{gathered}$$

(7)

$${\mathcal{L}}_B={\displaystyle \frac{1}{N_B}}\sum {(\mathit{u}\left({\mathbf{x}}^i,t^i\right)-\mathit{g}\left({\mathbf{x}}^i,t^i\right))}^2$$

If some ground truth data are available in the computational domain, an additional data-based loss term can also be included.

$${\mathcal{L}}_{Data}={\displaystyle \frac{1}{N_{Data}}}\sum {(\mathit{u}\left({\mathbf{x}}^{\mathit{i}},t^i\right)-{\mathit{u}}_{Data}\left({\mathbf{x}}^{\mathit{i}},t^i\right))}^2$$

(8)

Hence, the loss function of the PINN can be defined as the combination of these residuals:

$$\mathcal{L}={\mathcal{L}}_N+{\mathcal{L}}_I+{\mathcal{L}}_B+{\mathcal{L}}_{Data}$$

(9)

This approach allows PINNs to generalize beyond the training data and maintain consistency with underlying physics, making them particularly effective for thermal management problems with limited experimental data or unknown boundary conditions [40,41].

2.2. PINN Variants

While the standard PINN framework offers a powerful tool for solving PDE-governed problems with limited data, it still faces notable challenges when applied to complex real-world scenarios—such as those encountered in electronics and battery thermal management. These challenges include: (1) difficulty in accurately enforcing boundary conditions, which can degrade solution fidelity; (2) computational inefficiency when scaling to high-dimensional or multiscale problems; (3) poor convergence and susceptibility to local minima, particularly in stiff systems or extrapolation tasks; and (4) limited ability to capture complex physical phenomena like turbulence or Multiphysics interactions [42] To address these challenges, several variants of PINNs have been developed, each focusing on different limitations, which are reviewed in detail in the following subsections.

2.2.1. Balancing Residual and Boundary Losses

One of the most critical challenges in training PINNs is the imbalance between the PDE residual loss and the boundary condition loss, which can significantly hinder convergence and accuracy. This issue often arises because the residual loss, which stems from the PDE constraints across the entire domain, can dominate the boundary loss by several orders of magnitude, leading to poor satisfaction of boundary conditions. Wang et al. analyzed this phenomenon as a gradient pathology, showing that conventional training dynamics result in vanishing boundary loss gradients, thereby biasing the model towards interior solutions that violate boundary constraints. To address this, they proposed a learning rate annealing algorithm and a novel PINN architecture to rebalance gradient flows during training, which led to 50–100× improvements in predictive accuracy across various benchmark problems [43]. Building on this, Yao et al. introduced MultiAdam, a scale-invariant optimizer that adaptively rescales gradients using parameter-wise second-moment statistics. Unlike manual or static reweighting, MultiAdam automatically harmonizes the contributions of loss terms at different scales, maintaining consistent convergence across complex PDE domains. This method improved solution accuracy by 1–2 orders of magnitude across diverse physics scenarios, demonstrating robust performance in multiscale PINN training [44]. Together, these approaches mark a significant step forward in developing reliable and physically consistent PINNs, particularly for thermal management tasks that demand precision at boundary interfaces.

2.2.2. Adaptive Sampling Strategies

Sampling strategy plays a pivotal role in the training dynamics and accuracy of PINNs, as the locations of residual collocation directly influence how well the solution captures complex features of the PDE. Uniform sampling, while simple and widely adopted, often results in poor performance in regions with steep gradients or localized phenomena. To address this, several adaptive sampling strategies have been proposed. Nabian et al. introduced an importance sampling approach that selects collocation points proportional to the loss value, effectively focusing training on regions with greater residuals and accelerating convergence without additional hyperparameters [45]. Wu et al. conducted a comprehensive study and proposed RAD and RAR-D, which dynamically adjust point distributions based on residual magnitudes and outperform traditional strategies with fewer collocation points [46]. Tang et al. advanced this further with DAS-PINNs, a generative model-based method that learns the residual distribution, yielding strong results for high-dimensional or irregular PDEs [47]. More recently, Yu et al. proposed MCMC-PINNs, which use a modified Markov Chain Monte Carlo method to sample collocation points according to a canonical distribution based on PDE residuals. This method adapts the proposal distribution to domain geometry and ensures more thorough exploration of complex solution landscapes while maintaining convergence guarantees [48]. Together, these innovations in adaptive sampling significantly enhance both the efficiency and precision of PINNs, particularly in multiscale or unbounded domain problems.

2.2.3. Variational Formulations in PINNs

While traditional PINNs enforce PDEs through their strong form—minimizing residuals at discrete collocation points (equations (6) and (7))—this approach often suffers from instability, especially when high-order derivatives are involved or when the solution lacks smoothness. Variational formulations offer a powerful alternative by expressing the PDE in its weak form, where the equation is satisfied in an integrated sense against test functions. This allows for smoother losses, reduced differentiation order (via integration by parts), and improved stability, especially in complex or high-dimensional settings. The evolution of variational PINNs reflects growing recognition of these benefits. The earliest prominent example is the Deep Ritz Method by E and Yu, which recasts the PDE solution as the minimizer of a variational energy functional. This method constructs the trial solution using a deep neural network and optimizes an integral form of the PDE’s energy without enforcing pointwise residuals, thus avoiding high-order derivative computations and enabling efficient training even in high dimensions [49]. Following this, the VPINN framework by Kharazmi et al. generalized the approach by embedding PINNs in a Petrov-Galerkin setting. In VPINNs, the trial space consists of neural networks, while the test space is constructed using classical polynomial bases (e.g., Legendre polynomials). This variational residual reduces differential order via integration by parts and replaces dense collocation with sparse quadrature, leading to improved numerical stability and efficiency [50]. Building on VPINNs, the hp-VPINNs introduced adaptive domain decomposition and hierarchical polynomial refinement, enabling localized learning and better handling of sharp gradients or singularities in the solution [51]. Around the same time, VarNet proposed a variational training strategy that is fully discretization-free and operates over space-time volumes rather than isolated points. By training on integral residuals and using adaptive sampling driven by residual feedback, VarNet enables smoother, more sample-efficient learning and is particularly well-suited for parametric and control applications [52]. Collectively, variational approaches provide a powerful and more physically grounded alternative to classic PINNs, making them especially well-suited for problems with irregular domains, lower solution regularity, or high computational complexity.

2.2.4. Domain Decomposition PINNs

As PINNs are extended to large-scale or multi-physics systems, they often suffer from high computational costs and poor convergence, especially when trying to capture complex or discontinuous physical phenomena [53]. To address these limitations, domain decomposition techniques have been incorporated into the PINN framework, giving rise to variations such as Conservative PINNs (cPINNs) [54] and eXtended PINNs (XPINNs) [55]. These architectures divide the computational domain into smaller subdomains, within which localized PINNs are trained. This strategy not only enhances scalability and parallelizability but also enables tailored network architectures for different subregions of the problem domain.

The cPINN framework focuses on conservation laws, enforcing continuity of both the solution and flux across the boundaries of decomposed subdomains. Each subdomain employs a separate neural network, with interface conditions ensuring physical consistency by stitching local solutions together [54]. This includes enforcing average solution continuity and flux conservation at shared interfaces, a critical step for solving hyperbolic PDEs like the Euler equations (Figure 1a). Based on this, XPINNs further generalize the domain decomposition concept beyond conservation laws, supporting arbitrary space-time decompositions for any type of PDEs. This includes both convex and non-convex geometries, time-dependent or time-independent problems, and even cases with moving interfaces [55]. Each subdomain is governed by its own neural network and optimized independently. XPINNs introduced interface conditions such as residual continuity and average solution enforcement, allowing seamless stitching across irregular domains. In order to fully leverage the advantages of cPINN and XPINN, a parallelized implementation has also been proposed, based on a hybrid MPI + X programming model (where X can be CPUs or GPUs). This enables efficient training of PINNs on distributed hardware. The parallel framework supports both weak and strong scaling and significantly reduces training time by exploiting localized computation within subdomains.

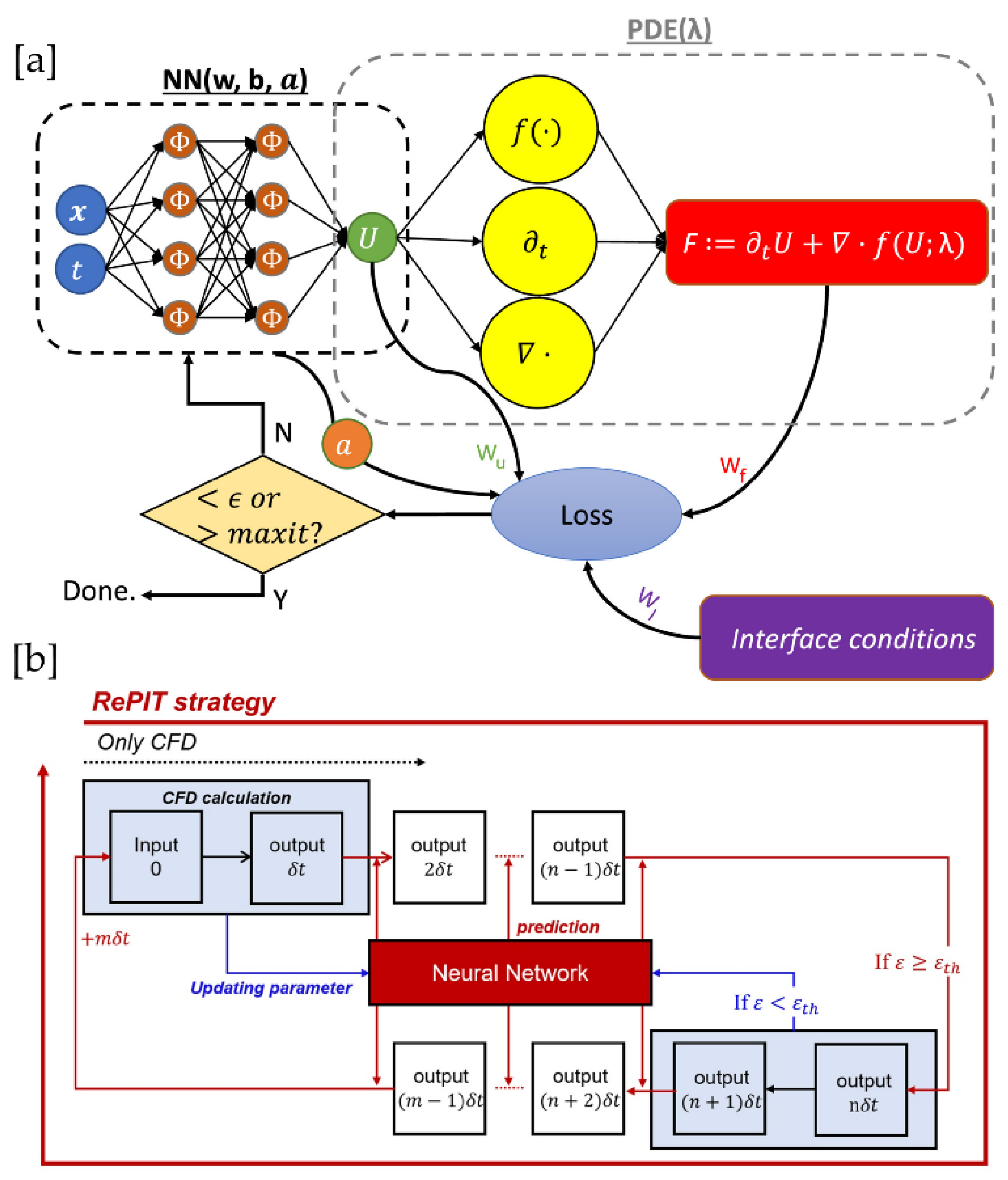
Figure 1. Schematics of PINN and its variations. (a) Schematic of the Conservative Physics-Informed Neural Network (cPINN) architecture [54]. The addition of interface loss distinguishes cPINNs from traditional PINNs, enabling improved performance on conservation laws and problems with sharp gradients. (b) The Residual-based Physics-Informed Transfer Learning (RePIT) strategy as a representative hybrid PINN approach [56]. The workflow alternates between conventional CFD computation and neural network-based predictions.

Figure 1. Schematics of PINN and its variations. (a) Schematic of the Conservative Physics-Informed Neural Network (cPINN) architecture [54]. The addition of interface loss distinguishes cPINNs from traditional PINNs, enabling improved performance on conservation laws and problems with sharp gradients. (b) The Residual-based Physics-Informed Transfer Learning (RePIT) strategy as a representative hybrid PINN approach [56]. The workflow alternates between conventional CFD computation and neural network-based predictions.

Physics-Informed Neural Networks (PINNs) have emerged as a powerful modeling framework for electronics thermal management (ETM), offering a compelling alternative to conventional numerical solvers. By embedding physical laws—such as Fourier’s law and the Navier–Stokes equations (equations (2)-(4))—directly into the training process, PINNs eliminate the need for large datasets and deliver fast, accurate solutions to partial differential equations, even in data-sparse or complex settings. As summarized in Table 1, adaptability of PINNs is further strengthened by a rich ecosystem of variants designed to overcome key training and scalability challenges. For instance, advanced optimizers like MultiAdam and reweighting strategies mitigate the imbalance between PDE residual and boundary losses, improving solution fidelity. Adaptive sampling methods such as importance sampling, DAS-PINNs, and MCMC-PINNs dynamically allocate collocation points where they are most needed, boosting convergence and efficiency in multiscale and sharp-gradient regions. Variational formulations—including the Deep Ritz Method, VPINNs, and VarNet—reformulate PINNs in a weak form, reducing the order of derivatives and enhancing stability for irregular geometries. Domain decomposition approaches like cPINNs and XPINNs enable parallelization and localized learning, making PINNs scalable to large or heterogeneous ETM problems. Together, these innovations make PINNs not only accurate and interpretable but also highly customizable, positioning them as a versatile tool for addressing the diverse modeling demands of modern ETM systems at chip, board, and system scales.

3. Application of PINN in Electronics Thermal Management

For general heat transfer physics, there are three modes of heat transfer: conduction, convection, and radiation, depending on the heat transfer medium [57]. Conduction heat transfer is governed by Fouries’ Law where heat flux is linearly dependent on temperature gradient if thermal conductivity is constant for steady state scenario or density and heat capacity. Temperature-dependent thermal conductivity or density or heat capacity will introduce non-linear physical character into this [58,59]. Convection is governed by Newton’s Law, and the heat transfer coefficient depends on fluid properties, such as temperature, fluid velocity, or flow regime (laminar or turbulent) [60]. Radiation is governed by Stefan-Boltzman Law and is non-linear due to the fourth-power dependence on temperature [61]. With various intensity power densities and different scale of cooling requirements, thermal management systems employed in electronics generally can be categorized into passive cooling and active cooling [62]. Passive cooling refers to the method that dissipates heat without any active energy inputs, and techniques in this category include heat sink, thermal pads/interfaces, heat pipes, vapor chambers. whereas active cooling will require additional power input, such as fan, liquid cooling, jet impingement cooling. Besides these traditional cooling mechanisms, two-phase liquid cooling is increasingly standard in data centers, while immersion cooling is gaining traction for its efficiency [63,64,65].

The advancement of cutting-edge information and digital technologies—including 5G, artificial intelligence, cloud computing, autonomous vehicles, and data centers—has greatly increased the need for functional electronics, driving a demand in their power densities and reliabilities [66,67]. Maintaining a safe operating temperature is essential for the proper functioning of each unit, making thermal management systems very critical. Depending on the physical size of the system, thermal management can be classified into three levels: chip, board, and system [68]. The thermal management challenges vary across the three levels. 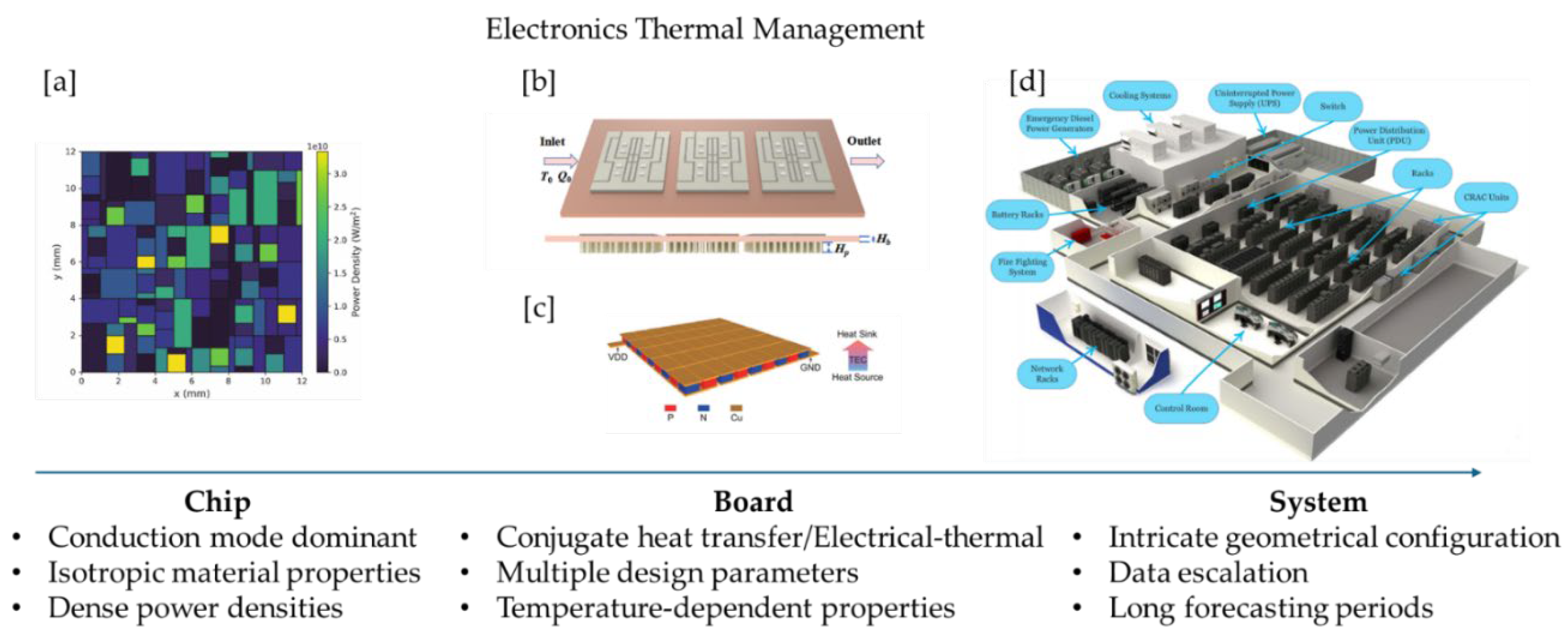As depicted in Figure 2, at the chip level (Figure 2a), densely packed power tiles represent each functional unit, with conduction as the dominant heat transfer mode and boundary conditions set by the heat transfer coefficient. Material properties may be isotropic and temperature-dependent, varying based on design accuracy requirements. At the board level (Figure 2b, 2c), heat transfer becomes more complex as various mediums—such as air or dielectric liquids—come into play. In addition, multiple components with varying power inputs are present, which can include factors like direct current internal resistance losses or electromagnetic power losses, involving Multiphysics consideration. Despite this increased complexity and the larger number of design parameters, board-level challenges are not necessarily greater than those at the chip level, largely because most passive electrical and heat-generating components exhibit isotropic characteristics. Finally, at the system level (Figure 2d), the intricate geometry of components not only increases the volume of data but also lengthens both the training and forecasting periods.

Figure 2. Electronics Thermal Management challenges. Image sources: [a] [69], [b] [70], [c] [71], [d] [72].

Figure 2. Electronics Thermal Management challenges. Image sources: [a] [69], [b] [70], [c] [71], [d] [72].

Following this scaling methodology, this chapter will analyze selective PINN applications at chip, board, and system level with electronics thermal management and aim to bridge the connections between different scales.

3.1. Chip Thermal Management

For chip thermal management, heat is generated at the nanoscale with intensive density and is mainly conducted through the die then reaches the chip surface and cooled through external multilayer package and thermal interface materials, eventually dissipated through external conduction or convection [73]. Therefore, conduction is the dominant heat transfer mode at the chip level, while external conduction or convection can be simplified and simulated with heat transfer coefficient boundary condition settings. Radiation is negligible due to the small surface area and low emissivity (polished surface) [68]. According to Fourier’s Law, conduction heat transfer is linear when thermal conductivity is constant. There are two main challenges posts with chip thermal management, namely temperature-dependent material properties (thermal conductivity, density, and heat capacity) and high-dimensional power densities due to the hierarchical structure or advanced 3D IC structure [74].

Chip nowadays has become very dense of power tiles and will require a very fine resolution for each tile of power to be captured correctly, which is not possible for current Finite Element Analysis (FEA) approach as discretization of the full chip level is extremely time-consuming and source intensive. The high-dimensional and nonlinear PDEs have also been researched to accelerate with machine learning approaches. Traditional machine learning approaches with chip thermal management require large data input. For example, Sadiqbatcha et al. build the long-short-term-memory (LSTM) to train experimental infrared thermal image results to estimate representative spatial features of the 2D heatmaps with similar accuracy and high efficiency [75]. Chen et al. [76] adopted graph convolution networks (GCN) with global features, skip connections, edge-based attention, and principle neighborhood aggregation to efficiently estimate thermal maps of 2.5D chiplet-based systems, while demonstrating strong generalization to unseen datasets.

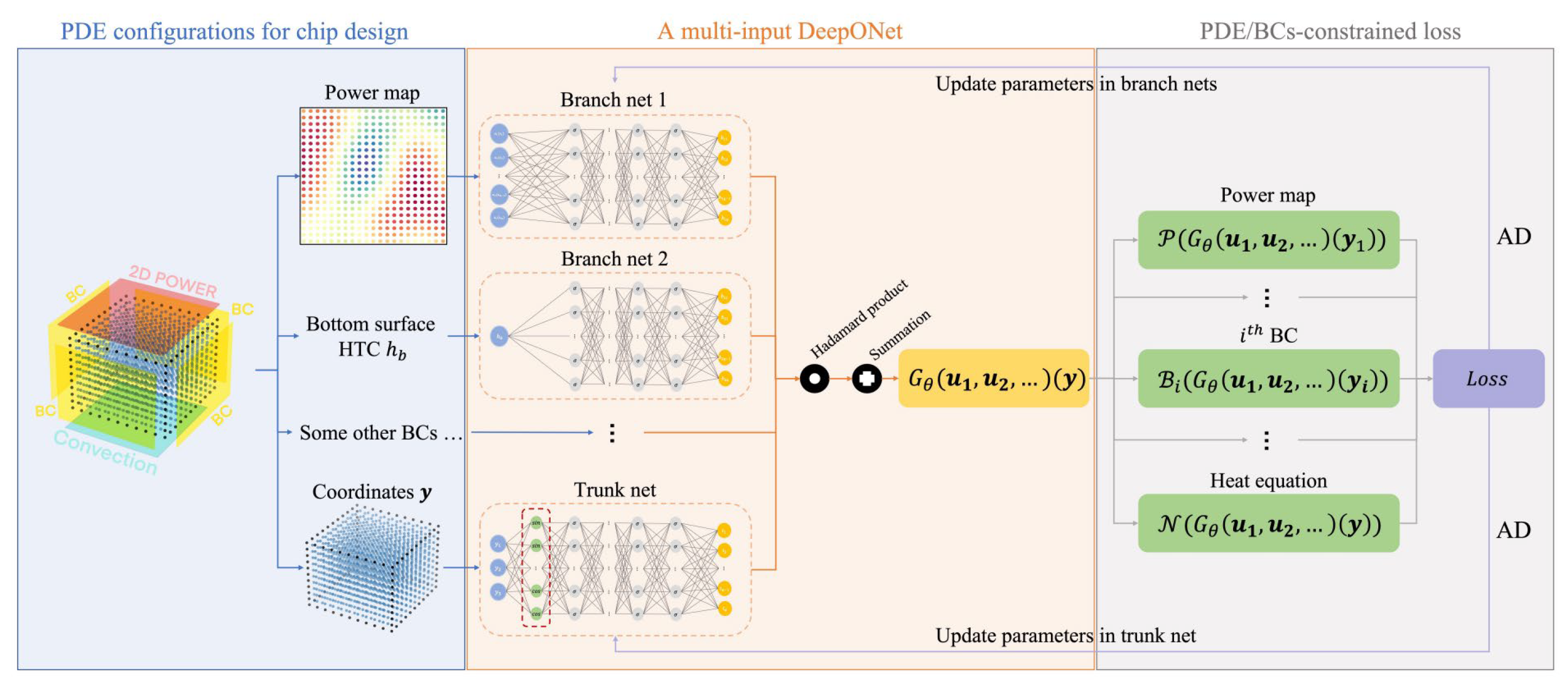
On the other hand, PINN presents to have good potential to overcome the data-intensive traditional machine learning shortages. Liu et al. applied physics-aware operator learning method (DeepONet) on a 21 x 21 x 11 mesh grid-based single-cuboid geometry with a 2D power map with constant HTC boundary condition [77]. In the study, firstly, two families of design configurations, namely, boundary condition for each individual surface and locations and intensity of external or internal heat sources were encoded as input functions as different “branch net” to be fed into the framework. While all the sampled coordinates are fed into another sub-network, namely, “trunk net”. Then the k branch nets, and one trunk net were combined via Hadamard (elementwise) product and summed to represent the predicted temperature field. The framework is then trained with multi-input DeepONet (Figure 3) [78]. The total loss was minimized by gradient descent based on automatic differentiation algorithm. The result showed 300,000 times faster than commercial Celsius 3D solver and max/min temperature difference less than 0.1K. However, this reveals limitations in scalabilities and generalization, as it does not include orthotropic or temperature-dependent material properties.

Figure 3. DeepOHeat framework.

Figure 3. DeepOHeat framework.

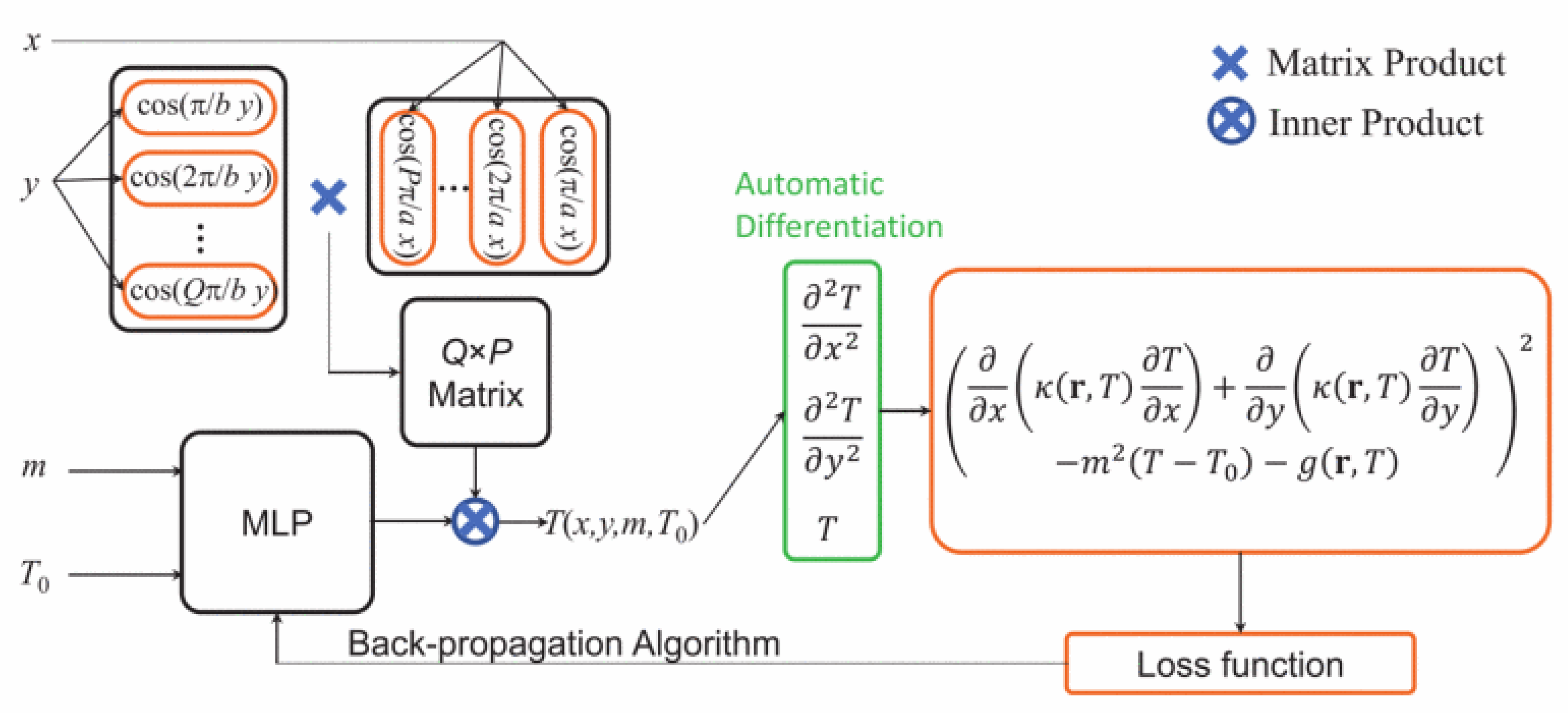
Another study conducted by Chen et al. was about an enhanced PINN approach designed for rapid and accurate full-chip thermal analysis of Very Large-Scale Integration (VLSI) chips, namely ThermPINN [79]. Standard PINNs, while innovative, suffer from slow training convergence. In Chen’s work, temperature distribution equation can be expressed with separation of variables into two variables along x- and y- directions to form two cosine vectors with a coefficient C_pq. The authors also considered that both thermal conductivity and leakage power vary with temperature and used appropriate models to depict their relationship to temperature across a specific temperature range. As shown in Figure 4, firstly spatial variables are separated into cosine vectors, forming a Q×P matrix whose inner product with the C_pq matrix yields the temperature value with a discrete cosine neural network. Second, effective convection coefficient m and ambient temperature T₀ are parameterized to connect with C_pq with multi-layer perception (MLP). Back-propagation algorithm is used to learn the MLP parameters. The thermal equation is then coupled into loss function and unsupervised learning method is used to train the networks. The author also applied a plain PINN as a benchmark where position, effective convection coefficient and ambient temperature are directly parametrized to trin the MLP.

Figure 4. ThermPINN framework.

Figure 4. ThermPINN framework.

The findings indicate that ThermPINN’s accuracy was slightly below that of plain PINN but in the same order of significance, while it demonstrated strong potential for faster training, making it more practical for EDA applications, with both PINNs outperforming traditional FEM solutions in speed. The model parameterizes key variables—ambient temperature and effective convection coefficient—enabling efficient design space exploration and uncertainty quantification (UQ).

3.2. Board Thermal Management

In board thermal management, the electrical components hosted on a printed circuit board—such as resistors, capacitors, memory cards, integrated circuits (ICs), heatsinks, and solder joints—vary widely by application and industry, with some being passive and others producing high-density, dynamic thermal power under different operating conditions [80]. Thermal management poses a significant challenge, though techniques like air cooling, cold plates, jet impingement, and immersion cooling are well-established, addressing the diverse safe temperature limits, space constraints, and power demands across components and product generations, which complicates redesign and simulation efforts. Simplified simulations on board thermal management using black-box reduced-order models (e.g., Linear time invariant [81], Linear parameter varying [82], singular value decomposition [83]) are possible but often lack field-specific accuracy or require extensive training data, whereas PINNs offer a promising approach for prescreening and estimating untested scenarios.

On the board, there can be power chips with different layers soldering with baseplate or printed circuit board (PCB). In a study conducted by Yang et al., four SiC MOSFET chips are sitting on DBC AIN substrates with integrated deionized water pin-fin colling channels on the top. 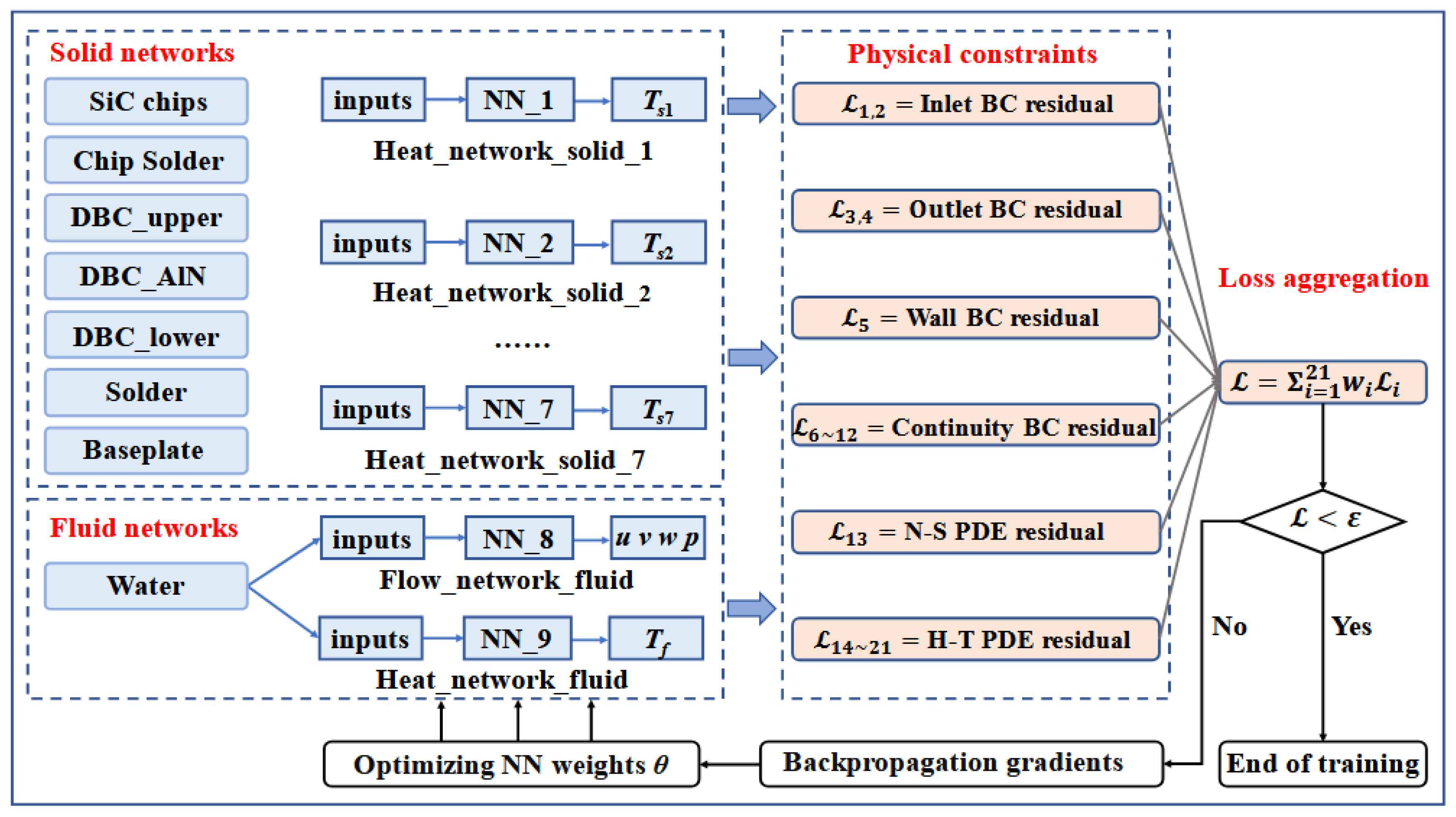5 parameters, including initial temperature, heat flux, chip total powers, and baseplate thickness and pin-fin heights are explored for design space [84]. For the SiC power module, due to the existence of layers with different material properties, representing to separate physical domain, the authors applied in total of 9 Fourier neural networks with soft coupling constraint in PINNs for rapid design exploration, outperforming traditional FEM solver for faster thermal profile prediction. As shown in Figure 5, 7 Fourier networks that represent and fit the thermal equations to each physical domain plus 2 Fourier networks for fluid flow and convective heat transfer PDEs consist of the total of 9 Fourier NN as training inputs. Random sampling points are then generated uniformly across the domain and boundaries to evaluate a loss function, which integrates PDE residuals, boundary condition errors, and interface continuity penalties, balanced using adaptive weights. The model undergoes iterative training via backpropagation with the Adam optimizer and an exponential decay learning rate, minimizing the loss below a threshold (10⁻⁵) for synchronized convergence across networks. Once trained, the PINNs model enables rapid inference of thermal fields for any input parameter combination without retraining, offering an efficient alternative to traditional numerical methods. The author suggested that in terms of scalability, PINNs delivered performance like COMSOL for 100 simulations. However, when expanding to a significantly larger set of simulations—such as 10,000 cases—the PINNs-based approach demonstrated substantially higher simulation efficiency, particularly for exploring expansive design spaces. However, PINNs were trained on GPU while benchmark COMSOL simulations are based on CPU, which is not a fair comparison due to the parallel computation capabilities of GPU. As the authors introduced geometrical parameters, mesh-dependent accuracy can be a potential risk when scaling.

Figure 5. PINNs with parameterized thermal simulation method on power module thermal management.

Figure 5. PINNs with parameterized thermal simulation method on power module thermal management.

Another application involves a cooling component on the board, thermoelectric cooler (TEC), which consists of N-type and P-type semiconductor materials in series [85]. When an electric current passes through these materials, heat is absorbed from one side (the cold side) and released on the opposite side (the hot side), which is also called Peltier effect. Simulating and Designing TECs can be challenging due to their complex physics and computational demands: (1) TECs operate based on intertwined thermal and electrical phenomena, governed by nonlinear PDEs, highly influenced by temperature-dependent material properties, including thermal conductivity, Seeback coefficient, and electrical conductivity; (2) 3D FEA simulation that requires fine spatial discretization results in large systems of equations and high demand of computer resources; (3) Identifying optimized parameters even escalates the complexity. 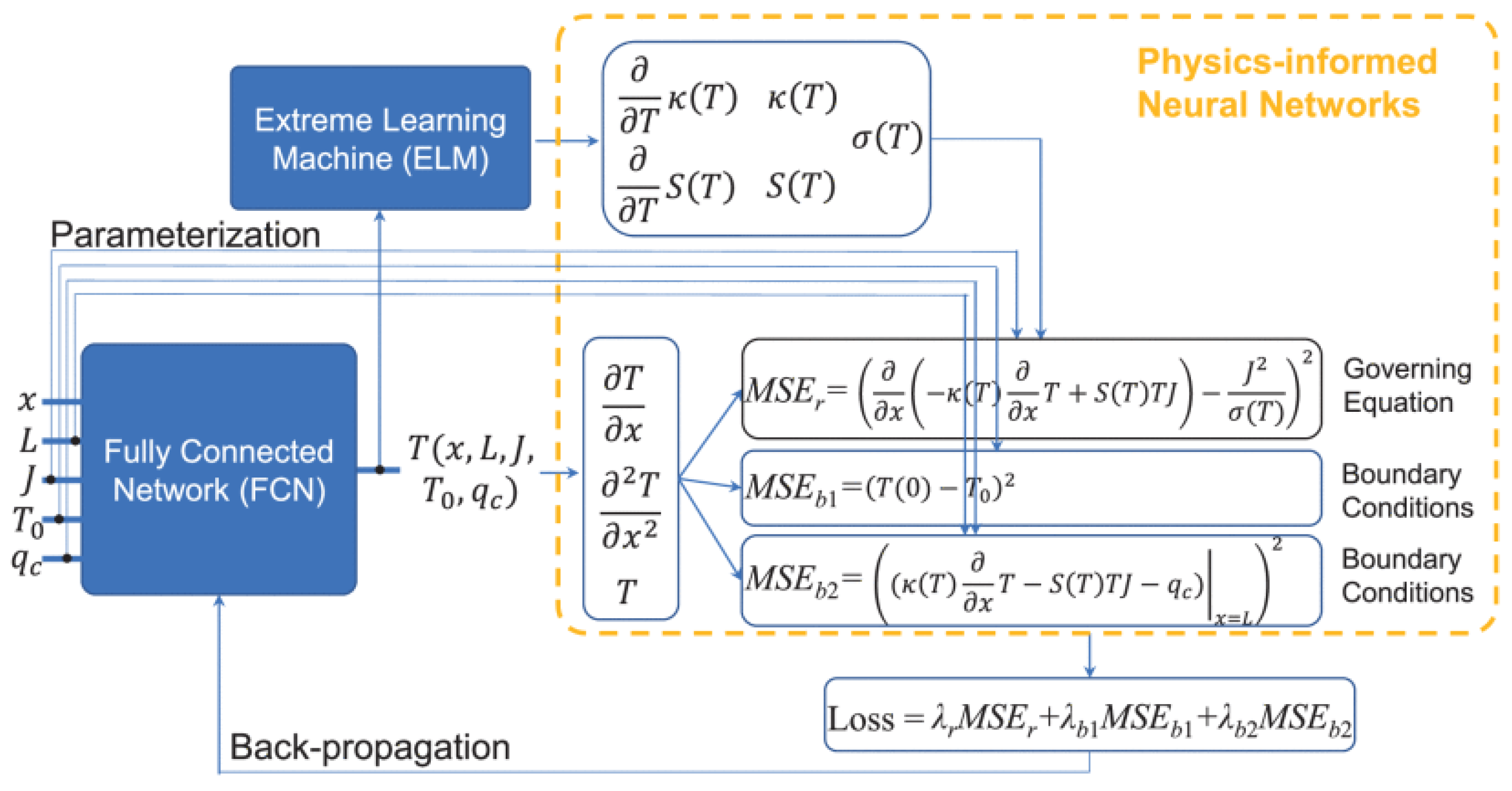The study conducted by Chen et.al introduced a surrogate model that reduces 3D TEC geometry to a 1D problem with key parameters like current density and thermal boundary conditions incorporated [86]. The implicit physics-constrained neural networks (IPCNN) framework proposed by the authors employs a two-stage training process (Figure 6). Firstly, temperature-dependent material properties are approximated with an extreme learning machine (ELM), followed by a PINN enforcing TEC-specific PDEs in the second stage. This method achieves an 8.5× speedup over traditional COMSOL simulations and enhances stability compared to conventional PINNs. Additionally, a hybrid finite element neural network (FENN) method integrates the surrogate model into COMSOL, yielding a 5.1× speedup and 5.4× memory reduction for VLSI chip thermal analysis. The author demonstrated that this IPCNN approach showed a much good convergence to a loss of 10⁻⁶ versus 10⁻¹ for traditional PINNs in smaller length ranges. It avoids the slow convergence and large errors of one-step PINN training by separating the modeling of material properties and PDE solutions, reducing the optimization search space. However, accuracy drop was observed as parameter ranges widen (e.g., length from 0.05–1.2 mm), suggesting scalability limitations, and the complexity of implementing a two-stage process compared to a single-step PINN. The scalability for broader parameter ranges based on this study can potentially be achieved by employing multiple neural networks for subregions, as suggested in the text. Further refinement could also involve adaptive learning rates or advanced network architectures to maintain accuracy across diverse conditions. Integrating more physics constraints or exploring alternative approximators beyond ELM could also boost performance. Overall, this study underscores IPCNN’s potential as a transformative tool in TEC modeling, balancing efficiency and precision, while identifying pathways for future enhancements in board thermal management.

Figure 6. IPCNNs for temperature-dependent TEC.

Figure 6. IPCNNs for temperature-dependent TEC.

Another research conducted Farrag et al. was on soldering reflow process (SRP) [87], which happens during the PCB manufacturing process. In SRP, solder paste is melted and then solidified to connect electronic components to PCB. Precise temperature control is critical to ensure the PCB’s quality. Due to the escalating complexity of the PCB and a greater number of different electrical components, monitoring and accommodating the SRP process becomes extremely difficult. The SRP-PINN model proposed by Farrag et al. leverages PINNs to predict the temperature distribution across PCBs, ensuring solder joints meet manufacturer-specified thermal profiles for quality assurance. Unlike traditional CFD approaches, which are computationally intensive, SRP-PINN integrates PDEs into a DNN to achieve accurate predictions with limited experimental data. The study uses a 1D heat transfer model along the PCB length, trains the PINN with sparse data from one recipe, and demonstrates its generalizability across different PCB designs and soldering recipes. Experimental results, conducted on a Heller 1707W reflow oven with SAC305 solder paste, show the model’s effectiveness, achieving 98% accuracy compared to 97% for a hybrid physics-ML benchmark, with potential applications in real-time manufacturing optimization.

3.3. System Thermal Management

When it comes to system scale, besides the above-mentioned challenges on the chip and board level challenges, intricate geometrical configurations can be a challenge due to the complexities of CAD geometries, such as electronics enclosure, large-scale cooling components [88,89,90,91]. To capture the fluid flow and temperature profile precisely, setting non-conformal mesh at different regions for balancing calculation accuracy and computer resources requires a lot of human instructions and experiences, let alone the time to even start a simulation [92,93]. PINN can be very useful in resolving repetitive work and save running time when only several parameters need to be modified for a new design.

In the data center field, energy consumption is long-term intensive and heat generation is significant due to the computing requirement. The primary cooling source is the Heating, Ventilation, and Air Conditioning (HVAC) system while the heat is generated from racks, power supplies, and power generators. Chen et al. demonstrated notable performance in a six-month case study on data center thermal modeling with adaptive physically consistent neural network (A-PCNN) [94] (Figure 7). The approach leveraged NN with Softplus activation functions, replacing traditional preset and fixed coefficients to reduce trial-and-error costs and increase flexibility. Specifically, it reduced the Mean Absolute Error by 17.3 % for a 15-min forecast and by 79.2 % over a 7-day period.

Figure 7. Adaptive physically consistent neural networks framework.

Figure 7. Adaptive physically consistent neural networks framework.

Tanaka et al. proposed a surrogate model for full-scale thermal models using data reduction via proper orthogonal decomposition and PIML. The prediction accuracy of the proposed method is evaluated using two types of thermal mathematical models to investigate the dependency of the training dataset and the size of the models. In addition, the prediction accuracy and training cost were compared between data-driven machine learning and physics-informed machine learning. As a result, the proposed method successfully predicted the full model temperature for both models under various heat input conditions. Moreover, the proposed method decreased the total training cost by 26% to 81% compared to data-driven machine learning [95].

Zhang et al. investigated the application of PINNs to simulate fluid flow and heat transfer in manifold microchannel (MMC) heat sinks designed for cooling high-power Insulated Gate Bipolar Transistors (IGBTs), critical components in power electronics [96]. The study develops a PINN model with two sub-networks—one for flow dynamics and another for thermal behavior—each employing a DNN with a sine activation function to capture high-order derivatives and mitigate vanishing gradient issues. Compared to traditional CFD simulations, PINNs show similar trends, such as increased pressure drop and decreased temperatures with higher inlet velocities, though discrepancies occur in regions with rapid flow changes and maximum temperature predictions. The mesh-free nature of PINNs and their ability to embed physical laws into the loss function enable efficient simulation of complex geometries with less data than purely data-driven approaches. Additionally, the paper explores PINNs’ potential in solving inverse problems, like estimating kinematic viscosity and thermal diffusivity, highlighting their versatility. Despite computational expense and sensitivity to geometry and hyperparameters, PINNs emerge as a promising alternative for thermal management in engineering applications.

All the above system thermal management benefits from implementing PINN framework. With emerging technologies and fast turn-around requests in high-tech consumer electronics, data centers, electrical vehicles, PINNs have more potential when the computational requests escalate.

4. Application of PINN in Battery Thermal Management

Battery systems involve multiple physical phenomena, such as electrochemical reactions, heat transfer, and mechanical stress, making simulation and analysis complex [97,98]. Use of PINNs include state estimation [99], degradation [100,101], aging estimation [101], proving the interest and potential of PINN in battery system. Finegan et al. outlined a perspective and discussed the challenge of scarce data for analysis thus recommended physics-based learning to predict battery failure more accurately and reliably [102]. Physics integration can include physics-based datasets, physics-informed training constraints and physics-guided algorithm structures, which are a hybrid approaches to merge data-driven and physics-based.

Thermal management in battery is critical as thermal runaway (TR) is one of the primary safety concerns in batteries [103,104]. It occurs when an increase in temperature accelerates internal chemical reactions, generating more heat and potentially causing an uncontrollable chain reaction that may result in fire or explosion. TR in a single LIB can rapidly propagate from the root cell to all adjacent cells, thus resulting in catastrophic accidents in large-scale battery pack and systems. Therefore, efficient battery thermal management system at different scales is critical to ensure safe temperature of each cell and mitigate the TR phenomenon overall.

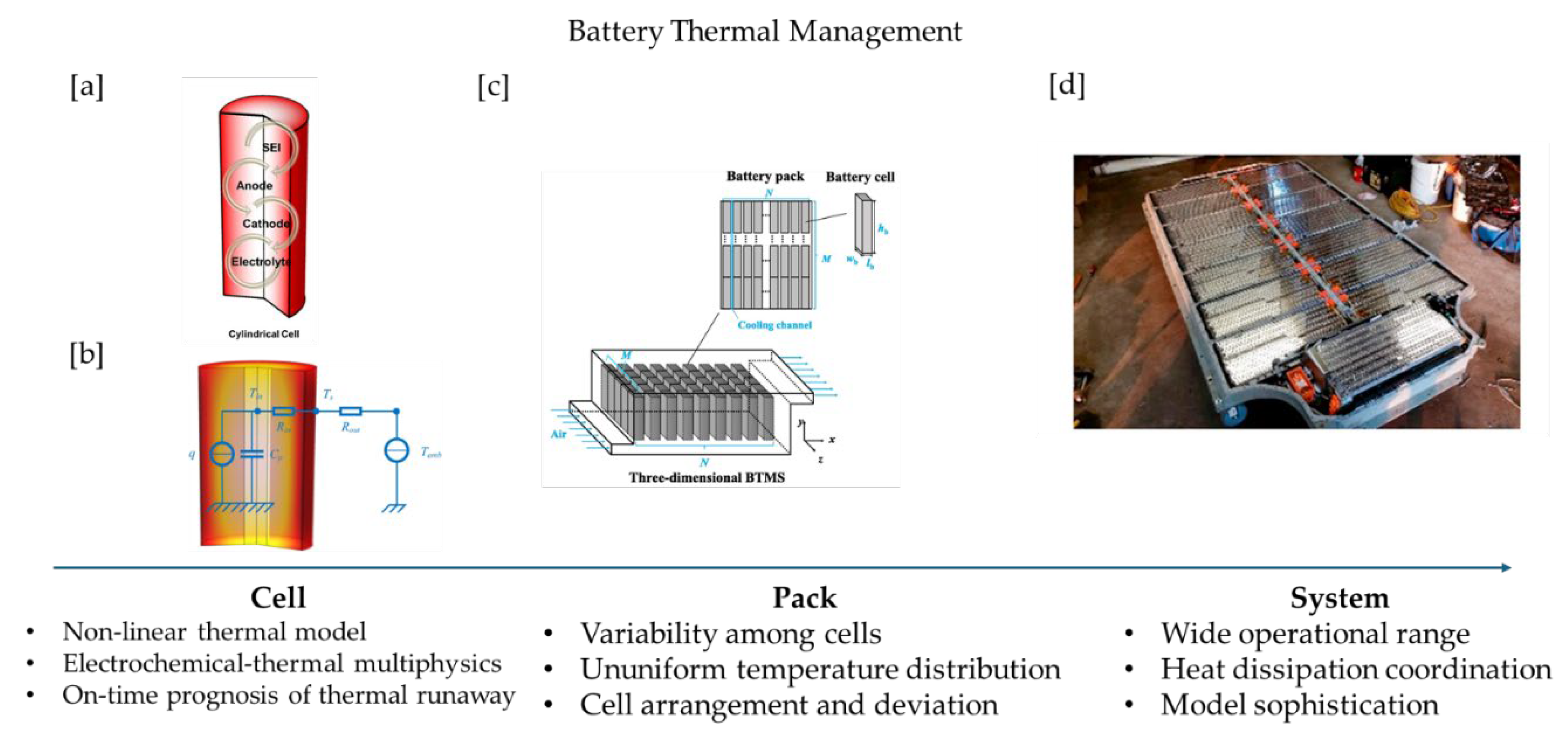
Battery thermal management simulation presents a range of challenges across different levels—from cell to pack to system (Figure 8). At the cell level, the need to capture non-linear thermal behavior and electrochemical-thermal Multiphysics interactions make modeling complex, especially for accurate real-time prediction of thermal runaway events. Moving to the pack level, cell-to-cell variability, non-uniform temperature distribution, and the impact of cell arrangement and manufacturing deviations complicate the prediction of thermal behavior and require detailed spatial resolution. At the system level, the challenges expand to modeling under wide operational conditions, ensuring effective heat dissipation coordination across components, and maintaining a high level of model sophistication to balance accuracy and computational efficiency. The challenges are not confined to a single scale; instead, they can play a role across different scales. In addition, different from electronics thermal management, the heat source is power loss from electrical components, traces, or frequency-varying process, the heat source in battery is mainly introduced through multiple endothermic and exothermic electrochemical processes and is dynamically changing due to the charging state, which makes capturing the exact source term and modeling battery thermal behavior even challenging.

Figure 8. Battery Thermal Management challenges. Image sources: [a] [105] , [b] [106], [c] [107], [d] [108].

Figure 8. Battery Thermal Management challenges. Image sources: [a] [105] , [b] [106], [c] [107], [d] [108].

This chapter will divide the PINN research into battery cells, battery packs, and battery system, following the same escalating order in Chapter 3.

4.1. Battery Cell Thermal Management

For battery thermal profile prediction, generally the source term is simplified with a uniform heat generation source, or thermal resistance network [109,110]. Many researchers have simplified PDEs to create lumped parameter models. Research can however be done by considering the realistic 3D battery thermal model at different charging states.

Deng et al. applied PINN to integrate electric–thermal mechanism of the battery and data information through a weight adaptive function [111]. It is done by integrating transient thermal equations with heat generation being uniformly calculated from the relationship between current and voltage. The thermal equation is relatively easy to train due to the constant material property and the battery heat generation rate is simply decided by joule heating without considering the various reactions and their exothermic rate in the formula. Wang et al. proposed a battery informed neural network (BINN), selected features (voltage, current, experiment time, etc.) to obtain cell surface temperature, open circuit voltage and internal resistance to reflect aging [112].

Kim et al. applied a Multiphysics-informed neural network (MPINN) in thermal runaway analysis with a simple cylindrical lithium-ion cell without any charge or discharge processes [105]. The MPINN addresses this by embedding physical laws—such as the energy balance equation and Arrhenius law—into the neural network, enabling it to estimate time- and space-dependent temperature and concentration profiles more effectively than purely data-driven models like standard artificial neural networks (ANNs). The study achieves significant advancements by demonstrating that MPINN outperforms ANNs in accuracy across various data availability scenarios (Figure 9). With fully labeled data, MPINN reduces mean absolute error (MAE) and root mean squared error (RMSE) compared to ANNs (e.g., MAE of 0.46 vs. 1.17 for temperature). In semi-supervised settings with limited labeled data, MPINN’s errors remain low (MAE of 0.08 vs. 47.46 for ANN), and it can even predict TR without labeled data for positive electrode decomposition, leveraging its physics-informed framework. This capability positions MPINN as a promising surrogate model for real-time TR prediction and battery safety optimization, validated through comparisons with high-fidelity COMSOL simulations. Looking forward, the paper suggests promising improvements, including expanding MPINN to model additional TR mechanisms like negative electrode and solid electrolyte interphase (SEI) layer decomposition for a more comprehensive representation. Reducing the computational cost of training, currently a bottleneck, would enhance its practicality. Additionally, applying MPINN to complex battery geometries or multi-cell systems could broaden its real-world applicability, advancing battery management systems and safety designs. These enhancements could solidify MPINN’s role in improving LIB reliability and safety.

Figure 9. Multiphysics-informed neural networks framework.

Figure 9. Multiphysics-informed neural networks framework.

4.2. Battery Pack Thermal Management

Cho et al. explores the use of a PINN to tackle significant challenges in managing lithium-ion battery packs, particularly the accurate prediction of temperature distributions [113]. The PINN approach addresses these issues by integrating physical laws, such as energy balance equations, directly into the neural network’s loss function. This hybrid method combines the strengths of physics-based and data-driven models, reducing the need for large datasets and extensive parameter tuning while maintaining accuracy, especially in scenarios with limited data or unknown initial conditions. The paper demonstrates notable success in applying the PINN method to improve temperature prediction accuracy within lithium-ion battery packs (Figure 10). By embedding physical constraints into the neural network, the PINN achieves a root mean square error (RMSE) of 0.57°C for the Direct Current Fast Charge (DCFC) test profile and 0.52°C for the Grade Load (GL) 100 test profile. These results mark a significant improvement over traditional methods, offering a more efficient and reliable way to monitor battery temperatures. Enhanced accuracy is particularly valuable for preventing thermal runaway and extending battery life, key concerns in battery management systems. The study also refines PINN’s performance by incorporating additional inputs, such as chamber temperature, and optimizing the neural network architecture. This hybrid approach not only outperforms conventional models in terms of precision but also reduces computational overhead, making it a practical solution for real-time temperature monitoring in battery packs.

Figure 10. LSTM-PINN hybrid framework.

Figure 10. LSTM-PINN hybrid framework.

Looking ahead, the paper suggests several avenues to further enhance the PINN approach for battery pack applications. One promising improvement is the integration of more comprehensive physical models into the neural network, such as those accounting for varying thermal properties or complex heat transfer mechanisms within the battery pack. This could lead to even greater prediction accuracy by capturing a broader range of physical phenomena. Another potential advancement lies in optimizing the neural network architecture, possibly by exploring hybrid models or alternative network types to better handle the nonlinear dynamics of battery systems. Additionally, expanding the dataset to encompass a wider variety of operating conditions and battery types could improve the model’s generalizability, making it adaptable to diverse real-world scenarios and battery configurations. These enhancements could solidify PINN’s role as a cornerstone in battery management systems, driving further improvements in safety, efficiency, and performance for lithium-ion battery applications.

4.3. Battery System Thermal Management

When batteries pack are embedded in large systems, such as electronics and electric vehicles, the simulation becomes more challenging.

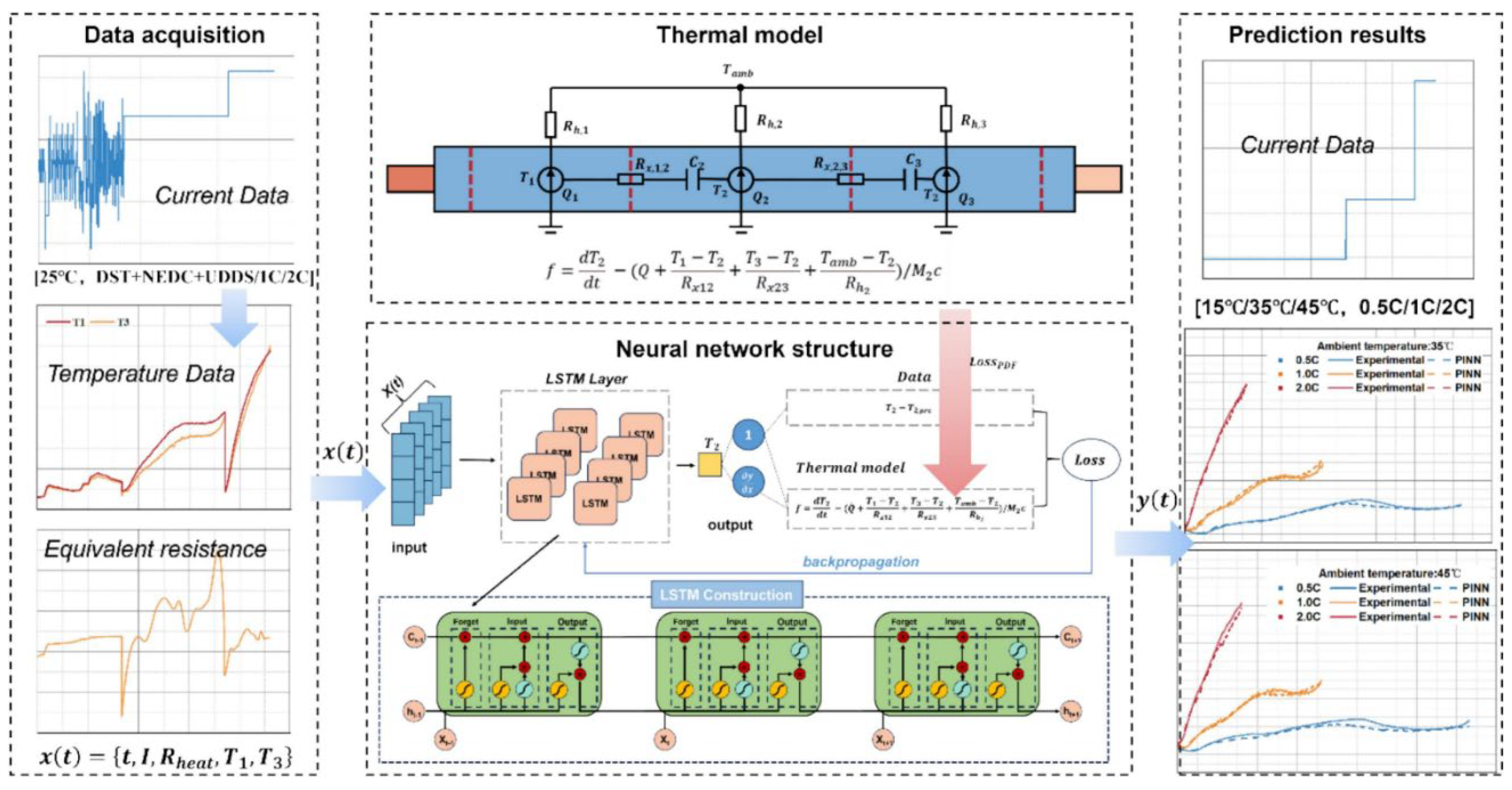
Shen et al. applied PINNs to address the challenge of accurately estimating temperature distributions in large-format lithium-ion blade batteries, a critical aspect of thermal management in electric vehicle battery packs [114]. Effective temperature control is vital because it directly impacts battery performance, safety, and lifespan, with excessive heat potentially leading to thermal runaway. Traditional physics-based models, while detailed, are computationally demanding and require extensive manual parameter tuning, making them impractical for real-time use. Conversely, data-driven models depend on large datasets, which may not always be available, especially under diverse operating conditions. The paper introduces a PINN model that integrates a simplified multi-node thermal model into a LSTM neural network, combining physical laws with machine learning (Figure 11). This hybrid approach reduces the need for extensive data and calibration by embedding heat transfer equations into the network’s loss function, enabling real-time temperature predictions with improved accuracy and interpretability, particularly for large-format batteries with non-uniform heat generation.

Figure 11. PINN-based real-time battery temperature estimation framework.

Figure 11. PINN-based real-time battery temperature estimation framework.

The paper demonstrates significant achievements through the development and testing of the PINN model for battery temperature estimation. By incorporating a one-dimensional thermal model with three nodes—accounting for heat generation, transfer, and dissipation—the PINN leverages LSTM to capture the time-series nature of temperature changes. Tested under various charging conditions (0.5C, 1.0C, and 2.0C), the model outperforms traditional approaches like Backpropagation Neural Networks (BP-NN) and standalone LSTM. For instance, at a 2.0C charging rate, it achieves an R² of 0.9863, a mean absolute error (MAE) of 0.2875°C, and a root mean square error (RMSE) of 0.3306°C, showcasing high predictive accuracy. A notable advantage is its ability to learn parameters such as equivalent internal resistance automatically via neural network training, eliminating manual calibration. These results, validated through a realistic experimental setup with a battery test bench, highlight PINN’s effectiveness in providing precise, real-time temperature estimates, enhancing battery management systems’ ability to prevent thermal issues. The paper outlines several promising directions for enhancing the PINN model’s capabilities. One key improvement is extending temperature estimation to the battery module level, predicting the overall temperature field across multiple cells in a pack. This would offer a more comprehensive thermal profile for practical applications but would require addressing increased complexity in modeling inter-cell interactions. Another avenue is refining the thermal model by incorporating additional physical phenomena, such as detailed heat transfer mechanisms or variable thermal properties, to further improve accuracy. Expanding the dataset to include a broader range of operating conditions (e.g., different charge rates, ambient temperatures, and battery aging states) could enhance the model’s generalizability and robustness. Additionally, optimizing the neural network architecture—potentially by exploring advanced hybrid designs—could improve its ability to handle complex, nonlinear thermal dynamics. These advancements would strengthen PINN’s role in real-time thermal management, supporting safer and more efficient battery pack operations in electric vehicles.

PINNs in battery thermal management have not been well understood due to the complexity of electrochemical-thermal Multiphysics that are different to identify the thermal source and corresponding PDEs, especially with different SOC. Data-driven experimental identifying is the current approach to identifying, which deviates from the PINNs intention that it is not data-driven.

5. Conclusions

In this review paper, we first discussed the working principles of the PINNs and variants, and their general applications in the physics simulation world in Chapter 2. Based on this understanding, we then discussed the challenges in both electronics and battery thermal management at three scale levels and how PINNs can tackle these challenges accordingly. Specially, we reviewed research that were conducted in the chip-level, board-level and system-level for electronics thermal management in Chapter 3. The PINNs are solving different analysis challenges at different scales. In Chapter 4, we then reviewed research conducted on battery thermal management, with the same scale categorizing standards, from battery-level to pack-level, to large-format. Being the most two heat-intensive components in the high-tech, automobile and industrial fields, thermal management on electronics and batteries should be considered together. Gaps clearly existed in the connections between these two components. For current research, the PINNs solved the challenges of data scarcity, prediction efficiency, and the critical idea is to figure out the correct PDEs to use, adjust the training algorithms for various operating conditions. Despite the promising advantages PINNs can bring over the traditional machine learning and flexibility of PINNs to combine with different techniques to enhance its performance, application of PINNs is not without challenges, as they can be computationally intensive, sensitive to the correct formulation of governing equations and neural network architecture, and may face convergence issues or require extensive hyperparameter tuning when dealing with stiff or highly nonlinear systems, making their deployment in real-time or large-scale industrial settings more challenging. Therefore, this review points out both pros and cons of application of PINNs, which will benefit from inspiration on applying advanced machine learning approaches to deal with the system-level electronics and battery systems thermal management.