A Mathematical Framework of a New Paradigm of Autonomous Organization: Constraint Emergence as the Origin of Life

1. Introduction

The origin of life remains one of the most profound and unresolved questions in science. Traditional approaches to this problem have largely focused on the spontaneous emergence of specific molecular subsystems: catalytic peptides (protein-first hypotheses), self-replicating RNA strands (RNA World hypothesis), or lipid bilayers forming primitive compartments (protocell models) [3,4,5]. While each of these perspectives has yielded critical insights, they remain fundamentally reductionist, seeking life’s explanation in the properties or behaviors of particular molecules or reactions.

Yet life, as it exists today, is not reducible to any single molecular species or isolated process. It is an organized, dynamic, and autonomous system: a network of processes that maintain and regenerate the conditions necessary for their own persistence [6,7]. Understanding life’s origins thus requires not merely explaining how molecules arise, but elucidating how matter and energy self-organize into self-producing, self-maintaining, and evolvable systems.

In this work, we propose a disruptive conceptual shift: Life did not emerge primarily from specific molecules, but from the spontaneous emergence of functional constraints. Constraints–localized, dynamically sustained structures that regulate chemical flows, stabilize reaction dynamics, and maintain internal organization, are treated as the primary actors in the transition from chemistry to biology.

We call this the Constraint Emergence Hypothesis. According to this framework:

• Life began when environmental energy gradients and stochastic chemical reactions gave rise to spontaneously organized constraint fields.
• These emergent constraints stabilized and structured chemical dynamics, forming proto-organizational systems prior to the appearance of traditional biological macromolecules.
• Feedback loops between constrained chemical flows and the reinforcement of organizational structures promoted persistence, robustness, and evolutionary potential.

This perspective unifies thermodynamics, self-organization, and biological autonomy into a new explanatory model. It reframes the origin of life as a phase transition in the organization of constraints, rather than the contingent emergence of particular molecules.

To formalize this hypothesis, we develop a comprehensive mathematical framework based on coupled reaction-diffusion equations, dynamic constraint field evolution, and feedback-modulated transport processes, extended to three-dimensional spatial domains. We analyze the system’s behavior through dynamical systems theory and phase space analysis, identifying critical thresholds for the spontaneous emergence of organizational closure and proto-individuality. Recent mathematical advances in non-equilibrium systems and emergent organizational structures [1,14] support the relevance of constraint-driven models.

In the following sections, we detail the conceptual foundations of this approach, present the mathematical structures underlying constraint-driven dynamics, and explore the broader implications for understanding life’s emergence as a universal organizational phenomenon, transcending purely chemical explanations.

2. Conceptual Foundations: Constraints as the Primary Drivers of Life’s Emergence

The Constraint Emergence Hypothesis reorients the study of life’s origins by elevating functional constraints–not specific molecules–to the central causal role in the transition from non-living to living systems.

2.1. What is a Functional Constraint?

A functional constraint is a localized, stable structure or pattern that modulates the behavior of underlying processes, channeling flows of matter, energy, and information without being fully reducible to them. Constraints do not passively exist; they actively regulate dynamics by:

• Selecting which reactions can occur within a region,
• Enhancing or suppressing reaction rates,
• Structuring spatial organization (e.g., confinement, selective permeability),
• Modulating energy dissipation pathways.

In this framework, constraints are physical yet organizational entities: they emerge from, and simultaneously regulate, the material processes they constrain.

2.2. Constraint-Driven Organization vs. Molecule-Driven Evolution

Traditional origin-of-life theories implicitly assume that specific molecules (RNA, proteins, lipids) carry the burden of initiating life. In contrast, we propose:

• Molecules are substrates.
• Constraints are organizers.

The emergence of life is not defined by the mere presence of complex molecules, but by the appearance of persistent constraints that organize and maintain complex, dynamic systems.

Constraints provide:

• Selective Retention: Not all chemical outcomes are equally probable; constraint fields bias the system toward stability and self-reinforcement.
• Operational Closure: By regulating chemical flows, constraints enable the local generation of further constraints, closing causal loops.
• Proto-Individuality: Constraints delimit a “self”–a bounded domain maintaining internal coherence against external fluctuations.

Thus, the emergence of constraints marks the beginning of biological individuality long before genetic inheritance mechanisms fully develop.

2.3. Constraints as Dynamic, Self-Sustaining Structures

Constraints are not static. Their emergence, maintenance, and evolution involve dynamical feedback processes:

• Environmental energy gradients drive initial fluctuations.
• Spontaneous local structures arise that selectively stabilize certain flows.
• Stabilized flows reinforce the persistence of the structure, deepening the constraint.
• Constraint fields themselves evolve, merge, or decay, depending on the robustness of feedbacks.

This self-sustaining dynamism distinguishes functional constraints from passive structures. Constraints capable of maintaining their own existence, by regulating the processes that regenerate them, are the seeds of autonomous organization.

2.4. From Proto-Constraints to Proto-Cells

Once constraint fields become sufficiently complex, they can:

• Support proto-metabolic cycles by stabilizing catalytic networks,
• Localize and protect informational molecules (e.g., RNA-like polymers),
• Guide the formation of semi-permeable membranes,
• Enable the system to resist entropy and maintain far-from-equilibrium organization.

Life, in this view, is the emergence of a network of dynamically maintained, mutually supporting constraints–a constraint-closed system–rather than a collection of molecules.

In the next section, we formalize these ideas mathematically by introducing a field-theoretic model for constraint emergence and coupling it with chemical reaction dynamics.

3. Mathematical Framework: Modeling Constraint-Driven Emergence

To formalize the Constraint Emergence Hypothesis, we develop a coupled dynamical model describing the co-evolution of chemical concentrations and constraint fields under environmental energy input.

3.1. State Variables

The system is characterized by coupled dynamical fields defined over a spatial domain $\Omega \subseteq {\mathbb{R}}^d$ (where $d=1,2,3$ dimensions) and over time $t\ge 0$. These fields capture both the chemical and organizational aspects of the proto-biological system.

3.1.1. Chemical Concentrations

We define:

$$x_i(\mathbf{r},t)\in {\mathbb{R}}^{+}\mathrm{for}i=1,\cdots ,N$$

where:

• $x_i(\mathbf{r},t)$ is the local concentration (molarity or number density) of the i-th chemical species at spatial position $\mathbf{r}\in \Omega$ and time t.
• N is the total number of distinct chemical species considered in the system.
• ${\mathbb{R}}^{+}$ indicates that concentrations are non-negative by physical constraint.

The collection $\mathbf{x}(\mathbf{r},t)=(x_1(\mathbf{r},t),\cdots ,x_N(\mathbf{r},t))$ forms the chemical state vector field, describing the material basis of the system’s dynamics.

3.1.2. Constraint Field

In addition to chemical concentrations, we introduce the constraint field:

$$C(\mathbf{r},t)\in \mathbb{R}$$

where:

• $C(\mathbf{r},t)$ measures the local intensity or “strength” of functional constraints acting on chemical processes at point $\mathbf{r}$ and time t.
• Positive values of C correspond to stronger constraints (higher modulation of chemical flows), while $C=0$ corresponds to unconstrained dynamics.
• In principle, C can be generalized to a multi-component field (vector or tensor) if multiple independent types of constraints (e.g., permeability, catalysis, confinement) are to be modeled separately.

Conceptually, $C(\mathbf{r},t)$ is not a passive background parameter, but an active, dynamical field shaped by, and shaping, the chemical processes it constrains.

3.1.3. Environmental Free Energy Gradient

Finally, we define the externally imposed driving forces:

$$\mathrm{\Phi }(\mathbf{r},t):\Omega \times {\mathbb{R}}^{+}\to \mathbb{R}$$

where:

• $\mathrm{\Phi }(\mathbf{r},t)$ represents the local free energy gradient available at position $\mathbf{r}$ and time t.
• It models environmental conditions such as chemical potential gradients, temperature gradients, redox potentials, or light fluxes that can drive chemical flows.
• $\mathrm{\Phi }$ is treated as an external (non-dynamical) field at this stage but could itself be dynamically coupled to system behavior in extended models.

3.1.4. Summary: State Space

At each point $(\mathbf{r},t)$, the full local state of the system is given by the tuple:

$$S(\mathbf{r},t)=\left({\left\{x_i(\mathbf{r},t)\right\}}_{i=1}^N,C(\mathbf{r},t),\mathrm{\Phi }(\mathbf{r},t)\right)$$

and the system as a whole is described by the time evolution of these fields over the spatial domain $\Omega$.

Thus, the full state space $\mathcal{S}$ of the system is:

$$\mathcal{S}={\left({\mathbb{R}}^{+}\right)}^N\times \mathbb{R}\times \mathbb{R}(\mathrm{at}\mathrm{each}\mathrm{point}\mathbf{r})$$

This formalization establishes the stage for modeling the coupled evolution of matter, energy, and organizational structure underlying the emergence of life.

3.2. Evolution Equations

The dynamics of the system are governed by a set of coupled, nonlinear partial differential equations (PDEs), describing the interaction between chemical species, constraint fields, and external energy gradients.

These equations reflect three intertwined physical processes:

• Diffusion and spatial transport of chemical species,
• Local chemical reactions governed by internal states and constraints,
• Energy-driven source and sink dynamics influenced by environmental gradients.

3.2.1. Chemical Species Dynamics

The temporal evolution of the concentration field $x_i(\mathbf{r},t)$ for each chemical species i is given by:

$${\displaystyle \frac{\partial x_i}{\partial t}}=D_i{\nabla }^2{x}_i+R_i(\left\{x_j\right\},C)+S_i(\mathrm{\Phi },C)$$

where each term has a distinct conceptual and mathematical role:

• Diffusion term:

  $$D_i{\nabla }^2{x}_i$$

  captures passive spreading of species i due to concentration gradients. Here, $D_i\in {\mathbb{R}}^{+}$ is the diffusion coefficient (constant or possibly dependent on C), and ${\nabla }^2$ is the Laplacian operator over the spatial domain $\Omega$.
  Conceptually, diffusion tends to homogenize the chemical field, opposing spatial structure. Constraints (via C) must counteract this natural tendency to enable localization.
• Reaction term:

  $$R_i(\left\{x_j\right\},C)$$

  represents the net local chemical production or consumption of species i through interactions with other species $x_j$, modulated by the local constraint field $C(\mathbf{r},t)$.
  Mathematically:

  $$R_i(\left\{x_j\right\},C)=\sum _{\mu }{\nu }_i^{\mu }{r}_{\mu }(\left\{x_j\right\},C)$$

  where:

  -

  $\mu$ indexes the reaction channels,

  -

  ${\nu }_i^{\mu }$ are stoichiometric coefficients,

  -

  $r_{\mu }(\left\{x_j\right\},C)$ are rate laws (e.g., mass action, Michaelis-Menten) possibly modified by C.

  In this way, C acts not only as a passive condition but can actively catalyze, inhibit, or otherwise bias reaction pathways.
• Source/Sink term:

  $$S_i(\mathrm{\Phi },C)$$

  describes the influence of external energy inputs and sinks (e.g., light absorption, redox potential, environmental fluxes) on the chemical species.
  Example model:

  $$S_i(\mathrm{\Phi },C)={\gamma }_i\left(C\right)\mathrm{\Phi }(\mathbf{r},t)$$

  where ${\gamma }_i\left(C\right)$ is an effective coupling coefficient that may itself depend on the local constraint field.
  Conceptually, this term allows environmental gradients to feed into localized chemical dynamics in a constraint-modulated fashion.

3.2.2. Interpretation: Tension Between Homogenization and Localization

The evolution of each $x_i$ embodies a competition between:

• Diffusive dispersion, driven by entropy and the tendency toward homogeneity,
• Reactive organization, driven by local chemistry and constraint amplification,
• Energy input, driven by the environment, modulated by constraints.

When constraints are weak, diffusion dominates and chemical structure dissipates. When constraints are sufficiently strong, self-organization can overcome diffusion, leading to localized, persistent patterns–the precursors of autonomous systems.

3.2.3. Mathematical Structure Summary

At a global level, the dynamics of all chemical species form a system of PDEs:

$${\displaystyle \frac{\partial \mathbf{x}}{\partial t}}=\mathbf{D}{\nabla }^2\mathbf{x}+\mathbf{R}(\mathbf{x},C)+\mathbf{S}(\mathrm{\Phi },C)$$

where:

• $\mathbf{x}(\mathbf{r},t)=(x_1,x_2,\cdots ,x_N)$,
• $\mathbf{D}=\mathrm{diag}(D_1,\cdots ,D_N)$,
• $\mathbf{R}(\mathbf{x},C)$ and $\mathbf{S}(\mathrm{\Phi },C)$ are vector-valued functions of chemical and constraint fields.

This compact notation allows systematic analysis of pattern formation, stability, bifurcations, and emergent spatial structures. We build upon recent developments in Wasserstein gradient flow structures [13], adapting these techniques to the evolution of constraint fields.

3.2.4. Constraint Field Dynamics

The evolution of the constraint field $C(\mathbf{r},t)$ captures how local organizational structures form, persist, and decay in response to chemical flows and environmental inputs.

We model the dynamics of C by the equation:

$${\displaystyle \frac{\partial C}{\partial t}}=\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })-\beta C+\xi (\mathbf{r},t)$$

where each term represents a fundamental physical or organizational process:

• Constraint Production Term:

  $$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })$$

  represents the local generation or amplification of functional constraints as a function of:
  • The local chemical composition $\left\{x_i\right\}$,
  • The existing constraint field C,
  • The available environmental free energy $\mathrm{\Phi }$.
  $\alpha \in {\mathbb{R}}^{+}$ is a sensitivity parameter controlling the efficiency of constraint production.
  Conceptually, this term captures the feedback loop: organized chemical flows reinforce local structures (e.g., by building semi-permeable boundaries, concentrating catalysts, establishing selective gradients).
• Constraint Decay Term:

  $$-\beta C$$

  models the natural degradation, dispersal, or weakening of constraints over time due to environmental fluctuations, diffusion, mechanical instability, or internal dissipation.
  Here, $\beta \in {\mathbb{R}}^{+}$ is a decay rate constant, representing the intrinsic instability of organizational structures in the absence of active maintenance.
• Stochastic Perturbation Term:

  $$\xi (\mathbf{r},t)$$

  represents random environmental noise, local fluctuations, or perturbations affecting the constraint field.
  It can be modeled, for example, as Gaussian white noise:

  $$\langle \xi (\mathbf{r},t)\xi ({\mathbf{r}}^{\prime },t^{\prime })\rangle ={\sigma }^2\delta (\mathbf{r}-{\mathbf{r}}^{\prime })\delta (t-t^{\prime })$$

  where $\sigma$ controls the noise strength.
  Including stochasticity allows for:

  -

  Spontaneous symmetry breaking,

  -

  Emergence of localized structures from fluctuations,

  -

  Realistic modeling of noisy prebiotic environments.

3.2.5. Constraint Production Function

The form of the production function F encodes the mechanisms by which chemical organization generates and maintains constraints. General properties include:

• F increases with concentrations of organizing species (e.g., catalysts, structural polymers),
• F may saturate (nonlinear feedback),
• F may depend multiplicatively on energy availability $\mathrm{\Phi }$,
• F may itself be enhanced by pre-existing C (positive reinforcement).

An example minimal form for F could be:

$$F(\left\{x_i\right\},C,\mathrm{\Phi })=\left(\sum _{i\in \mathrm{organizers}}{\lambda }_i{x}_i\right)\times \left({\displaystyle \frac{\mathrm{\Phi }}{\mathrm{\Phi }+{\mathrm{\Phi }}_0}}\right)\times (1+ϵC)$$

where:

• ${\lambda }_i$ are effectiveness coefficients for different chemical species,
• ${\mathrm{\Phi }}_0$ is a threshold parameter for energy dependence,
• $ϵ$ controls feedback amplification by existing constraints.

3.2.6. Interpretation: Constraint Self-Maintenance vs. Collapse

The stability of the constraint field hinges on the balance between production and decay:

$$\mathrm{If}\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })>\beta C\mathrm{locally},\mathrm{then}C\mathrm{grows}\mathrm{or}\mathrm{sustains}.$$

Otherwise, constraints decay and the system returns toward disorganized chemistry.

Thus, regions where the chemical organization is sufficiently strong and energy supply adequate can cross a critical threshold, leading to persistent localized constraints–the seeds of proto-individuality.

3.2.7. Global Mathematical Structure

The complete dynamics of the system are thus governed by a hybrid PDE-ODE system:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial \mathbf{x}}{\partial t}}& =\mathbf{D}{\nabla }^2\mathbf{x}+\mathbf{R}(\mathbf{x},C)+\mathbf{S}(\mathrm{\Phi },C)\hfill & \hfill (\mathrm{reaction}-\mathrm{diffusion}\mathrm{system})\\ \\ \hfill {\displaystyle \frac{\partial C}{\partial t}}& =\alpha F(\mathbf{x},C,\mathrm{\Phi })-\beta C+\xi (\mathbf{r},t)\hfill & \hfill (\mathrm{constraint}\mathrm{field}\mathrm{dynamics})\end{array}$$

Coupling chemical transport, reaction kinetics, constraint emergence, energy inflow, and stochasticity into a unified formalism.

4. Organizational Closure and Viability Domains

A key property distinguishing living from non-living systems is organizational closure: the self-production and self-maintenance of the very structures necessary for the system’s own persistence.

Here, we define viability rigorously in terms of the coupled chemical-constraint dynamics developed above.

4.1. Viability Domains in State Space

Recall that the full local system state at point $(\mathbf{r},t)$ is given by:

$$S(\mathbf{r},t)=\left({\left\{x_i(\mathbf{r},t)\right\}}_{i=1}^N,C(\mathbf{r},t),\mathrm{\Phi }(\mathbf{r},t)\right)$$

We define the viability domain $\mathcal{V}\subset \mathcal{S}$ as the subset of state space where the system can:

• Sustain the constraint field C above a critical threshold $C_{\mathrm{crit}}>0$,
• Maintain chemical concentrations $x_i$ within bounds that allow regeneration of C,
• Avoid collapse due to diffusion, decay, or depletion.

Formally, viability requires that for $S(\mathbf{r},t_0)\in \mathcal{V}$, the trajectory satisfies:

$$S(\mathbf{r},t)\in \mathcal{V},\forall t\ge t_0$$

provided environmental conditions $\mathrm{\Phi }$ remain within compatible ranges.

4.2. Mathematical Conditions for Organizational Closure

Organizational closure can now be expressed through three coupled conditions:

• Constraint Self-Maintenance Condition:

  $$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })\ge \beta C\mathrm{for}\mathrm{all}\mathbf{r}\in \mathcal{I}\left(t\right)$$

  where $\mathcal{I}\left(t\right)=\left\{\mathbf{r}\right|C(\mathbf{r},t)\ge C_{\mathrm{crit}}\}$ defines the spatial domain of the proto-individual.
• Chemical Stability Condition:

  $${\displaystyle \frac{\partial x_i}{\partial t}}\approx 0\mathrm{and}{x}_i\in [x_i^{\min },x_i^{\max }]\forall i,\forall \mathbf{r}\in \mathcal{I}\left(t\right)$$

  meaning that internal concentrations remain bounded and stable within a viable range.
• Energy Supply Condition:

  $$\mathrm{\Phi }(\mathbf{r},t)\ge {\mathrm{\Phi }}_{\min }\mathrm{for}\mathrm{all}\mathbf{r}\in \mathcal{I}\left(t\right)$$

  ensuring that external energy gradients are sufficient to sustain reaction dynamics and constraint regeneration.

4.3. Attractor Structure and Robustness

In a dynamical systems perspective, viability domains correspond to basins of attraction toward constraint-closed steady states or limit cycles.

Let $\mathcal{A}\subset \mathcal{V}$ denote the attractor associated with organizational closure.

Then, for initial conditions $S(\mathbf{r},t_0)\in \mathcal{U}\left(\mathcal{A}\right)$ (a neighborhood of $\mathcal{A}$), the system trajectory satisfies:

$$\underset{t\to +\infty }{lim}S(\mathbf{r},t)\to \mathcal{A}$$

where $\mathcal{A}$ represents a stable self-maintaining organizational regime.

Robustness against perturbations can be studied via:

• Linear stability analysis (e.g., eigenvalue spectra of linearized dynamics near $\mathcal{A}$),
• Stochastic resilience analysis (how constraint fields recover after noise-induced perturbations),
• Basin size estimation (measuring the volume of viable initial conditions).

4.4. Emergence of Individuality

When a localized region $\mathcal{I}\left(t\right)$ maintains autonomous internal organization against external disturbances, it functions as a proto-individual.

Key emergent properties include:

• Boundary Formation: Sharp gradients of $C(\mathbf{r},t)$ define an “inside” and “outside”.
• Selective Interaction: Internal states interact selectively with external flows based on constraint-mediated transport.
• Self-Maintenance: Internal reactions are organized to regenerate both chemical species and constraint structures.

Thus, individuality arises naturally as a dynamical property of constraint-organized domains within the broader prebiotic environment.

4.5. Phase Transition to Organizational Closure

Crossing the threshold into viability corresponds to a non-equilibrium phase transition in the system:

• Below critical conditions, chemical reactions and constraints dissipate.
• Above critical conditions, self-sustaining, self-producing constraint-chemical loops emerge.

This parallels known critical phenomena in physics (e.g., percolation, spontaneous symmetry breaking) but is rooted in the emergence of autonomous organization–not simply spatial order.

Thus, the origin of life is recast as a dynamical phase transition in constraint-mediated chemical systems under energy flow.

4.6. Minimal Requirements for Constraint Self-Maintenance

For a localized region $\mathcal{I}\left(t\right)\subset \Omega$ to achieve and maintain organizational closure, specific minimal conditions must be satisfied concerning constraint dynamics, chemical stability, and energy flow.

4.6.1. Constraint Production Must Outweigh Constraint Decay

A necessary condition for the persistence of local organizational structures is that, at each point $\mathbf{r}\in \mathcal{I}\left(t\right)$, the production rate of the constraint field exceeds its natural decay:

$$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })>\beta C$$

where:

• $\alpha$ is the efficiency of constraint generation from chemical organization,
• $F(\left\{x_i\right\},C,\mathrm{\Phi })$ is the local constraint production function (possibly nonlinear in $\left\{x_i\right\}$ and $\mathrm{\Phi }$),
• $\beta$ is the decay constant for constraint weakening.

Interpretation: This inequality ensures that the local constraint field $C(\mathbf{r},t)$ is either:

• Growing (${\partial }_{t}C>0$) when organizational processes reinforce the structure,
• Or at least sustained (${\partial }_{t}C\approx 0$) against natural decay.

Crossing this threshold defines a bifurcation point between constraint dissipation and constraint persistence– a critical precondition for the emergence of autonomous proto-systems.

4.6.2. Stabilization of Chemical Flows within Constrained Domains

Internal chemical processes must be localized and stable inside $\mathcal{I}\left(t\right)$. Specifically, effective chemical diffusion must be strongly suppressed relative to free-space diffusion:

$$D_i^{\mathrm{eff}}\left(C\right)\ll D_i\mathrm{for}\mathrm{all}i\mathrm{in}\mathcal{I}\left(t\right)$$

where:

• $D_i$ is the bare diffusion coefficient of species i in the unconstrained environment,
• $D_i^{\mathrm{eff}}\left(C\right)$ is the effective diffusion coefficient under the influence of the local constraint field $C(\mathbf{r},t)$.

Mechanism: The constraint field modifies the physical and chemical environment to:

• Reduce random diffusion,
• Enhance confinement and reactant localization,
• Facilitate high local concentrations for reaction dynamics.

For instance, constraints may arise from:

• Semi-permeable barriers,
• Catalytic scaffolds,
• Local energy traps.

Thus, chemical structures are protected against dispersive entropy-driven degradation, enabling sustained networked reactions.

4.6.3. Energy Flow Must Sustain Internal Reactions and Constraints

Finally, the availability of external free energy is critical. The environmental gradient $\mathrm{\Phi }(\mathbf{r},t)$ must supply sufficient energy to drive endergonic reactions and maintain organizational structure:

$$\mathrm{\Phi }(\mathbf{r},t)\ge {\mathrm{\Phi }}_{\mathrm{crit}}\mathrm{for}\mathbf{r}\in \mathcal{I}\left(t\right)$$

where ${\mathrm{\Phi }}_{\mathrm{crit}}$ is a minimal threshold determined by:

• The energetic cost of internal reactions,
• The energy required for constraint reinforcement,
• Dissipative losses due to leakage, decay, and noise.

Interpretation: Without sustained energy input:

• Reactions halt,
• Constraints decay ($\alpha F\to 0$),
• Organizational closure collapses.

Thus, stable proto-organisms require a continuous, but not necessarily massive, flux of usable energy through their internal networks.

4.6.4. Summary: Triple Minimal Conditions

In short, for constraint self-maintenance and proto-life emergence:

$$\begin{array}{|c|}\hline \begin{array}{cc}\hfill \left(\mathrm{i}\right)& \alpha F(\left\{x_i\right\},C,\mathrm{\Phi })>\beta C(\mathrm{Constraint}\mathrm{persistence})\hfill \\ \\ \hfill \left(\mathrm{ii}\right)& D_i^{\mathrm{eff}}\left(C\right)\ll D_i(\mathrm{Chemical}\mathrm{confinement})\hfill \\ \\ \hfill \left(\mathrm{iii}\right)& \mathrm{\Phi }(\mathbf{r},t)\ge {\mathrm{\Phi }}_{\mathrm{crit}}(\mathrm{Sufficient}\mathrm{energy}\mathrm{flow})\hfill \end{array}\\ \hline\end{array}$$

These three interlocking requirements define the minimal “triangle of viability” for the spontaneous emergence and persistence of constraint-organized systems.

They establish a precise mathematical and physical framework for identifying the conditions under which organization triumphs over entropy– the necessary stepping stone to the origin of life.

4.7. Toward Proto-Individuality: Constraint-Bounded Domains

The emergence of individuality–the distinction of a system from its environment–is a defining hallmark of life. In our framework, individuality arises naturally from the spatial organization of constraint fields.

4.7.1. Definition of Proto-Individuals

We define a proto-individual as a spatially localized domain $\mathcal{I}\left(t\right)\subset \Omega$ satisfying:

$$\mathcal{I}\left(t\right)=\{\mathbf{r}\in \Omega |C(\mathbf{r},t)\ge C_{\mathrm{crit}}\}$$

where:

• $C(\mathbf{r},t)$ is the local constraint field intensity,
• $C_{\mathrm{crit}}>0$ is the minimal threshold required for sustained chemical and constraint self-organization.

Thus, a proto-individual is a dynamically maintained, spatially bounded region where the concentration of organizational constraints is sufficiently high to preserve internal coherence against environmental noise and entropy.

4.7.2. Properties of Proto-Individuals

Each proto-individual $\mathcal{I}\left(t\right)$ is characterized by three essential features:

• Internal Chemical Coherence: Chemical concentrations $\left\{x_i(\mathbf{r},t)\right\}$ inside $\mathcal{I}\left(t\right)$ are stabilized and maintained within viable bounds, enabling sustained reaction dynamics.
• Sustained Constraint Regeneration: Internal chemical processes regenerate and maintain the constraint field C, ensuring organizational closure:

  $$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })\ge \beta C\mathrm{for}\mathrm{all}\mathbf{r}\in \mathcal{I}\left(t\right)$$

  thereby avoiding collapse due to natural decay.
• Selective Matter and Energy Exchange: The boundary of $\mathcal{I}\left(t\right)$ acts as an emergent semi- permeable membrane:

  -

  Nutrients and energy flow in,

  -

  Waste products flow out,

  -

  Diffusive losses of key internal components are minimized.

  Transport across the boundary is regulated dynamically by the structure and gradients of C.

4.7.3. Conceptual Interpretation: Birth of Individuality

From a deeper conceptual perspective, proto-individuals embody the emergence of:

• Self vs Environment Distinction:$\mathcal{I}\left(t\right)$ defines an “inside” (where organizational rules prevail) and an “outside” (dominated by unstructured chemistry).
• Operational Closure: Internal processes are organized such that they collectively maintain the boundary and internal conditions necessary for their own persistence.
• Autonomy: Proto-individuals exert causal control over their own material constitution and energy budget, rather than being passively shaped by external conditions.

Thus, individuality and autonomy emerge as dynamic consequences of constraint-bounded self-maintaining organization, without requiring an externally imposed membrane or genetic program.

4.7.4. Dynamic Behavior of Proto-Individuals

The dynamics of proto-individuals include:

• Growth: Expansion of $\mathcal{I}\left(t\right)$ as internal constraint strength and chemical resources increase.
• Division: Fission into two daughter proto-individuals if internal dynamics and spatial instabilities create multiple stable centers of constraint generation.
• Decay: Shrinkage or dissolution of $\mathcal{I}\left(t\right)$ when internal constraint production falls below viability thresholds.
• Evolutionary Variation: Differences in internal chemical compositions or constraint structures can lead to differential viability and adaptive evolution under environmental pressures.

Thus, proto-individuals exhibit the minimal necessary properties for selection, adaptation, and open-ended evolution– key criteria for life.

In summary, constraint-bounded domains where organizational closure is achieved function as primitive, autonomous units: they are not merely chemically structured objects, but dynamically sustained systems capable of survival, adaptation, and reproduction.

This natural emergence of proto-individuality provides a direct pathway from disorganized prebiotic chemistry to the first autonomous living systems.

In the following sections, we will analyze the stability, growth dynamics, and evolutionary potential of such constraint-driven proto-organisms.

5. Organizational Closure via Constraint Networks

In the Constraint Emergence Hypothesis, the origin of life is not attributed simply to the appearance of complex molecules, but to the emergence of organizational closure– a condition where internal processes collectively sustain the very conditions for their own persistence.

Organizational closure arises through the formation of constraint networks: interconnected dynamical structures that regulate chemical flows, energy transformations, and spatial organization, in a mutually reinforcing manner.

5.1. Definition of Organizational Closure

Formally, a system exhibits organizational closure when:

• Every critical functional process (e.g., constraint maintenance, catalytic activity, compartmental stability) is produced and maintained by other processes within the system,
• No critical component depends exclusively on uncontrolled environmental inputs for its regeneration,
• The system as a whole maintains its boundary conditions and identity despite fluctuations and perturbations.

In the context of constraint fields, this closure condition translates into:

$$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })\ge \beta C\mathrm{and}\mathrm{self}-\mathrm{sustained}\mathrm{cycles}\mathrm{of}\mathrm{constraint}-\mathrm{chemical}\mathrm{coupling}\mathrm{exist}$$

throughout the proto-individual $\mathcal{I}\left(t\right)$.

5.2. Structure of Constraint Networks

A constraint network is an emergent graph-like structure where:

• Nodes correspond to localized chemical processes or organizational structures (e.g., catalytic loops, selective barriers, energy sinks),
• Edges represent functional dependencies mediated by constraint fields (e.g., one process stabilizing or enabling another),
• Feedback Loops are closed cycles where processes mutually support each other’s continuation.

Mathematically, we can represent a constraint network as a directed graph $\mathcal{G}=(V,E)$ where:

• V is the set of organizational processes,
• $E\subset V\times V$ is the set of directed edges indicating “process A enables process B.”

Organizational closure then requires that $\mathcal{G}$ contains strongly connected components (SCCs)– subgraphs where every node is reachable from every other node via directed paths.

5.3. Feedback and Mutual Reinforcement

Critical to closure is the existence of:

• Positive feedback loops: Enhancing the persistence of constraint structures and chemical organization.
• Negative feedback loops: Regulating fluctuations and preventing destructive runaway dynamics (e.g., uncontrolled chemical explosions).
• Nonlinear Couplings: Enabling threshold behaviors, bistability, and multistability, essential for robustness against noise.

Such feedbacks convert otherwise dissipative chemical processes into self-sustaining organizations.

5.4. Stability of Constraint-Closed Systems

The stability of organizationally closed systems can be analyzed through:

• Linear Stability Analysis: Examining the eigenvalues of the Jacobian matrix of the coupled dynamical system near steady states.
• Attractor Structure: Identifying stable attractors (fixed points, limit cycles, or strange attractors) associated with constraint-closed regimes.
• Perturbation Resilience: Assessing how small environmental or internal perturbations are absorbed or amplified by the system dynamics.

Mathematically, stability requires that all perturbations around an organizational attractor $\mathcal{A}$ decay asymptotically:

$$\underset{t\to +\infty }{lim}\parallel S(\mathbf{r},t)-\mathcal{A}\parallel =0\mathrm{for}\mathrm{small}\mathrm{deviations}\mathrm{from}\mathcal{A}$$

5.5. Emergence of Viable Units of Evolution

Once constraint networks achieve organizational closure, proto-individuals become operationally autonomous, self-maintaining entities.

They can:

• Persist: Maintain coherence over time in fluctuating environments.
• Reproduce: Undergo fission or budding when internal constraint structures replicate.
• Evolve: Accumulate variations in internal network architecture leading to differential survival and reproduction.

Thus, organizational closure underpins the emergence of evolutionarily competent units– fulfilling the minimal requirements for Darwinian evolution in a prebiotic context.

5.6. Summary

Organizational closure transforms a mere chemical system into a proto-living system:

• It endows the system with autonomy, self-maintenance, and evolutionary potential.
• It emerges naturally from coupled constraint-chemical feedbacks under suitable energetic and material conditions.
• It defines the fundamental threshold that separates non-living matter from living organizations.

In the next sections, we analyze in more detail the dynamic conditions leading to the formation, persistence, and diversification of constraint-closed proto-individuals.

5.7. Defining Organizational Closure

Organizational closure is the core principle that transforms a chemically reactive environment into a self-sustaining, autonomous system capable of persistence and evolution.

5.7.1. Conceptual Definition

Organizational closure occurs when a system’s internal processes collectively:

• Produce, maintain, and regulate the very organizational structures (constraints) necessary for their own continuation,
• Stabilize internal dynamics despite environmental fluctuations,
• Maintain an operational boundary distinguishing “self” from “non-self.”

Thus, the system achieves a form of autonomy: it no longer passively follows external physical gradients, but actively maintains the conditions required for its own survival and reproduction.

5.7.2. Formal Mathematical Conditions

In our framework, organizational closure requires that the coupled dynamical fields $\left\{x_i(\mathbf{r},t)\right\}$ (chemical concentrations) and $C(\mathbf{r},t)$ (constraint field) admit self-sustaining solutions.

Specifically, in regions where $C(\mathbf{r},t)\ge C_{\mathrm{crit}}$, closure demands:

$${\displaystyle \frac{\partial C}{\partial t}}\approx 0\mathrm{and}{\displaystyle \frac{\partial x_i}{\partial t}}\approx 0\mathrm{for}\mathrm{all}\mathrm{relevant}\mathrm{species}i\mathrm{and}\mathrm{for}\mathrm{all}\mathbf{r}\in \mathcal{I}\left(t\right)$$

where:

• $\mathcal{I}\left(t\right)=\left\{\mathbf{r}\right|C(\mathbf{r},t)\ge C_{\mathrm{crit}}\}$ defines the spatial domain of the proto-individual,
• The approximate stationarity ($\approx 0$) reflects the maintenance of a steady dynamic regime (e.g., limit cycles or steady states), allowing small fluctuations around a stable core.

5.7.3. Self-Sustaining Constraint-Chemistry Feedback

Closure is achieved through a dynamical feedback loop:

• Constraint → Chemistry: The constraint field $C(\mathbf{r},t)$ modulates local reaction rates, stabilizes internal chemical compositions, and confines reactants.
• Chemistry → Constraint: Internal chemical processes regenerate and reinforce the constraint field, maintaining $C(\mathbf{r},t)$ against natural decay.

This creates a recursive, mutually supportive network of processes: constraints stabilize the flows that recreate the constraints.

Mathematically, this mutual maintenance is embedded in the coupled evolution equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial x_i}{\partial t}}& =D_i{\nabla }^2{x}_i+R_i(\left\{x_j\right\},C)+S_i(\mathrm{\Phi },C)\hfill \\ \\ \hfill {\displaystyle \frac{\partial C}{\partial t}}& =\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })-\beta C+\xi (\mathbf{r},t)\hfill \end{array}$$

where closure corresponds to finding nontrivial (nonzero) solutions where ${\displaystyle \frac{\partial }{\partial t}}\approx 0$ locally.

5.7.4. Critical Thresholds for Closure

Importantly, closure can only occur if:

• The constraint field strength $C(\mathbf{r},t)$ exceeds a critical value $C_{\mathrm{crit}}$,
• Chemical concentrations $x_i(\mathbf{r},t)$ fall within viability ranges supporting sufficient constraint regeneration,
• External energy flux $\mathrm{\Phi }(\mathbf{r},t)$ remains above a critical threshold ${\mathrm{\Phi }}_{\mathrm{crit}}$.

Thus, organizational closure is not a generic property of chemical systems– it emerges when sufficient material, energetic, and organizational conditions are simultaneously satisfied.

5.7.5. Interpretation: Emergent Autonomy and Selfhood

Once closure is achieved:

• The system no longer depends on continuous external scaffolding for survival,
• It sustains itself through internally organized, mutually supportive processes,
• It can maintain individuality, adapt, and even evolve in fluctuating environments.

Organizational closure thus marks the fundamental phase transition from prebiotic chemistry to proto-life.

5.7.6. Summary

Organizational closure can be seen as the emergence of a dynamical self– a self-maintaining, self-referential network of constraints and processes, capable of resisting entropic dissolution through continuous internal regeneration.

This principle is the cornerstone for understanding life not as a collection of molecules, but as an emergent regime of organization sustained through matter, energy, and information flows.

5.8. Feedback Loop Structure

At the heart of organizational closure lies a minimal, self-sustaining feedback loop– a causal cycle through which chemical and organizational processes reinforce and stabilize each other, giving rise to autonomy.

5.8.1. Minimal Organizational Feedback Loop

The basic causal sequence can be schematized as:

$$\mathrm{Environmental}\mathrm{Gradient}\to \mathrm{Chemical}\mathrm{Organization}\to \mathrm{Constraint}\mathrm{Field}\mathrm{Strengthening}\to \mathrm{Stabilized}\mathrm{Chemical}\mathrm{Flows}\to \mathrm{Sustained}\mathrm{Constraint}$$

Each element of the loop corresponds to a specific physical and organizational process:

• Environmental Gradient: External energy differentials (e.g., chemical potentials, thermal gradients, light fluxes) provide the driving forces necessary to power endergonic chemical reactions.
• Chemical Organization: Under the influence of energy flows, localized chemical networks (e.g., catalytic cycles, autocatalytic sets) emerge and organize, producing nontrivial spatial and functional patterns.
• Constraint Field Strengthening: Organized chemical networks generate and reinforce local constraint fields $C(\mathbf{r},t)$–structures that restrict, channel, or enhance specific reaction pathways and material flows.
• Stabilized Chemical Flows: The presence of strong constraints stabilizes internal chemical dynamics, enhancing reaction efficiencies, localizing reactants, and buffering against dispersive entropy.
• Sustained Constraint: Stabilized chemical flows, in turn, continually regenerate the constraint field, closing the causal loop and enabling self-maintenance.

5.8.2. Properties of the Feedback Loop

The minimal organizational feedback loop exhibits three fundamental properties:

• Closed: Every critical functional step in the loop is internally generated and maintained; no external agency or template is required beyond the basic environmental energy gradient.
  Mathematically, closure corresponds to the condition that all necessary variables $\{x_i,C\}$ are sustained dynamically through internal interactions:

  $${\displaystyle \frac{\partial x_i}{\partial t}}\approx 0,{\displaystyle \frac{\partial C}{\partial t}}\approx 0\mathrm{in}\mathcal{I}\left(t\right)$$
• Robust: The feedback loop can absorb small environmental perturbations (e.g., fluctuations in resource availability, temperature, noise) without systemic collapse.
  Stability analysis shows that perturbations $\delta S(\mathbf{r},t)$ decay over time:

  $$\underset{t\to +\infty }{lim}\parallel \delta S(\mathbf{r},t)\parallel \to 0\mathrm{for}\mathrm{small}\delta S$$
• Adaptive: Variations in the environmental gradient $\mathrm{\Phi }(\mathbf{r},t)$ can modulate internal chemical and constraint dynamics without disrupting overall organizational coherence.
  For moderate changes in $\mathrm{\Phi }$, the system dynamically adjusts its internal flows and constraint strengths to maintain viability.

5.8.3. Interpretation: Causal Self-Production

The feedback structure transforms the system from being a passive responder to external forces into an active, self-producing organization:

• Energy and matter are continuously transformed internally,
• Structural constraints are regenerated endogenously,
• The system persistently rebuilds itself from its own products and processes.

This recursive causality–where effects become causes for their own enabling conditions–is the hallmark of life and the fundamental mechanism through which autonomy emerges.

5.8.4. Comparison with Classical Systems

Unlike equilibrium systems (e.g., crystals) or simple dissipative structures (e.g., Bénard cells), constraint-organized proto-systems:

• Actively sustain non-equilibrium conditions rather than passively dissipating them,
• Self-referentially produce the organizational structures that maintain the system,
• Possess causal closure, forming autonomous operational units rather than merely reflecting external conditions.

Thus, the minimal feedback loop encodes the essential physical and organizational transition from passive chemistry to living, self-maintaining entities.

5.9. Mathematical Stability Conditions

For a localized region $\mathcal{I}\left(t\right)\subset \Omega$ to persist as a viable proto-individual exhibiting organizational closure, specific dynamical stability conditions must be satisfied simultaneously.

These conditions ensure that the system remains robust against both internal fluctuations and external environmental perturbations.

5.9.1. Constraint Regeneration Dominates Constraint Decay

The first and most fundamental requirement is that the local regeneration of constraints outpaces their natural degradation:

$$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })>\beta C\forall \mathbf{r}\in \mathcal{I}\left(t\right)$$

where:

• $\alpha$ is the constraint production efficiency,
• $F(\left\{x_i\right\},C,\mathrm{\Phi })$ encodes how chemical organization and energy flow generate constraints,
• $\beta$ is the intrinsic decay constant of the constraint field C.

Interpretation: Without continuous internal production fueled by chemical and energetic activity, the constraint structures would spontaneously decay, leading to loss of organizational closure and collapse of individuality.

Thus, active maintenance is a fundamental requirement for stability.

5.9.2. Chemical Stability within Constraint Domains

Chemical concentrations inside the proto-individual must achieve quasi-steady distributions, ensuring minimal net diffusion and stable reaction dynamics:

$${\nabla }^2{x}_i\approx 0\mathrm{for}\mathrm{all}\mathrm{species}i\mathrm{inside}\mathcal{I}\left(t\right)$$

This condition implies:

• Internal concentration gradients are small,
• Diffusive losses are negligible compared to local chemical reactions,
• Spatial homogeneity (or structured inhomogeneity) is dynamically stabilized by constraint-mediated confinement.

Mechanism: Constraints such as semi-permeable boundaries, localized catalysis, or microstructural scaffolds restrict molecule diffusion, maintaining chemical coherence and reaction specificity within the proto-organism.

5.9.3. Selective Exchange Across Proto-Individual Boundaries

While internal chemical processes must be stabilized, viability requires controlled interaction with the external environment.

Selective permeability must spontaneously emerge at the boundary $\partial \mathcal{I}\left(t\right)$, enabling:

• Import of nutrients, energy carriers, or building blocks from the environment,
• Export of waste products, dissipative byproducts, and excess energy.

Mathematically, selective exchange can be modeled as boundary conditions:

$${\left.{\mathbf{J}}_i·\mathbf{n}\right|}_{\partial \mathcal{I}\left(t\right)}={\Gamma }_i(C,\mathrm{\Phi })$$

where:

• ${\mathbf{J}}_i=-D_i\nabla x_i$ is the flux of species i,
• $\mathbf{n}$ is the outward normal vector at the boundary,
• ${\Gamma }_i(C,\mathrm{\Phi })$ is a function specifying controlled flux depending on constraint strength and local energy availability.

Key Features:

• Permeability is modulated by the local constraint field C, not imposed externally,
• Exchange remains selective, preventing catastrophic mixing or resource depletion.

5.9.4. Summary of Minimal Stability Conditions

Thus, mathematical viability of proto-individuals demands that:

$$\begin{array}{|c|}\hline \begin{array}{cc}\hfill \left(\mathrm{i}\right)& \alpha F(\left\{x_i\right\},C,\mathrm{\Phi })>\beta C(\mathrm{Constraint}\mathrm{persistence})\hfill \\ \\ \hfill \left(\mathrm{ii}\right)& {\nabla }^2{x}_i\approx 0(\mathrm{Chemical}\mathrm{confinement})\hfill \\ \\ \hfill \left(\mathrm{iii}\right)& {\left.{\mathbf{J}}_i·\mathbf{n}\right|}_{\partial \mathcal{I}\left(t\right)}={\Gamma }_i(C,\mathrm{\Phi })(\mathrm{Selective}\mathrm{exchange})\hfill \end{array}\\ \hline\end{array}$$

When these three stability criteria are simultaneously satisfied, constraint-organized proto-systems can sustain themselves far from thermodynamic equilibrium, maintaining individuality and paving the way for open-ended evolutionary processes.

5.10. Closure as a Phase Transition

Organizational closure in constraint-chemical systems represents a critical phase transition– a profound shift in the dynamical and causal structure of the system.

Unlike ordinary chemical phase changes (e.g., gas ↔ liquid), this transition involves a change in the system’s organizational regime: from environment-driven, dissipative chemistry to internally driven, self-sustaining autonomy.

5.10.1. Pre-Closure Regime: Open Dissipative System

Below a critical threshold of organizational density and constraint strength, the system behaves as an open, non-autonomous structure:

• Passive Dissipation: Energy from the environment is absorbed and dissipated without internal organization.
• Unstable Constraints: Any transient constraint structures decay rapidly (${\partial }_{t}C<0$).
• Chemical Homogenization: Diffusion dominates, leading to uniform chemical distributions without localized dynamics.
• No Individuality: There is no persistent boundary separating “self” from “environment.”

In this regime, the system is fully environment-driven: the environment imposes structure transiently, but the system has no internal causal closure.

5.10.2. Critical Threshold: Organizational Bifurcation

As the internal chemical organization and constraint field strength grow, a critical threshold is crossed where:

$$\alpha F(\left\{x_i\right\},C,\mathrm{\Phi })=\beta C$$

This point marks a bifurcation in the system’s dynamics:

• Self-reinforcing feedback loops become possible,
• Constraints can sustain themselves against decay,
• Chemical flows become localized and organized.

This transition is analogous to other non-equilibrium critical phenomena, such as:

• The emergence of convection rolls in Rayleigh-Bénard systems,
• The spontaneous magnetization of a ferromagnet below Curie temperature,
• Percolation transitions in random networks.

However, here the critical change is in the causal architecture of the system.

5.10.3. Post-Closure Regime: Autonomous Organization

Above the critical threshold:

• Self-Maintenance: Internal chemical processes continually regenerate constraints.
• Localized Persistence: Spatially bounded proto-individuals emerge and maintain internal coherence.
• Robustness and Adaptation: The system can absorb moderate environmental perturbations while preserving identity.
• Evolutionary Potential: Variations in organizational structures can propagate and be subject to selection.

In this regime, the system becomes self-driven: it actively shapes and maintains its own operational domain.

5.10.4. Causal Architecture Transformation

The phase transition to organizational closure corresponds to a fundamental shift in causality:

• Before closure: Environmental conditions fully determine internal dynamics (external causality dominates).
• After closure: Internal organizational dynamics maintain and regulate themselves (internal causality emerges).
• Mutual Modulation: The system can now modulate its own responses to environmental changes, enabling functional autonomy and adaptive evolution.

Thus, life does not emerge from molecular complexity alone, but from a critical shift in the causal regime governing matter and energy flows.

5.10.5. Summary

Organizational closure represents a non-equilibrium phase transition characterized by:

• Spontaneous emergence of constraint-maintaining cycles,
• Stabilization of localized chemical domains,
• Transition from passive dissipation to active autonomy,
• The birth of proto-individuals capable of evolution.

Understanding and modeling this phase transition is key to unraveling the true nature of life’s origin as an emergent organizational phenomenon.

5.11. Emergence of Evolutionary Potential

The establishment of organizational closure is not the end point of life’s emergence– it is the beginning of a new dynamical domain: evolution by variation, differential viability, and selection.

Once constraint-closed proto-individuals form, natural mechanisms allow evolutionary processes to take hold.

5.11.1. Variation in Constraint Architectures

Due to intrinsic stochasticity in chemical reactions, spatial fluctuations, and environmental perturbations, variations arise in the internal architectures of constraint-chemical systems.

These variations may include:

• Changes in the topology of constraint networks (e.g., addition or loss of nodes or feedback links),
• Alterations in the strength and spatial localization of constraint fields,
• Variations in chemical species abundances, reaction rates, or permeability profiles.

Mathematically, variations can be described as perturbations $\delta S(\mathbf{r},t)$ around the organizational attractor $\mathcal{A}$:

$$S(\mathbf{r},t)=\mathcal{A}\left(\mathbf{r}\right)+\delta S(\mathbf{r},t)$$

where $\delta S$ captures internal organizational diversity.

5.11.2. Differential Viability and Functional Selection

Variations affect the stability, resilience, and adaptability of constraint-closed systems.

Key points:

• Some variations may enhance constraint regeneration rates, robustness to noise, or efficiency of energy and matter use,
• Others may weaken organizational closure, making systems more prone to collapse under perturbations.

Thus, differential viability naturally emerges: constraint architectures that better maintain closure under fluctuating conditions are more likely to persist, grow, divide, or replicate.

Functional selection operates not at the level of isolated molecules, but at the level of whole organizational structures– constraint networks as cohesive, integrated wholes.

5.11.3. Evolutionary Dynamics Without Genetic Templates

Remarkably, evolutionary processes emerge here without requiring a pre-existing genetic code or template copying.

Instead, the evolutionary unit is:

• The self-sustaining constraint-chemical organization,
• Defined by its dynamic topology and material flows,
• Reproducing and varying through organizational fission, fragmentation, or extension.

This concept aligns with emerging theories of pre-Darwinian evolution, where structure-driven selection precedes sequence-based heredity.

5.11.4. Proto-Evolutionary Regime

The evolutionary regime arising from constraint-closed systems exhibits key features:

• Heritable Variability: Variations in organizational patterns are passed to offspring during fission or growth.
• Differential Persistence: More robust, efficient, or adaptable proto-individuals outlast less viable variants.
• Open-Ended Complexity: There is potential for cumulative organizational innovation over time.

Mathematically, this can be framed as an adaptive landscape $\mathcal{L}$ over the space of constraint network configurations, where selection drives drift toward regions of higher organizational viability.

5.11.5. Summary

Thus, once organizational closure is established, evolutionary dynamics emerge naturally:

• Variation arises from internal dynamics and environmental perturbations,
• Selection operates at the level of entire constraint-maintaining organizations,
• Adaptation, diversification, and complexity become possible even before the advent of genetic information systems.

This suggests that life and evolution are deeply rooted in organizational principles, and that the spontaneous emergence of constraint-closed systems was the true threshold crossing into the biological domain.

In the next section, we explore broader implications of this framework and outline directions for future research.

6. A Minimal Toy Model for Constraint-Driven Organization

We propose a simple model illustrating the core mechanisms of the Constraint Emergence Hypothesis.

6.1. State Variables

The system is defined by:

• $A(\mathbf{r},t)$: concentration of resource molecule A,
• $B(\mathbf{r},t)$: concentration of intermediate species B,
• $C(\mathbf{r},t)$: concentration of constraint-building molecule C,
• $\mathcal{C}(\mathbf{r},t)$: intensity of the local constraint field,
• $\mathrm{\Phi }\left(\mathbf{r}\right)$: external energy or resource gradient.

6.2. Reaction Scheme

The following chemical reactions are considered:

$$\begin{array}{cc}\hfill A+B& \stackrel{k_1}{\to }2B(\mathrm{autocatalytic}\mathrm{production}\mathrm{of}B),\hfill \\ \hfill B& \stackrel{k_2}{\to }C(\mathrm{transformation}\mathrm{of}B\mathrm{into}C),\hfill \\ \hfill C& \stackrel{k_d}{\to }\varnothing (\mathrm{decay}\mathrm{of}C).\hfill \end{array}$$

6.3. Evolution Equations

The spatiotemporal dynamics are governed by:

6.3.1. Chemical Species Dynamics

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial A}{\partial t}}& =D_A{\nabla }^{2}A-k_{1}AB+S_A\left(\mathrm{\Phi }\right),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial B}{\partial t}}& =D_B^{\mathrm{eff}}\left(\mathcal{C}\right){\nabla }^{2}B+k_{1}AB-k_{2}B,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial C}{\partial t}}& =D_C^{\mathrm{eff}}\left(\mathcal{C}\right){\nabla }^{2}C+k_{2}B-k_{d}C.\hfill \end{array}$$

(3)

where:

• $D_A,D_B,D_C$ are the baseline diffusion coefficients,
• $S_A\left(\mathrm{\Phi }\right)$ is a source term maintaining A under external gradient $\mathrm{\Phi }$,
• $D_B^{\mathrm{eff}}\left(\mathcal{C}\right)$ and $D_C^{\mathrm{eff}}\left(\mathcal{C}\right)$ are effective diffusion coefficients modulated by the constraint field.

The effective diffusion coefficients are given by:

$$D_B^{\mathrm{eff}}\left(\mathcal{C}\right)={\displaystyle \frac{D_B}{1+\lambda \mathcal{C}}},D_C^{\mathrm{eff}}\left(\mathcal{C}\right)={\displaystyle \frac{D_C}{1+\lambda \mathcal{C}}},$$

(4)

where $\lambda$ controls the strength of diffusion slowdown induced by constraints.

6.3.2. Constraint Field Dynamics

The constraint field evolves according to:

$${\displaystyle \frac{\partial \mathcal{C}}{\partial t}}=\alpha C-\beta \mathcal{C},$$

(5)

where:

• $\alpha$ is the constraint production efficiency,
• $\beta$ is the natural decay rate of the constraint field.

6.4. Summary of Parameters

• $k_1,k_2,k_d$ : reaction rates,
• $D_A,D_B,D_C$ : baseline diffusion coefficients,
• $\alpha ,\beta$ : constraint field dynamics parameters,
• $\lambda$ : constraint feedback strength on diffusion,
• $\mathrm{\Phi }\left(\mathbf{r}\right)$ : external resource/energy gradient.

6.5. Expected Dynamics

• Below a critical input energy threshold, no sustained organization arises: reactions dissipate randomly.
• Above the threshold, localized regions rich in C and $\mathcal{C}$ form.
• Within these regions, diffusion is slowed, allowing for the maintenance of internal reaction cycles.
• Proto-individuals emerge as dynamically maintained chemical-constraint domains.

This minimal toy model captures the essential features of autonomous constraint emergence and the transition from non-living chemistry to prebiotic organization.

7. Extension to Three-Dimensional Constraint Emergence

7.1. System Setup

We consider a three-dimensional cubic domain of size $L\times L\times L$, discretized into a regular grid. Each spatial point $(x,y,z)$ is characterized by the following fields:

• $A(x,y,z,t)$ : concentration of resource molecule,
• $B(x,y,z,t)$ : concentration of intermediate species,
• $C(x,y,z,t)$ : concentration of constraint-building molecule,
• $\mathcal{C}(x,y,z,t)$ : intensity of the constraint field,
• $\mathrm{\Phi }(x,y,z)$ : external energy/resource gradient (fixed or slowly varying).

7.2. Reaction Scheme

The chemical reactions are:

$$\begin{array}{cc}\hfill A+B& \stackrel{k_1}{\to }2B(\mathrm{autocatalytic}\mathrm{production}\mathrm{of}B),\hfill \\ \hfill B& \stackrel{k_2}{\to }C(\mathrm{transformation}\mathrm{of}B\mathrm{into}C),\hfill \\ \hfill C& \stackrel{k_d}{\to }\varnothing (\mathrm{decay}\mathrm{of}C).\hfill \end{array}$$

The constraint field evolves dynamically via:

$${\displaystyle \frac{\partial \mathcal{C}}{\partial t}}=\alpha C-\beta \mathcal{C},$$

(6)

where $\alpha$ and $\beta$ represent the production and decay rates of constraints, respectively.

7.3. Governing Equations

The spatiotemporal dynamics are governed by the following partial differential equations:

7.3.1. Chemical Species Dynamics

The concentrations of the three key chemical species, resource molecule $A(x,y,z,t)$, intermediate autocatalyst $B(x,y,z,t)$, and constraint-producing molecule $C(x,y,z,t)$, evolve according to a system of coupled reaction-diffusion equations.

Their spatiotemporal dynamics are governed by:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial A}{\partial t}}& =D_A{\nabla }^{2}A-k_{1}AB+S_A\left(\mathrm{\Phi }\right),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial B}{\partial t}}& =D_B^{\mathrm{eff}}\left(\mathcal{C}\right){\nabla }^{2}B+k_{1}AB-k_{2}B,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial C}{\partial t}}& =D_C^{\mathrm{eff}}\left(\mathcal{C}\right){\nabla }^{2}C+k_{2}B-k_{d}C,\hfill \end{array}$$

(9)

where:

• $D_A,D_B,D_C$ are the baseline (unconstrained) diffusion coefficients of species A, B, and C,
• $k_1,k_2,k_d$ are kinetic rate constants for the respective reactions,
• $S_A\left(\mathrm{\Phi }\right)$ is an external source term representing a supply of A, driven by the environmental energy gradient $\mathrm{\Phi }$.

7.3.1.1. Terms Explanation.

• $D{\nabla }^{2}f$: Represents isotropic spatial diffusion of chemical species, tending to homogenize concentrations.
• $k_{1}AB$: Autocatalytic production term for B, fueled by consumption of A.
• $k_{2}B$: Transformation of intermediate B into constraint-building molecule C.
• $k_{d}C$: Natural decay or degradation of C.

Thus, the dynamics combine diffusion, autocatalytic amplification, transformation, and decay processes. The analysis of trend to equilibrium in complex reaction-diffusion systems [2] informs our study of chemical concentration dynamics.

7.3.2. Modulation of Diffusion by Constraints

A crucial aspect of the model is that the diffusion coefficients of B and C are not constant, but dynamically modulated by the local intensity of the constraint field $\mathcal{C}(x,y,z,t)$.

Specifically, the effective diffusion coefficients are given by:

$$D_B^{\mathrm{eff}}\left(\mathcal{C}\right)={\displaystyle \frac{D_B}{1+\lambda \mathcal{C}}},D_C^{\mathrm{eff}}\left(\mathcal{C}\right)={\displaystyle \frac{D_C}{1+\lambda \mathcal{C}}},$$

(10)

where $\lambda >0$ quantifies the strength of constraint feedback on diffusive mobility.

7.3.2.1. Interpretation.

• In regions where $\mathcal{C}$ is low (weak constraints), diffusion proceeds close to baseline rates $D_B,D_C$.
• In regions where $\mathcal{C}$ is high (strong organizational constraints), diffusion is significantly reduced, leading to spatial confinement of chemical species.

This mechanism creates dynamically maintained compartments:

• Chemical flows are slowed and localized by self-generated constraints,
• Molecular species accumulate and interact more efficiently within organized domains,
• Autonomous regions (proto-individuals) emerge through self-reinforcing feedback between chemistry and organization.

7.3.2.2. Biophysical Analogy.

This constraint-dependent modulation of diffusion mimics biological phenomena such as:

• Reduced diffusion inside cellular compartments,
• Crowding effects in cytoplasm,
• Selective permeability of membranes and cytoskeletal scaffolds.

Thus, the model captures an essential feature of living systems: the ability to actively shape internal flows and structures, rather than being passively shaped by them.

7.3.2.3. Nonlinear Coupling.

The coupling between the chemical fields and the constraint field is highly nonlinear:

• Local concentrations influence constraint generation,
• Constraints, in turn, modify local transport properties,
• This two-way feedback creates the conditions for emergent organizational closure.

This mutual reinforcement is central to the emergence of autonomy and self-maintenance in the system.

7.3.3. Constraint Field Dynamics

The constraint field $\mathcal{C}(x,y,z,t)$ plays a central role in the organizational emergence of autonomous systems. It represents the local intensity of structural or dynamical constraints that regulate chemical flows, effectively shaping the behavior of the system at each spatial point.

Its evolution over time is governed by a local production-decay equation:

$${\displaystyle \frac{\partial \mathcal{C}}{\partial t}}=\alpha C-\beta \mathcal{C},$$

(11)

where:

• $\alpha >0$ is the rate at which the chemical species C generates or reinforces constraints,
• $\beta >0$ is the natural decay rate of constraints in the absence of sustaining chemical activity.

Interpretation.

At each point in space:

• The presence of C molecules actively promotes the build-up of organizational structures, represented by the local increase in $\mathcal{C}$.
• In the absence of continuous chemical support (i.e., if C vanishes), the constraint field spontaneously decays over time, modeling physical degradation or loss of functional structure.

Thus, constraint fields are not static; they require ongoing chemical activity for their persistence, embodying the principle that living organization must be actively maintained rather than passively assumed.

Steady-State Solution.

In the stationary limit $\partial \mathcal{C}/\partial t=0$, we find the local steady-state constraint intensity:

$${\mathcal{C}}_{\mathrm{ss}}(x,y,z)={\displaystyle \frac{\alpha }{\beta }}C(x,y,z).$$

(12)

This shows that at equilibrium, the constraint field is directly proportional to the concentration of the sustaining molecule C. Regions with higher C accumulation thus exhibit stronger constraints, leading to local modification of chemical flows (e.g., reduced diffusion rates) and spatial self-organization.

Non-Equilibrium and Dynamical Effects.

During the transient evolution toward steady-state:

• Rapid production of C can lead to the fast emergence of constraint-bounded domains.
• Variations in C can induce dynamic changes in $\mathcal{C}$, modulating the system’s organization over time.
• Spatial heterogeneity in C creates a patterned constraint landscape, supporting localized, autonomous behavior.

Mathematical Properties.

Equation (10) is a simple linear first-order ordinary differential equation (ODE) at each spatial point $(x,y,z)$, with solution:

$$\mathcal{C}\left(t\right)={\mathcal{C}}_0{e}^{-\beta t}+\alpha {\int }_0^t{e}^{-\beta (t-s)}C\left(s\right)ds,$$

(13)

where ${\mathcal{C}}_0$ is the initial constraint intensity at $t=0$. Thus, $\mathcal{C}$ behaves as a low-pass filter of the chemical field C, smoothing its variations over time depending on the decay constant $\beta$.

Biological and Physical Analogies.

This dynamics reflects the biological reality that:

• Cellular membranes, structural proteins, and regulatory complexes require continuous molecular turnover.
• Spatial organization in biological systems is inherently dynamic, arising from constant energy and matter flows.

The mathematical simplicity of the constraint field dynamics belies its fundamental importance: it embodies the principle of active self-maintenance ? the hallmark of living systems.

7.4. Laplacian Operator in Three Dimensions

The evolution of the chemical fields $A(x,y,z,t)$, $B(x,y,z,t)$, and $C(x,y,z,t)$ involves spatial diffusion processes, mathematically described by the three-dimensional Laplacian operator.

Given a scalar field $f(x,y,z,t)\in \{A,B,C\}$, its Laplacian ${\nabla }^{2}f$ is defined as:

$${\nabla }^{2}f={\displaystyle \frac{{\partial }^{2}f}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}f}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}f}{\partial z^2}},$$

(14)

where each term represents the second partial derivative along the respective spatial coordinate.

Interpretation.

The Laplacian measures the local curvature of the field f; intuitively, it quantifies how much f at a point differs from its average value in the immediate neighborhood. Regions with large Laplacian values correspond to sharp gradients or strong deviations from uniformity, thus driving diffusion flows that tend to flatten or equilibrate the field.

Fields Involved.

In the present model, the scalar fields f are the concentrations of chemical species:

• $f=A(x,y,z,t)$: concentration of the resource molecule,
• $f=B(x,y,z,t)$: concentration of the intermediate species,
• $f=C(x,y,z,t)$: concentration of the constraint-producing molecule.

Each field diffuses according to its own diffusion coefficient and local constraint conditions.

7.4.1. Numerical Discretization: 6-Point Stencil

For numerical simulations on a Cartesian grid with uniform spacing $\Delta x=\Delta y=\Delta z=dx$, the Laplacian is approximated using a second-order finite difference scheme (6-point stencil):

$${\nabla }^2{f}_{i,j,k}\approx {\displaystyle \frac{1}{d{x}^2}}\left(f_{i+1,j,k}+f_{i-1,j,k}+f_{i,j+1,k}+f_{i,j-1,k}+f_{i,j,k+1}+f_{i,j,k-1}-6f_{i,j,k}\right),$$

(15)

where $f_{i,j,k}$ denotes the value of f at grid indices $(i,j,k)$.

Boundary Conditions.

We impose Neumann (zero-flux) boundary conditions:

$${\left.{\displaystyle \frac{\partial f}{\partial n}}\right|}_{\mathrm{boundary}}=0,$$

(16)

meaning that no net flow crosses the system boundaries. Numerically, this is implemented by mirroring the nearest interior value across the boundary (copying the adjacent point).

Computational Considerations.

The 6-point stencil scheme is:

• Second-order accurate in space,
• Explicit and local (only nearest neighbors needed),
• Efficient for large-scale simulations,
• Easily parallelizable on CPUs or GPUs.

For higher accuracy or complex geometries, more sophisticated schemes (e.g., 27-point stencil, spectral methods) could be employed, but the 6-point stencil provides a good balance between accuracy and computational cost for the current modeling purposes.

7.5. Boundary Conditions

To model a finite, isolated chemical system without loss or gain of material at the boundaries, we impose Neumann (zero-flux) boundary conditions for all chemical and constraint fields.

Formally, for a generic field $f(x,y,z,t)\in \{A,B,C,\mathcal{C}\}$, we require that:

$${\displaystyle \frac{\partial f}{\partial \mathbf{n}}}=0\mathrm{at}\mathrm{the}\mathrm{domain}\mathrm{boundaries},$$

(17)

where $\mathbf{n}$ denotes the outward-pointing unit normal vector to the boundary surface.

Physical Interpretation.

The Neumann boundary condition expresses that:

• There is no net diffusive flux of matter or constraint across the boundaries.
• Chemical species and constraint fields are reflected at the domain edges rather than absorbed or transmitted.
• The system is effectively "closed" with respect to spatial transport, though external sources (e.g., energy input gradients) may still operate internally.

In biological terms, this approximates the behavior of compartments or microenvironments enclosed by impermeable membranes, or localized experimental setups where exchanges with the exterior are negligible.

Mathematical Implementation.

In finite difference schemes, the Neumann condition is typically enforced numerically by mirroring interior values at the boundary. For a field f, at the boundary grid points, we impose:

$$f_{\mathrm{boundary}}=f_{\mathrm{nearest}\mathrm{interior}\mathrm{point}}.$$

(18)

Explicitly, for grid indices:

• At the minimum boundary (e.g., $i=0$), set $f_{0,j,k}=f_{1,j,k}$,
• At the maximum boundary (e.g., $i=N-1$), set $f_{N-1,j,k}=f_{N-2,j,k}$,

and similarly for the j and k directions.

This discretization guarantees that:

$${\displaystyle \frac{f_{\mathrm{neighbor}}-f_{\mathrm{boundary}}}{dx}}=0,$$

(19)

thus satisfying $\partial f/\partial n=0$ at discrete level.

Computational Advantages.

The Neumann boundary condition offers several benefits:

• Simplicity: requires no additional ghost layers or complex extrapolations,
• Stability: preserves the internal dynamics without artificial losses,
• Physical relevance: appropriate for modeling proto-systems attempting to self-enclose.

Alternative Boundary Conditions.

While Neumann conditions are natural for isolated systems, other choices are possible depending on physical context:

• Dirichlet conditions ($f=\mathrm{const}$) model fixed boundary concentrations, e.g., contact with an infinite reservoir,
• Periodic conditions ($f(0,y,z)=f(L,y,z)$) model spatially continuous systems without boundaries (e.g., early ocean scenarios).

In this work, we focus on Neumann conditions to emphasize internal autonomous organization without boundary-driven flows.

7.6. Expected Phenomena in Three Dimensions

The three-dimensional extension enables:

• Emergence of volumetric constraint-bounded domains (proto-vesicles),
• True spatial separation of interior and exterior chemical environments,
• Dynamic stabilization of autonomous constraint-maintained structures,
• Possible self-division and budding events,
• Hierarchical organization and compartmentalization phenomena.

This 3D model is thus a crucial step toward realistically capturing the physical and topological conditions under which life-like organizational closure could emerge from purely physico- chemical processes.

8. Phase Space Structure for Constraint Emergence

8.1. Dimensionless Parameters

To analyze the regimes of behavior in our system, we introduce the following dimensionless groups:

• ${\mathcal{R}}_A={\displaystyle \frac{k_1{A}_0}{D_A}}$: ratio of autocatalytic production to diffusion for the resource molecule A,
• ${\mathcal{R}}_B={\displaystyle \frac{k_2}{D_B}}$: rate of transformation from B to C relative to diffusion,
• ${\mathcal{R}}_C={\displaystyle \frac{k_d}{D_C}}$: decay rate of C relative to its diffusion,
• $\Lambda =\lambda {\mathcal{C}}_{\mathrm{typ}}$: effective strength of constraint feedback on diffusion,
• $\Gamma ={\displaystyle \frac{\alpha }{\beta }}$: ratio of constraint production to constraint decay.

Here, $A_0$ is the typical background concentration of A, and ${\mathcal{C}}_{\mathrm{typ}}$ is the typical constraint field intensity expected during evolution.

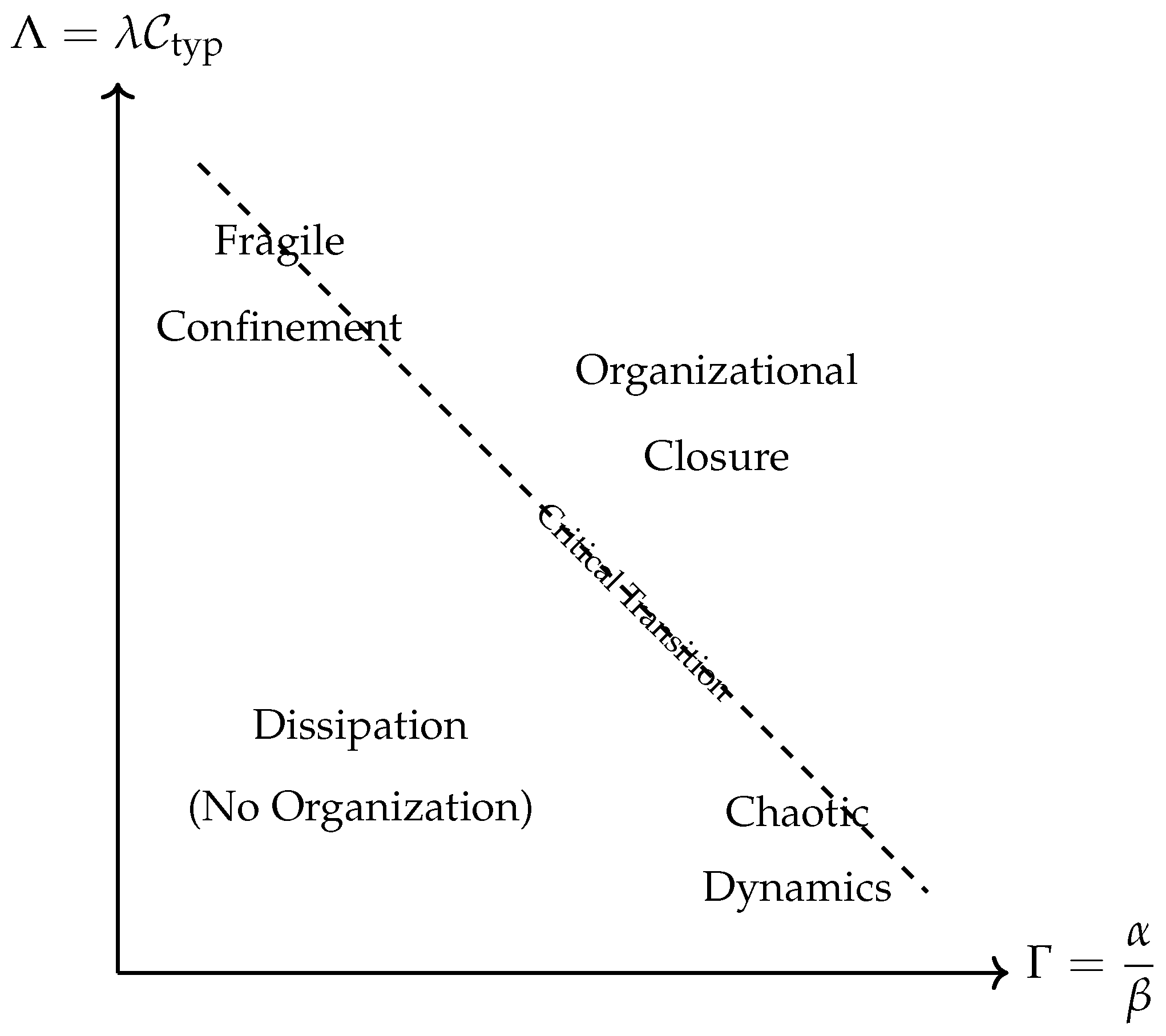
8.2. Phase Diagram Axes

We focus on the plane defined by $\Gamma$ and $\Lambda$, which control, respectively:

• The system’s ability to sustain self-generated constraints ($\Gamma$),
• The system’s ability to modulate internal diffusion based on constraint fields ($\Lambda$).

The behavior of the system qualitatively changes across this phase space.

8.3. Behavioral Regimes

We identify four major behavioral regimes:

• Low $\Gamma$, Low $\Lambda$: Diffusion dominates; no sustained organization; purely dissipative structures.
• High $\Gamma$, Low $\Lambda$: High constraint production, but insufficient spatial regulation; chaotic or unstable chemical patterns.
• Low $\Gamma$, High $\Lambda$: Strong spatial confinement, but insufficient self-maintenance; fragile, transient structures.
• High $\Gamma$, High $\Lambda$: Emergence of stable, localized, constraint-maintained domains; proto-autonomous individuals.

8.4. Critical Transition

Organizational closure occurs when the system crosses a critical surface in the $(\Gamma ,\Lambda )$ space, roughly characterized by:

$$\Gamma \times \Lambda \gtrsim \mathrm{Threshold}.$$

(20)

Beyond this threshold, the mutual reinforcement of chemical activity and constraints leads to the emergence of autonomous, self-maintaining organizational structures.

8.5. Implications for Simulations

To empirically map the phase structure, simulations can be performed by systematically varying:

• The constraint production rate $\alpha$ and decay rate $\beta$ (thus modifying $\Gamma$),
• The strength of constraint feedback $\lambda$ (thus modifying $\Lambda$).

Quantities such as:

• Average lifetime of constraint-bounded regions,
• Size distribution of organized domains,
• Degree of internal chemical coherence,

can be used as indicators to map the organizational phase diagram.

8.6. Summary Table

Regime	Behavior	Interpretation
Low $\Gamma$, Low $\Lambda$	Diffusion dominates	No organization, noise
High $\Gamma$, Low $\Lambda$	Chaotic chemical dynamics	Energy-rich but unstable
Low $\Gamma$, High $\Lambda$	Confinement but decay	Fragile compartments
High $\Gamma$, High $\Lambda$	Emergent autonomy	Proto-individuals, closure

9. Discussion and Implications

The Constraint Emergence Hypothesis reframes the origin of life not as the outcome of the spontaneous assembly of specific molecular subsystems, but as the result of the spontaneous formation of self-sustaining networks of functional constraints.

This shift from molecular reductionism to organizational realism provides both conceptual and mathematical innovations for understanding the fundamental nature of life.

Figure 1. Qualitative phase diagram of the system behavior in the $(\Gamma ,\Lambda )$ plane. Organizational closure emerges above a critical threshold surface, where constraint production and feedback strength are sufficiently high.

Figure 1. Qualitative phase diagram of the system behavior in the $(\Gamma ,\Lambda )$ plane. Organizational closure emerges above a critical threshold surface, where constraint production and feedback strength are sufficiently high.

9.1. From Molecules to Organization

Traditional origin-of-life theories often focus on identifying:

• The first replicators (e.g., RNA molecules),
• The first metabolic cycles (e.g., reverse citric acid cycle),
• The first compartments (e.g., lipid vesicles).

However, isolated replicators, metabolic loops, or vesicles are insufficient: they lack the integrated, self-reinforcing organization required for sustained autonomy, evolution, and individuation.

The Constraint Emergence Hypothesis proposes that:

• Life begins not with molecules, but with the self-organization of functional relationships,
• These relationships materialize as constraint networks regulating matter and energy flows,
• Chemical and spatial structures are shaped by, and sustain, internal organizational logic.

Thus, life is defined not by its material components, but by its organizational regime– a new kind of causal order emerging from far-from-equilibrium conditions.

9.2. Mathematical Contributions

Mathematically, this framework formalizes:

• The coupled dynamics of chemical fields $\left\{x_i\right\}$ and constraint fields C,
• The emergence of viability domains in state space,
• The conditions for organizational closure as a non-equilibrium phase transition,
• The robustness, resilience, and adaptive potential of proto-individuals.

This formalism allows the systematic study of:

• Stability and instability of organizational attractors,
• Bifurcation phenomena associated with closure and collapse,
• Evolutionary dynamics arising from constraint-driven selection.

By focusing on constraint generation and feedback structure, the model naturally incorporates the role of energy flow, stochastic fluctuations, and spatial localization– critical ingredients for realistic origin-of-life scenarios.

9.3. Philosophical and Foundational Implications

This perspective has profound implications for the definition and study of life:

• Life as Organization: Life is fundamentally an organizational phenomenon, not a molecular or thermodynamic anomaly.
• Causal Autonomy: True biological individuality emerges when systems gain internal causal closure, allowing them to maintain and regulate themselves despite environmental fluctuations.
• Continuity of Complexity: Life and non-life are not separated by a sharp molecular boundary, but by a phase transition in dynamical organization.
• Pre-Genetic Evolution: Evolution by selection on organizational structures predates the emergence of templated genetic replication.

These ideas align with and extend concepts from autopoiesis theory, theories of dissipative structures, and contemporary complex systems science.

9.4. Experimental and Synthetic Implications

The Constraint Emergence Hypothesis suggests new directions for experimental research:

• Designing Proto-Individuals: Constructing artificial systems where chemical reactions self-organize constraint fields, leading to sustained localized structures.
• Testing Phase Transition Hypotheses: Observing critical thresholds where passive chemical systems become autonomously organizing under varying environmental gradients.
• Minimal Life Simulations: Simulating constraint-chemical feedback systems to study the emergence of viability domains, robustness, and proto-evolutionary behaviors.
• Energy Flow Experiments: Testing how sustained energy gradients influence the emergence and maintenance of constraint-closed systems.

Such experimental approaches could recreate minimal models of life-like organization, independent of contemporary biomolecules, shedding new light on the origin of life.

9.5. Broader Implications

Beyond the origin of life, the organizational principles identified here may apply to:

• The evolution of biological complexity (e.g., emergence of multicellularity),
• The origin of cognitive and social systems (organizational closure at higher levels),
• Artificial life and synthetic biology (designing constraint-sustaining autonomous systems),
• The search for extraterrestrial life (identifying signs of organizational autonomy rather than specific molecular markers).

In all these domains, life is not substance, but process; not a set of molecules, but a sustained dynamic of self-producing constraints.

9.6. Summary

The Constraint Emergence Hypothesis offers a unified, physically grounded, and mathematically formalized framework for understanding life’s origins.

By identifying organizational closure–not molecule replication–as the critical transition, it reframes the origin of life as the spontaneous emergence of autonomous organizational regimes in matter and energy flows.

This approach opens new pathways for theoretical, experimental, and philosophical inquiry into one of the deepest questions in science: How does matter become autonomous?

9.7. Comparison with Traditional Theories

Traditional models of the origin of life typically emphasize one molecular subsystem as the privileged foundation for biological emergence:

• Metabolism-First Approaches: These theories focus on the spontaneous emergence of autocatalytic cycles and energy-driven reaction networks that could sustain themselves independently of genetic templates [8,10]. They highlight the thermodynamic necessity of maintaining far-from-equilibrium states through chemical fluxes.
• Replication-First Approaches: These theories emphasize the centrality of informational molecules–particularly RNA–as self-replicating entities capable of carrying heritable information and undergoing Darwinian evolution [3,4]. The “RNA World” hypothesis exemplifies this paradigm.
• Compartment-First Approaches: These models propose that spatial compartmentalization–the formation of lipid vesicles or protocells–was the first critical step, enabling localized reaction environments protected from external perturbations [5].

Each of these perspectives has contributed critical insights:

• Metabolism models elucidate how chemical networks could self-sustain energetically.
• Replication models explain how heredity and evolution could become possible.
• Compartmentalization models clarify how individuality and internal coherence could be achieved.

However, these traditional theories generally assume that one subsystem can precede and independently initiate life, with other functions emerging secondarily.

9.7.1. Limitations of Reductionist Approaches

This sequential or isolated view faces major conceptual challenges:

• Replication without metabolism lacks an energy and material basis for sustaining copying.
• Metabolism without information lacks directionality and evolutionary adaptability.
• Compartments without internal organization are merely passive enclosures, easily dissipated.

Thus, no single subsystem–metabolism, information, or membrane–is sufficient on its own to cross the threshold into living organization.

9.7.2. Constraint Emergence Hypothesis: A Holistic Framework

In contrast, the Constraint Emergence Hypothesis proposes that:

• Life emerged not from the dominance of one subsystem, but from the co-emergence and mutual reinforcement of metabolic, informational, and structural constraints.
• These subsystems were tightly coupled from the outset through dynamic feedback loops, enabled by environmental gradients and internal organizational dynamics.
• Organizational closure–not molecular replication or metabolic flux alone–defines the critical transition into autonomy and evolutionary competence.

In this view:

$$\mathbf{Organization}\mathrm{precedes}\mathit{molecular specialization}.$$

Material components (e.g., RNA, peptides, lipids) are important, but their biological significance arises only when embedded within a closed organizational regime capable of self-maintenance, individuation, and evolution.

9.7.3. Summary

The Constraint Emergence Hypothesis thus synthesizes and transcends traditional theories by emphasizing:

• The indispensability of integrating energy flow, information storage, and spatial organization from the outset,
• The central role of dynamical constraints and feedback structures,
• The emergence of life as a phase transition in organizational dynamics, not a simple molecular event.

This reframing suggests that life’s origin is best understood not as the appearance of a molecule, but as the spontaneous rise of a new causal regime– an autonomous, self-producing organization within matter.

9.8. Experimental Implications

The Constraint Emergence Hypothesis suggests novel experimental strategies for investigating the origin of life and the emergence of autonomous systems from prebiotic chemistry.

Rather than focusing exclusively on the spontaneous formation of individual molecular species (e.g., RNA, peptides, lipids), this approach emphasizes the spontaneous formation of functional constraint networks capable of sustaining organizational closure.

9.8.1. Focus on Constraint Formation

Experimental research should prioritize conditions that promote the spontaneous emergence of stable, dynamically maintained constraints.

Key experimental goals include:

• Identifying environmental gradients (chemical, thermal, redox, electrochemical) that drive self-organization,
• Observing how coupled reaction-diffusion systems generate localized regions of functional constraint (e.g., catalytic scaffolds, semi-permeable barriers, energy concentration zones),
• Measuring the persistence, robustness, and feedback effects of emergent constraint structures.

The critical focus shifts from molecular specificity to organizational dynamics.

9.8.2. Design of Synthetic Proto-Systems

Laboratory systems can be engineered to test the feasibility of constraint-closure emergence under controlled conditions.

Strategies could include:

• Coupled chemical networks embedded in spatially structured environments (e.g., microfluidic gradients, porous matrices),
• Energy-driven reaction systems (e.g., redox couples, light-activated reactions) under sustained non-equilibrium conditions,
• Incorporating materials or mechanisms that allow for self-assembling selective barriers and internal energy recycling loops.

The objective is not merely to assemble complex molecules, but to create experimental platforms where matter and energy flows spontaneously organize into self-sustaining constraint- regulated regimes.

9.8.3. Minimal Autonomy Experiments

An ultimate experimental test of the Constraint Emergence Hypothesis would be the construction of synthetic proto-individuals– spatially localized, autonomous systems that:

• Maintain internal organization via self-produced constraints,
• Regulate matter and energy intake and waste expulsion,
• Exhibit resilience to environmental perturbations,
• Possibly undergo fission or variation under suitable conditions.

Experimental observables include:

• The formation of spatially bounded, stable chemical domains,
• Fluctuation-driven transitions from passive dissipation to active self-organization,
• Measurements of constraint field strength, chemical stabilization, and persistence over time.

These “minimal autonomy experiments” would bridge the gap between synthetic biology, systems chemistry, and the physics of complex systems.

9.8.4. Toward a Unified Experimental Framework

This approach suggests a convergence between:

• Systems Chemistry: Understanding how chemical complexity arises and stabilizes under flow conditions,
• Synthetic Biology: Engineering life-like properties into non-living matter,
• Complex Systems Physics: Modeling critical transitions, emergent behaviors, and self- organized criticality.

By focusing on the emergence of autonomous organization–rather than molecular identity– experiments could reveal universal principles governing the spontaneous rise of living systems from prebiotic environments.

9.8.5. Summary

Experimental exploration of the Constraint Emergence Hypothesis offers the potential to:

• Test the minimal requirements for life-like autonomy,
• Reproduce critical organizational phase transitions in the laboratory,
• Discover alternative life-like systems independent of contemporary biochemistry,
• Illuminate the universal pathways through which matter self-organizes into living organization.

Thus, this approach not only advances our understanding of life’s origins but also lays the foundation for the design and discovery of novel autonomous systems.

9.9. Philosophical and Theoretical Implications

Beyond its scientific and experimental contributions, the Constraint Emergence Hypothesis invites a fundamental philosophical rethinking of life, organization, and autonomy.

9.9.1. Life as Organization of Constraints

In this framework, life is not defined by the presence of particular molecules (e.g., DNA, proteins, lipids) nor by the specific chemistry of carbon-based compounds.

Instead:

• Life is a property of organized constraints– dynamically maintained structures that regulate and shape flows of matter and energy to sustain themselves.
• Biological individuality arises from the emergence of autonomous constraint-maintaining systems, not from the passive aggregation of complex molecules.
• Material substrates matter, but only insofar as they support the self-production of organizational closure.

This view shifts the focus from substance to process, from components to relations, and from molecular identities to organizational dynamics.

9.9.2. Emergence without Design

The Constraint Emergence Hypothesis proposes that:

• No external design, teleology, or pre-existing genetic blueprint is necessary for the emergence of life-like systems.
• Self-producing organizations can spontaneously arise under suitable energetic and material conditions, driven by:

  -

  Environmental gradients (energy sources),

  -

  Stochastic fluctuations (variation and diversity),

  -

  Dynamical feedback (self-reinforcement of constraints).

• Purpose, functionality, and selfhood emerge a posteriori as properties of dynamically sustained constraint networks.

This aligns with the broader philosophy of complex systems science, where macroscopic order emerges from microscopic interactions without requiring external imposition.

It also extends the theoretical framework of autopoiesis [6] and biological autonomy [7] into a dynamically and experimentally testable model.

9.9.3. Universality of Life

A profound consequence of this framework is that life may be:

• Organizationally universal: Wherever matter and energy can self-organize into constraint-closed, self-maintaining systems, life-like phenomena could emerge.
• Chemically agnostic: Life may not require carbon, water, or Earth-like environments, but merely the right conditions for organizational closure and constraint generation.
• Emergent across scales: Similar principles may underlie the emergence of cognitive systems, ecosystems, social organizations, and even technological autonomous agents.

Thus, the Constraint Emergence Hypothesis not only reframes our understanding of terrestrial life, but expands the search for life in the universe to include fundamentally organizational signatures rather than specific molecular markers.

9.9.4. Toward a Unified Science of Autonomous Systems

The theoretical implications suggest the possibility of a unified framework for:

• Prebiotic chemistry,
• Biological origins,
• Cognitive emergence,
• Artificial life and synthetic autonomous systems,
• Universal evolutionary dynamics across substrates and scales.

By grounding life in the physics of constraint self-production and closure, this approach bridges gaps between chemistry, physics, biology, and philosophy, offering a coherent vision of autonomy as a general property of organized matter far from equilibrium.

9.9.5. Summary

The Constraint Emergence Hypothesis proposes a radical yet deeply grounded vision:

• Life is not a substance, but a dynamical process of autonomous constraint self-organization,
• No external design is needed; organization emerges naturally from internal dynamics under suitable conditions,
• Life may be a universal outcome of complex systems evolution, not a rare anomaly.

This philosophical shift opens new conceptual horizons for biology, physics, and the search for life beyond Earth.

9.10. Future Directions

The Constraint Emergence Hypothesis opens multiple promising avenues for further theoretical development, computational modeling, and experimental exploration.

By shifting focus from isolated molecular mechanisms to the dynamics of systemic constraint organization, this framework redefines the agenda for understanding and investigating the origin of autonomous systems, including life itself.

9.10.1. Detailed Mathematical Analysis

A crucial next step is the comprehensive mathematical study of constraint-chemical systems, focusing on:

• Stability Analysis: Characterizing the attractor structures corresponding to constraint-closed states and determining their domains of attraction under perturbations.
• Bifurcation Theory: Identifying critical parameters where transitions occur between dissipative, closed, and collapsed regimes; understanding phase diagrams and organizational thresholds.
• Pattern Formation: Studying spatial and temporal patterns arising from constraint-chemical feedbacks, including localization phenomena, wavefronts, and oscillatory structures. Analogous mechanisms have been mathematically modeled in biological pattern formation [15], although our emphasis is on organizational autonomy.
• Critical Phenomena: Investigating whether the transition to closure exhibits features of criticality, such as scaling laws, universality classes, and self-organized criticality.

This mathematical groundwork would solidify the theoretical basis for the spontaneous emergence of autonomous organization in chemical systems.

9.10.2. Simulation of Constraint Fields and Proto-Individual Dynamics

Computational modeling is essential to bridge theory and experiment.

Key goals include:

• Developing spatially resolved models of coupled reaction-diffusion-constraint systems,
• Simulating the spontaneous formation, growth, fission, and decay of constraint-bounded proto-individuals,
• Exploring the evolutionary dynamics of constraint networks under stochastic perturbations and resource limitations,
• Visualizing transitions from passive dissipation to autonomous closure across parameter spaces.

Agent-based models, lattice-Boltzmann simulations, and PDE solvers (finite-difference, finite-element) could be leveraged to explore these dynamics.

Such simulations could generate predictions testable by future laboratory experiments and guide the search for optimal experimental setups.

9.10.3. Synthesis of Proto-Constraints in Laboratory Systems

Experimental synthesis of constraint-driven systems represents a bold but feasible frontier.

Key directions include:

• Engineering chemical networks capable of generating localized constraints (e.g., catalytic scaffolds, microcompartment formation),
• Designing physical setups where environmental gradients can drive the emergence of organizational feedbacks,
• Demonstrating minimal systems exhibiting self-sustained constraint-chemical cycles and proto-individual behavior,
• Exploring transitions between organizational collapse, metastability, and robust autonomy.

This experimental strategy would complement and test the theoretical and computational predictions, paving the way toward a synthetic understanding of life’s fundamental organizational principles.

9.10.4. Interdisciplinary Integration

Realizing the full potential of the Constraint Emergence Hypothesis will require the convergence of multiple disciplines:

• Systems Chemistry: Understanding how chemical complexity arises and self-organizes under flow.
• Synthetic Biology: Designing life-like properties in non-living matter.
• Complex Systems Physics: Modeling criticality, emergence, and self-organization.
• Philosophy of Biology: Revisiting fundamental questions about individuality, autonomy, and the nature of life.

9.10.5. Summary

In summary, future work should:

• Develop rigorous mathematical frameworks for constraint-driven organization,
• Simulate the emergence and evolution of constraint fields in complex chemical systems,
• Build minimal synthetic systems demonstrating organizational closure in the laboratory,
• Integrate insights from chemistry, biology, physics, and philosophy to build a unified science of autonomous systems.

By addressing these directions, we may come closer to solving one of the deepest mysteries of science: How can matter organize itself into living autonomy?

10. Conclusions

In this work, we have proposed the Constraint Emergence Hypothesis as a new conceptual and mathematical framework for understanding the origin of life.

Departing from traditional reductionist models focused on isolated molecular subsystems, we argue that life emerges from the spontaneous formation of functional constraints that organize chemical, energetic, and spatial processes into autonomous, self-sustaining systems.

We developed a dynamical model coupling chemical reaction-diffusion processes with the evolution of constraint fields, demonstrating how mutual feedbacks between matter flows and constraint structures can lead to the stabilization of self-maintaining organizations. In this view, life is understood as a phase transition in the organization of matter and energy, marked by the closure of constraint networks capable of maintaining and reproducing their own enabling conditions.

This framework shifts the explanatory focus from molecular specificity to the dynamics of organizational autonomy, offering:

• A unified understanding of metabolism, information, and compartmentalization as emergent from constraint-driven self-organization,
• New experimental and computational avenues for the synthesis and study of minimal autonomous systems,
• A broader philosophical and scientific foundation for thinking about life as a universal phenomenon of complex systems.

Ultimately, life is not defined by the presence of particular molecules, but by the emergence of dynamic, self-reinforcing constraints that regulate and sustain flows of matter and energy against entropic dissipation.

This shift in perspective opens a new chapter in origins-of-life research, inviting us to explore not only the chemical possibilities, but the deeper organizational principles underlying all living systems.

In the spontaneous interplay of energy, matter, and emergent constraints, the cosmos first discovered the possibility of life.