1. Introduction
In modern 6–35 kV distribution networks, where isolated or compensated neutral configurations are predominantly used, the reliability of power supply largely depends on the effectiveness of ground fault protection systems. Statistical analysis shows that up to 70% of damage in such networks is caused by single-phase ground faults (SPGFs), often accompanied by significant transient resistances, which complicate their detection and localization [
1,
2,
3,
4]. The presence of transient resistance at the fault point can significantly reduce the fault current magnitude, leading to decreased sensitivity and delayed operation of traditional ground fault protection methods [
5,
6,
7,
8,
9]. Recent research has focused on developing protection algorithms that address these challenges by analyzing zero-sequence current (ZSC) and voltage signals [
10,
11,
12]. Methods such as the charge-voltage relationship [
11], improved symmetrical component analysis [
12], and hybrid compensation techniques [
13,
14] have been proposed to enhance fault detection reliability. However, these methods often require complex measurement systems or are not fully adapted to distribution networks with varying transient resistances. Superior methods, including adaptive threshold adjustment, multi-criteria decision algorithms, and transient-based approaches such as wavelet analysis, are increasingly recognized as effective means of detecting high-resistance faults while maintaining selectivity [
15,
16,26]. In particular, centralized protection architectures are gaining widespread adoption, where fault information from all feeders is collected at a centralized ground fault protection unit (CGFPU), enabling coordinated and selective decision-making [
17,
18,
19,
20]. The principle of comparing the angle and magnitude of zero-sequence currents among feeders offers a promising approach for accurate fault localization even under varying fault resistances [
21,
22,
23,
24]. Moreover, studies [
25,
26,
27,
28,
29,
30] emphasize the importance of considering the dynamic behavior of transient processes during SPGF for high-sensitivity protection schemes, particularly in high-impedance grounded networks. This study proposes a new selective method for identifying faulty feeders during SPGF with transient resistance based on the comparison of zero-sequence current angles and magnitudes. A protection algorithm is developed and implemented in a centralized relay protection device, ensuring selective, sensitive, and stable operation over a wide range of fault conditions. The method is validated through modeling in Matlab Simulink and laboratory testing. Furthermore, advanced principles from adaptive, transient-based, and high-resolution analysis methods are integrated into the design, ensuring the proposed solution remains robust for future developments, including smart grid and microgrid applications [
31]. The objective of this work is to develop a scientifically grounded and technically robust method for enhancing the protection of 6–35 kV electrical networks during SPGFs with transient resistance. Achieving effective detection and isolation of faulty elements will improve the overall reliability and efficiency of power supply. Additionally, it is critical to explore strategies for protecting network equipment against overvoltages under various neutral grounding configurations during such faults.
2. Relevance of the Topic
The primary advantage of the isolated neutral configuration in medium-voltage (MV) networks is the ability of the system to continue operating for an acceptable period during a single-phase ground fault (SPGF) before isolating the faulty feeder [
3,
4]. Damage to phase insulation in such networks leads to an increase in capacitive currents, which may reach magnitudes comparable to the normal operating current. This situation does not immediately create an emergency condition and typically does not necessitate immediate tripping by ground overcurrent protection.
However, intermittent arcing faults can cause dangerous overvoltages, the magnitude of which depends on the capacitive current during an SPGF. To mitigate these risks, it is critical to limit the capacitive current and associated overvoltages to permissible levels based on the network voltage class.
To achieve this, various neutral grounding techniques are employed, including grounding through:
- Arc-suppressing reactors (ASR);
- High- or low-resistance grounding;
- Combined grounding methods [
5,
6].
The use of an ASR reduces SPGF currents but is limited by its rated current capacity; excessive currents may threaten the reactor’s integrity. Advanced ASRs with controlled inductance can maintain detuning currents within acceptable limits, although they still present limitations in terms of power and the time needed to detect faults [
7]. Resistive neutral grounding through active resistance is also widely applied, significantly reducing the risk of arc-induced overvoltages. High-resistance grounding retains the main advantage of the isolated neutral system but is constrained to networks with relatively low intrinsic capacitive currents, typically within 5–7 A [
8]. Low-resistance grounding is applied in cases where it is crucial to clear SPGFs by isolating the faulty feeder as rapidly as possible. However, this method forfeits the isolated neutral system's operational advantages and is thus used selectively, particularly in networks where increased safety standards or high overvoltage risks exist [
8]. Combined neutral grounding, widely used in 3–69 kV MV networks in Europe, offers a balanced approach: it preserves the advantages of isolated neutral operation, limits residual currents at the fault location, and effectively controls both contact voltages and overvoltages. Nevertheless, this method involves high implementation costs and introduces challenges in ensuring the selectivity of protection systems [
5,
9]. While various methods exist to limit overvoltages arising from insulation failures, the most severe overvoltages are typically encountered during SPGFs in cable networks, owing to their high capacitive currents. For the reliable operation of isolated neutral MV networks, it is essential to properly select both the neutral grounding method and the corresponding protection schemes. Special attention must be paid to the impact of transient resistance at the fault location, as it significantly influences fault detection and protection system behavior.
Existing protection strategies for SPGF detection include:
- -
Methods based on residual voltage measurement and correction factors applied to inverse time delay curves [
10];
- -
Detection via the analysis of the charge-voltage curve during an SPGF [
11];
- -
Use of symmetrical components analysis [
12];
- -
Hybrid compensation techniques [
13,
14], although not yet widespread;
- -
More common methods focusing on zero-sequence current (ZSC) amplitude evaluation [
15];
- -
Measurement of fundamental harmonic components of ZSC on feeders [
16].
Despite these advances, current methods do not fully guarantee the required levels of reliability, sensitivity, and selectivity under SPGF conditions involving transient resistance. Moreover, comprehensive studies on the behavior and influence of transient resistance during SPGFs remain an urgent and underexplored research area.
3. Materials and Methods
To achieve the research objectives, it is necessary to:
- -
Analyze the influence of transient resistances during single-phase ground faults (SPGF) on the performance characteristics of protection systems;
- -
Assess the operation of protection systems under different transient resistance conditions, and;
- -
Develop a protection scheme and an algorithm for reliably detecting and protecting medium-voltage (MV) networks against SPGFs.
The research methodology is based on a detailed analysis of 6–35 kV networks, including the frequency and nature of fault occurrences, and the study of disturbance records during fault events. Existing protection methods applied in MV networks during SPGFs were comprehensively reviewed [
17,
18,
19,
20].
Relay protection in such networks generally operates based on the following algorithms:
- -
Magnitude of the residual (zero-sequence) voltage;
- -
Root mean square (RMS) value of the fundamental harmonic of the zero-sequence current in feeders;
- -
Direction of the zero-sequence power;
- -
Summation of the higher harmonics of the zero-sequence current.
Each protection method addresses specific factors influencing the controlled parameters. However, the analysis also revealed significant drawbacks in current protection strategies, particularly under SPGFs with transient resistance [
21,
22,
23,
24].
The presence of transient resistance during an SPGF leads to a reduction in protection sensitivity, thereby undermining the reliability and efficiency of MV networks configured with isolated neutrals. In practice, incomplete ground faults are frequently accompanied by transient resistance, which can range from a few Ohms to several kilo-Ohms [
22]. These resistance values are random and depend on various factors, such as the presence of moisture, icing, tree branches, and the soil's specific properties. During SPGFs with transient resistance, the magnitudes of zero-sequence current and voltage are significantly reduced. Since the settings for ground overcurrent protections are typically calculated assuming bolted faults (i.e., near-zero resistance faults), the failure to account for transient resistance may result in the protection system failing to detect and isolate the fault [
25,
26,
27]. Moreover, transient resistance affects not only traditional ground overcurrent protections but also protections based on detecting higher harmonic components in the steady-state SPGF current. Studies show that transient resistances of just a few Ohms can lead to substantial sensitivity degradation [
25]. Directional overcurrent protections that determine the direction of zero-sequence current under steady-state fault conditions offer somewhat better performance. Nonetheless, analysis reveals that even these protections exhibit low selectivity for SPGFs when transient resistances reach values between 600–700 Ohms, particularly in networks with a maximum distributed capacitance of around 6.5 μF.
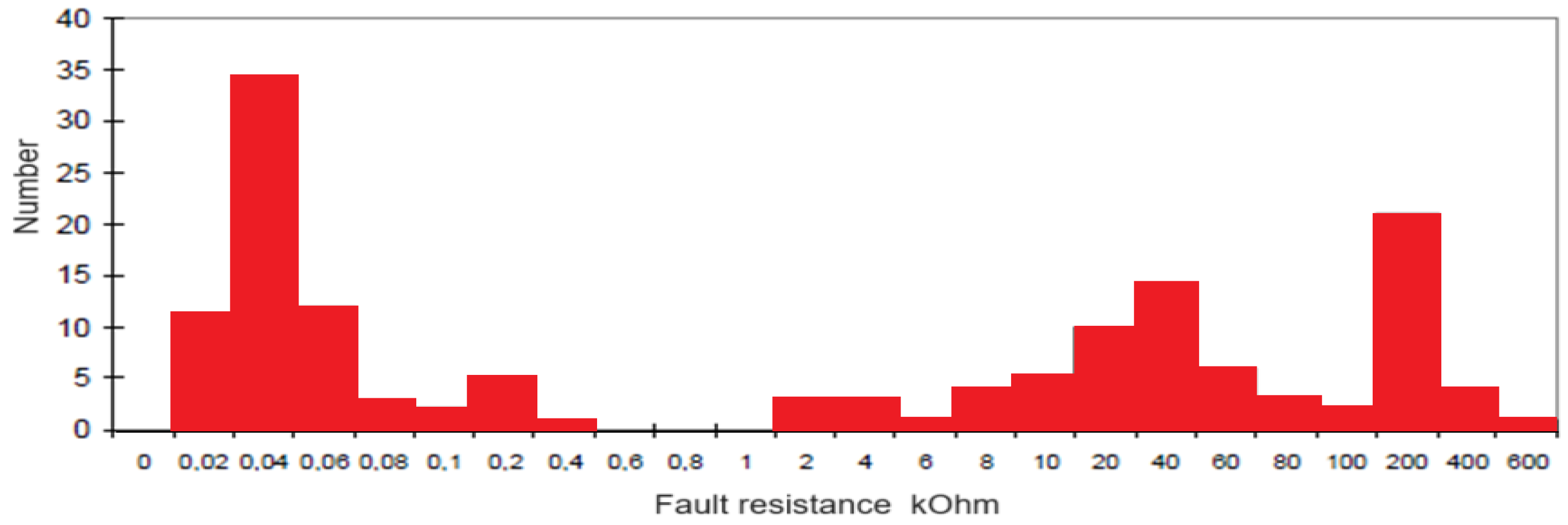
Figure 1 illustrates the relationship between SPGF conditions and transient resistance values for soils with high specific resistivity [
28].
The histogram in
Figure 1 shows the distribution of recorded SPGFs according to the transient resistance at the fault location [
10]. It can be observed that:
- -
A significant number of faults exhibit very low transient resistances, typically below 0.1 kOhm;
- -
Another notable cluster appears at higher resistance values between 20 kOhm and 400 kOhm, with a peak around 200 kOhm;
- -
Very few faults are recorded at intermediate resistance values between 0.2 kOhm and 10 kOhm.
This distribution confirms the random nature of transient resistance in SPGFs. It also emphasizes the challenge for conventional protection systems: low-resistance faults can generate detectable current levels, while high-resistance faults may significantly reduce the zero-sequence current, complicating reliable detection and requiring enhanced sensitivity in protection algorithms.
Data analysis shows that in most cases, SPGF occurs with the transient resistance, which is in the range from 0.02-200 kOhm.
3.1. Defining the Transient Resistance Values at the SPGF Location and Ground Overcurrent Settings
During transient processes associated with SPGFs, the ratio between the higher harmonic currents and the fundamental frequency current 50 Hz remains approximately constant [
29,
30]. The relationship between zero-sequence voltage and current is expressed as:
where І
0 (t) is the zero-sequence current at the SPGF location; u
0 (t) – is the zero-sequence voltage;
- is the total phase to ground capacitance of the network.
The current I
0 through unfaulted lines is determined by their self-capacitance:
where C
0S is the self-capacitance of the phase shorted to ground.
Thus, the total cumulative zero-sequence current during an SPGF can be written as:
For the root mean square (RMS) values, integrating over time
T, the expressions are:
where
– is the represents the derivative (rate of change) of the zero-sequence voltage.
The steady-state zero-sequence voltage
at the fault location, considering the transient resistance
, is given by:
where U
ph – is the phase voltage;
is the circuit completeness coefficient, defined as:
Thus, the zero-sequence fault current can be written as:
where
is the total capacitive current of the network in normal mode.
In networks with isolated neutral configurations, the ground fault current is determined by the difference between total capacitance and the capacitance of the faulted phase. Based on Eq. (4) and Eq. (5), the RMS current expressions for protection settings are:
Thus, the operational current setting
for the ground fault protection is defined as:
where K
off – is an offset coefficient that accounts for measurement inaccuracies, transducer errors, and calculation inaccuracies [
21,
23].
Finally, the sensitivity coefficient
of the ground fault protection is given by:
where K
s – defines the ability of the protection to reliably detect an SPGF even under varying transient resistance conditions.
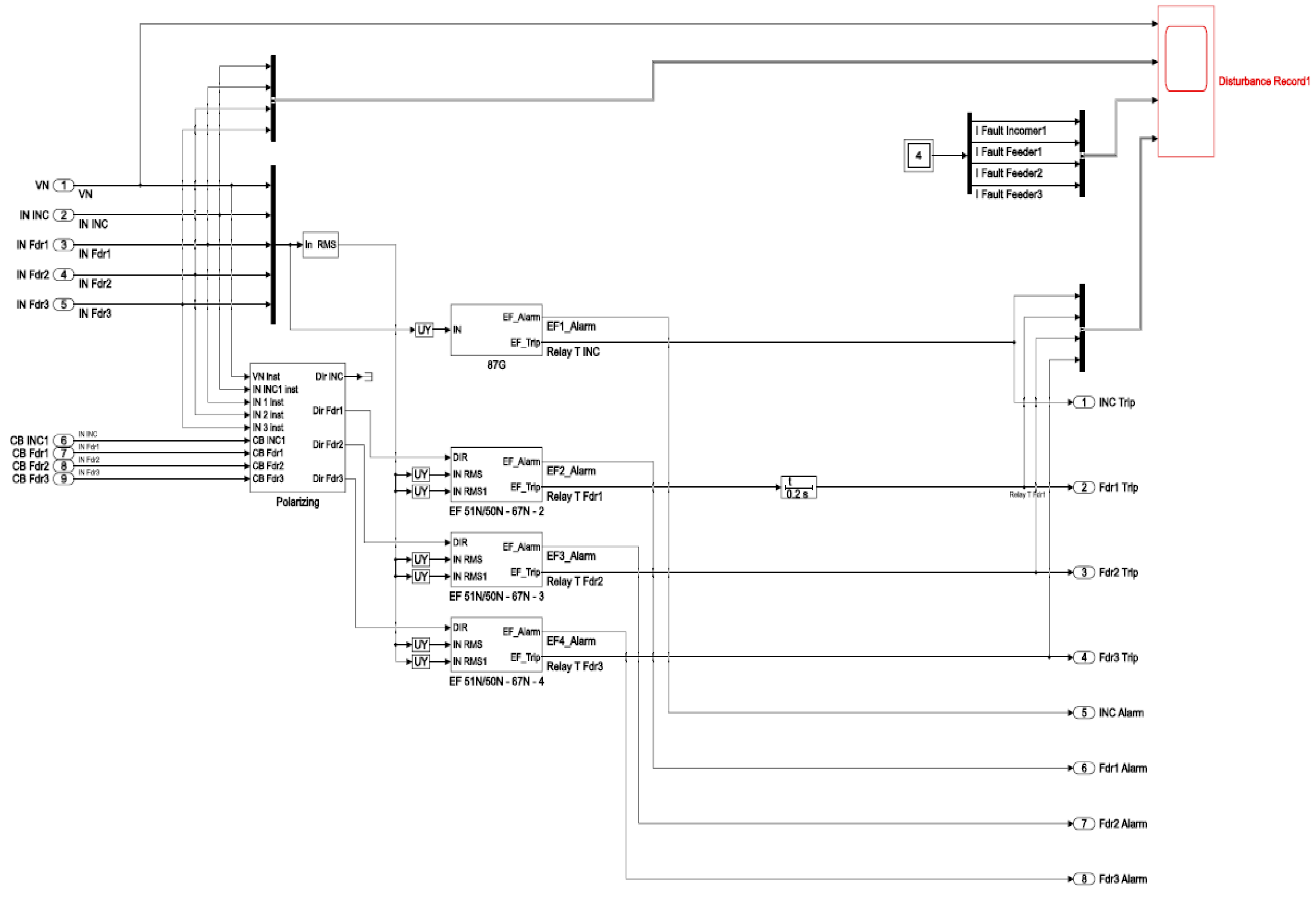
3.2. Development of Algorithm and Protective Device for Identifying a Faulty Feeder During SPGF with the Transient Resistance
A new method for identifying a faulty feeder during a single-phase ground fault (SPGF) with transient resistance is proposed. The method is based on the deployment of a centralized ground fault protection unit (CGFPU), which operates as a digital protective device designed for centralized control, monitoring, and protection of the medium-voltage (MV) distribution network. The CGFPU carries out the following key functions:
- Continuous measurement of zero-sequence currents and zero-sequence voltages at all feeders and bus sections;
- Comparison of zero-sequence current angles and magnitudes to detect characteristic changes caused by SPGFs;
- Fault location identification by analyzing the deviation patterns between normal and faulted states;
- Generation of alarm or trip signals depending on the severity and confirmation of the ground fault condition.
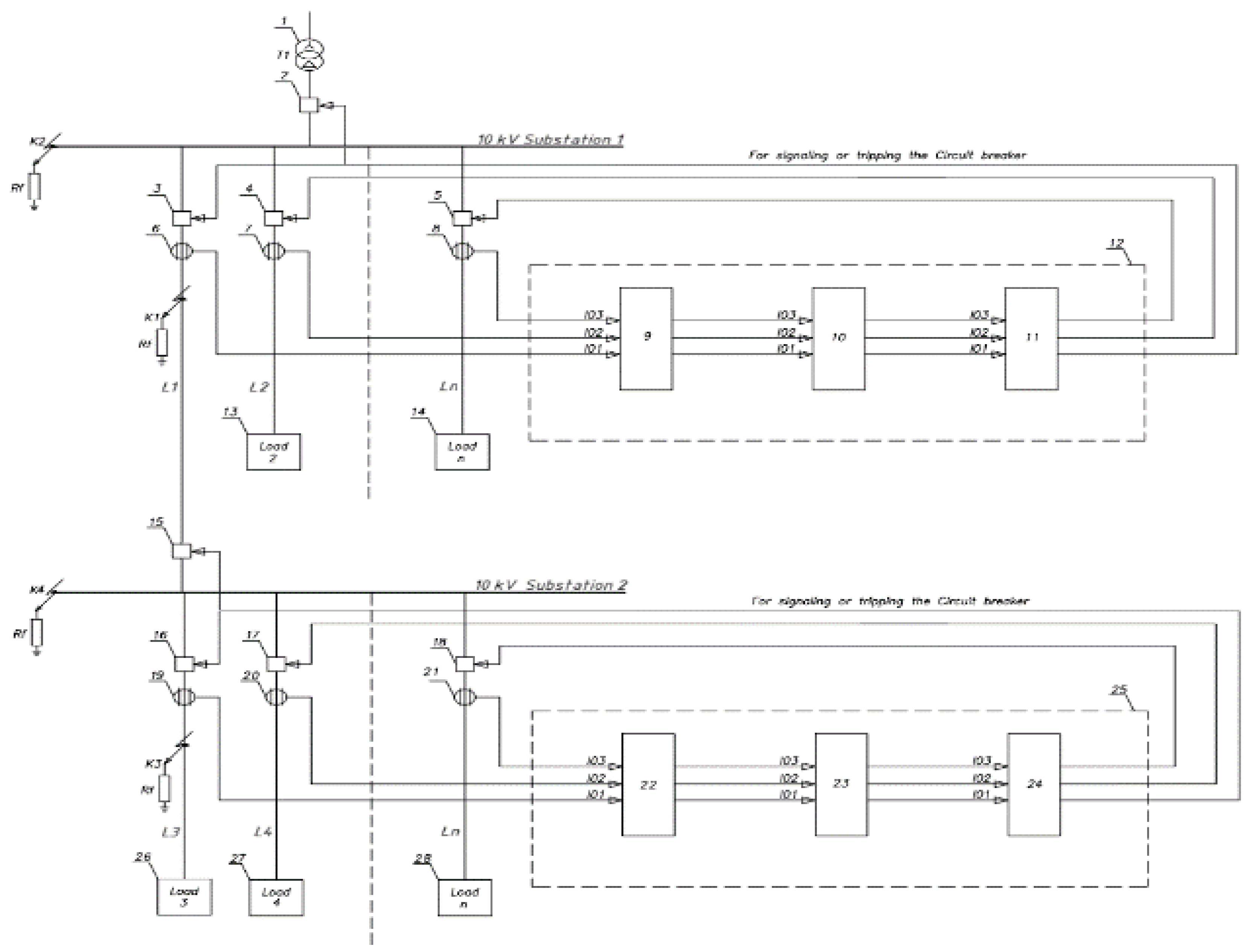
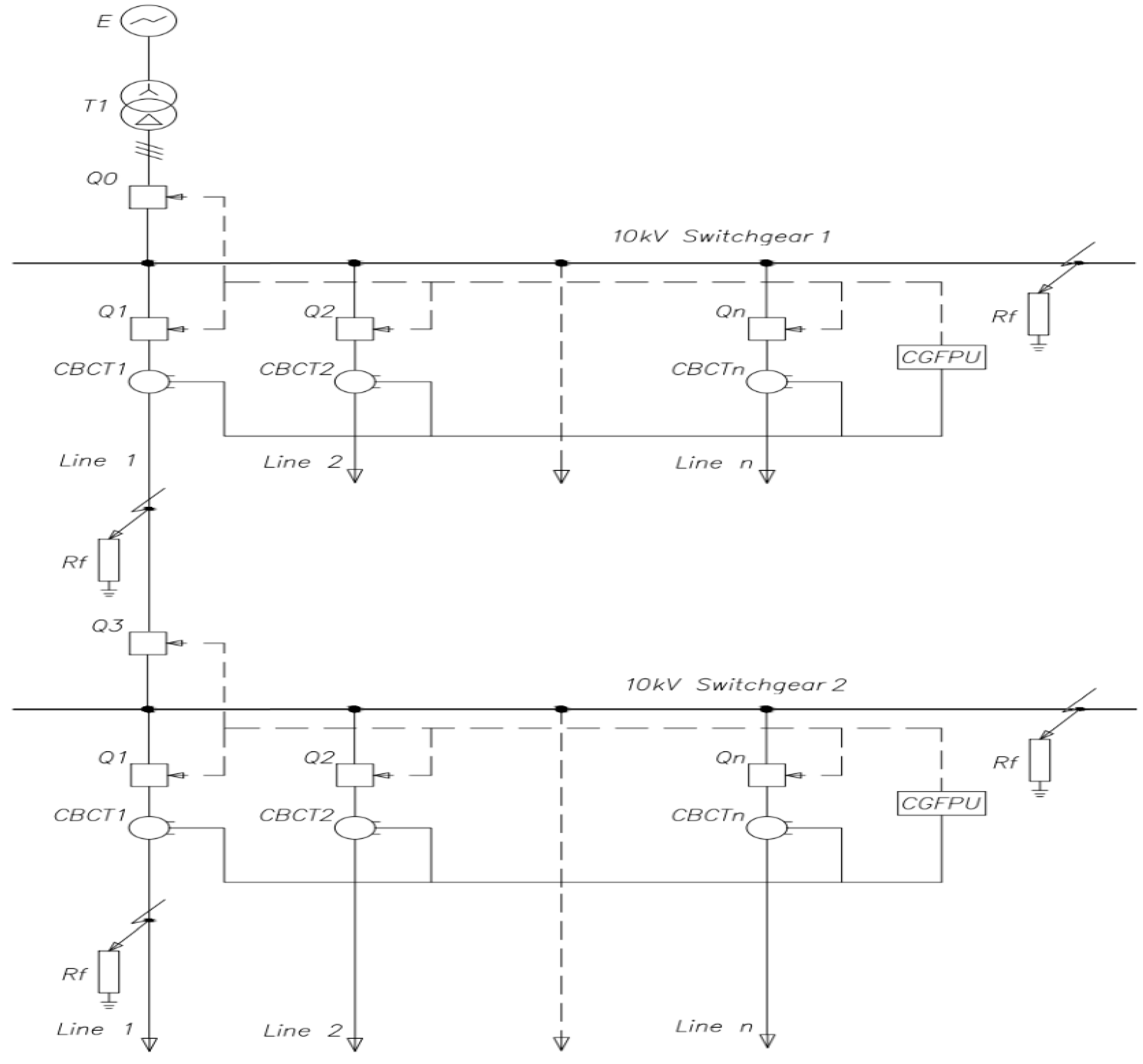
The functional diagram of the centralized ground fault protection unit is presented in
Figure 2.
Figure 2 shows the layout and components of the system: 1 - power transformer; 2 – incomer circuit breaker in the substation No.1; 3, 4, 5 - circuit breakers of outgoing feeders in the substation No.1; 6, 7, 8 - zero-sequence current transformers (ZCTs) of the outgoing feeders substation No.1; 9 - angle comparison module substation No.1; 10 - magnitude comparison module substation No.1; 11 - output module substation No.1; 12 - centralized ground fault protection unit substation No.1; 13, 14 – loads supplied by substation No.1; 15 – incomer circuit breaker substation No.2; 16, 17, 18 - circuit breakers of outgoing feeders substation No.2; 19, 20, 21 - zero-sequence current transformers of the outgoing feeders substation No.2; 22 - angle comparison module substation No.2; 23 - magnitude comparison module substation No.2; 24 - output module substation No.2; 25 - centralized ground fault protection unit substation No.2; 26, 27, 28 – loads supplied by substation No.2.
Zero-sequence currents are measured separately for each feeder. These currents are processed through angle comparison and magnitude comparison modules (blocks 9, 10, 22, and 23). The results are sent to an output module (blocks 11 and 24), which generates the final decision — either issuing a trip or an alarm signal.
The functioning of the CGFPU is organized according to the developed algorithm shown in
Figure 2, and operates as follows: Normal operation mode In the normal (fault-free) mode of network operation, imbalance currents or charging (capacitive) currents may arise. If the measured zero-sequence current (I
0) from the zero-sequence current (ZSC) transformers 6, 7, 8 (substation No.1) or 19, 20, 21 (substation No.2) exceeds the alarm or trip setting, the signals I
0 are transmitted to the angle comparison module 9 (substation No.1) or 22 (substation No.2).
In this situation:
- -
The phasors of the zero-sequence currents across all outgoing feeders are aligned in the same direction and have low magnitudes;
- -
No significant angle deviations or overcurrent conditions are detected;
- -
As a result, the output module 11 (substation No.1) or 24 (substation No.2) does not issue an alarm or trip command.
Thus, the CGFPU excludes false trips caused by network imbalance currents or line charging currents during normal operation.
Single-phase ground fault with transient resistance. In the event of an SPGF with transient resistance: A zero-sequence current appears on the faulty line; Together with capacitive currents from the unfaulted lines [
16], the currents are fed into the angle comparison module 9 (substation No.1) or 22 (substation No.2). In the angle comparison module: The measured zero-sequence current phasors from each feeder are compared by angle; An approximately 180° phase shift between the faulty line’s current and the unfaulted lines' capacitive currents is an indicator of the SPGF on that line [
22]. Next, in the magnitude comparison module 10 (substation No.1) or 23 (substation No.2): The magnitudes of the zero-sequence currents are compared; The line with the maximum zero-sequence current is selected. Finally, in the output module 11 (substation No.1) or 24 (substation No.2): The faulty feeder is identified; An alarm signal is generated or; If necessary, a trip command is sent to the corresponding circuit breaker to isolate the faulty feeder.
Thus, if an SPGF occurs, for instance, at the first outgoing line L
1 (at point K
1 in
Figure 2): The zero-sequence current phasor I
L1 of the faulty line will have a direction opposite (180° shift) to the capacitive current phasors I
L2, I
L3,...,I
Ln of the unfaulted lines.
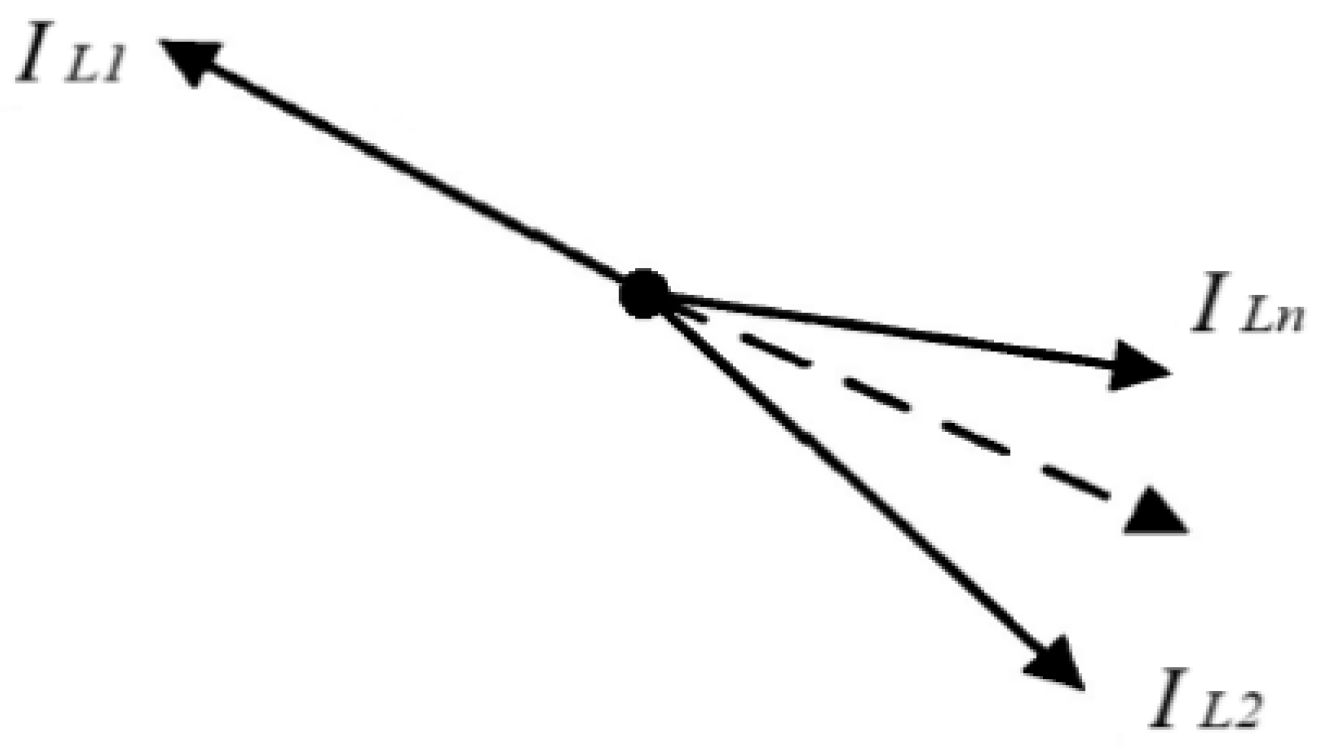
Phasor diagram illustration.
Figure 3 shows the phasor diagram of the capacitive currents of the outgoing lines during an SPGF occurring on the first outgoing feeder. The notations used in the diagram are: I
L2, I
L3,...,I
Ln phasors of the capacitive currents of the first, second, ..., n-th outgoing lines, respectively.
In the event of a single-phase ground fault (SPGF) on an outgoing feeder (e.g., Line L1): The phasor of the faulted line current IL1 is directed opposite (approximately 180° phase shift) to the phasors of the capacitive currents of the unfaulted lines IL2,…,ILn.
The unfaulted feeders’ capacitive current phasors are relatively aligned, forming a characteristic angle grouping. This phase opposition between the faulted line current and the unfaulted lines’ capacitive currents is the primary indicator used by the CGFPU to distinguish a faulty feeder from healthy feeders.
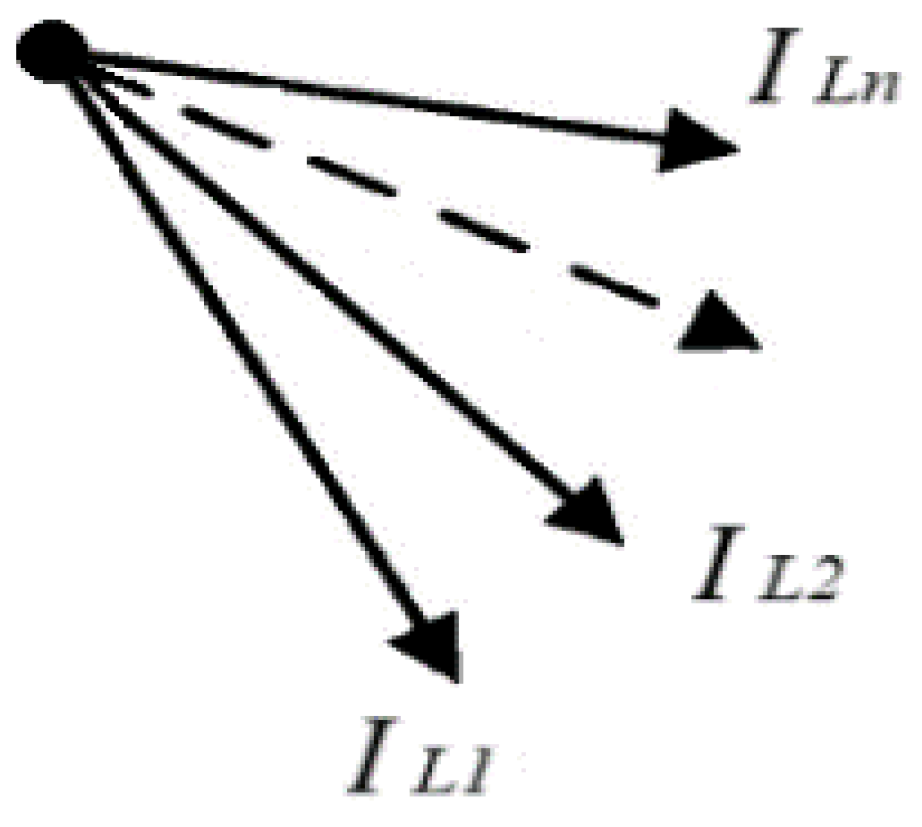
If an SPGF occurs directly on the substation busbars (point K
2) [
24], the scenario differs: The capacitive currents of all outgoing lines correspond only to their own self-capacitance; The directions of all capacitive current phasors will be aligned. No distinct 180° phase shift will be observed between any feeder currents. Thus, the CGFPU detects that no single outgoing line is faulted individually, but instead identifies the busbar fault condition.
Figure 4 illustrates the phasor diagram of capacitive currents during a ground fault occurring at the 10 kV busbars.
In the case of a busbar ground fault: All outgoing feeders' zero-sequence current phasors (IL1, IL2,…,ILn) are directed approximately in the same direction; The phasors represent only the capacitive currents of the feeders relative to ground. No distinct 180° opposition between feeders' phasors is observed. This alignment of all capacitive current phasors enables the CGFPU to recognize that the ground fault is located at the busbars, not at an individual outgoing line.
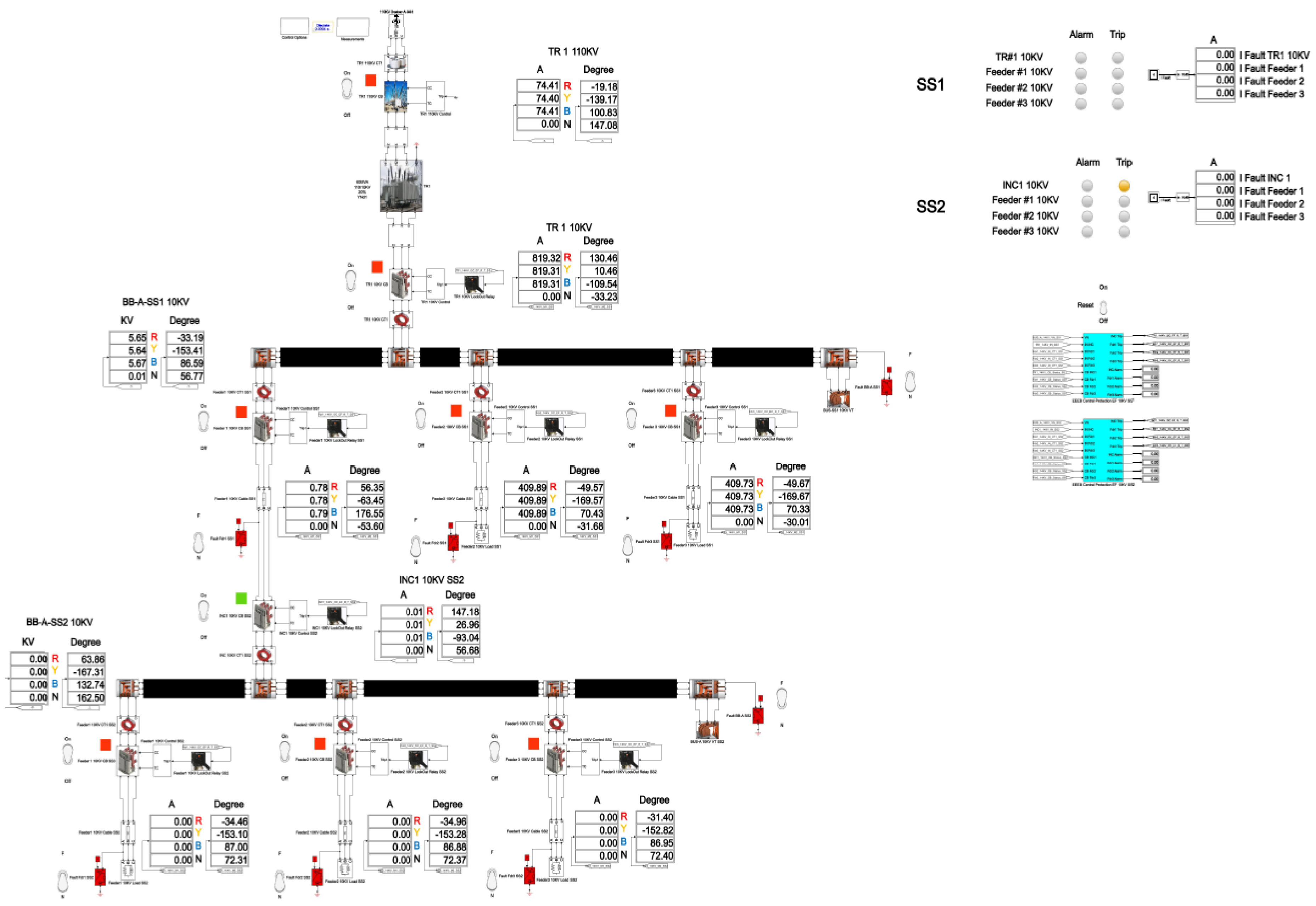
3.3. Description of Centralized Ground Fault Protection Unit
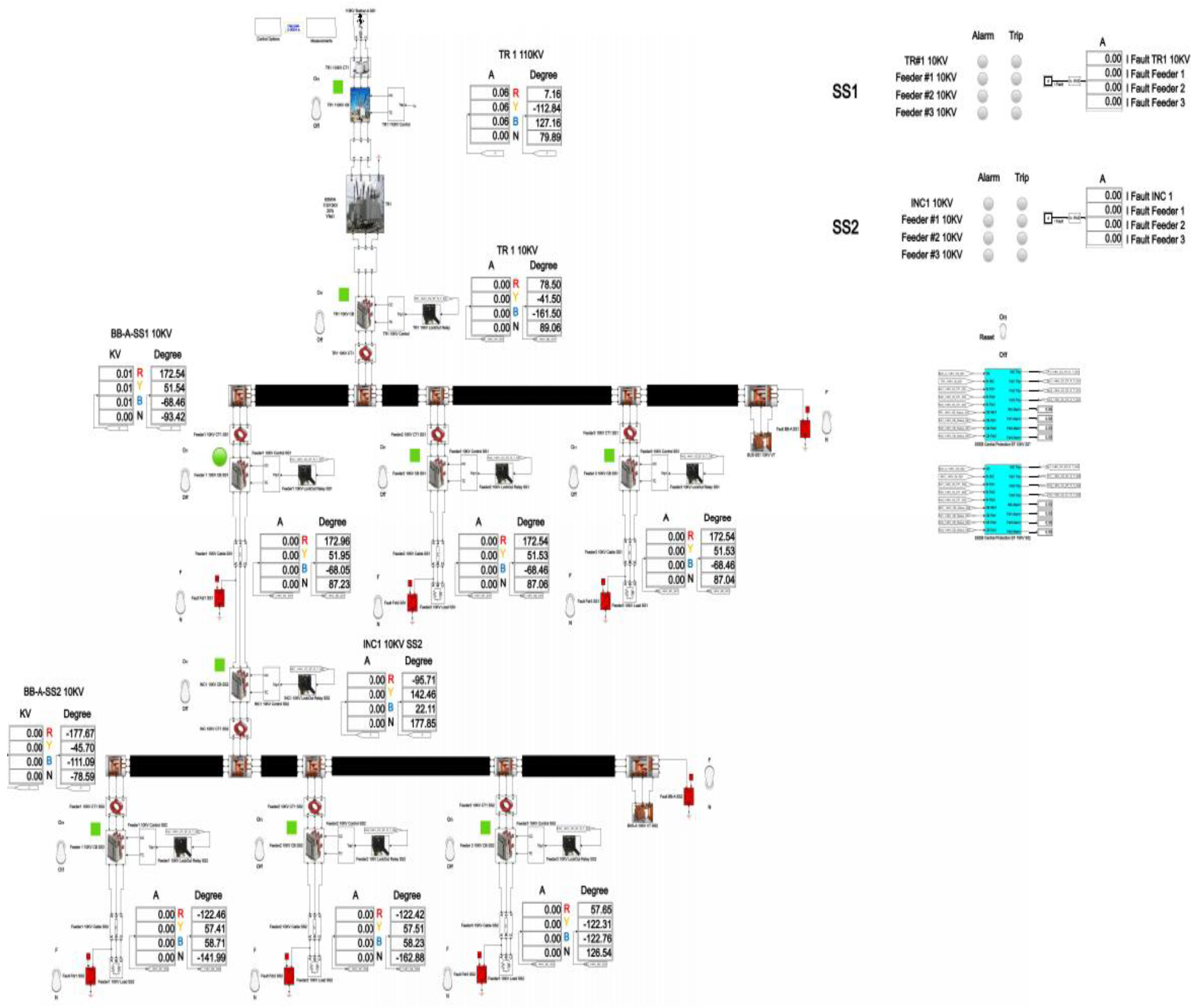
Building upon the functional diagram discussed previously (
Figure 2), a practical protection scheme based on zero-sequence current angle and magnitude comparison is developed and detailed. Zero-sequence current (ZSC) signals are transmitted from the zero-sequence current transformers: At substation No.1: from the incomer (TR1 10kV CT1) and feeders No.1, 2, and 3 (feeder 1 10kV CT1 SS1, feeder 2 10kV CT1 SS1, feeder 3 10kV CT1 SS1). At substation No.2: from the incomer (INC 10kV CT1 SS2) and feeders No.1, 2, and 3 (feeder 1 10kV CT1 SS2, feeder 2 10kV CT1 SS2, feeder 3 10kV CT1 SS2). These signals are sent to the respective centralized ground fault protection unit: Centralized ground fault protection 10kV SS1 (for substation No.1); Centralized ground fault protection 10kV SS2 (for substation No.2); The practical wiring scheme of these connections is illustrated in
Figure 5. Additionally, the block diagram representing the internal logical structure of the CGFPU operating in a 10 kV network [
23,
24,
25,
26,
27] with isolated neutral configuration for substations No.1 and No.2 is shown in
Figure 6.
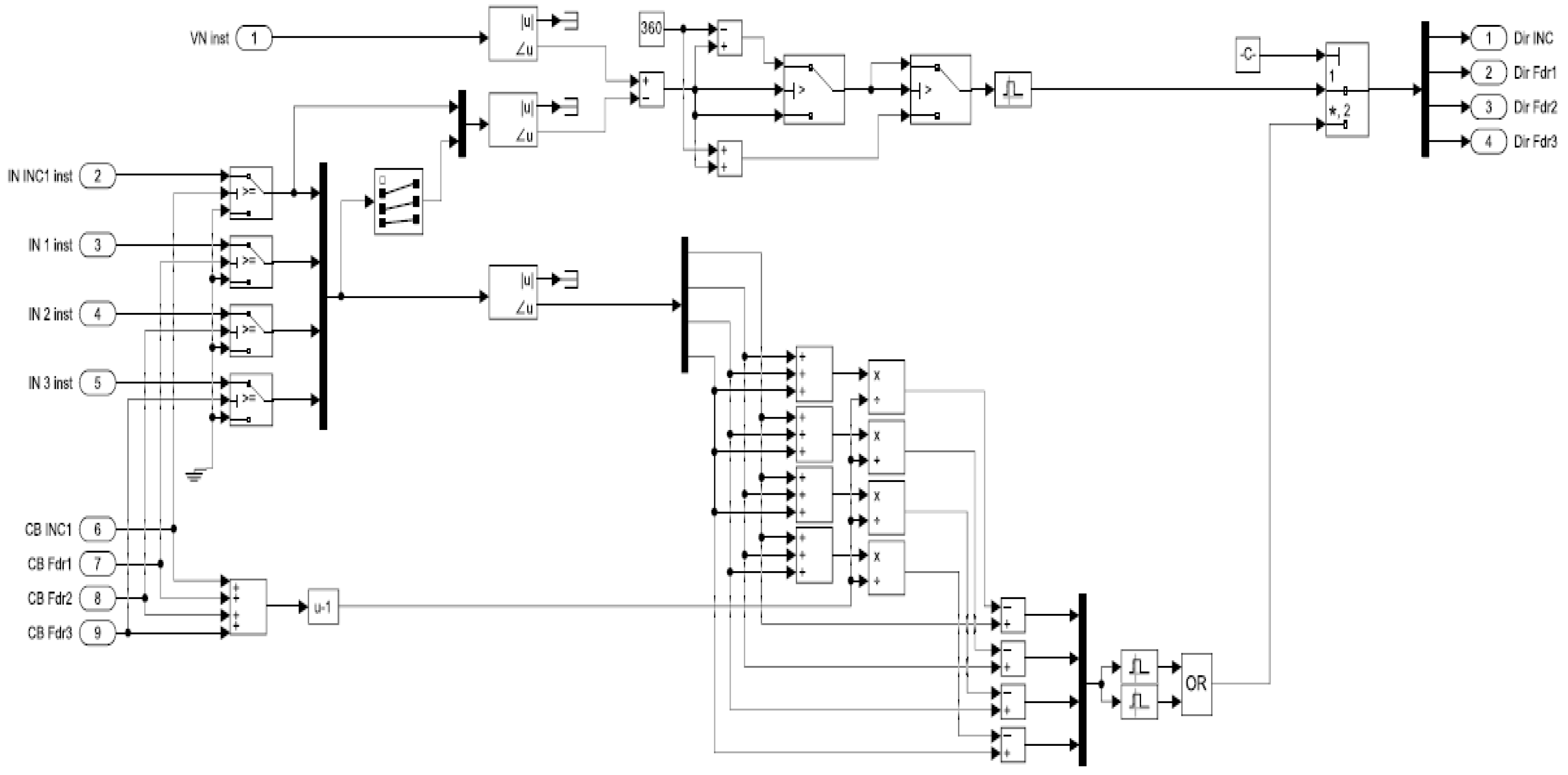
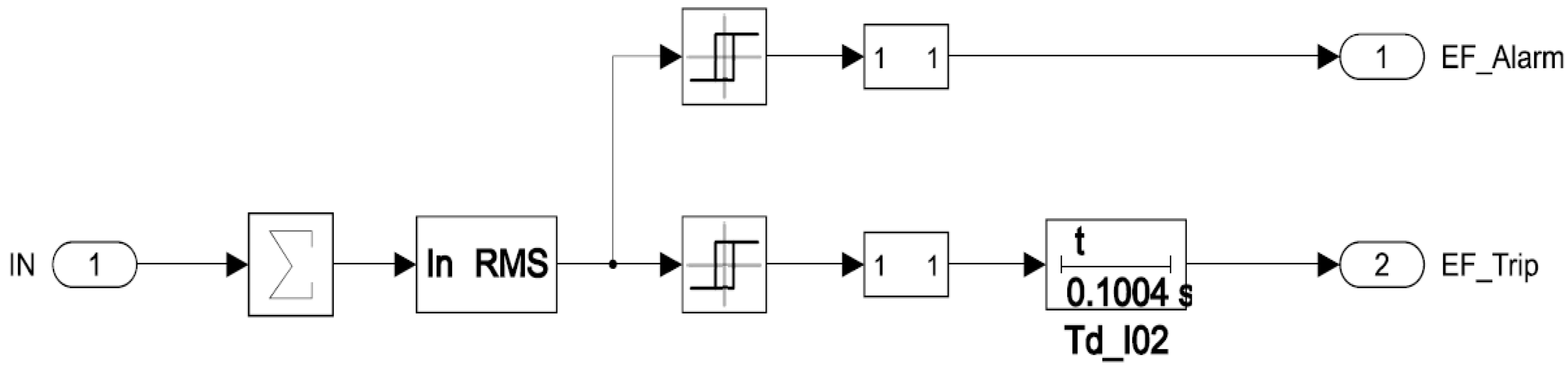
If the circuit breakers are in the service position, the auxiliary contacts are closed, then ZSC signals from the zero sequence current transformers (ZSCT) of the feeders participate in the circuit operation via the switch
. If any of the circuit breakers is tripped by protection or taken out for service, then the corresponding feeder will be removed from the protection scheme and at the switch output
there will be a logical zero.
In case of SPGF, the ZSC signals enter the polarization module (
Figure 7), pass through the switches
and are sent to the magnitude-angle to complex

, from there to the angle summation block

. Depending on the number of circuit breakers in the service position and put into operation

, the number of circuit breakers already switched on is subtracted

from the number of the unfaulted feeders.
In the summation block, division by the number of circuit breakers switched on occurs.

and the average angle value of the unfaulted feeders is obtained and in the comparison block, the ZSC signal of the faulty feeder is compared with the ZSC signals of the unfaulted feeders

, and the signals are sent to the angle calculation block

. If the angle is ±20% of +180
0, then at the output of OR operator

there is a logical one 1 and the signal will then go to the multiport switch

. From there the signal will go to the magnitude comparison module.
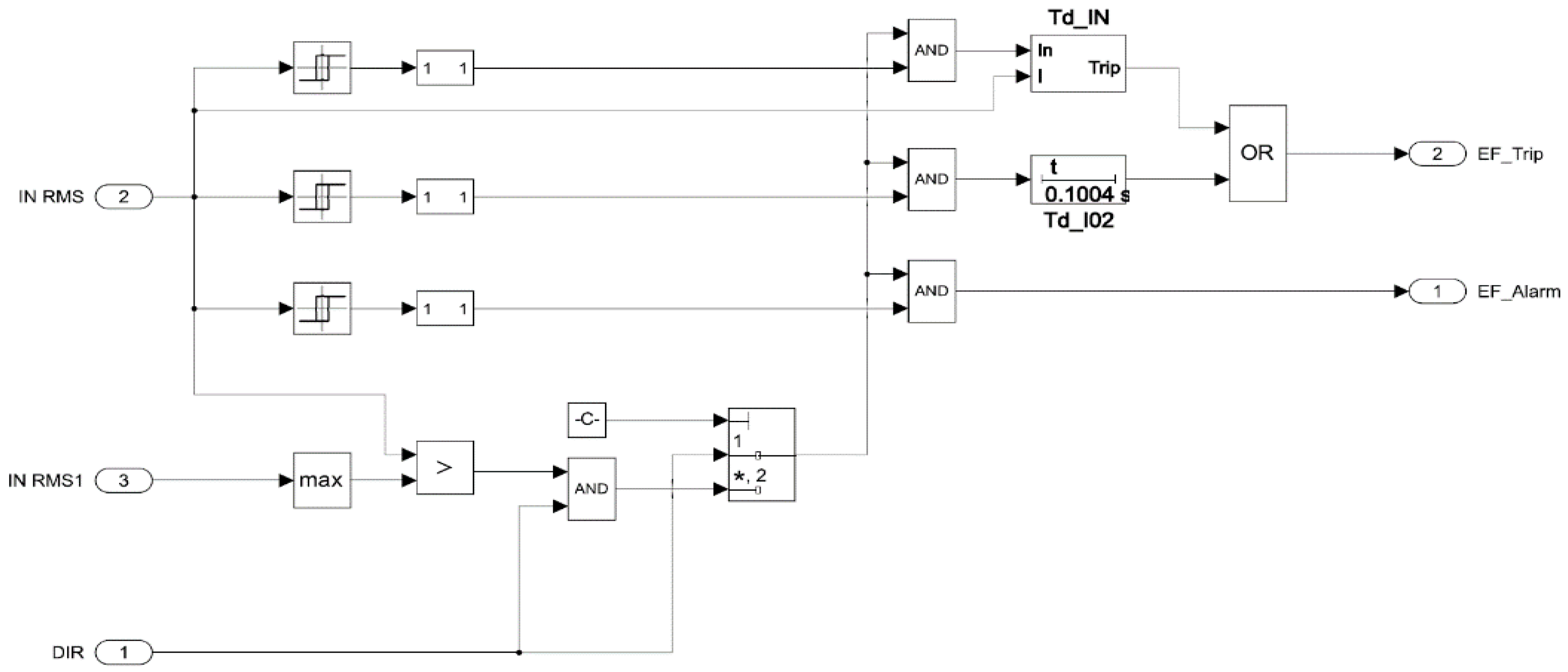
In the Magnitude comparison module, the ZSC signal with the maximum value (
Figure 8)

via the operator

will be sent to AND operator

. If the ZSC signal magnitude of the faulty feeder is higher than the specified setting and the angle is 180
0, then at the output of AND operator

there will be a logical one 1 and through the multiport switch

the ZSC signal will be directed to another operator AND

. If the alarm setting is exceeded

, then an SPGF signal will appear

. If the trip setting is exceeded

, then the operate delay time of the feeder No.1, in substation No.1, will be 300 ms, and for the remaining feeders, substations No.1 and No.2, it will be 100 ms
and a trip signal of the corresponding feeder will turn up

.
3.4. Algorithm of CGFPU Operation During Bus Ground Faults
In case of SPGF on buses, considering the direction and magnitude of the capacitive currents (
Figure 9), the zero-sequence current will have a maximum value and taking into account the summation of capacitive currents

and obtaining the rms value

, the ZSC signal will be directed to the magnitude comparison module. If the alarm setting is exceeded

, then an SPGF signal will appear

. If the trip protection setting is exceeded

, then after 100 ms
, a trip signal to open the incomer circuit breaker

will appear.
4. Results
We will calculate SPGF for different transient resistances, analyze and evaluate the obtained values and calculate the CGFPU settings at R
f= 5000 Ohm and R
f= 1 Ohm at the feeder No.1, substation No.1 bus and at the feeder No.1, substation No.2 bus. The SPGF calculation and analysis of ground fault protection was performed on sections of the 10 kV distribution network [
26] at the substations No.1 and 2, the single line diagram is shown in the
Figure 10. Power supply: short-circuit power S
sc = 40 MVA, voltage: U = 110 kV, ratio of reactive resistance to active resistance: X/R = 7.
High voltage side neutral mode: network with the solidly grounded neutral configuration.
Power transformer: transformer type: TM-60000/110/10, apparent power S = 60 MVA, voltage on the primary winding: U1 = 110 kV, voltage on the secondary winding: U2 = 10 kV.
Medium voltage neutral mode: isolated neutral configuration.
Substation No.1
Feeder 1: cable cross-section, S = 240 mm2, voltage: U1 = 6/10 kV, length l = 1 km.
Feeder 2: cable cross-section, S = 240 mm2, voltage: U1 = 6/10 kV, length l = 1.2 km.
Feeder 3: cable cross-section, S = 240 mm2, voltage: U1 = 6/10 kV, length l = 1.1 km.
Load 1, 2, 3: power consumption P = 7 MW, reactive power: Q = 2 MVAr, nominal voltage: U = 10 kV.
Substation No.2
Feeder 1: cable cross-section, S = 240 mm2, voltage: U1 = 6/10 kV, length l = 1.6 km.
Feeder 2: cable cross-section, S = 240 mm2, voltage: U1 = 6/10 kV, length l = 0.9 km.
Feeder 3: cable cross-section, S = 240 mm2, voltage: U1 = 6/10 kV, length l = 0.9 km.
Load 1, 2, 3: power consumption P = 7 MW, reactive power: Q = 2 MVAr, nominal voltage: U = 10 kV.
To analyze characteristics of changes in the SPGF currents and capacitive currents for different values of the transient resistances, it is required to evaluate the magnitude of the ground fault current flowing in the fault location, the zero-sequence voltage and the coefficient of ground fault incompleteness, which are determined by the following expressions:
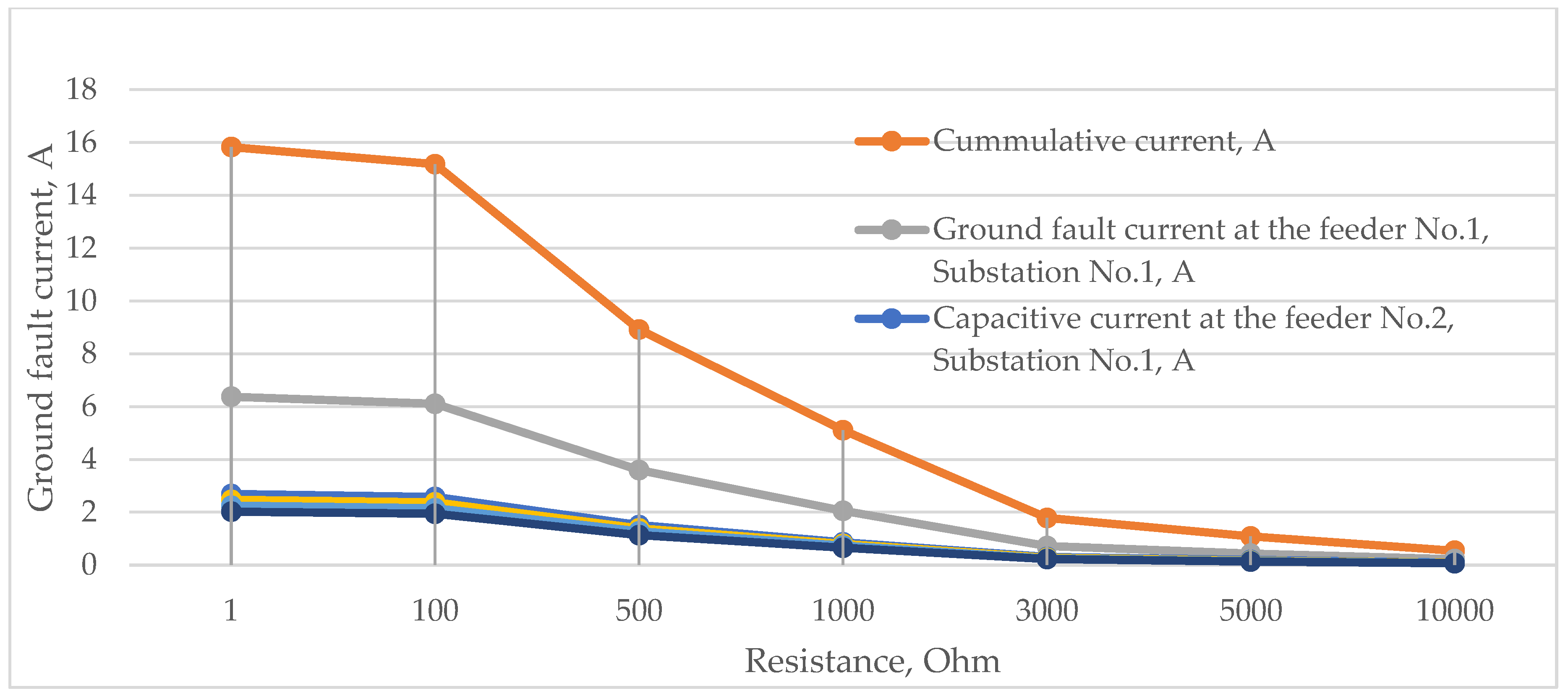
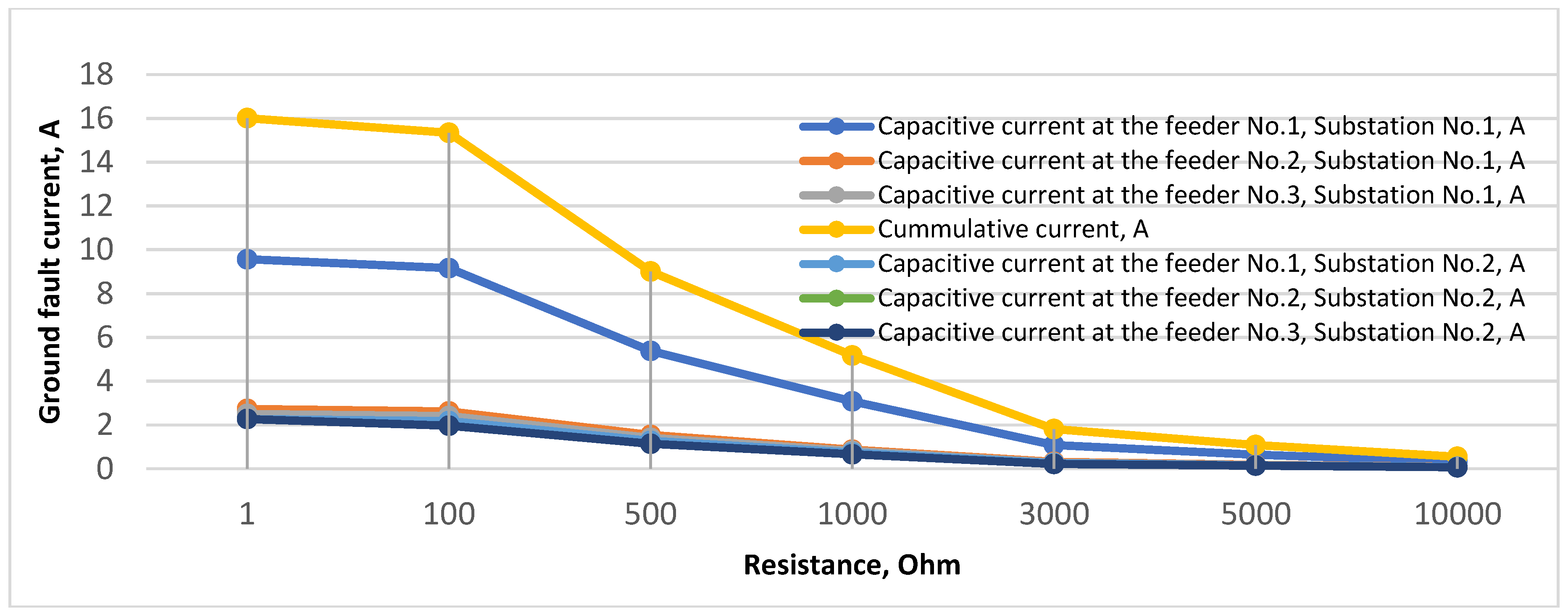
Table 1 shows the SPGF values with the different transient resistances at the feeder No.1, substation No.1.
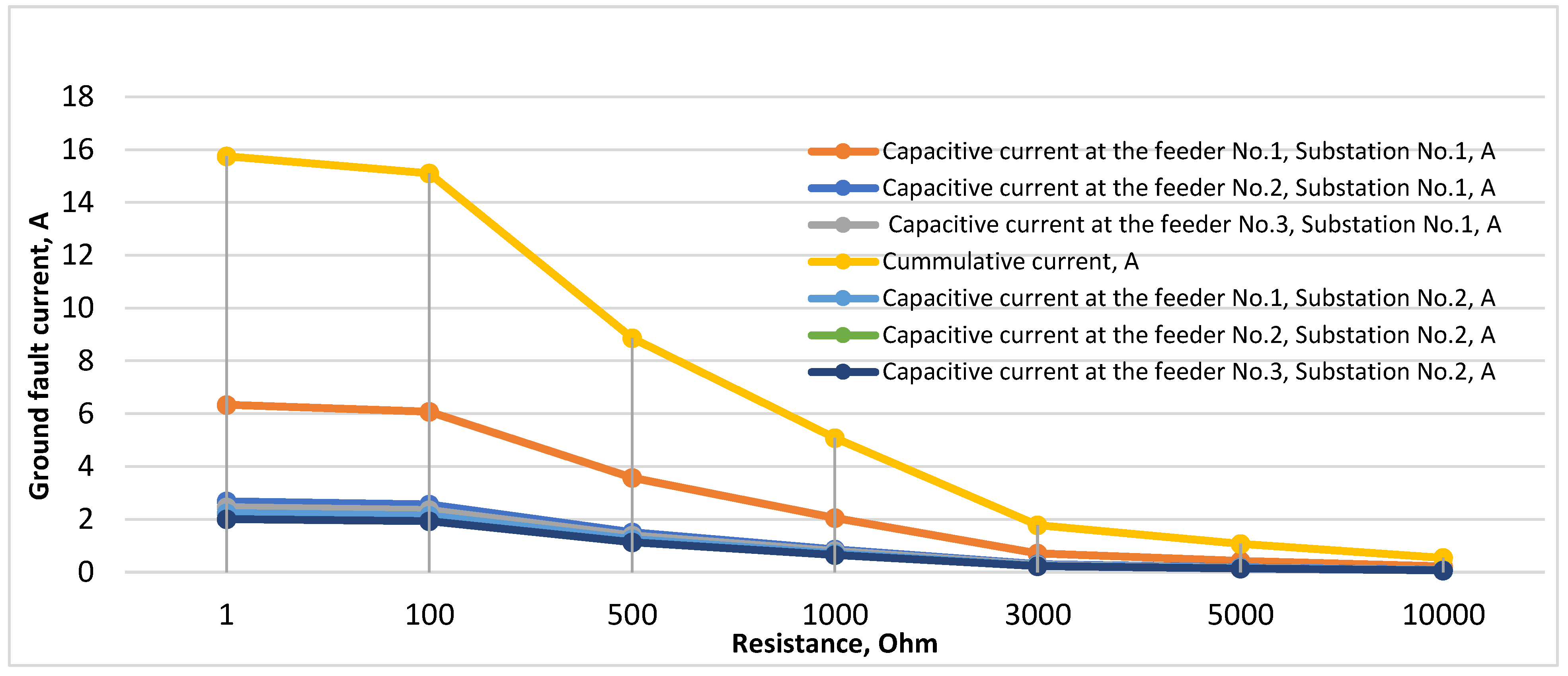
Figure 11 shows the change in the SPGF current and capacitive currents with the different transient resistances in the range of 1 Ohm to 10,000 Ohm at the feeder No.1, substation No.1. The total fault current, the current at the fault location, and the capacitive currents change sharply and nonlinearly with an increase in the transient resistance.
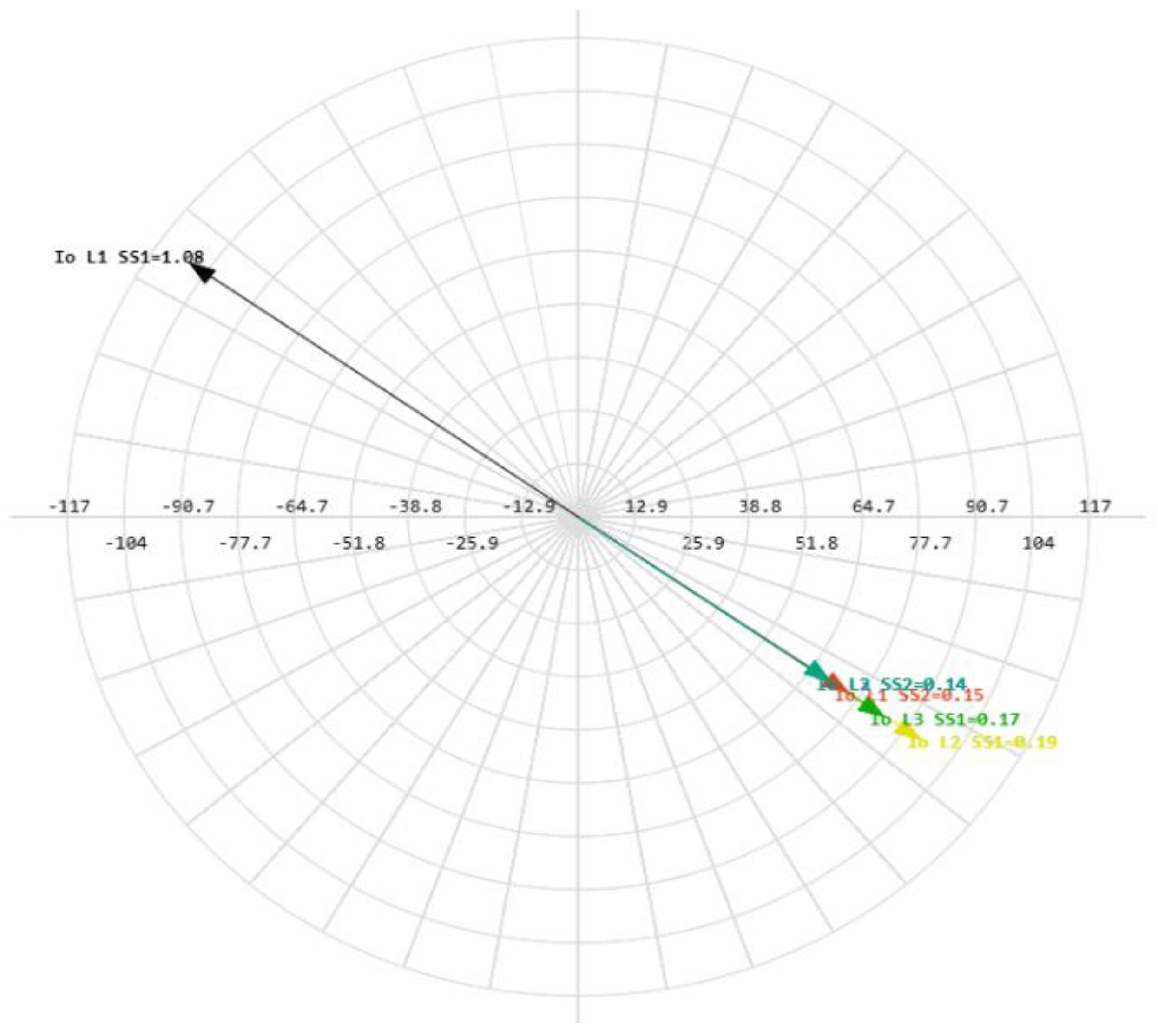
Figure 12 shows that the difference in angles between the fault current of the faulty feeder and the capacitive currents of the unfaulted feeders remains close to∠180°. In the case of a bolted SPGF at the feeder No.1, substation No.1, the SPGF current has a maximum value and is about ten amperes [
29], while in case of SPGF with the largest transient resistance, the SPGF current reaches tenths of an ampere.
Table 2 shows the SPGF values with the different transient resistances on substation No.1 buses.
Figure 13 shows a graph of SPGF and capacitive currents with the different transient resistances in the range of 1 Ohm to 10,000 Ohm on substation No.1 bus. The SPGF values, as well as capacitive currents, are nonlinear in nature and change depending on the transient resistance.
In case of SPGF, capacitive currents are proportional to their own capacitances, their direction is equal to each other, i.e., there is just slight angle shift (
Figure 14). In case of a bolted SPGF on the bus, the SPGF current is about tens of amperes, and in case of SPGF with the highest transient resistance, the SPGF current reaches tenths of an ampere.
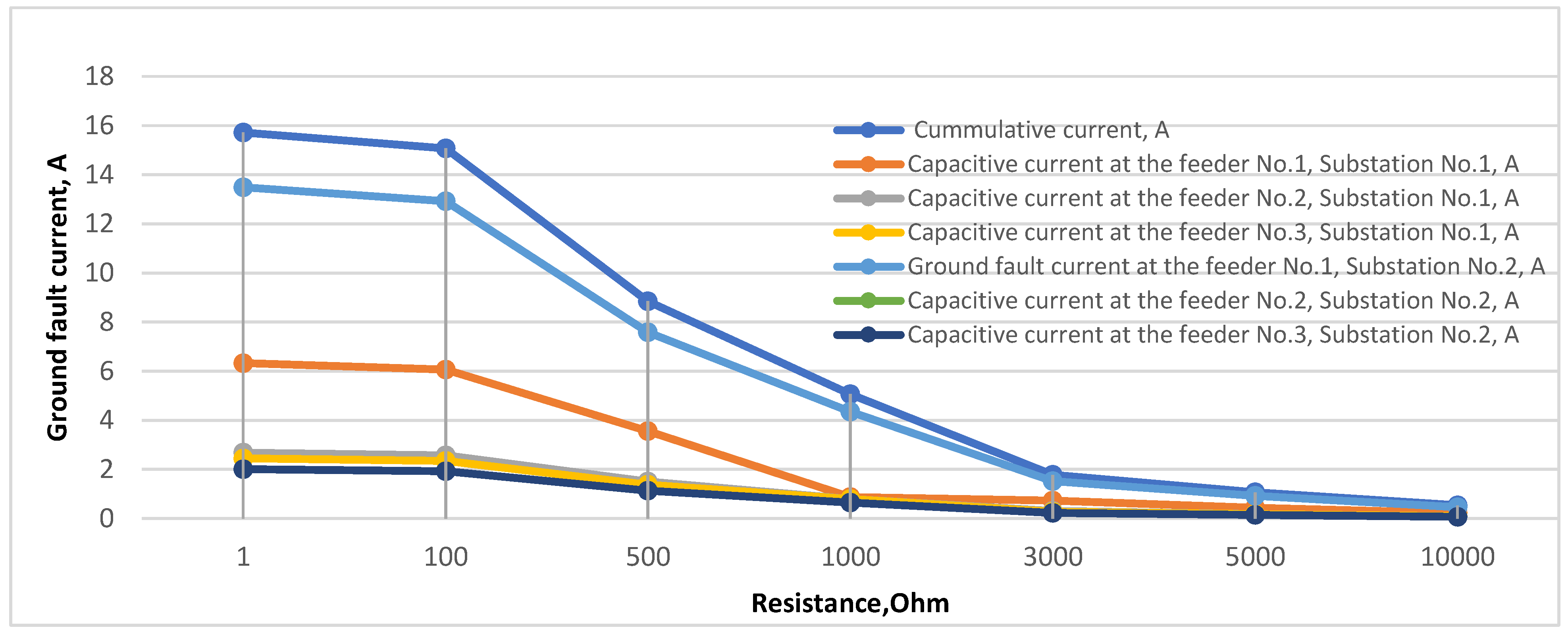
Table 3 shows the SPGF values with the different transient resistances at the feeder No.1, substation No.2.
Figure 15 shows the change in SPGF and capacitive currents with the different transient resistances from 1 Ohm to 10,000 Ohm at the feeder No.1, substation No.2. The faulty feeder No.1, substation No.2 has the highest SPGF current, the ZSCT installed at this faulty feeder, minus its own capacitive current, detects the total SPGF current. The total SPGF current, the current at the fault location, and the capacitive currents decrease with an increase in the transient resistance.
Figure 16 shows that the ZS current at the faulty feeder No.1, substation No.2 has a maximum value and has the same angle as the unfaulted feeder No.1, substation No.1, and is opposite to the capacitive currents of the unfaulted feeders and the difference in angles is close to∠180°. Due to the fact that the ZS current at the feeder No.1, substation No.2 has a greater value than the unfaulted feeder No.1, substation No1 and also at the feeder No.1, substation No.1 there is a time delay of 300 ms, therefore the protection at the substation No.2 will operate faster and issue an alarm signal at the feeder in case of SPGF with the high transient resistance or will issue a trip signal to open the CB in case of a bolted SPGF. In the case of the bolted SPGF at the feeder No.1, substation No.2, the SPGF current is tens of amperes. In the case of SPGF with the largest transient resistance, the SPGF current is tenths of an ampere.
Table 4 shows the SPGF values with the different transient resistances on the substation No.2 bus.
Figure 17 shows a graph of SPGF current and capacitive currents with the different transient resistances from 1 Ohm to 10,000 Ohm on the substation No.2 bus.
Figure 18 shows that the capacitive currents are equal to their own capacitances, the direction is the same, the angle shift is almost equal∠0°. However, from the phasor diagram it can be noted that the ZS current at the unfaulted feeder No.1, substation No.1 has the opposite angle as those of capacitive currents of the unfaulted feeders. It happens because the ground fault current flows through the unfaulted feeder No.1, substation No.1 to the ground fault location, which is the substation No.2 bus. The feeder No.1, substation No.1 has a time delay of 300 ms, therefore the protection at the Substation No.2 will operate faster and issue an alarm signal at the bus in case of SPGF with the high transient resistance or will issue a trip signal to open the incomer CB in case of a bolted SPGF.
In case of the bolted SPGF on the substation No.2 bus, the SPGF current is about ten amperes, and in case of SPGF with the highest transient resistance, the SPGF current reaches tenths of an ampere.
Let us calculate the SPGF considering the transient resistance at the feeder No.1, substation No.1 bus and at the feeder No.1, substation No.2 bus and calculate the ground overcurrent settings, analyze the protection operation and examine the disturbance records.
The minimum current in the secondary circuit that the ground overcurrent protection can detect depends on the relay sensitivity and the system configuration. Modern microprocessor relays can usually detect secondary currents of 0.01 to 0.05 A. Let us choose a transient resistance at the point of ground fault protection as shown in
Appendix A, Rf = 5000 Ohm. Let us calculate the ground overcurrent settings.
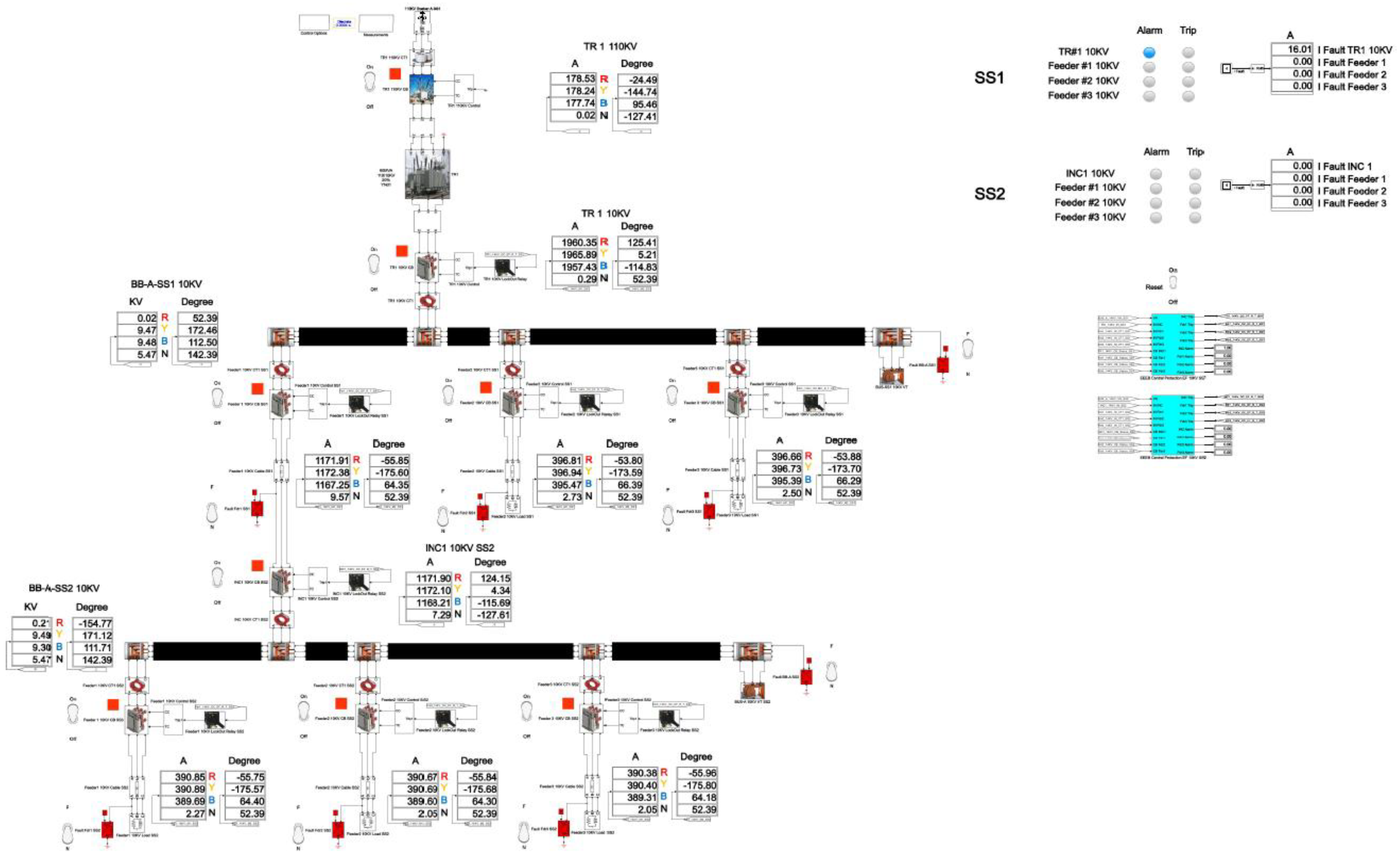
4.1. Modeling of SPGF with the Transient Resistance Rf = 5000 Ohm at the Feeder No.1, Substation No.1 in the 10 kV Network with the Isolated Neutral Configuration
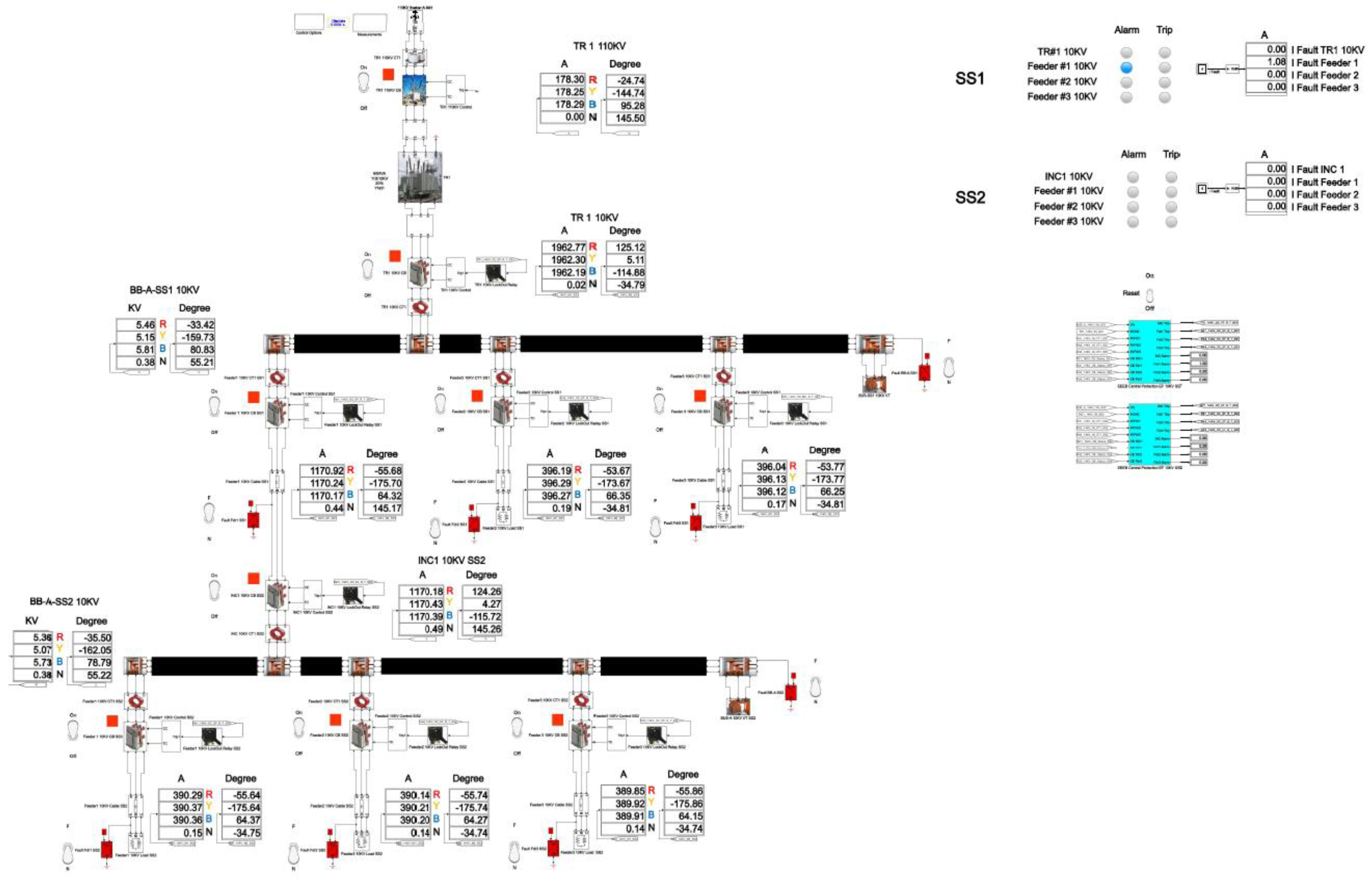
Figure 19 shows the Single line diagram with SPGF with the transient resistance R
f = 5000 Ohm at the feeder No.1, substation No.1 in the 10 kV network with the isolated neutral configuration [
26]. At the incomer, substation No.1, the zero-sequence current is I
ZSCT = 0.02 A, and the zero-sequence current angle is φ = -34.79°. At the feeder No.1, substation No.1, the zero sequence current is I
ZSCT = 0.44 A, and the zero sequence current angle is φ = 145.17°. At the feeder No.2, substation No.1, the zero sequence current is I
ZSCT = 0.19 A, and the zero sequence current angle is φ = -34.81°. At the feeder No.3, substation No.1, the zero-sequence current is I
ZSCT = 0.17 A, and the zero-sequence current angle is φ = -34.81°. At the incomer, substation No.2, the zero sequence current is I
ZSCT = 0.49 A, and the zero sequence current angle is φ = 145.26°. At the feeder No.1, substation No.2, the zero sequence current is I
ZSCT = 0.15 A, and the zero sequence current angle is φ = -34.75°. At the feeder No.2, substation No.2, the zero sequence current is I
ZSCT = 0.14 A, and the zero sequence current angle is φ = -34.74°. At the feeder No.3, substation No.2, the zero sequence current is I
ZSCT = 0.14 A, and the zero sequence current angle is φ = -34.74°.
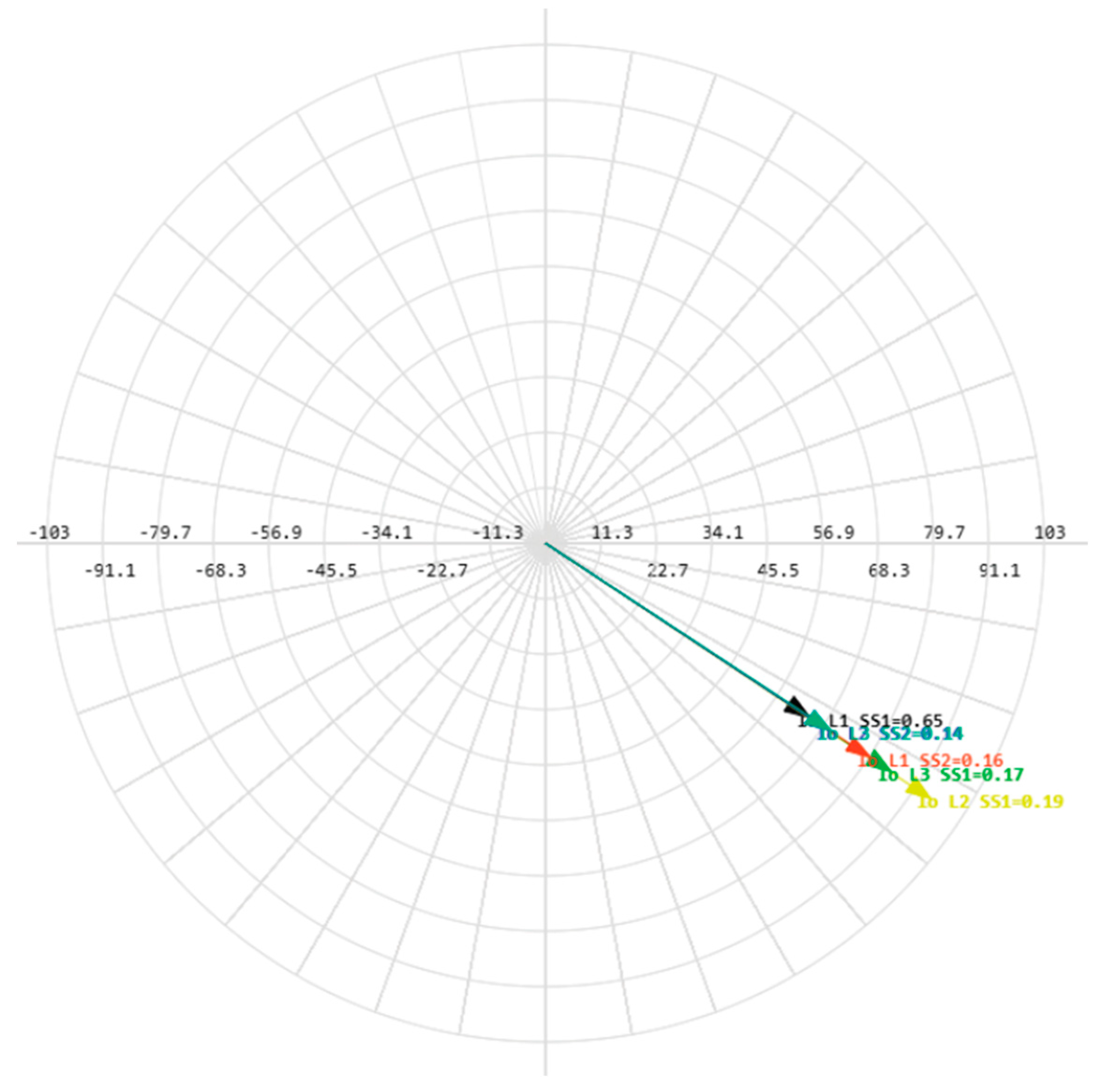
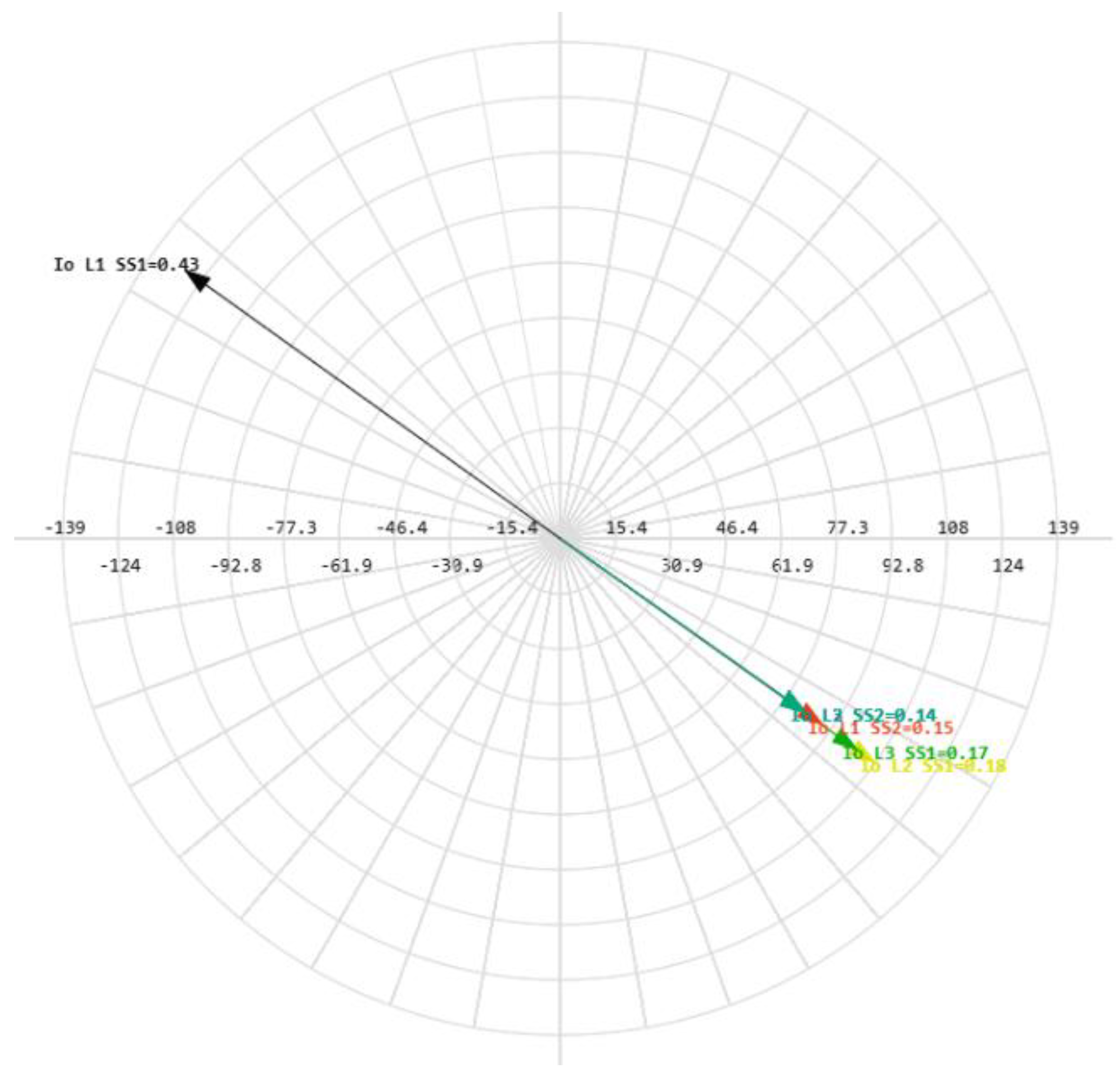
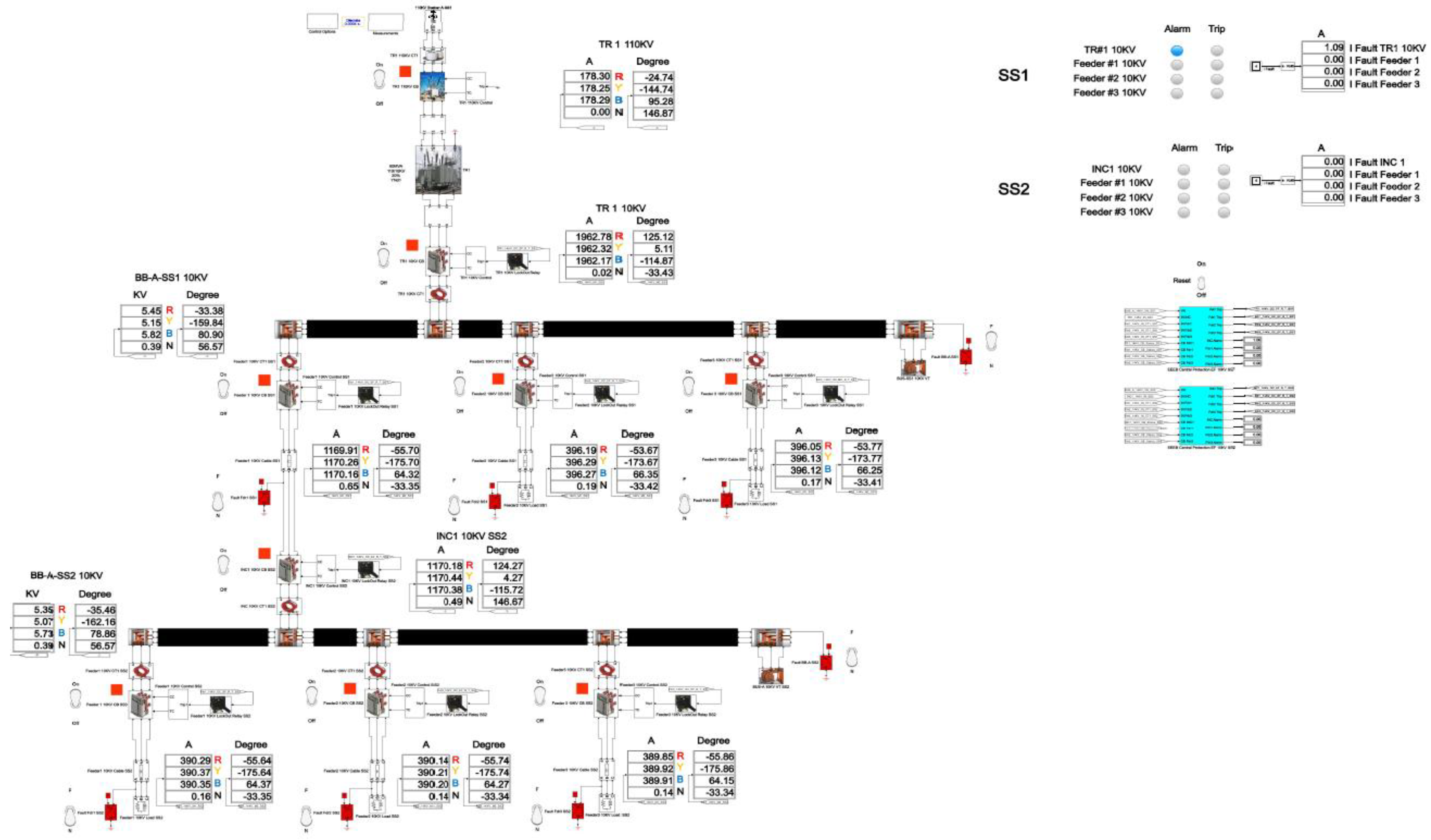
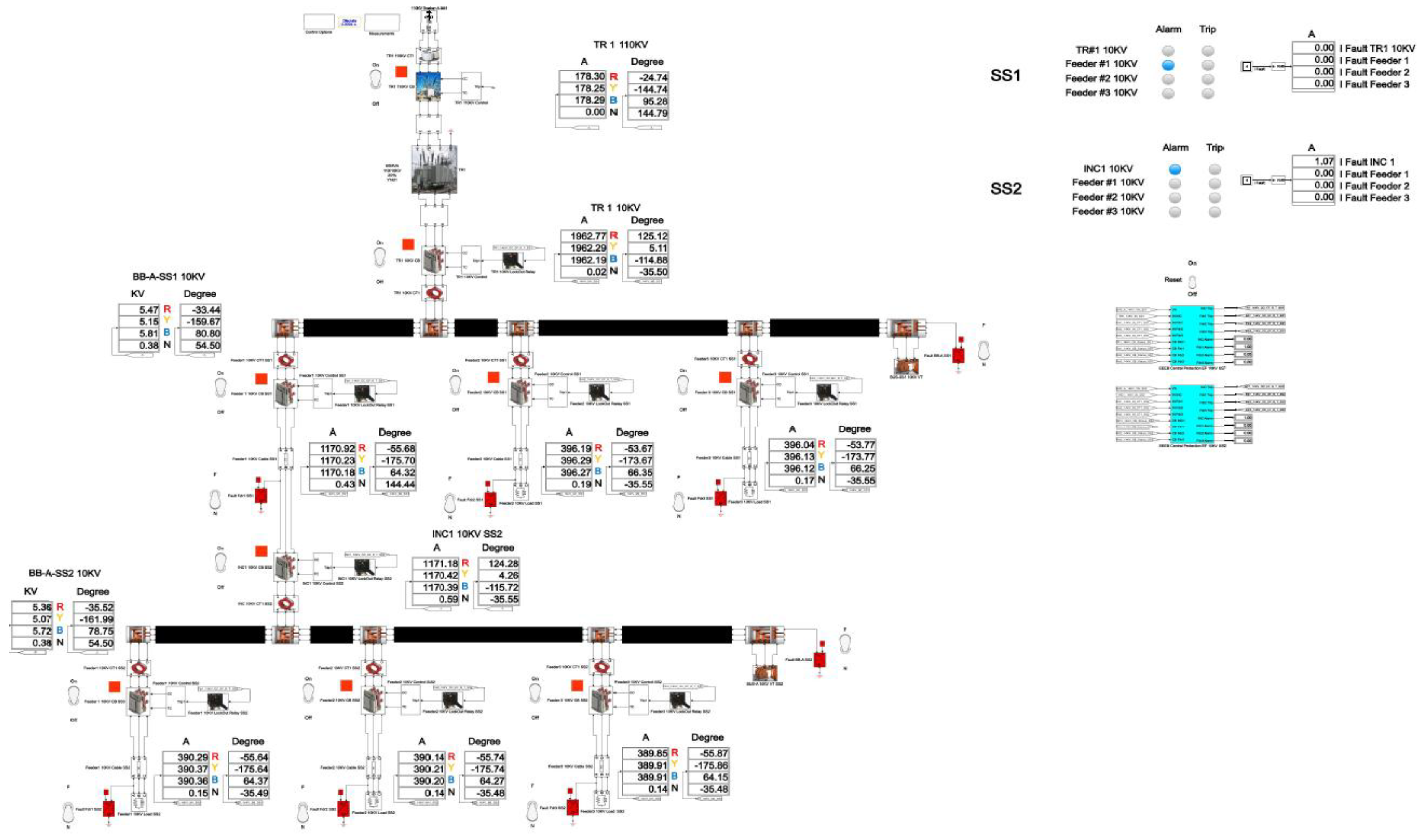
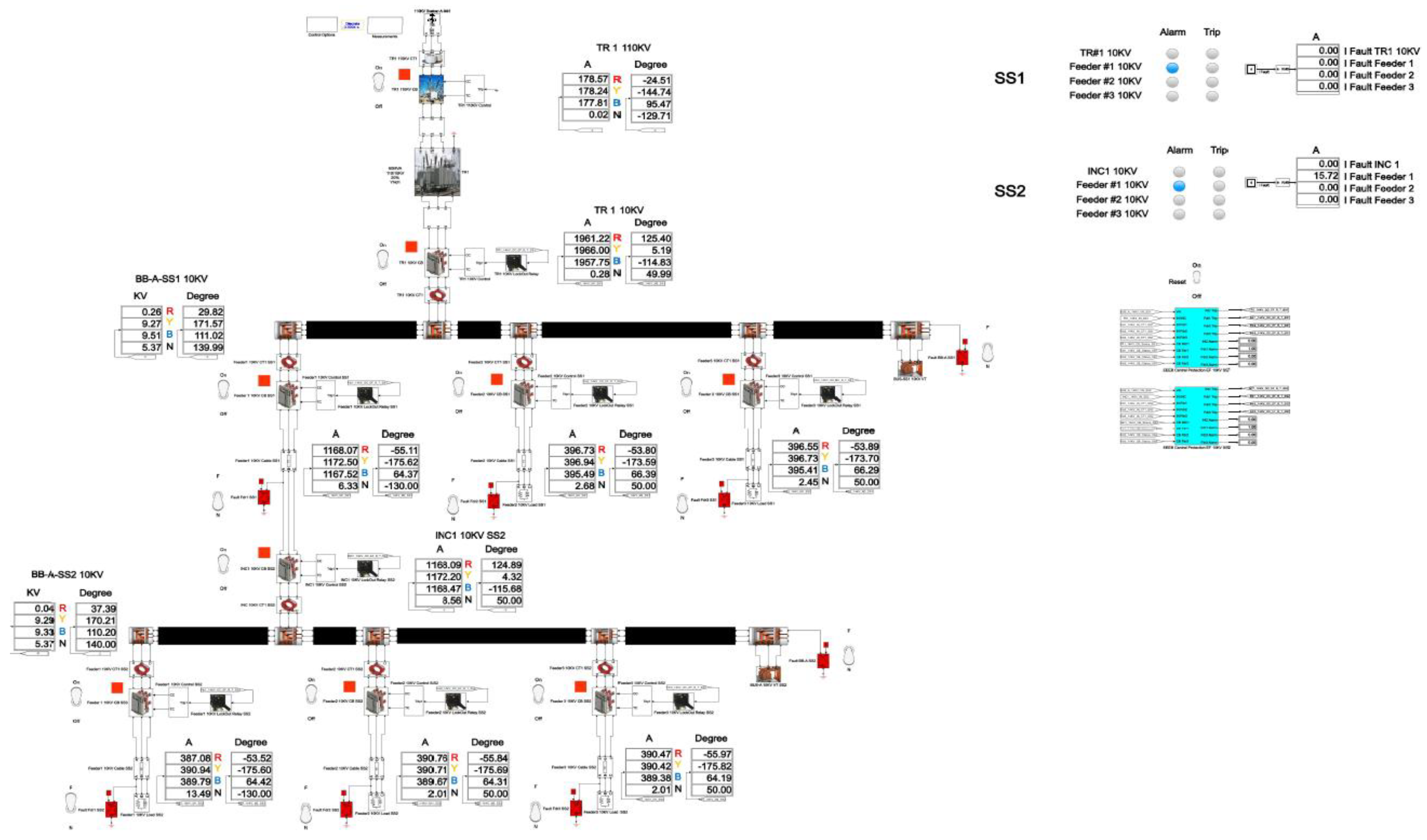
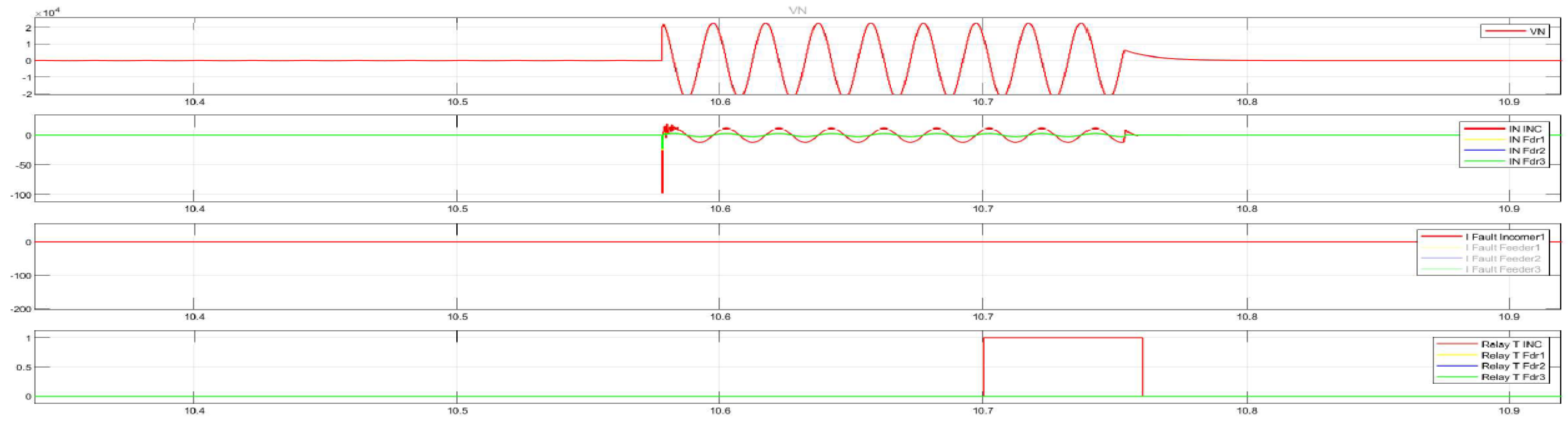
The total cumulative SPGF current on the phase A with the transient resistance Rf= 5000 Ohm is 1.09 A and the angle of the zero-sequence current is φ = 146.17°. The SPGF on the phase A with the transient resistance Rf= 5000 Ohm, has a greater magnitude and a shift of about 180-185° from the phasor of the capacitive currents of the unfaulted feeders No.2 and 3 in the substation No.1 and feeders No.1, 2 and 3 in the substation No.2. Due to the fact that the SPGF current exceeds the ground overcurrent setting, an alarm signal at the feeder No.1, substation No.1 is issued (
Figure 19).
4.2. Modeling of SPGF with the Transient Resistance of Rf = 5000 Ohm on the Substation No.1 Bus in the 10 kV Network with the Isolated Neutral Configuration
Figure 21 shows the single line diagram with SPGF with the transient resistance of Rf= 5000 Ohm on the substation No.1 bus in the 10 kV network with the isolated neutral configuration [
1,
2,
3]. At the incomer, substation No.1, the zero-sequence current is I
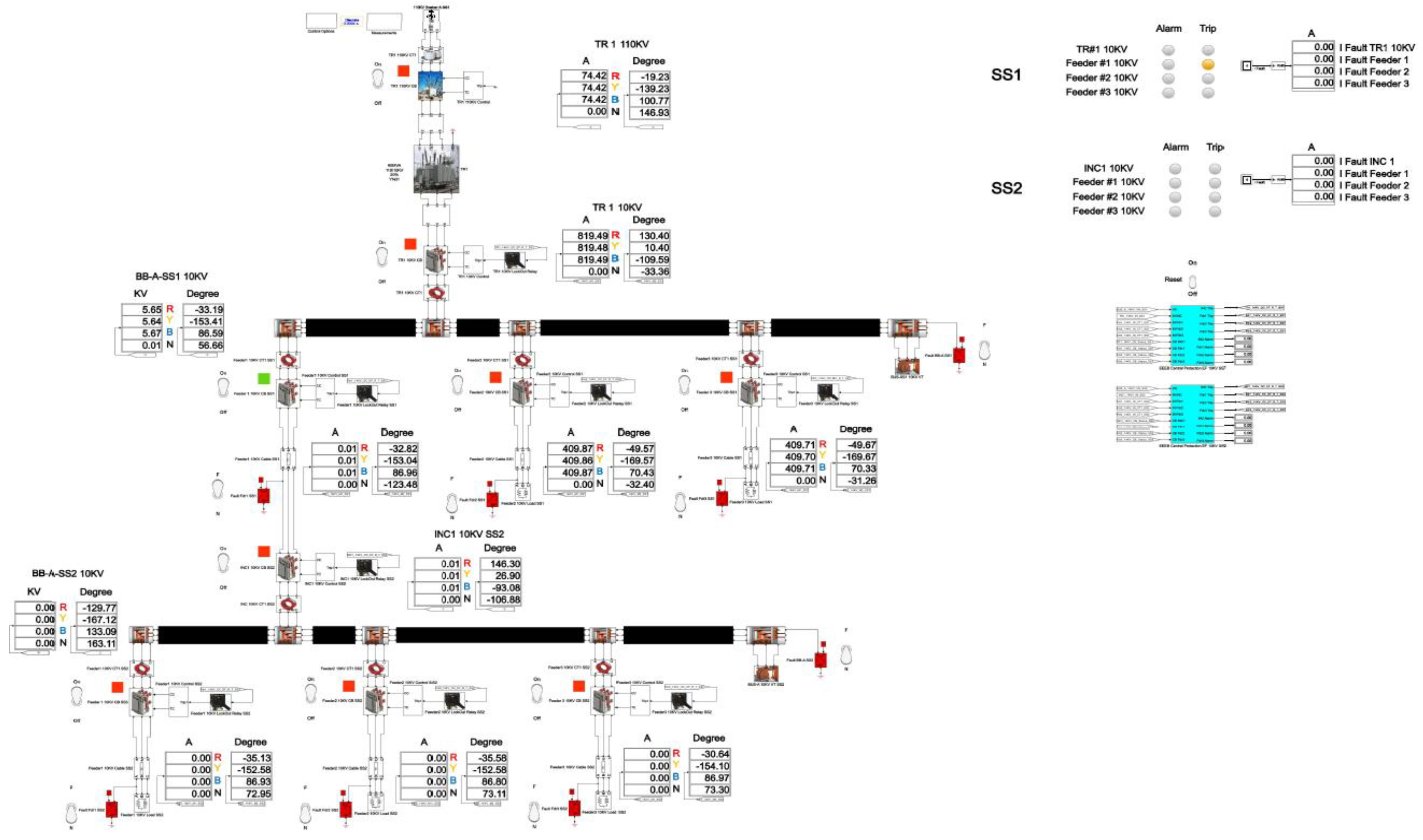
ZSCT = 0.02 A, and the zero-sequence current angle is φ = -33.43°. At the feeder No.1 , substation No.1, the zero sequence current is I
ZSCT = 0.65 A, and the zero sequence current angle is φ = -33.35°. At the feeder No.2, substation No.1, the zero sequence current is I
ZSCT = 0.19 A, and the zero sequence current angle is φ = -33.42°. At the feeder No.3, substation No.1, the zero-sequence current is I
ZSCT = 0.17 A, and the zero-sequence current angle is φ = -33.41°. At the incomer, substation No.2, the zero sequence current is I
ZSCT = 0.49 A, and the zero sequence current angle is φ = 146.67°. At the feeder No.1, substation No.2, the zero sequence current is I
ZSCT = 0.16 A, and the zero sequence current angle is φ = -33.35°. At the feeder No.2, substation No.2, the zero sequence current is I
ZSCT = 0.14 A, and the zero sequence current angle is φ = -33.34°. At the feeder No.3, substation No.2, the zero sequence current is I
ZSCT = 0.14 A, and the zero sequence current angle is φ = -33.34°.
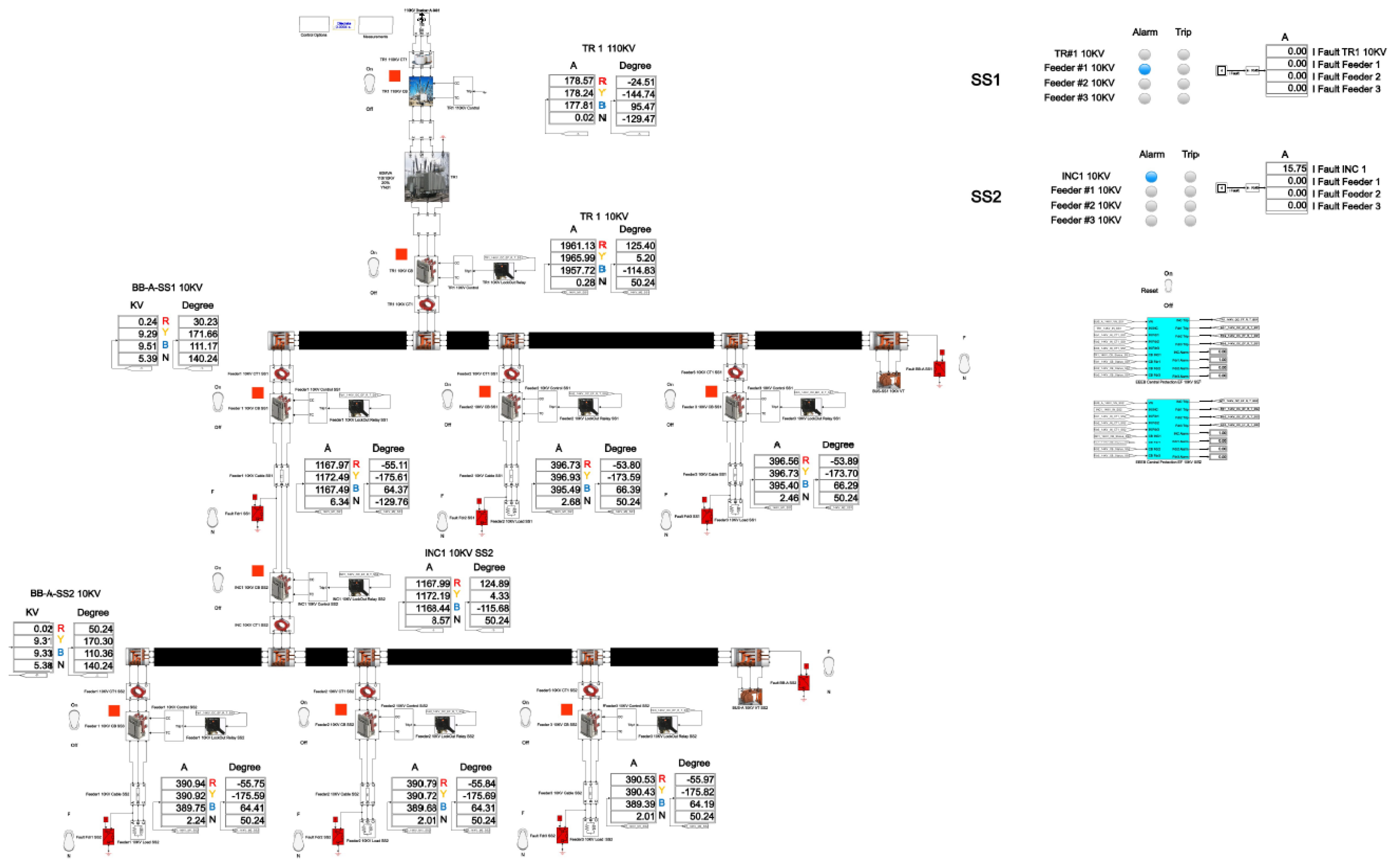
The total cumulative SPGF current on the phase A with the transient resistance of Rf= 5000 Ohm is 1.09 Aand the angle of the zero-sequence current is φ = -33.43°. The SPGF on the phase A with the transient resistance of Rf= 5000 Ohm, has a greater magnitude, has the same direction and a shift of about 0-5° from the phasor of the capacitive currents of the unfaulted feeders No.1, 2 and 3 in the substation No.1 and feeders No.1, 2 and 3 in the substation No.2. Due to the fact that the SPGF current exceeds the ground overcurrent setting, an alarm signal on the substation No.1 bus is issued (see
Figure 21 and
Appendix B).
4.3. Modeling of SPGF With the Transient Resistance of Rf = 5000 Ohm at the Feeder No.1, Substation No.2 in the 10 kV Network with the Isolated Neutral Configuration
Figure 23 shows the single line diagram with SPGF with the transient resistance of Rf = 5000 Ohm at the feeder No.1, substation No.2 in the 10 kV network with the isolated neutral configuration [
23,
24,
25,
26,
27]. At the incomer, substation No.1, the zero-sequence current is I
ZSCT = 0.02 A, and the zero-sequence current angle is φ = -35.73°. At the feeder No.1, substation No.1, the zero-sequence current is I
ZSCT = 0.43 A, and the zero-sequence current angle is φ = 144.20°. At the feeder No.2, substation No.1, the zero-sequence current is I
ZSCT = 0.19 A, and the zero-sequence current angle is φ = -35.78°. At the feeder No.3, substation No.1, the zero-sequence current is I
ZSCT = 0.17 A, and the zero-sequence current angle is φ = -35.79°. At the incomer, substation No.2, the zero-sequence current is I
ZSCT = 0.59 A, and the zero-sequence current angle is φ = -35.79°. At the feeder No.1, substation No.2, the zero-sequence current is I
ZSCT = 0.92 A, and the zero-sequence current angle is φ = 144.23°. At the feeder No.2, substation No.2, the zero-sequence current is I
ZSCT = 0.14 A, and the zero-sequence current angle is φ = -35.72°. At the feeder No.3, substation No.2, the zero-sequence current is I
ZSCT = 0.14 A, and the zero-sequence current angle is φ = -35.72°.
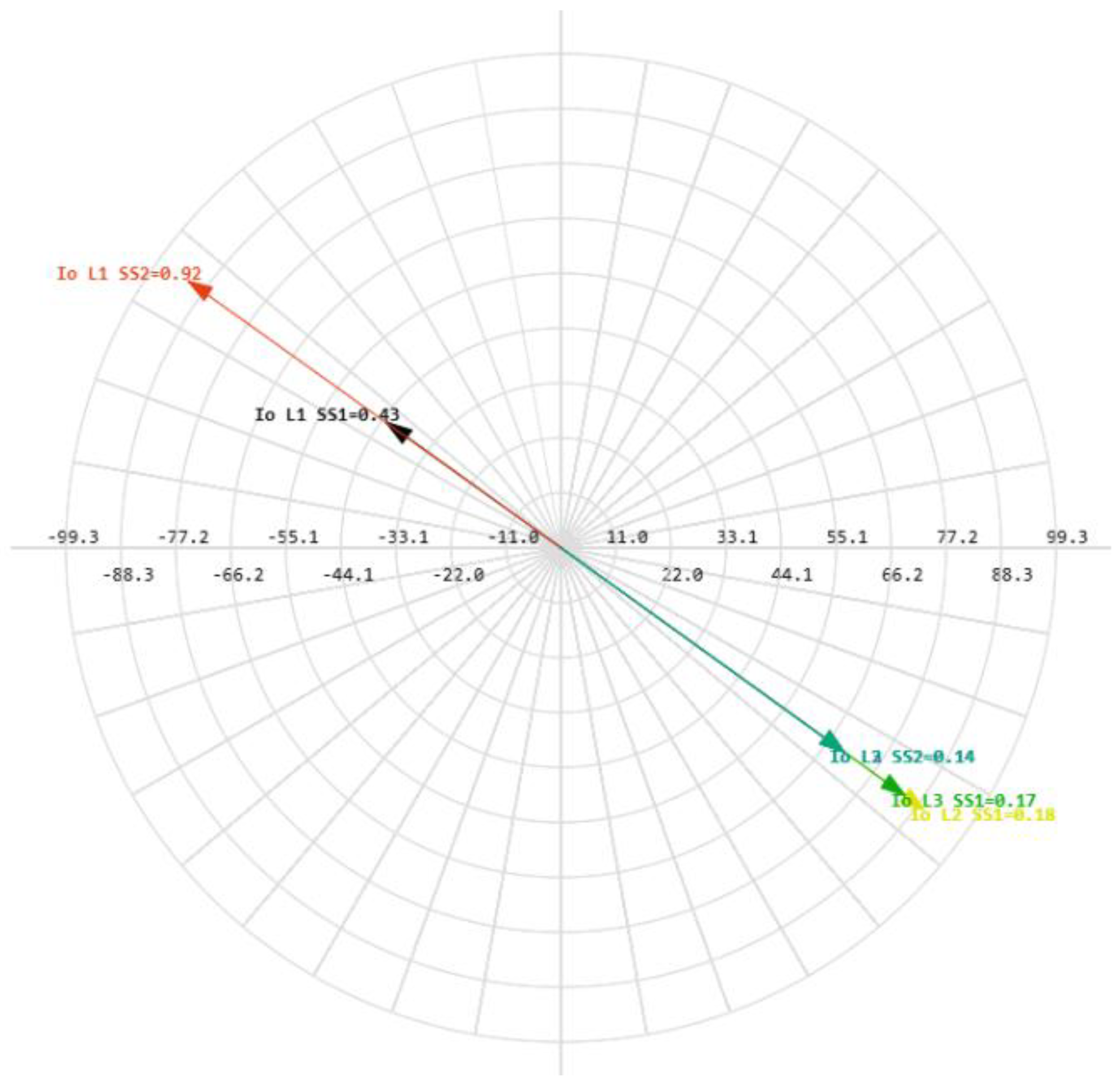
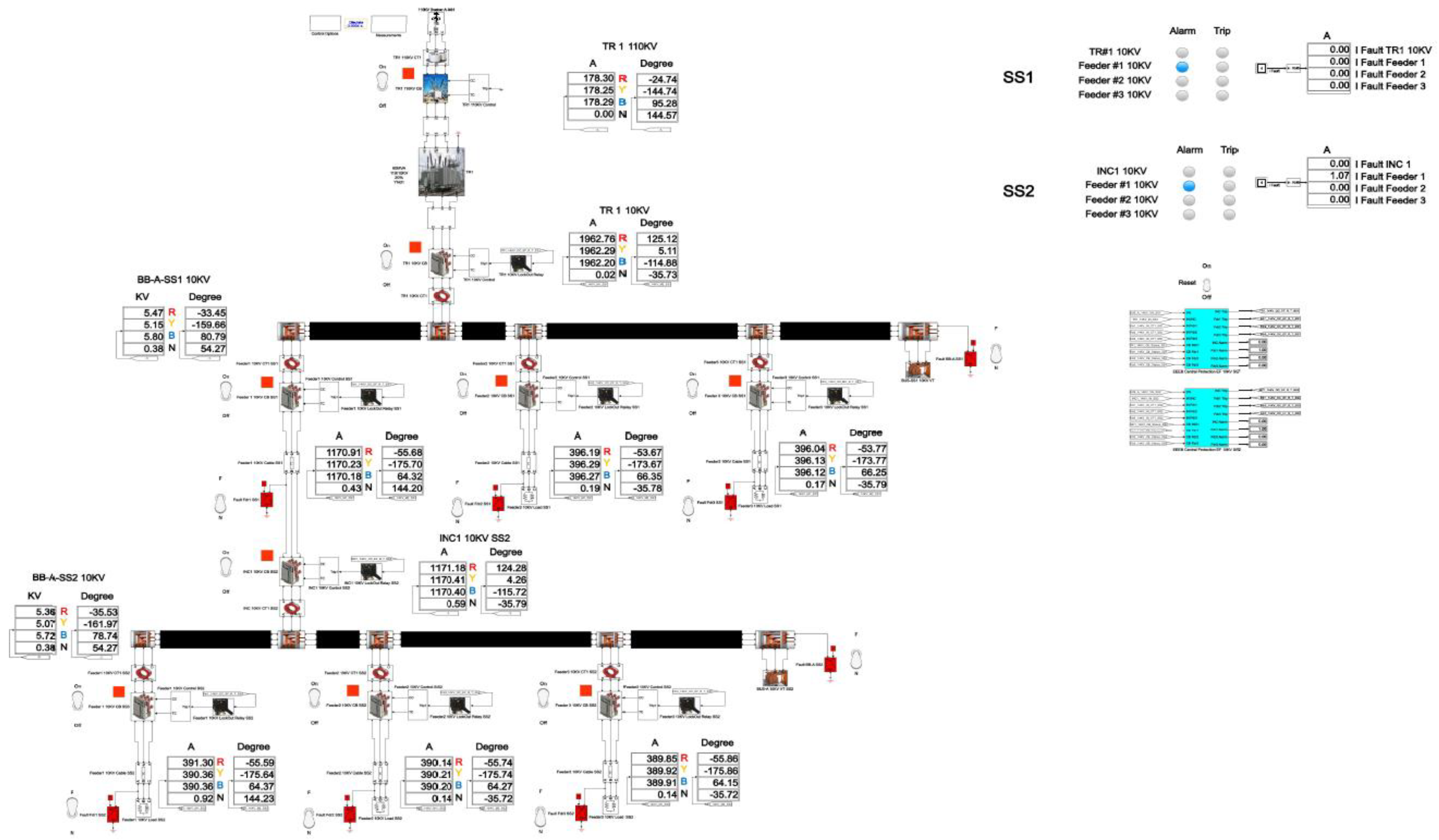
The total cumulative SPGF current on the phase A with the transient resistance Rf= 5000 Ohm is 1.07 A and the angle of the zero-sequence current is φ = 144.23°. The SPGF on the phase A with the transient resistance Rf= 5000 Ohm, has a greater magnitude and a shift of about 180-185° from the phasor of the capacitive currents of the unfaulted Feeders No.2 and 3 in the Substation No.2 and Feeders No.1, 2 and 3 in the Substation No.1. Due to the fact that the SPGF current exceeds the ground overcurrent setting, an alarm signal at the Feeder No.1, Substation No.2 is issued (
Figure 23).
4.4. Modeling of SPGF with the Transient Resistance of Rf = 5000 Ohm on the Substation No.2 Bus in the 10 kV Network with the Isolated Neutral Configuration
Figure 25 shows the Single line diagram with SPGF with the transient resistance of Rf = 5000 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration [
1,
2,
3]. At the Incomer, Substation No.1, the zero-sequence current is I
ZSCT = 0.02 A, and the zero-sequence current angle is φ = -35.50°. At the Feeder No.1, Substation No.1, the zero sequence current is I
ZSCT = 0.43 A, and the zero sequence current angle is φ = 144.44°. At the Feeder No.2, Substation No.1, the zero sequence current is I
ZSCT = 0.19 A, and the zero sequence current angle is φ = -35.55°. At the Feeder No.3 , Substation No.1, the zero-sequence current is I
ZSCT = 0.17 A, and the zero-sequence current angle is φ = -35.55°. At the Incomer, Substation No.2, the zero sequence current is I
ZSCT = 0.59 A, and the zero sequence current angle is φ = -35.55°. At the Feeder No.1, Substation No.2, zero sequence current is I
ZSCT = 0.15 A, and the zero sequence current angle is φ = -35.49°. At the Feeder No.2, Substation No.2, the zero sequence current is I
ZSCT = 0.14 A, and the zero sequence current angle is φ = -35.48°. At the Feeder No.3, Substation No.2, the zero sequence current is I
ZSCT = 0.14 A, and the zero sequence current angle is φ = -35.48°.
The total cumulative SPGF current on the phase A with the transient resistance of Rf= 5000 Ohm is 1.07 A and the angle of the zero-sequence current is φ = -33.50°. The SPGF on the phase A with the transient resistance of Rf= 5000 Ohm, has a greater magnitude, has the same direction and a shift of about 0-5° from the phasor of the capacitive currents of the unfaulted Feeders No.1, 2, 3 in the Substation No.1 and Feeders No.1, 2, 3 in the Substation No.2. Due to the fact that the SPGF current exceeds the ground overcurrent setting, an alarm signal on the Substation No.2 bus is issued (see
Figure 25 and
Appendix C).
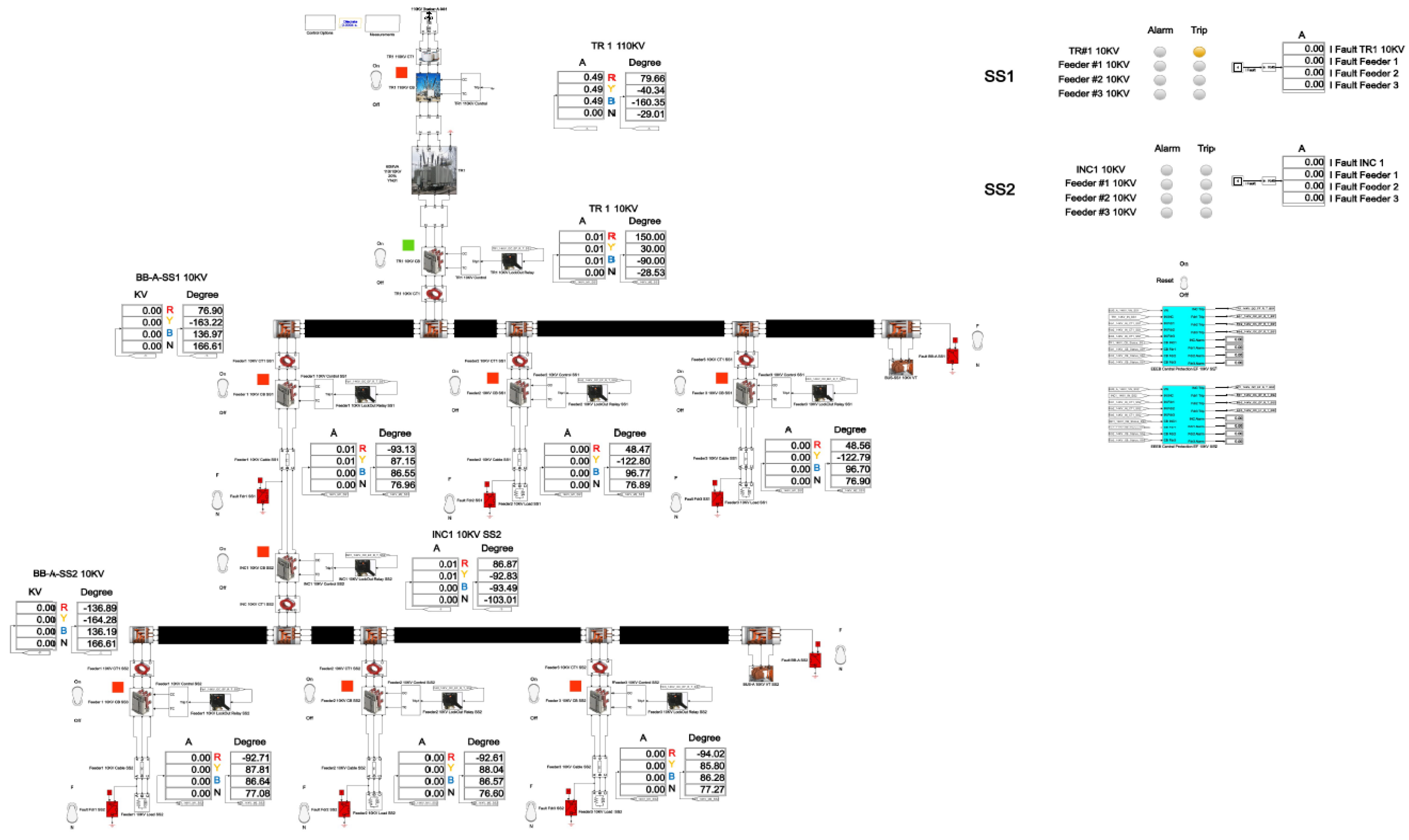
4.5. Modeling of SPGF with the Transient Resistance Rf = 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV Network with the Isolated Neutral Configuration
Figure 27 and
Figure 28 show the Single line diagrams with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration after clearing the ground fault. At the Incomer, Substation No.1, the zero-sequence current is I
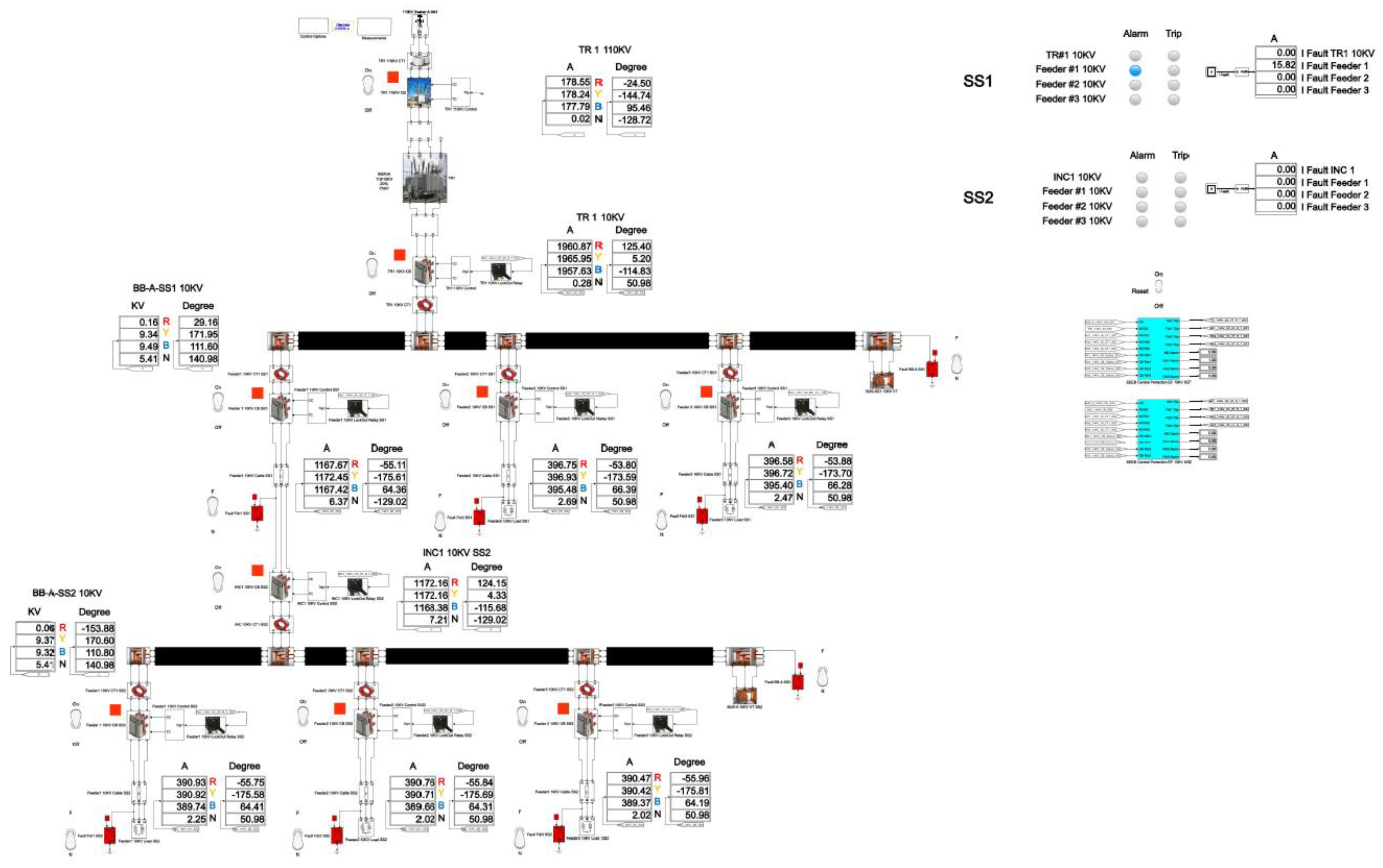
ZSCT = 0.28 A, and the zero-sequence current angle is φ = 50.98°. At the Feeder No.1, Substation No.1, the zero sequence current is I
ZSCT = 6.37 A, and the zero sequence current angle is φ = -129.02°. At the Feeder No.2, Substation No.1, the zero sequence current is I
ZSCT = 2.69 A, and the zero sequence current angle is φ = 50.98°. At the Feeder No.3, Substation No.1, the zero-sequence current is I
ZSCT = 2.47 A, and the zero-sequence current angle is φ = 50.98°. At the Incomer, Substation No.2, the zero sequence current is I
ZSCT = 7.21 A, and the zero sequence current angle is φ = -129.02°. At the Feeder No.1, Substation No.2, the zero sequence current is I
ZSCT = 2.25 A, and the zero sequence current angle is φ = 50.98°. At the Feeder No.2, Substation No.2, the zero sequence current is I
ZSCT = 2.02 A, and the zero sequence current angle is φ = 50.98°. At the Feeder No.3, Substation No.2, the zero sequence current is I
ZSCT = 2.02 A, and the zero sequence current angle is φ = 50.98°.
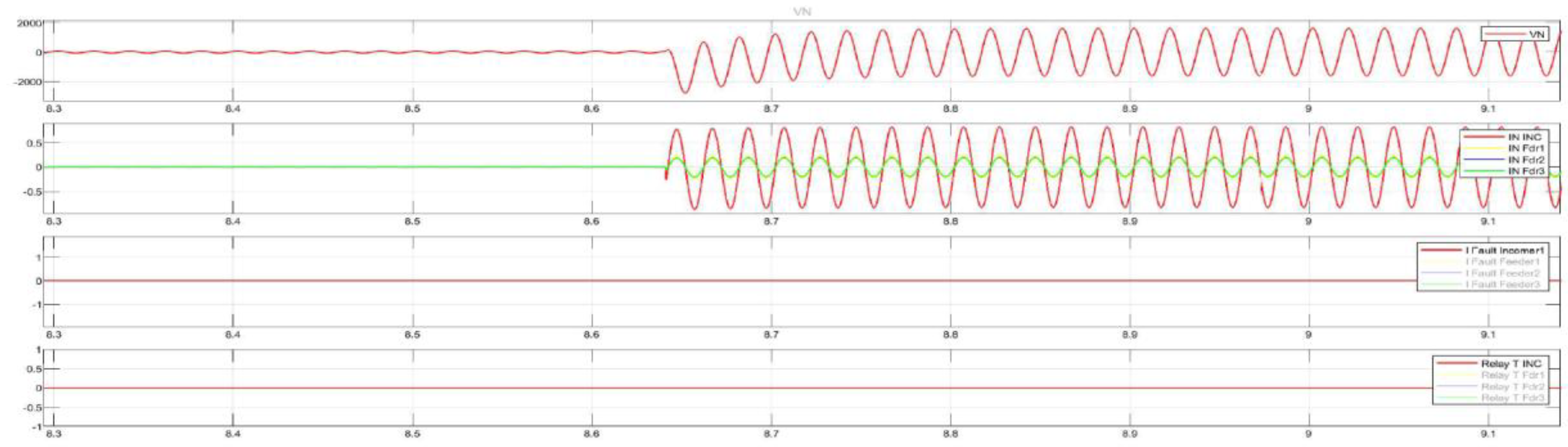
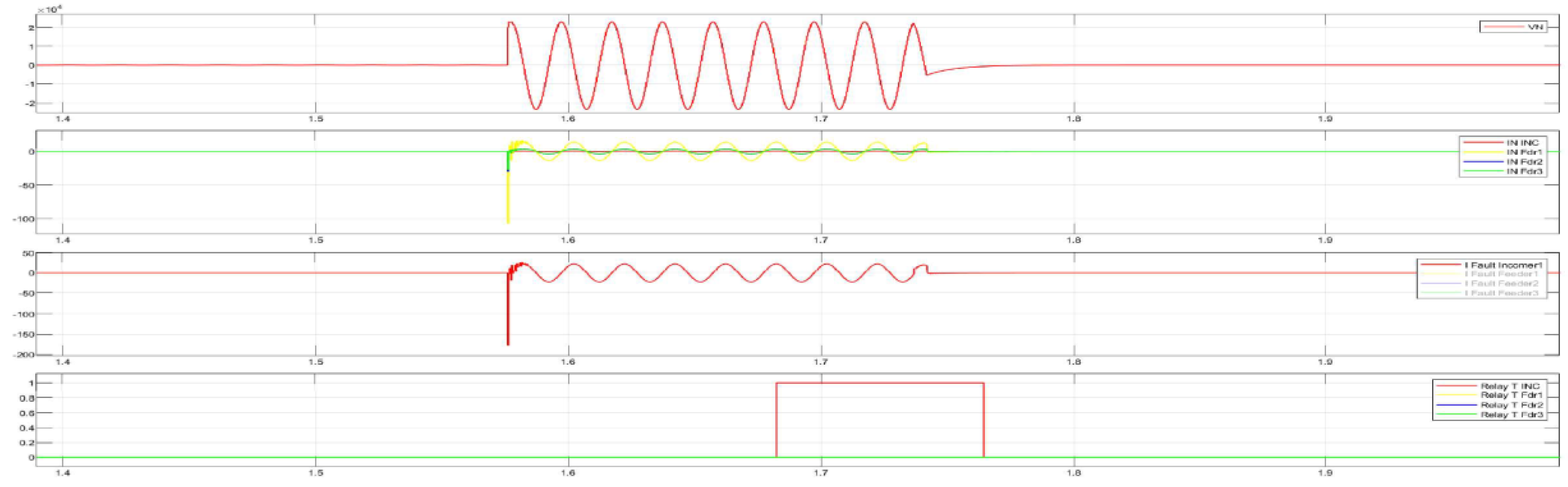
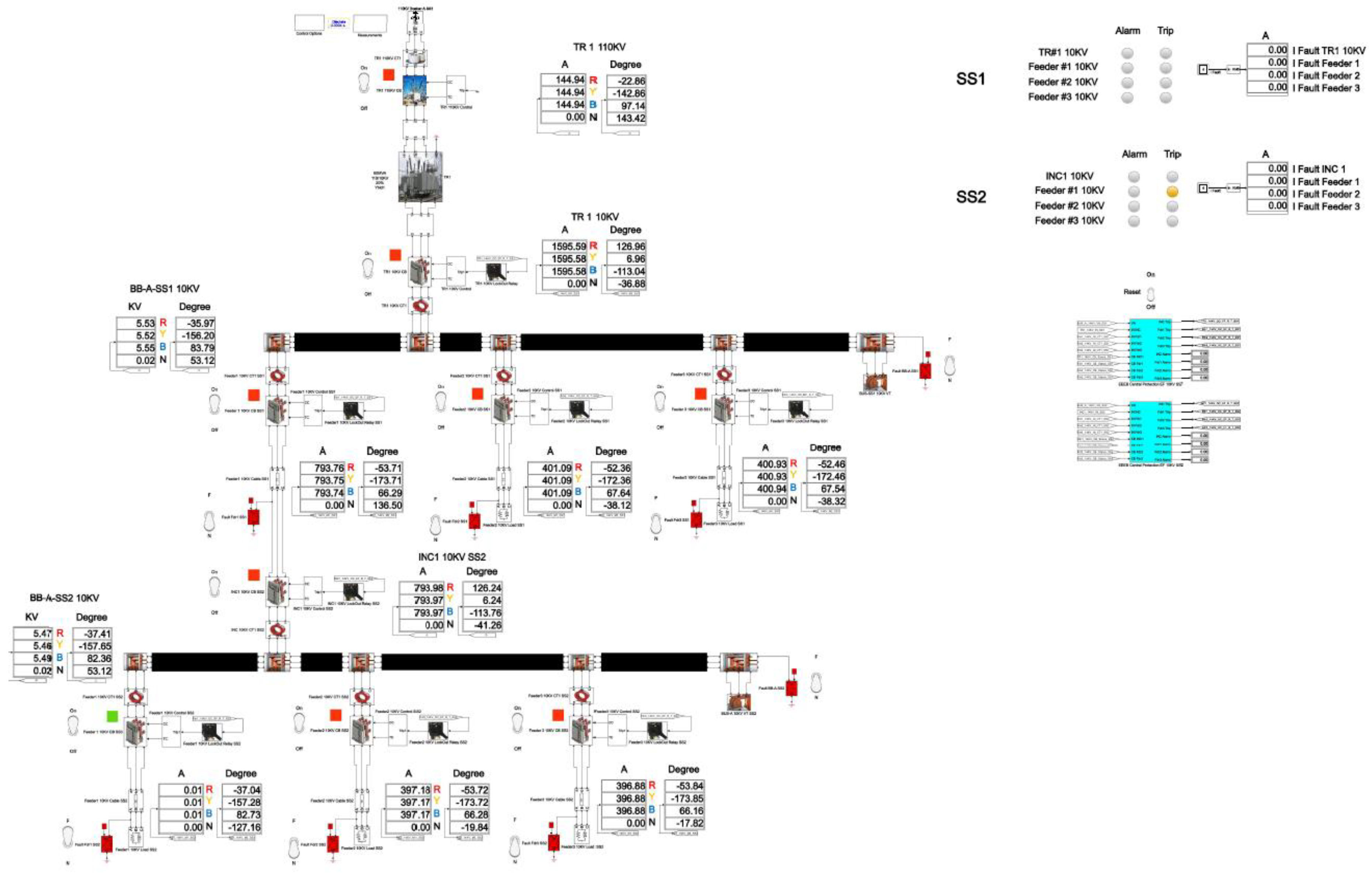
The total cumulative SPGF current on the phase A with the transient resistance Rf= 1 Ohm is 15.82 A and the angle of the zero-sequence current is φ = 129.02°. The SPGF on the phase A with the transient resistance Rf= 1 Ohm, has a greater magnitude and a shift of about 180-185° from the phasor of the capacitive currents of the unfaulted Feeders No.2 and 3 in the Substation No.1 and Feeders No.1, 2 and 3 in the Substation No.2. Due to the fact that the SPGF current exceeds the ground overcurrent setting, a trip signal at the Feeder No.1, Substation No.1 is issued.
4.6. Modeling of SPGF with the Transient Resistance of Rf = 1 Ohm on the Substation No.1 Bus in the 10 kV Network with the Isolated Neutral Configuration
Figure 30 and
Figure 31 show the Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral configuration during SPGF and after clearing the ground fault [
26]. At the Incomer, Substation No.1, the zero-sequence current is I
ZSCT = 0.29 A, and the zero-sequence current angle is φ = 52.39°. At the Feeder No.1, Substation No.1, the zero sequence current is I
ZSCT = 9.57 A, and the zero sequence current angle is φ = 52.39°. At the Feeder No.2, Substation No.1, the zero sequence current is I
ZSCT = 2.73 A, and the zero sequence current angle is φ = 52.39°. At the Feeder No.3, Substation No.1, the zero-sequence current is I
ZSCT = 2.50 A, and the zero-sequence current angle is φ = 52.39°. At the Incomer, Substation No.2, the zero sequence current is I
ZSCT = 7.29 A, and the zero sequence current angle is φ = -127.61°. At the Feeder No.1, Substation No.2, the zero sequence current is I
ZSCT = 2.27 A, and the zero sequence current angle is φ = 52.39°. At the Feeder No.2, Substation No.2, the zero sequence current is I
ZSCT = 2.05 A, and the zero sequence current angle is φ = 52.39°. At the Feeder No.3, Substation No.2, the zero sequence current is I
ZSCT = 2.05 A, and the zero sequence current angle is φ = 52.39°.
The total cumulative SPGF current on the phase A with the transient resistance of Rf= 1 Ohm is 16.01 A and the angle of the zero-sequence current is φ = 52.39°. The SPGF on the phase A with the transient resistance of Rf= 5000 Ohm, has a greater magnitude, has the same direction and a shift of about 0-5° from the phasor of the capacitive currents of the unfaulted Feeders No.1, 2 and 3 in the Substation No.1 and Feeders No.1, 2 and 3 in the Substation No.2. Due to the fact that the SPGF current exceeds the ground overcurrent setting, a trip signal on the Substation No.1 bus is issued (see
Figure 31 and
Appendix D).
4.7. Modeling of SPGF with the Transient Resistance Rf = 1 Ohm at the Feeder No.1, Substation No.2 in the 10 kV Network with the Isolated Neutral Configuration
Figure 33 and
Figure 34 show Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration during SPGF and after clearing the ground fault. At the Incomer, Substation No.2, the zero-sequence current is I
ZSCT= 0.28 A, and the zero-sequence current angle is φ = 49.99°. At the Feeder No.1 , Substation No.1, the zero sequence current is I
ZSCT= 6.33 A, and the zero sequence current angle is φ = -130.00°. At the Feeder No.2 , Substation No.1, the zero sequence current is I
ZSCT = 2.68 A, and the zero sequence current angle is φ = 50.00°.
At the Feeder No.3 , Substation No.1, the zero-sequence current is IZSCT = 2.45 A, and the zero-sequence current angle is φ = 50.00°. At the Incomer, Substation No.2, the zero sequence current is IZSCT= 8.56 A, and the zero sequence current angle is φ = 50.00°. At the Feeder No.1, Substation No.2, the zero sequence current is IZSCT = 13.49 A, and the zero sequence current angle is φ = -130.00°. At the Feeder No.2, Substation No.2, the zero sequence current is IZSCT = 2.01 A, and the zero sequence current angle is φ = 50.00°. At the Feeder No.3, Substation No.2, the zero sequence current is IZSCT = 2.01 A, and the zero sequence current angle is φ = 50.00°.
The total cumulative SPGF current on the phase A with the transient resistance Rf= 1 Ohm is 15.72 A and the angle of the zero-sequence current is φ = -130.00°. The SPGF on the phase A with the transient resistance Rf= 1 Ohm, has a greater magnitude and a shift of about 180-185° from the phasor of the capacitive currents of the unfaulted Feeders No.2 and 3 in the Substation No.2 and Feeders No.1, 2 and 3 in the Substation No.1. Due to the fact that the SPGF current exceeds the ground overcurrent setting, a trip signal at the Feeder No.1, Substation No.2 is issued (
Figure 33).
4.8. Modeling of SPGF with the Transient Resistance of Rf = 1 Ohm on the Substation No.2 bus in the 10 kV Network with the Isolated Neutral Configuration
Figure 36 and
Figure 37 show the Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration during SPGF and after clearing the ground fault. At the Incomer, Substation No.1, the zero-sequence current is I
ZSCT = 0.28 A, and the zero-sequence current angle is φ = 50.24°. At the Feeder No.1, Substation No.1, the zero sequence current is I
ZSCT = 6.34 A, and the zero sequence current angle is φ = -129.76°. At the Feeder No.2, Substation No.1, the zero sequence current is I
ZSCT = 2.68 A, and the zero sequence current angle is φ = 50.24°. At the Feede rNo.3, Substation No.1, the zero-sequence current is I
ZSCT = 2.46 A, and the zero-sequence current angle is φ = 50.24°. At the Incomer, Substation No.2, the zero sequence current is I
ZSCT = 8.57 A, and the zero sequence current angle is φ = 50.24°. At the Feeder No.1, Substation No.2, the zero sequence current is I
ZSCT = 2.24 A, and the zero sequence current angle is φ = 50.24°. At the Feeder No.2, Substation No.2, the zero sequence current is I
ZSCT = 2.01 A, and the zero sequence current angle is φ = 50.24°. At the Feeder No.3, Substation No.2, the zero sequence current is I
ZSCT = 2.01 A, and the zero sequence current angle is φ = 50.24°.
The total cumulative SPGF current on the phase A with the transient resistance of Rf= 1 Ohm is 15.75 A and the angle of the zero-sequence current is φ = 50.24°. The SPGF on the phase A with the transient resistance of Rf= 1 Ohm, has a greater magnitude, has the same direction and a shift of about 0-5° from the phasor of the capacitive currents of the unfaulted Feeders No.1, 2 and 3 in the Substation No.1 and Feeders No.1, 2 and 3 in the Substation No.2. Due to the fact that the SPGF current exceeds the ground overcurrent setting, a trip signal on the Substation No.2 bus is issued (
Figure 36).
Figure 1.
Distribution of the number of single-phase ground faults (SPGFs) versus transient resistance values at the fault location in a 10 kV network.
Figure 1.
Distribution of the number of single-phase ground faults (SPGFs) versus transient resistance values at the fault location in a 10 kV network.
Figure 2.
Functional diagram of the centralized ground fault protection unit (CGFPU) in the 10 kV network with isolated neutral configuration.
Figure 2.
Functional diagram of the centralized ground fault protection unit (CGFPU) in the 10 kV network with isolated neutral configuration.
Figure 3.
Phasor diagram of the ground fault current and capacitive currents during a ground fault on an outgoing feeder.
Figure 3.
Phasor diagram of the ground fault current and capacitive currents during a ground fault on an outgoing feeder.
Figure 4.
Phasor diagram of zero-sequence currents during ground fault on the 10 kV busbars.
Figure 4.
Phasor diagram of zero-sequence currents during ground fault on the 10 kV busbars.
Figure 5.
Single-line diagram of a 110/10 kV substation in a network with isolated neutral configuration.
Figure 5.
Single-line diagram of a 110/10 kV substation in a network with isolated neutral configuration.
Figure 6.
Block diagram of the centralized ground fault protection unit (CGFPU) in a 10 kV network with isolated neutral configuration for substations No.1 and No. 2.
Figure 6.
Block diagram of the centralized ground fault protection unit (CGFPU) in a 10 kV network with isolated neutral configuration for substations No.1 and No. 2.
Figure 7.
Functional diagram of the CGFPU polarization module in the 10 kV network with isolated neutral configuration for substation No.1 and No. 2.
Figure 7.
Functional diagram of the CGFPU polarization module in the 10 kV network with isolated neutral configuration for substation No.1 and No. 2.
Figure 8.
Functional diagram of the angle and magnitude comparison module for feeders No.1, 2 and 3 in substations No.1 and No. 2.
Figure 8.
Functional diagram of the angle and magnitude comparison module for feeders No.1, 2 and 3 in substations No.1 and No. 2.
Figure 9.
Functional diagram of the magnitude and angle comparison module for the incomers in substations No.1 and No. 2.
Figure 9.
Functional diagram of the magnitude and angle comparison module for the incomers in substations No.1 and No. 2.
Figure 10.
10 kV distribution network with isolated neutral configuration.
Figure 10.
10 kV distribution network with isolated neutral configuration.
Figure 11.
Ground fault current with the transient resistance at feeder No.1, substation No.1, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 11.
Ground fault current with the transient resistance at feeder No.1, substation No.1, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 12.
Phasor diagram for the single-phase ground fault (SPGF) at feeder No.1, substation No.1, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 12.
Phasor diagram for the single-phase ground fault (SPGF) at feeder No.1, substation No.1, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 13.
Ground fault current with transient resistance on the substation No.1 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 13.
Ground fault current with transient resistance on the substation No.1 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 14.
Phasor diagram for the single-phase ground fault (SPGF) on the substation No.1 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 14.
Phasor diagram for the single-phase ground fault (SPGF) on the substation No.1 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 15.
Ground fault current with the transient resistance at feeder No.1, substation No.2, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 15.
Ground fault current with the transient resistance at feeder No.1, substation No.2, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 16.
Phasor diagram for the single-phase ground fault (SPGF) at feeder No.1, substation No.2, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 16.
Phasor diagram for the single-phase ground fault (SPGF) at feeder No.1, substation No.2, and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 17.
Ground fault current with the transient resistance on the substation No.2 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 17.
Ground fault current with the transient resistance on the substation No.2 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 18.
Phasor diagram for the single-phase ground fault (SPGF) on the substation No.2 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Figure 18.
Phasor diagram for the single-phase ground fault (SPGF) on the substation No.2 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
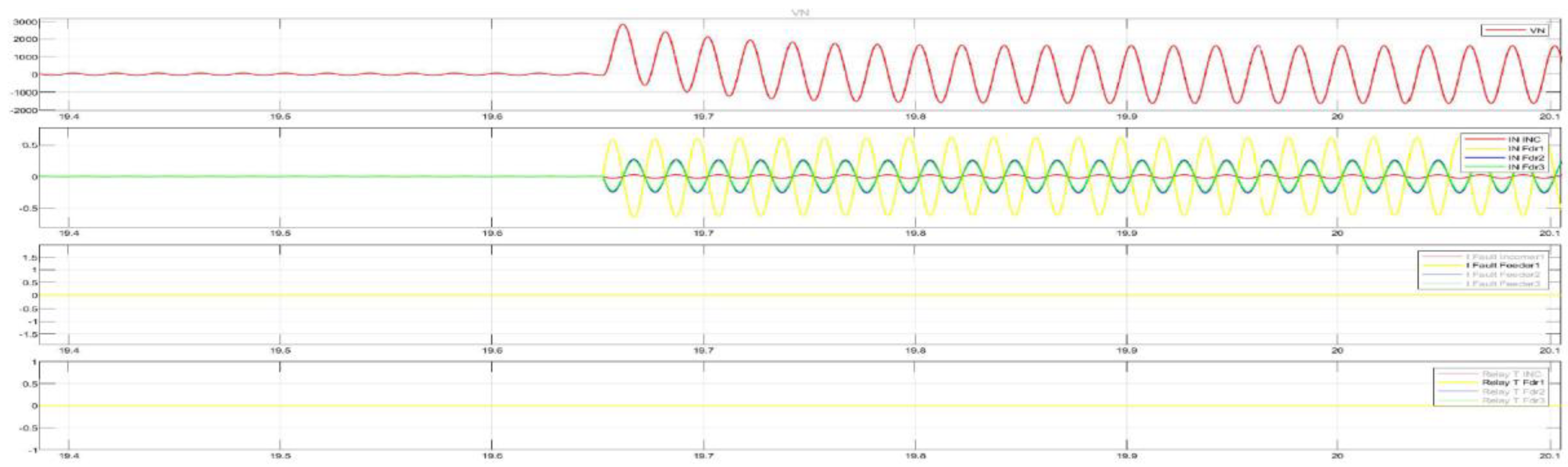
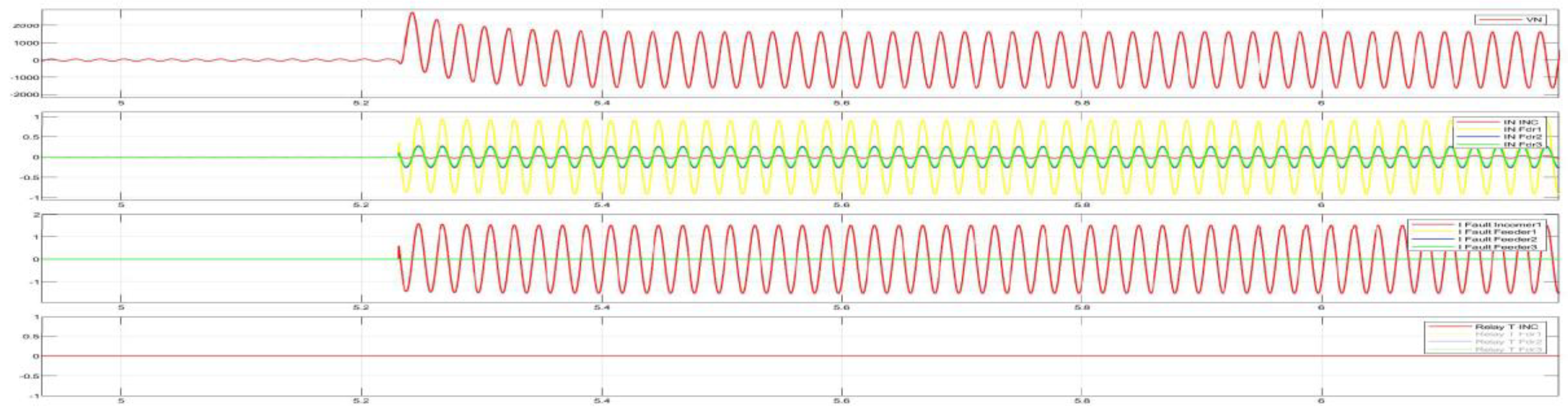
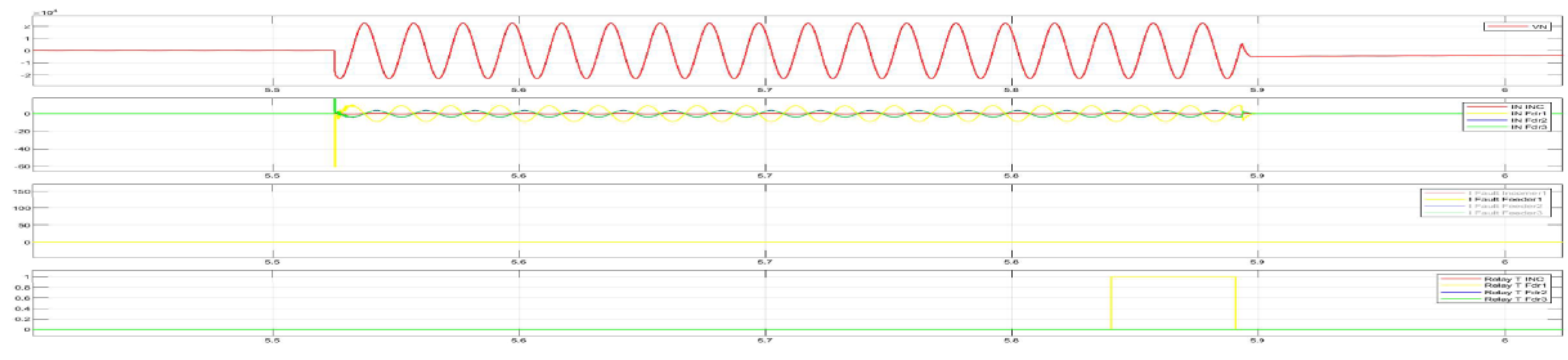
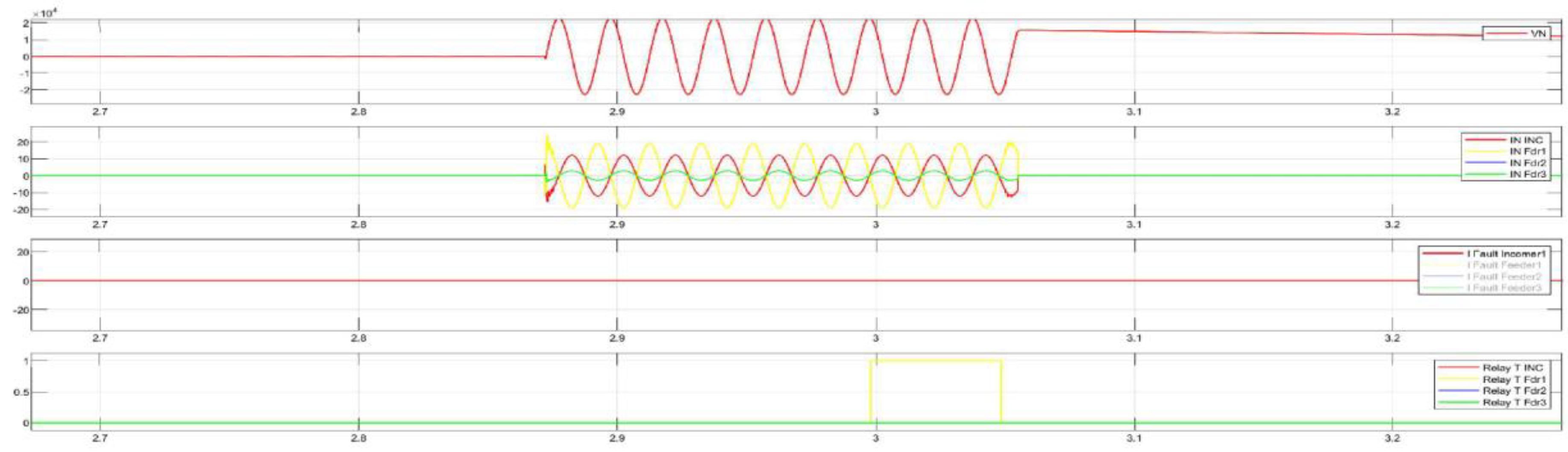
Figure 19.
demonstrates the disturbance recording of a single-phase ground fault (SPGF) with a transient resistance of Rf = 5000 Ohm at feeder No.1, substation No.1. The CGFPU accurately detects the ground fault, identifies the faulty feeder based on zero-sequence current magnitude and angle comparison, and selectively issues an alarm without nuisance trips of other feeders. This confirms the high sensitivity, selectivity, and operational reliability of the proposed protection scheme even in the presence of significant transient resistance.
Figure 19.
demonstrates the disturbance recording of a single-phase ground fault (SPGF) with a transient resistance of Rf = 5000 Ohm at feeder No.1, substation No.1. The CGFPU accurately detects the ground fault, identifies the faulty feeder based on zero-sequence current magnitude and angle comparison, and selectively issues an alarm without nuisance trips of other feeders. This confirms the high sensitivity, selectivity, and operational reliability of the proposed protection scheme even in the presence of significant transient resistance.
Figure 20.
Presents the disturbance recording of a single-phase ground fault (SPGF) with a transient resistance of Rf= 5000 Ohm at feeder No.1, substation No.1 in the 10 kV network with isolated neutral configuration.
Figure 20.
Presents the disturbance recording of a single-phase ground fault (SPGF) with a transient resistance of Rf= 5000 Ohm at feeder No.1, substation No.1 in the 10 kV network with isolated neutral configuration.
Figure 21.
Illustrates the correct detection and localization of a single-phase ground fault with a transient resistance of Rf = 5000 Ohm located on the substation No.1 bus. The CGFPU protection system correctly identifies the fault at the incomer by analyzing the magnitude and angle of the zero-sequence current and issues a selective alarm without false operation on unfaulted feeders, confirming high reliability and sensitivity even under high-resistance fault conditions.
Figure 21.
Illustrates the correct detection and localization of a single-phase ground fault with a transient resistance of Rf = 5000 Ohm located on the substation No.1 bus. The CGFPU protection system correctly identifies the fault at the incomer by analyzing the magnitude and angle of the zero-sequence current and issues a selective alarm without false operation on unfaulted feeders, confirming high reliability and sensitivity even under high-resistance fault conditions.
Figure 22.
Disturbance record of (SPGF) with a transient resistance of Rf= 5000 Ohm on the substation No.1 bus in the 10 kV network with isolated neutral configuration.
Figure 22.
Disturbance record of (SPGF) with a transient resistance of Rf= 5000 Ohm on the substation No.1 bus in the 10 kV network with isolated neutral configuration.
Figure 23.
Single line diagram with SPGF with the transient resistance of Rf = 5000 Ohm at the feeder No.1, substation No.2 in the 10 kV network with isolated neutral configuration.
Figure 23.
Single line diagram with SPGF with the transient resistance of Rf = 5000 Ohm at the feeder No.1, substation No.2 in the 10 kV network with isolated neutral configuration.
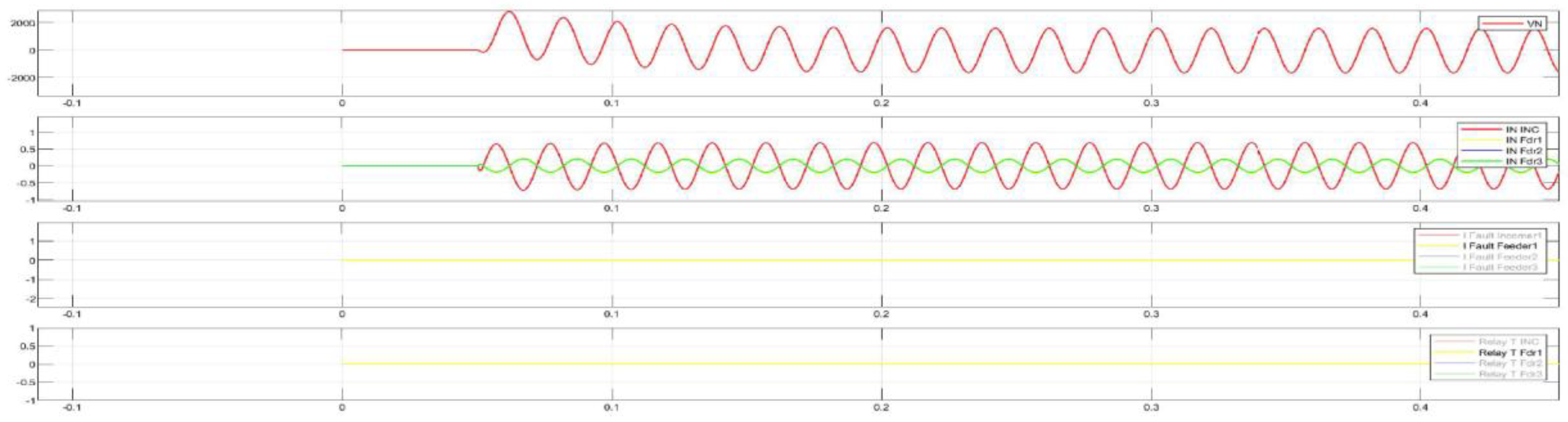
Figure 24.
Disturbance record of SPGF with the transient resistance of Rf= 5000 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration.
Figure 24.
Disturbance record of SPGF with the transient resistance of Rf= 5000 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration.
Figure 25.
Single line diagram with SPGF with the transient resistance of Rf = 5000 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration.
Figure 25.
Single line diagram with SPGF with the transient resistance of Rf = 5000 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration.
Figure 26.
Disturbance record of SPGF with the transient resistance of Rf= 5000 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration.
Figure 26.
Disturbance record of SPGF with the transient resistance of Rf= 5000 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration.
Figure 27.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 27.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 28.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 28.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 29.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration.
Figure 29.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration.
Figure 30.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 30.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 31.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 31.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 32.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral.
Figure 32.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm on the Substation No.1 bus in the 10 kV network with the isolated neutral.
Figure 33.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 33.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 34.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 34.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm at the Feeder No.1, Substation No.2 in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 35.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration.
Figure 35.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm at the Feeder No.1, Substation No.1 in the 10 kV network with the isolated neutral configuration.
Figure 36.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 36.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration (during SPGF).
Figure 37.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 37.
Single line diagram with SPGF with the transient resistance of Rf = 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration (after clearing the ground fault).
Figure 38.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration.
Figure 38.
Disturbance record of SPGF with the transient resistance of Rf= 1 Ohm on the Substation No.2 bus in the 10 kV network with the isolated neutral configuration.
Table 1.
Single-phase ground fault (SPGF) current values at feeder No.1, substation No.1 for different transient resistances, and capacitive currents in the 10 kV network with isolated neutral configuration [
26].
Table 1.
Single-phase ground fault (SPGF) current values at feeder No.1, substation No.1 for different transient resistances, and capacitive currents in the 10 kV network with isolated neutral configuration [
26].
| No |
Resistance Rf, Ohm |
Cumulative current, A |
Ground fault current at feeder No.1, substation No.1, A |
Capacitive current at feeder No.2, substation No.1, A |
Capacitive current at feeder No.3, substation No.1, A |
Capacitive current at feeder No.1, substation No.2, A |
Capacitive current at feeder No.2, substation No.2, A |
Capacitive current at feeder No.3, substation No.2, A |
|
| 1 |
1 |
15.82∠-129.02° |
6.37∠-129.02° |
2.69∠50.98° |
2.47∠50.98° |
2.25∠50.98° |
2.02∠50.98° |
2.02∠50.98° |
|
| 2 |
100 |
15.17∠-145.16° |
6.10∠-145.16° |
2.58∠34.84° |
2.37∠34.84° |
2.15∠34.84° |
1.94∠34.84° |
1.94∠34.84° |
|
| 3 |
500 |
8.91∠175.59° |
3.59∠175.59° |
1.52∠-4.41° |
1.39∠-4.41° |
1.27∠-4.40° |
1.14∠-4.40° |
1.14∠-4.40° |
|
| 4 |
1000 |
5.11∠160.15° |
2.06∠160.15° |
0.87∠-19.85° |
0.80∠-19.85° |
0.73∠-19.84° |
0.65∠-19.84° |
0.65∠-19.84° |
|
| 5 |
3000 |
1.79∠147.83° |
0.72∠147.78° |
0.31∠-32.21° |
0.28∠-32.21° |
0.25∠-32.17° |
0.23∠-32.17° |
0.23∠-32.17° |
|
| 6 |
5000 |
1.08∠145.18° |
0.43∠145.18° |
0.19∠-34.81° |
0.17∠-34.81° |
0.15∠-34.75° |
0.14∠-34.74° |
0.14∠-34.73° |
|
| 7 |
10000 |
0.54∠143.35° |
0.22∠143.18° |
0.09∠-36.79° |
0.09∠-36.79° |
0.08∠-36.67° |
0.07∠-36.65° |
0.07∠-36.64° |
|
Table 2.
Single-phase ground fault (SPGF) current values with different transient resistances at the substation No.1 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Table 2.
Single-phase ground fault (SPGF) current values with different transient resistances at the substation No.1 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
| No. |
Resistance Rf, Ohm |
Cumulative current, A |
Capacitive current at the Feeder No.1, Substation No.1, A |
Capacitive current at the Feeder No.2, Substation No.1, A |
Capacitive current at the Feeder No.3, Substation No.1, A |
Capacitive current at the Feeder No.1, Substation No.2, A |
Capacitive current at the Feeder No.2, Substation No.2, A |
Capacitive current at the Feeder No.3, Substation No.2, A |
|
| 1 |
1 |
16.01∠-127.61° |
9.57∠52.39° |
2.73∠52.39° |
2.50∠52.39° |
2.27∠52.39° |
2.27∠52.39° |
2.27∠52.39° |
|
| 2 |
100 |
15.35∠-143.75° |
9.17∠36.25° |
2.62∠36.25° |
2.40∠36.25° |
2.18∠36.25° |
1.96∠36.25° |
1.96∠36.25° |
|
| 3 |
500 |
9.02∠-177.01° |
5.39∠-2.99° |
1.54∠-3.00° |
1.41∠-3.00° |
1.28∠-2.99° |
1.15∠-2.99° |
1.15∠-2.99° |
|
| 4 |
1000 |
5.17∠167.57° |
3.09∠-18.43° |
0.88∠-18.44° |
0.81∠-18.44° |
0.73∠-18.43° |
0.66∠-18.43° |
0.66∠-18.43° |
|
| 5 |
3000 |
1.81∠149.24° |
1.08∠-30.77° |
0.31∠-30.81° |
0.28∠-30.81° |
0.26∠-30.77° |
0.23∠-30.76° |
0.23∠-30.76° |
|
| 6 |
5000 |
1.09∠146.67° |
0.65∠-33.34° |
0.19∠-33.41° |
0.17∠-33.41° |
0.16∠-33.35° |
0.14∠-33.34° |
0.14∠-33.33° |
|
| 7 |
10000 |
0.55∠144.77° |
0.33∠-35.26° |
0.09∠-35.41° |
0.09∠-35.40° |
0.08∠-35.28° |
0.07∠-35.25° |
0.07∠-35.24° |
|
Table 3.
Single-phase ground fault (SPGF) current values with different transient resistances at feeder No.1, substation No.2, and capacitive currents in the 10 kV network with isolated neutral configuration.
Table 3.
Single-phase ground fault (SPGF) current values with different transient resistances at feeder No.1, substation No.2, and capacitive currents in the 10 kV network with isolated neutral configuration.
| No. |
Resistance Rf, Ohm |
Cumulative current, A |
Capacitive current at the Feeder No.1, Substation No.1, A |
Capacitive current at the Feeder eder No.2, Substation No.1, A |
Capacitive current at the Feeder No.3, Substation No.1, A |
Ground fault current at the Feeder No.1, Substation No.2, A |
Capacitive current at the Feeder No.2, Substation No.2, A |
Capacitive current at the Feeder No.3, Substation No.2, A |
|
| 1 |
1 |
15.72∠-130.00° |
6.33∠-130.00° |
2.68∠50.00° |
2.45∠50.00° |
13.49∠-130.00° |
2.01∠50.00° |
2.01∠50.00° |
|
| 2 |
100 |
15.07∠-145.15° |
6.07∠-145.15° |
2.57∠33.85° |
2.35∠33.85° |
12.93∠-145.15° |
1.93∠33.85° |
1.93∠33.85° |
|
| 3 |
500 |
8.85∠-5.40° |
3.56∠174.60° |
1.51∠-5.40° |
1.38∠-5.40° |
7.59∠-174.60° |
1.13∠-5.39° |
1.13∠-5.39° |
|
| 4 |
1000 |
2.04∠159.16° |
0.87∠-20.84° |
0.79∠-20.84° |
0.79∠-20.84° |
4.35∠159.17° |
0.65∠-20.82° |
0.65∠-20.82° |
|
| 5 |
3000 |
1.78∠33.19° |
0.72∠146.80° |
0.30∠-33.18° |
0.28∠-33.19° |
1.52∠146.83° |
0.23∠-33.15° |
0.23∠-33.14° |
|
| 6 |
5000 |
1.07∠-35.79° |
0.43∠144.20° |
0.18∠-35.78° |
0.17∠-35.78° |
0.92∠144.24° |
0.14∠-35.72° |
0.14∠-35.71° |
|
| 7 |
10000 |
0.54∠-37.77° |
0.22∠142.21° |
0.09∠-37.75° |
0.09∠-37.75° |
0.46∠-142.28° |
0.07∠-37.63° |
0.07∠-37.62° |
|
Table 4.
Single-phase ground fault (SPGF) current values with different transient resistances on the substation No.2 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
Table 4.
Single-phase ground fault (SPGF) current values with different transient resistances on the substation No.2 bus and capacitive currents in the 10 kV network with isolated neutral configuration.
| No. |
Resistance Rf, Ohm |
Cummulative current, A |
Capacitive current at the Feeder No.1, Substation No.1, A |
Capacitive current at the Feeder No.2, Substation No.1, A |
Capacitive current at the Feeder No.3, Substation No.1, A |
Capacitive current at the Feeder No.1, Substation No.2, A |
Capacitive current at the Feeder No.2, Substation No.2, A |
Capacitive current at the Feeder No.3, Substation No.2, A |
|
| 1 |
1 |
15.75∠50.24° |
6.34∠-129.76° |
2.68∠50.24° |
2.46∠50.24° |
2.24∠50.24° |
2.01∠50.24° |
2.01∠50.24° |
|
| 2 |
100 |
15.10∠34.09° |
6.08∠-145.91° |
2.57∠34.09° |
2.36∠34.09° |
2.14∠34.10° |
1.93∠34.10° |
1.93∠34.10° |
|
| 3 |
500 |
8.87∠-5.15° |
3.57∠174.85° |
1.51∠-5.15° |
1.39∠-5.15° |
1.26∠-5.15° |
1.13∠-5.15° |
1.13∠-5.15° |
|
| 4 |
1000 |
5.08∠-20.60° |
2.05∠159.40° |
0.87∠-20.59° |
0.80∠-20.59° |
0.72∠-20.58° |
0.65∠-20.58° |
0.65∠-20.58° |
|
| 5 |
3000 |
1.78∠-32.95° |
0.72∠147.04° |
0.31∠-32.95° |
0.28∠-32.95° |
0.25∠-32.91° |
0.23∠-32.91° |
0.23∠-32.91° |
|
| 6 |
5000 |
1.07∠-35.55° |
0.43∠144.44° |
0.18∠-35.54° |
0.17∠-35.54° |
0.15∠-35.48° |
0.14∠-35.48° |
0.14∠-35.48° |
|
| 7 |
10000 |
0.54∠-37.53° |
0.22∠142.45° |
0.09∠-37.51° |
0.09∠-37.51° |
0.08∠-37.40° |
0.07∠-37.39° |
0.07∠-37.39° |
|
 . If any of the circuit breakers is tripped by protection or taken out for service, then the corresponding feeder will be removed from the protection scheme and at the switch output
. If any of the circuit breakers is tripped by protection or taken out for service, then the corresponding feeder will be removed from the protection scheme and at the switch output 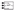 there will be a logical zero.
there will be a logical zero.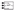 and are sent to the magnitude-angle to complex
and are sent to the magnitude-angle to complex  , from there to the angle summation block
, from there to the angle summation block  . Depending on the number of circuit breakers in the service position and put into operation
. Depending on the number of circuit breakers in the service position and put into operation  , the number of circuit breakers already switched on is subtracted
, the number of circuit breakers already switched on is subtracted  from the number of the unfaulted feeders.
from the number of the unfaulted feeders. and the average angle value of the unfaulted feeders is obtained and in the comparison block, the ZSC signal of the faulty feeder is compared with the ZSC signals of the unfaulted feeders
and the average angle value of the unfaulted feeders is obtained and in the comparison block, the ZSC signal of the faulty feeder is compared with the ZSC signals of the unfaulted feeders  , and the signals are sent to the angle calculation block
, and the signals are sent to the angle calculation block  . If the angle is ±20% of +1800, then at the output of OR operator
. If the angle is ±20% of +1800, then at the output of OR operator  there is a logical one 1 and the signal will then go to the multiport switch
there is a logical one 1 and the signal will then go to the multiport switch  . From there the signal will go to the magnitude comparison module.
. From there the signal will go to the magnitude comparison module. via the operator
via the operator  will be sent to AND operator
will be sent to AND operator  . If the ZSC signal magnitude of the faulty feeder is higher than the specified setting and the angle is 1800, then at the output of AND operator
. If the ZSC signal magnitude of the faulty feeder is higher than the specified setting and the angle is 1800, then at the output of AND operator  there will be a logical one 1 and through the multiport switch
there will be a logical one 1 and through the multiport switch  the ZSC signal will be directed to another operator AND
the ZSC signal will be directed to another operator AND  . If the alarm setting is exceeded
. If the alarm setting is exceeded  , then an SPGF signal will appear
, then an SPGF signal will appear  . If the trip setting is exceeded
. If the trip setting is exceeded  , then the operate delay time of the feeder No.1, in substation No.1, will be 300 ms, and for the remaining feeders, substations No.1 and No.2, it will be 100 ms
, then the operate delay time of the feeder No.1, in substation No.1, will be 300 ms, and for the remaining feeders, substations No.1 and No.2, it will be 100 ms 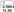 and a trip signal of the corresponding feeder will turn up
and a trip signal of the corresponding feeder will turn up  .
. and obtaining the rms value
and obtaining the rms value  , the ZSC signal will be directed to the magnitude comparison module. If the alarm setting is exceeded
, the ZSC signal will be directed to the magnitude comparison module. If the alarm setting is exceeded  , then an SPGF signal will appear
, then an SPGF signal will appear  . If the trip protection setting is exceeded
. If the trip protection setting is exceeded  , then after 100 ms
, then after 100 ms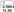 , a trip signal to open the incomer circuit breaker
, a trip signal to open the incomer circuit breaker  will appear.
will appear.