Fixation Time for Competing Beneficial Mutations and Their Genomic Footprint

1. Introduction

The speed of beneficial mutations on their way to fixation in natural populations is a fundamental topic in population genetics. Knowing how fast selection can act to change allele frequencies is essential for understanding evolution. The time for a beneficial allele to spread through a natural population was investigated early in the history of population genetics, using deterministic models $\left[1\right]$. Later, propertiies of the fixation time of individual advantageous mutations under the influence of positive directional selection and genetic drift in populations of finite size have been derived by several authors $\left[2-4\right]$.

However, the spread of two or more beneficial mutations that arise and interact during their fixation process is much less investigated. For two interacting mutations Otto and Barton $\left[5\right]$ have studied the case that the second mutation is less beneficial than the first one. In contrast, Cuthbertson et al. $\left[6\right]$ and Bossert and Pfaffelhuber $\left[7\right]$ considered the scenario that the second mutation is fitter than the first one. Furthermore, they assumed that there is a chance that the first and second mutant recombine such that the recombinant type has the highest fitness and eventually fixes. Here we will focus on this latter case.

We consider the mathematical analysis of the fixation time in conjunction with the theory of selective sweeps. Although beneficial mutations are a comparatively small fraction of all new mutations, some of them may reach fixation and are thus important in evolution. If the fitness effects of these beneficial mutations are sufficiently strong, they may cause selective sweeps, i.e. localized reductions of genetic variation along genomes $\left[8\right]$. Such localized patterns of reduced genetic variation have been convincingly described in a variety of organisms.

Detecting signatures of selective sweeps in genomes is a major goal of current population genetics, as it allows estimating the rate of beneficial mutations going to fixation and finding the genes involved in selection. The inference methods for detecting sweeps depend critically on assumptions on whether the benefical mutations occur sequentially (such that there is at most one beneficial allele on a chromosome on the way to fixation at a time) or whether beneficial alleles overlap with each other. Models of recurrent selective sweeps traditionally assume that in chromosomal regions of normal recombination rates at most one beneficial allele is on the way to fixation $\left[9-11\right]$.

Here we follow the scenario proposed by Bossert and Pfaffelhuber$\left[7\right]$. Thus we assume that, while a highly beneficial mutation spreads in a natural population, a second beneficial mutation arises before the first one has fixed. Furthermore, we envision that the first mutation is less fit than the second one and that recombination may occur between the two chromosomes. Under these conditions a haplotype may be formed that is fitter than the two individual mutations and may therefore eventually fix. To model this process for a population of finite size, Bossert and Pfaffelhuber $\left[7\right]$used stochastic differential equations and calculated the fixation time of a recombinant haplotype under the assumption that it fixes. In contrast, we use a deterministic approach based on ordinary differential equations (ODEs). Thus, in our analysis an explicit assumption about the fixation of a recombinant is not necessary.

We begin by formulating the differential equations for the basic allele frequency changes. Then we introduce nonnormalized variables (that are proportional to the allele frequencies) to find approximate solutions of this system of ODEs. Subsequently, we provide explicit formulas for the fixation time of the recombinant type. Finally, we apply our results to simulation data by Chevin et al. $\left[12\right]$ to describe patterns of selective sweeps in the genome caused by the joint fixation of two mutations due to selection and recombination.

2. Model

We consider a two-locus model, with alleles A and a at locus 1 and B and b at locus 2, respectively. The upper-case letters denote beneficial alleles with selection coefficient $s_2$ at locus 1 and $s_3$ at locus 2, whereas the alleles with lower-case letters are assumed to be neutral (wildtype). This model has four haplotypes AB, Ab, aB, and ab, with frequencies given by the variables $X_1,X_2,X_3$and $X_4$ (which add up to 1). Assuming additive selection, their relative fitnesses are $1+s_1$, $1+s_2$, $1+s_3$and 1, respectively, where $s_1=s_2+s_3$_. Recombination between locus 1 and locus 2 occurs at rate r. Since we are interested in closely linked loci, we assume that $r\ll s_i\ll 1$ for i = 2, 3. In our deterministic setting (without genetic drift) the ODEs for the time change of the variables X_i are obtained by adding the change due to selection and the change due to recombination ($\left[13\right]$, chapt. 2):

$$\begin{gathered} {\displaystyle \frac{d{X}_1}{dt}}=X_1\left(s_1-{\sum }_{j=1}^3{s}_j{X}_j\right)-r\left(X_1{X}_4-X_2{X}_3\right), \\ {\displaystyle \frac{d{X}_2}{dt}}=X_2\left(s_2-{\sum }_{j=1}^3{s}_j{X}_j\right)+r\left(X_1{X}_4-X_2{X}_3\right), \\ {\displaystyle \frac{d{X}_3}{dt}}=X_3\left(s_3-{\sum }_{j=1}^3{s}_j{X}_j\right)+r\left(X_1{X}_4-X_2{X}_3\right), \\ {\displaystyle \frac{d{X}_4}{dt}}=X_4\left(-{\sum }_{j=1}^3{s}_j{X}_j\right)-r\left(X_1{X}_4-X_2{X}_3\right), \end{gathered}$$

(1)

where $t$ measures time in generations.

For $r>0$, which we assume throughout this paper, an exact solution of this system of ODEs is not known. An approximate solution can be obtained using nonnormalized variables Y_i (i = 1, .... , 4) (see $\left[14\right]$ for mutation-selection and $\left[15\right]$ for recombination-selection equations). These are related to the original variables of equations (1) as:

$$X_i={\displaystyle \frac{Y_i}{{\sum }_{j=1}^4{Y}_j}}.$$

(2)

Using (2) it can be shown that the nonnormalized variables satisfy the following ODEs:

$$\begin{gathered} {\displaystyle \frac{d{Y}_1}{dt}}=s_1{Y}_1-{\displaystyle \frac{r}{{\sum }_{i=1}^4{Y}_i}}\left(Y_1{Y}_4-Y_2{Y}_3\right), \\ {\displaystyle \frac{d{Y}_2}{dt}}=s_2{Y}_2+{\displaystyle \frac{r}{{\sum }_{i=1}^4{Y}_i}}\left(Y_1{Y}_4-Y_2{Y}_3\right), \\ {\displaystyle \frac{d{Y}_3}{dt}}=s_3{Y}_3+{\displaystyle \frac{r}{{\sum }_{i=1}^4{Y}_i}}\left(Y_1{Y}_4-Y_2{Y}_3\right), \\ {\displaystyle \frac{d{Y}_4}{dt}}=-{\displaystyle \frac{r}{{\sum }_{i=1}^4{Y}_i}}\left(Y_1{Y}_4-Y_2{Y}_3\right). \end{gathered}$$

(3)

Note that rescaling all $Y_i$by a constant leaves $X_i$invariant. To fix this scaling, we use $X_i\left(0\right)=Y_i\left(0\right)$for all i = 1, ... , 4. As outlined in Appendix (A), the following approximate solutions of the ODEs (3) can be found, assuming that both mutations A and B arise on background ab (so that $X_1\left(0\right)=0)$:

$$\begin{gathered} Y_1\left(t\right)\approx r{X}_2\left(0\right)X_3\left(0\right)e^{s_{1}t}{\int }_0^t{\displaystyle \frac{1}{X_4\left(0\right)+X_2\left(0\right)e^{s_2\tau }+X_3\left(0\right)e^{s_3\tau }}}d\tau , \\ {Y}_2\left(t\right)\approx X_2\left(0\right)e^{s_{2}t}\left[1-r{X}_3\left(0\right){\int }_0^t{\displaystyle \frac{e^{s_3\tau }}{X_4\left(0\right)+X_2\left(0\right)e^{s_2\tau }+X_3\left(0\right)e^{s_3\tau }}}d\tau \right], \\ {Y}_3\left(t\right)\approx X_3\left(0\right)e^{s_{3}t}\left[1-r{X}_2\left(0\right){\int }_0^t{\displaystyle \frac{e^{s_2\tau }}{X_4\left(0\right)+X_2\left(0\right)e^{s_2\tau }+X_3\left(0\right)e^{s_3\tau }}}d\tau \right], \\ {Y}_4\left(t\right)\approx X_4\left(0\right)+r{X}_2\left(0\right)X_3\left(0\right){\int }_0^t{\displaystyle \frac{e^{s_1\tau }}{X_4\left(0\right)+X_2\left(0\right)e^{s_2\tau }+X_3\left(0\right)e^{s_3\tau }}}d\tau . \end{gathered}$$

(4)

These approximations were first established and tested by Yun Song (personal communication). Numerical analysis suggests that they are generally excellent for $r<min\left(s_2,s_3\right)$ /10.

3. Fixation time

Using equations (4) we can find the fixation time of two interfering mutations. We call an allele or haplotype fixed when it reaches frequency $1-\delta$and denote this time $T$. Thus $T$ measures the time from some initial frequency at $t=0$to $1-\delta$. The initial frequency may be the frequency of a newly arising mutation. In a haploid population of size $N$, which we consider here, this initial frequency is given by $1/N$. In our case, however, we are interested in the fixation of the double mutant $AB$whose initial frequency is $X_1\left(0\right)=0,$as $AB$ arises during the fixation process due to recombination. Thus, the fixation time of $AB$ is found by solving the equation

$$X_1\left(T\right)=1-\delta ,$$

(5)

where $\delta$ is a small number.

Next we express equation (5) in terms of nonnormalized variables and obtain

$$X_1\left(T\right)={\left(1+{\sum }_{i=2}^4{\displaystyle \frac{Y_i\left(T\right)}{Y_1\left(T\right)}}\right)}^{-1}=1-\delta .$$

Using (4) with $X_2\left(0\right){>X}_3\left(0\right)$ and $s_3>s_2$, this equation can be approximated by

$$\delta \approx {\displaystyle \frac{Y_2\left(T\right)}{Y_1\left(T\right)}}+{\displaystyle \frac{Y_3\left(T\right)}{Y_1\left(T\right)}}.$$

(6)

Evaluating the terms on the right-hand side of equation (6) requires that we find useful approxiations of the integrals in equations (4) because closed formulae for these integrals are not known (see Appendix (B)). Besides the two aforementioned assumptions, we assume that $T$is sufficiently large such that the second mutation is eventually dominating the first one; i.e. $X_2\left(0\right)e^{s_{2}T}\ll X_3\left(0\right)e^{s_{3}T}$, and population size is large $\left(N>{10}^5\right)$such that selection is strong $(N{s}_i>100).$Under these assumptions we find for the integrals $I_i\left(T\right)$ defined in Appendix (B):

$$\begin{gathered} I_1\left(T\right)\approx -{\displaystyle \frac{ln\left(X_2\left(0\right)\right)}{s_2\left(1-X_2\left(0\right)\right)}}, \\ {I}_2\left(T\right)<{\displaystyle \frac{T}{X_3\left(0\right)}}, \\ {I}_3\left(T\right)\approx {\displaystyle \frac{1}{X_2\left(0\right)}}\left[{\displaystyle \frac{s_3}{s_2\left(s_3-s_2\right)}}ln\left(X_2\left(0\right)\right)-{\displaystyle \frac{1}{s_3-s_2}}ln\left(X_3\left(0\right)\right)\right]. \end{gathered}$$

(7)

Inserting these formulas into equation (6), this equation can be written in the following form:

$$\delta I_1\left(T\right)\approx {\displaystyle \frac{1}{X_3\left(0\right)e^{s_{3}T}}}\left({\displaystyle \frac{1}{r}}-X_3\left(0\right)I_2\left(T\right)\right)+{\displaystyle \frac{1}{X_2\left(0\right)e^{s_{2}T}}}\left({\displaystyle \frac{1}{r}}-X_2\left(0\right)I_3\left(T\right)\right).$$

(8)

We can neglect the first term on the right-hand side of equation (8) for the following reasons: first, because we assumed that $X_2\left(0\right)e^{s_{2}T}\ll X_3\left(0\right)e^{s_{3}T},$ and second since $X_3\left(0\right)I_2\left(T\right)$ is bounded by ${\displaystyle \frac{1}{r}},$the term ${\displaystyle \frac{X_3\left(0\right)I_2\left(T\right)}{X_2\left(0\right)e^{s_{2}T}}}$ can be neglected compared to ${\displaystyle \frac{1}{X_2\left(0\right)e^{s_{2}T}}}{\displaystyle \frac{1}{r}}$. This leads to equation (9):

$$-{\displaystyle \frac{\delta X_2\left(0\right)ln\left(X_2\left(0\right)\right)}{s_2\left(1-X_2\left(0\right)\right)}}\approx e^{-s_{2}T}\left({\displaystyle \frac{1}{r}}-{\displaystyle \frac{s_{3}ln\left(X_2\left(0\right)\right)}{s_2\left(s_3-s_2\right)}}+{\displaystyle \frac{ln\left(X_3\left(0\right)\right)}{s_3-s_2}}\right).$$

(9)

Finally, we introduce population size $N$into this equation by writing $\delta ={\displaystyle \frac{1}{N}}{,X}_3\left(0\right)={\displaystyle \frac{1}{N}}$ and $X_2\left(0\right)={\displaystyle \frac{x_{20}}{N}}$ , where $x_{20}$is the number of $A$alleles at $t=0.$ Then solving the equation for $T$yields

$$T\approx {\displaystyle \frac{1}{s_2}}\left[2ln\left(N\right)-ln\left({\displaystyle \frac{x_{20}}{s_2}}\right)-ln\left({\displaystyle \frac{ln\left(\frac{N}{x_{20}}\right)}{1-\frac{x_{20}}{N}}}\right)+ln\left({\displaystyle \frac{1}{r}}+{\displaystyle \frac{s_3}{s_2}}{\displaystyle \frac{ln\left(\frac{N}{x_{20}}\right)}{s_3-s_2}}-{\displaystyle \frac{ln\left(N\right)}{s_3-s_2}}\right)\right].$$

(10)

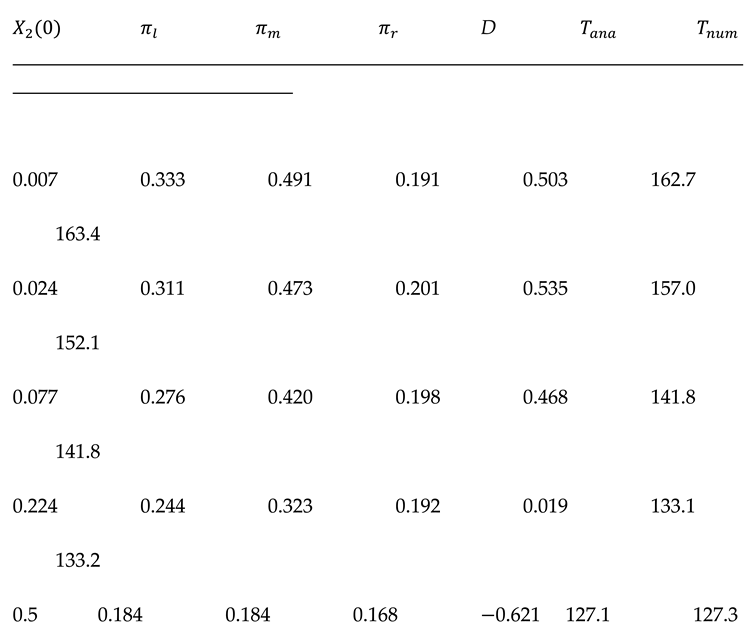
Table 1 shows that this result agrees very well with the numerical solution of equation (8).

As expected, the formula for $T$ is complex. However, in the interesting parameter range of small $r$values such that ${\displaystyle \frac{1}{r}}\gg \left|{\displaystyle \frac{s_3}{s_2}}{\displaystyle \frac{ln\left(\frac{N}{x_{20}}\right)}{s_3-s_2}}-{\displaystyle \frac{ln\left(N\right)}{s_3-s_2}}\right|$, we may approximate equation (10) as

$$T\approx {\displaystyle \frac{1}{s_2}}\left[2ln\left(N\right)-ln\left({\displaystyle \frac{r}{s_2}}{\displaystyle \frac{x_{20}}{1-\frac{x_{20}}{N}}}ln\left({\displaystyle \frac{N}{x_{20}}}\right)\right)\right]$$

(11)

The first term on the right-hand side of equation (11) equals the fixation time of a new allele starting at frequency ${\displaystyle \frac{1}{N}}$and ending at$1-{\displaystyle \frac{1}{N}}$ , driven by positive directional selection with selection coeffcient$s_2$. This term also appears in the result of Bossert and Pfaffelhuber $\left[7\right]$. The denominator $s_2$can be explained as follows. To go to fixation, the successful recombinant AB with fitness $1+s_2+s_3$has to compete against the – at the time – dominant aB type with fitness $1+s_3,$having a fitness advantage $s_2.$Furthermore, unless $r$is very small, the second term in equation (11) is negative such that $T$is smaller than ${\displaystyle \frac{2ln\left(N\right)}{s_2}}$. This is not surprising as we are dealing here with an equation describing continuous input of new $AB$alleles due to recombination, similar to the case of fixation under continuous mutation pressure and positive directional selection ($\left[16\right]$, equation (8)). Thus, based on equation (11) we obtain a relatively simple formula for the threshold of $r$

$$r_c={\displaystyle \frac{s_2}{x_{20}}}{\displaystyle \frac{1-\frac{x_{20}}{N}}{ln\left(\frac{N}{x_{20}}\right)}}$$

(12)

above which recombination speeds up fixation time, whereas for $r<r_c$the second term in equation (11) turns positive, such that the fixation time $T$ becomes larger than ${\displaystyle \frac{2ln\left(N\right)}{s_2}}$, meaning that the input of recombinants ceases.

4. Genomic footprint of competing mutations

As an application we analyze simulation data from a study of genetic variation at neutral sites located between two selected loci $\left[12\right]$. The data were obtained using Monte Carlo simulations of a Wright-Fisher model ($\left[13\right]$, chapt. 3) with two selected loci and three neutral loci. The three neutral sites are located between the selected loci as described in Table 1. Table 1 also contains the parameter values used in the simulations. They meet the assumptions of our analysis, except for the populaton size. In the simulations $N=20000$was used, while in our derivation $N>{10}^5$was suggested. To check whether this causes problems, we compared the analytical results for T from equation (10) with the numerical solutions of equation (8) for $N=20000.$ However, as Table 1 (columns 6 and 7) shows, no discrepancies could be found.

The first observation concerns T as a function of $X_2\left(0\right)$. Since $r=0.005$ was used in all simulations and in all cases $r$is larger than the threshold $r_c$ (equation 12), we expect that T is smaller than ${\displaystyle \frac{2ln\left(N\right)}{s_2}}=198.1$and decreases with increasing $X_2\left(0\right)={\displaystyle \frac{x_{20}}{N}}$. This is indeed the case. The most pronounced effect of $X_2\left(0\right)$on fixation time is observed for small values of $X_2\left(0\right)<0.1.$ For larger values of $X_2\left(0\right)$, however, fixation time is relatively constant. This observation is consistent with the formulas for T, especially equation (11), which shows that, for given${\displaystyle \frac{r}{s_2}}$ , fixation time depends about logarithmally on $x_{20}$. This formula also says that recombination is most important in speeding up fixation when the second mutation is introduced at low $X_2\left(0\right)$values. Here the interference between the two mutations is largest.

Next we discuss the simulation results of Chevin et al. $\left[12\right]$ in the light of our analysis. Variation at the neutral loci (close to the selected ones) shows typical hitchhiking effects $\left[8\right]$; i.e. variation is reduced relative to the neutral standard level such that stronger selection acting at locus 2 $\left(s_3>s_2\right)$leads to a greater reduction than at the neutral site near locus 1. Furthermore, variation at the neutral locus in the middle between the two selected loci is greater than that at the loci near the selected sites, which is also a typical hitchhiking effect, because the distance to the selected loci (and hence recombination rate) is larger.

Increasing $X_2\left(0\right)$generally leads to stronger hitchhiking effects such that levels of neutral variation decrease with $X_2\left(0\right)$. This can be clearly observed at the neutral locus close to locus 1, whereas at the neutral locus close to the stronger selected site this is hardly visible. At the neutral locus in the middle there is also a strong decay of variation with increasing levels of $X_2\left(0\right)$. The effect of $X_2\left(0\right)$ on hitchhiking is likely due to the interference of the two mutations. The longer they compete with each other on their way to fixation, the weaker their hitchhiking effect. This has already been observed in other studies (e.g. $\left[17\right]$).

Finally, we discuss D, a statistic introduced by Tajima $\left[18\right]$. In Table 1 (column 5) only the D values for the neutral locus in the middle between locus 1 and 2 are shown. All D values at the other two loci are negative as expected from the theory of genetic hitchhiking. A negative D is observed when an allele has either a lower or higher frequency than expected by the neutral theory. Interestingly, however, Chevin et al. $\left[12\right]$ observed strongly positive D values for $X_2\left(0\right)=0.007,0.024,$and 0.077, whereas D is around zero or negative for larger $X_2\left(0\right).$ Positive values of D indicate that alleles are at intermediate frequencies, such as predicted for balancing selection. In our case, however, this is probably not a valid hypothesis, at least concerning the standard models of balancing selection. A plausible hypothesis proposed by Bossert and Pfaffelhuber $\left[7\right]$ is that positive D may be observed when a haplotype structure arises in the genome through recombination between different haplotypes consisting of multiple polymorphic loci. Haplotype structures exist in populations only if polymorphisms at individual loci tend to be in intermediate frequency (such that the less frequent variants are not too rare). This may be the case for $X_2\left(0\right)=0.007,0.024,$and 0.077, but not for the larger $X_2\left(0\right)$ values, for which diversity is more heavily reduced (Table 1). An alternative, though related hypothesis postulates that the dynamics of the two selected mutations (while in repulsion) reaches nonnegligible frequencies at similar times such that recombination may produce haplotypes with the two favorable alleles in coupling $\left[12\right]$.

If these hypotheses are correct, a genomic footprint of competing beneficial mutations may be detected by measuring Tajima’s D and/or linkage disequilibrium. In general, footprints associated with selective sweeps caused by the fixation of beneficial mutations can be found in genetic data if their characteristic pattern of variation, such as a dip of nucleotide diversity around a selected site or a haplotype structure revealed by linkage disequilibrium, persist for some time. For Wright-Fisher populations such signatures may be detected for up to 0.1$N$ generations after fixation of the driving mutations $\left[19,20\right]$.

5. Discussion

For a highly beneficial mutation A at locus 1 spreading in a very large population, we have analyzed the scenario when a second beneficial mutant B arises in repulsion; i.e. on a chromosome carrying the wildtype a at locus 1. Under the assumptions that the fitness of B is greater than that of A and that A- and B-carrying chromosomes can recombine, recombinants AB may form and eventually fix. We present approximate formulas for the fixation time of AB under additive fitness of the mutations as a function of $X_2\left(0\right),$the frequency of A at the introduction of B. The latter parameter turns out to be useful for describing the interference between competing beneficial mutations.

Our analysis suggests that the effect of interference between beneficial mutations is most pronounced for small values of $X_2\left(0\right)<0.1.$In this parameter range fixation time decreases substantially with $X_2\left(0\right).$ However, for larger values fixation time is relatively constant (Table 1). This agrees with the formulas for T, especially equation (11), which shows that T depends about logarithmally on $X_2\left(0\right)$. Similarly, the effect of interference on the genomic footprint of competing mutations can be clearly discerned. For small values of $X_2\left(0\right)=0.007,0.024,$and 0.077, a strongly positive D was observed, whereas D is around zero or negative for larger $X_2\left(0\right)\left(\mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}1\right).$ Positive values of D indicate that alleles are in intermediate frequencies. This may be observed when a haplotype structure arises in the genome through recombination between different allelic types consisting of multiple polymorphic loci $\left[7,12\right]$.

Finally, we address the question whether we can expect observing patterns of overlapping selective sweeps due to competing mutations in genomes. Estimates of the average selection coefficient $s$and the rate $\nu$at which beneficial mutations arise and go to fixation (i.e. selective substitutions) are known for some species including Drosophila melanogaster. For instance, Jensen et al. $\left[21\right]$ analyzed a dataset of genetic variation from the euchromatic part of the genome of a D. melanogaster population from Africa, which is – roughly speaking – the recombining portion of chromosomes. They obtained the following estimates: $s=0.002$, $N=5\times {10}^6$and $\nu =4.2{\times 10}^{-11}$per generation per nucleotide site. Since under selection and genetic drift the mean fixation time (conditional on fixation) for a diploid species such as D. melanogaster is $T={\displaystyle \frac{4}{s}}ln\left(2Ns\right)$ $\left[3\right]$, we find that the probability of a second substitution arising on a chromosome during the sojourn of the first one to fixation is $T\nu =8.3\times {10}^{-7}$ per nucleotide site. Multiplying $T\nu$ with the size of the euchromatic part of a chromosome (in D. melanogaster approximately 24 Mb $=2.4\times {10}^7$base pairs), we find that on average at about 20 sites of a chromosome strongly selected substitutions could arise and compete with the first mutation during its sojourn to fixation.

An example that some of these selected substitutions occur in close proximity in the genome is found at the polyhomeotic locus of a European population of D. melanogaster. Voigt et al. $\left[22\right]$ report a case in which five selected substitutions (i.e. nearly fixed variants between Europe and Africa) are located in the 5-kb intergenic region between polyhomeotic proximal and the gene CG3835 within a segment of 2.28 kb. They showed that these five selected variants are involved in adaptation of D. melanogaster to the higher temperature in Europe compared to that of the ancestral species range in Africa. Variation is generally low in the whole polyhomeotic region and Tajima’s D is strongly negative, as expected after a sweep. However, using a larger dataset than in her previous study, Susanne Voigt (personal communication) found evidence that the five beneficial substitutions that likely caused the sweep did not act independently in a sequential manner but were selected as haplotype block. As a consequence, an elevated level of Tajima’s D in the fragment containing the five selected substitutions was not detected.

A more promising example in the context of interference between beneficial mutations may be the Agouti locus in deer mice. Here the precise mutations required for adaptation to light-colored soil of the Nebraska Sand Hills have been identified $\left[23\right]$. The authors claim that – contrary to the aforementioned Drosophila case – the light Sand Hills phenotype is the result of independent selection on many mutations within the Agouti locus spanning about 120 kb. Thus, in this case a genomic footprint of interference between beneficial mutations may be encountered in sequence data.