About Stability of SAIRP Epidemic Model Under Stochastic Perturbations of the Type of Poisson's Jumps

1. Introduction

So-called SAIRP epidemic model is described [1,2,3] by the system of five ordinary differential equations

$$\begin{array}{c}\dot{S}\left(t\right)=\Lambda -\left[\beta (1-p(1-u)){\displaystyle \frac{\theta A\left(t\right)+I\left(t\right)}{N\left(t\right)}}+\psi p(1-u)+\mu \right]S\left(t\right)+\omega P\left(t\right),\hfill \\ \dot{A}\left(t\right)=\beta (1-p(1-u)){\displaystyle \frac{\theta A\left(t\right)+I\left(t\right)}{N\left(t\right)}}S\left(t\right)-(\nu +\mu )A\left(t\right),\hfill \\ \dot{I}\left(t\right)=\nu A\left(t\right)-(\delta +\mu )I\left(t\right),\hfill \\ \dot{R}\left(t\right)=\delta I\left(t\right)-\mu R\left(t\right),\hfill \\ \dot{P}\left(t\right)=\psi p(1-u)S\left(t\right)-(\omega +\mu )P\left(t\right).\hfill \end{array}$$

(1)

Here it is assumed that the total population

$$N\left(t\right)=S\left(t\right)+A\left(t\right)+I\left(t\right)+R\left(t\right)+P\left(t\right),t\ge 0,$$

is subdivided into five distinct classes:

-

susceptible individuals ($S\left(t\right)$);

-

asymptomatic infected individuals ($A\left(t\right)$);

-

active infected individuals ($I\left(t\right)$);

-

removed (including recovered and deceased) individuals ($R\left(t\right)$);

-

protected individuals ($P\left(t\right)$).

Besides, the total population $N\left(t\right)$ has a variable size, the susceptible individuals $S\left(t\right)$ become infected by contact with active infected $I\left(t\right)$ and asymptomatic infected individuals $A\left(t\right)$, at a rate of infection

$$\beta {\displaystyle \frac{\theta A\left(t\right)+I\left(t\right)}{N\left(t\right)}},$$

where $\theta$ represents a modification parameter for the infectiousness of the asymptomatic infected individuals $A\left(t\right)$. It is assumed also that all parameters of the system (1) are positive and, besides, $p<1$, $u<1$.

In [1,2,3] some properties of the system (1) are studied in the deterministic case, in [4] the SAIRP epidemic model is studied by the assumption that the system (1) is exposed to stochastic perturbations of the white noise type [5]. It is supposed also that these stochastic perturbations are directly proportional to the deviation of the system state from one of the two system’s equilibria, that are defined [4] by the system of five algebraic equations

$$\begin{array}{c}\hfill \Lambda -\left[\beta (1-p(1-u)){\displaystyle \frac{\theta A+I}{N}}+\psi p(1-u)+\mu \right]S+\omega P=0,\\ \hfill \beta (1-p(1-u)){\displaystyle \frac{\theta A+I}{N}}S-(\nu +\mu )A=0,\\ \hfill \nu A-(\delta +\mu )I=0,\\ \hfill \delta I-\mu R=0,\\ \hfill \psi p(1-u)S-(\omega +\mu )P=0,\end{array}$$

(2)

with the two solutions:

1) disease-free equilibrium

$$E_0^{*}=(S_0^{*},A_0^{*},I_0^{*},R_0^{*},P_0^{*}),$$

where

$$\begin{gathered} S_0^{*}={\displaystyle \frac{(\omega +\mu )\Lambda }{\mu [\omega +\mu +\psi p(1-u\left)\right]}}, \\ {A}_0^{*}=I_0^{*}=R_0^{*}=0, \\ {P}_0^{*}={\displaystyle \frac{\psi p(1-u)\Lambda }{\mu [\omega +\mu +\psi p(1-u\left)\right]}}, \end{gathered}$$

(3)

and

2) endemic equilibrium

$$E_{+}^{*}=\left(S_{+}^{*},A_{+}^{*},I_{+}^{*},R_{+}^{*},P_{+}^{*}\right)$$

with

$$\begin{gathered} S_{+}^{*}={\displaystyle \frac{(\omega +\mu )\Lambda }{\mu [\omega +\mu +\psi p(1-u\left)\right]}}{R}_0^{-1}, \\ {A}_{+}^{*}={\displaystyle \frac{\Lambda }{\nu +\mu }}(1-R_0^{-1}), \\ {I}_{+}={\displaystyle \frac{\nu \Lambda }{(\nu +\mu )(\delta +\mu )}}(1-R_0^{-1}), \\ {R}_{+}^{*}={\displaystyle \frac{\delta \nu \Lambda }{\mu (\nu +\mu )(\delta +\mu )}}(1-R_0^{-1}), \\ {P}_{+}^{*}={\displaystyle \frac{\psi p(1-u)\Lambda }{\mu [\omega +\mu +\psi p(1-u\left)\right]}}{R}_0^{-1}, \end{gathered}$$

(4)

where $R_0$ is the basic reproduction number that is defined as follows:

$$R_0={\displaystyle \frac{\beta (1-p(1-u\left)\right)\left(\theta \right(\delta +\mu )+\nu )(\omega +\mu )}{(\nu +\mu )(\delta +\mu )(\omega +\mu +\psi p(1-u\left)\right)}}>1.$$

(5)

Note also that, summing all equations of the system (2), we obtain $N^{*}={\displaystyle \frac{\Lambda }{\mu }}$ for the both equilibria (3) and (4).

In contrast to [1,2,3,4], in this paper stability in probability of the both equilibria (3) and (4) of the SAIRP epidemic model (1) is studied for the first time under stochastic perturbations defined by a combination of the white noise and Poisson’s jumps. Following I.I. Gikhman and A.V. Skorokhod [5], the SAIRP model (1) becomes an object of the theory of stochastic differential equations with Poisson’s measure.

Remark 1.

Iosif Il’ich Gikhman (1918-1985) and Anatolij Vladimirovich Skorokhod (1930-2011) are two outstanding Ukrainian mathematicians, whose works have made an invaluable contribution to the development of the modern theory of stochastic processes, in particular, to the development of the theory of stochastic differential equations with Poisson’s measure. They are the authors of a large number of fundamental papers and books in the general theory of stochastic processes and in the theory of stochastic differential equations, in particular, [5,6,7,8].

2. Stochastic Perturbations

Let $\{\Omega ,\mathfrak{F},\mathbf{P}\}$ be a complete probability space, $\{{\mathfrak{F}}_t,t\ge 0\}$ be a nondecreasing family of sub-$\sigma$-algebras of $\mathfrak{F}$, i.e., ${\mathfrak{F}}_{t_1}\subset {\mathfrak{F}}_{t_2}\subset \mathfrak{F}$ for $t_1<t_2$, $\mathbf{E}$ be the mathematical expectation with respect to the measure $\mathbf{P}$.

Let us suppose that the system (1) is exposed to stochastic perturbations of the type of

$${\xi }_i\left(t\right)={\sigma }_i{w}_i\left(t\right)+{\gamma }_i{\tilde{\nu }}_i\left(t\right),i=1,...,5,$$

(6)

where ${\sigma }_i$ and ${\gamma }_i$ are arbitrary constants,

$${\tilde{\nu }}_i\left(t\right)={\nu }_i\left(t\right)-{\lambda }_{i}t,i=1,...,5,$$

$w_i\left(t\right)$ and ${\nu }_i\left(t\right)$ are respectively ${\mathfrak{F}}_t$-measurable and mutually independent the Wiener and the Poisson processes, $\mathbf{E}{\nu }_i\left(t\right)={\lambda }_{i}t$, ${\lambda }_i>0$ [5,6,7,8,9,10,11].

Remark 2.

Note that the Wiener processes describe continuous stochastic perturbations of the Brownian motion type, while the Poisson processes describe stochastic perturbations of the jumps type. Stability of some other models under stochastic perturbations of the type of Poisson’s jumps is studied in [9,10,11].

Let us suppose also that the stochastic perturbations (6) are directly proportional to the deviation of the system state $\left(S\right(t),A(t),I(t),R(t),P(t\left)\right)$ from one of the equilibria $(S^{*},A^{*},I^{*},R^{*},P^{*})$. As a result we obtain the system of stochastic differential equations [5,8]

$$\begin{array}{cc}\hfill dS\left(t\right)=& \left[\Lambda -\left(\beta (1-p(1-u)){\displaystyle \frac{\theta A\left(t\right)+I\left(t\right)}{N\left(t\right)}}\psi p(1-u)+\mu \right)S\left(t\right)+\omega P\left(t\right)\right]dt\hfill \\ & +(S\left(t\right)-S^{*})d{\xi }_1\left(t\right),\hfill \\ \hfill dA\left(t\right)=& \left[\beta (1-p(1-u)){\displaystyle \frac{\theta A\left(t\right)+I\left(t\right)}{N\left(t\right)}}S\left(t\right)-(\nu +\mu )A\left(t\right)\right]dt\hfill \\ & +(A\left(t\right)-A^{*})d{\xi }_2\left(t\right),\hfill \\ \hfill dI\left(t\right)=& [\nu A\left(t\right)-(\delta +\mu )I\left(t\right)]dt+(I\left(t\right)-I^{*})d{\xi }_3\left(t\right),\hfill \\ \hfill dR\left(t\right)=& [\delta I\left(t\right)-\mu R\left(t\right)]dt+(R\left(t\right)-R^{*})d{\xi }_4\left(t\right),\hfill \\ \hfill dP\left(t\right)=& [\psi p(1-u)S\left(t\right)-(\omega +\mu )P\left(t\right)]dt+(P\left(t\right)-P^{*})d{\xi }_5\left(t\right).\hfill \end{array}$$

(7)

Note that the equilibrium $(S^{*},A^{*},I^{*},R^{*},P^{*})$ of the deterministic system (1) is also the solution to the system of stochastic differential equations (7). Stochastic perturbations of this type were first proposed in [12] for the SIR epidemic model and later also for some other mathematical models in various applications (see, for instance, [13,14,15,16,17] and the references therein).

Let us note also, that unlike the present paper, where the considered system has a dimension 5, in the all mentioned previous works stochastic perturbations of the proposed type are used for systems of a dimension less than 5. This means, in particular, that the dimension of the system under consideration can in principle be increased even more.

3. Linear Approximation

Consider the nonlinear differential equation

$$\dot{x}\left(t\right)=F\left(x\left(t\right)\right),$$

(8)

where $x\left(t\right)\in {\mathbf{R}}^n$ and the equation $F\left(x\right)=0$ has a solution $x^{*}$ that is an equilibrium of differential Equation (8). Using the new variable $y\left(t\right)=x\left(t\right)-x^{*}$, represent Equation (8) in the form

$$\begin{array}{c}\dot{y}\left(t\right)=F(x^{*}+y\left(t\right)).\hfill \end{array}$$

(9)

It is clear that stability of the zero solution to Equation (9) is equivalent to stability of the equilibrium $x^{*}$ of Equation (8).

Let $J_F=∥{\displaystyle \frac{\partial F_i}{\partial x_j}}∥$, $i,j=1,...,n$, be the Jacobian matrix of the function $F=\{F_1,...,F_n\}$ and ${lim}_{\left|y\right|\to 0}{\displaystyle \frac{\left|o\right(y\left)\right|}{\left|y\right|}}=0$, where $\left|y\right|$ is the Euclidean norm in ${\mathbf{R}}^n$. Using Taylor’s expansion in the form

$$F(x^{*}+y)=F\left(x^{*}\right)+J_F\left(x^{*}\right)y+o\left(y\right)$$

and the equality $F\left(x^{*}\right)=0$, we obtain the linear approximation

$$\dot{z}\left(t\right)=J_F\left(x^{*}\right)z\left(t\right)$$

(10)

of the nonlinear differential Equation (9). So, a condition for the asymptotic stability of the zero solution of the linear Equation (10) is also a condition for the local stability of the equilibrium $x^{*}$ of the initial nonlinear Equation (8).

To construct the linear approximation of the system (7) let us put

$$\begin{array}{cc}x\left(t\right)=\hfill & {(S\left(t\right),A\left(t\right),I\left(t\right),R\left(t\right),P\left(t\right))}^{\prime },\\ x^{*}=\hfill & {(S^{*},A^{*},I^{*},R^{*},P^{*})}^{\prime },\\ y\left(t\right)=\hfill & x\left(t\right)-x^{*},\\ N^{*}=\hfill & S^{*}+A^{*}+I^{*}+R^{*}+P^{*}.\end{array}$$

(11)

Here and everywhere below ′ is the sign of transpose.

Representing the system (1) in the form (8) and calculating the Jacobian matrix, we obtain the linear part of the system (7) in the form

$$dz\left(t\right)=Az\left(t\right)dt+\sum _{i=1}^5{B}_{i}z\left(t\right)d{w}_i\left(t\right)+\sum _{i=1}^5{C}_{i}z\left(t\right)d{\tilde{\nu }}_i\left(t\right),$$

(12)

where $z\left(t\right)\in {\mathbf{R}}^5$, $B_i$ and $C_i$ are the $5\times 5$-matrices with all zero elements besides of respectively $b_{ii}={\sigma }_i$ and $c_{ii}={\gamma }_i$, $i=1,...,5$.

Note that for $C_i=0$, $i=1,...,5$, linear Equation (12) was obtained in [4] with

$$A=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& a_{14}& a_{15}\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}\\ 0& \nu & -(\delta +\mu )& 0& 0\\ 0& 0& \delta & -\mu & 0\\ \psi p(1-u)& 0& 0& 0& -(\omega +\mu )\end{array}\right],$$

(13)

where

$$\begin{array}{c}{a}_{11}=-\left[\beta (1-p(1-u)){\displaystyle \frac{\theta A^{*}+I^{*}}{N^{*}}}\left(1-{\displaystyle \frac{S^{*}}{N^{*}}}\right)+\psi p(1-u)+\mu \right],\hfill \\ a_{12}=-\beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}}\left(\theta -{\displaystyle \frac{\theta A^{*}+I^{*}}{N^{*}}}\right),\hfill \\ a_{13}=-\beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}}\left(1-{\displaystyle \frac{\theta A^{*}+I^{*}}{N^{*}}}\right),\hfill \\ a_{14}=\beta (1-p(1-u)){\displaystyle \frac{S^{*}(\theta A^{*}+I^{*})}{{\left(N^{*}\right)}^2}},\hfill \\ a_{15}=a_{14}+\omega ,\hfill \end{array}$$

(14)

and

$$\begin{array}{c}{a}_{21}=\beta (1-p(1-u)){\displaystyle \frac{\theta A^{*}+I^{*}}{N^{*}}}\left(1-{\displaystyle \frac{S^{*}}{N^{*}}}\right),\hfill \\ a_{22}=\beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}}\left(\theta -{\displaystyle \frac{\theta A^{*}+I^{*}}{N^{*}}}\right)-(\nu +\mu ),\hfill \\ a_{23}=\beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}}\left(1-{\displaystyle \frac{\theta A^{*}+I^{*}}{N^{*}}}\right),\hfill \\ a_{24}=a_{25}=-\beta (1-p(1-u)){\displaystyle \frac{S^{*}(\theta A^{*}+I^{*})}{{\left(N^{*}\right)}^2}}.\hfill \end{array}$$

(15)

In particular, for the equilibrium $E_0^{*}$ (3) the elements (14) and (15) of the matrix (13) are respectively

$$\begin{array}{c}{a}_{11}=-\left(\psi p(1-u)+\mu \right),\hfill \\ a_{12}=-\theta \beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}},\hfill \\ a_{13}=-\beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}},\hfill \\ a_{14}=0,a_{15}=\omega ,\hfill \end{array}$$

(16)

and

$$\begin{array}{c}{a}_{21}=a_{24}=a_{25}=0,\hfill \\ a_{22}=\theta \beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}}-(\nu +\mu ),\hfill \\ a_{23}=\beta (1-p(1-u)){\displaystyle \frac{S^{*}}{N^{*}}}.\hfill \end{array}$$

(17)

4. Stability

Following [13], let us consider the definitions of the different types of stability for the nonlinear system (7), linear Equation (12) and the relationship between these two types of definitions (see Remark 3).

Definition 1.

Put

$$\begin{array}{cc}\hfill y\left(t\right)& =(S\left(t\right),A\left(t\right),I\left(t\right),R\left(t\right),P\left(t\right))-(S^{*},A^{*},I^{*},R^{*},P^{*})\hfill \\ & =(S\left(t\right)-S^{*},A\left(t\right)-A^{*},I\left(t\right)-I^{*},R\left(t\right)-R^{*},P\left(t\right)-P^{*}).\hfill \end{array}$$

The solution $(S^{*},A^{*},I^{*},R^{*},P^{*})$ of the system (7) is called stable in probability if for any ${\epsilon }_1>0$ and ${\epsilon }_2>0$ there exists $\delta >0$ such that $y\left(t\right)$ satisfies the condition $\mathbf{P}\{\underset{t\ge 0}{sup}\left|y\left(t\right)\right|>{\epsilon }_1\}<{\epsilon }_2$ for any $y\left(0\right)$ such that $\mathbf{P}\left\{\right|y\left(0\right)|<\delta \}=1$.

Definition 2.

The zero solution to Equation (12) is called:

-mean square stable if for each $\epsilon >0$ there exists a $\delta >0$ such that ${\mathbf{E}\left|z\left(t\right)\right|}^2<\epsilon$, $t\ge 0$, provided that ${\mathbf{E}\left|z\left(0\right)\right|}^2<\delta$;

-asymptotically mean square stable if it is mean square stable and for each initial value $z\left(0\right)$ such that ${\mathbf{E}\left|z\left(0\right)\right|}^2<\infty$, the solution $z\left(t\right)$ to Equation (12) satisfies the condition $\underset{t\to \infty }{lim}\mathbf{E}{\left|z\left(t\right)\right|}^2=0$.

Remark 3.

It is known [13] that sufficient conditions for asymptotic mean square stability of the zero solution of the linear part of a stochastic nonlinear system with the order of nonlinearity higher than one at the same time are sufficient conditions for stability in probability of the solution of the initial nonlinear system. So, for investigation of stability in probability of the equilibrium $(S^{*},A^{*},I^{*},R^{*},P^{*})$ of the nonlinear system (7) it is enough to get conditions for asymptotic mean square stability of the zero solution of the linear Equation (12).

Remark 4.

Let the function $V\left(z\right)$, $z\in {\mathbf{R}}^5$, has two derivatives $\nabla V\left(z\right)$ and ${\nabla }^{2}V\left(z\right)$. The generator L of Equation (12) has the form [5,8,13]

$$\begin{array}{cc}\hfill LV\left(z\right)=& {(\nabla V\left(z\right))}^{\prime }Az+{\displaystyle \frac{1}{2}}\sum _{i=1}^5{z}^{\prime }{B}_i{\nabla }^{2}V\left(z\right)B_{i}z\hfill \\ & \hfill +\sum _{i=1}^5{\lambda }_i[V(z+C_{i}z)-V\left(z\right)-{(\nabla V\left(z\right))}^{\prime }{C}_{i}z].\end{array}$$

(18)

Theorem 1.([13]) Let there exist a function $V\left(z\right)$ and positive constants $c_1$, $c_2$, $c_3$ such that the following conditions hold:

$$\begin{gathered} \mathbf{E}V\left(z\left(t\right)\right)\ge c_1{\mathbf{E}\left|z\left(t\right)\right|}^2,\mathbf{E}V\left(z\left(0\right)\right)\le c_2{\left|z\left(0\right)\right|}^2, \\ \mathbf{E}LV\left(z\left(t\right)\right)\le -c_3\mathbf{E}{\left|z\left(t\right)\right|}^2. \end{gathered}$$

Then the zero solution to Equation (12) is asymptotically mean square stable.

Theorem 2.

Let for the matrices A, $B_i$ and $C_i$, $i=1,...,5$, of Equation (12) there exists a positive definite matrix Q such that the following LMI

$$QA+A^{\prime }Q+\sum _{i=1}^5(B_i^{\prime }Q{B}_i+{\lambda }_i{C}_i^{\prime }Q{C}_i)<0$$

(19)

holds. Then the equilibrium $(S^{*},A^{*},I^{*},R^{*},P^{*})$ of the system (7) is stable in probability.

Proof. 

Using the generator (18), for the Lyapunov function $V\left(z\right)=z^{\prime }Qz$, $Q>0$, we have

$$\begin{array}{cc}\hfill LV\left(z\right)& =2z^{\prime }QAz+{\displaystyle \sum _{i=1}^5}{z}^{\prime }{B}_i^{\prime }Q{B}_{i}z+{\displaystyle \sum _{i=1}^5}{\lambda }_i{z}^{\prime }{C}_i^{\prime }Q{C}_{i}z\hfill \\ & =z^{\prime }\left[QA+A^{\prime }Q+{\displaystyle \sum _{i=1}^5}\left(B_i^{\prime }Q{B}_i+{\lambda }_i{C}_i^{\prime }Q{C}_i\right)\right]z.\hfill \end{array}$$

(20)

So, if the LMI (19) holds then via (20)

$$LV\left(z\right)\le -{c\left|z\right|}^2$$

for some $c>0$ and, therefore, via Theorem 1 the zero solution to the linear stochastic differential Equation (12) is asymptotically mean square stable.

Via Remark 3 it means that the appropriate equilibrium $(S^{*},A^{*},I^{*},R^{*},P^{*})$ of the nonlinear system (7) is stable in probability. The proof is completed. □

5. Numerical Simulations

5.1. Difference analogue

For numerical simulation of solutions of the system (7) let us construct the difference analogue of this system. Put

$$\begin{gathered} t_j=\Delta j,\Delta >0, \\ {S}_j=S\left(t_j\right),A_j=A\left(t_j\right),I_j=I\left(t_j\right),R_j=R\left(t_j\right),P_j=P\left(t_j\right), \\ {w}_{i,j}=w_i\left(t_j\right),{\nu }_{i,j}={\nu }_i\left(t_j\right),i=1,...,5,j=0,1,2,.... \end{gathered}$$

(21)

Via (21) the difference analogue of the system (7) takes the form

$$\begin{array}{cc}\hfill S_{j+1}=& S_j+\left[\Lambda -\left(\beta (1-p(1-u)){\displaystyle \frac{\theta A_j+I_j}{N_j}}+\psi p(1-u)+\mu \right)S_j+\omega P_j\right]\Delta \hfill \\ & +(S_j-S^{*})[{\sigma }_1(w_{1,j+1}-w_{1,j})+{\gamma }_1({\nu }_{1,j+1}-{\nu }_{1,j}-{\lambda }_1\Delta )],\hfill \\ \hfill A_{j+1}=& A_j+\left[\beta (1-p(1-u)){\displaystyle \frac{\theta A_j+I_j}{N_j}}{S}_j-(\nu +\mu )A_j\right]\Delta \hfill \\ & +(A_j-A^{*})[{\sigma }_2(w_{2,j+1}-w_{2,j})+{\gamma }_2({\nu }_{2,j+1}-{\nu }_{2,j}-{\lambda }_2\Delta )],\hfill \\ \hfill I_{j+1}=& I_j+[\nu A_j-(\delta +\mu )I_j]\Delta \hfill \\ & +(I_j-I^{*})[{\sigma }_3(w_{3,j+1}-w_{3,j})+{\gamma }_3({\nu }_{3,j+1}-{\nu }_{3,j}-{\lambda }_3\Delta )],\hfill \\ \hfill R_{j+1}=& R_j+[\delta I_j-\mu R_j]\Delta \hfill \\ & +(R_j-R^{*})[{\sigma }_4(w_{4,j+1}-w_{4,j})+{\gamma }_4({\nu }_{4,j+1}-{\nu }_{3,j}-{\lambda }_4\Delta )],\hfill \\ \hfill P_{j+1}=& P_j+[\psi p(1-u)S_j-(\omega +\mu )P_j]\Delta \hfill \\ & +(P_j-P^{*})[{\sigma }_5(w_{5,j+1}-w_{5,j})+{\gamma }_5({\nu }_{5,j+1}-{\nu }_{5,j}-{\lambda }_5\Delta )],\hfill \\ & j=0,1,2,....\end{array}$$

(22)

5.2. Examples

Here two demonstrative numerical examples are considered, where (14), (15), (16), (17) are used to calculate the matrix (13).

Example 1.

Putting

$$\begin{gathered} \Lambda =15,\mu =1,\theta =1,\psi =0.4,\nu =0.15, \\ \delta =0.033,\omega =0.0013,p=0.7,u=0.3,\beta =1.5, \end{gathered}$$

(23)

we have $N_0^{*}={\displaystyle \frac{\Lambda }{\mu }}=15$ and via (3)

$$(S_0^{*},A_0^{*},I_0^{*},R_0^{*},P_0^{*})=(12.5445,0,0,0,2.4555).$$

(24)

Via MATLAB it was shown that for the values of the parameters

$$\begin{gathered} {\sigma }_1=1.4,{\sigma }_2=0.93,{\sigma }_3=1.2,{\sigma }_4=1.4, \\ {\sigma }_5=1.4,{\gamma }_i={\lambda }_i=1,i=1,...,5, \end{gathered}$$

(25)

the LMI (19) holds and, therefore, the equilibrium (24) is stable in probability.

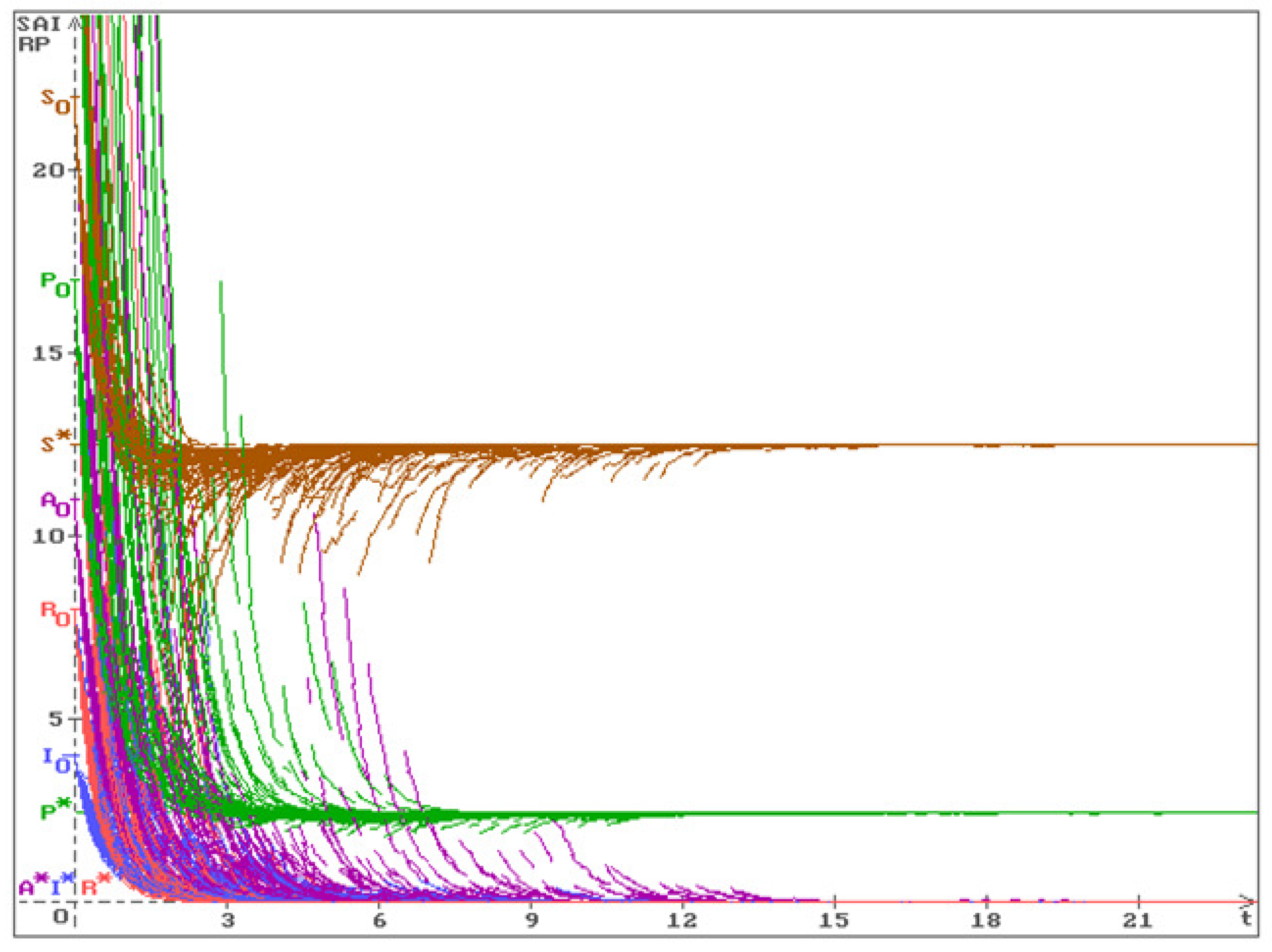
In Figure 1 50 trajectories of the solution of the system (7), obtained via the difference analogue (22) with the parameters (23), (25) and $\Delta =0.06$, are shown with the initial values

$$S\left(0\right)=22,A\left(0\right)=11,I\left(0\right)=4,R\left(0\right)=8,P\left(0\right)=17.$$

(26)

All trajectories ($S\left(t\right)$-brown, $A\left(t\right)$-violet, $I\left(t\right)$-blue, $R\left(t\right)$-red, $P\left(t\right)$-green) converge to the stable in probability equilibrium (24).

Example 2.

Putting

$$\begin{gathered} \Lambda =15,\mu =1,\theta =1,\psi =0.08, \\ \nu =0.18,\delta =0.33,\omega =0.0013,p=0.4,u=0.3,\beta =2, \end{gathered}$$

(27)

from (5) and (4) we obtain $R_0=1.3541>1$, $N_0^{*}={\displaystyle \frac{\Lambda }{\mu }}=15$ and

$$(S_{+}^{*},A_{+}^{*},I_{+}^{*},R_{+}^{*},P_{+}^{*})=(10.8264,3.3317,0.4509,0.1488,0.2422).$$

(28)

Via MATLAB it was shown that for the values of the parameters

$$\begin{gathered} {\sigma }_1=1.5,{\sigma }_2=0.79,{\sigma }_3=1.2,{\sigma }_4=1.3,{\sigma }_5=1.3, \\ {\gamma }_1=1.1,{\gamma }_2=0.95,{\gamma }_3=1.1,{\gamma }_4=0.5,{\gamma }_5=1, \\ {\lambda }_1=1.1,{\lambda }_2=1.59,{\lambda }_3=1.1,{\lambda }_4=1,{\lambda }_5=1.1, \end{gathered}$$

(29)

the LMI (19) holds and, therefore, the equilibrium (28) is stable in probability.

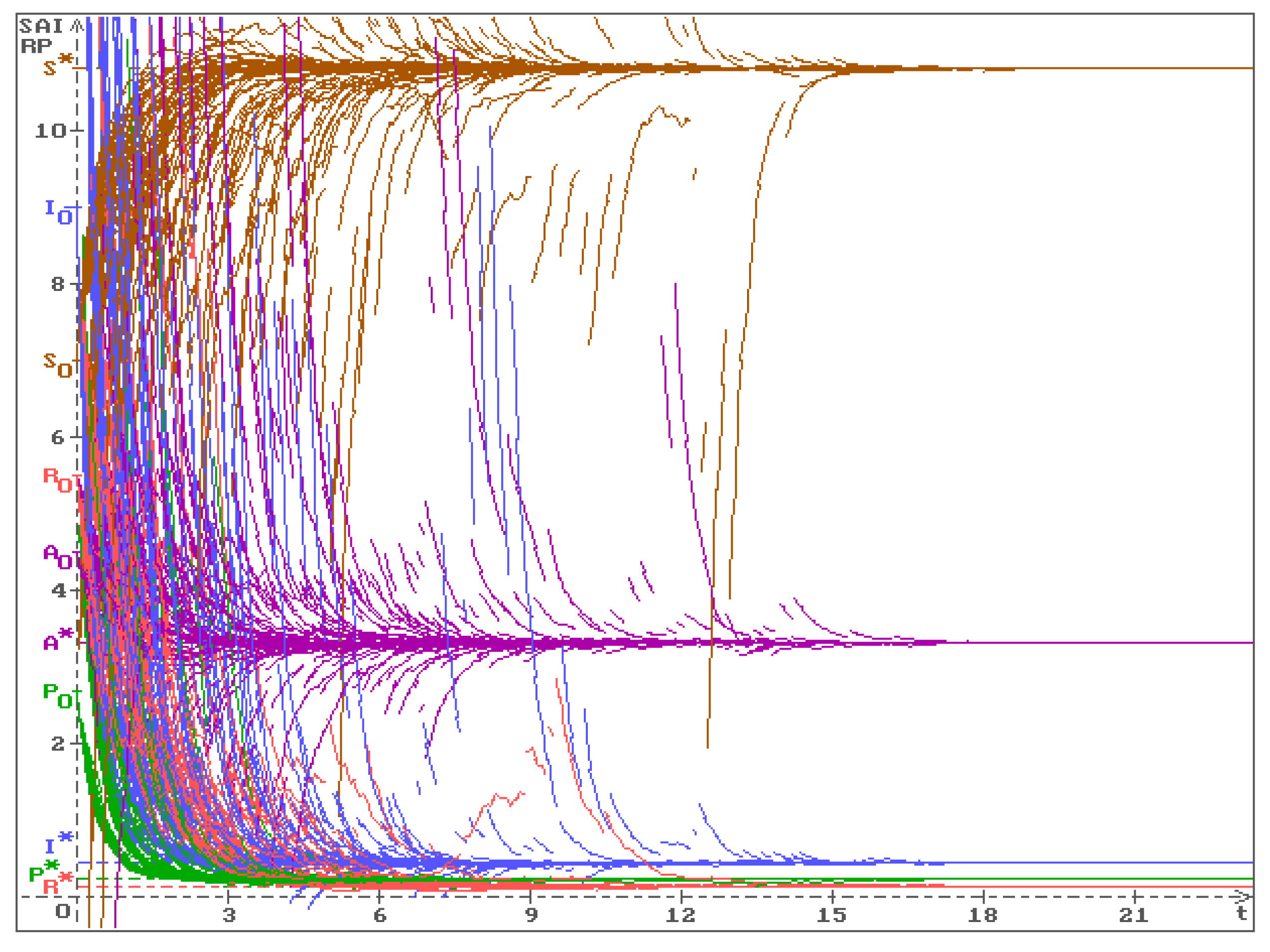
In Figure 2 50 trajectories of the solution of the system (7), obtained via the difference analogue (22) with the parameters (27), (29) and $\Delta =0.06$, are shown with the initial values

$$S\left(0\right)=7,A\left(0\right)=4.5,I\left(0\right)=9,R\left(0\right)=5.5,P\left(0\right)=2.7.$$

(30)

All trajectories ($S\left(t\right)$-brown, $A\left(t\right)$-violet, $I\left(t\right)$-blue, $R\left(t\right)$-red, $P\left(t\right)$-green) converge to the stable in probability equilibrium (28).

Remark 5.

Note that for the numerical simulation of trajectories of the Wiener processes $w_i\left(t\right)$, $i=1,...,5$, in Examples 1 and 2 a special algorithm has been used, described in detail in [13] (p.29-31).

Remark 6.

For the numerical simulation of the Poisson processes ${\nu }_i\left(t\right)$, $i=1,...,5$, similarly to [9,10,11] the continuous random variable ${\zeta }_i$ is used, uniformly distributed on the interval $(0,1)$: ${\nu }_{i,j+1}-{\nu }_{i,j}=1$ if ${\zeta }_i<{\lambda }_i\Delta$ and ${\nu }_{i,j+1}-{\nu }_{i,j}=0$ in the contrary case.

One can see that in difference from the similar pictures in [4], where only stochastic perturbations of the white noise type are considered, here in Figure 1 and Figure 2 the trajectories of all processes have discontinuities, that is a consequence of jumps in Poisson’s processes.

6. Conclusions

Asymptotic properties of the known SAIRP epidemic model, described by a system of five nonlinear differential equations, are studied under stochastic perturbations, given by a combination of the white noise and Poisson’s jumps. It is shown that a sufficient condition of stability in probability for two equilibria of the considered system is formulated in the form of a simple linear matrix inequality (LMI), which can be easily studied via MATLAB. Two examples with numerical simulation of solutions of the considered system illustrate the obtained results.

One of the goals of the proposed paper is to attract the attention of future researchers to extension of the use of Poisson’s type stochastic perturbations in their own research, to the use of the proposed algorithm of numerical simulation of this type of perturbations together with perturbations of the type of white noise and apply this method to many other more complicated nonlinear models of higher dimensional in various applications.