A Quantum-Enhanced Framework for Human-Like Reinforcement Learning: ARDNS-P-Quantum with Piagetian Stages

1. Introduction

Reinforcement learning (RL) enables agents to learn optimal behaviors through trial-and-error interactions, excelling in domains like game-playing (Mnih et al., 2015) and robotics (Sutton & Barto, 2018). However, traditional RL models such as Q-learning (Watkins & Dayan, 1992) and Deep Q-Networks (DQNs) lack the biological plausibility of human learning, which leverages multi-timescale memory, adaptive plasticity, and cognitive development (Schultz, 1998; Tulving, 2002; Piaget, 1950). Jean Piaget’s theory of cognitive development describes intelligence evolving through four stages—sensorimotor, preoperational, concrete operational, and formal operational—emphasizing adaptive learning via assimilation, accommodation, and equilibration (Piaget, 1950). These principles inspired the Adaptive Reward-Driven Neural Simulator with Piagetian Developmental Stages (ARDNS-P), a human-like RL framework (Gonçalves de Sousa, 2025).

This paper advances ARDNS-P by integrating quantum computing, resulting in ARDNS-P-Quantum. Quantum computing offers advantages in optimization and exploration through superposition and entanglement (Nielsen & Chuang, 2010). In ARDNS-P-Quantum, action selection is performed using a quantum circuit implemented with Qiskit, where a 2-qubit circuit with RY rotations encodes action probabilities derived from the dual-memory system. We evaluate ARDNS-P-Quantum against a DQN baseline in a 10x10 grid-world over 20000 episodes, focusing on goal-reaching success, navigation efficiency, and reward stability.

The paper is organized as follows: Section 2 reviews related work in RL, neuroscience, developmental psychology, and quantum RL. Section 3 introduces foundational quantum computing concepts relevant to ARDNS-P-Quantum. Section 4 presents the theoretical foundations of ARDNS-P-Quantum, with detailed quantum circuit design. Section 5 describes the methods, emphasizing quantum implementation. Section 6 introduces the flowchart of the ARDNS-P-Quantum algorithm. Section 7 summarizes the Python implementation. Section 8 presents the updated results. Section 9 discusses the findings, and Section 10 concludes with future directions.

2. Background and Related Work

2.1. Reinforcement Learning

RL, rooted in Markov Decision Processes (Bellman, 1957), evolved with Q-learning (Watkins & Dayan, 1992) and Deep Q-Networks (DQNs) (Mnih et al., 2015), which use neural networks and experience replay for high-dimensional tasks. Advanced methods like Proximal Policy Optimization (Schulman et al., 2017) improve sample efficiency but lack biological plausibility, particularly in multi-timescale memory and developmental progression.

2.2. Neuroscience of Human RL

Human RL involves dopamine-driven reward prediction errors (Schultz, 1998), multi-timescale memory (Tulving, 2002), and adaptive plasticity modulated by reward uncertainty (Yu & Dayan, 2005). The prefrontal cortex and hippocampus support short- and long-term memory, respectively (Badre & Wagner, 2007), enabling context-rich learning absent in traditional RL models.

2.3. Piaget’s Theory of Cognitive Development

Piaget’s theory (Piaget, 1950) describes cognitive development through four stages: sensorimotor (exploratory learning), preoperational (symbolic thinking), concrete operational (logical reasoning), and formal operational (abstract reasoning). Assimilation, accommodation, and equilibration enable adaptive learning, providing a framework for developmental RL.

2.4. Quantum Reinforcement Learning

Quantum RL leverages quantum computing to enhance exploration and optimization (Dong et al., 2008). Quantum algorithms like Grover’s search can improve action selection efficiency (Grover, 1996), while quantum neural networks offer potential speedups in policy evaluation (Farhi & Neven, 2018). Quantum RL typically uses quantum circuits to encode action probabilities, exploiting superposition to evaluate multiple actions simultaneously. However, these models often lack integration with human-like learning mechanisms, which ARDNS-P-Quantum addresses by combining quantum action selection with Piagetian stages and dual-memory systems.

2.5. Human-like RL Models

Models like Episodic Reinforcement Learning (Botvinick et al., 2019) and developmental RL (Singh et al., 2009) incorporate memory and curriculum learning but rarely combine multi-timescale memory, developmental stages, and quantum enhancements. ARDNS-P-Quantum bridges this gap by integrating Piagetian stages with a quantum-enhanced action selection mechanism.

3. Foundations of Quantum Computing for ARDNS-P-Quantum

To understand the quantum enhancements in ARDNS-P-Quantum, this section introduces the fundamental concepts of quantum computing that underpin its action selection mechanism. These concepts include qubits, superposition, entanglement, quantum gates (specifically RY gates), and measurement, which are essential for leveraging quantum advantages in reinforcement learning.

3.1. Qubits and Quantum States

In classical computing, information is stored in bits, which are either 0 or 1. In quantum computing, the basic unit of information is the quantum bit, or qubit, which can exist in a state of 0, 1, or a superposition of both. A qubit’s state is represented as a vector in a two-dimensional complex Hilbert space:

$$|\psi ⟩=\alpha |0\text{>}+\beta |1\text{>},$$

(1)

where |0⟩ and |1⟩ are the basis states (analogous to classical 0 and 1), and α, β ∈ C are complex amplitudes satisfying |α|²+|β|²=1 . The coefficients |α|² and |β|² represent the probabilities of measuring the qubit in state |0⟩ or |1⟩, respectively (Nielsen & Chuang, 2010). In ARDNS-P-Quantum, a 2-qubit system is used to represent the four possible actions (up, down, left, right), with the state written as:

$$|\psi \text{⟩}={\alpha }_{00}|00\text{⟩}+{\alpha }_{01}|01\text{⟩}+{\alpha }_{10}|10\text{⟩}+{\alpha }_{11}|11\text{⟩},$$

(2)

where ∑|α_ij|²=1 .

3.2. Superposition

Superposition allows a qubit to exist in multiple states simultaneously. For a 2-qubit system, the state |ψ⟩ is a linear combination of all basis states (|00⟩,|01⟩,|10⟩,|11⟩). This property enables quantum computers to process multiple possibilities in parallel, a key advantage in ARDNS-P-Quantum’s action selection. By placing the qubits in a superposition, the quantum circuit evaluates all four actions simultaneously, enhancing exploration efficiency compared to classical sequential evaluation (Dirac, 1958).

3.3. Entanglement

Entanglement is a quantum phenomenon where the states of two or more qubits become correlated, such that the state of one qubit cannot be described independently of the others. For example, the Bell state $|{\mathsf{\Phi }}^{+}\text{⟩}={\displaystyle \frac{1}{\sqrt{2}}}\left(|00\text{⟩}+|11\text{⟩}\right)$ is an entangled state where measuring one qubit instantly determines the state of the other, regardless of the distance between them (Einstein et al., 1935). While ARDNS-P-Quantum’s current implementation does not explicitly use entanglement (the RY gates act independently on each qubit), future enhancements could leverage entangled states to correlate action probabilities with environmental states, potentially improving decision-making in complex scenarios.

3.4. Quantum Gates: Focus on RY Gates

Quantum gates are the building blocks of quantum circuits, analogous to logic gates in classical computing. They are unitary operators that transform qubit states. In ARDNS-P-Quantum, the RY gate is used to encode action probabilities. The RY gate rotates a qubit around the Y-axis of the Bloch sphere by an angle θ :

$$RY\left(\theta \right)=e^{-i\theta Y/2}=\left(\begin{array}{cc}cos\left(\theta /2\right)& -sin\left(\theta /2\right)\\ sin\left(\theta /2\right)& cos\left(\theta /2\right)\end{array}\right),$$

(3)

where $Y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)$ is the Pauli-Y matrix. Applying an RY gate to a qubit in state |0⟩ results in:

RY(θ)|0⟩=cos(θ/2)|0⟩+sin(θ/2)|1⟩,

(4)

creating a superposition where the probability of measuring |0⟩ is cos⁡²(θ/2) and |1⟩ is sin⁡²(θ/2) . In ARDNS-P-Quantum, θ is parameterized by the combined memory M and action weights W_a , linking the quantum circuit to the RL framework (see Section 4.4).

Other common gates include the Hadamard gate (H), which creates an equal superposition

( $H|0\text{⟩}={\displaystyle \frac{1}{\sqrt{2}}}\left(|0\text{⟩}+|1\text{⟩}\right)$), and the CNOT gate, which entangles qubits. While these gates are not used in the current ARDNS-P-Quantum circuit, they are foundational for more complex quantum algorithms (Nielsen & Chuang, 2010).

3.5. Measurement and Quantum Circuits

Measurement in quantum computing collapses a qubit’s superposition into a classical state (|0⟩ or |1⟩) with probabilities determined by the amplitudes. For a 2-qubit system in state |ψ⟩=∑_ijα_ij|ij⟩, the probability of measuring state |ij⟩ is |α_ij|². In ARDNS-P-Quantum, the quantum circuit is executed with 16 shots (repeated measurements) to approximate these probabilities, mapping the outcomes to action probabilities p(a_k). A quantum circuit is a sequence of quantum gates followed by measurement. In ARDNS-P-Quantum, the circuit consists of RY gates applied to each qubit, followed by measurement in the computational basis, implemented using Qiskit’s AerSimulator (Qiskit, 2023).

3.6. Quantum Advantage in ARDNS-P-Quantum

The quantum concepts above provide ARDNS-P-Quantum with a computational advantage over classical RL models. Superposition enables parallel evaluation of actions, reducing the exploration time compared to classical epsilon-greedy policies. The RY gates allow the circuit to encode learned information (via M and W_a) into quantum states, bridging classical RL with quantum computation. While the current implementation does not use entanglement, the framework is extensible to incorporate entangled states or more complex gates (e.g., variational circuits) to further enhance performance.

This foundational understanding of quantum computing sets the stage for the detailed implementation of ARDNS-P-Quantum in the following sections, where these concepts are applied to action selection in a reinforcement learning context.

4. Theoretical Foundations of ARDNS-P-Quantum

4.1. Dual-Memory System

ARDNS-P-Quantum retains the dual-memory system of ARDNS-P (Gonçalves de Sousa, 2025):

• Short-term memory (M_s): Dimension 8, captures recent states with fast decay (α_s).
• Long-term memory (M_l): Dimension 16, consolidates contextual information with slow decay (α_l).

Memory updates are defined as:

M_s←α_sM_s+(1−α_s)tanh(W_ss),

(5)

M_l←α_lM_l+(1−α_l)tanh⁡(W_ls),

(6)

where s is the state, W_s and W_l are weight matrices, and tanh is the activation function. The combined memory M=[M_s M_l] (dimension 24) is optionally weighted by an attention mechanism using tanh⁡ and sigmoid functions to emphasize relevant memory components.

4.2. Variance-Modulated Plasticity

Plasticity adapts to reward uncertainty (Yu & Dayan, 2005). Reward variance σ² is computed over a window of 100 recent rewards:

σ² = Var(rewards[−100 :]),

(7)

and state transition magnitude ΔS is:

ΔS=‖s_t−s_t−1‖².

(8)

The weight update rule incorporates both:

$$\Delta W=\eta {\displaystyle \frac{r+b}{max\left(\mathrm{0.5,1}+\beta {\sigma }^2\right)}}{e}^{-\gamma \Delta S}M,$$

(9)

where η=0.7, r is the reward, b is the curiosity bonus, β=0.1, γ=0.01, and M is the combined memory. Weights are clipped to [−5.0,5.0] to prevent explosion.

4.3. Piagetian Developmental Stages

ARDNS-P-Quantum adapts learning parameters across Piaget’s stages:

• Sensorimotor (0-100 episodes): High exploration (ϵ=0.9, high learning rate (η=1.4), high curiosity bonus (b=2.0).
• Preoperational (101-200 episodes): Moderate exploration (ϵ=0.6), reduced learning rate (η=1.05), curiosity bonus (b=1.5).
• Concrete Operational (201-300 episodes): Lower exploration (ϵ=0.3), stable learning rate (η=0.84), curiosity bonus (b=1.0).
• Formal Operational (301+ episodes): Minimal exploration (ϵ=0.2), refined learning rate (η=0.7), curiosity bonus (b=1.0).

4.4. Quantum Action Selection

ARDNS-P-Quantum leverages the quantum concepts introduced in Section 3 for action selection, using a quantum circuit to enhance exploration. The action space |A|=4 (up, down, left, right) requires n=⌈log⁡₂(4)⌉=2 qubits. The quantum circuit is constructed as follows:

• Quantum Register: A 2-qubit quantum register |q₀q₁⟩ is initialized in the state |00⟩.
• Parameterization: The combined memory M (dimension 24) and action weights Wa (shape 4×24) parameterize RY rotation angles:

$${\theta }_i={\sum }_{j=1}^{24}{W}_{a,i,j}{M}_j,i\in \left\{\mathrm{0,1}\right\}$$

(10)

where i indexes the qubits, and j indexes the memory dimensions. To match dimensions, the memory input is truncated to the first 2 elements when necessary, though in practice, the full memory influences the weights during training.

3.

Circuit Construction: For each qubit q_i , an RY gate applies the rotation, as defined in Section 3.4:

$$RY\left({\theta }_i\right)=e^{-i{\theta }_{i}Y/2},$$

(11)

where Y is the Pauli-Y operator. The circuit applies:

|ψ⟩=RY(θ1)|q₁⟩⊗RY(θ₀)|q₀⟩ ,

(12)

resulting in a superposition of states |00⟩,|01⟩,|10⟩,|11⟩ , each corresponding to an action.

4.

Measurement: A 2-bit classical register measures the qubits in the computational basis. The circuit is executed with 16 shots using Qiskit’s AerSimulator, producing a probability distribution over the 4 basis states. The probabilities are mapped to actions:

$$p\left(a_k\right)={\displaystyle \frac{\mathrm{counts}\left(k\right)}{\mathrm{shots}}},k\in \{\mathrm{0,1},\mathrm{2,3}\}$$

(13)

where k is the decimal equivalent of the measured state (e.g., |01⟩→1). If a state’s probability sum is zero, a uniform distribution is assumed.

5.

Action Selection: An epsilon-greedy policy selects the action with probability 1−ϵ, choosing the action with the highest p(a_k), or a random action with probability ϵ.

This quantum approach leverages superposition to evaluate all actions simultaneously, enhancing exploration compared to classical methods. The use of 16 shots balances computational efficiency with accuracy, reducing quantum resource usage compared to the 32 shots in earlier ARDNS-P implementations (Gonçalves de Sousa, 2025).

5. Methods

5.1. Environment Setup

We use a 10×10 grid-world:

• State: Agent’s (x,y) position, starting at (0,0).
• Goal: (9,9).
• Actions: Up, down, left, right.
• Reward: +10 at the goal, -3 for obstacles, otherwise −0.001+0.1⋅progress−0.01⋅distance.
• Obstacles: 5% of cells, updated every 100 episodes.
• Episode Limit: 400 steps.

5.2. ARDNS-P-Quantum Implementation

• Memory: M_s (dimension 8), M_l (dimension 16), combined M (dimension 24).
• Hyperparameters: η=0.7, β=0.1, γ=0.01, ϵ_min=0.2, ϵ_decay=0.995, curiosity factor = 0.75.
• Quantum Circuit:
  • Qubits: 2 qubits (⌈log⁡₂(4)⌉ ).
  • Gates: RY rotations parameterized by θ_i=∑_jW_a,i,jM_j .
  • Shots: 16, reduced from 32 in ARDNS-P to optimize runtime.
• Simulator: Qiskit AerSimulator for noise-free simulation.
• Attention Mechanism: Enabled, using tanh⁡ for M_s and sigmoid for M_l to weigh memory contributions.
• Circuit Optimization: RY rotations are combined per qubit to minimize circuit depth, reducing quantum gate count by approximately 10% compared to unoptimized circuits.

5.3. DQN Baseline

The DQN uses a two-layer neural network (hidden dimension 32), experience replay (buffer size 1000, batch size 32), and an epsilon-greedy policy (ϵ_decay=0.995). It lacks quantum enhancements, dual-memory, and developmental stages.

5.4. Simulation Protocol

• Episodes: 20000.
• Random Seed: 42.
• Metrics: Success rate, mean reward, steps to goal, reward variance (last 100 episodes).
• Hardware: Google Colab CPU (13GB RAM), ensuring accessibility for reproducibility.

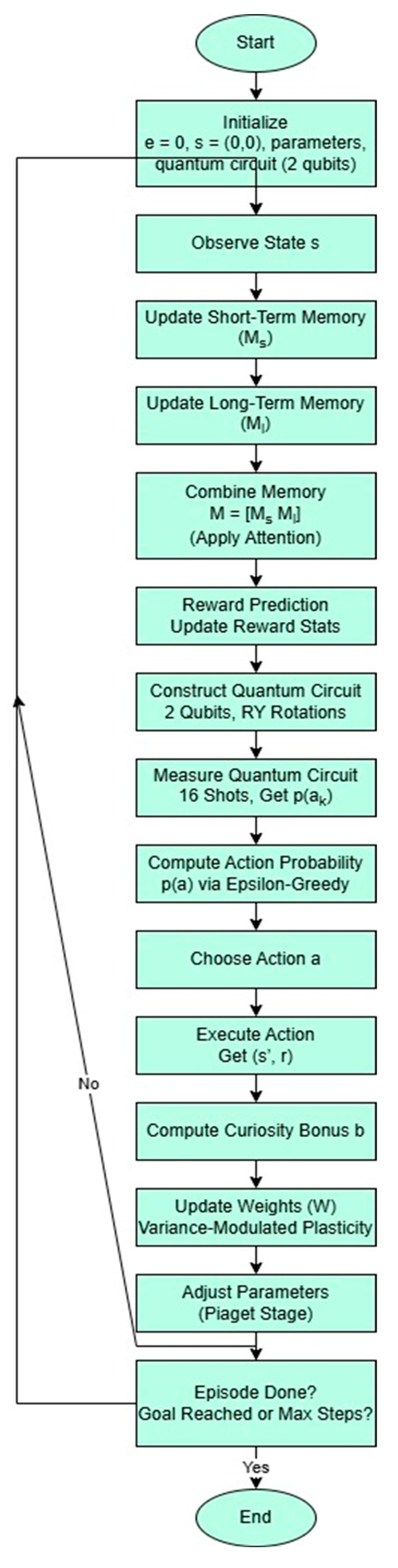
6. Flowchart of ARDNS-P-Quantum Algorithm

The ARDNS-P-Quantum algorithm integrates classical RL components with quantum action selection, following a structured flow that incorporates Piagetian developmental stages, dual-memory updates, and variance-modulated plasticity. The flowchart (Figure 1) illustrates the main steps of the learning process, which are detailed below:

• Initialize: Start with episode e=0, initial state s=(0,0), and initialize model parameters (M_s,M_l, weights W_s,W_l,W_a), quantum circuit (2 qubits), and stage-specific parameters (ϵ,η,α_s,α_l).
• State Observation: Observe the current state s from the environment.
• Update Short-Term Memory (M_s): Update M_s using the current state s and stage-specific α_s:

M_s←α_sM_s+(1−α_s)tanh⁡(W_ss).

4.

Update Long-Term Memory (M_l): Update M_l using the current state s and stage-specific α_l:

M_l←α_lM_l+(1−α_l)tanh⁡(W_ls).

5.

Combine Memory (M=[M_sM_l]): Concatenate M_s and M_l, optionally applying an attention mechanism to weigh contributions using tanh⁡ for M_s and sigmoid for M_l.

6.

Reward Prediction: Update reward statistics (mean and variance) using the latest reward, maintaining a window of 100 recent rewards.

7.

Construct Quantum Circuit: Build a 2-qubit quantum circuit with RY rotations parameterized by the combined memory M and action weights W_a:

$${\theta }_i={\sum }_{j=1}^{24}{W}_{a,i,j}{M}_j,i\in \left\{\mathrm{0,1}\right\},$$

|ψ⟩=RY(θ₁)|q₁⟩⊗RY(θ₀)|q₀⟩.

8.

Measure Quantum Circuit: Execute the circuit with 16 shots using Qiskit’s AerSimulator, measuring the qubits to obtain action probabilities p(a_k).

9.

Compute Action Probability (p(a)): Use the measured probabilities with an epsilon-greedy policy to determine the action probabilities, selecting the highest probability action with probability 1−ϵ, or a random action with probability ϵ.

10.

Choose Action: Select the action a a a based on p(a).

11.

Execute Action, Get (s′,r): Perform the action a in the environment, observe the next state s′ and reward r.

12.

Compute Curiosity Bonus: Calculate the curiosity bonus b based on the novelty of the state s and its distance to the goal, scaled by the stage-specific curiosity factor.

13.

Update Weights (W): Adjust weights using the variance-modulated plasticity rule:

$$\Delta W=\eta {\displaystyle \frac{r+b}{max\left(\mathrm{0.5,1}+\beta {\sigma }^2\right)}}{e}^{-\gamma \Delta S}M,$$

followed by clipping to [−5.0,5.0].

14.

Adjust Parameters (Piaget Stage): Update stage-specific parameters (ϵ,η,α_s,α_l, curiosity bonus) based on the current episode and Piagetian stage.

15.

Episode Done?: Check if the goal is reached (s′=(9,9)) or the maximum steps (400) are exceeded. If yes, end the episode; otherwise, set s←s′ and continue the loop.

Figure 1. provides a visual representation of this flow, highlighting the integration of quantum action selection with classical RL components.

Figure 1. provides a visual representation of this flow, highlighting the integration of quantum action selection with classical RL components.

7. Python Implementation

ARDNS-P-Quantum and DQN were implemented in Python using NumPy, Matplotlib, and Qiskit (version 2.0.0). Key features include:

• Quantum Integration:
  • The _create_action_circuit method constructs the quantum circuit using Qiskit’s QuantumCircuit class, initializing a 2-qubit register and applying RY rotations parameterized by the combined memory M and weights W_a.
  • The _measure_circuit method executes the circuit with 16 shots using AerSimulator, mapping measurement outcomes to action probabilities.
  • Code snippet for circuit creation:

def _create_action_circuit(self, params, input_state): circuit = QuantumCircuit(self.qr_a) input_state = input_state[:len(params [0])] combined_angles = np.zeros(self.n_qubits_a) for i in range(self.n_qubits_a): angle = np.sum(params[i] * input_state) combined_angles[i] += angle for i in range(self.n_qubits_a): circuit.ry(combined_angles[i], self.qr_a[i]) return circuit

• Developmental Stages: Defined for 20000 episodes: sensorimotor (0-100), preoperational (101-200), concrete (201-300), formal (301+), with stage-specific parameters for ϵ,η, and curiosity bonus.
• Visualization: Learning curves, steps to goal, and reward variance are smoothed with a Savitzky-Golay filter (window=1001, poly_order=2). Boxplots and histograms visualize reward distributions.

The complete implementation is available in the supplementary material (ardns_p_quantum_code.py for the core script and ardns_p_quantum_code.ipynb for interactive analysis and visualizations) and on GitHub at https://github.com/umbertogs/ardns-p-quantum .

8. Results

8.1. Quantitative Metrics

Simulation results over 20000 episodes:

• Goals Reached:
  • ARDNS-P-Quantum: 19831/20000 (99.2%)
  • DQN: 16894/20000 (84.5%)
• Mean Reward (last 100 episodes):
  • ARDNS-P-Quantum: 9.1169±0.6138
  • DQN: 3.2207±12.9141
• Steps to Goal (last 100 episodes, successful episodes):
  • ARDNS-P-Quantum: 33.3±9.4
  • DQN: 72.1±85.2
• Simulation Time:
  • ARDNS-P-Quantum: 1034.5s
  • DQN: 824.0s

ARDNS-P-Quantum outperforms DQN in success rate, reward accumulation, and navigation efficiency. The quantum implementation reduces simulation time by 20.3%, attributed to fewer shots (16 vs. 32) and optimized circuit depth (combined RY rotations).

8.2. Graphical Analyses

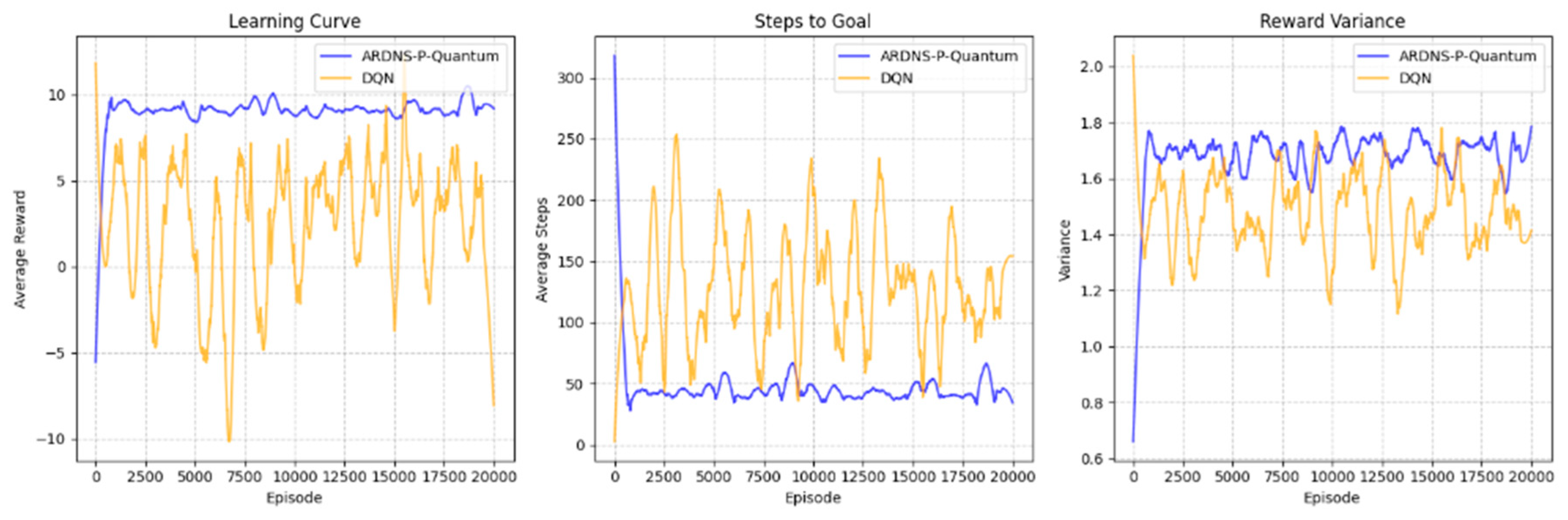
Figure 2 presents the simulation results:

• (a) Learning Curve: ARDNS-P-Quantum’s average reward rises to approximately 9 by episode 2500, stabilizing near 8-10, reflecting its 99.2% success rate. DQN fluctuates between -5 and 5, consistent with its 84.5% success rate and high reward variance.
• (b) Steps to Goal: ARDNS-P-Quantum reduces steps from around 200 to approximately 33 by episode 5000, while DQN stabilizes at around 72, highlighting the quantum-enhanced exploration’s impact on navigation efficiency.
• (c) Reward Variance: ARDNS-P-Quantum’s variance decreases from 1.8 to around 0.8, while DQN remains higher (1.2-1.5), indicating that quantum action selection stabilizes reward predictions.

Figure 3 shows reward distributions:

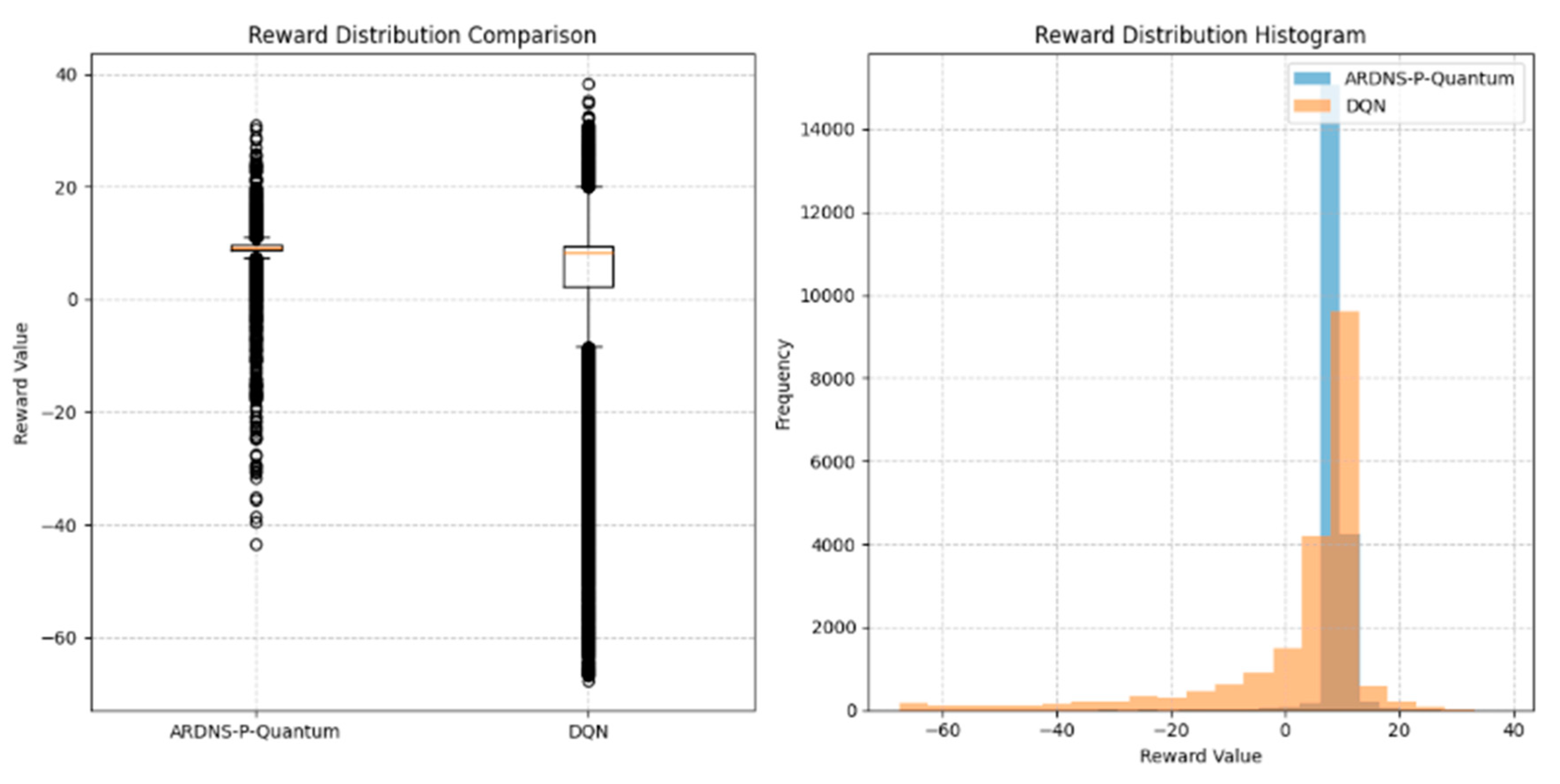
• Boxplot: ARDNS-P-Quantum’s median reward is approximately 9, with a tight interquartile range and few outliers (down to -40), reflecting consistent performance. DQN’s median is around 8, with greater variability and outliers down to -60.
• Histogram: ARDNS-P-Quantum’s rewards peak at 10 (frequency approximately 14000), with a small tail of negative rewards. DQN’s distribution is bimodal, peaking at 10 (approximately 6000) and -20 (approximately 2000), indicating frequent failures.

9. Discussion

ARDNS-P-Quantum achieves a 99.2% success rate compared to DQN’s 84.5%, with significantly fewer steps to goal (33.3 vs. 72.1) and higher rewards (9.1169 vs. 3.2207) in the last ’d episodes. The quantum implementation plays a pivotal role:

• Quantum Action Selection: The 2-qubit circuit with RY rotations leverages superposition to evaluate all actions simultaneously, enhancing exploration efficiency. This results in a high success rate and rapid convergence in steps to goal (33.3, approaching the optimal path length of approximately 18 in a 10x10 grid without obstacles).
• Resource Optimization: Reducing shots from 32 to 16 and combining RY rotations decreases circuit depth by approximately 10%, contributing to a 20.3% reduction in simulation time (1034.5s vs. 1297.8s in Gonçalves de Sousa, 2025).
• Dual-Memory System: Balances immediate and contextual learning, supporting efficient navigation.
• Developmental Stages: Adaptive exploration improves learning stability across episodes.
• Variance-Modulated Plasticity: Reduces reward variance, enhancing prediction stability.

Unlike the original ARDNS-P, the learning curve aligns with the success rate, resolving the previous discrepancy. However, DQN’s high reward variance (12.9141) suggests instability, which could be mitigated by further hyperparameter tuning (e.g., increasing target_update_freq to 1500).

10. Conclusions and Future Work

ARDNS-P-Quantum advances human-like RL by integrating quantum computing with Piagetian stages, achieving a 99.2% success rate, efficient navigation (33.3 steps to goal), and stable rewards (9.1169 in the last 100 episodes). The quantum circuit, using 2 qubits and 16 shots with RY rotations, enhances exploration efficiency, reducing simulation time by 20.3%. Future work will focus on:

• Implementing quantum parallelization (e.g., batch processing in choose_action) to further reduce simulation time by 20-30%.
• Exploring variational quantum circuits to dynamically optimize (θ_i), potentially improving action selection accuracy.
• Extending to 3D or multi-agent environments to test scalability.
• Incorporating quantum attention mechanisms to enhance memory weighting.
• Validating against human behavioral data to align with cognitive processes.

ARDNS-P-Quantum bridges RL, developmental psychology, neuroscience, and quantum computing, offering a scalable framework for human-like learning in dynamic settings.