Submitted:
17 April 2025
Posted:
18 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Electrical Aging Model for n-MOSFETS Structrues
2.1. Hole Trapping
2.2. Time-Dependent Hole Trap Density and Transconductance
3. Reliabilityanalyses of Total Ionizing Dose Effects ON n-MOSFET Current Mirrors
3.1. Electrical Aging Behavioral of an n-MOSFET
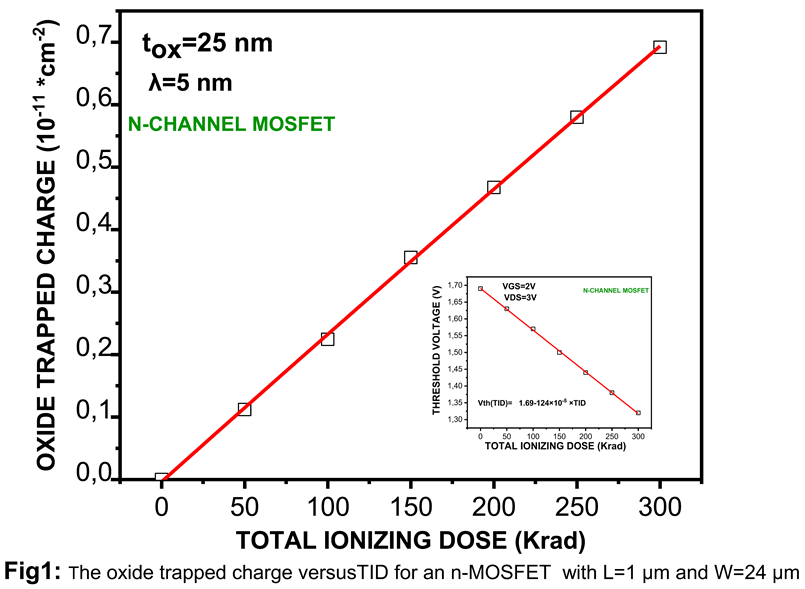
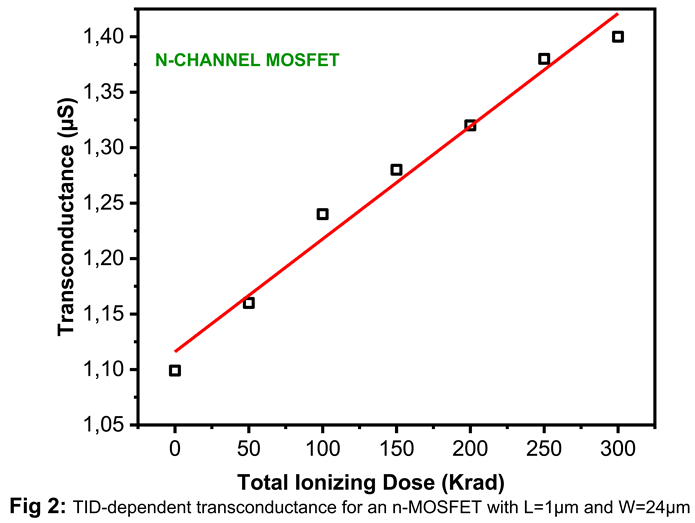
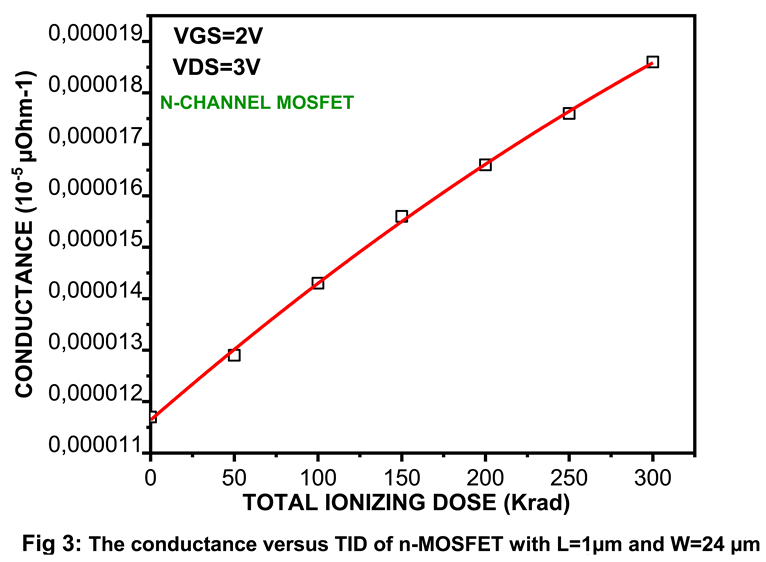
3.2. Electrical Degradation Mechanisms in n-MOSFET Current Mirrors
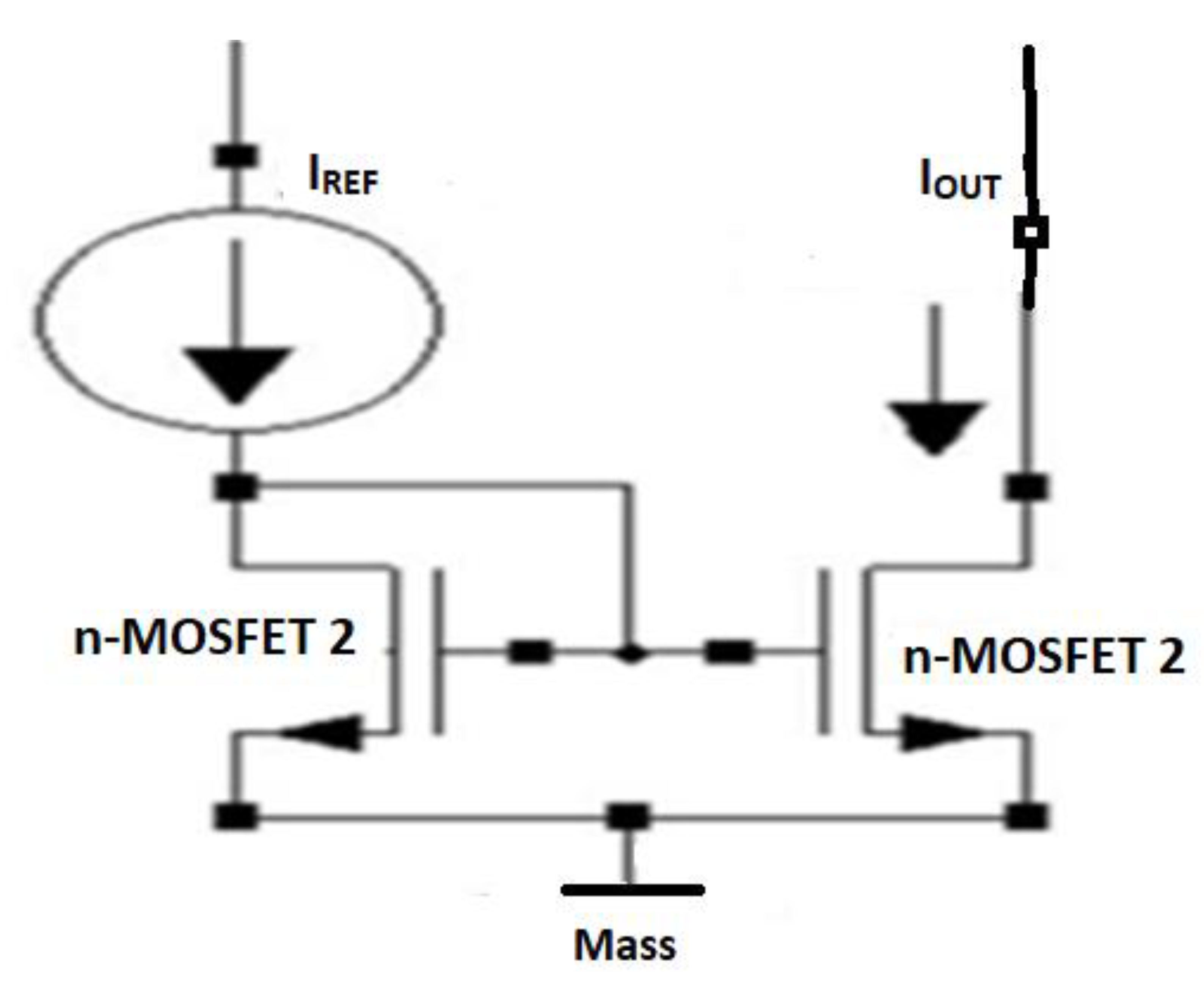
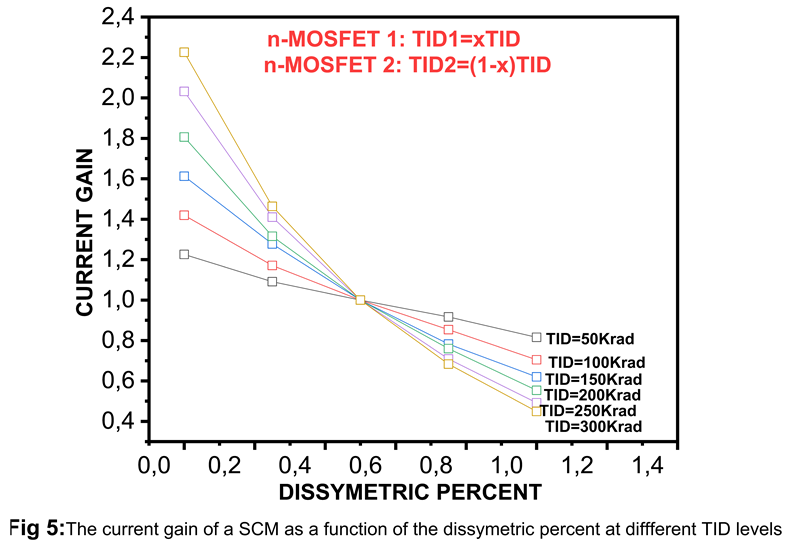
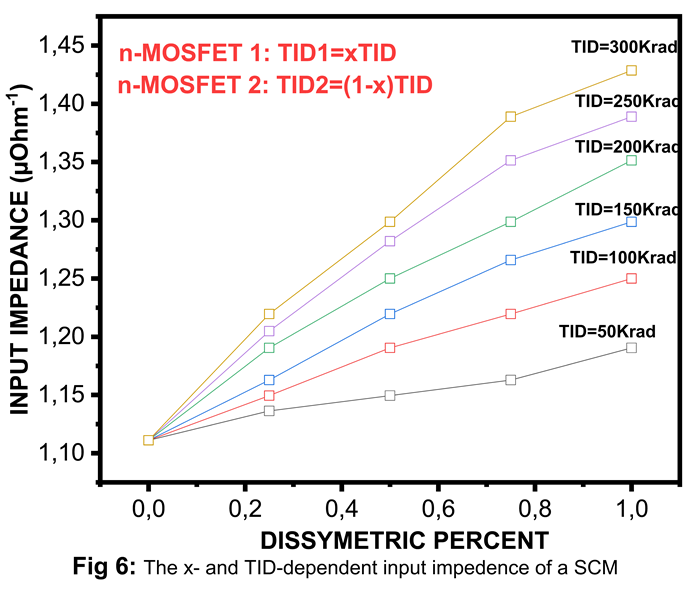
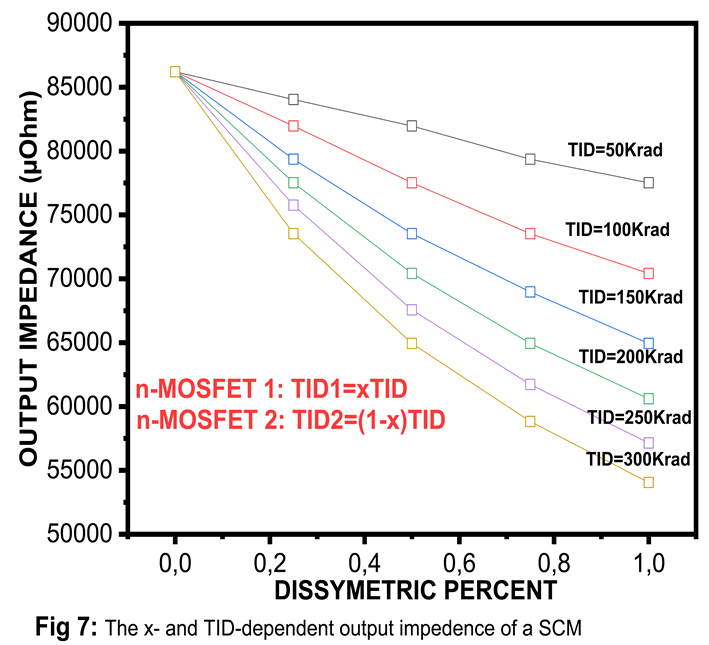
4. Conclusions
References
- Zhang, S.; Shi, J.; Wang, J.L. Satellite on-board failure statistics and analysis. Space cr. Eng. 2010, 19, 4l–46. [Google Scholar]
- Cao, Y.; Wang, M.; Zheng, X.; Zhang, E.; Lv, L.; Wang, L.; Ma, M.; Lv, H.; Wang, Z.; Wang, Y.; et al. Combined Effect of TID Radiation and Electrical Stress on NMOSFETs. Micromachines 2022, 13, 1860. [Google Scholar] [CrossRef] [PubMed]
- Gao, T.; Yin, C.; Chen, Y.; Chen, R.; Yan, C.; Liu, H. Simulation of Total Ionizing Dose Effects Technique for CMOS Inverter Circuit. Micromachines 2023, 14, 1438. [Google Scholar] [CrossRef]
- Bonaldo, S. TID effects in highly scaled gate-all-around Si nanowire CMOS transistors irradiated to ultra-high doses. IEEE Trans. Nucl. Sci. 2022, 69, 1444–1452. [Google Scholar] [CrossRef]
- Wang, S. Research and Modeling of Irradiation Characteristics of Ultra-Deep Submicron Devices. Ph.D. Thesis, Changchun University of Technology, Changchun, China, 2010. [Google Scholar]
- Zeng, C.; Li, X.; Gao, L. Research on High Temperature Characteristics of 28 nm Ultra-Thin FDSOI. Microelectronics 2021, 51, 577–581. [Google Scholar]
- Nasr, A.; Ashour, M. Experimental Studies for the Evaluation of Non-Ionizing Radiation Levels”, The Second All African IRPA Regional Radiation Protection Congress, 223 (2007).
- Nasr, Effect of ionizing radiation on the characteristics of photodetectors, The Second All African IRPA Regional Radiation Protection Congress, 231(2007).
- Prakash, G.; Ganesh, P.; Nagesha, Y.N.; Umakanth, D.; Arora, S.K.; Siddappa, K. Effect of 30 MeV Li3+ ion and 8 MeV electron irradiation on N-channel MOSFETs. Radiation Effects and Defects in Solids 2002, 157, 323–331. [Google Scholar] [CrossRef]
- Oldham, T.R.; Mclean, F.B. Total ionizing dose effects in MOS oxides and devices. IEEE. Trans. Nucl. Sci. 2003, 50, 483–499. [Google Scholar] [CrossRef]
- Schwank, J.R.; Shaneyfelt, M.R.; Fleetwood, D.M.; Felix, J.A.; Dodd, P.E.; Paillet, P.; Cavrois, V.F. Radiation effects in MOS oxides. IEEE. Trans. Nucl. Sci. 2008, 55, 1833–1853. [Google Scholar] [CrossRef]
- Grasser, T. Stochastic charge trapping in oxides: From random telegraph noise to bias temperature instabilities. Microelectronics Reliability 2012, 52, 39–70. [Google Scholar] [CrossRef]
- Guérin, C.; Huard, V.; Bravaix, A. General framework about defect creation at the Si/SiO2 interface. Journal of Applied Physics 2009, 105, 114513. [Google Scholar] [CrossRef]
- Rauch, S.E.; La Rosa, G. The energy-driven paradigm of NMOSFET hot-carrier effects. IEEE Transactions on Device and Materials Reliability 2005, 5, 701–705. [Google Scholar] [CrossRef]
- Tyaginov, S.; Jech, M.; Franco, J.; Sharma, P.; Kaczer, B.; Grasser, T. Understanding and Modeling the Temperature Behavior of Hot-Carrier Degradation in SiON nMOSFETs. IEEE Electron Device Letters 2016, 37, 84–87. [Google Scholar] [CrossRef]
- Zhicheng Wu, Jacopo Franco, Brecht Truijen, Philippe Roussel, Stanislav Tyaginov, Michiel Vandemaele1 , Erik Bury, Guido Groeseneken1 , Dimitri Linten, Ben Kaczer. Physics-based device aging modelling framework for accurate circuit reliability assessment.2021.
- Schroder, D.K.; Babcock, J.A. Negative bias temperature instability: Road to cross in deep submicron silicon semiconductor manufacturing. J. Appl. Phys. 2003, 94, 1–18. [Google Scholar] [CrossRef]
- Ullmann, B.; Jech, M.; Tyaginov, S.; Waltl, M.; Lllarionov, Y.Y.; Grill, A.; Puschkarsky, K.; Reisinger, H.; Grasser, T. The impact of mixed negative bias temperature instability and hot carrier stress on single oxide defects. IEEE. Inter. Reliab. Phys. Symp. 2017, XT-10.1–XT-10.6. [Google Scholar]
- Jech, M.; Ullmann, B.; Rzepa, G.; Tyaginov, S.; Grill, A.; Waltl, M.; Jabs, D.; Jungemann, C.; Grasser, T. Impact of mixed negative bias temperature instability and hot carrier stress on MOSFET characteristics—Part II: Theory. IEEE. Trans. Elec. Dev. 2019, 66, 241–248. [Google Scholar] [CrossRef]
- Zhou, X.J.; Fleetwood, D.M.; Felix, J.A.; Gusev, E.P.; Emic, D. Bias-temperature instabilities and radiation effects in MOS devices. IEEE. Trans. Nucl. Sci. 2006, 52, 2231–2238. [Google Scholar] [CrossRef]
- Zhao, X.; Gan, P.; Zhao, Q.; Liang, D.; Cao, Y.; Pan, X.; Bermak, A. A 124 fj/Bit cascode current mirror array based PUF with 1.50% native unstable bit ratio. IEEE Transaction on Circuits and Systems – I: Regular papers 2019, 66, 3494–3503. [Google Scholar] [CrossRef]
- Qin, Z.; Shintani, M.; Kuribara, K.; Ogasahara, Y.; Sato, T. Organic 2020, 20, 7569–7578.
- Lin, Z.; Fang, Y.; Peng, C.; Lu, W.; Li, X.; Wu, X.; Chen, J. Current mirror based compensation circuit for multi-row read inmemory computing. Electron. Lett. 2019, 55, 1176–1178. [Google Scholar] [CrossRef]
- F. Maloberti, Analog Design for CMOS VLSI Systems., International edition Springer, 2007.
- A.S. Sedra, K.C. Smith, and A.N. Chandokar, Microelectronic Circuits – Theory and Applications. Oxford University press, 2013.
- T.C. Carusone, and A. David, Analog Integrated Circuit Design, Wiley Student edition, 2015.
- Ning, T.H. Capture cross section and trap concentration of holes in siicon dioxide. J. Appl. 1976, 47, 1079–1081. [Google Scholar] [CrossRef]
- Viswanathan, C.R.; Maserjian, J. Model for thickness dependence of radiation charging in MOS structures. IEEE Trans. Nucl. Sci 1540, Ns-23, 1540–1545. [Google Scholar] [CrossRef]
- Sedki, A.; André, N.; Kilchytska, V.; Tounsi, F.; Mezghani, B.; Gérard, P.; Ali, Z.; Udrea, F.; Flandre, D.; Francis, L. In situ-Thermal Annealing of On-Membrane SOI Semiconducteur-Based Devices After High Gamma Dose irradiation. Nanotechnology 2017, 28, 184. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



