In this section, we use backward induction to solve the model. We first focus on the optimal subscription price and advertising intensity in the second stage. Then, based on these expected results, we analyze how the platform decides its investment strategy for original content and selects the appropriate business model to maximize profits in the first stage.
4.1. Stage 2: Subscription Price and Advertising Intensity
Let us assume that in the first stage the amount of original content developed by the platform is
. Now it decides how to maximize profits by choosing the advertising intensity
and the subscription price
. In particular, by substituting equations (2), (3) and (4) into the platform’s profit function (1), we can express the profit maximization problem as:
In the above maximization problem, the platform’s profit takes into account the money raised by subscriptions as well as the advertising revenues, minus the costs incurred in developing original content. The advertising intensity and the subscription price are the platform’s decision variables at this stage. The constraints on these two decision variables are necessary for the platform to have both non-empty sets of paid users and free users. Intuitively, the first constraint ensures that the platform’s advertising intensity must be non-negative and cannot exceed the maximum demand of advertisers. The second constraint is to ensure that both free and paid user segments can be formed. It can be seen from this constraint that if the subscription price is too high, so that the condition is satisfied, users will only pay for the premium service when their evaluation . However, the maximum value of does not exceed 1, so there will be no paying users. When the subscription price is too low and meets the condition , the indifference points mentioned above will satisfy . As a result, the utility of users choosing subscribe to the premium service is always higher than the utility of choosing free service, so all users will choose paid subscriptions and there will be no free users. Finally, the third constraint ensures that the advertising fees charged by the platform are always positive, otherwise introducing advertisements will not bring any revenue to the platform. For the convenience of subsequent analysis, we believe that the conditions stated in Assumption 1 hold throughout this paper.
Assumption 1.
, . Moreover, .
Firstly, we assume that the nuisance cost caused by advertisements to users, , is lower than the marginal revenue that users create for advertisers, . If not, the negative impact of advertisements will exceed the value it generates, and the platform will not be able to realize profits by introducing advertisements. And in order to be closer to the actual situation, we assume that the existing video content on the platform can only create limited intrinsic value for users. This implies that the platform cannot attract all user to participate solely based on existing content, and users need to weigh the intrinsic value provided by the platform and the nuisance cost caused by advertisements to make a participation decision. To focus on the existence of interior equilibrium results, we also assume that . Now, we can solve the profit maximization problem and summarize the results in the following lemma.
Lemma 1. Let . The optimal advertising intensity and subscription price of the online video platform have the following two cases:
If , then , the platform only provides the paid premium service and opts for a purely subscription-based model. At this time, the platform sets the optimal subscription price as .
If , the platforms offers both the free service and the premium service. In this case, the platform adopts a mixed model. The subscription price is and the advertising intensity is , where , , and .
Lemma 1 elaborates the platform’s optimal strategy for advertising intensity and subscription price in the second stage. It can be seen that the amount of original content provided by the platform in the first stage endogenously determines the business model it adopts. When there is less original content available, the platform tends to choose a mixed model, obtaining both advertising revenue and subscription revenue. On the contrary, when the amount of original content is large enough, the platform is more inclined to abandon advertising and rely entirely on user subscriptions for profit. The reason behind this that, as the amount of original content increases, the platform is able to create higher added value for subscribers, which greatly enhances users’ willingness to pay for subscription. As a result, more and more free users will switch to the premium service under the drive of original content. As the number of free users declines, the revenue of advertisers gradually decreases, causing more and more advertisers to leave the market because they cannot break even. The platform has to lower the advertising prices to maintain advertiser participation. In the extreme case, when the amount of original content increases to a certain threshold , the advertising fee drops to 0. At this point, the platform will lose the incentive to offer the free service, and thus transition to a purely subscription-based model.
Lemma 2. Let , where . If the advertising intensity threshold , when , although the platform still adopts a mixed mode, it always maintains the maximum advertising intensity , and sets the subscription price as . The advertising price becomes .
As mentioned in Lemma 1, when the amount of original content provided by the platform is limited, a mixed business model is more favorable. Under this model, the platform need to make a trade-off between subscription revenue and advertising revenue. As the amount of original content continues to decline, the number of subscription users and the subscription price decrease correspondingly, leading to a reduction in platform subscription revenue. Instead, the number of free users rises, which in turn helps the platform to attract more advertisers. Hence, the platform will consider increasing advertising intensity to expand advertising revenue. We define as the advertising intensity threshold, and find that under the condition of , when the amount of original content decreases to , the demand of advertisers will reach its maximum. Although with further reduction of original content, the scale of free users continues to expand, and the revenue brought to advertisers continues to rise, but the demand of advertisers cannot be further expanded. In this case, the platform will not continue to increase the supply of advertising space, but will keep the advertising intensity equal to the maximum demand of advertisers, and raise the advertising fee to to achieve profit growth.
However, it is not always the case that advertisers’ demand reaches its maximum. When the advertising intensity threshold is lower than 0, even if the amount of original content is reduced to 0, the demand of advertisers cannot achieve the maximum. Specifically, the markets that meet the above condition can be summarized into the following two types: (1) , or (2) , but . In the first type of market, the intrinsic value provided by the platform’s existing video content to users is relatively low, leading to fewer users choosing free services of the platform. And in the second type, although the existing video content provides higher intrinsic value to free users, the intrinsic value enjoyed by subscription users is significantly enhanced compared to free users. Therefore, regardless of original content, the enhancement of intrinsic value can drive enough users to switch from free services to paid subscriptions, resulting in a limited number of users choosing free services. In both situations, due to the smaller size of free users, advertisers are not able to earn sufficient revenue from participating in the platform, making advertisers with high fixed costs unable to break even and consequently exist the market. Only in the market where and , the platform is allowed to generate high enough advertising benefits for advertisers through a sufficient number of free users to attract the participation of all advertisers. Since has an important impact on the platform’s advertising intensity decision, we define as the advertising intensity threshold in the subsequent analysis.
Combining the conclusion in Lemma 1, we find that when the platform adopts the mixed model, it can choose to implement two strategies. In the first strategy, the platform provides relatively more original content to gain higher subscription revenue. At this time, users are more inclined to subscribe to premium services, and fewer users choose free services, so the platform can only achieve a moderate level of advertising intensity and correspondingly obtain lower advertising revenue. In contrast, in the second strategy, the platform is only willing to provide limited original content, placing greater emphasis on advertising revenue. Due to the fewer number of paid users, the platform gets lower subscription revenue. However, because of the huge size of free users, the platform can achieve maximum advertising intensity and further increase advertising revenue by charging higher advertising fees than the first strategy (i.e., ). It is worth noting that the second strategy is only available when the advertising intensity threshold is positive. Otherwise, when is negative, the platform only has the option of moderate advertising intensity strategy under the mixed model.
4.2. Stage 1: Original Content
In the first stage, the platform decides on how much original content to provide in order to maximize the total profit. Recall that the platform’s profit is expressed as the sum of subscription revenue and advertising revenue minus the production cost of original content, where the form of cost function is . To focus on the interior solution, we assume that the marginal production cost of original content satisfy the condition that , where . Based on this assumption, we can derive the optimal amount of original content under different models, and express the result in the following lemma.
Lemma 3. The optimal strategy for providing original content has the following three cases:
Under a subscription model, the optimal amount of original content is .
Under a mixed model, if the platform implements the maximum advertising intensity strategy, the optimal amount of original content is .
Under a mixed model, if the platform implements the moderate advertising intensity strategy, the optimal amount of original content is .
Indeed, in order to make users willing to pay subscription fees, the platform needs to provide sufficient original content. This ensures that users obtain enough utility growth from the premium service to offset the costs associated with subscribing. Consequently, the amount of original content under the purely subscription-based model, , is always higher than the amount of original content under the mixed model, and . However, in adopting this business model, although increasing the amount of original content can continuously raise the number of subscribers and subscription prices, it also expands the cost of producing original content. And the growth of subscription revenue cannot completely offset these additional production costs. Therefore, the platform tends to provide the minimum amount of original content for implementing this model, that is stated in Lemma 1. It is worth noting that is only affected by users’ utility, and is independent of the platform’s cost of producing original content.
Conversely, if the platform adopts a mixed model, the amount of original content reflects the utility difference between the free and paid options. More original content will incentivize users to switch from the free services to paid subscriptions. At this point, the platform needs to strike a balance between the following two decisions. On the one hand, by increasing the amount of original content, the platform can expand the number of subscribers and raise the subscription price, thereby enhancing subscription revenue. On the other hand, the platform can also increase the advertising intensity and obtain higher advertising revenue by reducing the amount of original content. Under the mixed model, the choice of original content is closely related to its production cost. Regardless of the strategy of advertising intensity, the optimal amount of original content, and both decreases with the production cost . This suggests that if the cost of creating original content is low, the subscription revenue generated by the increase in original content will be sufficient to cover the production cost, prompting the platform to provide more original content. On the contrary, if the production cost is high, producing more original content will exacerbate the cost burden of the platform. In this case, the platform will reduce the original content to alleviate the cost pressure, compensating for the loss in subscriptions by increasing adverting intensity.
However, under the condition where advertising intensity threshold , if the platform continues to reduce original content, the demand of advertisers will reach the maximum. Beyond this point, further reducing original content cannot stimulate more advertising demand. In this case, the production cost of original content becomes the key determinant of whether the platform adopts the strategy of maximum advertising intensity strategy or moderate advertising intensity. Let , we find that when , constrained by the higher production costs, the platform is more inclined to provide less original content and set maximum advertising intensity to maximize profit. Conversely, when , the production cost of original content is relatively low, and the subscription revenue brought an appropriate increase in the original content is enough to make up for the production cost and increase the profit. Therefore, the platform will increase the original content and reduce the advertising intensity, thus switching to the moderate advertising intensity strategy. As mentioned before, when the advertising intensity threshold , the platform cannot provide sufficient advertising benefits to attract all advertisers, leaving the moderate advertising intensity strategy as the only viable option.
Denote the platform’s optimal profit when choosing the subscription model as . Under the mixed model, if the platform opts for maximum advertising intensity, the optimal profit is denoted as , while the optimal profit when choosing moderate advertising intensity is . Use and to represent the differences between optimal profits, where and . We find that and , thus there exist and that make and hold respectively. and also satisfy and , thus meet the assumption. In previous analysis, we point out that the amount of original content will endogenously determine the business model chosen by the platform. However, the original content provided by the platform is primarily constrained by the production costs, thus making these costs a crucial factor influencing the platform’s choice of business model. The following propositions provide a systematic overview of the pathways of this influence.
Proposition 1. In the case of if , the platform only offers the premium service and chooses the subscription model. If , the platform offers a menu of free and premium services, chooses the mixed model and implements the strategy of moderate advertising intensity.
According to the previous analysis, when , the platform can only achieve moderate advertising intensity under the mixed model. In this case, the platform needs to decide the amount of original content to provide, which will further determine whether to choose the subscription model or the mixed model with moderate advertising intensity.
In our model, the benefits that advertisers derive from participating in the platform entirely come from the network externalities contributed by free users. The platform is unable to offer additional value to advertisers. But for users, not only existing video content on the platform can provide intrinsic value, but original content also generates additional value. As a result, the platform can always charge users a higher subscription price, compared to the advertising fee charged to advertisers. In the ad-free subscription model, the platform attracts more users to pay for subscription by providing more original content. In contrast, under the mixed model, the platform sacrifices some subscription users in exchange for more advertisers. Since the subscription price is always higher than the advertising price, when the cost of producing original content is low, the subscription model with more paying users always creates higher profits than the mixed model. However, as the production cost increases, since the optimal original content in the subscription model, , always stays at the value , the total cost of providing original content continually rises with . This increase gradually offsets the advantage brought by the higher subscription price, leading to a decline in platform profits. When increases to , the optimal profits under the subscription model drop to be equal to the optimal profit under the mixed model, that is, . Although as increases, the profits in the mixed model also decrease, the platform will correspondingly reduce the original content provided, thus slowing down the decline rate of profit. Therefore, when continues to increase beyond , will be lower than , and the platform will choose the mixed model and set moderate advertising intensity.
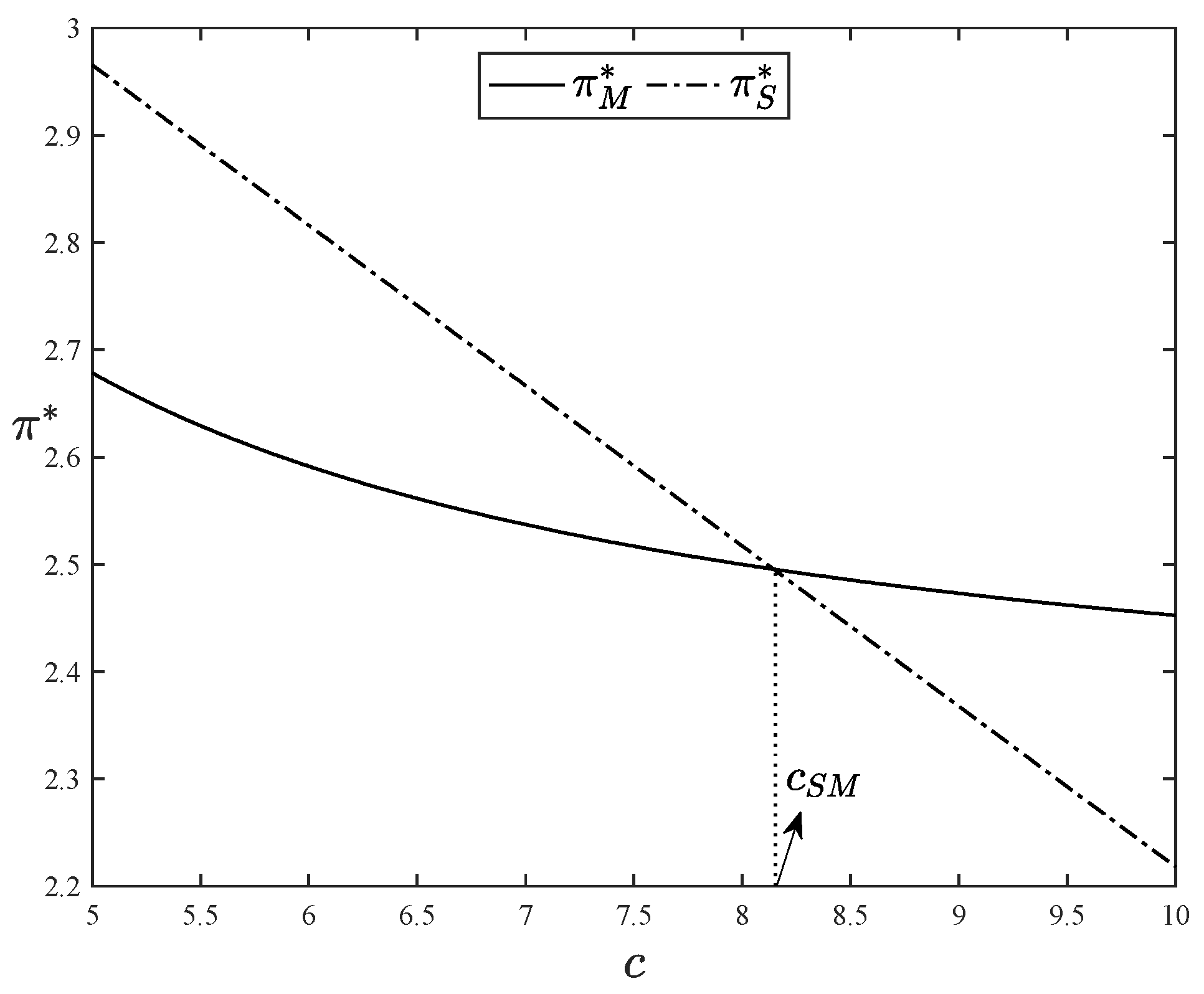
We then further illustrate the above results utilizing a numerical example. By setting
,
,
,
and
, we obtain the results shown in
Figure 2. Under these conditions, we can calculate that the advertising intensity threshold
is lower than 0, thus the platform is not able to achieve the maximum demand of advertisers. From the left-hand side of
Figure 2, we can observe that when the marginal production cost of original content is below a threshold value,
(approximately 8.1436 given our selected parameters), the optimal profits in a subscription model consistently surpasses those in a mixed model. Thus, when
remains below this threshold, the platform always chooses the subscription model to optimize profits. As
becomes larger, a decrease in the optimal profits in both models is observed. However, the rate of decline in the subscription model exceeds that of the mixed model. The right-hand side of
Figure 2 shows that, when
increases above 8.1436, the mixed model’s optimal profit outperforms that of the subscription model. Consequently, the platform transitions to the mixed model to maximize profits.
Proposition 2. In the case of :
If the improvement level of intrinsic value for subscribed users, , is greater than , when , the platform only offers the premium service and chooses the subscription model; when , the platform offers a menu of free and premium services, chooses the mixed model and implements the strategy of moderate advertising intensity; when , the platform chooses the mixed model with maximum advertising intensity.
However, if , when , the platform chooses the subscription model; otherwise, when , the platform chooses the mixed model and implements the strategy of maximum advertising intensity.
When , the platform has the potential to achieve maximum intensity of advertising under the mixed model. In this case, the platform needs to choose between an ad-free subscription model, a mixed model with moderate advertising intensity, and a mixed model with maximum advertising intensity. Among these three models, the optimal amount of original content shows a decreasing trend. As the marginal production cost of original content increases, providing more original content will lead to a rapid rise in costs, significantly cutting the total profits and thus reducing the platform’s willingness to produce original content. Therefore, as the cost continues to increase, the platform will gradually reduce the supply of original content while increasing the advertising intensity, transitioning from an ad-free subscription model to a mixed model with moderate advertising intensity, and ultimately shifting to maximum advertising intensity when the cost is sufficiently high.
However, the above result only applies when the platform provides a relatively high level of intrinsic value enhancement to its subscribers, i.e., when . When the promotion level of intrinsic value gained by subscribers is low, i.e., , the platform will only choose between the two extreme strategies of no advertising and maximum advertising, and will not consider adopting the moderate advertising intensity model. In the following, we will explore the reasons behind this phenomenon in detail.
From the utility function of users we can see that, compared with free users, the utility growth of subscribed users mainly comes from two aspects: the enhancement of intrinsic value provided by the platform and the supply of original content. Therefore, if subscribers can enjoy a higher intrinsic value increment, their utility can achieve greater growth, allowing the platform to charge them a higher subscription price. Conversely, if the increment level of intrinsic value is low, the subscription price that the platform can charge will decrease correspondingly. From this point of view, in the mixed model with moderate advertising intensity, since the platform only provides little original content, the subscription price charged by the platform is relatively limited. If is also very low at this time, the subscription price and ultimately the subscription revenue will be further reduced.
As mentioned in Lemma 3, when adopting the mixed model, if the marginal cost of producing original content exceeds a critical cost threshold, , the increased total production costs make the platform more inclined to provide less original content and take a maximum advertising intensity strategy for profit maximization. In contrast, if the marginal cost is low, i.e., , the platform will moderately increase the amount of original content to attract more subscribers, but can only achieve moderate advertising intensity. However, when is relatively low, the platform’s subscription revenue is limited when the advertising intensity is at a moderate level. Besides, due to the lower advertising intensity and the corresponding advertising fee, it also earns little advertising revenue. We observe that , which means that the cost threshold for the platform to switch from moderate advertising intensity to maximum advertising intensity decreases with . Therefore, in the case of lower , when is relatively small, the platform will become unable to provide more original content, thereby reducing the amount of original content and switching to a maximum advertising intensity strategy. Moreover, when , we find that . In other words, when , although the optimal profit at moderate advertising intensity is higher than the optimal profit at maximum advertising intensity, it is still lower than the optimal profit under a purely subscription-based model. This means that even if , the platform is less likely to choose the mixed model with moderate advertising intensity, but adopts a subscription model instead.
Therefore, when , the platform makes a choice between the subscription model and the mixed model with maximum adverting intensity. Under the ad-free subscription model, the optimal original content decreases with , implying that the platform needs to provide a relatively small amount of original content when is low. Even if the marginal production cost increases to , the subscription revenue can still cover the relatively low production costs and bring the maximum profit to the platform. However, as continues to increase above , the cost burden can no longer be ignored and the subscription model is no longer effective. The platform will then reduce the supply of original content and move to a mixed model with maximum advertising intensity.
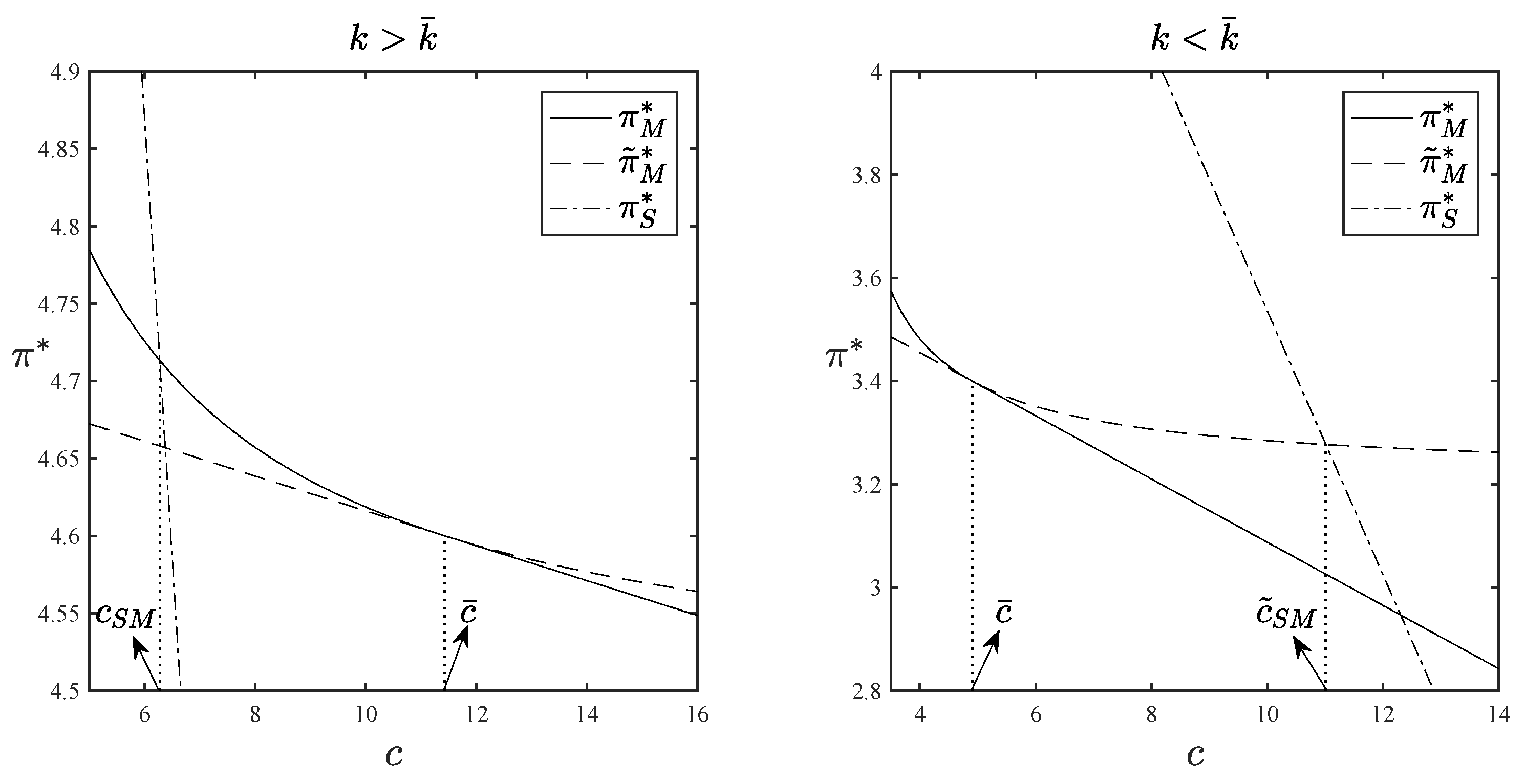
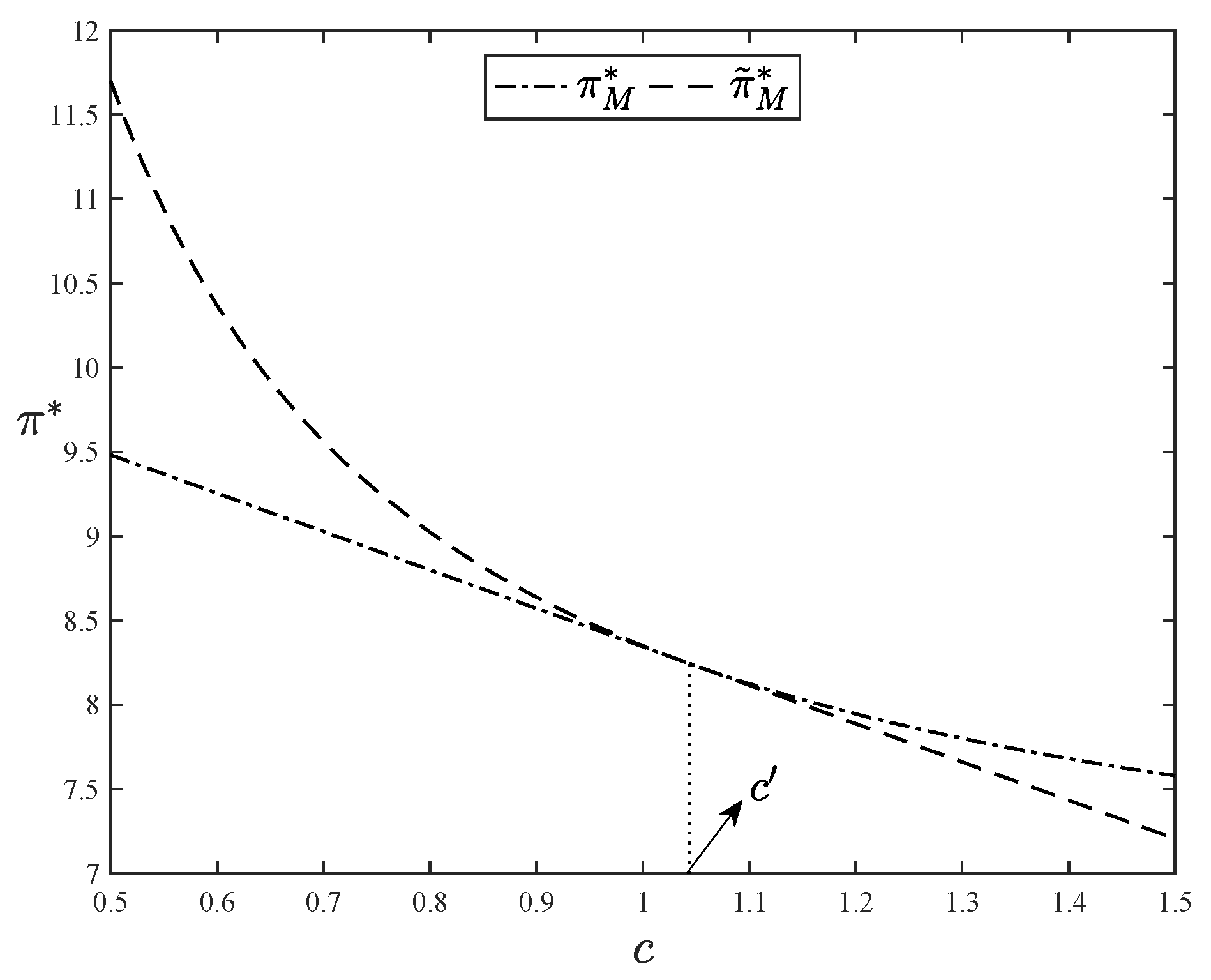
In order to better illustrate the above results, we present a numerical study in
Figure 3. We set
,
,
and
in this example, and these parameters yield a threshold
of approximately 0.35, i.e.,
in this case. By setting
in the left panel and
in the right panel, we can use the left and right panels of
Figure 3 to represent the cases of
and
, respectively. Then we plot how platform’s optimal profits under different business models changes with the production cost of original content in these two cases. From the left panel of
Figure 3, we observe that when
, the critical values of the marginal production cost of original content satisfies
. Additionally, when
is lower than
, the optimal profit in the subscription model,
, consistently surpasses those in the mixed models,
and
. Thus, if
falls below
, it is better for the platform to choose the subscription model. However, if
increases from
to
, the optimal profit in the moderate-advertising-intensity mixed model,
, overtakes
, becoming the maximum profits under the three business models. In such a scenario, the platform should adopt the mixed model with moderate advertising intensity when
lies in the interval
to maximize profits. Further, when
exceeds
, the optimal profit in the maximum-advertising-intensity mixed model,
, turns to be the maximum value among the three optimal profits. This shift prompts the platform to switch to the mixed model with maximum advertising intensity to obtain the largest revenue.
The right panel of
Figure 3 illustrates the case where
. In this situation, the critical values of the marginal production cost now align to
. We can observe that the optimal profit
is higher than
when
, and becomes lower than
when
. However, as long as
remains below
, these two optimal profits under the mixed model,
and
, consistently stay beneath the optimal profit in the subscription model,
, thus the platform always chooses the subscription model to optimize profits when
. When
surpasses
,
exceeds
, becoming the largest profit obtained by the platform under the three different business models. As a result, the platform transitions to the mixed model with maximum advertising intensity to maximize profits.
After discussing the strategic choice of the platform in equilibrium, we further investigate the influence of market characteristics on the platform’s choice of business model, and get the following findings.
Proposition 3. As the marginal revenue contributed by users to advertisers increases, the platform earns less profits under a subscription model but more profits under a mixed model, eventually switching from a subscription model to a mixed model.
This proposition describes the influence of network externalities that users contribute to advertisers on platform profits and business model. As increases, advertisers are willing to pay more for participating in the platform and the potential advertising revenue of the platform increases accordingly. This change makes the mixed model that introduces advertising more attractive relative to the ad-free subscription model. Thus, when is large, the platform will switch from the ad-free subscription model to the mixed model to earn both advertising and subscribing revenue. This strategic shift assists in increasing the platform’s profits. To understand this phenomenon, first recall that in Lemma 1, we find that when the market-clearing advertising fee drops to zero, the platform loses its motivation to attract advertisers by offering free services and thus shifts to a purely subscription-based model. However, advertisers’ revenue increases when increases, allowing the platform to charge higher advertising fees, thus it has enough incentives to choose the mixed model. With the growth of , the platform will only enable the subscription model when it further increases the supply of original content to reduce the number of free users, so that the advertising fee that advertisers are willing to pay is reduced to zero. Although increasing the amount of original content allows the platform to charge users more, due to the higher costs of producing original content, the growth in subscription revenue is insufficient to offset these costs, which eventually leads to a decline in platform profits. Secondly, under the mixed model, as increases, the platform will reduce investment in original content to boost the number of free users, thereby attracting more advertisers and collecting higher advertising fees. In this scenario, the platform’s advertising revenue increases, while the cost associated with providing original content decreases due to its reduced supply, contributing to an improvement of overall profits.
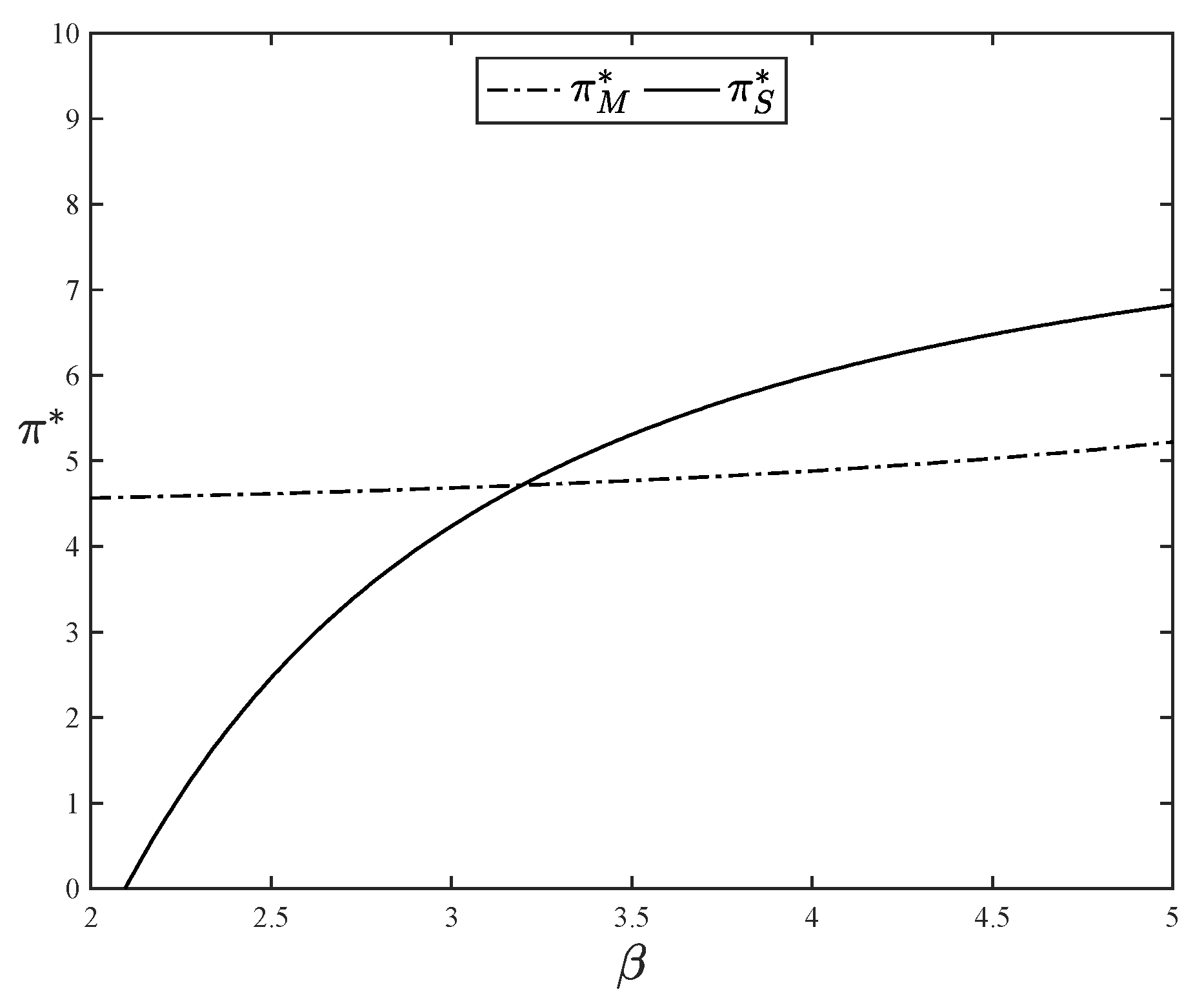
We use
Figure 4 to further illustrate the changing trend of optimal profits under the subscription model and the mixed model with respect to
. In order to meet the requirements in our assumptions and ensure the existence of equilibrium, we set the parameters as
,
,
,
and
. More importantly, we combine the two situations of moderate and maximum advertising intensity under the mixed model, and the optimal profit
is designated as
when
is lower than
and as
when
is higher than
. From
Figure 4, we can see that when
is low, the subscription model brings the highest profit to the platform, so the platform should choose the subscription model for profit maximization. As
increases, the optimal profit under the subscription mode gradually decreases, while the optimal profit under the mixed model keeps increasing. And eventually at sufficiently high values of
, the optimal profit in the mixed model surpasses the profit in the subscription model, causing the platform to shift to the mixed mode to maximize profits.
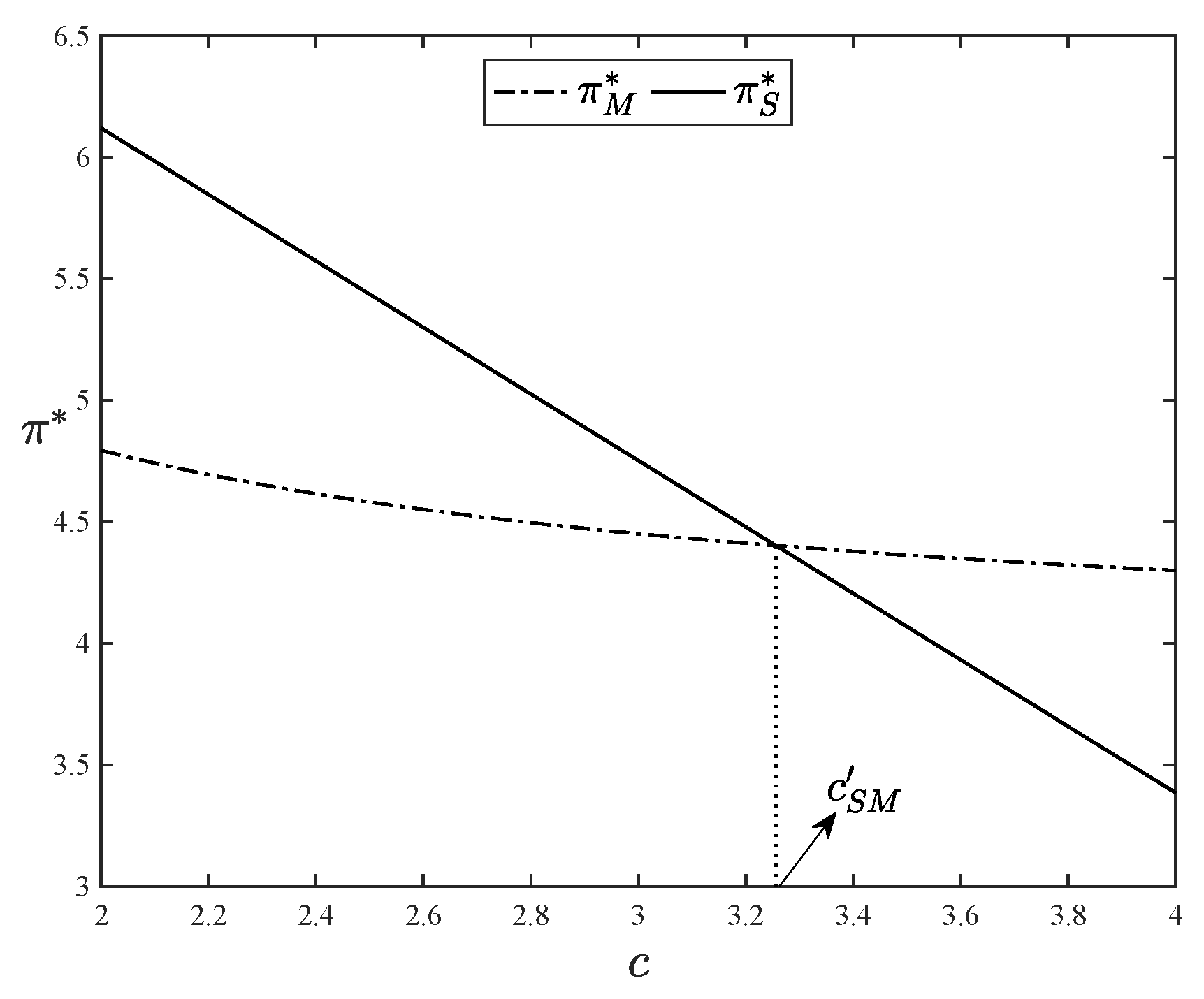
Proposition 4. As the marginal value of original content to users increases, the platform switches from a mixed model to a subscription model and earns more profits.
To understand this proposition, notice that the marginal value that original content delivers to users also reflects users’ desire for original content. As increases, users are willing to pay higher subscription fees and are more inclined to subscribe to the platform’s original content, gradually making the strategy of introducing advertising less attractive. With the growth of , an increasing number of users opt for subscription services. And the platform finally shifts from a mixed model to a subscription model with large . Under the mixed model, as increases, the platform will increase the supply of original content. This move helps to substantially enlarge the utility of subscribing users, enabling the platform to charge higher subscription fees. Such a price increase can significantly expand the platform’s profit, effectively offsetting the increased cost of providing original content. At the same time, with the increase of , a large number of free users convert to subscribing users, resulting in a continuous decrease in the revenue of advertisers as well as the market-clearing advertising fees. Therefore, under the subscription model, the amount of original content that the platform needs to provide decreases with the increase of . Such adjustments save costs for the platform and improve overall profits.
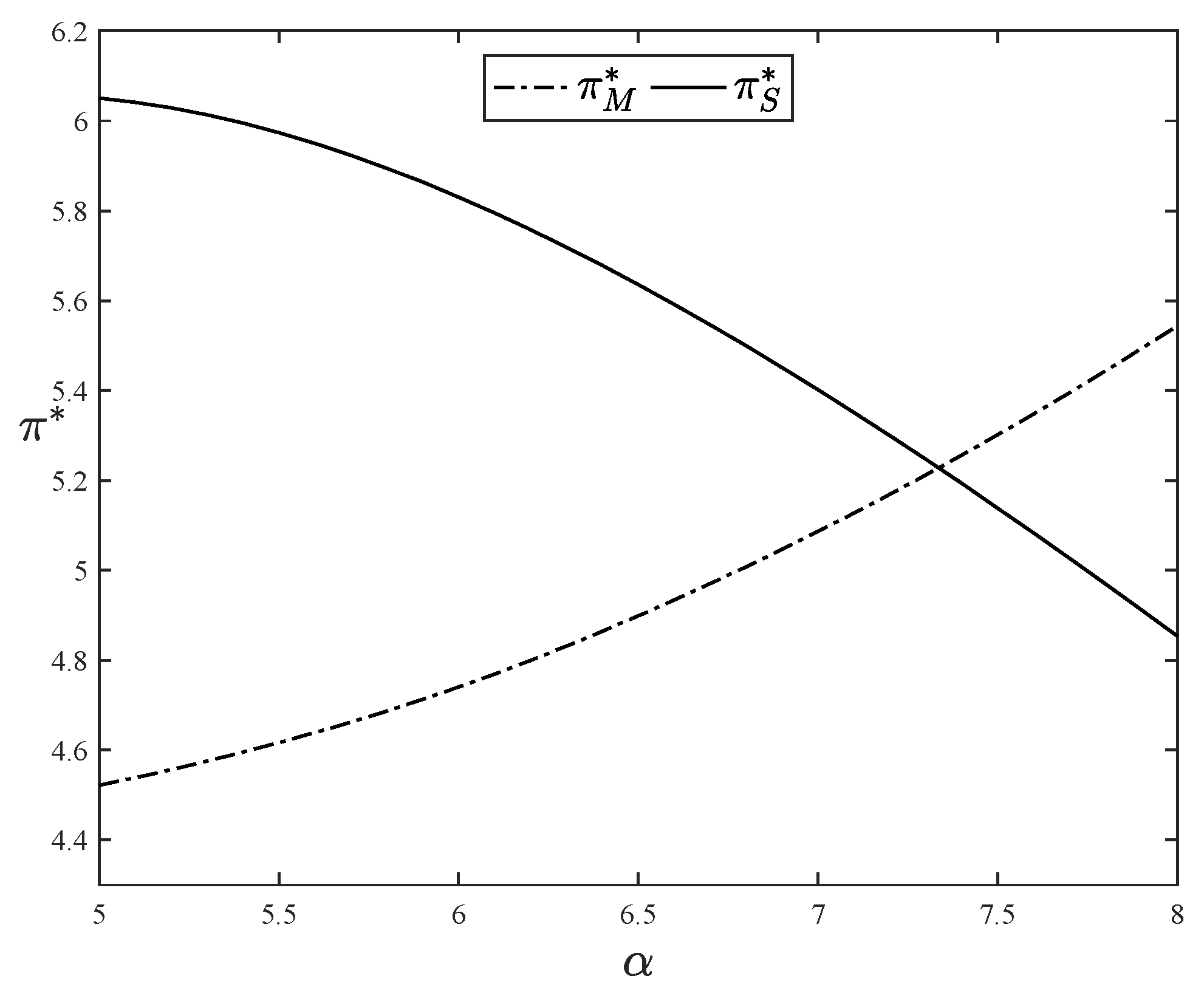
Figure 5 provides a more intuitive illustration of how optimal profits vary with respect to
in both the subscription and mixed models. The parameter setting is that
,
,
,
and
in
Figure 5. The expression of the optimal profit under the mixed model follows a pattern similar to that depicted in
Figure 4. It can be seen from
Figure 5 that as
grows, the optimal profit in both the subscription model and the mixed model keeps increasing. Besides, when
is low, the mixed model yields the maximum profit for the platform. However, when
becomes sufficiently large, the optimal profit of the subscription model outperforms that of the mixed model. This observation suggests that as
increases, the platform should shift from a mixed model to a subscription model to optimize profit.