Submitted:
11 April 2025
Posted:
14 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Big Data-Driven Characterization of Economic Cycles
2.1. Multidimensional Big Data Indicator Construction
2.2. Data Preprocessing and Feature Engineering
2.3. Identification of Key Features of the Economic Cycle
3. AI Intelligent Prediction Model Construction
3.1. Deep Learning Prediction Framework Design
3.2. Optimization of Neural Network Algorithm
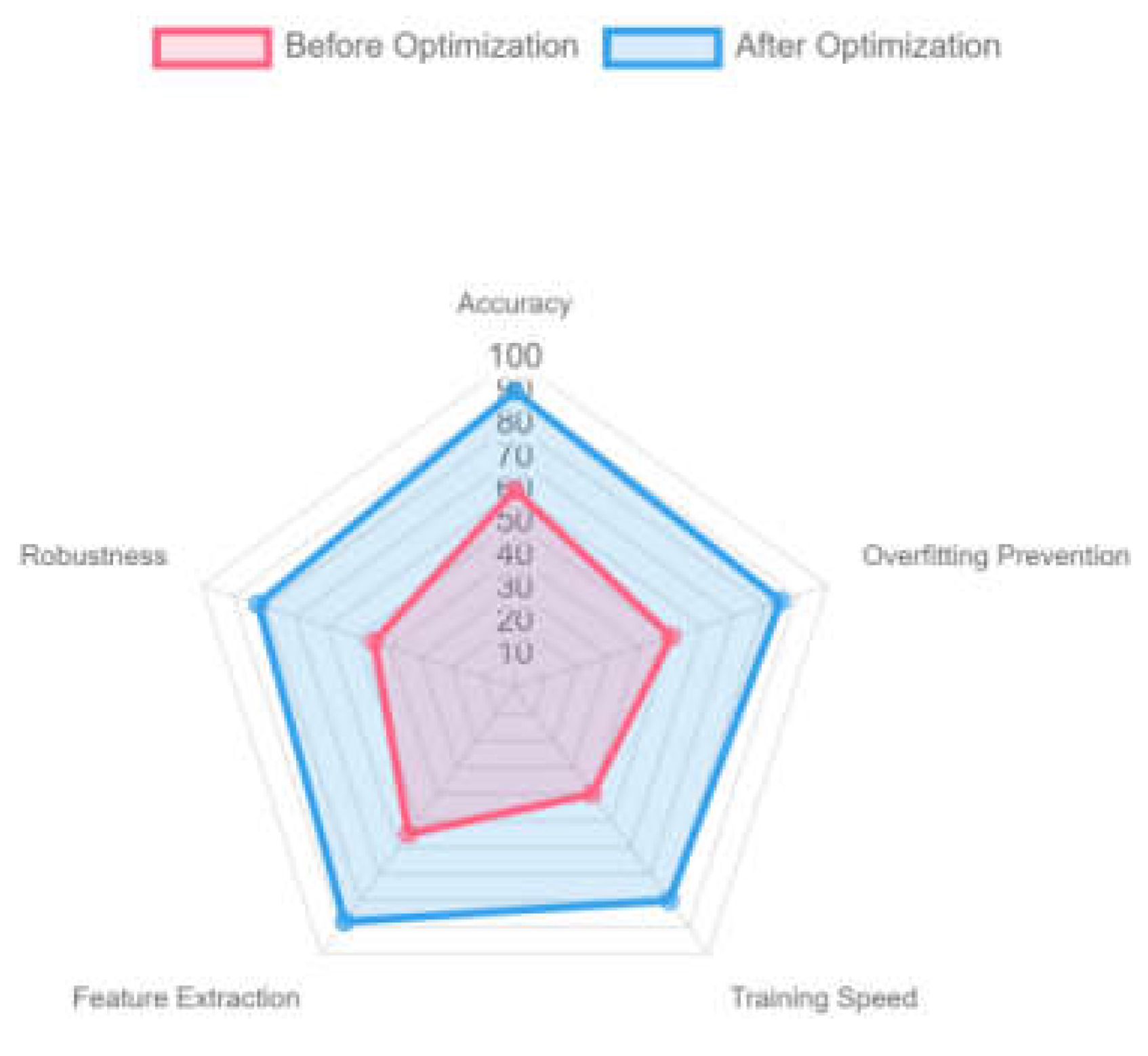
3.3. Model Training and Parameter Tuning
| Parameter name | Value range/set value | clarification |
| LSTM layers | 2-4 floors | Deep LSTM structure is used to improve the feature learning capability |
| Number of hidden units | 64, 128, 256 | Control network complexity to prevent overfitting |
| Dropout rate | 0.1-0.5 | Randomly Discarding Neurons to Improve Model Robustness |
| Learning rate (initial) | 0.001-0.01 | Adoption of dynamic learning rate adjustment strategies |
| Batch Size | 32, 64, 128 | Influence on the stability of gradient updates |
| Weight decay (L2) | 0.0001-0.001 | L2 regularization is used to prevent overfitting |
4. Validation of Economic Cycle Forecasting Methods
4.1. Predictive Model Performance Assessment
| Assessment of indicators | LSTM | Bi-LSTM | Bi-LSTM + Attention | Bi-LSTM + Transformer |
| MSE | 0.023 | 0.019 | 0.015 | 0.011 |
| MAE | 0.128 | 0.104 | 0.089 | 0.072 |
| R | 0.87 | 0.91 | 0.94 | 0.97 |
| TA | 83.5% | 87.2% | 90.4% | 93.1% |
4.2. Error Analysis of Prediction Results
| economic variable | Mean error (MAE) | Standard deviation (STD) | error contribution rate |
| GDP growth rate | 0.032 | 0.015 | 14.5% |
| CPI | 0.027 | 0.012 | 11.2% |
| unemployment rate | 0.045 | 0.020 | 18.7% |
| value added by industry | 0.038 | 0.017 | 16.1% |
| stock market index | 0.089 | 0.035 | 23.6% |
| Corporate credit spreads | 0.075 | 0.028 | 15.9% |
4.3. Model Robustness Test
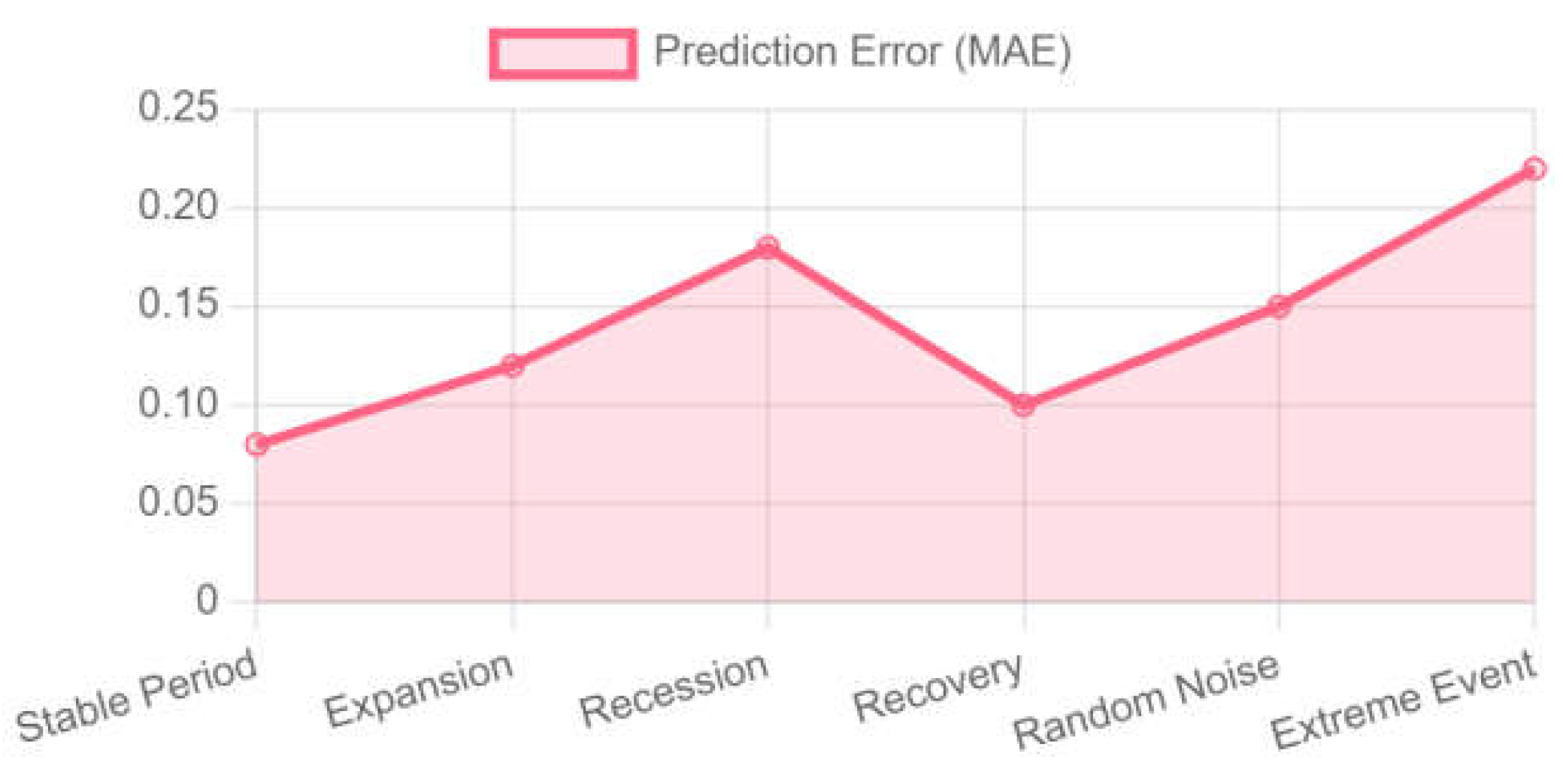
5. Conclusion
References
- Chen K, Zhao S, Jiang G, et al. The Green Innovation Effect of the Digital Economy. International Review of Economics & Finance, 2025: 103970. [CrossRef]
- Diao S, Huang S, Wan Y. Early detection of cervical adenocarcinoma using immunohistochemical staining patterns analyzed through computer vision technology//The 1st International scientific and practical conference “Innovative scientific research: theory, methodology, practice”(September 03–06, 2024) Boston, USA. International Science Group. 2024. 289 p. 2024: 256. [CrossRef]
- Diao S, Wan Y, Huang S, et al. Research on cancer prediction and identification based on multimodal medical image fusion//Proceedings of the 2024 3rd International Symposium on Robotics, Artificial Intelligence and Information Engineering. 2024: 120-124. [CrossRef]
- Gong C, Lin Y, Cao J, et al. Research on Enterprise Risk Decision Support System Optimization based on Ensemble Machine Learning//Proceeding of the 2024 5th International Conference on Computer Science and Management Technology. 2024: 1003-1007. [CrossRef]
- Gong C, Zhong Y, Zhao S, et al. Application of Machine Learning in Predicting Extreme Volatility in Financial Markets: Based on Unstructured Data//The 1st International scientific and practical conference “Technologies for improving old methods, theories and hypotheses”(January 07–10, 2025) Sofia, Bulgaria. International Science Group. 2025. 405 p. 2025: 47. [CrossRef]
- Huang S, Diao S, Wan Y, et al. Research on multi-agency collaboration medical images analysis and classification system based on federated learning//Proceedings of the 2024 International Conference on Biomedicine and Intelligent Technology. 2024: 40-44. [CrossRef]
- Huang S, Diao S, Zhao H, et al. The contribution of federated learning to AI development//The 24th International scientific and practical conference “Technologies of scientists and implementation of modern methods”(June 18–21, 2024) Copenhagen, Denmark. International Science Group. 2024. 431 p. 2024: 358. [CrossRef]
- Jian X, Zhao H, Yang H, et al. Self-Optimization of FDM 3D Printing Process Parameters Based on Machine Learning//The 24th International scientific and practical conference “Technologies of scientists and implementation of modern methods”(June 18––21, 2024) Copenhagen, Denmark. International Science Group. 2024. 431 p. 2024: 369.
- Jiang G, Huang S, Zou J. Impact of AI-driven data visualization on user experience in the internet sector. 2024. [CrossRef]
- Meng Q, Wang J, He J, et al. Research on Green Warehousing Logistics Site Selection Optimization and Path Planning based on Deep Learning. 2025. [CrossRef]
- Shimin L E I, Ke X U, Huang Y, et al. An Xgboost based system for financial fraud detection//E3S Web of Conferences. EDP Sciences, 2020, 214: 02042. [CrossRef]
- Shui H, Sha X, Chen B, et al. Stock weighted average price prediction based on feature engineering and Lightgbm model//Proceedings of the 2024 International Conference on Digital Society and Artificial Intelligence. 2024: 336-340. [CrossRef]
- Wang H, Li J, Li Z. AI-generated text detection and classification based on BERT deep learning algorithm. Theoretical and Natural Science, 2024, 39: 311-316. [CrossRef]
- Wang H, Li Z, Li J. Road car image target detection and recognition based on YOLOv8 deep learning algorithm. Applied and Computational Engineering, 2024, 69: 103-108. [CrossRef]
- Wang, H. Joint Training of Propensity Model and Prediction Model via Targeted Learning for Recommendation on Data Missing Not at Random//AAAI 2025 Workshop on Artificial Intelligence with Causal Techniques. 2025.
- Yang J, Tian K, Zhao H, et al. Wastewater treatment monitoring: Fault detection in sensors using transductive learning and improved reinforcement learning. Expert Systems with Applications, 2025, 264: 125805. [CrossRef]
- Zhao H, Chen Y, Dang B, et al. Research on Steel Production Scheduling Optimization Based on Deep Learning. 2024. [CrossRef]
- Zhao S, Lu Y, Gong C, et al. Research on Labour Market Efficiency Evaluation Under Impact of Media News Based on Machine Learning and DMP Model. 2025. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




