Towards Equilibrium in Human-AI Collaboration: A Dynamic Model of Performative Feedback and Empirical Insights

1. Introduction

Human-ML collaboration is increasingly applied in domains such as social media moderation (Lai et al., 2022), healthcare diagnosis (Jacobs et al., 2021; Dvijotham et al., 2023), and hiring decisions (Peng et al., 2022). However, deploying such systems introduces three key challenges: (1) ML models learn from human decisions, which may be noisy approximations of the ground truth; (2) deployed models influence future human decisions, altering the data used for subsequent training (Perdomo et al., 2020); and (3) collaborative performance depends on human incentives and behavior. These factors create a dynamic system where it’s unclear if learning will converge to an accurate representation of the truth or diverge. Consider a healthcare company deploying a diagnostic model trained on past doctor decisions—some of which may be incorrect. The model is then evaluated based on its agreement with those same decisions, potentially reinforcing errors. This feedback loop can lead to improvement or degradation over time, but without costly ground truth verification, it’s hard to tell which is occurring.

Contributions. In this paper, we present a novel framework for analyzing ML deployment in performative, human-AI collaborative systems. Central to our theory is the collaborative characteristic function, which maps ML performance to the resulting human+ML decision quality. We validate our framework with an empirical study involving 1,408 participants solving knapsack problems with ML assistance. Key results:

1) Humans often improve on ML suggestions.

2) Some human decisions are worse than the ML output, even when better options are apparent.

3) Financial incentives do not significantly influence decision quality.

These findings imply that ML models evaluated against human decisions may reinforce existing errors. Companies should invest in validating training labels and aim for deployment strategies that ensure convergence to higher-quality outcomes. A dynamic approach is essential when human decisions influenced by ML are used for future model updates.

2. Related Work

There is a growing literature on human-ML collaboration, from learning-to-defer systems (Cortes et al., 2016; Charusaie et al., 2022; Mozannar et al., 2023) to ML-assisted decision-making (Mozannar et al., 2024c; Dvijotham et al., 2023; Jacobs et al., 2021) and alternative mechanisms (Steyvers et al., 2022; Mozannar et al., 2024a). Applications span programming (Dakhel et al., 2023; Mozannar et al., 2024b), healthcare (Jacobs et al., 2021; Dvijotham et al., 2023), and business (Dell’Acqua et al., 2023). Related work explores explanations (Vasconcelos et al., 2023), incentives (Agarwal et al., 2023), fairness (Sühr et al., 2021), and adaptability (Bansal et al., 2019). We present the first theoretical study of dynamic human+ML systems where ML learns from prior collaborative decisions that may deviate from ground truth. Building on performative prediction (Perdomo et al., 2020; Mendler-Dünner et al., 2020; Hardt et al., 2022; Mendler-Dünner et al., 2022), we extend the framework by modeling proxy ground truth labels, introducing a utility-based view of stable points, and addressing unknown alignment to the true labels. Our empirical study provides a first step toward understanding these dynamics in practice.

3. Problem Statement

We consider a setting in which time is separable into discrete time epochs $t=1,...,T$. At each t, a firm deploys a machine learning model $M_t\in \mathcal{M}$ of a model class $\mathcal{M}$, with $M_t:\mathcal{X}\to \mathcal{Y}$. The model $M_t$ predicts a solution $Y\in \mathcal{Y}$ (e.g., a diagnosis) to a problem $X\in \mathcal{X}$ (e.g., the patient’s symptoms) as a function of past data.

The firm employs expert humans $H\in \mathcal{H}$, with $H:\mathcal{X}\times \mathcal{Y}\to \mathcal{Y}$, who solve problems with the help of ML predictions. We will write $M_t\left(X\right)=Y_{M_t}$ and $H(X,Y_{M_t})=Y_{H_t}$. We assume that for all $X\in \mathcal{X}$, there exists an optimal solution $Y^{*}$, which is the indisputable ground truth.

3.1. The Firm’s Learning Objective

In many real-world settings, obtaining the ground truth $Y^{*}$ is costly—e.g., accurate medical diagnoses may require input from multiple specialists and can still be prone to error. As a result, human label $Y_{H_t}$ are often the only practical proxy for training ML models. We allow the quality of $Y_{H_t}$ with respect to $Y^{*}$ to change. This means that two iterations of the ML model, $M_t$ and $M_{t+1}$, are trained on data from two different data-generating processes: $(X,Y_{H_{t-1}})\sim {\mathcal{D}}_{t-1}$ and $(X,Y_{H_t})\sim {\mathcal{D}}_t$, respectively.

Without access to $Y^{*}$, the only feasible learning objective for a firm updating its model parameters at time t is to compare the latest human-ML collaborative labels with the new predictions. For a given loss function $l:\mathcal{Y}\times \mathcal{Y}\to {\mathbb{R}}^{+}$, we can write this as follows:

$$L(Y_{M_t},Y_{H_{t-1}}):={\mathbb{E}}_{H\in \mathcal{H}}\left[{\mathbb{E}}_{(X,Y_{H_{t-1}})\sim {\mathcal{D}}_{t-1}}l(Y_{M_t},Y_{H_{t-1}})\right].$$

(1)

The firm aims to minimize the difference between the model predictions at time t and the human labels at time $t-1$. We can formulate the firm’s objective as selecting a model $M_t$ to minimize the loss function in Equation (1):

$$\underset{M_t\in \mathcal{M}}{min}L(Y_{M_t},Y_{H_{t-1}}).$$

(2)

For simplicity, we assume that at each time t, the firm collects enough data to perfectly learn the human-ML solution. In other words, with the optimal model, $L(Y_{M_t},Y_{H_{t-1}})=0$.

In our scenario, the firm cannot quantify the true quality of a solution Y with respect to $Y^{*}$. The loss in Equation (2) is a surrogate for the loss $L(Y,Y^{*})$, which is impossible or too costly to obtain. The firm thus defines the human label as the “ground truth” and maximizes the similarity between model and human solutions, without knowing how close the human or ML solutions are to the indisputable ground truth. To evaluate the firm’s progress in approximating $Y^{*}$, it is useful to define a measure of utility.

Definition 1. 

(Utility) Let $d_X$ be a distance measure on $\mathcal{Y}$ with respect to a given $X\in \mathcal{X}$. The function $U:\mathcal{X}\times \mathcal{Y}\to \mathbb{R}$ is a utility function on $\mathcal{X}\times \mathcal{Y}$ if $\forall X\in \mathcal{X},Y_{min},Y,Y^{\prime },Y^{*}\in \mathcal{Y}$:

• $\exists Y_{min}\in \mathcal{Y}$ such that $U(X,Y)\in [U(X,Y_{min}),U(X,Y^{*})]$ (bounded),
• $\exists ϵ>0$ such that $|d_X(Y,Y^{*})-d_X(Y^{\prime },Y^{*})|<ϵ\Rightarrow U(X,Y)=U(X,Y^{\prime })$ (ϵ-sensitive),
• $d_X(Y,Y^{*})+ϵ<d_X(Y^{\prime },Y^{*})\Rightarrow U(X,Y)>U(X,Y^{\prime })$ (proximity measure).

The utility of a solution for the firm is maximal if Y is $ϵ$-close to $Y^{*}$ with respect to the underlying problem X. The variable $ϵ$ should be interpreted as the threshold below which the firm perceives no difference between two outcomes, i.e., it does not care about infinitesimal improvements.

Collaborative Characteristic Function As time t increases, the firm hopes that the distributions ${\mathcal{D}}_t$ shift closer to the optimal distribution ${\mathcal{D}}^{*}$, where $(X,Y)=(X,Y^{*})$. In other words, for each model’s distance d, $d({\mathcal{D}}_t,{\mathcal{D}}^{*})>d({\mathcal{D}}_{t+1},{\mathcal{D}}^{*})$. For example, this could happen if humans were able to compare available solutions and select the one closest to the indisputable ground truth.

We translate this continuous improvement into properties of the human decision function H as follows: for all $t=1,...,T$ and $X\in \mathcal{X}$,

$${\mathbb{E}}_{H\in \mathcal{H}}\left[U(X,H(X,Y_{M_t}))\right]=U(X,Y_{M_t})+{\delta }_{M_t}.$$

(3)

The firm’s hope is that ${\delta }_{M_t}\ge 0$ for all $M_t$. Effectively, ${\delta }_{M_t}$ characterizes the human-ML collaboration for all utility levels of a model. If ${\delta }_{M_t}$ is positive, humans improve on ML predictions, allowing future models to approximate the ground truth more accurately. Conversely, if ${\delta }_{M_t}$ is negative, humans perform worse than ML recommendations, causing future models to diverge from the ground truth.

Definition 2. 

(Collaborative Characteristic Function) For a utility function U, humans $H\in \mathcal{H}$, and model $M\in \mathcal{M}$, the collaborative characteristic function ${\Delta }_U:\mathbb{R}\times \mathcal{M}\to \mathbb{R}$ is defined as:

$${\Delta }_U(U(X,Y_M),M)={\mathbb{E}}_{H\in \mathcal{H}}\left[U(X,H(X,Y_M))\right]=U(X,Y_M)+{\delta }_M.$$

(4)

The function ${\Delta }_U$ can take any arbitrary form. Several factors, such as ML explanations and monetary incentives, can influence ${\Delta }_U$ (as empirically explored in Section 4). Note that ${\Delta }_U$ depends on the ML model M, not just its utility, because equal utility levels across different ML models do not guarantee equal collaborative reactions from humans. For brevity, we write ${\Delta }_U\left(U(X,Y_M)\right)$.

4. Collaborative Learning Path and Stable Points

Although ${\Delta }_U$ has infinite support, a firm will only encounter a discrete set of utility values achieved by humans with ML recommendations. This is referred to as the collaborative learning path.

Definition 3. 

(Collaborative Learning Path) Let ${\Delta }_U$ be a collaborative characteristic function, $t=1,...,T\in {\mathbb{N}}_{\ge 1}$ the number of deployment cycles, and $s=U(X,Y_{M_1})$ the utility of the starting model. The collaborative learning path is defined as:

$$L_{{\Delta }_U}(s,t)={\mathbb{E}}_{H\in \mathcal{H}}\left[{\mathbb{E}}_{X\in \mathcal{X}}U\left(H(X,Y_{M_t})\right)\right].$$

(5)

Definition 4. 

(Stable Point) A stable point $L_{{\Delta }_U}(s,t)$ occurs at t if for all $t^{\prime }\ge t$, $L_{{\Delta }_U}(s,t^{\prime })=L_{{\Delta }_U}(s,t)$.

5. Stable Points and Collaborative Learning

Stable points are states where the utility remains constant across all future model deployments. If $Y^{*}$ is unique for all X, then this point also represents stability in terms of distribution shifts. The ability of a firm to achieve a stable point on its collaborative learning function depends on the shape of ${\Delta }_U$ and the initial model utility s.

Figure 1 illustrates two examples of collaborative characteristic functions and collaborative learning paths. The 45-degree line represents the points where:

$${\mathbb{E}}_{X,H}\left[U(X,H(X,Y))\right]={\mathbb{E}}_X\left[U(X,Y)\right],$$

(6)

mapping the human performance at $t-1$ to the ML performance at t under the assumption of perfect learning. This assumption implies $L(Y_{M_t},Y_{H_{t-1}})=0$.

Figure 1. Collaborative Improvement (left): The firm’s collaborative characteristic function and one collaborative learning path, if humans improve on the ML solution. The x-axis denotes the model expected utility, the y-axis denotes expected human+ML utility. The firm deploys a first model with utility (s). Then humans use the model and improve utility by $\delta$1, leading to expected human+ML utility (1). The firm learns a new model with utility (b) on the new data distribution. This is viable under the assumption that the new model has the same utility as the previous period’s human+ML labels, i.e., we can move horizontally from (1) to the 45-degree line at (b). Humans can further improve utility by $\delta$2, which leads to expected utility (2). The dynamic improvement process continues until it reaches stable point utility (6-d). Collaborative Harm (right): The firm deploys a model with expected utility (s) but the humans, when interacting with the model, decrease utility by $\delta$1, with expected utility (1). The firm will thus learn a model of utility (b) on the new distribution. The downward spiral continues until stable point (d).

Figure 1. Collaborative Improvement (left): The firm’s collaborative characteristic function and one collaborative learning path, if humans improve on the ML solution. The x-axis denotes the model expected utility, the y-axis denotes expected human+ML utility. The firm deploys a first model with utility (s). Then humans use the model and improve utility by $\delta$1, leading to expected human+ML utility (1). The firm learns a new model with utility (b) on the new data distribution. This is viable under the assumption that the new model has the same utility as the previous period’s human+ML labels, i.e., we can move horizontally from (1) to the 45-degree line at (b). Humans can further improve utility by $\delta$2, which leads to expected utility (2). The dynamic improvement process continues until it reaches stable point utility (6-d). Collaborative Harm (right): The firm deploys a model with expected utility (s) but the humans, when interacting with the model, decrease utility by $\delta$1, with expected utility (1). The firm will thus learn a model of utility (b) on the new distribution. The downward spiral continues until stable point (d).

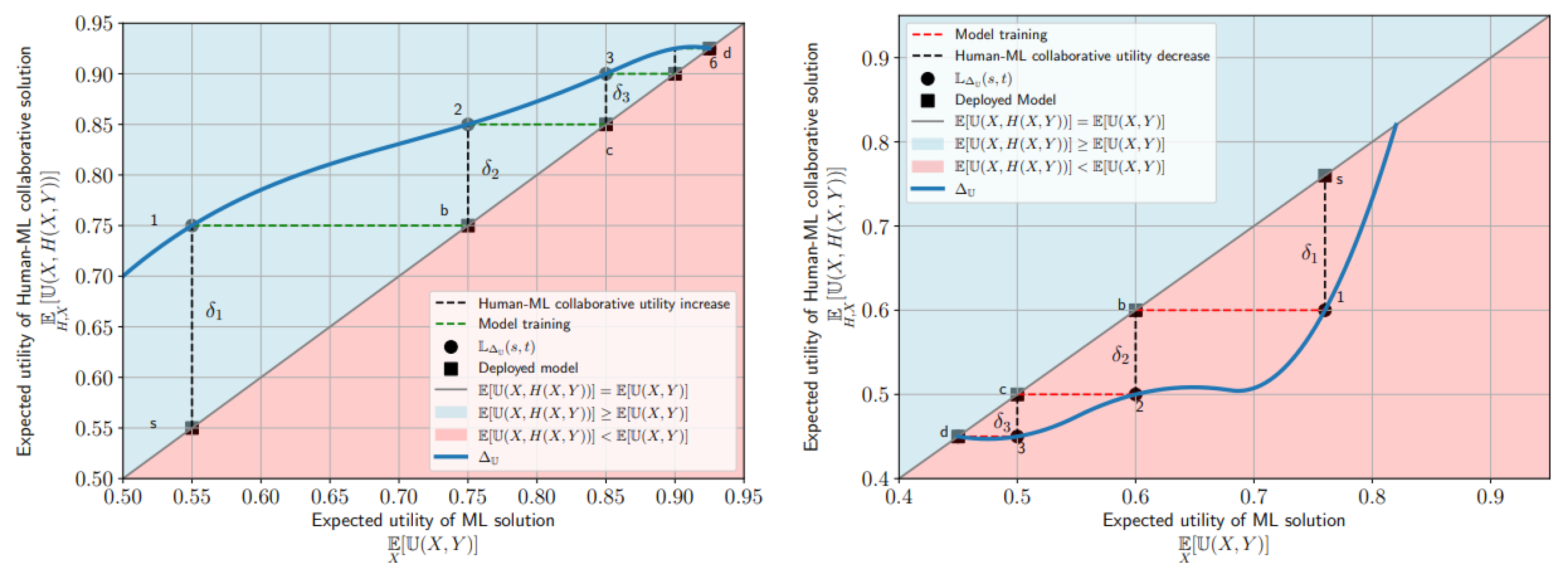
Stable points always lie on this line because such points require ${\delta }_t\approx 0$ (i.e., $|{\delta }_t|\le ϵ$), where $ϵ$ is the smallest detectable change in utility, as defined in Definition 1. If $|{\delta }_t|>ϵ$, this indicates that human intervention changes the labels Y relative to the most recent ML model, leading to a new data distribution. As a result, the subsequent model, $M_{t+1}$, will differ from $M_t$, thereby preventing stability. and maps the human performance at $t-1$ to the ML performance at t under the assumption of perfect learning, i.e., $L(Y_{M_t},Y_{H_{t-1}})=0$. Stable points will always lie on this line, as they require ${\delta }_t\approx 0$ (i.e., $|{\delta }_t|\le ϵ$), where $ϵ$ denotes the smallest detectable change in utility for a given $ϵ$ from Definition 1.

If $|{\delta }_t|>ϵ$, it indicates that human intervention alters the labels Y relative to the most recent ML model, leading to a new data distribution. Consequently, the model at $t+1$ will differ from $M_t$, preventing stability. When the model and human+ML labels diverge, two scenarios can arise:

• Case 1:${\delta }_{M_t}>ϵ$—The collaborative characteristic function ${\Delta }_U$ is above the 45-degree line on that portion of the domain (Figure ). In this case, human+ML labels are closer to the indisputable ground truth than the model alone, leading to improvements in subsequent model deployments.
• Case 2:${\delta }_{M_t}<-ϵ$—The collaborative characteristic function ${\Delta }_U$ is below the 45-degree line (Figure ). Here, human+ML labels are farther from the indisputable ground truth than the model alone, causing a deterioration in subsequent model deployments.

We formalize the best-case and worst-case scenarios from Figures and as Propositions 1 and 2:

Proposition 1 

(Collaborative Improvement). If ${\Delta }_U\left(U(X,Y_M)\right)\ge U(X,Y_M)$ for all $M\in \mathcal{M}$, $X\in \mathcal{X}$, then $L_{{\Delta }_U}(s,t)$ is non-decreasing with $t=1,\cdots ,T$. Furthermore, for sufficiently large T, there exists a $t^{\prime }\in [1,T]$ such that $L_{{\Delta }_U}(s,t^{\prime })$ is a stable point.

Sketch. 

Since U is bounded, ${\delta }_M$ must approach 0 at extreme points. Additionally, due to the $ϵ$-sensitivity of U, the number of steps t required to reach the maximum utility is also bounded. It follows that there exists a $t\in \mathbb{N}$ such that $L_{{\Delta }_U}(s,t)-L_{{\Delta }_U}(s,t+1)=0$, which represents a stable point. See Appendix A.6 for the complete proof. □

Proposition 2 

(Collaborative Harm). If ${\Delta }_U\left(U(X,Y_M)\right)\le U(X,Y_M)$ for all $M\in \mathcal{M}$, $X\in \mathcal{X}$, then $L_{{\Delta }_U}(s,t)$ is non-increasing with $t=1,\cdots ,T$. Furthermore, for sufficiently large T, there exists a $t^{\prime }\in [1,T]$ such that $L_{{\Delta }_U}(s,t^{\prime })$ is a stable point.

Proof. 

Similar to the proof of Proposition 1. □

A firm’s collaborative characteristic function may lie above or below the 45-degree line and can have multiple stable points if continuous. Without ground truth, the firm cannot identify which point yields the highest utility. We present a proof of concept in a setting where the ground truth is known, allowing us to approximate the function and examine how human behavior—especially incentives and selection strategies—shapes it. Participants solve challenging knapsack problems to address two key questions:

• RQ1: How do performance bonuses affect human utility $U\left(H\right(X,.\left)\right)$, without ML recommendations?
• RQ2: Can we approximate the collaborative characteristic function $\Delta U$? by testing human responses ${\delta }_M$ to ML of varying quality under fixed incentives?

6. Experimental Setup

6.1. The Knapsack Problem

We design a user study to simulate settings where ML supports users on difficult tasks, but the true solution $Y^{*}$, we use the 0-1 knapsack problem, which allows precise utility computation $U(X,Y)$. articipants select from 18 items to maximize value under a weight limit, a task that is intuitive yet cognitively demanding as complexity grows [1]. Optimal solutions are computed via dynamic programming, while ML models are trained to imitate human choices. This setup lets us approximate the collaborative characteristic function using multiple utility definitions.

Definition 5 

(Economic Performance). For a knapsack instance $X=((w_1,\cdots ,w_n),(v_1,\cdots ,v_n),W)$ with optimal solution

$$\underset{x_1,\cdots ,x_n}{max}\sum _{i=1}^n{x}_i{w}_i\le W\sum _{i=1}^n{x}_i{v}_i=Y^{*}$$

and a valid solution Y, we call the function

$$U_{\mathrm{Econ}}(X,Y)={\displaystyle \frac{Y}{Y^{*}}}$$

the economic performance of Y given X.

Table 1. Matrix of Treatment Conditions.

Model	None	q1	q2	q3	q4	q5	q6
Mean $U_{\mathrm{Econ}}(X,Y)$	.	0.717	0.800	0.844	0.884	0.899	0.920
SD	.	0.083	0.105	0.098	0.105	0.088	0.085
No Bonus	N = 102
2-cent Bonus	N = 98
10-cent Bonus*	N=100+117	N=64	N=78	N=194	N=179	N=70	N=191
20-cent Bonus	N = 96

Table 1. Matrix of Treatment Conditions.

Model	None	q1	q2	q3	q4	q5	q6
Mean $U_{\mathrm{Econ}}(X,Y)$	.	0.717	0.800	0.844	0.884	0.899	0.920
SD	.	0.083	0.105	0.098	0.105	0.088	0.085
No Bonus	N = 102
2-cent Bonus	N = 98
10-cent Bonus*	N=100+117	N=64	N=78	N=194	N=179	N=70	N=191
20-cent Bonus	N = 96

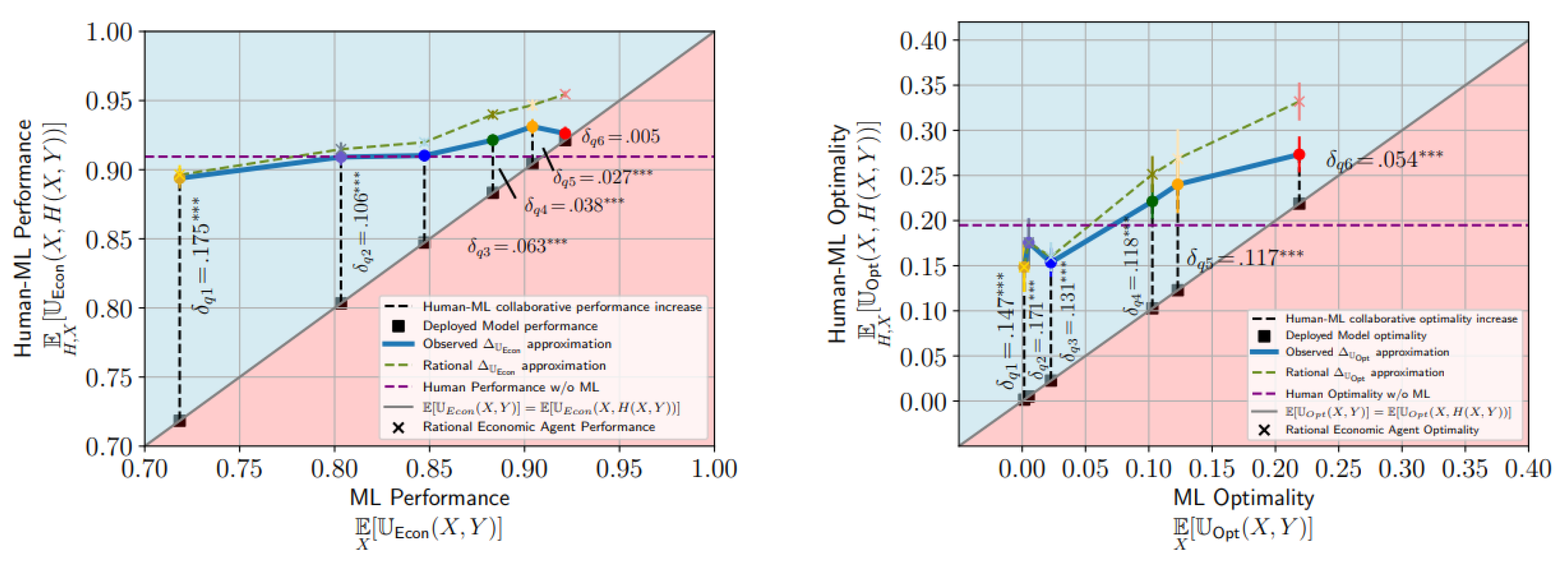
Study Design: We recruited 1,408 UK-based participants via Prolific to ensure familiarity with currency and weight units. After a tutorial and two practice tasks, participants completed 10 knapsack problems using a custom interface (Appendix A.11). We excluded 119 for browser violations, leaving 1,289 for analysis (Appendix A.9). Participants were randomly assigned to four monetary treatments and seven algorithmic recommendation levels (Table 1). Bonus conditions (No Bonus, 2¢, 10¢, 20¢ per point above 70% UEcon) were tested without ML to isolate incentive effects. The 10¢ Bonus condition was run twice, with the second including a comprehension quiz and randomization across models (q0–q6). ML models were trained on optimal solutions (Appendix A.8), and Appendix Figure 6 shows their utilities span the range of models trained on human data. These choices enable us to approximate collaborative characteristic functions, though they limit full theoretical replication.

7. Results

Monetary incentives had no significant effect on user performance (88.6%–90%), with all bonus treatments statistically indistinguishable from the control (Figure 2a). A comprehension quiz confirmed that users understood the incentive structure ($p=0.268$). ML recommendations improved human performance modestly as model quality increased—from 89.4% at 72% ML utility to 92.6% at 92% (Figure 2b)—though gains were often statistically indistinguishable. Even low-quality models (e.g., $q_1$) led to large improvements over the ML baseline (89.4% vs. 71.8%, $p=1.8\times {10}^{-28}$). Effort and time remained consistent across conditions (Appendix Figure 10 and 21). Together, the empirical approximations of the collaborative characteristic function (Figure 3) suggest convergence to stable points above human-only performance.

8. Conclusion

We propose a theoretical framework for human-ML collaboration in dynamic settings where human labels may deviate from the ground truth. At its core is the collaborative characteristic function, mapping ML utility to human+ML utility and defining learning paths that may converge to stable points. A large-scale knapsack user study shows that for models with 72–92% performance, paths likely converge near 92% utility. Monetary incentives had no effect, but simple post-processing (choosing the better of human or ML output) significantly improved outcomes. Limitations include assuming perfect replication in retraining and reliance on synthetic data. Empirical variations were limited to linear bonuses and independently varied ML quality. Future work should explore conditions for unique stable points, real-world applications, and fairness in convergence.