Theoretical Study of Salt Ion Transport in EMS with Ion-Exchange Membranes Having Geometrically Structured Surfaces

1. Introduction

Desalination is critical to providing access to clean water in water-stressed regions, especially in the face of population growth and climate change. Research shows that technologies such as reverse osmosis, solar desalination, etc. are becoming more efficient and cost-effective, but there are challenges associated with energy consumption and environmental impacts such as the formation of toxic brine.

According to the article [1], desalination, especially using reverse osmosis, has become a key solution for coastal regions with limited freshwater resources. They highlight that the cost of desalination has decreased by 50% over the past two decades, making it more affordable, but energy consumption and the formation of toxic brine remain significant drawbacks.

The article [1] discusses the potential reduction in energy consumption by modern seawater desalination technologies (reverse osmosis, electrodialysis) and their limitations, the potential role of advanced materials and innovative technologies in improving performance, and the environmental friendliness of desalination.

The [2] provides an overview of the challenges and opportunities for obtaining clean water based on solar desalination using photothermal materials. The paper describes the problem of salt accumulation, which is currently the main obstacle to the stable operation of solar evaporators.

The article in Frontiers [3] shows that desalination can support ecosystems if carbon dioxide emissions are minimized and brine is managed. However, the authors emphasize the need to monitor the impact on marine ecosystems, which requires further research.

It is known that membrane separation methods for water purification and desalination are increasingly used to solve global problems related to water shortage and aquatic pollution. However, progress in the field of membranes for water purification is hampered by the inherent limitations of traditional membrane materials. Recent advances in the field of methods for controlling the structure and chemical functionality of polymer films can potentially lead to the emergence of new classes of membranes for water purification. In the review [4], the authors first discuss the current state of existing membrane technologies for water purification and desalination, highlight their inherent limitations and determine the current requirements for next-generation membranes. They also offer promising approaches to modifying the membrane surface, which minimize interphase interactions and increase resistance to contamination.

The most environmentally friendly method of water desalination today is the use of electromembrane systems, in which electroconvection is the main mechanism of overlimit transport. Thus, in the work [5] an experimental confirmation of the role of electroconvection in porous media is presented. It is shown that vortex flows significantly increase the rate of salt removal.

The review [6] examines in detail recent studies of electroconvection with an emphasis on quantitative experimental and theoretical analysis and modeling of this phenomenon. Approaches to controlling this phenomenon under standard conditions are also discussed.

We will adhere to the definition of electroconvection given in [7,8]. Namely, by electroconvection we will mean any movement of an electrolyte solution caused by the effect of an external electric field on the solution. This effect is modeled as a spatial (volume) electric force in the Navier-Stokes equation. The origin and influence of spatial electric force can be explained as follows. The fixed charge of the matrix of ion-exchange membranes causes a high concentration of counterions and a low concentration of co-ions in the membrane volume. Due to the continuity of the concentration change, a double electric layer (DEL) is formed at the interface. The effect of the electric field on the spatial charge region (SCR) in the DEL of the solution leads to the movement of ions in this layer. Since the ions are hydrated, i.e. surrounded by a hydration shell, they move with it. We will assume that the solution is a viscous and incompressible liquid. In liquids, viscosity is a manifestation of the cohesion forces between molecules, therefore the hydration shell in turn is connected with the surrounding water molecules by the forces of molecular adhesion. Thus, part of the water surrounding the hydration shell of ions is also involved in the movement. Since the SCR contains almost exclusively counterions, the volume of water moving with them encounters almost no resistance from the counter-flow of volume carried by the co-ions. Therefore, the effect of the electric field on the SPR leads to the transport of the entire (or almost entire) volume of the solution located in this region (the phenomenon of electroosmosis). Note the significant difference compared to the volume of an electrically neutral solution, in which there is a counter-flow of water volumes associated with ions. Water molecules, not entering in the primary hydration shell, are affected by both cations moving from the anode to the cathode, and anions moving in the opposite direction. As a result, relatively free water molecules are not transportred at all, and the phenomenon of electroosmosis in an electrically neutral solution is absent. Dukhin and Mishchuk [9] distinguish two types of electroosmosis. Electroosmosis of the first type (classical electroosmosis) occurs as a result of the action of an electric field on the equilibrium DEL, which exists regardless of the presence of an external electric field. A different situation occurs with strong polarization of the ion-exchange membrane by an external electric field. In this case, as Rubinstein and Shtilman [10] first showed, the size of the SPE significantly exceeds the thickness of the equilibrium DEL, and can reach micrometer sizes [11]. Then electroosmosis of the second type occurs: the transport of the liquid volume under the action of an external electric field to the expanded SPE, which occurs as a result of the action of the same electric field. It is electroosmosis of the second kind that is the main mechanism that causes the overlimiting transport of salt counterions through the membrane. A large number of works are devoted to the study of the phenomenon of electroconvection [12,13,14,15,16]. In [16], the importance of the problem of intensifying the desalination process is discussed, including through geometric modification of the surface of ion-exchange membranes.

At present, the phenomenon of overlimiting mass transport is being intensively studied. However, many issues remain poorly understood. In particular, it is unclear what effect the geometric modification of the membrane surface and the forced flow of the solution in the desalination channel have on the development of electroconvection. This article attempts to advance the understanding of this phenomenon and to quantitatively describe the occurrence and development of electroconvection under conditions of forced convection and geometric modification of the membrane surface.

Modification of the membrane surface (nanostructuring, fractal patterns) allows to reduce concentration polarization, increase the area of ​​the active zone and improve selectivity. According to Zabolotsky et al. [17], the concept of profiled ion-exchange membranes was introduced and implemented in 1971 by Gnusin et al. [18] to accelerate the electrodialysis process by increasing the available membrane surface area and mass transport.

Later, Nikonenko et al. [19] compared the performance of the electrodialysis process in stacks with non-conductive spacers, ion-exchange resins or profiled ion-exchange membranes. They showed that in the case of profiled membranes, the production of drinking water is most efficient, the Sherwood number is up to five times higher than that of electrodialysis with non-conductive spacers.

Zabolotsky and Nikonenko used heterogeneous membranes with a specific pattern on the membrane surface, consisting of cones located at the nodes of rhombuses (diamond-shaped distribution).

Vasilyeva et al. [20] used similar profiling and investigated the mechanisms of selective transport of amino acids through ion-exchange membranes during the dialysis process and found a more than twofold increase in ion flux and separation factor. Loza et al. [21] confirmed the increased diffusion permeability of such membranes. Melnikov et al. used membranes with such a pattern to extract valuable components from dilute wastewater [22]. Liu et al. [23] changed the shape of the pattern from a rhombus to a square and obtained an approximately 35% increase in the power density in microbial ER cells.

The study by Wessling M., Stockmeier F. et al. [24] is devoted to the analysis of the direction of rotation and the position of electroconvective vortices using the surface patterning method or geometric and electrical inhomogeneity. Wessling M., Stockmeier F. et al. [24] compared the development of electroconvection on two membranes modified with patterns of different surface charges. They analyzed the increase in the area of ​​electroconvective vortices, the direction of their rotation and structural stability in a steady state, as well as the possibilities of controlling electroconvective vortices by introducing certain structural inhomogeneities of the membrane surface to reduce energy losses in the plateau region and more economical operation in EMS in overlimit modes, significantly increasing their efficiency. Recently, membranes with a fractal structure have been developed that increase the surface area by 300%. The efficiency of salt removal reached 99.5% at low pressure [25].

This paper discusses the most promising type of single-sided profiled membranes, which will significantly intensify mass transport and increase the efficiency of electrodialysis (ED) systems. Possible optimization paths are shown using numerical simulation of such a model. The article considers two 2D models of non-stationary electroconvection during binary electrolyte transport in the desalination channel of an electrodialysis apparatus (EDA) under extreme current conditions based on a boundary value problem for the Nernst-Planck-Poisson and Navier-Stokes equations. The first model considers half of the ED desalination flow channel on a cation-exchange membrane (CEM) with geometrically structural heterogeneity of the surface. The second model is half of the channel with the same flow rate and concentration, but without structural heterogeneity of the membrane surface. We calculated theoretical volt-ampere characteristics and determined the main patterns of salt ion transport.

2. Mathematical Model of Electroconvection in Potentiodynamic Mode in Half of Desalination Channel with Ideally Selective Cation Exchange Membrane (CEM) with Modified Surface

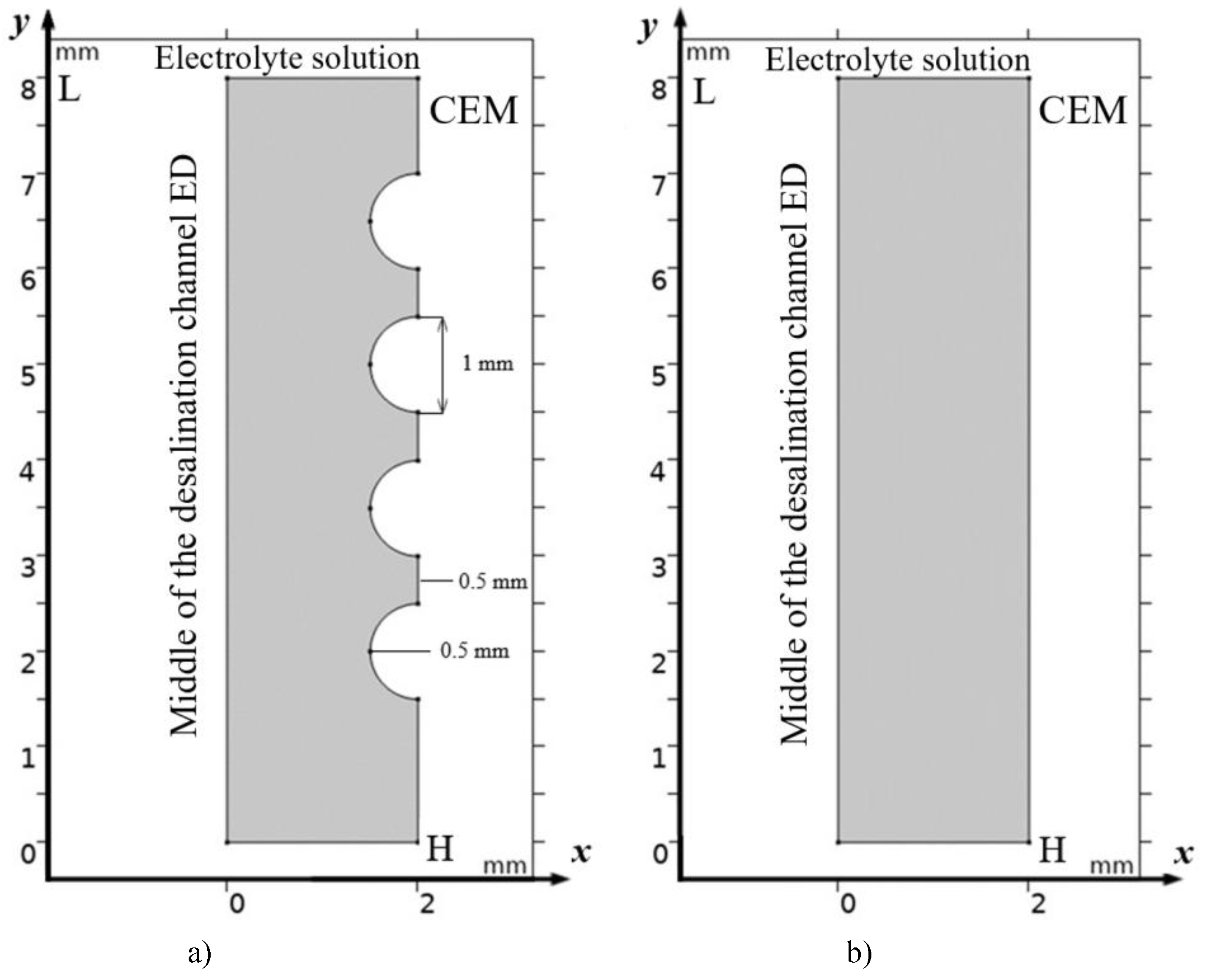
2.1. Physical Statement: Solution Domain

The potentiodynamic regime is modeled, half of the channel at the CEM (Figure 1) is considered. In the middle of the channel, the conditions of local electroneutrality are assumed to be fulfilled and the concentrations are known. In addition, the initial velocity is given by half of the Poiseuille parabola [7,8]$V_y(0,x,y)=6V_0{\displaystyle \frac{x}{H}}(1-{\displaystyle \frac{x}{H}}),V_x(t,x,y)=0,x\in [{\displaystyle \frac{1}{2}}H,H]$, where $V_0$ is the average (linear) flow velocity.

2.2. Boundary Value Problem for the System of Navier-Stokes and Nernst-Planck-Poisson Equations

Modeling of the electrolyte solution flow and the ion transport process for a binary electrolyte in the desalination channel EDA is performed simultaneously, using a system of Navier-Stokes and Nernst-Planck-Poisson equations, interconnected by an electric force. However, for convenience, the equations and boundary conditions modeling the solution flows and ion transport are considered separately below.

1. Modeling of the solution flow

The solution flowing in the desalination channel is affected by several forces:

1) the inertial force caused by the solution movement,

2) the friction force caused by the viscosity of the solution,

3) the spatial electric force caused by the effect of the electric field on the space charge region,

4) the lifting force arising from the density gradient caused by the concentration gradients (concentration polarization) and temperature (Joule heating, dissociation and recombination reactions).

In this paper, we will study the influence of only the first three forces (inertia, friction, and electric force) on the solution flow and their interaction. In doing so, we will adhere to the generally accepted approach, when the spatial force $\overrightarrow{f}$ is singled out separately. Under this condition, the flow in a sufficiently wide range of pressure and force changes is adequately described by the Navier-Stokes equations:

${\displaystyle \frac{\partial \overrightarrow{V}}{\partial t}}+(\overrightarrow{V}\nabla )\overrightarrow{V}=-{\displaystyle \frac{1}{{\rho }_0}}\nabla P+\nu \Delta \overrightarrow{V}+{\displaystyle \frac{1}{{\rho }_0}}\overrightarrow{f},$

$div(\overrightarrow{V})=0,$

where $\nabla$ is the gradient, $\Delta$ is the Laplace operator, $\overrightarrow{V}$ is the flow rate of the electrolyte solution, ${\rho }_0$ is the characteristic density of the solution, $P$ is the pressure, $t$ is the time, $\nu$ is the kinematic viscosity coefficient, $\overrightarrow{f}$ is the spatial force density. Below, as stated above, the electrical force is considered as the spatial force.

As boundary conditions for the Navier-Stokes equations we will use:

1) the conditions of solution adhesion on a solid boundary, namely, on the curved surface of the cation-exchange membrane $(x,y)\in \Gamma ,t\ge 0$:

$\overrightarrow{V}(x,y,t)=0$ at $(x,y)\in \Gamma ,t\ge 0$. And in the depth of the solution the velocity is considered constant and is specified as follows $V_x({\displaystyle \frac{H}{2}},y,t)=0,V_y({\displaystyle \frac{H}{2}},y,t)={\displaystyle \frac{3}{2}}{V}_0.$

2) At the inlet we will assume the velocity along the Poiseuille parabola.

3) Since non-stationary vortices can arise in this problem, the boundary conditions for the velocity at the outlet of the desalination channel can give computational artifacts near the outlet. To solve this problem, we use two different methods.

The first method is to extend the channel and extract data at some distance before the outlet. In this case, we can assume that the flow at the outlet is also Poiseuille.

This method is applicable when electroconvection begins at the inlet to the channel and the vortices die out before reaching the outlet. However, in some cases this leads to an unacceptable increase in the calculation time. In addition, this method is not applicable in the case where electroconvection begins at the channel outlet

In the second method, we consider the boundary to be open, and the normal voltage on it is taken to be zero. In this case, vortices can freely flow outside the modeled region. In numerical calculations with such a condition, difficulties arise in finding the initial approximation in the Newton method used to solve a nonlinear system of equations in the finite element method.

4) The initial flow at the channel inlet will be assumed to be a Poiseuille flow.

Initial and boundary conditions at corner points may, in some cases, be inconsistent. However, with a numerical solution, this is smoothed out fairly quickly, but they can initiate the emergence and development of electroconvective vortices that have a non-physical, i.e. artifactual, nature. Therefore, it is desirable to ensure the consistency of the initial and boundary conditions at corner points using correct mathematical methods.

When using the above boundary conditions, the influence of any non-hydrodynamic processes on the flow of the solution occurs only through the electrical force $\overrightarrow{f}$, which is not a potential force.

2. Modeling of the solution flow

The ion transport for a binary electrolyte in a desalination channel is described quite adequately by the system of Nernst-Planck and Poisson equations:

$${\overrightarrow{j}}_i=-{\displaystyle \frac{F}{RT}}{z}_i{D}_i{C}_i\nabla \phi -D_i\nabla C_i+C_i\overrightarrow{V},i=1,2,$$

(1)

$${\displaystyle \frac{\partial C_i}{\partial t}}=-div{\stackrel{\rightharpoonup }{j}}_i,i=1,2,$$

(2)

$${\epsilon }_0\Delta \varphi =-F\left(z_1{C}_1+z_2{C}_2\right),$$

(3)

$$\overrightarrow{I}=F\left(z_1{\overrightarrow{j}}_1+z_2{\overrightarrow{j}}_2\right),$$

(4)

where $C_1,C_2$ are the concentrations of cations and anions in the solution, respectively, $z_1,z_2$ are the charge numbers of cations and anions, $D_1,D_2$ are the diffusion coefficients of cations and anions, respectively, $j_1$, $j_2$ – is the fluxes of cations and anions, $\varphi$ is the electric field potential, ${\epsilon }_0$ is the permittivity of the electrolyte, $F$ is the Faraday constant, $R$ is the gas constant, $T$ is the absolute temperature. In this case, $P,$ $\overrightarrow{V},$$\varphi ,$$C_1,C_2$ – are unknown functions depending on time $t$ and coordinates $x,y$.

We will consider the potentiodynamic regime:

$\varphi ({\displaystyle \frac{H}{2}},y,t)=0,\varphi (H,y,t)=d_{\varphi }\cdot t,t\ge 0,y\in [0,L]$.

Along with this condition, we will also use the following boundary conditions

1) In the middle of the channel $x={\displaystyle \frac{H}{2}},y\in [0,L],t\ge 0$, we will consider the boundary concentrations of anions and cations to be known:

$${С}_1(t,{\displaystyle \frac{H}{2}},y)={С}_{01}$$

(5)

$${С}_2(t,{\displaystyle \frac{H}{2}},y)={С}_{02}$$

(6)

2) On the surface of the cation-exchange membrane, we will consider the boundary concentration of cations to be known, which is determined by its exchange capacity:

$${С}_1(t,x,y)={С}_{km},(x,y)\in \Gamma ,t\ge 0$$

(7)

and also, we will assume that the cation-exchange membrane is ideally selective, that is, impermeable to anions:

$\left({\displaystyle \frac{\partial C_2}{\partial x}}+{\displaystyle \frac{F}{RT}}{z}_2{C}_2{\displaystyle \frac{\partial \varphi }{\partial x}}\right)\left(t,H,y\right)=0.$

3) At the entrance to the channel, we will consider the ion concentrations to be given. Depending on the objectives of the study, they can be considered to be distributed either constantly or distributed according to another law. If the concentrations at the entrance are not constant, we will consider that their distribution corresponds to the maximum current density, and that the condition of electroneutrality is satisfied at the entrance.

We will consider the potential distribution at the entrance to be linear:

$$\varphi (t,x,0)=d_{\varphi }{\displaystyle \frac{2x-H}{H}}$$

(8)

4) At the exit from the region under consideration $y=L,x\in \left[0,H\right],t\ge 0$, we will use the condition for concentration, which determines the ion flow at the exit:

$-\overrightarrow{n}\cdot {\overrightarrow{j}}_i\left(t,x,L\right)=-V_2\left(t,x,L\right)C_i\left(t,x,L\right)$ or

$-{\displaystyle \frac{F}{RT}}{z}_i{D}_i{C}_i{\displaystyle \frac{\partial \phi }{\partial y}}-D_i{\displaystyle \frac{\partial C_i}{\partial y}}+C_i{V}_2=V_2\left(t,x,L\right)C_i\left(t,x,L\right),i=1,2$

For the potential, we will use a similar condition, which means that there is no current flow through the exit:

$-\overrightarrow{n}\cdot \nabla \phi \left(t,x,L\right)=0$ or ${\displaystyle \frac{\partial \phi \left(t,x,L\right)}{\partial y}}=0$.

5) We will accept the initial conditions at $t=0$, if possible, consistent with the remaining boundary conditions:

$$C_1(0,x,y)=C_2(0,x,y)=C_0$$

(9)

For the function $\varphi$, as an initial condition, we can take, for example, a linear function independent of $y$:

$$\varphi (0,x,y)=d_{\varphi }{\displaystyle \frac{2x-H}{H}}.$$

(10)

The influence of transport processes on the flow of the solution is manifested through the electric force, the density of which is equal to $\overrightarrow{f}={\displaystyle \frac{1}{{\rho }_0}}{\epsilon }_0\Delta \phi \nabla \phi$.

3. Results of Numerical Analysis

3.1. Calculation Parameters Used for Numerical Solution

To analyze the transport process, many different finite element calculations were performed with different parameters. The most typical results are given below. The width of the region under consideration H = 2 mm (channel width 6 mm), channel length L = 4H mm, average linear velocity V₀ = 1 mm/s, initial concentration C₀ varied from 0.01 to 10 mol/m³, potential scan rate 0.005 V/s. Cation diffusion coefficient D₁ = 1.331e^-9[m²/s], anion diffusion coefficient D₂ = 2.051e^-9[m²/s], cation charge number z₁ = 1, anion charge number z₂ = -1, $\nu$= 0.89371e^-3[Pas] is the kinematic viscosity coefficient, R is the universal gas constant, T is the absolute temperature, F is the Faraday constant.

Dimensionless characteristics of transport and flow are the Peclet number $Pe={\displaystyle \frac{V_{0}H}{D_2}},$ which is the ratio of convective transport to molecular transport, in this case $Pe\approx 976$, the Reynolds number $\mathrm{Re}={\displaystyle \frac{V_{0}H}{\nu }},$ which is the ratio of the inertial force $F_{in}={\rho }_0{H}^2{V}_0^2$ to the viscous friction force $F_{tr}=\nu {\rho }_0{V}_{0}H$, and in this case $\mathrm{Re}=8$. The Peclet number, as well as numerical calculations, show that the diffusion layer has been formed, while the Reynolds number, as well as numerical calculations, show that the hydrodynamic boundary layer has not yet been formed. It should be borne in mind that in the practice of electrodialysis, the Reynolds number can reach about 100, which is also too small for the formation of a boundary layer, and in experiments it rarely exceeds 10.

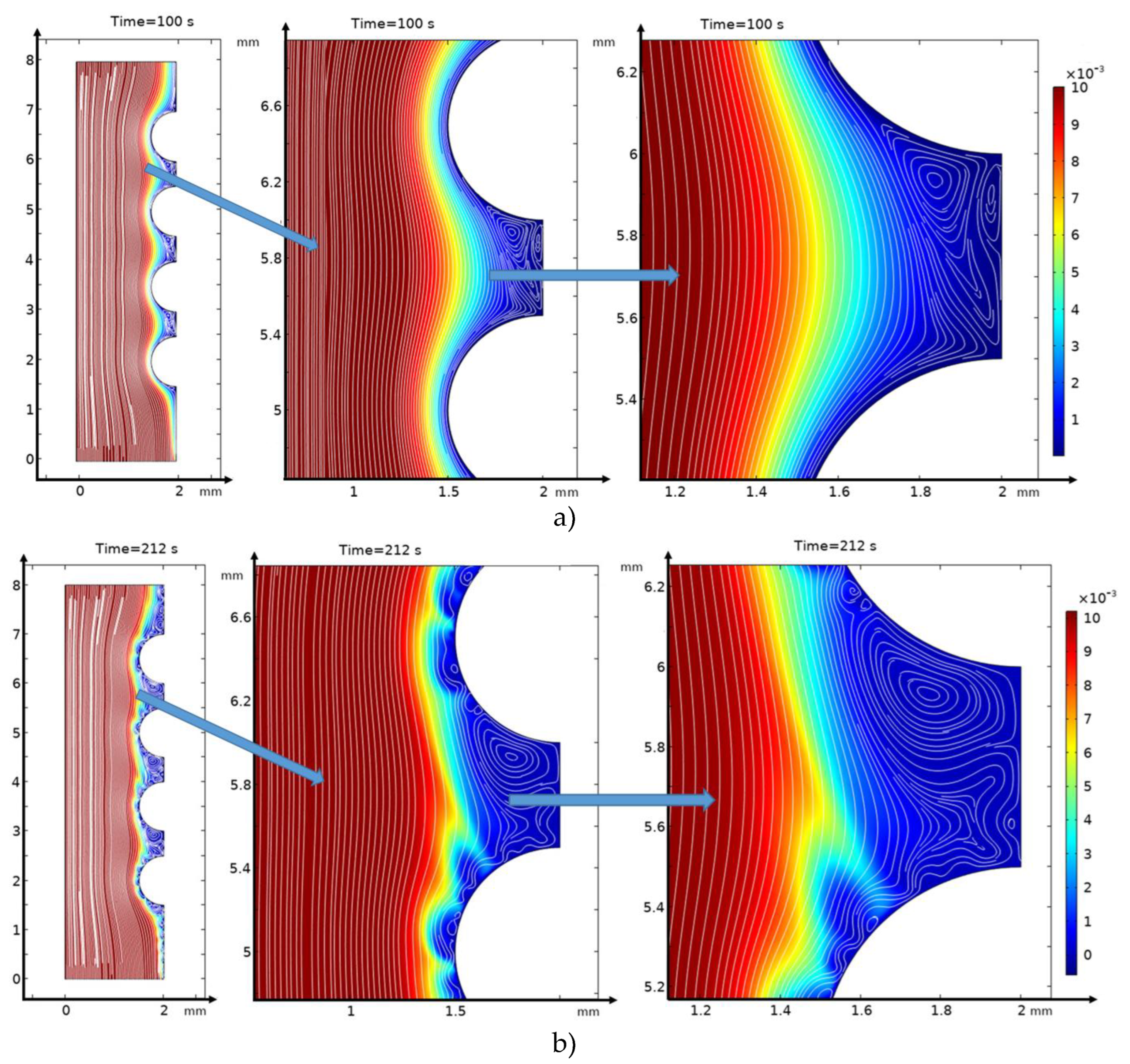
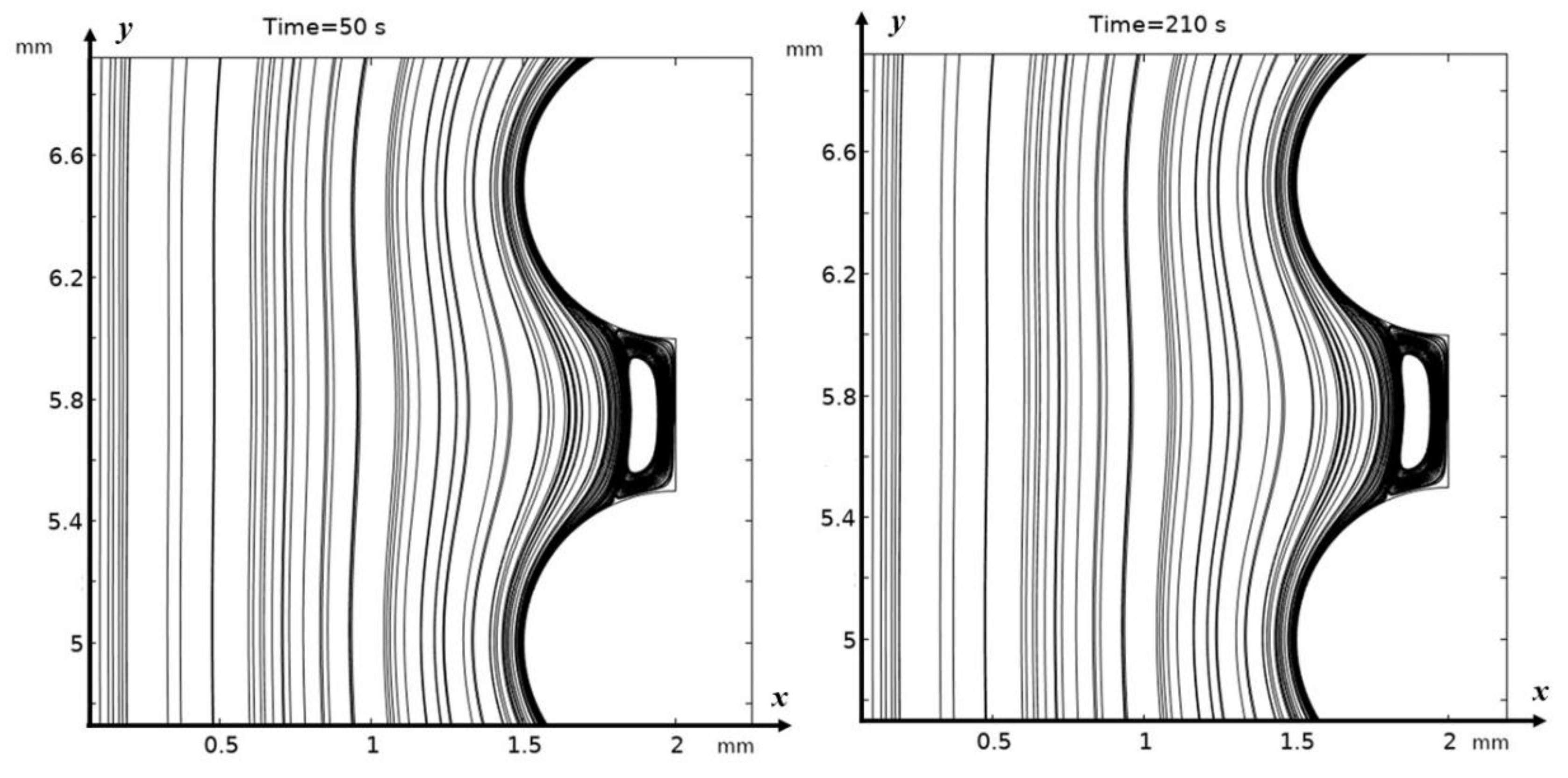
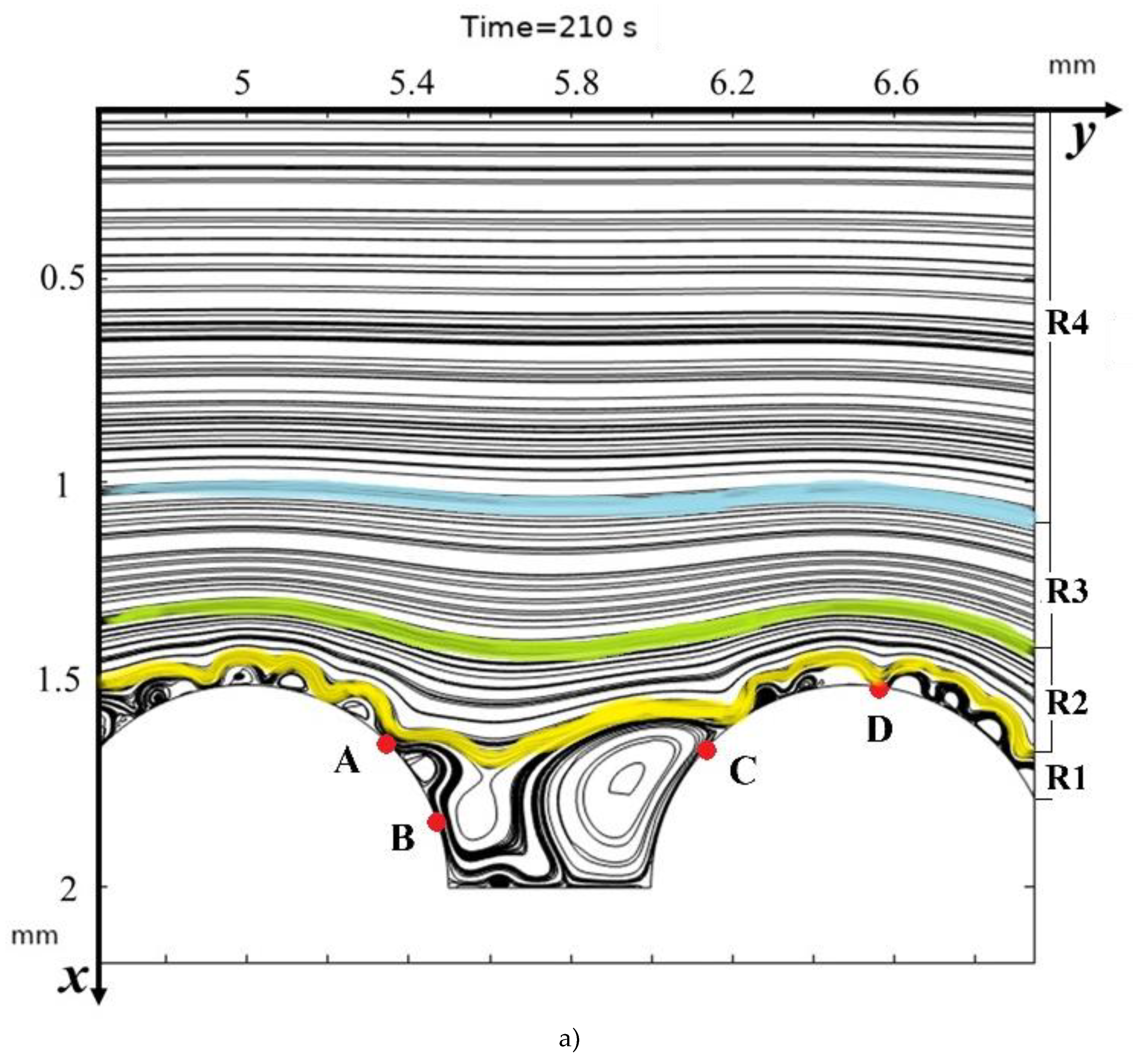
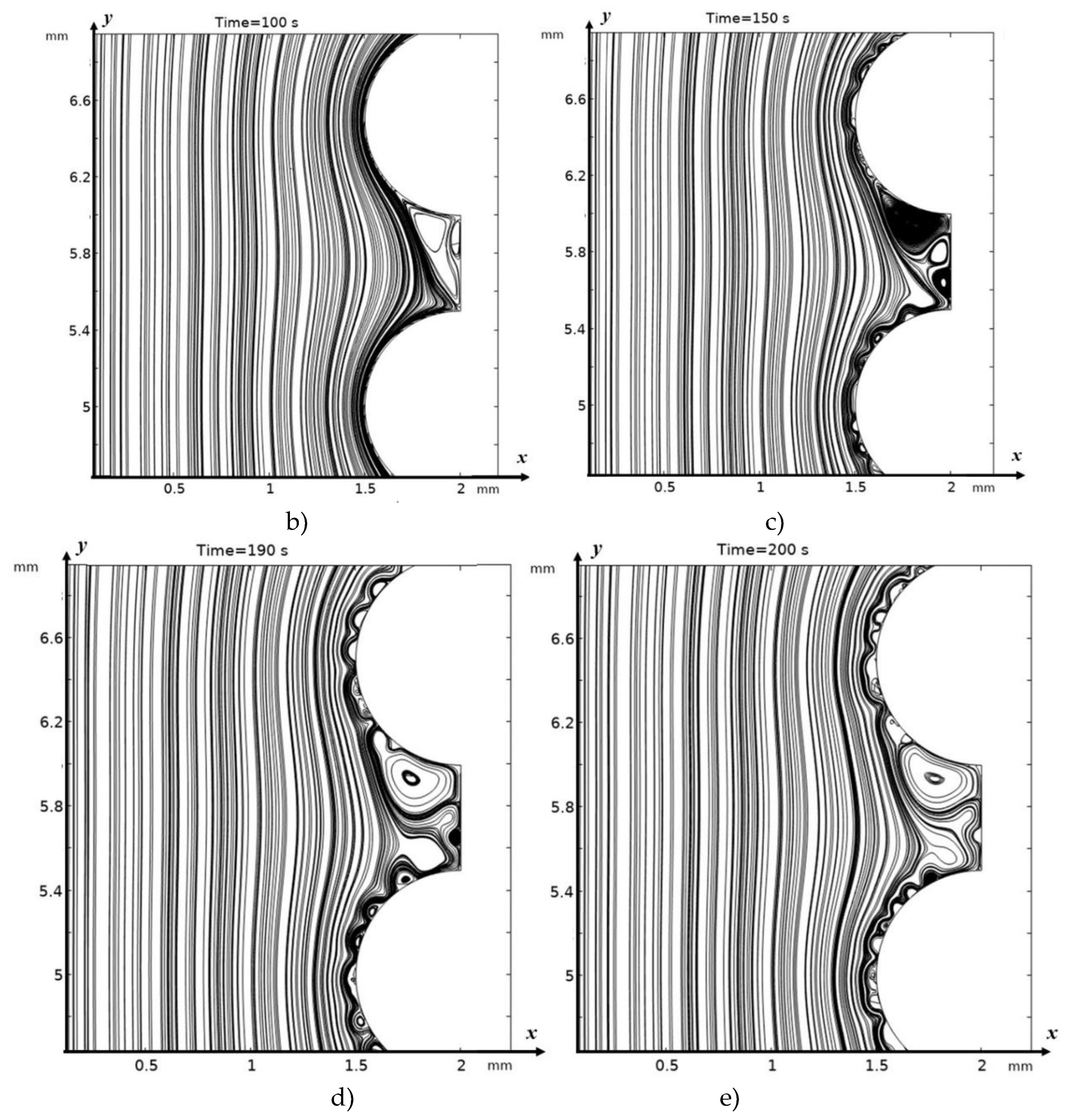
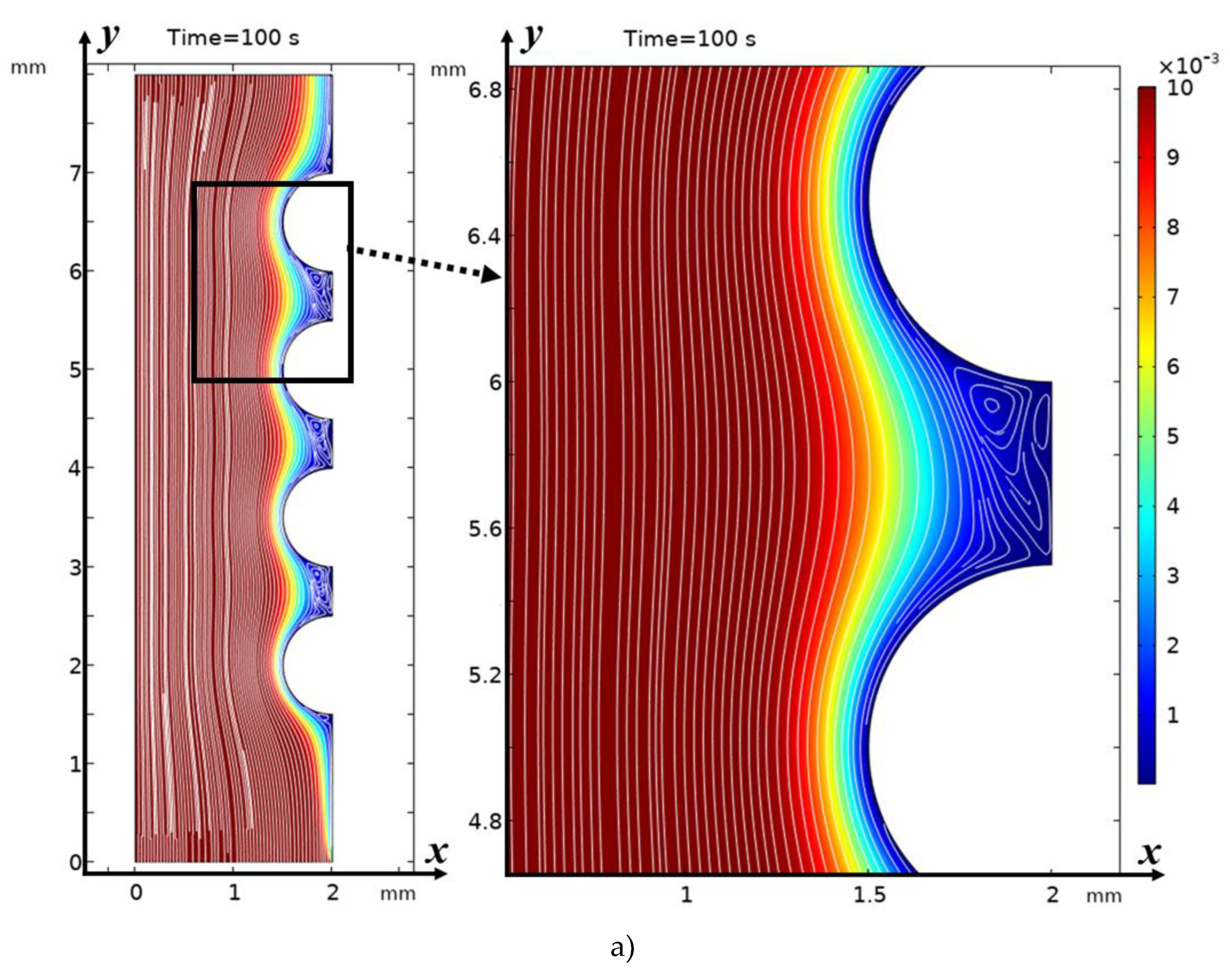
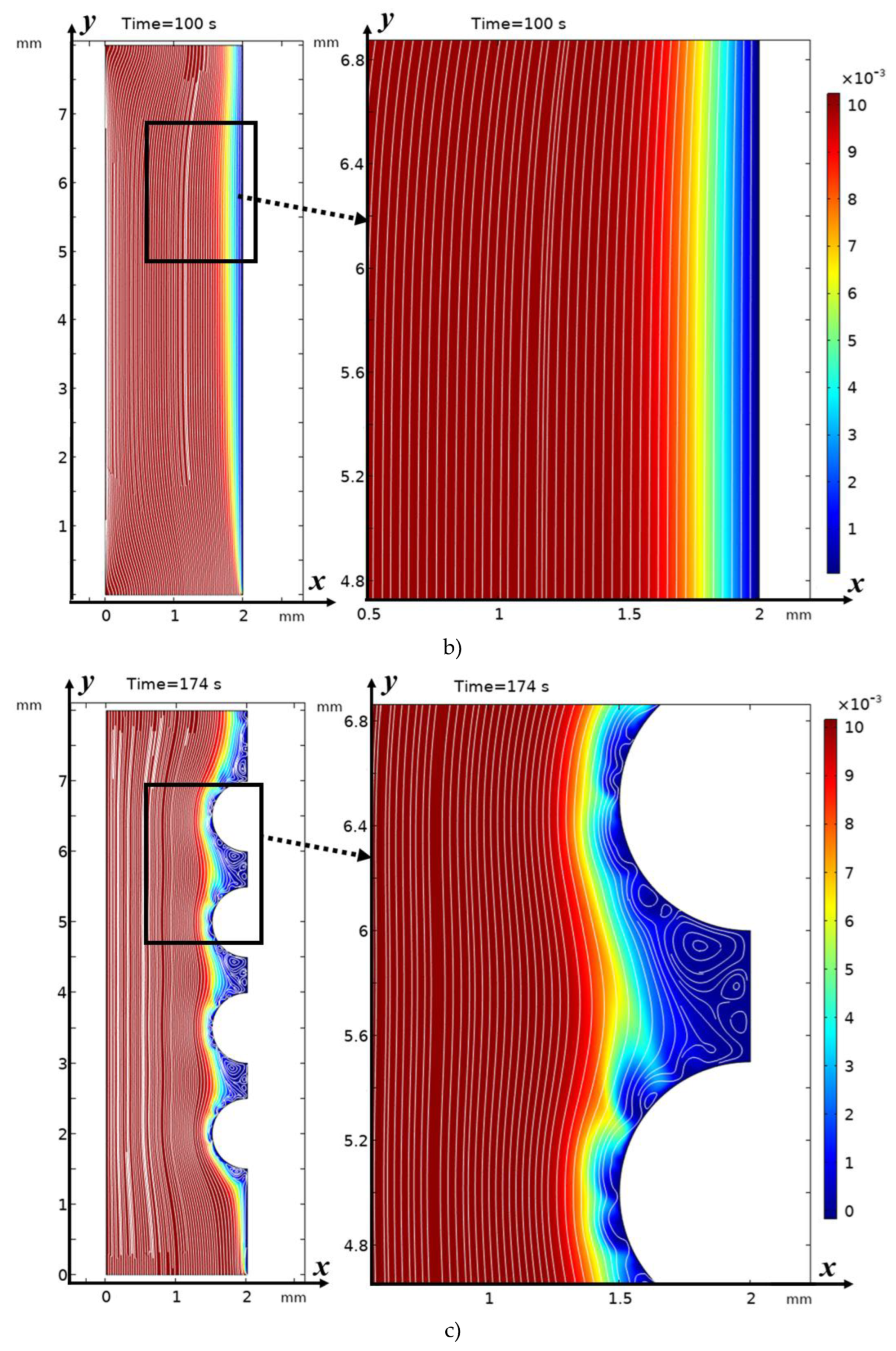
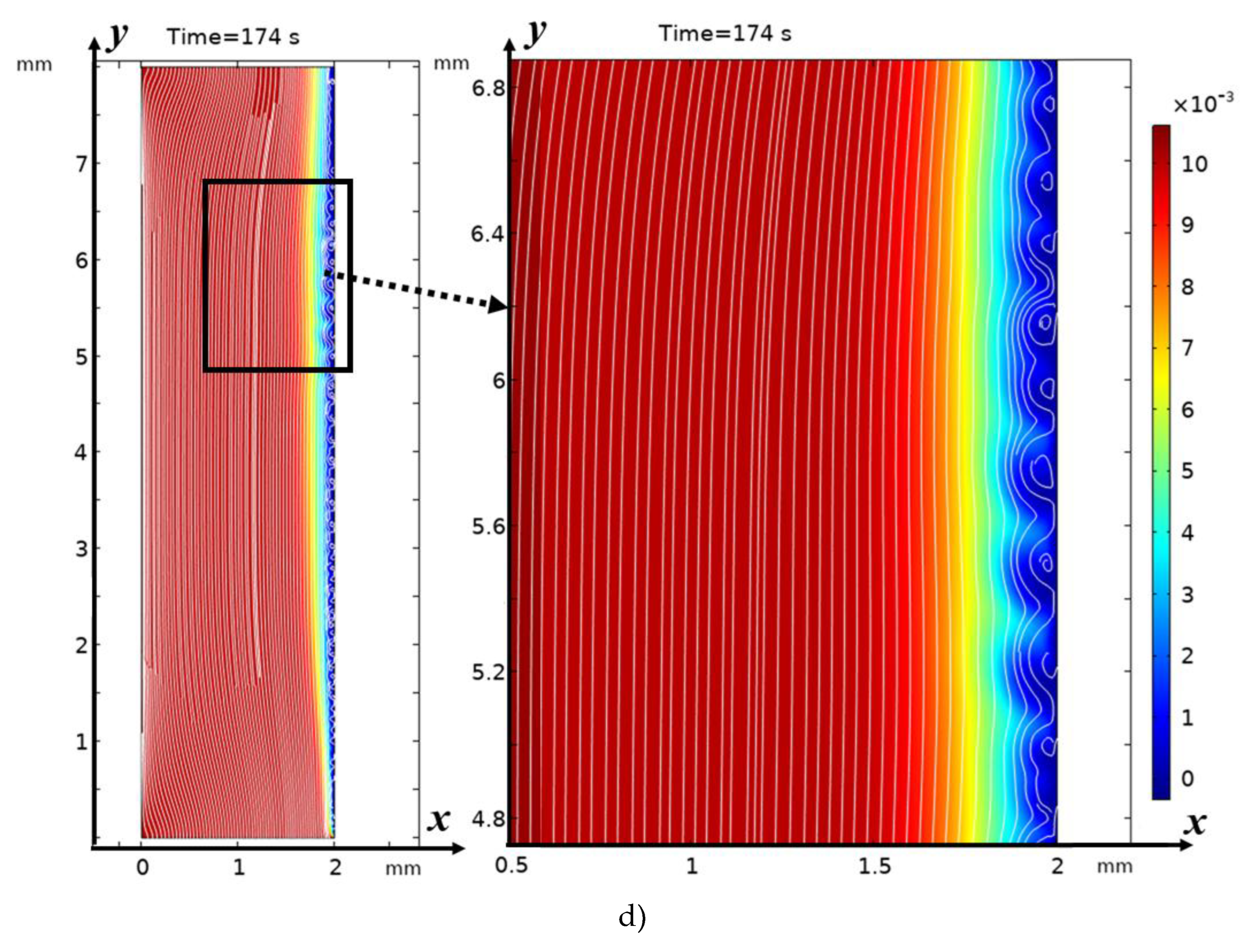
3.2. Structure of the Solution Flow

From Figure 2 it is seen that „stagnant” zones are formed in the valleys between the hills, where the flow velocity is significantly lower, but the main change in the direction of the flow is towards the membrane, and the flow disturbance is noticeable almost to the core of the flow, but the zone of electroconvective vortices over most of the hill occupies a narrow strip. However, in the lower part of the hill and above the valley, the vortex zone significantly expands. Here both electroconvective vortices and purely hydrodynamic vortices are formed.

In the absence of electroconvection, a steady state is reached in the valley fairly quickly and a purely stagnant zone is formed (see Figure 3. a and b). In the presence of electroconvection, electroconvective vortices penetrate into the „stagnant” zone in the valley, carrying with them a more concentrated solution, which is desalinated in the valley, and flow out of it, carrying out the desalinated solution, i.e. this zone is no longer stagnant (Figure 4a). Electroconvective vortices and purely hydrodynamic vortices influence each other in a complex, nonlinear and non-stationary manner, a change in the size and number of vortex structures, the formation of vortex clusters and their bifurcation (Figure 4.b-e) occur. All this leads to the fact that in the valley between the elevations, the desalination of the electrolyte solution is enhanced.

From Figure 4 (a) it is evident that the general structure of the flow if moving across the channel, starting from the middle to the membrane contains several regions: the flow core (in Figure 4 (a) this region is designated as R4), where the flow is practically not disturbed and is a Poiseuille flow. Region R1, in which the flow lines are the envelopes of the vortex zone and are directly adjacent to the vortex zone. The region of curved flow – R2, enclosed between the envelopes and the flow core, where the flow differs from the Poiseuille flow and where the solution flow lines are gradually deformed from the envelope flow lines to the Poiseuille flow lines – R3.

The structure of the flow directly above the hills and between the hills, i.e. below the region of the envelopes, has a different character in three different regions (Figure 4. a): in the upper slope of the hill to point A, in the lower slope of the hill to point B and in the valley itself between the hills (between points B and C). In the area of ​​point A and after point C there are no hydrodynamic vortices, and electroconvective vortices have the same structure as in the case of a membrane with a smooth surface (Figure 5). These areas are located in the upper part of the hill. In the lower part of the hill slope and the valley itself, the flow has a different character. In the lower part of the hill slope, two separation points are visible: the upper (point A) and the lower (point B) almost at the bottom. The left boundary of the lower part of the right slope of the hill is determined by the first separation point of the envelope of electroconvective vortices, and the right boundary is determined by the second separation point. The left boundary of the lower part of the left slope of the next hill is determined when the lower envelope approaches the hill surface at a distance approximately corresponding to the quasi-equilibrium SCD (point C). And the right boundary is determined similarly to point D, where the upper envelope approaches the membrane. The flow above the valley itself, as noted above, is characterized by non-stationarity and instability, constant bifurcation of vortices due to the interaction of electroconvective and purely hydrodynamic vortices. Let us compare the distribution of concentrations (highlighted in color) and the solution flow lines for models with a structured surface (on the left in the figure) and without modification (on the right in the figure) at different moments in time (Figure 5).

It is evident from Figure 5 (a, b) that from the very beginning the region where concentrations change quite significantly is considerably wider at the surface of the modified membrane. This tendency is maintained further (Figure 5 c, d). Moreover, the concentration of the solution drops considerably faster at the surface of the modified membrane (Figure 5). Thus, it is possible to conclude about the intensification of electroconvection and, accordingly, about the increase in the efficiency of desalination due to the modification of the membrane surface, including due to the increase in the conductive surface of the cation exchange membrane, which occurs during the modification of the membrane surface.

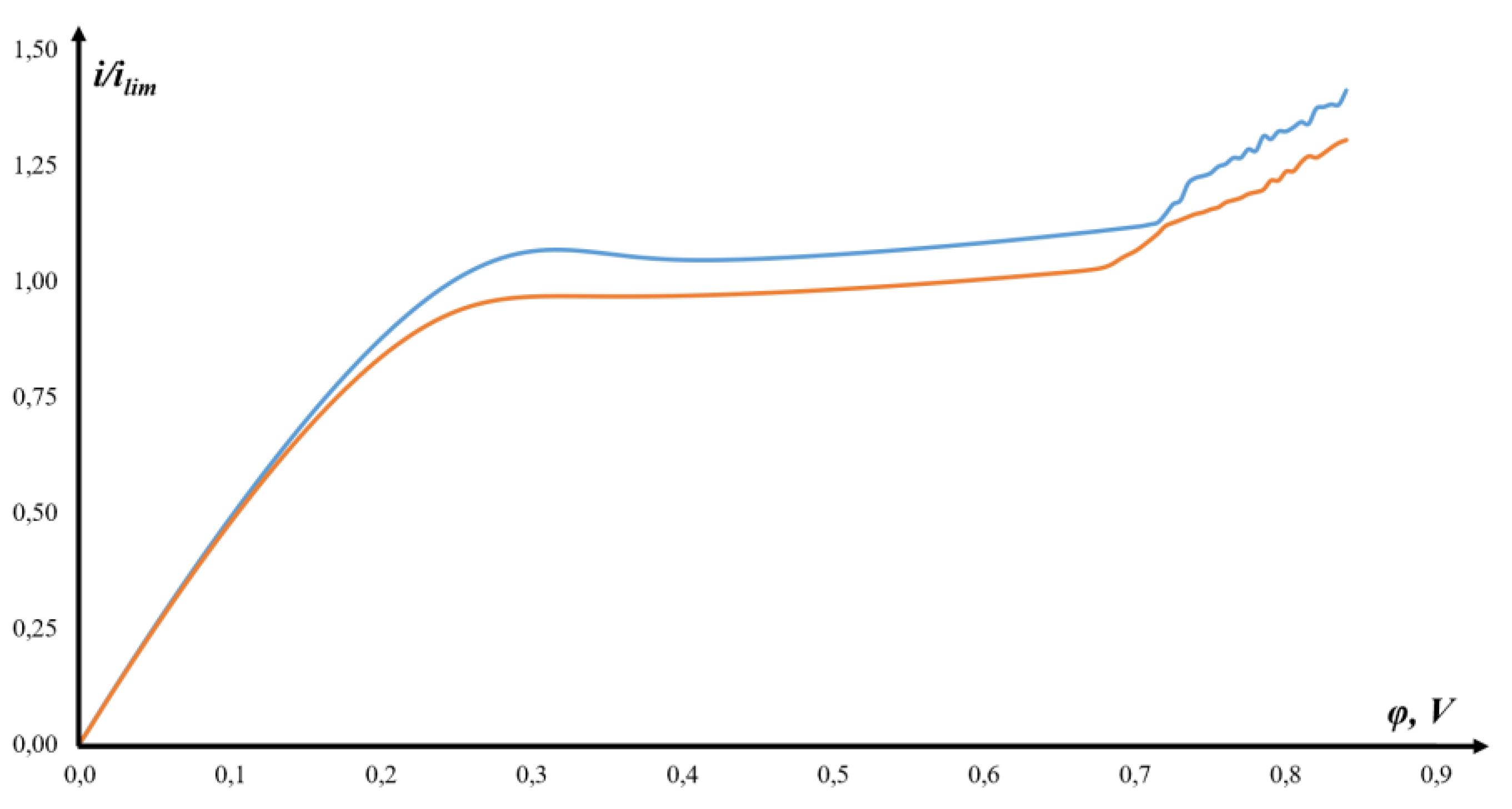
3.2. CVC and Its Description

In works [26,27,28,29,30], the authors derived and justified a special formula for calculating the theoretical current-voltage characteristic (CVC) of electromembrane systems (EMS), based on the law of charge conservation in potentiodynamic mode. For a given one $t$, the potential drop is determined $\varphi (t,H,y)=d_{\varphi }\cdot t$ ($d_{\varphi }$– speed of sweep of the potential drop). Solving the boundary value problem, we find the current density in the channel $\overrightarrow{I}(t,x,y)$. Then, to calculate the CVC, it is proposed to use the formula:

$$i(t)={\displaystyle \frac{1}{HL}}{\displaystyle \underset{0}{\overset{H}{\int }}{\displaystyle \underset{0}{\overset{L}{\int }}{I}_x(t,s,y)dy}}ds+{\displaystyle \frac{1}{2HL}}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{H}{\int }}(H-2x)div\overrightarrow{I}dxdy}}$$

(11)

Let’s designate

$$i_{av}(t)={\displaystyle \frac{1}{HL}}{\displaystyle \underset{0}{\overset{H}{\int }}{\displaystyle \underset{0}{\overset{L}{\int }}{I}_x(t,s,y)dy}}ds$$

(12)

$$i_d(t)={\displaystyle \frac{1}{2HL}}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{H}{\int }}(H-2x)div\overrightarrow{I}dxdy}}$$

(13)

Then $i(t)=i_{av}(t)+i_d(t)$.

In [29,30,31] it is shown that the term $i_{av}(t)$ is the averaged conduction current carried by ions, the second term $i_d(t)$ is the averaged displacement current.

Although the total current in the CVC calculation is not constant over time, its change can be made slow if the potential drop sweep rate is small. In this case $i_d(t)$, it is small and when calculating the CVC, it is not necessary to take into account the bias current and the CVC must be calculated using the formula $i_{av}(t)={\displaystyle \frac{1}{HL}}{\displaystyle \underset{0}{\overset{H}{\int }}{\displaystyle \underset{0}{\overset{L}{\int }}{I}_x(t,s,y)dy}}ds$.

In Figure 6, the abscissa shows the values ​​of the potential drop, and the ordinate shows the current density value, dimensionless by the limiting diffusion current according to Leveck [32]: $i_{\lim }={\displaystyle \frac{FD{C}_0}{H\left(T_1-t_1\right)}}\left[1.47{\left({\displaystyle \frac{H^2{V}_0}{LD}}\right)}^{1/3}-0.2\right],T_1=1,t_1=0.5$.

As can be seen from Figure 6, the CVC in both cases has a classical form - a linear ohmic section, a „plateau” and a secondary over-limiting rise associated with the onset and development of electroconvection. For models with a structured surface (blue color), the membrane is higher than the CVC of an unstructured (smooth) surface (red color), and, accordingly, the mass transport is higher.

A small convexity at the beginning of the „plateau” for the model with a structured surface is due to the fact that it reacts more sensitively to changes in the potential sweep rate, i.e. it is more sensitive to non-stationarity effects.

3.3. Verification of Results

To verify the results, a comparison was made with the experiment described in [33]. In this work, images of its section in the swollen state were taken, which were used to model the cation-exchange membrane. Images of electroconvective vortices arising in a depleted solution near the membranes at a current of i = 2.4 mA and t = 22 ± 1 s show that the average size of the vortex structures of the unprofiled membrane is approximately 200 μm, while for the profiled membrane it is approximately one and a half times larger, i.e. about 300 μm. This is in good qualitative and quantitative agreement with the numerical results.

4. Conclusion

The 2D mathematical model of the transport process in half of the desalination channel with geometric modification of the surface by the cation-exchange membrane is constructed based on the boundary value problem for the coupled system of Nernst-Planck-Poisson and Navier-Stokes equations. A theoretical analysis of the effect of geometric modification of the surfaces of ion-exchange membranes on the transport of salt ions was carried out and the main patterns of salt ion transport were established taking into account diffusion, electromigration, forced convection, and electroconvection. Using the current-voltage characteristics, it was shown that geometric modification of the surface of ion-exchange membranes enhances the transport of salt ions.