Submitted:
28 March 2025
Posted:
31 March 2025
You are already at the latest version
Abstract
Keywords:
MSC:
1. Introduction
- a)
- in the 1st of them, we have a sample (the “The Garden of flowers… in [24]”) of “products (papers)” produced by various production lines (authors)
- b)
- while, in the other, we have some few products produced by the same production line (same author)
- c)
- several inspectors (Peer Reviewers, PRs) analyse the “quality of the products” in the two departments; the PRs can be the same (but we do not know) for both the departments
- d)
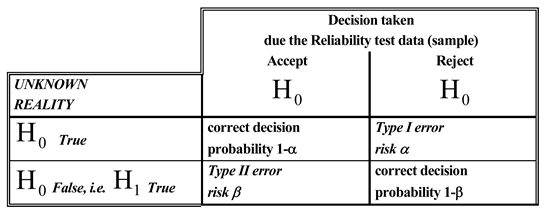
- The final result, according to the judgment of the inspectors (PRs), is the following: the products stored in the 1st dept. are good, while the products in the 2nd dept. are defective. It is a very clear situation, as one can guess by the following statement of a PR: “Our limits [in the 1st dept.] are calculated using standard mathematical statistical results/methods as is typical in the vast literature of similar papers [24].” See the standard mathematical statistical results/methods in the Appendix C and meditate (see the formulae there)!
2. Materials and Methods
2.1. A reduced Background of Statistical Concepts

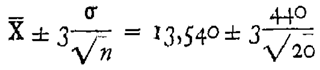
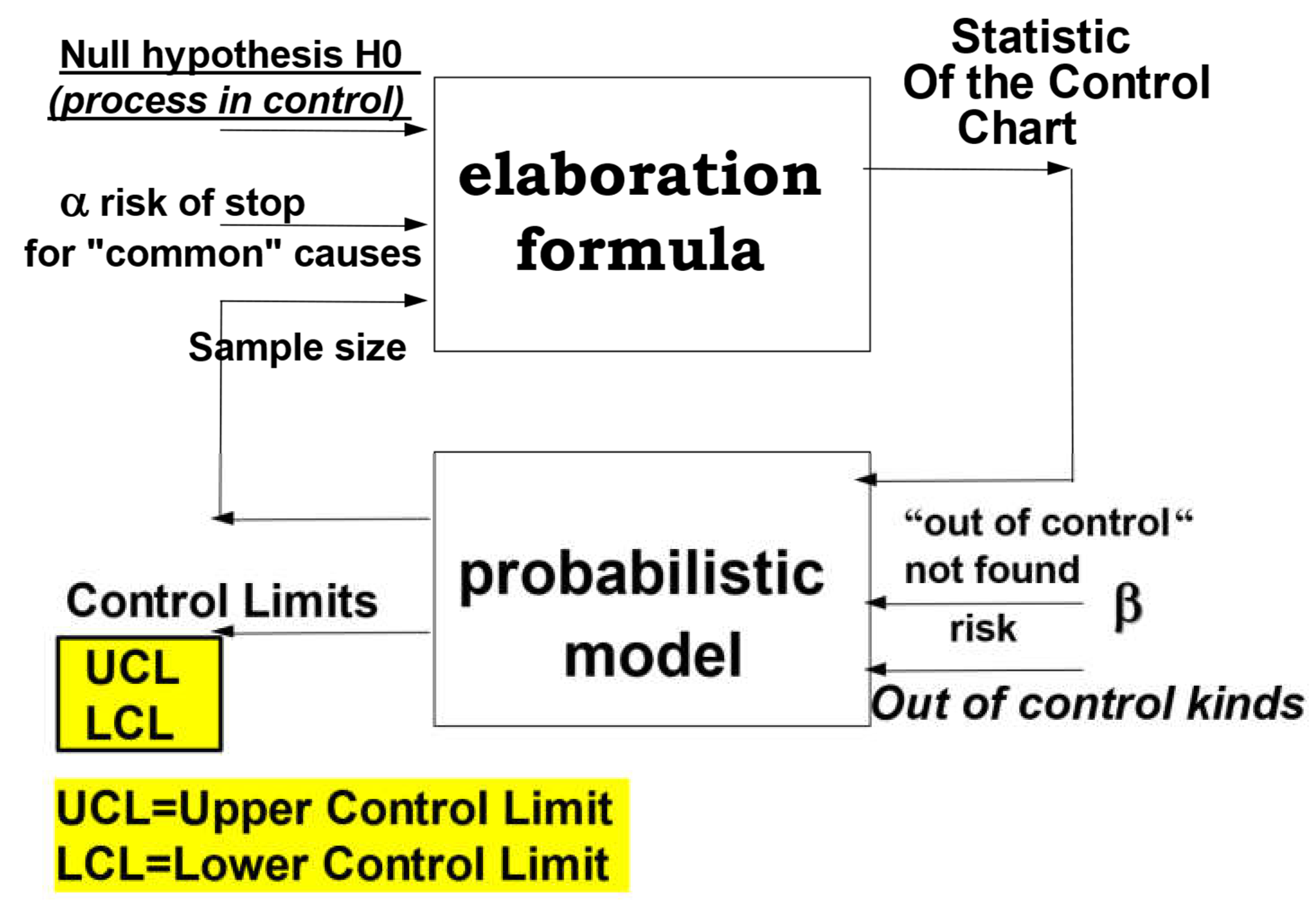
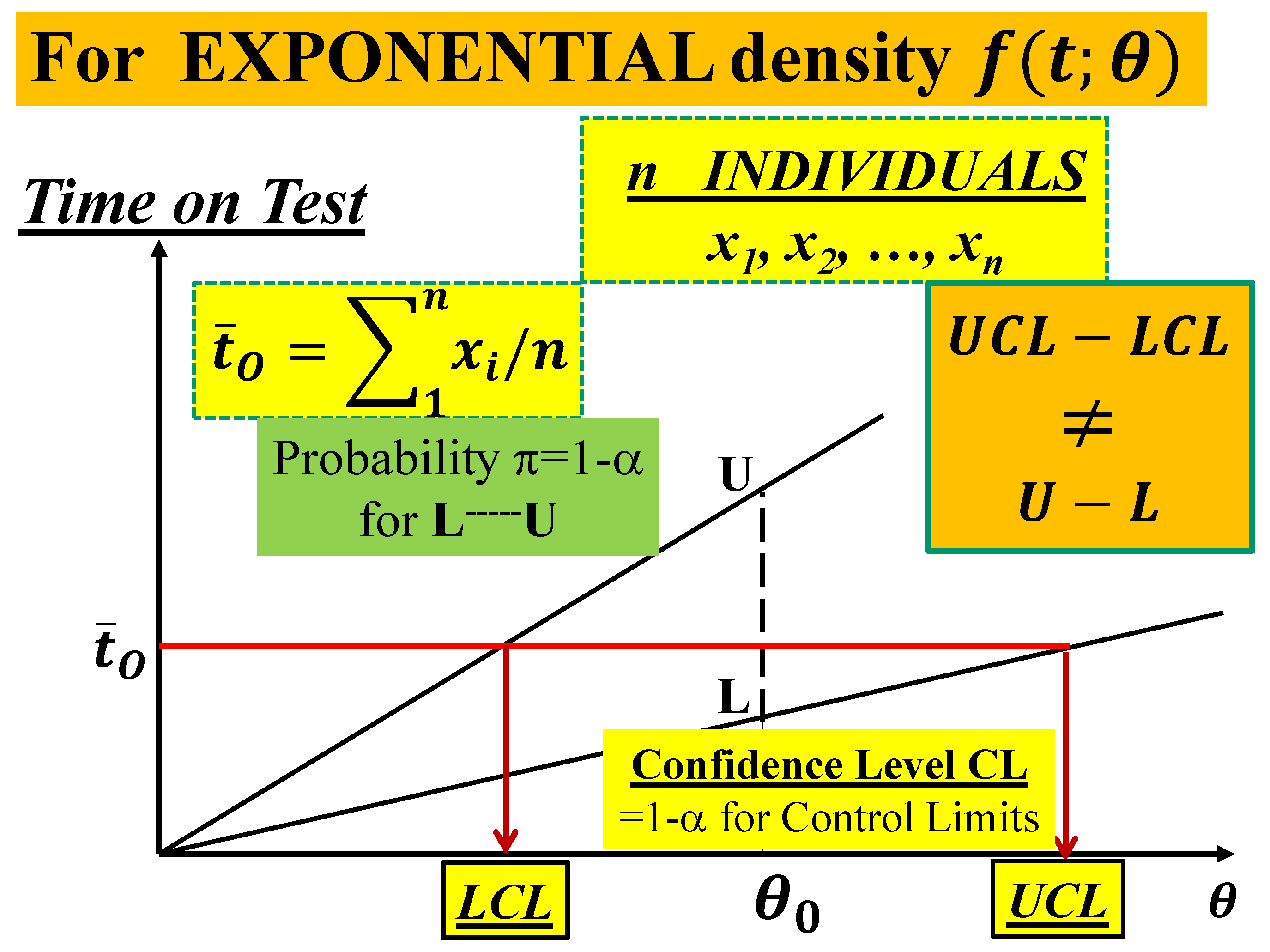
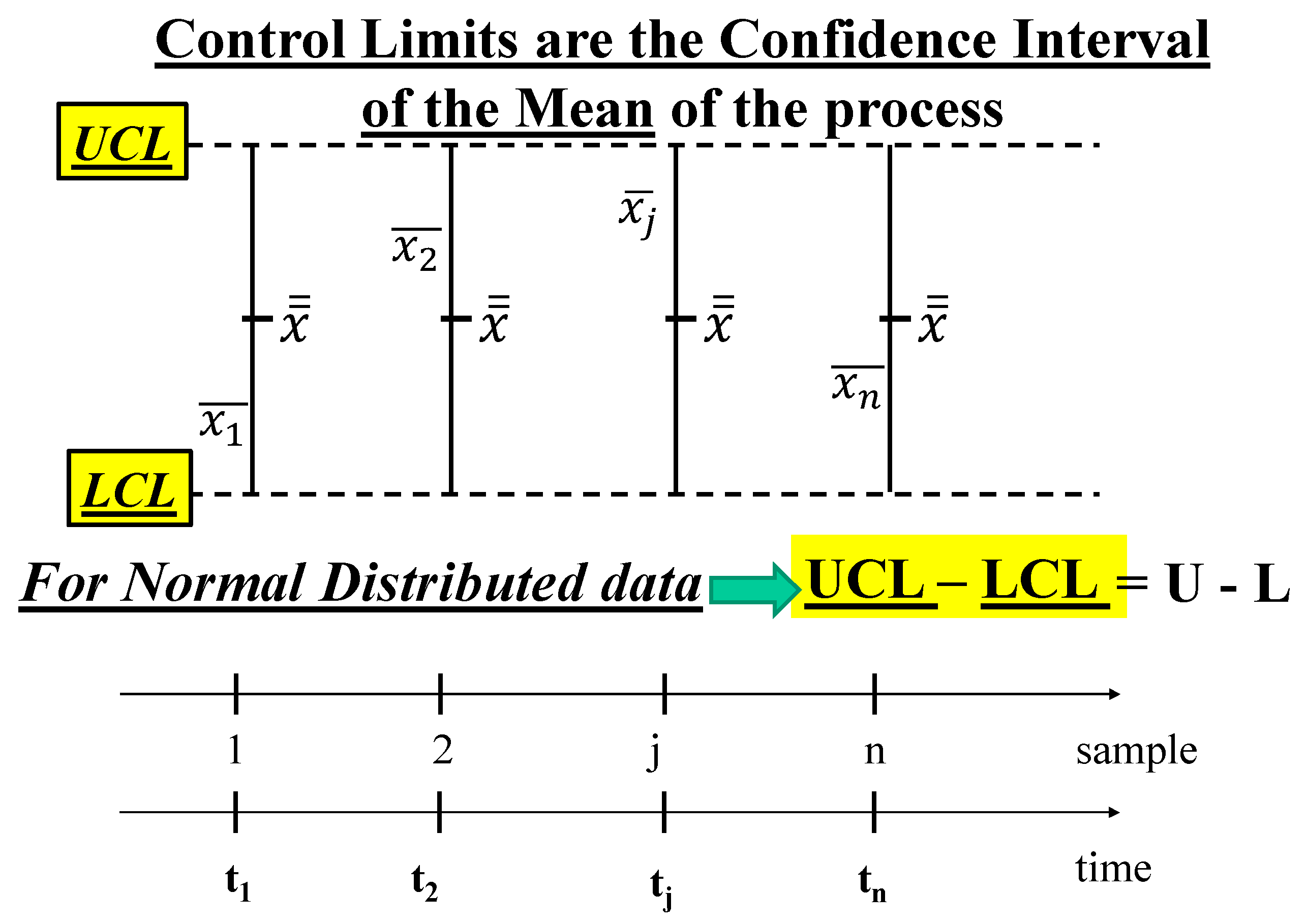
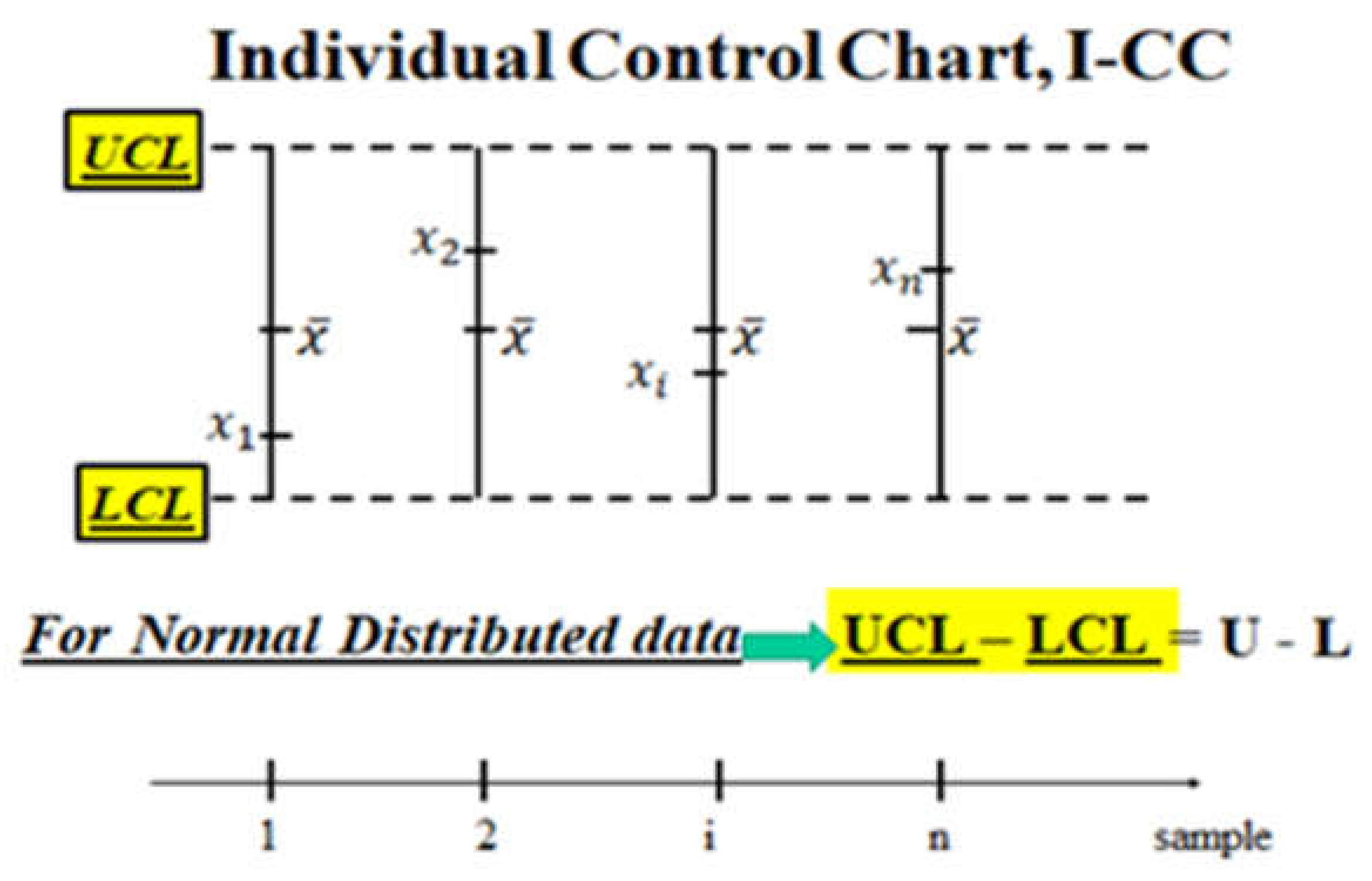
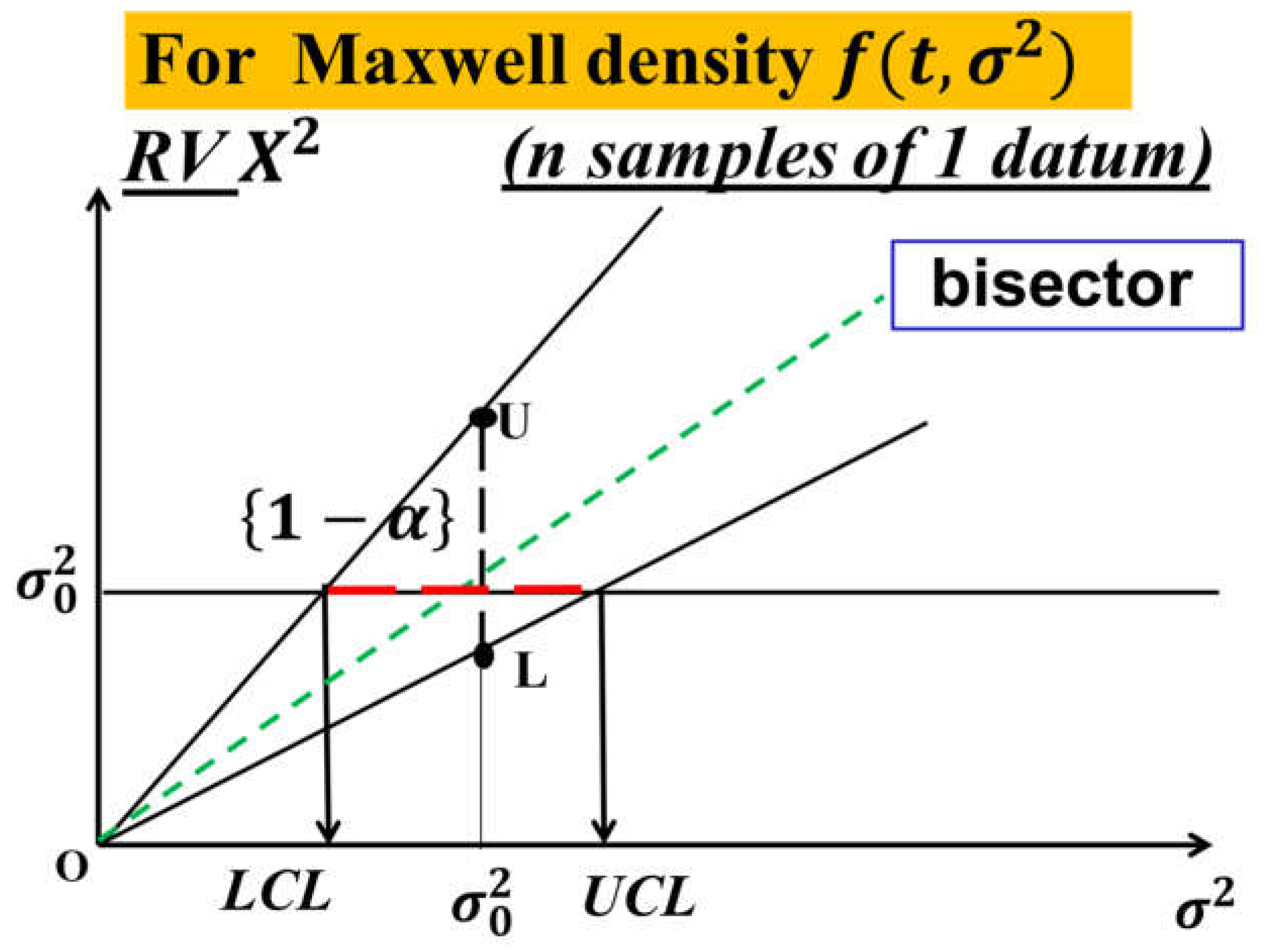
2.2. Control Charts for Process Management



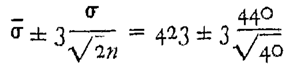

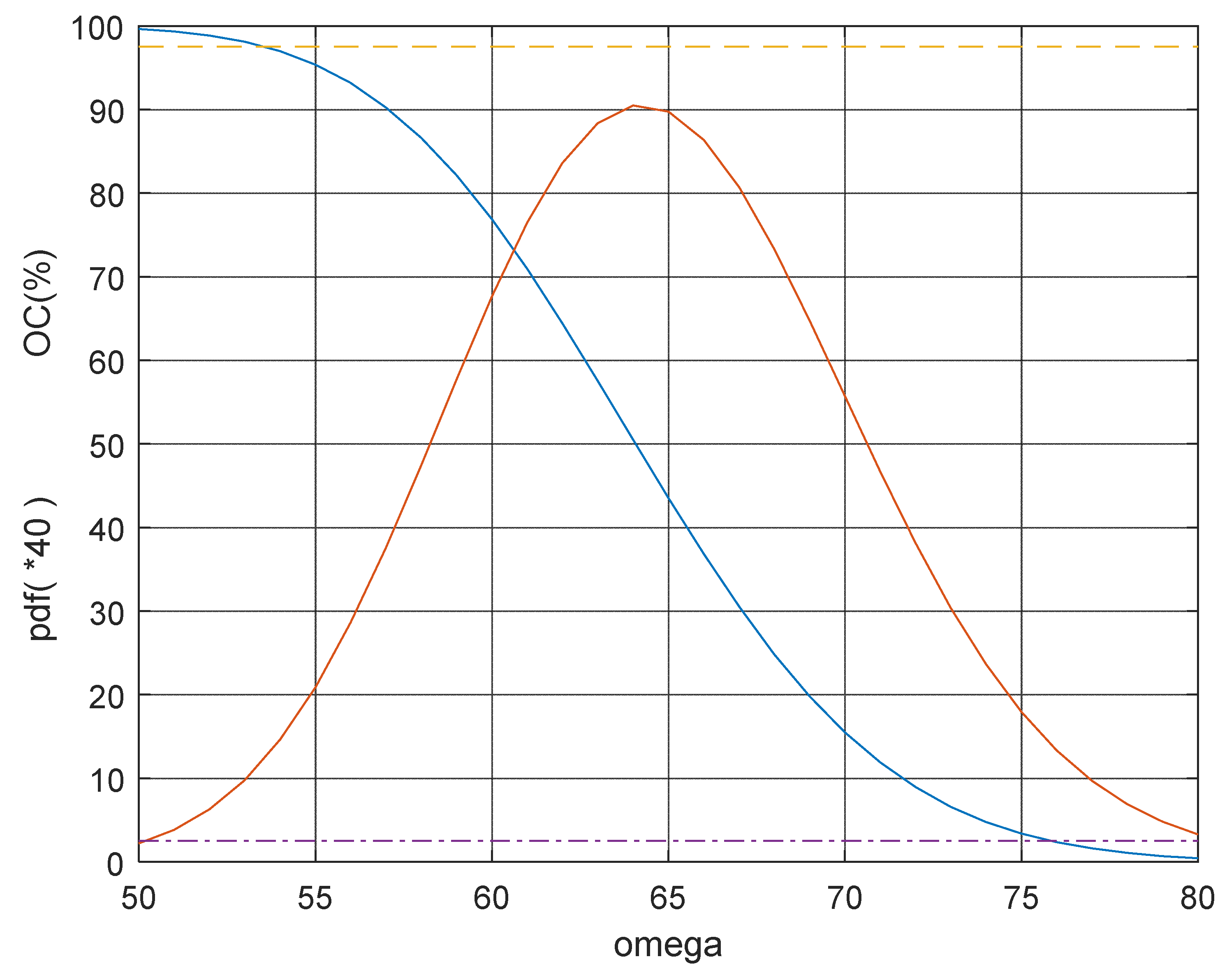
2.3. Statistics and RIT
2.4. Control Charts for TBE Data. Some Ideas for Phase I Analysis
3. Results
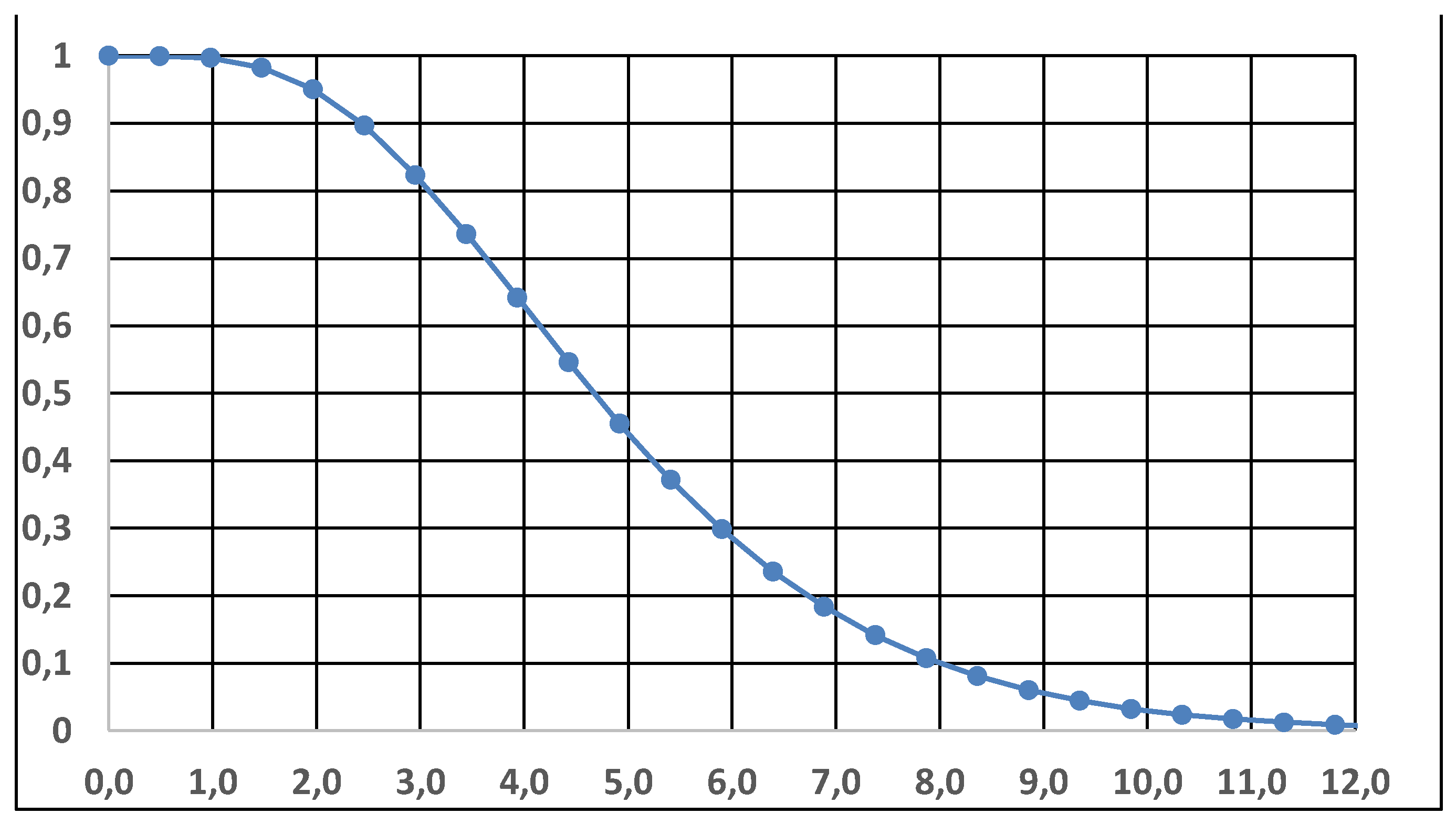
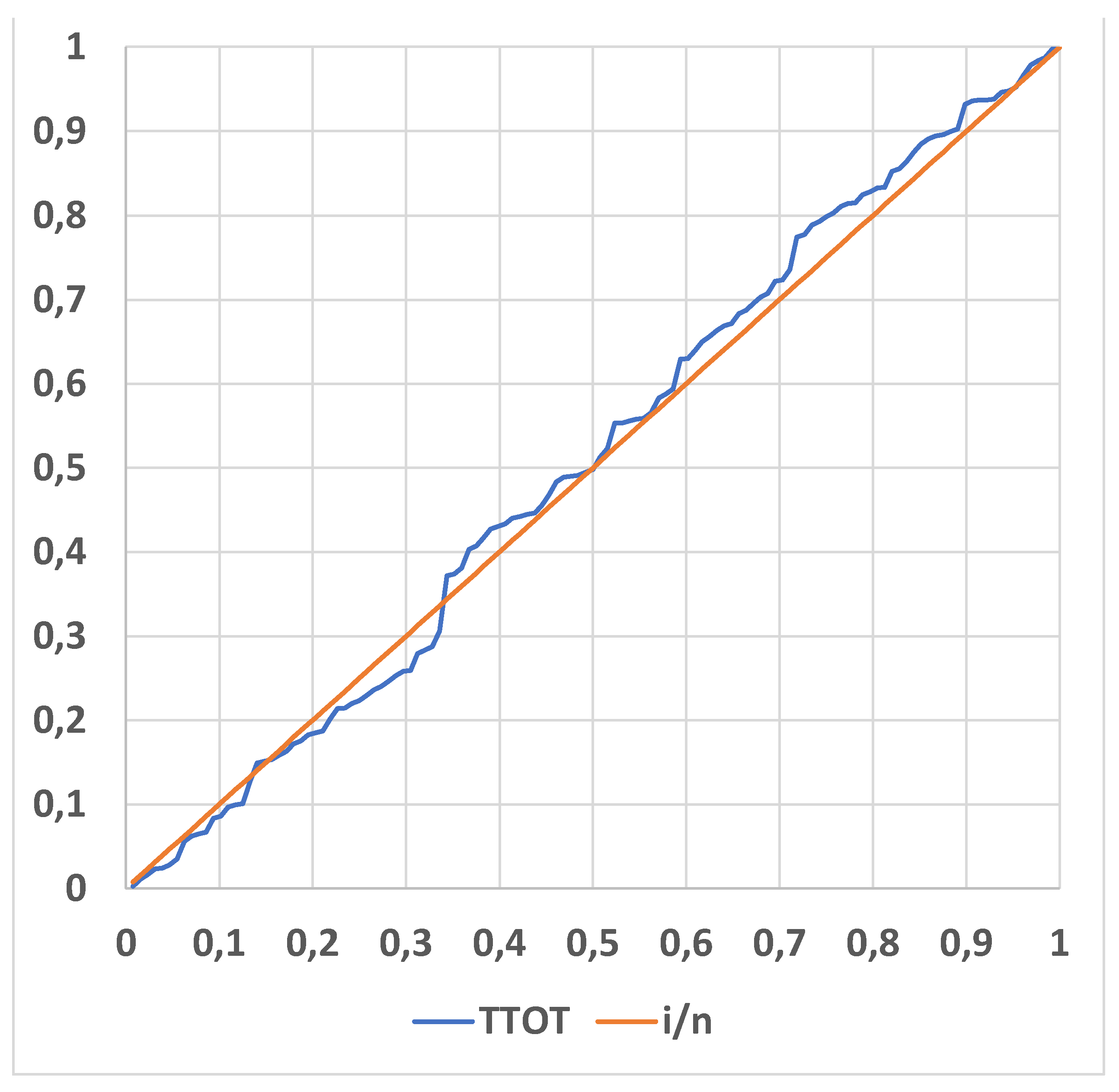
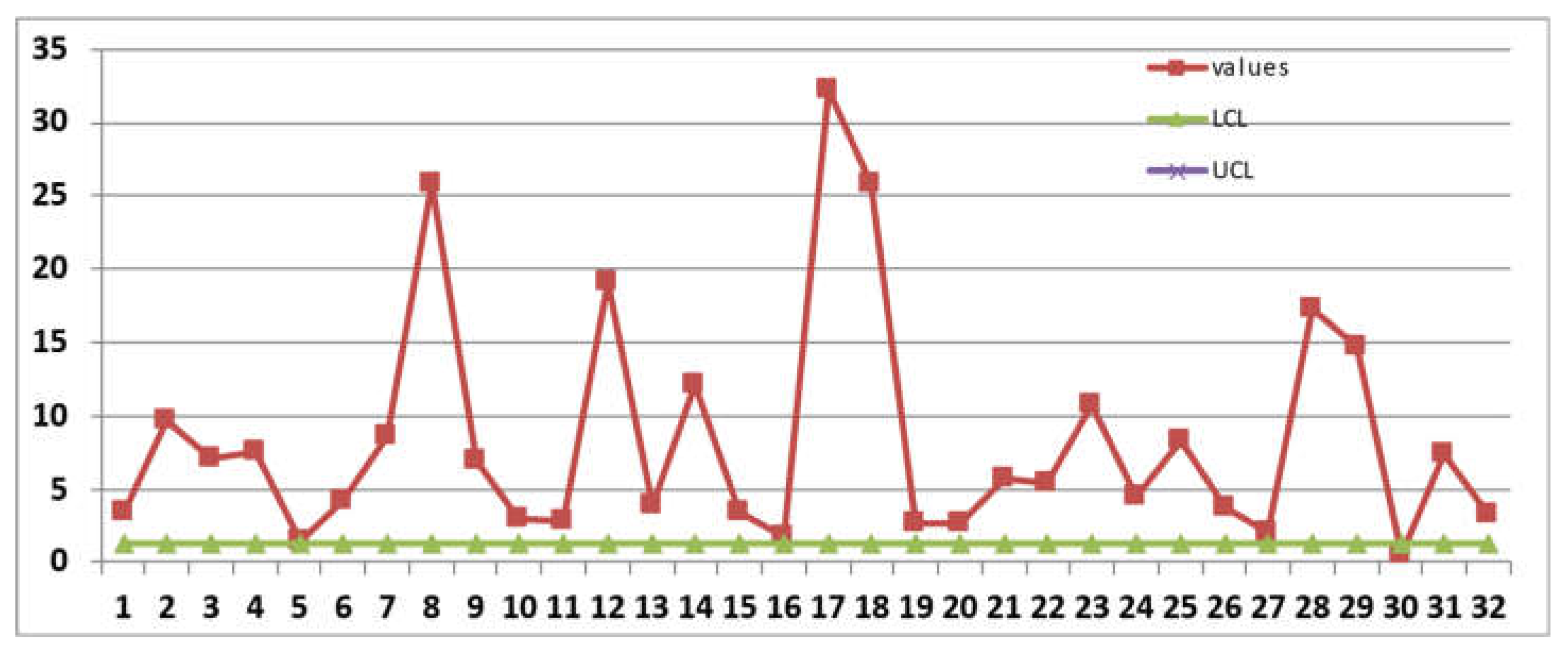
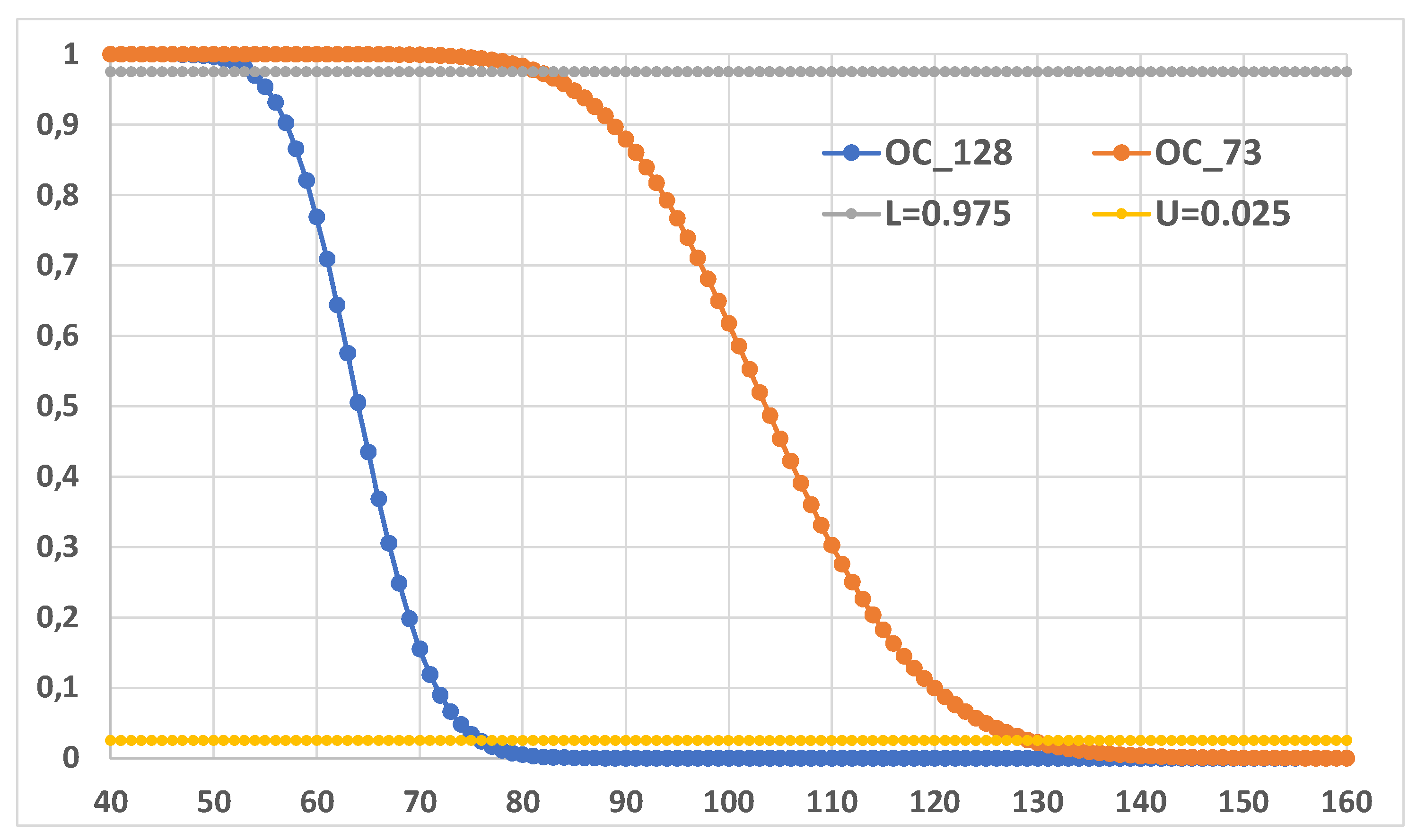
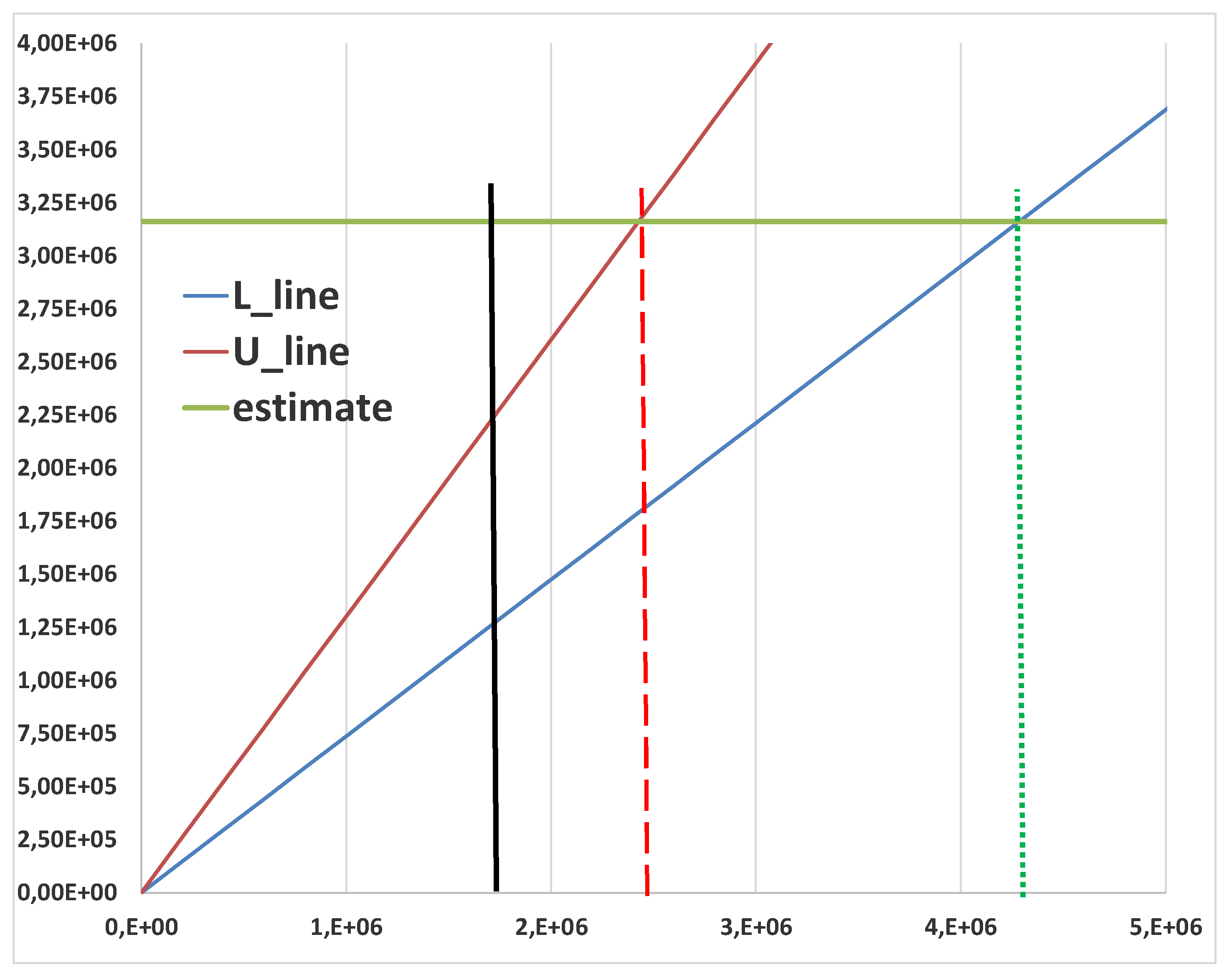
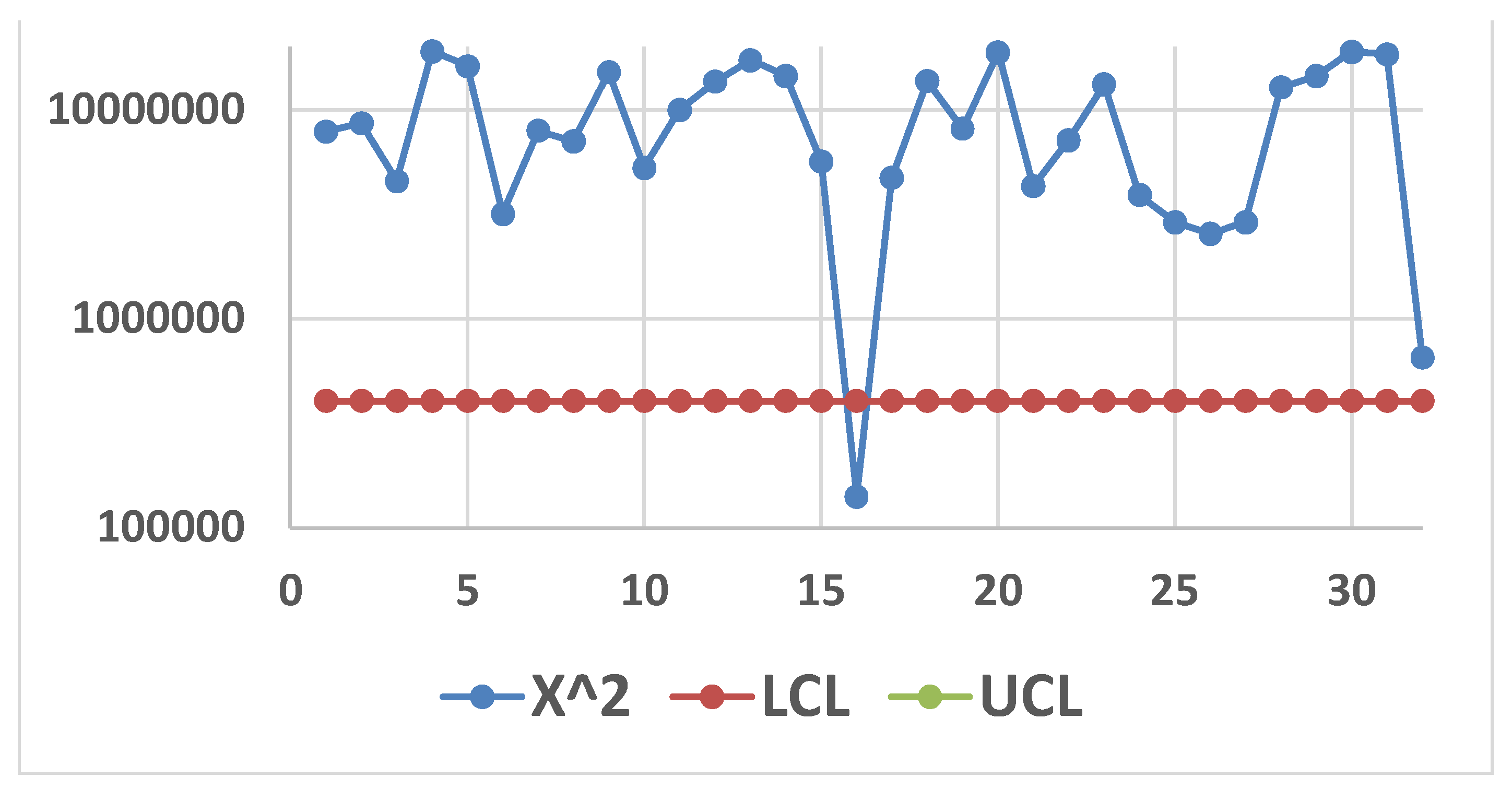
3.1. Control Charts for TBE Data. Phase I Analysis
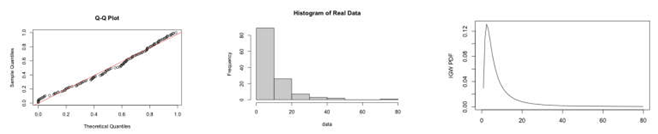
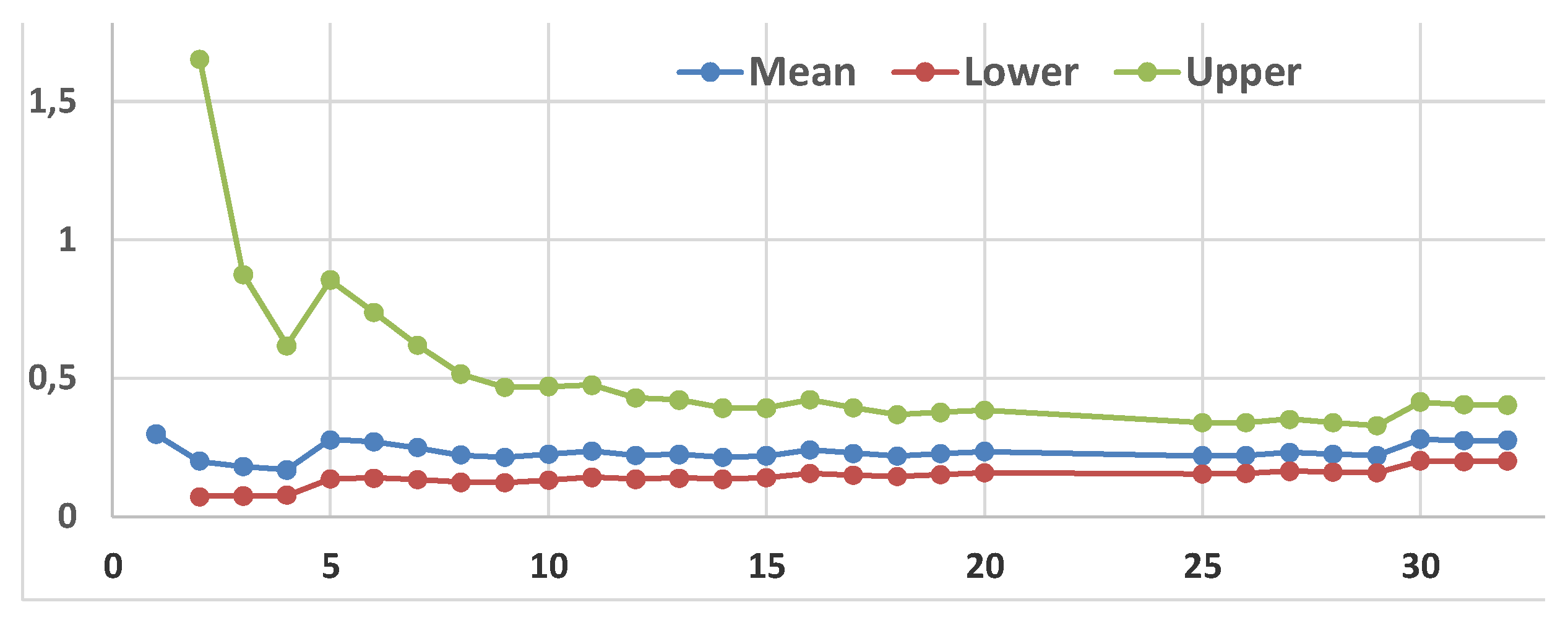
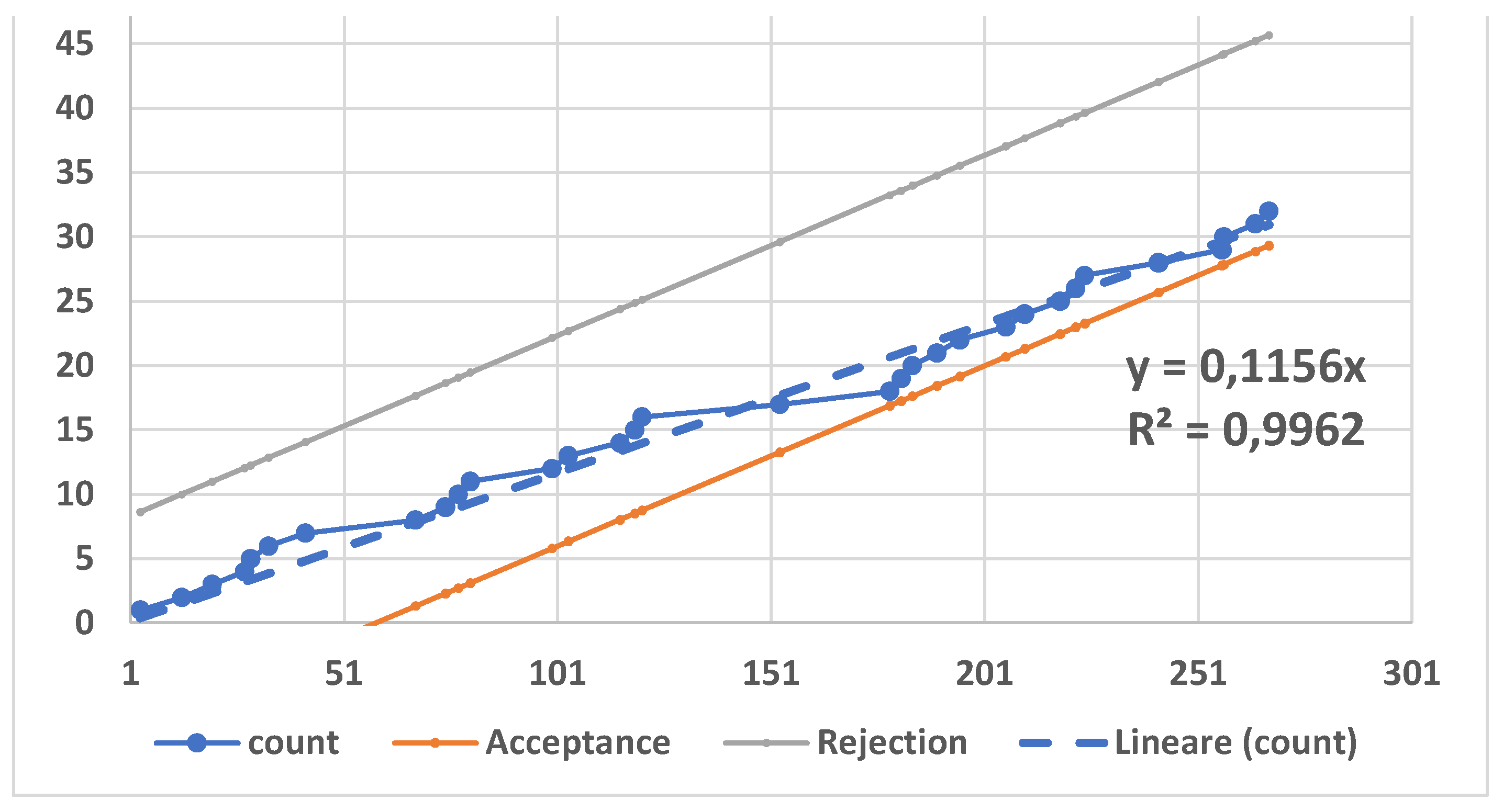
3.2. Control Charts for TBE Data. Phase II Analysis
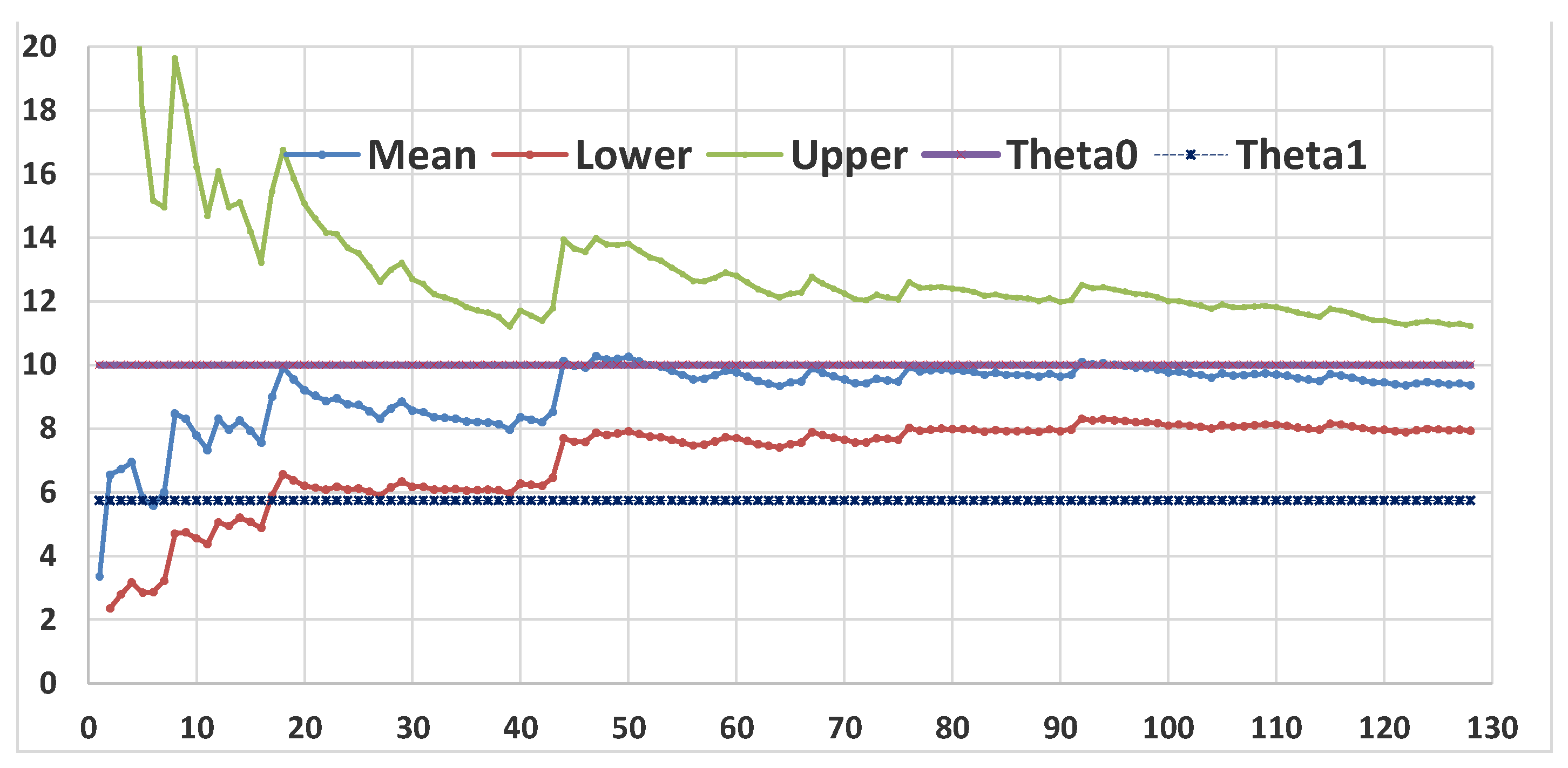
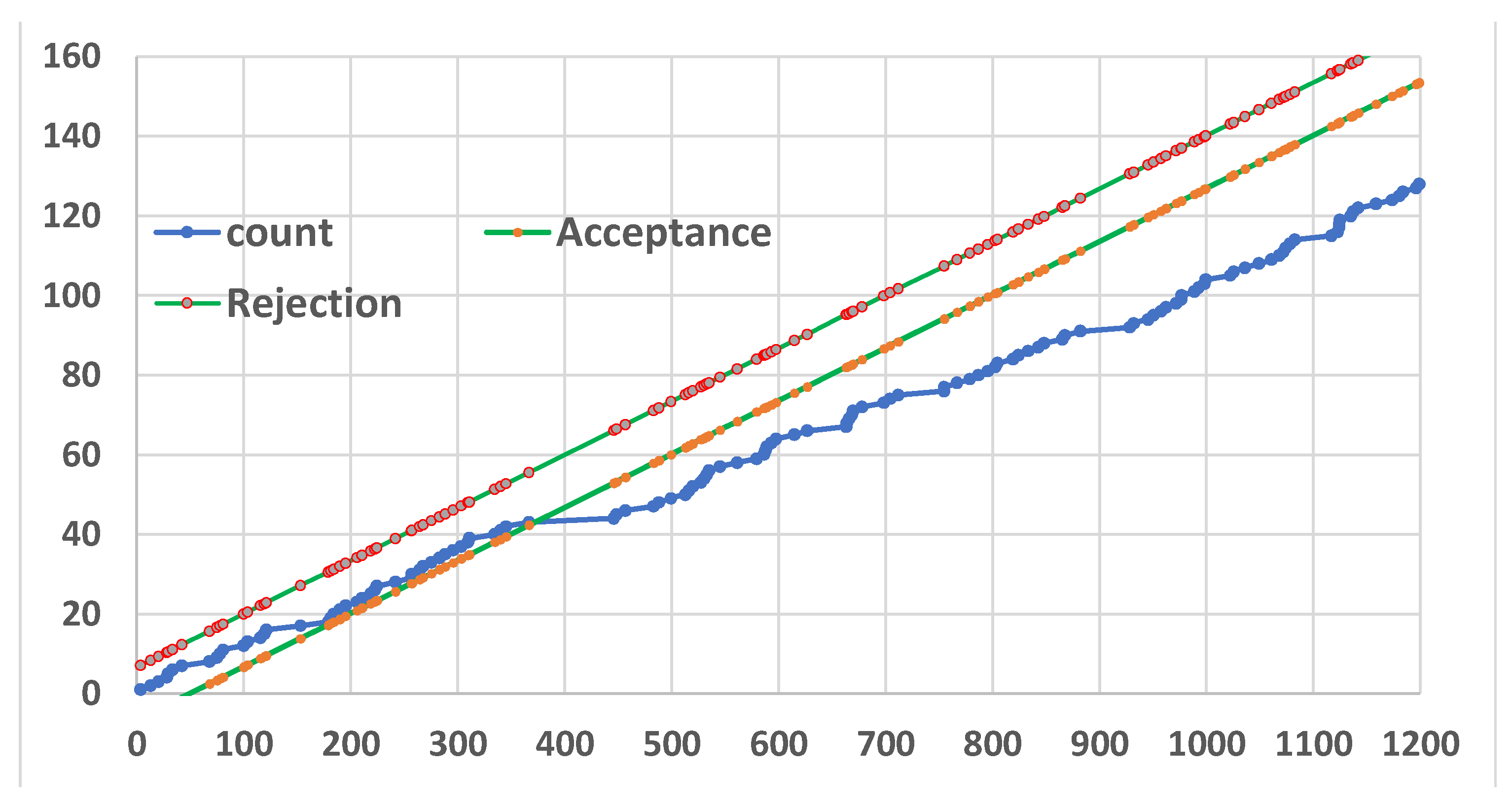
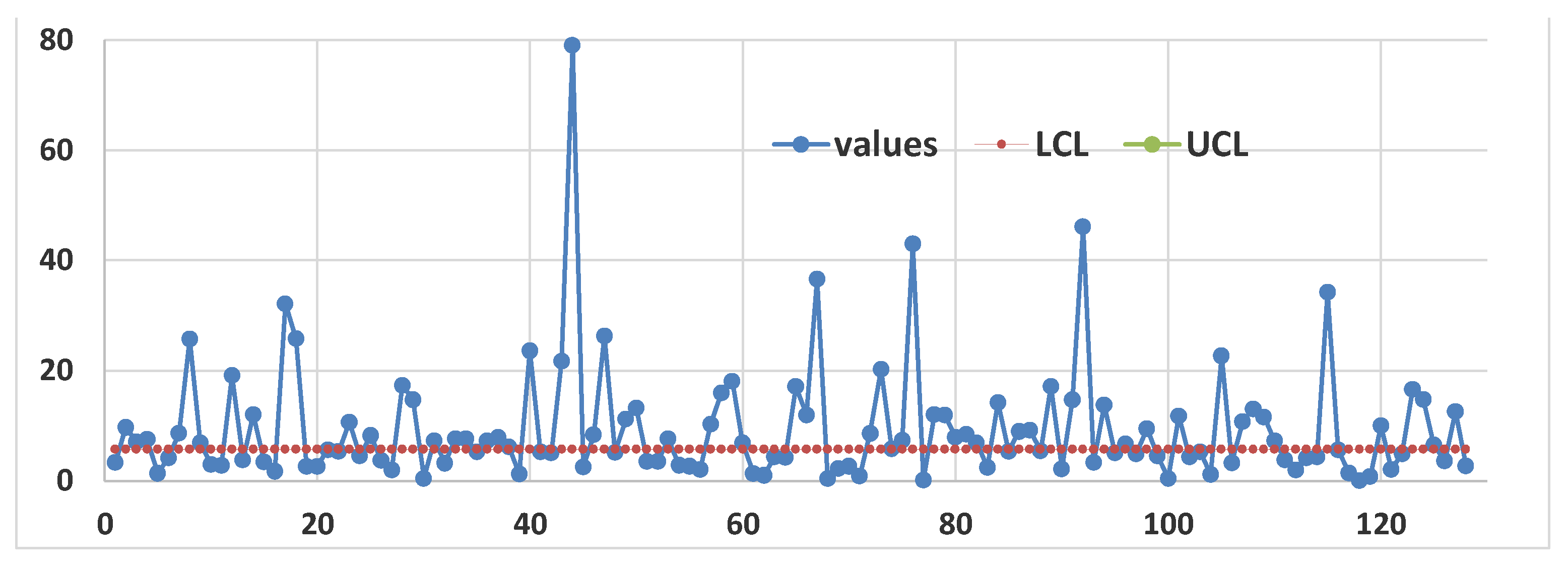
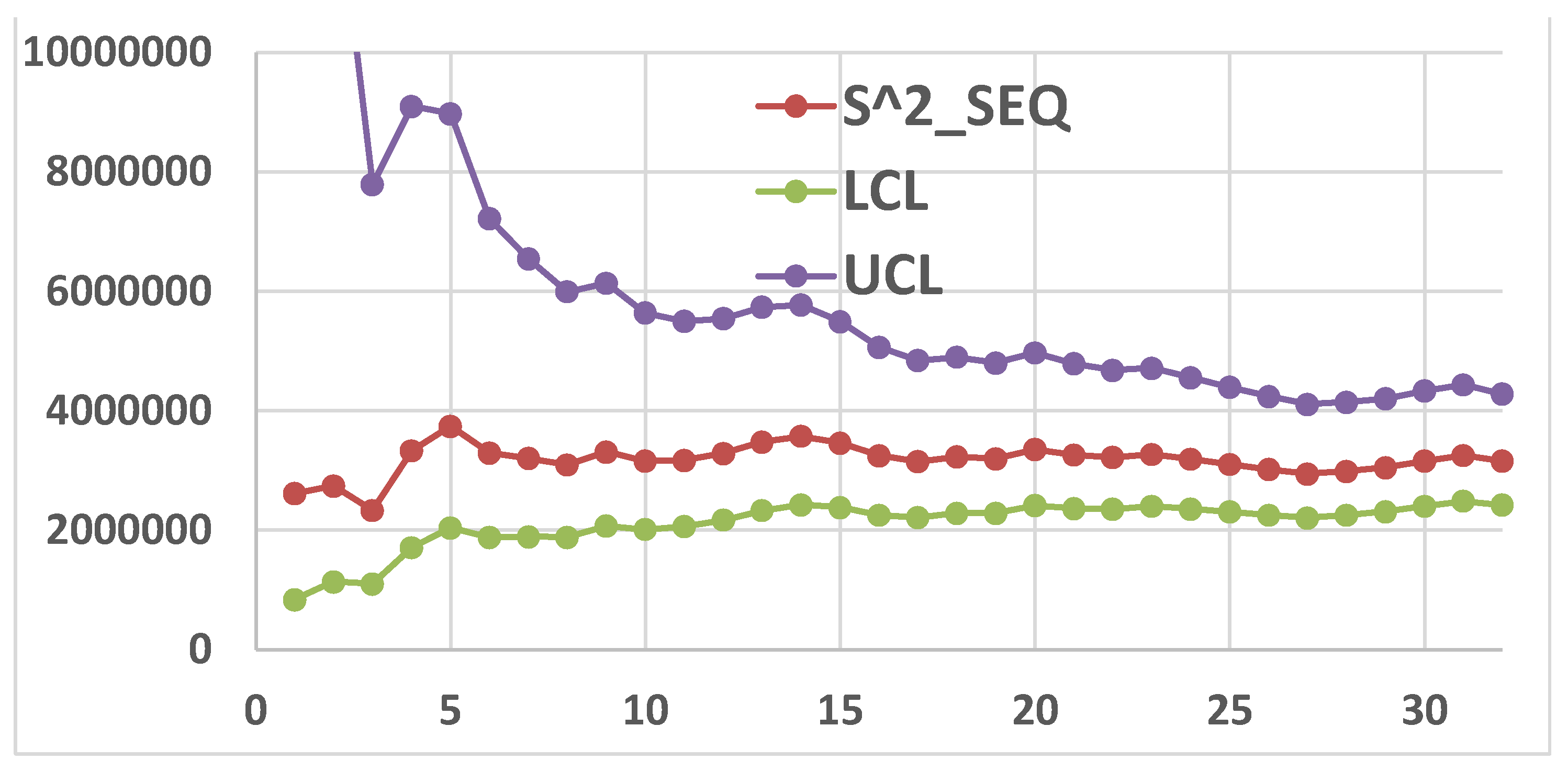
3.3. Sequential Test by the Authors of [3]
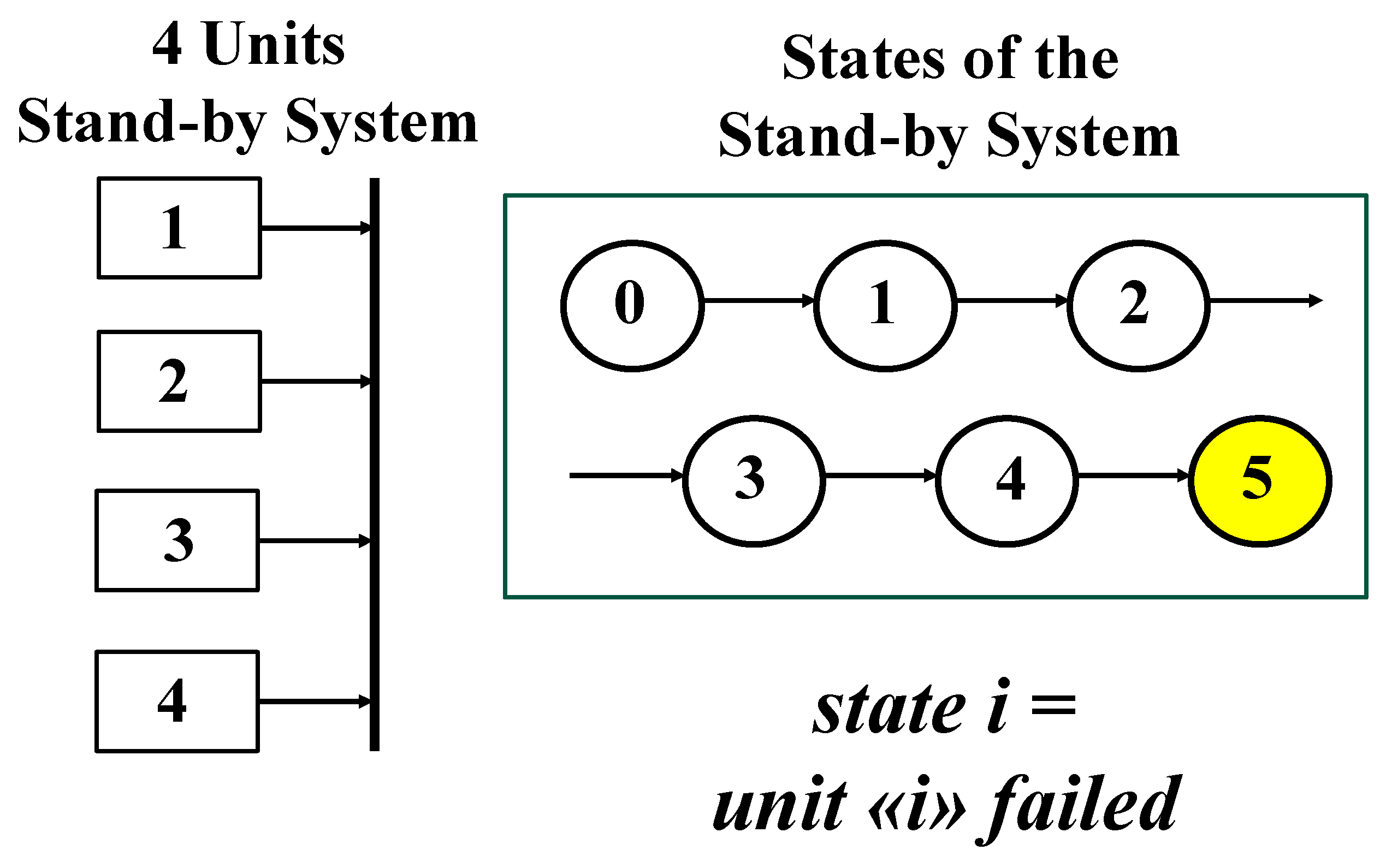
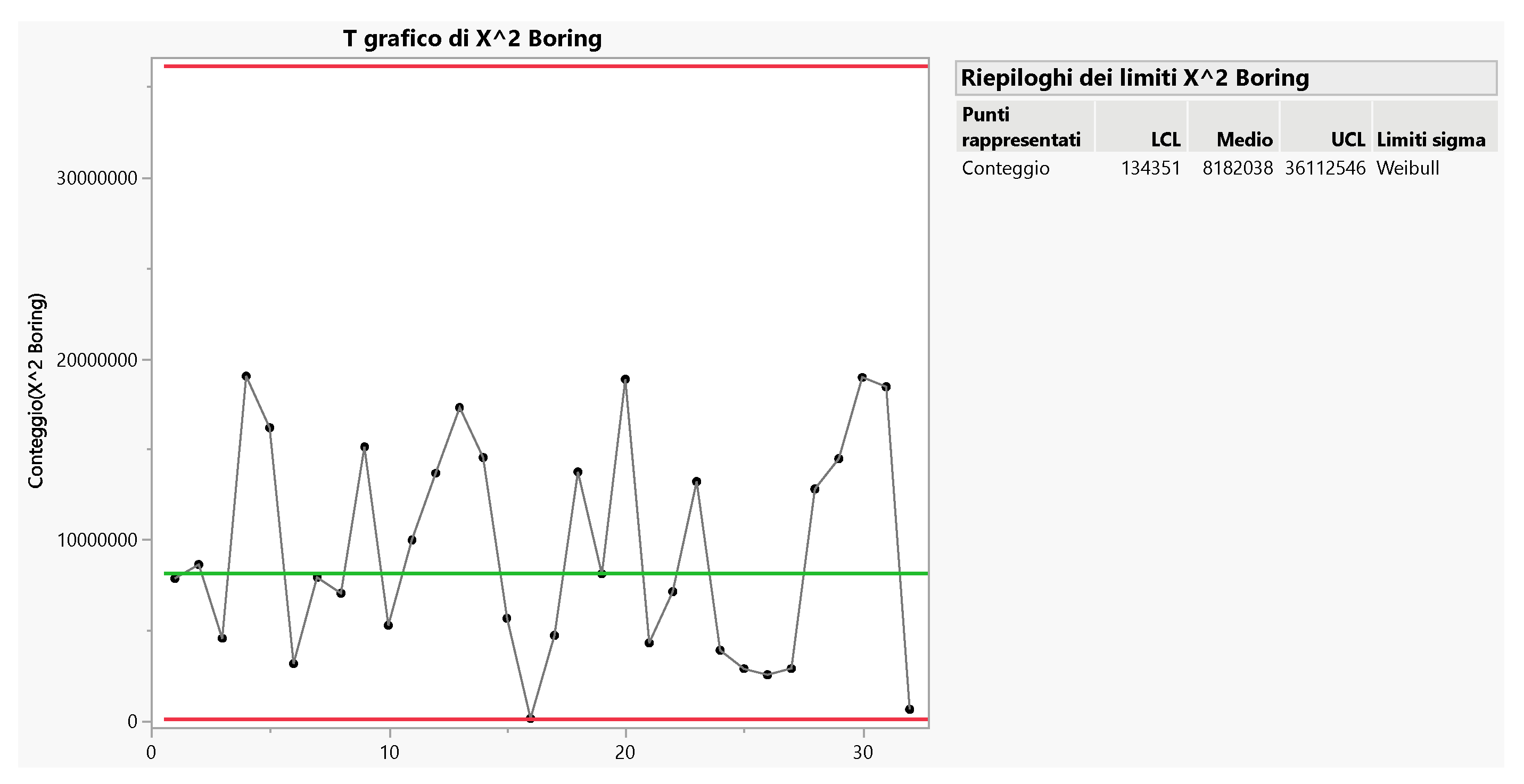
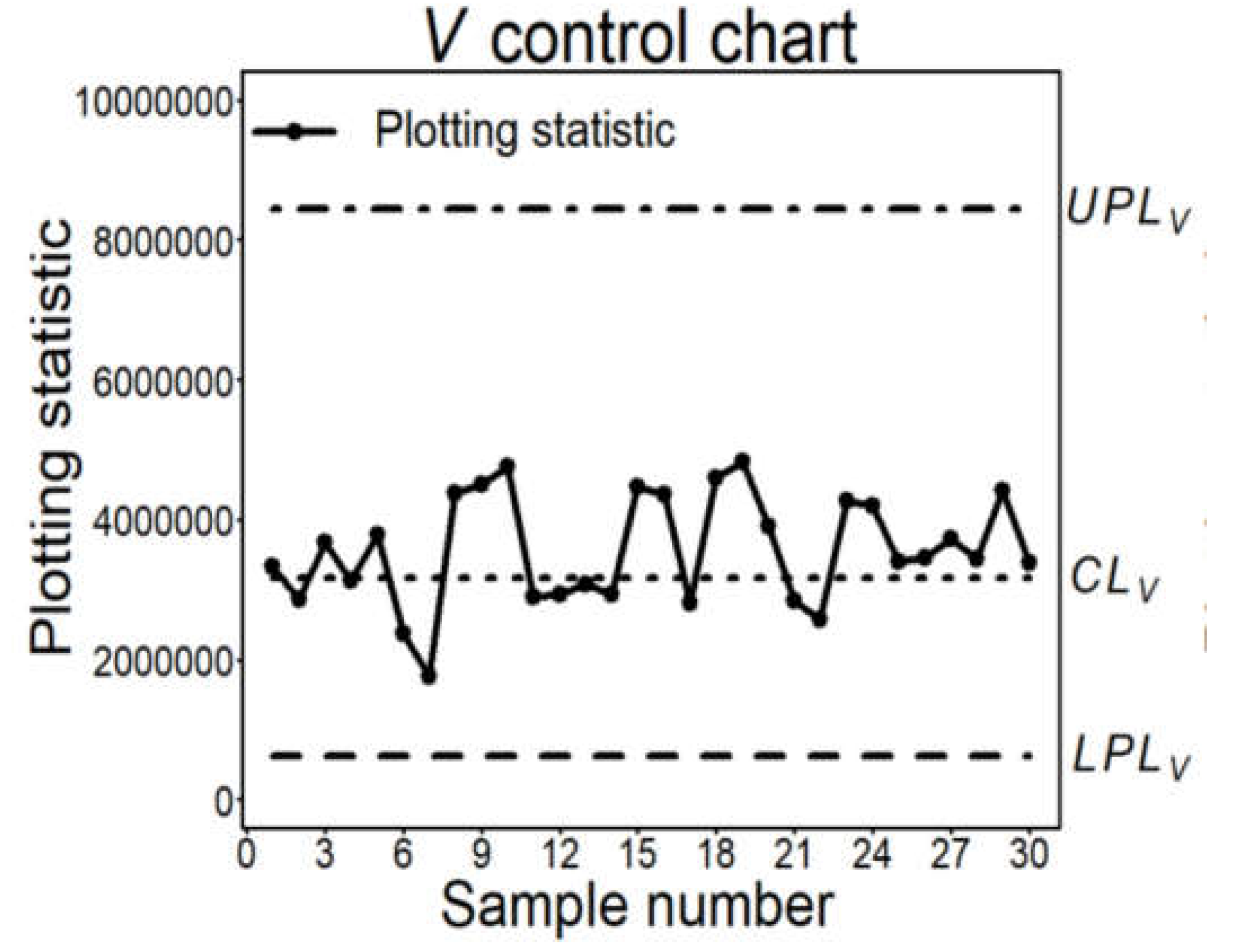
3.4. Other Cases
4. Discussion
5. Conclusions

Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
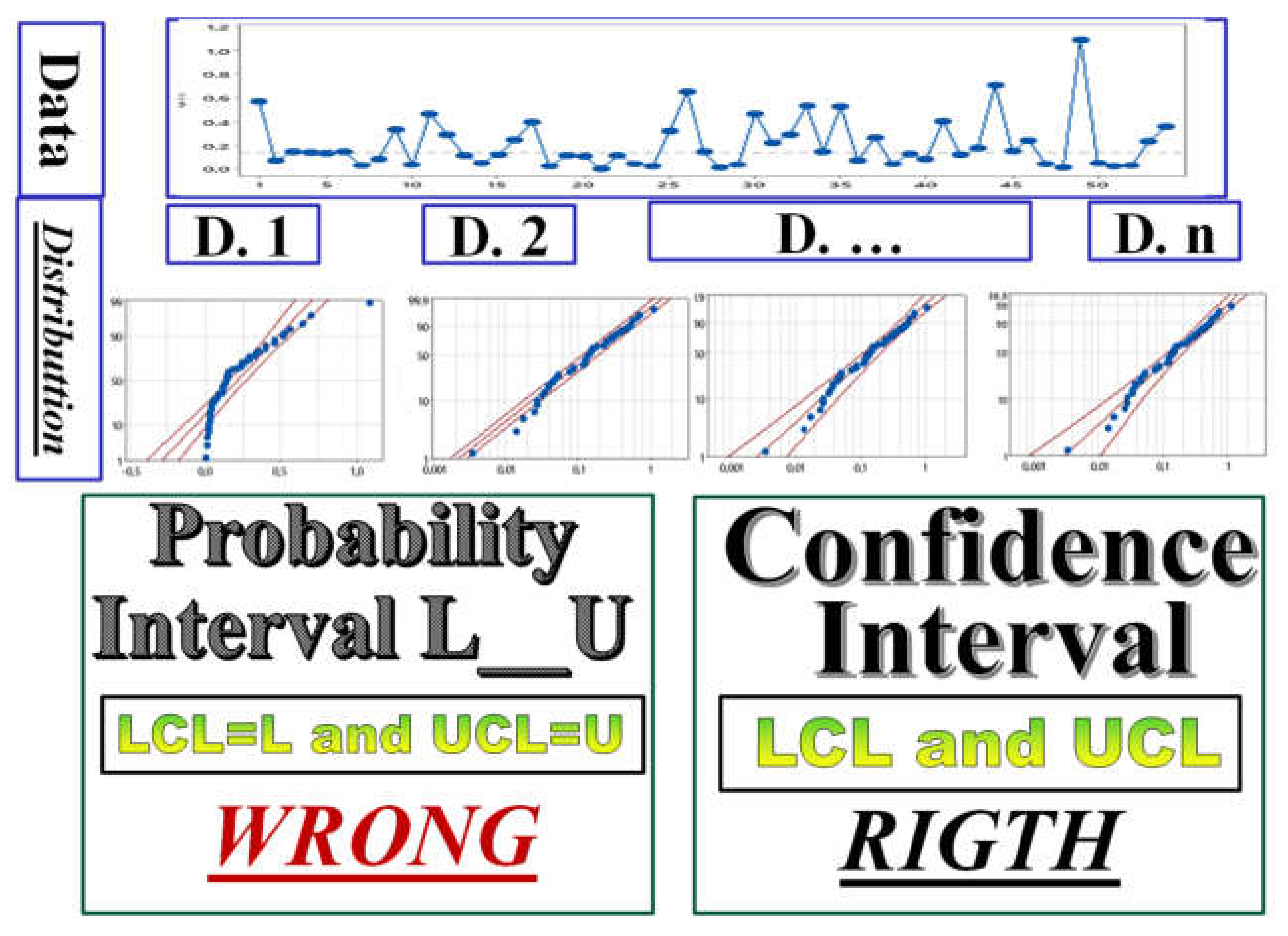
| LCL, UCL | Control Limits of the Control Charts (CCs) |
| L, U | Probability Limits related to a probability 1-α |
| θ | Parameter of the Exponential Distribution |
| θL-----θU | Confidence Interval of the parameter θ |
| RIT | Reliability Integral Theory |
Appendix A
A very illuminating case
| UTI | UTI | UTI | UTI | UTI | UTI | ||||||
| 1 | 0.57014 | 11 | 0.46530 | 21 | 0.00347 | 31 | 0.22222 | 41 | 0.40347 | 51 | 0.02778 |
| 2 | 0.07431 | 12 | 0.29514 | 22 | 0.12014 | 32 | 0.29514 | 42 | 0.12639 | 52 | 0.03472 |
| 3 | 0.15278 | 13 | 0.11944 | 23 | 0.04861 | 33 | 0.53472 | 43 | 0.18403 | 53 | 0.23611 |
| 4 | 0.14583 | 14 | 0.05208 | 24 | 0.02778 | 34 | 0.15139 | 44 | 0.70833 | 54 | 0.35972 |
| 5 | 0.13889 | 15 | 0.12500 | 25 | 0.32639 | 35 | 0.52569 | 45 | 0.15625 | ||
| 6 | 0.14931 | 16 | 0.25000 | 26 | 0.64931 | 36 | 0.07986 | 46 | 0.24653 | ||
| 7 | 0.03333 | 17 | 0.40069 | 27 | 0.14931 | 37 | 0.27083 | 47 | 0.04514 | ||
| 8 | 0.08681 | 18 | 0.02500 | 28 | 0.01389 | 38 | 0.04514 | 48 | 0.01736 | ||
| 9 | 0.33681 | 19 | 0.12014 | 29 | 0.03819 | 39 | 0.13542 | 49 | 1.08889 | ||
| 10 | 0.03819 | 20 | 0.11458 | 30 | 0.46806 | 40 | 0.08681 | 50 | 0.05208 |
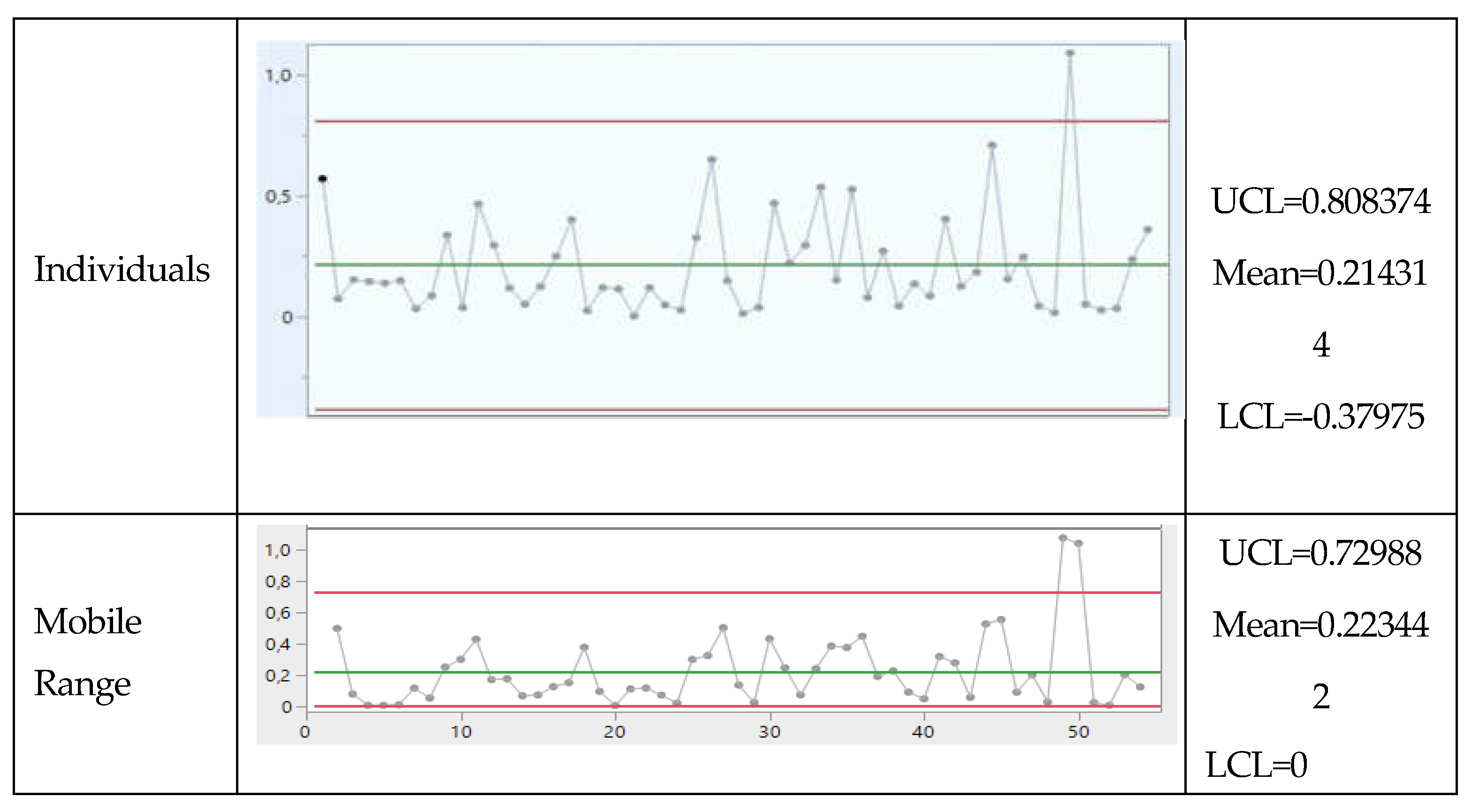
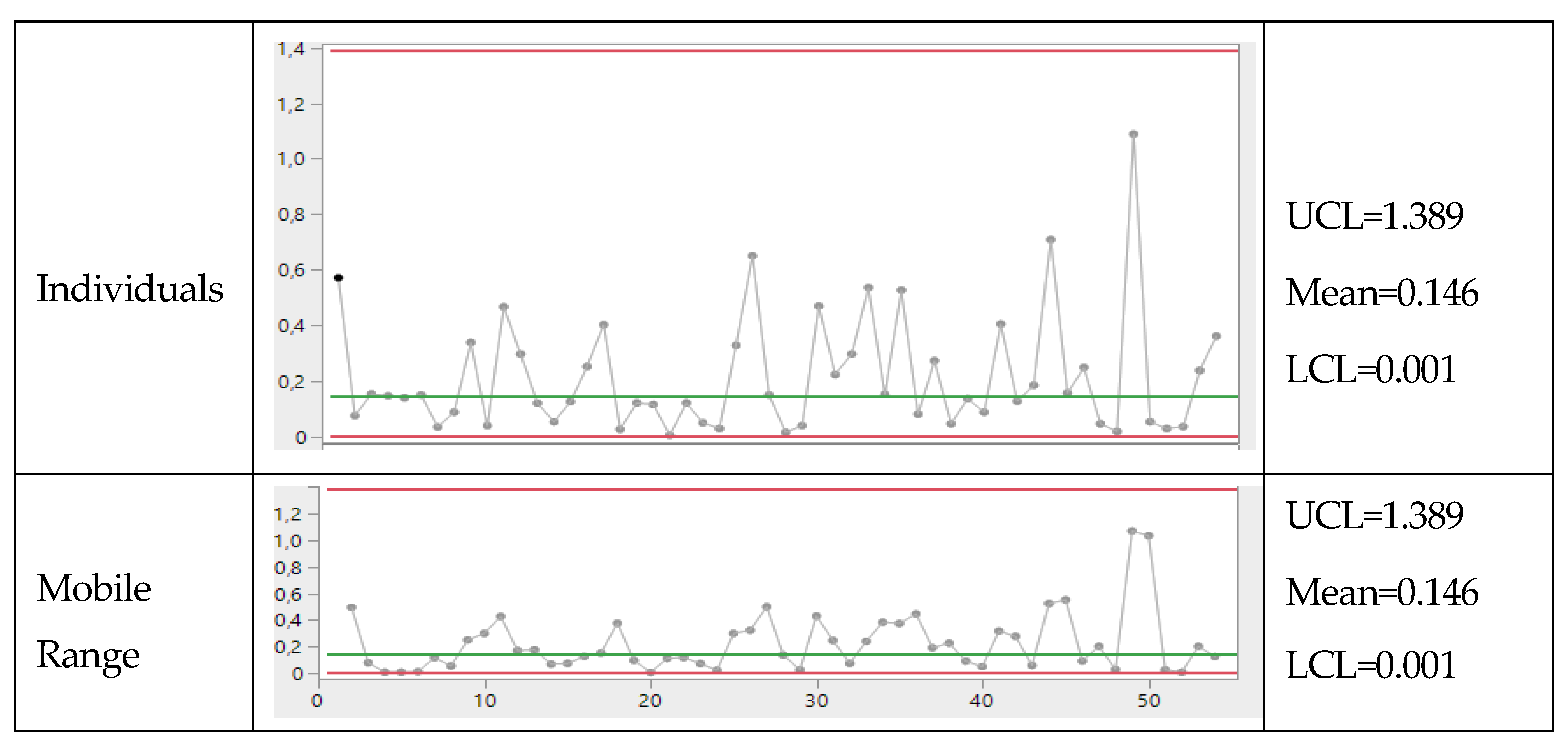

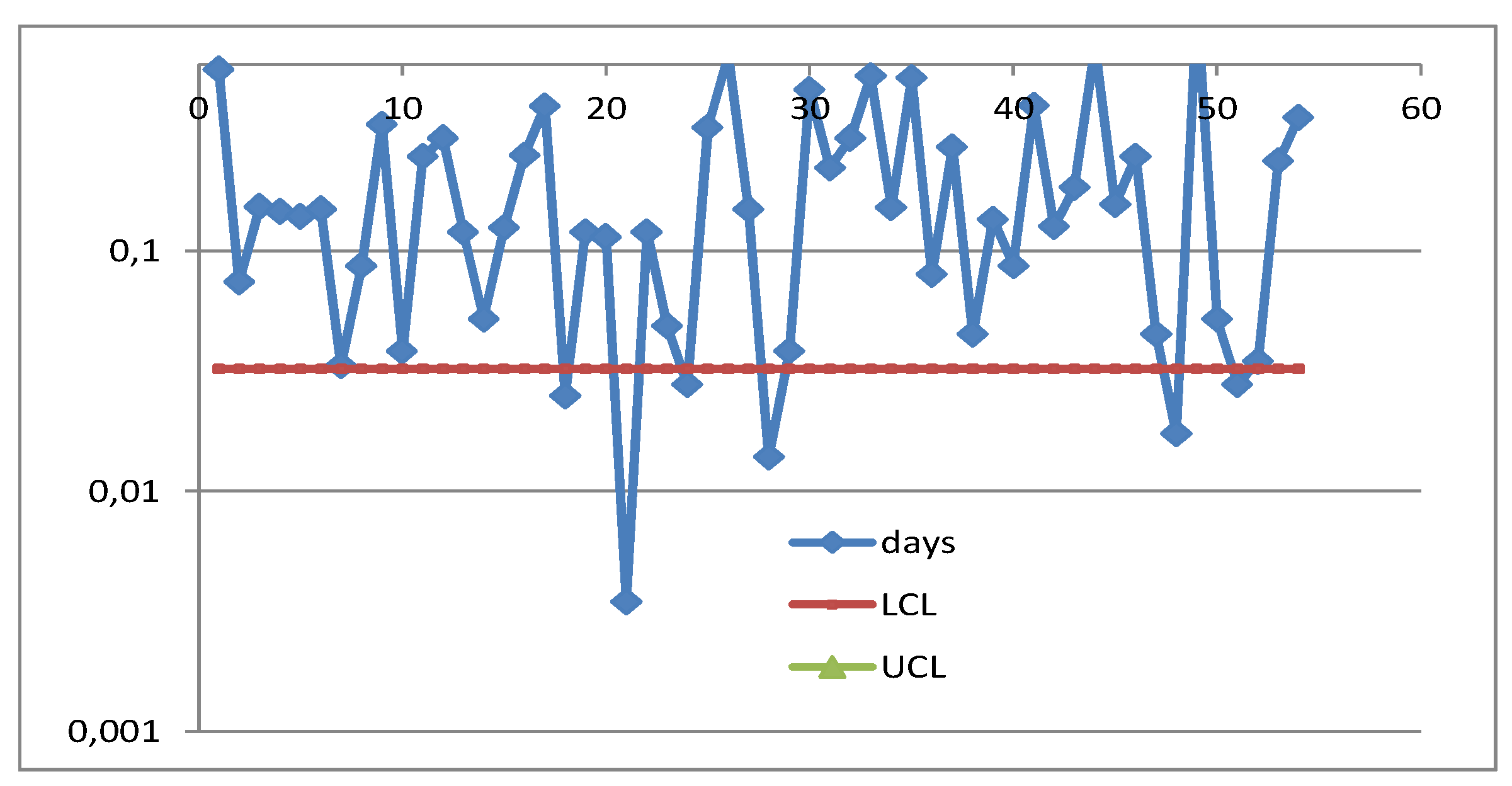
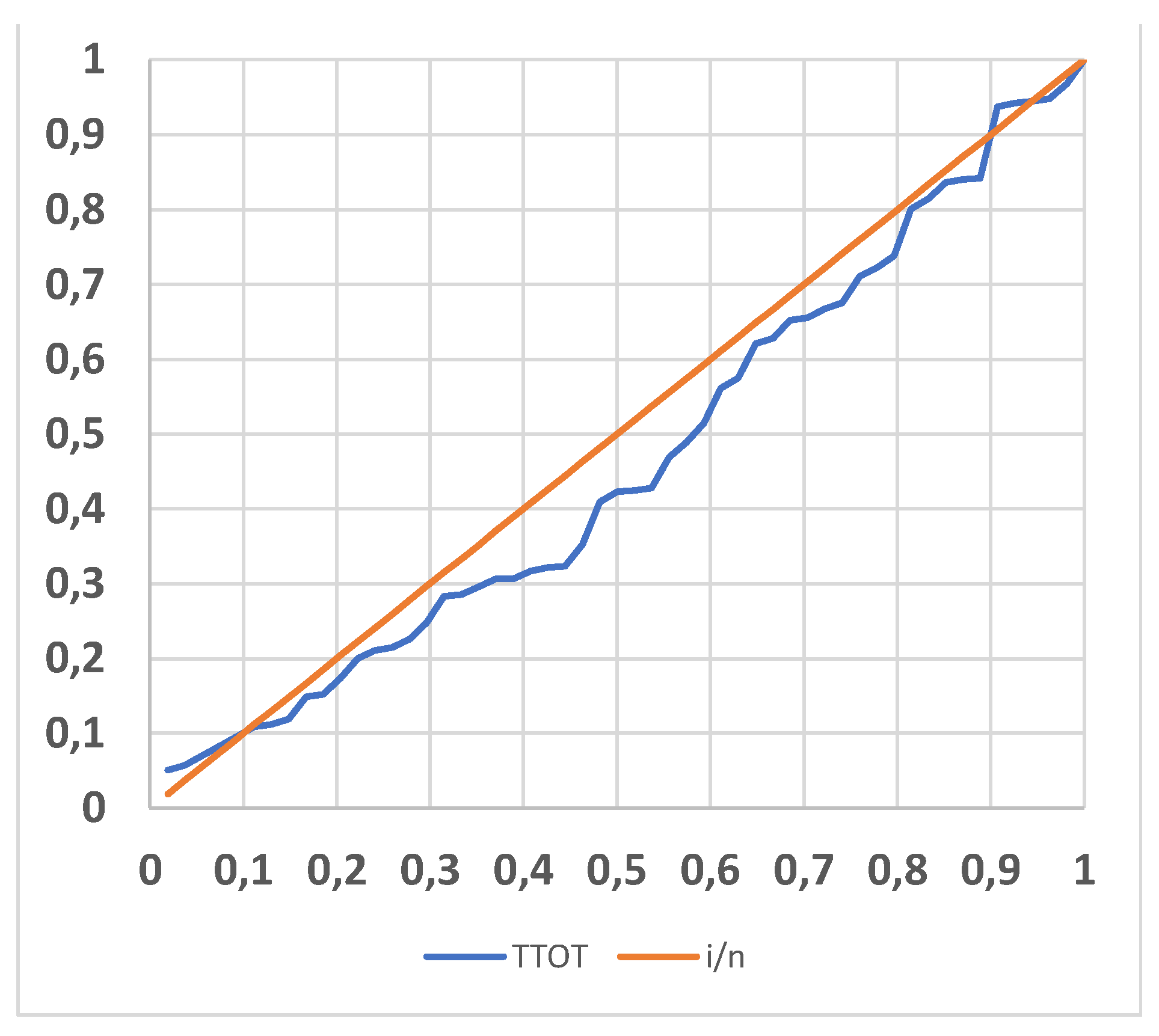
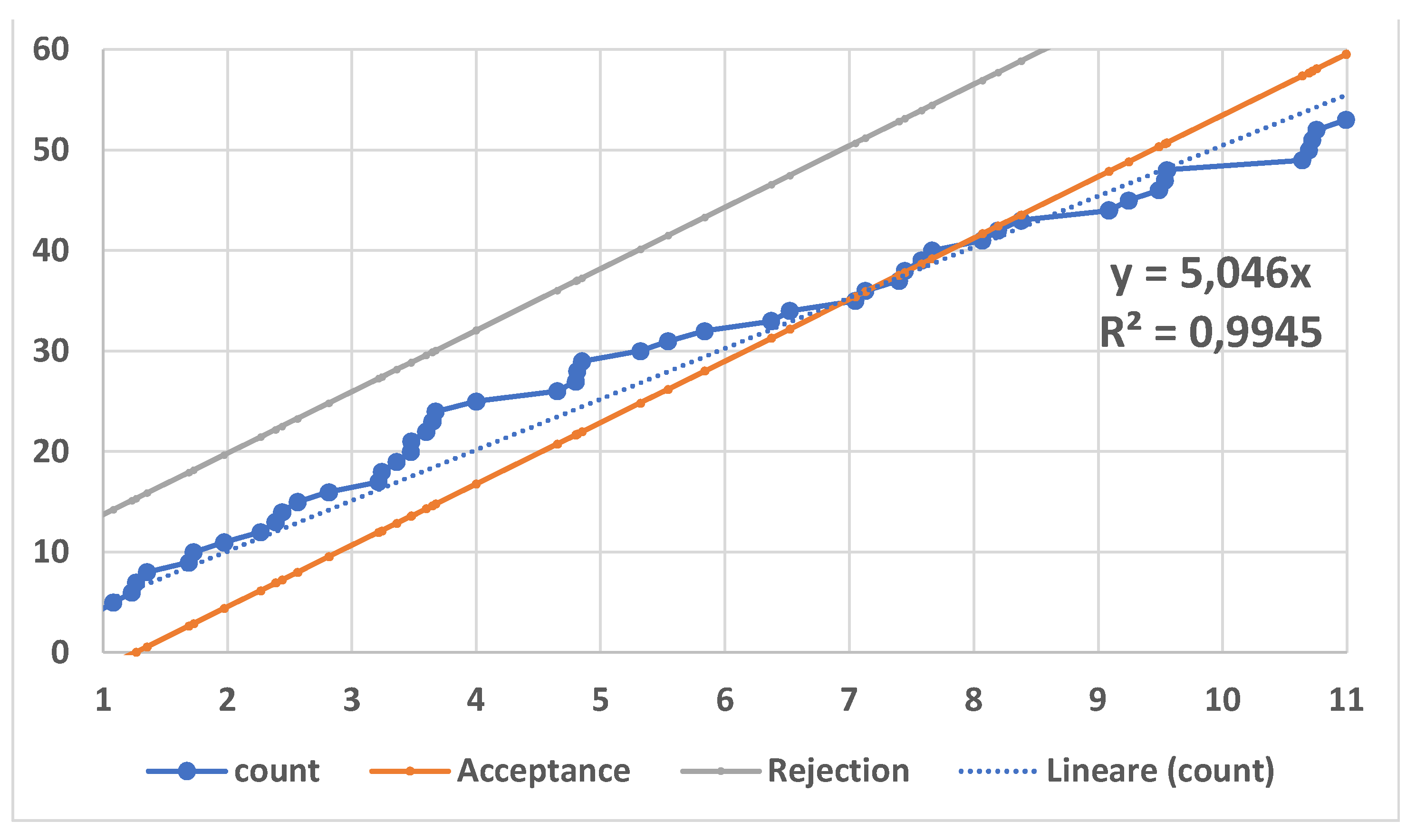

Appendix B
Appendix C. (related to [24])

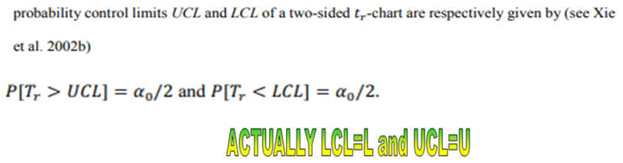

References
- Galetto, F., Quality of methods for quality is important. European Organisation for Quality Control Conference, Vienna. 1989.
- Galetto, F., GIQA, the Golden Integral Quality Approach: from Management of Quality to Quality of Management. Total Quality Management (TQM), Vol. 10, No. 1; 1999.
- Zhuang, Y., Bapat, S.R.; Wang, W. Statistical Inference on the Shape Parameter of Inverse Generalized Weibull Distribution. Mathematics 2024, 12, 3906. [CrossRef]
- Hu, J., Zheng, L.; Alanazi, I. Sequential Confidence Intervals for Comparing Two Proportions with Applications in A/B Testing. Mathematics 2025, 13, 161. [CrossRef]
- Alshahrani, F., Almanjahie, I.M.; Khan, M.; Anwar, S.M.; Rasheed, Z.; Cheema, A.N. On Designing of Bayesian Shewhart-Type Control Charts for Maxwell Distributed Processes with Application of Boring Machine. Mathematics 2023, 11, 1126. [CrossRef]
- Belz, M. Statistical Methods in the Process Industry: McMillan; 1973.
- Casella, Berger, Statistical Inference, 2nd edition: Duxbury Advanced Series; 2002.
- Cramer, H. Mathematical Methods of Statistics: Princeton University Press; 1961.
- Deming W. E., Out of the Crisis, Cambridge University Press; 1986.
- Deming W. E., The new economics for industry, government, education: Cambridge University Press; 1997.
- Dore, P., Introduzione al Calcolo delle Probabilità e alle sue applicazioni ingegneristiche, Casa Editrice Pàtron, Bologna; 1962.
- Juran, J., Quality Control Handbook, 4th, 5th ed.: McGraw-Hill, New York: 1988-98.
- Kendall, Stuart, (1961) The advanced Theory of Statistics, Volume 2, Inference and Relationship:, Hafner Publishing Company; 1961.
- Meeker, W. Q., Hahn, G. J., Escobar, L. A. Statistical Intervals: A Guide for Practitioners and Researchers. John Wiley & Sons. 2017.
- Mood, Graybill, Introduction to the Theory of Statistics, 2nd ed.: McGraw Hill; 1963.
- Rao, C. R., Linear Statistical Inference and its Applications: Wiley & Sons; 1965.
- Rozanov, Y., Processus Aleatoire, Editions MIR: Moscow, (traduit du russe); 1975.
- Ryan, T. P., Statistical Methods for Quality Improvement: Wiley & Sons; 1989.
- Shewhart W. A., Economic Control of Quality of Manufactured Products: D. Van Nostrand Company; 1931.
- Shewhart W.A., Statistical Method from the Viewpoint of Quality Control: Graduate School, Washington; 1936.
- D. J. Wheeler, Various posts, Online available from Quality Digest.
- Galetto, F., (2014), Papers, and Documents of FG, Research Gate.
- Galetto, F., (2015-2024), Papers, and Documents of FG, Academia.edu.
- Galetto, F., (2024), The garden of flowers, Academia.edu.
- Galetto, F., Affidabilità Teoria e Metodi di calcolo: CLEUP editore, Padova (Italy); 1981-94.
- Galetto, F., Affidabilità Prove di affidabilità: distribuzione incognita, distribuzione esponenziale: CLEUP editore, Padova (Italy); 1982, 85, 94.
- Galetto, F., Qualità. Alcuni metodi statistici da Manager: CUSL, Torino (Italy; 1995-99).
- Galetto, F., Gestione Manageriale della Affidabilità: CLUT, Torino (Italy); 2010.
- Galetto, F., Manutenzione e Affidabilità: CLUT, Torino (Italy); 2015.
- Galetto, F., Reliability and Maintenance, Scientific Methods, Practical Approach, Vol-1: www.morebooks.de.; 2016.
- Galetto, F., Reliability and Maintenance, Scientific Methods, Practical Approach, Vol-2: www.morebooks.de.; 2016.
- Galetto, F., Statistical Process Management, ELIVA press ISBN 9781636482897; 2019.
- Galetto F., Affidabilità per la manutenzione, Manutenzione per la disponibilità: tab edizioni, Roma (Italy), ISBN 978-88-92-95-435-9, www.tabedizioni.it; 2022.
- Galetto, F., (2015) Hope for the Future: Overcoming the DEEP Ignorance on the CI (Confidence Intervals) and on the DOE (Design of Experiments), Science J. Applied Mathematics and Statistics, Vol. 3, No. 3, pp. 99-123. [CrossRef]
- Galetto, F., (2015) Management Versus Science: Peer-Reviewers do not Know the Subject They Have to Analyse, Journal of Investment and Management. Vol. 4, No. 6, pp. 319-329. [CrossRef]
- Galetto, F., (2015) The first step to Science Innovation: Down to the Basics., Journal of Investment and Management. Vol. 4, No. 6, pp. 319-329. [CrossRef]
- Galetto F., (2021) Minitab T charts and quality decisions, Journal of Statistics and Management Systems. [CrossRef]
- Galetto, F., (2012) Six Sigma: help or hoax for Quality?, 11th Conference on TQM for HEI, Israel.
- Galetto, F., (2020) Six Sigma_Hoax against Quality_Professionals Ignorance and MINITAB WRONG T Charts, HAL Archives Ouvert, 2020.
- Galetto, F., (2021) Control Charts for TBE and Quality Decisions, Academia.edu.
- Galetto F. (2021) ASSURE: Adopting Statistical Significance for Understanding Research and Engineering, Journal of Engineering and Applied Sciences Technology, ISSN: 2634 – 8853, 2021 SRC/JEAST-128. [CrossRef]
- Galetto F. (2023) Control Charts, Scientific Derivation of Control Limits and Average Run Length, International Journal of Latest Engineering Research and Applications (IJLERA) ISSN: 2455-7137 Volume – 08, Issue – 01, January 2023, PP – 11-45.
- Galetto, F., (2006) Quality Education and quality papers, IPSI, Marbella (Spain).
- Galetto, F., (2006) Quality Education versus Peer Review, IPSI, Montenegro.
- Galetto, F., (2006) Does Peer Review assure Quality of papers and Education? 8th Conference on TQM for HEI, Paisley (Scotland).
- Galetto, F., (1998), Quality Education on Quality for Future Managers, 1st Conference on TQM for HEI (Higher Education Institutions), Toulon (France).
- Galetto, F., (2000), Quality Education for Professors teaching Quality to Future Managers, 3rd Conference on TQM for HEI, Derby (UK).
- Galetto, F., (2001), Looking for Quality in "quality books", 4th Conference on TQM for HEI, Mons (Belgium).
- Galetto, F., (2001), Quality and Control Carts: Managerial assessment during Product Development and Production Process, AT&T (Society of Automotive Engineers), Barcelona (Spain).
- Galetto, F., (2001), Quality QFD and control charts, Conference ATA, Florence (Italy).
- Galetto, F., (2002), Business excellence Quality and Control Charts”, 7th TQM Conference, Verona (Italy).
- Galetto, F., (2002), Fuzzy Logic and Control Charts, 3rd ICME Conference, Ischia (Italy).
- Galetto, F., (2002), Analysis of "new" control charts for Quality assessment, 5th Conference on TQM for HEI, Lisbon (Portugal).
- Galetto, F., (2009), The Pentalogy, VIPSI, Belgrade (Serbia).
- Galetto, F., (2010),The Pentalogy Beyond, 9th Conference on TQM for HEI, Verona (Italy).
- Galetto, F., (2024), News on Control Charts for JMP, Academia.edu.
- Galetto, F., (2024), JMP and Minitab betray Quality, Academia.edu.
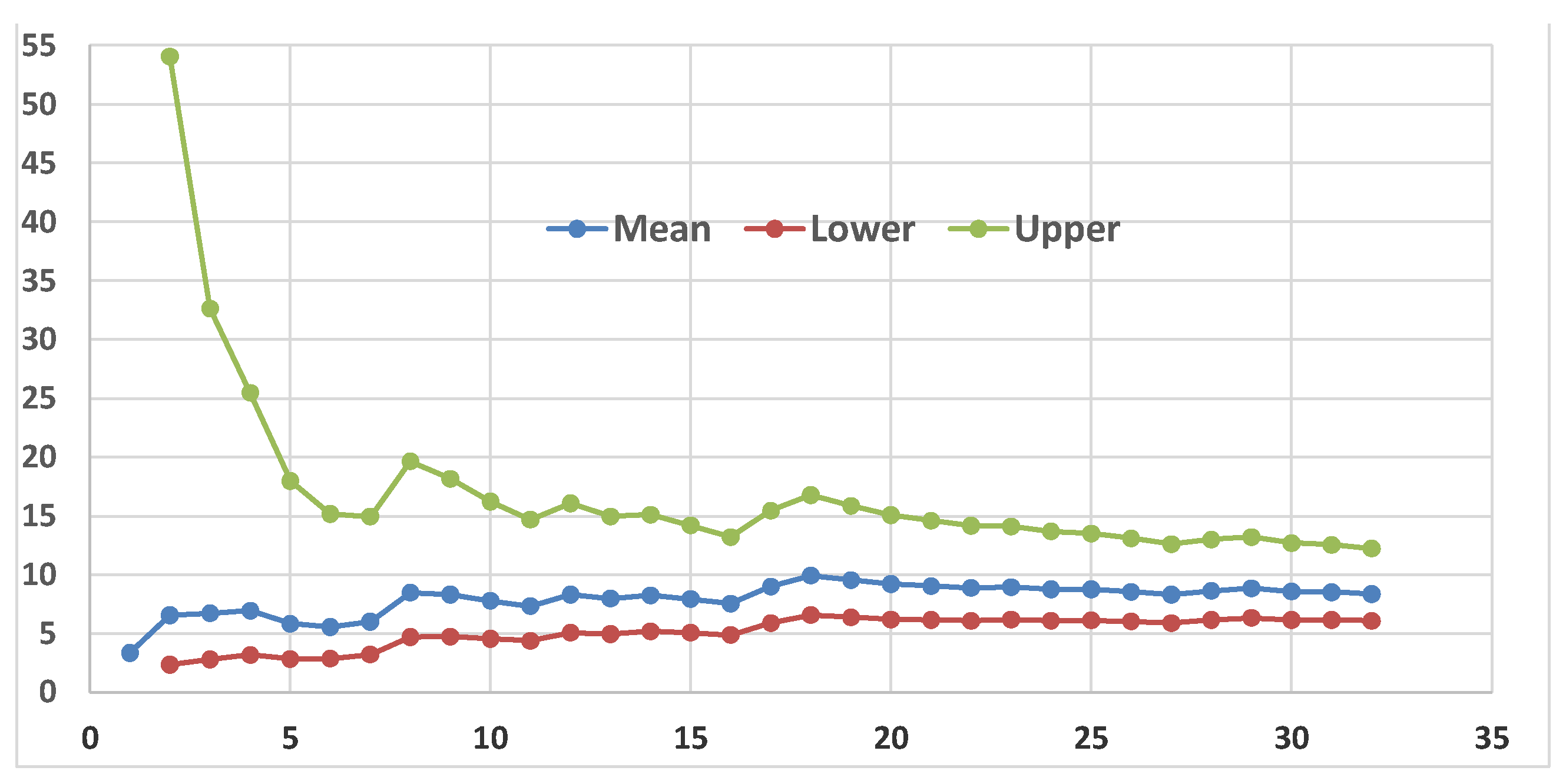
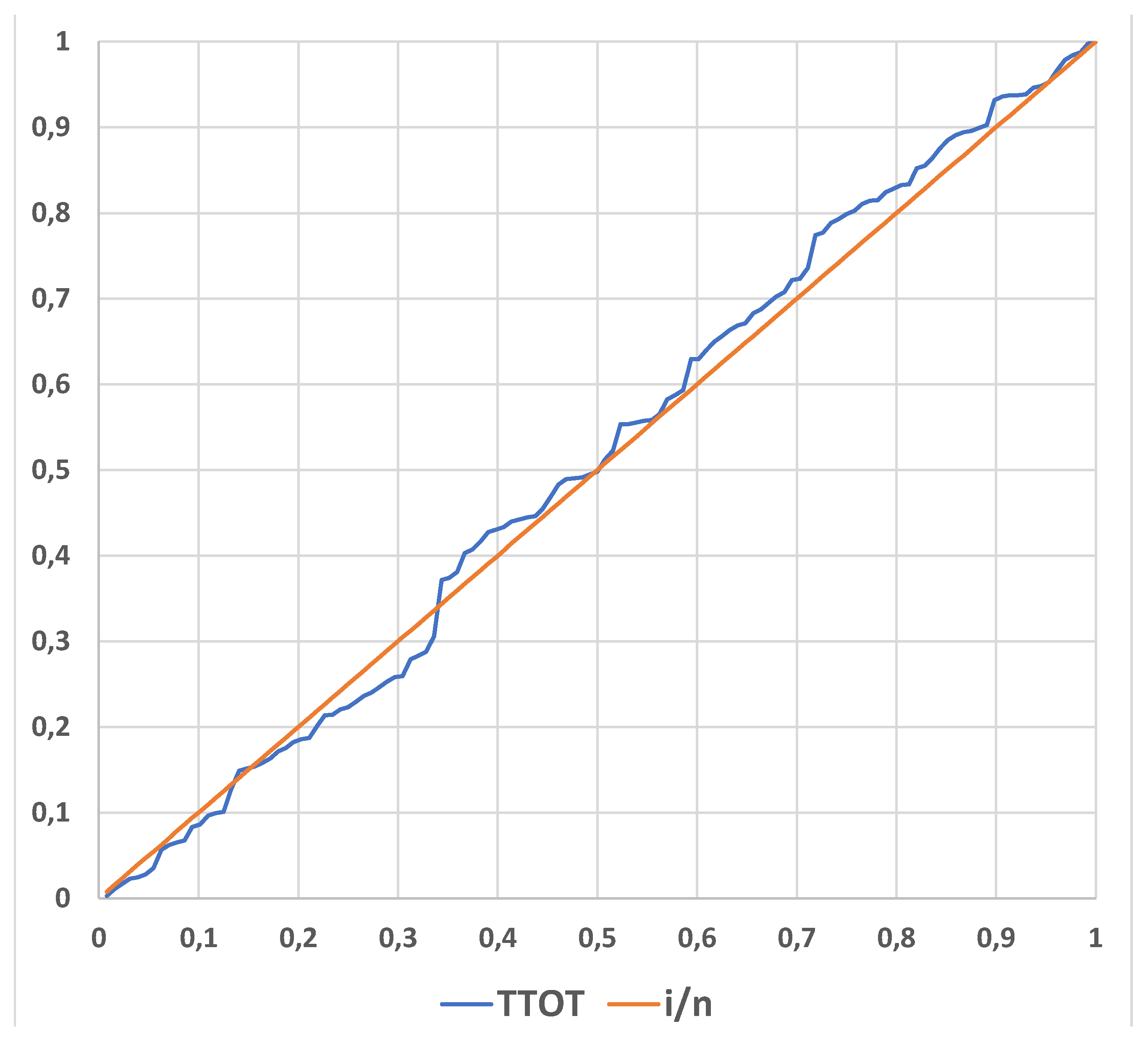
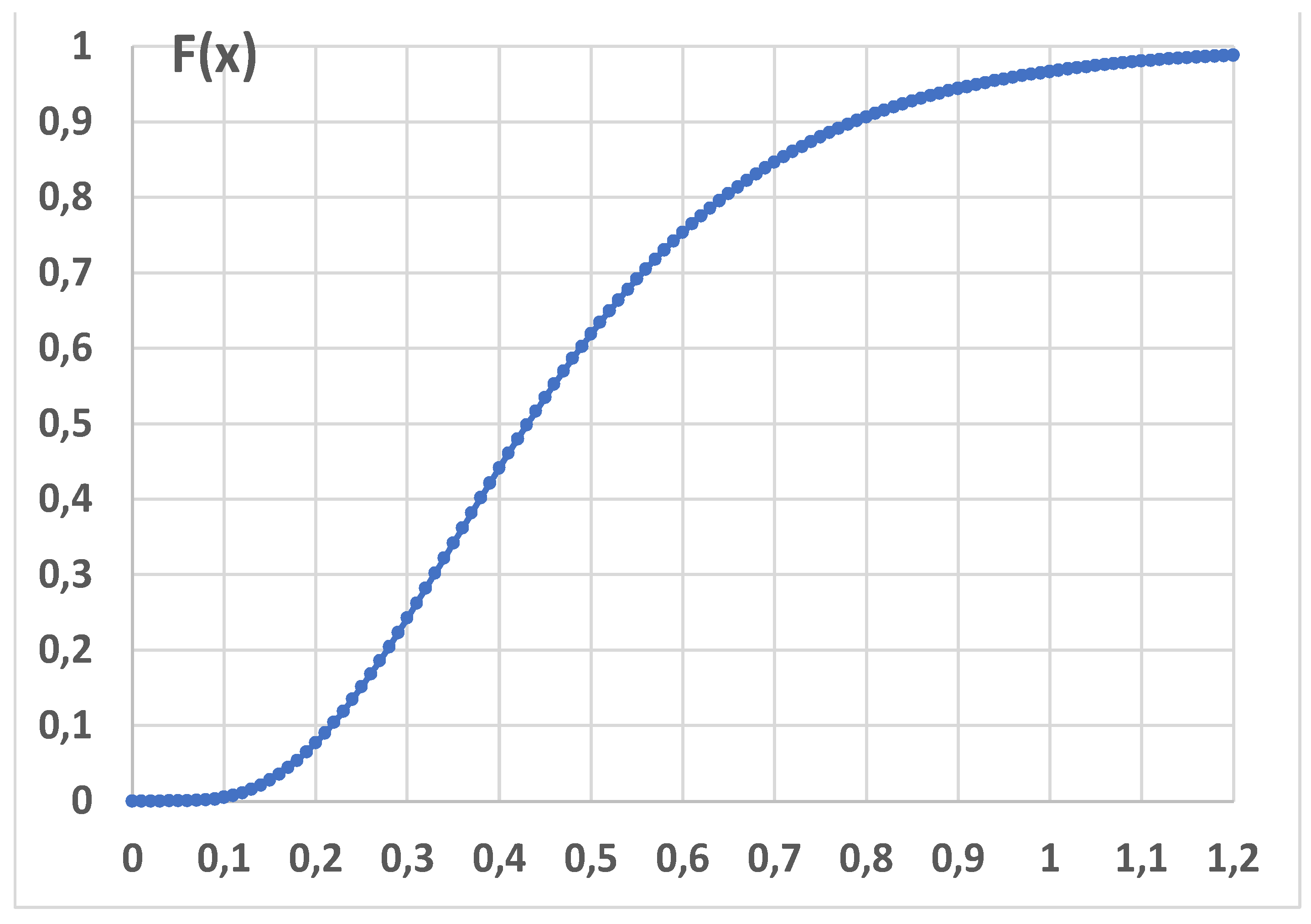
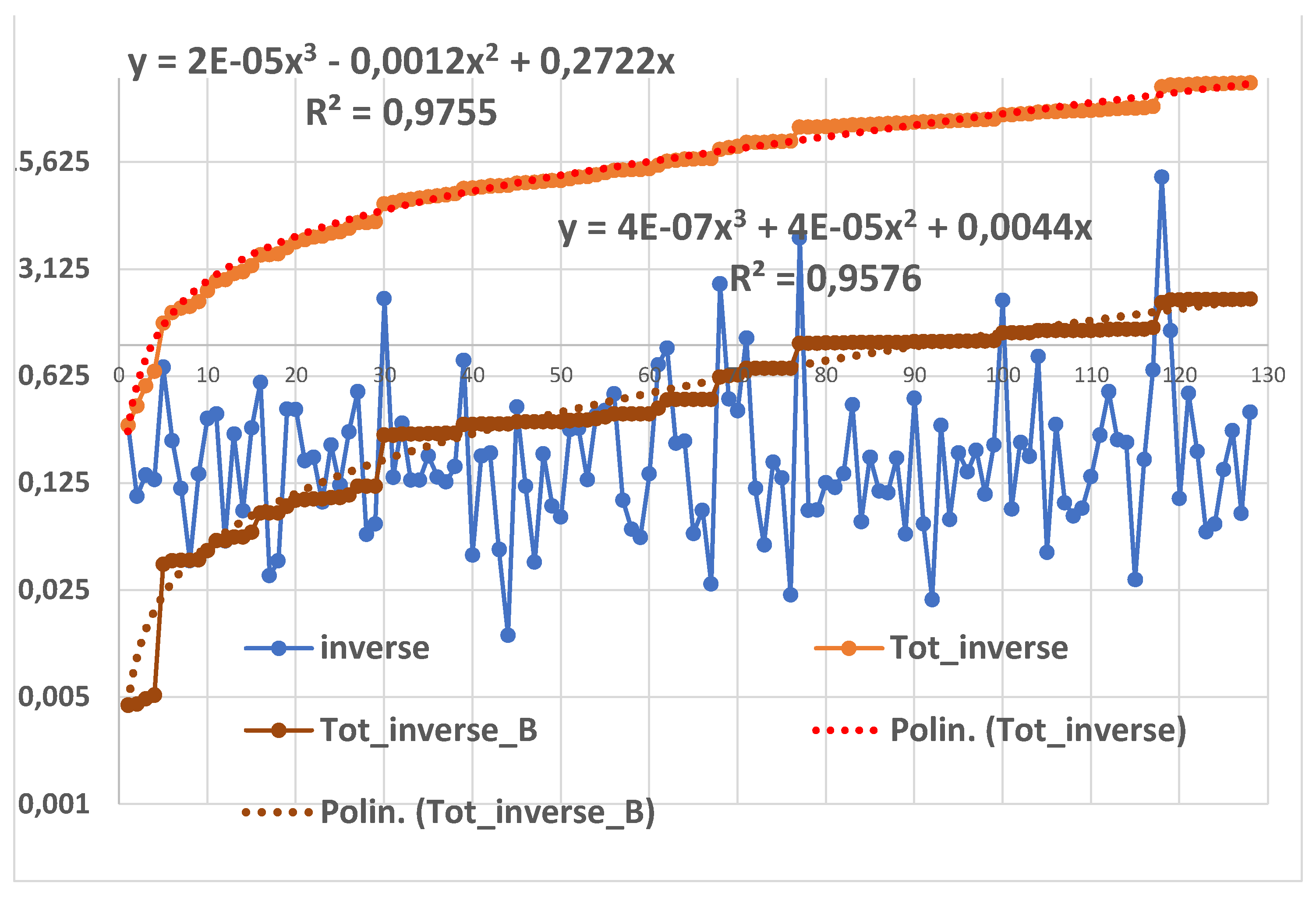
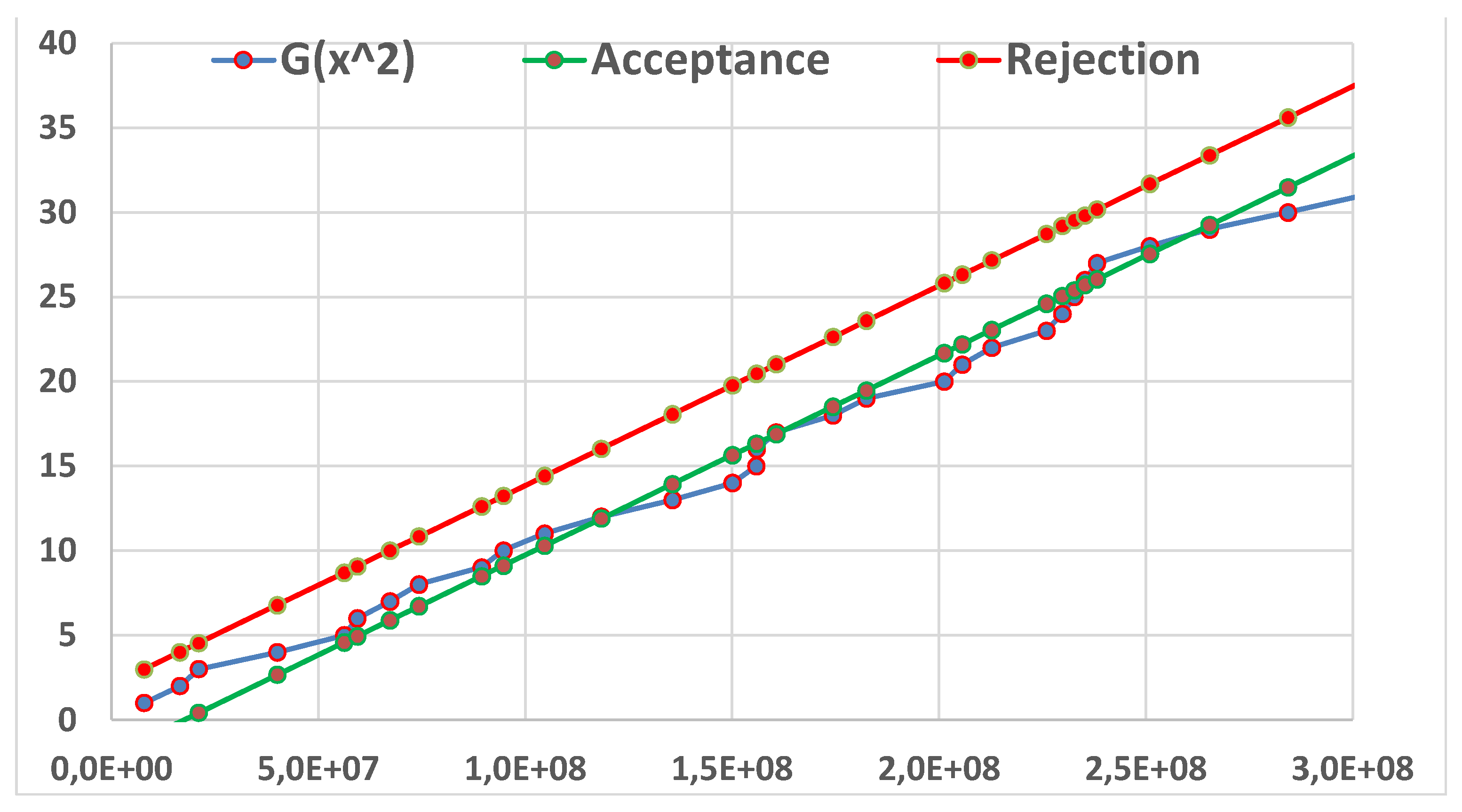
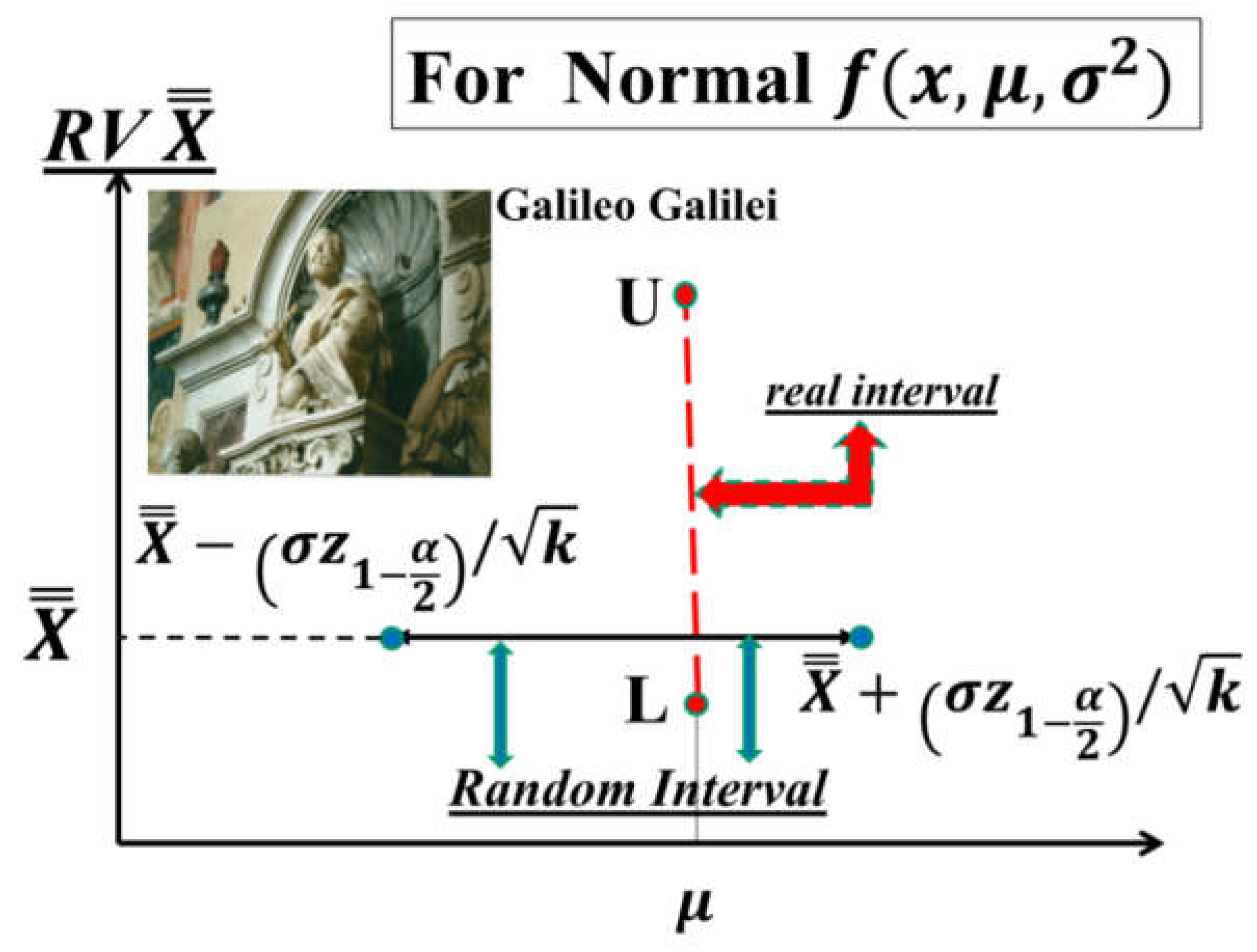

| Name | parameters | Symbol | |||
| Exponential | E(x|θ) | ||||
| Weibull | W(x|β,η) | ||||
| Inverted Weibull | IW(x|β,η) | ||||
| General Inverted W | GIW(x|β,η,ω) | ||||
| Maxwell | σ2 | MW(x|σ) | |||
| Normal | μ | σ2 | N(x|μ, σ2) | ||
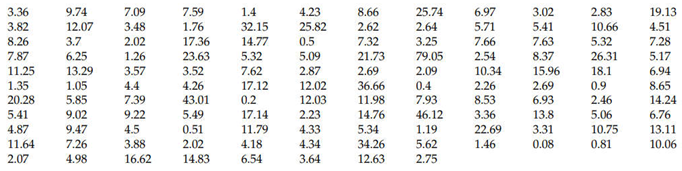 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).