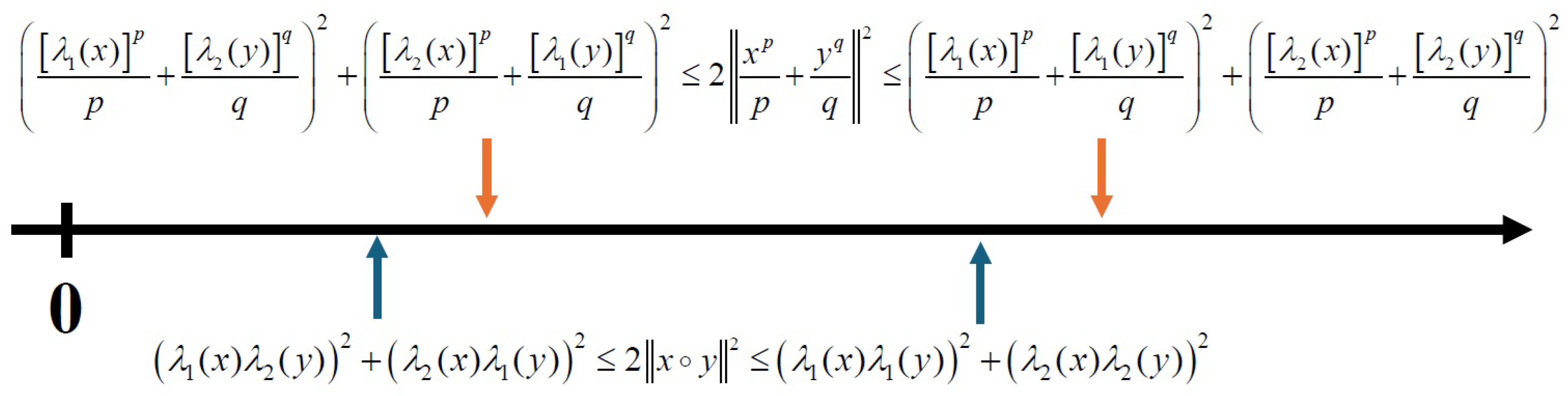Young and Inverse Young Inequalities on Euclidean Jordan Algebra

1. Introduction

Optimization theory primarily explores the existence of an optimal solution for an objective function under specific conditions and the methods for finding it. The content includes studying the conditions for the existence of the optimal solution and some related criteria and designing the corresponding algorithm to find the optimal solution. Now, we consider the following nonlinear symmetric cone programming (SCP):

$$\begin{array}{cc}min\hfill & f(x)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & x\in \mathcal{K},\hfill \end{array}$$

where $\mathbb{V}$ is a Euclidean Jordan algebra, $\mathcal{K}\subset \mathbb{V}$ denotes the associated symmetric cone of invertible squares, $f:\mathbb{V}\to \mathbb{R}\cup \{+\infty \}$ is a proper lower semicontinuous convex function. A popular approach to deal with SCP is the proximal point algorithm, which generates a sequence $\left\{x^n\right\}$ via the following iterative scheme:

$$x^{k+1}=\underset{x\in \mathcal{K}}{\arg \min }\{f(x)+{\lambda }_{k}D(x,x^k)\}.$$

Here, $D(·,·)$ is a certain function that satisfies some desirable properties and ${\left\{{\lambda }_k\right\}}_{k\in \mathbb{N}}$ a positive sequence. The choice of $D(·,·)$ is important, and several well-known examples $D(·,·)$ are the distances induced by the Euclidean norm, the Bregman distance, the proximal distance, the quasi-distance and the $\phi$ -divergence.

We recall that a distance function (or called metric) on a set X is a function $d:X\times X\to [0,\infty )$ satisfying that, for all $x,y,z\in X$,

$$\begin{array}{ccc}(\mathrm{D}1)\hfill & d(x,y)\ge 0;\hfill & \hfill (\mathrm{N}\mathrm{o}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e})\\ (\mathrm{D}2)\hfill & d(x,y)=0⟺x=y;\hfill & \hfill (\mathrm{I}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{s})\\ (\mathrm{D}3)\hfill & d(x,y)=d(y,x);\hfill & \hfill (\mathrm{S}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{y})\\ (\mathrm{D}4)\hfill & d(x,z)\le d(x,y)+d(y,z).\hfill & \hfill (\mathrm{T}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e} \mathrm{i}\mathrm{n}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y})\end{array}$$

There are several ways of relaxing the axioms of distance. For example, a semi-distance is defined as a function that satisfies all axioms for a distance with the possible exception of (D4). A quasi-distance is defined as a function that satisfies all axioms for a distance with the exception of (D3).

In the previous research, it can be observed that when an algorithm is designed to solve symmetric cone programming problems and investigate its convergence, it is essential to consider inequalities on symmetric cones. Most of these inequalities differ from those in real numbers. Due to the special algebraic structure, deriving inequalities analogous to fundamental ones in real numbers is not always feasible, such as the most fundamental arithmetic-geometric mean inequality and the Cauchy-Schwarz inequality, among others. Historically, the development of inequalities associated with symmetric cones has been mainly centered on matrix inequalities, as detailed in [1,2].

In fact, there are only a few known inequalities associated with second-order cones. For several years, one of our main research focuses on deriving inequalities associated with second-order cones, including defining the mean and weighted mean, and establishing trace inequalities associated with second-order cones. The main goal of this paper is to establish a series of results analogous to well-known inequalities in matrix analysis. So far, we have accumulated numerous studies on this topic; see [3,4,5,6,7,8].

In this paper, we derive various trace and norm inequalities related to second-order cones. Section 2 provides a review of fundamental concepts concerning symmetric cones, with a particular focus on second-order cones. In Section 3, we explore the Young and inverse Young inequalities associated with second-order cones. Finally, Section 4 discusses potential directions for future research.

Throughout this paper, we denote the n-dimensional Euclidean space endowed with the canonical inner product $\langle ·,·\rangle$ by ${\mathbb{R}}^n$, and the norm of x given by $\parallel x\parallel ={\langle x,x\rangle }^{\frac{1}{2}}$ is the Euclidean norm. In addition, for any nonempty subset K of ${\mathbb{R}}^n$, the interior of K is denoted by $\mathrm{int}(K)$, and the boundary of K is denoted by $\partial K$.

2. Preliminaries

In this section, we review some fundamental concepts and properties of Jordan algebras, as presented in [9] on symmetric cones and in [10,11,12] on second-order cones (Lorentz cones), which are essential for the subsequent analysis.

A Euclidean Jordan algebra is a finite-dimensional inner product space $(\mathbb{V},\langle ·,·\rangle )$ ($\mathbb{V}$ for short) over the field of real numbers $\mathbb{R}$ equipped with a bilinear map $(x,y)\mapsto x\circ y:\mathbb{V}\times \mathbb{V}\to \mathbb{V}$, which satisfies the following conditions:

(i)

$x\circ y=y\circ x$ for all $x,y\in \mathbb{V}$;

(ii)

$x\circ (x^2\circ y)=x^2\circ (x\circ y)$ for all $x,y\in \mathbb{V}$;

(iii)

$\langle x\circ y,z\rangle =\langle x,y\circ z\rangle$ for all $x,y,z\in \mathbb{V}$,

where $x^2:=x\circ x$, and $x\circ y$ is called the Jordan product of x and y. If a Jordan product only satisfies conditions (i) and (ii) in the above definition, the algebra $\mathbb{V}$ is said to be a Jordan algebra. If there is a (unique) element $e\in \mathbb{V}$ such that $x\circ e=x$ for all $x\in \mathbb{V}$, the element e is called the identity element in $\mathbb{V}$. Note that a Jordan algebra does not necessarily have an identity element. Throughout this paper, we assume that $\mathbb{V}$ is a Euclidean Jordan algebra with an identity element e.

In a given Euclidean Jordan algebra $\mathbb{V}$, the set of squares $\mathcal{K}:=\{x^2:x\in \mathbb{V}\}$ is a symmetric cone[9], TheoremIII.2.1. That is, $\mathcal{K}$ is a self-dual, closed convex cone, and homogeneous, which means that for any two elements $x,y\in \mathrm{int}(\mathcal{K})$, there exists an invertible linear transformation $\Gamma :\mathbb{V}\to \mathbb{V}$ such that $\Gamma (x)=y$ and $\Gamma (\mathcal{K})=\mathcal{K}$.

• An element $e^{(i)}\in \mathbb{V}$ is an idempotent if ${(e^{(i)})}^2=e^{(i)}$,
• An element is called a primitive idempotent if it is nonzero and cannot be written as a sum of two nonzero idempotents.
• The idempotents $e^{(i)}$ and $e^{(j)}$ are said to be orthogonal if $e^{(i)}\circ e^{(j)}=0$.

In addition, we say that a finite set $\{e^{(1)},e^{(2)},\cdots ,e^{(r)}\}$ of primitive idempotents in $\mathbb{V}$ is a Jordan frame if

$$e^{(i)}\circ e^{(j)}=0\mathrm{for}i\ne j,\mathrm{and}\sum _{i=1}^r{e}^{(i)}=e.$$

Note that $\langle e^{(i)},e^{(j)}\rangle =\langle e^{(i)}\circ e^{(j)},e\rangle =0$ whenever $i\ne j$. With the above definitions, there is the spectral decomposition of an element x in $\mathbb{V}$.

Theorem 1. 

[9], heoremIII.1.2 (The Spectral Decomposition Theorem) Let $\mathbb{V}$ be a Euclidean Jordan algebra. Then there is a number r such that, for every $x\in \mathbb{V}$, there exists a Jordan frame $\{e^{(1)},\cdots ,e^{(r)}\}$ and real numbers ${\lambda }_1(x),\cdots ,{\lambda }_r(x)$ with

$$x={\lambda }_1(x)e^{(1)}+\cdots +{\lambda }_r(x)e^{(r)}.$$

Here, the numbers ${\lambda }_i(x)$$(i=1,\cdots ,r)$ are called the eigenvalues of x, the expression ${\lambda }_1(x)e^{(1)}+\cdots +{\lambda }_r(x)e^{(r)}$ is called the spectral decomposition of x. Moreover, $\mathbf{tr}(x):={\sum }_{i=1}^r{\lambda }_i(x)$ is called the trace of x, and $det(x):={\lambda }_1(x){\lambda }_2(x)\cdots {\lambda }_r(x)$ is called the determinant of x.

The second-order cone (in short SOC), in ${\mathbb{R}}^n$ is an important example of symmetric cones, which is defined as follows:

$${\mathcal{K}}^n=\left\{x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}|x_1\ge \parallel x_2\parallel \right\}.$$

For $n=1$, ${\mathcal{K}}^n$ denotes the set of nonnegative real number ${\mathbb{R}}_{+}$. Since ${\mathcal{K}}^n$ is a pointed closed convex cone, for any $x,y$ in ${\mathbb{R}}^n$, we define a partial order on it:

$$\begin{array}{ccc}\hfill x{⪯}_{{\mathcal{K}}^n}y& ⟺& y-x\in {\mathcal{K}}^n;\hfill \\ \hfill x{\prec }_{{\mathcal{K}}^n}y& ⟺& y-x\in \mathrm{int}({\mathcal{K}}^n).\hfill \end{array}$$

Note that the relation ${⪯}_{{\mathcal{K}}^n}$ (or ${\prec }_{{\mathcal{K}}^n}$) is only a partial ordering, not a linear ordering in ${\mathcal{K}}^n$. To see this, a counterexample occurs by taking $x=(1,1)$ and $y=(1,0)$ in ${\mathbb{R}}^2$. It is clear to see that $x-y=(0,1)\notin {\mathcal{K}}^2$, $y-x=(0,-1)\notin {\mathcal{K}}^2$. For any $x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$ and $y=(y_1,y_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$, we define the Jordan product as

$$x\circ y=\left(x^{T}y,y_1{x}_2+x_1{y}_2\right).$$

We note that $e=(1,0)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$ acts as the Jordan identity. Besides, the Jordan product is not associative in general. However, it is power associative, i.e., $x\circ (x\circ x)=(x\circ x)\circ x$ for all $x\in {\mathbb{R}}^n$. Without loss of ambiguity, we may denote $x^m$ for the product of m copies of x and $x^{m+n}=x^m\circ x^n$ for any positive integers m and n. Here, we set $x^0=e$. In addition, ${\mathcal{K}}^n$ is not closed under Jordan product.

Given any $x\in {\mathcal{K}}^n$, it is known that there exists a unique vector in ${\mathcal{K}}^n$ denoted by $x^{\frac{1}{2}}$ such that ${(x^{\frac{1}{2}})}^2=x^{\frac{1}{2}}\circ x^{\frac{1}{2}}=x$. Indeed,

$$x^{\frac{1}{2}}=\left(s,\frac{x_2}{2s}\right),\mathrm{where}s=\sqrt{\frac{1}{2}\left(x_1+\sqrt{x_1^2-{\parallel x_2\parallel }^2}\right)}.$$

In the above formula, the term $x_2/s$ is defined to be the zero vector if $s=0$, i.e., $x=0$. For any $x\in {\mathbb{R}}^n$, we always have $x^2\in {\mathcal{K}}^n$, i.e., $x^2{⪰}_{{\mathcal{K}}^n}0$. Hence, there exists a unique vector ${(x^2)}^{\frac{1}{2}}\in {\mathcal{K}}^n$ denoted by $\left|x\right|$. It is easy to verify that $\left|x\right|{⪰}_{{\mathcal{K}}^n}0$ and $x^2={\left|x\right|}^2$ for any $x\in {\mathbb{R}}^n$. It is also known that $\left|x\right|{⪰}_{{\mathcal{K}}^n}x$. For more details, please refer to [9,13].

In the setting of second-order cone in ${\mathbb{R}}^n$, the vector $x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$ can be decomposed as

$$x={\lambda }_1(x)u_x^{(1)}+{\lambda }_2(x)u_x^{(2)},$$

(1)

where ${\lambda }_1(x),{\lambda }_2(x)$ and $u_x^{(1)},u_x^{(2)}$ are the eigenvalues (or spectral values) and the associated eigenvectors (or spectral vectors) of x, respectively, given by

$${\lambda }_i(x)=x_1+{(-1)}^i\parallel x_2\parallel ,$$

(2)

$$u_x^{(i)}=\left\{\begin{array}{ccc}\frac{1}{2}\left(1,{(-1)}^i\frac{x_2}{\parallel x_2\parallel }\right)\hfill & \mathrm{if}\hfill & x_2\ne 0,\hfill \\ \frac{1}{2}\left(1,{(-1)}^i\overline{v}\right)\hfill & \mathrm{if}\hfill & x_2=0.\hfill \end{array}\right.$$

(3)

for $i=1,2$ with $\overline{v}$ being any vector in ${\mathbb{R}}^{n-1}$ satisfying $\parallel \overline{v}\parallel =1$. The decomposition is unique if $x_2\ne 0$. Accordingly, the determinant, the trace, and the Euclidean norm of x can all be represented in terms of ${\lambda }_1(x)$ and ${\lambda }_2(x)$:

$$\begin{array}{ccc}\hfill det(x)& =& {\lambda }_1(x){\lambda }_2(x)=x_1^2-{\parallel x_2\parallel }^2,\hfill \\ \hfill \mathbf{tr}(x)& =& {\lambda }_1(x)+{\lambda }_2(x)=2x_1,\hfill \\ \hfill {\parallel x\parallel }^2& =& \frac{1}{2}\left({\lambda }_1{(x)}^2+{\lambda }_2{(x)}^2\right).\hfill \end{array}$$

For any function $f:\mathbb{R}\to \mathbb{R}$, the following vector-valued function associated with ${\mathcal{K}}^n$ ($n\ge 1$) was considered in [10,11]:

$$f^{\mathrm{soc}}(x)=f({\lambda }_1(x))u_x^{(1)}+f({\lambda }_2(x))u_x^{(2)},\forall x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}.$$

(4)

If f is defined only on a subset of $\mathbb{R}$, then $f^{\mathrm{soc}}$ is defined on the corresponding subset of ${\mathbb{R}}^n$. The definition (4) is unambiguous whether $x_2\ne 0$ or $x_2=0$. The cases of $f^{\mathrm{soc}}(x)=x^{\frac{1}{2}}$, $x^2$, $exp(x)$ are discussed in [9]. Let m be any real number and $x\in {\mathcal{K}}^n$, we could define the $m^{th}$ power of x as

$$x^m={\left({\lambda }_1(x)\right)}^m{u}_x^{(1)}+{\left({\lambda }_2(x)\right)}^m{u}_x^{(2)}.$$

With this definition, we can explore the properties of the Young inequality associated with second-order cones.

In a Euclidean Jordan algebra $\mathbb{V}$, for any $x\in \mathbb{V}$, the linear transformation $L(x):\mathbb{V}\to \mathbb{V}$ is called Lyapunov transformation, which is defined as $L(x)y:=x\circ y$ for all $y\in \mathbb{V}$. The so-called quadratic representation $P(x)$ is defined by

$$P(x):=2L^2(x)-L(x^2).$$

For any $x\in \mathbb{V}$, the endomorphisms $L(x)$ and $P(x)$ are self-adjoint. We say that two elements x and y of a Euclidean Jordan algebra $\mathbb{V}$operator commute if $x\circ (y\circ z)=y\circ (x\circ z)$ for all $z\in \mathbb{V}$, which is equivalent to stating that $L(x)L(y)=L(y)L(x)$. For the quadratic representation $P(x)$, if x is invertible, then $P(x)$ is invertible with $P{(x)}^{-1}=P(x^{-1})$ and

$$P(x)\mathcal{K}=\mathcal{K}\mathrm{and}P(x)\mathrm{int}(\mathcal{K})=\mathrm{int}(\mathcal{K}).$$

To close this section, we summarize some fundamental properties as follows. The proofs are omitted because they can be found in [9,10,13].

Lemma 1. 

For any $x,y\in {\mathbb{R}}^n$ with spectral decomposition given as in (1)-(3), the following hold.

(a) 

$\left|x\right|=|{\lambda }_1(x)|u_x^{(1)}+\left|{\lambda }_2(x)\right|u_x^{(2)}$;

(b) 

If $x{⪯}_{{\mathcal{K}}^n}y$, then ${\lambda }_i(x)\le {\lambda }_i(y)$ for all $i=1,2$.

(c) 

$\mathbf{tr}(\alpha x+\beta y)=\alpha \mathbf{tr}(x)+\beta \mathbf{tr}(y)$.

(d) 

${\lambda }_1(x){\lambda }_2(y)+{\lambda }_1(y){\lambda }_2(x)\le \mathbf{tr}(x\circ y)\le {\lambda }_1(x){\lambda }_1(y)+{\lambda }_2(x){\lambda }_2(y)$.

Lemma 2. 

For any $x,y\in {\mathcal{K}}^n$ with spectral decomposition given as in (1)-(3), the following results hold.

(a) 

$x^{\frac{1}{2}}=\sqrt{{\lambda }_1(x)}{u}_x^{(1)}+\sqrt{{\lambda }_2(x)}{u}_x^{(2)}$ whenever $x\in {\mathcal{K}}^n$.

(b) 

$det(x\circ y)\le det(x)det(y)$.

3. Young Inequality and Inverse Young Inequality

Suppose that $a,b\ge 0$ and $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$, the Young inequality states that

$$ab\le \frac{a^p}{p}+\frac{b^q}{q}.$$

In 1995, Ando [14] showed the singular value version of Young inequality that

$$s_j(AB)\le s_j\left(\frac{A^p}{p}+\frac{B^q}{q}\right)\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} 1\le j\le n,$$

where A and B are positive definite matrices. Huang, Chen, and Hu[7] propose some trace version of Young inequality associated with second-order cones. The authors conjectured the existence of an eigenvalue version of the Young inequality.

Conjecture 1. 

For any $x,y\in {\mathcal{K}}^n$, there holds

$${\lambda }_j(x\circ y)\le {\lambda }_j\left(\frac{x^p}{p}+\frac{y^q}{q}\right),j=1,2.$$

Recently, Huang et al. [8] establish that the Young inequality under the partial order

$$x\circ y{⪯}_{{\mathcal{K}}^n}\frac{x^p}{p}+\frac{y^q}{q}$$

holds if x and y share the same Jordan frame. Furthermore, it deduces the trace, determinant, and norm version of Young inequalities.

In the following, for any $x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$ and $y=(y_1,y_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$, we may assume that $x_2\ne \mathbf{0}$, $y_2\ne \mathbf{0}$. In fact, x and y will share the same Jordan frame if $x_2=\mathbf{0}$ or $y_2=\mathbf{0}$. We first illustrate some inequalities of eigenvalue associated with second-order cones, and establish the condition that the equality holds.

Lemma 3. 

For any $x,y\in {\mathbb{R}}^n$, the followings hold

(a) 

${\lambda }_1(x)+{\lambda }_1(y)\le {\lambda }_1(x+y)\le min\left\{{\lambda }_1(x)+{\lambda }_2(y),{\lambda }_2(x)+{\lambda }_1(y)\right\}$.

(b) 

$max\left\{{\lambda }_1(x)+{\lambda }_2(y),{\lambda }_2(x)+{\lambda }_1(y)\right\}\le {\lambda }_2(x+y)\le {\lambda }_2(x)+{\lambda }_2(y)$.

Proof. 

For any $x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$ and $y=(y_1,y_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$, we note

$$\begin{array}{ccc}\hfill {\lambda }_1(x+y)& =& x_1+y_1-\parallel x_2+y_2\parallel ,\hfill \\ \hfill {\lambda }_2(x+y)& =& x_1+y_1+\parallel x_2+y_2\parallel .\hfill \end{array}$$

(a) It is known that by triangle inequality of norm, we have

$$\left|\parallel x_2\parallel -\parallel y_2\parallel \right|\le \parallel x_2+y_2\parallel \le \parallel x_2\parallel +\parallel y_2\parallel .$$

Hence, we obtain

$$\begin{array}{ccc}\hfill {\lambda }_1(x+y)& \ge & x_1-\parallel x_2\parallel +y_1-\parallel y_2\parallel ={\lambda }_1(x)+{\lambda }_1(y),\hfill \\ \hfill {\lambda }_1(x+y)& \le & x_1+y_1-|\parallel x_2\parallel -\parallel y_2\parallel |=min\left\{{\lambda }_1(x)+{\lambda }_2(y),{\lambda }_2(x)+{\lambda }_1(y)\right\}.\hfill \end{array}$$

(b) Similarly, the desired inequality follows by

$$\begin{array}{ccc}\hfill {\lambda }_2(x+y)& \le & x_1+\parallel x_2\parallel +y_1+\parallel y_2\parallel ={\lambda }_2(x)+{\lambda }_2(y),\hfill \\ \hfill {\lambda }_2(x+y)& \ge & x_1+y_1+|\parallel x_2\parallel -\parallel y_2\parallel |=max\left\{{\lambda }_1(x)+{\lambda }_2(y),{\lambda }_2(x)+{\lambda }_1(y)\right\}.\hfill \end{array}$$

We complete the proof. □

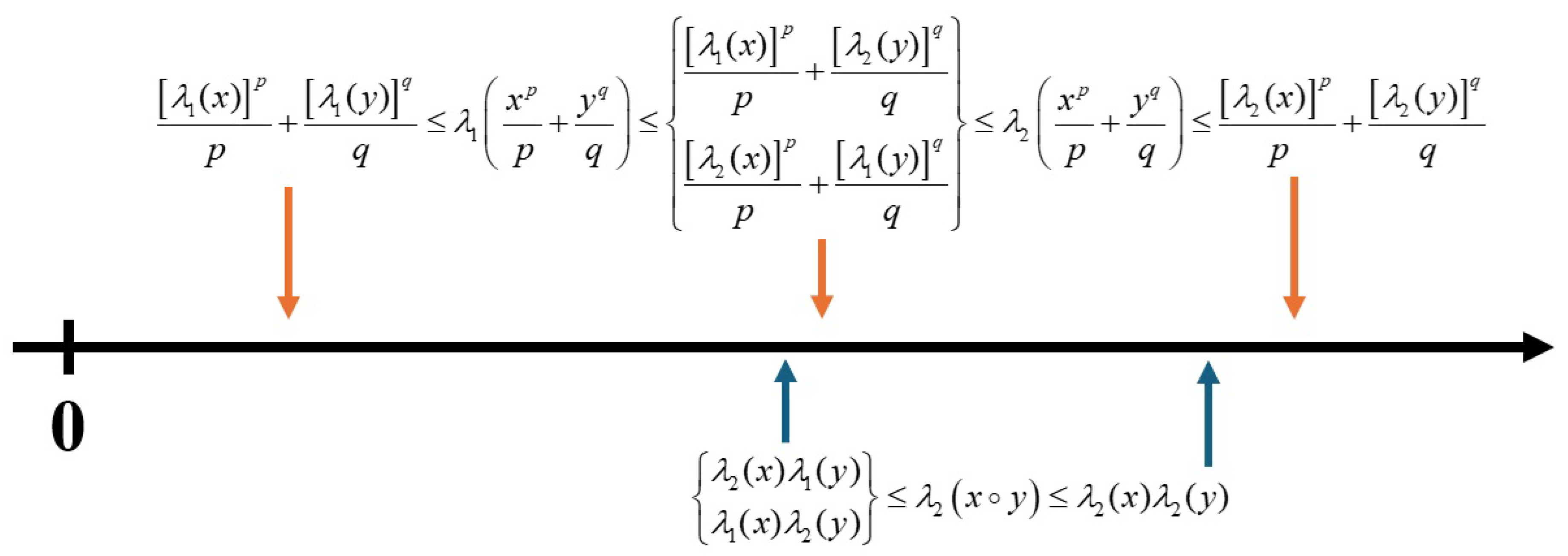
Proposition 1. 

For any $x,y\in {\mathcal{K}}^n$, $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$, the followings hold

(a) 

$\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\le {\lambda }_1\left(\frac{x^p}{p}+\frac{y^q}{q}\right)\le min\left\{\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q},\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right\}.$

(b) 

$max\left\{\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q},\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right\}\le {\lambda }_2\left(\frac{x^p}{p}+\frac{y^q}{q}\right)\le \frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}.$

Proof. 

According to the decomposition of $x,y$, it is clear that

$$\begin{array}{ccc}& & {\lambda }_1\left(\frac{x^p}{p}\right)=\frac{{\left[{\lambda }_1(x)\right]}^p}{p},{\lambda }_2\left(\frac{x^p}{p}\right)=\frac{{\left[{\lambda }_2(x)\right]}^p}{p},\hfill \\ & & {\lambda }_1\left(\frac{y^q}{q}\right)=\frac{{\left[{\lambda }_1(y)\right]}^q}{q},{\lambda }_2\left(\frac{y^q}{q}\right)=\frac{{\left[{\lambda }_2(y)\right]}^q}{q},\hfill \end{array}$$

since p, q are positive and ${\lambda }_j(x),{\lambda }_j(y)\ge 0$ for $j=1,2$.

(a) It follows by Lemma 3 that

$$\begin{array}{ccc}\hfill {\lambda }_1\left(\frac{x^p}{p}+\frac{y^q}{q}\right)& \ge & {\lambda }_1\left(\frac{x^p}{p}\right)+{\lambda }_1\left(\frac{y^q}{q}\right)=\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q},\hfill \\ \hfill {\lambda }_1\left(\frac{x^p}{p}+\frac{y^q}{q}\right)& \le & min\left\{{\lambda }_1\left(\frac{x^p}{p}\right)+{\lambda }_2\left(\frac{y^q}{q}\right),{\lambda }_2\left(\frac{x^p}{p}\right)+{\lambda }_1\left(\frac{y^q}{q}\right)\right\}\hfill \\ & =& min\left\{\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q},\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right\}.\hfill \end{array}$$

(b) Similarly, the desired inequality follows by

$$\begin{array}{ccc}\hfill {\lambda }_2\left(\frac{x^p}{p}+\frac{y^q}{q}\right)& \le & {\lambda }_2\left(\frac{x^p}{p}\right)+{\lambda }_2\left(\frac{y^q}{q}\right)=\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q},\hfill \\ \hfill {\lambda }_2\left(\frac{x^p}{p}+\frac{y^q}{q}\right)& \ge & max\left\{{\lambda }_1\left(\frac{x^p}{p}\right)+{\lambda }_2\left(\frac{y^q}{q}\right),{\lambda }_2\left(\frac{x^p}{p}\right)+{\lambda }_1\left(\frac{y^q}{q}\right)\right\}\hfill \\ & =& max\left\{\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q},\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right\}.\hfill \end{array}$$

The proof is complete. □

Proposition 2. 

For any $x,y\in {\mathcal{K}}^n$, there holds

$$max\left\{{\lambda }_1(x){\lambda }_2(y),{\lambda }_2(x){\lambda }_1(y)\right\}\le {\lambda }_2(x\circ y)\le {\lambda }_2(x){\lambda }_2(y).$$

Proof. 

We note that

$$\begin{array}{ccc}\hfill x\circ y& =& \left(x_1{y}_1+x_2^T{y}_2,x_1{y}_2+y_1{x}_2\right),\hfill \\ \hfill {\lambda }_2(x\circ y)& =& x_1{y}_1+x_2^T{y}_2+\parallel x_1{y}_2+y_1{x}_2\parallel .\hfill \end{array}$$

Then, the result follows by

$$\begin{array}{ccc}& & max\left\{{\lambda }_1(x){\lambda }_2(y),{\lambda }_2(x){\lambda }_1(y)\right\}\hfill \\ & =& x_1{y}_1-\parallel x_2\parallel ·\parallel y_2\parallel -|x_1\parallel y_2\parallel -y_1\parallel x_2\parallel |\hfill \\ & \le & x_1{y}_1+x_2^T{y}_2+\parallel x_1{y}_2+y_1{x}_2\parallel \hfill \\ & \le & x_1{y}_1+\parallel x_2\parallel ·\parallel y_2\parallel +x_1\parallel y_2\parallel +y_1\parallel x_2\parallel \hfill \\ & =& {\lambda }_2(x){\lambda }_2(y),\hfill \end{array}$$

where the inequalities hold by triangle inequality and Schwarz inequality. □

Remark 1. 

Based on Proposition 1-2, for $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$, we can establish a picture of the ordered relationship between the eigenvalues of x, y, $x\circ y$, $\frac{x^p}{p}+\frac{y^q}{q}$ as depicted in Figure 1. However, we have no results regarding the relationship between ${\lambda }_1(x\circ y)$ and ${\lambda }_1(x){\lambda }_1(y)$. In fact, $x\circ y$ does not always belong to ${\mathcal{K}}^n$ even if $x,y\in {\mathcal{K}}^n$. That is, it is possible that ${\lambda }_1(x\circ y)\le {\lambda }_1(x){\lambda }_1(y)$.

Proposition 3. 

For any $x,y\in {\mathcal{K}}^n$, $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$, there holds

$$\begin{array}{ccc}& & \left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)\hfill \\ & \le & det\left(\frac{x^p}{p}+\frac{y^q}{q}\right)\hfill \\ & \le & \left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right).\hfill \end{array}$$

Proof. 

First, we write $\frac{x^p}{p}+\frac{y^q}{q}=(w_1,w_2)$, where

$$\begin{array}{cc}\hfill w_1& =\frac{{\left[{\lambda }_2(x)\right]}^p+{\left[{\lambda }_1(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_2(y)\right]}^q+{\left[{\lambda }_1(y)\right]}^q}{2q},\hfill \\ \hfill w_2& =\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}\frac{x_2}{\parallel x_2\parallel }+\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\frac{y_2}{\parallel y_2\parallel }.\hfill \end{array}$$

(5)

By triangle inequality of norm, it implies that

$$\begin{array}{ccc}& & {\left(\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}-\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & \le & \parallel w_2{\parallel }^2\hfill \\ & \le & {\left(\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2.\hfill \end{array}$$

Then, the first inequality follows by

$$\begin{array}{ccc}& & det\left(\frac{x^p}{p}+\frac{y^q}{q}\right)\hfill \\ & \ge & {\left(\frac{{\left[{\lambda }_1(x)\right]}^p+{\left[{\lambda }_2(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_1(y)\right]}^q+{\left[{\lambda }_2(y)\right]}^q}{2q}\right)}^2\hfill \\ & & -{\left(\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & =& \frac{4{\left[{\lambda }_1(x)\right]}^p{\left[{\lambda }_2(x)\right]}^p}{4p^2}+\frac{4{\left[{\lambda }_1(y)\right]}^q{\left[{\lambda }_2(y)\right]}^q}{4q^2}+\frac{4{\left[{\lambda }_1(x)\right]}^p{\left[{\lambda }_2(y)\right]}^q+4{\left[{\lambda }_2(x)\right]}^p{\left[{\lambda }_1(y)\right]}^q}{4pq}\hfill \\ & =& \left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right).\hfill \end{array}$$

Similarly, the second inequality holds since

$$\begin{array}{ccc}& & det\left(\frac{x^p}{p}+\frac{y^q}{q}\right)\hfill \\ & \le & {\left(\frac{{\left[{\lambda }_1(x)\right]}^p+{\left[{\lambda }_2(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_1(y)\right]}^q+{\left[{\lambda }_2(y)\right]}^q}{2q}\right)}^2\hfill \\ & & -{\left(\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}-\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & =& \frac{4{\left[{\lambda }_1(x)\right]}^p{\left[{\lambda }_2(x)\right]}^p}{4p^2}+\frac{4{\left[{\lambda }_1(y)\right]}^q{\left[{\lambda }_2(y)\right]}^q}{4q^2}+\frac{4{\left[{\lambda }_1(x)\right]}^p{\left[{\lambda }_1(y)\right]}^q+4{\left[{\lambda }_2(x)\right]}^p{\left[{\lambda }_2(y)\right]}^q}{4pq}\hfill \\ & =& \left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right).\hfill \end{array}$$

Therefore, we conclude the desired inequalities. □

Remark 2. 

According to Lemma 2(b) and the classical Young inequality for real numbers, we can obtain the determinant version of Young inequality in the setting of second-order cone, that is, for $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$,

$$\begin{array}{ccc}\hfill det(x\circ y)& \le & det(x)det(y)\hfill \\ & =& {\lambda }_1(x){\lambda }_2(x){\lambda }_1(y){\lambda }_2(y)\hfill \\ & \le & \left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)\hfill \\ & \le & det\left(\frac{x^p}{p}+\frac{y^q}{q}\right).\hfill \end{array}$$

In fact, Huanget al.[4] establish the determinant version of Young inequality based on the SOC weighted mean inequality. However, we obtain a refined inequality by direct computation.

Proposition 4. 

For any $x,y\in {\mathcal{K}}^n$, $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$, the following holds

$$\begin{array}{ccc}& & {\left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)}^2+{\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)}^2\hfill \\ & \le & 2{∥\frac{x^p}{p}+\frac{y^q}{q}∥}^2\hfill \\ & \le & {\left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)}^2+{\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)}^2.\hfill \end{array}$$

Proof. 

Let $\frac{x^p}{p}+\frac{y^q}{q}$ be expressed as in (5). Thus, we have

$$\begin{array}{ccc}\hfill 2{∥\frac{x^p}{p}+\frac{y^q}{q}∥}^2& =& 2\left(w_1^2+{\parallel w_2\parallel }^2\right)\hfill \\ & \le & 2{\left(\frac{{\left[{\lambda }_2(x)\right]}^p+{\left[{\lambda }_1(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_2(y)\right]}^q+{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & & +2{\left(\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & =& {\left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)}^2+{\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)}^2.\hfill \end{array}$$

Similarly, the other inequality follows by

$$\begin{array}{ccc}\hfill 2{∥\frac{x^p}{p}+\frac{y^q}{q}∥}^2& \ge & 2{\left(\frac{{\left[{\lambda }_2(x)\right]}^p+{\left[{\lambda }_1(x)\right]}^p}{2p}+\frac{{\left[{\lambda }_2(y)\right]}^q+{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & & +2{\left(\frac{{\left[{\lambda }_2(x)\right]}^p-{\left[{\lambda }_1(x)\right]}^p}{2p}-\frac{{\left[{\lambda }_2(y)\right]}^q-{\left[{\lambda }_1(y)\right]}^q}{2q}\right)}^2\hfill \\ & =& {\left(\frac{{\left[{\lambda }_1(x)\right]}^p}{p}+\frac{{\left[{\lambda }_2(y)\right]}^q}{q}\right)}^2+{\left(\frac{{\left[{\lambda }_2(x)\right]}^p}{p}+\frac{{\left[{\lambda }_1(y)\right]}^q}{q}\right)}^2.\hfill \end{array}$$

We conclude the desired result. □

Proposition 5. 

For any $x,y\in {\mathcal{K}}^n$, the following holds

$${\left({\lambda }_1(x){\lambda }_2(y)\right)}^2+{\left({\lambda }_2(x){\lambda }_1(y)\right)}^2\le 2{∥x\circ y∥}^2\le {\left({\lambda }_1(x){\lambda }_1(y)\right)}^2+{\left({\lambda }_2(x){\lambda }_2(y)\right)}^2$$

Proof. 

Suppose that $x=(x_1,x_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$ and $y=(y_1,y_2)\in \mathbb{R}\times {\mathbb{R}}^{n-1}$. It is evident that the inequalities hold if $x_2=\mathbf{0}$ or $y_2=\mathbf{0}$. In fact, the equality will hold if $x_2=\mathbf{0}$ or $y_2=\mathbf{0}$. We assume that $x_2\ne \mathbf{0}$, $y_2\ne \mathbf{0}$, which imply $x_1>0$ and $y_1>0$. Then,

$$\begin{array}{ccc}\hfill {∥x\circ y∥}^2& =& {(x_1{y}_1+x_2^T{y}_2)}^2+{\parallel x_1{y}_2+y_1{x}_2\parallel }^2\hfill \\ & =& x_1^2{y}_1^2+{(x_2^T{y}_2)}^2+x_1^2\parallel y_2{\parallel }^2+y_1^2{\parallel x_2\parallel }^2+4x_1{y}_1{x}_2^T{y}_2\hfill \\ & =& x_1^2{y}_1^2+\parallel x_2{\parallel }^2\parallel y_2{\parallel }^2{cos}^2\theta +x_1^2\parallel y_2{\parallel }^2+y_1^2\parallel x_2{\parallel }^2+4x_1{y}_1\parallel x_2\parallel \parallel y_2\parallel cos\theta ,\hfill \end{array}$$

where $\theta$ is the angle between $x_2$ and $y_2$ in ${\mathbb{R}}^{n-1}$. We notice that the value of $2{∥x\circ y∥}^2$ is determined by $\theta$ if $x_1$, $y_1$, $\parallel x_2\parallel$, $\parallel y_2\parallel$ are fixed. Let $f:[0,\pi ]\to \mathbb{R}$ be defined by

$$f(\theta )=\parallel x_2{\parallel }^2\parallel y_2{\parallel }^2{cos}^2\theta +4x_1{y}_1\parallel x_2\parallel \parallel y_2\parallel cos\theta .$$

The derivative of f is

$$\begin{array}{ccc}\hfill f^{\prime }(\theta )& =& -2\parallel x_2{\parallel }^2\parallel y_2{\parallel }^{2}cos\theta sin\theta -4x_1{y}_1\parallel x_2\parallel \parallel y_2\parallel sin\theta .\hfill \\ & =& -2\parallel x_2\parallel \parallel y_2\parallel sin\theta (\parallel x_2\parallel \parallel y_2\parallel cos\theta +2x_1{y}_1).\hfill \end{array}$$

Then, it is clear that 0, $\pi$ are the only two critical points of f since

$$\begin{array}{ccc}\hfill \parallel x_2\parallel \parallel y_2\parallel cos\theta +2x_1{y}_1& =& x_1{y}_1+(x_1{y}_1+\parallel x_2\parallel \parallel y_2\parallel cos\theta )\hfill \\ & \ge & x_1{y}_1+(\parallel x_2\parallel \parallel y_2\parallel +\parallel x_2\parallel \parallel y_2\parallel cos\theta )\hfill \\ & >& 0.\hfill \end{array}$$

Therefore, the extreme values of $2{∥x\circ y∥}^2$ occur at $\theta =0,\pi$. For $\theta =0$, we have

$$\begin{array}{ccc}\hfill 2{∥x\circ y∥}^2& =& 2\left(x_1^2{y}_1^2+\parallel x_2{\parallel }^2\parallel y_2{\parallel }^2+x_1^2\parallel y_2{\parallel }^2+y_1^2\parallel x_2{\parallel }^2+4x_1{y}_1\parallel x_2\parallel \parallel y_2\parallel \right)\hfill \\ & =& {\left({\lambda }_1(x){\lambda }_1(y)\right)}^2+{\left({\lambda }_2(x){\lambda }_2(y)\right)}^2.\hfill \end{array}$$

On the other hand, for $\theta =\pi$, we obtain

$$\begin{array}{ccc}\hfill 2{∥x\circ y∥}^2& =& 2\left(x_1^2{y}_1^2+\parallel x_2{\parallel }^2\parallel y_2{\parallel }^2+x_1^2\parallel y_2{\parallel }^2+y_1^2\parallel x_2{\parallel }^2-4x_1{y}_1\parallel x_2\parallel \parallel y_2\parallel \right)\hfill \\ & =& {\left({\lambda }_1(x){\lambda }_2(y)\right)}^2+{\left({\lambda }_2(x){\lambda }_1(y)\right)}^2.\hfill \end{array}$$

Thus, the norm $2{∥x\circ y∥}^2$ attains the maximum and minimum at $\theta =0$ and $\theta =\pi$, respectively. The proof is complete. □

Remark 3. 

According to the proof of Proposition 4, we remark that the maximum and minimum of the norm $2{∥\frac{x^p}{p}+\frac{y^q}{q}∥}^2$ also occur at $\theta =0$ and $\theta =\pi$, respectively. In addition, for $1<p,q<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$, we could obtain the relationship between these two maxima and minima by applying the classical Young inequality, see Figure 2. However, we have not reached a conclusion whether the inequality $∥x\circ y∥\le ∥\frac{x^p}{p}+\frac{y^q}{q}∥$ is true or not.

Next, we consider the inverse Young inequality, namely

$$ab\ge \nu b^{\frac{1}{\nu }}+(1-\nu )a^{\frac{1}{1-\nu }}$$

for $a,b>0$ and $\nu >1$. Manjegani and Norouzi [15] prove an inverse Young inequality for eigenvalues of positive definite matrices, that is,

$$s_j(AB)\ge s_j\left(\nu A^{\frac{1}{\nu }}+(1-\nu )B^{\frac{1}{1-\nu }}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}1\le j\le n,$$

(6)

where A and B are positive definite matrices, and $\nu >1$. However, Drury[16] provides counterexamples to (6) for $\nu =2$, and slightly modifies inequality (6). He proves that the results hold only for $1<\nu <\frac{3}{2}$. In the following, we discuss the trace version of inverse Young inequality in the setting of second-order cone.

Theorem 2. 

(Inverse Young inequality-Type I) For any $x,y\in \mathrm{int}({\mathcal{K}}^n)$, there holds

$$\mathbf{tr}(x\circ y)\ge \mathbf{tr}\left(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}\right)$$

where $\nu >1$.

Proof. 

According to Lemma 1(c)(d), the desired result follows by

$$\begin{array}{ccc}\hfill \mathbf{tr}(x\circ y)& \ge & {\lambda }_1(x){\lambda }_2(y)+{\lambda }_2(x){\lambda }_1(y)\hfill \\ & \ge & \left(\nu {\lambda }_1{(x)}^{\frac{1}{\nu }}+(1-\nu ){\lambda }_2{(y)}^{\frac{1}{1-\nu }}\right)+\left(\nu {\lambda }_2{(x)}^{\frac{1}{\nu }}+(1-\nu ){\lambda }_1{(y)}^{\frac{1}{1-\nu }}\right)\hfill \\ & =& \nu \left({\lambda }_1{(x)}^{\frac{1}{\nu }}+{\lambda }_2{(x)}^{\frac{1}{\nu }}\right)+(1-\nu )\left({\lambda }_1{(y)}^{\frac{1}{1-\nu }}+{\lambda }_2{(y)}^{\frac{1}{1-\nu }}\right)\hfill \\ & =& \mathbf{tr}(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}),\hfill \end{array}$$

where the last inequality is due to the inverse Young inequality for positive numbers. □

Corollary 1. 

(Inverse Young inequality-Type II) For any $x,y\in \mathrm{int}({\mathcal{K}}^n)$, there holds

$$\mathbf{tr}(|x\circ y|)\ge \mathbf{tr}\left(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}\right)$$

where $\nu >1$.

Proof. 

The results follow immediately from the fact that $|x\circ y|{⪰}_{{\mathcal{K}}^n}x\circ y$ and Lemma 1(b). □

Theorem 3. 

(Inverse Young inequality-Type II) For any $x,y\in {\mathbb{R}}^n$, if $x,y$ are not in $\partial ({\mathcal{K}}^n)\cup (-\partial ({\mathcal{K}}^n))$, there holds

$$\mathbf{tr}(|x|\circ \left|y\right|)\ge \mathbf{tr}\left({\nu \left|x\right|}^{\frac{1}{\nu }}+(1-\nu ){\left|y\right|}^{\frac{1}{1-\nu }}\right)$$

where $\nu >1$.

Proof. 

We note that both $\left|x\right|$ and $\left|y\right|$ are in $\mathrm{int}({\mathcal{K}}^n)$. The desired inequality follows by applying Theorem 2 to $\left|x\right|$ and $\left|y\right|$. □

Now, we construct a counterexample to elaborate that for any $x,y\in \mathrm{int}({\mathcal{K}}^n)$, the eigenvalue version of inverse Young inequality in the SOC setting , that is,

$${\lambda }_j(x\circ y)\ge {\lambda }_j\left(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}\right).j=1,2.$$

is false if $v=2$.

Example 1. 

Let $x=(5,0,-2)$, $y=(5,-4,2)$. Then we have

$$\begin{array}{ccc}\hfill x\circ y& =& (21,-20,0)\hfill \\ \hfill x^{\frac{1}{2}}& =& (2.1889,0,-0.4569)\hfill \\ \hfill y^{-1}& =& (1,0.8,-0.4),\hfill \end{array}$$

and hence, $2x^{\frac{1}{2}}-y^{-1}\approx (3.3778,-0.8,-0.5137)$. Therefore,

$${\lambda }_1(x\circ y)=1<2.42707\approx {\lambda }_1(2x^{\frac{1}{2}}-y^{-1}).$$

Example 2. 

Let $x=(5.5,0,-4)$, $y=(5.5,-3,4)$. Then we have

$$\begin{array}{ccc}\hfill x\circ y& =& (14.25,-16.5,0)\hfill \\ \hfill x^{\frac{1}{2}}& \approx & (2.1535,0,-0.9287)\hfill \\ \hfill y^{-1}& \approx & (1.0476,0.5714,-0.7619),\hfill \end{array}$$

which says that $2x^{\frac{1}{2}}-y^{-1}\approx (3.2593,-0.5714,-1.0956)$. Hence,

$$\begin{array}{ccc}\hfill {\lambda }_1(x\circ y)=-2.25& ,& {\lambda }_1(2x^{\frac{1}{2}}-y^{-1})\approx 2.0237\hfill \\ \hfill {\lambda }_2(x\circ y)=30.75& ,& {\lambda }_2(2x^{\frac{1}{2}}-y^{-1})\approx 4.4950,\hfill \end{array}$$

Which implies $det(x\circ y)=-69.1875<9.0965\approx det(2x^{\frac{1}{2}}-y^{-1})$

In Example2, we note that it is also a counterexample to the determinant version of inverse Young inequality, that is,

$$det(x\circ y)\ge det\left(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}\right)$$

is false for $\nu =2$. However, for the other type of determinant version of inverse Young inequality, namely,

$$det(|x\circ y|)\ge det\left(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}\right),$$

we have no conclusion yet.

4. Conclusion

In this paper, we establish several inequalities associated with second-order cones. We discuss the relationship between the eigenvalue and norm of x, y, $x\circ y$, $\frac{x^p}{p}+\frac{y^q}{q}$ in Proposition 1-2 and Proposition 4, respectively. we derive a refined inequality for the determinant version of Young inequality through direct computation. Moreover, we explore the inverse Young inequality in the setting of second-order cones. Our conclusions align with the results established for the positive semidefinite cone, which is also a symmetric cone. We believe that Conjecture1 holds, as computational verification has found no counterexample in ${\mathbb{R}}^3$. However, directly proving the inequality is challenging due to the algebraic complexity of the expression $\frac{x^p}{p}+\frac{y^q}{q}$. There are several directions that are worth further exploration. We outline them as follows.

(Q1) 

Does the inequality $∥x\circ y∥\le ∥\frac{x^p}{p}+\frac{y^q}{q}∥$ hold or not?

(Q2) 

Does the inequality $det(|x\circ y|)\ge det\left(\nu x^{\frac{1}{\nu }}+(1-\nu )y^{\frac{1}{1-\nu }}\right)$ hold or not?

We note that Conjecture1 would be wrong if we could show that Q1 is false.