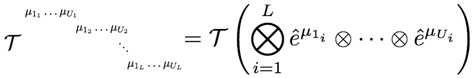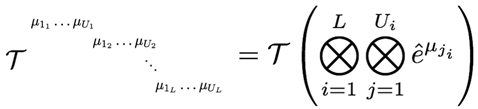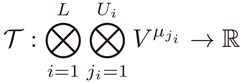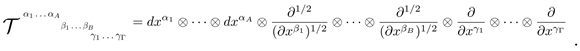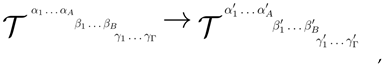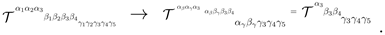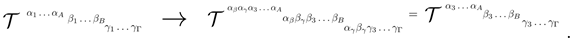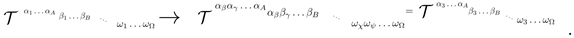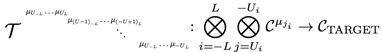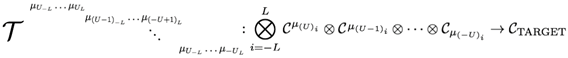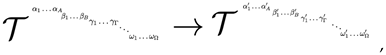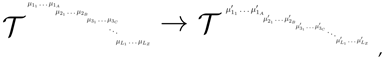Advancing Tensor Theories

1. Introduction

This manuscript focuses on the core concepts rooted on tensor theory and category theory, integral components of mathematical logic, topology, algebraic geometry, foundations and philosophy. These mathematical disciplines hold significant relevance in elucidating innovative mathematical and scientific ideas. Here, we expand upon foundational tensor and category theory concepts.

In 1975, Gregorio Ricci-Curbastro and Tullio Levi-Civita’s seminal work, “Methodes de Calculs Differentiel Absolute et Leur Application” 1, marked a significant milestone in the development of tensor calculus, now recognized as tensor theory. Over time, diverse investigations have delved into tensor theory’s intersections with mathematical analysis, differential geometry, and topology, including the study by 2, which introduced tensors with maximal symmetries, extending into realms like representation theory, computer science, computational complexity, and algebraic geometry. In this paper, we further advance the concepts established in prior research by extending the tensor framework. Specifically, we introduce the generalized tensor index, a versatile descriptor encompassing various tensor indices. This novel notation, is useful to describe concepts beyond tensors which only have input vectors and their dual vectors. In particular, E. J. Cartan [3], proposed the triality as an extension of the concept of duality of vector spaces. In this work we extend the concept to the D-ality, which extends further the concepts of dualities, and trialities.

Category theory provides a vantage point akin to a “far-distant observer view” in mathematics [4], where intricate details fade into obscurity, revealing previously hidden patterns. It beckons us to ponder: How does the direct sum of vector spaces relate to the least common multiple of numbers? What unites free groups, fields of fractions, and discrete topological spaces? Category theory not only explores these inquiries but also unveils profound connections in mathematics and physics that elude closer scrutiny [5]. This document draws inspiration from modern category theory Definitions [6] and refines them, ushering in a new perspective. In particular, we redefine categories with brevity, introduce the concept of a signature, and employ graphical representations. These novel viewpoints shed fresh light on categories, akin to how algebra bridges diverse mathematical realms. Moreover, contemporary developments in category theory have given rise to sophisticated notions like ∞-categories, ∞-functors, and ∞-cosmoi [7,8], expanding the horizons of mathematical exploration.

The concept of fractional derivatives was introduced by a letter written to Guillaume de l’Hôpital by Gottfried Wilhelm Leibniz in 1695. It found applications on fractional dynamical systems [9]. Then it found applications in fractional differential geometrical aspects [10,11]. In particular, Calcagni [12], focused on explaining that the fractional derivative describes a new sub-manifold to a point of an original manifold, which is not the same sub-manifold as the one described by a standard derivative. Fractional calculus was successfully applied to physics [13] and in particular to quantum mechanics, creating the concepts of fractional schrodinger equation[14]. In this study we develop further fractional calculus, and we introduce generalised tensors which have the concept of fractional differentials. In extend we develop further tensor calculus and tensor theories.

Furthermore, we establish a linkage between category theory, tensor theory, and set theory, investigating amalgamations of sets, tensors, categories, functors, and their extended counterparts. We will forge categories and functors employing generalized tensors, crafting categorial tensors (tensors with categories as elements) and functorial tensors (tensors with functors as elements).

Category theory and tensor theory, with their rich contemporary and recent applications spanning fields like physics, as evidenced in Feynman diagrams [15], cosmology, and the study of functors of actions [16], statistics, and computer science 3, as well as epidemiology 4, underscore their paramount significance. Thus, it is imperative to further cultivate and solidify the foundational concepts within category and tensor theories, encompassing the fundamental notions of categories, functors, tensors, and their multifaceted interplay.

According to the criteria presented in [19], our manuscript is a description of a good, important, and novel mathematical and philosophical concepts for the following reasons. We describe the criteria and then we give at least one Example from our paper, that renders our work mathematically and philosophically important. The satisfied criteria are the following:

• Good mathematical problem solving (e.g., a major breakthrough on an important mathematical problem); This paper solves the problem of how to find further what are the foundations of tensor theory and category theory, by implementing generalised concepts within these theories, and ultimately combining them.
• Good mathematical technique (e.g., a masterful use of existing methods or the development of new tools); We use the substitution method, where the simple index is substituted with an index of index and so on. We construct generalised components of the tensors which results to the generalised tensor theory structures. We also use the substitution method to both category theory and tensor theory to create the generic concepts such as tensorial set, setorial tensor, tensorial category, categorial tensor, tensorial functor, and functorial tensor.
• Good mathematical insight (e.g., a major conceptual simplification or the realisation of a unifying principle, heuristic, analogy, or theme); In this study, we considered a heuristic argument to construct a generic concepts such as the generalised tensor, as well as the categorial tensor and the tensorial category, but the unifying principle of the method of substitution.
• Good mathematical discovery (e.g., the revelation of an unexpected and intriguing new mathematical phenomenon, connection, or counterExample); This study finds an unexpected results such as the generalised tensor, as well as the connections between the concepts of category theory and tensor theory, such as the tensorial category and categorial tensor.
• Good mathematical application (e.g., to important problems in physics, engineering, computer science, statistics, etc., or from one field of mathematics to another); This study finds important applications in physics since it connects the concepts of category theory and tensor theory, and their combinations, since both category theory and tensor theory find applications in physics. Furthermore, we expect that the combination of the concepts between the two theories will find further applications in physics.
• Rigorous mathematics (with all details correctly and carefully given in full); This paper is mathematical rigorous, since it construct every Definition, Theorems, and proofs in detail.
• Beautiful mathematics (e.g., the amazing identities of Ramanujan, results which are easy (and pretty) to state but not to prove); The construction of the Definition of the generalised concepts in tensor theory and category theory, such as functors of functors, generalised tensor, categorial tensor, and tensorial category are easy to state, but difficult to prove, since we need to make several substitution in their individual components.
• Elegant mathematics (e.g., Paul Erdos concept of proofs from The Book, achieving a difficult result with a minimum of effort); The construction of the Definition of the generalised concepts in tensor theory and category theory, such as generalised tensor, categorial tensor, and tensorial category, with the minimum effort, i.e., using the simple substitution method makes them easy to prove, and creates a difficult result. We also use the functor of proof, which is a generalisation of the substitution method, in order to prove the Theorem 1.
• Creative mathematics (e.g., a radically new and original technique, viewpoint, or species of result); The structure of the Definitions of the generalised concepts in category theory and tensor theory, such as generalised tensor, setorial tensor, and tensorial set shows the creativity of our work. The creativity is also shown by the connection between the category theory and tensor theory with the creation of categorial tensor and tensorial category. We have created the functor of proof.
• Useful mathematics (e.g., a lemma or method which will be used repeatedly in future work on the subject); The method of substitution of simple components with more generalised ones was used, and it is going to be used in the future repeatedly. The generalised tensors are used to compress information, more than a standard tensor does. Generalised tensors are capturing aspects of fractional geometry, in a economical way.
• Deep mathematics (e.g., a result which is manifestly non-trivial, for instance by capturing a subtle phenomenon beyond the reach of more elementary tools); The creation of the generic concepts of generalised tensor, with and without the use of fractional derivatives, categorial tensor, and tensorial category, as a foundation, as well as the application of connecting category theory and tensor theory show the mathematical deepness of our study.

The structured path of this paper is as follows. Section 2 introduces fresh insights into tensor theory. In Section 3, we present the properties of these tensors. In Section 4, we describe the geometrical interpretation of the general tensors using fractional derivatives in Section 4, while in Section 4.1, we describe the geometrical interpretation in some generic way. In Section 5 we shed light on noteworthy applications stemming from tensor and category theories. Lastly, in Section 6, we draw our paper to a close.

2. Tensor Theory

In this section, we present a review of the Definition of a tensor, and we develop further some novel Definitions on generalised tensors concepts.

2.1. Standard Tensor Definitions

In this section, we introduce the standard tensor Definitions, that we are going to generalise in the next sessions.

Definition 1. 

The generalization of the dual vector is called a tensor and is defined as the multi-linear object that maps distinct vectors and dual vectors to a scalar. A tensor of type $(q,p)$ is a multilinear representation that maps p dual vectors and q vectors to $\mathbb{R}$, and we write

$$\begin{array}{c}\hfill T:\underset{i=1}{\overset{p}{⨂}}{V}_i^{*}\underset{j=1}{\overset{q}{⨂}}{V}_j\to \mathbb{R}.\end{array}$$

(1)

Example 1. 

A tensor $(1,0)$ represents a real number vector. Thus can be recognized as a dual vector. A tensor of type $(1,0)$ is a vector. If ω represents a map of two binary vectors and a vector to a scalar, i.e., $\omega :V^{*}\times V^{*}\times V\to \mathbb{R}$, then it is a (1,2) tensor.

Definition 2. 

The set of all tensors of type (q,p) is called the tensor space of type (q,p) and it is denoted with ${\mathcal{T}}_q^p$.

Definition 3. 

Let two tensors, $\mu \in {\mathcal{T}}_q^p$ and $\nu \in {\mathcal{T}}_{q^{\prime }}^{p^{\prime }}$. Then the tensor product is defined as

$$\begin{array}{c}\hfill \tau =\mu \otimes \nu \end{array}$$

(2)

or

$$\begin{array}{cc}\hfill \tau & =\tau \left({\omega }_1,\cdots ,{\omega }_p,{\xi }_1,\cdots ,{\xi }_{p^{\prime }};u_1,\cdots ,u_q,v_1,\cdots ,v_{q^{\prime }}\right)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \tau & =\mu \left({\omega }_1,\cdots ,{\omega }_p;u_1,\cdots ,u_q\right)\otimes \nu \left({\xi }_1,\cdots ,{\xi }_{p^{\prime }};v_1,\cdots ,v_{q^{\prime }}\right)\hfill \end{array}$$

(4)

and it is the element of the tensor space, ${\mathcal{T}}_{q+q^{\prime }}^{p+p^{\prime }}$. Thus we write $\tau \in {\mathcal{T}}_{q+q^{\prime }}^{p+p^{\prime }}$.

By introducing a basis for the tensors $(q,p)$ as

$$\begin{array}{c}\hfill \overrightarrow{e}={\overrightarrow{e}}_{{\mu }_1}\otimes \cdots \otimes {\overrightarrow{e}}_{{\mu }_p}\otimes {\overrightarrow{e}}^{*{\nu }_1}\otimes \cdots \otimes {\overrightarrow{e}}^{*{\nu }_q}\end{array}$$

(5)

we can write the tensor in the form of components. Therefore, we write

$$\begin{array}{c}\hfill T={T^{{\mu }_1\cdots {\mu }_p}}_{{\nu }_1\cdots {\nu }_q}{\overrightarrow{e}}_{{\mu }_1}\otimes \cdots \otimes {\overrightarrow{e}}_{{\mu }_p}\otimes {\overrightarrow{e}}^{*{\nu }_1}\otimes \cdots \otimes {\overrightarrow{e}}^{*{\nu }_q}\end{array}$$

(6)

or we can also write

$$\begin{array}{c}\hfill {T^{{\mu }_1\cdots {\mu }_p}}_{{\nu }_1\cdots {\nu }_q}=T({\overrightarrow{e}}^{*{\nu }_1},\cdots ,{\overrightarrow{e}}^{*{\nu }_q};{\overrightarrow{e}}_{{\mu }_1},\cdots ,{\overrightarrow{e}}_{{\mu }_p})\end{array}$$

(7)

A tensor in a d-dimensional space will have $d^{p+q}$ components. A tensor acts on a set of vectors $(v^{\left(j\right)}\in V)$ and dual vectors $({\omega }^{\left(i\right)}\in \mathrm{\Omega })$ as

$$\begin{array}{c}\hfill T({\omega }^{\left(1\right)},\cdots ,{\omega }^{\left(p\right)};v^{\left(1\right){\nu }_1},\cdots ,v^{\left(q\right){\nu }_q})={T^{{\mu }_1\cdots {\mu }_p}}_{{\nu }_1\cdots {\nu }_q}{\omega }_{{\mu }_1}^{\left(1\right)}\cdots {\omega }_{{\mu }_p}^{\left(p\right)}{v}^{\left(1\right){\nu }_1}\cdots v^{\left(q\right){\nu }_q}\end{array}$$

(8)

Another operation that tensor have is the operation of contraction. A contraction of first order of a tensor of $(q,p)$-rank is a map between a tensor of $(q,p)$-rank to a tensor of $(q-1,p-1)$-rank, and we write

$$\begin{array}{c}\hfill {T^{{\mu }_1\cdots \lambda \cdots {\mu }_p}}_{{\nu }_1\cdots \lambda \cdots {\nu }_q}=T({\overrightarrow{e}}^{*{\nu }_1},\cdots ,{\overrightarrow{e}}^{*\lambda },\cdots ,{\overrightarrow{e}}^{*{\nu }_q};{\overrightarrow{e}}_{{\mu }_1},\cdots ,{\overrightarrow{e}}_{\lambda },\cdots ,{\overrightarrow{e}}_{{\mu }_p})\end{array}$$

(9)

Therefore a contraction of k-order of a tensor of $(q,p)$-rank is a map between a tensor of $(q,p)$-rank to a tensor of $(q-k,p-k)$-rank, and we write

$$\begin{array}{c}\hfill {T^{{\mu }_1\cdots {\lambda }_1\cdots {\lambda }_k\cdots {\mu }_p}}_{{\nu }_1\cdots {\lambda }_1\cdots {\lambda }_k\cdots {\nu }_q}=T({\overrightarrow{e}}^{*{\nu }_1},\cdots ,{\overrightarrow{e}}^{*{\lambda }_1},\cdots ,{\overrightarrow{e}}^{*{\lambda }_k},\cdots ,{\overrightarrow{e}}^{*{\nu }_q};{\overrightarrow{e}}_{{\mu }_1},\cdots ,{\overrightarrow{e}}_{{\lambda }_1},\cdots ,{\overrightarrow{e}}_{{\lambda }_k},\cdots ,{\overrightarrow{e}}_{{\mu }_p})\end{array}$$

(10)

2.2. Generalisation of a Tensor

We can think of a generalisation of a tensor, by simply introducing a collection of distinct vectors, among which there are vectors and dual vectors, and a map between the collection of vectors to the collection of generic number set. Below we express these ideas in Theorems and proofs.

Theorem 1 

(Informa). Let $\mathcal{T}$ be a generic generalised tensor, $\mathcal{V}$ be a generic vector, and $\mathbb{G}$ be a generic number set, then the generic generalised tensor maps the generic vector to the generic number set, and we write

$$\begin{array}{c}\hfill \mathcal{T}:\mathcal{V}\to \mathbb{G}.\end{array}$$

(11)

Proof. 

To prove Theorem 1, we consider that the ($U,L$) rank tensor is a map between the combination of vectors, V to the real number set, $\mathbb{R}$ and we write in functional notation:

$$\begin{array}{c}\hfill T:V\to \mathbb{R}\end{array}$$

(12)

By considering the simple functor of substitution $S_F$ as follows

$$\begin{array}{c}\hfill S_F:\left\{\begin{array}{cc}T& \to \mathcal{T}\\ V& \to \mathcal{V}\\ \mathbb{R}& \to \mathbb{G}\end{array}\right.\end{array}$$

(13)

we have that the generic generalised tensor, $\mathcal{T}$ is a map between the generic vector, $\mathcal{V}$ to the generic number set, $\mathbb{G}$ and we write

$$\begin{array}{c}\hfill \mathcal{T}:\mathcal{V}\to \mathbb{G}\end{array}$$

(14)

□

In other words we can state the previous Theorem in a more detailed way.

Theorem 2. 

In accordance with informal Theorem 1, let $\mathcal{T}$ be a generic generalised tensor, and $\mathbb{G}$ be a generic number set. Let $\mathcal{V}$ be a generic vector, $V^{{\ell }_{k_{{\cdots }_{j_i}}}}$ denote an element of the generic vector, with generic index, $\mathcal{I}={\ell }_{k_{{\cdots }_{j_i}}}$, where i is the index of j which is the index of the indices of k, of the indices, ℓ, for any $i,j,\cdots ,k,\ell \in \mathbb{Z}$, and $-L$ is the lower bound of the lowest index i, while $+U_{k_{{\cdots }_{j_i}}}$ is the maximum bound of the highest index, $k_{{\cdots }_{j_i}}$, and

$$\begin{array}{c}\hfill \underset{\mathcal{I}\in \mathbb{Z}}{⨂}=\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}\end{array}$$

(15)

be a generic vector product operator. If the generic vector is constructed via

$$\begin{array}{c}\hfill \mathcal{V}=\underset{\mathcal{I}\in \mathbb{Z}}{⨂}{\mathcal{V}}^{\mathcal{I}}=\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{V}^{{\ell }_{k_{{\cdots }_{j_i}}}}\end{array}$$

(16)

then the generic generalised tensor maps the generic vector to the generic number set, and we write

$$\begin{array}{c}\hfill \mathcal{T}:\underset{\mathcal{I}\in \mathbb{Z}}{⨂}{\mathcal{V}}^{\mathcal{I}}\to \mathbb{G},\end{array}$$

(17)

or in short

$$\begin{array}{c}\hfill \mathcal{T}:\mathcal{V}\to \mathbb{G}.\end{array}$$

(18)

Proof. 

Sketch. To prove Theorem 1 , we consider the following. Let ($U,L$) rank tensor be a map between the combination of vectors, V to the real number set, $\mathbb{R}$ and we write in functional notation:

$$\begin{array}{c}\hfill T:V\to \mathbb{R}\end{array}$$

(19)

or in more detail

$$\begin{array}{c}\hfill T:\underset{i\in \mathbb{Z}}{⨂}{V^{*}}^i\underset{j\in \mathbb{Z}}{⨂}{V}^j\to \mathbb{R}\end{array}$$

(20)

where the vector

$$\begin{array}{cc}\hfill V& =\underset{i\in \mathbb{Z}}{⨂}{V^{*}}^i\underset{j\in \mathbb{Z}}{⨂}{V}^j\hfill \end{array}$$

(21)

while the generic vectors is

$$\begin{array}{cc}\hfill \mathcal{V}& =\underset{\mathcal{I}\in \mathbb{Z}}{⨂}{\mathcal{V}}^{\mathcal{I}}.\hfill \end{array}$$

(22)

By considering the simple functor of substitution, as defined in [20], we write

$$\begin{array}{c}\hfill S_F:\left\{\begin{array}{cc}T& \to \mathcal{T}\\ V& \to \mathcal{V}\\ \mathbb{R}& \to \mathbb{G}\end{array}\right.\end{array}$$

(23)

we have that the generalised tensor, $\mathcal{T}$ is a map between the generic vector, $\mathcal{V}$ to the generic number set, $\mathbb{G}$ and we write

$$\begin{array}{c}\hfill \mathcal{G}:\mathcal{V}\to \mathbb{G}\end{array}$$

(24)

□

Proof. 

To prove the Theorem 2, in formal mathematical language, we consider the following. The tensor of vectors and their duals is defined, as stated before in Section 2.1, as

$$\begin{array}{cc}\hfill {T^{{\mu }_1\cdots {\mu }_U}}_{{\nu }_1\cdots {\nu }_L}& =T\left(\widehat{e}\right)=T({\widehat{e}}_{{\mu }_1},\cdots ,{\widehat{e}}_{{\mu }_U},{\widehat{e}}^{{\nu }_1},\cdots ,{\widehat{e}}^{{\nu }_L})\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=T({\widehat{e}}_{{\mu }_1}\otimes \cdots \otimes {\widehat{e}}_{{\mu }_U}\otimes {\widehat{e}}^{{\nu }_1}\otimes \cdots \otimes {\widehat{e}}^{{\nu }_L})\hfill \end{array}$$

(26)

To generalise this concept, we introduce the space between upper, U, and lower, L, indices by assuming that we have the first upper layer of indices, $U_1$, then $U_2$, and so on up to the lowest layer of indices, $U_L$, and we write

(27)

where $\widehat{e}$ is the basis of the ($U_1,U_2,\cdots ,U_L$)-rank tensor, which is simply defined as

$$\begin{array}{cc}\hfill \widehat{e}={\widehat{e}}^{\mu }& =\underset{i=1}{\overset{L}{⨂}}\underset{j_i=1_i}{\overset{U_i}{⨂}}{\widehat{e}}^{{\mu }_{j_i}}=\underset{i=1}{\overset{L}{⨂}}{\widehat{e}}^{{\mu }_{1_i}}\otimes \cdots \otimes {\widehat{e}}_{{\mu }_{U_i}}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\widehat{e}}^{{\mu }_{1_1}}\otimes \cdots \otimes {\widehat{e}}^{{\mu }_{U_1}}\otimes {\widehat{e}}^{{\mu }_{1_2}}\otimes \cdots \otimes {\widehat{e}}^{{\mu }_{U_2}}\otimes {\widehat{e}}_{{\mu }_{U_L}}\otimes \cdots \otimes {\widehat{e}}_{{\mu }_{U_L}}\hfill \end{array}$$

(29)

Therefore, the generalised tensor is simply written as

(30)

Note that if this tensor has dimension d, then it will have $d^{{\sum }_{i=1}^L{U}_i}$ components. In this case, we write the generalised tensor in functor notation as

(31)

This means in functor notation that we have the vector $V^{{\mu }_{j_i}}$, where the index ${\mu }_{j_i}$ specifies each vector for every j, while the index i indicates the indexation or how lower is the index from the most upper index. Now we generalise the initial value of the indices,

$$\begin{array}{cc}\hfill (i=1)& \to (i=-L)\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill (j_i=1)& \to (j_i=U_i).\hfill \end{array}$$

(33)

Considering another layer of generalisation of the generalised tensor, we can think of the generic generalised tensor, $\mathcal{T}$, using the functor notation as

$$\begin{array}{c}\hfill \mathcal{T}:\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{V}^{{\ell }_{k_{{\cdots }_{j_i}}}}\to \mathbb{R}\end{array}$$

(34)

where $V^{{\ell }_{k_{{\cdots }_{j_i}}}}$ is a generic vector, and $k_{{\cdots }_{j_i}}$ denotes the index of the indices, ℓ, namely a generalised index, ${\ell }_{k_{{\cdots }_{j_i}}}=\mathcal{I}$. Now what we need to do is that we can build another layer of generalisation since the previous generic generalised tensor only maps the combination of vectors to the real numbers $\mathbb{R}$. Therefore we can make the generic generalised tensor to map the combination of vectors to the complex numbers, $\mathbb{C}$, or a generic space of numbers named as $\mathbb{G}$, therefore we have that the generic generalised tensor is defined as

$$\begin{array}{c}\hfill \mathcal{T}:\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{V}^{{\ell }_{k_{{\cdots }_{j_i}}}}\to \mathbb{G}\end{array}$$

(35)

At this instance, we can define the generic vector

$$\begin{array}{c}\hfill \mathcal{V}=\underset{\mathcal{I}\in \mathbb{Z}}{⨂}{\mathcal{V}}^{\mathcal{I}}\end{array}$$

(36)

and in details the generic vector is written as

$$\begin{array}{c}\hfill \mathcal{V}=\underset{\mathcal{I}\in \mathbb{Z}}{⨂}{\mathcal{V}}^{\mathcal{I}}=\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{V}^{{\ell }_{k_{{\cdots }_{j_i}}}}\end{array}$$

(37)

where $\mathcal{I}={\ell }_{k_{{\cdots }_{j_i}}}$, and i is the index of j which is the index of the indices of k, and $-L$ is the lower bound of the lowest index, i, and $U_{k_{{\cdots }_{j_i}}}$ the maximum bound of the highest index ${\ell }_{k_{{\cdots }_{j_i}}}$. Consider that the generic vector is defined as ${\mathcal{V}}^{\mathcal{I}}=V^{{\ell }_{k_{{\cdots }_{j_i}}}}$. Therefore, by collecting this information together, it is easy to show that the generic generalised tensor is simply the map between the generic vector to the generic number set, written in generic notation as

$$\begin{array}{c}\hfill \mathcal{T}:\mathcal{V}\to \mathbb{G}.\end{array}$$

(38)

□

Remark 1. 

The basis vector of this generic generalised tensor is defined as

$$\begin{array}{c}\hfill \widehat{\mathcal{E}}=\underset{\mathcal{I}\in \mathbb{Z}}{⨂}{\widehat{\mathcal{E}}}^{\mathcal{I}}=\underset{I=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{\widehat{e}}^{{\ell }_{k_{{\cdots }_{j_i}}}}\end{array}$$

(39)

where ${\widehat{e}}^{{\ell }_{k_{{\cdots }_{j_i}}}}$ denotes the components of basis vector.

2.3. Generic Generalised Tensor in Respect of Indices

We can think of a generalisation of a tensor, by simply introducing a collection of distinct vectors, among which there are vectors and dual vectors, and a map between the collection of vectors to the collection of generic number set. Below we express these ideas in Theorems and proofs.

Theorem 3. 

In generic notation, the generic generalised tensor, $\mathcal{G}$ is the tensor which maps the generic vector, $\mathcal{V}$, to the generic number set, $\mathbb{G}$, and we write

$$\begin{array}{c}\hfill \mathcal{G}:\mathcal{V}\to \mathbb{G}.\end{array}$$

(40)

In other words we can state the previous informal Theorem in a more detailed way.

Theorem 4. 

In accordance with the informal Theorem 3, the generic generalised tensor, $\mathcal{G}$, is the tensor which maps the generic vector, $\mathcal{V}$, to the generic number set, $\mathbb{G}$, and we write

$$\begin{array}{cc}\hfill \mathcal{G}& :\underset{\mathcal{I}\in \mathbb{G}}{⨂}{\mathcal{V}}^{\mathcal{I}}\to \mathbb{G}\hfill \end{array}$$

(41)

when the generic vector is defined as

$$\begin{array}{c}\hfill \underset{\mathcal{I}\in \mathbb{G}}{⨂}{\mathcal{V}}^{\mathcal{I}}=\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{V}^{{\ell }_{k_{{\cdots }_{j_i}}}}\end{array}$$

(42)

where $V^{{\ell }_{k_{{\cdots }_{j_i}}}}$ denotes an element of the generic vector, with generic index, $\mathcal{I}={\ell }_{k_{{\cdots }_{j_i}}}$, where i is the index of j which is the index of the indices of k, which is the index of ℓ, for any $i,j,\cdots ,k,\ell \in \mathbb{G}$, where $\mathcal{I},L,U_{k_{{\cdots }_{j_i}}}\in \mathbb{G}$, and $-L$ is the lower bound of the lower index, i, while, $+U_{k_{{\cdots }_{j_i}}}$ is the bound of the highest index, ${\ell }_{k_{{\cdots }_{j_i}}}$. We also consider that ${⨂}_{\mathcal{I}\in \mathbb{G}}{\mathcal{V}}^{\mathcal{I}}$ is the generic tensorial product of generic vector elements ${\mathcal{V}}^{\mathcal{I}}$.

Proof. 

The proof of Theorem 3 and Theorem 4 are exactly the same as the proves of the previous Theorems, Theorem 1 and Theorem 2, respectively. The two distinctions are the following

• All indices in Theorem 4 belong to the collection of the generic numbers, $\mathbb{G}$, instead to the integer number set, $\mathbb{Z}$.
• The generalised tensor, $\mathcal{T}$, in the proof of Theorem 3, is substituted by the generic generalised tensor, $\mathcal{G}$, in the proof of Theorem 4.

□

3. Properties

In this section we review the concept of the Definition of a tensor using using 1-forms and partial derivatives, and their corresponding transformations. Then we introduce the concept of generalised tensors, using 1-forms, partial derivatives, and fractional partial derivatives. Then we construct the transformation of generalised tensors, using 1-forms, partial derivatives, and fractional partial derivatives. We construct the tensors via the infinitesimal elements and their corresponding derivatives.

3.1. Definition of Standard Tensors

A $(1,0)$-rank tensor is defined as

$$\begin{array}{c}\hfill V^{\mu }=d{x}^{\mu }\end{array}$$

(43)

while a $(0,1)$-rank tensor is defined as

$$\begin{array}{c}\hfill V_{\mu }={\displaystyle \frac{\partial }{x^{\mu }}}\end{array}$$

(44)

A $(1,1)$-rank tensor is defined as

$$\begin{array}{c}\hfill {T^{\mu }}_{\nu }=d{x}^{\mu }\otimes {\displaystyle \frac{\partial }{\partial x^{\nu }}}\end{array}$$

(45)

A $(U,L)$-rank tensor is defined as

$$\begin{array}{c}\hfill {T^{{\mu }_1\cdots {\mu }_U}}_{{\nu }_1\cdots {\nu }_L}\to {T^{{{\mu }_1}^{\prime }\cdots {{\mu }_U}^{\prime }}}_{{{\nu }_1}^{\prime }\cdots {{\nu }_L}^{\prime }}=d{x}^{{\mu }_1}\otimes \cdots \otimes d{x}^{{\mu }_U}\otimes {\displaystyle \frac{\partial }{\partial x^{{\nu }_1}}}\otimes \cdots \otimes {\displaystyle \frac{\partial }{\partial x^{{\nu }_L}}}\end{array}$$

(46)

3.2. Definition of Generalised Tensors

Let $\alpha ,\beta ,\gamma ,{\alpha }_1,\cdots ,{\alpha }_A,{\beta }_1,\cdots ,{\beta }_1,\cdots ,{\beta }_B,{\gamma }_1,\cdots ,{\gamma }_{\Gamma },\cdots ,{\omega }_1,\cdots ,{\omega }_{\mathrm{\Omega }}$, be indices.

We consider the generalised $(1,1,1)$-rank tensor as

$$\begin{array}{c}\hfill \mathcal{T}={{{\mathcal{T}}_{\alpha }}^{\beta }}^{\gamma }d{x}^{\alpha }\otimes {\displaystyle \frac{{\partial }^{1/2}}{{\left(\partial x^{\beta }\right)}^{1/2}}}\otimes {\displaystyle \frac{\partial }{\partial x^{\gamma }}}\end{array}$$

(47)

where we have used the notation of the fractional derivative, ${\displaystyle \frac{{\partial }^{1/2}}{{(\partial x^{\beta })}^{1/2}}}$ to consider the index, $\beta$, which is in between the upper index, $\alpha$ and the lower index, $\gamma$.

We consider the generalised $(A,B,\Gamma )$-rank tensor as

(48)

where $A,B,\Gamma \in \mathbb{Z}$.

$$\begin{array}{c}\hfill \mathcal{T}={{{\mathcal{T}}_{{\alpha }_1\cdots {\alpha }_A}}^{{\beta }_1\cdots {\beta }_B}}^{{\gamma }_1\cdots {\gamma }_{\Gamma }}d{x}^{{\alpha }_1}\otimes \cdots \otimes d{x}^{{\alpha }_A}\otimes {\displaystyle \frac{{\partial }^{1/2}}{{\left(\partial x^{{\beta }_1}\right)}^{1/2}}}\otimes \cdots \otimes {\displaystyle \frac{{\partial }^{1/2}}{{\left(\partial x^{{\beta }_B}\right)}^{1/2}}}\otimes {\displaystyle \frac{\partial }{\partial x^{{\gamma }_1}}}\otimes \cdots \otimes {\displaystyle \frac{\partial }{\partial x^{{\gamma }_{\Gamma }}}}\end{array}$$

(49)

We consider the generalised $(A,B,\Gamma ,\cdots ,\mathrm{\Omega })$-rank tensor as

$$\begin{array}{c}\hfill \mathcal{T}={{{{{\mathcal{T}}_{{\alpha }_1\cdots {\alpha }_A}}^{{\beta }_1\cdots {\beta }_B}}^{{\gamma }_1\cdots {\gamma }_{\Gamma }}}^{\ddots }}^{{\omega }_1\cdots {\omega }_{\mathrm{\Omega }}}d{x}^{{\alpha }_1}\otimes \cdots \otimes d{x}^{{\alpha }_A}\otimes {\displaystyle \frac{{\partial }^{1/z}}{{\left(\partial x^{{\beta }_1}\right)}^{1/z}}}\otimes \cdots \otimes {\displaystyle \frac{{\partial }^{1/z}}{{\left(\partial x^{{\beta }_B}\right)}^{1/z}}}\otimes {\displaystyle \frac{{\partial }^{2/z}}{{\left(\partial x^{{\gamma }_1}\right)}^{2/z}}}\otimes \cdots \otimes {\displaystyle \frac{{\partial }^{2/z}}{{\left(\partial x^{{\gamma }_{\Gamma }}\right)}^{2/z}}}\otimes \cdots \otimes {\displaystyle \frac{\partial }{\partial x^{{\omega }_1}}}\otimes \cdots \otimes {\displaystyle \frac{\partial }{\partial x^{{\omega }_{\mathrm{\Omega }}}}}\end{array}$$

(50)

in which tensor there are $1+z$ ranks. Note that we have partial derivatives in which the denominator of the fraction of the derivative is one more than the number of fractional derivatives that the tensor is defined on.

Note the previous tensor can be describe with L ranks in a more compact form as follows. Let ${\mu }_{1_1},\cdots ,{\mu }_{1_A},{\mu }_{2_1},\cdots ,{\mu }_{2_B},{\mu }_{3_1},\cdots ,{\mu }_{3_C},\cdots ,{\mu }_{L_1},\cdots ,{\mu }_{L_Z}$ are indices. In particular we can built a generalised ($1,2,\cdots ,L$)-rank tensor as

$$\begin{array}{c}\hfill \mathcal{T}={{{{{\mathcal{T}}_{{{\mu }_1}_1\cdots {{\mu }_1}_A}}^{{{\mu }_2}_1\cdots {{\mu }_2}_B}}^{{{\mu }_3}_1\cdots {{\mu }_3}_C}}^{\ddots }}^{{{\mu }_L}_1\cdots {{\mu }_L}_Z}d{x}^{{{\mu }_1}_1}\otimes \cdots \otimes d{x}^{{{\mu }_1}_A}\otimes {\partial }_{{{\mu }_2}_1}^{1/z}\otimes \cdots \otimes {\partial }_{{{\mu }_2}_B}^{1/z}\otimes {\partial }_{{{\mu }_3}_1}^{2/z}\cdots \otimes {\partial }_{{{\mu }_3}_C}^{2/z}\otimes \cdots \otimes {\partial }_{{{\mu }_L}_1}\otimes \cdots \otimes {\partial }_{{{\mu }_L}_Z}\end{array}$$

(51)

where we have defined

$$\begin{array}{c}\hfill {\partial }_{{\mu }_{i_j}}={\displaystyle \frac{\partial }{\partial x^{{\mu }_{i_j}}}}\end{array}$$

(52)

where i index defines the type of rank, while j index defines the amount of indices in the specific rank. Note that i is the index which defines the amount of fractional derivative, i.e., how many times the indices is lowered from the upper index, ${\mu }_{1_j}$. Note also that the power

$$\begin{array}{c}\hfill p=(i-1)/z\end{array}$$

(53)

defines the level of fractional derivative. For Example we have

$$\begin{array}{c}\hfill {\left({\partial }_{{\mu }_{i_j}}\right)}^{1/z}={\left({\displaystyle \frac{\partial }{\partial x^{{\mu }_{i_j}}}}\right)}^{1/z}\end{array}$$

(54)

the one zth fractional derivative, while

$$\begin{array}{c}\hfill {\left({\partial }_{{\mu }_{i_j}}\right)}^{3/z}={\left({\displaystyle \frac{\partial }{\partial x^{{\mu }_{i_j}}}}\right)}^{3/z}\end{array}$$

(55)

the three zth fractional derivative.

3.3. Transformation

We introduce the concept of transformations of standard tensors. Then we construct the transformation of generalised tensors, using 1-forms, partial derivatives, and fractional partial derivatives.

3.3.1. Transformation of standard tensors

The $(1,0)$-rank tensor is transformed as

$$\begin{array}{c}\hfill V^{\mu }\to V^{{\mu }^{\prime }}=V^{\mu }{\displaystyle \frac{\partial x^{{\mu }^{\prime }}}{\partial x^{\mu }}}\end{array}$$

(56)

The $(0,1)$-rank tensor is transformed as

$$\begin{array}{c}\hfill V_{\mu }\to V_{{\mu }^{\prime }}=V_{\mu }{\displaystyle \frac{\partial x^{\mu }}{\partial x^{{\mu }^{\prime }}}}\end{array}$$

(57)

A $(1,1)$-rank tensor is transformed as

$$\begin{array}{c}\hfill {T^{\mu }}_{\nu }\to {T^{{\mu }^{\prime }}}_{{\nu }^{\prime }}={T^{\mu }}_{\nu }{\displaystyle \frac{\partial x^{{\mu }^{\prime }}}{\partial x^{\mu }}}{\displaystyle \frac{\partial x^{\nu }}{\partial x^{{\nu }^{\prime }}}}\end{array}$$

(58)

A $(U,L)$-rank tensor is transformed as

$$\begin{array}{c}\hfill {T^{{\mu }_1\cdots {\mu }_U}}_{{\nu }_1\cdots {\nu }_L}\to {T^{{{\mu }_1}^{\prime }\cdots {{\mu }_U}^{\prime }}}_{{{\nu }_1}^{\prime }\cdots {{\nu }_L}^{\prime }}={T^{{\mu }_1\cdots {\mu }_U}}_{{\nu }_1\cdots {\nu }_L}{\displaystyle \frac{\partial x^{{\mu }_1^{\prime }}}{\partial x^{{\mu }_1}}}\cdots {\displaystyle \frac{\partial x^{{\mu }_U^{\prime }}}{\partial x^{{\mu }_U}}}{\displaystyle \frac{\partial x^{{\nu }_1}}{\partial x^{{\nu }_1^{\prime }}}}\cdots {\displaystyle \frac{\partial x^{{\nu }_L}}{\partial x^{{\nu }_L^{\prime }}}}\end{array}$$

(59)

3.4. Transformations of Generalised Tensors

We consider the generalised $(1,1,1)$-rank tensor, the generalised $(A,B,\Gamma )$-rank, and the generalised $(A,B,\Gamma ,\cdots ,\mathrm{\Omega })$-rank tensor.

This generalised $(1,1,1)$-rank tensor is transformed as follows:

$$\begin{array}{c}\hfill {{{\mathcal{T}}^{{\alpha }^{\prime }}}_{{\beta }^{\prime }}}_{{\gamma }^{\prime }}={{{\mathcal{T}}^{\alpha }}_{\beta }}_{\gamma }{\displaystyle \frac{\partial x^{{\alpha }^{\prime }}}{\partial x^{\alpha }}}{\displaystyle \frac{{\partial }^{1/2}{x}^{\beta }}{{\left(\partial x^{{\beta }^{\prime }}\right)}^{1/2}}}{\displaystyle \frac{\partial x^{\gamma }}{\partial x^{{\gamma }^{\prime }}}}\end{array}$$

(60)

This $(A,B,\Gamma )$-rank generalised tensor is transformed as

(61)

where

$$\begin{array}{c}\hfill {{{\mathcal{T}}^{{\alpha }_1^{\prime }\cdots {\alpha }_A^{\prime }}}_{{\beta }_1^{\prime }\cdots {\beta }_B^{\prime }}}_{{\gamma }_1^{\prime }\cdots {\gamma }_{\Gamma }^{\prime }}={{{\mathcal{T}}^{{\alpha }_1\cdots {\alpha }_A}}_{{\beta }_1\cdots {\beta }_B}}_{{\gamma }_1\cdots {\gamma }_{\Gamma }}{\displaystyle \frac{\partial x^{{\alpha }_1^{\prime }}}{\partial x^{{\alpha }_1}}}\cdots {\displaystyle \frac{\partial x^{{\alpha }_A^{\prime }}}{\partial x^{{\alpha }_A}}}{\displaystyle \frac{{\partial }^{1/2}{x}^{{\beta }_1}}{{\left(\partial x^{{\beta }_1^{\prime }}\right)}^{1/2}}}\cdots {\displaystyle \frac{{\partial }^{1/2}{x}^{{\beta }_B}}{{\left(\partial x^{{\beta }_B^{\prime }}\right)}^{1/2}}}{\displaystyle \frac{\partial x^{{\gamma }_1}}{\partial x^{{\gamma }_1^{\prime }}}}\cdots {\displaystyle \frac{\partial x^{{\gamma }_{\Gamma }}}{\partial x^{{\gamma }_{\Gamma }^{\prime }}}}\end{array}$$

(62)

The generalised $(A,B,\Gamma ,\cdots ,\mathrm{\Omega })$-rank tensor, defined in Equation (50), is transformed as

(63)

where

$$\begin{array}{c}\hfill {{{{{\mathcal{T}}^{{\alpha }_1^{\prime }\cdots {\alpha }_A^{\prime }}}_{{\beta }_1^{\prime }\cdots {\beta }_B^{\prime }}}_{{\gamma }_1^{\prime }\cdots {\gamma }_{\Gamma }^{\prime }}}_{\ddots }}_{{\omega }_1^{\prime }\cdots {\omega }_{\mathrm{\Omega }}^{\prime }}={{{{{\mathcal{T}}^{{\alpha }_1\cdots {\alpha }_A}}_{{\beta }_1\cdots {\beta }_B}}_{{\gamma }_1\cdots {\gamma }_{\Gamma }}}_{\ddots }}_{{\omega }_1\cdots {\omega }_{\mathrm{\Omega }}}{\displaystyle \frac{\partial x^{{\alpha }_1^{\prime }}}{\partial x^{{\alpha }_1}}}\cdots {\displaystyle \frac{\partial x^{{\alpha }_A^{\prime }}}{\partial x^{{\alpha }_A}}}{\displaystyle \frac{{\partial }^{1/z}{x}^{{\beta }_1}}{{\left(\partial x^{{\beta }_1^{\prime }}\right)}^{1/z}}}\cdots {\displaystyle \frac{{\partial }^{1/z}{x}^{{\beta }_B}}{{\left(\partial x^{{\beta }_B^{\prime }}\right)}^{1/z}}}{\displaystyle \frac{{\partial }^{2/z}{x}^{{\gamma }_1}}{{\left(\partial x^{{\gamma }_1^{\prime }}\right)}^{2/z}}}\cdots {\displaystyle \frac{{\partial }^{2/z}{x}^{{\gamma }_{\Gamma }}}{{\left(\partial x^{{\gamma }_{\Gamma }^{\prime }}\right)}^{2/z}}}{\displaystyle \frac{\partial x^{{\omega }_1}}{\partial x^{{\omega }_1^{\prime }}}}\cdots {\displaystyle \frac{\partial x^{{\omega }_{\mathrm{\Omega }}}}{\partial x^{{\omega }_{\mathrm{\Omega }}^{\prime }}}}\end{array}$$

(64)

The generalised $(A,B,C,\cdots ,Z)$-rank tensor, defined in Equation (51), is transformed as

(65)

where

$$\begin{array}{c}\hfill {{{{{\mathcal{T}}^{{{\mu }_1}_1^{\prime }\cdots {{\mu }_1}_A^{\prime }}}_{{{\mu }_2}_1^{\prime }\cdots {{\mu }_2}_B^{\prime }}}_{{{\mu }_3}_1^{\prime }\cdots {{\mu }_3}_C^{\prime }}}_{\ddots }}_{{{\mu }_L}_1^{\prime }\cdots {{\mu }_L}_Z^{\prime }}={{{{{\mathcal{T}}^{{{\mu }_1}_1\cdots {{\mu }_1}_A}}_{{{\mu }_2}_1\cdots {{\mu }_2}_B}}_{{{\mu }_3}_1\cdots {{\mu }_3}_C}}_{\ddots }}_{{{\mu }_L}_1\cdots {{\mu }_L}_Z}{\displaystyle \frac{\partial x^{{{\mu }_1}_1^{\prime }}}{\partial x^{{{\mu }_1}_1}}}\cdots {\displaystyle \frac{\partial x^{{{\mu }_1}_A^{\prime }}}{\partial x^{{{\mu }_1}_A}}}{\displaystyle \frac{{\partial }^{1/z}{x}^{{{\mu }_2}_1}}{{\left(\partial x^{{{\mu }_2}_1^{\prime }}\right)}^{1/z}}}\cdots {\displaystyle \frac{{\partial }^{1/z}{x}^{{{\mu }_2}_B}}{{\left(\partial x^{{{\mu }_2}_B^{\prime }}\right)}^{1/z}}}{\displaystyle \frac{{\partial }^{2/z}{x}^{{{\mu }_3}_1}}{{\left(\partial x^{{{\mu }_3}_1^{\prime }}\right)}^{2/z}}}\cdots {\displaystyle \frac{{\partial }^{2/z}{x}^{{{\mu }_3}_C}}{{\left(\partial x^{{{\mu }_3}_C^{\prime }}\right)}^{2/z}}}{\displaystyle \frac{\partial x^{{{\mu }_L}_1}}{\partial x^{{{\mu }_L}_1^{\prime }}}}\cdots {\displaystyle \frac{\partial x^{{{\mu }_L}_Z}}{\partial x^{{{\mu }_L}_Z^{\prime }}}}\end{array}$$

(66)

3.5. Basic Operations

We introduce the concept of basic operations of standard tensors. Then we construct the basic operations of generalised tensors, using 1-forms, partial derivatives, and fractional partial derivatives.

The basic operations include, tensor product, contraction, raising or lowering an index

3.5.1. Standard Tensor Product

We consider the $(L,K)$-rank tensor, S , and the $(N,M)$-rank tensor, T. Then, the standard tensor product, ⊗, is defined as

$$\begin{array}{c}\hfill {{(S\otimes T)}^{i_1\cdots i_L{i}_{L+1}\cdots i_{L+N}}}_{j_1\cdots j_K{j}_{K+1}\cdots j_{K+M}}={S^{i_1\cdots i_L}}_{j_1\cdots j_K}\otimes {T^{i_{L+1}\cdots i_{L+N}}}_{j_{K+1}\cdots j_{K+M}}\end{array}$$

(67)

3.5.2. Standard Tensor Contraction

We consider the $(L,K)$-rank tensor, S , and the $(N,M)$-rank tensor, T. Then, the standard tensor contraction of tensor, S, is defined as follows. The contraction of the first index is defined as

$$\begin{array}{c}\hfill {S^{i_1{i}_2\cdots i_L}}_{i_1{j}_2\cdots j_K}=\sum _{i_1}{S^{i_1{i}_2\cdots i_L}}_{i_1{j}_2\cdots j_K}={S^{i_2\cdots i_L}}_{j_2\cdots j_K}\end{array}$$

(68)

The contraction up to p-index is defined as

$$\begin{array}{c}\hfill {S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_L}}_{i_1\cdots i_p{j}_{p+1}\cdots j_K}=\sum _{i_1\cdots i_p}{S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_L}}_{i_1\cdots i_p{j}_{p+1}\cdots j_K}={S^{i_{p+1}\cdots i_L}}_{j_{p+1}\cdots j_K}\end{array}$$

(69)

The contraction up to p-up index and q-down index of two tensor is defined as

$$\begin{array}{cc}\hfill & {S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_L}}_{i_1\cdots i_q{j}_{q+1}\cdots j_K}{T_{i_1\cdots i_p{i}_{L+p+1}\cdots i_{L+N}}}^{i_1\cdots i_q{j}_{K+q+1}\cdots j_{K+M}}\hfill \\ \hfill =\\ \hfill & {S^{i_{p+1}\cdots i_L}}_{j_{q+1}\cdots j_K}{T_{i_{L+p+1}\cdots i_{L+N}}}^{j_{K+q+1}\cdots j_{K+M}}\hfill \end{array}$$

(70)

3.5.3. Standard Tensors’ Lowering and Rising Indices

We consider the $(L,K)$-rank tensor, S , and the $(N,M)$-rank tensor, T. Then, the standard tensor contraction of tensor, S, is defined as follows. The lower the first p upper indices rising the first q lower indices is defined as

$$\begin{array}{cc}\hfill & {S^{i_1\cdots i_p{i}_{p+1}\cdots i_L}}_{j_1\cdots j_q{j}_{q+1}\cdots j_K}\hfill \\ \hfill & ={{S_{i_1^{\prime }\cdots i_p^{\prime }}}^{i_{p+1}\cdots i_L{j}_1^{\prime }\cdots j_q^{\prime }}}_{j_{q+1}\cdots j_K}{g}^{i_1^{\prime }{i}_1}\cdots g^{i_p^{\prime }{i}_p}{g}_{j_1^{\prime }{j}_1}\cdots g^{j_q^{\prime }{i}_q}\hfill \end{array}$$

(71)

The contraction up to p-index is defined as

$$\begin{array}{c}\hfill {S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_L}}_{i_1\cdots i_p{j}_{p+1}\cdots j_K}=\sum _{i_1\cdots i_p}{S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_L}}_{i_1\cdots i_p{j}_{p+1}\cdots j_K}={S^{i_{p+1}\cdots i_L}}_{j_{p+1}\cdots j_K}\end{array}$$

(72)

The contraction up to p-up index and q-down index of two tensor is defined as

$$\begin{array}{cc}\hfill & {S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_L}}_{j_1\cdots j_q{j}_{q+1}\cdots j_K}{T_{i_1\cdots i_p{i}_{L+p+1}\cdots i_{L+N}}}^{j_1\cdots j_q{j}_{K+q+1}\cdots j_{K+M}}\hfill \\ \hfill =\\ \hfill & {S^{i_{p+1}\cdots i_L}}_{j_{q+1}\cdots j_K}{T_{i_{L+p+1}\cdots i_{L+N}}}^{j_{K+q+1}\cdots j_{K+M}}\hfill \end{array}$$

(73)

3.5.4. Generalised Tensor Contraction

We consider the generalised $(3,4,5)$- rank tensor, which is given via

$$\begin{array}{c}\hfill \mathcal{T}={{{\mathcal{T}}_{{\alpha }_1{\alpha }_2{\alpha }_3}}^{{\beta }_1{\beta }_2{\beta }_3{\beta }_4}}^{{\gamma }_1{\gamma }_2{\gamma }_3{\gamma }_4{\gamma }_5}d{x}^{{\alpha }_1}\otimes d{x}^{{\alpha }_2}\otimes d{x}^{{\alpha }_3}\otimes {\left({\partial }_{{\beta }_1}\right)}^{1/2}\otimes {\left({\partial }_{{\beta }_2}\right)}^{1/2}\otimes {\left({\partial }_{{\beta }_3}\right)}^{1/2}\otimes {\left({\partial }_{{\beta }_4}\right)}^{1/2}\otimes {\partial }_{{\gamma }_1}\otimes {\partial }_{{\gamma }_2}\otimes {\partial }_{{\gamma }_3}\otimes {\partial }_{{\gamma }_4}\otimes {\partial }_{{\gamma }_5}.\end{array}$$

(74)

Then the contraction of this object from $(3,4,5)$-rank tensor to a $(1,2,3)$-rank tensor, is given by

(75)

We consider the generalised $(A,B,\Gamma )$-rank. The contraction from generalised $(A,B,\Gamma )$-rank to generalised $(A-2,B-2,\Gamma -2)$-rank is given by

(76)

We consider the generalised $(A,B,\Gamma ,\cdots ,\mathrm{\Omega })$-rank tensor. The contraction from generalised $(A,B,\cdots ,\mathrm{\Omega })$-rank to generalised $(A-2,B-2,\cdots ,\mathrm{\Omega }-2)$-rank is given by

(77)

3.5.5. Generalised Tensors’ Lowering and Rising Indices

We can consider the tensor

$$\begin{array}{c}\hfill {{{\mathcal{T}}^{\alpha }}_{\beta }}_{\gamma }\end{array}$$

(78)

Then we can consider a standard metric, which is

$$\begin{array}{c}\hfill {g^{\alpha }}_{\beta }\end{array}$$

(79)

which the upper indices will increase one layer upwards an index of a tensor, while the lower, will move an index one layer downward for a tensor.

Then we can make the tensor to have the upper index to move to the middle, while the middle to move to the upper layer by the following operation

$$\begin{array}{c}\hfill {{{\mathcal{T}}^{{\beta }^{\prime }}}_{{\alpha }^{\prime }}}_{\gamma }={{{\mathcal{T}}^{\alpha }}_{\beta }}_{\gamma }{g}^{{\beta }^{\prime }\beta }{g}_{{\alpha }^{\prime }\alpha }\end{array}$$

(80)

while we can also have

$$\begin{array}{c}\hfill {{{\mathcal{T}}^{\alpha }}_{{\gamma }^{\prime }}}_{{\beta }^{\prime }}={{{\mathcal{T}}^{\alpha }}_{\beta }}_{\gamma }{g}_{{\beta }^{\prime }\beta }{g}^{{\gamma }^{\prime }\gamma }\end{array}$$

(81)

or

$$\begin{array}{c}\hfill {{{\mathcal{T}}^{{\gamma }^{\prime }}}_{{\beta }^{\prime }}}_{{\alpha }^{\prime }}={{{\mathcal{T}}^{\alpha }}_{\beta }}_{\gamma }{g}_{{\alpha }^{\prime }\alpha }{g}^{{\gamma }^{\prime }\gamma }\end{array}$$

(82)

Then we can lower and upper the indices as follows

We consider the $(I,J,K)$-rank tensor, S , and the $(N,M,P)$-rank tensor, T. Then, the standard tensor contraction of tensor, S, is defined as follows. The lower the first p upper indices rising the first q lower indices is defined as

$$\begin{array}{cc}\hfill & {{S^{i_1\cdots i_p{i}_{p+1}\cdots i_I}}_{j_1\cdots j_q{j}_{q+1}\cdots j_J}}_{k_1\cdots k_r{k}_{r+1}\cdots k_K}\hfill \\ \hfill & ={{{{S_{i_1^{\prime }\cdots i_p^{\prime }}}^{i_{p+1}\cdots i_I{j}_1^{\prime }\cdots j_q^{\prime }}}_{j_{q+1}\cdots j_J}}_{i_1\cdots i_r{i}_{r+1}\cdots i_A}}_{k_1\cdots k_r{k}_{r+1}\cdots k_K}{g}^{i_1^{\prime }{i}_1}\cdots g^{i_p^{\prime }{i}_p}{g}_{j_1^{\prime }{j}_1}\cdots g^{j_q^{\prime }{i}_q}\hfill \end{array}$$

(83)

The contraction up to p-index is defined as

$$\begin{array}{cc}\hfill {{S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_I}}_{i_1\cdots i_p{j}_{p+1}\cdots j_J}}_{k_1\cdots k_r{k}_{r+1}\cdots k_K}& =\sum _{i_1\cdots i_p}{{S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_I}}_{i_1\cdots i_p{j}_{p+1}\cdots j_J}}_{k_1\cdots k_r{k}_{r+1}\cdots k_K}\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill & ={{S^{i_{p+1}\cdots i_I}}_{j_{p+1}\cdots j_J}}_{k_1\cdots k_r{k}_{r+1}\cdots i_K}\hfill \end{array}$$

(85)

The contraction up to p-up index and q-down index of two tensor is defined as

$$\begin{array}{cc}\hfill & {{S^{i_1{i}_2\cdots i_p{i}_{p+1}\cdots i_I}}_{j_1\cdots j_q{j}_{q+1}\cdots j_J}}_{k_1\cdots k_r{k}_{r+1}\cdots k_K}{{T_{i_1\cdots i_p{i}_{I+s+1}\cdots i_{I+N}}}^{j_1\cdots j_q{j}_{J+t+1}\cdots j_{J+M}}}^{k_1\cdots k_r{k}_{K+u+1}\cdots k_{K+P}}\hfill \\ \hfill & ={{S^{i_{p+1}\cdots i_I}}_{j_{q+1}\cdots j_J}}_{k_{r+1}\cdots k_K}{{T_{i_{I+s+1}\cdots i_{I+N}}}^{j_{J+t+1}\cdots j_{J+M}}}^{k_{K+u+1}\cdots k_{K+P}}\hfill \end{array}$$

(86)

4. Geometrical Interpretation of Generalised Tensors Using Fractional Derivatives

In this section, we introduce the geometrical interpretation of the generalised tensors.

Following [12], we propose the following geometrical interpretation of fractional derivatives.

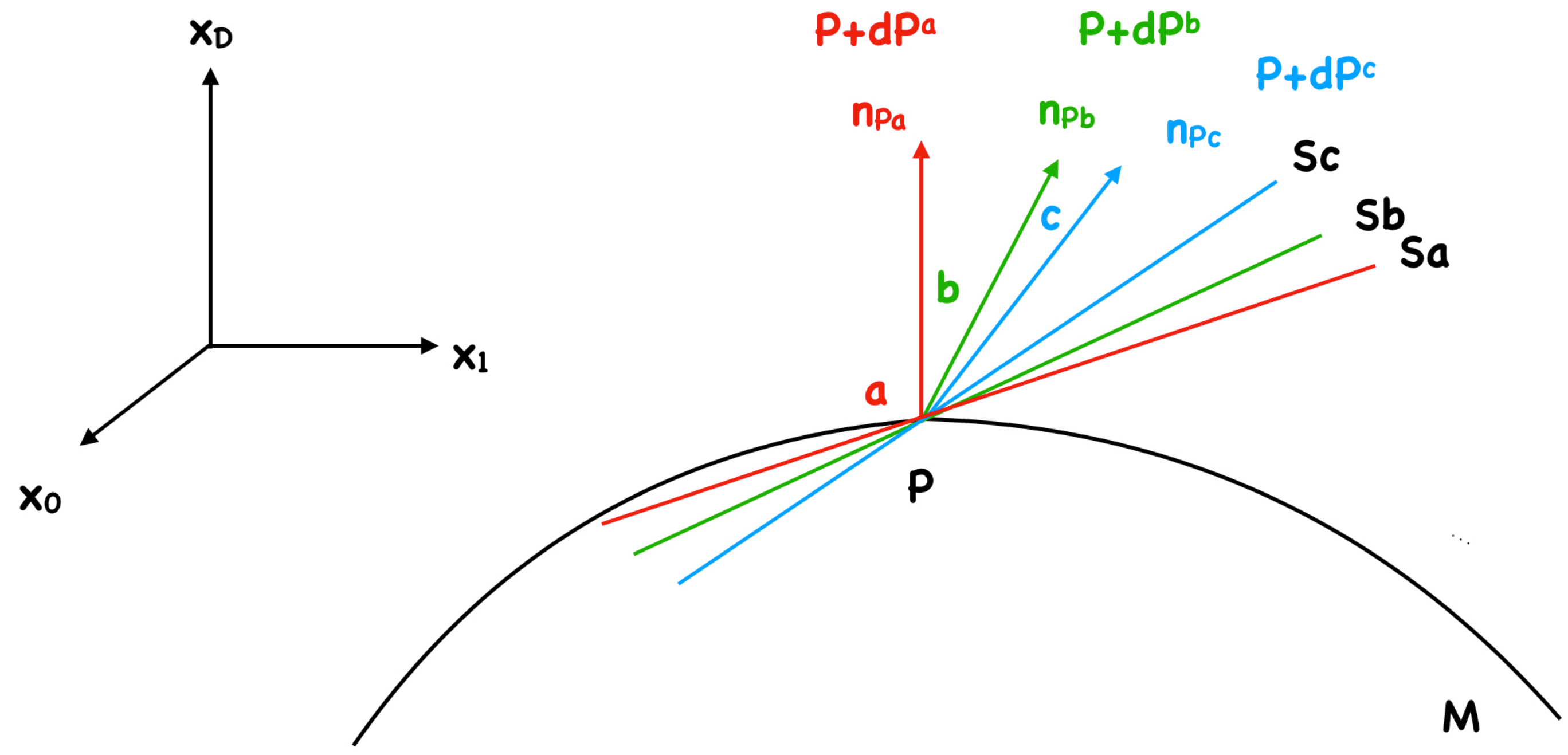
Let $\mathcal{M}$ be a Manifold, of D-dimensions, with $(x_0,x_1,\cdots ,x_D$ coordinates. Let $\mathcal{P}$ be a point, and $d\mathcal{P}$ is an infinitesimal space away from this point, $\mathcal{P}$. Then the actual derivative will construct a tangent sub-manifold, $\mathcal{TM}$, to this point, according to the operation on any functor, $\mathcal{F}$, that passes from $\mathcal{P}$, to be

$$\begin{array}{c}\hfill d\mathcal{F}={\partial }_{\mu }\mathcal{F}d{P}^{\mu }.\end{array}$$

(87)

Then this derivative will have an associated normal vector which is perpendicular to the tangent sub-manifold, $\mathcal{TM}$. This normal vector is n.

Now a fractional derivative, of fraction, a, will have a derivative at point $\mathcal{P}$, as

$$\begin{array}{c}\hfill d^a\mathcal{F}={\left({\partial }_{\mu }\right)}^a\mathcal{F}{\left(d{P}^{\mu }\right)}^a.\end{array}$$

(88)

which will correspond to a Tangent sub-manifold ${\mathcal{TM}}^a$, with a vector which has some angle, $a\ne {90}^o$.

Then we can have a submanifold, which corresponds to a fractional derivative of fraction, b, or c and so on. We illustrate this result to Figure 1.

Following the duality to triality extension [3], we can extend triality to any D-ality property.

Remark 2. 

The $(1,1,1)$ and $(A,B,\Gamma )$-rank tensors conceptualise in tensor formalism the concept of triality of vectors [3]. Note that the $(A,B,\Gamma ,\cdots ,\mathrm{\Omega })$ and $(A,B,C,\cdots ,Z)$-rank tensors conceptualise in tensor formalism the concept of Ω-ality and Z-ality relations of vectors spaces, which is an extension of the work of triality found in [3].

4.1. Geometrical Interpretation

Let’s consider the following generalised tensor:

$$T={{T_{{\mu }_{\mathrm{down}}}}^{{\mu }_{\mathrm{middle}}}}^{{\mu }_{\mathrm{up}}}d{x}^{{\mu }_{\mathrm{up}}}\otimes {\displaystyle \frac{{\partial }^{1/2}}{{\left(\partial x^{{\mu }_{\mathrm{middle}}}\right)}^{1/2}}}\otimes {\displaystyle \frac{\partial }{\partial x^{{\mu }_{\mathrm{up}}}}}$$

This generalised tensor correctly represents a tensor with three indices, where:

- ${\mu }_{\mathrm{up}}$ is the upper index.

- ${\mu }_{\mathrm{middle}}$ is the middle index.

- ${\mu }_{\mathrm{down}}$ is the lower index.

4.1.1. Geometrical Interpretation of a Tensor with Three Indices: One Up, One Middle, One Down

To interpret a tensor with three indices one upper, one middle, and one lower. Let’s think about what each index represents geometrically:

1. Traditional Tensors:

- Contravariant Index (Upper Index ${\mu }_{\mathrm{up}}$): Represents components that transform oppositely to coordinate transformations (basis vectors), such as vectors.

- Covariant Index (Lower Index ${\mu }_{\mathrm{down}}$): Represents components that transform similarly to coordinate transformations (dual basis vectors), such as covectors or one-forms.

2. “Middle” Index Interpretation:

- The “middle” index ${\mu }_{\mathrm{middle}}$ suggests a different kind of interaction or relationship that isn’t purely contravariant or covariant in the traditional sense.

In the following subsubsection we represent some possible interpretations.

4.1.2. Geometric Interpretation Possibilities

- Transformation Between Two Different Spaces or Layers:

1) A tensor with three indices can be thought of as an operator that takes input from one vector space and maps it to another while taking into account a transformation or relationship given by the middle index.

2) For Example, if the upper index ${\mu }_{\mathrm{up}}$ corresponds to a contravariant vector in one vector space, and the lower index ${\mu }_{\mathrm{down}}$ corresponds to a covariant vector in another space, the middle index ${\mu }_{\mathrm{middle}}$ could represent a mapping or transformation between these two spaces. This is akin to a mixed transformation tensor or an object that mediates between two different layers of geometric structures.

- Multi-Layered Tensor Product or Interaction: The “middle” index could represent an intermediate interaction between the upper and lower indices. For Example, in a physical context, if the upper and lower indices represent different fields or states, the middle index could represent a coupling constant, an intermediate field interaction, or a basis that bridges the contravariant and covariant components. This interpretation might be used in areas like quantum field theory or complex geometrical structures where such intermediate states or interactions are crucial.

- Higher-Order Differential Forms or Geometrical Objects: In differential geometry, higher-order tensors often involve combinations of forms and vectors. The “middle” index might represent an additional layer of structure that combines aspects of both vectors and covectors. In this case, the tensor might represent a higher-order differential form that acts differently depending on the direction of the middle index.

- Curvature-like Structures: In more abstract geometrical frameworks (such as those in advanced differential geometry or complex manifold theory), the “middle” index could denote a type of curvature or torsion that acts upon different tensor components. It might represent how a space curves or twists differently depending on the position or layer represented by the middle index. This can be seen as a generalization of objects like the Riemann curvature tensor.

4.1.3. Conclusion

The tensor with three indices – one upper, one middle, and one lower – could represent a variety of complex geometric or physical structures, depending on the specific nature and transformation properties of the “middle” index. It might denote a transformation between different vector spaces, an intermediate interaction, or even a curvature-like structure that combines and interacts with different geometrical objects or fields. The precise interpretation depends on the context in which this tensor is being used.

5. Applications

Immediate trivial applications of generalised tensor, are similar to the ones of standard tensors. In particular, generalised tensors can be used to compress the information of multiple tensors, much like tensors compress the information of vectors, and much like the vectors compress the informations of scalars. Note also that the structure of information of a vector from scalars, has immediate geometrical implications and interpretations. In the same way the generalised tensors have also geometrical implications and interpretations. However, we will not discuss these concepts in this study, and we will focus on expanding the more abstract applications. In particular, in this section, we construct informal Definitions and their corresponding Examples for combinations of tensors, generalised tensors, generic generalised tensors, categories, functors, and sets.

5.1. Sets and tensors

Basically a tensorial set is the standard application of the Definition of a set which is applied to tensors.

Definition 4. 

Informally, a tensorial set is a collection of tensors.

Example 2. 

Let $T_1$ and $T_2$ be two tensors with distinct ranking and number of elements. Then a tensorial set is defined as

$$\begin{array}{c}\hfill S_T=\left\{T_1,T_2\right\}.\end{array}$$

(89)

On the other hand, we can define a novel concept, the concept of the setorial tensor.

Definition 5. 

A setorial tensor, $T_S$ is a tensor with elements sets, using a generic operation between the sets, denoted with o.

Example 3. 

Let’s consider an Example of a setorial tensor of (2,2)-rank. Let $S_{jk}^{\left(i\right)}$ be the elements of the ith setorial tensors, and j,k indices show the element position of the set in respect of the setorial tensor. These elements are basically distinct sets. Let the operation between these sets be the union operation $o=\cup$. Let a setorial tensor be defined as

$$\begin{array}{c}\hfill T_S^{\left(1\right)}=\left[\begin{array}{cc}{S}_{11}^{\left(1\right)}& S_{12}^{\left(1\right)}\\ S_{21}^{\left(1\right)}& S_{22}^{\left(1\right)}\end{array}\right]\end{array}$$

(90)

Let another setorial tensor be defined as

$$\begin{array}{c}\hfill T_S^{\left(2\right)}=\left[\begin{array}{cc}{S}_{11}^{\left(2\right)}& S_{12}^{\left(2\right)}\\ S_{21}^{\left(2\right)}& S_{22}^{\left(2\right)}\end{array}\right]\end{array}$$

(91)

Then, we can define two operation between the two setorial tensors, the summation or sum, and the product operations. The generic summation operation is defined as

$$\begin{array}{cc}\hfill T_S^{\mathrm{sum}}& =T_S^{\left(1\right)}\oplus T_S^{\left(2\right)}\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}{S}_{11}^{\left(1\right)}& S_{12}^{\left(1\right)}\\ S_{21}^{\left(1\right)}& S_{22}^{\left(1\right)}\end{array}\right]\oplus \left[\begin{array}{cc}{S}_{11}^{\left(2\right)}& S_{12}^{\left(2\right)}\\ S_{21}^{\left(2\right)}& S_{22}^{\left(2\right)}\end{array}\right]\hfill \end{array}$$

(93)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}{S}_{11}^{\left(1\right)}\cup S_{11}^{\left(2\right)}& S_{12}^{\left(1\right)}\cup S_{12}^{\left(2\right)}\\ S_{21}^{\left(1\right)}\cup S_{21}^{\left(2\right)}& S_{22}^{\left(1\right)}\cup S_{22}^{\left(2\right)}\end{array}\right]\hfill \end{array}$$

(94)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}{S}_{11}^{(1\oplus 2)}& S_{12}^{(1\oplus 2)}\\ S_{21}^{(1\oplus 2)}& S_{22}^{(1\oplus 2)}\end{array}\right]\hfill \end{array}$$

(95)

where

$$\begin{array}{c}\hfill S_{jk}^{(1\oplus 2)}=S_{jk}^{\left(1\right)}\cup S_{jk}^{\left(2\right)},\end{array}$$

(96)

is the union of set, $S_{jk}^{\left(1\right)}$ and $S_{jk}^{\left(2\right)}$.

Furthermore we can define the generic product operation between two setorial tensors. In this case, we consider both the union operation, ∪, and the intersection operation ∩. The generic product operation between two setorial tensors can be defined as

$$\begin{array}{cc}\hfill T_S^{\mathrm{product}}& =T_S^{\left(1\right)}\otimes T_S^{\left(2\right)}\hfill \end{array}$$

(97)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}{S}_{11}^{\left(1\right)}& S_{12}^{\left(1\right)}\\ S_{21}^{\left(1\right)}& S_{22}^{\left(1\right)}\end{array}\right]\otimes \left[\begin{array}{cc}{S}_{11}^{\left(2\right)}& S_{12}^{\left(2\right)}\\ S_{21}^{\left(2\right)}& S_{22}^{\left(2\right)}\end{array}\right]\hfill \end{array}$$

(98)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}\left(S_{11}^{\left(1\right)}\cup S_{11}^{\left(2\right)}\right)\cap \left(S_{12}^{\left(1\right)}\cup S_{21}^{\left(2\right)}\right)& \left(S_{11}^{\left(1\right)}\cup S_{12}^{\left(2\right)}\right)\cap \left(S_{12}^{\left(1\right)}\cup S_{22}^{\left(2\right)}\right)\\ \left(S_{12}^{\left(1\right)}\cup S_{11}^{\left(2\right)}\right)\cap \left(S_{22}^{\left(1\right)}\cup S_{21}^{\left(2\right)}\right)& \left(S_{12}^{\left(1\right)}\cup S_{12}^{\left(2\right)}\right)\cap \left(S_{22}^{\left(1\right)}\cup S_{22}^{\left(2\right)}\right)\end{array}\right]\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}{S}_{11}^{(1\otimes 2)}& S_{12}^{(1\otimes 2)}\\ S_{21}^{(1\otimes 2)}& S_{22}^{(1\otimes 2)}\end{array}\right]\hfill \end{array}$$

(100)

where

$$\begin{array}{cc}\hfill S_{11}^{(1\otimes 2)}& =\left(S_{11}^{\left(1\right)}\cup S_{11}^{\left(2\right)}\right)\cap \left(S_{12}^{\left(1\right)}\cup S_{21}^{\left(2\right)}\right)\hfill \end{array}$$

(101)

$$\begin{array}{cc}\hfill S_{12}^{(1\otimes 2)}& =\left(S_{11}^{\left(1\right)}\cup S_{12}^{\left(2\right)}\right)\cap \left(S_{12}^{\left(1\right)}\cup S_{22}^{\left(2\right)}\right)\hfill \end{array}$$

(102)

$$\begin{array}{cc}\hfill S_{21}^{(1\otimes 2)}& =\left(S_{12}^{\left(1\right)}\cup S_{11}^{\left(2\right)}\right)\cap \left(S_{22}^{\left(1\right)}\cup S_{21}^{\left(2\right)}\right)\hfill \end{array}$$

(103)

$$\begin{array}{cc}\hfill S_{22}^{(1\otimes 2)}& =\left(S_{12}^{\left(1\right)}\cup S_{12}^{\left(2\right)}\right)\cap \left(S_{22}^{\left(1\right)}\cup S_{22}^{\left(2\right)}\right)\hfill \end{array}$$

(104)

are the corresponding union and intersections of the corresponding combinations of sets, $S_{jk}^{\left(i\right)}$.

5.2. Categories and tensors

Basically a tensorial category is the standard application of the Definition of a category which is applied to tensors.

Definition 6. 

A tensorial category, ${\mathcal{C}}_T$, is a category with elements which are tensors and a morphism between the tensors which is a functor built with the tensor product.

Example 4. 

We can construct the tensorial category which is given by the following signature:

$$\begin{array}{c}\hfill {\mathcal{C}}_T=\left\{{\mathbb{o}}_T,{\mathbb{m}}_F;\mathbb{c},\mathbb{i},\mathbb{a}\right\}\end{array}$$

(105)

where $\mathbb{c},\mathbb{i}$ and $\mathbb{a}$ are the standard properties of composition, identity, and associativity, while ${\mathbb{o}}_T$ is the collection of objects which objects are tensors, and ${\mathbb{m}}_F$ is the collection of morphisms which is basically the tensorial product.

On the other hand, we can define a novel concept, the concept of categorial tensor.

Definition 7. 

A categorial tensor, ${\mathcal{T}}_C$ is a tensor with elements which are categories, and a generic morphism between categories, i.e., a functor F.

Example 5. 

Since categories are used as entities and functors as map from one such entity to another then a functorial tensor can map a collection of categorial vectors to a category.

$$\begin{array}{cc}\hfill \mathcal{T}& :{\mathcal{C}}_{\mathrm{SOURCE}}\to {\mathcal{C}}_{\mathrm{TARGET}}\hfill \end{array}$$

(106)

$$\begin{array}{cc}\hfill {{\mathcal{T}}^{\alpha }}_{\beta }& :{\mathcal{C}}^{\alpha }\otimes {\mathcal{B}}_{\beta }\to {\mathcal{C}}_{\mathrm{TARGET}}\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill {{\mathcal{T}}^{{\alpha }_{-U}\cdots {\alpha }_U}}_{{\beta }_{-L}\cdots {\beta }_L}& :\underset{i=-U}{\overset{U}{⨂}}{\mathcal{C}}^{{\alpha }_i}\otimes \underset{j=-L}{\overset{L}{⨂}}{\mathcal{B}}_{{\beta }_j}\to {\mathcal{C}}_{\mathrm{TARGET}}\hfill \end{array}$$

(108)

where ${\mathcal{C}}_{\mathrm{TARGET}}$ is the target category, ${\mathcal{C}}_{\mathrm{SOURCE}}$ is the source category, and the index is just a name in these two cases.

This lead us to the construction of the generalised tensor of categories written as:

(109)

which means

(110)

. Having this generalised tensor, we can proceed to a more generic generalised tensor.

Now we can build the generic generalised tensor of categories by considering another layer of generalisation, in which we have index of the index of the index repeatedly. We consider the aforementioned index, $\mathcal{I}={\ell }_{k_{{\cdots }_{j_i}}}$. This is basically defined as

$$\begin{array}{c}\hfill \mathcal{T}:\mathcal{C}\to \mathcal{D}\end{array}$$

(111)

or

$$\begin{array}{cc}\hfill \mathcal{T}& :\underset{\mathcal{I}}{⨂}{\mathcal{C}}^{\mathcal{I}}\to \mathcal{D}\hfill \end{array}$$

(112)

or

$$\begin{array}{cc}\hfill \mathcal{T}& :\underset{i=-L}{\overset{L}{⨂}}\underset{j_i=-L_{j_i}}{\overset{L_{j_i}}{⨂}}\cdots \underset{{\ell }_{k_{{\cdots }_{j_i}}}=U_{k_{{\cdots }_{j_i}}}}{\overset{-U_{k_{{\cdots }_{j_i}}}}{⨂}}{\mathcal{C}}^{{\ell }_{k_{{\cdots }_{j_i}}}}\to \mathcal{D}\hfill \end{array}$$

(113)

where ${\mathcal{C}}^{\mathcal{I}}={\mathcal{C}}^{{\ell }_{k_{{\cdots }_{j_i}}}}$ is a vector with category elements, and $\mathcal{D}$ is the target category.

5.3. Functors and tensors

Basically a tensorial functor is the standard application of the Definition of a functor which is applied to tensors.

Definition 8. 

A tensorial functor is a functor which is constructed with tensorial product which maps tensor elements from one set to a real number.

Example 6. 

Let $F_T$ be a functor and T a tensor. Then, $F_T$ is a tensorial functor if

$$\begin{array}{cc}\hfill F_T& =T\hfill \end{array}$$

(114)

where

$$\begin{array}{cc}\hfill T& :\underset{i=1}{\overset{p}{⨂}}{V}_i^{*}\underset{j=1}{\overset{q}{⨂}}{V}_j\to \mathbb{R},\hfill \end{array}$$

(115)

is a simple tensor, as defined by Equation (1).

Another Example of a tensorial functor would be a tensorial functor which is applied to a generic generalised tensor.

Definition 9. 

A tensorial functor is a functor which is constructed with generic tensorial product which maps tensor elements from one set to a generic number, $\mathbb{G}$.

Example 7. 

Let $F_{GT}$ be a functor and $T_G$ a generic generalised tensor. Then, $F_{GT}$ is a generic generalised tensorial functor if

$$\begin{array}{cc}\hfill F_{GT}& =T_G\hfill \end{array}$$

(116)

where

$$\begin{array}{cc}\hfill T_G& :\underset{\mathcal{I}\in \mathbb{G}}{⨂}{\mathcal{V}}^{\mathcal{I}}\to \mathbb{G}\hfill \end{array}$$

(117)

is a generic generalised tensor, as defined by Equation (41).

On the other hand, we can define a novel concept, the concept of the functorial tensor.

Definition 10. 

A functorial tensor, $T_F$ is a tensor with elements functors, and a generic morphism between functors, i.e., a functor of functors $\mathbb{F}$.

Example 8. 

Let $T_F^{\left(i\right)}$ be a collection of tensors of ($2,2$)-rank, with functors as elements, where $i=1,2$. Let $F_{jk}^{\left(i\right)}$ is a collection of functors, where the upper index shows which tensor these elements belong to, while the two lower indices, $j,k$ denote the position of the functor inside the tensor. We can construct a simple functorial tensor, $T_F$, of ($2,2$)-rank, as

$$\begin{array}{c}\hfill T_F^{\left(1\right)}=\left[\begin{array}{cc}{F}_{11}^{\left(1\right)}& F_{12}^{\left(1\right)}\\ F_{21}^{\left(1\right)}& F_{22}^{\left(1\right)}\end{array}\right]\end{array}$$

(118)

and another one as

$$\begin{array}{c}\hfill T_F^{\left(2\right)}=\left[\begin{array}{cc}{F}_{11}^{\left(2\right)}& F_{12}^{\left(2\right)}\\ F_{21}^{\left(2\right)}& F_{22}^{\left(2\right)}\end{array}\right]\end{array}$$

(119)

Then the morphism between the two tensors would be a functor of functors, denoted with $\stackrel{\mathbb{F}}{\to }$, since this objects represents the morphism which maps a functor to another functor. Then the operation between the two tensor is defined as

$$\begin{array}{cc}\hfill T_F^{\mathrm{operation}}& :T_F^{\left(1\right)}\stackrel{\mathbb{F}}{\to }{T}_F^{\left(2\right)}\hfill \end{array}$$

(120)

$$\begin{array}{cc}\hfill T_F^{\mathrm{operation}}& =\left[\begin{array}{cc}{F}_{11}^{\left(1\right)}& F_{12}^{\left(1\right)}\\ F_{21}^{\left(1\right)}& F_{22}^{\left(1\right)}\end{array}\right]\stackrel{\mathbb{F}}{\to }\left[\begin{array}{cc}{F}_{11}^{\left(2\right)}& F_{12}^{\left(2\right)}\\ F_{21}^{\left(2\right)}& F_{22}^{\left(2\right)}\end{array}\right]\hfill \end{array}$$

(121)

$$\begin{array}{cc}\hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{cc}{F}_{11}^{\left(1\right)}\stackrel{\mathbb{F}}{\to }{F}_{11}^{\left(2\right)}& F_{12}^{\left(1\right)}\stackrel{\mathbb{F}}{\to }{F}_{12}^{\left(2\right)}\\ F_{21}^{\left(1\right)}\stackrel{\mathbb{F}}{\to }{F}_{21}^{\left(2\right)}& F_{22}^{\left(1\right)}\stackrel{\mathbb{F}}{\to }{F}_{22}^{\left(2\right)}\end{array}\right]\hfill \end{array}$$

(122)

$$\begin{array}{cc}\hfill & =\left[\begin{array}{cc}{F}_{11}^{\left(1\stackrel{\mathbb{F}}{\to }2\right)}& F_{12}^{\left(1\stackrel{\mathbb{F}}{\to }2\right)}\\ F_{21}^{\left(1\stackrel{\mathbb{F}}{\to }2\right)}& F_{22}^{\left(1\stackrel{\mathbb{F}}{\to }2\right)}\end{array}\right]\hfill \end{array}$$

(123)

where

$$\begin{array}{c}\hfill F_{jk}^{\left(1\stackrel{\mathbb{F}}{\to }2\right)}=F_{jk}^{\left(1\right)}\stackrel{\mathbb{F}}{\to }{F}_{jk}^{\left(2\right)}\end{array}$$

(124)

is the elements of the sum of the two functorial tensors. Diagrammatically, Equation (124) this is written also in the form of functor of functors as

$$\begin{array}{cc}\hfill \mathbb{F}:F_{jk}^{\left(1\right)}& \to F_{jk}^{\left(2\right)}\hfill \end{array}$$

(125)

$$\begin{array}{cc}\hfill F_{jk}^{\left(1\right)}& \stackrel{\mathbb{F}}{\to }{F}_{jk}^{\left(2\right)}\hfill \end{array}$$

(126)

for every $j,k$.

6. Conclusion

In this study, we have delved into the foundational principles of tensor theory and category, inovatively crafting new concepts based on these fundamentals.

Our work extends prior conventions by generalizing the tensor concept, introducing the versatile generalized tensor index that encapsulates diverse tensor indices. After introducing the concept of transformation of tranditional tensors, we constructed the transformation of generalised tensors using fractional derivatives. Furthermore we describe the geometrical interpretation of these generalised tensors. We’ve also forged a deep connection between category theory and tensor theory, exploring the fusion of sets, tensors, categories, functors, and their extensions. Notably, we’ve introduced novel concepts like setorial tensors, functorial tensors, and categorial tensors. These extensions find applications to partial differention and integration.

In conclusion, this study paves the way for fresh perspectives in mathematical analysis, tensor theory, set theory, functor calculus, category theory, mathematical logic, partial differentiation, integration, physics and philosophy.