Nonconforming Finite Elements and Multigrid Methods for Maxwell Eigenvalue Problem

1. Introduction

Let $\mathrm{\Omega }$ be a bounded polynomial domain in ${\mathbb{R}}^2$. We consider the following Maxwell eigenvalue problem:

Find $(u,\lambda )\in H_0(\mathrm{curl};\mathrm{\Omega })\cap H({\mathrm{div}}^0;\mathrm{\Omega })$ such that

$$(\mathrm{\nabla }\times u,\mathrm{\nabla }\times \mathbf{v})=\lambda (u,\mathbf{v})\forall v\in H_0(\mathrm{curl};\mathrm{\Omega })\cap H({\mathrm{div}}^0;\mathrm{\Omega }),$$

(1.1)

where $(·,·)$ denotes the inner product in ${\left[L_2\left(\mathrm{\Omega }\right)\right]}^2$, and the function spaces are defined as follows.

$$\begin{array}{cc}\hfill H(\mathrm{curl};\mathrm{\Omega })& =\left\{\mathbf{v}=\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\in {\left[L_2\left(\mathrm{\Omega }\right)\right]}^2:\mathrm{\nabla }\times \mathbf{v}={\displaystyle \frac{\partial v_2}{\partial x_1}}-{\displaystyle \frac{\partial v_1}{\partial x_2}}\in L_2\left(\mathrm{\Omega }\right)\right\},\hfill \\ \hfill H(\mathrm{div};\mathrm{\Omega })& =\left\{\mathbf{v}=\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\in {\left[L_2\left(\mathrm{\Omega }\right)\right]}^2:\mathrm{\nabla }·\mathbf{v}={\displaystyle \frac{\partial v_2}{\partial x_1}}+{\displaystyle \frac{\partial v_1}{\partial x_2}}\in L_2\left(\mathrm{\Omega }\right)\right\},\hfill \\ \hfill H_0(\mathrm{curl};\mathrm{\Omega })& =\{\mathbf{v}\in H(\mathrm{curl};\mathrm{\Omega }):\mathbf{n}\times \mathbf{v}=0\mathrm{on}\partial \mathrm{\Omega }\},\hfill \\ \hfill H({\mathrm{div}}^0;\mathrm{\Omega })& =\{\mathbf{v}\in H(\mathrm{div};\mathrm{\Omega }):\mathrm{\nabla }·\mathbf{v}=0\}.\hfill \end{array}$$

Here, the vector $\mathbf{n}$ is the unit outer normal on $\partial \mathrm{\Omega }$.

Since the eigenfunction u has divergence-free constraint, it is not easy to achieve in numerical approximations. [1,2,3,4,5,6,7,8,9,10] replace the Maxwell eigenvalue problem with the following by neglecting the divergence-free condition:

Find $(u,\lambda )\in H_0(\mathrm{curl};\mathrm{\Omega })\times \mathbb{R}$ such that $u\ne 0$,

$$(\mathrm{\nabla }\times u,\mathrm{\nabla }\times \mathbf{v})=\lambda (u,\mathbf{v})\forall v\in H_0(\mathrm{curl};\mathrm{\Omega }).$$

(1.2)

However, (1.2) introduces a non-physical zero eigenvalue into the spectrum. It will add more complexity when we analyze the eigensolvers.

In this paper, we present a numerical scheme by relating eigensolvers to a curl-curl problem. The scheme was proposed early in [11]. Note that the curl-curl problem is solved by different methods such as a nonconforming finite element [12], a mixed finite element methods [13] and a nonconforming penalty method [14]. In addition, [15,16] also give optimal order error estimates in $L_2$-norm and energy norm.

In order to simplify the problem into several scalar elliptic boundary value problems, we turn to introduce the Hodge decomposition, which has been applied to many problems. For example, the quad-curl Problem in [17], the Maxwell’s equations in [18] and the two-dimensional time-harmonic Maxwell’s equations with impedance boundary condition in [19]. Besides, [5] and [18] discuss the Hodge decomposition for three-dimensional vector fields. Furthermore, the multigrid method is proposed for solving some boundary value problems in this work. It has been used in many works such as quantum eigenvalue problems [21], nonlinear eigenvalue problems based on Newton iteration [22] and coupled semilinear elliptic equation [23].

The rest of the paper is organized as follows. We analyze discrete problems based on graded meshes in Section 2. Then we introduce multigrid methods and derive related convergence rates in Section 3. In Section 4, we report the numerical results.

2. Discrete Problems Based on Graded Meshes

In this section, we present an eigensolver which is related to a curl-curl problem. Furthermore, by applying the Hodge decomposition and the nonconforming finite elements, the convergence results are given.

2.1. Construction of Maxwell Eigensolver

We introduce a bounded linear operator $T:{\left[L_2\left(\mathrm{\Omega }\right)\right]}^2\to {\left[L_2\left(\mathrm{\Omega }\right)\right]}^2$ for the Maxwell eigenvalue problem (1.1). Given any function $f\in {\left[L_2\left(\mathrm{\Omega }\right)\right]}^2$, we define $Tf$ with the condition

$$(\mathrm{\nabla }\times Tf,\mathrm{\nabla }\times v)+(Tf,v)=(f,v),$$

(2.1)

for all $v\in H_0(curl;\mathrm{\Omega })\cap H({div}^0;\mathrm{\Omega })$. Obviously, T is a symmetric positive and compact operator from ${\left[L_2\left(\mathrm{\Omega }\right)\right]}^2$ to ${\left[L_2\left(\mathrm{\Omega }\right)\right]}^2$. In addition, $(u,\lambda )$ satisfies equation (1.1) if and only if

$$Tu={\displaystyle \frac{1}{1+\lambda }}u.$$

Note that the eigenfunctions of T are exactly the eigenfunctions of the Maxwell equations.

2.2. Hodge Decomposition

We define $\xi =\mathrm{\nabla }\times Tf\in H^1\left(\mathrm{\Omega }\right)$, where $\xi$ satisfies

$$(\mathrm{\nabla }\times \xi ,\mathrm{\nabla }\times \psi )+(\xi ,\psi )=(f,\mathrm{\nabla }\times \psi )\forall \psi \in H^1\left(\mathrm{\Omega }\right).$$

(2.2)

Therefore, the Hodge decomposition of $Tf$ is

$$Tf=\mathrm{\nabla }\times \varphi +\sum _{j=1}^m{c}_j\mathrm{\nabla }{\phi }_j.$$

(2.3)

Here

$${\displaystyle \frac{\partial \varphi }{\partial \mathrm{n}}}=0\mathrm{on}\partial \mathrm{\Omega }$$

(2.4)

with the constraint

$$(\varphi ,1)={\int }_{\mathrm{\Omega }}\varphi dx=0,$$

(2.5)

and m is a non-negative integer.

Suppose that $\partial \mathrm{\Omega }$ has $m+1$ components. ${\mathrm{\Gamma }}_0$ denotes the outward boundary of $\mathrm{\Omega }$ and ${\mathrm{\Gamma }}_1,\dots ,{\mathrm{\Gamma }}_m$ denote the m parts of the interior boundaries. The functions ${\phi }_1,\dots ,{\phi }_m$ are defined as

$$\begin{array}{cc}\hfill \left(\mathrm{\nabla }{\phi }_j,\mathrm{\nabla }v\right)& =0\forall v\in H_0^1\left(\mathrm{\Omega }\right),\hfill \\ \hfill {\left.{\phi }_j\right|}_{{\mathrm{\Gamma }}_0}& =0,\hfill \\ \hfill {\left.{\phi }_j\right|}_{{\mathrm{\Gamma }}_i}& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}i=j\hfill \\ 0\hfill & \mathrm{if}i\ne j\hfill \end{array}\right.1\le i\le m.\hfill \end{array}$$

(2.6)

The function $\varphi$ satisfies (2.5) and is determined by

$$(\mathrm{\nabla }\times \varphi ,\mathrm{\nabla }\times \psi )=(\xi ,\psi )\forall \psi \in H^1\left(\mathrm{\Omega }\right).$$

(2.7)

The constants $c_1,\dots ,c_m$ in (2.3) are determined by

$$\sum _{j=1}^m{c}_j\left(\mathrm{\nabla }{\phi }_j,\mathrm{\nabla }{\phi }_j\right)=(f,\mathrm{\nabla }{\phi }_i)1\le i\le m.$$

(2.8)

Thus, (2.3) can be solved by the following five steps:

label=

Compute the numerical approximation ${\xi }_h$ of $\xi$ by solving problem (2.2).

lbbel=

Replace $\xi$ with ${\xi }_h$ and solve for the numerical approximation ${\varphi }_h$ of $\varphi$ by using (2.7).

lcbel=

Compute the approximations ${\phi }_{1,h},\dots ,{\phi }_{m,h}$ of ${\phi }_1,\dots ,{\phi }_m$ by solving the boundary value problems (2.6).

ldbel=

Obtain the approximations $c_{1,h},\dots ,c_{m,h}$ of $c_1,\dots ,c_m$ by solving the symmetric positive problem (2.8).

lebel=

Compute the numerical approximation $T_{h}f$ of $Tf$ as

$$T_{h}f=\mathrm{\nabla }\times {\varphi }_h+\sum _{j=1}^m{c}_{j,h}\mathrm{\nabla }{\phi }_{j,h}.$$

(2.9)

2.3. A Nonconforming Finite Element Method

Let ${\tau }_h$ be a family of triangulations of $\mathrm{\Omega }$. We define the weight ${\mathrm{\Phi }}_{\mu }\left(T\right)$ associated with $T\in {\tau }_h$ as

$${\mathrm{\Phi }}_{\mu }\left(T\right)=\prod _{i=1}^L{\left|c_l-c_T\right|}^{1-{\mu }_l},$$

where $c_1,\dots ,c_L$ are the corners of $\mathrm{\Omega }$ with interior angles ${\omega }_1,\dots ,{\omega }_L$, and ${\mu }_l(1\le l\le L)$ is the grading parameter which is chosen by

$$\begin{array}{cc}\hfill {\mu }_l& =1{\omega }_l\le {\displaystyle \frac{\pi }{2}},\hfill \end{array}$$

(2.10)

$$\begin{array}{cc}\hfill {\mu }_l& <{\displaystyle \frac{\pi }{2{\omega }_l}}{\omega }_l>{\displaystyle \frac{\pi }{2}}.\hfill \end{array}$$

(2.11)

The graded mesh ${\tau }_h$ satisfies the following condition

$$h_T=diam\left(T\right)\approx {\mathrm{\Phi }}_{\mu }\left(T\right)h\forall T\in {\tau }_h,$$

(2.12)

where h is the mesh parameter.

Define a weighted Sobolev space

$$L_{2,\mu }\left(\mathrm{\Omega }\right)=\left\{\zeta \in L_{2,\mathrm{loc}}\left(\mathrm{\Omega }\right):{\parallel \zeta \parallel }_{L_{2,\mu }\left(\mathrm{\Omega }\right)}^2={\int }_{\mathrm{\Omega }}{\varphi }_{\mu }^2\left(x\right){\zeta }^2\left(x\right)dx<\infty \right\},$$

where the weight function ${\mathrm{\Phi }}_{\mu }$ is determined by

$${\mathrm{\Phi }}_{\mu }\left(x\right)=\prod _{l=1}^L{\left|x-c_l\right|}^{1-{\mu }_l}.$$

Clearly $L_2\left(\mathrm{\Omega }\right)\subset L_{2,\mu }\left(\mathrm{\Omega }\right)$ and

$${\parallel \zeta \parallel }_{L_{2,\mu }\left(\mathrm{\Omega }\right)}\le C_{\mathrm{\Omega }}{\parallel \zeta \parallel }_{L_2\left(\mathrm{\Omega }\right)}\forall \zeta \in L_2\left(\mathrm{\Omega }\right).$$

(2.13)

Hence (2.3) has a unique solution for any $f\in L_{2,\mu }\left(\mathrm{\Omega }\right)$. Moreover, the norm of the dual space $L_{2,-\mu }\left(\mathrm{\Omega }\right)$ of $L_{2,\mu }\left(\mathrm{\Omega }\right)$ is defined by

$${\parallel \xi \parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}^2={\int }_{\mathrm{\Omega }}{\varphi }_{\mu }^{-2}\left(x\right){\xi }^2\left(x\right)dx.$$

The nonconforming $P_1$ finite element space $V_h$ associated with $T_h$ is defined by

$$\begin{array}{cc}\hfill V_h=\{& v\in L_2\left(\mathrm{\Omega }\right):v_T{=v|}_T\in P_1\left(T\right)\forall T\in {\tau }_h,\hfill \\ \hfill & v\mathrm{is}\mathrm{continuous}\mathrm{at}\mathrm{the}\mathrm{midpoints}\mathrm{of}\mathrm{the}\mathrm{edges}\mathrm{of}{\tau }_h,\hfill \\ & v=0\mathrm{is}\mathrm{continuous}\mathrm{at}\mathrm{the}\mathrm{midpoints}\mathrm{of}\mathrm{the}\mathrm{edges}\mathrm{on}\partial \mathrm{\Omega }\}.\hfill \end{array}$$

Let ${\Pi }_h:C\left(\overline{\mathrm{\Omega }}\right)\to V_h$ be a weak interpolation operator for the nonconforming $P_1$ finite element. Therefore, ${\Pi }_h$ satisfies the following interpolation error estimate for the Neumann problem (2.7) and the Dirichlet problem (2.6), which are similar to [24,25,26]. We have

$$\parallel \phi -{\Pi }_h{\phi \parallel }_{L_2\left(\mathrm{\Omega }\right)}+h{|\phi -{\Pi }_h\phi |}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}^2.$$

(2.14)

Moreover,

$$\parallel \beta -{\Pi }_h{\beta \parallel }_{L_2\left(\mathrm{\Omega }\right)}+h|\beta -{\Pi }_h{\beta |}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}^2{\parallel g\parallel }_{L_{2,\mu }\left(\mathrm{\Omega }\right)},$$

(2.15)

where $\beta$ is the solution of the Laplace equation with Neumann Boundary condition and g is the right hand side function (cf. [18]).

Let $E_h$ be a set of all edges in $T_h$. We define $E_h^i=E_h\setminus \partial \mathrm{\Omega }$ be the set of all interior edges. Let $e\in E_h^i$ be the edge shared by two triangles $T_1$, $T_2$$\in T_h$ and $v_j{=v|}_{T_j},j=1,2$. Define the jump on e by

$$〚v〛=n_1{v}_1+n_2{v}_2,$$

where $n_1,n_2$ are the unit outward normal vector.

If e is a boundary edge of $\mathrm{\Omega }$, then

$$〚v〛=vn.$$

Next we consider the nonconforming $P_1$ finite element method for (2.2), which is to find ${\xi }_h\in V_h$ such that

$$a_h({\xi }_h,v)=F\left(v\right)\forall v\in V_h,$$

(2.16)

where

$$\begin{array}{cc}\hfill a_h({\xi }_h,v)& =\sum _{T\in {\tau }_h}{\int }_T\mathrm{\nabla }\times {\xi }_h·\mathrm{\nabla }\times vdx+({\xi }_h,v),\hfill \end{array}$$

(2.17)

$$\begin{array}{cc}\hfill F\left(v\right)& =(f,\mathrm{\nabla }\times v)\forall v\in V_h.\hfill \end{array}$$

(2.18)

The nonconforming $P_1$ finite element method for (2.7) is to find ${\varphi }_h\in V_h$ such that

$$\widehat{a_h}({\varphi }_h,v)=({\xi }_h,v)\forall v\in V_h,$$

(2.19)

where

$$\begin{array}{cc}\hfill \widehat{a_h}({\varphi }_h,v)& =\sum _{T\in {\tau }_h}{\int }_T\mathrm{\nabla }{\varphi }_h·\mathrm{\nabla }vdx,\hfill \\ \hfill ({\varphi }_h,1)& =0.\hfill \end{array}$$

When $m\ge 1$, the approximation ${\phi }_{j,h}\in V_h$ of the harmonic function ${\phi }_j$ in (2.6) is defined by

$$\begin{array}{cc}\hfill \left(\mathrm{\nabla }{\phi }_{j,h},\mathrm{\nabla }v\right)& =0\forall v\in H_0^1\left(\mathrm{\Omega }\right),\hfill \\ \hfill {\left.{\phi }_{j,h}\right|}_{{\mathrm{\Gamma }}_0}& =0,\hfill \\ \hfill {\left.{\phi }_{j,h}\right|}_{{\mathrm{\Gamma }}_i}& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}i=j\hfill \\ 0\hfill & \mathrm{if}i\ne j\hfill \end{array}\right.1\le i\le m.\hfill \end{array}$$

(2.20)

To compute $c_{j,h}$, we introduce the following system:

$$\sum _{j=1}^m{c}_{j,h}(\mathrm{\nabla }{\phi }_{j,h},\mathrm{\nabla }{\phi }_{i,h})=(f,\mathrm{\nabla }{\phi }_{i,h})1\le i\le m.$$

(2.21)

Finally, we define the piecewise constant vector field $T_{h}f$ of $Tf$ as

$$T_{h}f=\mathrm{\nabla }\times {\varphi }_h+\sum _{j=1}^m{c}_{j,h}\mathrm{\nabla }{\phi }_{j,h}.$$

(2.22)

2.4. Error Analysis

We start this section by defining a mesh-dependent energy norm ${\parallel ·\parallel }_h$ for any $v\in H^1\left(\mathrm{\Omega }\right)+V_h$ as follows

$${\parallel v\parallel }_h=\sqrt{a_h(v,v)}.$$

Combining with the Cauchy-Schwarz inequality, we observe that the form $a_h(v,v)$ is bounded with respect to ${\parallel ·\parallel }_h$ , i.e.,

$$|a_h{(\omega ,v)|\le \parallel \omega \parallel }_h{\parallel v\parallel }_h\forall v,w\in H^1\left(\mathrm{\Omega }\right)+V_h.$$

Next we turn to the error estimate. The following lemma, whose proof is similar to the proof of Theorem 10.3.11 in [27].

Lemma 1. 

Let ${\xi }_h$ be the solution of (2.16). Then the following discrete error estimate holds

$$\parallel \xi -{\xi }_h{\parallel }_h\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)},$$

(2.23)

where C is a positive constant.

Proof. 

Let $\omega \in V_h$ be arbitrary. Combining with (2.2), (2.17) and the partial integration, we obtain

$$\begin{array}{cc}\hfill a_h(\xi ,\omega )& =\sum _{T\in {\tau }_h}{\int }_T\mathrm{\nabla }\times \xi ·\mathrm{\nabla }\times \omega dx+(\xi ,\omega )\hfill \\ & =F\left(\omega \right)+\sum _{e\in {\epsilon }^h}{\int }_e\mathrm{\nabla }\xi ·〚\omega 〛ds,\hfill \\ \hfill a_h(\xi -{\xi }_h,\omega )& =\sum _{e\in {\epsilon }^h}{\int }_e\mathrm{\nabla }\xi ·〚\omega 〛ds.\hfill \end{array}$$

From Theorems 4.4.20, 10.1.10 and 10.3.10 in [27], we have

$$\begin{array}{cc}\hfill |a_h(\xi -{\xi }_h,\omega )|& \le {Ch\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}{\parallel \omega \parallel }_h,\hfill \end{array}$$

(2.24)

$$\begin{array}{cc}\hfill \parallel \xi -{\xi }_h{\parallel }_h& \le \underset{{\xi }_h\in V_h}{inf}{\parallel \xi -{\xi }_h\parallel }_h+\underset{w\in V_h\setminus \left\{0\right\}}{sup}{\displaystyle \frac{\left|a_h\left(\xi -{\xi }_h,w\right)\right|}{{\parallel w\parallel }_h}},\hfill \end{array}$$

(2.25)

$$\begin{array}{cc}\hfill \underset{{\xi }_h\in V_h}{inf}{\parallel \xi -{\xi }_h\parallel }_h& \le {∥\xi -{\Pi }_h\xi ∥}_h\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.\hfill \end{array}$$

(2.26)

The estimate (2.23) follows from (2.24), (2.25) and (2.26). □

Theorem 2.1. 

For the solution ${\xi }_h$ of (2.16), the following discrete error estimate holds

$$\parallel \xi -{\xi }_h{\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(2.27)

Proof. 

Let the dual argument $\zeta \in H^1\left(\mathrm{\Omega }\right)$ be defined by

$$(\mathrm{\nabla }\times \zeta ,\mathrm{\nabla }\times v)+(\zeta ,v)=({\varphi }_{\mu }^{-2}(\xi -{\xi }_h),v)\forall v\in H^1\left(\mathrm{\Omega }\right).$$

Hence

$$\begin{array}{cc}\hfill \parallel \xi -{\xi }_h{\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}^2& =(\mathrm{\nabla }\times \zeta ,\mathrm{\nabla }\times (\xi -{\xi }_h))+(\zeta ,\xi -{\xi }_h)\hfill \\ & =(\mathrm{\nabla }\times (\zeta -{\Pi }_h\zeta ),\mathrm{\nabla }\times (\xi -{\xi }_h))+(\zeta -{\Pi }_T\zeta ,\xi -{\xi }_h)\hfill \\ & =a_h(\zeta -{\Pi }_h\zeta ,\xi -{\xi }_h)\hfill \\ & \le \parallel \zeta -{\Pi }_h{\zeta \parallel }_h{\parallel \xi -{\xi }_h\parallel }_h.\hfill \end{array}$$

In view of the definition of ${\Pi }_h$, combining with Theorem 4.4.20 in [27], we have

$$\parallel \zeta -{\Pi }_h{\zeta \parallel }_h\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

The estimate (2.1) follows from (2.23) and (2.28). □

Corollary 1. 

Suppose the condition in Theorem 2.1 holds, we have

$$\parallel \xi -{\xi }_h{\parallel }_{L_2\left(\mathrm{\Omega }\right)}\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(2.28)

Lemma 2. 

Assume $f\in {\left[L_2\left(\mathrm{\Omega }\right)\right]}^2$. Then

$$|\varphi -{\varphi }_h{|}_{H^1\left(\mathrm{\Omega }\right)}\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(2.29)

Proof. 

It follows from Theorem 10.3.21 in [27], we have

$$\parallel \varphi -{\varphi }_h{\parallel }_{L_2\left(\mathrm{\Omega }\right)}\le Ch{\parallel \xi \parallel }_{H^1\left(\mathrm{\Omega }\right)}.$$

(2.30)

Since ${\parallel \xi \parallel }_{H^1\left(\mathrm{\Omega }\right)}\le C{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)},$ we have

$$\parallel \varphi -{\varphi }_h{\parallel }_{L_2\left(\mathrm{\Omega }\right)}\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(2.31)

Combining (2.28), (2.31), and the Cauchy-Schwarz inequality, we have

$$\begin{array}{cc}\hfill |{\varphi }_h{-\varphi |}_{H^1\left(\mathrm{\Omega }\right)}^2& =\parallel \mathrm{\nabla }\times (\varphi -{\varphi }_h){\parallel }_{L_2\left(\mathrm{\Omega }\right)}^2\hfill \\ & =(\xi -{\xi }_h,\varphi -{\varphi }_h)\hfill \\ & \le \parallel \xi -{\xi }_h{\parallel }_{L_2\left(\mathrm{\Omega }\right)}{\parallel \varphi -{\varphi }_h\parallel }_{L_2\left(\mathrm{\Omega }\right)}\hfill \\ & \le {Ch\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)},\hfill \end{array}$$

which means

$$|\varphi -{\varphi }_h{|}_{H^1\left(\mathrm{\Omega }\right)}\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

□

Next we compare ${\phi }_j$ with ${\phi }_{j,h}$ in $H^1\left(\mathrm{\Omega }\right)$. Clearly, we obtain ${\phi }_{j,h}$ by solving the Dirichlet problem (2.20).

Lemma 3. 

For $1\le j\le m$, we have

$$|{\phi }_j-{\phi }_{j,h}{|}_{H^1\left(\mathrm{\Omega }\right)}\le Ch.$$

(2.32)

Proof. 

By using (2.14) , we know

$$\parallel \phi -{\Pi }_h{\phi \parallel }_{L_2\left(\mathrm{\Omega }\right)}+h{|\phi -{\Pi }_h\phi |}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}^2.$$

(2.33)

Let ${\zeta }_2\in H^1\left(\mathrm{\Omega }\right)$ which is determined by

$$(\mathrm{\nabla }{\zeta }_2,\mathrm{\nabla }v)=(\mathrm{\nabla }({\phi }_h-\phi ),v)\forall v\in H^1\left(\mathrm{\Omega }\right).$$

There exists a unique solution ${\tilde{\phi }}_h$ of (2.6) such that

$$\begin{array}{cc}\hfill |{\tilde{\phi }}_h{-\phi |}_{H^1\left(\mathrm{\Omega }\right)}^2& =\parallel \mathrm{\nabla }\times ({\tilde{\phi }}_h-{\phi }_h){\parallel }_{L_2\left(\mathrm{\Omega }\right)}^2\hfill \\ & =(\mathrm{\nabla }{\zeta }_2,\mathrm{\nabla }({\tilde{\phi }}_h-{\phi }_h))\hfill \\ & \le \parallel \mathrm{\nabla }{\zeta }_2{\parallel }_{L_2\left(\mathrm{\Omega }\right)}{\parallel \mathrm{\nabla }({\tilde{\phi }}_h-{\phi }_h)\parallel }_{L_2\left(\mathrm{\Omega }\right)}\hfill \\ & \le |{\zeta }_2-{\Pi }_h{\zeta }_2{|}_{H^1\left(\mathrm{\Omega }\right)}{\parallel {\tilde{\phi }}_h-{\phi }_h\parallel }_{H^1\left(\mathrm{\Omega }\right)}\hfill \\ & \le Ch\parallel {\tilde{\phi }}_h{-\phi \parallel }_{H^1\left(\mathrm{\Omega }\right),}\hfill \end{array}$$

which means

$$|{\tilde{\phi }}_h{-\phi |}_{H^1\left(\mathrm{\Omega }\right)}\le Ch.$$

(2.34)

By (2.33), we know

$$|{\phi }_j-{\tilde{\phi }}_h{|}_{H^1\left(\mathrm{\Omega }\right)}\le {|{\phi }_j-{\Pi }_h{\phi }_j|}_{H^1\left(\mathrm{\Omega }\right)}\le Ch.$$

(2.35)

The estimate (2.32) follows from (2.34) and (2.35). □

Combining with (2.8), (2.21) and (2.32), we have the following lemma with respect to the error estimate of $c_{j,h}$. The proof is similar to the Lemma 4.7 in [26].

Lemma 4. 

For $1\le j\le m$, $c_{j,h}$ is the solution of (2.21) , we have

$$|c_j-c_{j,h}{|\le Ch\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(2.36)

Theorem 2.2. 

Suppose h is small enough and $T_{h}f$ is the solution of (2.22). Then

$$\parallel Tf-T_h{f\parallel }_{L_2\left(\mathrm{\Omega }\right)}\le Ch{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(2.37)

Proof. 

The discrete error estimate holds bases on Lemma2-Lemma4, the proof is similar to [15]. □

3. Multigrid Methods

In this section, we establish the multigrid algorithm for solving discrete problems (2.16) and (2.23) on graded meshes. For the initial triangulation ${\tau }_0$ on an L-shaped domain, we chose a properly grading factor ${\mu }_l$ according to (2.10) and consider the procedure to generate the triangulation ${\tau }_k(k\ge 1)$ which is the same as [25,26,28].

(a)

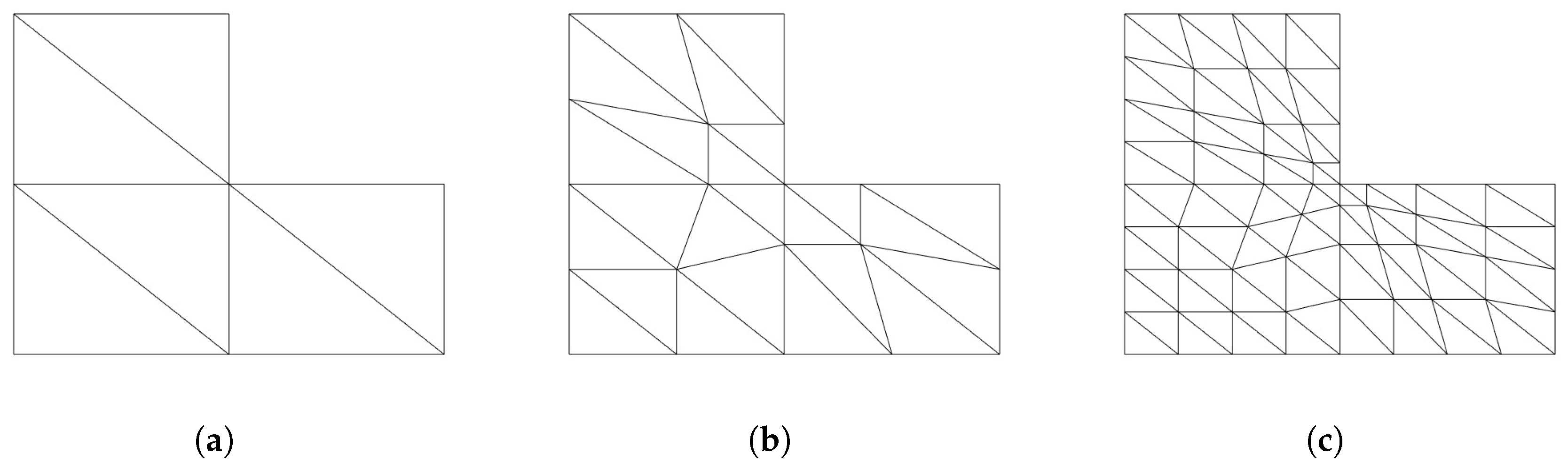
If any vertex of $T\in T_k$ is not a reentrant corner, then $T\in T_k$ is divided uniformly by connecting midpoints of the edges of T.

(b)

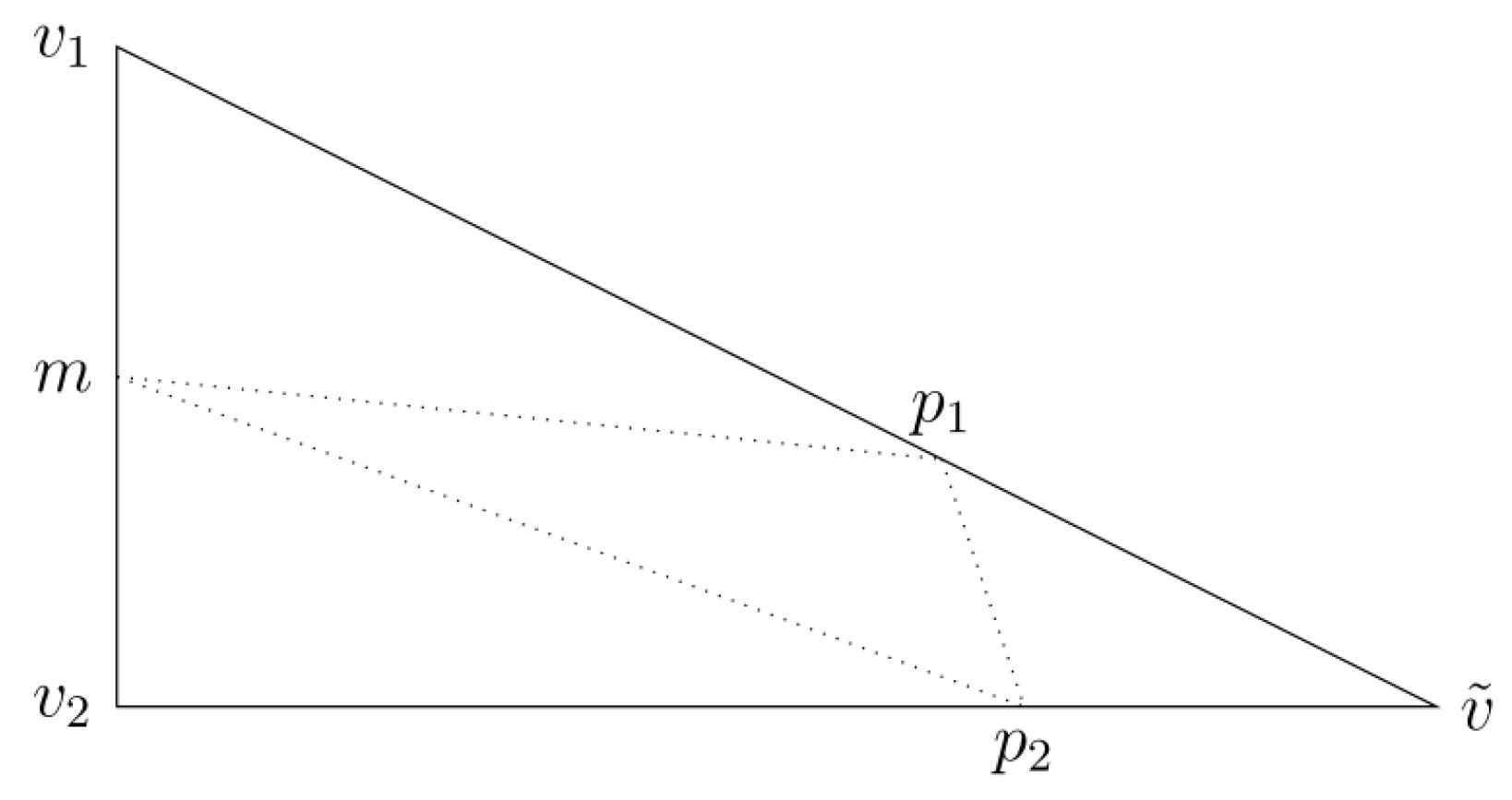
Suppose $v_1,v_2,\tilde{v}$ are the vertexes of $T\in {\tau }_k$. For the midpoint of the edge $v_1{v}_2$, we denote as m. If $\tilde{v}$ is a reentrant corner, then $T\in T_k$ is divided by connecting $p_1,p_2$ and m, where $p_i(i=1,2)$ is a point on the edge $\tilde{v}{v}_i(i=1,2)$ (cf. Figure 1) such that

$$\left|{\displaystyle \frac{\tilde{v}-p_i}{\tilde{v}-v_i}}\right|=2^{-\left(1/{\mu }_l\right)}i=1,2.$$

We take ${\mu }_l$ as ${\displaystyle \frac{2}{3}}$ when depicting the triangulation $T_0,T_1$ and $T_2$ on the L-shaped domain in Figure 2.

3.1. W-Cycle Multigrid Algorithm

3.1.1. The k-th Level Multigrid Algorithm

Since these triangulations ${\tau }_k(k\ge 0)$ satisfy the condition (2.12), we turn to suppose

$$h_k={\displaystyle \frac{1}{2}}{h}_{k-1}k\ge 1.$$

(3.1)

Let $V_k$ be the nonconforming $P_1$ finite element space associated with $T_k$. For each k, the bilinear form $a_k(u,v)$ is defined on $V_k+H^1\left(\mathrm{\Omega }\right)$ as follows

$$a_k(u,v)=\sum _{T\in {\tau }_h}{\int }_T\mathrm{\nabla }u·\mathrm{\nabla }vdx+(u,v).$$

(3.2)

The norm ${\parallel v\parallel }_k$ defines as the analog of ${\parallel v\parallel }_h$, i.e.,

$${\parallel v\parallel }_k=\sqrt{a_k(v,v)},$$

and the analog of ${\Pi }_h$ is defined by ${\Pi }_k$.

We introduce the operator $A_k:V_k\to V_k^{\prime }$ as

$$\langle A_k\omega ,v\rangle =a_k(\omega ,v)\forall \omega ,v\in V_k,$$

where $\langle ·\rangle$ denotes the canonical bilinear form on $V_k^{\prime }\times V_k$. The k-th level nonconforming finite element method for (2.2) is to find ${\xi }_k\in V_k$ such that

$$A_k{\xi }_k=f_k,$$

(3.3)

where $f_k\in V_k^{\prime }$ satisfies

$$\langle f_k,v\rangle =(f,\mathrm{\nabla }\times v)\forall v\in V_k.$$

It is clear that (3.3) can be solved by the multigrid algorithms.

Since $V_k$ is a nonconforming finite element space, $V_k\neg \subset V_{k+1}$ and $V_k\neg \subset H^1\left(\mathrm{\Omega }\right)$, we cannot directly use the natural injection transfer as in the finite element spaces. Moreover, we define a proper intergrid transfer operator $I_{k-1}^k:V_{k-1}\to V_k$ as a natural injection (cf. [29]). But the actual value of $\left(I_{k-1}^{k}v\right)\left(p\right)$ is determined by

$$\left(I_{k-1}^{k}v\right)\left(p\right)=\left\{\begin{array}{cc}v\left(p\right)\hfill & p\in S_{k-1},\hfill \\ {\displaystyle \frac{1}{2}}\left[{v|}_{T_1}{\left(p\right)+v|}_{T_2}\left(p\right)\right]\hfill & p\notin S_{k-1}\mathrm{and}p\mathrm{is}\mathrm{shared}\mathrm{by}{T}_1,T_2\in {\tau }_k,\hfill \\ v\left(p\right)\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where $S_{k-1}$ is the vertices set of ${\tau }_{k-1}$ for any $p\in S_k.$

Define the fine to coarse intergrid transfer operator $I_k^{k-1}:V_k^{\prime }\to V_{k-1}^{\prime }$ to be the transpose of $I_{k-1}^k$ which is related to $\langle ·,·\rangle$, i.e.,

$$\langle I_k^{k-1}\omega ,v\rangle =\langle \omega ,I_{k-1}^{k}v\rangle \forall \omega \in V_k^{\prime },v\in V_{k-1}.$$

(3.4)

In order to analyze the error estimate, we define an operator $B_k:V_k\to V_k^{\prime }$ such that

$$\langle B_k\omega ,v\rangle =h_k^2\sum _{T\in {\tau }_k}\sum _{m\in M_T}\omega \left(m\right)\nu \left(m\right),$$

(3.5)

where $M_T$ is the set of vertices on the triangle T. It is easy to know that the spectral radius of $B_k^{-1}{A}_k$ satisfies

$$\rho \left(B_k^{-1}{A}_k\right)<C{h}_k^{-2}\forall k\ge 0.$$

An appropriate damping factor $\lambda$ is chosen such that the spectral radius $\rho \left(\lambda h_k^2{B}_k^{-1}{A}_k\right)$ satisfies

$$\rho \left(\lambda h_k^2{B}_k^{-1}{A}_k\right)<1\forall k\ge 0.$$

(3.6)

Next we introduce a W-cycle algorithm for the equation

$$A_{k}z=g\forall z\in V_k,\forall g\in V_k^{\prime }.$$

(3.7)

Algorithm 3.1. 

$M{G}_W(k,g,z_0,m_1,m_2)$denote the output of the algorithm, where $z_0\in V_k$ is the initial guess. Furthermore, the pre-smoothing and post-smoothing steps are denoted as $m_1$ and $m_2$.

$\begin{array}{cc}& \mathrm{For}k=0,M{G}_W(0,g,z_0,m_1,m_2)=A_0^{-1}g.\hfill \\ & \mathrm{For}k>0,M{G}_W(0,g,z_0,m_1,m_2)\mathrm{is}\mathrm{compute}\mathrm{by}\mathrm{following}\mathrm{procedure}.\hfill \end{array}$

Pre-smoothing. With the condition $1\le l\le m_1$, $z_l\in V_k$ is computed by

$$z_l=z_{l-1}+\left(\lambda h_k^2\right)B_k^{-1}(g-A_k{z}_{l-1}).$$

Error correction. Let $q_0=0$. For $1\le i\le 2$, compute $z_{m_1+1}$ recursively by

$$\begin{array}{cc}\hfill r_{k-1}& =I_k^{k-1}(g-A_k{z}_{m_1}),\hfill \\ \hfill q_i& =MG(k-1,r_{k-1},q_{i-1},m_1,m_2),\hfill \\ \hfill z_{m_1+1}& =z_{m_1}+I_{k-1}^k{q}_2.\hfill \end{array}$$

Post-smoothing. For $m_1+2\le l\le m_1+m_2+1$, $z_l$ is determined by

$$z_l=z_{l-1}+\left(\lambda h_k^2\right)B_k^{-1}(g-A_k{z}_{l-1}).$$

(3.8)

Finally, the output of the k-th level iteration is

$$M{G}_W(k,g,z_0,m_1,m_2)=z_{m_1+m_2+1}.$$

The multigrid Algorithm 3.1 can also be modified to solve the singular Neumann problem (2.7).

The space $\widehat{V_k}$ is defined by $\widehat{V_k}=\{v\in V_k:(v,1)=0\}$. We denote the orthogonal projection $\widehat{P_k}:V_k\to {\widehat{V}}_k$ with respect to ${(·,·)}_k$. Moreover, for any $v\in V_k,\widehat{P_k}v\in \widehat{V_k}$ satisfies

$${(w,\widehat{P_k}v)}_k={(w,v)}_k\forall \omega \in V_k.$$

(3.9)

We turn to compute $\widehat{P_k}v$ explicitly as follows

$$\widehat{P_k}v=v-{\displaystyle \frac{{(v,s_k)}_k}{{(s_k,s_k)}_k}}{s}_k,$$

(3.10)

where $s_k\in V_k$ spans the orthogonal complement of ${\widehat{V}}_k$ with respect to ${(·,·)}_k$. In addition, we take $N_k$ as the set of all the nodes associated with $V_k$ and define $s_k$ as the finite element function

$$s_k\left(p\right)={\displaystyle \frac{1}{3h_k^2·n\left(T_p\right)}}\sum _{T\in T_p}\left|T\right|\forall p\in N_k,$$

where $T_p$ is the set of triangles in ${\tau }_k$ sharing p as a common vertex, $n\left({\tau }_p\right)$ is the number of triangles in ${\tau }_p$, and $\left|T\right|$ is the area of T.

The natural injection is denoted by $\widehat{I_k}:{\widehat{V}}_k\to V_k$. Moreover, an operator

$$\widehat{A_k}={\widehat{P}}_k\circ B_k^{-1}\circ A_k\circ \widehat{I_k}$$

(3.11)

is determined by

$${(\widehat{A_k}w,v)}_k=\sum _{T\in {\tau }_k}{\int }_T\mathrm{\nabla }w·\mathrm{\nabla }vdx\forall w,v\in {\widehat{V}}_k.$$

Now we define a W-cycle algorithm for

$$\widehat{A_k}z=gz\in {\widehat{V}}_k,g\in {\widehat{V}}_k^{\prime }.$$

(3.12)

Algorithm 3.2. 

$M{G}_W^1(k,g,z_0,m_1,m_2)$ denote the output of the algorithm, where $z_0\in V_k$ is the initial guess. Furthermore, the pre-smoothing and post-smoothing steps are denoted as $m_1$ and $m_2$.

$\begin{array}{cc}& \mathrm{For}k=0,M{G}_W^1(0,g,z_0,m_1,m_2)={\left(\widehat{A_0}\right)}^{-1}\left(\widehat{P_0}{B}_0^{-1}g\right).\hfill \\ & \mathrm{For}k>0,M{G}_W^1(0,g,z_0,m_1,m_2)\mathrm{is}\mathrm{compute}\mathrm{by}\mathrm{following}\mathrm{procedure}.\hfill \end{array}$

Pre-smoothing.With the condition $1\le l\le m_1$, $z_l\in V_k$ is computed by

$$z_l=z_{l-1}+\left(\lambda h_k^2\right)({\widehat{P}}_k{B}_k^{-1}g-\widehat{A_k}{z}_{l-1}).$$

(3.13)

Error correction. Let $q_0=0$. For $1\le i\le 2$, compute $z_{m_1+1}$ recursively by

$$\begin{array}{cc}\hfill r_{k-1}& =I_k^{k-1}({\widehat{P}}_k{B}_k^{-1}g-\widehat{A_k}{z}_{m_1}),\hfill \\ \hfill q_i& =M{G}_W^1(k-1,r_{k-1},q_{i-1},m_1,m_2),\hfill \\ \hfill z_{m_1+1}& =z_{m_1}+I_{k-1}^k{q}_2.\hfill \end{array}$$

Post-smoothing. For $m_1+2\le l\le m_1+m_2+1$, $z_l$ is determined by

$$z_l=z_{l-1}+\left(\lambda h_k^2\right)({\widehat{P}}_k{B}_k^{-1}g-\widehat{A_k}{z}_{l-1}).$$

(3.14)

Finally, the output of the k-th level iteration is

$$M{G}_W^1(k,g,z_0,m_1,m_2)=z_{m_1+m_2+1}.$$

The construction of the operators $\widehat{P_k}$ and $\widehat{I_k}$ are used to perform all the calculations in Algorithm 3.2 in the space $V_k$ instead of $\widehat{V_k}$. With (3.11), (3.13) and (3.14) can be rewritten as

$$z_l=z_{l-1}+\left(\lambda h_k^2\right){\widehat{P}}_k{B}_k^{-1}(g-A_k{z}_{l-1}).$$

Obviously, Algorithm 3.1 is identical with Algorithm 3.2.

3.1.2. Full Multigrid Methods

In the application of the k-th level iteration to (2.16), we use the following multigrid algorithm, applying p times at each level.

Algorithm 3.3.(Full multigrid methods for (2.16)) For $k=0,A_0{\tilde{\xi }}_0=f_0.$

For $k\ge 1$, the approximate solution ${\tilde{\xi }}_k\in {\widehat{v}}_k$ is obtained by the following iterative procedure

$$\begin{array}{cc}\hfill {\xi }_0^k& =I_{k-1}^k{\tilde{\xi }}_{k-1},\hfill \\ \hfill {\xi }_q^k& =M{G}_W(k,f_k,{\xi }_{q-1}^k,m_1,m_2)1\le q\le p,\hfill \\ \hfill {\tilde{\xi }}_k& ={\xi }_p^k.\hfill \end{array}$$

Then we introduce the k-th level nonconforming finite element method for (2.7), which is to find ${\varphi }_k\in \widehat{V_k}$ such that

$$\widehat{A_k}{\varphi }_k=g_k,$$

(3.15)

where $g_k\in V_k^{\prime }$ satisfies

$$\langle g_k,v\rangle =({\tilde{\xi }}_k,v)\forall v\in V_k.$$

Here ${\tilde{\xi }}_k$ is obtained by Algorithm 3.3. In order to solve (3.15), we introduce the following Algorithm.

Algorithm 3.4.(Full multigrid methods for (3.15)) For $k=0$, $\widehat{A_0}{\tilde{\varphi }}_0=g_0.$

For $k\ge 1$, the approximate solution ${\tilde{\varphi }}_k$ is obtained by the following iterative process

$$\begin{array}{cc}\hfill {\varphi }_0^k& =I_{k-1}^k{\tilde{\varphi }}_{k-1},\hfill \\ \hfill {\varphi }_q^k& =M{G}_W^1(k,g_k,{\varphi }_{q-1}^k,m_1,m_2)1\le q\le p,\hfill \\ \hfill {\tilde{\varphi }}_k& ={\varphi }_p^k.\hfill \end{array}$$

3.2. Error Analysis

We establish the error analysis of the W-cycle multigrid algorithm for discrete problems.

Firstly, we define the operator $R_k:V_k\to V_k$ which is used to measure the effect of smoothing steps as

$$R_k=I_d^k-\left(\lambda h_k^2\right)B_k^{-1}{A}_k,$$

(3.16)

and $I_d^k$ is the identity operator on $V_k$. Then the k-th level error propagation operator $E_k:V_k\to V_k$ for Algorithm 3.1 is determined by the following famous recursive relation ([10,20])

$$E_k=R_k^{m_2}(I_d^k-I_{k-1}^k{P}_k^{k-1}+I_{k-1}^k{E}_{k-1}^2{P}_k^{k-1})R_k^{m_1},$$

(3.17)

where $P_k^{k-1}:V_k\to V_{k-1}$ denotes the transpose of $I_{k-1}^k$ in the variational form

$$a_{k-1}(P_k^{k-1}\omega ,v)=a_k(\omega ,I_{k-1}^{k}v)\forall \omega \in V_k,v\in V_{k-1}.$$

(3.18)

Finally, the mesh-dependent norm is denoted as

$${\left|\left|\left|v\right|\right|\right|}_{j,k}=\sqrt{\langle B_k{\left(B_k^{-1}{A}_k\right)}^{j}v,v\rangle }\forall v\in V_k,k\ge 1,j=0,1,2.$$

(3.19)

Obviously, we have

$$\begin{array}{cc}\hfill {\left|\left|\left|v\right|\right|\right|}_{0,k}^2& =\langle B_{k}v,v\rangle \approx {\parallel v\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}\forall v\in V_k,\hfill \end{array}$$

(3.20)

$$\begin{array}{cc}\hfill {\left|\left|\left|v\right|\right|\right|}_{1,k}^2& =\langle A_{k}v,v\rangle =a_k(v,v)\forall v\in V_k.\hfill \end{array}$$

(3.21)

By the Cauchy-Schwarz inequality

$${\left|\left|\left|v\right|\right|\right|}_{2,k}=\underset{\omega \in V_k\setminus \left\{0\right\}}{max}{\displaystyle \frac{\langle A_{k}v,\omega \rangle }{{\left|\left|\left|\omega \right|\right|\right|}_{0,k}}}\forall v\in V_k.$$

(3.22)

Note that (3.6), (3.16) and (3.19) imply the following lemmas whose proof are standard in [10,20].

Lemma 5. 

There exist constants C independent of k such that

$$\begin{array}{cc}\hfill {\left|\left|\left|R_{k}v\right|\right|\right|}_{j,k}& \le C{\left|\left|\left|v\right|\right|\right|}_{j,k},\hfill \end{array}$$

(3.23)

$$\begin{array}{cc}\hfill {\left|\left|\left|R_k^{m}v\right|\right|\right|}_{1,k}& \le C{h}_k^{-1}{m}^{-{\displaystyle \frac{1}{2}}}{\left|\left|\left|v\right|\right|\right|}_{0,k},\hfill \end{array}$$

(3.24)

$$\begin{array}{cc}\hfill {\left|\left|\left|R_k^{m}v\right|\right|\right|}_{2,k}& \le C{h}_k^{-1}{m}^{-{\displaystyle \frac{1}{2}}}{\left|\left|\left|v\right|\right|\right|}_{1,k},\hfill \end{array}$$

(3.25)

where $v\in V_k$ , $k\ge 1$ and $j=0,1.$

We now use a duality argument to prove the following lemma.

Lemma 6. 

For any given $v\in V_k$$(k\ge 1)$, there exists a constant C independent of k such that

$${\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{0,k}\le C{h}_k{\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{1,k}\le C{h}_k^2{\left|\left|\left|v\right|\right|\right|}_{2,k}.$$

(3.27)

Proof. 

For any given $v\in V_k$, let $ϵ={\varphi }_{\mu }^{-2}(I_d^k-I_{k-1}^k{P}_k^{k-1})v,$ then we have

$${\parallel ϵ\parallel }_{L_{2,\mu }\left(\mathrm{\Omega }\right)}={\parallel (I_d^k-I_{k-1}^k{P}_k^{k-1})v\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}.$$

(3.28)

We introduce an argument ${\zeta }_3\in H^1\left(\mathrm{\Omega }\right)$ which is determined by

$$(\mathrm{\nabla }\times {\zeta }_3,\mathrm{\nabla }\times v)+({\zeta }_3,v)=(ϵ,v)\forall v\in H^1\left(\mathrm{\Omega }\right).$$

(3.29)

It is clear that ${\zeta }_3$ also satisfies

$$a_k({\zeta }_3,v)=(ϵ,v)\forall v\in V_k.$$

From (3.1), (2.15) and (3.28), we find that

$$\begin{array}{cc}\hfill \parallel {\zeta }_3-I_{k-1}^k{\Pi }_{k-1}{\zeta }_3{\parallel }_k& \le C\parallel {\zeta }_3-{\Pi }_{k-1}{\zeta }_3{\parallel }_{k-1}\hfill \\ & \le C{h}_{k-1}{\parallel ϵ\parallel }_{L_{2,\mu }\left(\mathrm{\Omega }\right)}\hfill \\ & \le C{h}_k{\parallel (I_d^k-I_{k-1}^k{P}_k^{k-1})v\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right),}\hfill \end{array}$$

which means

$$\parallel {\zeta }_3-I_{k-1}^k{\Pi }_{k-1}{\zeta }_3{\parallel }_k\le C{h}_k{\parallel (I_d^k-I_{k-1}^k{P}_k^{k-1})v\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right).}$$

(3.30)

At first, we prove

$${\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{0,k}\le C{h}_k{\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{1,k}.$$

(3.31)

It follows from (3.20) and (3.28) that

$$\begin{array}{cc}\hfill {\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{0,k}^2& =\langle B_k(I_d^k-I_{k-1}^k{P}_k^{k-1})v,(I_d^k-I_{k-1}^k{P}_k^{k-1})v\rangle \hfill \\ & \approx \parallel (I_d^k-I_{k-1}^k{P}_k^{k-1}){v\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}^2\hfill \\ & ={\int }_{\mathrm{\Omega }}{\varphi }_{\mu }^{-2}{\left[(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right]}^{2}dx\hfill \\ & ={\int }_{\mathrm{\Omega }}ϵ(I_d^k-I_{k-1}^k{P}_k^{k-1})vdx\hfill \\ & =a_k({\zeta }_3,(I_d^k-I_{k-1}^k{P}_k^{k-1})v).\hfill \end{array}$$

Moreover, (3.30) and(3.20) imply

$$\begin{array}{cc}\hfill & a_k({\zeta }_3,(I_d^k-I_{k-1}^k{P}_k^{k-1})v)\hfill \\ & =a_k({\zeta }_3-I_{k-1}^k{\Pi }_{k-1}{\zeta }_3,(I_d^k-I_{k-1}^k{P}_k^{k-1})v)\hfill \\ \hfill & \le \parallel {\zeta }_3-I_{k-1}^k{\Pi }_{k-1}{\zeta }_3{\parallel }_k{\parallel (I_d^k-I_{k-1}^k{P}_k^{k-1})v\parallel }_k\hfill \\ \hfill & \le Ch\parallel (I_d^k-I_{k-1}^k{P}_k^{k-1}){v\parallel }_{L_{2,-\mu }\left(\mathrm{\Omega }\right)}{\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{1,k}\hfill \\ \hfill & \approx Ch{\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{0,k}{\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{1,k}.\hfill \end{array}$$

Next we prove

$${\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{1,k}\le C{h}_k{\left|\left|\left|v\right|\right|\right|}_{2,k}.$$

(3.32)

Combining with duality and (3.22), we obtain

$${\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})v\right|\right|\right|}_{1,k}=\underset{w\in V_k\setminus \left\{0\right\}}{sup}{\displaystyle \frac{a_k((I_d^k-I_{k-1}^k{P}_k^{k-1})v,w)}{{\left|\left|\left|w\right|\right|\right|}_{1,k}}}.$$

(3.33)

Since

$$\begin{array}{cc}\hfill a_k((I_d^k-I_{k-1}^k{P}_k^{k-1}v),w)& =a_k((I_d^k-I_{k-1}^k{P}_k^{k-1}w),v)\hfill \\ & \le \parallel (I_d^k-I_{k-1}^k{P}_k^{k-1}){w\parallel }_{0,k}{\parallel v\parallel }_{2,k}\hfill \\ & \le Ch{\left|\left|\left|w\right|\right|\right|}_{1,k}{\left|\left|\left|v\right|\right|\right|}_{2,k},\hfill \end{array}$$

we finish the proof of (3.22). Finally, the Lemma 6 is a consequence of (3.21) and (3.22). □

Two preliminary approximation properties with respect to the operators $P_k^{k-1}\mathrm{and}{I}_{k-1}^k$ are given in the following lemma.

Lemma 7. 

$${\left|\left|\left|P_k^{k-1}v\right|\right|\right|}_{1,k-1}\le {\left|\left|\left|v\right|\right|\right|}_{1,k}\forall v\in V_k,$$

(3.34)

$${\left|\left|\left|I_{k-1}^{k}v\right|\right|\right|}_{1,k}\le {\left|\left|\left|v\right|\right|\right|}_{1,k-1}\forall v\in V_{k-1}.$$

(3.35)

Proof. 

The proof is identical with Lemma 4.5 in [25]. □

With $m_1$ pre-smoothing steps and $m_2$ post-smoothing steps on the two-grid algorithm, we introduce the following convergence.

Theorem 3.1. 

There exists a constant C independent of $k\ge 1$ such that the following holds

$${\left|\left|\left|R_k^{m_2}(I_d^k-I_{k-1}^k{P}_k^{k-1})R_k^{m_1}v\right|\right|\right|}_{1,k}\le C{\left[(1+m_1)(1+m_2)\right]}^{-{\displaystyle \frac{1}{2}}}{\left|\left|\left|v\right|\right|\right|}_{1,k}\forall v\in V_k.$$

(3.36)

Proof. 

If follows from Lemma 5 and 6, we have

$$\begin{array}{cc}& {\left|\left|\left|R_k^{m_2}(I_d^k-I_{k-1}^k{P}_k^{k-1})R_k^{m_1}v\right|\right|\right|}_{1,k}\hfill \\ & \le C{\left[(1+m_2)\right]}^{-1/2}{\left|\left|\left|(I_d^k-I_{k-1}^k{P}_k^{k-1})R_k^{m_1}v\right|\right|\right|}_{0,k}\hfill \\ & \le C{\left[(1+m_2)\right]}^{-1/2}{\left|\left|\left|R_k^{m_1}v\right|\right|\right|}_{2,k}\hfill \\ & \le C{\left[(1+m_1)(1+m_2)\right]}^{-1/2}{\left|\left|\left|v\right|\right|\right|}_{1,k}.\hfill \end{array}$$

□

Then we have the following convergence theorem for the W-cycle algorithm.

Theorem 3.2. 

For any $\gamma \in (0,1)$, there exists a positive integer m independent of k such that

$${\left|\left|\left|z-M{G}_w(k,g,z_0,m_1,m_2)\right|\right|\right|}_{1,k}\le \gamma {\left|\left|\left|z-z_0\right|\right|\right|}_{1,k},$$

(3.37)

provided $m_1+m_2\ge m$.

Proof. 

Based on Theorem 3.1 and Lemma 7, we can find an estimate similar in [26]. □

Furthermore, () becomes

$${\left|\left|\left|v\right|\right|\right|}_{1,k}^2=\langle {\widehat{A}}_{k}v,v\rangle \approx {\left|v\right|}_{H^1\left(\mathrm{\Omega }\right)}\forall v\in {\widehat{V}}_k,$$

which implies

$$\begin{array}{cc}\hfill |\varphi -{\varphi }_k{|}_{H^1\left(\mathrm{\Omega }\right)}& =\underset{v\in {\widehat{V}}_K}{inf}{|\varphi -v|}_{H^1\left(\mathrm{\Omega }\right)}\hfill \\ \hfill & \le |\varphi -{\Pi }_k{\varphi |}_{H^1\left(\mathrm{\Omega }\right).}\hfill \end{array}$$

Therefore, if we replace $V_k$ with ${\widehat{V}}_k$, Theorem 3.2 also valid.

Now we analyze the error estimate of the k-th level iterations.

Theorem 3.3. 

Suppose p is sufficiently large and $h_1$ is small enough, there exists a constant C such that

$$\parallel \xi -{\tilde{\xi }}_k{\parallel }_{L_2\left(\mathrm{\Omega }\right)}\le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

Proof. 

The proof is identical to Theorem 7.2 in [26]. □

The following theorem compares the exact solution $\varphi$ of (2.7) with the approximate solution ${\tilde{\varphi }}_k$ obtained by Algorithm 4.4.

Theorem 3.4. 

Suppose p is sufficiently large and $h_1$ is small enough, we have

$${\left|\varphi -{\tilde{\varphi }}_k\right|}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)},$$

(3.38)

where C is a constant.

Proof. 

We find that ${\varphi }_0-{\tilde{\varphi }}_0=0$ and suppose ${\alpha }^{r+1}<{\displaystyle \frac{1}{2}}$, then

$$\begin{array}{cc}\hfill |{\varphi }_k-{\tilde{\varphi }}_k{|}_{H^1\left(\mathrm{\Omega }\right)}& ={\left|\left|\left|{\varphi }_k-{\tilde{\varphi }}_k\right|\right|\right|}_{1,k}\hfill \\ & \le {\alpha }^r{\left|\left|\left|{\varphi }_k-{\tilde{\varphi }}_{k-1}\right|\right|\right|}_{1,k}\hfill \\ & \le C{\alpha }^r\left(\right|{\varphi }_k{-\varphi |}_{H^1\left(\mathrm{\Omega }\right)}+|\varphi -{\varphi }_{k-1}{|}_{H^1\left(\mathrm{\Omega }\right)}+{\left|\left|\left|{\varphi }_{k-1}-{\tilde{\varphi }}_k-1\right|\right|\right|}_{1,k})\hfill \\ & \le C{h}_k{\alpha }^r{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}+C^2{h}_{k-1}{\alpha }^{2r}{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}+\cdots \hfill \\ & +C^{k+1}{h}_0{\alpha }^{(k+1)r}{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}+{|{\varphi }_0-{\tilde{\varphi }}_0|}_{H^1\left(\mathrm{\Omega }\right)}\hfill \\ & \le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}{\displaystyle \frac{{\alpha }^r}{1-2{\alpha }^r}}+{|{\varphi }_0-{\tilde{\varphi }}_0|}_{H^1\left(\mathrm{\Omega }\right)}\hfill \\ & \le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}\hfill \end{array}$$

which means

$$|{\varphi }_k-{\tilde{\varphi }}_k{|}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

Combining with the triangle inequality and (2.23), we obtain

$$\begin{array}{cc}\hfill {\left|\varphi -{\tilde{\varphi }}_k\right|}_{H^1\left(\mathrm{\Omega }\right)}& \le |{\varphi }_k-{\tilde{\varphi }}_k{|}_{H^1\left(\mathrm{\Omega }\right)}+{|\varphi -{\varphi }_k|}_{H^1\left(\mathrm{\Omega }\right)}\hfill \\ & \le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.\hfill \end{array}$$

□

In the case that $\mathrm{\Omega }$ is not simply connected, we have the following lemmas.

Lemma 8. 

Suppose p is sufficiently large and $h_1$ is small enough, we have

$${\left|{\phi }_j-{\tilde{\phi }}_{j,k}\right|}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}_k,$$

(3.39)

where C is a constant.

Proof. 

The proof is similar to Theorem 3.4, and hence will be omitted. □

Note that ${\tilde{c}}_{j,k}(1\le j\le m)$ is computed by

$$\sum _{j=1}^m{\tilde{c}}_{j,k}(\mathrm{\nabla }{\tilde{\phi }}_{j,k},\mathrm{\nabla }{\tilde{\phi }}_{i,j})=(f,\mathrm{\nabla }{\tilde{\phi }}_{i,k})1\le i\le m.$$

(3.40)

Moreover, the estimate of ${\tilde{c}}_{j,k}$ is shown by next lemma and the proof is similar to Theorem 4.

Lemma 9. 

Suppose p is sufficiently large and $h_1$ is small enough, we have

$$|c_j-{\tilde{c}}_{j,k}{|}_{H^1\left(\mathrm{\Omega }\right)}\le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)},$$

(3.41)

where C is a constant.

For any k-th level iteration, the approximate value $\widetilde{T_k}f$ of $Tf$ is determined as

$$\widetilde{T_k}f=\mathrm{\nabla }\times \widetilde{{\varphi }_k}+\sum _{j=1}^m{\tilde{c}}_{j,k}\mathrm{\nabla }{\tilde{\phi }}_{j,k}.$$

(3.42)

According to (3.42), (3.38), (3.39) and (3.41), we are ready to compare $Tf$ and $\widetilde{T_k}f$. The proof is similar to Theorem 2.2.

Theorem 3.5. 

$${∥Tf-\widetilde{T_k}f∥}_{L_2\left(\mathrm{\Omega }\right)}\le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

For the problem (1.1), the following theorem holds provided $Tu={\displaystyle \frac{1}{1+\lambda }}u$.

Theorem 3.6. 

Suppose ${\tilde{u}}_k$ is the approximation of u, we have

$${∥u-{\tilde{u}}_k∥}_{L_2\left(\mathrm{\Omega }\right)}\le C{h}_k{\parallel f\parallel }_{L_2\left(\mathrm{\Omega }\right)}.$$

(3.43)

4. Numerical Experiments

In this section, we present the contraction numbers of the W-cycle algorithms on the L-shaped domain ${(-1,1)}^2\setminus {[0,1]}^2$. We create the triangulations ${\tau }_0,{\tau }_1,\dots$ as the rules in Section 3, and the grading parameter at the reentrant corner $(0,0)$ is chosen as ${\displaystyle \frac{2}{3}}$.

The damping factor $\lambda$ is taken to be ${\displaystyle \frac{1}{2}}$ in (3.6). Moreover, report the numerical solution in Table 1 and Table 2. The numerical results confirm the theoretical results given in Theorem 3.2, where p is taken to be 7, and the number of smoothing steps is taken to be 40.

The first experiment is applied on the L-shaped domain ${(-1,1)}^2\setminus {[0,1]}^2$ with graded meshes. The exact solution is taken to be

$$u=\mathrm{\nabla }\times \left(r^{{\displaystyle \frac{2}{3}}}cos\left({\displaystyle \frac{2}{3}}\theta -{\displaystyle \frac{\pi }{3}}\right)\varphi \left(x\right)\right),$$

(4.1)

where $(r,\theta )$ are the polar coordinates at the origin and $\varphi \left(x\right)={(1-x_1^2)}^2{(1-x_2^2)}^2$. The results are tabulated in Table 1. We find that the order of convergence for ${\widehat{u}}_k$ is 1 as predicted by Theorem 3.6.

For examining the numerical result on a doubly connected domain $\mathrm{\Omega }$, we present the second set of experiments. Let $\mathrm{\Omega }={(0,4)}^2\setminus {[1,3]}^2$ and the harmonic function $\varphi$ satisfies the following boundary conditions

$${\varphi |}_{{\mathrm{\Gamma }}_0}{=0\mathrm{and}\varphi |}_{{\mathrm{\Gamma }}_1}=1,$$

where ${\mathrm{\Gamma }}_0$ (resp. ${\mathrm{\Gamma }}_1$) is the boundary of ${(0,4)}^2$ (resp. ${(1,3)}^2$). The solution can be written as

$$(1+\lambda )Tu=\mathrm{\nabla }\times \varphi +c\mathrm{\nabla }\varphi ,$$

(4.2)

where c is a constant.

The right-hand side function is taken to be

$$f=\left\{\begin{array}{cc}\left(\begin{array}{c}1+x_1\\ 0\end{array}\right)\hfill & \mathrm{if}{x}_1\le x_2\mathrm{and}3\le x_1\le 4,\hfill \\ \left(\begin{array}{c}0\\ 1+x_2\end{array}\right)\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4.3)

The results are presented in Table 2. The orders of convergence for ${\widehat{u}}_k$ is 1 as predicted by Theorem 3.6. If a smaller mesh size is chosen, we believe the results will be better.

5. Discussion

The results are tabulated in Table 1 and Table 2. We find that the order of convergence for ${\widehat{u}}_k$ is both 1 as predicted by Theorem 3.6. If a smaller mesh size is chosen, we believe the results will be better.