A Categorical Model of General Consciousness

1. Introduction

Consciousness is an object of philosophy, science and common sense. However, science sometimes concedes defining consciousness to philosophy, even everyday common sense, and modestly regards its studies on consciousness only as relatives to, or the biological basis of [1] consciousness, regardless of remarkable advances of consciousness. Meanwhile, AI seems to essentially emulate consciousness, which calls for a scientific, not (only) philosophic definition of consciousness, so that there should be a clear and tangible definition of consciousness what the in-physical and everyday consciousness refers to is. In as much as consciousness is empirical matters appealed to science ----notice that both philosophy (conservatively, as a part) and common sense do not refuse consciousness as a scientific object. That is, in contrast to meta-physics, science should be “philosophy-inclusive”, at least answer what the relationship of meanings of consciousness between philosophy and of science is. In fact, the paradigm of consciousness study is evolving that science is not only addressing the question “what is the basis of consciousness?”, but also “what is consciousness?”. ----seeing that science studies nature, consciousness as the natural activities spontaneously is included as no extra-nature exists, and it should no be treated only as a basis to the concept that philosophy mentioned, as the supervenience to philosophy, as epiphenomena or as only explananda of the concept. Hence, it is indispensable to scientifically make a definition of consciousness, in detail, mathematically, physically even technically for AI, biologically etc., which should be overall compatible with the deep-rooted concept no matter it used in which disciplines.

The relationship of consciousness between philosophy and science has been proposed by Uriah Kriegel as follows.

Philosophy may have a more significant role to play in shaping our understanding of consciousness; that even a complete science of consciousness may involve certain lacunae calling for philosophical supplementation [1](pp. 1–13).

This paradigm gives an architectural scheme that is naturally (physically, chemically, biologically, etc.) to analyze phenomena corresponding to philosophical ideas. It establishes a scheme where philosophy to explain consciousness on the hypothesis that the philosophical ideas on consciousness are relatively clear, not controversary for an integrated and objective world. However, as philosophy is too imaginary and controversy always, the paradigm calls for a new improvement that puts philosophy in analyzing too to entertain the natural analysis----this paradigm is, as hereby proposed, mathematics-assistant. That is, a mathematical frame, with its infusing methods comprehensive in knowing world, parallel to the natural analysis and also on philosophy, is desired. The present study is in attempt to establish an algebraic model, which serves as such a frame and as the assistant methods to mathematically, therefor epistemologically describe and analyze consciousness, including the relevant philosophical ideas. Against the controversy definitions or interpretations on it, mathematical methods may achieve a “Greatest Common Divisor” ---- the widest consensus drawn from various statements on consciousness by modeling common and intrinsic features inner the statements, descriptions with more exactness.

[2](pp.3-45) abstracts two semantics of consciousness, which summarizes the essence of consciousness well. One is the transitivity, meaning being sensing or aware of objects; another one is non-transitive, meaning a mental state yet not unconscious. If we regard the non-transitive as of capability of performing the transitive, we can simplify consciousness as transitivity of experiential objects or some mental states. Therefore, could we acquire a mathematical description of consciousness in the sense of transitivity? Fortunately, in this way, mathematically modeling consciousness, have been attempted in the history. Piaget, the psychologist influenced by the mathematical school Bourbaki, established a mathematical model to depict consciousness generated from growing of the young child. Piaget’s consciousness model properly reflects the essence of consciousness---transitivity with established psychological logic [3,4,5].

Piaget gave his definition of consciousness in terms of “cognizance”, a type of behavior which is a psychological structure holding a logic that a cognized object is homomorphic to the type:

In general, when a psychologist speak of a subject being conscious of a situation, he means that the subject is fully aware of it.

…cognizance (or the act of becoming conscious) of an action scheme transforms it into a concept and therefore that cognizance consists basically in a conceptualization.

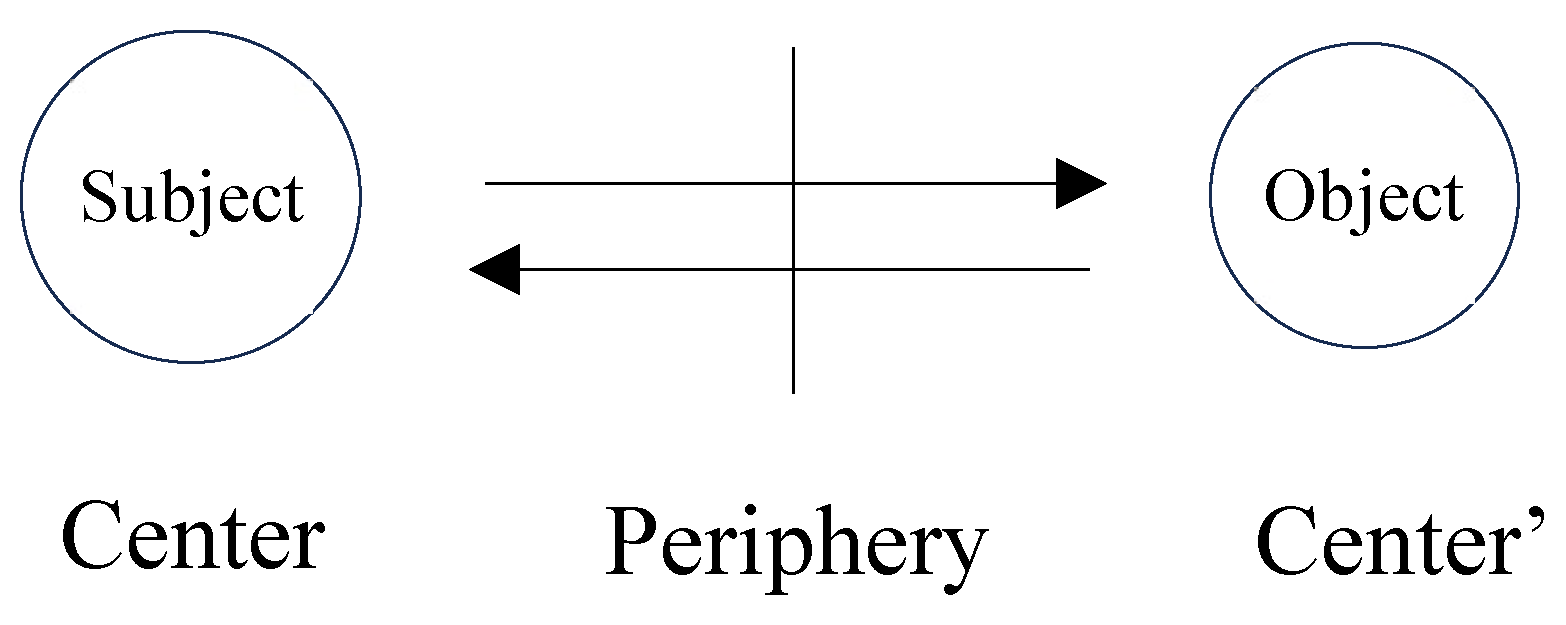
…Thus, cognizance, starting from the periphery (goals or results) moves in the direction of the central regions of the action in order to reach its internal mechanism: recognition of the means employed, reasons for their selection or their modification en route, and the like. [3](pp.332-352)

Piaget explained the mechanism of a cognizance by Figure 1 [3](pp.332-352), where the interaction between the subject and object is given, accompanying double centers as the cores of the corresponding classifications and the abstracted environment.

Concerning homomorphism between the subject and object, respectively with own operations or movements, Piaget gave an example of setting up causality of consciousness [6]:

Returning to the problems with which we begin, one can wonder what the relationships are between the correspondences or transformations that the child discovers in reality and those that he discoverers in his own operations or actions. In particular, one can ask whether there exists, as we suppose, a correspondence between causality contributed to objects and the subject’s operatory structure.

…

Correspondences of this sort between causality and the subject’s deductive productions become conscious only tardily, of course.

As same as Malcolm referring the essence of consciousness to as the transitivity (“being aware of”) between a psychological state and the corresponded objects, Piaget’s cognizance interaction between the two sides of the periphery is the transitivity too; moreover, the pairs in interaction, Center and Center’, remain their own transitivity on a level, and the double transitivity on their own levels, constructs a homomorphism. 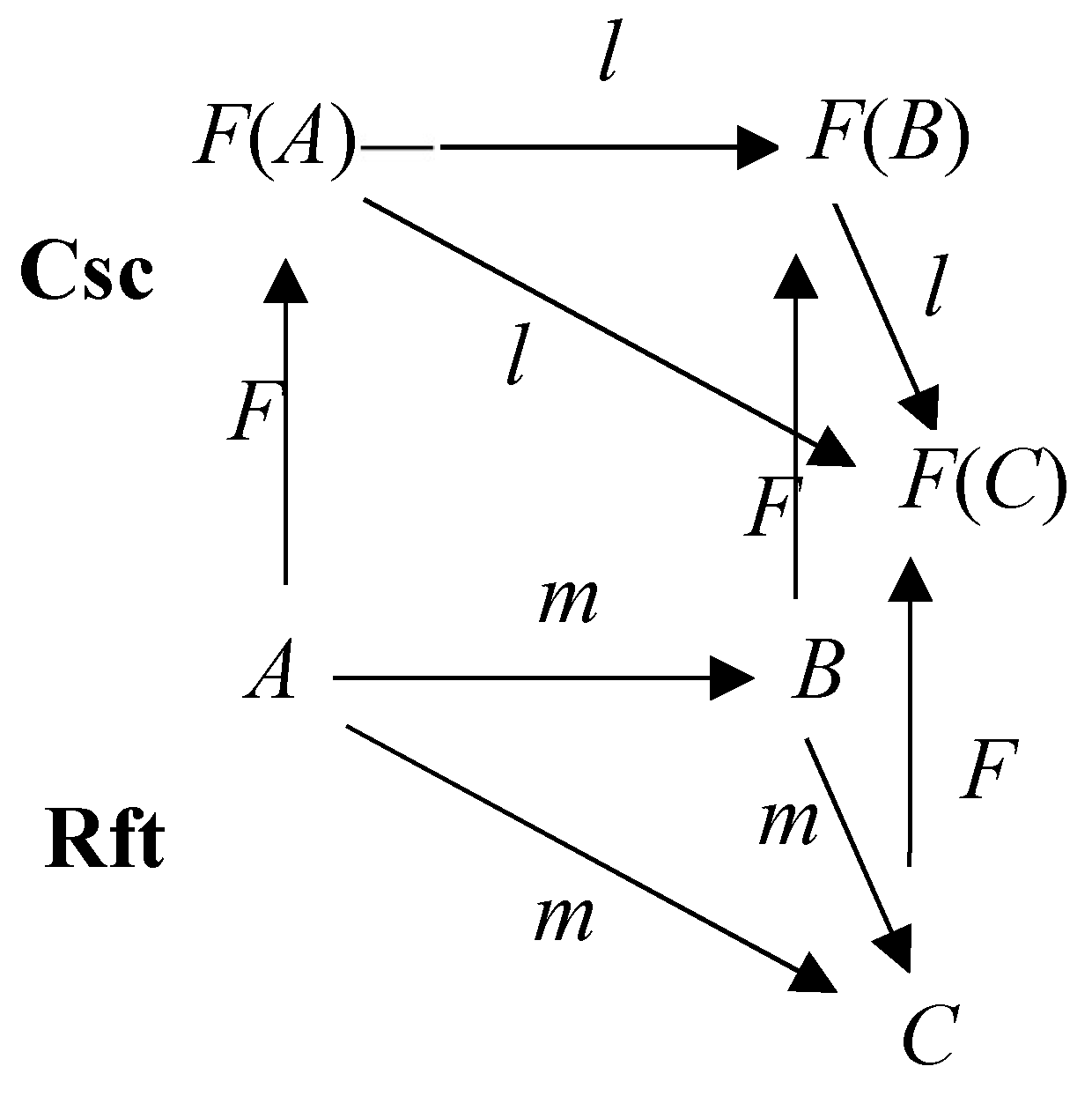So, we can express Piaget’s categorical thought about consciousness [7] as (1), with the diagram as Figure 2.

Csc := ({Rft, Csc}, F: Rft → Csc)

(1)

Expressions in (1) contain

Csc: consciousness;

Objects: Rft, referents;

Morphism: l(A,B), m(C,D), A,B∈ Csc, C,D∈Rft,…(l represents psychological operation like “logic” as Piaget described, m represents objective “movement” or behavior of the subject) ,…

The objects and morphisms satisfy:

f(A,B) × f(B,C) → f(A,C) , … (transitivity----Piaget typically instantiates the transitivity as operations which have the identical or equivalent effects to the composition);

Iden(A,A) , …(Identity).

F is a natural transform, which looks like sensing objects (like a projection of, say, a ball) and generating the corresponding mind, being the mappings from the objects into psychological statements. F represents the transitivity as mentioned by Malcolm. The morphisms l, m, and the transformer F are all compositing/ed or expanding/ed such that the image is flexible in function selves, in the levels and for the levels.

(1) exhibits a homomorphism between referents and its subject, or consciousness and its reflected objects in a categorical scheme, as stated in (2).

Rft ≅ Scs

(2)

In other words, albeit (1) and (2) do not describe an inner characteristic of what is to be determined as consciousness, like features or structures, they give a composite relation structure, by which consciousness can be determined by these outer relationships (like l, F in Figure 2). So, it is the relationship, varying with each other between the information F(A) as the reflex in line of logic l and the periphery worlds (an object A, referred to by a mind event F(A)), confirmed by a function or effect, that consciousness is defined in languages and thoughts, including philosophic or scientific. In particular, Piaget described consciousness as realizing some logic operations like inferences, by the process, a reflex (like F(A)) in brain resulted from an input gives rise to predicting a position of the referent object (say C in Figure 2 after a movement of A). Thus, a simply stimulus-reaction can be mapped by F though, it lacks sufficient relevant operation logic l to predict a movement of stimulus (m), causing that such a too simple reaction not always can be determined as a conscious event. Similarly, unconsciousness might go through F but lack sufficient {l}, causing F(A) failing to become a conscious event made up of {F(B), F(C)}. The transitivity on one layer like F(A)→F(C) guarantees equivalency arising in the operations on the layers, so that logic can generate.

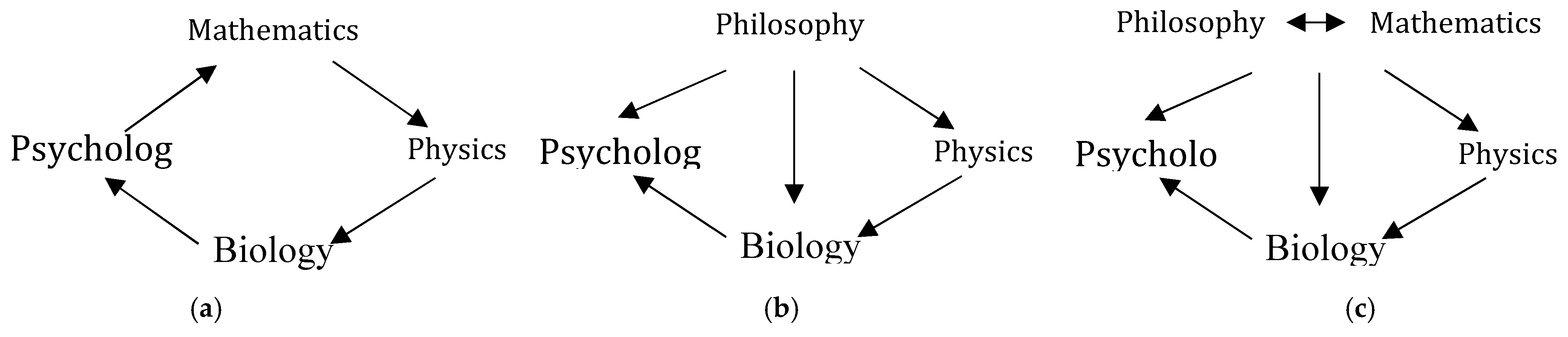
(1) and (2) show a paradigm of mathematical modeling of consciousness, in parallel, there exists a paradigm of Kriegel [1], where mathematics is weaker than Piaget’ model, and philosophy----its notations and questions--- inspires science (including that of consciousness) to be confirmed and resolved it. The two schemes of Piaget and Kriegel, as visually represented by (a)(b) in Figure 3, call for an evolved paradigm so that mathematic and philosophic approaches are all sufficiently applied in defining and explaining consciousness, as proposed by Figure 3(c).

2. A 3-Layer Categorical Model of General Consciousness (3-CGCM)

2.1. The Outline of 3-CGCM

(1) with Figure 1 omits materials (neurons, machine units, etc.) processing the mappings from outer objects into psychological states for generating consciousness, which need to insert a material layer to represent the substance implementing the processing.

(3) with Figure 4 makes an attempt to insert such a material layer, Unt, representing material bodies, like neurons, artefact units, etc.

Csc: = ({Rft, Unt, Csc}, F₁, F₂: Rft →Unt→Csc)

(3)

The novel paradigm (3) serves as an improvement of homomorphism as expressed by (4).

Rft ≅ Unt ≅ Csc

(4)

(3) define the consciousness as a kind of psychologic or artificial states grounding in the phenomena of matters like neurons, software; (4) states a homomorphism between the consciousness Csc and its reductive matters Unt and its referents (objects projecting to the Rft, like the periphery for the subject).

(3) and (4) are a result from the epistemological paradigm of modeling consciousness as stated in (c) in Figure 3, which belongs to a monism that regards consciousness as identity of both psychologic and material entity, and the two entities are representable in virtue of physical methods.

When the model applies to artificial objects like robots, AI, artificial consciousness, the artifacts are viewed as the conscious. So, the model is viewed as one of general consciousness, named as 3-layer categorical model of general consciousness (3-CMGC).

2.2. A Direct Depiction of Reductive Physicalism

(3) and (4) are also a result from the epistemological paradigm of modeling consciousness, they belong to a reductive physicalism that regards consciousness as the phenomena of the material entity-----just for deambiguity from the term “materialism” which excessively highlights social meanings, “physicalism” is chosen while holding the essentially material characteristics of consciousness with the principle of materialism departing from the social meanings.

The reductive physicalism of consciousness, typically as elaborated by [8,9], has been refuted for such a gap of explanation between mental or similar properties and physical properties, or between mind and brain, here represented as between Csc and Unt, that at least not all consciousness can be essentially subsumed under physical (biological, chemical, etc.) phenomena, that is, consciousness is physically inexplicable, or partly is, forever [10](pp.455-484) [11](p.117).

This refutation, however, is facing objection such as from [12](pp. 14–36). Here, we further verify that the functor Csc ↔Unt ↔ Rft, linking to the consciousness Csc with exact correspondence of neurons Unt, and optionally linked with the objective periphery world Rft, exist truly, wherein, Csc ↔Unt primarily implies the identification of the two factors as monism and reductive physicalism deem.

Verifying existence of Unt for biological bodies has to figure out the neurons {F₁}, which definitely play a role deputizing for certain objects to participate in thinking in brain to complete some functions of generating consciousness.

The thought that a physical (biological) unit representing an object has originated for a long term. “Psychophysics”, advocated by Friedrich Albert Lange, Neo-Kantianism regards the sensation from the objects as “The transcendent basis of our organization remains therefore just as unknown to us as the things which act upon it. We have always before us only the product of both” [13], which implies that organs are especially representing objectives, or certain objectives may own their own cells in the organs in terms of the schemes Csc↔Unt.

The subsequent development of science has confirmed this prediction that exist neurons which play a role to stand for the special kinds of objects. In particular some space-representative neurons are explored.

In 1959, David Hubel and Torsten Wiesel revealed that in various cat’s striate cortex areas (receptive fields) discharging accordingly the map with angles of stimuli, so the certain cells were space-feature related [14].

In this case, let α indicate the angles which are stimuli in David Hubel and Torsten Wiesel’s experiment, and F₁(α), the receptive fields of single neurons in the cat’s striate cortex definitely react to α. Suppose that the cat had a conscious activity F₂. Thus, a function between Rft, Unt and Csc can be expressed as (5), with reference of Figure 4.

$${\displaystyle \genfrac{}{}{0pt}{}{\genfrac{}{}{0pt}{}{\mathit{\alpha }}{\downarrow }}{\genfrac{}{}{0pt}{}{\mathbf{R}\mathbf{f}\mathbf{t}}{}}}{\displaystyle \genfrac{}{}{0pt}{}{\underset{\downarrow }{\underbrace{F_1\left(\mathit{\alpha }\right)F_2\left(F_1\left(\mathit{\alpha }\right)\right)}}}{\mathbf{U}\mathbf{n}\mathbf{t}}}{\displaystyle \genfrac{}{}{0pt}{}{\genfrac{}{}{0pt}{}{\mathrm{P}\mathrm{s}\mathrm{y}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{t}}{\downarrow }}{\genfrac{}{}{0pt}{}{\mathbf{C}\mathbf{s}\mathbf{c}}{}}}$$

(5)

Another discovery of space-positioning cells in the brain of rat was achieved by John O ́Keefe and May-Britt Moser & Edvard Moser in 1971 and 2005 respectively. Let α₁,α₂,α₃ denote direction, position and velocity of a space object as stimuli respectively in their experiment, then, (5) still holds with the Rft variables α₁,α₂,α₃ in replace of α [15,16,17,18].

Recent similar discovers figuring out neurons of orientation and positioning by means of functional magnetic resonance imaging (fMRI) are achieved [19,20,21].

A topological object is projected into the neurons holding and acting as its primary topological geological characteristics was unveiled latter by Tootell, Roger BH, et al., which makes a composition of the neurons with 2-D topological shape same to the shape of the object. This well displays a fractional (omitting the transitivity like {l}, {u} in a layer) homomorphism between Rft and Unt [22,23].

The neurons representing an object not only in neuron reflection but also in thinking by means of using the representing neurons are called “Mirror Neurons”, which was discovered by [24]. This displays an intact homomorphism between Rft and Unt.

As time and space are not only objective parameters in physical laws, but also subjective consciousness functions, as Kant systematically came up with his theory that reason is consciousness reorganizing sensory information by time and space [25](p.61), it is believable that existence of neurons definitely acting to certain objects, and play a representing role in thinking to form consciousness.

2.3. A Reductive-Physicalism Explanation of Qualia

As stated in the section 2.2, the reductive physicalism of consciousness is being doubted for a claimed gap of explanation between mental properties and physical properties, wherein an important point is that sensation, or qualia of a process, upon a pain-resulting stimuli for a salient example, is taken as unexplained, as some persist in that nociceptive-specific neurons firing is regarded as pain is unintelligible [12]. The present study proposes that the gap is overstated, and it is physically explainable as it is semantically calibrated. It is noteworthy that “consciousness” is a notation in a usage of context of thoughts, its explanation is limited the usage in languages so that the language makes sense. So, consciousness is a referrer different from the referent as objects like the cosmos, an apple etc., because a referrer is for explanation to meet the usage in the context, and a referent is to meet objective laws. (The relationship between the referrer and the referent as delineated in (Scs, Unt) and Rft in Figure 4.) Then, the physical explanation, in particular upon the troubling problem qualia, should suffice semantics of “consciousness” in referring. It means that the first semantics of the transitivity in [2](pp.3-45) is more essential in the definition of consciousness. Hence, we should make a position that the second semantics of consciousness without referring to something, should be treated as for a confirmation of the transitive usage of “consciousness”, rather than a consciousness itself. That is, one in pain is conscious for referring (secondly aware of to the pain), when one cannot say “being conscious of a molecular of a certain chunk of neurons in the pain”, it means that the result of the pain is conscious rather than the pain per se. Thus, the result is physically explainable with physical means; and a result of subject conscious experience for semantically explaining consciousness consists in the relationship in the 3-layer construct. Therefore, a narrowed gap is explainable with and for physical features.

3. The Construct of Consciousness in View of 3-CMGC

3-CMGC raises a question if it can develop, or has contained, a construct of consciousness.

Constructs and compositions of consciousness have been uncovered by many philosophers and psychologists, among which, Kant has a priority for that he regarded the mind as a cognition process which conforms to objectivity with physical laws, as the paradigm of Cognitive Theory of Consciousness (CTC), not to mention that Kant referred to his thoughts as a “future scientific metaphysics”, which just includes the contemporary’s cognition science cross disciplines of philosophy, psychology, AI, neuroscience, etc., as remarked by [26] that it had been argued by Kitcher, Brook, Sellars and others that Kant’s philosophy of mind has valuable contributions to make to contemporary cognitive science and artificial intelligence .

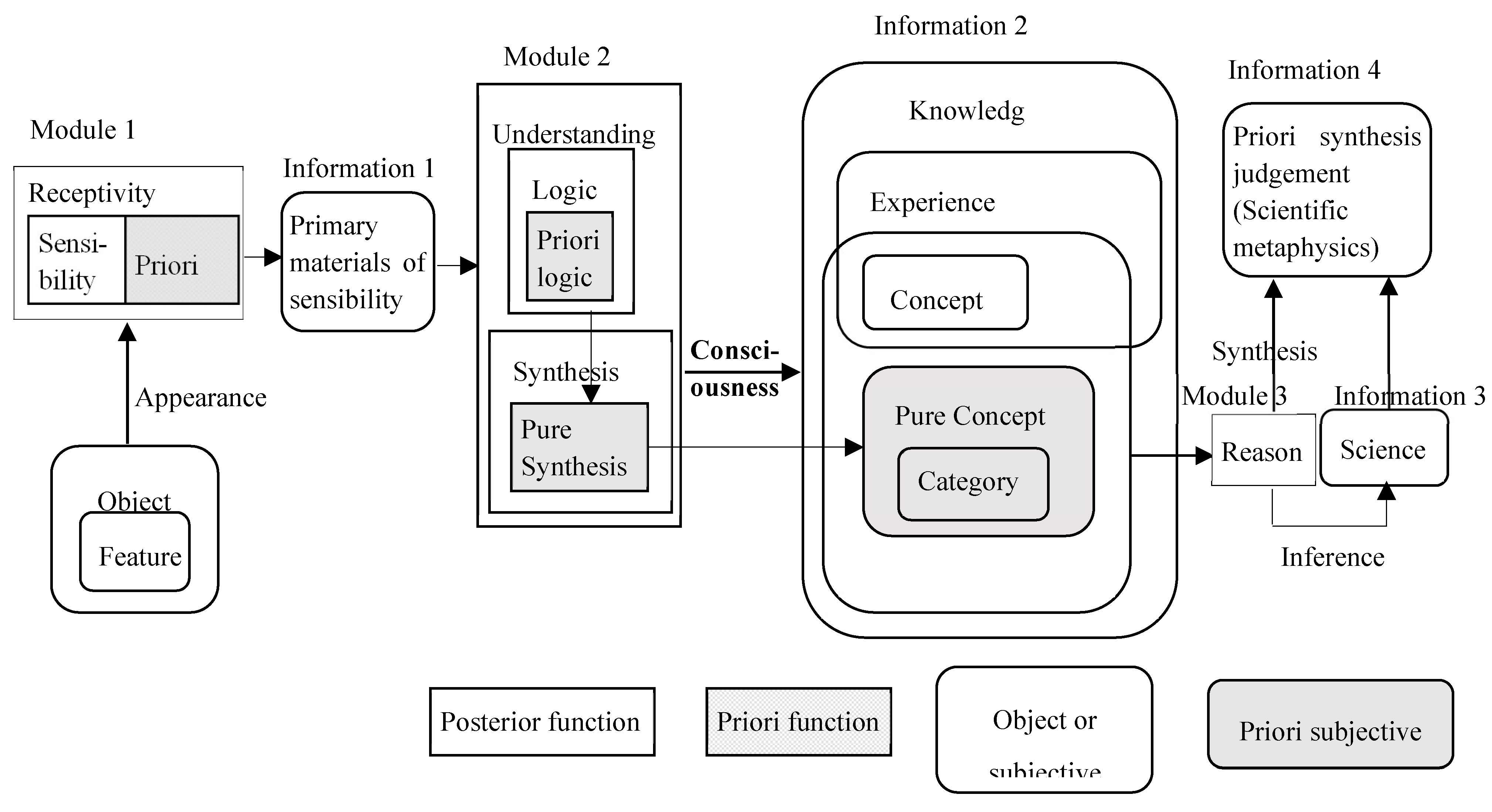
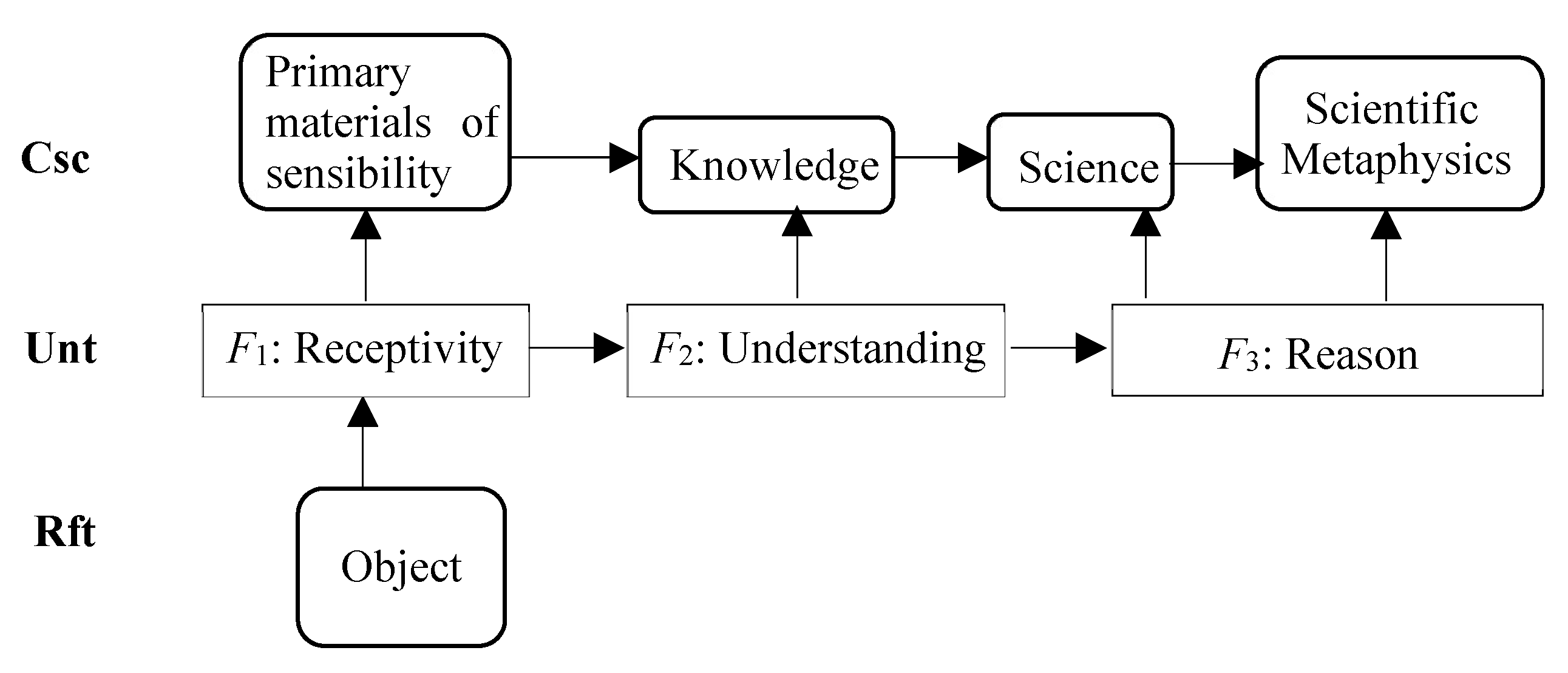
Kant viewed consciousness as a complex process which follows receptivity and understanding to generate knowledge and its synthesis. He thought consciousness as only matter lending appearance to be thoughts, or appeared form of knowledge. [27] These thoughts interpret the process of consciousness in line with the description as Figure 5.

For explaining meanings of (represented as modules in Figure 5) functions in mind, Kant gave definitions or statements, among which some key notations are chosen as following.

Concerning Module 1[25](pp.59-61)：

Whatever the process and the means may be by which knowledge refers to its objects, intuition is that through which it refers to them immediately, and at which all thought aims as a means. But intuition takes place only insofar as the object is given to us.

The capability (receptivity) to obtain representation through the way in which we are affected by objects is called sensibility. Objects are therefore given as by means of our sensibility. Sensibility alone supplies us with intuitions.

The effect produced by an object upon the capacity for representation, insofar as we are affected by the object, is sensation.

I call all representation pure (in a transcendental sense) in which there is nothing that belongs to sensation. …this pure form of sensibility may it self be called pure intuition. …These belong to pure intuition, which even without an actual object of the senses, exists a priori in the mind, as a mere form of sensibility.

…there are two forms of sensible intuition, which are principles of a priori knowledge, namely space and time.

Concerning Module 2:

We call sensibility the receptivity of our mind to receive representation insofar as it is in some wise affected, while the understanding, on the other hand, is our faculty of producing representations by ourselves, or the spontaneity of knowledge. [25](p. 86)

The thought of consciousness appealing to reason, as section 2.3 analyzes that sensation, which contains qualia, not wholly serves as consciousness, but as an intermediary nature extracted for generating consciousness. However, in the former process of receptivity and understanding, there are priori functions infused, they are priori intuition and priori logic, the two should be classified into consciousness. This is because of that priori intuition, referred by Kant as time and space to tidy up intuition, has been confirmed as participation in generation of consciousness by means of time-intermediary “script” [28] or as space feature’s cognition or remaining as the section 2.2 introduced; and of that logic, a human holds, is confirmed as consciousness by Piaget. [6] Therefore, the developed Kant’s model of mind should be conceivable in (3)(4), such that (3)(4) obtain a more detailed categorical form as (6).

({F_1,2, _…n }, →, (→, →)) ≅ ($ℱ$, →, (→, →))

(6)

where,

→ denotes the meaning of logic implication;

(→, →) denotes the morphisms like A→B, B→C, and A→C, or a liner process of objects by natural laws;

$ℱ$ is natural laws, which supports the functions in F_1,2…,n;

{F_1,2…,n: x→y} is the individual psychological contents, basically in long-term memories as if the factors in Global Workspace Theory (GWT [29]), like logic, knowledge base or culture in terms of Kant’s priori generating or appealing to Reason and Science, such that a conscious event F_i calls {F_1,2…,n }, as (7) shows

F_i ∈{F_1,2…,n}

(7)

That is, {F_i} are specific experience, as originated from the Object with their Features in Figure 5, which accompany their individual long-term psychological contents like logic, knowledge or culture as the priori function.

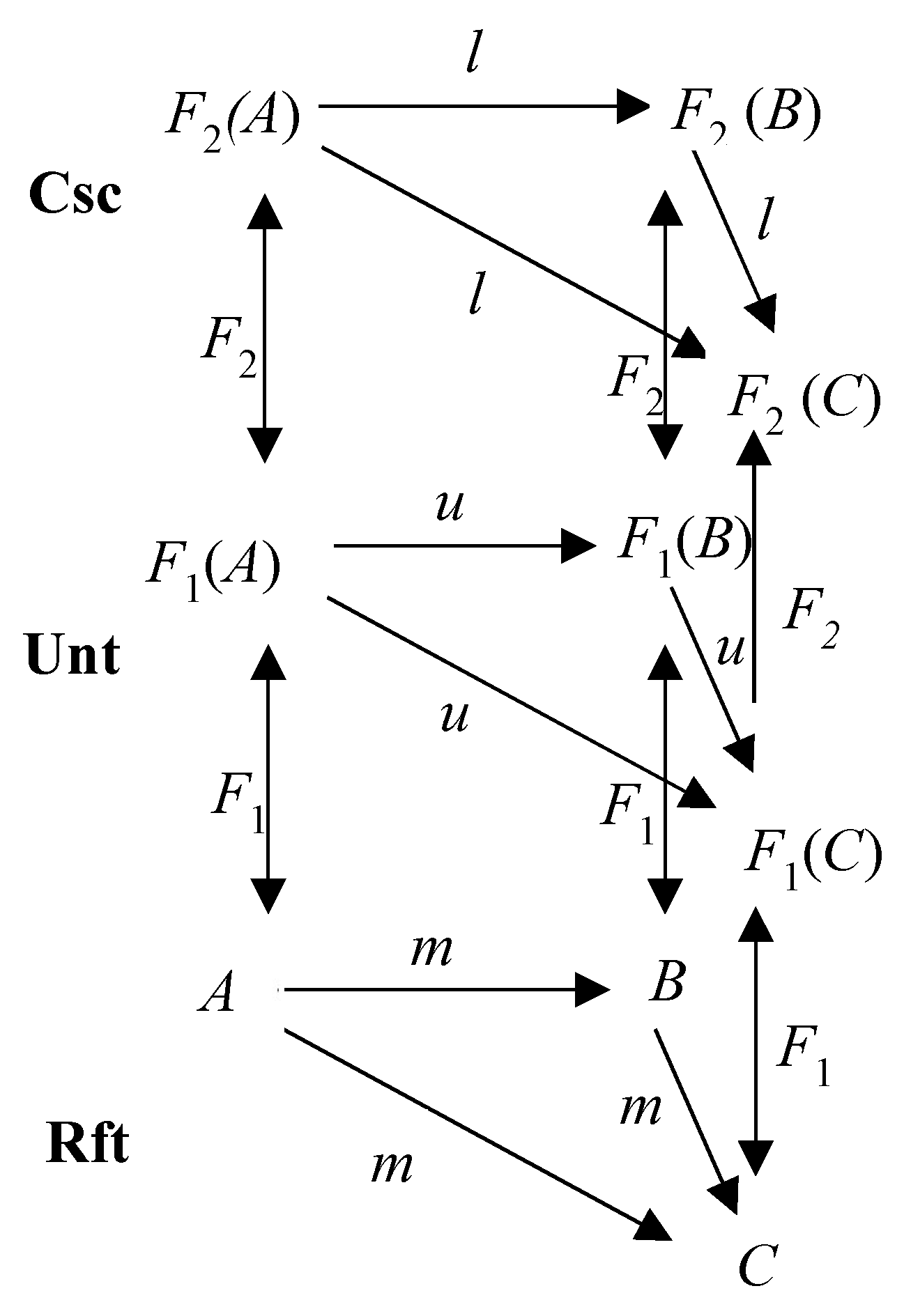
Consequently, Kant’s model of consciousness can be represented as a homomorphism as Figure 6, which is a simplified version of Figure 4 for simplifying a transitivity in a layer.

After converging (Neo-)Kant’s model with correction of Piaget on turning the priori into generation in constructing consciousness, 3-CMGC becomes delineating a conscious even with a static frame of construct of consciousness as (6)(7) stated, which should be an addition to the models of consciousness based on Cognitive Theory of Consciousness (CTC) and GWT, as be an inner construct to add (3)(4).

4. Computability of Consciousness in View of 3-CMGC

4.1. Current Computability Models of Consciousness

Now that consciousness is regarded as a cognitive activity according to CTC, it should be computable, as Charles Wallis expounded that the exact nature of cognition lies in dynamic computationalism. [30]

Actually, viewing consciousness as computable has been given for a longtime since Turing Machine proposed. At least, strong AI favors this proposition, as David J. Chamers said:

The strong AI thesis is cast in term computation, telling us that implementation of the appropriate computation suffices for consciousness. To evaluate this claim, we need to know just what it is for a physical system to implement a computation. [31]

And David J. Chamers predicated that the computation implementing consciousness is a Turing Machine (TM) in the form of combinational-state automata (CSA).

Recently, consciousness-represented brain neurons are modeled by Lenore Blum and Manuel Blumin in more detail as the Conscious Turing Machine (CTM) [32]. The model proposes that conscious neurons according to GWT is presented by neuron networks, and the connexity of the networks are regression, that is, Turing computable. CTM describes consciousness-relating neurons as a six-tuple as

< STM, LTM, Up Tree, Down Tree, Links, Input, Output >

(8)

where,

STM: Short Term Memory that at any moment in time contains CTM’s conscious content;

LTM: Long Term Memory, like expertise making up processors;

Env → LTM: directed edges from the environment via sensors to processors of the sensory data, Env is an environment for the neurons;

LTM → STM: via the Up Tree;

STM → LTM: via the Down Tree;

LTM → LTM: bidirectional edges (links) between processors; and

LTM → Env: directed edges from specific processors (like those that generate instructions for finger movement) to the environment via actuators (like the fingers that receive instructions from these processors) that act on the environment (via the actions of the fingers from these processors).

According to the theory of CTM, the stage is represented by STM that at any moment in time contains CTM’s conscious content. The audience members are represented by an enormous collection of powerful processors –each with its own expertise – that make up LTM processors which make predictions and get feedback from CTM’s world. Based on this feedback, learning algorithms internal to each processor improve that processor’s behavior. So, LTM processors, each with their own specialty, compete to get their questions, answers, and information in the form of chunks on the stage for immediate broadcast to the audience.

Conscious awareness is defined formally in the CTM as the reception by the LTM processors of the broadcast of conscious content. In time, some of these processors become connected by links turning conscious communication (through STM) into unconscious communication (through links) between LTM processors. Communication via links about a broadcasted chunk reinforces its conscious awareness, a process as an ignition.

A conscious neuron phenomenon is explained as a chunk of linked nodes in the Up Tree, an up-directed binary tree, as the chunk wins a competence of neurons through a function f holding, expanding or curtailing its nodes such that the chunk acquires sufficient |weight| and weight, respectively called intensity (the sum of the sub-node weights after a duration) and mood----a node’s weight in virtue of assigning probability in a coin-flip neuron node. Therefore, f is regressive, so, Turing computable.

CTM neuron dynamics of a conscious event shows a more competitive neuron network in a GWT. Spontaneously, it raises two questions that

(i).

if a (pure) mathematical representation of CTM can be made ---note that the mode of TM is an extractive mechanism model, rather than a (pure) mathematical one (compare notations like (of transition function) “turning left”, “turning right”, “tape writer”, “tape reader”, etc. in TM with “prime number”, “triangle” etc. in pure mathematics);

(ii).

if there exists a common model depicting consciousness of both brain and machines (if the machine or artificial consciousness is putative), note that the mode of CTM explains only biological brains, or similar mechanism model rather than a mathematical model.

4.2. A Proposed Computability Models of General Consciousness of 3-CGCM

In this section, a computability model of general consciousness is proposed for answering the questions (i) and (ii).

Church-Turing Thesis has been proved as a theorem by [33] with the help of [34] which proves that a TM equivalently serves as a general recursion function [35,36,37], defined by Godël [38], making up of primitive recursions in a recursion, or a composition way as expressed by (9)(10), wherein, the general recursion function f is achieved by means of recursion of h and g, and x is a vector.

f(x, 0)= g(x）

(9)

f(x, y+1= h(x , y, f(x,y))

(10)

(9)(10) describe a definitely decision, which are different from rough or flexible values as {l}{u}in an interval stage as a logic in generating described by Piaget, or as a script for a final version of a conscious event described by Deniel Dannett, or as a moving scheme in a competence for winning as CTM predicates. Moreover, a swarm computation is not targeted for (9)(10), which is resulting in a reason of emergence of AI’s new strands ----connectionism.

Upon this insufficiency in depicting rough or flexible values in a network computation, a mathematical model of neuron network computation hereby proposed. Consider a kind of machine learning-----artificial neuron network (ANN), which simulates natural neurons. A common formulas of ANN can be expressed as (11)(12).

{f₀(x,0)}={g(x)}

(11)

{f₂(x,y+1)}={h(x, y, ε, f₁(x, y))}

(12)

where,

x is certain elements in Rft;

g is to initialize informalization of x for inputting, as nodes of neurons in 0 layer;

{g(x)} indicates inputting examples of g(x) many times in training;

f : x→ f(x) is a recursion function, for example, the function like reflex of nodes;

f₀(x, 0) is to get the connection weight of elements of x from the 0 layer of the ANN;

{f₀(x, 0)} indicates inputting f₀(x, 0) many times of training;

f₁ = w^Tx+ε+y is to get the connection weight of elements of x with bias ε based on y;

y, regression vector of neurons next to x;

f₂ is the recursion function for the next layer of f₁; {f₂} refers to f₂ for multiple training;

ε is a bias for adjusting weights of nodesw;

h is a threshold function, including iterate ε for a multiple-time training {h}.

(11)(12) give a result of a neuron network {x, y} in recursion satisfying (9)(10), constituting a general recursion of multiple training. Considering the neuron network given by (8), it is plausible that CTM is amendable to (11)(12).

(11)(12) follow that a learned outcomes {f} on the primary structure {g} in a similarity emerges, as (13) says.

{f} ≈ L({g})

(13)

(13) says {f} learn, viz. L, from {g}, which is a proposing relation beyond Godël recursion model (9)(10).

The anatomy evidence of human (brain) neuron network (HNN) holding the structure same as ANN and showing the same mechanism with ANN in learning has been given and modeled by Kali and Dayan. [39]

More detailed evidence that HNN is same with ANN in construction recently confirmed by Jane X. Wang et.al. who claim that there exists a learning system----meta-reinforcement learning system in prefrontal cortex of human brain [40], wherein, even the correspondence matters of the weights in HNN are narrowed at participation of dopamine (DA), which is the molecular level evidence mapping the molecular Unt into the Csc, which could be formalized in (14)(15).

{Consc₀(photons,0)}={info(photons)}

(14)

{Consc₂((photons), y+1)}={h(Consc(photons, y, amount(DA), Consc₁(photons, y))}

(15)

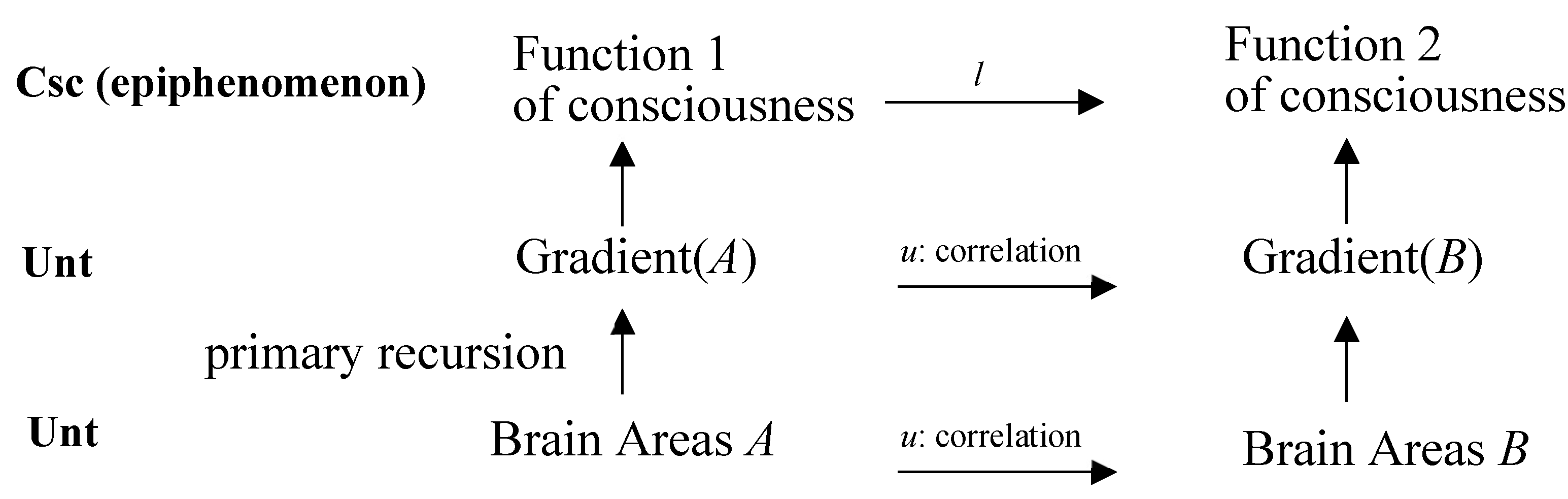
(14)(15) are an instance of learning of HNN-ANN, which contains a core of recursion on swarm computation (second-order variables of sets in contrast to (11)(12)). Corresponding to 3-CGCM, (14)(15) implements the following diagram from a learning unit to the classified result:

Or a diagram with 3-layers as (16).

(16)

(13) (14) (15) (16) describe sets as recursion variables in replace of individual variables as in (9)(10), and for brains or machines learning so of a general consciousness of species of natural and artificial units. Hence, question (i)(ii) should be considered as solved. This implies the swarm characteristics variables has been joined as TM model, such that cognitive theories based on swarm characteristics variables in terms of TM are mathematically represented. For example, “multiple scripts” [29] for editing into consciousness can be mathematically represented as the type of {f} in (11)(12)(13).

4.3. The Biological Positive of Recursion for 3-CMGC

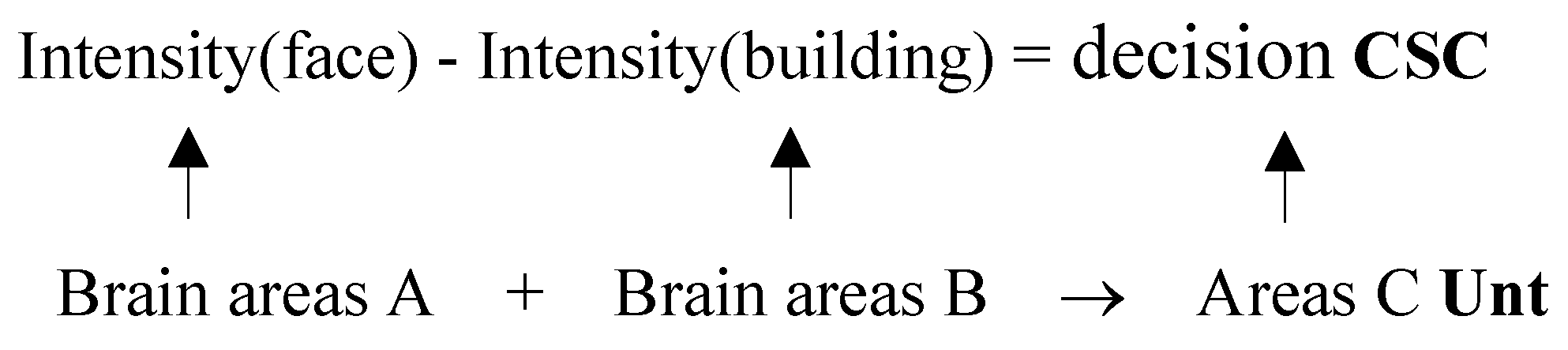
Empirical arguments which confirm that neurons make natural computation to perform a recursion were authenticated. Here we cite a study by H. R. Heekeren, S. Marrett, et.al. who conducted an experiment making the subjects to decide if the stimuli were a face or a house given an image with noise. [41]

With decrease of noise of images in showing a face or a building, the brain fMRI signals in an area of dorsolateral prefrontal cortex (DLPFC) of a subject is proportional to the gaps of cognition cells of face or house, which shows a decision of neurons do subtraction for maximizing a characteristics difference. If by “Intensity” we mean the intensity of fMRI signals for a special object (face or building), using “Areas” to denote reflecting region in the subject’s brain, the experiment demonstrates a homomorphism as (17).

(17)

The quantification relation in (17) (up formula) is a mathematical expression, which is a primitive recursion function, implemented by the brain neurons (as down expression says). This shows an instance of material layer Unt (neutrons and their properties) running computations {u} and homomorphic to Csc (like making a decision).

Recently, more and more discoveries of the functional neutrons are achieved, where, mathematical features are verified to be gradient-characteristic and -relative for functional neutrons [42], which implies natural computations belonging to {u}. The relations between the two gradients are primitive recursion (projection), as (18) shows.

(18)

In (18), the recursion function is of regression, that is, running in two steps. If an input α in Rft was supposed, the mappings between layers is given as (5), showing that the Unt operation is composite.

5. The Unity of Natural and Artificial Consciousness in 3-CMGC)

Functionalism and computationalism, therefore physicalism in the view of the present study, all argue that the mind, in particular consciousness, is computable, according to which there exists a common algorithm like (11)(12) depicting a machine or artificial system functionally equivalent to a natural consciousness by the algorithm. The recent advance shows an attempt to establish artificial consciousness model with the extracted pillars: Data, Information, Knowledge, Wisdom, and Purposes, DIKWP [43,44], which has the essence similar with physicalism in the unity of the artificial and natural consciousness, and so does 3-CMGC with the homomorphism thought. The viewpoint of the unity seems to be reasonable, however, there is still a “conservative” instance that insists on that the gap between natural consciousness and the technologies claiming “possessing consciousness” cannot be filled out, for example, as [45,46] hold.

The characteristic of the first person with the private is treated as one of essential factor of consciousness, which is not conceding physicalism like the model (3)(4). Here, we give an argument that “the first person” is accessed, not private.

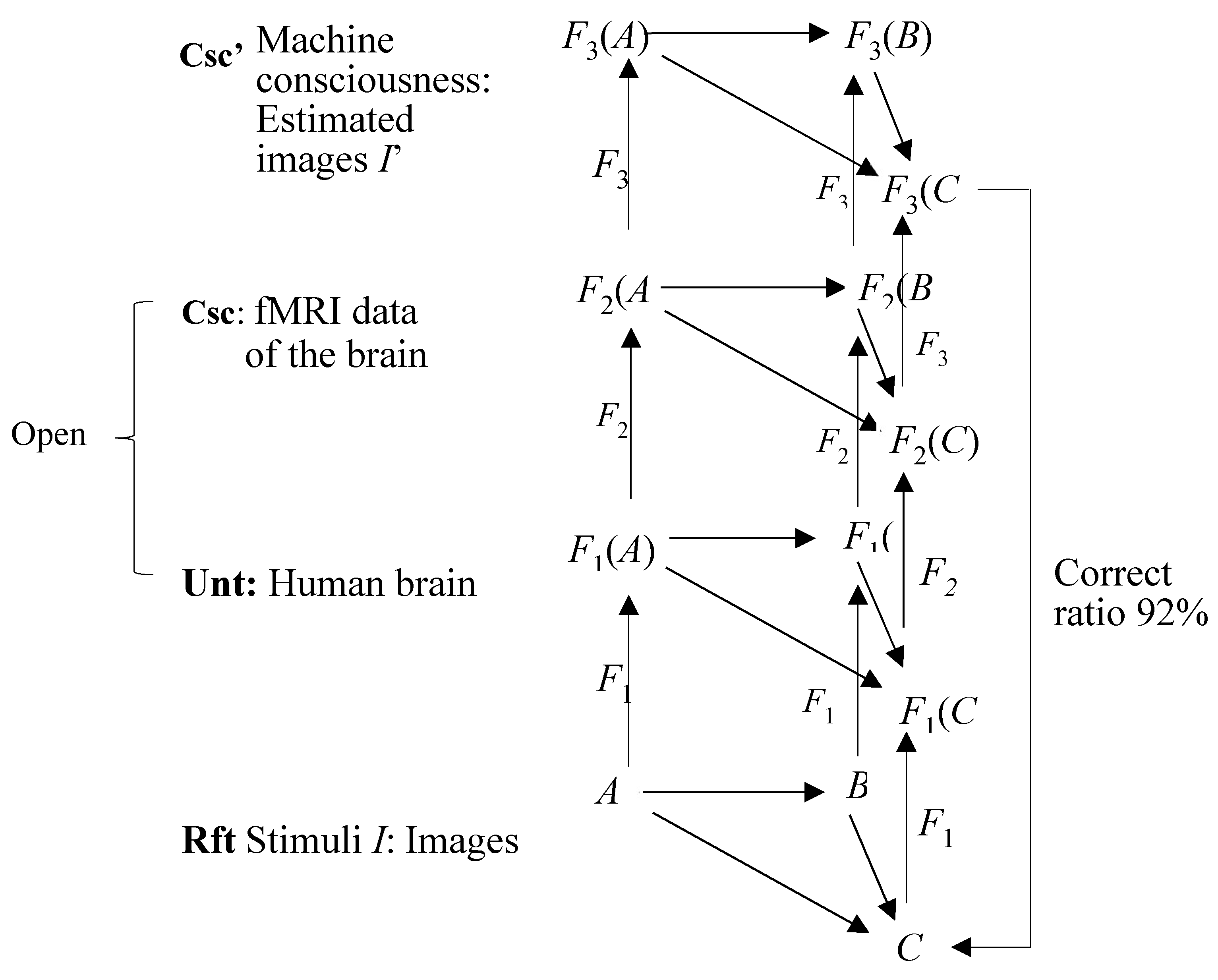
Consider a case of brain-computer interface (BCI). The experiment was made to read out mental contents from brain activity through fMRI [47]. In the experiment, brain fMRI data were recorded while the subject viewed a large collection of natural images I. The data was used to estimate a quantitative receptive-field model F₂ for each voxel for space, orientation and spatial frequency from responses evoked by stimuli of the natural images. The model F₃ predicts the brain activity seeing potential images I’ that matches the stimuli images I with a maximum 92% correct ratio. In other word, the images in Rft were being coded in Unt by brain fMRI as F₁, to generate image variables I in Csc by the brain-receptive-field models, say F₂; F₂ was to be estimated by the brain-receptive-field models F₃, giving the potential (objective) images I ’ in Csc’ (machine consciousness). The result is confirmed that I ≈ I ’ with a maximum 92% correct ratio as if Csc ≈ Csc’, as Figure 7 framed.

As a result, private Csc becomes open to a high extent (92%) as Csc-simulated Csc’. In other words, the experiment accessed the brain of the subject by means of fMRI, and its signals were verified as the consciousness about space. Then, the first-person characteristic of consciousness was broken, really becoming open to a high extent.

Similarly, collecting signals from the brain, no matter of interference, semi-interference or non-interference in BCI, all may be regarded as breaking “first person” for breaching the private and make the brain’s function to be common. In other words, BCI makes first-person access is fully authorizing, and their outputs, mostly with appliable outcomes, show a conscious result such as an everyday action etc., which undermines the monopoly of “first person” of biological entities, which delivers pursuable evidences to confirm the unity of general consciousness by filling out the gap between the artificial and the natural consciousness.

6. Conclusions

Mathematically modeling consciousness is feasible. Although consciousness (as the specific mind) is considered as the most complex in the world, and many aspects of consciousness are hidden, it is reasonable to set up a frame determining the essence of consciousness. According to the transitivity, the essential meaning based on the commonsense and learning from Piaget’s 2-layer consciousness model, 3-CMGC of homomorphism between the objects and the materials of implementing consciousness and the consciousness per se has been proposed here, which is not only for live matters, say, neutrons, but also for AI technologies such as artificial consciousness, robots and BCI technologies.

The expectation of 3-CMGC is giving a space classifying local and stepwise studies of consciousness with its artefacts into a global view. Further, the model delivers mathematical formulas about consciousness, which should be beneficial for applications on quantitative determinations in what measure machines possess consciousness.