Numerous Multi–Wave Solutions of the Time–Fractional Boussinesq–Like System via a Variant of the Extended Simple Equations Method (SEsM)

1. Introduction

Over the past two decades, the fractional nonlinear partial differential equations (FNPPDEs) have gained considerable popularity in the scientific community for modeling and analyzing a wide range of phenomena observed in the real world. This efficient framework allows for more accurately reproducing the complex wave dynamics of model systems encountered in diverse fields such as biology and ecology [1]–3], fluid dynamics [4]–7], finance and economics [8]–10], engineering [11]–13], among others. These systems often exhibit features such as memory effects, spatial heterogeneity and nonlocal interactions that integer-order models fail to adequately address. One approach to better understand this unconventional dynamic behavior is to find analytical solutions to the such models and their expert analysis. Finding exact solutions to FNPDEs, unlike those of NPDEs, is more difficult due to the necessary combination of elements from nonlinear dynamics with those arising from the fractional derivative’s order.

To date, two main approaches to finding exact and approximate analytical solutions of FNPDEs dominate the scientific literature: (1) Using fractional transformations, which allow reducing the studied NFPDEs to integer order nonlinear ODEs. Then, various well–known approaches from the ODE theory can be applied to the latter to obtain exact general and particular solutions of NPDEs. The most famous and applied methodologies in this direction use the so–called ansatz techniques [14]. Based on ansatz techniques, numerous analytical methods have been developed, including the Hirota method [15], the homogeneous balance method [16], the auxiliary equation method [17], the Jacobi elliptic function expansion method [18], the (G′/G)-expansion method [19], the F–expansion method [20], the tanth–function method [21], the first integral method [22], the exponential function method [23], the simplest equation method [24], the modified method of simplest equation [25]–27], etc. There are also numerous studies that apply these methods to find analytical solutions to various single NPDEs and systems of NPDEs. The SEsM, used in this study, is a relatively new methodology [28,29]. It is an extension of the Modified Method of Simple Equation, and has an almost universal nature. This is because most of the above–mentioned methods in this category are its particular cases, as proven in [30,31,32,33]; (2) Using standard traveling wave transformations, which allow reducing the studied FNPDEs to simpler fractional PDEs or fractional ODEs, whose analytical solutions are known (For instance, see Ref. [34]). Then, similarly to the first approach, analytical solutions of the studied FNPDEs are constructed on the basis of known analytical solutions of fractional ODEs. Among the methods in this category, the most widely used is so called fractional sub–equation method [35,36,37,38]. This method is based on known solutions of the fractional ODE of Riccati and its sub–variants. Another popular method in this category is the fractional elliptic Jacobi equation method [39,40], which uses Jacobi elliptic functions to derive analytical solutions of the studied FPDEs. When using the second approach, the Mittag–Leffler functions often appear in solutions of the studied FNPDEs, because they effectively describe the behavior of systems with fractional order.

The extended SEsM used in the current study follows the first approach, above given. In detail, we shall adapt the SEsM [41]–44], which is established for finding exact solutions of integer–order NPDEs to find exact solutions of a known system of FNPDEs by introducing an appropriate fractional transformation. The new and different emphasis in this methodology is that the solutions of the studied equations are presented as complex composite functions, including series of solutions of two (or more) simple equations or two (or more) special functions. In addition, we extend the current version of the SEsM by assuming that the simple equations used have different independent variables. The latter is a new approach that firstly has been applied to find analytical solutions of the extended integer–order KDV equation [45]. Numerous traveling wave solutions have been derived in [45] using an ODE of Abel, an ODE of Bernoulli, an ODE of Riccati and its sub–variants. Later, in [46], the authors independently proposed a similar methodology based on the extended Kudryashov method, as it was applied to find exact solutions of an integer-order Boussinesq-like system and the integer-order shallow-water wave equation. To obtain exact analytical solutions of the aforementioned models, the authors in [46], used two sub–variants of the ODE of Riccati as simple equations. In terms of finding exact solutions to systems of FNPDEs, a similar version of the extended SEsM was applied in [47,48] to dynamical models describing natural processes in fluid mechanics and ecology. In these studies, the obtained traveling wave solutions were presented by sums of two single composite functions containing the solutions of two distinct simple equations with the same independent variable. In [49,50], another version of the extended SEsM was applied to an extended variant of a popular ecological system of FNPDEs. In these studies, the obtained analytical solutions of the studied system are presented by distinct single composite functions with different independent variables (different wave coordinates) for each system variable.

In this study we shall apply the extended SEsM to the time–fractional version of the Boussinesq–like system [51]

$$\begin{array}{ccc}\hfill & & D_t^{\alpha }u+v_x+u{u}_x=0\hfill \\ & & D_t^{\alpha }v+u{v}_x+v{u}_x+k{u}_{xxx}=0\hfill \end{array}$$

(1)

where $u(x,t)$ is the elevation of a water wave and $v(x,t)$ is the surface velocity of water along x-direction, $\alpha$ is a time–fractional number and k is a coefficient, related to the depth of water. For the case $k=-1/3$, Equation (1) reduces to the classical Boussinesq system. Equation (1) is a very useful model for coastal and civil engineering in predicting the propagating nonlinear water waves in harbour and coastal zones.

Following the extended SEsM algorithm given bellow, we shall search for analytical solutions of Equation (1) in more specific manner taking into account the special wave characteristics of the studied time–fractional Boussinesq model. It is known that most fluid systems exhibit simultaneously nonlinear and dispersive properties. These distinct properties support diverse wave modes like solitary waves, periodic waves, and dispersive wave trains. In addition, variation in wave speeds of the distinct waves can be appeared due to factors such as the dispersion relation and the nonlinear interactions. Thus, such systems can demonstrate multi–scale dynamics, involving fast and slow wave components in accordance with its dispersion and nonlinear components. Taking into account these arguments, bellow we shall present the analytical solutions for each system variable of Equation (1) as a composition of two single composite functions with different wave coordinates. These composite functions contain power series of solutions of two distinct simple equations. We hope that such a presentation of the aforementioned solutions provides more accurate and insightful depiction of the complex behaviors inherent in the studied fluid system.

2. Preliminaries

In this section we present several important definitions of the modified Riemann-Liouville derivatives that we will use in the current study. These definitions are stated according to the basic results obtained by G. Jumarie in [52]–54]

2.1. Fractional derivative via fractional difference

Definition 2.1. Let $f:R\to R,x\to f\left(x\right)$, denote a continuous (but not necessarily differentiable) function, and let $h>0$ denote a constant discretization span. Define the forward operator $FW\left(h\right)$ by the equality (the symbol $:=$ means that the left side is defined by the right side)

$$FW\left(h\right)f\left(x\right):=f(x+h);$$

(2)

then the fractional difference of order $\alpha$, $0<\alpha <1$, of $f\left(x\right)$ is defined by the expression

$${\Delta }^{\alpha }f\left(x\right):={(FW-1)}^{\alpha }=\sum _{k=0}^{\infty }{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{k}}\right)f[x+(\alpha -k)h]$$

(3)

and its fractional derivative of order $\alpha$ is defined by the limit

$$f^{\alpha }\left(x\right)=\underset{h\downarrow 0}{lim}{\displaystyle \frac{{\Delta }^{\alpha }f\left(x\right)}{h^{\alpha }}}$$

(4)

2.2. Modified fractional Riemann–Liouville derivative

Definition 2.2. Refer to the function $f\left(x\right)$ of Definition 2.1.

(i) Assume that $f\left(x\right)$ is a constant K . Then its fractional derivative of order $\alpha$ is

$$\begin{array}{c}\hfill D_x^{\alpha }=K{\Gamma }^{-1}(1-\alpha )x^{-\alpha },\alpha \le 0,\\ \hfill =0,\alpha \ge 0.\end{array}$$

(5)

(ii) When $f\left(x\right)$ is not a constant, then we will set

$$f\left(x\right)=f\left(0\right)+\left[f\right(x)-f(0\left)\right],$$

(6)

and its fractional derivative will be defined by the expression

$$f^{\alpha }\left(x\right)=D_x^{\alpha }\left(0\right)+D_x^{\alpha }\left(f\left(x\right)-f\left(0\right)\right),$$

(7)

in which, for negative $\alpha$, one has

$$D_x^{\alpha }(f\left(x\right)-f\left(0\right)):={\displaystyle \frac{1}{{\Gamma }^{-\alpha }}}{\int }_0^x{(x-\zeta )}^{-\alpha -1}f\left(\zeta \right)d\zeta ,\alpha \le 0$$

(8)

whilst for positive $\alpha$, we will set

$$D_x^{\alpha }(f\left(x\right)-f\left(0\right))=D_x^{\alpha }\left(f\left(x\right)\right)=D_x^{\alpha }\left(f^{(\alpha -1)}\left(x\right)\right),\alpha \ge 0.$$

(9)

When $n\le \alpha <n+1$,

$$f^{\alpha }\left(x\right):=f^{(\alpha -1)}{\left(x\right)}^n,n\le \alpha ,n+1$$

(10)

In order to find the fractional derivative of compound functions, the following equation holds:

$$d^{\alpha }f\approx \Gamma (1+\alpha )df,0<alpha<1.$$

(11)

2.3. Taylor’s series of fractional order

Definition 2.3. The continuous function $f:R\to R,x\to f\left(x\right)$ has a fractional derivative of order $k\alpha$. For any positive integer k and for any $\alpha$, $0<\alpha \le 1$, then the following equality holds

$$f(x+h)=\sum _{k=0}^{\infty }{\displaystyle \frac{h^{\alpha k}}{\left(\alpha k\right)!}}{f}^{\left(\alpha k\right)}\left(x\right),$$

(12)

where $\Gamma (1+k\alpha )=\left(\alpha k\right)!,0<\alpha \le 1$.

Definition 2.4. If $0<\alpha \le 1$, then

$$D_x^{\alpha }{x}^{\gamma }=\Gamma (\gamma +1){\Gamma }^{-1}(\gamma +1-\alpha )x^{\gamma -\alpha },\gamma >0$$

(13)

or, if $\alpha =n+\theta ,n\in N$, then

$$D_x^{n+\theta }{x}^{\gamma }=\Gamma (\gamma +1){\Gamma }^{-1}(\gamma +1-n-\theta )x^{\gamma -n-\theta },0<\theta <1.$$

(14)

3. Description of the Generalized SEsM Algorithm

In this section, we present the generalized algorithm of a specific version of SEsM, exposing all the possibilities it provides for obtaining various complex analytical solutions to systems of FNPDEs (or single FNPDEs), depending on the selected fractional transformation and simple equation’s types used by the implementer. As it is demonstrated below, unlike the original SEsM algorithm outlined in [41]–43], we have swapped its first and second steps, incorporating methodological extensions into both steps of the original SEsM algorithm. In addition, the proposed SEsM algorithm presented below covers both approaches to the chosen traveling wave transformation discussed earlier in the paper. Our goal is to allow the user to choose which of the two approaches to use when extracting exact solutions to systems of FNPDEs similar to Equation (1).

Taking into account the problem we set out to solve in this study, we shall demonstrate all the possible steps of the algorithm above mentioned for a system of two NPPDEs with two independent variables:

$$\begin{array}{ccc}\hfill & & {\Psi }_1(u,v,D_t^{\alpha }u,D_t^{\alpha }v,D_{tt}^{2\alpha }u,D_{tt}^{2\alpha }v,D_x^{\beta }u,D_x^{\beta }v,D_{xx}^{2\beta }u,D_{xx}^{2\beta }v,...)=0\hfill \\ & & {\Psi }_2(u,v,D_t^{\alpha }u,D_t^{\alpha }v,D_{tt}^{2\alpha }u,D_{tt}^{2\alpha }v,D_x^{\beta }u,D_x^{\beta }v,D_{xx}^{2\beta }u,D_{xx}^{2\beta }v,...)=0,0<\alpha ,\beta \le 1\hfill \end{array}$$

(15)

where D denotes the arbitrary fractional order derivative operator, as superscripts $\alpha ,2\alpha ,\beta ,2\beta ,...$ give its fractional number and subscripts denote time and partial derivatives. Here, ${\Psi }_1$ and ${\Psi }_2$ are polynomials of u and v and their derivatives, respectively, where $u=u(t,x)$ and $v=v(t,x)$ are unknown functions.

Remark: We note that the variant of SEsM presented below is suitable to be applied mainly to real-world dynamical models of the type (15), where the system variables are expected to exhibit complex synchronized multi–layered wave behavior.

The generalized extended SEsM algorithm which is adopted for finding exact solutions of FNPDEs includes the following basic steps:

1.

Construction of the solutions of Equation (15). The solution of Equation (15) can be constructed as a complex composite function of two or more single composite functions, involving solutions of two or more simple equations with different independent variables. There are many variants of combination between the single composite function in constructing the corresponding solution, but below we will present only a few of its simplest forms:

Variant 1:

$$u({\xi }_1,{\xi }_2)=F_1\left({\xi }_1\right)+F_2\left({\xi }_2\right),v({\xi }_1,{\xi }_2)=F_3\left({\xi }_1\right)+F_4\left({\xi }_2\right),$$

(16)

Variant 2:

$$u({\xi }_1,{\xi }_2)=F_1\left({\xi }_1\right)F_2\left({\xi }_2\right),v({\xi }_1,{\xi }_2)=F_3\left({\xi }_1\right)F_4\left({\xi }_2\right),$$

(17)

Variant 3:

$$u({\xi }_1,{\xi }_2)={\displaystyle \frac{F_1\left({\xi }_1\right)}{F_2\left({\xi }_2\right)}},v({\xi }_1,{\xi }_2)={\displaystyle \frac{F_3\left({\xi }_1\right)}{F_4\left({\xi }_2\right)}},$$

(18)

where

$$\begin{array}{c}\hfill F_1\left({\xi }_1\right)=\sum _{i_1=1}^{n_1}{ϵ}_{i_1}{\left[f_1\left({\xi }_1\right)\right]}^{i_1},F_2\left(\xi \right)=\sum _{i_2=1}^{n_2}{\eta }_{i_2}{\left[f_2\left({\xi }_2\right)\right]}^{i_2},\\ \hfill F_3\left(\xi \right)=\sum _{i_3=1}^{n_3}{\theta }_{i_3}{\left[f_1\left({\xi }_1\right)\right]}^{i_3},F_4\left(\xi \right)=\sum _{i_4=1}^{n_4}{\iota }_{i_4}{\left[f_2\left({\xi }_2\right)\right]}^{i_4},\end{array}$$

(19)

as $f_1\left({\xi }_1\right)$ and $f_2\left({\xi }_2\right)$ are solutions of simple equations , which are presented in Step 3 of the SEsM algorithm.

2.

Selection of the traveling wave type transformation. To apply the SEsM to Equation (15), it is crucial to define the fractional derivatives in those equations. The choice of fractional derivatives (e.g., Riemann-Liouville, Caputo, conformable, etc) is essential for accurately modeling wave dynamics and reflecting the system’s physical properties, based on factors like the process nature, boundary conditions, and memory effects interpretation. In this context, the following variants of transformations are possible:

• Variant 1: Use a fractional transformation. The choice of explicit form of the fractional traveling wave transformation depends on how the fractional derivatives in Equation (15) are defined. Bellow, the most used fractional traveling wave transformations are selected:
  – Conformable fractional traveling wave transformation: ${\xi }_1={\kappa }_1{\displaystyle \frac{x^{\beta }}{\beta }}+{\omega }_1{\displaystyle \frac{t^{\alpha }}{\alpha }},{\xi }_2={\kappa }_2{\displaystyle \frac{x^{\beta }}{\beta }}+{\omega }_2{\displaystyle \frac{t^{\alpha }}{\alpha }}$, defined for conformable fractional derivatives [55];
  – Fractional complex transform: ${\xi }_1={\kappa }_1{\displaystyle \frac{x^{\beta }}{\Gamma (\beta +1)}}+{\omega }_1{\displaystyle \frac{t^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2={\kappa }_2{\displaystyle \frac{x^{\beta }}{\Gamma (\beta +1)}}+{\omega }_2{\displaystyle \frac{t^{\alpha }}{\Gamma (\alpha +1)}}$, defined for modified Riemann–Liouville fractional derivatives [52], which can applied for Caputo fractional derivatives and other fractional derivative types in studied FNPDEs [56].
  In the both cases, the studied FNPDEs are reduced to integer–order nonlinear ODEs.
• Variant 2: Use a standard traveling wave transformation. In this case, by introducing a traveling wave ansatz ${\xi }_1={\kappa }_{1}x+{\omega }_{1}t,{\xi }_2={\kappa }_{2}x+{\omega }_{2}t$ in the selected variant solutions from Step 1, the studied FNPDEs are reduced to fractional nonlinear ODEs.

3.

Selection of the forms of the used simple equations.

• For Variant 1 of Step 2: The general form of the integer–order simple equations used is:

  $${\left({\displaystyle \frac{d^{k_1}{f}_1}{d{\xi }_1^{k_1}}}\right)}^{l_1}=\sum _{j_1=0}^{m_1}{\mu }_{j_1}{f}_1^{j_1},{\left({\displaystyle \frac{d^{k_2}{f}_2}{d{\xi }_2^{k_2}}}\right)}^{l_2}=\sum _{j_2=0}^{m_2}{\nu }_{j_2}{f}_2^{j_2}.$$

  (20)
  By fixing $l_1,l_2$ and $m_1,m_2$ (at $k_1=k_2=1$) in Equation (20), different types integer–order ODEs can be used as simple equations, such as:
  – ODEs of first order with known analytical solutions (For example, an ODE of Riccati, an ODE of Bernoulli, an ODE of Abel of first kind, an ODE of tanh–function, etc);
  – ODEs of second order with known analytical solutions (For example, elliptic equations of Jaccobi and Weiershtrass and their sub–variants, an ODE of Abel of second kind, etc.). This scenario can be applied to specific classes FNPDEs (or NPDEs) (For instance, see [57]).
• For Variant 2 of Step 2: The general form of the fractional simple equations used is:

  $$D_{{\xi }_1}^{\alpha }=\sum _{j_1=0}^{m_1}{\mu }_{j_1}{f}_1^{j_1},D_{{\xi }_2}^{\alpha }=\sum _{j_2=0}^{m_2}{\nu }_{j_2}{f}_2^{j_2},$$

  (21)
  By fixing and $m_1,m_2$ in Equation (21), different types fractional ODEs can be used as simple equations, such as a fractional ODE of Riccati, a fractional ODE of Bernoulli or other polynomial or elliptic form equations, which solutions are available in the literature.

4.

Derivation of the balance equations and the system of algebraic equations. The fixation of the explicit form of solutions of Equation (15) presented in Step 1 of the SEsM algorithm depends on the balance equations derived. Substitutions of the selected variants from Steps 1,2 and 3 in Equation (15) leads to obtaining polynomials of the functions $f_1$ and $f_2$. The coefficients in front of these functions include the coefficients of the solution of the considered FNPDEs as well as the coefficients of the simple equations used. Analytical solutions of Equation (15) can be extracted only if each coefficient in front of the functions $f_1$ and $f_2$ contains almost two terms. Equating these coefficients to zero leads to formation of a system of nonlinear algebraic equations for each variant chosen according Steps 1,2 and 3 of the SEsM algorithm.

5.

Derivation of the analytical solutions. Any non–trivial solution of the algebraic system above mentioned leads to a solution of the studied FNPDEs by replacing the specific coefficients in the corresponding variant solutions, given in Step 1 as well as by changing the traveling wave coordinates chosen by the variants given in Step 2. For simplicity, these solutions are expressed through special functions. For a Variant 1 of the Step 3, these special functions are $V_{{\mu }_0,{\mu }_1,...,{\mu }_{j_1}}({\xi }_1;k_1,l_1,m_1)$ and $V_{{\nu }_0,{\nu }_1,...,{\nu }_{j_2}}({\xi }_2;k_2,l_2,m_2)$, as their explicit forms are determined on the basis of the specific form of the simple equations chosen (For reference, see Equation (20)). For a Variant 2 of the Step 3, the special functions are $V_{{\mu }_0,{\mu }_1,...,{\mu }_{j_1}}({\xi }_1,\alpha ;m_1)$ and $V_{{\nu }_0,{\nu }_1,...,{\nu }_{j_2}}({\xi }_2,\alpha ;m_2)$, whose exact forms are determined by the type of fractional simple equations used (For reference, see Equation (21)).

In this study, we shall demonstrate only some of the possibilities provided by the generalized SEsM algorithm, presented above, by applying only one of its variants to Equation (1).

4. Exact Solutions of the Time Fractional Boussinesq–Like System Using a Fractional Wave Transformation

According to the generalized SEsM algorithm, presented above, we choose to present the general solution of Equation (1) by Equation (16) in the way:

$$\begin{array}{ccc}\hfill & & u({\xi }_1,{\xi }_2)=\sum _{i_1=0}^{n_1}{ϵ}_{i_1}{\left[f_1\left({\xi }_1\right)\right]}^{i_1}+\sum _{i_2=0}^{n_2}{\eta }_{i_2}{\left[f_2\left({\xi }_2\right)\right]}^{i_2}\hfill \\ & & v({\xi }_1,{\xi }_2)=\sum _{i_1=0}^{n_3}{\theta }_{i_1}{\left[f_1\left({\xi }_1\right)\right]}^{i_1}+\sum _{i_2=0}^{n_4}{\iota }_{i_2}{\left[f_2\left({\xi }_2\right)\right]}^{i_2}\hfill \end{array}$$

(22)

In view of the studied shallow water problem, we choose to present the memory effects occurring in the system (1) in sense of modified Riemann–Liouville fractional derivatives, presented in Section 2. Thus, the fractional transformations take the form:

$${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$$

(23)

In the simple equations (20), we choose to fix $k_1=k_2=1$, $l_1=l_2=2$ and $m_1=4,m_2=3$. Then, Equation (20) is reduced to

$${\left({\displaystyle \frac{d{f}_1}{d{\xi }_1}}\right)}^2=\sum _{j_1=0}^4{\mu }_{j_1}{\left[f_1\left({\xi }_1\right)\right]}^{j_1},{\left({\displaystyle \frac{d{f}_2}{d{\xi }_2}}\right)}^2=\sum _{j_2=0}^3{\nu }_{j_2}{\left[f_2\left({\xi }_2\right)\right]}^{j_2}$$

(24)

The balance equations are $n_1=n_3=m_1-2$ and $n_2=n_4=m_2-2$. Substitution of Equations (22)–(24) in Equation (1) leads to a system of nonlinear equations. There are many variants and sub–variants of Equation (24) depending on the numerical values of their coefficients. For each of these variants or sub–variants, there are specific solutions, which are available in the literature. Below, we shall present only a few examples of specific sub–variants of simple equations of type (24). For example, as a starting point, we shall choose to use the first simple equation of Equation (24) in its complete form with respect to the coefficients ${\mu }_{j_1}$, i.e. ${\mu }_{j_1}\ne 0,j_1=0,1,..,4$. Regarding to the second simple equation of (24), however, we shall chose to use its simplest sub–variant, where ${\nu }_0=0,{\nu }_1=0,{\nu }_2\ne 0,{\nu }_3\ne 0$. Then, the system of nonlinear algebraic equations is:

$$\begin{array}{ccc}\hfill & & {{ϵ}_2}^2-12k{ϵ}_2{\mu }_4+2{ϵ}_2{\theta }_2=0\hfill \\ & & {ϵ}_1{\theta }_2+{ϵ}_1{ϵ}_2+{ϵ}_2{\theta }_1-5k{ϵ}_2{\mu }_3-2k{ϵ}_1{\mu }_4=0\hfill \\ & & {ϵ}_2{\iota }_1+{ϵ}_2{\eta }_1+{\theta }_2{\eta }_1=0\hfill \\ & & {ϵ}_1{\eta }_1+{ϵ}_1{\iota }_1+{\theta }_1{\eta }_1=0\hfill \\ & & {\omega }_1{\theta }_2+2{{ϵ}_1}^2+4{ϵ}_2+2{ϵ}_0{ϵ}_2+2{\eta }_0{ϵ}_2+2{\eta }_0{\theta }_2+2{ϵ}_1{\theta }_1-8k{ϵ}_2{\mu }_2\hfill \\ & & +2{ϵ}_0{\theta }_2-{\omega }_2{ϵ}_2+2{\iota }_0{ϵ}_2+4{\theta }_2+2{\theta }_0{ϵ}_2-3k{ϵ}_1{\mu }_3+{\omega }_2{\theta }_2-{\omega }_1{ϵ}_2=0\hfill \\ & & 4{ϵ}_1+4{\theta }_1-{\omega }_1{ϵ}_1-{\omega }_2{ϵ}_1+2{ϵ}_0{ϵ}_1+2{\eta }_0{ϵ}_1+{\omega }_1{\theta }_1+{\omega }_2{\theta }_1\hfill \\ & & +2{ϵ}_0{\theta }_1+2{\eta }_0{\theta }_1+2{\theta }_0{ϵ}_1+2{\iota }_0{ϵ}_1-2k{ϵ}_1{\mu }_2-6k{ϵ}_2{\mu }_1=0\hfill \\ & & {{\eta }_1}^2+2{\eta }_1{\iota }_1-12k{\eta }_1{\nu }_3=0\hfill \\ & & 4{\iota }_1-{\omega }_2{\eta }_1+2{\eta }_0{\eta }_1+2{\eta }_0{\iota }_1+{\omega }_1{\iota }_1+{\omega }_2{\iota }_1\hfill \\ & & +2{ϵ}_0{\iota }_1+2{ϵ}_0{\eta }_1+2{\theta }_0{\eta }_1+2{\iota }_0-{\omega }_1{\eta }_1-8k{\eta }_1{\nu }_2=0\hfill \end{array}$$

(25)

In the rest of this article, we shall present only a part of off-beat possible solutions which can be derived on dependence of the numerical values of the coefficients in polynomial parts of Equation (24) for this specific case.

4.1. Case 1: When ${\mu }_0={\mu }_1=0,{\mu }_2\ne 0,{\mu }_3=0,{\mu }_4\ne 0$ and ${\nu }_0=0,{\nu }_1=0,{\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (24)

Let us consider the case, where ${\mu }_0={\mu }_1=0,{\mu }_2\ne 0,{\mu }_3=0,{\mu }_4\ne 0$ and ${\nu }_0=0,{\nu }_1=0,{\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (24). Then Equation (24) is reduced to

$${\left({\displaystyle \frac{d{f}_1}{d{\xi }_1}}\right)}^2={\mu }_2{f}_1^2+{\mu }_4{f}_1^4,{\left({\displaystyle \frac{d{f}_2}{d{\xi }_2}}\right)}^2={\nu }_2{f}_2^2+{\nu }_3{f}_2^3$$

(26)

We present the general solution of Equation (1) by special functions in the following manner:

$$\begin{array}{ccc}\hfill & & u({\xi }_1,{\xi }_2)={ϵ}_0+{ϵ}_1{V}_{0,0,{\mu }_2,0,{\mu }_4}({\xi }_1;1,2,4)+{ϵ}_2{V}_{0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\eta }_0+{\eta }_1{V}_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)\hfill \\ & & v({\xi }_1,{\xi }_2)={\theta }_0+{\theta }_1{V}_{0,0,{\mu }_2,0,{\mu }_4}({\xi }_1;1,2,4)+{\theta }_2{V}_{0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\iota }_0+{\iota }_1{V}_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)\hfill \end{array}$$

(27)

For this specific case, several families of solutions of Equation (1) can be obtained depending on numerical values of the coefficients ${\mu }_2,{\mu }_4$ and ${\nu }_2,{\nu }_3$.

4.1.1. Variant 1: When ${\mu }_2=1,{\mu }_4=-1$ and ${\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (26)

Let us consider the case, where ${\mu }_2=1,{\mu }_4=-1$ and ${\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (26). Then, Equation (27) reduces to

$$\begin{array}{ccc}\hfill & & u({\xi }_1,{\xi }_2)={ϵ}_0+{ϵ}_1{V}_{0,0,1,0,-1}({\xi }_1;1,2,4)+{ϵ}_2{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & +{\eta }_0+{\eta }_1{V}_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)\hfill \\ & & v({\xi }_1,{\xi }_2)={\theta }_0+{\theta }_1{V}_{0,0,1,0,-1}({\xi }_1;1,2,4)+{\theta }_2{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & +{\iota }_0+{\iota }_1{V}_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)\hfill \end{array}$$

(28)

where the special function $V_{0,0,1,0,-1}({\xi }_1;1,2,4)$ is a particular solution of an ODE of second order, given in [57,58], and the special function $V_{0,0,{\nu }_2,{\nu }_3}({\xi }_1;1,2,3)$ presents particular solutions of an ODE of second order, which can be found in [59].

We solve the algebraic system (25) by fixing ${\mu }_0={\mu }_1=0,{\mu }_2=1,{\mu }_3=0,{\mu }_4=-1$. Many solutions of the system (25) can be derived, but we aim to find those solutions, where the coefficients ${\nu }_2,{\nu }_3$ are free parameters. In this way, one non–trivial solution of this system is:

$$\begin{array}{ccc}\hfill & & {ϵ}_0=4k{\nu }_2+4k-2-{\eta }_0-2{\theta }_0-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_1+{\displaystyle \frac{3}{2}}{\omega }_2,{ϵ}_1={\theta }_1={\eta }_0={\theta }_0={\iota }_0=0,\hfill \\ & & {ϵ}_2=-{\displaystyle \frac{6(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}},{\eta }_1=-{\displaystyle \frac{6{\nu }_3\left(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k\right)}{{\nu }_2+1}},\hfill \\ & & {\theta }_2={\displaystyle \frac{3(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}},{\iota }_1=-{\displaystyle \frac{3{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{{\nu }_2+1}}\hfill \end{array}$$

(29)

According to all possible variant solutions $V_{0,0,{\nu }_2,{\nu }_3}({\xi }_1;1,2,3)$, the following families of solutions (28) of Equation (1) are possible:

$$\begin{array}{ccc}\hfill & & u^{\left(1\right)}({\xi }_1,{\xi }_2)=4k{\nu }_2+4k-2-{\eta }_0-2{\theta }_0-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_1+{\displaystyle \frac{3}{2}}{\omega }_2\hfill \\ & & -{\displaystyle \frac{6(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6{\nu }_3\left(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k\right)}{{\nu }_2+1}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(1\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{3{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{{\nu }_2+1}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(30)

where [57]

$$V_{0,0,1,0,-1}({\xi }_1;1,2,4)={\displaystyle \frac{1}{cosh\left({\xi }_1\right)}},$$

(31)

and [59]

$$V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)={\displaystyle \frac{1}{(p_1{\xi }_2+p_2)e^{\frac{{\nu }_2{\xi }_2}{2}}-\frac{{\nu }_3}{4}}},\Delta ={\nu }_2^2+2{\nu }_3=0$$

(32)

In Equation (32), $p_1$ and $p_2$ are arbitrary constants.

$$\begin{array}{ccc}\hfill & & u^{\left(2\right)}({\xi }_1,{\xi }_2)=4k{\nu }_2+4k-2-{\eta }_0-2{\theta }_0-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_1+{\displaystyle \frac{3}{2}}{\omega }_2\hfill \\ & & -{\displaystyle \frac{6(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6{\nu }_3\left(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k\right)}{{\nu }_2+1}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(2\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{3{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{{\nu }_2+1}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(33)

where $V_{0,0,1,0,-1}({\xi }_1;1,2,4)$ is presented in Equation (31) and [59]

$$V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)={\displaystyle \frac{1}{p_1{e}^{\frac{{\nu }_2+\sqrt{\Delta }{\xi }_2}{2}}+p_2{e}^{\frac{{\nu }_2-\sqrt{\Delta }{\xi }_2}{2}}-\frac{1}{2}\frac{{\nu }_3}{{\nu }_2}}},\Delta >0$$

(34)

In Equation (34), $p_1$ and $p_2$ are arbitrary constants.

$$\begin{array}{ccc}\hfill & & u^{\left(3\right)}({\xi }_1,{\xi }_2)=4k{\nu }_2+4k-2-{\eta }_0-2{\theta }_0-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_1+{\displaystyle \frac{3}{2}}{\omega }_2\hfill \\ & & -{\displaystyle \frac{6(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6{\nu }_3\left(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k\right)}{{\nu }_2+1}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(3\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3(2k{\nu }_2+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0+2k)}{{\nu }_2+1}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{3{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{{\nu }_2+1}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(35)

where $V_{0,0,1,0,-1}({\xi }_1;1,2,4)$ is presented in Equation (31) and [59]

$$V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)={\displaystyle \frac{1}{e^{\frac{{\nu }_2{\xi }_2}{2}}(p_{1}cos[-\frac{\sqrt{\Delta }{\xi }_2}{2}]+p_{2}sin[-\frac{\sqrt{\Delta }{\xi }_2}{2}]-\frac{1}{2}\frac{{\nu }_3}{e_2})}},\Delta <0$$

(36)

In Equation (36), $p_1$ and $p_2$ are arbitrary constants. In all the solutions provided in this subsection, ${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$.

4.1.2. Variant 2: When ${\mu }_2=1,{\mu }_4=-1$ and ${\nu }_2=1,{\nu }_3\ne 0$ in Equation (26)

Let us consider the particular case, where ${\mu }_2=1,{\mu }_4=-1$ and ${\nu }_2=1,{\nu }_3\ne 0$ in Equation (26). Then, Equation (29) is reduced to:

$$\begin{array}{ccc}\hfill & & {ϵ}_0=8k-2-{\eta }_0-2{\theta }_0-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_1+{\displaystyle \frac{3}{2}}{\omega }_2,{ϵ}_1={\theta }_1={\eta }_0={\theta }_0=0,\hfill \\ & & {ϵ}_2=-{\displaystyle \frac{6(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0)}{2}},{\eta }_1=-{\displaystyle \frac{6{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{2}},\hfill \\ & & {\theta }_2={\displaystyle \frac{3(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0)}{2}},{\iota }_1=-{\displaystyle \frac{3{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{2}}\hfill \end{array}$$

(37)

In this specific case, the solution of Equation (1) is reduced to:

$$\begin{array}{ccc}\hfill & & u^{\left(4\right)}({\xi }_1,{\xi }_2)=8k-2-{\eta }_0-2{\theta }_0-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_1+{\displaystyle \frac{3}{2}}{\omega }_2\hfill \\ & & -{\displaystyle \frac{6(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0)}{2}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{2}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(4\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0)}{2}}{V}_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{3{\nu }_3\left(4k+{\omega }_1+{\omega }_2-{\theta }_0-{\iota }_0\right)}{2}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(38)

where $V_{0,0,1,0,-1}({\xi }_1;1,2,4)$ is presented in Equation (31) and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is a particular solution of an ODE of second order, given in [60].

$$V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)={\displaystyle \frac{2}{{\nu }_3}}csc{h}^2\left({\xi }_2\right)\pm {\displaystyle \frac{2}{{\nu }_3}}csch\left({\xi }_2\right)cosh\left({\xi }_2\right)$$

(39)

In Equation (38), ${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$.

4.1.3. Variant 3: When ${\mu }_2=1,{\mu }_4=-1$ and ${\nu }_2=4,{\nu }_3=-4$ in Equation (26)

Let us consider the case, where ${\mu }_2=1,{\mu }_4=-1$ and ${\nu }_2=4,{\nu }_3=-4$ in Equation (26). Then, Equation (29) is reduced to:

$$\begin{array}{ccc}\hfill & & {ϵ}_0=20k-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_2+{\displaystyle \frac{3}{2}}{\omega }_1-{\eta }_0-2-2{\theta }_0,{ϵ}_1={\eta }_0={\theta }_0={\theta }_1={\iota }_0=0,\hfill \\ & & {ϵ}_2=-2{\theta }_0+2{\omega }_1+2{\omega }_2-2{\iota }_0+20k,{\eta }_1=8{\theta }_0-8{\omega }_1-8{\omega }_2+8{\iota }_0-80k,\hfill \\ & & {\theta }_2=-16k+{\theta }_0-{\omega }_1-{\omega }_2+{\iota }_0,{\iota }_1=16k-4{\theta }_0+4{\omega }_1+4{\omega }_2-4{\iota }_0\hfill \end{array}$$

(40)

In this specific case, the solution of Equation (1) is reduced to:

$$\begin{array}{ccc}\hfill & & u^{\left(5\right)}({\xi }_1,{\xi }_2)=20k-2{\iota }_0+{\displaystyle \frac{3}{2}}{\omega }_2+{\displaystyle \frac{3}{2}}{\omega }_1-{\eta }_0-2-2{\theta }_0\hfill \\ & & +(-2{\theta }_0+2{\omega }_1+2{\omega }_2-2{\iota }_0+20k)V_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & +(8{\theta }_0-8{\omega }_1-8{\omega }_2+8{\iota }_0-80k)V_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(5\right)}({\xi }_1,{\xi }_2)=(-16k+{\theta }_0-{\omega }_1-{\omega }_2+{\iota }_0)V_{0,0,1,0,-1}^2({\xi }_1;1,2,4)\hfill \\ & & +(16k-4{\theta }_0+4{\omega }_1+4{\omega }_2-4{\iota }_0)V_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(41)

where $V_{0,0,1,0,-1}({\xi }_1;1,2,4)$ is presented in Equation (31) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is a particular solution of an ODE of second order, given in [57,58].

$$V_{0,0,4,-4}({\xi }_2;1,2,3)={\displaystyle \frac{1}{cos{h}^2\left({\xi }_2\right)}}$$

(42)

In Equation (41), ${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$.

4.2. Case 2: When ${\mu }_0\ne 0,{\mu }_1=0,{\mu }_2\ne 0,{\mu }_3=0,{\mu }_4\ne 0$ and ${\nu }_0={\nu }_1=0,{\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (24)

Let us consider the case, where ${\mu }_0\ne 0,{\mu }_1=0,{\mu }_2\ne 0,{\mu }_3=0,{\mu }_4\ne 0$ and ${\nu }_0=0,{\nu }_1=0,{\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (24). Then, Equation (24) is reduced to

$${\left({\displaystyle \frac{d{f}_1}{d{\xi }_1}}\right)}^2={\mu }_0+{\mu }_2{f}_1^2+{\mu }_4{f}_1^4,{\left({\displaystyle \frac{d{f}_2}{d{\xi }_2}}\right)}^2={\nu }_2{f}_2^2+{\nu }_3{f}_2^3$$

(43)

We present the general solution of Equation (1) by special functions in the following manner:

$$\begin{array}{ccc}\hfill & & u({\xi }_1,{\xi }_2)={ϵ}_0+{ϵ}_1{V}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}({\xi }_1;1,2,4)+{ϵ}_2{V}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\eta }_0+{\eta }_1{V}_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)\hfill \\ & & v({\xi }_1,{\xi }_2)={\theta }_0+{\theta }_1{V}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}({\xi }_1;1,2,4)+{\theta }_2{V}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\iota }_0+{\iota }_1{V}_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)\hfill \end{array}$$

(44)

In Equation (44), we choose to express the special function $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}({\xi }_1;1,2,4)$ (the solutions of the first equation in (43)), in terms of Weierstrass–elliptic functions [61].The special function $V_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)$ presents the same solutions, as those given in the previous section. Depending on variant solutions $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}({\xi }_1;1,2,4)$ and $V_{0,0,{\nu }_2,{\nu }_3}({\xi }_2;1,2,3)$, various families of solutions of Equation (1) can be selected.

4.2.1. Variant 1. When ${\mu }_0\ne 0,{\mu }_2\ne 0,{\mu }_4\ne 0$ and ${\nu }_2\ne 0,{\nu }_3\ne 0$ in Equation (43)

One non–trivial solution of the algebraic system (25) at ${\mu }_0\ne 0,{\mu }_1=0,{\mu }_2\ne 0,{\mu }_3=0,{\mu }_4\ne 0$ and ${\nu }_2\ne 0,{\nu }_3\ne 0$, including the coefficients ${\mu }_0,{\mu }_2,{\mu }_4$ and ${\nu }_2,{\nu }_3$ as free parameters, is:

$$\begin{array}{ccc}\hfill & & {ϵ}_0={ϵ}_1=0,{ϵ}_2={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}},{\eta }_1={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}},\hfill \\ & & {\eta }_0={\theta }_0={\theta }_1=0,{\theta }_2=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}},\hfill \\ & & {\iota }_0=-{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0,\hfill \\ & & {\iota }_1={\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}\hfill \end{array}$$

(45)

Then, substitution of Equation (45) in Equation (44) leads to the following solutions of Equation(1):

$$\begin{array}{ccc}\hfill & & u^{\left(6\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(6\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(46)

where

$$\begin{array}{ccc}\hfill & & V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(1\right)}({\xi }_1;1,2,4)=\sqrt{{\displaystyle \frac{1}{{\mu }_4}}(\wp ({\xi }_1;g_2,g_3)-{\displaystyle \frac{1}{3}}{\mu }_2)}\hfill \\ & & g_2={\displaystyle \frac{4}{3}}({\mu }_2^2-3{\mu }_4{\mu }_0),g_3={\displaystyle \frac{4{\mu }_2}{27}}(-2{\mu }_2^2+9{\mu }_4{\mu }_0)\hfill \end{array}$$

(47)

and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)$ is presented in Equation (32).

$$\begin{array}{ccc}\hfill & & u^{\left(7\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(7\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(48)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(1\right)}({\xi }_1;1,2,4)$ is presented in Equation (47) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)$ is presented in Equation (34).

$$\begin{array}{ccc}\hfill & & u^{\left(8\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(8\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(49)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(1\right)}({\xi }_1;1,2,4)$ is presented in Equation (47) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)$ is presented in Equation (36).

$$\begin{array}{ccc}\hfill & & u^{\left(9\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(9\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(50)

where

$$\begin{array}{ccc}\hfill & & V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(2\right)}({\xi }_1;1,2,4)=\sqrt{{\displaystyle \frac{3{\mu }_0}{3\wp ({\xi }_1;g_2,g_3)-{\mu }_2}}},\hfill \\ & & g_2={\displaystyle \frac{4}{3}}({\mu }_2^2-3{\mu }_4{\mu }_0),g_3={\displaystyle \frac{4{\mu }_2}{27}}(-2{\mu }_2^2+9{\mu }_4{\mu }_0)\hfill \end{array}$$

(51)

and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)$ is presented in Equation (32).

$$\begin{array}{ccc}\hfill & & u^{\left(10\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(10\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(52)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(2\right)}({\xi }_1;1,2,4)$ is presented in Equation (51) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)$ is presented in Equation (34).

$$\begin{array}{ccc}\hfill & & u^{\left(11\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(11\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(53)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(2\right)}({\xi }_1;1,2,4)$ is presented in Equation (51) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)$ is presented in Equation (36).

$$\begin{array}{ccc}\hfill & & u^{\left(12\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(12\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(54)

where

$$\begin{array}{ccc}\hfill & & V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(3\right)}({\xi }_1;1,2,4)={\displaystyle \frac{\sqrt{12{\mu }_0\wp ({\xi }_1;g_2,g_3)+2{\mu }_0(2{\mu }_2+D)}}{12\wp ({\xi }_1;g_2,g_3)+D}},D={\displaystyle \frac{1}{2}}(5{\mu }_2\pm \sqrt{9{\mu }_2^2-36{\mu }_0{\mu }_4}),\hfill \\ & & g_2=-{\displaystyle \frac{-(5{\mu }_{2}D+4{\mu }_2^2+33{\mu }_0{\mu }_2{\mu }_4)}{12}},g_3={\displaystyle \frac{21{\mu }_2^{2}D-63{\mu }_0{\mu }_{4}D+20{\mu }_2^3-27{\mu }_0{\mu }_2{\mu }_4}{216}}\hfill \end{array}$$

(55)

and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)$ is presented in Equation (32).

$$\begin{array}{ccc}\hfill & & u^{\left(13\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(13\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(56)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(3\right)}({\xi }_1;1,2,4)$ is presented in Equation (55) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)$ is presented in Equation (34).

$$\begin{array}{ccc}\hfill & & u^{\left(14\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(14\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(57)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(3\right)}({\xi }_1;1,2,4)$ is presented in Equation (55) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)$ is presented in Equation (36).

$$\begin{array}{ccc}\hfill & & u^{\left(15\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(15\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(58)

where

$$\begin{array}{ccc}\hfill & & V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(4\right)}({\xi }_1;1,2,4)={\displaystyle \frac{\sqrt{{\mu }_0}[6\wp ({\xi }_{;}{g}_2,g_3)+{\mu }_2]}{3{\wp }^{\prime }({\xi }_1;g_2,g_3)}},\hfill \\ & & g_2=-{\displaystyle \frac{1}{12}}{\mu }_2^2+{\mu }_0{\mu }_4,g_3={\displaystyle \frac{1}{216}}{\mu }_2(36{\mu }_0{\mu }_4-{\mu }_2^2)\hfill \end{array}$$

(59)

and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)$ is presented in Equation (32).

$$\begin{array}{ccc}\hfill & & u^{\left(16\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(16\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(60)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(4\right)}({\xi }_1;1,2,4)$ is presented in Equation (59) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)$ is presented in Equation (34).

$$\begin{array}{ccc}\hfill & & u^{\left(17\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(17\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(61)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(4\right)}({\xi }_1;1,2,4)$ is presented in Equation (59) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)$ is presented in Equation (36).

$$\begin{array}{ccc}\hfill & & u^{\left(18\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(18\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(62)

where

$$\begin{array}{ccc}\hfill & & V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(5\right)}({\xi }_1;1,2,4)={\displaystyle \frac{3{\wp }^{\prime }({\xi }_1;g_2,g_3)}{\sqrt{{\mu }_4}[6\wp ({\xi }_{;}{g}_2,g_3)+{\mu }_2]}},\hfill \\ & & g_2=-{\displaystyle \frac{1}{12}}{\mu }_2^2+{\mu }_0{\mu }_4,g_3={\displaystyle \frac{1}{216}}{\mu }_2(36{\mu }_0{\mu }_4-{\mu }_2^2)\hfill \end{array}$$

(63)

and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)$ is presented in Equation (32).

$$\begin{array}{ccc}\hfill & & u^{\left(19\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(19\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(64)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(5\right)}({\xi }_1;1,2,4)$ is presented in Equation (63) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)$ is presented in Equation (34).

$$\begin{array}{ccc}\hfill & & u^{\left(20\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(20\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(65)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(5\right)}({\xi }_1;1,2,4)$ is presented in Equation (63) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)$ is presented in Equation (36).

$$\begin{array}{ccc}\hfill & & u^{\left(21\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(21\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(66)

where

$$V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(6\right)}({\xi }_1;1,2,4)={\displaystyle \frac{{\mu }_2\sqrt{-15{\mu }_0/2{\mu }_4}\wp ({\xi }_1,g_2,g_3)}{3\wp ({\xi }_1;g_2,g_3)+{\mu }_2}},{\mu }_0={\displaystyle \frac{5{\mu }_2^2}{36{\mu }_4}},g_2={\displaystyle \frac{2{\mu }_2^2}{9}},g_3={\displaystyle \frac{{\mu }_2^3}{54}}$$

(67)

and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(1\right)}({\xi }_2;1,2,3)$ is presented in Equation (32).

$$\begin{array}{ccc}\hfill & & u^{\left(22\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(22\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(68)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(6\right)}({\xi }_1;1,2,4)$ is presented in Equation (67) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(2\right)}({\xi }_2;1,2,3)$ is presented in Equation (34).

$$\begin{array}{ccc}\hfill & & u^{\left(23\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(23\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k{\nu }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k{\nu }_2+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8{\mu }_2-8{\nu }_2+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-{\nu }_2}}{V}_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(69)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(6\right)}({\xi }_1;1,2,4)$ is presented in Equation (67) and $V_{0,0,{\nu }_2,{\nu }_3}^{\left(3\right)}({\xi }_2;1,2,3)$ is presented in Equation (36). In all the solutions, presented in this subsection, ${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$

4.2.2. Variant 2: When ${\mu }_0\ne 0,{\mu }_2\ne 0,{\mu }_4\ne 0$ and ${\nu }_2=1,{\nu }_3\ne 0$ in Equation (43)

When ${\nu }_2=1,{\nu }_3\ne 0$, Equation (45) is reduced to:

$$\begin{array}{ccc}\hfill & & {ϵ}_0={ϵ}_1=0,{ϵ}_2={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}},{\eta }_1={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}},\hfill \\ & & {\eta }_0={\theta }_0={\theta }_1=0,{\theta }_2=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}},\hfill \\ & & {\iota }_0=-{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0,\hfill \\ & & {\iota }_1={\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}\hfill \end{array}$$

(70)

Substitution of Equation (70) in the particular variant of Equation (44) leads to the following solutions of Equation (1):

$$\begin{array}{ccc}\hfill & & u^{\left(24\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(24\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(71)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(1\right)}({\xi }_1;1,2,4)$ is presented in Equation (47), and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is presented in Equation (39).

$$\begin{array}{ccc}\hfill & & u^{\left(25\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(25\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(72)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(2\right)}({\xi }_1;1,2,4)$ is presented in Equation (51), and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is presented in Equation (39).

$$\begin{array}{ccc}\hfill & & u^{\left(26\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(26\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(73)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(3\right)}({\xi }_1;1,2,4)$ is presented in Equation (55), and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is presented in Equation (39).

$$\begin{array}{ccc}\hfill & & u^{\left(27\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(27\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(74)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(4\right)}({\xi }_1;1,2,4)$ is presented in Equation (59), and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is presented in Equation (39).

$$\begin{array}{ccc}\hfill & & u^{\left(28\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(28\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(75)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(5\right)}({\xi }_1;1,2,4)$ is presented in Equation (63), and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is presented in Equation (39).

$$\begin{array}{ccc}\hfill & & u^{\left(29\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & +{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\nu }_3\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(29\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+8k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+2k+{\displaystyle \frac{3}{4}}{\omega }_1+2k{\mu }_2-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\nu }_3\left(8k{\mu }_2-8k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-1}}{V}_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)\hfill \end{array}$$

(76)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(6\right)}({\xi }_1;1,2,4)$ is presented in Equation (67), and $V_{0,0,1,{\nu }_3}^{\left(4\right)}({\xi }_2;1,2,3)$ is presented in Equation (39). In all the solutions presented in this subsection, ${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$.

4.2.3. Variant 3: When ${\mu }_0\ne 0,{\mu }_2\ne 0,{\mu }_4\ne 0$ and ${\nu }_2=4,{\nu }_3=-4$ in Equation (43)

When ${\nu }_2=4,{\nu }_3=-4$, Equation (45) is reduced to:

$$\begin{array}{ccc}\hfill & & {ϵ}_0={ϵ}_1=0,{ϵ}_2={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}},{\eta }_1=-{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}},\hfill \\ & & {\eta }_0={\theta }_0={\theta }_1=0,{\theta }_2=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}},\hfill \\ & & {\iota }_0=-{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0,\hfill \\ & & {\iota }_1={\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}\hfill \end{array}$$

(77)

Substitution of Equation (77) in the particular variant of Equation (44) leads to the following solutions of Equation (1):

$$\begin{array}{ccc}\hfill & & u^{\left(30\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(30\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}}{V^{\left(1\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(78)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(1\right)}({\xi }_1;1,2,4)$ is presented in Equation (47) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is presented in Equation (42).

$$\begin{array}{ccc}\hfill & & u^{\left(31\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(31\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}}{V^{\left(2\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(79)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(2\right)}({\xi }_1;1,2,4)$ is presented in Equation (51) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is presented in Equation (42).

$$\begin{array}{ccc}\hfill & & u^{\left(32\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(32\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}}{V^{\left(3\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(80)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(3\right)}({\xi }_1;1,2,4)$ is presented in Equation (55) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is presented in Equation (42).

$$\begin{array}{ccc}\hfill & & u^{\left(33\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(33\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}}{V^{\left(4\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(81)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(4\right)}({\xi }_1;1,2,4)$ is presented in Equation (59) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is presented in Equation (42).

$$\begin{array}{ccc}\hfill & & u^{\left(34\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(34\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}}{V^{\left(5\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(82)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(5\right)}({\xi }_1;1,2,4)$ is presented in Equation (63) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is presented in Equation (42).

$$\begin{array}{ccc}\hfill & & u^{\left(35\right)}({\xi }_1,{\xi }_2)={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\mu }_4\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{6\left(4+2{\eta }_0+{\omega }_2+2{ϵ}_0+{\omega }_1\right)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \\ & & v^{\left(35\right)}({\xi }_1,{\xi }_2)=-{\displaystyle \frac{3}{4}}{\displaystyle \frac{{\mu }_4\left(-8k{\mu }_2+4+2{ϵ}_0+{\omega }_2+32k+{\omega }_1+2{\eta }_0\right)}{{\mu }_2-4}}{V^{\left(6\right)}}_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^2({\xi }_1;1,2,4)\hfill \\ & & -{\displaystyle \frac{1}{2}}{ϵ}_0-{\theta }_0+{\displaystyle \frac{3}{4}}{\omega }_2-1+16k+{\displaystyle \frac{3}{4}}{\omega }_1-{\displaystyle \frac{1}{2}}{\eta }_0\hfill \\ & & +{\displaystyle \frac{3(8k{\mu }_2-32k+4+2{ϵ}_0+{\omega }_2+{\omega }_1+2{\eta }_0)}{{\mu }_2-4}}{V}_{0,0,4,-4}({\xi }_2;1,2,3)\hfill \end{array}$$

(83)

where $V_{{\mu }_0,0,{\mu }_2,0,{\mu }_4}^{\left(6\right)}({\xi }_1;1,2,4)$ is presented in Equation (67) and $V_{0,0,4,-4}({\xi }_2;1,2,3)$ is presented in Equation (42). In all the solutions, presented in this subsection, ${\xi }_1=x+{\displaystyle \frac{{\omega }_1{t}^{\alpha }}{\Gamma (\alpha +1)}},{\xi }_2=x+{\displaystyle \frac{{\omega }_2{t}^{\alpha }}{\Gamma (\alpha +1)}}$.

For all analytical and numerical calculations in this article, we use the computational software Maple (https://www.maplesoft.com).

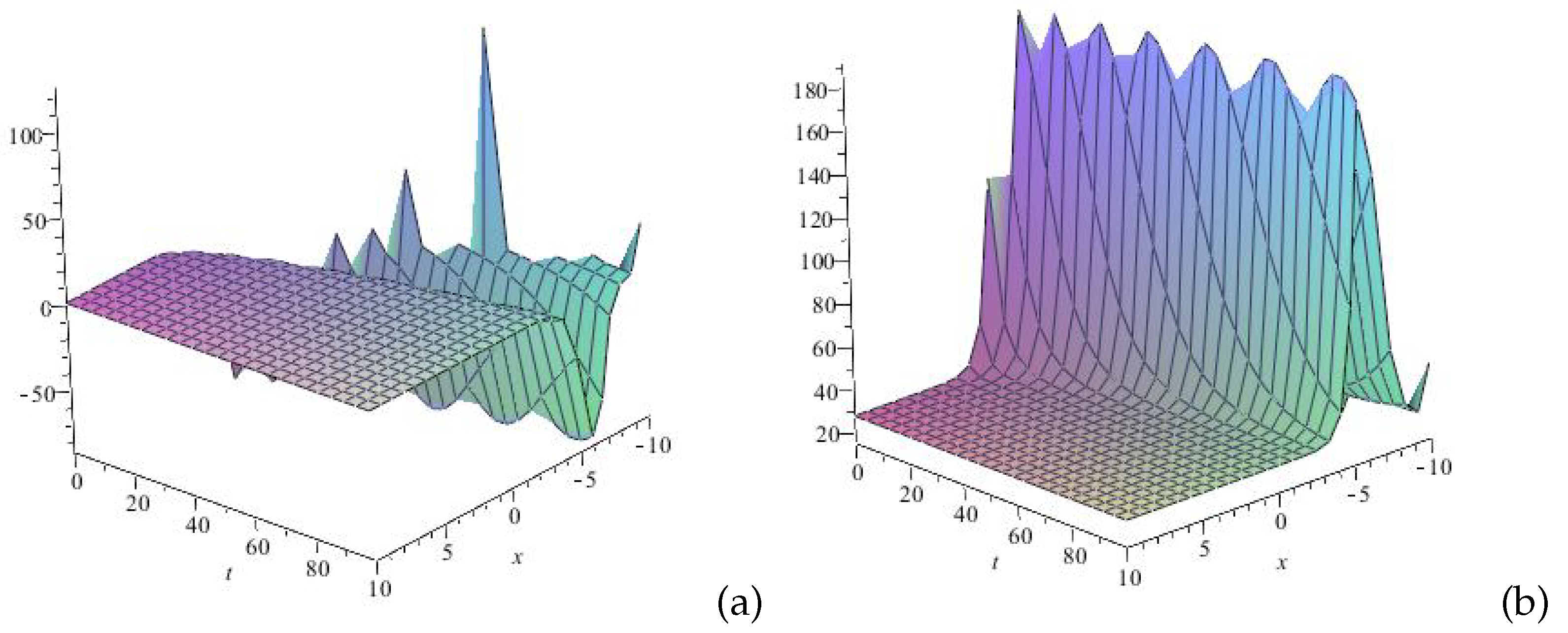
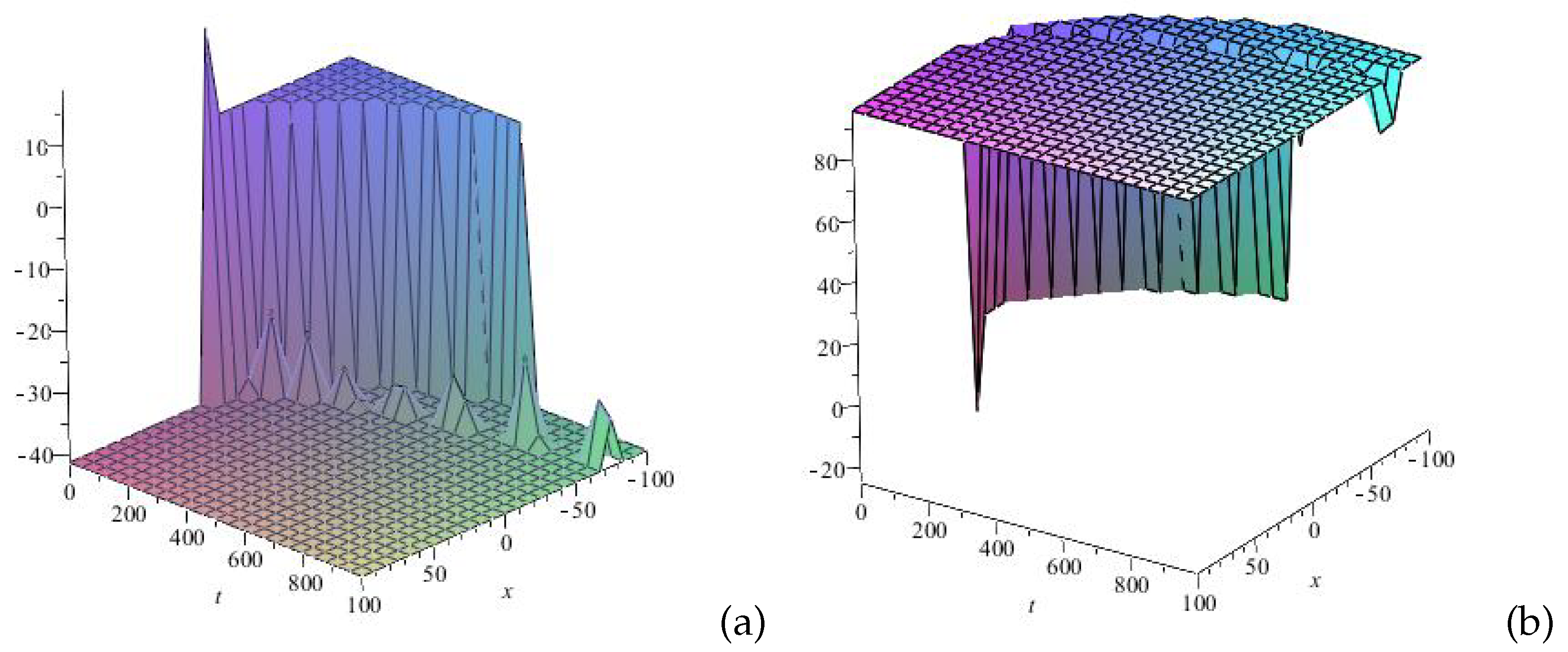
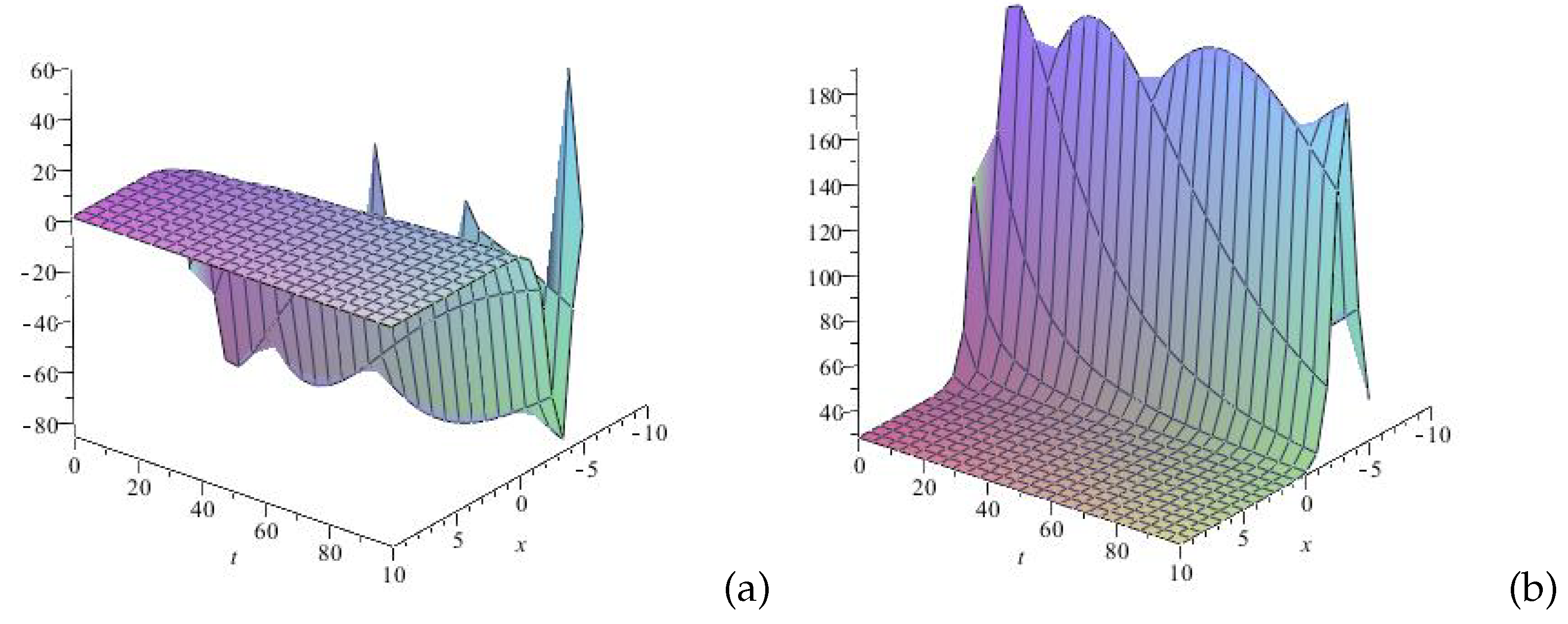
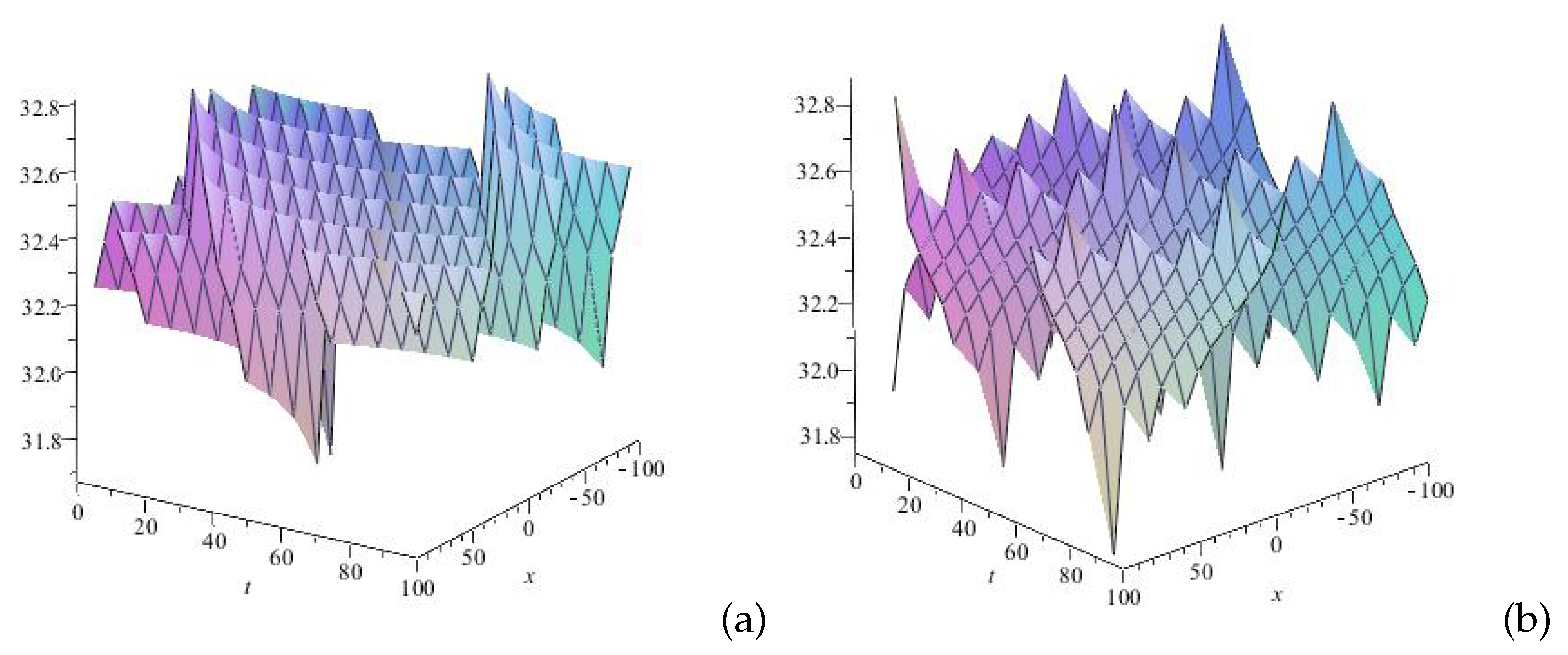
5. Numerical Simulations

In this section, we present visualizations of some analytical solutions presented in Section 4. In accordance with the obtained exact solutions of Equation (1), which are combinations of various special functions, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 illustrate combinations of different type’s waves, propagating in the studied water medium. It is obvious that Equation (1) demonstrates complex wave behavior, which can vary significantly depending on the specific exact solution. Here, we have shown the more interesting variants of mixed waves, trying to summarize them briefly depending on their wave type. For example, in the simplest case, one can observe combinations of waves of one type, such as single solitons (Figure 1) or complex multi-soliton structures (Figure 3) with different amplitudes and wavelengths. A more complex scenario involves the propagation of soliton wave packets combined with single solitons, as shown in Figure 4 and Figure 7. Of particular interest are combinations of synchronized kink and anti-kink waves and periodic structures (Figure 2 and Figure 5 ), as well as kink and anti-kink wave packets combined with multiple single solitons of different amplitude and wavelength (Figure 6 and Figure 8). The complex wave dynamics of the system (1) is also demonstrated in Figure 9, where combinations of kinks, anti-kinks, and multi–soliton wave packets are observed. We note, that the multi-wave behavior of the system (1), based on any analytical solution, presented in this section, can change qualitatively depending on the choice of the numerical values of the coefficients in it, the fractional derivative order, as well as the time and spatial numerical intervals of the plots. In this context, a more realistic picture of the wave dynamics of the studied system for prediction or control purposes can only be obtained if numerical values or numerical intervals of the above-mentioned parameters are specified.

6. Conclusions

In this study, we have proposed an extended version of the SEsM, which is applicable for obtaining analytical solutions of FNPDEs (in particular, NPDEs), that model dynamics of real-world processes with complex wave behavior. The solutions to such NPDEs are expressed as combinations of single composite functions, which involve solutions to two distinct simple equations or two distinct special functions with different independent variables. A generalized algorithm of the methodology has been presented, allowing the researcher to flexibly choose an appropriate traveling wave transformation and appropriate simple equations’ types to extract exact solutions to the studied models. This highlights the universality of the method in its application to both systems of FNPDEs and single FNPDEs of various types.

One variant of the extended SEsM has been applied to the time-fractional Boussinesq–like system, introducing a fractional traveling wave transformation and utilizing two second-order ODEs with different coordinates in their generalized form as simple equations. It has been demonstrated, that for different numerical values of the coefficients in polynomial parts of these equations, they reduce to various forms, each yielding distinct analytical solutions. By different combinations of these solutions, we have derived a part of the possible analytical solutions to the studied system of FNPDEs, including diverse combinations of hyperbolic, elliptic, and trigonometric functions. In this way, the investigated water medium exhibits a variety of mixed waves, such as single solitons, multi-solitons with different amplitudes and wavelengths, complex kink and anti-kink structures, and periodic wave packets. The propagation of different types of waves in the studied medium, analytically and numerically illustrated in this paper, is explained by the interplay of nonlinear interactions and dispersion effects present in Equation (1).

It is important to note, that the analytical solutions obtained in this study, present only a a part of the possible solutions under the selected simple equations (24). For instance, the solutions of Jacobi elliptic equation, along with its hyperbolic and trigonometric analogues, or the solutions of the Abel equation of second kind, could also be used in extracting the solutions of Equation (1). Additionally, the construction solutions to Equation (1) can incorporate also combinations of series of known solutions of different ODEs of first order, or mixture combinations of series of known solutions of ODEs of first order and ODEs of second order. Following another variant of the extended SEsM, proposed in [50], it is also feasible to construct the solution of Equation (1) by distinct single composite functions that include series of solutions of two distinct simple equations with different independent variables for each system variable. These ideas, however, will be the subject of our furture investigations.