Surface Inflows Toward Active Regions in Solar Dynamo Models

1. Introduction

Both large- and small-scale flows govern the magnetic field and surface activity of the Sun. Differential rotation and meridian flow constitute large-scale flows [1,2,3]. Observations on the solar surface reveal the presence of converging flows surrounding Bipolar Magnetic Regions (BMRs) [4,5]. These inflows collectively generate average flows around the activity belt, [6,7], and their intensity is contingent on the level of flux within the solar cycle, as demonstrated by [8] and [7]. Additionally, these inflows can reach a substantial fraction of the mean axisymmetric poleward meridional flow at mid-latitudes, but their spatial extent remains confined to the belts where the active regions are located. The magnetic influence on surface flows can induce variations in the transportation of magnetic flux towards the pole, consequently affecting the dynamo efficiency of decaying bipolar active regions. This variation is attributed, at least in part, to surface inflows directed towards large active regions [8,9,10], which lead to a reduction in the cross-equatorial cancellations of BMRs and suppress the effectiveness of the Babcock–Leighton process. In the case of a strong solar cycle, this effect becomes more pronounced and imparts a stabilising influence on the dynamo, as demonstrated by [11] and [12].

Surface inflows toward active regions have also been identified using local correlation tracking of solar granules observed in continuum images. These inflows are characterized by converging flows of about 20-30 m/s, which become visible approximately one day before the emergence of an active region [13]. From one solar cycle to the next, the mean poleward meridional flow changes by about 25%, [14,15].

To modulate the surface inflows toward active regions in the Solar dynamo models, one should identify these models, which can be separated into three main categories:

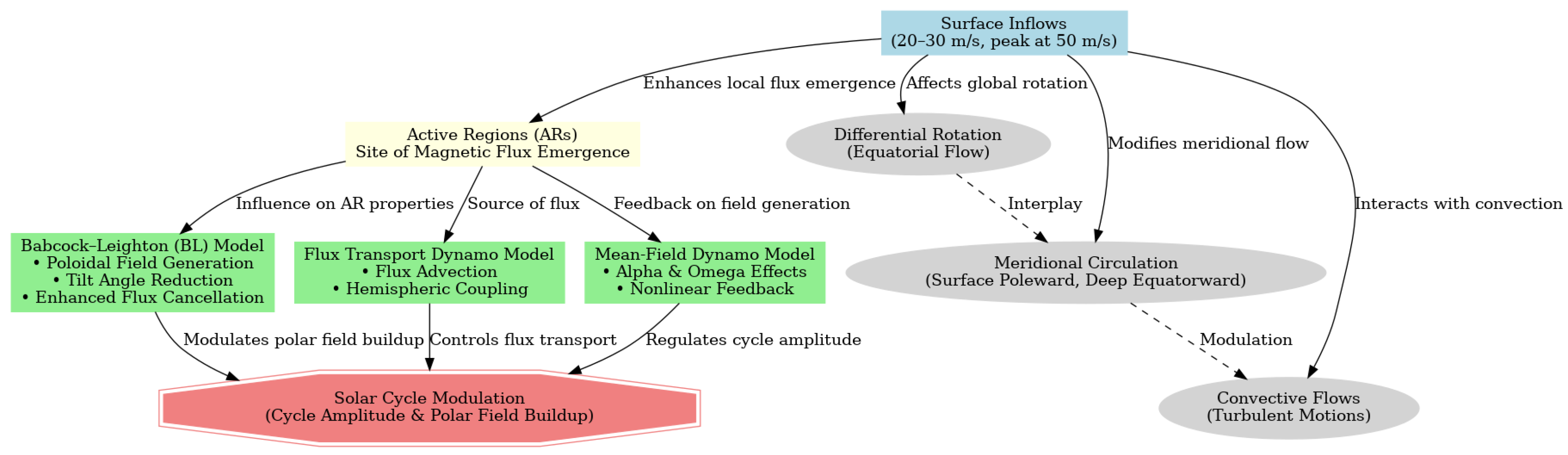
• Babcock-Leighton (BL) Dynamo Modelswhich explain the solar cycle through the generation of the poloidal magnetic field near the solar surface and the toroidal field in the solar interior. The coupling of these fields introduces a memory effect, allowing for short-term predictions of solar activity, [16]. Generating a poloidal field from the toroidal field is considered a nonlinear process, [17]; the nonlinear mechanisms included in the models are tilt quenching, latitude quenching and surface inflows (see Figure 3 in [18]. The accuracy of these models can be affected by turbulent pumping, which degrades the memory of the dynamo, limiting long-term predictions. Additionally, the depth variation of equatorward flow and strong turbulent diffusivity pose challenges, [19]. The recent development of the model was described in [18].
• Flux Transport Dynamo Models focus on the transport of magnetic flux by large-scale flows, such as differential rotation and meridional circulation. They are particularly useful for explaining the cyclic nature of solar magnetic activity, [20]. The emergence and growth of the flux transport dynamo model of the sunspot cycle were described in [21]. Recent advancements include three-dimensional non-kinematic simulations, which incorporate the emergence of BMRs and their tilt angles, influenced by the Coriolis force, [22]. These models of flux transport dynamo and meridional circulation in the Sun and stars were reviewed by [23].
• Mean-Field Dynamo Models use mean-field electrodynamics to describe the generation of magnetic fields through the $\alpha$-effect (helical turbulence) and $\Omega$-effect (differential rotation). They can reproduce irregularities in solar cycles, including grand minima [24]. Incorporating additional turbulent induction effects, such as the $\Omega \times J$ effect, can improve the agreement with observed solar cycle periods and magnetic field concentrations at low latitudes [25]. These models and how inflows influence the dynamo processes are summarized in Figure 1.

Solar active regions exhibit complex surface inflows that influence dynamo processes, yet their role remains debated. This short review aims to synthesize current knowledge on these inflows within solar dynamo models, highlight trends in observational and theoretical advances, and identify gaps where further research could refine our understanding of solar magnetic activity.

2. Background

Solar ARs are areas on the Sun with very strong magnetic fields where various solar activities, such as solar flares and coronal mass ejections (CMEs) occur [26,27]. ARs exhibit self-similar structures with fractal dimensions ranging from 1.2 to 1.7, indicating complex magnetic field configurations [28]. The magnetic field in ARs is significantly stronger than in surrounding regions, leading to the formation of giant arches of hot plasma that emit strong UV and X-ray radiation [29]. ARs often host sunspots, which are regions of intense magnetic activity and appear darker due to lower temperatures compared to their surroundings [30]. They typically contain regions of opposite magnetic polarity [26]. The locations, areas, heights, and widths of ARs vary and can be analyzed to predict solar activities [31]. The heights of ARs refer to a characteristic measure of how far an AR extends radially from the solar limb. They were obtained by first segmenting the AR region using a deep-learning (U-Net) method, then extracting the AR’s spatial extent along the radial (vertical) direction, and finally calculating the geometric center (or characteristic height) of the AR, which represents the average radial distance of the AR’s pixels above the limb..

Observations from instruments like the Helioseismic and Magnetic Imager (HMI) and the Solar Dynamics Observatory (SDO) provide high-resolution data for monitoring ARs [32] [33]. Various models, including those based on deep learning and machine learning, have been developed to predict solar flares and CMEs by analyzing the magnetic and geometric features of ARs [34]. Historical data and statistical models help in understanding the evolution and characteristics of ARs, aiding in the prediction of solar activities [35].

Surface inflows toward ARs feature converging horizontal flows with speeds of roughly 20-30 m/s, becoming noticeable about a day before the ARs appear. These inflows keep developing after the regions emerge, with their strength and reach tied to the region’s total magnetic flux. Within the first six days following emergence, the inflows can extend as far as 7^∘ from the centre of the active region, with speeds peaking at 50 m/s. The strength of inflows along the latitude grows with the region’s magnetic flux, peaking between one and four days after emergence. These inflows occur consistently, regardless of the AR’s latitude or flux, suggesting a predictable pattern. While they boost flux cancellation, this is balanced by reduced flux movement away from the region, as noted in [13].

The inflows act as a saturation mechanism for the global dynamo by decreasing the amplitude of the axial dipole moment [11]. This reduction is more pronounced after strong cycles, supporting the idea that inflows help in saturating the dynamo and modulating the solar cycle [36]. Inflows decrease the amplitude of the axial dipole moment by approximately 30%, relative to a no-inflows scenario [11]. The relative amplitude of the generated axial dipole is about 9% larger after very weak cycles than after very strong cycles, indicating the non-linear impact of inflows on the solar dynamo [37]. [12] show that for solar-like inflow speeds, a decrease of 10–20% in the strength of the global dipole builds up at the end of an activity cycle, in agreement with earlier simulations based on linear surface flux transport models.[38] confirmed that including inflows produces a lower net contribution to the dipole moment (10-25%) using a 1D surface flux transport model. Recently, [36] confirmed that these inflows enhance flux cancellation in BMRs by bringing together the opposite magnetic polarities. Stronger inflows lead to more flux cancellation, which suppresses polar field generation. A similar result was early reported by [7]. Surface inflows toward ARs provide a nonlinear feedback mechanism that limits the amplitude of the solar dynamo [7]. This feedback is crucial in modulating the strength of solar cycles by affecting the build-up of polar fields and the axial dipole moment [39]. Inflows reduce the tilt angles of bipolar magnetic regions and influence the cross-equator transport of magnetic flux, which in turn affects the amplitude of the solar cycles [11]. The inflows are believed to play a role in the diffusion of the magnetic field within ARs, although the exact mechanisms and effects are still under investigation.

These inflows impede the dispersal of magnetic flux into the surrounding network, influencing the larger-scale and longer-term patterns of the surface magnetic field [40]. Simulations incorporating these inflows show that they lead to a strong correlation between the simulated axial dipole strength and the observed cycle amplitude. This supports the hypothesis that inflows are a key ingredient in determining the amplitude of solar cycles [39]. Inflows into ARs alter the global surface pattern of the meridional circulation, contributing to the observed anti-phase variation with the solar cycle [41]. [42] proposed that the near-surface meridional flow consists of a three-component flow: a constant baseline flow, variations due to inflows around active regions, and solar-cycle-scale variations.

3. Current Understanding and Open Questions

Meridional flows are essential in transporting magnetic flux from low to high latitudes, influencing the solar cycle’s amplitude and period [10,43,44,45]. These flows are poleward at the surface and equatorward at deeper layers, forming a circulation pattern that is vital for the dynamo process [43,44,46]. Based on helioseismic data, the meridional circulation may form multiple cells along the radius in the convection zone, which can significantly impact dynamo models [47]. Incorporating helioseismically inferred meridional flow profiles into dynamo models has shown compatibility with observed solar cycle properties, such as the butterfly diagram and the 11-year cycle period [44]. Helioseismic techniques lack the sensitivity to capture the dynamics of weak, large-scale flows deep inside the convection zone. This limitation hinders our understanding of the behaviour of meridional circulation at greater depths [41].

The Babcock-Leighton model, which includes surface flux transport and meridional flows, remains a robust framework for explaining solar cycles. These models have been enhanced by including observed surface inflows and their effects on magnetic field evolution [7,36,48]. Surface inflows towards ARs and sunspot zones provide a nonlinear feedback mechanism that limits the amplitude of the solar dynamo, affecting the cycle strength [7]. These inflows modulate the build-up of polar fields by reducing the tilt angles of bipolar magnetic regions and influencing the cross-equator transport of magnetic flux [7]. Observations of inflows around active regions show that these inflows extend up to 30^∘ from the AR centroids. However, excluding ARs reduces the observed solar-cycle-scale variation in the background meridional flow, indicating that more comprehensive coverage is needed to fully understand these variations [42].

Recent studies suggest that even shallow meridional flows, when combined with turbulent pumping, can sustain solar-like magnetic cycles, challenging the necessity of deep equatorward flows [48,49]. Advanced 3D dynamo models have been developed to capture the buoyant emergence of tilted bipolar sunspot pairs and cyclic large-scale field reversals [50].

High-resolution observations are necessary to detect and analyze persistent inflows and their impact on solar dynamics. However, even with advanced instruments like the SDO and Hinode, there are challenges in consistently identifying and tracking these inflows over long periods [51]. The BL dynamo model needs to incorporate more accurate meridional flow profiles and account for the loss of toroidal flux through the solar surface to align better with observations [44]. The influence of magnetic torques on the global angular momentum distribution and the development of upward flows at mid-latitudes during the solar cycle maximum are not fully captured in conventional kinematic models; [41]. Turbulent pumping, which affects the transport of magnetic flux, is not fully integrated into many solar dynamo models. This mechanism is crucial for understanding the storage and latitudinal distribution of magnetic fields [49]. Non-local convection models often rely on assumptions like the quasi-normal approximation, which may not accurately represent the dynamics in the superadiabatic and quasi-adiabatic layers of the Sun [52].

The exact drivers of solar surface inflows and their feedback on the dynamo process remain unresolved, with ongoing debates about the relative contributions of magnetic forces versus thermal effects. Observations indicate systematic horizontal inflows near the photosphere surrounding ARs, which are likely driven by magnetic forces. These inflows impede the dispersal of magnetic flux, influencing larger-scale patterns and the evolution of the surface magnetic field [7,40]. Additionally, the solar surface exhibits convective motions forming granular patterns, with magnetic fields accumulating in inter-granular lanes. These motions, driven by thermal effects, are believed to generate and maintain quiet Sun magnetic features through local dynamo action [11,36].

Magnetic mechanisms where strong magnetic fields in active regions can generate Lorentz-force-driven inflows, which suppress further flux emergence and modulate the global solar cycle. These magnetically driven flows are expected to correlate with emerging BMRs’ strength. Alternatively, the thermal mechanisms where thermal effects such as radiative cooling and convective interactions could drive inflows through baroclinic forces. In this scenario, thermal perturbations alter pressure and density distributions, indirectly affecting flux transport dynamics. Studies such as [53] suggest that both mechanisms may play a role, but their relative contributions remain an open debate. Recent studies (e.g., [54]) highlight a deep-seated thermal regulation mechanism within the overshoot region, where convective overshooting generates thermal perturbations. These perturbations could influence BMR tilts before their emergence, thereby affecting the latitudinal distribution of AR’s and contributing to long-term solar cycle variations.

Numerical simulations show that inflows around regions of concentrated magnetic flux can be driven by reducing the surface temperature as a function of local magnetic flux, indicating a thermal effect [40]. BMR inflows can regulate the amplitudes and periods of magnetic cycles by reducing the buildup of the global poloidal field through local flux cancellation, acting as a nonlinear feedback mechanism that saturates the dynamo [11,36] (i.e. , this mechanism limits the amplitude of the solar dynamo and determines the variation of cycle strength). This modulation is achieved by reducing the tilt angles of bipolar magnetic regions and affecting the cross-equator transport of magnetic flux [7].

The inclusion of inflows in solar cycle models leads to a strong correlation between the simulated axial dipole strength during the activity minimum and the observed amplitude of the subsequent cycle, supporting the role of inflows in modulating the solar cycle [7].

Inflows stabilize cycle characteristics, reducing the scatter in individual cycle amplitudes and enhancing cross-hemispheric coupling, which decreases hemispheric cycle amplitude asymmetries and temporal lags [12].

Several improvements can be proposed to handle the previous aspects and give more robust results. Firstly, developing more sensitive helioseismic methods and combining them with machine learning techniques could improve the detection of internal solar flows and reduce the need for extensive temporal averaging [55]. Secondly, increasing the temporal and spatial resolution of observations, particularly around active regions, can provide better insights into the dynamics of solar surface inflows [42,51]. Thirdly, incorporating more realistic meridional flow profiles, accounting for magnetic field interactions, and integrating turbulent pumping mechanisms can enhance the accuracy of solar dynamo models [44,49].

Despite significant advancements in understanding solar dynamo processes, several key challenges remain:

• Uncertainty in the Role of Inflows: The impact of large-scale inflows around active regions on the global magnetic field and the solar cycle is still debated. While observational evidence suggests that these flows influence flux transport, their precise role in modulating solar activity remains unclear.
• Observational Limitations: Helioseismology provides essential insights into the Sun’s internal dynamics, but its spatial and temporal resolution constraints limit our ability to resolve fine-scale features crucial for dynamo modelling. Additionally, direct observations of subsurface flows and deep-seated magnetic fields remain a major challenge.
• Modelling Complexities: Different dynamo models—including Babcock-Leighton, flux transport, and mean-field approaches—offer varied interpretations of solar cycle evolution. However, integrating multi-scale processes, such as turbulence, differential rotation, and meridional circulation, into a unified framework remains an open challenge.
• Cycle Predictability: Despite improvements in dynamo models and data assimilation techniques, predicting solar cycles remains an imperfect science. Discrepancies between different forecasting methods and observed cycle variability highlight gaps in our understanding of long-term solar activity [56].

To overcome these challenges, future studies should focus on the following aspects:

• Advancing Helioseismic Observations: Higher-resolution helioseismic techniques and next-generation space missions will provide more detailed measurements of subsurface flows, improving constraints on dynamo models.
• Data-Driven Dynamo Modelling: The integration of observational data with advanced computational models, including machine learning approaches, can refine predictions of solar cycles and magnetic field evolution.
• Enhanced Global and Local Dynamo Simulations: Future models must incorporate small-scale turbulent processes, improved boundary conditions, and multi-layer interactions to achieve a more comprehensive understanding of the solar magnetic cycle.
• Interdisciplinary Approaches: Insights from stellar magnetism, geodynamo studies, and plasma physics could offer new perspectives on solar dynamo mechanisms.
• Long-Term Solar Activity Studies: Expanding databases with historical solar cycle reconstructions and comparisons with stellar analogs may improve our understanding of extreme solar events and long-term cycle variations.

4. Conclusions

Surface inflows toward solar ARs represent a critical yet complex component of solar dynamics, influencing the evolution of magnetic fields and the broader solar cycle. These inflows, characterized by converging horizontal flows with velocities of 20-30 m/s—peaking at 50 m/s post-emergence—consistently emerge approximately one day before AR formation and persist thereafter, with their strength and spatial extent (up to 7^∘ from AR centres) closely tied to the region’s magnetic flux. This review synthesizes observational and theoretical insights, revealing a consistent pattern: inflows are a ubiquitous feature across ARs, regardless of latitude or flux, and they play a dual role by enhancing local flux cancellation while reducing flux dispersal, thus acting as a nonlinear feedback mechanism within solar dynamo processes.

In the context of dynamo models; Babcock-Leighton, Flux Transport, and Mean-Field models, these inflows modulate key processes such as the buildup of polar fields and the axial dipole moment, which ultimately shape cycle amplitude and stability. Notably, their impact is more pronounced in strong cycles, where they contribute to dynamo saturation, while their nonlinear influence is evident in the 9% larger dipole amplitude following weak cycles compared to strong ones. Advanced observations, including helioseismic data and high-resolution imaging from instruments like the Solar Dynamics Observatory, alongside 3D simulations, have bolstered our understanding by linking inflows to meridional circulation variations and magnetic flux transport. However, gaps persist: the precise drivers of inflows—whether magnetic forces or thermal effects—remain debated, and their integration into dynamo models is incomplete, particularly regarding turbulent pumping and deep meridional flow dynamics. This synthesis highlights the need for refined observational techniques, such as enhanced helioseismic sensitivity and machine learning-driven flow detection, alongside improved model realism incorporating magnetic-thermal interactions and multi-cell meridional profiles. Addressing these gaps could clarify the inflows’ role in cycle modulation and enhance solar activity predictions. Ultimately, while significant progress has been made in understanding the drivers and feedback mechanisms of solar surface inflows, the exact contributions of magnetic forces versus thermal effects remain unresolved. Further observational and modelling studies are needed to clarify these mechanisms and their impact on the solar dynamo process.