Cooperative Optimization Strategies for Data Collection and Machine Learning in Large-Scale Distributed Systems

1. Introduction

With the rapid amount of data generated every day in our current data-based age and the growing complexity of machine learning pipelines, the classical approach of collecting and processing data in one centralized storage and processing site is becoming inadequate. To ensure efficient data processing, large-scale distributed systems have emerged as a key technology that disperses data and computing tasks across multiple nodes, enabling resource allocation optimization and task processing in parallel [1]. Design and implementing distributed systems is no easy task though.

There are many other things to consider when constructing his own distributed system, such as the reasonable distribution of computing load, the optimization of communication between nodes, and the extensibility and fault tolerance of the system. As a result of these hurdles, researchers have been evaluating new algorithms and architectures that enhance the reliability and scalability of distributed systems repeatedly.

Nevertheless, the collaborative optimization of data collection and machine learning tasks in a distributed setting is a challenging problem. First, data privacy and security issues are paramount in distributed systems, especially when sensitive data is in play. How to protect the privacy and integrity of data during multi-node data exchange to prevent being leaked and malicious tampered by any participant is an urgent and difficult problem to be solved [2]. Second, more communication latency and bandwidth constraints are also one of the performance bottlenecks in a distributed environment between the nodes. As the nodes increase, the network transmission, which is the main factor restricting the system efficiency, is more significant.

To solve these problems, researchers focus on proposing new data compression and communication optimization methods, which aim to reduce the cost and time of exchanging data between nodes as much as possible. Moreover, it is also an issue worthy of further discussion on how to efficiently manage the status of nodes and the scheduling of computing tasks, so that the computing and storage resources of each node can be reasonably allocated. Efficient algorithms is important for optimizing the coordination strategy, but it also need to take full account of the actual conditions of hardware and network [3].

To solve the communication bottleneck of distributed optimization, an algorithm based on local data similarity is proposed. Other algorithms (only few, though, and almost no distributed ones) minimize the total cost that combines communication and computation. The algorithm optimally partitions the data between the server and the local machine [4]. The inherent nature of distributed systems is such that multiple nodes continuously exchange data, and this can adversely affect the performance of the system if the bandwidth is limited.

Local data similarity allows nodes to intelligently determine whether they need to transfer data for computation, which helps them choose to pre-calculate and delay data transfer, or keeps them independent from other nodes. This approach helps decrease unneeded network flows and increases computer performance. Moreover, with the rise of deep learning and image recognition technology, data locality and similarity are playing increasingly important roles in distributed machine learning [5]. And it can further accelerate the model training speed and the system response through optimized data distribution strategy in the specific manner.

Distributed optimization algorithms have a huge potential in large-scale datasets processing. Since the distributed optimization algorithm can decompose an optimization problem into several sub-problems, and these sub-problems can be solved parallelly on different computing nodes, it can significantly reduce the computation time and enhance the efficiency of model training. Each subtask can be computed in parallel on different nodes, significantly enhancing the computing power of the system.

They can launch multiple threads in parallel, which can minimize computing pressure on a single node and avoid dominating bottlenecks in computing. Actually, distributed optimization algorithms have been supporting more complex tasks like large-scale image recognition and natural language processing, and the processing power is still improving with the continuous development of technology.

2. Related Work

Deshmukh et al. [6] adopted collaborative learning to enhance lag using ADMM for resource optimization and task scheduling. It can achieve dynamic adjustment of resource allocation so as to alleviate the lag influence on computing performances. Wang et al. [7] proposed cooperative optimization and cooperative/non-cooperative games in multi-agent systems. After introducing the background of collaborative optimization, they first introduced their research progress on distributed optimization and federated optimization, and then they focused on distributed online optimization (DOO) and its application in protecting privacy.

Li et al. [8] presented a data acquisition scheme based on Deep Reinforcement Learning (DRLR) for optimizing efficiency and cost of data collection through intelligent resource management and scheduling By building a model of deep reinforcement learning, this device can autonomously select the appropriate upload time in a complex network environment, as well as maximize the effect of data collection. Nguyen et al. [9] The authors proposed a 3D drone trajectory optimization approach using deep reinforcement learning, which is focused on maximizing the information collected from IoT devices by rationalizing the drone flight. Based on this, a deep reinforcement learning model was established in this paper to obtain the shortest flight path of UAV under data acquisition task, taking into account factors such as flight distance, energy consumption, communication delay.

Wang et al. [10] by using a long short term memory network (LSTM) to conduct an in-depth analysis of educational big data to evaluate students’ academic performance, which presents a machine learning-based analysis method for students’ academic performance. LSTM is a deep learning model that can be processed effectively with time series data that can process the time series dependence and long-term trends in students’ learning activities, which is of great significance for understanding the students’ learning progress, engagement and other behavior patterns.

Furthermore, Wang et al. [11] proposed an approach to recommending teaching strategy personalized using deep-learning, which aims profile with a recommendation based approach to identify the most appropriate teaching strategy according to the different characteristics of At the heart of this approach is the creation of a multi-layered neural network model to analyze students’ multi-faceted learning data and behavioral patterns, in order to recommend the best teaching strategy for each student.

3. Methodologies

3.1. Optimize Data Processing and Task Scheduling

This subsection proposes a novel collaborative optimization model that integrates data acquisition and machine learning tasks in a unified framework. The core goal of the model is to optimize resource allocation, data collection, and machine learning task execution in a large-scale distributed system through an adaptive feedback mechanism. In this model, the system is assumed to be composed of $N$ nodes, each node $i$ has a local dataset $D_i$ and a label set $Y_i$, and is trained by a local model. We define the global loss function as Equation 1:

$$L\left(\theta \right)=\sum _{i=1}^N({\alpha }_i{L}_i\left({\theta }_i\right)+{\lambda }_i{\mathcal{R}}_i({\theta }_i\left)\right)+\beta \sum _{i=1}^{N}CommCos{t}_i\left({\theta }_i\right),$$

(1)

where $L_i\left({\theta }_i\right)$ is the local loss function of node $i$, ${\mathcal{R}}_i\left({\theta }_i\right)$ is the regularization term, $CommCos{t}_i\left({\theta }_i\right)$ is the communication cost, ${\alpha }_i$ and ${\lambda }_i$ are the weight coefficients, and $\beta$ is the moderating factor of the communication cost. The optimization goal is to minimize the global loss function, considering both the quality of local training and the control of communication costs and resource consumption.

In order to better handle data acquisition and task execution, an adaptive data selection mechanism is introduced. The data acquisition priority for each node $i$ is determined by the following Equation 2:

$$S_i={\left({\displaystyle \frac{f_i\left(\theta \right)\bullet r_i}{{\sum }_{i=1}^N{f}_i\left(\theta \right)}}\right)}^{\gamma }\bullet \left({\displaystyle \frac{1}{1+{\lambda }_i\bullet CommCos{t}_i\left({\theta }_i\right)}}\right),$$

(2)

where $f_i\left(\theta \right)$ is the feedback signal of the node, indicating the importance of the node’s training; $r_i$ represents the computing resources of the node, $\gamma$ is the factor that adjusts the priority of data selection, and ${\lambda }_i$ is the adjustment factor of the communication cost. The purpose of this formula is to dynamically adjust the data collection priority through the feedback information of the nodes, so as to ensure that the data of important nodes can be selected first, so as to improve the efficiency of model training

In order to achieve more intelligent resource scheduling, the feedback mechanism $f_i\left(\theta \right)$ of the node is designed as a combination of gradient information and communication costs. Specifically, the feedback signal is calculated as Equation 3:

$$f_i\left(\theta \right)=\alpha \bullet {\nabla }_{{\theta }_i}{L}_i\left({\theta }_i\right)-\beta \bullet CommCos{t}_i\left({\theta }_i\right),$$

(3)

where ${\nabla }_{{\theta }_i}{L}_i\left({\theta }_i\right)$ is the local gradient of node $i$, $CommCos{t}_i\left({\theta }_i\right)$ is the communication cost, and $\alpha$ and $\beta$ are the moderators. This feedback mechanism ensures that nodes can dynamically adjust their data acquisition and task execution strategies based on their gradient information and communication costs, thereby reducing unnecessary waste of resources while maintaining efficiency.

In the process of model optimization, distributed reinforcement learning methods are introduced to further improve the adaptive ability of the system. Each node, when interacting with the environment, adjusts its decisions based on its immediate reward to maximize its long-term reward. The desired form of the reward function is Equation 4:

$$R_i=\mathbb{E}\left[\sum _{t=0}^T{\gamma }^t{r}_t^{\left(i\right)}\right],$$

(4)

where $r_t^{\left(i\right)}$ is the instant reward of node $i$ at time step $t$, $\gamma$ is the discount factor, and $T$ is the total number of steps trained. Through distributed reinforcement learning, nodes are able to adjust resource allocation and data selection based on feedback, thereby optimizing the overall training process.

3.2. Distributed Gradient Descent and Communication Optimization

In order to further optimize the training efficiency, the system adopts a distributed gradient descent algorithm. Each node $i$ will be based on its local data set $D_i$; and the current model parameter ${\theta }_i$ to update the local parameter. The update rule for nodes is Equation 5:

$${\theta }_i^{\left(t+1\right)}={\theta }_i^{\left(t\right)}-{\eta }_i{\nabla }_{{\theta }_i}{L}_i\left({\theta }_i^{\left(t\right)}\right),$$

(5)

where ${\eta }_i$ is the learning rate of node $i$, and ${\nabla }_{{\theta }_i}{L}_i\left({\theta }_i^{\left(t\right)}\right)$ is the local gradient of node $i$ at time step $t$. In the update of the global model, the gradients of each node are aggregated according to the following Equation 6:

$${\theta }^{\left(t+1\right)}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\theta }_i^{\left(t\right)}-\eta \sum _{i=1}^N{\nabla }_{{\theta }_i}{L}_i\left({\theta }_i^{\left(t\right)}\right).$$

(6)

This approach effectively aggregates the local gradients of nodes, reduces the frequency of communication, and optimizes the global model through multiple iterations. The training speed and communication efficiency of nodes have been significantly improved. In distributed learning, the cost of communication is an issue that cannot be ignored. In order to reduce the communication cost, we designed a communication scheduling strategy based on gradient difference. The communication cost per node is defined by the following Equation 7:

$$CommCos{t}_i\left({\theta }_i\right)=\alpha \bullet {\parallel {\theta }_i^{\left(t\right)}-{\theta }^{\left(t-1\right)}\parallel }^2,$$

(7)

where ${\parallel {\theta }_i^{\left(t\right)}-{\theta }^{\left(t-1\right)}\parallel }^2$ represents the difference between the global model of node $i$ at time step $t$ and the last synchronization, and $\alpha$ is the moderating factor of the communication cost. Through this formula, the system can decide whether to synchronize globally based on the update rate of the node, avoiding unnecessary communication overhead.

The task scheduling and resource allocation of nodes need to be adjusted according to the priority of the task. To optimize this process, we calculate task priority $P_i$ for each node and adjust its resource allocation strategy $R_i$ according to the priority, as shown in Equation 8:

$$R_i={\displaystyle \frac{P_i}{{\sum }_{j=1}^N{P}_j}}\bullet r_i,$$

(8)

where $P_i$ represents the task priority of node $i$, and $r_i$ is the available computing resources of the node. With this formula, high-priority tasks will receive more computing resources, which will improve the overall efficiency of the system.

Load balancing is an important issue in distributed systems, especially if the load on nodes varies greatly. In order to achieve load balancing, we design a scheduling strategy based on the load difference between nodes, and the load $L_i$ of the nodes is calculated by the following Equation 9:

$$L_i=\sum _{j=1}^N{\parallel {\theta }_i-{\theta }_j\parallel }^2.$$

(9)

Through this formula, the system can reasonably distribute tasks according to the load difference between nodes, avoid overloading some nodes, and improve the stability and reliability of the system.

4. Experiments

4.1. Experimental Setup

Using GeoSOC, we performed an experiment using real-world simulated geospatial data based on an OpenStreetMap (OSM) dataset, with a test scenario on the ability of the system to facilitate machine learning tasks for data acquisition in a large-scale distributed system. The OSM dataset has map records in various geographical locations globally, is sparse and heterogeneous to a great extent, and provides supporting data for numerous task types, including but not limited to path planning and urban traffic flow prediction.

To thoroughly analyze our proposed co-optimization strategy, we chose four related comparative methods, namely the traditional distributed data acquisition method (TDDC), data selection and scheduling strategy (DSS), decentralized gradient descent (DGD) and reinforcement learning optimization strategy (RLOS).

In tightly-coupled environments, such as DC deployments, TDDC is not effective because it fails to coordinate resources across nodes. DSS alleviates the strain on bandwidth by optimizing data transmission, but responds poorly to environmental changes. While the data grouping discovered (DGD) enhances the training efficiency, it does not provide much help in solving the dilemma of data collection and resource allocation. RLOS can dynamically and optimally allocate resources, but the training time is long and consumes high computational resources.

4.2. Experimental Analysis

In various training rounds, comparison of the performance of each method was performed, where accuracy was the principal evaluation index. Accuracy is a measure of the performance of a model by comparing how well the predicted labels from the model correspond to the real labels.

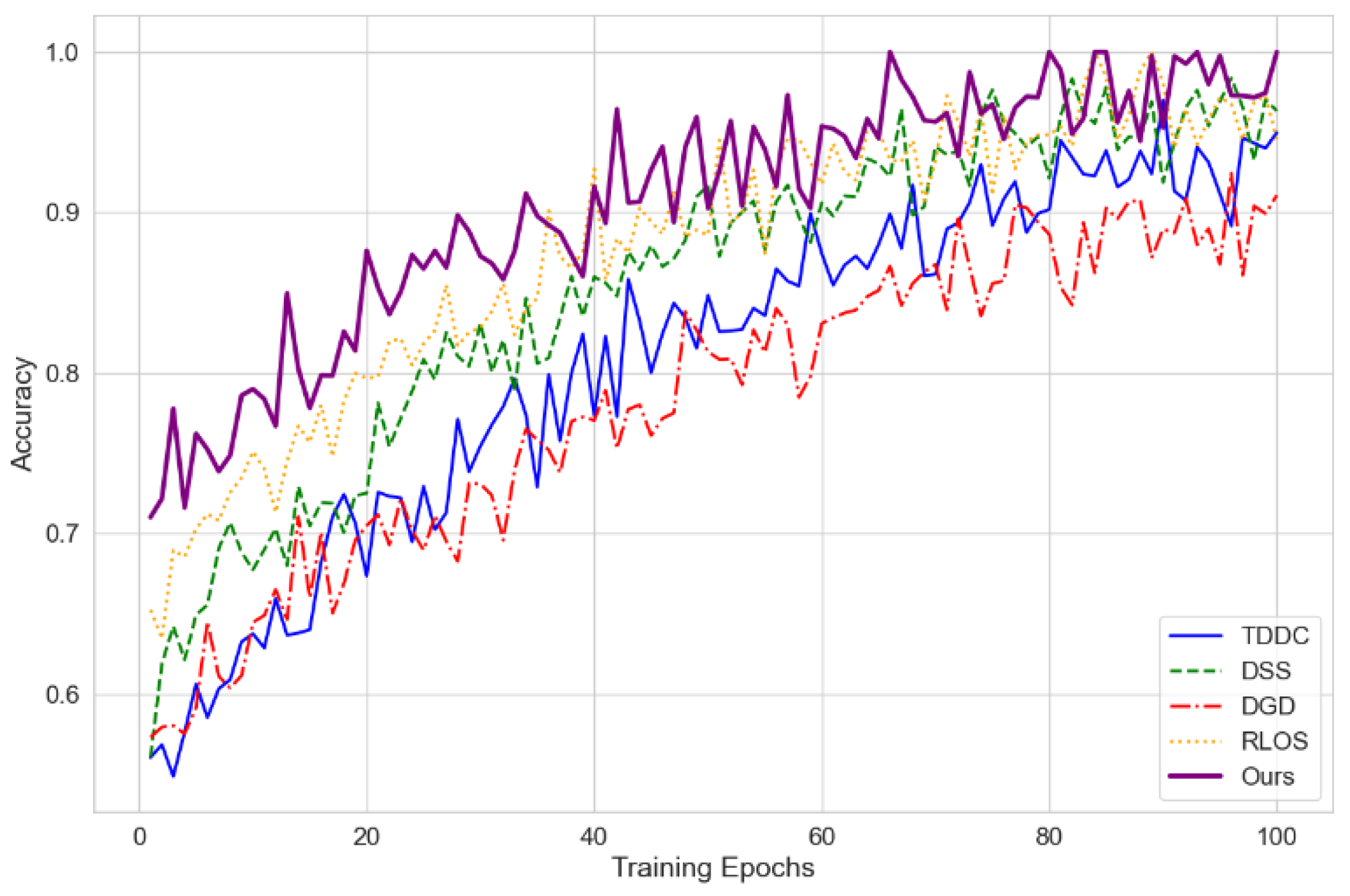
As shown in Figure 1, with the increase of number of training rounds, the accuracy of all methods has a gradual convergence trend, and the speed of convergence and the final accuracy is different for different methods. Our method had good solutions in early-stage training and maintained strong stability and high final accuracy during later accuracy improvement, which was significantly better than that of comparison methods. While TDDC and DSS gained rapid accuracy in the early stage, the accuracy of the later stage dropped significantly, showing weak optimization ability.

Convergence time is the time it takes for different methods in various iterations. With more iterations, the convergence time increases in the sense that more calculations and updates need to be done for each iteration. Although the actual convergence time is not compared in this work, but we compare the convergence times of the different methods to show their efficiency while working with large-scale distributed tasks.

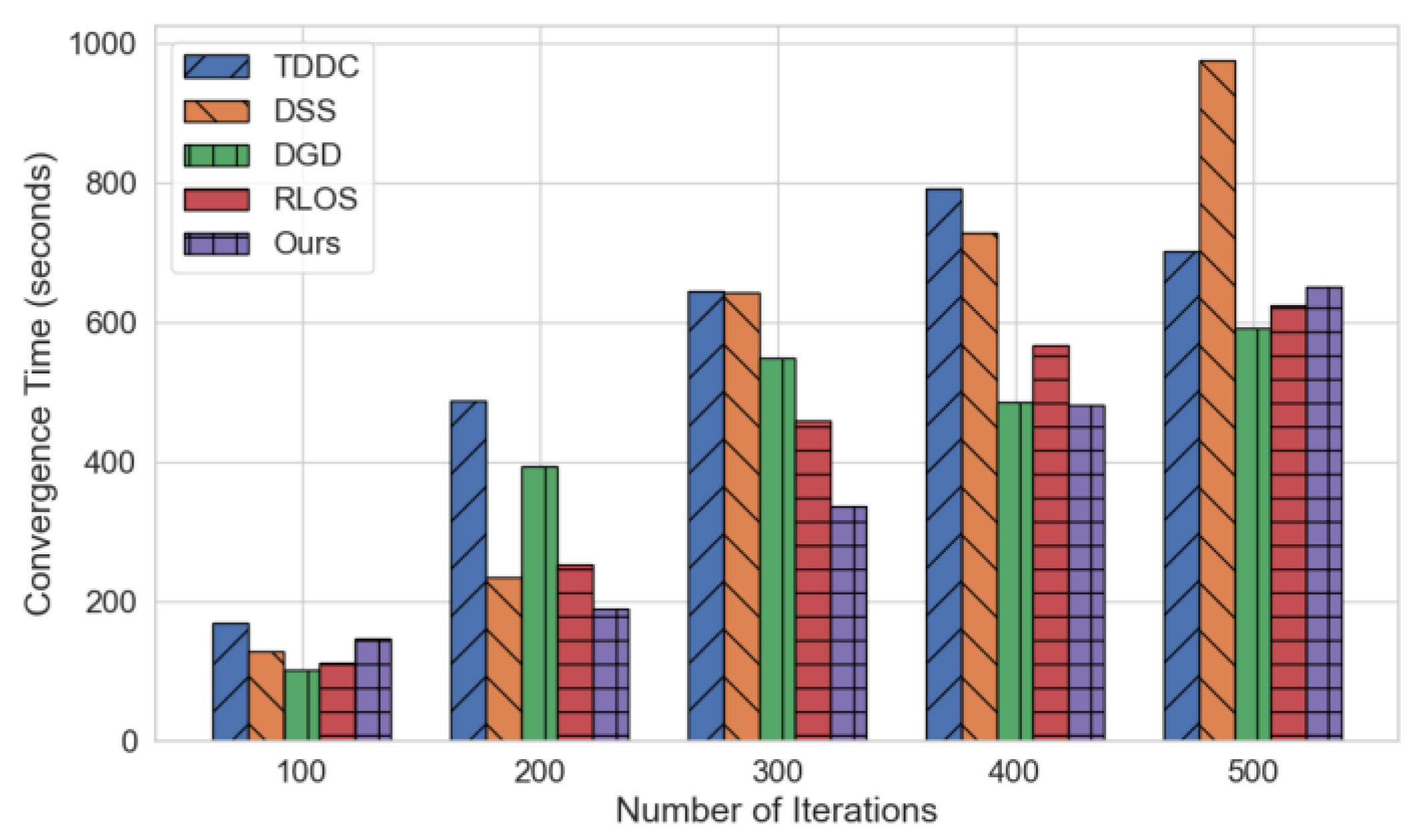
As evidenced in the results from Figure 2, it can be seen that the Ours method demonstrates lower convergence time than all other methods when it comes to increasing the number of iterations, primarily in cases where the number of iterations is high, which indicates that the method has advantages on the utilization of computing resources and task optimization, that can effectively reduce the computational burden and optimization time of the system, and improve the processing efficiency of large-scale datasets. TDDC, DSS, DGD and RLOS all have a significant increase in time for a large number of iterations meaning that they might have performance bottlenecks when tackling more complex tasks.

Finally, the system computation is also influencing the complexity and performance of large-scale distributed systems. Therefore, we illustrate the average processing cost for different models with identical 50MB, 100MB data for 10 times in following Table 1.

5. Conclusions

In conclusion, we validate correctness of our Ours method by outperforming the state of the art TDDC, DSS, DGD & RLOS methods that have been known in the literature for large-scale distributed systems in terms of accuracy and convergence time. Indeed, the Ours method can increase efficiency when it comes to capturing data as well as implementing the machine learning in shades of same tasks and solving the respective problem, especially as the number of iterations as well as framework grows; computational overhead can be reduced, which can lead to optimize resource usage. Dynamic resource scheduling algorithms can help enrich the adaptability of the system under diverse workloads.