Some Uniformly Smooth Approximating Functions for Absolute Value Function

1. Introduction

The absolute value function $\varphi (t)=\left|t\right|$ is not differentiable at $t=0$. Absolute value function is of great significance in non-smooth optimization theory and variational inequality. Therefore, it is of great practical significance to study the smooth approximation function of absolute value function. $\varphi (t)=\left|t\right|$ is equivalent to $\varphi (t)=\max \{t,-t\}$. Literature [7] gave the smoothing processing method of absolute value function and its application in friction contact problems. Some approximation functions of absolute value function $\varphi (t)=\left|t\right|$ are gave in literature [8,9,10,11,12,13], and applied to solve absolute value equation respectively. Literature [14] studied a class of smooth approximation functions of maximum function $\max \{0,t\}$. Literature [15] studied the uniformly smooth approximation function for absolute value function.

On the basis of the above literatures, this paper systematically gives seven uniformly smooth approximation functions of absolute value functions, analyzes the properties and approximation degrees of these smooth approximation functions theoretically, and finally points out the application prospects of uniformly smooth approximation functions.

Definition 1 (Smooth approximation function [15].) Given a non-smooth function$f:R\to R$.We call the smooth function$f(\mu ,t),\mu >0$ the smooth approximation function of $f(t)$. If for any $t\in R$, there exists $\kappa >0$, such that

$$\left|f(\mu ,t)-f(t)\right|\le \kappa \mu ,\forall \mu >0.$$

If $\kappa$ does not depend on $t$, then $f(\mu ,t)$ is said to be a uniformly smooth approximation function of $f(t)$.

Uniformly smooth approximation function can be divided into two classes: from above and from below. Let $f(\mu ,t)$ be the uniformly smooth approximation function of $f(t)$. If $f(\mu ,t)$ satisfies $f(\mu ,t)\ge f(t)$, and$\underset{\mu \to 0^{+}}{\lim }f(\mu ,t)=f(t)$, then $f(\mu ,t)$ is said to be uniformly approximated from above. If $f(\mu ,t)$ satisfies $f(\mu ,t)\le f(t)$, and $\underset{\mu \to 0^{+}}{\lim }f(\mu ,t)=f(t)$, then $f(\mu ,t)$ is said to be uniformly approximated from below. The following we use $(\mu ,t)\in R_{++}\times R$ to express $\mu >0,t\in R$.

2. Some Uniformly Smooth Approximating Functions

Following we give seven uniformly smooth approximating functions ${\varphi }_i(\mu ,t)$ of the absolute value function $\varphi (t)=\left|t\right|$. They are continuously differentiable on $(\mu ,t)\in R_{++}\times R$, and ${\varphi }_i(\mu ,t),i=1,2,\cdots ,7$ are defined as follows:

$${\varphi }_1(\mu ,t)=\mu \left[\ln \left(1+e^{-{\displaystyle \frac{t}{\mu }}}\right)+\ln \left(1+e^{{\displaystyle \frac{t}{\mu }}}\right)\right]$$

(1)

$${\varphi }_2(\mu ,t)=\sqrt{{\mu }^2+t^2}$$

(2)

$${\varphi }_3(\mu ,t)=\mu \ln \left(e^{{\displaystyle \frac{t}{\mu }}}+e^{-{\displaystyle \frac{t}{\mu }}}\right)$$

(3)

$${\varphi }_4(\mu ,t)=\left\{\begin{array}{l}t, t\ge \mu ,\\ \mu \ln \left(1+{\left({\displaystyle \frac{t}{\mu }}\right)}^2\right)+\mu (1-\ln 2),-\mu <t<\mu ,\\ -t, t\le -\mu .\end{array}\right.$$

(4)

$${\varphi }_5(\mu ,t)=\left\{\begin{array}{l}t, t\ge {\displaystyle \frac{\mu }{2}},\\ {\displaystyle \frac{t^2}{\mu }}+{\displaystyle \frac{\mu }{4}},-{\displaystyle \frac{\mu }{2}}<t<{\displaystyle \frac{\mu }{2}},\\ -t, t\le -{\displaystyle \frac{\mu }{2}}.\end{array}\right.$$

(5)

$${\varphi }_6(\mu ,t)=\left\{\begin{array}{c}{\displaystyle \frac{t^2}{2\mu }},\left|t\right|\le \mu ,\\ \left|t\right|-{\displaystyle \frac{\mu }{2}},\left|t\right|>\mu .\end{array}\right.$$

(6)

$${\varphi }_7(\mu ,t)=\mu \ln \left({\displaystyle \frac{1}{2}}{e}^{{\displaystyle \frac{t}{\mu }}}+{\displaystyle \frac{1}{2}}{e}^{-{\displaystyle \frac{t}{\mu }}}\right)$$

(7)

2.1. Properties of Function ${\varphi }_1(\mu ,t)$

Proposition 2.1 The function ${\varphi }_1(\mu ,t)=\mu \left[\ln \left(1+e^{-{\displaystyle \frac{t}{\mu }}}\right)+\ln \left(1+e^{{\displaystyle \frac{t}{\mu }}}\right)\right]$ on $(\mu ,t)\in R_{++}\times R$ has the following properties:

(1)$0<{\varphi }_1(\mu ,t)-\varphi (t)\le \mu \ln 4$;

(2)${\varphi }_1(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$, and

$\left|{\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial t}}\right|<1$ , ${\left.{\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)${\varphi }_1(\mu ,t)$ decreases with decreasing parameter $\mu$, and when$\mu \to 0^{+}$, $\underset{\mu \to 0^{+}}{\lim }{\varphi }_1(\mu ,t)=\left|t\right|$.

Proof (1) ${\varphi }_1(\mu ,t)-\varphi (t)=\mu \ln \left(2+e^{{\displaystyle \frac{t}{\mu }}}+e^{-{\displaystyle \frac{t}{\mu }}}\right)-\mu \ln e^{{\displaystyle \frac{\left|t\right|}{\mu }}}=\mu \ln \left(2e^{-{\displaystyle \frac{\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{t-\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{-t-\left|t\right|}{\mu }}}\right)$

Since $\left|t\right|=\max \{t,-t\}$, then $t-\left|t\right|\le 0,-t-\left|t\right|\le 0$, and at least one of $t-\left|t\right|$ and $-t-\left|t\right|$ is equal to 0, thus $0<2e^{-{\displaystyle \frac{\left|t\right|}{\mu }}}\le 2$,$1<e^{{\displaystyle \frac{t-\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{-t-\left|t\right|}{\mu }}}\le 2$. So $1<2e^{-{\displaystyle \frac{\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{t-\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{-t-\left|t\right|}{\mu }}}\le 4$.

Thereby $\mu \ln 1<{\varphi }_1(\mu ,t)-\varphi (t)\le \mu \ln 4$. So $0<{\varphi }_1(\mu ,t)-\varphi (t)\le \mu \ln 4$.

(2) A simple calculation leads to

${\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial t}}={\displaystyle \frac{-e^{-\frac{t}{\mu }}}{1+e^{-\frac{t}{\mu }}}}+{\displaystyle \frac{e^{\frac{t}{\mu }}}{1+e^{\frac{t}{\mu }}}},$

${\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial \mu }}=\left[\ln \left(1+e^{-{\displaystyle \frac{t}{\mu }}}\right)+\ln \left(1+e^{{\displaystyle \frac{t}{\mu }}}\right)\right]+{\displaystyle \frac{t}{\mu }}\left[{\displaystyle \frac{e^{-\frac{t}{\mu }}}{1+e^{-\frac{t}{\mu }}}}+{\displaystyle \frac{-e^{\frac{t}{\mu }}}{1+e^{\frac{t}{\mu }}}}\right].$

Since ${\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial t}}$ and ${\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial \mu }}$ are continuous on $(\mu ,t)\in R_{++}\times R$.Therefore, ${\varphi }_1(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$. And

$\left|{\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial t}}\right|=\left|{\displaystyle \frac{e^{\frac{t}{\mu }}-e^{-\frac{t}{\mu }}}{2+e^{-\frac{t}{\mu }}+e^{\frac{t}{\mu }}}}\right|<\left|{\displaystyle \frac{e^{\frac{t}{\mu }}-e^{-\frac{t}{\mu }}}{e^{-\frac{t}{\mu }}+e^{\frac{t}{\mu }}}}\right|\le 1,$ ${\left.{\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)To prove that the ${\varphi }_1(\mu ,t)$ decreases with decreasing parameter $\mu$, it is sufficient to prove that ${\displaystyle \frac{\partial {\varphi }_1(\mu ,t)}{\partial \mu }}>0,(\mu ,t)\in R_{++}\times R$ (see Appendix 1). Use$0<{\varphi }_1(\mu ,t)-\varphi (t)\le \mu \ln 4$, combined with Squeeze Theorem. Then there is$\underset{\mu \to 0^{+}}{\lim }{\varphi }_1(\mu ,t)=\left|t\right|$.

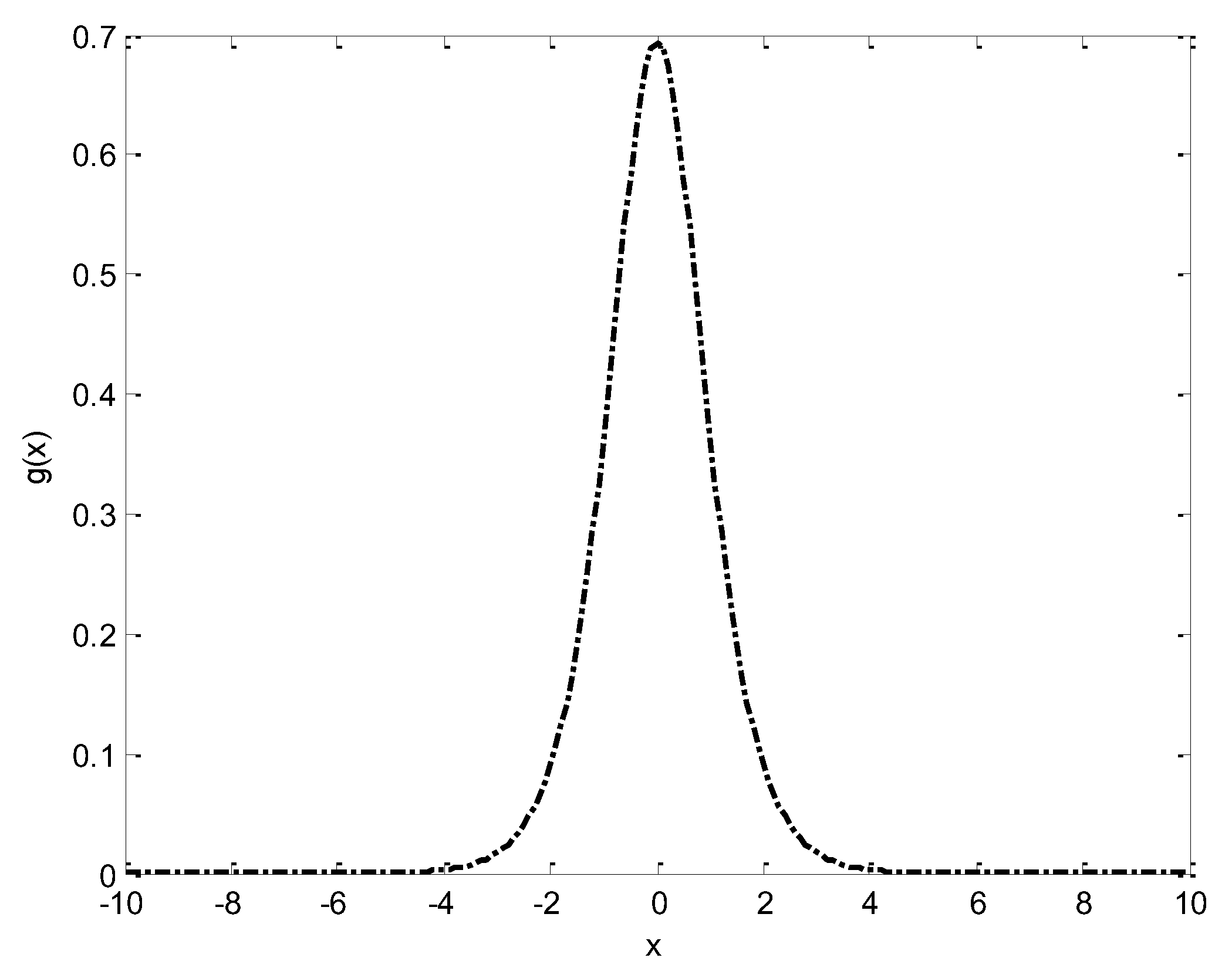
Figure 1 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_1(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_1(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from above.

2.2. Properties of Function ${\varphi }_2(\mu ,t)$

Proposition 2.2 The function ${\varphi }_2(\mu ,t)=\sqrt{{\mu }^2+t^2}$ in $(\mu ,t)\in R_{++}\times R$ has the following properties：

(1)$0<{\varphi }_2(\mu ,t)-\varphi (t)\le \mu$;

(2)${\varphi }_2(\mu ,t)$ is differentiable on ,and

$\left|{\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial t}}\right|<1$ , ${\left.{\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)${\varphi }_2(\mu ,t)$ decreases with the decrease parameter $\mu$,and when$\mu \to 0^{+},\underset{\mu \to 0^{+}}{\lim }{\varphi }_2(\mu ,t)=\left|t\right|$.

Proof (1) Since ${\varphi }_2(\mu ,t)-\varphi (t)={\displaystyle \frac{{\mu }^2}{\sqrt{{\mu }^2+t^2}+\sqrt{t^2}}}$,then$0<{\varphi }_2(\mu ,t)-\varphi (t)\le \mu$.

(2) A simple calculation leads to

${\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial t}}={\displaystyle \frac{t}{\sqrt{{\mu }^2+t^2}}},$${\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial \mu }}={\displaystyle \frac{\mu }{\sqrt{{\mu }^2+t^2}}}.$

Apparently, ${\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial t}}$ and ${\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial \mu }}$ is continuous, so ${\varphi }_2(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$. And

$\left|{\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial t}}\right|=\left|{\displaystyle \frac{t}{\sqrt{{\mu }^2+t^2}}}\right|<1,$${\left.{\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial t}}\right|}_{t=0}={\left.{\displaystyle \frac{t}{\sqrt{{\mu }^2+t^2}}}\right|}_{t=0}=0$

(3) For any $(\mu ,t)\in R_{++}\times R$, ${\displaystyle \frac{\partial {\varphi }_2(\mu ,t)}{\partial \mu }}={\displaystyle \frac{\mu }{\sqrt{{\mu }^2+t^2}}}>0$.Thus the value of ${\varphi }_2(\mu ,t)$ decreases with the decrease parameter $\mu$. Using $0<{\varphi }_2(\mu ,t)-\varphi (t)\le \mu$, combined with Squeeze Theorem. Then there is$\underset{\mu \to 0^{+}}{\lim }{\varphi }_2(\mu ,t)=\left|t\right|$.

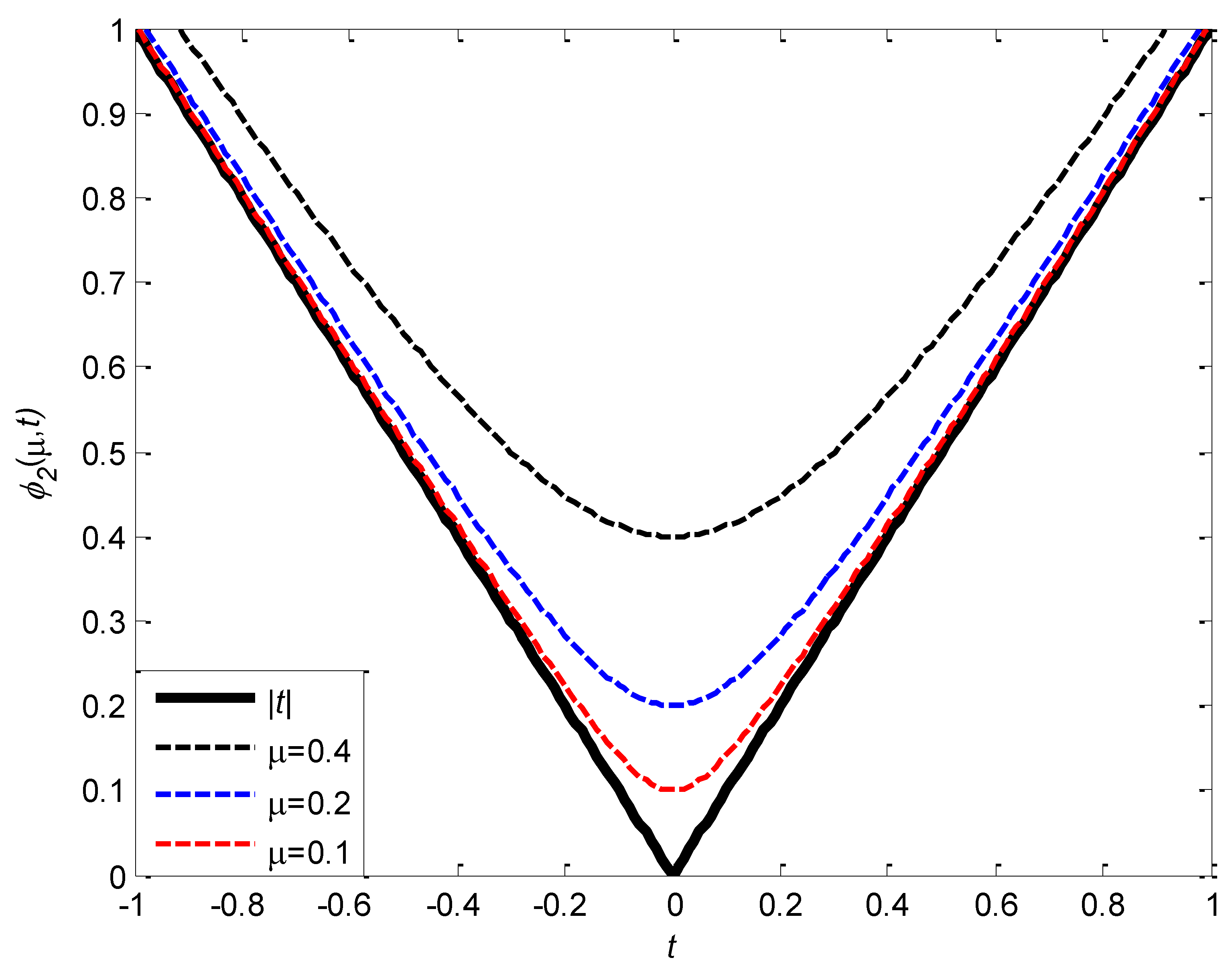
Figure 2 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_2(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_2(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from above.

2.3. Properties of Function ${\varphi }_3(\mu ,t)$

Proposition 2.3 The function ${\varphi }_3(\mu ,t)=\mu \ln \left(e^{{\displaystyle \frac{t}{\mu }}}+e^{-{\displaystyle \frac{t}{\mu }}}\right)$ in $(\mu ,t)\in R_{++}\times R$ has the following properties:

(1)$0<{\varphi }_3(\mu ,t)-\varphi (t)\le \mu \ln 2$.

(2)${\varphi }_3(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$,and

$\left|{\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}}\right|<1$ , ${\left.{\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)${\varphi }_3(\mu ,t)$ decreases with the decrease parameter $\mu$,and when$\mu \to 0^{+},\underset{\mu \to 0^{+}}{\lim }{\varphi }_3(\mu ,t)=\left|t\right|$.

Proof (1)${\varphi }_3(\mu ,t)-\varphi (t)=\mu \ln \left(e^{{\displaystyle \frac{t}{\mu }}}+e^{-{\displaystyle \frac{t}{\mu }}}\right)-\mu \ln e^{{\displaystyle \frac{\left|t\right|}{\mu }}}=\mu \ln \left(e^{{\displaystyle \frac{t-\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{-t-\left|t\right|}{\mu }}}\right)$.

Since $\left|t\right|=\max \{t,-t\}$,then $t-\left|t\right|\le 0,-t-\left|t\right|\le 0$, and at least one of $t-\left|t\right|$ and $-t-\left|t\right|$ is equal to 0,so$1<e^{{\displaystyle \frac{t-\left|t\right|}{\mu }}}+e^{{\displaystyle \frac{-t-\left|t\right|}{\mu }}}\le 2$.Thus$\mu \ln 1<{\varphi }_3(\mu ,t)-\varphi (t)\le \mu \ln (1+1)$.That is

$0<{\varphi }_3(\mu ,t)-\varphi (t)\le \mu \ln 2$.

(2)A simple calculation leads to

${\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}}={\displaystyle \frac{e^{\frac{t}{\mu }}-e^{-\frac{t}{\mu }}}{e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}},$${\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial \mu }}=\ln \left(e^{{\displaystyle \frac{t}{\mu }}}+e^{-{\displaystyle \frac{t}{\mu }}}\right)+{\displaystyle \frac{t}{\mu }}\left({\displaystyle \frac{-e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}{e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}}\right)$.

Since ${\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}}$ and${\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial \mu }}$ continuous on $(\mu ,t)\in R_{++}\times R$.So ${\varphi }_3(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$. And

$\left|{\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}}\right|=\left|{\displaystyle \frac{e^{\frac{t}{\mu }}-e^{-\frac{t}{\mu }}}{e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}}\right|=\left|{\displaystyle \frac{e^{\frac{2t}{\mu }}-1}{e^{\frac{2t}{\mu }}+1}}\right|<1$, ${\left.{\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}}\right|}_{t=0}={\left.\left({\displaystyle \frac{e^{\frac{t}{\mu }}-e^{-\frac{t}{\mu }}}{e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}}\right)\right|}_{t=0}=0$.

(3) To prove that the value of ${\varphi }_3(\mu ,t)$ decreases with decreasing parameter $\mu$. It is sufficient to prove that ${\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial \mu }}>0,(\mu ,t)\in R_{++}\times R$ (see Appendix 2).

Using$0<{\varphi }_3(\mu ,t)-\varphi (t)\le \mu \ln 2$, combined with Squeeze Theorem, thus $\underset{\mu \to 0^{+}}{\lim }{\varphi }_3(\mu ,t)=\left|t\right|$.

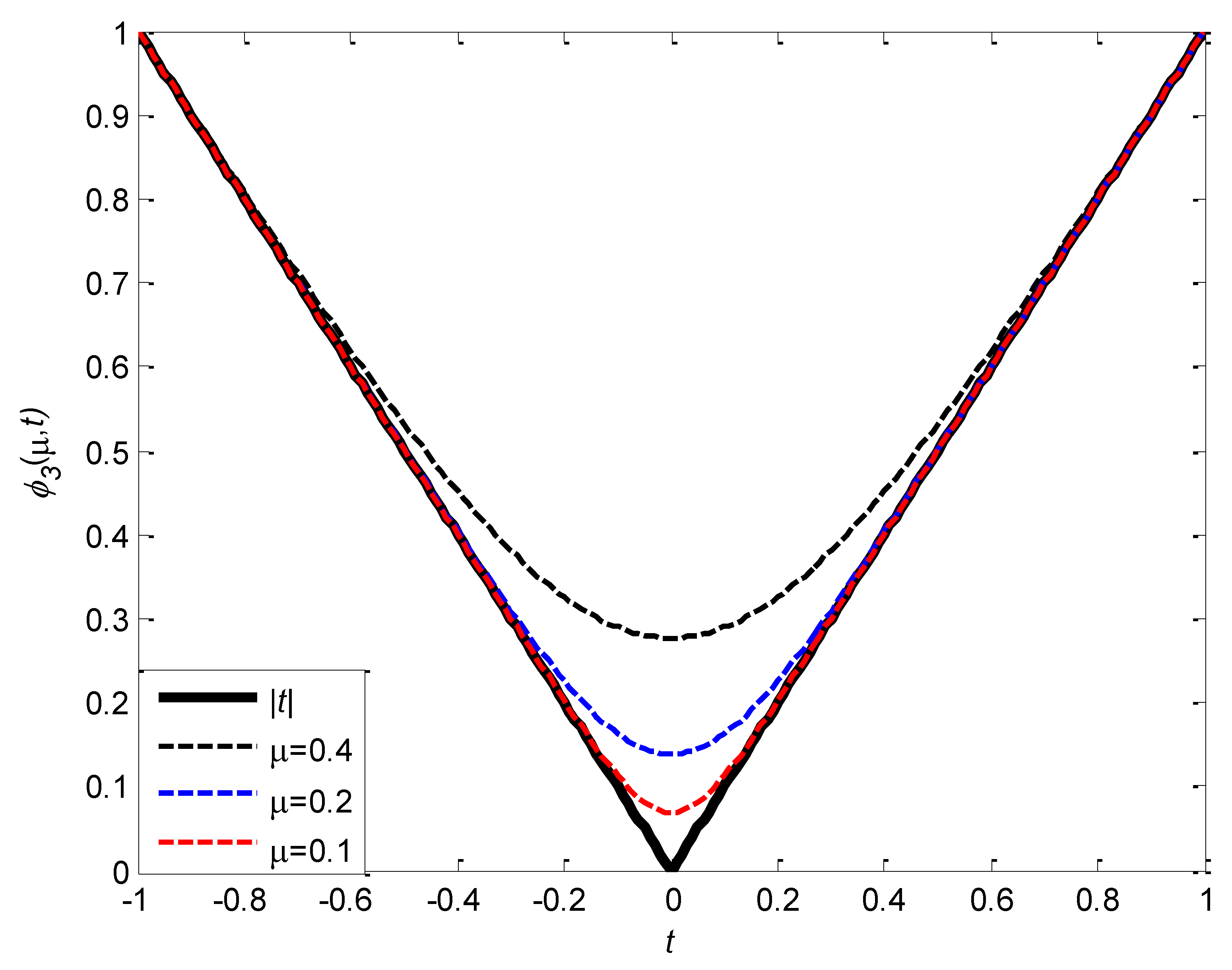
Figure 3 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_3(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_3(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from above.

2.4. Properties of Function ${\varphi }_4(\mu ,t)$

Proposition 2.4 The function ${\varphi }_4(\mu ,t)=\left\{\begin{array}{c}t,t\ge \mu ,\\ \mu \ln \left(1+{\left({\displaystyle \frac{t}{\mu }}\right)}^2\right)+\mu (1-\ln 2),-\mu <t<\mu ,\\ -t,t\le -\mu .\end{array}\right.$ in $(\mu ,t)\in R_{++}\times R$ has the following properties:

(1)$0\le {\varphi }_4(\mu ,t)-\varphi (t)\le \mu (1-\ln 2)$;

(2)${\varphi }_4(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$,and

$\left|{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}\right|\le 1$,${\left.{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)${\varphi }_4(\mu ,t)$ decreases with the decrease parameter $\mu$,and when$\mu \to 0^{+},\underset{\mu \to 0^{+}}{\lim }{\varphi }_4(\mu ,t)=\left|t\right|$.

Proof (1) When$\left|t\right|\ge \mu$,${\varphi }_4(\mu ,t)-\varphi (t)\equiv 0$. When $-\mu <t<\mu$,

${\varphi }_4(\mu ,t)-\varphi (t)=$$\mu \ln \left(1+{\left({\displaystyle \frac{t}{\mu }}\right)}^2\right)+\mu (1-\ln 2)-\left|t\right|\le \mu (1-\ln 2)$.

Thus, for any$(\mu ,t)\in R_{++}\times R$, we have $0\le {\varphi }_4(\mu ,t)-\varphi (t)\le \mu (1-\ln 2)$.

(2) A simple calculation gives

${\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}=\left\{\begin{array}{l}1, t\ge \mu ,\\ {\displaystyle \frac{2\mu t}{t^2+{\mu }^2}},-\mu <t<\mu ,\\ -1, t\le -\mu .\end{array}\right.$

${\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial \mu }}=\left\{\begin{array}{l}0, t\ge \mu ,\\ \ln \left(1+{\displaystyle \frac{t^2}{{\mu }^2}}\right)-2{\displaystyle \frac{t^2}{{\mu }^2+t^2}}+(1-\ln 2),-\mu <t<\\ 0, t\le -\mu .\end{array}\right.\mu ,$

Since $\underset{t\to \mu }{\lim }{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}=\underset{t\to \mu }{\lim }{\displaystyle \frac{2\mu t}{t^2+{\mu }^2}}=1$,$\underset{t\to -\mu }{\lim }{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}=\underset{t\to -\mu }{\lim }{\displaystyle \frac{2\mu t}{t^2+{\mu }^2}}=-1$,so ${\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}$ is continuous. Since $\underset{t\to \mu }{\lim }{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial \mu }}=0,$$\underset{t\to -\mu }{\lim }{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial \mu }}=0$,so${\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial \mu }}$ is continuous. Thus ${\varphi }_4(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$. From the expression for ${\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}$, we get $\left|{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}\right|\le 1$ and${\left.{\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3) To prove that the value of ${\varphi }_4(\mu ,t)$ decreases with decreasing parameter $\mu$. Only proof ${\displaystyle \frac{\partial {\varphi }_4(\mu ,t)}{\partial \mu }}>0,(\mu ,t)\in R_{++}\times R$ is required (see Appendix 3).

Using $0\le {\varphi }_4(\mu ,t)-\varphi (t)\le \mu (1-\ln 2)$, combined with Squeeze, thus $\underset{\mu \to 0^{+}}{\lim }{\varphi }_4(\mu ,t)=\left|t\right|$.

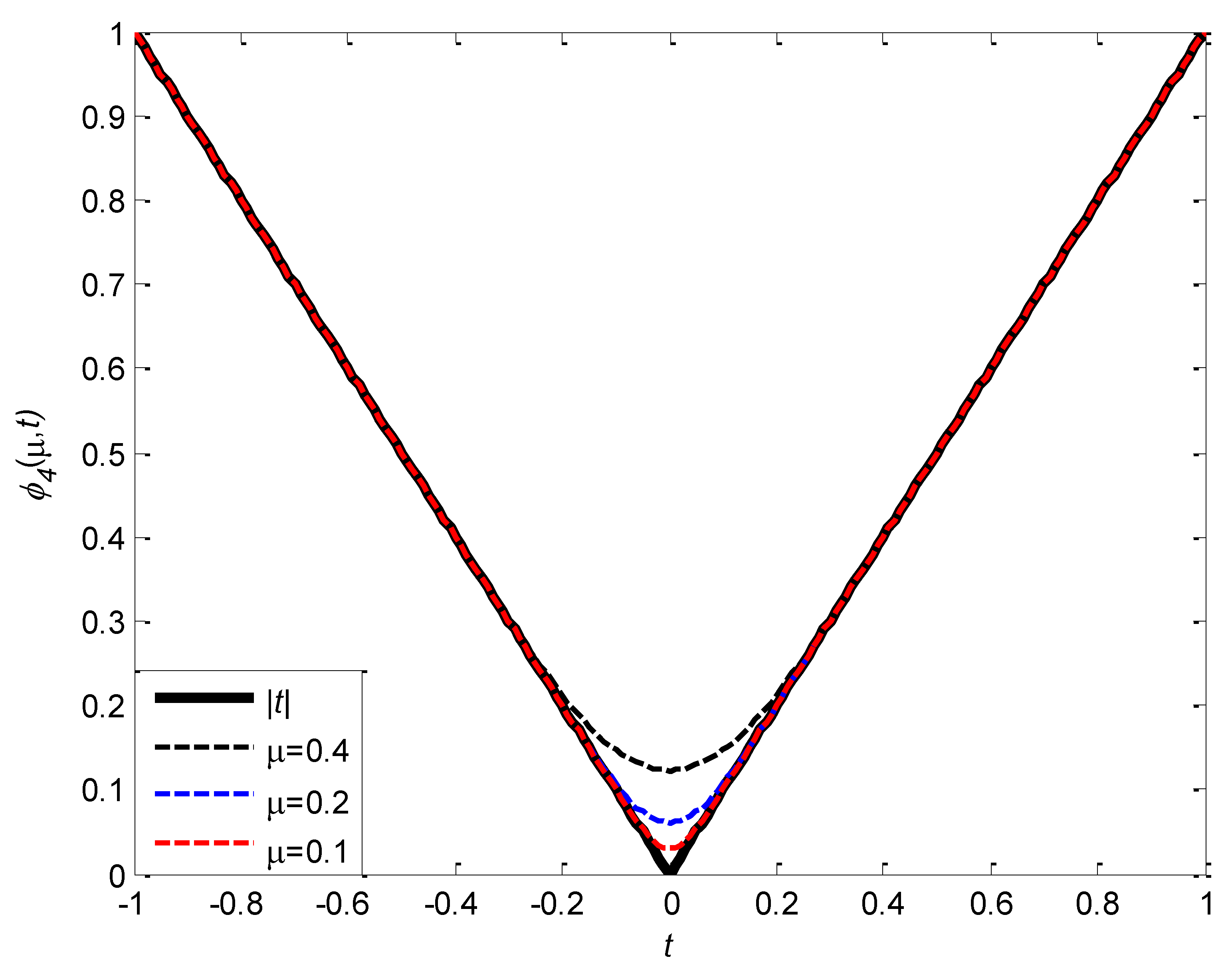
Figure 4 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_4(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_4(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from above.

2.5. Properties of Function ${\varphi }_5(\mu ,t)$

Proposition 2.5 The function ${\varphi }_5(\mu ,t)=\left\{\begin{array}{l}t, t\ge {\displaystyle \frac{\mu }{2}},\\ {\displaystyle \frac{t^2}{\mu }}+{\displaystyle \frac{\mu }{4}},-{\displaystyle \frac{\mu }{2}}<t<{\displaystyle \frac{\mu }{2}},\\ -t, t\le -{\displaystyle \frac{\mu }{2}}.\end{array}\right.$ in $(\mu ,t)\in R_{++}\times R$ has the following properties:

(1) $0\le {\varphi }_5(\mu ,t)-\varphi (t)\le {\displaystyle \frac{1}{4}}\mu$;

(2) ${\varphi }_5(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$,and

$\left|{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}\right|\le 1$ ,${\left.{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)${\varphi }_5(\mu ,t)$ decreases with the decrease parameter $\mu$,and when$\mu \to 0^{+},\underset{\mu \to 0^{+}}{\lim }{\varphi }_5(\mu ,t)=\left|t\right|$.

Proof (1)When$\left|t\right|\ge {\displaystyle \frac{\mu }{2}}$,${\varphi }_5(\mu ,t)-\varphi (t)\equiv 0$.When $-{\displaystyle \frac{\mu }{2}}<t<{\displaystyle \frac{\mu }{2}}$,$0<{\displaystyle \frac{{\left(2\left|t\right|-\mu \right)}^2}{4\mu }}\le {\displaystyle \frac{1}{4}}\mu$, while ${\varphi }_5(\mu ,t)-\varphi (t)={\displaystyle \frac{{\left(2\left|t\right|-\mu \right)}^2}{4\mu }}$. So when$-{\displaystyle \frac{\mu }{2}}<t<{\displaystyle \frac{\mu }{2}}$, $0<{\varphi }_5(\mu ,t)-\varphi (t)\le {\displaystyle \frac{1}{4}}\mu$.

From above, for any$(\mu ,t)\in R_{++}\times R$,we have $0\le {\varphi }_5(\mu ,t)-\varphi (t)\le {\displaystyle \frac{1}{4}}\mu$.

(2) Simple calculation gives

${\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}=\left\{\begin{array}{c}1,t\ge {\displaystyle \frac{\mu }{2}},\\ {\displaystyle \frac{2t}{\mu }},-{\displaystyle \frac{\mu }{2}}<t<\\ -1,t\le -{\displaystyle \frac{\mu }{2}}.\end{array}\right.{\displaystyle \frac{\mu }{2}},$${\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial \mu }}=\left\{\begin{array}{c}0,t\ge {\displaystyle \frac{\mu }{2}},\\ -{\left({\displaystyle \frac{t}{\mu }}\right)}^2+{\displaystyle \frac{1}{4}},-{\displaystyle \frac{\mu }{2}}<t<\\ 0,t\le -{\displaystyle \frac{\mu }{2}}.\end{array}\right.{\displaystyle \frac{\mu }{2}},$

Since $\underset{t\to {\displaystyle \frac{\mu }{2}}}{\lim }{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}=\underset{t\to {\displaystyle \frac{\mu }{2}}}{\lim }{\displaystyle \frac{2t}{\mu }}=1,$$\underset{t\to -{\displaystyle \frac{\mu }{2}}}{\lim }{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}=\underset{t\to -{\displaystyle \frac{\mu }{2}}}{\lim }{\displaystyle \frac{2x}{\mu }}=-1$, so${\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}$ is continuous. Since

$\underset{t\to {\displaystyle \frac{\mu }{2}}}{\lim }{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial \mu }}=\underset{t\to {\displaystyle \frac{\mu }{2}}}{\lim }\left[-{\left({\displaystyle \frac{t}{\mu }}\right)}^2+{\displaystyle \frac{1}{4}}\right]=0,$$\underset{t\to -{\displaystyle \frac{\mu }{2}}}{\lim }{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial \mu }}=\underset{t\to -{\displaystyle \frac{\mu }{2}}}{\lim }\left[-{\left({\displaystyle \frac{t}{\mu }}\right)}^2+{\displaystyle \frac{1}{4}}\right]=0$,

So ${\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial \mu }}$ is continuous. Thus, ${\varphi }_5(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$. From the expression of${\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}$, we have $\left|{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}\right|\le 1$ and ${\left.{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)When$-{\displaystyle \frac{\mu }{2}}<t<{\displaystyle \frac{\mu }{2}}$,$0<-{\left({\displaystyle \frac{t}{\mu }}\right)}^2+{\displaystyle \frac{1}{4}}\le {\displaystyle \frac{1}{4}}$, so $0<{\displaystyle \frac{\partial {\varphi }_5(\mu ,t)}{\partial \mu }}\le {\displaystyle \frac{1}{4}}.$ This indicates that ${\varphi }_5(\mu ,t)$ decreases with the decrease parameter $\mu$.

Using $0\le {\varphi }_5(\mu ,t)-\varphi (t)\le {\displaystyle \frac{1}{4}}\mu$,combined with Squeeze Theorem, thus$\underset{\mu \to 0^{+}}{\lim }{\varphi }_5(\mu ,t)=\left|t\right|$.

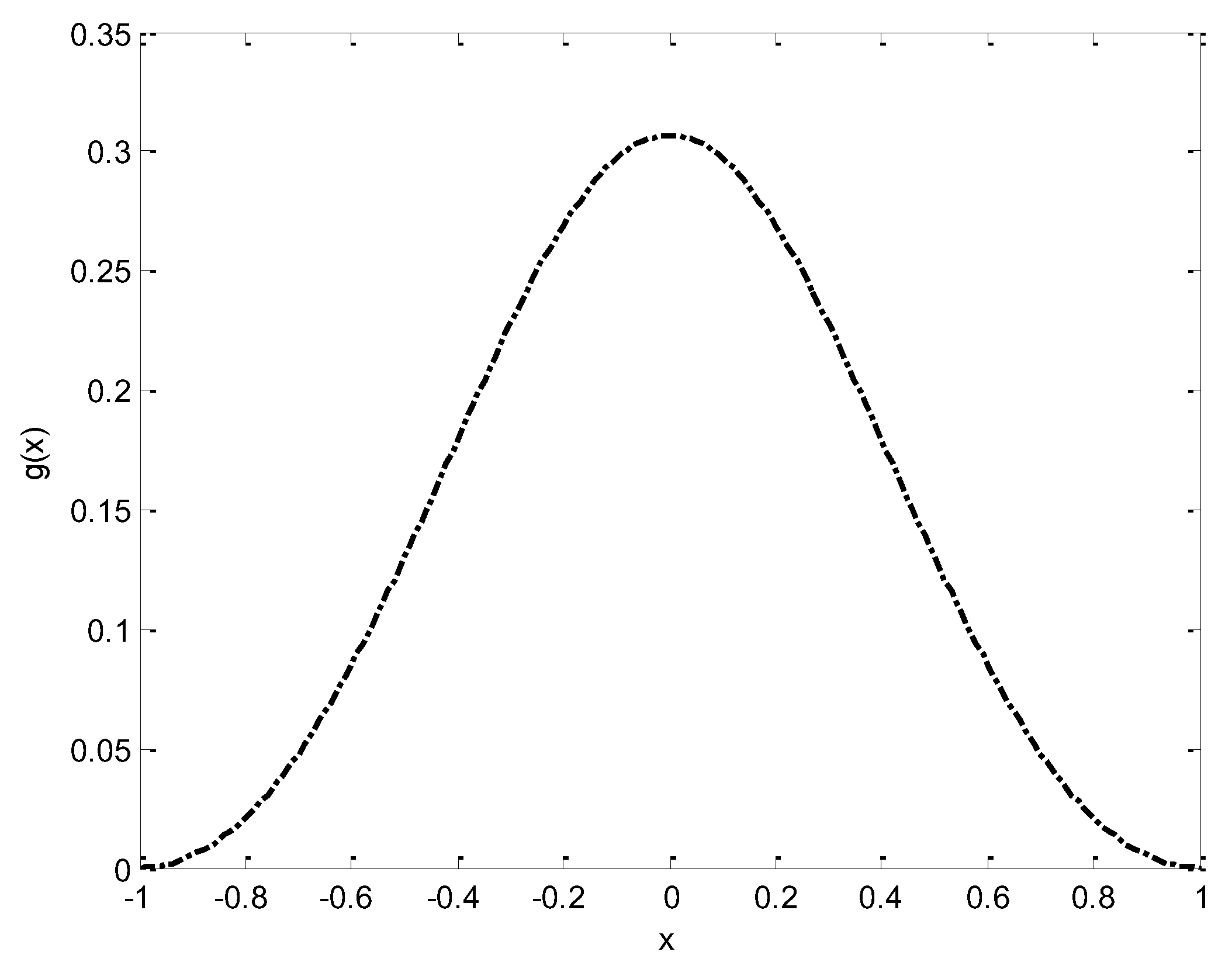
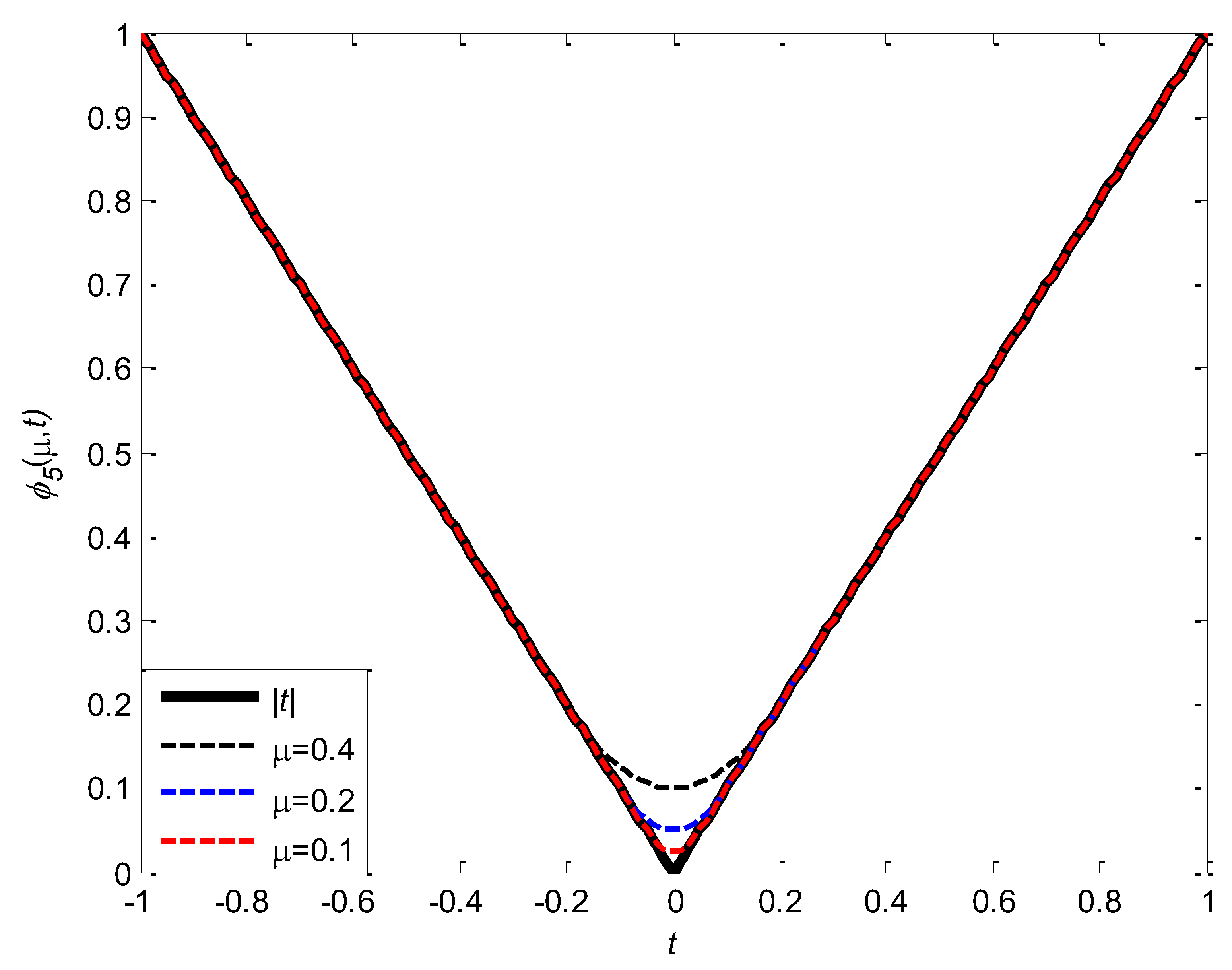
Figure 5 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_5(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_5(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from above.

2.6. Properties of Function ${\varphi }_6(\mu ,t)$

Proposition 2.6 The function ${\varphi }_6(\mu ,t)=\left\{\begin{array}{c}{\displaystyle \frac{t^2}{2\mu }},\left|t\right|\le \mu ,\\ \left|t\right|-{\displaystyle \frac{\mu }{2}},\left|t\right|>\mu .\end{array}\right.$ in $(\mu ,t)\in R_{++}\times R$ has the following properties：

(1)$-{\displaystyle \frac{1}{2}}\mu \le {\varphi }_6(\mu ,t)-\varphi (t)\le 0$;

(2)${\varphi }_6(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$, and

$\left|{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}\right|\le 1$ ,且${\left.{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)${\varphi }_6(\mu ,t)$ increases with decreasing parameter $\mu$. When$\mu \to 0^{+}$,$\underset{\mu \to 0^{+}}{\lim }{\varphi }_6(\mu ,t)=\left|t\right|$.

Proof (1)When $\left|t\right|>\mu$,${\varphi }_6(\mu ,t)-\varphi (t)=-{\displaystyle \frac{\mu }{2}}$. When $\left|t\right|\le \mu$, ${\varphi }_6(\mu ,t)-\varphi (t)={\displaystyle \frac{t^2}{2\mu }}-\left|t\right|$. Using the properties of the parabolic function yields $-{\displaystyle \frac{1}{2}}\mu \le {\displaystyle \frac{t^2}{2\mu }}-\left|t\right|\le 0$, so $-{\displaystyle \frac{1}{2}}\mu \le {\varphi }_6(\mu ,t)-\varphi (t)\le 0$.

Form above, for any$(\mu ,t)\in R_{++}\times R$,we have $-{\displaystyle \frac{1}{2}}\mu \le {\varphi }_6(\mu ,t)-\varphi (t)\le 0$.

(2) A simple calculation gives

${\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}=\left\{\begin{array}{c}1,t>\mu ,\\ {\displaystyle \frac{t}{\mu }},-\mu \le t\le \\ -1,t<-\mu .\end{array}\right.\mu ,$${\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial \mu }}=\left\{\begin{array}{c}-{\displaystyle \frac{1}{2}},t>\mu ,\\ -{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{t}{\mu }}\right)}^2,-\mu \le t\le \\ -{\displaystyle \frac{1}{2}},t<-\mu .\end{array}\right.\mu ,$

Since $\underset{t\to \mu }{\lim }{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}=\underset{t\to \mu }{\lim }{\displaystyle \frac{t}{\mu }}=1,$$\underset{t\to -\mu }{\lim }{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}=\underset{t\to -\mu }{\lim }{\displaystyle \frac{t}{\mu }}=-1$. thus ${\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}$ is continuous. Since $\underset{t\to \mu }{\lim }{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial \mu }}=\underset{t\to \mu }{\lim }\left[-{\displaystyle \frac{1}{2}}\times {\left({\displaystyle \frac{t}{\mu }}\right)}^2\right]=-{\displaystyle \frac{1}{2}},$$\underset{t\to -\mu }{\lim }{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial \mu }}=\underset{t\to -\mu }{\lim }\left[-{\displaystyle \frac{1}{2}}\times {\left({\displaystyle \frac{t}{\mu }}\right)}^2\right]=-{\displaystyle \frac{1}{2}}.$

Thus ${\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial \mu }}$ is continuous. So ${\varphi }_6(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$. From the expression of ${\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}$,we have $\left|{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}\right|\le 1$ and ${\left.{\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3)For any $(\mu ,t)\in R_{++}\times R$, there are $-{\displaystyle \frac{1}{2}}\le {\displaystyle \frac{\partial {\varphi }_6(\mu ,t)}{\partial \mu }}\le 0$. So ${\varphi }_6(\mu ,t)$ increases with decreasing parameter $\mu$. Using $-{\displaystyle \frac{1}{2}}\mu \le {\varphi }_6(\mu ,t)-\varphi (t)\le 0$, combined with Squeeze Theorem, thus$\underset{\mu \to 0^{+}}{\lim }{\varphi }_6(\mu ,t)=\left|t\right|$.

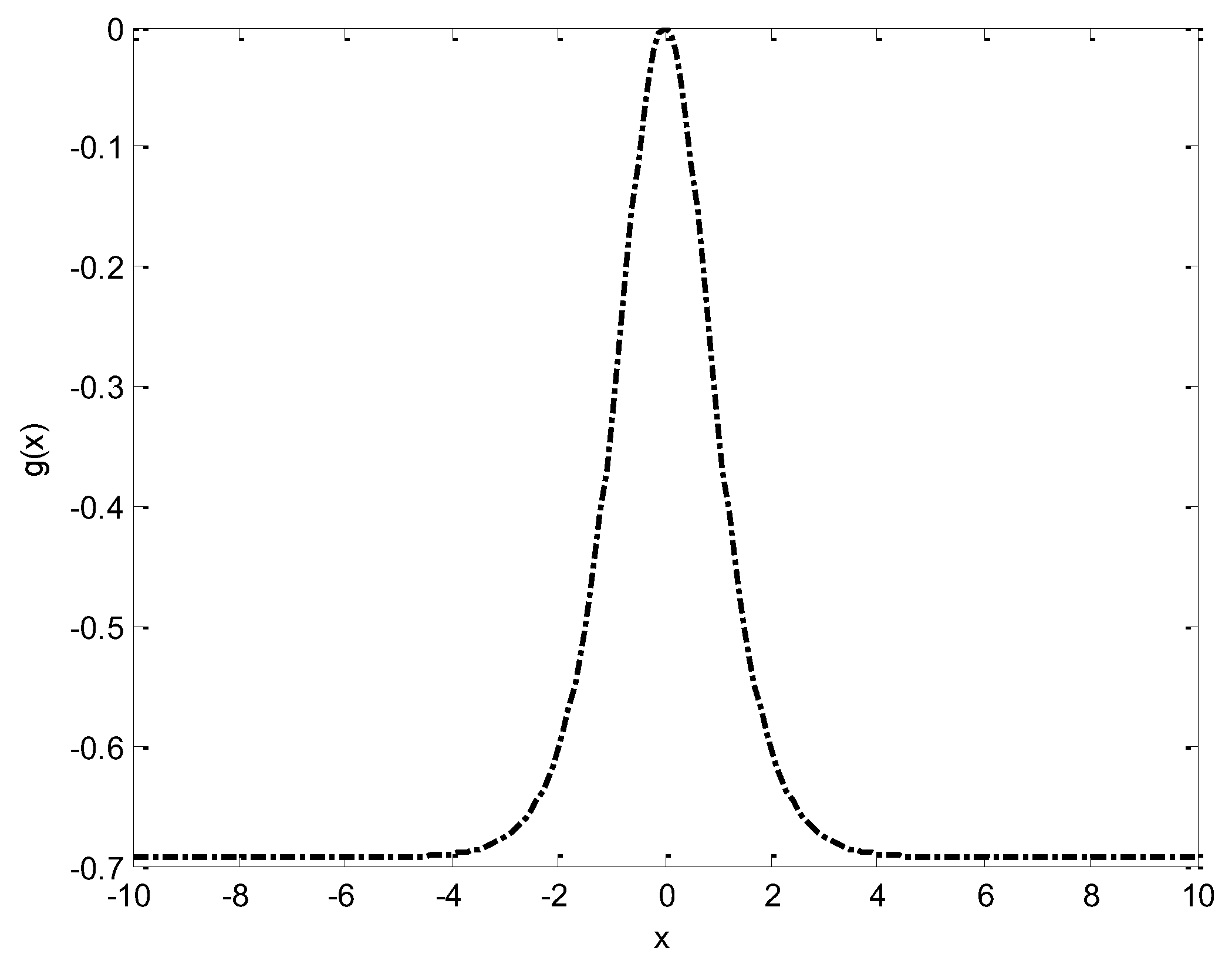
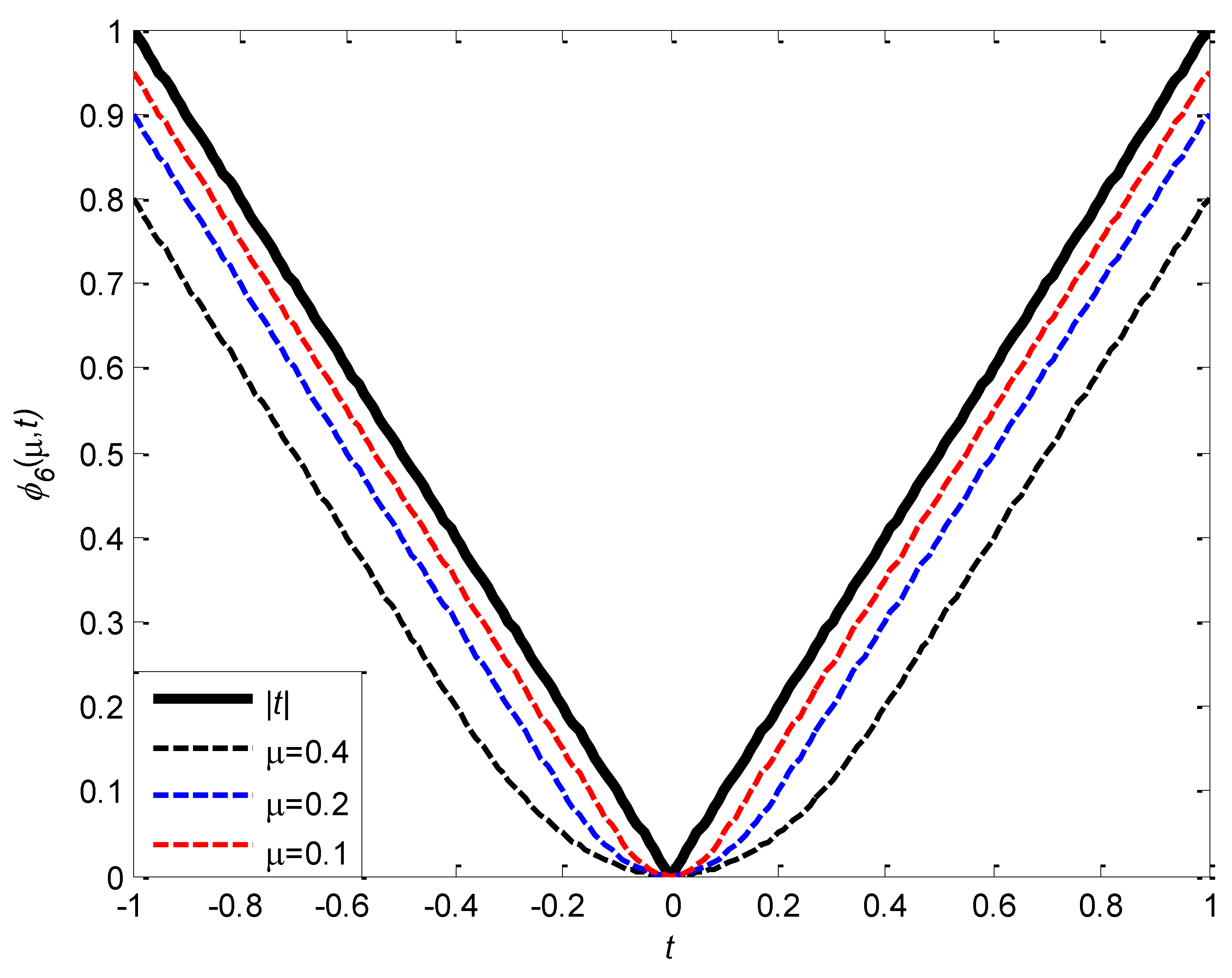
Figure 6 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_6(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_6(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from below.

2.7. Properties of Function ${\varphi }_7(\mu ,t)$

Proposition 2.7 The function ${\varphi }_7(\mu ,t)=\mu \ln \left({\displaystyle \frac{1}{2}}{e}^{{\displaystyle \frac{t}{\mu }}}+{\displaystyle \frac{1}{2}}{e}^{-{\displaystyle \frac{t}{\mu }}}\right)$ in $(\mu ,t)\in R_{++}\times R$ has the following properties：

(1)$-\mu \ln 2<{\varphi }_7(\mu ,t)-\varphi (t)\le 0$;

(2)${\varphi }_7(\mu ,t)$ is differentiable on $(\mu ,t)\in R_{++}\times R$,and

$\left|{\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial t}}\right|<1$ , ${\left.{\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3) ${\varphi }_7(\mu ,t)$ increases with decreasing parameter $\mu$. When$\mu \to 0^{+}$,$\underset{\mu \to 0^{+}}{\lim }{\varphi }_7(\mu ,t)=\left|t\right|$.

Proof (1)${\varphi }_7(\mu ,t)={\varphi }_3(\mu ,t)+\mu \ln {\displaystyle \frac{1}{2}}$,${\varphi }_7(\mu ,t)-\varphi (t)=\mu \ln {\displaystyle \frac{1}{2}}+{\varphi }_3(\mu ,t)-\varphi (t)$.

Combined $0<{\varphi }_3(\mu ,t)-\varphi (t)\le \mu \ln 2$.Then there are $-\mu \ln 2<{\varphi }_7(\mu ,t)-\varphi (t)\le 0$.

(2) Simple calculation gives

${\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial t}}={\displaystyle \frac{e^{\frac{t}{\mu }}-e^{-\frac{t}{\mu }}}{e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}}={\displaystyle \frac{\partial {\varphi }_3(\mu ,t)}{\partial t}},$${\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial \mu }}=\ln \left({\displaystyle \frac{1}{2}}{e}^{{\displaystyle \frac{t}{\mu }}}+{\displaystyle \frac{1}{2}}{e}^{-{\displaystyle \frac{t}{\mu }}}\right)+{\displaystyle \frac{t}{\mu }}\left({\displaystyle \frac{-e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}{e^{\frac{t}{\mu }}+e^{-\frac{t}{\mu }}}}\right)$.

So $\left|{\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial t}}\right|<1$ and ${\left.{\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3) To prove that the value of ${\varphi }_7(\mu ,t)$ increases with decreasing parameter $\mu$. It is sufficient to prove ${\displaystyle \frac{\partial {\varphi }_7(\mu ,t)}{\partial \mu }}<0,(\mu ,t)\in R_{++}\times R$ (see Appendix 4).

Using $-\mu \ln 2<{\varphi }_7(\mu ,t)-\varphi (t)\le 0$, combined with Squeeze Theorem,thus $\underset{\mu \to 0^{+}}{\lim }{\varphi }_7(\mu ,t)=\left|t\right|$.

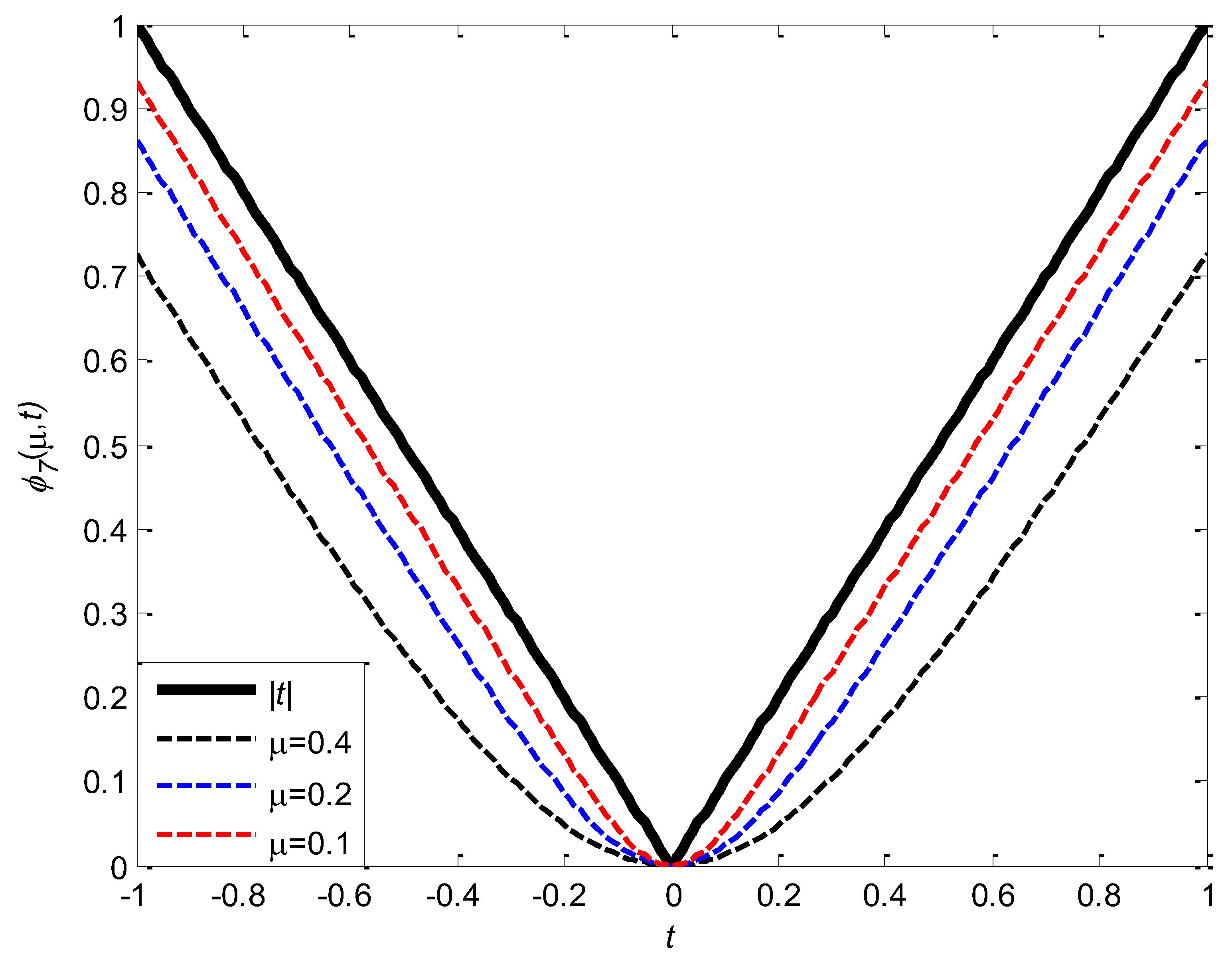
Figure 7 gives the graph of $\varphi (t)=\left|t\right|$ and ${\varphi }_7(\mu ,t)$,when$\mu =0.4,\mu =0.2,\mu =0.1$.It can also be observed from the figure, ${\varphi }_7(\mu ,t)$ is uniformly approximates $\varphi (t)=\left|t\right|$ from below.

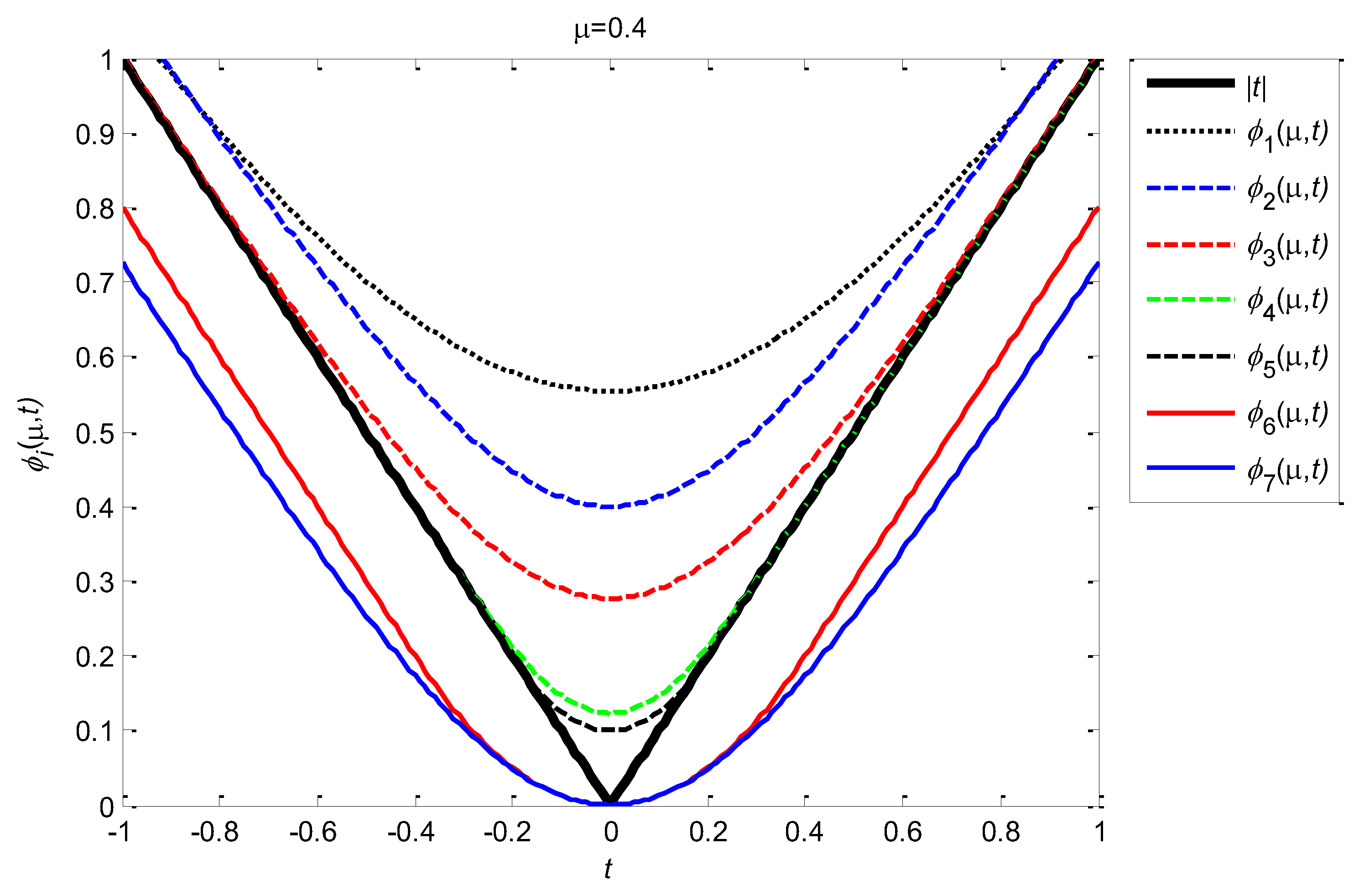
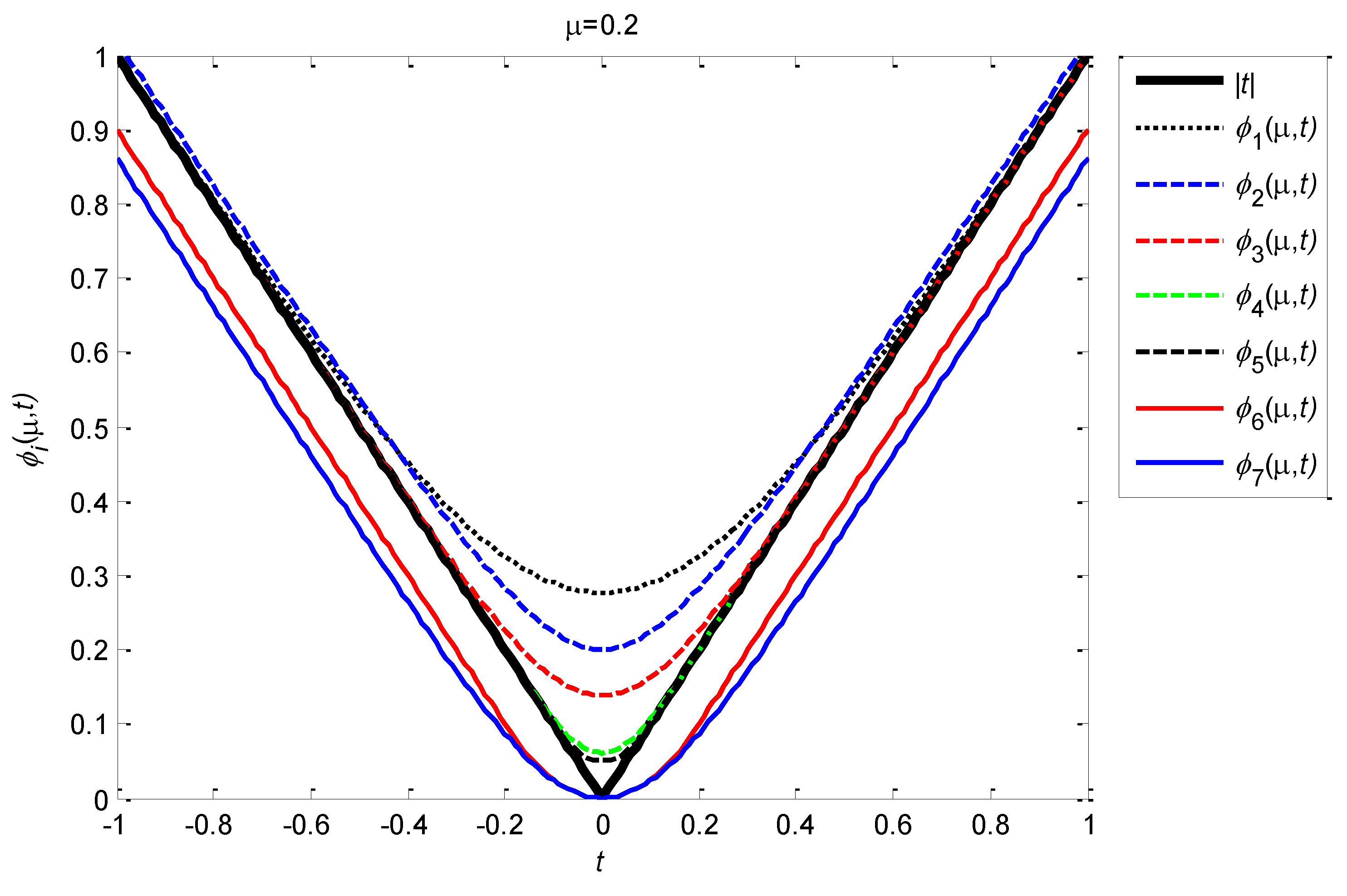
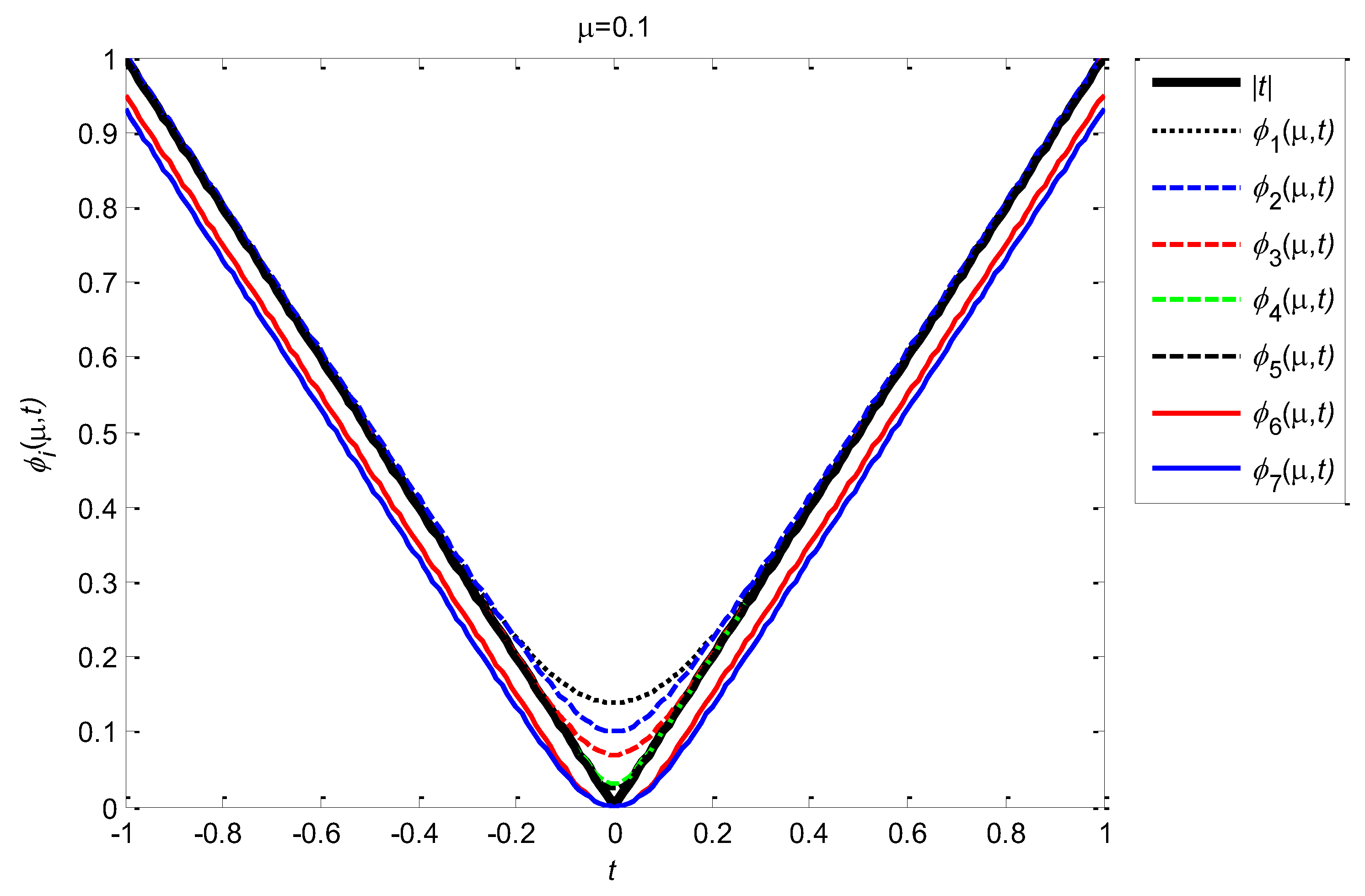
Some properties of these 7 uniformly smooth approximate functions are given above, and the common properties of these 7 uniformly smooth approximation functions are given in the form of theorems.

Theorem 2.1 ${\varphi }_i(\mu ,t),i=1,\cdots ,7$, as defined above, satisfies the following properties:

(1) ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ is uniformly smooth approximate function of $\varphi (t)$ on $(\mu ,t)\in R_{++}\times R$. Among which ${\varphi }_i(\mu ,t),$$i=1,2,3,4,5$ is uniformly smooth approximate functions of $\varphi (t)$ from above, while ${\varphi }_i(\mu ,t),i=6,7$ is uniformly smooth approximate functions of $\varphi (t)$ from below.

(2) ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ is continuously differentiable on $(\mu ,t)\in R_{++}\times R$, and all satisfies

$\left|{\displaystyle \frac{\partial {\varphi }_i(\mu ,t)}{\partial t}}\right|\le 1$,${\left.{\displaystyle \frac{\partial {\varphi }_i(\mu ,t)}{\partial t}}\right|}_{t=0}=0$.

(3) For any $t\in R$,$\underset{\mu \to 0^{+}}{\lim }{\varphi }_i(\mu ,t)=\left|t\right|,i=1,\cdots ,7$.

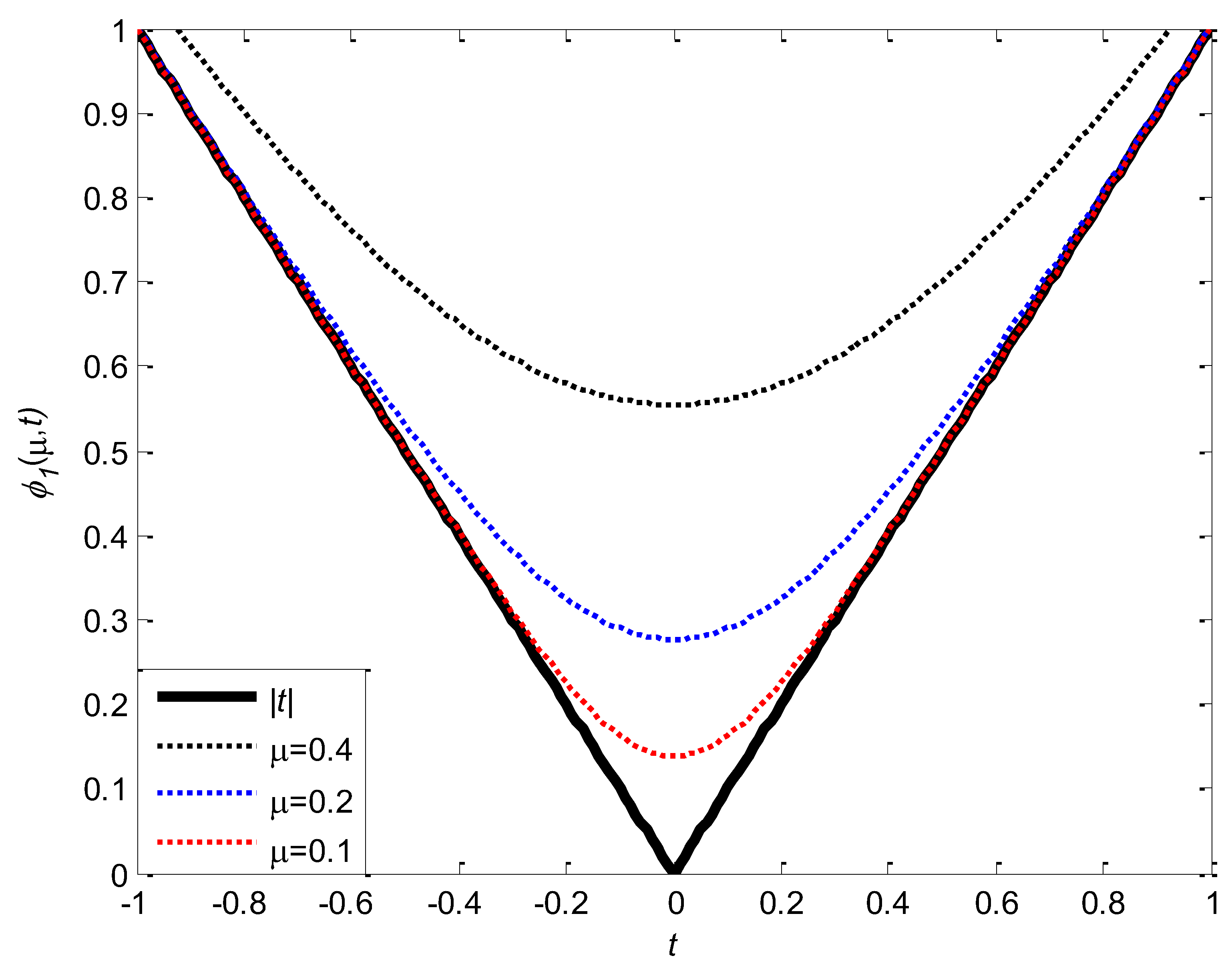
3. Approximation Degree of Uniformly Smooth Approximation Function

Following we describes the approximation degree between the ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$ on $\mu \to 0^{+}$.From Theorem 2.1 and Figure 5, we can see that ${\varphi }_5(\mu ,t)$ approximates $\varphi (t)=\left|t\right|$ most well. To prove this conclusion, firstly we define the distance between two real-valued functions by using infinite norm, that is, for the given two real-valued functions $f(t)$ and $g(t)$,we define the distance between them as

${‖f-g‖}_{\infty }=\underset{t\in R}{\max }\left\{\left|f(t)-g(t)\right|\right\}$

For any given $\mu >0$.Since:

$\underset{\left|t\right|\to \infty }{\lim }\left|{\varphi }_i(\mu ,t)-\left|t\right|\right|=0,i=1,2,3,4,5.$

and

$\underset{t\in R}{\max }\left|{\varphi }_i(\mu ,t)-\left|t\right|=\left|{\varphi }_i(\mu ,0)\right|\right|,i=1,2,3,4,5.$

Since

${\varphi }_1(\mu ,0)=\mu \ln 4,{\varphi }_2(\mu ,0)=\mu ,{\varphi }_3(\mu ,0)=\mu \ln 2,{\varphi }_4(\mu ,0)=\mu (1-\ln 2),{\varphi }_5(\mu ,0)={\displaystyle \frac{1}{4}}\mu$,

Thus

${‖{\varphi }_1(\mu ,t)-\left|t\right|‖}_{\infty }=\mu \ln 4$

${‖{\varphi }_2(\mu ,t)-\left|t\right|‖}_{\infty }=\mu$

${‖{\varphi }_3(\mu ,t)-\left|t\right|‖}_{\infty }=\mu \ln 2$

${‖{\varphi }_4(\mu ,t)-\left|t\right|‖}_{\infty }=\mu (1-\ln 2)$

${‖{\varphi }_5(\mu ,t)-\left|t\right|‖}_{\infty }={\displaystyle \frac{1}{4}}\mu$

Therefore, it is concluded from the above approximation we get

${‖{\varphi }_1(\mu ,t)-\left|t\right|‖}_{\infty }>{‖{\varphi }_2(\mu ,t)-\left|t\right|‖}_{\infty }>{‖{\varphi }_3(\mu ,t)-\left|t\right|‖}_{\infty }>{‖{\varphi }_4(\mu ,t)-\left|t\right|‖}_{\infty }>{‖{\varphi }_5(\mu ,t)-\left|t\right|‖}_{\infty }$.

Thus, ${\varphi }_5(\mu ,t)$ approximates $\varphi (t)=\left|t\right|$ most well among ${\varphi }_i(\mu ,t),i=1,2,3,4,5$.

In fact, for any fixed $\mu >0$,

${\varphi }_1(\mu ,t)>{\varphi }_2(\mu ,t)>{\varphi }_3(\mu ,t)>{\varphi }_4(\mu ,t)>{\varphi }_5(\mu ,t)>\left|t\right|.$

On the other hand, for any$\mu >0$,since

$\underset{t\to \infty }{\lim }\left|{\varphi }_6(\mu ,t)-\left|t\right|\right|={\displaystyle \frac{1}{2}}\mu ,{\varphi }_6(\mu ,0)=0,$

It means

$\underset{t\in R}{\max }\left|{\varphi }_6(\mu ,t)-\left|t\right|\right|={\displaystyle \frac{1}{2}}\mu .$

Thus

${‖{\varphi }_6(\mu ,t)-\left|t\right|‖}_{\infty }={\displaystyle \frac{1}{2}}\mu .$

In addition

$\underset{t\to \infty }{\lim }\left|{\varphi }_7(\mu ,t)-\left|t\right|\right|=\mu \ln 2,{\varphi }_7(\mu ,0)=0$.

It means

$\underset{t\in R}{\max }\left|{\varphi }_7(\mu ,t)-\left|t\right|\right|=\mu \ln 2.$

Thus

${‖{\varphi }_7(\mu ,t)-\left|t\right|‖}_{\infty }=\mu \ln 2$.

Therefore, it is concluded from the below approximation that

${‖{\varphi }_6(\mu ,t)-\left|t\right|‖}_{\infty }>‖{\varphi }_7(\mu ,t)-\left|t\right|‖$.

It shows that in all the lower approximation functions ${\varphi }_i(\mu ,t),i=6,7$, ${\varphi }_6(\mu ,t)$ approximates best to $\varphi (t)=\left|t\right|$. In fact, for any fixed $\mu >0$,

${\varphi }_7(\mu ,t)<{\varphi }_6(\mu ,t)<\left|t\right|.$

In summary, we have the following conclusions

${\varphi }_1(\mu ,t)>{\varphi }_2(\mu ,t)>{\varphi }_3(\mu ,t)>{\varphi }_4(\mu ,t)>{\varphi }_5(\mu ,t)>\left|t\right|>{\varphi }_6(\mu ,t)>{\varphi }_7(\mu ,t)$.

Following, the images of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$ are given respectively with $\mu =0.4,\mu =0.2,\mu =0.1$.

Figure 8. Graph of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$,when$\mu =0.4$.

Figure 8. Graph of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$,when$\mu =0.4$.

Figure 9. Graph of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$,when$\mu =0.2$.

Figure 9. Graph of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$,when$\mu =0.2$.

Figure 10. Graph of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$,when$\mu =0.1$.

Figure 10. Graph of ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$,when$\mu =0.1$.

Table 1 gives the distance between ${\varphi }_i(\mu ,t),i=1,\cdots ,7$ and $\varphi (t)=\left|t\right|$ when $\mu$ takes different values.

It can also be derived from the data in Table 1 that the distance between ${\varphi }_5(\mu ,t)$ and $\varphi (t)=\left|t\right|$ is the smallest, thus ${\varphi }_5(\mu ,t)$ approximates $\varphi (t)=\left|t\right|$ most well.

4. Conclusions

The uniformly smooth approximation function of absolute value function plays important scientific significance in the fields of numerical approximation[16], non-smooth optimization[17], neural network [18,19,20], etc. Limited by space, the application of uniformly smooth approximation functions for absolute value functions will be discussed separately. In addition, among the above uniformly smooth approximation function ${\varphi }_i(\mu ,t),i=1,\cdots ,7$,the approximation degree will be better if $\mu$ is replaced by its equivalent infinitesimal quantity $\sin \mu , 0<\mu <1$.