2. Some Uniformly Smooth Approximating Functions
Following we give seven uniformly smooth approximating functions
of the absolute value function
. They are continuously differentiable on
, and
are defined as follows:
2.1. Properties of Function
Proposition 2.1 The function on has the following properties:
(1);
(2) is differentiable on , and
, .
(3) decreases with decreasing parameter , and when, .
Proof (1)
Since , then , and at least one of and is equal to 0, thus ,. So .
Thereby . So .
(2) A simple calculation leads to
Since and are continuous on .Therefore, is differentiable on . And
.
(3)To prove that the
decreases with decreasing parameter
, it is sufficient to prove that
(see
Appendix 1). Use
, combined with Squeeze Theorem. Then there is
.
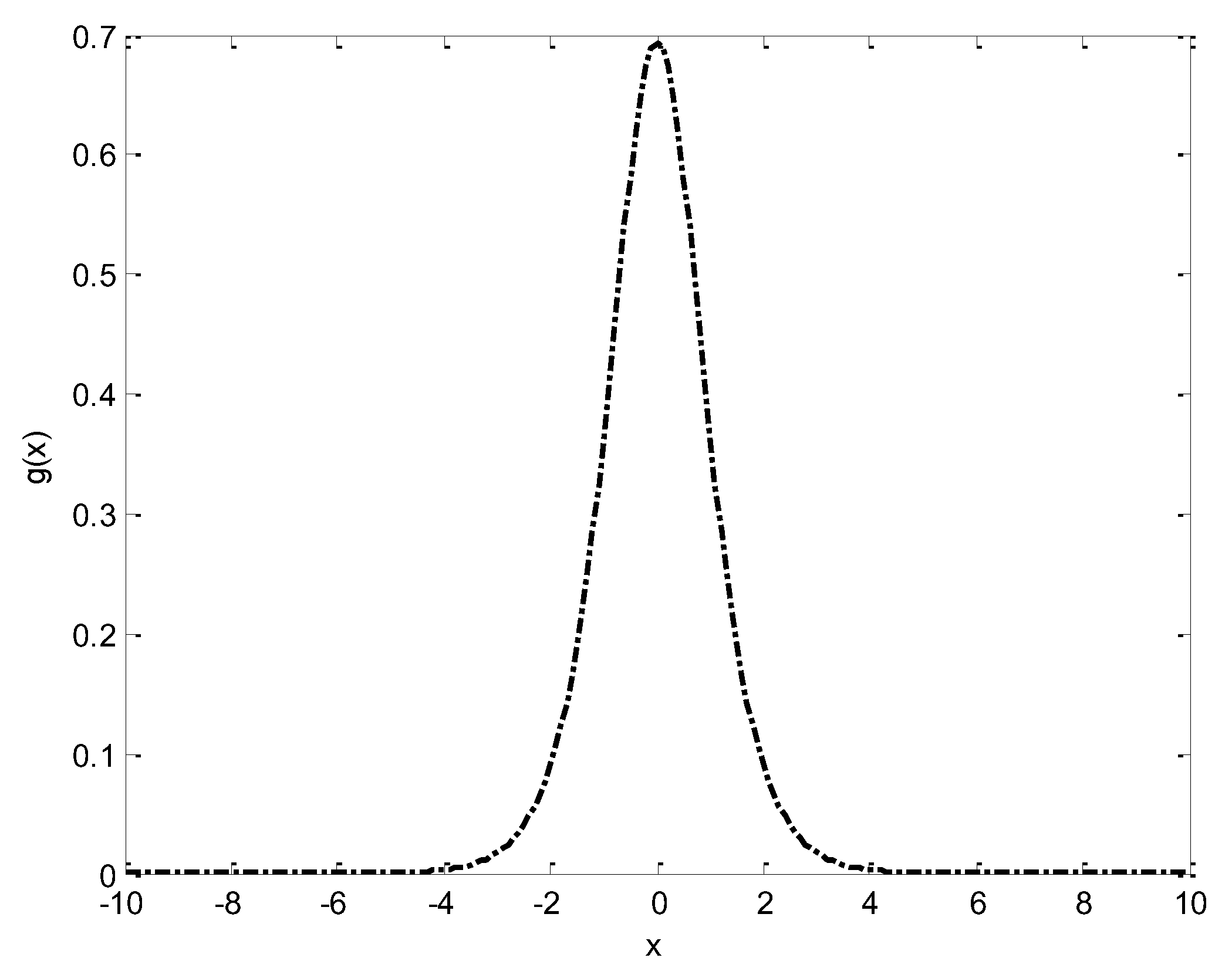
Figure 1 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from above.
2.2. Properties of Function
Proposition 2.2 The function in has the following properties:
(1);
(2) is differentiable on ,and
, .
(3) decreases with the decrease parameter ,and when.
Proof (1) Since ,then.
(2) A simple calculation leads to
Apparently, and is continuous, so is differentiable on . And
(3) For any , .Thus the value of decreases with the decrease parameter . Using , combined with Squeeze Theorem. Then there is.
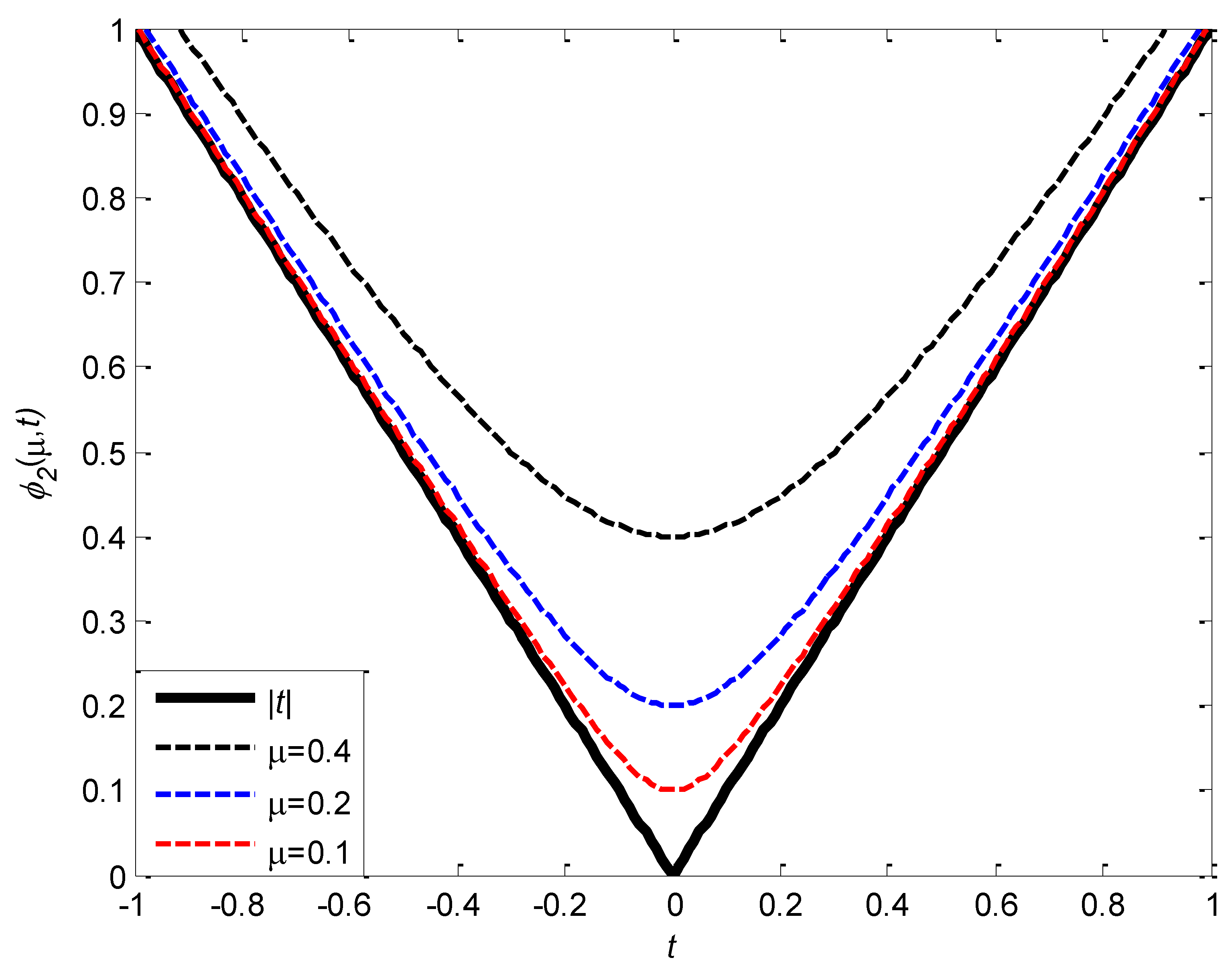
Figure 2 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from above.
2.3. Properties of Function
Proposition 2.3 The function in has the following properties:
(1).
(2) is differentiable on ,and
, .
(3) decreases with the decrease parameter ,and when.
Proof (1).
Since ,then , and at least one of and is equal to 0,so.Thus.That is
.
(2)A simple calculation leads to
.
Since and continuous on .So is differentiable on . And
, .
(3) To prove that the value of
decreases with decreasing parameter
. It is sufficient to prove that
(see
Appendix 2).
Using, combined with Squeeze Theorem, thus .
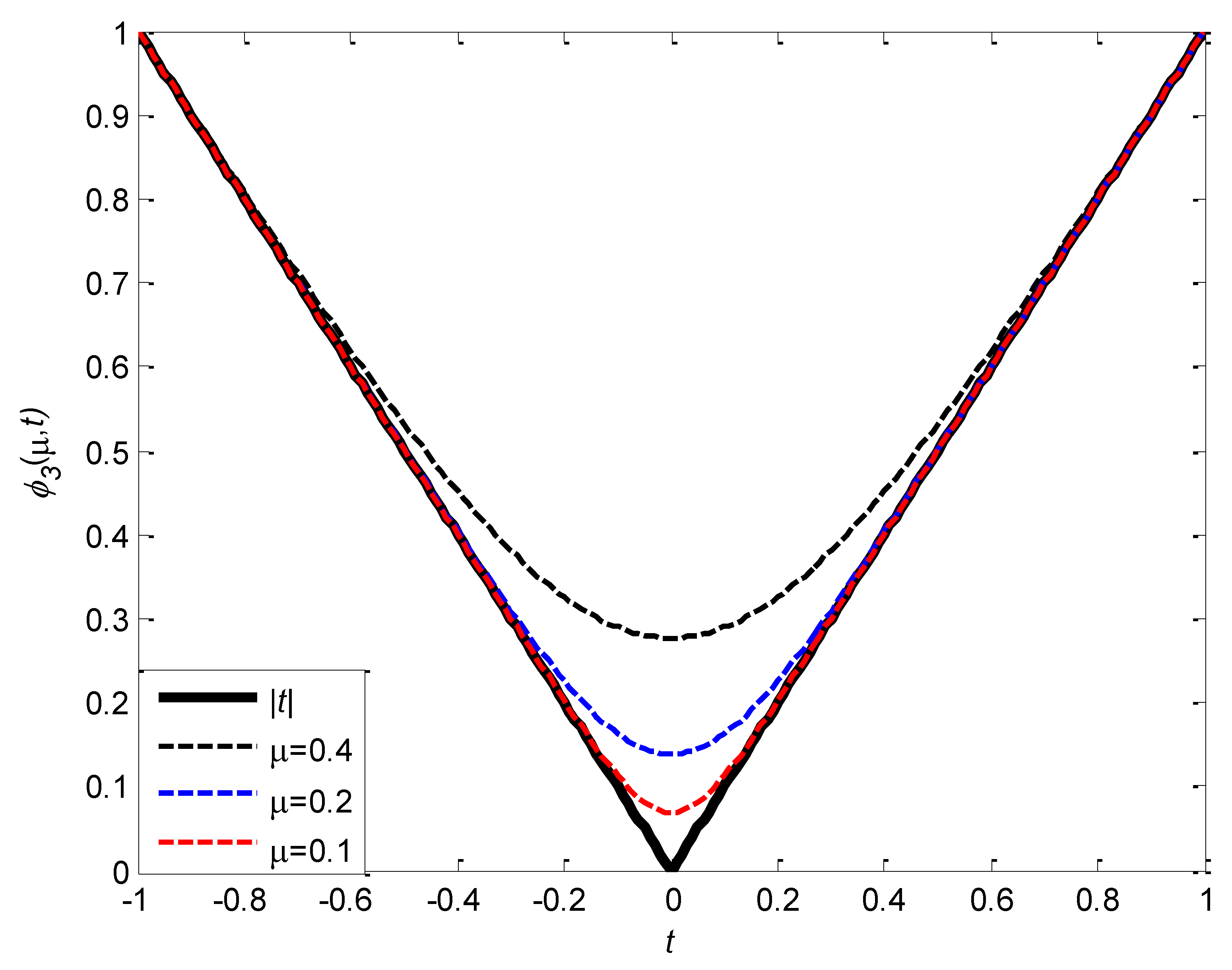
Figure 3 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from above.
2.4. Properties of Function
Proposition 2.4 The function in has the following properties:
(1);
(2) is differentiable on ,and
,.
(3) decreases with the decrease parameter ,and when.
Proof (1) When,. When ,
.
Thus, for any, we have .
(2) A simple calculation gives
Since ,,so is continuous. Since ,so is continuous. Thus is differentiable on . From the expression for , we get and.
(3) To prove that the value of
decreases with decreasing parameter
. Only proof
is required (see
Appendix 3).
Using , combined with Squeeze, thus .
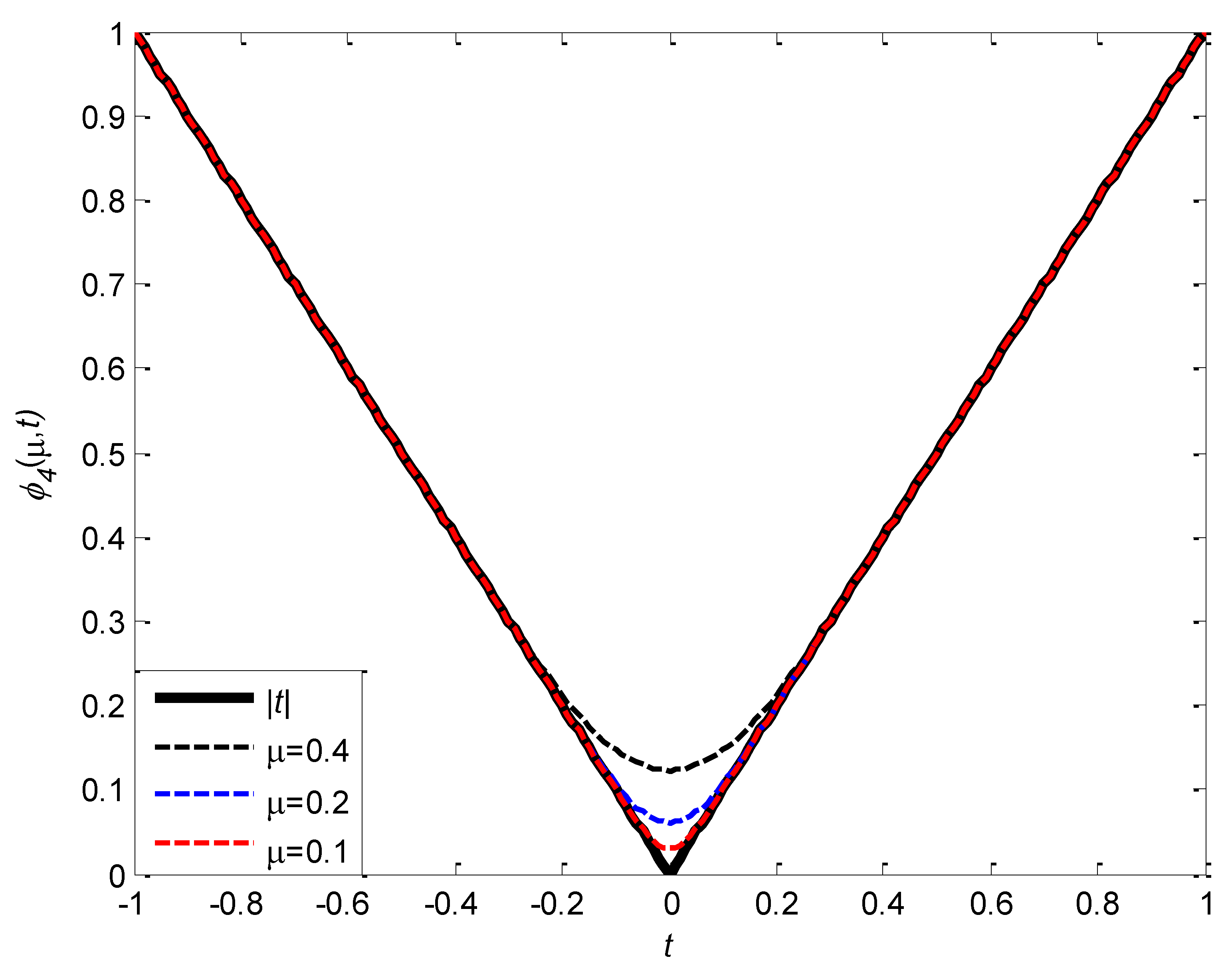
Figure 4 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from above.
2.5. Properties of Function
Proposition 2.5 The function in has the following properties:
(1) ;
(2) is differentiable on ,and
,.
(3) decreases with the decrease parameter ,and when.
Proof (1)When,.When ,, while . So when, .
From above, for any,we have .
(2) Simple calculation gives
Since , so is continuous. Since
,
So is continuous. Thus, is differentiable on . From the expression of, we have and .
(3)When,, so This indicates that decreases with the decrease parameter .
Using ,combined with Squeeze Theorem, thus.
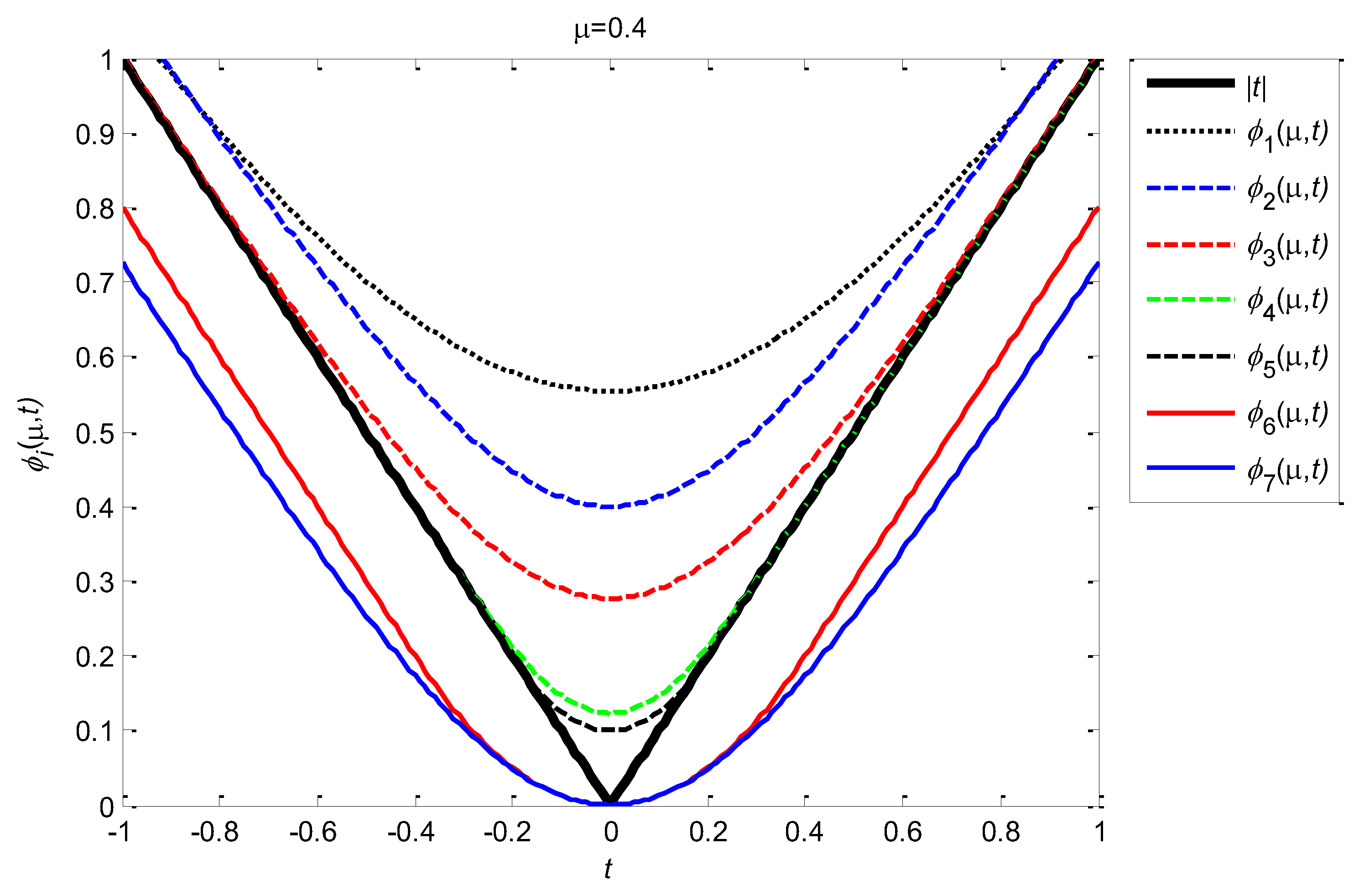
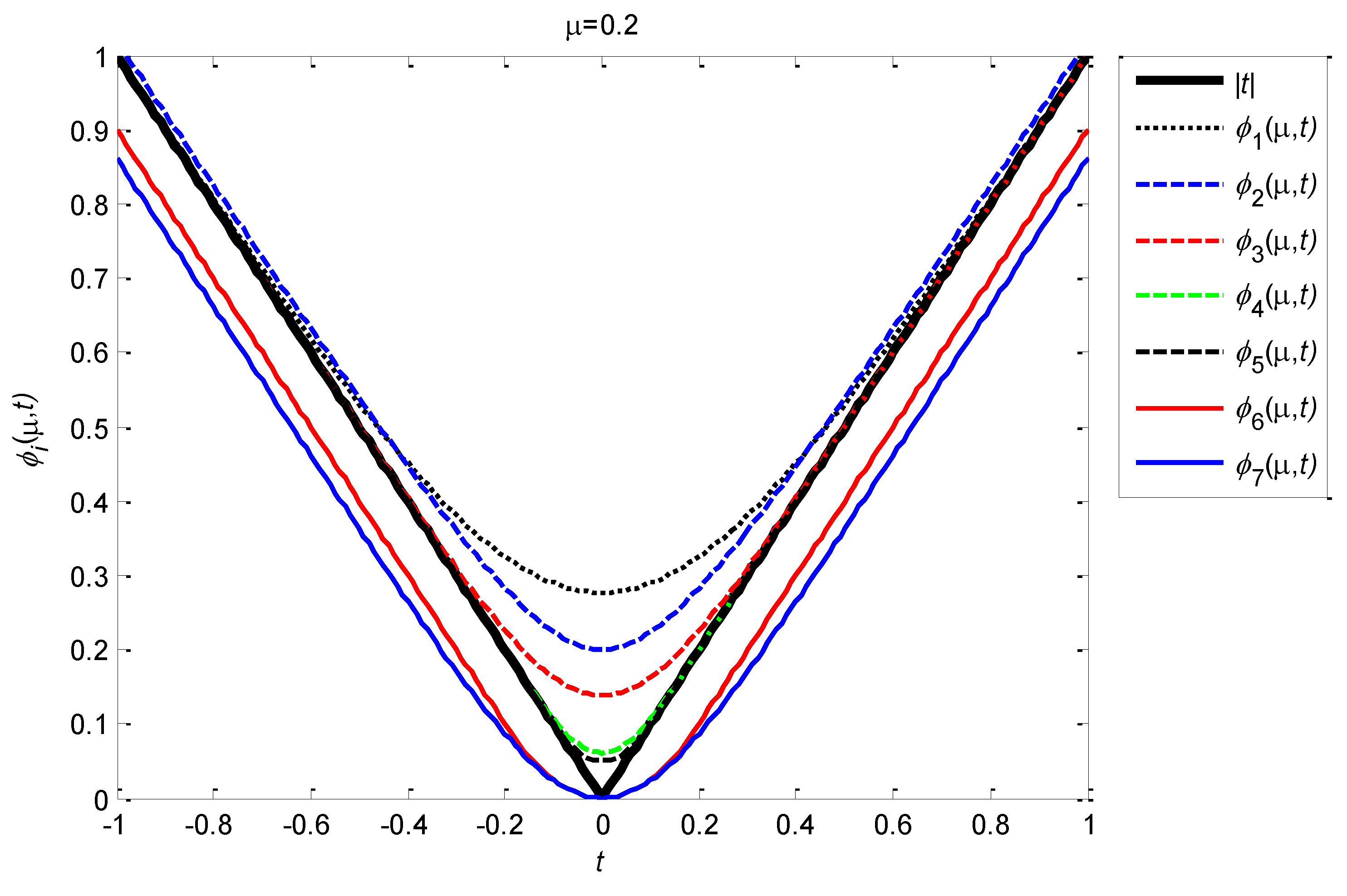
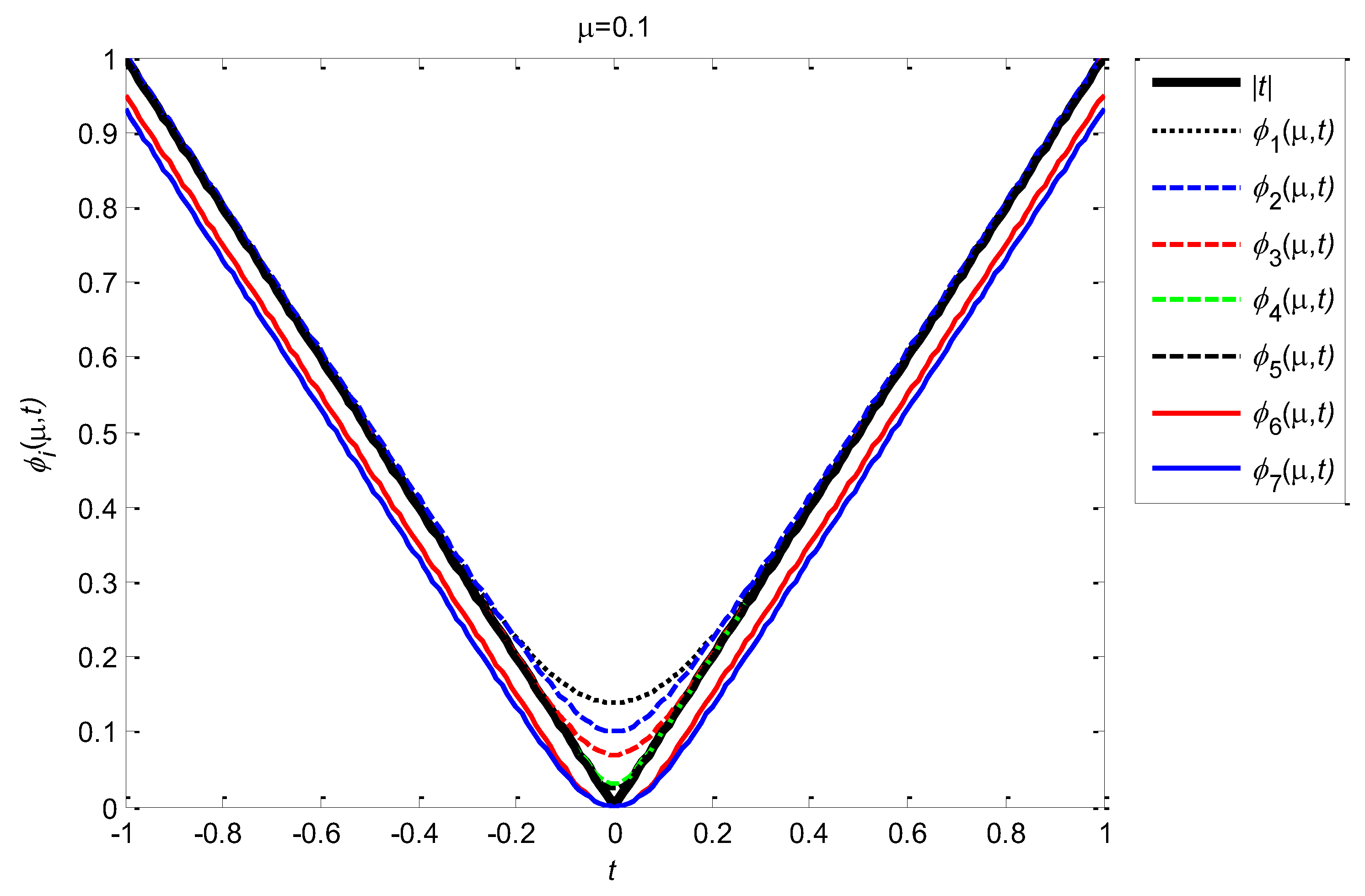
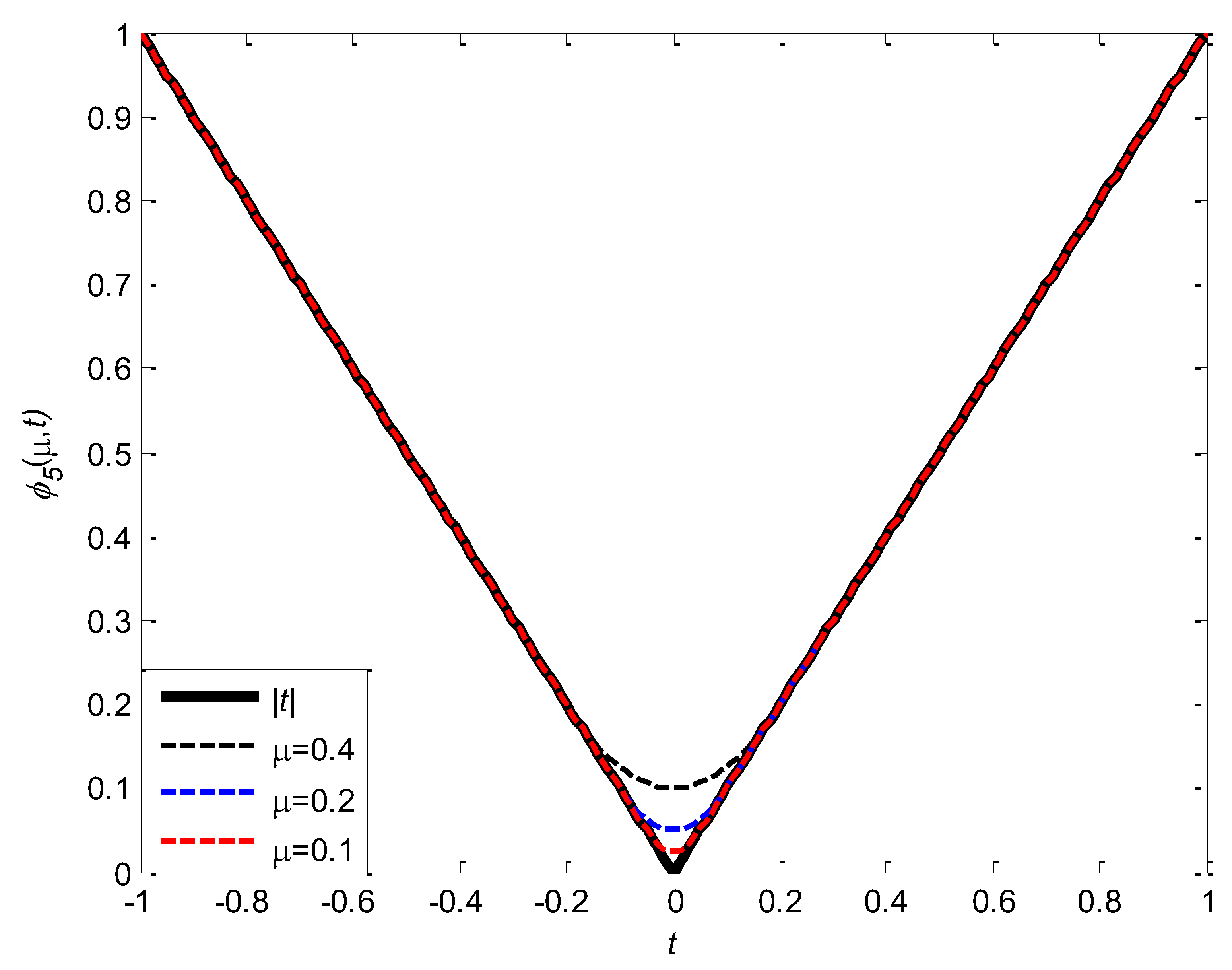
Figure 5 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from above.
2.6. Properties of Function
Proposition 2.6 The function in has the following properties:
(1);
(2) is differentiable on , and
,且.
(3) increases with decreasing parameter . When,.
Proof (1)When ,. When , . Using the properties of the parabolic function yields , so .
Form above, for any,we have .
(2) A simple calculation gives
Since . thus is continuous. Since
Thus is continuous. So is differentiable on . From the expression of ,we have and .
(3)For any , there are . So increases with decreasing parameter . Using , combined with Squeeze Theorem, thus.
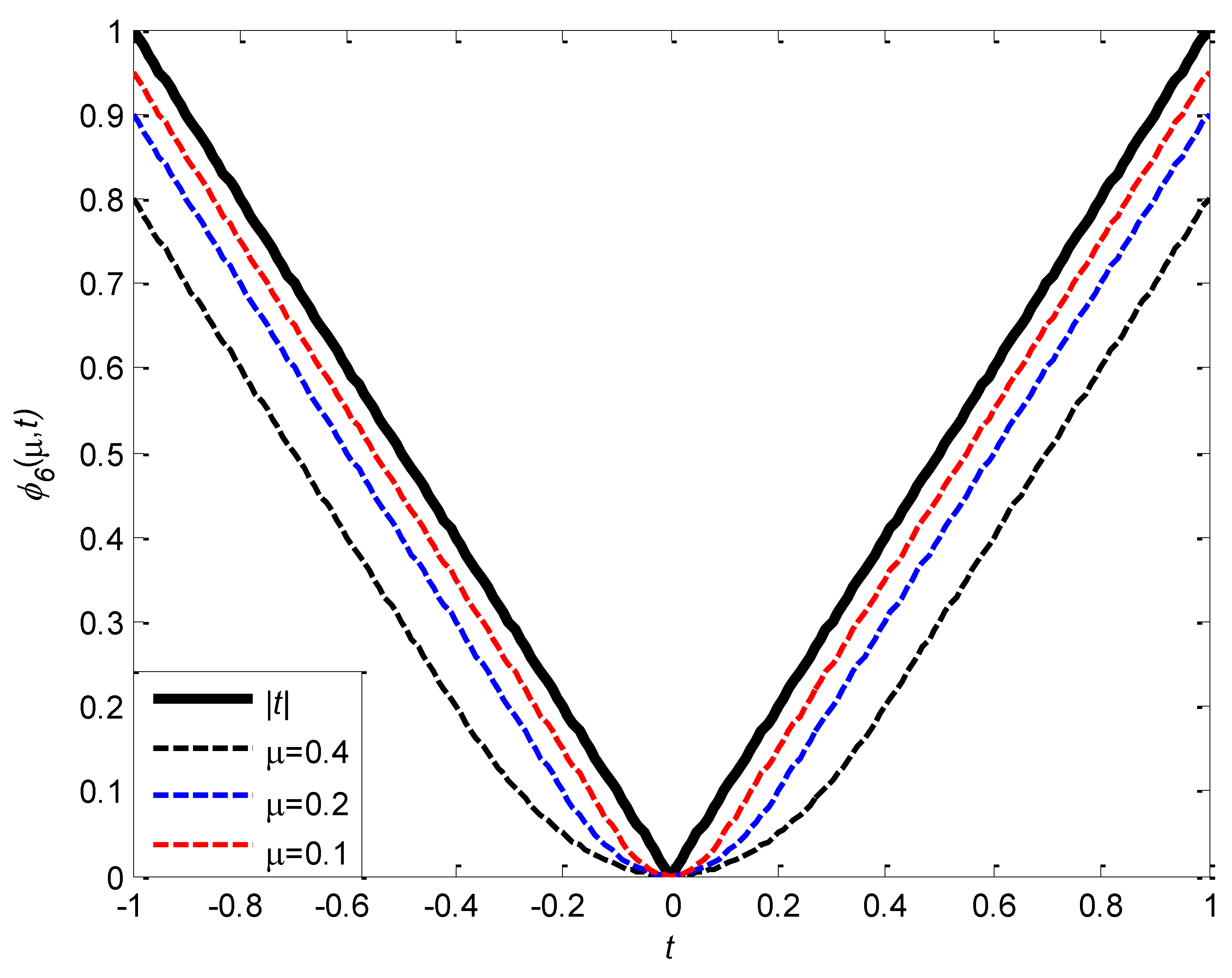
Figure 6 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from below.
2.7. Properties of Function
Proposition 2.7 The function in has the following properties:
(1);
(2) is differentiable on ,and
, .
(3) increases with decreasing parameter . When,.
Proof (1),.
Combined .Then there are .
(2) Simple calculation gives
.
So and .
(3) To prove that the value of
increases with decreasing parameter
. It is sufficient to prove
(see
Appendix 4).
Using , combined with Squeeze Theorem,thus .
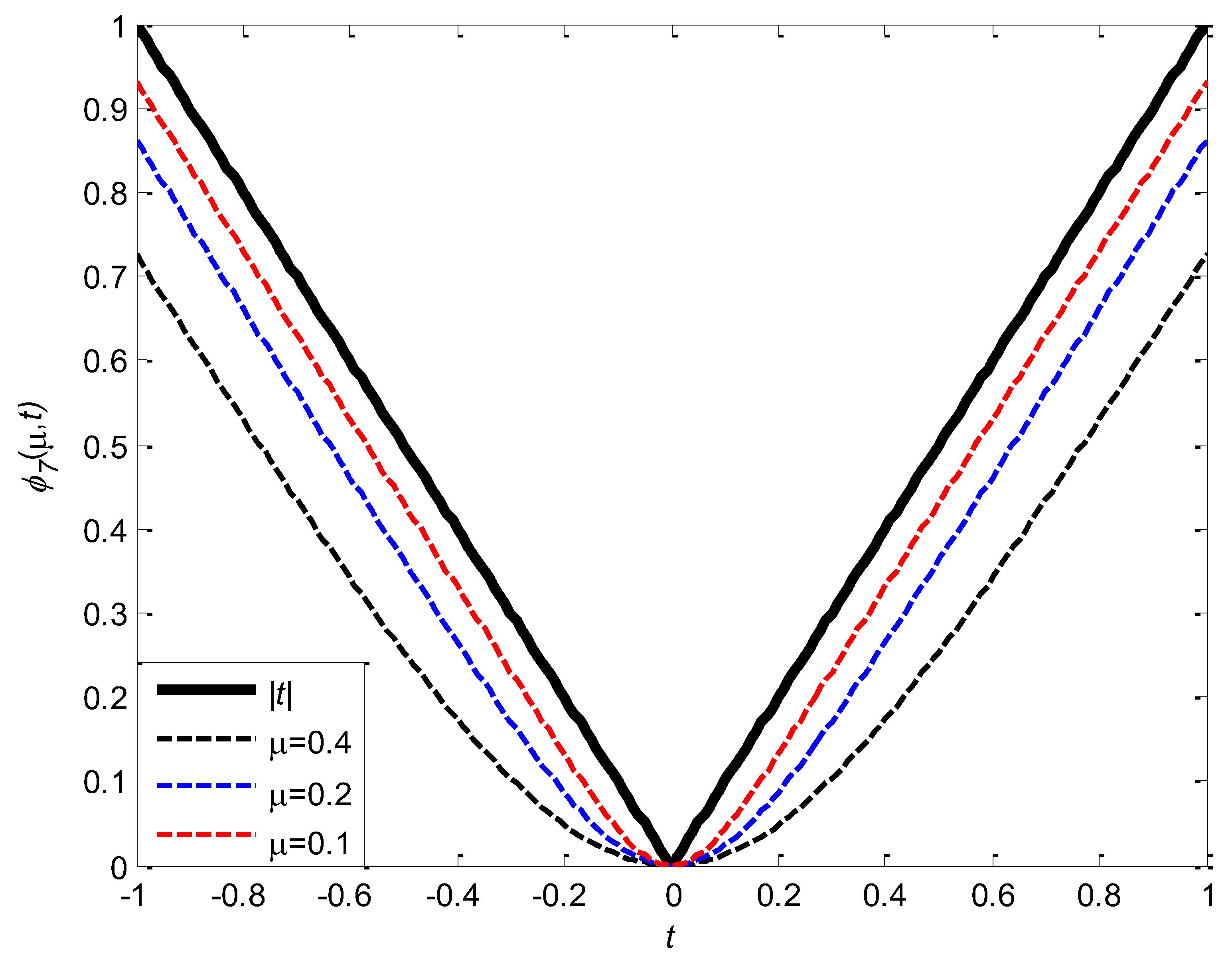
Figure 7 gives the graph of
and
,when
.It can also be observed from the figure,
is uniformly approximates
from below.
Some properties of these 7 uniformly smooth approximate functions are given above, and the common properties of these 7 uniformly smooth approximation functions are given in the form of theorems.
Theorem 2.1 , as defined above, satisfies the following properties:
(1) is uniformly smooth approximate function of on . Among which is uniformly smooth approximate functions of from above, while is uniformly smooth approximate functions of from below.
(2) is continuously differentiable on , and all satisfies
,.
(3) For any ,.
3. Approximation Degree of Uniformly Smooth Approximation Function
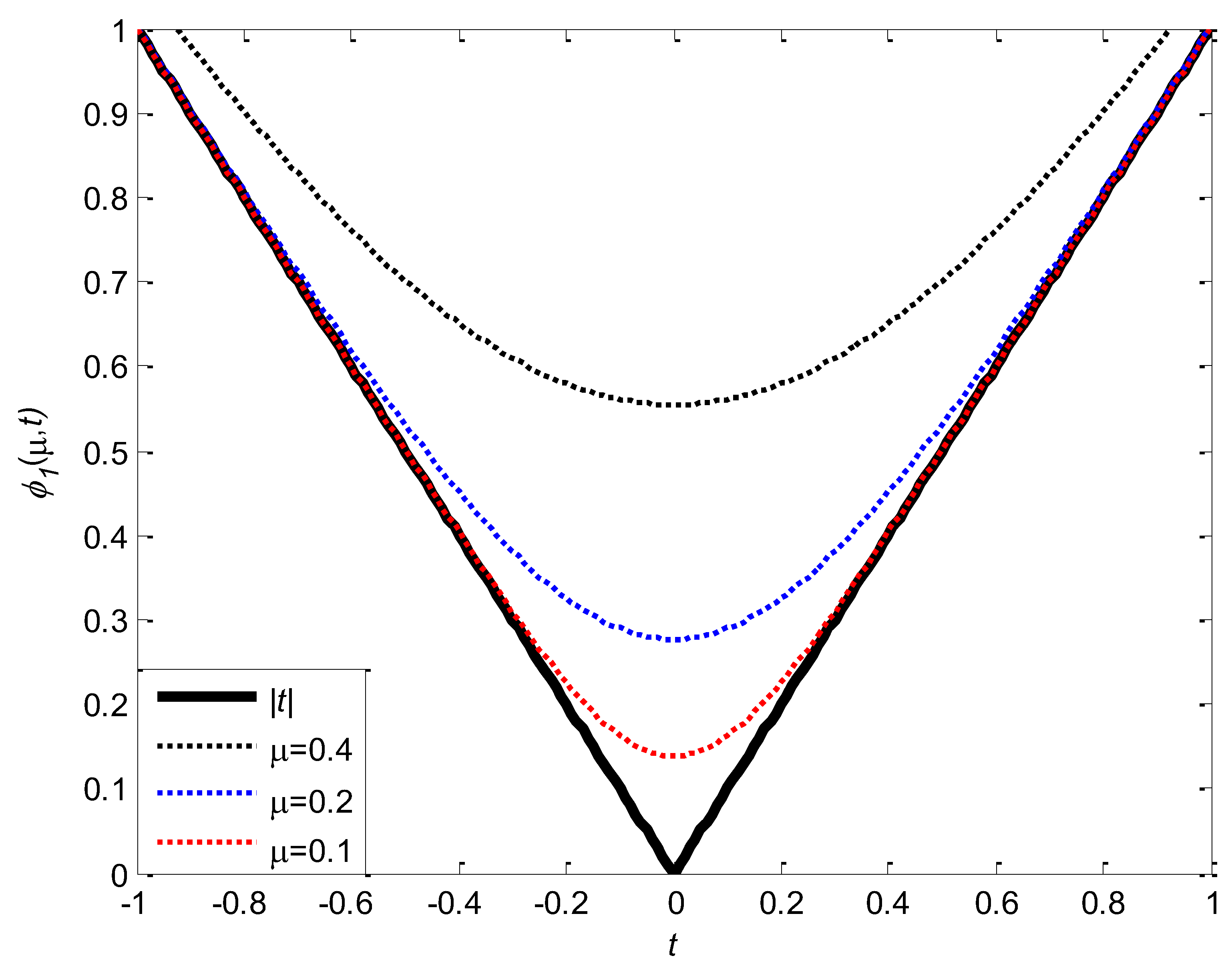
Following we describes the approximation degree between the
and
on
.From Theorem 2.1 and
Figure 5, we can see that
approximates
most well. To prove this conclusion, firstly we define the distance between two real-valued functions by using infinite norm, that is, for the given two real-valued functions
and
,we define the distance between them as
For any given .Since:
and
Since
,
Thus
Therefore, it is concluded from the above approximation we get
.
Thus, approximates most well among .
In fact, for any fixed ,
On the other hand, for any,since
It means
Thus
In addition
.
It means
Thus
.
Therefore, it is concluded from the below approximation that
.
It shows that in all the lower approximation functions , approximates best to . In fact, for any fixed ,
In summary, we have the following conclusions
.
Following, the images of and are given respectively with .
Figure 8.
Graph of and ,when.
Figure 8.
Graph of and ,when.
Figure 9.
Graph of and ,when.
Figure 9.
Graph of and ,when.
Figure 10.
Graph of and ,when.
Figure 10.
Graph of and ,when.
Table 1 gives the distance between
and
when
takes different values.
It can also be derived from the data in
Table 1 that the distance between
and
is the smallest, thus
approximates
most well.
4. Some Appendixes
Appendix 1
,
Following we prove .
Proof For an any , we need to prove
.
Let , .
Thus we only need to prove .
Since ,.
For any, when ,; when ,, and
.
Thus we have, that is .
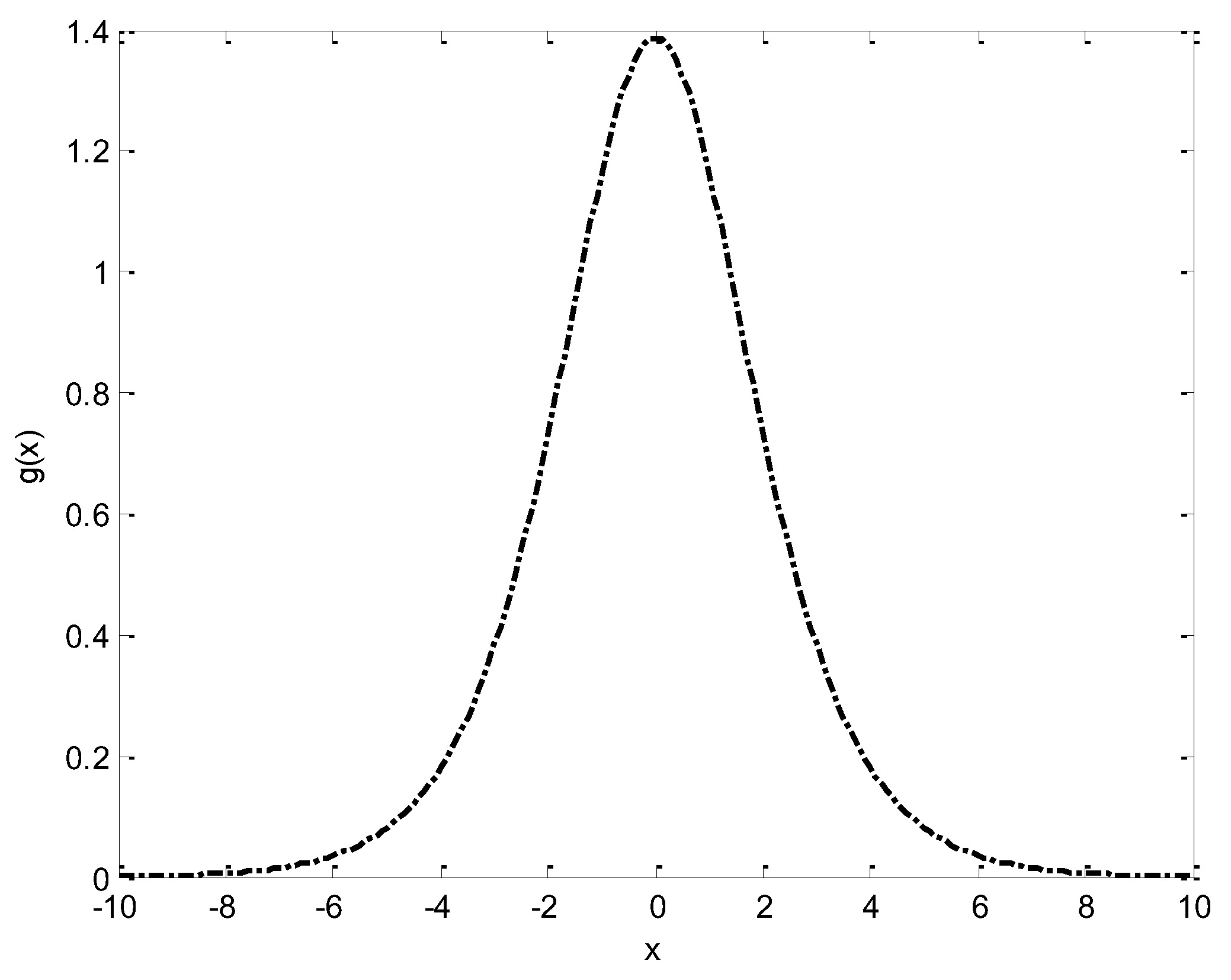
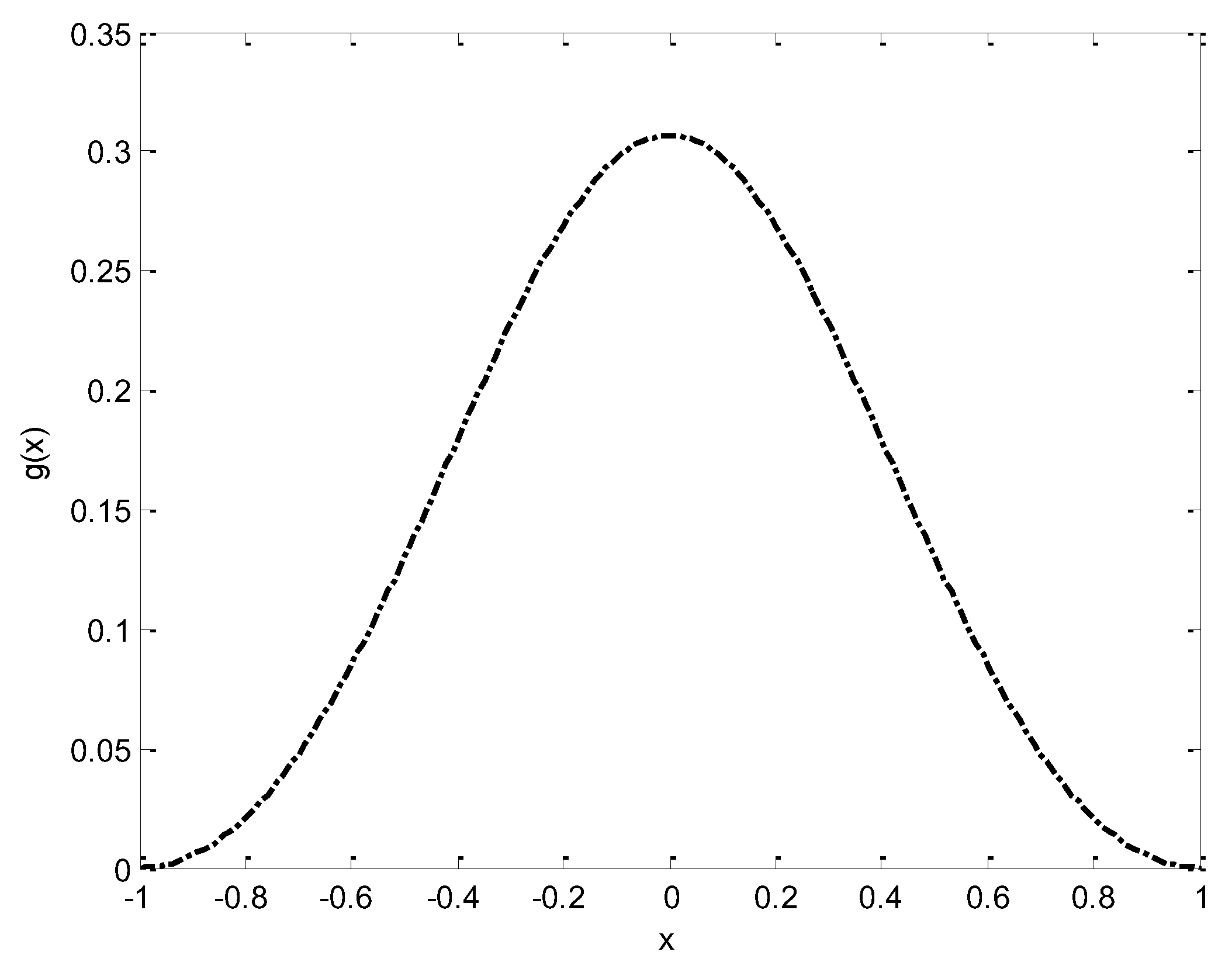
The image of
with
is shown in the
Figure A1.
Figure A1.
The image of with .
Figure A1.
The image of with .
Appendix 2
.
Following we prove .
Proof For any, we need to prove
.
Let
,.
Thus we only need to prove .
Since ,.
For any,when ,,when ,, and
.
Thus we have , that is .
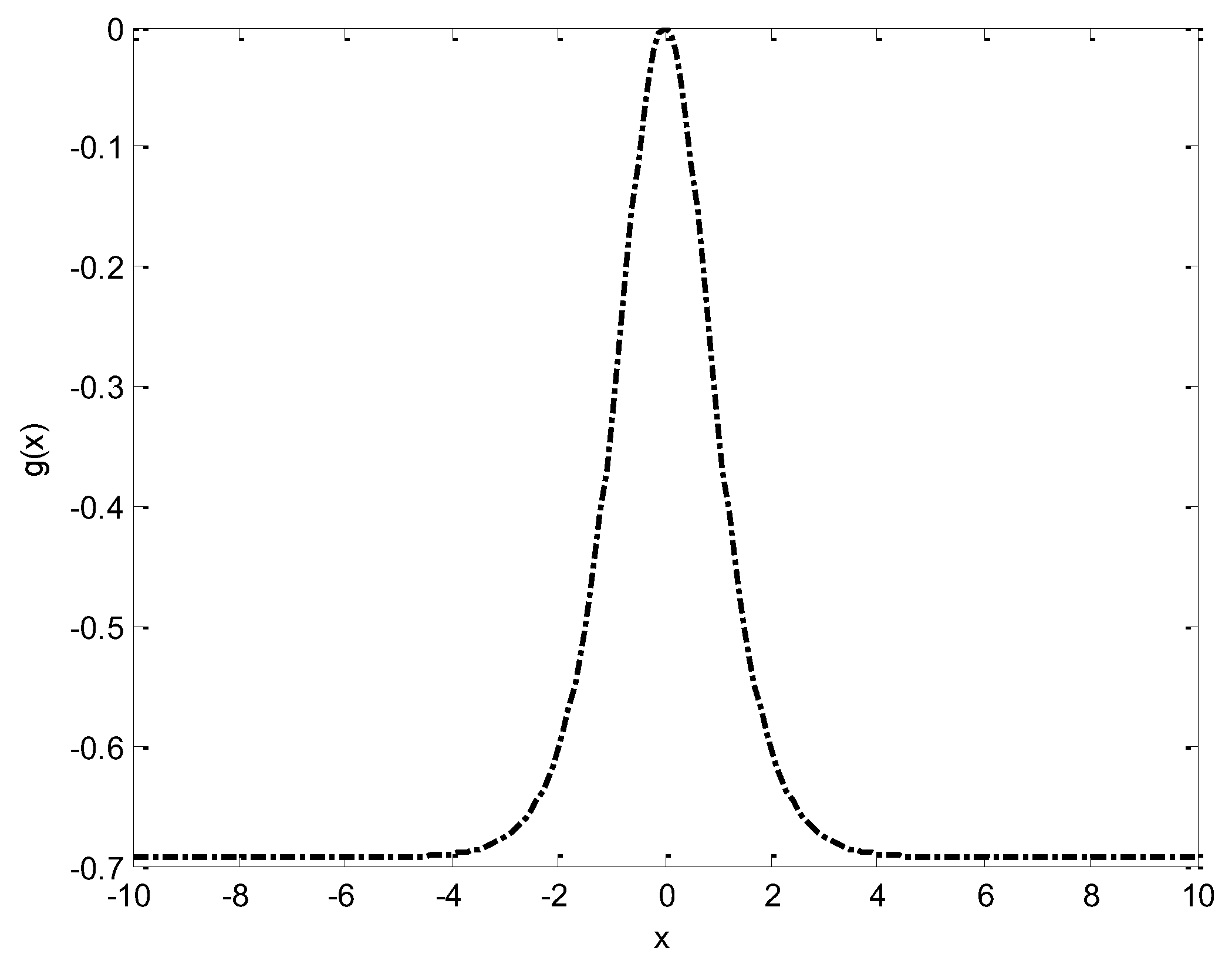
The image of
with
is shown in the
Figure A2.
Figure A2.
The image of with .
Figure A2.
The image of with .
Appendix 3
Following we prove .
Proof It is only necessary to prove that for any
Let
,.
Thus we only need to prove .
Since ,.
For any,when ,,when ,.
So when ,, when , .
Thus when
,
, the image of
is shown in the
Figure A3.
Figure A3.
The image of with .
Figure A3.
The image of with .
Appendix 4
Following we prove .
Proof For any, we need to prove
.
Let
, .
Thus we only need to prove .
Since ,.
For any,when ,, thus . When , , so . In addition, .
The image of
with
is shown in the
Figure A4.
Figure A4.
The image of with .
Figure A4.
The image of with .